| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913247 | |
| Published online | 20 September 2010 | |
Microlensing in H1413+117: disentangling
line profile emission
and absorption in a broad absorption line quasar![[*]](/icons/foot_motif.png)
D. Hutsemékers1,![]() - B. Borguet1,
- B. Borguet1,![]() - D. Sluse2
- P. Riaud1 - T. Anguita2,3
- D. Sluse2
- P. Riaud1 - T. Anguita2,3
1 - Institut d'Astrophysique et de Géophysique, Université de Liège,
Allée du 6 Août 17, B5c, 4000 Liège, Belgium
2 - Astronomisches Rechen-Institut, Zentrum für Astronomie der
Universität Heidelberg (ZAH), Mönchhofstr. 12-14, 69120 Heidelberg,
Germany
3 - Departamento de Astronomía y Astrofísica, Pontificia Universidad
Católica de Chile, Santiago, Chile
Received 4 September 2009 / Accepted 1 June 2010
Abstract
On the basis of 16 years of spectroscopic observations of the four
components of the gravitationally lensed broad absorption line (BAL)
quasar H1413+117, covering the ultraviolet to visible rest-frame
spectral
range, we analyze the spectral differences observed in the
P Cygni-type line profiles and have used the microlensing
effect to
derive new clues to the BAL profile formation. We first find that the
absorption gradually decreases with time in all components and that
this intrinsic variation is accompanied by a decrease in the intensity
of the emission. We confirm that the spectral differences observed in
component D can be attributed to a microlensing effect lasting
at
least a decade. We show that microlensing magnifies the continuum
source in image D, leaving the emission line region essentially
unaffected. We interpret the differences seen in the absorption
profiles of component D as the result of an emission line
superimposed
onto a nearly black absorption profile. We also find that the
continuum source and a part of the broad emission line region are
likely de-magnified in component C, while components A and B
are not
affected by microlensing. Differential dust extinction is measured
between the A and B lines of sight. We show that microlensing of the
continuum source in component D has a chromatic dependence
compatible
with the thermal continuum emission of a standard Shakura-Sunyaev
accretion disk. Using a simple decomposition method to separate the
part of the line profiles affected by microlensing and coming from a
compact region from the part unaffected by this effect and coming from
a larger region, we disentangle the true absorption line profiles from
the true emission line profiles. The extracted emission line profiles
appear double-peaked, suggesting that the emission is occulted by a
strong absorber, narrower in velocity than the full absorption
profile, and emitting little by itself. We propose that the outflow
around H1413+117 is constituted by a high-velocity polar flow and a
denser, lower velocity disk seen nearly edge-on. Finally, we report on
the first ground-based polarimetric measurements of the four
components of H1413+117.
Key words: gravitational lensing: micro - quasars: general - quasars: absorption lines - quasars: individual: H1413+117
1 Introduction
The broad absorption lines (BALs) observed in the spectra of quasars (or QSOs, quasi-stellar objects), blueshifted with respect to the broad emission lines (BELs), reveal massive, high-velocity outflows in active galactic nuclei (AGN). Such powerful winds can strongly affect the formation and evolution of the host galaxy, enrich the intergalactic medium, and regulate the formation of the large-scale structures (e.g. Silk & Rees 1998; Furlanetto & Loeb 2001; Scannapieco & Oh 2004; Scannapieco et al. 2005).
About 15% of optically selected quasars have BALs in their spectra (Reichard et al. 2003). Outflows may be present in all quasars if the wind is confined into a small solid angle so that BALs are only observed when the flow appears along the line of sight (Weymann et al. 1991; Gallagher et al. 2007). On the other hand, BAL QSOs could be quasars in an early evolutionary stage, washing out their cocoons (Voit et al. 1993; Becker et al. 2000).
Despite many high-quality observational studies, in particular from spectropolarimetry (Ogle et al. 1999), no clear view of the geometry and kinematics of the BAL phenomenon has emerged yet. While pure spherically symmetric winds appeared too simple to account for the variety of observations (Hamann et al. 1993; Ogle et al. 1999), equatorial disks, rotating winds, polar flows, or combinations thereof have been proposed more or less successfully to interpret the observations of individual objects or small groups of them (e.g. Murray et al. 1995; Schmidt & Hines 1999; Lamy & Hutsemékers 2004; Zhou et al. 2006). Given the large parameter space characterizing non spherically symmetric winds, BAL profile modeling must then be combined with other techniques to determine the outflow properties in individual objects (e.g. Young et al. 2007).
An interesting method that can bring independent information
on the
quasars' internal regions is the use of gravitational microlensing.
Indeed, in a typical gravitationally lensed quasar, a solar mass star
belonging to the lensing galaxy has an Einstein radius ![]() (the
microlensing cross section) on the order of 10-2 pc,
which is
comparable to the size of the continuum source. The microlens, moving
across the quasar core in projection, can successively magnify regions
of area
(the
microlensing cross section) on the order of 10-2 pc,
which is
comparable to the size of the continuum source. The microlens, moving
across the quasar core in projection, can successively magnify regions
of area ![]()
![]() ,
inducing spectroscopic variations that
could be used to extract information on the quasar structure
(Schneider et al. 1992,
and references therein). Several
studies, based on simulations, have demonstrated the interest of
microlensing analyses for understanding BAL QSOs (Hutsemékers
et al. 1994;
Lewis & Belle 1998;
Belle & Lewis
2000; Chelouche 2005).
,
inducing spectroscopic variations that
could be used to extract information on the quasar structure
(Schneider et al. 1992,
and references therein). Several
studies, based on simulations, have demonstrated the interest of
microlensing analyses for understanding BAL QSOs (Hutsemékers
et al. 1994;
Lewis & Belle 1998;
Belle & Lewis
2000; Chelouche 2005).
H1413+117 is a BAL QSO of redshift ![]() showing typical
P Cygni-type profiles, i.e., profiles where the absorption is
not
detached from the emission. Turnshek et al. (1988) discussed
the spectrum of H1413+117 in detail and made the first attempts to
disentangle the emission from the absorption assuming an intrinsic
blue/red symmetry of the emission lines. H1413+117 is also a
gravitationally lensed quasar constituted of four images (Magain
et al. 1988;
see Fig. 1).
The lensing galaxy is
faint and its redshift poorly known: indirect estimates give
showing typical
P Cygni-type profiles, i.e., profiles where the absorption is
not
detached from the emission. Turnshek et al. (1988) discussed
the spectrum of H1413+117 in detail and made the first attempts to
disentangle the emission from the absorption assuming an intrinsic
blue/red symmetry of the emission lines. H1413+117 is also a
gravitationally lensed quasar constituted of four images (Magain
et al. 1988;
see Fig. 1).
The lensing galaxy is
faint and its redshift poorly known: indirect estimates give ![]() (Kneib et al. 1998)
or
(Kneib et al. 1998)
or ![]() (Goicoecha
& Shalyapin 2010).
Evidence of microlensing in
component D has been suggested from both photometry and
spectroscopy
(Angonin et al. 1990;
Østensen et al. 1997).
In
particular, Angonin et al. (1990)
found that the equivalent
width of the emission lines is systematically smaller in
component D
than observed in the other components, a result which can be
interpreted by microlensing of the continuum source, the larger region
at the origin of the emission lines being unaffected. This effect,
which appeared to last at least a decade (Chae et al. 2001;
Anguita et al. 2008a),
offers the possibility to separate the
microlensed attenuated continuum (i.e. the absorption profile) from
the true emission line profile, thus providing new clues to the
formation of BAL profiles (Hutsemékers 1993; Hutsemékers
et al. 1994).
(Goicoecha
& Shalyapin 2010).
Evidence of microlensing in
component D has been suggested from both photometry and
spectroscopy
(Angonin et al. 1990;
Østensen et al. 1997).
In
particular, Angonin et al. (1990)
found that the equivalent
width of the emission lines is systematically smaller in
component D
than observed in the other components, a result which can be
interpreted by microlensing of the continuum source, the larger region
at the origin of the emission lines being unaffected. This effect,
which appeared to last at least a decade (Chae et al. 2001;
Anguita et al. 2008a),
offers the possibility to separate the
microlensed attenuated continuum (i.e. the absorption profile) from
the true emission line profile, thus providing new clues to the
formation of BAL profiles (Hutsemékers 1993; Hutsemékers
et al. 1994).
In the present paper, we homogeneously analyze the spectra of the four components of H1413+117 obtained from 1989 to 2005. The spectra cover the ultraviolet to visible rest-frame spectral range. In Sect. 3, we show that the spectral differences observed between the images can be consistently attributed to microlensing in spite of intrinsic variations. In Sect. 4, using a simple method, we separate the parts of the spectra affected and unaffected by microlensing, which basically correspond to the attenuated continuum and the emission lines. From these results, we derive a consistent view of the macro- and microlensing in H1413+117 (Sect. 5). Finally, with the ``pure'' absorption and emission profiles in hand, we discuss the formation of the BAL profiles and the implications for the geometry and the kinematics of the outflow (Sect. 6).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13247f01.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg19.png)
|
Figure 1:
A deconvolved near-infrared image of the gravitationally
lensed quasar H1413+117 with the four images and the lensing galaxy
labelled (from Chantry & Magain 2007). The image has
been
obtained in the F160W filter (
|
| Open with DEXTER | |
2 Data collection
Spectra of the four components of H1413+117 were gathered from archived
and published data. Table 1 summarizes
the
characteritics of the spectra obtained over a period of 16 years, with
the date of observation, the spectral range, the average resolving
power ![]() ,
and the instrument used.
,
and the instrument used.
The visible spectra secured in 1989 with the bidimensional
spectrograph SILFID at the Canada-France-Hawaii Telescope (CFHT) are
described in Angonin et al. (1990)
and Hutsemékers
(1993). These
spectra were obtained under optimal seeing
conditions (0
![]() 6
FWHM). They provided the first spectroscopic
evidence of microlensing in H1413+117.
6
FWHM). They provided the first spectroscopic
evidence of microlensing in H1413+117.
A series of spectra were obtained in 1993-1994 with the Hubble Space Telescope (HST) feeding the Faint Object spectrograph (FOS). They cover the UV-visible spectral range (gratings G400H and G570H). These data are described in Monier et al. (1998). A second series of HST spectra, yet unpublished, were obtained in 2000 using the Space Telescope Imaging Spectrograph (STIS) and the G430L grating (principal investigator: Monier; proposal # 8127). All HST data were retrieved from the archive and reduced using standard procedures for long slit spectroscopy and prescriptions by Monier et al. (1998).
In 2005, visible spectra were obtained with the integral field
unit of
the Visible MultiObject Spectrograph (VIMOS) attached to the European
Southern Observatory (ESO) Very Large Telescope (VLT). The data were
obtained under medium quality seeing conditions (1
![]() 2
FWHM). Details on the observations and reductions
are given in Anguita
et al. (2008a).
For this data set, it was not possible to
separate the spectra of images A and B of H1413+117.
2
FWHM). Details on the observations and reductions
are given in Anguita
et al. (2008a).
For this data set, it was not possible to
separate the spectra of images A and B of H1413+117.
The 2005 near-infrared spectra obtained with the integral
field
spectrograph SINFONI at the VLT were retrieved from the ESO archive
(principal investigator: Verma; proposal 075.B-0675(A)). Only the
spectra obtained with the best seeing (0
![]() 5 FWHM
on May 22, 2005
in the H and K spectral bands) are considered here. The pixel
size was
5 FWHM
on May 22, 2005
in the H and K spectral bands) are considered here. The pixel
size was
![]() on the sky. The observations consist
of four exposures per spectral band. The object was positionned at
different locations on the detector for sky subtraction. The data
were reduced using the SINFONI pipeline. Telluric absorptions were
corrected using standard star spectra normalized to a blackbody. The
individual spectra were extracted by fitting a 4-Gaussian function
with fixed relative positions and identical widths to each image plane
of the data cube using a modified MPFIT package (Markwardt
2009).
Astrometric positions were taken from HST observations
(Chantry & Magain 2007).
The spectra which appeared affected
by detector defects and/or important cosmic ray hits were
discarded. The good spectra were finally filtered to remove remaining
spikes.
on the sky. The observations consist
of four exposures per spectral band. The object was positionned at
different locations on the detector for sky subtraction. The data
were reduced using the SINFONI pipeline. Telluric absorptions were
corrected using standard star spectra normalized to a blackbody. The
individual spectra were extracted by fitting a 4-Gaussian function
with fixed relative positions and identical widths to each image plane
of the data cube using a modified MPFIT package (Markwardt
2009).
Astrometric positions were taken from HST observations
(Chantry & Magain 2007).
The spectra which appeared affected
by detector defects and/or important cosmic ray hits were
discarded. The good spectra were finally filtered to remove remaining
spikes.
In addition, we have observed H1413+117 on
May 10, 2008 with the
polarimetric mode of the Focal Reducer and low dispersion
Spectrograph 1 (FORS1) installed at the Cassegrain focus of
the VLT. Observations
have been carried out with the ![]() filter, under excellent
seeing conditions (0
filter, under excellent
seeing conditions (0
![]() 6).
Linear polarimetry has been performed
by inserting in the parallel beam a Wollaston prism, which splits the
incoming light rays into two orthogonally polarized beams, and a
half-wave plate rotated to four position angles (e.g. Sluse
et al. 2005).
In order to measure the polarization of the four
images, the MCS deconvolution procedure devised by Magain
et al. (1998)
has been applied. We used a version of the
algorithm that allows for a simultaneous fit of different individual
frames obtained with the same observational setup (Burud
2001). We
constructed the PSF using a bright point-like object
located
6).
Linear polarimetry has been performed
by inserting in the parallel beam a Wollaston prism, which splits the
incoming light rays into two orthogonally polarized beams, and a
half-wave plate rotated to four position angles (e.g. Sluse
et al. 2005).
In order to measure the polarization of the four
images, the MCS deconvolution procedure devised by Magain
et al. (1998)
has been applied. We used a version of the
algorithm that allows for a simultaneous fit of different individual
frames obtained with the same observational setup (Burud
2001). We
constructed the PSF using a bright point-like object
located ![]() 15
15
![]() from
H1413+117. Since this object is close to
our target and is similar in brightness to the individual components
of H1413+117, it provided a good estimate of the PSF. The Stokes
parameters have been calculated from the photometry of the quasar
lensed images derived from the deconvolution process.
from
H1413+117. Since this object is close to
our target and is similar in brightness to the individual components
of H1413+117, it provided a good estimate of the PSF. The Stokes
parameters have been calculated from the photometry of the quasar
lensed images derived from the deconvolution process.
Table 1: Spectroscopic data.
![\begin{figure}
\par\includegraphics[angle=90,width=15cm,clip]{13247f02.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg25.png)
|
Figure 2: Intercomparison, at different epochs, of the Si IV and C IV line profiles illustrating the spectral differences between some images of H1413+117. Ordinates are relative fluxes. Vertical dotted lines indicate the positions of the spectral lines at the redshift z = 2.553. The scaling factors needed to superimpose the continua are indicated. AB refers to the average spectrum of the A and B components (which could not be separated in the 2005 spectra). The upper left panel illustrates the time variation of the AB spectrum. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=14.2cm,clip]{13247f03.eps}
\includegraphics[angle=90,width=14.2cm,clip]{13247f04.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg26.png)
|
Figure 3:
Intercomparison of the Ly |
| Open with DEXTER | |
3 Description of the spectra
At the redshift of H1413+117, spectra obtained in the UV-visible
contain
C IV
![]() 1548,1550, Si IV
1548,1550, Si IV
![]() 1393,1402,
N V
1393,1402,
N V
![]() 1238,1242,
P V
1238,1242,
P V
![]() 1117,1128, O VI
1117,1128, O VI
![]() 1031,1037,
Ly
1031,1037,
Ly![]()
![]() 1216 and Ly
1216 and Ly![]()
![]() 1026, while
the near-infrared spectra contain H
1026, while
the near-infrared spectra contain H![]()
![]() 6563, H
6563, H![]()
![]() 4861 and [O III]
4861 and [O III]
![]() 4959,5007
(Figs. 2
and 3).
From the [O III] lines we measure
the
redshift z = 2.553. The UV resonance lines show
typical P
Cygni-type profiles with deep absorption while the Balmer lines show
broad emission possibly topped with a narrower feature. Ly
4959,5007
(Figs. 2
and 3).
From the [O III] lines we measure
the
redshift z = 2.553. The UV resonance lines show
typical P
Cygni-type profiles with deep absorption while the Balmer lines show
broad emission possibly topped with a narrower feature. Ly![]() and Ly
and Ly![]() lines are weak due to absorption by the N V
and
O VI ions, respectively (e.g. Surdej
& Hutsemékers
1987).
lines are weak due to absorption by the N V
and
O VI ions, respectively (e.g. Surdej
& Hutsemékers
1987).
3.1 Evidence for microlensing
In Figs. 2 and 3, we compare the profiles of various spectral lines observed in the different images A, B, C, and D of H1413+117. A scaling factor is applied to superimpose at best the continua, considering in particular the continuum windows 4525-4545 Å and 5165-5220 Å (i.e. 1275-1280 Å and 1450-1470 Å rest-frame, Kuraszkiewicz et al. 2002). If the four images are only macrolensed, the line profiles observed in the spectra of the four components must be identical up to the scaling factor. On the other hand, line profile differences between some components may be indicative of microlensing, which is expected to magnify the - small - continuum region and not the - larger - broad emission line region.
We first note that the line profiles in components A and B are
essentially identical up to the scaling factor. This suggests that
neither A nor B are strongly affected by microlensing. The small
difference observed in the [O III] lines
may be related to the
fact that the narrow line region could be partially resolved (Chantry
& Magain 2007).
The wavelength dependence of the scaling
factor reveals higher dust extinction along the B line of sight than
along the A one, as discussed in detail in Sect. 3.2. In
the following we consider the average spectrum of components A and B,
denoted AB, as the reference spectrum unaffected by microlensing
effects. As seen in the upper panel of Fig. 2, the
spectrum of H1413+117 changes regularly with time, suggesting intrinsic
variations in the quasar outflow (this is further discussed in
Sect. 3.3).
These changes are observed in all components,
indicating that the time scale of the intrinsic line profile variation
is longer than the time delays between the four images. In fact, the
longest time delay is not larger than one month according to the
observations of Goicoecha & Shalyapin (2010) and in
agreement with models![]() (Kayser et al. 1990;
Chae & Turnshek
1999).
(Kayser et al. 1990;
Chae & Turnshek
1999).
The spectrum of component D is clearly different when compared to AB. After scaling the continua, the emission appears less intense in D. This behavior is observed at all epochs and in the different spectral lines, superimposed onto the intrinsic time variations seen in all components. This is a clear signature of a long-term microlensing effect in D with amplification of the continuum with respect to the emission lines. The timescale of the effect is in agreement with previous estimates, i.e. on the order of 10 years (e.g. Hutsemékers 1993). As first pointed out by Angonin et al. (1990), a difference is also observed in the absorption profiles. This difference is especially strong in the 1989 and 1993 spectra. This is a priori not expected since the region at the origin of the observed absorption lines has the same spatial extent as the continuum source. Differential microlensing of absorbing clouds smaller in projection than the continuum source has been proposed (Angonin et al. 1990). However the timescale of such an event is expected to be smaller than 1 year (Hutsemékers 1993), ruling out this interpretation. Instead, we interpret the difference in the absorption profiles as due to the superposition of an emission line onto a nearly black absorption profile (Sect. 6.1).
Although not as strong as in component D, spectral
differences are
also observed when comparing C to AB. After scaling the continua, the
emission lines appear slightly stronger in C at all epochs, with a
possible differential effect between the broad H![]() and the
narrower [O III] lines. This suggests that
microlensing also
affects component C, de-amplifying the continuum with respect
to the
emission lines.
and the
narrower [O III] lines. This suggests that
microlensing also
affects component C, de-amplifying the continuum with respect
to the
emission lines.
The scaling factor used to fit the continuum of D to that one of AB clearly depends on wavelength. This can be explained either by chromatic microlensing (the source of UV continuum is less extended than the source of visible continuum and then more magnified), differential extinction (the extinction along the AB line of sight is higher than along the line of sight to D), wavelength-dependent dilution of the quasar continuum by the host galaxy light, or a combination thereof. Such a strong wavelength dependence of the scaling factor is not observed when comparing C to AB. The origin of this effect is further discussed in Sect. 5.2.
3.2 The extinction curve from A/B
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13247f05.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg29.png)
|
Figure 4:
The flux ratio |
| Open with DEXTER | |
Since images A and B are not significantly affected by microlensing,
the wavelength dependence of their flux ratio can be interpreted in
terms of differential extinction in the lensing
galaxy. Figure 4
illustrates the observed flux ratio
![]() using all available spectroscopic data
(slightly filtered and smoothed). Photometric data are
superimposed. They were collected from Angonin et al. (1990),
Østensen et al. (1997;
the ratios
using all available spectroscopic data
(slightly filtered and smoothed). Photometric data are
superimposed. They were collected from Angonin et al. (1990),
Østensen et al. (1997;
the ratios ![]() are
averaged per filter), Turnshek et al. (1997), Chae &
Turnshek (2001),
Kneib et al. (1998),
Chantry &
Magain (2007),
MacLeod et al. (2009).
are
averaged per filter), Turnshek et al. (1997), Chae &
Turnshek (2001),
Kneib et al. (1998),
Chantry &
Magain (2007),
MacLeod et al. (2009).
There is a lot of dispersion in the measured flux ratios which
arises
not only from inacurracies in the data but also from a possible
combined effect of intrinsic photometric variations and time delay
(cf. Østensen et al. 1997).
A clear trend is nevertheless
observed, indicating higher extinction along the line of sight to
image B, as suggested by Turnshek et al. (1997). The flux
ratio is reasonably well modeled using
| (1) |
where
3.3 Intrinsic line profile variations
Time variations in the absorption line profiles of BAL quasars are not uncommon (Barlow et al. 1989,1992; Gibson et al. 2008). In H1413+117, Turnshek et al. (1988) reported a deepening of the Si IV BAL between 1981 and 1985. On the contrary, between 1989 and 2005 (Fig. 2), variations are observed as a gradual decrease of the depth of the BAL high-velocity part, the deepest component of the profile being essentially unaffected. Variations appear more complex in Si IV than in C IV, affecting a larger part of the absorption profile (see also Fig. 6).
The strongest change occurs between 1989 and 1993 and
corresponds to
an increase of the luminosity (Remy et al. 1996; Østensen
et al. 1997).
Moreover, stronger absorption is accompanied by
stronger emission, which is an indication that resonance line
scattering can play an important role in the emission line formation.
In the C IV line of the AB spectrum, the
high-velocity
absorption appears ![]() 15%
larger in 1989 than in 2005 while the
emission is
15%
larger in 1989 than in 2005 while the
emission is ![]() 25%
more intense. In the framework of resonance
scattering where each absorbed photon is re-emitted, this may suggest
that the high-velocity outflow has more scattering material
perpendicular to the line of sight than absorbing material along the
line of sight. This also requires a large covering factor.
25%
more intense. In the framework of resonance
scattering where each absorbed photon is re-emitted, this may suggest
that the high-velocity outflow has more scattering material
perpendicular to the line of sight than absorbing material along the
line of sight. This also requires a large covering factor.
4 Decomposition of the line profiles
4.1 The method
We follow a method similar to that used in Sluse
et al. (2007).
Assuming that the observed spectra Fi
of
the different images are made of a superposition of a spectrum ![]() which is
only macrolensed and of a spectrum
which is
only macrolensed and of a spectrum ![]() which is both
macro- and microlensed, it is possible to extract the components
which is both
macro- and microlensed, it is possible to extract the components ![]() and
and ![]() by using pairs of observed spectra. Indeed, considering
a line profile, we can write
by using pairs of observed spectra. Indeed, considering
a line profile, we can write
| F1 | = | (2) | |
| F2 | = | (3) |
where M=M1/M2 is the macro-amplification ratio between images 1 and 2 and
|
|
= | (4) | |
| = | (5) |
where
|
|
= | 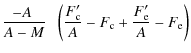
|
(6) |
| = | 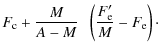
|
(7) |
Up to a scaling factor,
Equations (6) and (7) show that if the
emission profile is only macro-amplified
(i.e. if ![]() ),
),
![]() only contains the
underlying continuum
only contains the
underlying continuum ![]() ,
while
,
while ![]() contains the full emission
profile
contains the full emission
profile ![]() .
If the emission profile is micro-amplified to some
extent, parts of it will appear in both
.
If the emission profile is micro-amplified to some
extent, parts of it will appear in both ![]() and
and ![]() (see
Appendix A). More specifically,
(see
Appendix A). More specifically, ![]() can be seen as the
part of the emission profile which is not only macro-amplified, and
can be seen as the
part of the emission profile which is not only macro-amplified, and
![]() as the part
of the emission profile which is not amplified like
the continuum.
as the part
of the emission profile which is not amplified like
the continuum.
The micro-amplification factor ![]() and the macro-amplification
factor M possess some specific chromatic behaviors.
While
and the macro-amplification
factor M possess some specific chromatic behaviors.
While ![]() is
assumed constant over the small wavelength range spanned by a line
profile, it can be different at the wavelengths corresponding to
different line profiles. Indeed, the micro-amplification of the
continuum is related to the effective size of the continuum source
which can be wavelength-dependent. The macro-amplification factor Mmay
also contain a wavelength-dependent contribution due to
differential extinction in the lensing galaxy, since extinction, like
macrolensing, acts on the line profile as a whole. Finally,
concerning the time dependence properties, M is
expected to remain
identical at different epochs of observation while
is
assumed constant over the small wavelength range spanned by a line
profile, it can be different at the wavelengths corresponding to
different line profiles. Indeed, the micro-amplification of the
continuum is related to the effective size of the continuum source
which can be wavelength-dependent. The macro-amplification factor Mmay
also contain a wavelength-dependent contribution due to
differential extinction in the lensing galaxy, since extinction, like
macrolensing, acts on the line profile as a whole. Finally,
concerning the time dependence properties, M is
expected to remain
identical at different epochs of observation while ![]() can be
time-dependent.
can be
time-dependent.
4.2 The results
4.2.1 Line profile decomposition from the (D, AB) pair
Table 2: Amplification factors determined from the (D, AB) pair.
We extract ![]() and
and ![]() from the spectra of H1413+117 using
from the spectra of H1413+117 using ![]() and
and ![]() in Eqs. (4) and (5). We have M
< 1and
in Eqs. (4) and (5). We have M
< 1and ![]() since D is fainter than AB and its continuum amplified
(Sect. 3.1).
A is computed as the value for which
since D is fainter than AB and its continuum amplified
(Sect. 3.1).
A is computed as the value for which
![]() in the continuum windows adjacent to the line profiles
(cf. Sect. 3.1).
Within the uncertainties, A is the
inverse of the scaling factor determined in Figs. 2
and 3.
M is computed as the largest value for
which
in the continuum windows adjacent to the line profiles
(cf. Sect. 3.1).
Within the uncertainties, A is the
inverse of the scaling factor determined in Figs. 2
and 3.
M is computed as the largest value for
which ![]() over the whole line profile. For the
resonance line profiles, the continuum may be completely absorbed at
some wavelengths such that
over the whole line profile. For the
resonance line profiles, the continuum may be completely absorbed at
some wavelengths such that ![]() must also be larger than
zero. Measurements of A and M
are given in Table 2
with
must also be larger than
zero. Measurements of A and M
are given in Table 2
with ![]() .
Taking into account the noise and possible
contaminating features in the observed spectra, a range of acceptable
values is obtained which provides a rough estimate of the
uncertainties. These are typically 2-3% for A and
4-10% for M.
As expected, the macro-amplification factor M is
independent of the
epoch of observation, the dispersion of the values being in agreement
with the uncertainties. The temporal variation of A
then
essentially comes from the variation of the micro-amplification of the
continuum. This is shown in Fig. 5. This figure
also
suggests that, within the uncertainties, there is no significant
wavelength dependence of M due to a differential
reddening between
AB and D (see also Sect. 5.1).
.
Taking into account the noise and possible
contaminating features in the observed spectra, a range of acceptable
values is obtained which provides a rough estimate of the
uncertainties. These are typically 2-3% for A and
4-10% for M.
As expected, the macro-amplification factor M is
independent of the
epoch of observation, the dispersion of the values being in agreement
with the uncertainties. The temporal variation of A
then
essentially comes from the variation of the micro-amplification of the
continuum. This is shown in Fig. 5. This figure
also
suggests that, within the uncertainties, there is no significant
wavelength dependence of M due to a differential
reddening between
AB and D (see also Sect. 5.1).
With the measured A and M,
we then compute ![]() and
and ![]() from Eqs. (4)
and (5). The results of the line profile decompositions are
given in Figs. 6
to 8.
Over large parts
of the emission profile (mainly in the wings),
from Eqs. (4)
and (5). The results of the line profile decompositions are
given in Figs. 6
to 8.
Over large parts
of the emission profile (mainly in the wings), ![]() .
This
indicates that at least a part of the observed emission line profile
is unaffected by microlensing and that M actually
represents the
macro-amplification factor. We emphasize that the
derived
.
This
indicates that at least a part of the observed emission line profile
is unaffected by microlensing and that M actually
represents the
macro-amplification factor. We emphasize that the
derived ![]() and
and ![]() profiles are robust against small
changes of A or M.
profiles are robust against small
changes of A or M.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13247f06.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg66.png)
|
Figure 5:
The relation between A and |
| Open with DEXTER | |
Figure 6
illustrates the spectral decomposition for the
Si IV-C IV
region. Although different values of A(or ![]() )
are found at different epochs, the extracted spectra are
remarkably consistent. The microlensed part of the spectrum,
)
are found at different epochs, the extracted spectra are
remarkably consistent. The microlensed part of the spectrum,
![]() ,
contains the continuum with the full absorption profiles
as well as a small contribution from the core (not the wings) of the
emission profiles. The bulk of the emission lines appears in the
macrolensed-only part of the spectrum
,
contains the continuum with the full absorption profiles
as well as a small contribution from the core (not the wings) of the
emission profiles. The bulk of the emission lines appears in the
macrolensed-only part of the spectrum ![]() ,
clearly showing a
two-peak structure in C IV (at
5350 Å and 5500 Å).
Recall that
,
clearly showing a
two-peak structure in C IV (at
5350 Å and 5500 Å).
Recall that ![]() shows the flux emitted from a large region of the
quasar (much larger than the Einstein radius of the microlens) whereas
shows the flux emitted from a large region of the
quasar (much larger than the Einstein radius of the microlens) whereas
![]() shows the flux emitted from a smaller region (comparable to
and smaller than the Einstein radius). Interestingly enough, the
small part of the emission profile observed in
shows the flux emitted from a smaller region (comparable to
and smaller than the Einstein radius). Interestingly enough, the
small part of the emission profile observed in ![]() is the core,
i.e. the low-velocity part. The temporal variations of the absorption
are particularly well seen in the
is the core,
i.e. the low-velocity part. The temporal variations of the absorption
are particularly well seen in the ![]() spectrum of Si IV.
spectrum of Si IV.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13247f07.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg67.png)
|
Figure 6:
The microlensed |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13247f08.eps}
\vspace*{1.5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg68.png)
|
Figure 7:
Same as Fig. 6,
but for the Ly |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{13247f09.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg69.png)
|
Figure 8:
Same as Fig. 6,
but for the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{13247f10.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg70.png)
|
Figure 9:
Same as Figs. 6
and 7
but the
microlensed |
| Open with DEXTER | |
The rest-frame UV spectra, and more particularly the Ly![]() +
N V region, are similarly analyzed
(Fig. 7).
Although the decomposition is less accurate due to structures in the
continuum blueward of Ly
+
N V region, are similarly analyzed
(Fig. 7).
Although the decomposition is less accurate due to structures in the
continuum blueward of Ly![]() (possibly due to narrow absorption
features and inaccuracies in the wavelength calibration), the
extracted spectra
(possibly due to narrow absorption
features and inaccuracies in the wavelength calibration), the
extracted spectra ![]() and
and ![]() show the same qualitative
behavior as observed in the C IV and Si IV
line
profiles.
show the same qualitative
behavior as observed in the C IV and Si IV
line
profiles.
Figure 8
shows the decomposition for the H![]() +
[O III] and H
+
[O III] and H![]() line profiles. The micro-amplified
spectrum is clearly a flat continuum in the H
line profiles. The micro-amplified
spectrum is clearly a flat continuum in the H![]() + [O III]
spectral region while there is some evidence that the core (and not
the wings) of the H
+ [O III]
spectral region while there is some evidence that the core (and not
the wings) of the H![]() emission line is micro-amplified.
emission line is micro-amplified.
4.2.2 Line profile decomposition from the (C, AB) pair
The same kind of analysis can be done using the pair (C, AB).
However
the line profile differences are more subtle
(cf. Figs. 2
and 3)
so that the value
of M is closer to the value of A
(i.e. ![]() closer
to 1) in
Eqs. (4) and (5), making the extracted spectra
noisier. Only the spectra
obtained in 2000, which show the most conspicuous profile differences,
are considered here. A de-magnification of the continuum explains the
observations (Sect. 3.1)
and the resulting
closer
to 1) in
Eqs. (4) and (5), making the extracted spectra
noisier. Only the spectra
obtained in 2000, which show the most conspicuous profile differences,
are considered here. A de-magnification of the continuum explains the
observations (Sect. 3.1)
and the resulting ![]() and
and
![]() are illustrated in Fig. 9.
They are roughly
similar to those derived from the pair (D, AB) but the part of
the
emission profile which is micro-amplified is different. While only a
small part of the core of the emission is seen in the
are illustrated in Fig. 9.
They are roughly
similar to those derived from the pair (D, AB) but the part of
the
emission profile which is micro-amplified is different. While only a
small part of the core of the emission is seen in the ![]() profile
derived from the (D, AB) pair, the red wing of the emission
profile is also observed in
profile
derived from the (D, AB) pair, the red wing of the emission
profile is also observed in ![]() computed from (C, AB). This red
wing and the blue emission peak are not seen in
computed from (C, AB). This red
wing and the blue emission peak are not seen in ![]() ,
suggesting
that the high-velocity component of the C IV
resonance line is
micro-deamplified like the continuum. This is not unexpected since,
for a given Einstein radius, demagnification regions with relatively
smooth
,
suggesting
that the high-velocity component of the C IV
resonance line is
micro-deamplified like the continuum. This is not unexpected since,
for a given Einstein radius, demagnification regions with relatively
smooth ![]() variations can extend on larger scales than amplification
regions (e.g. Lewis & Ibata 2004).
The emission line core,
which appears in both
variations can extend on larger scales than amplification
regions (e.g. Lewis & Ibata 2004).
The emission line core,
which appears in both ![]() and
and ![]() ,
should originate, at
least in part, from a region more extended than the high-velocity
component.
,
should originate, at
least in part, from a region more extended than the high-velocity
component.
From the 2005 near-infrared spectra (the decomposition of
which is not
shown), we measure A = 0.74 for both the H![]() +[O III]
and
H
+[O III]
and
H![]() regions. The condition
regions. The condition ![]() is verified at
the wavelengths of H
is verified at
the wavelengths of H![]() or H
or H![]() with
with ![]() ,
while
,
while
![]() is obtained at the wavelength of the
[O III] lines with
is obtained at the wavelength of the
[O III] lines with ![]() .
The latter value is
comparable to the value of M derived from the
UV-visible resonance
lines. Although the narrow line region may be partially resolved
(Chantry & Magain 2007),
the [O III] emission lines
are expected to originate from a larger region and then less affected
by microlensing, making
.
The latter value is
comparable to the value of M derived from the
UV-visible resonance
lines. Although the narrow line region may be partially resolved
(Chantry & Magain 2007),
the [O III] emission lines
are expected to originate from a larger region and then less affected
by microlensing, making ![]() a more plausible estimate. In
this case, with
a more plausible estimate. In
this case, with ![]() for the micro-amplification
factor of the continuum, the Balmer emission lines do appear in both
for the micro-amplification
factor of the continuum, the Balmer emission lines do appear in both
![]() and
and ![]() .
This means that they are also
micro-deamplified although not as much as the continuum.
.
This means that they are also
micro-deamplified although not as much as the continuum.
5 Lensing in H1413+117
5.1 The macro-amplification factors
In principle, the variation of M with the
wavelength can be
attributed to differential extinction. Unfortunately, for the
(D, AB)
pair, the wavelength dependence is not clear enough to extract an
extinction curve, given the uncertainties on the determination of M(Fig. 5 and
Table 2).
The results
nevertheless suggest that the differential extinction between AB and D
is lower than between A and B for which the extinction at Ly![]() is
is ![]() 1.2 times
the extinction at H
1.2 times
the extinction at H![]() (Fig. 4). As a
consequence, the value M(D, AB
(Fig. 4). As a
consequence, the value M(D, AB
![]() determined at the wavelength of H
determined at the wavelength of H![]() ,
i.e. in the
reddest part of our spectra, should not differ from the true
macro-amplification factor by more than 2%.
,
i.e. in the
reddest part of our spectra, should not differ from the true
macro-amplification factor by more than 2%.
For the (C, AB) pair, we conservatively adopt M(C, AB
![]() at
the wavelength of H
at
the wavelength of H![]() .
Comparing with M(C, AB
.
Comparing with M(C, AB
![]() and M(C, AB
and M(C, AB
![]() at the wavelengths of
Ly
at the wavelengths of
Ly![]() and C IV, respectively (Fig. 9),
M(C, AB) might be slightly wavelength
dependent, providing marginal
evidence that extinction is lower for C than for AB.
Since the
differential extinction remains low, we also assume that it does not
affect the macro-amplification factor determined at the wavelength of
H
and C IV, respectively (Fig. 9),
M(C, AB) might be slightly wavelength
dependent, providing marginal
evidence that extinction is lower for C than for AB.
Since the
differential extinction remains low, we also assume that it does not
affect the macro-amplification factor determined at the wavelength of
H![]() by more than 2%.
by more than 2%.
The flux ratios with respect to component A are then ![]() /
/
![]() .02
(Fig. 4),
.02
(Fig. 4),
![]() /
/
![]() .10
and
.10
and ![]() /
/
![]() .04.
The fact that
.04.
The fact that ![]() /
/
![]() and
and ![]() /
/
![]() are different from the values estimated from
photometry is due to a significant de-amplification of the C continuum
and to a significant amplification of the D continuum, as derived from
the analysis of the spectral lines. This emphasizes the need to
properly correct for microlensing before interpreting the flux ratios.
are different from the values estimated from
photometry is due to a significant de-amplification of the C continuum
and to a significant amplification of the D continuum, as derived from
the analysis of the spectral lines. This emphasizes the need to
properly correct for microlensing before interpreting the flux ratios.
MacLeod et al. (2009) determined ![]() ,
,
![]() and
and ![]() at 11
at 11 ![]() m
in the mid-infrared,
i.e., where microlensing and extinction are thought to be negligible.
Although only marginally different, the flux ratios of the B and C
components relative to A seem slightly smaller than ours. If real,
the origin of such a discrepancy is not clear but could be related to
the intense starburst activity detected in the host galaxy of H1413+117
(Lutz et al. 2007;
Bradford et al. 2009),
which
possibly contaminates with PAH emission the 11.2
m
in the mid-infrared,
i.e., where microlensing and extinction are thought to be negligible.
Although only marginally different, the flux ratios of the B and C
components relative to A seem slightly smaller than ours. If real,
the origin of such a discrepancy is not clear but could be related to
the intense starburst activity detected in the host galaxy of H1413+117
(Lutz et al. 2007;
Bradford et al. 2009),
which
possibly contaminates with PAH emission the 11.2 ![]() m
(3.2
m
(3.2 ![]() m
rest-frame) flux measurements.
m
rest-frame) flux measurements.
5.2 Microlensing of the continuum source
The micro-amplification factor ![]() determined in component D depends
on both the date and the wavelength (Table 2).
determined in component D depends
on both the date and the wavelength (Table 2).
Considering the Si IV-C IV
spectral region, the
strongest variation of ![]() occurs between 1989 and 1993 (see
also Figs. 2
and 6).
It roughly
corresponds to a relative photometric variation between A and D which
can be observed in the V light curves of
H1413+117 presented by Remy et al. (1996) and Østensen
et al. (1997),
superimposed
onto the common intrinsic variation of the 4 components. Between 1993
and 2000, the variation of
occurs between 1989 and 1993 (see
also Figs. 2
and 6).
It roughly
corresponds to a relative photometric variation between A and D which
can be observed in the V light curves of
H1413+117 presented by Remy et al. (1996) and Østensen
et al. (1997),
superimposed
onto the common intrinsic variation of the 4 components. Between 1993
and 2000, the variation of ![]() is weaker, in agreement with the HST
photometry in the F555W filter reported by
Turnshek et al. (1997)
and Chae et al. (2001).
is weaker, in agreement with the HST
photometry in the F555W filter reported by
Turnshek et al. (1997)
and Chae et al. (2001).
At a given epoch, ![]() decreases with increasing wavelength,
suggesting chromatic magnification of the continuum source. This is
best seen in the 2005 data (obtained within a 2 month
interval) which
span the largest wavelength range. We emphasize that
decreases with increasing wavelength,
suggesting chromatic magnification of the continuum source. This is
best seen in the 2005 data (obtained within a 2 month
interval) which
span the largest wavelength range. We emphasize that ![]() ,
when
determined from the line profiles, is not contaminated by differential
extinction (Sect. 4.1).
In Fig. 10,
we
plot the values of
,
when
determined from the line profiles, is not contaminated by differential
extinction (Sect. 4.1).
In Fig. 10,
we
plot the values of ![]() as a function of the wavelength of
observation in the quasar rest-frame.
as a function of the wavelength of
observation in the quasar rest-frame.
The magnification ![]() of an extended source close to a caustic can
be written
of an extended source close to a caustic can
be written
| (8) |
where
| (9) |
As seen in Fig. 10, this model nicely reproduces the data using C = -0.55 and assuming for simplicity
In principle, we could have used the Ly![]() +N V
and the
C III]
+N V
and the
C III] ![]() 1909 emission lines,
also present in the 2005
visible spectra, to measure
1909 emission lines,
also present in the 2005
visible spectra, to measure ![]() at other wavelengths. Although
tentative estimates do agree with the observed trend, the quality of
the data is not sufficient to derive reliable values of
at other wavelengths. Although
tentative estimates do agree with the observed trend, the quality of
the data is not sufficient to derive reliable values of ![]() at
these wavelengths, due to the insufficient spectral resolution in the
complex Ly
at
these wavelengths, due to the insufficient spectral resolution in the
complex Ly![]() +N
V region and to the fact that the
C III] line is truncated. Clearly, with
better quality data, it
could be possible to separate M and
+N
V region and to the fact that the
C III] line is truncated. Clearly, with
better quality data, it
could be possible to separate M and ![]() at other wavelengths using
additional line profiles and thus derive the temperature profile of the
accretion disk.
at other wavelengths using
additional line profiles and thus derive the temperature profile of the
accretion disk.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13247f11.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg95.png)
|
Figure 10:
The micro-amplification factor |
| Open with DEXTER | |
Dilution of the quasar continuum - microlensed - by the host
galaxy light - not microlensed - can affect the interpretation of
the wavelength dependence of ![]() .
Denoting
.
Denoting ![]() the ratio of the host and quasar continua at
a given wavelength, we find that the micro-amplification factor of the
quasar continuum
the ratio of the host and quasar continua at
a given wavelength, we find that the micro-amplification factor of the
quasar continuum ![]() is related to the measured
is related to the measured ![]() by
by
| (10) |
if the host galaxy is unresolved and macrolensed as the quasar (i.e. if
| (11) |
if the host galaxy is resolved and not macrolensed (i.e. if
5.3 Microlensing of a scattering region?
Chae et al. (2001) have obtained the first polarization mesurements of the four images of H1413+117 using the HST. The F555W filter was used. They noted that, in March 1999, the polarization degree of component D might be higher that the polarization degree of the other components (Table 3). From this result, they suggested that microlensing also affects the scattering region. The measurements obtained in June 1999 possibly indicate an intrinsic variation of the polarization observed in all components. Similar variations have been reported by Goodrich & Miller (1995).
Table 3: Polarimetry of the four images.
Taking advantage of an excellent seeing, we were able to measure the polarization of the 4 components of H1413+117 in the V filter, from the ground. Our measurements are also reported in Table 3. Within the uncertainties, the polarization degree of components A, B and C do agree with the March 1999 values of Chae et al. (2001), while the polarization degree of component D does not. Instead, we find that the difference between the polarization degrees measured in A and C and those ones measured in B and D is significant. The difference between A and B is especially intriguing since we found no significant microlensing effect neither in A nor in B (at least before 2005). Possible interpretations could involve the polarization due to an extended scattering region resolved by the macrolens (possibly in the host galaxy, see Borguet et al. 2008), or a differential polarization induced by aligned dust grains in the lens galaxy. More data are clearly needed to correctly understand the meaning of these measurements.
6 Consequences for the BAL formation
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{13247f12.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg110.png)
|
Figure 11:
Selected |
| Open with DEXTER | |
In the previous sections we derived a consistent picture of
microlensing in H1413+117, showing that the continuum of
component D (or
more precisely all the regions of the quasar located in a cylinder of
diameter ![]()
![]() oriented along the line of sight and
containing the continuum source) is magnified with respect to the more
extended regions at the origin of the emission lines. This allowed us
to disentangle the absorption part of the BAL profiles, essentially
oriented along the line of sight and
containing the continuum source) is magnified with respect to the more
extended regions at the origin of the emission lines. This allowed us
to disentangle the absorption part of the BAL profiles, essentially
![]() ,
from the emission part, essentially
,
from the emission part, essentially ![]() (Figs. 6 to 8). The observed
profiles
are equal to the sum of the
(Figs. 6 to 8). The observed
profiles
are equal to the sum of the ![]() and
and ![]() spectra (Eq. (3)).
The separation is robust against the uncertainties of the
amplification factors. It is however not perfect since emission which
originates from regions close to the continuum source in projection
appears in
spectra (Eq. (3)).
The separation is robust against the uncertainties of the
amplification factors. It is however not perfect since emission which
originates from regions close to the continuum source in projection
appears in
![]() .
Selected spectra are illustrated in
Fig. 11
on a velocity scale.
.
Selected spectra are illustrated in
Fig. 11
on a velocity scale.
The absorption profile of the C IV
BAL appears nearly black
extending from ![]() km s-1
to
km s-1
to ![]() km s-1.
It is especially interesting to note
that the flow does not start at v = 0 in the
rest-frame defined
by the [O III] emission lines. The part of
the profile between
-8000 and -10 000 km s-1
is clearly variable between 1993 and
2000, showing a smaller depth in 2000. At a given epoch (1993-1994),
the absorption appears stronger in N V and
weaker in
Si IV; this is best seen in the velocity
range -2000 to
-4000 km s-1 and indicates an
ionization dependence of the
optical depth. The extracted emission profiles show a double-peaked
structure which extends to the blue as far as the absorption profile
does. The blue peak at -8000 km s-1
appears much fainter than
the red peak at -1000 km s-1.
The full emission profile
(represented by the green line in Fig. 11) is roughly
centered on the onset velocity of the flow (-2000 km s-1),
thus
blueshifted with respect to the [O III]
rest-frame. In fact,
the full absorption + emission line profile appears in a rest-frame
blueshifted by -2000 km s-1
with respect to the rest-frame
defined by the [O III] emission lines. H
km s-1.
It is especially interesting to note
that the flow does not start at v = 0 in the
rest-frame defined
by the [O III] emission lines. The part of
the profile between
-8000 and -10 000 km s-1
is clearly variable between 1993 and
2000, showing a smaller depth in 2000. At a given epoch (1993-1994),
the absorption appears stronger in N V and
weaker in
Si IV; this is best seen in the velocity
range -2000 to
-4000 km s-1 and indicates an
ionization dependence of the
optical depth. The extracted emission profiles show a double-peaked
structure which extends to the blue as far as the absorption profile
does. The blue peak at -8000 km s-1
appears much fainter than
the red peak at -1000 km s-1.
The full emission profile
(represented by the green line in Fig. 11) is roughly
centered on the onset velocity of the flow (-2000 km s-1),
thus
blueshifted with respect to the [O III]
rest-frame. In fact,
the full absorption + emission line profile appears in a rest-frame
blueshifted by -2000 km s-1
with respect to the rest-frame
defined by the [O III] emission lines. H![]() ,
on the other
hand, appears redshifted (Fig. 3). Although
not
clearly understood, these line shifts are common in quasars
(e.g. Corbin 1990;
McIntosh et al. 1999)
and
particularly strong in BAL QSOs (Richards et al. 2002), in
agreement with our observations. Interestingly enough, Nestor
et al. (2008)
found a deficit of intrinsic C IV Narrow
Absorption Line (NAL) systems at outflowing velocities lower
than 2000 km s-1,
possibly due to overionization close to the
accretion disk.
,
on the other
hand, appears redshifted (Fig. 3). Although
not
clearly understood, these line shifts are common in quasars
(e.g. Corbin 1990;
McIntosh et al. 1999)
and
particularly strong in BAL QSOs (Richards et al. 2002), in
agreement with our observations. Interestingly enough, Nestor
et al. (2008)
found a deficit of intrinsic C IV Narrow
Absorption Line (NAL) systems at outflowing velocities lower
than 2000 km s-1,
possibly due to overionization close to the
accretion disk.
The shape of the emission suggests that it is occulted by a
strong
absorber, narrower in velocity than the full absorption profile, and
emitting little by itself. Very similar absorption and emission
profiles are produced in the outflow model of Bjorkman et al. (1994) proposed for
early-type stars. We build on this
model to interpret our observations. A toy model, detailed in
Appendix B, is used for illustrative purposes (a full
radiative transfer
modeling is beyond the scope of the present paper; it is
presented in Borguet & Hutsemékers 2010, where details
on
the flow geometry are also given). We assume that the outflow in
H1413+117 is constituted of two components: a quasi-spherically
symmetric
``polar'' outflow, and a denser disk seen nearly edge-on. The
equatorial disk expands slower than the polar wind and partly covers
it. The polar outflow produces typical P Cygni line profiles
constituted of the superposition of a deep absorption extending from
-2000 to roughly -10 000 km s-1
and a symmetric emission due
to resonantly scattered photons (e.g. Lamers & Cassinelli
1999). This
emission (assumed Gaussian shaped for simplicity)
is centered on ![]() km s-1
and extends from
-10 000 to +6000 km s-1.
Both the remaining continuum and the
emission from the polar wind are absorbed in the equatorial disk. A
double-peaked emission line is then produced (Fig. 11),
little emission being expected from the edge-on disk. As we can see
from Fig. 11,
this simple model is able to reproduce the
main characteristics of the intrinsic emission line profiles extracted
from the microlensing analysis. Since the disk is expected to also
absorb the continuum, its absorption profile must be contained within
the total polar+equatorial absorption profile, as illustrated.
Variability of the polar outflow optical depth will generate
variations at the high velocity end of the absorption accompanied by a
change in the resonantly scattered emission, as observed
(Sect. 3.3;
see also Bjorkman et al. 1994,
for
simulations). Note that two-component winds have good
theoretical
grounds (e.g. Murray et al. 1995;
Proga & Kallman
2004) and are
supported by many observations interpreted with
either disks or polar flows (cf. Sect. 1).
km s-1
and extends from
-10 000 to +6000 km s-1.
Both the remaining continuum and the
emission from the polar wind are absorbed in the equatorial disk. A
double-peaked emission line is then produced (Fig. 11),
little emission being expected from the edge-on disk. As we can see
from Fig. 11,
this simple model is able to reproduce the
main characteristics of the intrinsic emission line profiles extracted
from the microlensing analysis. Since the disk is expected to also
absorb the continuum, its absorption profile must be contained within
the total polar+equatorial absorption profile, as illustrated.
Variability of the polar outflow optical depth will generate
variations at the high velocity end of the absorption accompanied by a
change in the resonantly scattered emission, as observed
(Sect. 3.3;
see also Bjorkman et al. 1994,
for
simulations). Note that two-component winds have good
theoretical
grounds (e.g. Murray et al. 1995;
Proga & Kallman
2004) and are
supported by many observations interpreted with
either disks or polar flows (cf. Sect. 1).
Spectropolarimetric observations of H1413+117 (e.g. Goodrich & Miller 1995; Lamy & Hutsemékers 2004) provide additional evidence favoring this kind of scenario. First, the polarization angle rotates within the absorption line profiles, suggesting the existence of at least two sources and/or mechanisms of polarization. The polar outflow and the disk, expected to produce perpendicular polarizations, can play this role, especially in the case of BAL QSOs with P Cygni-type profiles (Goodrich 1997; Hutsemékers et al. 1998; Lamy & Hutsemékers 2004). Furthermore, the absorption in the polarized spectrum is clearly narrower than the absorption in the direct spectrum (this is best observed in Fig. 3 of Goodrich & Miller 1995), supporting the existence of a slowly expanding equatorial disk which absorbs the polar-scattered flux.
6.1 Microlensing in the BAL
The difference observed in the BAL profiles of images AB and D (best seen in C IV, Fig. 2) can also be interpreted in the framework of this outflow model. In 1989 and 1993, the intrinsic absorption at 5330 Å (-9000 km s-1) due to the high-velocity ``polar'' outflow is nearly black (Figs. 6 and 11). In classical P Cygni line profile formation (e.g. Lamers & Cassinelli 1999; Hutsemékers & Surdej 1990), this absorption is partially filled in with emission resonantly scattered at the same velocity (the blueward peak of the intrinsic emission, not absorbed by the slower disk, and seen in Figs. 6 and 11). Since the emission line and the absorbed continuum react differently to the magnification by the microlens, a spectral difference is observed in the high-velocity part of the BALs seen in AB and D. Later, in 2000 and 2005, the high-velocity part of the BAL profile is less optically thick: the absorption is not as deep as in the nineties and the blue wing of the resonantly scattered emission which fills in the absorption is accordingly weaker (the blue emission peak appears narrower or less intense in 2000 and 2005, Figs. 6 and 11). As a consequence, the microlens-induced spectral difference observed in the high-velocity part of the BALs appears smaller at these epochs.
7 Conclusions
Using 16 years of spectroscopic observations of the 4 components of the gravitationally lensed BAL quasar H1413+117, we derived the following results.
- -
- The strength of the BAL profiles gradually decreases with time in all components. This intrinsic variation is accompanied by a decrease of the intensity of the emission.
- -
- The spectral differences observed in component D can be attributed to a long-term microlensing effect, in agreement with previous studies. This effect consistently magnifies the continuum source of image D, leaving the broad emission line region essentially unaffected. We also find that the continuum of component C is most likely de-magnified, while components A and B are not affected by microlensing. Differential extinction is found between A and B.
- -
- Using a simple decomposition method to separate the part of the line profiles affected by microlensing from the part unaffected by this effect, we were able to disentangle the intrinsic absorption (affected) from the emission line profile (unaffected). Consistent results are obtained for the different epochs of observation.
- -
- Considering the macro- and micro-amplification factors estimated with this method, we obtain a coherent view of lensing in H1413+117. In particular, we show that microlensing of the D continuum source has a chromatic dependence which is compatible with a continuum emitted by a standard Shakura-Sunyaev accretion disk.
- -
- To interpret the extracted absorption and emission line profiles, we propose that the outflow from H1413+117 is constituted of a high-velocity polar flow (at the origin of the intrinsic variations) and a dense disk expanding at lower velocity and seen nearly edge-on. This is in agreement with spectropolarimetric data and supports the idea that BAL outflows can have large covering factors.
It is a pleasure to thank Virginie Chantry for providing us with the image illustrated in Fig. 1. A fellowship from the Alexander von Humboldt Foundation to D.S. is gratefully acknowledged.
Appendix A: Example of a line profile decomposition
We consider a line profile constituted of an underlying continuum
![]() (absorbed or not at some wavelengths) and an emission
profile
(absorbed or not at some wavelengths) and an emission
profile ![]() .
We assume the
continuum
.
We assume the
continuum ![]() micro-amplified by a constant factor
micro-amplified by a constant factor ![]() ,
the
component
,
the
component ![]() of the emission micro-amplified by a constant factor
of the emission micro-amplified by a constant factor
![]() ,
and the component Eb
unaffected by
microlensing
,
and the component Eb
unaffected by
microlensing![]() . We consider a typical
case with
. We consider a typical
case with ![]() .
If M is the relative macro-amplification factor
between
images 1 and 2, we have
.
If M is the relative macro-amplification factor
between
images 1 and 2, we have
| F1 | = | (A.1) | |
| F2 | = | (A.2) |
Using these expressions with
|
|
= | (A.3) | |
| = | (A.4) |
with
To effectively compute Eqs. (4) and (5) and to
determine the
profile of ![]() ,
we need to know M
,
we need to know M![]() (or
(or ![]() ).
Practically, we consider M as a free parameter in
Eq. (5) and, by varying it, we adopt the value of M
closest to Asuch that
).
Practically, we consider M as a free parameter in
Eq. (5) and, by varying it, we adopt the value of M
closest to Asuch that ![]() at all wavelengths (Eq. (7)). This is
equivalent to adopt a value of
at all wavelengths (Eq. (7)). This is
equivalent to adopt a value of ![]() as close as possible to 1, thus
ensuring that the macro- and micro-amplifications are best separated
(see also Sluse et al. 2007). Unless
as close as possible to 1, thus
ensuring that the macro- and micro-amplifications are best separated
(see also Sluse et al. 2007). Unless ![]() ,
this
method provides a reasonably accurate estimate of M,
and then of
,
this
method provides a reasonably accurate estimate of M,
and then of
![]() .
Indeed, denoting the free parameter M' and using
expressions A.1 and A.2 in Eq. (5), we write
.
Indeed, denoting the free parameter M' and using
expressions A.1 and A.2 in Eq. (5), we write
|
|
= | 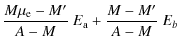
|
(A.5) |
such that
| M
= |
(A.6) |
with
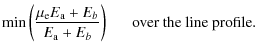
|
(A.7) |
If
Appendix B: The absorption / emission toy model
For a given line profile, we adopt for the disk optical depth ![]() the
functional form
the
functional form
| (B.1) |
where w is the velocity.
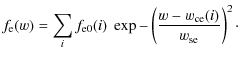
|
(B.2) |
The disk absorption profile is computed as
For all line profiles shown in Fig. 11, we use ![]() 5000 km s-1,
5000 km s-1,
![]() km s-1,
km s-1,
![]() 2000 km s-1,
2000 km s-1,
![]() km s-1,
i=1 corresponding
to the reddest line of the profiles, the position of the other ones
being fixed by the doublet separation and/or by the Ly
km s-1,
i=1 corresponding
to the reddest line of the profiles, the position of the other ones
being fixed by the doublet separation and/or by the Ly![]() -
N V velocity separation.
-
N V velocity separation. ![]() and
and ![]() are
choosen to fit the observations. The parameters are not unique and
may be different at other epochs.
are
choosen to fit the observations. The parameters are not unique and
may be different at other epochs.
References
- Angonin, M.-C., Vanderriest, C., Remy, M., & Surdej, J. 1990, A&A, 233, L5
- Anguita, T., Faure, C., Yonehara, A., et al. 2008a, A&A, 481, 615
- Anguita, T., Schmidt, R. W., Turner, E. L., et al. 2008b, A&A, 480, 327
- Barlow, T. A., Junkkarinen, V. T., & Burbidge, E. M. 1989, ApJ, 347, 674
- Barlow, T. A., Junkkarinen, V. T., Burbidge, E. M., et al. 1992, ApJ, 397, 81
- Becker, R. H., White, R. L., Gregg, M. D., et al. 2000, ApJ, 538, 72
- Belle, K. E., & Lewis, G. F. 2000, PASP, 112, 320
- Bjorkman, J. E., Ignace, R., Tripp, T. M., & Cassinelli, J. P. 1994, ApJ, 435, 416
- Borguet, B., & Hutsemékers, D. 2010, A&A, 515, A22
- Borguet, B., Hutsemékers, D., Letawe, G., Letawe, Y., & Magain, P. 2008, A&A, 478, 321
- Bradford, C. M., Aguirre, J. E., Aikin, R., et al. 2009, ApJ, 705, 112
- Burud, I. 2001, Ph.D. Thesis
- Chae, K.-H., & Turnshek, D. A. 1999, ApJ, 514, 587
- Chae, K.-H., Turnshek, D. A., Schulte-Ladbeck, R. E., Rao, S. M., & Lupie, O. L. 2001, ApJ, 561, 653
- Chantry, V., & Magain, P. 2007, A&A, 470, 467
- Chelouche, D. 2005, ApJ, 629, 667
- Corbin, M. R. 1990, ApJ, 357, 346
- Eigenbrod, A., Courbin, F., Meylan, G., et al. 2008, A&A, 490, 933
- Furlanetto, S. R., & Loeb, A. 2001, ApJ, 556, 619
- Gallagher, S. C., Hines, D. C., Blaylock, M., et al. 2007, ApJ, 556, 619
- Gibson, R. R., Brandt, W. N., Schneider, D. P., & Gallagher, S. C. 2008, ApJ, 675, 985
- Goicoechea, L. J., & Shalyapin, V. N. 2010, ApJ, 708, 995
- Goodrich, R. W., & Miller, J. S. 1995, ApJ, 448, L73
- Goodrich, R. W. 1997, ApJ, 474, 606
- Hamann, F., Korista, K. T., & Morris, S. L. 1993, ApJ, 415, 541
- Hutsemékers, D. 1993, A&A, 280, 435
- Hutsemékers, D., & Surdej, J. 1990, ApJ, 361, 367
- Hutsemékers, D., Surdej, J., & van Drom, E. 1994, Ap&SS, 216, 361
- Hutsemékers, D., Lamy, H., & Remy, M. 1998, A&A, 340, 371
- Kayser, R., Surdej, J., Condon, J. J., et al. 1990, ApJ, 364, 15
- Kneib, J.-P., Alloin, D., & Pello, R. 1998, A&A, 339, L65
- Kuraszkiewicz, J. K., Green, P. J., Forster, K., et al. 2002, ApJS, 143, 257
- Lamers, H. J. G. L. M., & Cassinelli, J. P. 1999, Introduction to stellar winds (Cambridge University Press)
- Lamy, H., & Hutsemékers, D. 2004, A&A, 427, 107
- Lewis, G. F., & Belle, K. E. 1998, MNRAS, 297, 69
- Lewis, G. F., & Ibata, R. A. 2004, MNRAS, 348, 24
- Lutz, D., Sturm, E., Tacconi, L. J., Valiante, E., et al. 2007, ApJ, 661, L25
- MacLeod, C. L., Kochanek, C. S., & Agol, E. 2009, ApJ, 699, 1578
- Magain, P., Surdej, J., Swings, J.-P., Borgeest, U., & Kayser, R. 1988, Nature, 334, 325
- Magain, P., Courbin, F., & Sohy, S. 1998, ApJ, 494, 472
- Markwardt, C. B. 2009, XVIII ASP Conf. Ser., 411, 251
- McIntosh, D. H., Rix, H.-W., Rieke, M. J., & Foltz, C. B. 1999, ApJ, 517, L73
- Monier, E. M., Turnshek, D. A., & Lupie, O. L. 1998, ApJ, 496, 177
- Murray, N., Chiang, J., Grossman, S. A., & Voit, G. M. 1995, ApJ, 451, 498
- Nestor, D., Hamann, F., & Rodriguez Hidalgo, P. 2008, MNRAS, 386, 2055
- Ogle, P. M., Cohen, M. H., Miller, J. S., et al. 1999, ApJS, 125, 1
- Østensen, R., Remy, M., Lindblad, P. O., et al. 1997, A&AS, 126, 393
- Pei, Y. C. 1992, ApJ, 395, 130
- Poindexter, S., Morgan, N., & Kochanek, C. S. 2008, ApJ, 673, 34
- Proga, D., & Kallman, T. R. 2004, ApJ, 616, 688
- Reichard, T. A., Richards, G. T.; Hall, P. B.; et al. 2003, AJ, 126, 2594
- Remy, M., Gosset, E., Hutsemékers, D., Revenaz, B., & Surdej, J. 1996, Astrophysical Applications of Gravitational Lensing, 173, 261
- Richards, G. T., Vanden Berk, D. E., Reichard, T. A., et al. 2002, AJ, 124, 1
- Saha, P., & Williams, L. L. R. 2004, AJ, 127, 2604
- Scannapieco, E., & Oh, S. P. 2004, ApJ, 608, 62
- Scannapieco, E., Silk, J., & Bouwens, R. 2005, ApJ, 635, L13
- Schmidt, G. D., & Hines, D. C. 1999, ApJ, 512, 125
- Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses (Berlin, Heidelberg, New York: Springer-Verlag)
- Schramm, M., Wisotzki, L., & Jahnke, K. 2008, A&A, 478, 311
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337
- Silk, J., & Rees, M. 1993, A&A, 331, L1
- Sluse, D., Hutsemékers, D., Lamy, H., Cabanac, R., & Quintana, H. 2005, A&A, 433, 757
- Sluse, D., Claeskens, J.-F., Hutsemékers, D., & Surdej, J. 2007, A&A, 468, 885
- Surdej, J., & Hutsemékers, D. 1987, A&A, 177, 42
- Turnshek, D. A., Lupie, O. L., Rao, S. M., Espey, B. R., & Sirola, C. J. 1997, ApJ, 485, 100
- Turnshek, D. A., Grillmair, C. J., Foltz, C. B., & Weymann, R. J. 1988, ApJ, 325, 651
- Voit, G. M., Weymann, R. J., & Korista, K. T. 1993, ApJ, 413, 95
- Witt, H. J., Kayser, R., & Refsdal, S. 1993, A&A, 268, 501
- Weymann, R. J., Morris, S. L., Foltz, C. B., & Hewett, P. C. 1991, ApJ, 373, 23
- Young, S., Axon, D. J., Robinson, A., Hough, J. H., & Smith, J. E. 2007, Nature, 450, 74
- Zhou, H., Wang, T., Wang, H., et al. 2006, ApJ, 639, 716
Footnotes
- ... quasar
![[*]](/icons/foot_motif.png)
- Based on observations made with the Canada-France-Hawaii Telescope (Hawaii), with ESO Telescopes at the Paranal Observatory (Chile) and with the NASA/ESA Hubble Space Telescope, and obtained from the data archive at the Space Telescope Institute. ESO program ID: 074.A-0152, 075.B-0675, 081.A-0023.
- ...
![[*]](/icons/foot_motif.png)
- Maître de Recherches du FNRS.
- ...
![[*]](/icons/foot_motif.png)
- Boursier du FNRS.
- ... models
![[*]](/icons/foot_motif.png)
- We also estimate small time delays, typically less than 10 days, considering a classical singular isothermal ellipsoid (SIE)+shear model, a SIE+shear+galaxy model proposed by MacLeod et al. (2009), as well as using pixellated models with a symmetric mass distribution (Saha & Williams 2004).
- ...
microlensing
![[*]](/icons/foot_motif.png)
- It is always possible to write
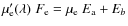 where
where
 =
max(
=
max(
 ).
).
- ...M
![[*]](/icons/foot_motif.png)
- As
discussed in Sect. 4.1, the factor A and then the
profile of
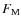 are more easily determined.
are more easily determined.
- ...
micro-lensing
![[*]](/icons/foot_motif.png)
- The amplification factors can be renormalized
as follows:
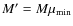 ,
,
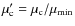 and
and
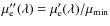 .
Note that
.
Note that
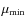 = min(
= min(
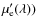 .
.
All Tables
Table 1: Spectroscopic data.
Table 2: Amplification factors determined from the (D, AB) pair.
Table 3: Polarimetry of the four images.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13247f01.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg19.png)
|
Figure 1:
A deconvolved near-infrared image of the gravitationally
lensed quasar H1413+117 with the four images and the lensing galaxy
labelled (from Chantry & Magain 2007). The image has
been
obtained in the F160W filter (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=15cm,clip]{13247f02.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg25.png)
|
Figure 2: Intercomparison, at different epochs, of the Si IV and C IV line profiles illustrating the spectral differences between some images of H1413+117. Ordinates are relative fluxes. Vertical dotted lines indicate the positions of the spectral lines at the redshift z = 2.553. The scaling factors needed to superimpose the continua are indicated. AB refers to the average spectrum of the A and B components (which could not be separated in the 2005 spectra). The upper left panel illustrates the time variation of the AB spectrum. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=14.2cm,clip]{13247f03.eps}
\includegraphics[angle=90,width=14.2cm,clip]{13247f04.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg26.png)
|
Figure 3:
Intercomparison of the Ly |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13247f05.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg29.png)
|
Figure 4:
The flux ratio |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13247f06.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg66.png)
|
Figure 5:
The relation between A and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13247f07.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg67.png)
|
Figure 6:
The microlensed |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{13247f08.eps}
\vspace*{1.5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg68.png)
|
Figure 7:
Same as Fig. 6,
but for the Ly |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{13247f09.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg69.png)
|
Figure 8:
Same as Fig. 6,
but for the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{13247f10.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg70.png)
|
Figure 9:
Same as Figs. 6
and 7
but the
microlensed |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13247f11.eps}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg95.png)
|
Figure 10:
The micro-amplification factor |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{13247f12.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/11/aa13247-09/Timg110.png)
|
Figure 11:
Selected |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


