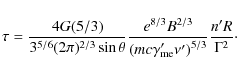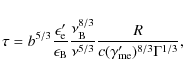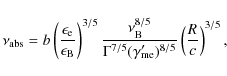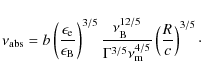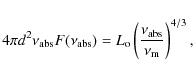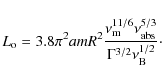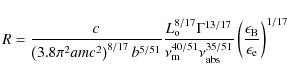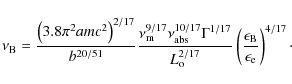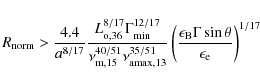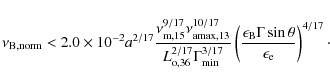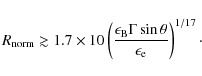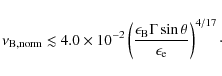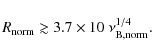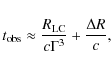| Issue |
A&A
Volume 516, June-July 2010
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 6 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201014049 | |
| Published online | 29 June 2010 | |
The location of the Crab pulsar emission region: restrictions on synchrotron emission models
C.-I. Björnsson - A. Sandberg - J. Sollerman
The Oskar Klein Centre, Department of Astronomy, Stockholm University, AlbaNova, 106 91 Stockholm, Sweden
Received 12 January 2010 / Accepted 25 March 2010
Abstract
Recent observations of the Crab pulsar show no evidence of a spectral
break in the infrared regime. It is argued that the observations are
consistent with a power-law spectrum in the whole observable
infrared-optical range. This is taken as the starting point for
evaluating of how self-consistent incoherent synchrotron models fare in
a comparison with observations. Inclusion of synchrotron
self-absorption proves important as does the restriction on the
observed size of the emission region imposed by the relativistic
beaming thought to define the pulse profile. It is shown that the
observations can be used to derive two independent constraints on the
distance from the neutron star to the emission region; in addition to a
direct lower limit, an indirect measure is obtained from an upper limit
to the magnetic field strength. Both of these limits indicate
that the emission region is located at a distance considerably greater
than the light cylinder radius. The implications of this result are
discussed, and it is emphasized that, for standard incoherent
synchrotron models to fit inside the light cylinder, rather special
physical conditions need to be invoked.
Key words: pulsars: individual: PSR B0531+21 - radiation mechanisms: non-thermal - stars: neutron - pulsars: general
1 Introduction
Incoherent synchrotron radiation was recognized early on as a likely emission mechanism for the infrared-optical pulses in the Crab pulsar (e.g., Shklovsky 1970; Pacini 1971). However, as discussed by O'Dell & Sartori (1970) and Epstein & Petrosian (1973), some of the model constraints imposed by the pulsed nature of the emission were initially not explicitly included; e.g., the assumption that the pulses are due to a combination of rotation and relativistic streaming/small pitch angles implies that the frequency of the observed emission should be at least as high as the Doppler boosted cyclotron frequency. This puts an upper limit on the magnetic field in the emission region. With a dipolar magnetic field structure, this results in a minimum distance to the emission region corresponding roughly to the light cylinder radius or even somewhat larger (e.g., Golden et al. 2000).The spectral characteristics in the infrared-optical range
have long been a matter of debate. The discussion has centred on two
issues (see, e.g., Sandberg &
Sollerman 2009, hereafter SS09); namely, (i) the value of the
spectral index ![]() ,
defined such that the flux
,
defined such that the flux ![]() ,
in the optical and (ii) the existence of a possible break and/or bump
in the infrared. The main question regarding
,
in the optical and (ii) the existence of a possible break and/or bump
in the infrared. The main question regarding ![]() is whether it is consistent with a value of 1/3. Since this value is
the highest possible for optically thin incoherent synchrotron
radiation, such a spectrum would indicate that the distribution of
electron energies has a sharp, low-energy cut-off and that the typical
synchrotron frequencies for these electrons lie above the optical
frequency band. In addition to its implication for the acceleration
process, it has consequences for the deduced upper limit of the
magnetic field in the emission region.
is whether it is consistent with a value of 1/3. Since this value is
the highest possible for optically thin incoherent synchrotron
radiation, such a spectrum would indicate that the distribution of
electron energies has a sharp, low-energy cut-off and that the typical
synchrotron frequencies for these electrons lie above the optical
frequency band. In addition to its implication for the acceleration
process, it has consequences for the deduced upper limit of the
magnetic field in the emission region.
The value of the magnetic field discussed above assumes that
the observed frequencies correspond to the typical synchrotron
frequencies, i.e., that the observed spectral range is determined by
the range of electron energies. As a result, the lower frequency limit
corresponds to electrons being non-relativistic in the frame where
there is no streaming (i.e., the average pitch-angle is ![]() ). This
contrasts to the case of a low-energy cut-off for which the lowest
energy electrons are highly relativistic also in the no-streaming
frame. Since the inertial mass of the electron increases with the
Lorentz factor, the synchrotron spectrum extends below the cyclotron
frequency. The arguments leading to the upper limit of the magnetic
field and the associated lower limit of the distance to the emission
region are therefore no longer valid and, a priori, no
restrictions regarding the location of the emission region can be set.
). This
contrasts to the case of a low-energy cut-off for which the lowest
energy electrons are highly relativistic also in the no-streaming
frame. Since the inertial mass of the electron increases with the
Lorentz factor, the synchrotron spectrum extends below the cyclotron
frequency. The arguments leading to the upper limit of the magnetic
field and the associated lower limit of the distance to the emission
region are therefore no longer valid and, a priori, no
restrictions regarding the location of the emission region can be set.
The synchrotron self-absorption frequency is an important parameter for restricting the properties of the emission region. This was already used by Shklovsky (1970, see also Pacini & Salvati 1983), together with the expected brightness temperature to estimate the source size, i.e., its lateral extent. Simple scaling relations have also been derived for the expected emission outside the infrared-optical range for the Crab pulsar itself (e.g., Pacini & Salvati 1987), as well as for the infrared-optical emission in other pulsars. In this case, the synchrotron self-absorption frequency plays a central role (O'Connor et al. 2005).
Another important constraint in the synchrotron scenario is the relation imposed by the geometry of the emission region between the observed lateral extent of the source and its distance from the neutron star. Although some aspects of this have been considered, for example, by Pacini & Salvati (1987) in their scaling relations, a more extensive discussion including synchrotron self-absorption still seems to be lacking. Motivated by recent observational progress regarding the spectral properties of the Crab pulsar, it is the aim of the present paper to provide such an analysis.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14049fig1.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14049-10/Timg9.png)
|
Figure 1:
Best fit of an |
| Open with DEXTER | |
In Sect. 2
the observational situation is summarized and evaluated. It is
concluded that ![]() is consistent with, although not required by, the observations.
Furthermore, it emphasizes that recent observations
show no indications of either a break or a bump in the infrared. The
temporal structure of the Crab pulses is also briefly discussed.
Standard synchrotron theory is applied to a few different settings for
the emission region in Sect. 3.
We show that the observations can be used to derive two independent
constraints on the properties of the emission region. The first is an
upper limit to the strength of the magnetic field, even in the case of
a low-energy cut-off in the electron energy distribution, while the
second one is a direct lower limit of the distance to the emission
region. Although the various settings give somewhat different limits,
they all suggest that the distance to the emission region is
considerably larger than the light cylinder radius. The implications of
these results are discussed in Sect. 4. We conclude that an
incoherent synchrotron radiation scenario is still tenable although
severely restricted. A few alternative origins for the infrared-optical
emission are also suggested. Throughout this paper, cgs-units are used.
is consistent with, although not required by, the observations.
Furthermore, it emphasizes that recent observations
show no indications of either a break or a bump in the infrared. The
temporal structure of the Crab pulses is also briefly discussed.
Standard synchrotron theory is applied to a few different settings for
the emission region in Sect. 3.
We show that the observations can be used to derive two independent
constraints on the properties of the emission region. The first is an
upper limit to the strength of the magnetic field, even in the case of
a low-energy cut-off in the electron energy distribution, while the
second one is a direct lower limit of the distance to the emission
region. Although the various settings give somewhat different limits,
they all suggest that the distance to the emission region is
considerably larger than the light cylinder radius. The implications of
these results are discussed in Sect. 4. We conclude that an
incoherent synchrotron radiation scenario is still tenable although
severely restricted. A few alternative origins for the infrared-optical
emission are also suggested. Throughout this paper, cgs-units are used.
2 Observations
2.1 Spectral energy distribution
In this section we review some of the observations of the Crab pulsar spectral energy distribution in the infrared-optical regime. We start by restating the lack of evidence for a spectral break in the observed infrared. As mentioned by SS09, since the early observations by Middleditch et al. (1983), the existence of such a break has permeated pulsar textbooks and literature. This has had large consequences for the theoretical interpretation of the synchrotron emission, as seen e.g., in O'Connor et al. (2005) and Crusius-Wätzel et al. (2001).
More recent observations of the infrared SED discussed a smooth levelling or a rollover towards the IR (Sollerman 2003; Temim et al. 2006). However, looking afresh at the new observations (SS09), in particular the corrected data from the Spitzer Space Telescope (Temim et al. 2009), there is actually no evidence of any spectral break in the observed infrared (Fig. 1).
For characterizing the SED, we list in
Table 1
results from some of the previous observations of the
spectral index, ![]() ,
of the Crab pulsar, and indicate for which wavelength ranges these
observations were made
(compare Fordham et al. 2002,
their Table 6). The uppermost part are spectroscopic
observations and the lower part are photometric. For dereddening E(B-V)=0.51-0.52 mag
and R = 3.1 were used for all observations. A quick
glance at
Table 1
shows that there are many observed values
of
,
of the Crab pulsar, and indicate for which wavelength ranges these
observations were made
(compare Fordham et al. 2002,
their Table 6). The uppermost part are spectroscopic
observations and the lower part are photometric. For dereddening E(B-V)=0.51-0.52 mag
and R = 3.1 were used for all observations. A quick
glance at
Table 1
shows that there are many observed values
of ![]() on both sides of a totally flat spectrum. There are a few more
observations not included in Table 1, e.g., those by Middleditch et al. (1983),
since these data were not well fit by a power law.
on both sides of a totally flat spectrum. There are a few more
observations not included in Table 1, e.g., those by Middleditch et al. (1983),
since these data were not well fit by a power law.
The observations behind the estimated spectral indices in
Table 1
were obtained using many different
techniques, which can explain at least part of the differences.
The procedure for dereddening also has strong effects on the deduced
values.
Sollerman et al. (2000, hereafter
S00) derived a value for the reddening towards the Crab
pulsar of
E(B-V)=0.52 mag,
by smoothing out the 2200 ![]() dust feature in the near-UV,
and show that within reasonable limits their spectral index had error
bars of
dust feature in the near-UV,
and show that within reasonable limits their spectral index had error
bars of ![]() 0.2
due to the uncertainty in extinction.
0.2
due to the uncertainty in extinction.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{14049fig2.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14049-10/Timg12.png)
|
Figure 2: Multiwavelength spectrum of the Crab pulsar. This figure is partly adopted from Serafimovich et al. (2004), with the data from SS09 added. |
| Open with DEXTER | |
A general trend among the measurements in Table 1
is a lower value of ![]() for higher frequencies. S00 derived
for higher frequencies. S00 derived ![]() for the UV-optical range, whereas the UV alone
had a spectral index that was essentially flat.
The SED of the Crab pulsar thus seems to level out
(and peak, see Fig. 2)
somewhere in the ultraviolet, and the wavelength range will
therefore also be an important factor for the derived value of
for the UV-optical range, whereas the UV alone
had a spectral index that was essentially flat.
The SED of the Crab pulsar thus seems to level out
(and peak, see Fig. 2)
somewhere in the ultraviolet, and the wavelength range will
therefore also be an important factor for the derived value of ![]() .
.
Table 1:
Summary of previous observations of the spectral index ![]() of the Crab pulsar.
of the Crab pulsar.
Another large uncertainty in determining the shape of the
pulsar spectrum
comes from the difficulties in subtracting the nebular contribution.
Some of the measurements have
used time-resolved data to estimate the phase-averaged spectral index,
while most observations have been time-integrated making them
susceptible to bad seeing.
In, Beskin & Neustroev (2001),
among others, the spectrum
displays clear residuals from nebular subtraction.
Since the surrounding nebula appears redder than the pulsar at these
wavelengths
(e.g. Tziamtzis et al. 2009),
observations at mediocre seeing may
result in a redder spectral index.
In particular, all time-integrated estimates for ![]() also include contributions from the nearby
(
also include contributions from the nearby
(
![]() )
knot (Hester et al. 1995).
The knot is known to be a very red feature (
)
knot (Hester et al. 1995).
The knot is known to be a very red feature (
![]() )
and also to be variable over time (Sollerman
2003; SS09). The knot may thus also have affected these
measurements in different ways, depending on how much of the knot has
been included and on how strong this feature was at the time of
observation.
)
and also to be variable over time (Sollerman
2003; SS09). The knot may thus also have affected these
measurements in different ways, depending on how much of the knot has
been included and on how strong this feature was at the time of
observation.
It is not clear whether the knot could contribute
significantly to the
emission seen in the mid-IR regime.
By extrapolating a conservative spectral index for the knot
of ![]() into this regime, we can estimate that the pulsar optical
spectral index continues at least to a frequency of
into this regime, we can estimate that the pulsar optical
spectral index continues at least to a frequency of ![]() ,
and we use this number below as an upper limit for the synchrotron
self-absorption frequency (
,
and we use this number below as an upper limit for the synchrotron
self-absorption frequency (
![]() ).
).
There is an offset in Fig. 1 between the infrared flux measured with ground-based observations using NACO (SS09) and the space-based Spitzer data. This is likely the result of problems with absolute flux calibration between different instruments. The complex background inside the Crab Nebula make the resolution important for correctly sampling the contribution of the spatially varying nebular background close to the pulsar. Clearly, the actual shape of the SED from the Spitzer measurements is less affected than the absolute flux.
We argue, thus, that the simplest possible picture for the
knot-subtracted pulsar SED is that it can
be described as a single power law
below the UV (optical towards infrared) and that the value of
![]() is consistent with the
multitude of published observations of the Crab pulsar.
The best value in the
optical-IR regime is
is consistent with the
multitude of published observations of the Crab pulsar.
The best value in the
optical-IR regime is ![]() (SS09), where
emission from the knot has been subtracted. Figure 1 shows the best
fit of a spectral index of
(SS09), where
emission from the knot has been subtracted. Figure 1 shows the best
fit of a spectral index of
![]() to the observations of SS09, including the near-UV spectrum from S00.
to the observations of SS09, including the near-UV spectrum from S00.
Figure 2
shows a multiwavelength, phase-averaged spectrum of the Crab pulsar.
From this spectrum, we estimated that the
peak of the emission lies at a frequency of ![]() .
This peak frequency is also used below to derive constraints on the
emission model.
.
This peak frequency is also used below to derive constraints on the
emission model.
2.2 Temporal resolution of the pulse
Another restriction on pulsar emission theory that is important for our
purposes is given
by the temporal extent and shape of the pulse peaks.
Early data from Papaliolios et
al. (1970) described a cusp-like behaviour of the pulse at a
resolution of 32 ![]() s.
More recent data, with a much better time resolution of only
s.
More recent data, with a much better time resolution of only ![]() 1
1 ![]() s, instead
give an approximation
of the temporal extent of the plateau on the main pulse of
s, instead
give an approximation
of the temporal extent of the plateau on the main pulse of ![]() 55
55 ![]() s (Golden et al. 2000).
s (Golden et al. 2000).
3 Incoherent synchrotron models
The spectral shape of the emission from the Crab pulsar is thus
consistent with incoherent synchrotron radiation from a distribution of
relativistic electrons with a sharp low-energy cut-off. For the
rotation of the neutron star to give rise to pulses, relativistic
beaming is necessary. We denote the frame, in which the total momentum
of the relativistic electrons is zero (i.e., the no-streaming frame),
with a prime (') and let ![]() be the Lorentz factor of this frame as measured in the observer's
frame.
be the Lorentz factor of this frame as measured in the observer's
frame.
A few standard approximations are useful to simplify the
treatment: (1) the electron distribution is isotropic and
mono-energetic in the primed frame with an electron energy
corresponding to a Lorentz factor ![]() ;
(2) the intensity leaving the source is confined within a cone with
opening angle
;
(2) the intensity leaving the source is confined within a cone with
opening angle ![]() .
Inside this cone, the intensity is constant; (3) frequencies in the two
frames are related by
.
Inside this cone, the intensity is constant; (3) frequencies in the two
frames are related by ![]() .
Furthermore,
.
Furthermore, ![]() is assumed.
is assumed.
The observed intensity is then (e.g., Pacholczyk
1970)
where
where d is the distance to the pulsar.
3.1 Emission from within the light cylinder
Since the magnetic field is dynamically dominant in this case, the
particles are streaming along the magnetic field lines with a Lorentz
factor ![]() .
Let
.
Let ![]() denote the radius of curvature of the magnetic field. The distance over
which particles and radiation can interact is then
denote the radius of curvature of the magnetic field. The distance over
which particles and radiation can interact is then ![]() ,
which implies a column density of particles given by
,
which implies a column density of particles given by ![]() ,
where n is the number density of particles.
However, due to the relativistic streaming of the particles, the
emitted photons experience only a fraction
,
where n is the number density of particles.
However, due to the relativistic streaming of the particles, the
emitted photons experience only a fraction ![]() of this column density. The optical depth, which is a relativistic
invariant, is (e.g., Pacholczyk 1970)
of this column density. The optical depth, which is a relativistic
invariant, is (e.g., Pacholczyk 1970)
Here,
With the use of ![]() ,
the optical depth can also be expressed as
,
the optical depth can also be expressed as
where
where
The value of
The flux at ![]() is obtained from
is obtained from
where
Expressions for R and
and
For the values of
and
Here,
As discussed above, ![]() is expected. From the discussion in Sect. 2,
is expected. From the discussion in Sect. 2, ![]() and the observed minimum pulse structure of
and the observed minimum pulse structure of ![]() 55
55 ![]() s corresponds to
s corresponds to ![]() (Golden et al. 2000). It is
likely that the X-ray flux is a continuation of the optical emission
(see Fig. 2),
i.e., that
(Golden et al. 2000). It is
likely that the X-ray flux is a continuation of the optical emission
(see Fig. 2),
i.e., that ![]() is the low-energy cut-off of a power-law distribution of electron
energies. As a result,
is the low-energy cut-off of a power-law distribution of electron
energies. As a result, ![]() and Fig. 2
suggests
and Fig. 2
suggests ![]() for a
for a ![]() -spectrum
in the optical frequency range. The peak flux in a single pulse was
estimated from Fig. 2,
together with the pulse profile in S00, to be 43 mJy
at
-spectrum
in the optical frequency range. The peak flux in a single pulse was
estimated from Fig. 2,
together with the pulse profile in S00, to be 43 mJy
at ![]() Hz. Extrapolating
this value to
Hz. Extrapolating
this value to ![]() results in
results in ![]() .
When these values are inserted into Eq. (11), one obtains
.
When these values are inserted into Eq. (11), one obtains
The value of
The conclusion regarding the upper limit for the value of
Independent of the detailed physics (i.e., the value of
One implicit assumption underlying the results in
Eqs. (13)
and (14)
is that the pulse profile is independent of frequency. Although the
minimum pulse structure, as well as the full width half maximum (FWHM)
are consistent with being constant in the UBV-range, there is an
indication of a decreasing FWHM with frequency (e.g., Golden et al. 2000). The
suggested variation is small enough to be caused by the relativistic
streaming itself, since it induces an anti-correlation between
frequency and angular width. If real, this variation could indicate
that the value of ![]() is not much higher than
is not much higher than ![]() .
Furthermore, a pulse profile varying with frequency would result in an
observed spectrum flatter than the intrinsic one due to overlapping
emission regions. Since observations of the Crab pulsar are consistent
with a
.
Furthermore, a pulse profile varying with frequency would result in an
observed spectrum flatter than the intrinsic one due to overlapping
emission regions. Since observations of the Crab pulsar are consistent
with a ![]() -spectrum,
this limits the magnitude of possible frequency variations of the
pulsar profile in a synchrotron scenario.
-spectrum,
this limits the magnitude of possible frequency variations of the
pulsar profile in a synchrotron scenario.
It should also be remembered that the low-frequency part of
the pulsar spectrum shown in Fig. 1, hence, the
value of ![]() used above, is from Spitzer-observations. Since
these data cannot resolve individual pulses, it could be that this
emission is not pulsed. Although there are no indications that this is
the case, a conservative approach is therefore to use only the
NACO-data, since Eikenberry et
al. (1997) have shown that the pulse profiles in
used above, is from Spitzer-observations. Since
these data cannot resolve individual pulses, it could be that this
emission is not pulsed. Although there are no indications that this is
the case, a conservative approach is therefore to use only the
NACO-data, since Eikenberry et
al. (1997) have shown that the pulse profiles in ![]() are similar to the optical ones. Taking the K-band
observations as the lower limit to the pulsed emission would increase
the value of
are similar to the optical ones. Taking the K-band
observations as the lower limit to the pulsed emission would increase
the value of ![]() by a factor
by a factor ![]() 3.
As can be seen from Eqs. (11)
and (12),
the limits of
3.
As can be seen from Eqs. (11)
and (12),
the limits of ![]() and
and ![]() are then changed only by a factor
are then changed only by a factor ![]() 2. Neither the possible
frequency dependence of the pulsar profile nor the unconstrained nature
of the emission measured by Spitzer is therefore
likely to substantially change the conclusion about the location of the
emission region.
2. Neither the possible
frequency dependence of the pulsar profile nor the unconstrained nature
of the emission measured by Spitzer is therefore
likely to substantially change the conclusion about the location of the
emission region.
The above discussion assumes that ![]() is either the Lorentz factor of a mono-energetic electron distribution
or the low-energy cut-off in a power-law distribution of electron
energies. The reason for this choice is that the observed
infrared-optical flux from the Crab pulsar increases with frequency
consistent with a
is either the Lorentz factor of a mono-energetic electron distribution
or the low-energy cut-off in a power-law distribution of electron
energies. The reason for this choice is that the observed
infrared-optical flux from the Crab pulsar increases with frequency
consistent with a ![]() -spectrum.
However, as discussed in Sect. 2,
a flatter spectrum cannot be excluded. The brightness temperature at
-spectrum.
However, as discussed in Sect. 2,
a flatter spectrum cannot be excluded. The brightness temperature at ![]() is proportional to
is proportional to ![]() .
A spectrum flatter than
.
A spectrum flatter than ![]() would, therefore, decrease the brightness temperature at
would, therefore, decrease the brightness temperature at ![]() ,
since it will be determined by electrons with Lorentz factors
,
since it will be determined by electrons with Lorentz factors ![]() .
Furthermore, for a given value of peak luminosity (i.e.,
.
Furthermore, for a given value of peak luminosity (i.e., ![]() ), the flux
below the peak frequency (i.e.,
), the flux
below the peak frequency (i.e., ![]() )
would be larger than in the
)
would be larger than in the ![]() case. Both of these effects result in an increase in the lower limit of
case. Both of these effects result in an increase in the lower limit of
![]() ,
as well as a decrease in the upper limit of
,
as well as a decrease in the upper limit of ![]() .
Since a
.
Since a ![]() -spectrum
is the hardest possible for optically thin synchrotron radiation, a
spectrum flatter than this would strengthen the above conclusions.
-spectrum
is the hardest possible for optically thin synchrotron radiation, a
spectrum flatter than this would strengthen the above conclusions.
3.2 Emission from the light cylinder
An alternative site for the pulsed emission is close to the light
cylinder. The physical setting is here considerably more uncertain than
for emission from within the light cylinder; for example, the energy
densities in particles and electric field are expected to be of the
same magnitude as that in the magnetic field. This could affect both
the emission process and the beaming of the radiation in several ways.
Both of these effects are crucially dependent on the details of the
particle motion. To allow a simplified discussion of these issues, the
motion of the particles is divided into three components: (1) random
motion in the zero-momentum (i.e., primed) frame in addition to the
gyration of the particles around the magnetic field (
![]() ); (2) streaming or bulk
motion as measured in the frame co-rotating with the neutron star (
); (2) streaming or bulk
motion as measured in the frame co-rotating with the neutron star (
![]() ). In the observer's frame,
this component differs from that in Sect. 3.1 mainly because
of the importance of aberration effects, which make it likely that the
motion is at large angles to the magnetic field; (3) the motion due to
the rotation of the neutron star (
). In the observer's frame,
this component differs from that in Sect. 3.1 mainly because
of the importance of aberration effects, which make it likely that the
motion is at large angles to the magnetic field; (3) the motion due to
the rotation of the neutron star (
![]() ).
).
The origin of ![]() could be small-scale irregularities in the magnetic and/or the electric
field. Such deviations from pure gyration in the large-scale magnetic
field mainly affect the low-frequency emission from an individual
particle. An example of such a situation is ``jitter'' radiation (Medvedev 2000), which corresponds to
small-scale magnetic irregularities. As shown by Medvedev
(2000), the low-frequency part of the spectrum is determined
by the statistical properties of the magnetic field; in particular, the
spectral distribution is expected to differ substantially from the
synchrotron case (e.g., ``jitter'' radiation has
could be small-scale irregularities in the magnetic and/or the electric
field. Such deviations from pure gyration in the large-scale magnetic
field mainly affect the low-frequency emission from an individual
particle. An example of such a situation is ``jitter'' radiation (Medvedev 2000), which corresponds to
small-scale magnetic irregularities. As shown by Medvedev
(2000), the low-frequency part of the spectrum is determined
by the statistical properties of the magnetic field; in particular, the
spectral distribution is expected to differ substantially from the
synchrotron case (e.g., ``jitter'' radiation has ![]() as compared to
as compared to ![]() for the synchrotron case). Although the statistical properties of
possible small-scale irregularities close to the light cylinder are
hard to predict, it is unlikely that they would result in a spectral
index close to that of synchrotron radiation. The observation of a
spectral index for the Crab pulsar close to
for the synchrotron case). Although the statistical properties of
possible small-scale irregularities close to the light cylinder are
hard to predict, it is unlikely that they would result in a spectral
index close to that of synchrotron radiation. The observation of a
spectral index for the Crab pulsar close to ![]() therefore suggests that
therefore suggests that ![]() does not seriously affect the emission from individual particles and,
in particular, that the basic frequency is the cyclotron one.
does not seriously affect the emission from individual particles and,
in particular, that the basic frequency is the cyclotron one.
A situation where ![]() plays a significant role is similar to the one discussed in
Sect. 3.1.
There are two main differences: (1) the angle
plays a significant role is similar to the one discussed in
Sect. 3.1.
There are two main differences: (1) the angle ![]() does not correspond to the angular distance of the emission site from
the magnetic axis; instead,
does not correspond to the angular distance of the emission site from
the magnetic axis; instead, ![]() is now a free parameter determining the value of
is now a free parameter determining the value of ![]() ;
(2) the energy density associated with the magnetic field (
;
(2) the energy density associated with the magnetic field (
![]() )
is not necessarily an invariant even for Lorentz boosts along the
magnetic field lines. Both of these effects are contained in the factor
)
is not necessarily an invariant even for Lorentz boosts along the
magnetic field lines. Both of these effects are contained in the factor
![]() (cf.
Eqs. (11)
and (12)).
As already emphasized, by suitably varying the value of this factor,
the limit for either
(cf.
Eqs. (11)
and (12)).
As already emphasized, by suitably varying the value of this factor,
the limit for either ![]() or
or ![]() can be made to come closer to what is expected for a source distance
corresponding to the light cylinder radius; however, this occurs at the
expense of the other limit, which will then correspond to an even
greater distance to the emission region (cf. Eq. (15)). The physical
differences in this case are therefore not expected to affect the main
conclusions from Sect. 3.1.
can be made to come closer to what is expected for a source distance
corresponding to the light cylinder radius; however, this occurs at the
expense of the other limit, which will then correspond to an even
greater distance to the emission region (cf. Eq. (15)). The physical
differences in this case are therefore not expected to affect the main
conclusions from Sect. 3.1.
When the effects of ![]() are negligible, the pulsar profile is mainly determined by rotation and
are negligible, the pulsar profile is mainly determined by rotation and
![]() .
Since the emission site is now moving towards the observer, the
observed duration of a pulse is
.
Since the emission site is now moving towards the observer, the
observed duration of a pulse is
where
For an emission site in the vicinity of the last closed magnetic field
lines, one expects ![]() and
and ![]() .
In the general case when both
.
In the general case when both ![]() and
and ![]() contribute to the effective value of
contribute to the effective value of ![]() ,
the result is expected to fall in between the two extremes discussed
above. It is clear that the lower value of
,
the result is expected to fall in between the two extremes discussed
above. It is clear that the lower value of ![]() in the rotational scenario contributes most to diminishing the
discrepancies between the expected values for
in the rotational scenario contributes most to diminishing the
discrepancies between the expected values for ![]() and
and ![]() and their lower and upper limits, respectively, derived from
observations; for example, the lower value of
and their lower and upper limits, respectively, derived from
observations; for example, the lower value of ![]() reduces the lower limit of
reduces the lower limit of ![]() by a factor
by a factor ![]() 10
and only marginally decreases the upper limit on
10
and only marginally decreases the upper limit on ![]() .
However, even in this case, the lower limit of R
is a factor
.
However, even in this case, the lower limit of R
is a factor ![]() 2
larger than
2
larger than ![]() ,
while the upper limit of the magnetic field is a factor
,
while the upper limit of the magnetic field is a factor ![]() 10 smaller
than expected for an emission site close to the light cylinder.
Therefore, even with the low value of
10 smaller
than expected for an emission site close to the light cylinder.
Therefore, even with the low value of ![]() allowed by the rotational scenario, it is not straightforward to make
an emission site close to the light cylinder consistent with
observations.
allowed by the rotational scenario, it is not straightforward to make
an emission site close to the light cylinder consistent with
observations.
4 Discussion
Several explicit scenarios for the emission site of the Crab pulsar
have been developed in the past, including the outer gap model
(Cheng et al. 1986) and the
polar cap model (e.g., Harding 1981).
In this paper we have instead focused on the fundamental constraints
inherent to any synchrotron emission model.
The main result from Sect. 3
is that, in the incoherent synchrotron scenario, the implied distance
to the emission region is considerably greater than the light cylinder
radius. This conclusion is supported by two independent pieces of
evidence; namely, a direct lower limit of the distance and an indirect
one through the upper limit to the magnetic field strength. Most of the
uncertain physics is contained in one parameter, which affects these
limits in the same way. By changing its value, one of the limits will
indicate a shorter distance to the emission site, while, at the same
time, the other limit would suggest an even greater distance. It is
therefore impossible to make both limits compatible with a distance
comparable to or shorter than the light cylinder radius by invoking a
particular value for this parameter (cf. Eq. (15)). Furthermore,
these limits are quite robust; in particular, both of them are valid
using anyone of three independent observations: (1) the upper limit on
the self-absorption frequency (
![]() ); (2) the upper
limit on the spectral index (i.e., a
); (2) the upper
limit on the spectral index (i.e., a ![]() -spectrum); or
(3) the lower limit on the streaming (
-spectrum); or
(3) the lower limit on the streaming (
![]() )
obtained from the pulse profile.
)
obtained from the pulse profile.
Although the distance to the emission region may be much
greater than the light cylinder radius (i.e., ![]() ),
it can still be situated within the light cylinder. This requires a
small inclination angle (i) between the rotation and
magnetic axes. The allowed values for i are bounded
from below (
),
it can still be situated within the light cylinder. This requires a
small inclination angle (i) between the rotation and
magnetic axes. The allowed values for i are bounded
from below (
![]() )
to assure pulsed emission and from above (
)
to assure pulsed emission and from above (
![]() )
by the requirement that the emission region lies within the light
cylinder. These inequalities are satisfied in the streaming scenario,
since
)
by the requirement that the emission region lies within the light
cylinder. These inequalities are satisfied in the streaming scenario,
since ![]() is needed for the lateral extent of the emission region to be less than
the light cylinder radius. It is seen from Eq. (11) that
is needed for the lateral extent of the emission region to be less than
the light cylinder radius. It is seen from Eq. (11) that ![]() is possible for
is possible for ![]() .
A streaming scenario together with a small inclination angle are
therefore compatible with observations but certainly for much smaller
inclinations than typically envisioned in most models for an oblique
rotator (e.g., Cheng et al. 1986).
.
A streaming scenario together with a small inclination angle are
therefore compatible with observations but certainly for much smaller
inclinations than typically envisioned in most models for an oblique
rotator (e.g., Cheng et al. 1986).
The constraints imposed by observations on an emission region
located close to the light cylinder are qualitatively similar to those
corresponding to streaming along the magnetic field lines within the
pulsar magnetosphere. In models with the emission site in the vicinity
of the last closed magnetic field lines, ![]() is expected; as a result, small inclination angles cannot be invoked to
make such scenarios compatible with observations. The limits discussed
above for the distance to the emission region hinge on the size of the
emitting surface and it was argued that an upper bound to this size
could be found in the streaming scenario. A similar upper bound is also
likely to apply to emission sites close to the light cylinder, in which
case such models would be untenable. However, the magnetospheric
properties in the vicinity of the light cylinder remain rather
uncertain, which leaves open the possibility that this upper bound
could be exceeded.
is expected; as a result, small inclination angles cannot be invoked to
make such scenarios compatible with observations. The limits discussed
above for the distance to the emission region hinge on the size of the
emitting surface and it was argued that an upper bound to this size
could be found in the streaming scenario. A similar upper bound is also
likely to apply to emission sites close to the light cylinder, in which
case such models would be untenable. However, the magnetospheric
properties in the vicinity of the light cylinder remain rather
uncertain, which leaves open the possibility that this upper bound
could be exceeded.
The restrictions on potential incoherent synchrotron models are quite severe. The main problem afflicting them is that their maximum brightness temperature is too low to easily fit the emission region inside the light cylinder. The brightness temperature can be increased by invoking coherent/amplified radiation. An alternative that would preserve many of the attractive features of the standard synchrotron scenario is, therefore, coherent/amplified synchrotron radiation. The conditions needed for synchrotron radiation to be amplified within a pulsar magnetosphere have been discussed by Stoneham (1982). In this case, the emission would likely come from well within the light cylinder and a connection to the radio emission is possible. Anotherpossibility is emission regions located outside the light cylinder. Lerche (1970) has considered a scenario, in which the dipole field of the rotating neutron star induces oscillations at the interface with an external plasma. Although the properties of the synchrotron-like emission expected from such models have not been worked out in any detail, their applicability should not be constrained by the size of the emission region.
AcknowledgementsThis research was supported by grants from the Swedish Natural Science Research Council. The Oskar Klein Centre is also funded by the Swedish Natural Science Research Council. The Dark Cosmology Centre is funded by the Danish National Research Foundation. J.S. is a Royal Swedish Academy of Sciences Research Fellow supported by a grant from the Knut and Alice Wallenberg Foundation. We would also like to thank the referee, Marco Salvati, for a thorough reading of the manuscript, as well as many constructive comments, that helped to improve the paper substantially.
References
- Beskin, G. M., & Neustroev, V. V. 2001, A&A, 374, 584 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carramiñana, A., Cadez, A., & Zwitter, T. 2000, ApJ, 542, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Ho, C., & Ruderman, M. 1986, ApJ, 300, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Crusius-Wätzel, A. R., Kunzl, T., & Lesch, H. 2001, ApJ, 546, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Eikenberry, S. S., Fazio, G. G., Ransom, S. M., et al. 1997, ApJ, 477, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Epstein, R. I., & Petrosian, V. 1973 ApJ, 183, 611 [Google Scholar]
- Fordham, J. L. A., Vranesevic, N., Carramiñana, A., et al. 2002, ApJ, 581, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Gull, T. R., Lindler, D. J., Crenshaw, D. M., et al. 1998, ApJ, 495, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Golden, A., Shearer, A., Redfern, R. M., et al. 2000, A&A, 363, 617 [NASA ADS] [Google Scholar]
- Harding, A. K. 1981, ApJ, 245, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Hester, J. J., Scowen, P. A., Sankrit, R., et al. 1995, ApJ, 448, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, L., Hermsen, W., Cusumano, G., et al. 2001, A&A, 378, 918 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lerche, I. 1970, ApJ, 162, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Medvedev, M. 2000, ApJ, 540, 704 [Google Scholar]
- Middleditch, J., Pennypacker, C., & Burns, M. S. 1983, ApJ, 273, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Nasuti, F. P., Mignani, R., Caraveo, P. A., & Bignami, G. F. 1996, A&A, 314, 849 [NASA ADS] [Google Scholar]
- O'Connor, P., Golden, A., & Shearer, A. 2005, ApJ, 631, 471 [NASA ADS] [CrossRef] [Google Scholar]
- O'Dell, S. L., & Sartori, L. 1970, ApJ, 161, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Pacholczyk, A. G. 1970, Radio Astrophysics (San Francisco: Freeman) [Google Scholar]
- Pacini, F. 1971, ApJ, 163, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Pacini, F., & Salvati, M. 1983, ApJ, 274, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Pacini, F., & Salvati, M. 1987, ApJ, 321, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Papaliolios, C., Carleton, N. P., & Horowitz, P. 1970, Nature, 228, 445 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Penny, A. J. 1982, MNRAS, 198, 773 [NASA ADS] [Google Scholar]
- Percival, J. W., Biggs, J. D., Dolan, J. F., et al. 1993, ApJ, 407, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Sandberg, A., & Sollerman, J. 2009, A&A, 504, 525 (SS09) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serafimovich, N. I., Shibanov, Y. A., Lundqvist, P., & Sollerman, J. 2004, A&A, 425, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shklovsky, I. S. 1970, ApJ, 159, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Sollerman, J. 2003, A&A, 406, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sollerman, J., Lundqvist, P., Lindler, D., et al. 2000, ApJ, 537, 861 (S00) [NASA ADS] [CrossRef] [Google Scholar]
- Stoneham, R. J. 1982, MNRAS, 199, 219 [Google Scholar]
- Temim, T., Gehrz, R. D., Woodward, C. E., et al. 2006, AJ, 132, 1610 [NASA ADS] [CrossRef] [Google Scholar]
- Temim, T., Gehrz, R. D., Woodward, C. E., et al. 2009, AJ, 137, 5155 [NASA ADS] [CrossRef] [Google Scholar]
- Tziamtzis, A., Schirmer, M., Lundqvist, P., & Sollerman, J. 2009, A&A, 497, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Table 1:
Summary of previous observations of the spectral index ![]() of the Crab pulsar.
of the Crab pulsar.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{14049fig1.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14049-10/Timg9.png)
|
Figure 1:
Best fit of an |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{14049fig2.eps}
\end{figure}](/articles/aa/full_html/2010/08/aa14049-10/Timg12.png)
|
Figure 2: Multiwavelength spectrum of the Crab pulsar. This figure is partly adopted from Serafimovich et al. (2004), with the data from SS09 added. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}I(\nu) = \frac{3}{2} m \nu^{2} \gamma [1-\exp(-\tau)],
\end{displaymath}](/articles/aa/full_html/2010/08/aa14049-10/img39.png)
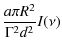
![$\displaystyle \frac{3a \pi R^2}{2 d^2} m \nu^2 \frac{\gamma_{\rm me}'}{\Gamma}[1-\exp(-\tau)],$](/articles/aa/full_html/2010/08/aa14049-10/img46.png)