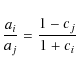The stability of ultra-compact planetary systems

B. Funk; G. Wuchterl; R. Schwarz; E. Pilat-Lohinger; S. Eggl

doi:10.1051/0004-6361/200912698

Free Access

Issue		A&A Volume 516, June-July 2010


Article Number		A82
Number of page(s)		6
Section		Planets and planetary systems
DOI		https://doi.org/10.1051/0004-6361/200912698
Published online		19 July 2010

A&A 516, A82 (2010)

The stability of ultra-compact planetary systems

B. Funk¹ - G. Wuchterl² - R. Schwarz^1,3 - E. Pilat-Lohinger³ - S. Eggl³

1 - Department of Astronomy, Eötvös Loránd University, Pázmány Péter Sétány 1/A, 1117 Budapest, Hungary
2 - Thüringer Landessternwarte, Sternwarte 5, 07778 Tautenburg, Germany
3 - Institute for Astronomy, University of Vienna, Türkenschanzstrasse 17, 1180 Vienna, Austria

Received 15 June 2009 / Accepted 15 March 2010

Abstract
Aims. We investigate the dynamical stability of compact planetary systems in the CoRoT discovery space, i.e., with orbital periods of less than 50 days, including a detailed study of the stability of systems, which are spaced according to Hill's criteria.
Methods. The innermost fictitious planet was placed close to the Roche limit from the star ( $M_{{\rm Star}} = 1~M_{{\rm Sun}}$ ) and all other fictitious planets are lined up according to Hill's criteria up to a distance of 0.26 AU, which corresponds to a 50 day period for a Sun-massed star. For the masses of the fictitious planets, we chose a range of 0.33-17 $m_{{\rm Earth}}$ , where in each simulation all fictitious planets have the same mass. Additionally, we tested the influence of both the semi-major axis of the innermost planet and of the number of planets. In a next step we also included a gas giant in our calculations, which perturbs the inner ones and investigated their stability.
Results. With numerous integrations of many different configurations we could show that long-time stable motion is possible for up to 10 planets with 17 $m_{{\rm Earth}}$ within a distance of 0.26 AU. Further investigations show that the fictitious planets remain stable under certain circumstances even if a close-in gas giant is present.

Key words: planets and satellites: general - celestial mechanics

1 Introduction

For more than one decade of ground-based observations of extra-solar planets, the radial velocity (RV) method dominated the exciting search for far away planetary systems. Nowadays, another observational method - the transit method - gains importance from the discoveries of the space mission CoRoT (see e.g. Baglin et al. 2006; Barge et al. 2008). CoRoT searches for short-period planets with a maximum period of 50 days, which approximately corresponds to a maximum distance of 0.26 AU to a Sun-massed host star.

The stability of such close-in planets is the subject of the present paper, which studies fictitious planetary systems, where several (up to 10) planets move in the discovery space of CoRoT. While CoRoT 7 b was discovered by the CoRoT satellite (see Léger et al. 2009; and Bouchy et al. 2009), CoRoT 7 c was found through follow-up observations by the radial velocity technique (see Queloz et al. 2009). The host star has a mass of 0.93 $M_{\rm Sun}$ , so that both planets lie within a 50-day period ( $\approx$ 0.26 AU) radius. The parameters of the CoRoT 7 b system are summarized in Table 1, where we list additional close-in multiplanetary systems that have been discovered so far. In the case of Gliese 581, the host star has just a mass of 0.31 $m_{\rm Sun}$ , which leads to a distance of 0.18 AU for a 50-day period. Three of the known planets are within this distance and extremely tightly packed, and even the fourth planet lies just slightly outside 0.18 AU. With a mass of 0.32 $m_{\rm Sun}$ , Gliese 876 habours two planets within and one planet slightly outside a 50-day period's orbit. For such low-mass M-stars even the habitable zone lies partly within the discovery space of CoRoT. A dynamical study of the orbital stability of planets inside the habitable zone of M-stars was done by Schwarz et al. (2010). Finally in the case of HD 40307, all three known planets clearly lie inside a 50-day period ( $\approx$ 0.24 AU for a host stars mass of 0.77 $M_{\rm Sun}$ ).

It is also worth mentioning the existence of hot Jupiters (Gliese 876) or at least quite massive planets (Gliese 581) inside the orbits of terrestrial planets. Many articles dealing with the formation of such systems have shown, that the existence of a hot Jupiter does not necessarily mean there are no terrestrial planets farther out (e.g. Fogg & Nelson 2007, 2009; Raymond et al. 2008; Raymond 2008).

Encouraged by the existence of such systems, the goal of our work was to find out how many planets can populate a system with a maximum period of 50 days. Therefore we created compact close-in planetary systems of terrestrial planets with masses up to 30 Earth masses ( $m_{{\rm Earth}}$ ) around a solar massed star and studied the gravitational interactions in this region.

Table 1: Example systems with known close-in planets.

In a first attempt our fictitious systems consisted of equal-mass-planets, where we used 4, 17, or 30 $m_{{\rm Earth}}$ in different numerical runs to generate information on the number of small planets that could hide in the area observed by CoRoT.

Applying Hill's radius criteria, we placed as many equal massed fictitious planets in the region from 0.01 AU to 0.26 AU as possible, and studied the stability of the systems via numerical orbital integration up to 10⁶ years. Earlier studies have already shown that placing planets according to Hill's criteria leads - depending on a parameter k - either to stable or unstable motion. Chambers et al. (1996) found that the stability time can be estimated with the following formula (in the case of a system of 10 planets):

$\begin{displaymath}\log t = (0.756\pm0.027) k - (0.358\pm0.176). \end{displaymath}$

(1)

In their work different numbers of planets were placed according to Hill's criteria starting at 1 AU. In our study we derive and compare a similar formula for close-in planetary systems complementing real planetary masses.

In a second step we included a gas giant (GG) of 1 Jupiter-mass ( $m_{\rm Jup}$ ) in the system, moving at distances from the host star between 0.3 and 0.5 AU and examined its perturbation on the compact close-in planetary system. Finally, we calculated planetary systems, where a GG (of 0.5-6.5 $m_{\rm Jup}$ ) was placed in an orbit with a 50-day period and an eccentricity between 0 to 0.26 and determined the stable region for small planets orbiting the host-star within the CoRoT discovery space.

Before presenting the results, we will discuss Hill's criteria in Sect. 2 and the dynamical model and methods in Sect. 3.

2 Hill's criteria and number of planets

Hill's exclusion criteria offer a convenient rough proxy for the stability of planetary systems, such as in Hayes & Tremaine (1998). In its simplest form for planets of equal mass, m_i=m on circular orbits around a stellar mass, M, with semi-major axes a_i it requires for the separation $\Delta a_i = a_{i+1} - a_{i}$ of two adjacent orbital radii to fulfill

$\begin{displaymath}a_{i+1} = a_i + 2 k R_{\rm Hill}. \end{displaymath}$

(2)

This expresses that spherical volumes of k times Hill's radius, centred on each one of the two neighbouring planets, must never overlap. The factor k is typically 4-15. It depends on the structure of the systems, in particular the number of planets, and is used to include stability-properties that go beyond the simple scaling considerations; see Smith & Lissauer (2009) for recent determinations relevant to our context here. For small orbital separations, we clearly see the mass-dependency due to $R_{\rm Hill} = a_i (m/(3M))^{1/3}$ :

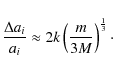
$\begin{displaymath}\frac{\Delta a_i}{a_i} \approx 2 k \left(\frac{m}{3M}\right)^\frac{1}{3}\cdot \end{displaymath}$

(3)

It shows the well known fact that stable systems allow closer spacings for lower mass planets. Using Kepler's third law in its log-differential version, ${\rm d} \ln P = 3/2 ~ {\rm d} \ln a$ , we obtain for the periods, P_i of low-mass planetary systems:

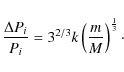
$\begin{displaymath}\frac{\Delta P_i}{P_i} = 3^{2/3} k \left(\frac{m}{M}\right)^\frac{1}{3}\cdot \end{displaymath}$

(4)

The above expression gives the relative change in period from one planet to the next, thus the inverse, $(\Delta P_i/P_i)^{-1}$ , gives the period scaling for the number of planets, i.e., in the differential form the increase of planet number per e-folding of the orbital period. Integrating of ${\rm d} \ln P$ for a range in period (or semi-major axis) gives the respective maximum total number of (low-mass) planets that can be sustained in a stable planetary system of equally massed planets in the period-range $[P_{\rm l},P_{\rm u}]$ :

$\begin{displaymath}n \!=\! \frac{1}{3^{2/3} k} \left(\frac{M}{m}\right)^{\frac{1... ... \frac{m}{[M_\oplus]}\right)^{-\frac{1}{3}} \! \Delta \lg P. ~ \end{displaymath}$

(5)

For CoRoT, $P_{\rm l}$ is typically 0.5 d (Roche-limit of a solar-mass star) and $P_{\rm u}$ is about 50 d owing to the requirement of detecting three planetary transits during a CoRoT-long-run with a duration of about 150 d. For k=8.5, respectively k=6.1, we estimate for the maximum total number of planets with 4 $m_{{\rm Earth}}$ on a circular orbit in the CoRoT-discovery space:

$\begin{displaymath}N_{\rm planet, [0.5,50] d} \approx 11 \rm ,~respectively \approx 15. \end{displaymath}$

(6)

The above considerations are rough approximations but serve as an overview of possible planetary system architectures in the CoRoT discovery space in particular when going down to terrestrial planet masses. The many simplifications make a detailed dynamical analysis necessary for checking whether the picture that is obtained is plausible. A key question when deriving characteristic spacings of planetary systems as above is that of characteristic planet masses. The classification of giant planet equilibria show a bimodal mass distribution in the CoRoT discovery space (Broeg 2007), that has been derived explicitly for the simple case of isothermal planets (Schönke 2007), and a mass scale is introduced by the feeding-zone mass in planetesimal disks also for terrestrial planets. Thus the study of equal-mass planet systems is physically plausible from planet formation considerations, because the planetary equilibria have typical masses in relatively narrow bins. The planetary system architecture may well be dominated by the dynamics rather than the mass-distributions.

2.1 Scalability

Let a_i and a_j be the semi-major axes of two adjacent planets i and j with masses m_i and m_j. Their mutual distance $\Delta a = a_j-a_i$ is determined by the sum of both planet's Hill's radii with respect to their host star with mass M. Let us further assume that a_j>a_i, $a_i\gg\Delta a$ , and M>m_i,m_j. Applying the definition of Hill's radius ( $R_{\rm Hill}$ ) from the previous section, one can easily derive

$\begin{displaymath}\frac{a_i}{a_j}=\frac{1-c_j}{1+c_i} \end{displaymath}$

(7)

with c_j the mass-dependent factor of $R_{\rm Hill,j}$ , namely ( $\frac{m_j}{3M})^{1/3}$ , and c_i the $i{\rm th}$ counterpart. For fixed mass ratios $\frac{m_i}{M},\frac{m_j}{M}$ , the fraction $\frac{a_i}{a_j}$ is therefore constant. Since this relation is valid for any pair of adjacent planets i,j, the problem can be considered scalable.

3 The dynamical model and methods

We performed long-term integrations up to 10⁶ years, which is equivalent to approximately 10⁹ periods for the innermost and $7 \times 10^{6}$ periods for the outermost planet. For these calculations we used two different dynamical models:

1.

In the first step, we integrated the orbits of fictitious planetary systems, consisting of a Sun-massed star and up to 20 massive fictitious planets ( 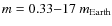$m = 0.33{-}17~m_{{\rm Earth}}$ ). All fictitious planets were lined according to Hill's criteria. To find out how many planets can be stable within a given region, we calculated their escape times for different values of the parameter k (see Sect. 4.1).

2.

In the next step, we perturbed the system with a GG and investigated two different models (see Sect. 4.2):

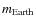
Configuration 1: consists of a Sun-massed star, 8 fictitious planets with 17 $m_{{\rm Earth}}$ lined according to Hill's criteria, and a GG. By varying the semi-major axis and the eccentricity of the GG, we analysed the interactions with the fictitious planets.
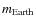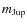Configuration 2: In the second model, we examine the case of a GG being detected at 0.26 AU. Therefore we investigate the stable region within this distance by again using Hill's criteria, starting from a = 0.01 AU. For the mass of the fictitious planets we again choose 17 $m_{{\rm Earth}}$ . The eccentricity of the GG was varied from 0.0 to 0.26 and its mass from 0.5 to 6.5 $m_{\rm Jup}$ .

All calculations were performed by direct numerical integrations with the Lie integration method (see Hanslmeier & Dvorak 1984; Lichtenegger 1984; Eggl 2010), which is able to deal with highly eccentric orbits and close encounters between the bodies. For all integrations without a perturbing GG, we defined the system as unstable, when the first major irregularities in the semi-major axis occurred.

For the systems with a perturbing GG we distinguished between stable and unstable motions by a direct test of the orbits using the eccentricity. This orbital element is a good indicator of the probability of orbital crossing and close encounters of two planets. We examined the behaviour of the eccentricity of the planet throughout the integration, and used the highest value denoted as maximum eccentricity. A low value indicates stable motion for the fictitious planet. A higher maximum eccentricity means that the fictitious planet is heavily perturbed and moves on a chaotic orbit. Such maximum eccentricity results were compared with results of different chaos indicators on many previous occations (see e.g. Érdi et al. 2004; Schwarz et al. 2007; Sándor et al. 2006), where the different results were in good agreement.

4 Results

4.1 Systems without a perturbing gas giant

As shown in Eq. (5) the number of stable orbits within a given region (in our case CoRoT's discovery space: 0.01-0.26 AU) depends on the masses of the star and the planets, on the semi-major axis of the innermost planet, and on the value of the parameter k. The smaller k, the more planets can be packed in the given region, yet the stability still needs to be checked for these configurations. To tackle the question of how sensitive such systems are at the starting positions (given by different mean anomalies M) of the fictitious planets, we performed two test runs, one with randomized mean anomalies and one where the mean anomalies of all planets were set to 0. Figure 3b shows the results for the first case and Fig. 1 the results for the second case.

$\begin{figure} \par\includegraphics[width=9cm,clip]{R12698fg1.eps} \end{figure}$

Figure 1:

Log t in dependence of k for a system of 10 fictitious planets with 17 $m_{{\rm Earth}}$ . All fictitious planets were started with mean anomaly = 0.

While one can see that the individual escape times may differ quite a lot, the overall structure, as well as the slope of the least squares fit, remains almost the same, so we decided to use single runs with randomized mean anomalies for the rest of the integrations.

In the next step we integrated three systems containing 10 planets using the parameters of Table 2 with lower mass ( m = 10^-7 $m_{\rm Sun}$ ) for different semi-major axis of the innermost planet ( a = 0.0207, 0.2, and 1.0 AU (Systems 1, 2, and 3)) to be able to compare our results with earlier results from Chambers et al. 1996 and test the predicted scalability of such systems (Figs. 2a-c). For the sake of comparability, we plotted the common logarithm of the escape times in periods of the innermost planet (log time) for all three systems.

Table 2: Initial conditions for the fictitious planets with 10^-7 $m_{\rm Sun}$ .

$\begin{figure} \par\includegraphics[width=9cm]{R12698fg2.eps}\par\includegraphics[width=9cm]{R12698fg3.eps}\par\includegraphics[width=9cm]{R12698fg4.eps} \end{figure}$

Figure 2:

log time in dependence of k for three systems with 10 planets each for different starting positions of the innermost planet: a) a = 0.0207 AU (System 1); b) a = 0.2 AU (System 2); c) a = 1.0 AU (System 3).

For all plots we calculated a least squares fit in the form

$\begin{displaymath}\log time = a \cdot k + b. \end{displaymath}$

(8)

In Table 3 we summarize the values for the constants a and b for the three investigated systems.

Table 3: Values for the constants a and b in the formula 8 for the three investigated systems (see Fig. 2) as well as the errors from the least square fit.

Systems 1, 2, and 3 reach the first stable run between k = 6 and k = 6.1. It turns out when comparing systems 1, 2, and 3 that the slope of the least squares fit as well as the value of the parameter k for the first configuration, which remains stable for the integration time of 10⁷ (= $k_{\rm st}$ ) is - considering the error bars - the same for all three systems. We can thus assume that the results for comparable systems (equal number of planets with the same mass) are scalable for different semi-major axis of the innermost planet (see also Sect. 2.1).

After comparing our results to the results from Chambers et al. (1996) (same configuration as system 5), it turns out that there is very good agreement between both values, considering the different definitions for the planet's mutual distances. While we use the parameter k, Chambers et al. (1996) uses a parameter $\Delta$ corresponding to $1.59 \times k$ . With this in mind, our value of $k_{\rm st} = 6.1$ corresponds to a value of $\Delta = 9.7$ , which lies quite close to the given value ( $\Delta$ $\approx$ 9) in Chambers et al. (1996).

To investigate the dynamical behaviour of systems with actual planetary masses (17 $m_{{\rm Earth}}$ ), we determined the mean expected stability fit up to an integration time of 10⁶ years (which corresponds to $\approx$ $3 \times 10^{8}$ periods for the innermost planet ( a = 0.0207 AU)). This was done for the planetary systems 4 and 5 (the initial conditions are given in Table 4). Our first system consists of 8 fictitious planets with 17 $m_{{\rm Earth}}$ each. Figure 3a shows the decadal logarithm of the escape times (log t) versus the value of the parameter k, starting with k = 3.5. The escape time gives the time of the first close encounter between two bodies. The second system contains 10 fictitious planets with 17 $m_{{\rm Earth}}$ each, and the escape times (log t) are plotted in Fig. 3b.

$\begin{figure} \par\includegraphics[width=9cm,clip]{R12698fg5.eps}\par\includegraphics[width=9cm,clip]{R12698fg6.eps} \end{figure}$

Figure 3:

Log t in dependence of k for a system of a) 8 fictitious planets with 17 $m_{{\rm Earth}}$ each (System 4); b) 10 fictitious planets with 17 $m_{{\rm Earth}}$ each (System 5). The large scattering in the values of the parameter k follows from mean motion resonances (see end of Sect. 4.1).

Table 4: Initial conditions for the fictitious planets with 17 $m_{{\rm Earth}}$ .

For both plots we calculated a least squares fit in the form

$\begin{displaymath}\log t = a \cdot k + b. \end{displaymath}$

(9)

In Table 5 we summarize the value for the constants a and b for systems 4 and 5.

Table 5: Values for the constants a and b in the formula 9 for systems 4 and 5 (see Fig. 3), as well as the errors from the least square fit.

By comparing the results, one can see that the behaviour of the systems is quite similar. On the one hand, system 4 reaches its first stable configuration for $k_{\rm st} = 6.1$ and system 5 just for a slightly higher value of $k_{\rm st} = 6.4$ ; on the other hand, the least squares fits lead to the same results (see Table 5) regarding the error bars, so it seems that the values of the parameter $k_{\rm st}$ do not rise to a much higher number of planets. To test this assumption we determined the value of the parameter $k_{\rm st}$ (integration time 10⁶ years) for systems with up to 20 planets. The results are summarized in Fig. 4.

$\begin{figure} \par\includegraphics[width=9cm,clip]{R12698fg7.eps} \vspace*{-1mm} \end{figure}$

Figure 4:

Number of planets versus the value of $k_{\rm st}$ (integration time 10⁶ years).

While for planetary systems with less than approximately 10 planets, one can see a linear increase in the value $k_{\rm st}$ , the value $k_{\rm st}$ remains almost the same for systems with more than 10 planets. We can conclude that the number of planets does not play an important role for systems with more than $\approx$ 10 planets. Comparison of Figs. 2 and 3b shows results that are not very sensitive to changes in the planets' masses. Chambers et al. (1996) found a weak dependency of the slope of the least squares fit on the mass ( $\propto$ m^1/R12). Due to the strong influence of mean motion resonances, we were not able to find any meaningful power law.

Furthermore, one can see the strong influence of some mean motion resonances for all 5 systems, which has already been described by Chambers et al. (1996). In our work we investigated these resonances in more detail for system 4. Therefore we calculated the resonances for each planet for some values of the parameter k (k = 4.7, 5.0, 5.5, and 5.9). In the case of k = 5.0 and k = 5.9, we found that the planets are quite close to a mean motion resonance (7:5 for k = 5.0 and 3:2 for k = 5.9), while for k values of 4.7 and 5.5, the planets are farther away from these resonances. Thus we can conclude that these extremely unstable points results from the influence of some mean motion resonances.

4.2 Systems with a perturbing GG

For all further investigations with the presence of a GG, we choose system 4 with k = 8.5. According to equation 9 this will lead to a mean stability-time of approximately $7 \times 10^{7}$ years.

4.2.1 Configuration 1 - GG between 0.3 and 0.5 AU

Configuration 1 consists of a Sun-massed star, 8 fictitious planets with 17 $m_{{\rm Earth}}$ (lined according to Hill's criteria, starting from a = 0.0207 AU), and a GG with different initial conditions (see Table 6).

Table 6: Initial conditions for the GG and the fictitious planets in configuration 1.

The orbits were calculated over 10⁵ years, and the results are summarized in Fig. 5. On the x-axis, we plotted the semi-major axis of the GG, and on the y-axis its eccentricity.

$\begin{figure} \par\includegraphics[width=9cm,clip]{R12698fg8.ps}\vspace*{-3mm} \end{figure}$

Figure 5:

The GGs' semi-major axis versus its eccentricity. The colour code corresponds to the mean maximum eccentricity of all eight fictitious planets. The initial conditions are given in Table 6.

The colour code corresponds to the mean maximum eccentricity of all 8 fictitious planets, where red marks regions with low eccentricities, hence stable motion of all fictitious planets, and blue indicates high eccentricities, therefore unstable motion of the fictitious planets. Colours from orange to green show configurations for which not all fictitious planets were disturbed. As one can see, the border between blue and red is quite narrow. Therefore we can conclude that the existence of one unstable orbit of a fictitious planet would destroy the whole system in most cases. For the two stability islands around a = 0.3 AU and 0.32 AU, the outermost planet quickly collides with the GG and therefore did not disturb the other planets; nevertheless, these two islands only remain stable up to an integration time of approximately $8 \times 10^{5}$ years. Some test calculations in the stable stripes around a = 0.38 AU and a = 0.46 AU also showed that these regions does not remain stable for a longer time span.

4.2.2 Configuration 2 - GG at 0.26 AU

In the second model we investigated the case of a GG being detected at 0.26 AU. Similar to configuration 1 the system consists of a Sun-massed star, fictitious planets with 17 $m_{{\rm Earth}}$ , and a GG at 0.26 AU for which we varied the mass and the eccentricity (see Table 7). We found out that a GG at a distance of 0.26 AU does not exclude other low-mass planets inside its orbit. The computations showed 7 fictitious planets with 17 $m_{{\rm Earth}}$ (lined according to Hill's criteria, starting from a = 0.01 AU) in stable motion.

Table 7: Initial conditions for the GG and the fictitious planets in configuration 2.

The orbits were calculated over 10⁴ years, and the results are summarized in Fig. 6, where we plot the mass of the GG versus its eccentricity. For the colour scale we again used the mean of the maximum eccentricity values of all seven fictitious planets with the same colour code as in Fig. 5. The calculations showed that for low eccentricities (below approximately 0.08), the fictitious planets remain very stable on nearly circular orbits even for quite massive GGs. For eccentricities >0.1, the stable region shrinks quite fast and disappears when e = 0.26.

$\begin{figure} \par\includegraphics[width=9cm,clip]{R12698fg9.ps} \end{figure}$

Figure 6:

The GGs' mass versus its eccentricity. The colour code corresponds to the mean maximum eccentricity of all seven fictitious planets. The initial conditions are given in Table 7.

5 Conclusions

Via calculations of escape times for numerous different configurations, we find that compact multiplanetary systems are stable in the CoRoT discovery space, if they satisfy their respective Hill's exclusion stability criteria. We could show furthermore that similar systems (same number of equal massed planets) are scalable, which means that they reach their first stable configuration for the same value $k_{\rm st}$ independent of the semi-major axis of the innermost planet.

In the second test we investigated the interplay between $k_{\rm st}$ and the number of planets. For systems with only a few planets (up to $\approx$ 10 planets) we could find an almost linear growth of the value $k_{\rm st}$ with the number of planets, but for a higher number of planets ( $\geq$ 10), it turned out that $k_{\rm st}$ reaches a plateau, indicating that the number of planets is no longer relevant for the system's stability time.

For two systems (8 and 10 planets with 17 $m_{{\rm Earth}}$ each), we tested the interplay between the value of the parameter k and the escape time and could find linear behaviour. According to these results we chose k such that it leads to stability times of approximately $7 \times 10^{7}$ years for a system with 8 fictitious planets (innermost planet at 0.0207 AU), in order to investigate the influence of a GG.

Introducing a perturbing GG, we found stable regions for certain initial conditions. Thus - from a dynamical point of view - ultra-compact planetary systems with numerous low-mass planets complying with periods of less than 50 days are possible and thus may be discovered by the CoRoT transit search.

Acknowledgements

B. Funk wants to acknowledge the support by the AUstrian FWF Erwin Schrödinger grant No. J2892-N16. G. Wuchterl acknowledges support by the DLR grants 50 OW 0205, 50 OW 0501, 50 OW 0603. R. Schwarz wants to acknowledge the support by the MOEL grant No. 309. E. Pilat-Lohinger wants to acknowledge the support by the Austrian FWF project No. P19569-N16. S. Eggl wants to acknowledge the support by the Austrian FWF project No. P20216.

References

Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, in COSPAR, Plenary Meeting, 36, 36th COSPAR Scientific Assembly, 3749 [Google Scholar]
Barge, P., Baglin, A., Auvergne, M., et al. 2008, A&A, 482, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bouchy, F., Moutou, C., Queloz, D., et al. 2009, Transiting Planets, Proceedings of the International Astronomical Union, IAU Symp., 253, 129 [Google Scholar]
Broeg, C. 2007, MNRAS, 377, L44 [NASA ADS] [Google Scholar]
Chambers, J. E., Wetherill, G. W., & Boss, A. P. 1996, ICARUS, 119, 261 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Eggl, S., & Dvorak, R. 2010, LNP, 790 [Google Scholar]
Érdi, B., Dvorak, R., Sándor, Zs., Pilat-Lohinger, E., & Funk, B. 2004, MNRAS, 351, 1043 [NASA ADS] [CrossRef] [Google Scholar]
Fogg, M. J., & Nelson, R. P. 2007, A&A, 472, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
Fogg, M. J., & Nelson, R. P. 2009, A&A, 498, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Hanslmeier, A., & Dvorak, R. 1984, A&A, 132, 203 [NASA ADS] [Google Scholar]
Hayes, W., & Tremaine, S. 1998, Icarus, 135, 549 [NASA ADS] [CrossRef] [Google Scholar]
Léger, A., Rouan, D., Schneider, J., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
Lichtenegger, H. 1984, CeMDA, 34, 357 [Google Scholar]
Mayor, M., Bonfils, X., Forveille, T., et al. 2009a, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mayor, M., Udry, S., Lovis, C., et al. 2009b, A&A, 493, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Murray, C. D., & Dermott S. F. 2000, Solar System Dynamics (Cambridge, UK: University Press), 104 [Google Scholar]
Queloz, D., Bouchy, F., Moutou, C., et al. 2009, A&A, 506, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Raymond, S. N. 2008, Exoplanets: Detection, Formation and Dynamics, Proceedings of the International Astronomical Union, IAU Symp., 249, 233 [Google Scholar]
Raymond, S. N., Barnes, R., & Mandell, A. M. 2008, MNRAS, 384, 663 [NASA ADS] [CrossRef] [Google Scholar]
Rivera, E. J., Lissauer, J. J., Butler, R. P., et al. 2005, ApJ, 634, 625 [NASA ADS] [CrossRef] [Google Scholar]
Sándor, Zs., Süli, Á., Érdi, B., Pilat-Lohinger, E., & Dvorak, R. 2007, MNRAS, 375, 1495 [NASA ADS] [CrossRef] [Google Scholar]
Schönke, J. 2007, Planet. Space Sci., 55, 1299 [NASA ADS] [CrossRef] [Google Scholar]
Schwarz, R., Dvorak, R., Pilat-Lohinger, E., Süli, Á., & Érdi, B. 2006, A&A, 462, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Schwarz, R., Funk, B., & Pilat-Lohinger, E. 2010, ASPCS, in press [Google Scholar]
Smith, A. W., & Lissauer, J. J. 2009, Icarus, 201, 381 [NASA ADS] [CrossRef] [Google Scholar]
Yoshida, H. 1993, CMDA, 56, 27 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... 0.01 AU: A distance of 0.01 AU from a solar-massed star corresponds approximately to the Roche radius (see also Murray & Dermott 2000).
... formula: For details see Sect. 2.
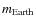
... $m_{{\rm Earth}}$: The value was chosen as more likely to be detected.
... 0.0207: For reasons of computational feasibility, we used the third planet's position (see Table 7) as a starting point for Hill's line-up without changing the total number of planets. This should not change the dynamical properties of the system due to its scalability (see Eq. (7)).
...configuration: For all our calculations we used a integration time of 10⁷ periods of the innermost planet.

All Tables

Table 1: Example systems with known close-in planets.

Table 2: Initial conditions for the fictitious planets with 10^-7 $m_{\rm Sun}$ .

Table 3: Values for the constants a and b in the formula 8 for the three investigated systems (see Fig. 2) as well as the errors from the least square fit.

Table 4: Initial conditions for the fictitious planets with 17 $m_{{\rm Earth}}$ .

Table 5: Values for the constants a and b in the formula 9 for systems 4 and 5 (see Fig. 3), as well as the errors from the least square fit.

Table 6: Initial conditions for the GG and the fictitious planets in configuration 1.

Table 7: Initial conditions for the GG and the fictitious planets in configuration 2.

All Figures

$\begin{figure} \par\includegraphics[width=9cm,clip]{R12698fg1.eps} \end{figure}$	Figure 1: Log t in dependence of k for a system of 10 fictitious planets with 17 $m_{{\rm Earth}}$ . All fictitious planets were started with mean anomaly = 0.
In the text

$\begin{figure} \par\includegraphics[width=9cm]{R12698fg2.eps}\par\includegraphics[width=9cm]{R12698fg3.eps}\par\includegraphics[width=9cm]{R12698fg4.eps} \end{figure}$	Figure 2: log time in dependence of k for three systems with 10 planets each for different starting positions of the innermost planet: a) a = 0.0207 AU (System 1); b) a = 0.2 AU (System 2); c) a = 1.0 AU (System 3).
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{R12698fg5.eps}\par\includegraphics[width=9cm,clip]{R12698fg6.eps} \end{figure}$	Figure 3: Log t in dependence of k for a system of a) 8 fictitious planets with 17 $m_{{\rm Earth}}$ each (System 4); b) 10 fictitious planets with 17 $m_{{\rm Earth}}$ each (System 5). The large scattering in the values of the parameter k follows from mean motion resonances (see end of Sect. 4.1).
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{R12698fg7.eps} \vspace*{-1mm} \end{figure}$	Figure 4: Number of planets versus the value of $k_{\rm st}$ (integration time 10⁶ years).
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{R12698fg8.ps}\vspace*{-3mm} \end{figure}$	Figure 5: The GGs' semi-major axis versus its eccentricity. The colour code corresponds to the mean maximum eccentricity of all eight fictitious planets. The initial conditions are given in Table 6.
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{R12698fg9.ps} \end{figure}$	Figure 6: The GGs' mass versus its eccentricity. The colour code corresponds to the mean maximum eccentricity of all seven fictitious planets. The initial conditions are given in Table 7.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.