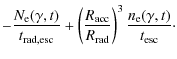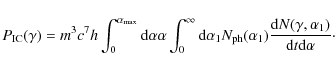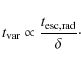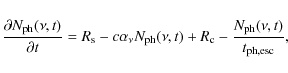| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 4 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201014299 | |
| Published online | 02 June 2010 | |
Modelling the variability of 1ES1218+30.4
(Research Note)
M. Weidinger - F. Spanier
Lehrstuhl für Astronomie, University of Würzburg, Am Hubland, 97074 Würzburg, Germany
Received 22 February 2010 / Accepted 6 April 2010
Abstract
Context. The blazar 1 ES 1218+30.4 has been previously
detected by the VERITAS and MAGIC telescopes in the very high energies.
The new detection of VERITAS from December 2008 to April 2009 proves
that 1 ES 1218+30.4 is not static, but shows short-time variability.
Aims. We show that the time variability may be explained in the
context of a self-consistent synchrotron-self Compton model, while the
long time observation do not necessarily require a time-resolved
treatment.
Methods. The kinetic equations for electrons and photons in a
plasma blob are solved numerically including Fermi acceleration for
electrons as well as synchrotron radiation and Compton scattering.
Results. The light curve observed by VERITAS can be reproduced
in our model by assuming a changing level of electron injection
compared to the constant state of 1 ES 1218+30.4. The multiwavelength
behaviour during an outburst becomes comprehensible by the model.
Conclusions. The long time measurements of VERITAS are still
explainable via a constant emission in the SSC context, but the short
outbursts each require a time-resolved treatment.
Key words: galaxies: jets - relativistic processes - radiation mechanisms: non-thermal - BL Lacertae objects: individual: 1 ES 1218+30.4 - galaxies: active
1 Introduction
Blazars are a special class of active galactic nuclei (AGN) exhibiting a spectral energy distribution (SED) that is strongly dominated by nonthermal emission across a wide range of wavelengths, from radio waves to gamma rays, and rapid, large-amplitude variability. The source of this emission is presumably the relativistic jet emitted at a narrow angle to the line of sight to the observer.
In high-peaked BL Lac objects (HBLs) the SED shows a double hump structure as the most notable feature with the first hump in the UV- to X-ray regime and the second hump in the gamma-ray regime. Indeed, a substantial fraction of the known nearby HBLs have already been discovered with Cherenkov telescopes like HESS, MAGIC or VERITAS. The origin of the first hump is mostly undisputed: nonthermal, relativistic electrons in the jet are emitting synchrotron radiation. The origin of the second hump is still controversially debated. Up to now two kinds of models are discussed: leptonic (e.g. Maraschi et al. 1992) and hadronic (e.g. Mannheim 1993) ones, which are mostly applied for other subclasses of blazars.
Another important feature of AGNs in general and HBLs in particular is their strong variability. The dynamical timescale may range from minutes to years. This requires complex models, which obviously have to include time dependence, but this gives us also the chance to understand the mechanisms that drive AGNs. We will apply a self-consistent leptonic model to new data observed for the source 1 ES 1218+30.4, because those are the ones favoured for HBLs.
The source HBL 1 ES 1218+30.4 has been discovered as a candidate BL Lac object on the basis of its X-ray emission and has been identified with the X-ray source 2A 1219+30.5 (Wilson et al. 1979; Ledden et al. 1981). For the first time, 1 ES 1218+30.4 has been observed at VHE energies using the MAGIC telescope in January 2005 (Albert et al. 2006) and later from VERITAS (Acciari et al. 2009). Coverage of the optical/X-ray regime is provided by BeppoSAX (Donato et al. 2005) and SWIFT (Tramacere et al. 2007), unfortunately the data are not always simultaneous. During the observations from December 2008 to April 2009 VERITAS also observed 1 ES 1218+30.4 showing a time-variability (the VERITAS collaboration et al. 2010). The observations from the MAGIC telescope have previously been modelled by Rüger et al. (2010). the VERITAS collaboration et al. (2010) claim that their new observations exhibiting variability challenge the previous models. We will show that a timedependent model using a self-consistent treatment of electron acceleration is able to model the new VERITAS data.
We present the kinetic equation, which we solve numerically, describing the synchrotron-self Compton emission (Sect. 2). In Sect. 3 we apply our code to 1 ES 1218+30.4, taking the VERITAS data into account and give a set of physical parameters for the most acceptable fit. Finally, we discuss our results in the light of particle acceleration theory and the multiwavelength features.
2 Model
Here we will give a brief description of the model used, for a complete overview see (Weidinger et al. 2010; Weidinger & Spanier 2010).
We start with the relativistic Vlasov equation (see e.g. Schlickeiser 2002) in the one dimensional diffusion approximation (e.g. Schlickeiser 1984), here the relativistic approximation
![]() is
used. This kinetic equation will then be solved time-dependently in two
spatially different zones, the smaller acceleration zone and the
radiation zone, which are assumed to be spherical and homogeneous. Both
contain isotropically distributed electrons and a randomly oriented
magnetic field as common for these models. All calculations are made in
the rest frame of the blob.
is
used. This kinetic equation will then be solved time-dependently in two
spatially different zones, the smaller acceleration zone and the
radiation zone, which are assumed to be spherical and homogeneous. Both
contain isotropically distributed electrons and a randomly oriented
magnetic field as common for these models. All calculations are made in
the rest frame of the blob.
Electrons entering the acceleration zone (radius
![]() )
from the upstream of the jet are continuously accelerated through diffusive shock acceleration. This extends the model of Kirk et al. (1998)
with a stochastic part. The energy gain due to the acceleration is
balanced by radiative (synchrotron) and escape losses, the latter
scaling with
)
from the upstream of the jet are continuously accelerated through diffusive shock acceleration. This extends the model of Kirk et al. (1998)
with a stochastic part. The energy gain due to the acceleration is
balanced by radiative (synchrotron) and escape losses, the latter
scaling with
![]() with
with ![]() as an empirical factor reflecting the diffusive nature of particle
loss. Escaping electrons completely enter the radiation zone (radius
as an empirical factor reflecting the diffusive nature of particle
loss. Escaping electrons completely enter the radiation zone (radius
![]() )
downstream of the acceleration zone.
)
downstream of the acceleration zone.
Here the electrons are suffering synchrotron losses as in the
acceleration zone and also inverse-Compton losses, but they do not
undergo acceleration. Pair production and other contributions do not
alter the SED in typical SSC conditions and are neglected (Chiang & Böttcher 2002).
The SED in the observer's frame is calculated by boosting the
selfconsistently calculated photons towards the observer's frame and
correcting for the redshift z:
![]() with
with
![]() .
The acceleration zone will have no contribution to
.
The acceleration zone will have no contribution to
![]() directly, due to the
directly, due to the
![]() dependence of the observed flux at a distance r (
dependence of the observed flux at a distance r (
![]() )
and the small size of the acceleration zone. The kinetic equation in the acceleration zone is
)
and the small size of the acceleration zone. The kinetic equation in the acceleration zone is
The injected electrons at
with the Thomson cross-section
This model takes account of a much more confined shock region. Fermi-I
acceleration will probably not occur over the whole blob when
considering a real blazar but rather at a small region in the blob's
front.
Neglecting acceleration simplifies the kinetic equation in the
radiation zone to
The photon energies are rewritten in terms of the electron rest mass,
To determine the time-dependent model SED of blazars the partial differential equation for the differential photon number density has to be solved time-dependently, which can be done numerically. The PDE (6) can be obtained from the radiative transfer equation making use of the isotropy of the blob
where
3 Results
Using the parameters summed up in Table 1 we were able to fit the emission of 1 ES 1218+30.4 as a steady state with our SSC model, see Fig. 1. We used all the archival data from BeppoSAX, SWIFT in the X-ray band and the MAGIC 2006, VERITAS 2009 as well as the new released VERITAS 2010 data in the VHE to model the SED of 1 ES 1218+30.4 (Donato et al. 2005; Albert et al. 2006; the VERITAS collaboration et al. 2010; Acciari et al. 2009; Tramacere et al. 2007). The derived SED is absorbed in the VHE using the EBL model of Primack et al. (2005) for the corresponding redshift of 1 ES 1218+30.4.
The parameters of our SSC model are well winthin the standard SSC
parameter region with an equipartition parameter of 0.02. Even though
PIC and MHD simulations suggest a higher magnetic field compared to
particle energy (in the range of 0.1), this is a common assumption in
SSC models, but has to be kept in mind with regard e.g. the stability
of the blob. If one wishes to enforce higher equipartition parameters
one could to use the model of Schlickeiser & Lerche (2007). In order to allow strong shocks to form
![]() must be fulfilled, which is the case for a=10.
must be fulfilled, which is the case for a=10.
Due to relatively small deviation (within the error margins) between
the MAGIC 2005/VERITAS 2008 and the averaged VHE data from the VERITAS
2009 campaign we find a steady state the most plausible way to model
the emission, i.e. the small fluctuations (see the overall lightcurve
in the VERITAS collaboration et al. 2010)
are not contributing significantly to the averaged observed SEDs. In
the Fermi LAT energy regime our model yields a photon index of
![]() ,
whichagrees well with the Fermi measurement of
,
whichagrees well with the Fermi measurement of
![]() (Abdo et al. 2009).
(Abdo et al. 2009).
Table 1: Model parameters for the low-state SED, basis to model the outburst by varying Q0.
The lightcurve of the VERITAS collaboration et al. (2010) shows a relatively strong outburst at ![]() MJD 54 861. Starting with the steady state emission (solid line, Fig. 1; parameters: Table 1) we injected more electrons Q0 into the emission region at low
MJD 54 861. Starting with the steady state emission (solid line, Fig. 1; parameters: Table 1) we injected more electrons Q0 into the emission region at low
![]() .
As the blob evolves in time the emission in the model at higher
energies rises and drops off again when the injected electrons finally
relax to the initial Q0. This process can be explained as density fluctuations along the jet axis and finally fits the flare.
.
As the blob evolves in time the emission in the model at higher
energies rises and drops off again when the injected electrons finally
relax to the initial Q0. This process can be explained as density fluctuations along the jet axis and finally fits the flare.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14299_f1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa14299-10/Timg56.png)
|
Figure 1: Model SED of 1 ES 1218+30.4 (black solid line) as derived using the described model (see Sect. 2) and the parameters shown in Table 1. The VHE parts of the model SEDs have been absorbed using the EBL model of Primack et al. (2005). The BeppoSAX data are from Donato et al. (2005), SWIFT from Tramacere et al. (2007), MAGIC from Albert et al. (2006), VERITAS 2009 from Acciari et al. (2009) and the blue dots are the new VERITAS 2010 data from the VERITAS collaboration et al. (2010). The dashed red curve shows the time integrated SED over the strong outburst shown in Fig. 2, as measured by VERITAS in 2009. |
| Open with DEXTER | |
We found that nearly doubling the injected electron number density in a
![]() way with a timescale
way with a timescale
![]() days (as measured in the observer's frame) and then decreasing them to the initial Q0
in an almost linear way on the same timescale fits the strong outburst
of 1 ES 1218+30.4. The corresponding lightcurve of the model as well as
the observed one are summarized in Figs. 2, 3.
Figure 3
shows a more detailed view of the lightcurve in the VHE (above
200 GeV) as well as the corresponding lightcurves in the X-ray
(between 1.2 keV and 11 keV) regime of BeppoSAX/SWIFT and the lower
tail of the Fermi LAT energy range (between 0.2 GeV and 22 GeV) as
predicted by our model. The latter two have been scaled down to the
flux level of the VERITAS measurement, see Fig. 3,
because the real fluxes are higher than the VHE flux. The model
predicts the peak of the lightcurve in the Fermi regime to be
1.26 h ahead of the VHE one, where the X-ray regime is delayed by
0.97 h for 1 ES 1218+30.4. The delay of the X-ray band can be used
to verify the model when multiwavelength data of the flaring behaviour
of 1 ES 1218+30.4 is available, while the derivation of the
0.2 GeV to 22 GeV lightcurve is beyond the resolution of
Fermi for this source.
days (as measured in the observer's frame) and then decreasing them to the initial Q0
in an almost linear way on the same timescale fits the strong outburst
of 1 ES 1218+30.4. The corresponding lightcurve of the model as well as
the observed one are summarized in Figs. 2, 3.
Figure 3
shows a more detailed view of the lightcurve in the VHE (above
200 GeV) as well as the corresponding lightcurves in the X-ray
(between 1.2 keV and 11 keV) regime of BeppoSAX/SWIFT and the lower
tail of the Fermi LAT energy range (between 0.2 GeV and 22 GeV) as
predicted by our model. The latter two have been scaled down to the
flux level of the VERITAS measurement, see Fig. 3,
because the real fluxes are higher than the VHE flux. The model
predicts the peak of the lightcurve in the Fermi regime to be
1.26 h ahead of the VHE one, where the X-ray regime is delayed by
0.97 h for 1 ES 1218+30.4. The delay of the X-ray band can be used
to verify the model when multiwavelength data of the flaring behaviour
of 1 ES 1218+30.4 is available, while the derivation of the
0.2 GeV to 22 GeV lightcurve is beyond the resolution of
Fermi for this source.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14299_f2.eps} \vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa14299-10/Timg59.png)
|
Figure 2:
Lightcurve of the photon flux above 200 GeV as measured by the VERITAS collaboration et al. (2010)
(inset of their figure) in January 2009 to February 2009 and our model
(red solid line). The outburst was modelled by injecting more electrons
into the blob by varying Q0 at a timescale of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14299_f3}
\end{figure}](/articles/aa/full_html/2010/07/aa14299-10/Timg60.png)
|
Figure 3: Detailed view of the high outburst shown already in Fig. 2 as well as the behaviour of 1 ES 1218+30.4 in the lower Fermi LAT energy band and the synchrotron regime, measurable by BeppoSAX/SWIFT during such a flare. |
| Open with DEXTER | |
Additionally we plotted the time averaged SED (over the outburst from
MJD54860 until MJD54864) into the SED of 1 ES 1218+30.4, Fig. 1
(dashed red line). As one can see only when separately considering the
strongest outburst of 1 ES 1218+30.4 within the VERITAS campaign in
2009 the aberration from a presumed steady state is significant. In
contrast an average over the whole observation of the VERITAS collaboration et al. (2010), which is low-state most of the time, will result in a steady state as shown here or in Rüger et al. (2010). For the IC photon index ![]() (
(
![]() )
above 200 GeV we get
)
above 200 GeV we get
![]() for the low-state (solid curve in Fig. 1), which slightly softens to
for the low-state (solid curve in Fig. 1), which slightly softens to
![]() when considering the high-state as the time-average over the single outburst shown in the lightcurve, Fig. 2
in the VERITAS range. Note that the photon index and its behaviour
during an outburst in this energy range is very sensitive to the EBL
absorption and thus to the EBL model used and shows a strong dependency
on the considered energy range. With our model we are able to compute
the spectral behaviour in the X-ray energy range of the BeppoSAX/SWIFT
satellites (i.e. 1.2 keV < E < 11 keV). The model predicts the source to be spectrally steady in this regime with a photon index
when considering the high-state as the time-average over the single outburst shown in the lightcurve, Fig. 2
in the VERITAS range. Note that the photon index and its behaviour
during an outburst in this energy range is very sensitive to the EBL
absorption and thus to the EBL model used and shows a strong dependency
on the considered energy range. With our model we are able to compute
the spectral behaviour in the X-ray energy range of the BeppoSAX/SWIFT
satellites (i.e. 1.2 keV < E < 11 keV). The model predicts the source to be spectrally steady in this regime with a photon index
![]() for outbursts on timescales of days. Considering shorter averaging
timescales of the outburst of 1 ES 1218+30.4, e.g. the first or last
two hours, two hours around the peak in the lightcurve, the maximum
derivation from
for outbursts on timescales of days. Considering shorter averaging
timescales of the outburst of 1 ES 1218+30.4, e.g. the first or last
two hours, two hours around the peak in the lightcurve, the maximum
derivation from
![]()
![]() predicted by the model is
predicted by the model is ![]() (-0.07), which could not be measured with current experiments and thus is considered as spectrally steady in this case.
(-0.07), which could not be measured with current experiments and thus is considered as spectrally steady in this case.
4 Discussion
Our results clearly show that the latest observations from the VERITAS telescope for 1 ES 1218+30.4 still agree with a constant (steady state) emission from a SSC model when averaged over a long observation period. This is due to the relatively moderate variability of 1 ES 1218+30.4 compared to the observation time.
The variability may be well explained in the context of the self-consistent treatment of acceleration of electrons in the jet. We are aware that an outburst of the timescale of roughly five days as measured from 1 ES 1218+30.4 does not necessarily require a shock in jet model, which scales down to a few minutes depending on the SSC parameters (Weidinger & Spanier 2010), but may also be explained as e.g. different accretion states. Nevertheless the fundamental statement remains the same: long time observation of slightly variable blazars will result in a steady state emission, while an average over a single outburst will, of course, result in a significantly different SED for the source. We are not yet able to rule out different emission models or even complex geometries of the emitting region. But we are able to model the influence of short outbursts of a source on the SED and the lightcurves in the different energy bands selfconsistently.
The VERITAS collaboration only shows an integrated spectrum for 1 ES 1218+30.4, which is due to the low flux of the source and the photon index behaviour of the combined high-states. This integrated spectrum does not show strong variations with regard to the known low-state observed by MAGIC. Our model now predicts a clear change in the spectrum, which is indicated by the dashed line in Fig. 1, which shows the average over one outburst with a slight, currently not detectable spectral softening in the VHE range, while the synchrotron peak in the BeppoSAX/SWIFT regime remains spectrally constant. This situation changes for shorter and/or stronger outbursts of an overall timescale of hours, which will result in measurable spectral evolutions in all energy regimes when considered with the presented model. Furthermore the time-resolved SEDs during a flare are comprehensible with our model. Hence with better time-resolved spectra or/and better multiwavelength coverage it should be possible to prove this model, and if the model is indeed applicable it will be a good tool to investigate the whole SED during an outburst without having all energy regimes observationally covered.
AcknowledgementsM.W. wants to thank the Elitenetzwerk Bayern and GK1147 for their support. F.S. acknowledges support from the Deutsche Forschungsgemeinschaft (DFG) through grant SP 1124/1.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 707, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2009, ApJ, 695, 1370 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2006, ApJ, 642, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, J., & Böttcher, M. 2002, ApJ, 564, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Donato, D., Sambruna, R. M., & Gliozzi, M. 2005, A&A, 433, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drury, L. O., Duffy, P., Eichler, D., & Mastichiadis, A. 1999, A&A, 347, 370 [NASA ADS] [Google Scholar]
- Jones, F. C. 1968, Phys. Rev., 167, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Kerrick, A. D., Akerlof, C. W., Biller, S. D., et al. 1995, ApJ, 438, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Rieger, F. M., & Mastichiadis, A. 1998, A&A, 333, 452 [NASA ADS] [Google Scholar]
- Ledden, J. E., Odell, S. L., Stein, W. A., & Wisniewski, W. Z. 1981, ApJ, 243, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Mannheim, K. 1993, A&A, 269, 67 [NASA ADS] [Google Scholar]
- Maraschi, L., Ghisellini, G., & Celotti, A. 1992, ApJ, 397, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Primack, J. R., Bullock, J. S., & Somerville, R. S. 2005, in High Energy Gamma-Ray Astronomy, ed. F. A. Aharonian, H. J. Völk, & D. Horns, AIP Conf. Ser., 745, 23 [Google Scholar]
- Rüger, M., Spanier, F., & Mannheim, K. 2010, MNRAS, 401, 973 [Google Scholar]
- Schlickeiser, R. 1984, A&A, 136, 227 [NASA ADS] [Google Scholar]
- Schlickeiser, R. 2002, Cosmic ray astrophysics, Astronomy and Astrophysics Library, Physics and Astronomy Online Library (Berlin: Springer), 519 [Google Scholar]
- Schlickeiser, R., & Lerche, I. 2007, A&A, 476, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- VERITAS collaboration, et al. 2010, ApJ, 709, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Tramacere, A., Giommi, P., Massaro, E., et al. 2007, A&A, 467, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidinger, M., Rüger, M., & Spanier, F. 2010, Astrophys. Space Sci. Trans., 6, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Weidinger, M., & Spanier, F. 2010, in HEPRO II Conf. Proc., ed. G. Romero, F. Aharonian, & J. Paredes, Int. J. Mod. Phys. D, submitted, [Google Scholar]
- Wilson, A. S., Ward, M. J., Axon, D. J., Elvis, M., & Meurs, E. J. A. 1979, MNRAS, 187, 109 [NASA ADS] [Google Scholar]
All Tables
Table 1: Model parameters for the low-state SED, basis to model the outburst by varying Q0.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14299_f1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa14299-10/Timg56.png)
|
Figure 1: Model SED of 1 ES 1218+30.4 (black solid line) as derived using the described model (see Sect. 2) and the parameters shown in Table 1. The VHE parts of the model SEDs have been absorbed using the EBL model of Primack et al. (2005). The BeppoSAX data are from Donato et al. (2005), SWIFT from Tramacere et al. (2007), MAGIC from Albert et al. (2006), VERITAS 2009 from Acciari et al. (2009) and the blue dots are the new VERITAS 2010 data from the VERITAS collaboration et al. (2010). The dashed red curve shows the time integrated SED over the strong outburst shown in Fig. 2, as measured by VERITAS in 2009. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14299_f2.eps} \vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa14299-10/Timg59.png)
|
Figure 2:
Lightcurve of the photon flux above 200 GeV as measured by the VERITAS collaboration et al. (2010)
(inset of their figure) in January 2009 to February 2009 and our model
(red solid line). The outburst was modelled by injecting more electrons
into the blob by varying Q0 at a timescale of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14299_f3}
\end{figure}](/articles/aa/full_html/2010/07/aa14299-10/Timg60.png)
|
Figure 3: Detailed view of the high outburst shown already in Fig. 2 as well as the behaviour of 1 ES 1218+30.4 in the lower Fermi LAT energy band and the synchrotron regime, measurable by BeppoSAX/SWIFT during such a flare. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



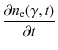
![$\displaystyle \frac{\partial}{\partial \gamma} \left[\left( \beta_{\rm s} \gamma^2 - t_{{\rm acc}}^{-1}\gamma \right) \cdot n_{\rm e}(\gamma, t) \right]$](/articles/aa/full_html/2010/07/aa14299-10/img13.png)
![$\displaystyle +\frac{\partial}{\partial \gamma} \left[ [(a+2)t_{{\rm acc}}]^{-1}\gamma^2 \frac{\partial n_{\rm e}(\gamma, t)}{\partial \gamma}\right]$](/articles/aa/full_html/2010/07/aa14299-10/img14.png)
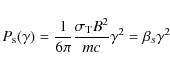

![$\displaystyle \frac{\partial}{\partial \gamma}\left[\left(\beta_{\rm s} \gamma^2 + P_{{\rm IC}}(\gamma)\right) \cdot N_{\rm e}(\gamma, t) \right]$](/articles/aa/full_html/2010/07/aa14299-10/img30.png)