| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913946 | |
| Published online | 10 June 2010 | |
On the physical properties of z 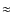 6-8 galaxies
6-8 galaxies
D. Schaerer1,2 - S. de Barros1
1 - Geneva Observatory, University of Geneva,
51, Ch. des Maillettes, 1290 Versoix, Switzerland
2 -
Laboratoire d'Astrophysique de Toulouse-Tarbes,
Université de Toulouse, CNRS,
14 Avenue E. Belin,
31400 Toulouse, France
Received 22 December 2009 / Accepted 3 February 2010
Abstract
Aims. We analyse the spectral energy distributions (SEDs) of
the most distant galaxies discovered with the Hubble Space telescope
and from the COSMOS survey and determine their physical properties,
such as stellar age and mass, dust attenuation, and star-formation
rate.
Methods. We use our SED fitting tool including the effects of nebular emission to analyse three samples of
![]() galaxies with observed magnitudes
galaxies with observed magnitudes
![]() to 29. Our models cover a wide parameter space.
to 29. Our models cover a wide parameter space.
Results. We find that the physical parameters of most galaxies
cover a wide range of acceptable values. Stellar ages, in particular,
are not strongly constrained, even for objects detected longward of the
Balmer break. As already pointed out earlier, the effects of nebular
lines significantly affect the age determinations of star-forming
galaxies at
![]() .
We find no need for stellar populations with extreme metallicities or
other non-standard assumptions (IMF, escape fraction) to explain the
observed properties of faint z-dropout galaxies. Albeit with large uncertainties, our fit results show indications of dust attenuation in some of the
.
We find no need for stellar populations with extreme metallicities or
other non-standard assumptions (IMF, escape fraction) to explain the
observed properties of faint z-dropout galaxies. Albeit with large uncertainties, our fit results show indications of dust attenuation in some of the
![]() galaxies, which have best-fit values of AV up to
galaxies, which have best-fit values of AV up to ![]() 1.
Furthermore, we find a possible trend of increasing dust attenuation
with galaxy mass, and a relatively large scatter in specific
star-formation rates, SFR/
1.
Furthermore, we find a possible trend of increasing dust attenuation
with galaxy mass, and a relatively large scatter in specific
star-formation rates, SFR/![]() .
.
Conclusions. The physical parameters of very high-z galaxies may be more uncertain than indicated by previous studies. Dust attenuation seems also to be present in some
![]() galaxies, and may be correlated with galaxy mass, as is also the case for SFR.
galaxies, and may be correlated with galaxy mass, as is also the case for SFR.
Key words: galaxies: starburst - galaxies: high-redshift - Galaxies: ISM - ultraviolet: galaxies
1 Introduction
Finding and studying the most distant galaxies formed during the epoch of reionisation, more recent than 1 Gyr after the Big Bang, is one of the challenges of contemporary observational astrophysics. Over the past few years considerable progress has been made in this field, pushing the observable limits beyond redshift 6 with the use of ground-based facilities and satellites.
A variety of observational programs have tried to locate z > 6 galaxies
using different observational techniques, mostly involving either searches for
Ly![]() emission through narrow-band filters or searches using the Lyman break
technique - also called the dropout technique.
These have been performed either in blank fields or in fields with galaxy clusters,
which act as strong gravitational lenses, targetting different depths and survey areas.
The objects found in this way are line emitters or Lyman break galaxies (LBGs).
emission through narrow-band filters or searches using the Lyman break
technique - also called the dropout technique.
These have been performed either in blank fields or in fields with galaxy clusters,
which act as strong gravitational lenses, targetting different depths and survey areas.
The objects found in this way are line emitters or Lyman break galaxies (LBGs).
Although Ly![]() emitters are among the most distant galaxies
with spectroscopically confirmed redshifts (see Ota et al. 2008; Iye et al. 2006),
few have been found at
emitters are among the most distant galaxies
with spectroscopically confirmed redshifts (see Ota et al. 2008; Iye et al. 2006),
few have been found at ![]() (see e.g. Stark et al. 2007b; Hibon et al. 2009; Willis et al. 2008; Cuby et al. 2007; Sobral et al. 2009).
Furthermore, because of their faintness the photometry available is
inadequate in terms of depth to allow studies of their stellar populations.
(see e.g. Stark et al. 2007b; Hibon et al. 2009; Willis et al. 2008; Cuby et al. 2007; Sobral et al. 2009).
Furthermore, because of their faintness the photometry available is
inadequate in terms of depth to allow studies of their stellar populations.
Surveys using strong gravitational lensing were among the first
to pave the way in the of study z>6 galaxies
(see Pelló et al. 2004; Kneib et al. 2004; Bradley et al. 2008; Egami et al. 2005; Zheng et al. 2009; Richard et al. 2008,2006).
Ultra-deep fields with the Hubble Space Telescope (HST) including
near-IR observations with NICMOS have uncovered a handful of ![]() candidates in blank fields (Henry et al. 2008; Labbé et al. 2006; Bouwens et al. 2004).
These pilot studies also showed that some of the
candidates in blank fields (Henry et al. 2008; Labbé et al. 2006; Bouwens et al. 2004).
These pilot studies also showed that some of the ![]() galaxies
could be detected at 3.6 and 4.5
galaxies
could be detected at 3.6 and 4.5 ![]() m with Spitzer,
thus probing the rest-frame optical emission from these objects
(Labbé et al. 2006; Egami et al. 2005).
m with Spitzer,
thus probing the rest-frame optical emission from these objects
(Labbé et al. 2006; Egami et al. 2005).
Since then, surveys of z-dropout galaxies (targeting ![]() objects) have been extended to cover larger areas, primarily with ground-based instruments
(Hickey et al. 2010; Castellano et al. 2010; Ouchi et al. 2009; Capak et al. 2009; Wilkins et al. 2009; Mannucci et al. 2007),
but also with HST (Henry et al. 2009; Gonzalez et al. 2010; Henry et al. 2007).
In most cases, however, only a few near-IR photometric bands are
available, providing so far information only on source counts
and luminosity functions, but precluding more detailed studies of the physical
properties of the sources.
Notable exceptions are the work of Capak et al. (2009), who present
three bright (
objects) have been extended to cover larger areas, primarily with ground-based instruments
(Hickey et al. 2010; Castellano et al. 2010; Ouchi et al. 2009; Capak et al. 2009; Wilkins et al. 2009; Mannucci et al. 2007),
but also with HST (Henry et al. 2009; Gonzalez et al. 2010; Henry et al. 2007).
In most cases, however, only a few near-IR photometric bands are
available, providing so far information only on source counts
and luminosity functions, but precluding more detailed studies of the physical
properties of the sources.
Notable exceptions are the work of Capak et al. (2009), who present
three bright (![]() )
)
![]() galaxy candidates from the COSMOS 2 square
degree field, and the study of Gonzalez et al. (2010) finding 11
fainter (
galaxy candidates from the COSMOS 2 square
degree field, and the study of Gonzalez et al. (2010) finding 11
fainter (
![]()
![]() )
)
![]() galaxies in the two GOODS fields.
Both studies benefit from a coverage including optical, near-IR, and Spitzer
bands.
galaxies in the two GOODS fields.
Both studies benefit from a coverage including optical, near-IR, and Spitzer
bands.
Observations taken recently with the newly installed WFC3 camera
on-board HST have just been released, resulting in publications from
four independent groups identifying faint (
![]()
![]() 27-29)
27-29) ![]() galaxies, based on the combination of the deepest available ACS/HST and
WFC3 data (Oesch et al. 2010; Bouwens et al. 2010a; Bunker et al. 2009; McLure et al. 2010; Yan et al. 2009).
While these objects are too faint to be detected at the current
limits of the deepest Spitzer images, a stack of 14 z-dropout galaxies
from Oesch et al. (2010) shows tentative (5.4 and 2.6
galaxies, based on the combination of the deepest available ACS/HST and
WFC3 data (Oesch et al. 2010; Bouwens et al. 2010a; Bunker et al. 2009; McLure et al. 2010; Yan et al. 2009).
While these objects are too faint to be detected at the current
limits of the deepest Spitzer images, a stack of 14 z-dropout galaxies
from Oesch et al. (2010) shows tentative (5.4 and 2.6 ![]() )
detections
at 3.6 and 4.5
)
detections
at 3.6 and 4.5 ![]() m, respectively (Labbé et al. 2010).
m, respectively (Labbé et al. 2010).
Given these detected ![]() galaxies (or candidates) with
available multi-band photometry, it is of interest to
determine their physical properties such as stellar ages, reddening,
stellar masses, star-formation rates, and related properties such as
their formation redshift, specific star-formation rate, and others.
Several studies have addressed these questions using
different modeling tools (see Labbé et al. 2010; Gonzalez et al. 2010; Capak et al. 2009; Bouwens et al. 2010b).
However, some consider only special types of star-formation
histories (constant star-formation rate), or zero dust extinction, and except for
Capak et al. (2009) none of them
accounts for the effects of nebular emission (lines and continua)
present in star-forming galaxies. Neglecting the latter may
in particular lead to systematically older stellar ages,
to lower dust extinction, and differences in stellar masses, as shown
by Schaerer & de Barros (2009) for
galaxies (or candidates) with
available multi-band photometry, it is of interest to
determine their physical properties such as stellar ages, reddening,
stellar masses, star-formation rates, and related properties such as
their formation redshift, specific star-formation rate, and others.
Several studies have addressed these questions using
different modeling tools (see Labbé et al. 2010; Gonzalez et al. 2010; Capak et al. 2009; Bouwens et al. 2010b).
However, some consider only special types of star-formation
histories (constant star-formation rate), or zero dust extinction, and except for
Capak et al. (2009) none of them
accounts for the effects of nebular emission (lines and continua)
present in star-forming galaxies. Neglecting the latter may
in particular lead to systematically older stellar ages,
to lower dust extinction, and differences in stellar masses, as shown
by Schaerer & de Barros (2009) for ![]() galaxies.
Furthermore, the uncertainties in the derived physical parameters
are not always determined or addressed.
Last, but not least, no ``uniform'' study of the entire data sets
of
galaxies.
Furthermore, the uncertainties in the derived physical parameters
are not always determined or addressed.
Last, but not least, no ``uniform'' study of the entire data sets
of ![]() galaxies has yet been undertaken using the
same methodology and modeling tools.
For all these reasons, we present a critical analysis of the physical
properties of the majority of
galaxies has yet been undertaken using the
same methodology and modeling tools.
For all these reasons, we present a critical analysis of the physical
properties of the majority of
![]() galaxies that have been
discovered recently.
galaxies that have been
discovered recently.
Nebular emission can significantly alter the physical parameters of distant star-forming galaxies derived from broad-band photometry. The main reason for this is that the emission lines, which are invariably present in the H II regions accompanying massive star-formation, strengthen with redshift, because their observed equivalent width scales with (1+z). Since the main emission lines are in the optical (rest-frame) domain and few are in the UV, their presence can mimick a Balmer break in absorption, a signature usually interpreted as an age indicator for stellar populations (Wiklind et al. 2008; Kauffmann et al. 2003). This effect of emission lines, and to a lesser extent also nebular continuum emission, can lead to degeneracies in broad-band SED fits of high-z galaxies as e.g., shown by Zackrisson et al. (2008) and Schaerer & de Barros (2009). The presence of both nebular lines and continua and their contribution to broad-band photometry is well known in nearby star-forming galaxies, such as very metal-poor objects (e.g., I Zw 18, SBS 0335-052, and others), blue compact dwarf galaxies and related objects (cf. Papaderos et al. 2006; Izotov et al. 1997; Papaderos et al. 2002; Pustilnik et al. 2004). The strongest evidence of a significant contribution of the nebular continuum in some nearby star-forming galaxies is the observational finding of a Balmer jump in emission (see Guseva et al. 2007). For these reasons, it is important to include nebular emission in SED fits of distant starbursts and to examine their effect on the derived physical properties.
In the present paper, we analyse samples of
![]() galaxies discovered
recently. The data are compiled from the literature,
including the brightest objects from the sample of Capak et al. (2009),
the ``intermediate'' sample of Gonzalez et al. (2010), and
the faintest z-dropouts recently found with the WFC3 camera.
Applying our up-to-date spectral energy distribution
(SED) fitting tool, we search in particular for possible trends
in the physical parameters of
galaxies discovered
recently. The data are compiled from the literature,
including the brightest objects from the sample of Capak et al. (2009),
the ``intermediate'' sample of Gonzalez et al. (2010), and
the faintest z-dropouts recently found with the WFC3 camera.
Applying our up-to-date spectral energy distribution
(SED) fitting tool, we search in particular for possible trends
in the physical parameters of ![]() galaxies over a range of
galaxies over a range of
![]() 6 mag, i.e., a range of
6 mag, i.e., a range of ![]() 250 in flux. First results
from our analysis are presented here. A more detailed and extensive
study of the properties of z-dropout galaxies and comparisons with
objects at lower redshift will be published elsewhere.
250 in flux. First results
from our analysis are presented here. A more detailed and extensive
study of the properties of z-dropout galaxies and comparisons with
objects at lower redshift will be published elsewhere.
In Sect. 2, we summarise the galaxy sample and the SED
fitting method. In Sect. 3, we present our results for the three
subsamples. The overall results of the whole ![]() LBG sample
and implications are discussed in Sect. 4, where we also
compare our results to those for LBGs at lower redshift.
Our main conclusions are discussed and summarised in Sect. 5.
We assume a flat
LBG sample
and implications are discussed in Sect. 4, where we also
compare our results to those for LBGs at lower redshift.
Our main conclusions are discussed and summarised in Sect. 5.
We assume a flat ![]() CDM cosmology with H0=70 km s-1 Mpc-1,
CDM cosmology with H0=70 km s-1 Mpc-1,
![]() ,
and
,
and
![]() .
All magnitudes are given in the AB system.
.
All magnitudes are given in the AB system.
2 Observational data and modelling tools
2.1 z 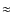 7 galaxy samples
7 galaxy samples
To determine the physical properties of
- two of the three bright (
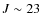 )
z dropout galaxies from the COSMOS survey, discovered
by Capak et al. (2009). We refer to these as the ``bright sample''.
)
z dropout galaxies from the COSMOS survey, discovered
by Capak et al. (2009). We refer to these as the ``bright sample''.
- The 11
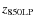 dropout objects identified by Gonzalez et al. (2010) from the HST ACS
and NICMOS data in the GOODS and HUDF fields, plus their mean SED.
These objects typically have
dropout objects identified by Gonzalez et al. (2010) from the HST ACS
and NICMOS data in the GOODS and HUDF fields, plus their mean SED.
These objects typically have
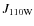
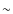 26.-27.5, and are referred to as the
``intermediate sample'';
26.-27.5, and are referred to as the
``intermediate sample'';
- the ``faint sample'', including 15 of the 16
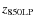 dropout candidates
found by Oesch et al. (2010) in the HUDF using the newly installed WFC3 camera of HST,
and the 15 additional objects identified as
dropout candidates
found by Oesch et al. (2010) in the HUDF using the newly installed WFC3 camera of HST,
and the 15 additional objects identified as
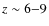 candidates by McLure et al. (2010).
The photometry is taken from McLure et al. (2010).
They typically span a range from
candidates by McLure et al. (2010).
The photometry is taken from McLure et al. (2010).
They typically span a range from
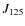
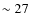 to 29.
We also include the stacked SED obtained by Labbé et al. (2010) for 14 objects
from the Oesch et al. (2010) sample, which shows tentative (5.4 and 2.6
to 29.
We also include the stacked SED obtained by Labbé et al. (2010) for 14 objects
from the Oesch et al. (2010) sample, which shows tentative (5.4 and 2.6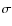 )
detections in the 3.6 and 4.5
)
detections in the 3.6 and 4.5 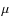 m bands of Spitzer.
m bands of Spitzer.
Except for the 3 objects in the bright sample for which one spectral line was found for each of them, no spectroscopic redshifts are available for these objects. We therefore treat the redshift as a free parameter for all objects.
2.2 SED fitting tool
To analyse the broad-band photometry, we use a modified version of the Hyperz photometric redshift code of Bolzonella et al. (2000) described in Schaerer & de Barros (2009). The main improvement with respect to both earlier versions and other SED fitting codes is the treatment of nebular emission (lines and continua), which can have a significant impact on the broad-band photometry of high redshift galaxies and hence their derived properties (see Schaerer & de Barros 2009). We use a large set of spectral templates (primarily the GALAXEV synthesis models of Bruzual & Charlot 2003), covering different metallicities and a wide range of star formation (SF) histories (bursts, exponentially decreasing, or constant SF), and we add the effects of nebular emission. Models with a more sophisticated description of stellar populations, chemical evolution, dust evolution, and different geometries (see e.g., Schurer et al. 2009) are not used, given the small number of observational constraints.
We adopt a Salpeter IMF from 0.1 to 100 ![]() ,
and we accurately consider the returned ISM mass from stars.
Nebular emission from continuum processes and lines is added to the predicted spectra
from the GALAXEV models, as described in Schaerer & de Barros (2009), proportional
to the Lyman continuum photon production.
The relative line intensities of He and metals are taken from Anders & Fritze-v. Alvensleben (2003),
including galaxies grouped into three metallicity intervals covering
,
and we accurately consider the returned ISM mass from stars.
Nebular emission from continuum processes and lines is added to the predicted spectra
from the GALAXEV models, as described in Schaerer & de Barros (2009), proportional
to the Lyman continuum photon production.
The relative line intensities of He and metals are taken from Anders & Fritze-v. Alvensleben (2003),
including galaxies grouped into three metallicity intervals covering
![]() 1/50
1/50 ![]() to
to ![]() .
Hydrogen lines from the Lyman to the Brackett series are included
with relative intensities given by case B.
Our treatment therefore covers the main emission lines of H, He, C, N, O, and S from the
UV (Ly
.
Hydrogen lines from the Lyman to the Brackett series are included
with relative intensities given by case B.
Our treatment therefore covers the main emission lines of H, He, C, N, O, and S from the
UV (Ly![]() )
to 2
)
to 2 ![]() m (rest-frame), necessary for fitting the SED of
galaxies at z>4 up to 10
m (rest-frame), necessary for fitting the SED of
galaxies at z>4 up to 10 ![]() m (IRAC channel 4).
m (IRAC channel 4).
The free parameters of our SED fits are:
the redshift z,
the metallicity Z (of stars and gas),
the SF history described by the timescale ![]() (where the SF rate is
(where the SF rate is
![]() ),
the age t defined since the onset of star-formation,
the extinction AV described here by the Calzetti law (Calzetti et al. 2000),
and whether or not nebular emission is included.
In some cases, we exclude the Ly
),
the age t defined since the onset of star-formation,
the extinction AV described here by the Calzetti law (Calzetti et al. 2000),
and whether or not nebular emission is included.
In some cases, we exclude the Ly![]() line from the synthetic
spectra, since this line may be attenuated by radiation transfer processes
inside the galaxy or by the intervening intergalactic medium.
line from the synthetic
spectra, since this line may be attenuated by radiation transfer processes
inside the galaxy or by the intervening intergalactic medium.
Here we consider
![]() in steps of 0.1, three metallicities
in steps of 0.1, three metallicities
![]() ,
1/5, 1/20,
,
1/5, 1/20,
![]() ,
7, 10, 30, 50, 70, 100, 300, 500, 700, and 1000 Myr in addition to
bursts and
,
7, 10, 30, 50, 70, 100, 300, 500, 700, and 1000 Myr in addition to
bursts and
![]() ,
ages up to the Hubble time, and
AV= 0-2 (or 4) mag in steps of 0.2.
In general, the combination of all parameters leads to
,
ages up to the Hubble time, and
AV= 0-2 (or 4) mag in steps of 0.2.
In general, the combination of all parameters leads to ![]()
![]() models for each object.
models for each object.
Non-detections are included in the SED fit with Hyperz by setting the
flux in the corresponding filter to zero, and the error to the ![]() upper limit.
For all the above combinations we compute the
upper limit.
For all the above combinations we compute the ![]() and the scaling
factor of the template, which provides information about the SFR and
and the scaling
factor of the template, which provides information about the SFR and ![]() ,
from the fit to the observed SED.
Minimisation of
,
from the fit to the observed SED.
Minimisation of ![]() over the entire parameter space yields the best-fit
parameters.
over the entire parameter space yields the best-fit
parameters.
To illustrate the uncertainties in the resulting fit parameters,
we examine the distribution of ![]() across the entire parameter
space. To determine confidence intervals from the
across the entire parameter
space. To determine confidence intervals from the
![]() distribution, the degree of freedom must be known to
determine the
distribution, the degree of freedom must be known to
determine the
![]() values corresponding to different
confidence levels, or Monte Carlo simulations must be carried out.
In any case, the photometric uncertainties, typically taken
from SExtractor, would also need to be examined critically, since
these may be underestimated, and since errors in the relative
photometric calibration between different telescopes/instruments,
which affect SED fits, are usually not taken into account.
We chose to plot the 1D
values corresponding to different
confidence levels, or Monte Carlo simulations must be carried out.
In any case, the photometric uncertainties, typically taken
from SExtractor, would also need to be examined critically, since
these may be underestimated, and since errors in the relative
photometric calibration between different telescopes/instruments,
which affect SED fits, are usually not taken into account.
We chose to plot the 1D ![]() distribution for the parameter
of interest, marginalised over all other parameters, so that the reader
is able to appreciate these distributions.
Illustrative confidence intervals are determined by assuming
distribution for the parameter
of interest, marginalised over all other parameters, so that the reader
is able to appreciate these distributions.
Illustrative confidence intervals are determined by assuming
![]() ,
the value for one degree of freedom.
This should provide a lower limit to the true uncertainties.
More quantitative estimates of the uncertainties will be given in
a subsequent publication, which will include the analysis of a larger sample
of LBGs at different redshift.
,
the value for one degree of freedom.
This should provide a lower limit to the true uncertainties.
More quantitative estimates of the uncertainties will be given in
a subsequent publication, which will include the analysis of a larger sample
of LBGs at different redshift.
3 Results
3.1 Photometric redshifts: overview of the full sample
The photometric redshifts
![]() of the objects from the three subsamples
were discussed by Capak et al. (2009), Gonzalez et al. (2010), and McLure et al. (2010). Since these
authors use different spectral templates and methods, it is useful
to examine briefly the redshifts we derive from our SED fits,
and their dependence om nebular emission.
Figure 1 shows the best-fit model values for
of the objects from the three subsamples
were discussed by Capak et al. (2009), Gonzalez et al. (2010), and McLure et al. (2010). Since these
authors use different spectral templates and methods, it is useful
to examine briefly the redshifts we derive from our SED fits,
and their dependence om nebular emission.
Figure 1 shows the best-fit model values for
![]() using
either standard templates (i.e., neglecting nebular emission), or including
nebular emission (lines and continua), and the latter but neglecting
the contribution from Ly
using
either standard templates (i.e., neglecting nebular emission), or including
nebular emission (lines and continua), and the latter but neglecting
the contribution from Ly![]() .
Clearly, the contribution of Ly
.
Clearly, the contribution of Ly![]() can lead to higher photometric
redshifts, since it can compensate for the drop of the flux
shortward of Ly
can lead to higher photometric
redshifts, since it can compensate for the drop of the flux
shortward of Ly![]() ,
and hence lead to drop-out at higher
,
and hence lead to drop-out at higher
![]() .
With the prescription used for Ly
.
With the prescription used for Ly![]() in our models (i.e. maximum
emission according to Case B recombination) this typically leads to
in our models (i.e. maximum
emission according to Case B recombination) this typically leads to
![]() .
In some cases, e.g., for 4 objects from the Gonzalez et al. (2010) sample,
the shift is larger. The reason for this large shift is the
available filter set, which include
.
In some cases, e.g., for 4 objects from the Gonzalez et al. (2010) sample,
the shift is larger. The reason for this large shift is the
available filter set, which include
![]() and
and
![]() for this sample,
whereas
for this sample,
whereas
![]() ,
a filter that is intermediate between
,
a filter that is intermediate between
![]() and
and
![]() ,
is available
for the WFC3/HST (faint) subsample.
By including the nebular continuum and all spectral lines except Ly
,
is available
for the WFC3/HST (faint) subsample.
By including the nebular continuum and all spectral lines except Ly![]() (blue symbols) one recovers essentially the same photometric redshifts
as with standard templates. This is expected, since the Lyman break
- the main feature determining
(blue symbols) one recovers essentially the same photometric redshifts
as with standard templates. This is expected, since the Lyman break
- the main feature determining
![]() - can only be strongly affected
by Ly
- can only be strongly affected
by Ly![]() .
.
We compared our photometric redshifts against objects
with known spectroscopic redshifts, where possible. For a sample of B, V, and
i-dropouts from the GOODS fields, we find good agreement for the
majority of objects using the GOODS-MUSIC photometry (Santini et al. 2009).
For this sample, spanning objects with
![]() ,
our results are essentially the same with/without nebular emission,
and with/without Ly
,
our results are essentially the same with/without nebular emission,
and with/without Ly![]() .
Since Ly
.
Since Ly![]() emission may be weaker than predicted by the models,
because of the multiple scattering in the presence of dust (Verhamme et al. 2008)
and/or because of the intervening IGM, we subsequently consider
models including all nebular lines except Ly
emission may be weaker than predicted by the models,
because of the multiple scattering in the presence of dust (Verhamme et al. 2008)
and/or because of the intervening IGM, we subsequently consider
models including all nebular lines except Ly![]() .
It must, however, be noted that for objects with strong Ly
.
It must, however, be noted that for objects with strong Ly![]() emission
the true redshift may be higher than
emission
the true redshift may be higher than
![]() obtained from photometric codes
neglecting this line.
obtained from photometric codes
neglecting this line.
3.2 Bright sample
Our SED fits for these objects yield results (redshift probability distributions
and physical parameters) broadly in agreement with Capak et al. (2009), which is
unsurprising since these authors also include nebular lines in their
analysis using the Le Phare code.
Since we include SEDs spanning metallicities from ![]() to 1/50
to 1/50 ![]() (in contrast to
(in contrast to ![]() only), we obtain a wider range of acceptable
fit parameters.
only), we obtain a wider range of acceptable
fit parameters.
For example, we find evidence of significant reddening in object 1,
with
![]() ,
in agreement with the best-fit value of AV=1.2
given by Capak et al. (2009). The corresponding
,
in agreement with the best-fit value of AV=1.2
given by Capak et al. (2009). The corresponding ![]() distribution
is shown in Fig. A.1.
The situation is similar for object 3, although for
more moderate extinction (
distribution
is shown in Fig. A.1.
The situation is similar for object 3, although for
more moderate extinction (
![]() ).
).
The corresponding range of ages, SFRs, and stellar masses for both
objects, obtained with and without nebular emission, are illustrated in
Figs. A.2 to A.4.
Approximately (within
![]() )
object number 1 (3) has thee best-fit model parameters
)
object number 1 (3) has thee best-fit model parameters
![]() (10-200) Myr,
(10-200) Myr,
![]() .
(10.6-11.6)
.
(10.6-11.6) ![]() ,
and
,
and
![]() (10-104)
(10-104) ![]() yr-1.
We note that a very large range in SFR is obtained from the SED fits
since both the SF history and the extinction are kept free.
The high SFR tail is related to solutions with high extinction
and very young populations, where the UV output per unit SFR remains
below the equilibrium value reached after typically
yr-1.
We note that a very large range in SFR is obtained from the SED fits
since both the SF history and the extinction are kept free.
The high SFR tail is related to solutions with high extinction
and very young populations, where the UV output per unit SFR remains
below the equilibrium value reached after typically ![]() 100 Myr.
For comparison, using the standard SFR(UV) calibration of Kennicutt (1998)
and assuming z=8, one obtains
100 Myr.
For comparison, using the standard SFR(UV) calibration of Kennicutt (1998)
and assuming z=8, one obtains
![]()
![]() yr-1 without extinction correction for object 1, and
yr-1 without extinction correction for object 1, and
![]()
![]() yr-1 adopting AV=1.2 and Calzetti's attenuation law.
yr-1 adopting AV=1.2 and Calzetti's attenuation law.
As noted by Capak et al. (2009), object 3 is not detected in H, possibly indicating
a dip in the flux between J and K (see Fig. 2). If real, this
dip could be explained by the 2175 Å dust absorption feature, as also mentioned
by Capak et al. (2009). Using the Galactic extinction law from Seaton (1979)
provides excellent fits with
![]() ,
as shown in Fig. 2.
The possible indication for a 2175 Å dust absorption feature at such a high redshift
is in contrast to evidence so far, suggesting the absence of this feature
(see e.g., Maiolino et al. 2004).
,
as shown in Fig. 2.
The possible indication for a 2175 Å dust absorption feature at such a high redshift
is in contrast to evidence so far, suggesting the absence of this feature
(see e.g., Maiolino et al. 2004).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg76.png)
|
Figure 1:
Comparison of best-fit model photometric redshifts for the three samples using SEDs
without (x-axis) and with nebular emission (y-axis). Circles, squares, and triangles
indicate the bright, intermediate, and faint samples, respectively. Black symbols show the
comparison with all nebular lines, i.e. including also Ly |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg77.png)
|
Figure 2:
Observed (blue points) and fitted SEDs (solid lines) of object 3
from Capak et al. (2009) using our spectral templates with nebular
emission. Ly |
| Open with DEXTER | |
3.3 Intermediate sample
The redshift probability distribution of the objects from the Gonzalez et al. (2010)
sample is shown in Fig. 3. All objects have a best-fit
photometric redshift at high z (
![]() ). However, 6 of the 11 objects
(ID 4, 5, 6, 7, 8, 10) also have an acceptable fit at low redshift (
). However, 6 of the 11 objects
(ID 4, 5, 6, 7, 8, 10) also have an acceptable fit at low redshift (
![]() )
with a probability comparable to the high-z solution;
the most unreliable objects being ID 6, 7, and 8.
The 3 brightest objects in
)
with a probability comparable to the high-z solution;
the most unreliable objects being ID 6, 7, and 8.
The 3 brightest objects in
![]() (ID 1, 9, 11) favour clearly high-z solutions,
since they provide the largest ``leverage'' on the Lyman-break between
(ID 1, 9, 11) favour clearly high-z solutions,
since they provide the largest ``leverage'' on the Lyman-break between
![]() and the optical data.
and the optical data.
Figure 4 shows an example of an object with
both acceptable low- or high-redshift solutions of similar quality.
The observed SED is reproduced well by a low extinction,
young, starburst at high-z (z=7.14 here) or by a 4.5 Gyr old
stellar populations with AV=0.4 at z=1.29.
Reducing the probability of a low-z interloper would obviously
be possible with deeper optical photometry, which would place tighter constraints
on the Lyman break.
Deep K-band data (not available for this object) or other
constraints on the shape of the SED between 2 and 3.6 ![]() m, may allow us
to distinguish between the two solutions shown here, and provide stronger
constraints on the possible Balmer break - hence the age - of this
object.
m, may allow us
to distinguish between the two solutions shown here, and provide stronger
constraints on the possible Balmer break - hence the age - of this
object.
Object 1 (UDF-640-1417) from Gonzalez et al. (2010) is such an example,
benefiting from deeper optical imaging and Ks data, as shown in
Fig. 5. The former leads to a well-defined and clearly
most probable high-z solution at
![]() .
However, here the observed spectral shape between the rest-frame UV and
optical range (probed by JHK and 3.6-4.5
.
However, here the observed spectral shape between the rest-frame UV and
optical range (probed by JHK and 3.6-4.5 ![]() m, respectively)
may imply a degeneracy between age and extinction.
While Gonzalez et al. (2010) fit this SED with a dust-free
population of several 100 Myr age (cf. our magenta line),
we obtain a tighter fit with models including nebular emission
for a young population plus dust reddening
(typically
m, respectively)
may imply a degeneracy between age and extinction.
While Gonzalez et al. (2010) fit this SED with a dust-free
population of several 100 Myr age (cf. our magenta line),
we obtain a tighter fit with models including nebular emission
for a young population plus dust reddening
(typically ![]() Myr,
Myr,
![]() ).
The distribution of
).
The distribution of ![]() for AV and other parameters are shown
in the Appendix (Figs. B.1 to B.4).
for AV and other parameters are shown
in the Appendix (Figs. B.1 to B.4).
In total, we find three objects
(UDF-640-1417, GNS-zD5, HDFN-3654-1216)
with best-fit solutions for
![]() and relatively young age (
and relatively young age (![]() Myr).
Incidentally these are the three brightest objects in
Myr).
Incidentally these are the three brightest objects in
![]() ,
which may
suggest a trend of extinction with magnitude (cf. below).
However, the significance of non-zero extinction is not very high,
in particular for GNS-zD5 and HDFN-3654-1216, where the 3.6
,
which may
suggest a trend of extinction with magnitude (cf. below).
However, the significance of non-zero extinction is not very high,
in particular for GNS-zD5 and HDFN-3654-1216, where the 3.6 ![]() m flux is affected by a bright neighbouring source (cf. Gonzalez et al. 2010).
m flux is affected by a bright neighbouring source (cf. Gonzalez et al. 2010).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg3.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg84.png)
|
Figure 3:
Redshift probability distribution
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg4.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg85.png)
|
Figure 4:
Observed (blue points) and fitted SEDs (solid lines) of object 8
(GNS-zD4) from Gonzalez et al. (2010) using standard Bruzual & Charlot solar metallicity
models. The best-fit (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg86.png)
|
Figure 5:
Observed (blue points) and best-fit SEDs (solid lines) of object 1
(UDF-640-1417) from Gonzalez et al. (2010) using standard Bruzual and Charlot solar metallicity
models.
The magenta line shows the best-fit for templates without nebular emission, and
assuming that
|
| Open with DEXTER | |
Considering the entire parameter space for the whole sample
(cf. Figs. B.1 to B.4), we
find that age and dust extinction of most objects are not well constrained,
and could reach from few Myr up to the age of the universe at that redshift,
and from
![]() to
to ![]() 1.6 mag for some objects.
In particular, the data does not allow us to conclude that these
galaxies show no sign of dust extinction.
Furthermore, their age and hence formation redshift remains poorly constrained.
The same is also true for the mean SED from Gonzalez et al. (2010), which
yields results compatible with those of the individual objects, as expected
(see thick line in the plots).
For comparison, Gonzalez et al. (2010) find fairly old best-fit stellar-mass-weighted ages
1.6 mag for some objects.
In particular, the data does not allow us to conclude that these
galaxies show no sign of dust extinction.
Furthermore, their age and hence formation redshift remains poorly constrained.
The same is also true for the mean SED from Gonzalez et al. (2010), which
yields results compatible with those of the individual objects, as expected
(see thick line in the plots).
For comparison, Gonzalez et al. (2010) find fairly old best-fit stellar-mass-weighted ages
![]() Myr
Myr![]() typically.
Both the assumption of
typically.
Both the assumption of
![]() and Av=0 lead to the highest age, since both
effects minimise the ratio of the rest-frame visible/UV light, the main age constraint.
and Av=0 lead to the highest age, since both
effects minimise the ratio of the rest-frame visible/UV light, the main age constraint.
Allowing for wide range of SF histories, variable extinction, and for nebular emission
yields, on average, a broader age range (between a few Myr and up to the maximum age),
room for
extinction up to
![]() ,
stellar masses from 108.5 to 1010
,
stellar masses from 108.5 to 1010 ![]() ,
and
,
and
![]()
![]() yr-1. In other words, the properties of the galaxies
from this sample of intermediate brightness (
yr-1. In other words, the properties of the galaxies
from this sample of intermediate brightness (
![]()
![]() ), are clearly
more uncertain than indicated by Gonzalez et al. (2010), who consider only a restricted
range of the parameter space.
), are clearly
more uncertain than indicated by Gonzalez et al. (2010), who consider only a restricted
range of the parameter space.
3.4 Faint sample
Using the first UDF observations taken with the newly installed WFC3 camera
onboard HST, four studies have identified ![]() 11 to 20
11 to 20
![]() galaxy candidates (or
galaxy candidates (or
![]() drop-outs) (Oesch et al. 2010; Bunker et al. 2009; McLure et al. 2010; Yan et al. 2009).
What can be said about their physical properties?
drop-outs) (Oesch et al. 2010; Bunker et al. 2009; McLure et al. 2010; Yan et al. 2009).
What can be said about their physical properties?
3.4.1 Photometric redshifts
McLure et al. (2010) had previously examined the photometric redshifts and uncertainties
for their sample, which also covers the majority of ![]() galaxies found
by the other groups (Oesch et al. 2010; Bunker et al. 2009; Yan et al. 2009).
Unsurprisingly, our results using a modified version of the Hyperz code
also used by McLure et al. (2010) and a slightly more extended template library,
confirm their findings. In particular, for the
galaxies found
by the other groups (Oesch et al. 2010; Bunker et al. 2009; Yan et al. 2009).
Unsurprisingly, our results using a modified version of the Hyperz code
also used by McLure et al. (2010) and a slightly more extended template library,
confirm their findings. In particular, for the ![]() sample of Oesch et al. (2010)
we find that their objects consistently show photometric redshifts with well-defined
probability distributions peaking between
sample of Oesch et al. (2010)
we find that their objects consistently show photometric redshifts with well-defined
probability distributions peaking between
![]() and 7.6.
For fainter z-dropouts and Y-dropouts, the photometric redshift becomes
far more uncertain, and a significant fraction of the objects could
also be low-z galaxies. As already pointed out by McLure et al. (2010) and Capak et al. (2009),
the depth of the optical imaging becomes the limiting factor for objects
that faint in the near-IR.
and 7.6.
For fainter z-dropouts and Y-dropouts, the photometric redshift becomes
far more uncertain, and a significant fraction of the objects could
also be low-z galaxies. As already pointed out by McLure et al. (2010) and Capak et al. (2009),
the depth of the optical imaging becomes the limiting factor for objects
that faint in the near-IR.
3.4.2 UV slope
One group pointed out that the fainter of these objects
had very blue UV-continuum slopes, ![]() ,
indicative of
``non-standard'' properties of these galaxies (Bouwens et al. 2010b).
Their data, shown as red squares in Fig. 6, exhibits
a trend of decreasing
,
indicative of
``non-standard'' properties of these galaxies (Bouwens et al. 2010b).
Their data, shown as red squares in Fig. 6, exhibits
a trend of decreasing ![]() (as estimated from their (
(as estimated from their (
![]() -
-
![]() )
colour) towards fainter
magnitudes.
From the very steep slopes (i.e., low values of
)
colour) towards fainter
magnitudes.
From the very steep slopes (i.e., low values of
![]() )
reached
in faint objects, Bouwens et al. (2010b) claim that extremely low metallicities and
large Lyman continuum escape fractions seem to be
required to understand these objects, since ``standard'' evolutionary synthesis models
predict minimum values of
)
reached
in faint objects, Bouwens et al. (2010b) claim that extremely low metallicities and
large Lyman continuum escape fractions seem to be
required to understand these objects, since ``standard'' evolutionary synthesis models
predict minimum values of
![]() for young stellar populations.
As the data and the errorbars from different groups plotted
in Fig. 6 show, we cannot reach similar conclusions,
given the uncertainties in the colour measurement used to determine
for young stellar populations.
As the data and the errorbars from different groups plotted
in Fig. 6 show, we cannot reach similar conclusions,
given the uncertainties in the colour measurement used to determine ![]() .
For the bulk of the sources, the
.
For the bulk of the sources, the ![]() -slope is compatible within
-slope is compatible within ![]() with
normal values of
with
normal values of
![]() or flatter slopes.
Furthermore, it is unclear whether the (
or flatter slopes.
Furthermore, it is unclear whether the (
![]() -
-
![]() )
colour exhibits any
systematic trend towards fainter magnitudes.
The observations do not exclude different properties such as
extremely low metallicities and large Lyman continuum escape fractions
for some of the objects at
)
colour exhibits any
systematic trend towards fainter magnitudes.
The observations do not exclude different properties such as
extremely low metallicities and large Lyman continuum escape fractions
for some of the objects at ![]() .
However, the low significance of these deviations do not justify
making assumptions that differ significantly from those commonly adopted for
the analysis of lower redshift objects.
.
However, the low significance of these deviations do not justify
making assumptions that differ significantly from those commonly adopted for
the analysis of lower redshift objects.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg97.png)
|
Figure 6:
UV slope |
| Open with DEXTER | |
With the WFC3 filters used in this survey, it is possible
to generate unusually blue (
![]() -
-
![]() )
colours in certain
circumstances from spectral templates including nebular emission.
Such a case is illustrated in Fig. 7, showing
a fit to object 2502 from the McLure et al. (2010) sample.
Shown here is a model of a very young stellar population
with solar metallicity including lines and nebular continuum
emission redshifted to either z=6.96 (dashed, magenta line) or
z=7.97 (solid, black line). In the latter case, the strong
intrinsic Ly
)
colours in certain
circumstances from spectral templates including nebular emission.
Such a case is illustrated in Fig. 7, showing
a fit to object 2502 from the McLure et al. (2010) sample.
Shown here is a model of a very young stellar population
with solar metallicity including lines and nebular continuum
emission redshifted to either z=6.96 (dashed, magenta line) or
z=7.97 (solid, black line). In the latter case, the strong
intrinsic Ly![]() emission (with
emission (with
![]() Å)
boosts the flux in both
Å)
boosts the flux in both
![]() and
and
![]() since
these filters overlap by
since
these filters overlap by ![]() 0.1
0.1 ![]() m.
This provides a very blue (
m.
This provides a very blue (
![]() -
-
![]() )
colour, and enough
flux in
)
colour, and enough
flux in
![]() to ensure that this object does not appear as a
to ensure that this object does not appear as a
![]() -drop
even at
-drop
even at ![]() .
If at
.
If at ![]() ,
as implied by SED fits excluding
the Ly
,
as implied by SED fits excluding
the Ly![]() line (magenta line) or from simple colour-criteria
designed to select
line (magenta line) or from simple colour-criteria
designed to select ![]() galaxies (e.g Oesch et al. 2010),
the (
galaxies (e.g Oesch et al. 2010),
the (
![]() -
-
![]() )
colour is not affected by Ly
)
colour is not affected by Ly![]() .
However, this is not necessarily the case for all z-dropout galaxies
since strong Ly
.
However, this is not necessarily the case for all z-dropout galaxies
since strong Ly![]() emission, if present, may mimic a lower
redshift (cf. Sect. 3.1).
The likelyhood of this situation remains difficult to establish,
especially since Ly
emission, if present, may mimic a lower
redshift (cf. Sect. 3.1).
The likelyhood of this situation remains difficult to establish,
especially since Ly![]() may be differentially affected by dust,
and scattered by the IGM.
may be differentially affected by dust,
and scattered by the IGM.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg7.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg100.png)
|
Figure 7:
Best-fit SEDs of object 2502 (photometry in blue symbols) of
McLure et al. (2010) for solar metallicity models including nebular emission.
The black solid line shows the model including all lines (Ly |
| Open with DEXTER | |
3.4.3 Age and reddening
For the 15 objects in common between the Oesch and McLure samples, we find young
stellar populations (![]() Myr) as best-fits, and zero extinction, except for objects
688, 835, and 1092, with
Myr) as best-fits, and zero extinction, except for objects
688, 835, and 1092, with
![]() .
However, as for the objects from the intermediate sample, the distribution of
.
However, as for the objects from the intermediate sample, the distribution of ![]() is
very flat (cf. Figs. C.1 to C.4), allowing a
wide range of extinctions (
is
very flat (cf. Figs. C.1 to C.4), allowing a
wide range of extinctions (
![]() ), ages of
), ages of ![]() to several 100 Myr,
stellar masses from 107 to few times 109
to several 100 Myr,
stellar masses from 107 to few times 109 ![]() ,
and SFRs from 0.1 (or less) to
,
and SFRs from 0.1 (or less) to ![]() 200
200 ![]() yr-1, for most objects in the faint sample.
The wide age range, is possible, e.g., since the upper limits at 3.6 and 4.5
yr-1, for most objects in the faint sample.
The wide age range, is possible, e.g., since the upper limits at 3.6 and 4.5 ![]() m do not provide a strong enough constraint on the optical to UV flux of these faint
objects. Given the rapid evolution with time in the mass/light ratio involved here
(mostly the UV-optical
domain), the uncertainty in the ages translates into a large spread in
stellar masses, as show by Fig. C.3. The wide range of
acceptable SFR values is due to both age and SF history (parametrised
here by the e-folding timescale
m do not provide a strong enough constraint on the optical to UV flux of these faint
objects. Given the rapid evolution with time in the mass/light ratio involved here
(mostly the UV-optical
domain), the uncertainty in the ages translates into a large spread in
stellar masses, as show by Fig. C.3. The wide range of
acceptable SFR values is due to both age and SF history (parametrised
here by the e-folding timescale ![]() )
being kept free, in contrast e.g., to
commonly used SFR(UV) calibrations assuming
)
being kept free, in contrast e.g., to
commonly used SFR(UV) calibrations assuming
![]() and ages
and ages ![]() 0 Myr.
0 Myr.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg8.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg105.png)
|
Figure 8:
Best-fit SEDs to the SED of the stack of 14 z-dropout galaxies
from Oesch et al. (2010) measured by Labbé et al. (2010).
Photometry is shown by blue symbols; including the 1 |
| Open with DEXTER | |
3.4.4 Physical properties from the stacked SED
The individual z-dropout candidates of Oesch et al. (2010) and McLure et al. (2010) are
undetected in the deep, available 3.6 and 4.5 ![]() m Spitzer images, but
Labbé et al. (2010) stacked the images of 14 of the 16 z-dropout galaxies from Oesch et al. (2010),
obtaining 5.4 and 2.6
m Spitzer images, but
Labbé et al. (2010) stacked the images of 14 of the 16 z-dropout galaxies from Oesch et al. (2010),
obtaining 5.4 and 2.6![]() detections in these bands.
Fitting the SED of this stack, we find that the physical parameters
are more tightly constrained, as the thick line in Figs. C.1 to C.4 show.
Overall our best-fit values (with or without nebular
emission) are very similar to those obtained by Labbé et al. (2010),
bearing the different definitions of stellar ages t and tW in
mind. Furthermore, the values of the physical parameters derived for
the majority of the individual objects is compatible with the values
determined from the stack.
detections in these bands.
Fitting the SED of this stack, we find that the physical parameters
are more tightly constrained, as the thick line in Figs. C.1 to C.4 show.
Overall our best-fit values (with or without nebular
emission) are very similar to those obtained by Labbé et al. (2010),
bearing the different definitions of stellar ages t and tW in
mind. Furthermore, the values of the physical parameters derived for
the majority of the individual objects is compatible with the values
determined from the stack.
An uncertainty remains, however, in the age and consequently also in the stellar
mass determination. We first obtain secondary solutions with
![]() with young ages (
with young ages (![]() 4-5 Myr) and a small extinction (
4-5 Myr) and a small extinction (
![]() )
as we consider all metallicities, both with our without nebular
emission. Furthermore, if we suppress the Ly
)
as we consider all metallicities, both with our without nebular
emission. Furthermore, if we suppress the Ly![]() line we improve the fit, leading
to a best-fit at young ages (
line we improve the fit, leading
to a best-fit at young ages (![]() 2-7 Myr).
The corresponding
2-7 Myr).
The corresponding ![]() distributions illustrating these results are shown
in Figs. C.5 to C.8, and
SED fits from these models are shown in Fig. 8.
This figure clearly illustrates how an apparent Balmer break can
be explained by an old population (here
distributions illustrating these results are shown
in Figs. C.5 to C.8, and
SED fits from these models are shown in Fig. 8.
This figure clearly illustrates how an apparent Balmer break can
be explained by an old population (here
![]() Myr) or by nebular
emission from a younger population, as already shown by Schaerer & de Barros (2009).
A suppression of the Ly
Myr) or by nebular
emission from a younger population, as already shown by Schaerer & de Barros (2009).
A suppression of the Ly![]() line is justified since Ly
line is justified since Ly![]() may be attenuated by radiation transfer processes inside the galaxy or by the
intervening intergalactic medium.
In any case, neglecting nebular emission is inconsistent for spectral
templates with recent (
may be attenuated by radiation transfer processes inside the galaxy or by the
intervening intergalactic medium.
In any case, neglecting nebular emission is inconsistent for spectral
templates with recent (![]() 10 Myr) or ongoing star formation.
Finally, in comparison with the bright and intermediate samples
we may also question why the faintest
10 Myr) or ongoing star formation.
Finally, in comparison with the bright and intermediate samples
we may also question why the faintest ![]() objects
should have the oldest stellar populations, whereas the ages
of brighter objects are compatible with a broad range of ages,
including young ones.
objects
should have the oldest stellar populations, whereas the ages
of brighter objects are compatible with a broad range of ages,
including young ones.
The uncertainty in the age also translates into an uncertainty in stellar mass.
Whereas the estimated average mass is
![]()
![]() for the old population (cf. Labbé et al. 2010), it is more than a factor of 10 lower for young ages (see Fig. C.7), since nebular
emission contributes partly to the rest-frame optical domain.
The SFR is, however, hardly affected by this uncertainty (see Fig. C.8),
since it is more sensitive to the rest-frame UV light present in
both young and old star-forming populations.
In consequence, the specific SFR (SFR
for the old population (cf. Labbé et al. 2010), it is more than a factor of 10 lower for young ages (see Fig. C.7), since nebular
emission contributes partly to the rest-frame optical domain.
The SFR is, however, hardly affected by this uncertainty (see Fig. C.8),
since it is more sensitive to the rest-frame UV light present in
both young and old star-forming populations.
In consequence, the specific SFR (SFR![]() )
could be significantly higher
than advocated by Labbé et al. (2010).
Before performing spectroscopy for these objects - a currently
impossible task - to examine if the 3.6
)
could be significantly higher
than advocated by Labbé et al. (2010).
Before performing spectroscopy for these objects - a currently
impossible task - to examine if the 3.6 ![]() m filter is truly
affected by emission lines as predicted by the model, the present data
does not allow us to completely rule out one or the other solution.
m filter is truly
affected by emission lines as predicted by the model, the present data
does not allow us to completely rule out one or the other solution.
4 Discussion
We discuss the effects of varying the model assumptions on the physical parameters derived. We then examine the main derived properties and possible correlations among them for the ensemble of galaxies studied here, and compare any correlations found to those of lower redshift galaxies. Finally, we discuss some implications of our results.![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg9.eps}
\vspace*{6mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg110.png)
|
Figure 9:
Comparison of best-fit values for the age t ( upper left), extinction AV ( upper right),
stellar mass |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg10.eps}
\vspace*{6mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg111.png)
|
Figure 10:
Best-fit value for the age (upper left), extinction ( upper right),
stellar mass ( lower left), and star-formation rate ( lower right) as a function of
the observed
|
| Open with DEXTER | |
4.1 Effects of varying model assumptions
Varying the model assumptions in broad-band SED fits affects the inferred
physical parameters of distant galaxies in ways that
have been discussed in several studies, e.g.,
by Yabe et al. (2009) in quite some detail (cf. also Gonzalez et al. 2010; Papovich et al. 2001; Sawicki et al. 2007, and others).
The most relevant assumptions are the star-formation histories, metallicity, the inclusion
of dust extinction, and the adopted extinction law. Furthermore, the inclusion
of nebular emission and the assumptions made to do so also affect the results
as shown here and in (cf. also Yabe et al. 2009; Schaerer & de Barros 2009, and the latter for a discussion of the
effect of H![]() ).
).
The impact of different model assumptions on the best-fit parameters of our sample is shown
in Fig. 9, where we plot the values from our ``reference model'' (including
nebular emission, Ly![]() suppressed, all SF histories, all ages, all extinction values, and all
metallicities) on the x-axis, and the same from comparison models on the y-axis.
The models we consider here for comparison are:
1) models with
suppressed, all SF histories, all ages, all extinction values, and all
metallicities) on the x-axis, and the same from comparison models on the y-axis.
The models we consider here for comparison are:
1) models with
![]() Myr (yellow),
2) models with Ly
Myr (yellow),
2) models with Ly![]() (blue),
3) models without nebular emission (red), and
4) same as 3), but for
(blue),
3) models without nebular emission (red), and
4) same as 3), but for
![]() only (green).
SEDs without nebular emission (3) may be taken as an extreme case of
models with a very large escape fraction (
only (green).
SEDs without nebular emission (3) may be taken as an extreme case of
models with a very large escape fraction (
![]() )
of ionising
radiation from the Lyman continuum, whereas in the other cases
we implicitly assume no escape (
)
of ionising
radiation from the Lyman continuum, whereas in the other cases
we implicitly assume no escape (
![]() ), maximising
thus nebular emission if young massive stars are present.
One may theoretically expect an evolution of
), maximising
thus nebular emission if young massive stars are present.
One may theoretically expect an evolution of
![]() with redshift,
galaxy mass, and other properties, although large differences remain even
between simulations (see e.g., Wise & Cen 2009; Gnedin et al. 2008; Razoumov & Sommer-Larsen 2010).
Intermediate values of
with redshift,
galaxy mass, and other properties, although large differences remain even
between simulations (see e.g., Wise & Cen 2009; Gnedin et al. 2008; Razoumov & Sommer-Larsen 2010).
Intermediate values of
![]() may be included in future models.
may be included in future models.
Circles, squares, and triangles in Fig. 9 represent objects from the bright, intermediate, and faint samples, respectively. In Figs. 9 to 12, we now include all objects of McLure et al. (2010) in the faint sample, i.e. 15 objects in addition to the 15 of Oesch et al. (2010), to maximise the sample size and because the results with the additional sample do not show noticeable differences. We do not show the effect of fixing metallicity, since it is small compared to the other effects discussed here. We now discuss the dependence of the physical parameters on these models assumptions one-by-one.
4.1.1 Stellar mass
As noted and discussed by Yabe et al. (2009) and others, the
stellar mass ![]() is the least sensitive parameter to the model assumptions,
especially when measurements
for the rest frame optical domain are available. This is mainly because
it is derived from the absolute scaling of the overall SED, and that the
mass-to-light ratio in the optical does not change much with age and star-formation
history.
is the least sensitive parameter to the model assumptions,
especially when measurements
for the rest frame optical domain are available. This is mainly because
it is derived from the absolute scaling of the overall SED, and that the
mass-to-light ratio in the optical does not change much with age and star-formation
history.
4.1.2 Age
In contrast, age is the most sensitive quantity (cf. Yabe et al. 2009). From Fig. 9 it is clear that models without nebular emission (red and green) yield older ages in most cases, as already discussed above (cf. Schaerer & de Barros 2009). By assuming constant SFR, we also tend to infer older ages, as is well known, but not in all cases (see green symbols). The inclusion (suppression) of Ly4.1.3 Extinction
Although a spread is obtained in AV for the different model assumptions,
the best-fit model values of AV correlate reasonably well around our ``reference value''
for most objects. The greatest differences arise when the SF history is varied
- here imposing
![]() Myr leads to lower AV and higher ages (because of the
age-extinction degeneracy), as shown by the yellow symbols - and, for the same reason,
when nebular lines are omitted, as shown by some outliers with red symbols.
The largest differences in stellar mass are found for some objects where
nebular emission leads to a strong age reduction and hence a lower M/L ratio.
Myr leads to lower AV and higher ages (because of the
age-extinction degeneracy), as shown by the yellow symbols - and, for the same reason,
when nebular lines are omitted, as shown by some outliers with red symbols.
The largest differences in stellar mass are found for some objects where
nebular emission leads to a strong age reduction and hence a lower M/L ratio.
4.1.4 SFR
The star-formation rate SFR deserves special comment. The value of the current SFR (SFR(t)) obtained from SED fits depends strongly on both SFH and age. Formally,The comparisons shown here all include a marginalisation over the three
metallicities Z considered in our models. As already mentioned, fixing Zleads to small differences.
Given our limited knowledge of high-z galaxies, other variations in the input physics,
e.g., for the star-formation history or the reddening law, could be considered.
Quantifying this is beyond the scope of this paper. The effect of
different reddening laws on the physical parameters, however, can be understood
quite simply, and is e.g., illustrated in Yabe et al. (2009).
Rising SF histories, which are not considered here, have, e.g., been advocated
by Finlator et al. (2007). We note, that these SF histories would in general
correspond to a higher extinction than decreasing ones, to reproduce the observed
SEDs of LBGs (cf. Finlator et al. 2007). This would strengthen our arguments
in favour of dust at ![]() .
.
4.2 Correlations between physical properties in z  7 galaxies
7 galaxies
Although the uncertainties in the physical parameters are relatively large for most
objects, it is helpful to search for correlations between them, and
with observed quantities.
Figure 10 shows the best-fit values for age, AV, stellar mass, and
SFR of all objects from the 3 samples, plotted as a function of the J-band magnitude,
which traces approximately the rest-frame UV at 1500 Å.
The values plotted here are taken from our model 1, i.e., the reference
model plus the constraint that
![]() Myr, in particular to assure
that SFR is properly defined.
We also compare the best-fit values obtained by Gonzalez et al. (2010) and Labbé et al. (2010)
for the mean/stacked SED for the intermediate and faint samples, and the available
fit results from Capak et al. (2009) for the bright objects. The origin of the
differences with these authors have already been discussed above.
Myr, in particular to assure
that SFR is properly defined.
We also compare the best-fit values obtained by Gonzalez et al. (2010) and Labbé et al. (2010)
for the mean/stacked SED for the intermediate and faint samples, and the available
fit results from Capak et al. (2009) for the bright objects. The origin of the
differences with these authors have already been discussed above.
As is clear for the different samples, stellar ages and
extinction cover a wide range of values with no clear or strong trend.
It is possible that a tendency of increasing AV for brighter objects exists, as
would be expected from other studies at lower redshift (cf. below).
This trend becomes clearer when AV is plotted as a function of stellar mass,
as shown in Fig. 11.
We also find a tentative trend of the extinction AV with galaxy mass ![]() ,
as shown in Fig. 11.
,
as shown in Fig. 11.
Both the stellar mass and SFR show clear trends with the J-band magnitude, albeit
with a significant scatter. We note
that the scatter in the mass-magnitude relation for the ![]() objects
does not significantly decrease when 3.6 or 4.5
objects
does not significantly decrease when 3.6 or 4.5 ![]() m photometry is used.
Deviations of the best-fit SFR from the simple ``standard'' calibration, also indicated
in Fig. 10 for AV=0, are caused by non-zero extinction, age effects,
and exponentially decreasing SF histories, or combinations thereof, as already discussed above.
Figure 12 shows the corresponding correlation between stellar
mass and SFR, suggesting a fairly well-defined mass-SFR relation at
m photometry is used.
Deviations of the best-fit SFR from the simple ``standard'' calibration, also indicated
in Fig. 10 for AV=0, are caused by non-zero extinction, age effects,
and exponentially decreasing SF histories, or combinations thereof, as already discussed above.
Figure 12 shows the corresponding correlation between stellar
mass and SFR, suggesting a fairly well-defined mass-SFR relation at ![]() .
Our best-fit values yield on average higher specific star-formation rates
(
.
Our best-fit values yield on average higher specific star-formation rates
(
![]() )
than the values derived by Gonzalez et al. (2010) and Labbé et al. (2010)
shown by large open circles, and tend to indicate a relatively large
spread in SSFR.
)
than the values derived by Gonzalez et al. (2010) and Labbé et al. (2010)
shown by large open circles, and tend to indicate a relatively large
spread in SSFR.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg11.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg123.png)
|
Figure 11:
Black circles, green squares, blue triangles show best-fit values of
AV versus |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg12.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg124.png)
|
Figure 12:
Stellar mass-SFR relation for the |
| Open with DEXTER | |
4.3 Comparison with lower redshift galaxies
Although an exhaustive comparison with studies of the physical
properties of LBGs at lower redshift is clearly beyond the scope
of the present paper, it is worthwhile comparing briefly
our results with those obtained at ![]() ,
and at lower redshift.
To do so we refer to the detailed SED fitting analysis and discussions
of Yabe et al. (2009, and references therein), who have compared the physical parameters of
z=2, 3, 5, and 6 LBGs from different samples.
,
and at lower redshift.
To do so we refer to the detailed SED fitting analysis and discussions
of Yabe et al. (2009, and references therein), who have compared the physical parameters of
z=2, 3, 5, and 6 LBGs from different samples.
The analysis of both Yabe et al. and Verma et al. (2007)
of ![]() galaxies find
clear signs of significant extinction. The former study finds E(B-V) values ranging
from 0 to
galaxies find
clear signs of significant extinction. The former study finds E(B-V) values ranging
from 0 to ![]() 0.5, with a median of
E(B-V)-0.22, corresponding to
AV=0.89 i.e. a factor 9 attenuation of the UV flux!
Our typical AV values are lower and the uncertainties are large;
but in many cases the best-fit model extinction is AV>0 for the
0.5, with a median of
E(B-V)-0.22, corresponding to
AV=0.89 i.e. a factor 9 attenuation of the UV flux!
Our typical AV values are lower and the uncertainties are large;
but in many cases the best-fit model extinction is AV>0 for the ![]() LBGs.
For comparison, Bouwens et al. (2010b,2009) advocate
an attenuation of the UV flux by a factor 1.35-1.6 (corresponding
to
LBGs.
For comparison, Bouwens et al. (2010b,2009) advocate
an attenuation of the UV flux by a factor 1.35-1.6 (corresponding
to
![]() for the Calzetti law) at
for the Calzetti law) at
![]() ,
and
an attenuation by 2.7 (
,
and
an attenuation by 2.7 (
![]() )
at
)
at
![]() .
The extinction obtained by Yabe et al. (2009) and from our analysis is thus typically
higher by a factor 3 than in the work of Bouwens and collaborators,
who estimate the dust attenuation from the UV slope.
.
The extinction obtained by Yabe et al. (2009) and from our analysis is thus typically
higher by a factor 3 than in the work of Bouwens and collaborators,
who estimate the dust attenuation from the UV slope.
We find a trend of increasing extinction with galaxy mass (Fig. 11).
At
![]() ,
it is known that dust extinction increases with
bolometric luminosity (i.e., also with SFR), which in turn increases with stellar
mass (e.g., Reddy et al. 2006; Daddi et al. 2007; Reddy et al. 2008; Buat et al. 2005; Burgarella et al. 2007; Buat et al. 2008).
Luminosity-dependent dust corrections have been proposed, e.g., by
Reddy & Steidel (2009) and Bouwens et al. (2009), based on observed variations of the UV slope
with
,
it is known that dust extinction increases with
bolometric luminosity (i.e., also with SFR), which in turn increases with stellar
mass (e.g., Reddy et al. 2006; Daddi et al. 2007; Reddy et al. 2008; Buat et al. 2005; Burgarella et al. 2007; Buat et al. 2008).
Luminosity-dependent dust corrections have been proposed, e.g., by
Reddy & Steidel (2009) and Bouwens et al. (2009), based on observed variations of the UV slope
with
![]() .
From these results, it is not surprising to find a
similar relation at
.
From these results, it is not surprising to find a
similar relation at ![]() ,
here expressed as extinction versus
stellar mass. The origin of a mass-extinction relation is most likely
related to that of the mass-metallicity relation
(cf. Tremonti et al. 2004; Finlator et al. 2007; Maiolino et al. 2008; Erb et al. 2006).
The data of Yabe et al. (2009) at
,
here expressed as extinction versus
stellar mass. The origin of a mass-extinction relation is most likely
related to that of the mass-metallicity relation
(cf. Tremonti et al. 2004; Finlator et al. 2007; Maiolino et al. 2008; Erb et al. 2006).
The data of Yabe et al. (2009) at ![]() ,
also plotted in
Fig. 11, may show a less clear trend with mass and some offset.
A systematic differential analysis of LBG samples at different redshifts,
will be necessary to shed more light on these issues.
,
also plotted in
Fig. 11, may show a less clear trend with mass and some offset.
A systematic differential analysis of LBG samples at different redshifts,
will be necessary to shed more light on these issues.
The best-fit model values of the other physical parameters (age, mass, and SFR)
span a similar range as found by Yabe et al. (2009) for ![]() LBGs.
In contrast to the results of Gonzalez et al. (2010) and Labbé et al. (2010), our relatively
young ages resemble those found by Verma et al. (2007) and Yabe et al. (2009) for
LBGs.
In contrast to the results of Gonzalez et al. (2010) and Labbé et al. (2010), our relatively
young ages resemble those found by Verma et al. (2007) and Yabe et al. (2009) for ![]() ,
which are younger than
,
which are younger than
![]() LBGs (cf. Shapley et al. 2005; Yabe et al. 2009; Shapley et al. 2001; Sawicki et al. 2007). However, other studies (e.g., Stark et al. 2007a,2009; Eyles et al. 2007), find relatively
old ages at
LBGs (cf. Shapley et al. 2005; Yabe et al. 2009; Shapley et al. 2001; Sawicki et al. 2007). However, other studies (e.g., Stark et al. 2007a,2009; Eyles et al. 2007), find relatively
old ages at ![]() ,
and Yabe et al. (2009) confirm some of them with
their method. Whether LBGs show a clear trend of decreasing age with
increasing redshift, as one may naively expect, thus remains to be clarified.
,
and Yabe et al. (2009) confirm some of them with
their method. Whether LBGs show a clear trend of decreasing age with
increasing redshift, as one may naively expect, thus remains to be clarified.
For the IRAC-detected objects at ![]() (the bright and intermediate
samples), the relation between stellar mass
and absolute optical magnitude (derived from the 4.5
(the bright and intermediate
samples), the relation between stellar mass
and absolute optical magnitude (derived from the 4.5 ![]() m flux)
is very similar to that of the
m flux)
is very similar to that of the ![]() objects. The lower masses of the
faint
objects. The lower masses of the
faint ![]() subsample - undetected by IRAC - provide a natural
extension towards fainter objects.
A similar behaviour is also found for the SFR, when comparing our
subsample - undetected by IRAC - provide a natural
extension towards fainter objects.
A similar behaviour is also found for the SFR, when comparing our
![]() results to those of Yabe et al. (2009).
results to those of Yabe et al. (2009).
The ![]() -SFR relation found at
-SFR relation found at ![]() resembles that of
resembles that of
![]() LBGs
(see Fig. 12).
We note that most objects lie above the
LBGs
(see Fig. 12).
We note that most objects lie above the ![]() -SFR relation found
at
-SFR relation found
at
![]() (cf. Daddi et al. 2007; Sawicki et al. 2007).
However, both the behaviour and the scatter found for the
(cf. Daddi et al. 2007; Sawicki et al. 2007).
However, both the behaviour and the scatter found for the ![]() objects resembles
that of
objects resembles
that of
![]() LBGs, also shown in this plot.
Given the large uncertainties for the
LBGs, also shown in this plot.
Given the large uncertainties for the ![]() objects, and the different
methods used in these analysis, it is possible that the same
objects, and the different
methods used in these analysis, it is possible that the same ![]() -SFR
relation (with a similar scatter) is in place from
-SFR
relation (with a similar scatter) is in place from ![]() to 2
and that the specific SFR declines to lower redshift
(cf. Gonzalez et al. 2010; Daddi et al. 2007; Elbaz et al. 2007; Noeske et al. 2007).
to 2
and that the specific SFR declines to lower redshift
(cf. Gonzalez et al. 2010; Daddi et al. 2007; Elbaz et al. 2007; Noeske et al. 2007).
A detailed study of the physical parameters of LBGs over a wide redshift domain with our modeling tools, including more in-depth comparisons of the results from different methods/groups, will be presented elsewhere.
4.4 Implications
An important result of this study is the possible discovery of dust extinction
in LBGs at ![]() from detailed SED modeling, which contrasts with claims of
basically dust-free objects from studies of their UV slope or from too
restrictive SED modeling (cf. Labbé et al. 2010; Gonzalez et al. 2010; Bouwens et al. 2010b).
If this were correct, the UV attenuation - up to
from detailed SED modeling, which contrasts with claims of
basically dust-free objects from studies of their UV slope or from too
restrictive SED modeling (cf. Labbé et al. 2010; Gonzalez et al. 2010; Bouwens et al. 2010b).
If this were correct, the UV attenuation - up to
![]() (factor 20)
for the brightest objects - would imply a higher SFR
density at high redshift than previously inferred.
However, to quantify the average dust correction remains difficult, especially
given the large uncertainties for the individual objects and the possible
dependence of AV on the UV luminosity and/or stellar mass.
Even if our results imply that a non-negligible dust correction
is required at
(factor 20)
for the brightest objects - would imply a higher SFR
density at high redshift than previously inferred.
However, to quantify the average dust correction remains difficult, especially
given the large uncertainties for the individual objects and the possible
dependence of AV on the UV luminosity and/or stellar mass.
Even if our results imply that a non-negligible dust correction
is required at ![]() ,
it is possible that the SFR density decreases with
redshift from
,
it is possible that the SFR density decreases with
redshift from
![]() on, at least if the median attenuation of
on, at least if the median attenuation of
![]() found by Yabe et al. (2009) at
found by Yabe et al. (2009) at
![]() is representative.
is representative.
Our analysis, covering a wider domain in parameters space than previous studies
and also allowing for the effects of nebular emission, shows that a wide range
of stellar ages is acceptable for most ![]() LBGs.
The Balmer break observed for some objects does not always imply old ages,
or correspondingly high formation redshifts as already pointed out
by Schaerer & de Barros (2009). It can often equally well
be explained by nebular emission, younger populations at non-solar
metallicity, extinction, or a combination thereof.
LBGs.
The Balmer break observed for some objects does not always imply old ages,
or correspondingly high formation redshifts as already pointed out
by Schaerer & de Barros (2009). It can often equally well
be explained by nebular emission, younger populations at non-solar
metallicity, extinction, or a combination thereof.
Younger ages and variations in the star-formation history can lead to solutions
with lower masses and higher SFR for many of the ![]() LBGs than
estimated by other groups (Labbé et al. 2010; Gonzalez et al. 2010).
The specific star-formation rate (
LBGs than
estimated by other groups (Labbé et al. 2010; Gonzalez et al. 2010).
The specific star-formation rate (
![]() )
of
these high-z galaxies may also be higher than thought.
)
of
these high-z galaxies may also be higher than thought.
In short, our SED analysis including in particular the effects
of nebular emission and considering a wide parameter space
(SF histories, extinction etc., shows that the physical
parameters of ![]() galaxies may differ significantly
from those advocated by other groups, with possibly many
implications for our picture of galaxy formation and evolution
in the early universe.
However, we emphasize that the physical properties of
these objects are affected by large uncertainties (cf. Sect. 3 and Appendix), given their faintness and the available data.
Furthermore, comparisons with results for lower redshifts may
be problematic because of the use of different methods.
galaxies may differ significantly
from those advocated by other groups, with possibly many
implications for our picture of galaxy formation and evolution
in the early universe.
However, we emphasize that the physical properties of
these objects are affected by large uncertainties (cf. Sect. 3 and Appendix), given their faintness and the available data.
Furthermore, comparisons with results for lower redshifts may
be problematic because of the use of different methods.
Obviously, additional and higher quality data, and a detailed differential study of the physical parameters of LBGs over a wide redshift domain using state-of-the-art tools will be very helpful in providing a clearer and more accurate picture of the properties and evolution of high-z galaxies in the distant universe, and their link to lower redshift galaxy populations.
5 Conclusions
We have presented a homogeneous and detailed analysis of broad-band
photometry for three samples of
![]() galaxies discovered
by the COSMOS survey and with HST
(see Oesch et al. 2010; Gonzalez et al. 2010; Capak et al. 2009; Bunker et al. 2009; McLure et al. 2010). Their J-band
magnitude span a range from
galaxies discovered
by the COSMOS survey and with HST
(see Oesch et al. 2010; Gonzalez et al. 2010; Capak et al. 2009; Bunker et al. 2009; McLure et al. 2010). Their J-band
magnitude span a range from ![]() 23 to 29, the bulk of them having
23 to 29, the bulk of them having
![]() .
The broad-band SEDs have been fitted using our
modified version of the Hyperz photometric redshift code
described in Schaerer & de Barros (2009), which accounts for the effects of nebular
emission.
.
The broad-band SEDs have been fitted using our
modified version of the Hyperz photometric redshift code
described in Schaerer & de Barros (2009), which accounts for the effects of nebular
emission.
In contrast to earlier studies that assumed, e.g., constant
star formation and/or no extinction, we have explored a wide
range of the parameter space without using priors.
The free parameters (and range) of our SED fits are:
the redshift z ([0,12]),
the metallicity Z (
![]() ,
1/5, 1/20),
the SF history described by the e-folding timescale
,
1/5, 1/20),
the SF history described by the e-folding timescale ![]() ([0, 1000] Myr,
([0, 1000] Myr, ![]() ),
the age t defined since the onset of star-formation (
),
the age t defined since the onset of star-formation (![]() tH),
the extinction AV ([0,2] in general) described by the Calzetti law (Calzetti et al. 2000),
and whether or not nebular emission is included
tH),
the extinction AV ([0,2] in general) described by the Calzetti law (Calzetti et al. 2000),
and whether or not nebular emission is included![]() .
.
Our main results can be summarised as follows:
- Overall, we find that the physical parameters of most
galaxies studied here cover a wide range of acceptable values, e.g., within
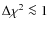 from the best-fit modeling. This finding is independent of
whether nebular emission is included or not.
from the best-fit modeling. This finding is independent of
whether nebular emission is included or not.
- Stellar ages, in particular, are not tightly constrained, even for objects detected with Spitzer, i.e., with photometry both blue- and redward of the Balmer break. When nebular emission is taken into account, we find that the majority of the objects (and the stacked SEDs as well) are most accurately reproduced by ages t < 100, which are younger than derived in other studies of the same objects (Labbé et al. 2010; Gonzalez et al. 2010). The younger ages are due to the contribution of nebular lines to the broad-band rest-frame optical filters, which mimic to some extent a Balmer break, as already shown by Schaerer & de Barros (2009).
- Examination of the UV slope and SEDs of faint z-dropout galaxies found with WFC3/HST shows no need for ``unusual'' stellar populations, extreme metallicities, or other physical processes, advocated previously by Bouwens et al. (2010b), when the uncertainties are taken into account (see also Finkelstein et al. 2009).
- Albeit with large uncertainties, our fit results show indications
of dust attenuation in some of the
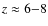 galaxies, with
best-fit model values of AV up to
galaxies, with
best-fit model values of AV up to 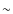 1, even among relatively faint
objects (
1, even among relatively faint
objects (
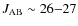 ;
cf. Fig. 10).
;
cf. Fig. 10).
- We find a possible trend of increasing dust attenuation with
the stellar mass of the galaxy (Fig. 11) and a
relatively large scatter in specific star-formation rates, SFR/
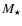 .
.
- Our results, including the evidence of dust in
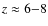 galaxies, are consistent with the results and trends from other SED studies
of LBG samples at
galaxies, are consistent with the results and trends from other SED studies
of LBG samples at 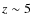 (see e.g. Yabe et al. 2009; Verma et al. 2007).
(see e.g. Yabe et al. 2009; Verma et al. 2007).
We would like to thank Matthew Hayes, David Valls-Gabaud, Rychard Bouwens, and Masami Ouchi for interesting discussions, and Roser Pelló for regular discussions and support with Hyperz. This work was supported by the Swiss National Science Foundation.
Appendix A: Bright sample Capak et al. (2009)
![\begin{figure}
%
\par\includegraphics[width=9cm,clip]{13946fga1.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg140.png)
|
Figure A.1:
Distribution of the minimum |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fga2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg141.png)
|
Figure A.2: Same as Fig. A.1 as a function of stellar age. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fga3.eps} \vspace*{6mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg142.png)
|
Figure A.3: Same as Fig. A.1 as a function of stellar mass. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fga4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg143.png)
|
Figure A.4: Same as Fig. A.1 as a function of the star-formation rate. |
| Open with DEXTER | |
Appendix B: Intermediate sample Gonzalez et al. (2009)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13946fgb1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg144.png)
|
Figure B.1:
Distribution of the minimum |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13946fgb2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg145.png)
|
Figure B.2: Same as Fig. B.1 as a function of the stellar age. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13946fgb3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg146.png)
|
Figure B.3: Same as Fig. B.1 as a function of the stellar mass. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13946fgb4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg147.png)
|
Figure B.4: Same as Fig. B.1 as a function of the star-formation rate. |
| Open with DEXTER | |
Appendix C: Faint sample
C.1 Oesch et al. (2010) objects
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13946fgc1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg148.png)
|
Figure C.1:
Distribution of the minimum |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13946fgc2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg149.png)
|
Figure C.2: Same as Fig. C.1 as a function of the stellar age. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13946fgc3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg150.png)
|
Figure C.3: Same as Fig. C.1 as a function of the stellar mass. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13946fgc4.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg151.png)
|
Figure C.4: Same as Fig. C.1 as a function of the star-formation rate. |
| Open with DEXTER | |
C.2 Stacked SED Labbé et al. (2010)
![\begin{figure}
%
\par\includegraphics[width=8.2cm,clip]{13946fgc5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg152.png)
|
Figure C.5:
Distribution of the minimum |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13946fgc6.eps}
\vspace*{4.5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg153.png)
|
Figure C.6: Same as Fig. C.5 as a function of the stellar age. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13946fgc7.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg154.png)
|
Figure C.7: Same as Fig. C.5 as a function of the stellar mass. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13946fgc8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg155.png)
|
Figure C.8: Same as Fig. C.5 as a function of the star-formation rate. |
| Open with DEXTER | |
References
- Anders, P., & Fritze-v. Alvensleben, U. 2003, A&A, 401, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolzonella, M., Miralles, J.-M., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Franx, M., et al. 2009, ApJ, 705, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2010a, ApJ, 709, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2010b, ApJ, 708, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Thompson, R. I., Illingworth, G. D., et al. 2004, ApJ, 616, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, L. D., Bouwens, R. J., Ford, H. C., et al. 2008, ApJ, 678, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Boissier, S., Burgarella, D., et al. 2008, A&A, 483, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buat, V., Iglesias-Páramo, J., Seibert, M., et al. 2005, ApJ, 619, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Bunker, A., Wilkins, S., Ellis, R., et al. 2009, MNRAS [arXiv:0909.2255] [Google Scholar]
- Burgarella, D., Le Floc'h, E., Takeuchi, T. T., et al. 2007, MNRAS, 380, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Mobasher, B., Scoville, N. Z., et al. 2009, ApJ, submitted[arXiv:0910.0444] [Google Scholar]
- Castellano, M., Fontana, A., Boutsia, K., et al. 2010, A&A, 511, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuby, J., Hibon, P., Lidman, C., et al. 2007, A&A, 461, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Egami, E., Kneib, J.-P., Rieke, G. H., et al. 2005, ApJ, 618, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Eyles, L. P., Bunker, A. J., Ellis, R. S., et al. 2007, MNRAS, 374, 910 [NASA ADS] [CrossRef] [Google Scholar]
- Finkelstein, S. L., Papovich, C., Giavalisco, M., et al. 2009, ApJ, submitted[arXiv:0912.1338] [Google Scholar]
- Finlator, K., Davé, R., & Oppenheimer, B. D. 2007, MNRAS, 376, 1861 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, N. Y., Kravtsov, A. V., & Chen, H. 2008, ApJ, 672, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, V., Labbe, I., Bouwens, R. J., et al. 2010, ApJ, 713, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Guseva, N. G., Izotov, Y. I., Papaderos, P., & Fricke, K. J. 2007, A&A, 464, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henry, A. L., Malkan, M. A., Colbert, J. W., et al. 2008, ApJ, 680, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, A. L., Malkan, M. A., Colbert, J. W., et al. 2007, ApJ, 656, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, A. L., Siana, B., Malkan, M. A., et al. 2009, ApJ, 697, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Hibon, P., Cuby, J., Willis, J., et al. 2009, A&A, accepted [arXiv:0907.3354] [Google Scholar]
- Hickey, S., Bunker, A., Jarvis, M. J., Chiu, K., & Bonfield, D. 2010, MNRAS, 404, 212 [NASA ADS] [Google Scholar]
- Iye, M., Ota, K., Kashikawa, N., et al. 2006, Nature, 443, 186 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Izotov, Y. I., Lipovetsky, V. A., Chaffee, F. H., et al. 1997, ApJ, 476, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kneib, J., Ellis, R. S., Santos, M. R., & Richard, J. 2004, ApJ, 607, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Labbé, I., Bouwens, R., Illingworth, G. D., & Franx, M. 2006, ApJ, 649, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Labbé, I., González, V., Bouwens, R. J., et al. 2010, ApJ, 708, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Schneider, R., Oliva, E., et al. 2004, Nature, 431, 533 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mannucci, F., Buttery, H., Maiolino, R., Marconi, A., & Pozzetti, L. 2007, A&A, 461, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLure, R. J., Dunlop, J. S., Cirasuolo, M., et al. 2010, MNRAS, 403, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [Google Scholar]
- Oesch, P. A., Bouwens, R. J., Illingworth, G. D., et al. 2010, ApJ, 709, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Ota, K., Iye, M., Kashikawa, N., et al. 2008, ApJ, 677, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Mobasher, B., Shimasaku, K., et al. 2009, ApJ, 706, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Papaderos, P., Izotov, Y. I., Thuan, T. X., et al. 2002, A&A, 393, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaderos, P., Guseva, N. G., Izotov, Y. I., et al. 2006, A&A, 457, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papovich, C., Dickinson, M., & Ferguson, H. C. 2001, ApJ, 559, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Pelló, R., Schaerer, D., Richard, J., Le Borgne, J., & Kneib, J. 2004, A&A, 416, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pustilnik, S. A., Pramskij, A. G., & Kniazev, A. Y. 2004, A&A, 425, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Razoumov, A. O., & Sommer-Larsen, J. 2010, ApJ, 710, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., & Steidel, C. C. 2009, ApJ, 692, 778 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Fadda, D., et al. 2006, ApJ, 644, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Pettini, M., et al. 2008, ApJS, 175, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, J., Pelló, R., Schaerer, D., Le Borgne, J., & Kneib, J. 2006, A&A, 456, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richard, J., Stark, D. P., Ellis, R. S., et al. 2008, ApJ, 685, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Fontana, A., Grazian, A., et al. 2009, A&A, 504, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sawicki, M., Iwata, I., Ohta, K., et al. 2007, in Deepest Astronomical Surveys, ed. J. Afonso, H. C. Ferguson, B. Mobasher, & R. Norris, ASP Conf. Ser., 380, 433 [Google Scholar]
- Schaerer, D., & de Barros, S. 2009, A&A, 502, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schurer, A., Calura, F., Silva, L., et al. 2009, MNRAS, 394, 2001 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J. 1979, MNRAS, 187, 73P [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Adelberger, K. L., et al. 2001, ApJ, 562, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Erb, D. K., et al. 2005, ApJ, 626, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Best, P. N., Geach, J. E., et al. 2009, MNRAS, 398, L68 [Google Scholar]
- Stark, D. P., Bunker, A. J., Ellis, R. S., Eyles, L. P., & Lacy, M. 2007a, ApJ, 659, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Richard, J., et al. 2007b, ApJ, 663, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Bunker, A., et al. 2009, ApJ, 697, 1493 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Verhamme, A., Schaerer, D., Atek, H., & Tapken, C. 2008, A&A, 491, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verma, A., Lehnert, M. D., Förster Schreiber, N. M., Bremer, M. N., & Douglas, L. 2007, MNRAS, 377, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Wiklind, T., Dickinson, M., Ferguson, H. C., et al. 2008, ApJ, 676, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, S. M., Bunker, A. J., Ellis, R. S., et al. 2009, MNRAS, accepted [arXiv:0910.1098] [Google Scholar]
- Willis, J. P., Courbin, F., Kneib, J., & Minniti, D. 2008, MNRAS, 384, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., & Cen, R. 2009, ApJ, 693, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Yabe, K., Ohta, K., Iwata, I., et al. 2009, ApJ, 693, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, H., Windhorst, R., Hathi, N., et al. 2009, ApJ, submitted[arXiv:0910.0077] [Google Scholar]
- Zackrisson, E., Bergvall, N., & Leitet, E. 2008, ApJ, 676, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W., Bradley, L. D., Bouwens, R. J., et al. 2009, ApJ, 697, 1907 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ...
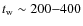 Myr
Myr![[*]](/icons/foot_motif.png)
- With their definition, one has
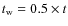 for
for
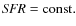 assumed by these authors, where t is our definition of the stellar age.
assumed by these authors, where t is our definition of the stellar age.
- ... redshift
![[*]](/icons/foot_motif.png)
- In addition, there is the well-known age-extinction degeneracy.
- ...
differ
![[*]](/icons/foot_motif.png)
- In general, one has
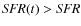 (UV), since stars over a broad
age range contribute to the UV output, and since
(UV), since stars over a broad
age range contribute to the UV output, and since
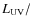 SFR is lower
at young ages.
SFR is lower
at young ages.
- ... included
![[*]](/icons/foot_motif.png)
- In some cases, we exclude the Ly
 line from the synthetic
spectra, since this line may be attenuated by radiation transfer processes
inside the galaxy or by the intervening intergalactic medium.
line from the synthetic
spectra, since this line may be attenuated by radiation transfer processes
inside the galaxy or by the intervening intergalactic medium.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg76.png)
|
Figure 1:
Comparison of best-fit model photometric redshifts for the three samples using SEDs
without (x-axis) and with nebular emission (y-axis). Circles, squares, and triangles
indicate the bright, intermediate, and faint samples, respectively. Black symbols show the
comparison with all nebular lines, i.e. including also Ly |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg77.png)
|
Figure 2:
Observed (blue points) and fitted SEDs (solid lines) of object 3
from Capak et al. (2009) using our spectral templates with nebular
emission. Ly |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg3.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg84.png)
|
Figure 3:
Redshift probability distribution
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg4.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg85.png)
|
Figure 4:
Observed (blue points) and fitted SEDs (solid lines) of object 8
(GNS-zD4) from Gonzalez et al. (2010) using standard Bruzual & Charlot solar metallicity
models. The best-fit (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg86.png)
|
Figure 5:
Observed (blue points) and best-fit SEDs (solid lines) of object 1
(UDF-640-1417) from Gonzalez et al. (2010) using standard Bruzual and Charlot solar metallicity
models.
The magenta line shows the best-fit for templates without nebular emission, and
assuming that
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg97.png)
|
Figure 6:
UV slope |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg7.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg100.png)
|
Figure 7:
Best-fit SEDs of object 2502 (photometry in blue symbols) of
McLure et al. (2010) for solar metallicity models including nebular emission.
The black solid line shows the model including all lines (Ly |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg8.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg105.png)
|
Figure 8:
Best-fit SEDs to the SED of the stack of 14 z-dropout galaxies
from Oesch et al. (2010) measured by Labbé et al. (2010).
Photometry is shown by blue symbols; including the 1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg9.eps}
\vspace*{6mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg110.png)
|
Figure 9:
Comparison of best-fit values for the age t ( upper left), extinction AV ( upper right),
stellar mass |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg10.eps}
\vspace*{6mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg111.png)
|
Figure 10:
Best-fit value for the age (upper left), extinction ( upper right),
stellar mass ( lower left), and star-formation rate ( lower right) as a function of
the observed
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg11.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg123.png)
|
Figure 11:
Black circles, green squares, blue triangles show best-fit values of
AV versus |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fg12.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg124.png)
|
Figure 12:
Stellar mass-SFR relation for the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
%
\par\includegraphics[width=9cm,clip]{13946fga1.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg140.png)
|
Figure A.1:
Distribution of the minimum |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fga2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg141.png)
|
Figure A.2: Same as Fig. A.1 as a function of stellar age. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fga3.eps} \vspace*{6mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg142.png)
|
Figure A.3: Same as Fig. A.1 as a function of stellar mass. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13946fga4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg143.png)
|
Figure A.4: Same as Fig. A.1 as a function of the star-formation rate. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13946fgb1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg144.png)
|
Figure B.1:
Distribution of the minimum |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13946fgb2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg145.png)
|
Figure B.2: Same as Fig. B.1 as a function of the stellar age. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13946fgb3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg146.png)
|
Figure B.3: Same as Fig. B.1 as a function of the stellar mass. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13946fgb4.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg147.png)
|
Figure B.4: Same as Fig. B.1 as a function of the star-formation rate. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13946fgc1.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg148.png)
|
Figure C.1:
Distribution of the minimum |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13946fgc2.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg149.png)
|
Figure C.2: Same as Fig. C.1 as a function of the stellar age. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13946fgc3.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg150.png)
|
Figure C.3: Same as Fig. C.1 as a function of the stellar mass. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13946fgc4.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg151.png)
|
Figure C.4: Same as Fig. C.1 as a function of the star-formation rate. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
%
\par\includegraphics[width=8.2cm,clip]{13946fgc5.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg152.png)
|
Figure C.5:
Distribution of the minimum |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13946fgc6.eps}
\vspace*{4.5mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg153.png)
|
Figure C.6: Same as Fig. C.5 as a function of the stellar age. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13946fgc7.eps}
\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg154.png)
|
Figure C.7: Same as Fig. C.5 as a function of the stellar mass. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{13946fgc8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13946-09/Timg155.png)
|
Figure C.8: Same as Fig. C.5 as a function of the star-formation rate. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


