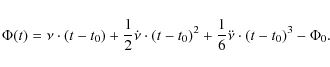EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 515 (June 2010) A&A, 515 (2010) A34 Full HTML
Free Access
Issue
A&A
Volume 515, June 2010
Article Number A34
Number of page(s) 10
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200913851
Published online 04 June 2010
A&A 515, A34 (2010)

Hard X-ray timing and spectral characteristics of the energetic pulsar PSR J0205+6449 in supernova remnant 3C 58

An RXTE PCA/HEXTE and XMM-Newton view on the 0.5-250 keV band

L. Kuiper1 - W. Hermsen1,2 - J. O. Urama3 - P. R. den Hartog1,4 - A. G. Lyne5 - B. W. Stappers5

1 - RON-Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA, Utrecht, The Netherlands
2 - Astronomical Institute ``Anton Pannekoek'', University of Amsterdam, PO Box 94249, 1090 GE, Amsterdam, The Netherlands
3 - Dept. of Physics & Astronomy, University of Nigeria, Nsukka, Nigeria
4 - Stanford University HEPL/KIPAC Physics, 382 via Pueblo Mall Stanford, 94305, USA
5 - Jodrell Bank Center for Astrophysics, School of Physics and Astronomy, The University of Manchester Manchester M13 9PL, UK

Received 11 December 2009 / Accepted 1 February 2010

Abstract
Context. PSR J0205+6449 is a young rotation-powered pulsar in SNR 3C 58. It is one of only three young (<10 000 year old) pulsars that have so far been detected in the radio and the classical X-ray bands, as well as at hard X-rays above 20 keV and at high-energy (>100 MeV) $\gamma $-rays. The other two young pulsars are the Crab and PSR B1509-58.
Aims. Our aim is to derive the timing and spectral characteristics of PSR J0205+6449 over the broad X-ray band from $\sim $0.5 to $\sim $270 keV.
Methods. We used all publicly available RXTE observations of PSR J0205+6449 to first generate accurate ephemerides over the period September 30, 2000-March 18, 2006. We then employed phase-folding procedures yielded pulse profiles using data from RXTE PCA and HEXTE, and XMM-Newton EPIC PN. All profiles were phase aligned with a radio profile derived from the Jodrell Bank Observatory data, and the time-averaged timing and spectral characteristics of the pulsed X-ray emission were derived.
Results. Our timing solutions are consistent with earlier results, but we detect sharper structures in the PCA X-ray profile. The X-ray pulse profile consists of two sharp pulses, separated in phase by $0.488 \pm 0.002$, that can be described by 2 asymmetric Lorentzians, each with the rising wing steeper than the trailing wing, and full-width-half-maximum $1.41 \pm 0.05$ ms and $2.35 \pm 0.22$ ms, respectively. For the second, weaker pulse we find an indication of a flux increase by a factor $\sim $2, about $3.5\sigma $ above the time-averaged value, over a two-week interval, during which its pulse shape did not change. The spectrum of the pulsed X-ray emission is non-thermal in origin, exhibiting a power-law shape with photon index $\Gamma = 1.03 \pm 0.02$ over the energy band $\sim $0.5 to $\sim $270 keV. In the energy band covered with the PCA ($\sim $3-30 keV), the spectra of the two pulses have the same photon index, namely, $1.04 \pm 0.03$ and $1.10 \pm 0.08$, respectively. Comparisons of the detailed timing and spectral characteristics of PSR J0205+6449 in the radio, hard X-ray, and gamma-ray bands with those of the Crab pulsar, PSR B1509-58 and the middle-aged Vela pulsar uncover more differences than similarities.

Key words: stars: neutron - pulsars: general - X-rays: general - gamma rays: general - radiation mechanisms: non-thermal

1 Introduction

PSR J0205+6449 is a young rotation-powered pulsar. Its pulsations were first detected in X-rays by a 2002 Chandra X-ray observatory (CXO) observation (Murray et al. 2002) and confirmed by archival Rossi X-Ray Timing Explorer (RXTE) data. Its weak radio signal was subsequently detected by Camilo et al. (2002). Located at the center of supernova remnant/pulsar wind nebula (PWN) 3C 58, PSR J0205+6449 is a young, 65-ms pulsar and one of the most energetic pulsars in the Galaxy with a spin-down luminosity $\dot{E}\sim{2.7}\times 10^{37}$ erg s-1. Its characteristic age of $\tau\sim{5.4}$ kyr, which was estimated from its period and period derivative, places in doubt its possible association with 3C 58, coinciding positionally with the historical 828 yr old supernova SN1191 (Stephenson & Green 2002). However, an age of several thousand years for 3C 58, which is closer to the characteristic age of the pulsar, can be derived from the velocities of both the radio expansion of the PWN (Bietenholz 2006) and the optical knots (Fesen et al. 2008).

For PSR J0205+6449, Livingstone et al. (2009) presented phase-coherent timing analyses of X-ray data from the Proportional Counter Array (PCA; 2-60 keV) aboard RXTE and radio data from both the Jodrell Bank Observatory and the Green Bank Telescope (GBT), spanning 6.4 yrs. This work uncovered timing noise and two spin-up glitches. Furthermore, they presented detailed characteristics of the X-ray profile, which was detected up to $\sim $40 keV. Their X-ray profile template consisted of two Gaussian-shaped pulses, a narrow (full-width-half-maximum (FWHM) $\sim $1.6 ms), more intense pulse and a broader ( ${\it FWHM} \sim 3.8$ ms), weak pulse separated 0.505 in phase, the single radio pulse leading the main X-ray pulse by $ \phi = 0.10 \pm 0.01$. Earlier results from an analysis of part of the RXTE and GBT data were reported by Ransom et al. (2004). These authors also presented spectral fits over the energy band 3-16 keV for both pulses: the best-fit power-law model photon indices were hard, namely $\Gamma = 0.84_{-0.15}^{+0.06}$ for the main pulse and $\Gamma = 1.0_{-0.3}^{+0.4}$ for the second (weaker) pulse.

Finally, high-energy $\gamma $-ray pulsations ($\geq$0.1 GeV) from PSR J0205+6449 were discovered with the Large Area Telescope (LAT) aboard the Fermi Gamma-ray Space Telescope (Abdo et al. 2009a), folding the $\gamma $-ray arrival times with the radio rotational ephemeris from, again, the GBT and Jodrell Bank. The $\gamma $-ray light curve for energies $\geq$0.1 GeV also has two peaks with intensities differing by a factor $\sim $2, aligned with the X-ray peaks, However, the main X-ray pulse coincides in phase with the weakest $\gamma $-ray pulse, which has the softest spectrum of the two at high-energy $\gamma $-rays. The total pulsed $\gamma $-ray spectrum exhibits a simple power-law shape with index $\Gamma \sim 2.1$ and exponential cutoff at $\sim $3.0 GeV.

PSR J0205+6449 is now one of only three young (<10 000 year old) pulsars that have been detected in the classical X-ray band, at hard X-rays above 20 keV, and at high-energy (>0.1 GeV) $\gamma $-ray energies, the others being the Crab pulsar and PSR B1509-58 (PSR J1513-5908). The Crab pulsar has been studied across the full high-energy band in great detail (for a coherent high-energy picture from soft X-rays up to high-energy $\gamma $-rays, see Kuiper et al. 2001), with a detection even of pulsed $\gamma $-rays above 25 GeV (Aliu et al. 2008).

The detection of pulsed emission above 100 MeV from PSR B1509-58 had a wait a new generation of $\gamma $-ray telescopes (Pellizzoni et al. 2009). However, these three young pulsars have very different timing and spectral characteristics. This makes it particularly interesting to determine the timing and spectral characteristics of PSR J0205+6449 across the high-energy band of the electromagnetic spectrum to compare with those of Crab and PSR B1509-58 and with theoretical predictions. In this work, our aim is to extend the coverage in the hard X-ray band to higher energies by exploiting the data of the High Energy X-ray Timing Experiment (HEXTE; 15-250 keV) onboard RXTE, and extend the energy window to lower energies by analysing data from XMM-Newton. We present the results of our timing study performed using only the multi-year PCA/RXTE monitoring data, which we performed in parallel to the work reported by Livingstone et al. (2009). Our timing solutions are consistent with those of the latter authors, but our work uncovered sharper structures in the PCA X-ray pulse profile. Furthermore, we derive the spectral characteristics over the total X-ray band. In the discussion, we compare our findings with the characteristics of PSR J0205+6449 reported in the radio band and at high-energy $\gamma $-rays, as well as with the timing and spectral characteristics of the Crab pulsar, PSR B1509-58, and the middle-aged Vela pulsar.

Table 1:   RXTE PSR J0205+6449 observation summary.

2 Instruments and observations

2.1 RXTE

In this study, extensive use is made of data from monitoring observations of PSR J0205+6449 with the two non-imaging X-ray instruments aboard RXTE, the Proportional Counter Array (PCA; 2-60 keV) and the High Energy X-ray Timing Experiment (HEXTE; 15-250 keV). The PCA (Jahoda et al. 1996) consists of five collimated Xenon proportional counter units (PCUs) with a total effective area of $\sim $6500 cm2 over a $\sim $ $1\hbox{$^\circ$ }$ (FWHM) field of view. Each PCU has a front propane anti-coincidence layer and three xenon layers, which provide the basic scientific data, and is sensitive to photons with energies in the range 2-60 keV. The energy resolution is about 18% at 6 keV. All data used in this work were collected from observations in GoodXenon or GoodXenonwithPropane mode allowing high-time-resolution ($0.9~\mu$s) studies in 256 spectral channels.

The HEXTE instrument (Rothschild et al. 1998) consists of two independent detector clusters A and B, each containing four Na(Tl)/ CsI(Na) scintillation detectors. The HEXTE detectors are mechanically collimated to a $\sim $ $1\hbox{$^\circ$ }$ (FWHM) field of view and cover the 15-250 keV energy range with an energy resolution of $\sim $15% at 60 keV. The collecting area is 1400 cm2 taking into account the loss of the spectral capabilities of one of the detectors. The finest time resolution of the tagged events is $7.6~\mu$s. In its default operation mode, the field of view of each cluster is switched on and off source to provide instantaneous background measurements. Because of the co-alignment of the HEXTE and the PCA, both instruments simultaneously observe the same field of view.

For the first time, RXTE observed PSR J0205+6449  on Sept. 30, 1997 (MJD 50 721) for about 17 ks. Data from this observation were used by Murray et al. (2002) to confirm the pulsation discovered with Chandra. A dedicated much deeper observation was performed in the period August 17-19, 2001 (MJD 52 138-52 141), providing about 80 ks of high quality exposure time. A monitoring campaign then started on March 10, 2003 (MJD 52 343) and ended on April 23, 2003 (MJD 52 752). The total (good) exposure time for this period was about 269 ks. A second monitoring round commenced on Feb. 28, 2004 and continued until March 18, 2006 (MJD 53 063-53 813) yielding a total (good) exposure time of about 572 ks. A summary of all RXTE observations of PSR J0205+6449 is given in Table 1. The total high quality exposure (after screening; see Sect. 3.1) equals 938.23 ks.

2.2 XMM-Newton

We searched the XMM-Newton observation database for observations of the field around PSR J0205+6449 in which the EPIC-PN camera (Strüder et al. 2001) operated in small-window (SW) mode. This mode ( $4\hbox{$.\mkern-4mu^\prime$ }4 \times 4\hbox{$.\mkern-4mu^\prime$ }4$ field of view) offers sufficient time resolution ($\sim $5.67 ms) to sample the pulse-profile of PSR J0205+6449 over the $\sim $0.3-12 keV range. We found two observations (observation ids. 0004010101/0004010201) both performed on February 22, 2001 at $1\hbox{$.\mkern-4mu^\prime$ }2$ offset from PSR J0205+6449 with durations of about 9.2 and 23.6 ks, respectively.

Table 2:   Phase-coherent ephemerides for PSR J0205+6449 as derived from RXTE PCA (monitoring) data.

3 Timing

3.1 RXTE PCA timing analysis

The first step in the RXTE PCA data analysis was the screening of the data. We generated good-time intervals (GTI) for each PCU separately, because the number of active PCU's at any instant was changing. Good time intervals were determined for each PCU by including only time periods when the PCU in question was on, during which the pointing direction is within $0\hbox{$.\!\!^\circ$ }05$ from the target, the elevation angle above Earth's horizon is greater than $5\hbox{$^\circ$ }$, a time delay of 30 min since the peak of a South-Atlantic-Anomaly passage holds, and a low background level due to contaminating electrons is observed. These good time intervals have subsequently been applied in the screening process to the data streams from each of the PCUs (e.g., see Table 1 for the resulting screened exposure of PCU-2 per observation run).

We selected event data from all three xenon layers of each PCU, which allowed us to characterize the hard (>10 keV) X-ray properties of PSR J0205+6449. The TT (Terrestrial Time) arrival times of the selected events (for each sub-observation and PCU unit) were converted to arrival times at the solar system barycenter (in Barycentric Dynamical Time (TDB) time scale) using 1) the JPL DE200 solar system ephemeris, 2) the instantaneous spacecraft position, and 3) the sub-arcsecond celestial position of PSR J0205+6449. The position used is: $(\alpha,\delta)=(02^{\hbox{\scriptsize h}}05^{\hbox{\scriptsize m}}37\hbox{$.\!\!^{\rm s}$ }92,+64\degr49\hbox{$^\prime$ }42~\hbox{$.\!\!^{\prime\prime}$ }8)$ for epoch J2000 (Slane et al. 2002), which corresponds to (l,b)=(130.71931,3.08456) in Galactic coordinates.

3.2 Timing solutions: ephemerides

We generated pulsar timing models (ephemerides) specifying the rotation behaviour of the pulsar over a certain time stretch. The pulse frequency and its first two time derivatives $(\nu,\dot\nu,\ddot\nu)$ were determined from PCA X-ray data solely[*], demanding a maximum RMS value of only 0.01 period in the time-of-arrival (TOA) analysis. This requirement resulted in 13 timing models with validity intervals of typically 100 days. The ephemerides are listed in Table 2. In the TOA analysis, we followed the steps outlined in Sect. 4 of Kuiper & Hermsen (2009); in this case, however, we compiled a high quality correlation template (showing clearly the two X-ray pulses) from the 80 ks observation during run 60 130. Our models are fully consistent with those derived by Livingstone et al. (2009), who used a combination of X-ray (RXTE PCA) and radio (GBT and JBO) data. Using X-ray data alone, we found evidence of two timing glitches, one occurring somewhere between MJD 52 515 and 52 571 and a much stronger one in the RXTE monitoring gap between MJD 52 752 and 53 063; we refer to Livingstone et al. (2009) for more details of these glitches, which they report to have fractional magnitudes of ${\Delta}{\nu}/\nu \sim 3.4 \times 10^{-7}$ and ${\Delta}{\nu}/\nu \sim 3.8 \times 10^{-6}$, respectively. The frequency evolution history over the RXTE observation time stretch MJD 52 138-53 813 is shown in Fig. 1.

\begin{figure} \par\includegraphics[width=9cm,clip]{13851fig1.ps} \end{figure} Figure 1:

Evolution of the spin-frequency of PSR J0205+6449 as derived from RXTE PCA data over the period MJD 52 138-53 813 with respect to the linear trend of the phase coherent timing model of period MJD 52 433-52 515 (entry #3 of Table 2). As solid lines, the entries #1-12 of Table 2 are plotted, while for the period 52 571-52 752 the linear fit to the incoherent frequency measurements is also shown as a solid line. Incoherent frequency measurements over the period MJD 52 544-52 752 are shown as data points. Note the presence of (at least) two timing glitches: one in the period 52 515 to 52 571 and a second stronger one between 52 752 and 53 063 (see text).

Open with DEXTER

The main difference between our work and that performed by Livingstone et al. (2009) is that we selected an accurate (rms < 0.01) description of the rotation behaviour of the pulsar that has at most 3 timing parameters over a limited time period instead of using many more timing parameters over a much wider time interval. In the latter approach, the need for the (unphysical) higher order timing parameters reflects the presence of (strong) timing noise.

3.3 X-ray/radio pulse profile phase alignment

The Jodrell Bank observatory (JBO) was used to perform observations at a radio frequency of 1.4 GHz from MJD 53 725 to 54 666, and therefore overlaps for about 89 days with the second RXTE monitoring cycle in the period MJD 53725 to 53813. For two time segments in this interval, MJD 53 726-53 764 (number of TOAs, 28) and MJD 53 750-53 814 (number of TOAs, 29), accurate (rms < 0.01) timing models are constructed with 3 timing parameters (see also Table 2). The 1.4 GHz single-pulse radio profile (in 400 bins) is shown in Fig. 3a with a fiducial point (defining radio-phase 0.0) corresponding to the centre of gravity of the single pulse (just before the pulse maximum). Folding the barycentered X-ray time tags from period MJD 53726 to 53813 on these radio-ephemerides places the main X-ray pulse (pulse-1) at phase $0.089\pm0.001$ (statistical error only), which is consistent with the value quoted for the JBO-PCA offset in Livingstone et al. (2009), namely $0.085\pm 0.010$. We determine by means of correlation analysis the phase shifts to be applied to the X-ray pulse profiles from the data periods of entries 0-12 of Table 2 to align these to the radio-aligned X-ray profile of period MJD 53 726-53 813. These shifts ($\Phi_{0}$) are given in Table 2.

3.4 Combined X-ray event matrix from PCA observations

Barycentered PCA X-ray event times are finally folded on an appropriate timing model composed of $\nu,\dot\nu,\ddot\nu$, and the epoch t0, as shown in Table 2. Proper X-ray/radio phase alignment, $\Phi(t)$, is obtained by subtracting $\Phi_{0}$ as shown in the formula

\begin{displaymath}\Phi(t)=\nu\cdot (t-t_0) + \frac{1}{2}\dot\nu\cdot (t-t_0)^2+\frac{1}{6}\ddot\nu\cdot (t-t_0)^3 - \Phi_0. \end{displaymath} (1)

By combining the radio-aligned phase information for all PCA-data covered with a proper ephemeris (see Table 2), we obtained an event matrix $N(\Phi,E)$ of $(180\times256)$ elements by binning the pulse-phase interval [0,1] into 180 phase bins for all 256 PCA PHA channels. From this matrix a high-statistics pulse-phase distribution was extracted for the PHA channels 5-44 ($\sim $2-20 keV). This distribution is shown in Fig. 2.

\begin{figure} \par\includegraphics[width=9cm,clip]{13851fig2.ps} \vspace*{-2mm} \end{figure} Figure 2:

High-statistics radio-aligned PCA pulse phase distribution in 180 bins for PHA range 5-44 ($\sim $2-20 keV) combining all available radio-aligned pulse phase distributions from different data segments. Error bars represent $1\sigma $ uncertainties. The best-fit ( $\chi ^2=199.47$ for 171 degrees of freedom) model composed of two asymmetric Lorentzians plus background is superimposed as a dashed red line. The rising wings of the pulses are steeper than the trailing wings.

Open with DEXTER

3.5 X-ray pulse profile characterization

In an analogous way to Livingstone et al. (2009), we initially fitted our high-statistics RXTE PCA pulse profile shown in Fig. 2 with a model consisting of 2 Gaussians, each with free scale, width, and position, in addition to a background. However, this model rendered a poor/unacceptable fit ( $\chi^2=265.48$for 180-7 degrees of freedom). We then attempted to fit a double symmetric Lorentzian model plus background to give more weight to the wings of the pulses. This model provided a more accurate description of the measured pulse-phase distribution ( $\chi^2=239.13$for 180-7 degrees of freedom), but is still poor. Finally, we abandoned a description in terms of symmetric functions and used a combination of 2 asymmetric Lorentzians plus background. This model (9 free parameters) is specified to be

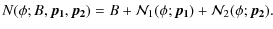
$\displaystyle N(\phi;B,\vec{p_1},\vec{p_2})=B+{\cal{N}}_1(\phi;\vec{p_1})+{\cal{N}}_2(\phi;\vec{p_2}).$     (2)

In this formula, $\vec{p_1}$ represents the 4 model parameters, $(N_1,\phi_1,\Gamma_{1l},\Gamma_{1r})$, of the first asymmetric Lorentzian, $\vec{p_2}$ the equivalent parameters, $(N_2,\phi_2,\Gamma_{2l},\Gamma_{2r})$, describing the second asymmetric Lorentzian, and B is the value of the background level. The first asymmetric Lorentzian is described by the expression
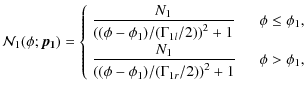
$\displaystyle {\cal{N}}_1(\phi;\vec{p_1})= \left\{ \begin{array}{lcr} \displays... ...hi_1)/(\Gamma_{1r}/2)\right)^2+1} & \ \ & \phi > \phi_1, \\ \end{array}\right.$     (3)

where N1 is the maximum value of pulse-1 reached at $\phi_1$, the location of the maximum of pulse-1, $\Gamma_{1l}/2$ is the width of the left wing of the pulse-1, and finally $\Gamma_{1r}/2$ is the width of the right wing of the pulse-1. A similar expression and equivalent definitions hold for the second asymmetric Lorentzian.

This composite model provided an excellent fit, $\chi ^2=199.47$ for 171 degrees of freedom, its best-fit model parameters and their $1\sigma $ error estimates being listed in Table 3 (see also the best-fit model superimposed on the data in Fig. 2). A description in terms of two asymmetric Lorentzians and a background provides a $7.7\sigma$ improvement to the two-Gaussians-plus-background model and a $6\sigma$improvement to the two-Lorentzians-plus-background model, taking into account the two (=9-7) additional degrees of freedom in both cases. Therefore, our analysis does not support the assumption made by Livingstone et al. (2009) of an underlying double Gaussian shape for the X-ray profile. We find the X-ray pulses to be sharper, especially for pulse-2. For both pulses, the rising wings are significantly steeper than the trailing wings.

The X-ray peak separation $\phi_2-\phi_1$ derived in this work is 0.488(2), significantly smaller than the value estimated by Livingstone et al. (2009), but consistent with the separation of $0.49 \pm 0.01 \pm 0.01$[*] measured at high-energy $\gamma $-rays by Abdo et al. (2009a) using Fermi LAT >100 MeV data. The comparison of the shapes and absolute phases of the JBO radio, our RXTE-PCA X-ray, and the Fermi-LAT profiles is shown in Fig. 3. The main X-ray pulse (P1) appears to be the sharpest pulse in this comparison.

Table 3:   X-ray pulse profile characterization of PSR J0205+6449 from a fit involving two asymmetric Lorentzians plus background.

\begin{figure} \par\includegraphics[width=7.cm,height=13cm,clip]{13851fig3.ps} \end{figure} Figure 3:

A comparison in absolute phase of the JBO radio (1.4 GHz), RXTE-PCA ($\sim $2-20 keV) and Fermi LAT (>100 MeV) pulse profiles. Note the change in the relative contributions of P1 and P2 in the X-ray and $\gamma $-ray windows.

Open with DEXTER

3.6 X-ray pulse profile variability

We investigated the stability of the X-ray pulse-shape as a function of time. We fitted the measured X-ray pulse-phase distribution (PHA range $[4,27] \sim 2$-11 keV) for 15 time periods in terms of a constant background and the shapes of pulse-1 and pulse-2, separately. The times of these data points correspond to those of the X-ray timing models shown in Table 2 (entries 0 to 11; 12 points), augmented with two measurements during the last RXTE monitoring period, MJD 53 726-53 813, covering entry #12 and finally, with a data point covering the post-glitch-1 period MJD 52 544-52 607, yielding eventually 15 independent measurements. The splitting of period MJD 53 726-53 813 into the intervals MJD 53 736-53 749 (2 RXTE sub-observations) and MJD 53 760-53 813 (5 sub-observations) was driven by the detection of a ``timing anomaly'' in the former interval during the phase-coherent timing analysis. At a later stage of this work, it turned out that this ``anomaly'' was caused by incorrect RXTE clock corrections just after the introduction of a leap second on 2006, January 1.

The profile-fitting procedure yields the flux ratio R=I1/I2 (see for the definition Table 3) for each time interval. The results, R(t) versus t, are shown in Fig. 4, the P1/P2-flux ratio from the time-averaged high-statistics profile ( $R=2.2\pm0.1$; see Table 3) being superimposed as a long-dashed line along with its 1-$\sigma$ error region (shaded area). One data point, corresponding to the ``anomaly'' period, deviates $\sim $$3.5\sigma $ from the time-averaged value. Taking into account the number of trials (15), its significance reduces to $2.7\sigma$, which is still indicative of variability. The pulse-phase distribution during the ``anomaly'' period is shown in Fig. 5. In this figure, we also superimposed as a dotted line the best-fit model in which the shapes (two asymmetric Lorentzians) of each of the two pulses are identical to those derived for the time-averaged profile in Fig. 2 and detailed in Table 3.

Compared to the other measurements, where P2 is sometimes hardly visible, we see strongly enhanced P2 emission during this period. From the spectral analysis of the P1 and P2 emissions during the ``anomaly'' period, the P1 flux is found to be comparable to its time-averaged value in contrast to the P2 flux, which shows a clear enhancement by almost a factor 2.

This infers that we see an interesting indication for flux variability for P2 without any change in its pulse shape. Finally, we checked the JBO radio profile assembled during the ``anomaly'' period for possible morphology changes e.g., the appearance of a new feature, but we found none.

\begin{figure} \par\includegraphics[angle=90,width=9cm,clip]{13851fig4.ps} \end{figure} Figure 4:

The ratio of the integrated flux in pulse-1 to pulse-2 as a function of time for the PCA energy band $\sim $2-11 keV. At time interval MJD 53 736-53 749 (i.e., the ``anomaly'' period) one data point deviates $\sim $$3.5\sigma $ (single trial) from the time-averaged value of $2.2\pm 0.1$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=9cm,clip]{13851fig5.ps} \end{figure} Figure 5:

The pulse profile of PSR J0205+6449 (60 bins) in the $\sim $2-11 keV band during the ``anomaly'' interval (MJD 53 736-53 749; 2 RXTE sub-observations). Strongly enhanced P2 emission is detected. The best fit model, composed of a background plus two asymmetric Lorentzians of the same shapes as shown in Fig. 2, is superimposed as dashed line.

Open with DEXTER

3.7 RXTE HEXTE timing analysis

During the observations listed in Table 1 HEXTE operated in its default rocking mode, allowing the collection of real-time background data from two independent positions $\pm 1\hbox{$.\!\!^\circ$ }5$ to either side of the on-source position. For the timing analysis, we selected only the on-source data from both clusters. Good-time intervals were determined using similar screening filters as used in the case of the PCA. The selected on-source HEXTE event times were subsequently barycentered and folded on the ephemerides listed in Table 2 taking into account proper radio-phase referencing. Thus, we obtained time-averaged HEXTE pulse phase distributions in 256 spectral channels (15-250 keV) for the combination of observations listed in Table 1. The total dead-time corrected exposure time collected for clusters A and B amounts to 400.6 ks and 426.3 ks, respectively. Pulse profiles for the bands[*] 14.7-28 and 33.1-132.6 keV are shown in panels c and d of Fig. 6. Fitting a model comprising the (asymmetric) Lorentzians shapes of Pulses 1 and 2 and a flat background to these phase distributions yielded detection significances of $7.8\sigma$ and $3.8\sigma$ for the 14.7-28 and 33.1-132.6 keV bands, respectively ($2.9\sigma$ for the band, 64.1-132.6 keV). Therefore, pulsed emission of PSR J0205+6449 was detected up to $\sim $132 keV, well above the sensitivity band of the PCA.

3.8 XMM-Newton timing analysis

The XMM EPIC-PN data were screened for solar (soft proton) flares by creating a light curve for events with energies in excess of 10 keV. From the resulting count rate distribution, assumed to be Gaussian in absence of any flares, we could identify periods during which the rate exceeds its mean value plus three times the width of the distribution. These periods are ignored in subsequent analyses. We then selected events from a sufficiently large circular region centered on PSR J0205+6449 of radius $60\hbox{$^{\prime\prime}$ }$ to ensure that all pulsar counts are included and barycentered the event times of these events. Because the XMM-Newton observations were performed before the 80 ks RXTE observation (60 130), no valid ephemeris was available for the XMM data period. Therefore, we performed a limited periodicity search around the predicted frequency value based on entry-1 of Table 2. We found a $\sim $$10\sigma$ signal right at the predicted frequency using only events with energies between 4 and 12 keV. The folded pulse profile was compatible with the high-statistics PCA profile (see Fig. 2) taking into account the blurring of the pulse profile caused by the limited time resolution of 5.67 ms (=0.086 in phase units). For subsequent studies, we used an extraction radius of $15\hbox{$^{\prime\prime}$ }$ because the signal-to-noise ratio reaches a maximum at that value. We created pulse-phase distributions by combining both adjacent XMM observations in 30 bins (i.e., oversampled by a factor of $\sim $3) for 585 energy intervals over the 0.3 to 12 keV range, each 0.02 keV wide. The (radio-aligned) EPIC-PN pulse profiles for the 0.5-3 and 3-12 keV bands are shown in the panels a and b of Fig. 6 and have significances of 5.8 and $9.7\sigma$ (adopting Z72-test; Buccheri et al. 1983), respectively. Pulsed emission was detected down to $\sim $0.95 keV.

\begin{figure} \par\includegraphics[width=7cm,clip]{13851fig6.ps} \end{figure} Figure 6:

XMM-Newton EPIC-PN pulse profiles (30 bins) of PSR J0205+6449 for the 0.5-3 and 3-12 keV energy bands (panels a, b). Panels c) and d) show the RXTE HEXTE profiles (60 bins) for the 14.7-28 and 33.1-132.8 keV energy bands. Significant pulsed emission is detected up to $\sim $130 keV and down to $\sim $0.95 keV.

Open with DEXTER

4 Pulsed spectra from RXTE PCA/HEXTE and XMM-Newton data: total pulsed, P1 and P2

From the pulse-phase distributions $N(\Phi,E)$ derived for RXTE PCA, HEXTE, and XMM-Newton EPIC PN, we extracted pulsed excess counts by fitting the following model function (analoguous to our X-ray pulse profile variability study shown in Sect. 3.6) to the measured pulse-phase distribution, ${\cal{N}}(\Phi)$, in various user-selected energy bands:

\begin{displaymath}{\cal{N}}(\Phi)=b+c_1\times T_1(\Phi)+c_2\times T_2(\Phi). \end{displaymath} (4)

In this formula, b represents the (constant) unpulsed/DC level, c1 and c2 the scales of the two asymmetric Lorentzian templates, T1 and T2 (both normalized to 1), respectively (see Sect. 3.5). This model provided statistically good fits to all PCA and HEXTE profiles. Good fits could be achieved for the EPIC-PN profiles after convolving the Lorentzian templates with the poorer time resolution.

For each instrument, the pulsed excess counts in the various energy bands for the first (P1) and the second pulse (P2) and the sum (=total pulsed, TP) can be translated into photon fluxes provided that proper energy response matrices are used.

In the case of the PCA, we constructed time-averaged energy response matrices for each PCU by separately taking into account the different (screened) exposure times of the involved PCU's during the time period of interest. For this purpose, we used the ftools version 6.4 programs pcarsp and addrmf. To convert PHA channels to measured energy values, $E_{\hbox{\scriptsize PHA}}$, for PCU combined/stacked products, we also generated a weighted PCU-combined energy response matrix.

For HEXTE, we employed cluster A and B energy-response matrices separately, taking into account the different screened on-source exposure times and the reduction in efficiency in the case of off-axis observations. The on-source exposure times of both clusters were corrected for considerable dead-time effects.

Finally, we created energy response files (effective area (arf) and energy redistribution matrix (rmf)) for the EPIC PN operating in small window mode taking into account the reduction in effective area given the $15\hbox{$^{\prime\prime}$ }$ source extraction radius used. For this purpose, we employed the XMM SAS (vrs. 7.1.0) software tools arfgen 1.73.3 and rmfgen 1.55.1.

We assume simple power-law models of the form, $F_{\gamma }= K\cdot (E_{\gamma }/E_0)^{-\Gamma }$ where $\Gamma$ is the photon index and K the normalization in ph/cm2 s keV at the pivot energy E0 for the underlying photon spectra of P1, P2, and its sum TP. We fixed the absorbing interstellar hydrogen column $N_{\rm H}$ to $3.4~\times ~10^{21}$ cm-2 (see the ``PL-model for neutron star'' entry in Table 2 of Slane et al. 2004). These models were fitted by a forward folding procedure using the appropriate response matrices to obtain the optimum spectral parameters, K and $\Gamma$, and the reconstructed spectral flux points from the observed pulsed count rates. We verified that the measured high-statistics RXTE-PCA spectrum, the EPIC-PN spectrum, and the total spectrum including HEXTE data are fully consistent with this non-thermal simple power-law model. In the pulsed X-ray spectrum above $\sim $0.5 keV, there is no indication of a thermal black-body component, a conclusion also reached for the total emission from the compact source by Slane et al. (2002) and Slane et al. (2004), who reported a power-law spectral index of $\sim $1.7. In their Table I, we note that Kargaltsev & Pavlov (2008) erroneously mark this pulsar to have a black-body component. Furthermore, we only show the unabsorbed spectra i.e., the effect of the interstellar absorption has been removed from the observed spectra.

In Table 4, the best-fit spectral model parameters are listed for the total pulsed emission TP, and emissions of P1 and P2 using PCA data only, and for TP using the EPIC PN, PCA, and HEXTE combination over the extended energy band from 0.56 to 267.5 keV. All spectra have a consistent shape with index $\sim $1.03. For energies >100 MeV, we note for comparison that the Fermi LAT measures for TP a much softer spectrum with spectral index 2.1 and a cutoff at $\sim $3 GeV (Abdo et al. 2009a), and that P2 exhibits at high-energy $\gamma $-rays a significantly harder spectrum than P1.

The photon spectrum ( $\nu F_{\nu}$ representation) over the 0.56-267.5 keV energy band of the total pulsed emission combining XMM-Newton EPIC-PN, RXTE-PCA and HEXTE data, as derived in this work, is shown in Fig. 7 for a much wider energy frame (0.1 keV-10 GeV) by including the best fit and its uncertainty range measured by Fermi for energies >100 MeV (Abdo et al. 2009a). The luminosity of the pulsed emission of PSR J0205+6449 apparently reaches a maximum in the MeV band. For comparison, we also plotted the total pulsed emission spectra of the Crab, PSR B1509-58 as well as the ``middle-aged'' Vela pulsar.

Table 4:  Best fit values for the photon flux spectra of the total pulsed emission (TP), the first (P1) and second (P2) pulse emissions of PSR J0205+6449 assuming a power-law model of the form $F_{\gamma }= K\cdot (E_{\gamma }/E_0)^{-\Gamma }$.

\begin{figure} \par\includegraphics[width=9cm,clip]{13851fig7.ps} \end{figure} Figure 7:

Broad-band total-pulsed photon spectrum of PSR J0205+6449 (aqua colored) compared with the pulsed spectra of PSR B0531+21 (Crab; red), PSR B0833-45 (Vela; dark blue), and PSR B1509-58 (purple). The (hard) X-ray spectrum (0.56-267.5 keV) of PSR J0205+6449 was derived in this work, and the best-fit power-law model (index $\sim $1.03) has been superimposed. The >100 MeV spectrum of PSR J0205+6449 is the model fit to the Fermi spectrum from Abdo et al. (2009a). For Crab and Vela, the best-model fits to the recently published Fermi spectra for energies >100 MeV are also shown (see Abdo et al. 2010b,2009b, respectively). For all spectra, the effect of the interstellar absorption has been removed (only effective below $\sim $5 keV).

Open with DEXTER

5 Summary

For the young rotation-powered pulsar PSR J0205+6449, we have derived the timing and spectral characteristics across the broad X-ray band from $\sim $0.5 to $\sim $270 keV, using data from the RXTE PCA and HEXTE, and XMM-Newton EPIC PN. These X-ray characteristics complement our knowledge about this pulsar in the radio domain and the high-energy $\gamma $-ray band for energies above 100 MeV in the following ways:

  • Our phase-coherent ephemerides (see Table 2) are consistent with those derived by Livingstone et al. (2009) with the main difference that we used solely X-ray data (from the RXTE PCA) and fitted at most three timing parameters 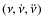$(\nu,\dot\nu,\ddot\nu)$ over more limited time intervals.

  • The X-ray pulse profile consists of two sharp pulses that can be described by 2 asymmetric Lorentzians, each with the rising wing steeper than the trailing wing, and full-width-half-maximum 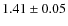$1.41 \pm 0.05$ ms and 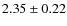$2.35 \pm 0.22$ ms, respectively. These profiles are sharper than reported by Livingstone et al. (2009).

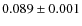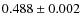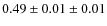  • The first X-ray pulse lags the single radio pulse in phase by $0.089\pm0.001$ (statistical error), and the phase separation between the two X-ray pulses equals $0.488 \pm 0.002$, which is fully consistent with the value $0.49 \pm 0.01 \pm 0.01$ (statistical and systematic errors) reported for high-energy 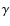$\gamma $-rays above 100 MeV (Abdo et al. 2009a).

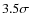  • We found an indication of a flux increase by a factor $\sim $2, $\sim $$3.5\sigma $ above the time-averaged value, for the second, weaker pulse during a two-week time interval, while its pulse shape did not change. During this time window, the morphology of the JBO radio profile of PSR J0205+6449 did not change, and there was no indication of a second pulse.

  • We detected the pulsed signal significantly for the first time down to $\sim $0.95 keV with XMM-Newton EPIC PN, and up to $\sim $130 keV by analysing RXTE HEXTE data. The morphologies of the EPIC PN (taking into account the coarser timing resolution) and the HEXTE profiles are consistent with that measured with the PCA.

    Table 5:   Characteristics of the three young (<10 kyr) X-ray and $\gamma $-ray emitting pulsars in comparison with the middle-aged Vela pulsar (PSR B0833-045).

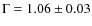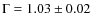  • The spectrum of the pulsed X-ray emission is of non-thermal origin, exhibiting a power-law shape with photon index $\Gamma = 1.06 \pm 0.03$ when fitting just the high-statistics PCA data, and $\Gamma = 1.03 \pm 0.02$ when fitting across the broader energy band from $\sim $0.5 to $\sim $270 keV by including also the EPIC-PN and HEXTE flux values. There is no indication of a black-body component in the soft X-ray spectrum above 0.5 keV.

  • We do not see any spectral difference between the spectra of the two X-ray pulses in the PCA data. Both spectral photon indices are fully consistent with the time-averaged value for the total pulsed emission (see Table 4). We note that the relative strengths of P1 and P2 in the X-ray and high-energy 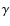$\gamma $-ray windows differ (see Fig. 3), such that the spectrum of P2 has to harden significantly with respect to that of P1 between a few hundred keV and 100 MeV.

6 Discussion and conclusions

In the introduction, we noted that PSR J0205+6449 is one of only three young (<10 000 year old) pulsars that have been detected in the classical X-ray band and at hard X-rays above 20 keV, as well as at high-energy (>100 MeV) $\gamma $-rays, the others being the Crab pulsar and PSR B1509-58. Figure 7 shows that these three young pulsars reach their maximum luminosities below 100 MeV, while the ``middle-aged'' Vela pulsar (characteristic age 11.4 kyr) reaches its maximum at GeV energies. For the latest results on the Vela pulsar at energies above 100 MeV, we refer to the Fermi results by Abdo et al. (2009b). The latter spectrum is characteristic for older pulsars reported to be detected above 100 MeV (e.g., see the first Fermi Large Area Telescope catalog of $\gamma $-ray pulsars by Abdo et al. 2010a).

Comparing in more detail the high-energy spectra of the young pulsars in Fig. 7, we notice large differences. For energies below 10 keV the flux values of PSR J0205+6449 are $\sim $4 orders of magnitude below those of the Crab, while around 10 MeV the difference is reduced to about a factor of 10. The X-ray spectrum of PSR J0205+6449 is, thus, very much harder than that of the Crab. The total high-energy spectrum of PSR J0205+6449 appears to reach its maximum luminosity at MeV energies. This is also the case for PSR B1509-58/PSR J1513-5908 whose spectral break measured by Kuiper et al. (1999) between 10 MeV and 100 MeV (see flux values in Fig. 7) with COMPTEL and EGRET aboard the Compton Gamma-Ray Observatory was confirmed by Pellizzoni et al. (2009). For PSR B1509-58, the latter authors report a softening of the photon index $\Gamma$ from $\sim $1.7 to $\sim $2.5 going from tens to hundreds of MeV but do not provide pulsed-flux values.

Interestingly, the X-ray spectrum above 2 keV of PSR J0205+6449 resembles that of the slightly older Vela pulsar (similar spectral index), but the $L_{\rm X}/L_{\gamma}$ ratio for the pulsed component differs by a factor $\sim $50 (larger for PSR J0205+6449; see Table 5, which is introduced below). The $L_{\rm X}/L_{\gamma}$ ratio of PSR J0205+6449 is in-between those of Vela and PSR B1509-58, namely, the $L_{\rm X}/L_{\gamma}$ ratio for PSR J0205+6449 is a factor $\sim $50 smaller than that for PSR B1509-58. We note, that for the quoted flux ratios it is assumed that the beaming fractions in the X-ray and $\gamma $-ray bands are the same. We know, however, that these are in many cases different. More importantly, in the X-ray spectra below e.g., 2 keV there are no indications of black-body components in the spectra of Crab, PSR B1509-58, and PSR J0205+6449. In contrast, below 2 keV the (pulsed) Vela spectrum exhibits a black-body peak (not shown in Fig. 7; see e.g., Pavlov et al. 2001), which is characteristic of middle-aged and older rotation powered pulsars. Therefore, the spectral properties of PSR J0205+6449 confirm that we are dealing with a young pulsar, and suggest a real age between those of Vela and PSR B1509-58, favouring its characteristic age of 5.4 kyr over that of SN 1181 (828 yr).

Table 5 lists for the four pulsars discussed above in order of characteristic age ( $\tau=P/2\dot{P}$) the spin-down luminosities $L_{\rm sd}$ and fluxes F and luminosities L in the X-ray 2-100 keV and gamma-ray 0.1-10 GeV bands, as well as the corresponding efficiencies to convert spin-down energy into emission in these energy bands. The luminosities are calculated to be $L = 4\pi d^2Ff_{\Omega}$, where the values of the distance d are taken from the table, and the values of beaming fraction, $f_\Omega$, are set to 1. At first sight, one could argue that there is an anticorrelation between characteristic age and X-ray luminosity, independent of differences in the beaming fractions, but this becomes less obvious when we consider the X-ray efficiencies instead of luminosities. In the gamma-ray band, there is no indication of a correlation. The listed gamma-ray efficiencies differ by less than a factor $\sim $10, ignoring differences in beaming fraction, that can also be substantial.

There are also large differences in the morphologies of the pulse profiles of the three young pulsars. Comparing the pulse profiles detected for the Crab and PSR J0205+6449 at X-ray energies and high-energy $\gamma $-rays, there are some simularities: both exhibit two pulses with peaks separated $\sim $0.5 and $\sim $0.4 in pulse phase, respectively, and the X-ray and $\gamma $-ray pulses are aligned in phase. However, the pulses in the Crab profile are significantly broader than those of PSR J0205+6449  and emission is also detected between the two Crab pulses. The latter is not the case for the X-ray profile of PSR J0205+6449, but, interestingly, emission between the pulses has been detected in the Fermi profile at the $5\sigma$ level.

Furthermore, the Crab main radio pulse is generally in phase coincidence with the broad X-ray/$\gamma $-ray pulse. The peak of this main radio pulse lags that of the first X-ray/$\gamma $-ray pulse in phase by only $\sim $0.008 or 280 $\mu$s; for consistent estimates from INTEGRAL, RXTE, and EGRET, we refer to Kuiper et al. (2003), and from Fermi, Abdo et al. (2010b). On the other hand, the Crab radio precursor precedes the first, main X-ray/$\gamma $-ray pulse in phase by $\sim $0.09, or 3.2 ms, being located around the start of the leading wing of the high-energy pulse. In the case of PSR J0205+6449, the single radio pulse also precedes the first narrow X-ray/$\gamma $-ray pulse in phase by $\sim $0.083 or 5.4 ms, and is fully separated in phase, the radio pulse being located just before the onset of the first high-energy pulse (see Fig. 3). This strongly suggests that the analogue of the radio pulse of PSR J0205+6449 is the weak radio precursor of the Crab. In contrast to the situation for the Crab, there are no counterparts in the radio profile of PSR J0205+6449 to the two high-energy pulses of PSR J0205+6449. This means that for this young pulsar exhibiting sharp non-thermal high-energy pulses, we do not see evidence of radio emission originating from the same site in the magnetosphere, e.g., in slot gaps (two-pole caustic emission, Dyks & Rudak 2003) or outer gaps (outer-magnetosphere emission; see Hirotani 2006; Cheng et al. 1986; Romani 1996, from a region close to the light cylinder). The radio component of PSR J0205+6449 is possibly just too weak to be detectable, but might be found in a search for giant radio pulses in the phase intervals of the high-energy pulses. For a number of young and milli-second radio pulsars phase coincidences between the high-energy pulses and giant radio pulses have indeed been reported. Two examples are the Crab for which the distribution of giant radio pulses is remarkably similar to the average emission profile of the radio main and interpulse (Popov et al. 2006), and the milli-second pulsar PSR B1937+21 for which Cusumano et al. (2003) reported the phase coincidence of two sharp high-energy X-ray pulses with two phase intervals exhibiting giant radio pulses, which trail the two normal radio pulses. The latter example might be applicable PSR J0205+6449.

The high-energy pulse profile of PSR B1509-58 differs totally from those of the Crab and PSR J0205+6449. At hard X-rays and soft $\gamma $-rays below 10 MeV, the profile consists of a single structured broad pulse, which can be explained as consisting of two Gaussian pulse profiles separated $\sim $0.14 in phase with different spectra (Cusumano et al. 2001; Kuiper et al. 1999), the second broader pulse peaking at $\sim $0.35, and the main radio pulse being at phase 0. Above 10 MeV, the COMPTEL profile between 10 and 30 MeV and the EGRET profile between 30 and 100 MeV are indicative of an additional high-energy pulse at phase $\sim $0.85 (Kuiper et al. 1999). The latter seems now to be confirmed in the AGILE profile of PSR B1509-58 Pellizzoni et al. (2009), which shows the main pulse for energies above 100 MeV at phase $\sim $0.35, and a second possible pulse at $\sim $0.85. It is now ambiguous which phase difference between high-energy pulses of PSR B1509-58 ($\sim $0.14 or $\sim $0.5) should be considered for comparison with the morphology of pulse profiles of the other young pulsars.

The various models cited above aim to explain the production of non-thermal high-energy emission in the magnetospheres of rotation-powered pulsars without addressing flux variability. There was indeed no observational evidence of variability until the magnetar-like outburst of the high-field pulsar PSR J1846-0258 (Gavriil et al. 2008), which decayed with an 1/e-time constant of $\sim $55 days. It was shown by Kuiper & Hermsen (2009) that the radiative outburst was triggered by a major spin-up glitch, and that, most interestingly, the shape of the X-ray pulse profile did not change during the outburst. For the flux increase by a factor of $\sim $2 of the non-thermal emission from the second pulse of PSR J0205+6449 during a two-week time period, we also saw no variation in pulse shape. However, there was no indication of glitching activity. The significance of the variability is insufficient to draw strong conclusions, but it appears warranted to begin searching for this variability in the emission from the increasing sample of rotation-powered pulsars emitting non-thermal high-energy emission.

In conclusion, we have accurately measured for the young rotation powered pulsar PSR J0205+6449 the morphology of the X-ray light curve and the spectrum over the broad X-ray band $\sim $0.5-$\sim $270 keV. The PSR J0205+6449 X-ray spectrum above 2 keV has the same power-law shape ( $\Gamma \sim 1.03$) as the middle-aged Vela pulsar, but the overall high-energy spectral shape, considering also the Fermi $\gamma $-ray spectrum, resembles more clsoely the spectrum expected for a younger pulsar, i.e., it exhibits no evidence of a thermal black-body component, and has maximum luminosity at MeV energies and not at GeV energies.

The morphology of the double-pulse PSR J0205+6449 light curve can be explained in a conventional outer-gap scenario for a rotating dipole in vacuum assuming low-altitude radio emission. This is similar to the case of the Crab pulsar when taking the Crab precursor radio pulse as the counterpart to the single radio pulse detected for PSR J0205+6449. This can be verified in the ``atlas'' of model $\gamma $-ray light curves simulated by Watters et al. (2009). However, we refer also to the alternative atlas by Bai & Spitkovsky (2010a), who point out an inconsistency in the model calculations by Watters et al. (2009) and earlier reports, affecting particularly the profile shapes calculated for the two-pole caustic model.

Furthermore, it should be realized that the sharp pulses in the high-energy profile of this young pulsar PSR J0205+6449 do not have radio counterparts similar to those we see for the Crab, and we encourage a search for giant radio pulses in the phase intervals of these high-energy pulses. Model calculations by Bai & Spitkovsky (2010b) using a force-free field instead of the vacuum dipole field show that alternative scenarios, such as their annular-gap model, are required to reproduce for a wide range of parameters two sharp high-energy pulses as exhibited by PSR J0205+6449. More extensive 3-D simulations including the physics of the production processes are required before more detailed comparisons with the spectral and timing characteristics can be made.



Acknowledgements
This research has made use of data obtained from the High Energy Astrophysics Science Archive Research Center (HEASARC), provided by NASA's Goddard Space Flight Center. We have extensively used NASA's Astrophysics Data System (ADS). J.O.U. acknowledges the IAU Travel Grant that enabled him to visit SRON; and the support and hospitality of SRON Netherlands Insitute for Space Research.

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, ApJ, 699, L102 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abdo, A. A., Ackermann, M., Atwood, W. B., et al. 2009b, ApJ, 696, 1084 [Google Scholar]
  3. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJS, 187, 460 [NASA ADS] [CrossRef] [Google Scholar]
  4. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 708, 1254 [NASA ADS] [CrossRef] [Google Scholar]
  5. Aliu, E., Anderhub, H., Antonelli, L. A., et al. (The MAGIC Collaboration) 2008, Science, 322, 1221 [Google Scholar]
  6. Bai, X.-N., & Spitkovsky, A. 2010a, ApJ, 715, 1270 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bai, X.-N., & Spitkovsky, A. 2010b, ApJ, 715, 1282 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bietenholz, M. F. 2006, ApJ, 645, 1180 [NASA ADS] [CrossRef] [Google Scholar]
  9. Buccheri, R., Bennett, K., Bignami, G., et al. 1983, A&A, 128, 245 [NASA ADS] [Google Scholar]
  10. Camilo, F., Stairs, I. H., Lorimer, D. R., et al. 2002, ApJ, 571, L41 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cheng, K. S., Ho, C., & Ruderman, M. A. 1986, ApJ, 300, 522 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cusumano, G., Mineo, T., Massaro, E., et al. 2001, A&A, 375, 379 [Google Scholar]
  13. Cusumano, G., Hermsen, W., Kramer, M., et al. 2003, A&A, 410, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Dyks, J., & Rudak, B. 2003, ApJ, 598, 1201 [NASA ADS] [CrossRef] [Google Scholar]
  15. Fesen, R., Rudie, G., Hurford, A., & Soto, A. 2008, ApJS, 174, 379 [NASA ADS] [CrossRef] [Google Scholar]
  16. Gavriil, F. P., Gonzales, M. E., Gotthelf, E. V., et al. 2008, Science, 319, 1802 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  17. Hirotani, K. 2006, ApJ, 652, 1475 [NASA ADS] [CrossRef] [Google Scholar]
  18. Jahoda, K., Swank, J. H., Giles, A. B., et al. 1996, Proc. SPIE, 2808, 59 [NASA ADS] [CrossRef] [Google Scholar]
  19. Kargaltsev, O., & Pavlov, G. G. 2008, AIP Conf. Proc., 983, 171 [Google Scholar]
  20. Kuiper, L., & Hermsen, W. 2009, A&A, 501, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Kuiper, L., Hermsen, W., Krijger, J. M., et al. 1999, A&A, 351, 119 [NASA ADS] [Google Scholar]
  22. Kuiper, L., Hermsen, W., Cusumano, G., et al. 2001, A&A, 378, 918 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Kuiper, L., Hermsen, W., Walter, R., & Foschini, L. 2003, A&A, 411, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Livingstone, M. A., Ransom, S. M., Camilo, F., et al. 2009, ApJ, 706, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  25. Murray, S. S., Slane, P. O., Seward, F. D., et al. 2002, ApJ, 568, 226 [NASA ADS] [CrossRef] [Google Scholar]
  26. Pavlov, G. G., Zavlin, V. E., Sanwal, D., et al., 2001, ApJ, 552, L129 [Google Scholar]
  27. Pellizzoni, A., Pilia, M., Possenti, A., et al. 2009, ApJ, 695, L115 [NASA ADS] [CrossRef] [Google Scholar]
  28. Popov, M., Soglasnov, V., Kondrat'ev, V., et al. 2006, Astron. Lett., 50, 55 [Google Scholar]
  29. Ransom, S., Camilo, F., Kaspi, V., et al. 2004, in X-ray Timing 2003: Rossi and Beyond, AIP Conf. Proc., 714, ed. P. Kaaret, F. K. Lamb, & J. H. Swank [Google Scholar]
  30. Romani, R. W. 1996, ApJ, 470, 469 [NASA ADS] [CrossRef] [Google Scholar]
  31. Rothschild, R. E., Blanco, P. R., Gruber, D. E., et al. 1998, ApJ, 496, 538 [NASA ADS] [CrossRef] [Google Scholar]
  32. Slane, P. O., Helfand, D. J., & Murray, S. S. 2002, ApJ, 571, L45 [NASA ADS] [CrossRef] [Google Scholar]
  33. Slane, P. O., Helfand, D. J., van der Swaluw, E., & Murray, S. S. 2004, ApJ, 616, 403 [NASA ADS] [CrossRef] [Google Scholar]
  34. Stephenson, F. R., & Green, D. A. 2002, Historical Supernovae and Their Remnants (Oxford: Clarendon) [Google Scholar]
  35. Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Watters, K., Romani, R. W., Weltevrede, P., & Johnston, S. 2009, ApJ, 695, 1289 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... solely[*]
X-ray timing data are not hampered by time-variable dispersion measure (DM) variations, as is the case for the radio data, and therefore the remaining scatter in the obtained timing solutions is smaller. This has been verified for the Crab pulsar.
...$0.49 \pm 0.01 \pm 0.01$[*]
The first error specifies the statistical error and the second the systematical error (see Abdo et al. 2009a, for more details).
... bands[*]
We ignored spectral data from the band 28-33.1 keV because of a huge background line originating from the activation of iodine.
Copyright ESO 2010

All Tables

Table 1:   RXTE PSR J0205+6449 observation summary.

Table 2:   Phase-coherent ephemerides for PSR J0205+6449 as derived from RXTE PCA (monitoring) data.

Table 3:   X-ray pulse profile characterization of PSR J0205+6449 from a fit involving two asymmetric Lorentzians plus background.

Table 4:   Best fit values for the photon flux spectra of the total pulsed emission (TP), the first (P1) and second (P2) pulse emissions of PSR J0205+6449 assuming a power-law model of the form $F_{\gamma }= K\cdot (E_{\gamma }/E_0)^{-\Gamma }$.

Table 5:   Characteristics of the three young (<10 kyr) X-ray and $\gamma $-ray emitting pulsars in comparison with the middle-aged Vela pulsar (PSR B0833-045).

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{13851fig1.ps} \end{figure} Figure 1:

Evolution of the spin-frequency of PSR J0205+6449 as derived from RXTE PCA data over the period MJD 52 138-53 813 with respect to the linear trend of the phase coherent timing model of period MJD 52 433-52 515 (entry #3 of Table 2). As solid lines, the entries #1-12 of Table 2 are plotted, while for the period 52 571-52 752 the linear fit to the incoherent frequency measurements is also shown as a solid line. Incoherent frequency measurements over the period MJD 52 544-52 752 are shown as data points. Note the presence of (at least) two timing glitches: one in the period 52 515 to 52 571 and a second stronger one between 52 752 and 53 063 (see text).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13851fig2.ps} \vspace*{-2mm} \end{figure} Figure 2:

High-statistics radio-aligned PCA pulse phase distribution in 180 bins for PHA range 5-44 ($\sim $2-20 keV) combining all available radio-aligned pulse phase distributions from different data segments. Error bars represent $1\sigma $ uncertainties. The best-fit ( $\chi ^2=199.47$ for 171 degrees of freedom) model composed of two asymmetric Lorentzians plus background is superimposed as a dashed red line. The rising wings of the pulses are steeper than the trailing wings.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.cm,height=13cm,clip]{13851fig3.ps} \end{figure} Figure 3:

A comparison in absolute phase of the JBO radio (1.4 GHz), RXTE-PCA ($\sim $2-20 keV) and Fermi LAT (>100 MeV) pulse profiles. Note the change in the relative contributions of P1 and P2 in the X-ray and $\gamma $-ray windows.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=9cm,clip]{13851fig4.ps} \end{figure} Figure 4:

The ratio of the integrated flux in pulse-1 to pulse-2 as a function of time for the PCA energy band $\sim $2-11 keV. At time interval MJD 53 736-53 749 (i.e., the ``anomaly'' period) one data point deviates $\sim $$3.5\sigma $ (single trial) from the time-averaged value of $2.2\pm 0.1$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13851fig5.ps} \end{figure} Figure 5:

The pulse profile of PSR J0205+6449 (60 bins) in the $\sim $2-11 keV band during the ``anomaly'' interval (MJD 53 736-53 749; 2 RXTE sub-observations). Strongly enhanced P2 emission is detected. The best fit model, composed of a background plus two asymmetric Lorentzians of the same shapes as shown in Fig. 2, is superimposed as dashed line.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13851fig6.ps} \end{figure} Figure 6:

XMM-Newton EPIC-PN pulse profiles (30 bins) of PSR J0205+6449 for the 0.5-3 and 3-12 keV energy bands (panels a, b). Panels c) and d) show the RXTE HEXTE profiles (60 bins) for the 14.7-28 and 33.1-132.8 keV energy bands. Significant pulsed emission is detected up to $\sim $130 keV and down to $\sim $0.95 keV.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13851fig7.ps} \end{figure} Figure 7:

Broad-band total-pulsed photon spectrum of PSR J0205+6449 (aqua colored) compared with the pulsed spectra of PSR B0531+21 (Crab; red), PSR B0833-45 (Vela; dark blue), and PSR B1509-58 (purple). The (hard) X-ray spectrum (0.56-267.5 keV) of PSR J0205+6449 was derived in this work, and the best-fit power-law model (index $\sim $1.03) has been superimposed. The >100 MeV spectrum of PSR J0205+6449 is the model fit to the Fermi spectrum from Abdo et al. (2009a). For Crab and Vela, the best-model fits to the recently published Fermi spectra for energies >100 MeV are also shown (see Abdo et al. 2010b,2009b, respectively). For all spectra, the effect of the interstellar absorption has been removed (only effective below $\sim $5 keV).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.