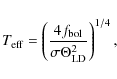| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 8 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200913736 | |
| Published online | 31 May 2010 | |
Ellipsoidal primary of the RS CVn binary  Andromedae
Andromedae
Investigation using high-resolution spectroscopy and optical
interferometry![[*]](/icons/foot_motif.png)
H. Korhonen1 - M. Wittkowski1 - Zs. Kovári2 - Th. Granzer3 - T. Hackman4 - K. G. Strassmeier3
1 - European Southern Observatory, Karl-Schwarzschild-Str. 2,
85748 Garching bei München, Germany
2 -
Konkoly Observatory, 1525 Budapest, PO Box 67, Hungary
3 -
Astrophysical Institute Potsdam, An der Sternwarte 16, 14482 Potsdam,
Germany
4 -
Observatory, PO Box 14, 00014 University of Helsinki, Finland
Received 24 November 2009 / Accepted 24 January 2010
Abstract
Aims. We have obtained high-resolution spectroscopy, optical
interferometry, and long-term broad band photometry of the
ellipsoidal primary of the RS CVn-type binary system ![]() And.
These observations are used to obtain fundamental stellar parameters
and to study surface structures and their temporal evolution.
And.
These observations are used to obtain fundamental stellar parameters
and to study surface structures and their temporal evolution.
Methods. Temperature maps of the stellar surface were obtained
from high-resolution spectra with Doppler imaging techniques. These
spectra were also used to investigate the chromospheric activity using
the H![]() line and to correlate it with the photospheric activity. The possible
cyclicity in the spot activity was investigated from the long-term
broad band photometry. Optical interferometry was obtained during
the same time period as the high-resolution spectra. These observations
were used to derive the size and fundamental parameters of
line and to correlate it with the photospheric activity. The possible
cyclicity in the spot activity was investigated from the long-term
broad band photometry. Optical interferometry was obtained during
the same time period as the high-resolution spectra. These observations
were used to derive the size and fundamental parameters of ![]() And.
And.
Results. Based on the optical interferometry the apparent limb darkened diameter of ![]() And is
And is
![]() mas using a uniform disk fit. The expected
mas using a uniform disk fit. The expected ![]() 4%
maximum difference between the long and short axes of the ellipsoidal
stellar surface cannot be confirmed from the current data which have 4%
errors. The Hipparcos distance and the limb-darkened diameter obtained
with a uniform disk fit give stellar radius of
4%
maximum difference between the long and short axes of the ellipsoidal
stellar surface cannot be confirmed from the current data which have 4%
errors. The Hipparcos distance and the limb-darkened diameter obtained
with a uniform disk fit give stellar radius of
![]() ,
and combined with bolometric luminosity, it implies an effective temperature of
,
and combined with bolometric luminosity, it implies an effective temperature of
![]() K.
The temperature maps obtained from Doppler imaging show a strong belt
of equatorial spots and hints of a cool polar cap. The equatorial spots
show a concentration around the phase 0.75, i.e., 0.25 in phase from
the secondary, and another concentration spans the phases 0.0-0.4. This
spot configuration is reminiscent of the one seen in the earlier
published temperature maps of
K.
The temperature maps obtained from Doppler imaging show a strong belt
of equatorial spots and hints of a cool polar cap. The equatorial spots
show a concentration around the phase 0.75, i.e., 0.25 in phase from
the secondary, and another concentration spans the phases 0.0-0.4. This
spot configuration is reminiscent of the one seen in the earlier
published temperature maps of ![]() And. Investigation of the H
And. Investigation of the H![]() line
reveals both prominences and cool clouds in the chromosphere. These
features do not seem to have a clearly preferred location in the binary
reference frame, nor are they strongly associated with the cool
photospheric spots. The investigation of the long-term photometry
spanning 12 years shows hints of a spot activity cycle, which is also
implied by the Doppler images, but the cycle length cannot be reliably
determined from the current data.
line
reveals both prominences and cool clouds in the chromosphere. These
features do not seem to have a clearly preferred location in the binary
reference frame, nor are they strongly associated with the cool
photospheric spots. The investigation of the long-term photometry
spanning 12 years shows hints of a spot activity cycle, which is also
implied by the Doppler images, but the cycle length cannot be reliably
determined from the current data.
Key words: stars: activity -
stars: chromospheres -
stars: fundamental parameters -
stars: individual: ![]() Andromedae -
starspots
Andromedae -
starspots
1 Introduction
Because of the enhanced dynamo action in stars with thick, turbulent
outer-convection zones, rapidly rotating cool stars, both evolved and young,
exhibit significantly stronger magnetic activity than is seen in the Sun.
This activity means that the spots are also much larger than the spots observed
in the Sun. The largest starspot recovered with Doppler imaging is on the
active RS CVn-type binary HD 12545 which, in January 1998, had a spot that
extended approximately
![]() solar radii (Strassmeier 1999). The
lifetime of the large starspots/spot groups can also be much longer than that
of the sunspots, even years instead of weeks for sunspots (e.g., Rice &
Strassmeier 1996; Hussain 2002). The most typical dynamo
signature is the presence of an activity cycle. Cyclic changes in the level of
magnetic activity are well documented for the Sun, as well as for many
solar-type stars (see, e.g., Oláh et al. 2009). It is also
interesting that, according to theoretical calculations, cyclic
variations in the stellar magnetic activity can only be produced when
differential rotation is present (Rüdiger et al. 2003).
solar radii (Strassmeier 1999). The
lifetime of the large starspots/spot groups can also be much longer than that
of the sunspots, even years instead of weeks for sunspots (e.g., Rice &
Strassmeier 1996; Hussain 2002). The most typical dynamo
signature is the presence of an activity cycle. Cyclic changes in the level of
magnetic activity are well documented for the Sun, as well as for many
solar-type stars (see, e.g., Oláh et al. 2009). It is also
interesting that, according to theoretical calculations, cyclic
variations in the stellar magnetic activity can only be produced when
differential rotation is present (Rüdiger et al. 2003).
Table 1: Log of the VLTI/AMBER observations.
In this work ![]() Andromedae, a long-period (17.8 day), single-lined
spectroscopic RS CVn binary (Campbell 1911; Cannon 1915),
is investigated in detail. In this system the primary is of spectral type
K1 III, and the unseen companion possibly of type F (Strassmeier et al. 1993). The primary fills approximately 80% of its Roche lobe,
so it has a non-spherical shape. The estimated ellipticity gives a
Andromedae, a long-period (17.8 day), single-lined
spectroscopic RS CVn binary (Campbell 1911; Cannon 1915),
is investigated in detail. In this system the primary is of spectral type
K1 III, and the unseen companion possibly of type F (Strassmeier et al. 1993). The primary fills approximately 80% of its Roche lobe,
so it has a non-spherical shape. The estimated ellipticity gives a ![]() 4%
difference between the long and short axes of the ellipsoid (Kovári
et al. 2007, from here on Paper I). The mean angular diameter of
4%
difference between the long and short axes of the ellipsoid (Kovári
et al. 2007, from here on Paper I). The mean angular diameter of
![]() And has been derived to
And has been derived to
![]() mas using spectro-photometry
(Cohen et al. 1999)
mas using spectro-photometry
(Cohen et al. 1999)
An earlier detailed Doppler imaging study (Paper I) revealed that the spots on
the surface of ![]() And have a temperature contrast of approximately 1000 K
and that they occur on a wide latitude range from the equator to an asymmetric
polar cap. The strength of the features changed with time, with the polar cap
dominating the beginning of the two-month observing period in 1996/97, while
the activity during the second half was dominated by medium-to-high latitude
features. Also, the investigation revealed a weak solar-type differential
rotation.
And have a temperature contrast of approximately 1000 K
and that they occur on a wide latitude range from the equator to an asymmetric
polar cap. The strength of the features changed with time, with the polar cap
dominating the beginning of the two-month observing period in 1996/97, while
the activity during the second half was dominated by medium-to-high latitude
features. Also, the investigation revealed a weak solar-type differential
rotation.
Here, results from Doppler imaging, optical interferometry, and long-term
photometry of ![]() And are presented. We discuss the reduction of the
interferometric data and the obtained fundamental stellar parameters. The
high-resolution spectra are used with Doppler-imaging techniques to obtain a
surface temperature map. This surface map is compared to the earlier published
temperature maps and also with the chromospheric activity based on observations
of the H
And are presented. We discuss the reduction of the
interferometric data and the obtained fundamental stellar parameters. The
high-resolution spectra are used with Doppler-imaging techniques to obtain a
surface temperature map. This surface map is compared to the earlier published
temperature maps and also with the chromospheric activity based on observations
of the H![]() line. Finally, the long-term broad band photometry is used to
study the temporal evolution of the spottedness, hence the possible spot cycles.
line. Finally, the long-term broad band photometry is used to
study the temporal evolution of the spottedness, hence the possible spot cycles.
2 Observations
Simultaneous observations were carried out at the European Southern Observatory with UVES (UV-Visual Echelle Spectrograph; Dekker et al. 2000) mounted on the 8-m Kueyen telescope of the VLT, and the AMBER (Astronomical Multi BEam combineR; Petrov et al. 2007) instrument of the VLT Interferometer (VLTI). Additionally broad and intermediate band photometry in V, Ic and y bands were obtained with the automatic photoelectric telescopes Wolfgang and Amadeus in Arizona, USA (Strassmeier et al. 1997; Granzer et al. 2001). For all the photometric observations HD 5516 was used as the comparison star.
All the observations were phased using the same ephemeris as in Paper I,
referring to the time of the conjunction.
2.1 Optical interferometry
The AMBER observations were obtained during the second part of the nights
starting on September 14, 16, and 18, 2008, corresponding to orbital phases
![]() (secondary in front),
(secondary in front), ![]() (intermediate case), and
(intermediate case), and
![]() (secondary to the side), respectively. The details of the
observations are listed in Table 1.
During the night starting September 18 the coherence time was very short, so
the data quality is lower than during the other half nights. For all the
observations, AMBER was used in the low-resolution mode at J, H, and K
passbands, giving a resolving power (
(secondary to the side), respectively. The details of the
observations are listed in Table 1.
During the night starting September 18 the coherence time was very short, so
the data quality is lower than during the other half nights. For all the
observations, AMBER was used in the low-resolution mode at J, H, and K
passbands, giving a resolving power (
![]() )
of
)
of ![]() 35
and recording data between about 1.1-2.5
35
and recording data between about 1.1-2.5 ![]() m. Only the H and K band
data (
m. Only the H and K band
data (![]() 1.5-2.5
1.5-2.5 ![]() m) were used for the data analysis. The J band
data were of poor quality owing to vanishing detected flux. The fringe tracker
FINITO (Le Bouquin et al. 2008) was used for most observations. During
the night starting September 14, data were also taken without the use of FINITO
in order to confirm the calibration of the visibility. The Auxiliary Telescopes
(ATs) were placed at the stations A0, K0, and G1, giving ground-baseline
lengths of 128 m (A0-K0) and 90 m (A0-G1 and K0-G1). The A0-G1 and K0-G1
baselines have the same ground length, but differ in position angle by
90
m) were used for the data analysis. The J band
data were of poor quality owing to vanishing detected flux. The fringe tracker
FINITO (Le Bouquin et al. 2008) was used for most observations. During
the night starting September 14, data were also taken without the use of FINITO
in order to confirm the calibration of the visibility. The Auxiliary Telescopes
(ATs) were placed at the stations A0, K0, and G1, giving ground-baseline
lengths of 128 m (A0-K0) and 90 m (A0-G1 and K0-G1). The A0-G1 and K0-G1
baselines have the same ground length, but differ in position angle by
90 ![]() .
.
In addition to ![]() And, a circular check star was observed every night. For
this
And, a circular check star was observed every night. For
this ![]() Andromedae was chosen because it is at a similar position on the
sky as
Andromedae was chosen because it is at a similar position on the
sky as ![]() And and it is expected to have a similar angular diameter
(
And and it is expected to have a similar angular diameter
(
![]() mas; Nordgren et al. 2001;
Mozurkewich et al. 2003). Observations of
mas; Nordgren et al. 2001;
Mozurkewich et al. 2003). Observations of ![]() And and
And and
![]() Peg were interleaved with observations of the interferometric calibration
stars
Peg were interleaved with observations of the interferometric calibration
stars ![]() Psc (K1 III, K=1.86,
Psc (K1 III, K=1.86,
![]() mas), 41 Psc (K3 III, K=2.43,
mas), 41 Psc (K3 III, K=2.43,
![]() mas), HD 7087 (G9 III, K=2.48,
mas), HD 7087 (G9 III, K=2.48,
![]() mas), and HD 15694 (K3 III, K=2.48,
mas), and HD 15694 (K3 III, K=2.48,
![]() mas). The angular diameters for
mas). The angular diameters for
![]() Psc and 41 Psc are from Bordé et al. (2002) and those
for HD 7087 and HD 15694 are from Mérand et al. (2006).
Psc and 41 Psc are from Bordé et al. (2002) and those
for HD 7087 and HD 15694 are from Mérand et al. (2006).
2.2 Spectroscopy
The UVES observations of ![]() And were carried out during 10 nights between
September 13, 2008 and October 1, 2009. The red arm in the standard wavelength
setting of 600 nm was used with the imageslicer #3. This instrument setup
gives a spectral resolution (
And were carried out during 10 nights between
September 13, 2008 and October 1, 2009. The red arm in the standard wavelength
setting of 600 nm was used with the imageslicer #3. This instrument setup
gives a spectral resolution (
![]() )
of 110 000 and a
wavelength coverage of 5000-7000 Å. Each observation consists of three
exposures of 8 s that were later combined to one very high
signal-to-noise ratio (S/N) spectrum. The S/N of combined observations was
between 586 and 914 around 6400 Å. The data were reduced using the UVES
pipeline. A summary of the spectroscopic observations is given in
Table 2.
)
of 110 000 and a
wavelength coverage of 5000-7000 Å. Each observation consists of three
exposures of 8 s that were later combined to one very high
signal-to-noise ratio (S/N) spectrum. The S/N of combined observations was
between 586 and 914 around 6400 Å. The data were reduced using the UVES
pipeline. A summary of the spectroscopic observations is given in
Table 2.
Table 2: The high-resolution spectroscopy with UVES at VLT.
3 Reduction and analysis of the interferometric data
3.1 Data reduction
Raw visibility and closure phase values were computed using the latest version of the amdlib data reduction package (version 2.2) and the yorick interface, both provided by the Jean-Marie Mariotti Center (JMMC). The data reduction principles are described in Tatulli et al. (2007).
Absolute wavelength calibration was performed by correlating the raw spectra
with a model of the atmospheric transmission, resulting in a correction of
![]() in the K-band with respect to the original
wavelength table (cf. Wittkowski et al. 2008). For each observation
mentioned in Table 1, only some of the individual frames were
selected for further analysis. Only those frames were used that had a flux
ratio under 3 between the telescopes of the concerned baseline and that had an
estimated absolute piston of less than 4
in the K-band with respect to the original
wavelength table (cf. Wittkowski et al. 2008). For each observation
mentioned in Table 1, only some of the individual frames were
selected for further analysis. Only those frames were used that had a flux
ratio under 3 between the telescopes of the concerned baseline and that had an
estimated absolute piston of less than 4 ![]() m. Finally, out of these only
the 30% of the frames with the highest fringe signal-to-noise ratio were kept.
The selected frames were averaged.
m. Finally, out of these only
the 30% of the frames with the highest fringe signal-to-noise ratio were kept.
The selected frames were averaged.
The resulting differential phase and visibility values were significantly
affected by chromatic piston effects caused by the dispersion of the air
(cf. Millour et al. 2008; Le Bouquin et al. 2009).
This effect was relatively strong for our data because of the combination of
long baselines and large airmasses. We used the measured differential phase to
estimate the amount of chromatic piston ![]() using
using
![]() ,
where
,
where ![]() is the differential phase and
is the differential phase and ![]() the
wavenumber. The loss of the squared visibility amplitude
the
wavenumber. The loss of the squared visibility amplitude ![]() was estimated
using formula (1) of Millour et al. (2008). The averaged visibility
data were compensated using the estimated
was estimated
using formula (1) of Millour et al. (2008). The averaged visibility
data were compensated using the estimated ![]() .
Millour et al. note that
.
Millour et al. note that
![]() is the absolute piston value relative to the white light fringe. The
absolute piston also includes the frame-by-frame piston that is estimated by
the regular AMBER data reduction. This quantity is determined with respect to
the pixel-to-visibility matrix (P2VM) reference, which can have an offset to
the white light fringe. We selected frames with an estimated piston of less
than 4
is the absolute piston value relative to the white light fringe. The
absolute piston also includes the frame-by-frame piston that is estimated by
the regular AMBER data reduction. This quantity is determined with respect to
the pixel-to-visibility matrix (P2VM) reference, which can have an offset to
the white light fringe. We selected frames with an estimated piston of less
than 4 ![]() m, and verified that the piston of our P2VM measurements is less
than 2
m, and verified that the piston of our P2VM measurements is less
than 2 ![]() m in the H band and less than 4
m in the H band and less than 4 ![]() m in the K band. In
total, we assumed an error of the piston estimate of 5
m in the K band. In
total, we assumed an error of the piston estimate of 5 ![]() m and propagated
it to the final visibility amplitude. We also used an alternative compensation
of the loss of the squared visibility amplitude
m and propagated
it to the final visibility amplitude. We also used an alternative compensation
of the loss of the squared visibility amplitude ![]() that was based on a
parametrization of the calibrator star data as a function of optical path
difference, i.e., an estimate that does not depend on the measured differential
phase of the science target. We obtained results well within the adopted error.
that was based on a
parametrization of the calibrator star data as a function of optical path
difference, i.e., an estimate that does not depend on the measured differential
phase of the science target. We obtained results well within the adopted error.
As a final data reduction step, the squared visibility amplitudes were calibrated for the interferometric transfer function, which was estimated using an average of the computed transfer functions based on the closest calibration star measurement before that of each science target and the closest thereafter. The final error of the calibrated data includes the statistical error of the frames, the error in the correction for chromatic piston, and the standard deviation of the two transfer function measurements.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13736fg1a.ps} \includegraphics[width=8cm,clip]{13736fg1b.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg31.png)
|
Figure 1:
VLTI/AMBER visibility data of |
| Open with DEXTER | |
3.2 Analysis of interferometric data
Figure 1 shows the resulting visibility data of ![]() And and of
the check star
And and of
the check star ![]() Peg obtained from all three observing nights and compared
to models of a uniform disk (UD). Because of the relative large errors in the
observations, no differences were seen in the measurements from different
baselines. Thus all the baselines were used together in the analysis.
Table 3 lists the resulting uniform disk diameters of
Peg obtained from all three observing nights and compared
to models of a uniform disk (UD). Because of the relative large errors in the
observations, no differences were seen in the measurements from different
baselines. Thus all the baselines were used together in the analysis.
Table 3 lists the resulting uniform disk diameters of
![]() And and
And and ![]() Peg for each of the nights separately, as well as for all
three observing nights. When using the data from all the nights together, the
diameter is estimated from the data obtained during the nights starting on
September 14 and 16, but the error is from all the data, i.e., including the
data from the night starting on September 18. This is done because the data
quality is significantly lower on the night starting on September 18 than
during the two other observing nights.
Peg for each of the nights separately, as well as for all
three observing nights. When using the data from all the nights together, the
diameter is estimated from the data obtained during the nights starting on
September 14 and 16, but the error is from all the data, i.e., including the
data from the night starting on September 18. This is done because the data
quality is significantly lower on the night starting on September 18 than
during the two other observing nights.
During the night of September 14, we obtained data with and without the use of
the fringe tracker FINITO. The results for these two data sets agree well
within the errors for both targets, and we do not see any systematic
calibration effects that are caused by the use of FINITO. Deviations between
observed visibility values and the UD model are mostly caused by residuals of
the compensation of the chromatic piston effect, which was most noticeable on
the baseline A0-G1, and by systematic calibration uncertainties due to varying
atmospheric conditions. Within the obtained errors of the UD diameter of about
4%, we do not see indications of any elliptical intensity distribution of
![]() And. However, the ellipticity of
And. However, the ellipticity of ![]() 4% expected for the night of
September 18 is consistent with our data.
4% expected for the night of
September 18 is consistent with our data.
Table 3: Uniform disk fit results for the VLTI/AMBER data.
Correction factors between UD diameter and limb-darkened (LD) disk diameters
were computed using ATLAS 9 model atmospheres (Kurucz 1993). For the
spectral types of our target stars ![]() And and
And and ![]() Peg and the wavelength
range used for our observations, we obtain values for
Peg and the wavelength
range used for our observations, we obtain values for
![]() of 0.974 and 0.976, respectively. The
resulting LD diameters are
of 0.974 and 0.976, respectively. The
resulting LD diameters are
![]() mas and
mas and
![]() mas, respectively. Cohen et al.
(1999) give a diameter of
mas, respectively. Cohen et al.
(1999) give a diameter of
![]() mas for
mas for ![]() And, based
on spectro-photometry. This diameter is significantly larger, but the error
smaller, than what was obtained in this work. Still, the spectro-photometric
observations could be affected by the significant magnetic activity exhibited
by
And, based
on spectro-photometry. This diameter is significantly larger, but the error
smaller, than what was obtained in this work. Still, the spectro-photometric
observations could be affected by the significant magnetic activity exhibited
by ![]() And. The LD diameter of
And. The LD diameter of ![]() Peg obtained here is consistent
with the earlier interferometric measurements of
Peg obtained here is consistent
with the earlier interferometric measurements of
![]() mas obtained with the NPOI and
mas obtained with the NPOI and
![]() mas
obtained with the Mark III interferometers (Nordgren et al. 2001;
and Mozurkewich et al. 2003), increasing the confidence in the
results presented here.
mas
obtained with the Mark III interferometers (Nordgren et al. 2001;
and Mozurkewich et al. 2003), increasing the confidence in the
results presented here.
4 Fundamental parameters
4.1 Radius
The limb darkened diameter of ![]() And, obtained from the interferometric
observations, is
And, obtained from the interferometric
observations, is
![]() mas. Together with the Hipparcos parallax of
mas. Together with the Hipparcos parallax of
![]() mas (van Leeuwen 2007) this can be used to determine the
stellar radius with the following formula:
mas (van Leeuwen 2007) this can be used to determine the
stellar radius with the following formula:
![]() ,
where
,
where
![]() is the
limb-darkened angular diameter in radians,
is the
limb-darkened angular diameter in radians,
![]() the parallax in
arcseconds, and C the conversion from parsecs to meters. For
the parallax in
arcseconds, and C the conversion from parsecs to meters. For ![]() And
this gives stellar radius of
And
this gives stellar radius of
![]() ,
which is
consistent with the 16.0
,
which is
consistent with the 16.0 ![]() estimated in Paper I.
estimated in Paper I.
![\begin{figure}
\par\includegraphics[width=5.7cm,clip]{13736fg2a.ps}\hspace*{2mm}...
...m}
\includegraphics[width=5.7cm,clip]{13736fg2f.ps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg46.png)
|
Figure 2:
Doppler imaging results of |
| Open with DEXTER | |
4.2 Effective temperature
The effective temperature of a star can be calculated from the interferometric
diameter determination when combined with a bolometric flux measurement using
the formula
where
The bolometric flux of ![]() And was estimated using measurements on all
the available photometric passbands and the getCal tool of the NASA
Exoplanet Science Institute's interferometric observation planning tool suite.
The bolometric flux of
And was estimated using measurements on all
the available photometric passbands and the getCal tool of the NASA
Exoplanet Science Institute's interferometric observation planning tool suite.
The bolometric flux of
![]() W/m2
was obtained. Inserting this value to Eq. (1), together with the
limb-darkened angular diameter, gives
W/m2
was obtained. Inserting this value to Eq. (1), together with the
limb-darkened angular diameter, gives
![]() of
of
![]() K. This
value is very close to, and the same within errors, as the
K. This
value is very close to, and the same within errors, as the
![]() K used for Doppler imaging in Paper I and the
current work.
K used for Doppler imaging in Paper I and the
current work.
5 Doppler imaging
For Doppler imaging we used the code T EMPM AP, which was originally written
by Rice et al. (1989). The code performs a full LTE spectrum synthesis
by solving the equation of transfer through a set of ATLAS-9 (Kurucz
1993) model atmospheres at all aspect angles and for a given set of
chemical abundances. Simultaneous inversions of the spectral lines, as well as
of the two photometric bandpasses, are then carried out using a maximum-entropy
regularization. For the non-spherical ![]() And, a new version of the code
was applied: T EMPM AP
And, a new version of the code
was applied: T EMPM AP![]() (see Paper I and the references therein)
takes the distorted geometry of the evolved component in a close binary into
account through the distortion parameter
(see Paper I and the references therein)
takes the distorted geometry of the evolved component in a close binary into
account through the distortion parameter ![]() .
The elliptical distortion
is approximated by a rotation ellipsoid, elongated towards the secondary star:
.
The elliptical distortion
is approximated by a rotation ellipsoid, elongated towards the secondary star:
![]() where a and b are the long and the short axes of the ellipsoid,
respectively. The appropriate value of
where a and b are the long and the short axes of the ellipsoid,
respectively. The appropriate value of ![]() for
for ![]() And, 0.27, as
well as the overall system and stellar parameters, were adopted from Paper I
(Table 2 therein).
And, 0.27, as
well as the overall system and stellar parameters, were adopted from Paper I
(Table 2 therein).
The 30 available UVES spectra (three exposures per night) covered 18 days,
i.e., one full rotation cycle, thus allowing one Doppler reconstruction. The
three nightly observations were averaged, since they were taken within
approximately 120 s. Thus, for further investigation we used the ten
averaged spectra with an enhanced S/N value of ![]() 600 or more (see
Table 2 for more details on observations).
600 or more (see
Table 2 for more details on observations).
Doppler imaging was performed for the well-known mapping lines within the
6392-6440 Å spectral range. Doppler maps for Fe I 6393, 6400, 6411,
6421, 6430, and Ca I 6439 are shown in Fig. 2. The
individual maps revealed similar spot distributions, i.e., mainly cool spots
at low latitudes with temperature contrasts of 600-900 K with respect to the
unspotted surface of 4600 K. Cool polar features are also recovered, however,
with significantly weaker contrast ranging from ![]() 100 K (Fe I 6400)
to a maximum of
100 K (Fe I 6400)
to a maximum of ![]() 700 K (cf. the Fe I 6430 map). Numerous bright
features also appear in the iron maps; however, as they occur near dominant
cool spots they can be artifacts, so-called ``rebound'' features (see, e.g.,
Rice 2002).
700 K (cf. the Fe I 6430 map). Numerous bright
features also appear in the iron maps; however, as they occur near dominant
cool spots they can be artifacts, so-called ``rebound'' features (see, e.g.,
Rice 2002).
Despite the small difference between the temperature contrasts of the
respective maps and the spurious bright features, the resulting six Doppler
maps are in very good agreement. This similarity is more conspicuous in
Fig. 3, where the average of the six individual maps is plotted.
Averaging did not blur the overall structure. The most prominent feature is the
belt of cool spots at the equatorial region, with the strongest concentration
of spots located at the phase ![]() and at another cool region ranging
between phases
and at another cool region ranging
between phases
![]() .
Also a weak polar feature can be detected. This
result is reminiscent of the result in Paper I, where low-latitude dominant
features also tended to concentrate at quadrature positions of opposite
hemispheres for both observing seasons.
.
Also a weak polar feature can be detected. This
result is reminiscent of the result in Paper I, where low-latitude dominant
features also tended to concentrate at quadrature positions of opposite
hemispheres for both observing seasons.
6 Discussion
6.1 Comparison between spherical and ellipsoidal surface geometry in the inversion
Another Doppler imaging code, INVERS7PD, which was written by Piskunov
(see, e.g., Piskunov et al. 1990) and modified by Hackman (Hackman
et al. 2001), was also used to obtain a temperature map of ![]() And.
In this inversion spherical geometry and only the Fe I 6400 Å line
were used. The observations are compared to a grid of local line profiles
calculated with the SPECTRUM spectral synthesis code (Gray & Corbally
1994) and Kurucz model atmospheres (Kurucz 1993). In the
calculations, 10 limb angles and nine temperatures between 3500 K and 5500 K
were used. Photometry was not used as a constraint in this inversion as the
ellipticity effect seen in the light curves cannot be properly taken into
account when using spherical geometry.
And.
In this inversion spherical geometry and only the Fe I 6400 Å line
were used. The observations are compared to a grid of local line profiles
calculated with the SPECTRUM spectral synthesis code (Gray & Corbally
1994) and Kurucz model atmospheres (Kurucz 1993). In the
calculations, 10 limb angles and nine temperatures between 3500 K and 5500 K
were used. Photometry was not used as a constraint in this inversion as the
ellipticity effect seen in the light curves cannot be properly taken into
account when using spherical geometry.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13736fg3.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg56.png)
|
Figure 3: Average map produced from all the maps shown in Fig. 2. |
| Open with DEXTER | |
| Figure 4:
Temperature map of |
|
| Open with DEXTER | |
The result of this inversion is shown in Fig. 4. The main spot
structures and the temperature range are similar to the ones in the map
obtained with T EMPM AP![]() from the Fe I 6400 Å line.
The cool spots concentrate on the equatorial region and especially on the
quadrature points. The main spot is seen at the phase
from the Fe I 6400 Å line.
The cool spots concentrate on the equatorial region and especially on the
quadrature points. The main spot is seen at the phase ![]() in the
equatorial region, and there is also a prominent spot at the phase
in the
equatorial region, and there is also a prominent spot at the phase ![]() at higher latitudes. This is missing from the map obtained using
T EMPM AP
at higher latitudes. This is missing from the map obtained using
T EMPM AP![]() ,
so it is most likely an artifact caused by
using spherical geometry on an ellipsoidal star (cf. Fig. 3 in Paper I).
Furthermore, at the phase
,
so it is most likely an artifact caused by
using spherical geometry on an ellipsoidal star (cf. Fig. 3 in Paper I).
Furthermore, at the phase ![]() ,
the equatorial region has a temperature
close to that of the unspotted surface, unlike in the map obtained using
ellipsoidal geometry. Also, the whole temperature scale is shifted by 100 K
towards the cooler temperatures. On the whole, the temperature map obtained
with the spherical geometry is very similar to the one obtained using
ellipsoidal geometry and T EMPM AP
,
the equatorial region has a temperature
close to that of the unspotted surface, unlike in the map obtained using
ellipsoidal geometry. Also, the whole temperature scale is shifted by 100 K
towards the cooler temperatures. On the whole, the temperature map obtained
with the spherical geometry is very similar to the one obtained using
ellipsoidal geometry and T EMPM AP![]() .
As expected, the main
differences occur at the quadrature points and especially at the phase
.
As expected, the main
differences occur at the quadrature points and especially at the phase
![]() .
Also, one has to keep in mind that the tests with
T EMPM AP
.
Also, one has to keep in mind that the tests with
T EMPM AP![]() show that neglecting the ellipticity in the Doppler
imaging reconstruction yields
show that neglecting the ellipticity in the Doppler
imaging reconstruction yields ![]() 50-240% higher
50-240% higher ![]() values in
comparison to using the correct surface geometry.
values in
comparison to using the correct surface geometry.
| Figure 5:
Observed V magnitude of |
|
| Open with DEXTER | |
The main differences between the results from the spherical and ellipsoidal
codes can be seen in the photometry. Figure 5 shows the
normalised V observations of ![]() And compared to the ones calculated from
the temperature map obtained with the code using spherical geometry. Only
around the phases 0.4-0.6 the two light curves show similar behaviour,
and the photometry calculated from the INVERS7PD temperature map shows
completely different behaviour than the observed one especially around the
quadrature points.
And compared to the ones calculated from
the temperature map obtained with the code using spherical geometry. Only
around the phases 0.4-0.6 the two light curves show similar behaviour,
and the photometry calculated from the INVERS7PD temperature map shows
completely different behaviour than the observed one especially around the
quadrature points.
6.2 Chromospheric activity
Chromospheric activity of ![]() And was investigated using the H
And was investigated using the H![]() line
profiles, which appeared in absorption during the observations, similarly to
the other Balmer lines. Variations in the H
line
profiles, which appeared in absorption during the observations, similarly to
the other Balmer lines. Variations in the H![]() line through the rotation
cycle are shown in Fig. 6a. Both the red and the blue wings show
strong variation at one, but different, phase. Also, most line profiles clearly
show variable behaviour between velocities -100 km s-1 and +100 km s-1. These
variations are clearly seen already in the spectra, which have not been
corrected to the continuum level. All the spectra show identical continuum
shapes, except approximately
line through the rotation
cycle are shown in Fig. 6a. Both the red and the blue wings show
strong variation at one, but different, phase. Also, most line profiles clearly
show variable behaviour between velocities -100 km s-1 and +100 km s-1. These
variations are clearly seen already in the spectra, which have not been
corrected to the continuum level. All the spectra show identical continuum
shapes, except approximately ![]() 5 Å from the H
5 Å from the H![]() line, corresponding
to the variation also seen in the normalised spectra used in the following
analysis.
line, corresponding
to the variation also seen in the normalised spectra used in the following
analysis.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{13736fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg61.png)
|
Figure 6:
Variations in the H |
| Open with DEXTER | |
To investigate the line-profile variations in more detail, the average profile was subtracted from all the profiles, thus creating the residual profiles shown in Fig. 6b. The temporal variations are clearly seen in these profiles. The most prominent features are the two strong absorption features seen at the velocities -350-0 km s-1 and 0-100 km s-1. A dynamic spectrum, shown in Fig. 7, was also created from the difference profiles. Brighter colours in the plot correspond to enhanced emission and the darker colours to the enhanced absorption. The heliocentric Julian dates of the observations are shown with crosses in the plot. The data for the times where there are no observations are interpolations between the closest timepoints with data. The plotting over the heliocentric Julian date instead of the rotational phase was chosen, as some events are short lived, and the observations in any case cover only slightly more than one rotation. The observational phases are given on the left side of the plot.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13736fg7.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg62.png)
|
Figure 7:
Dynamic spectrum of the H |
| Open with DEXTER | |
The most noticeable feature in the dynamical spectrum is the strong enhanced absorption around the phase 1.6 at the velocity +100 km s-1. If the velocity seen in this absorption system was caused by the stellar rotation, it would be outside the stellar disk and would not be seen in absorption. Thus it must be a cloud of cool gas in the stellar atmosphere that is falling into the star. This could be the final stages of a flare event. No evidence of such an event is seen in the earlier observations, but it could have occurred during the one-night gap in the observations. More enhanced absorption is seen at the first observation (phase 0.94) extending to the very blue, to -300 km s-1 and beyond. This could be caused by a mass ejection event with a strong line of sight component. In the following observation, more enhanced absorption is seen spanning the velocities -100-+100 km s-1.
Enhanced emission occurs at three main locations: around the phases 1.15-1.30 at the velocities -40--70 km s-1, around the phases 1.2-1.4 at the velocities +60-100 km s-1 and at the phases 1.7-1.8 at the velocities +40-70 km s-1. These features have velocities that place them slightly outside the stellar disk, and thus they could be caused by prominences seen at the stellar limb. The prominence seen at the blue edge around phases 1.1-1.3 is most likely the same one as seen at the red edge 0.5 in a later phase (i.e., at phases 1.7-1.8). Also, a weak enhanced absorption feature is seen at phase 1.4 around the velocity -20 km s-1, which could be caused by the prominence starting to cross the stellar disk. This prominence could be centred around phase 1.5, which in the binary reference frame is the phase pointing away from the secondary. The enhanced emission seen in the red around phases 1.2-1.4 are, based on their velocities, also most likely caused by prominences. However, they have to be short lived in nature, as no evidence of them is seen in the observations before or after. These prominences would be at the disk centre approximately at phases 1.0 and 1.1, which places them on the side phasing the secondary. They also coincide with the weaker cool region seen around the phases 0.0-0.4 in the Doppler image.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13736fg8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg63.png)
|
Figure 8:
All the differential V and y magnitudes of |
| Open with DEXTER | |
6.3 Long-term magnetic activity of  And
And
The long-term activity in ![]() And is investigated based on the photometric
V and y band observations obtained with the Wolfgang and Amadeus automatic
photometric telescopes. The observations between December 1996 and October 2002
were already used in Paper I. Here, we also use observations obtained between
June 27, 2003 and October 25, 2008, in total 211 new V magnitudes.
And is investigated based on the photometric
V and y band observations obtained with the Wolfgang and Amadeus automatic
photometric telescopes. The observations between December 1996 and October 2002
were already used in Paper I. Here, we also use observations obtained between
June 27, 2003 and October 25, 2008, in total 211 new V magnitudes.
When all the instrumental differential magnitudes are plotted against the phase, see plot Fig. 8, the variation caused by the ellipticity effect is clearly seen. Still, the observations show much larger scatter around the ellipticity curve than is expected from the measurement error of 0.01-0.02 mag. This indicates that there are also significant variations due to starspots. Evidence of changes in the activity level are also seen when all the observations are plotted against the Julian date in Fig. 9. In this plot the small crosses give the individual observations and the large crosses the mean of that time period. No mean is given for some time periods, as there are so few measurements, or they are grouped such, that the full light-curve was not sampled.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13736fg9.eps}\vspace*{-1mm}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg64.png)
|
Figure 9: All the differential V and y magnitudes plotted against the heliocentric Julian date. The large crosses show the mean magnitudes for that time. |
| Open with DEXTER | |
Changes in the mean magnitudes could be interpreted as a solar-like activity
cycle. A spectral analysis of the mean measurements was carried out using the
Lomb method (Press et al. 1992). The result indicates a presence of a
cycle with a cycle length of
![]() years, but the false alarm
probability is 0.36. Thus the period can be spurious, and more measurements are
needed for confirming it.
years, but the false alarm
probability is 0.36. Thus the period can be spurious, and more measurements are
needed for confirming it.
As can be seen from Fig. 9, ![]() And is on average brighter by 0.014 mag during the VLT observations presented here than during the
December 1997-January 1998 KPNO observations presented in Paper I. This
implies that the spot coverage, and/or the spot temperature, is different
between the two epochs. For studying this further, the temperature maps
obtained with the Ca I 6439 Å line, were investigated both from the
VLT and KPNO observations. The hottest temperature is basically the same in
both maps, 4600 K for VLT and 4620 K for KPNO. Still, the coolest temperatures
are very different. For the VLT observations, the coolest spots are 3710 K and
for the KNPO map 3480 K. Also, the number of surface elements having a
temperature of 4000 K or less in the map obtained from the VLT is 75% of the
surface elements with those temperatures in the KPNO map. This investigation
supports the existence of a activity cycle, which is also indicated by the
long-term photometry of
And is on average brighter by 0.014 mag during the VLT observations presented here than during the
December 1997-January 1998 KPNO observations presented in Paper I. This
implies that the spot coverage, and/or the spot temperature, is different
between the two epochs. For studying this further, the temperature maps
obtained with the Ca I 6439 Å line, were investigated both from the
VLT and KPNO observations. The hottest temperature is basically the same in
both maps, 4600 K for VLT and 4620 K for KPNO. Still, the coolest temperatures
are very different. For the VLT observations, the coolest spots are 3710 K and
for the KNPO map 3480 K. Also, the number of surface elements having a
temperature of 4000 K or less in the map obtained from the VLT is 75% of the
surface elements with those temperatures in the KPNO map. This investigation
supports the existence of a activity cycle, which is also indicated by the
long-term photometry of ![]() And. Still, one must keep in mind that the
temperatures in the Doppler images are very sensitive to the data quality, and
the VLT data are superior to the KPNO ones.
And. Still, one must keep in mind that the
temperatures in the Doppler images are very sensitive to the data quality, and
the VLT data are superior to the KPNO ones.
7 Conclusions
The following conclusions can be drawn from the optical interferometry, high-resolution spectroscopy and broad band photometry presented in this work.
- 1.
- Optical interferometry gives an apparent diameter of
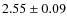 mas
for
mas
for 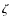 And. Using the Hipparcos parallax, this translates into a
stellar radius of
And. Using the Hipparcos parallax, this translates into a
stellar radius of
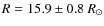 ,
which is in line with the
earlier radius determinations.
,
which is in line with the
earlier radius determinations.
- 2.
- Combining the interferometrically determined diameter and bolometric
flux gives an effective temperature of
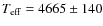 ,
which is
consistent with the values determined through Doppler imaging.
,
which is
consistent with the values determined through Doppler imaging.
- 3.
- The expected ellipsoidal stellar geometry with
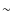 4% difference
between the long and short axes cannot be confirmed with the current
interferometric observations, which have errors of about 4% in the diameter
measurement. However, the highest ellipticity expected for the night
of September 18 is consistent with the data.
4% difference
between the long and short axes cannot be confirmed with the current
interferometric observations, which have errors of about 4% in the diameter
measurement. However, the highest ellipticity expected for the night
of September 18 is consistent with the data.
- 4.
- The Doppler images reveal cool spots on the surface of the primary
of the
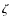 And binary. The spots are located in the equatorial
region, and the main concentration of spots is seen around phase 0.75,
i.e., 0.25 in phase from the secondary. Another weaker cool region spans the
phases 0.0-0.4, again around the equator. There are also indications of a
cool polar cap. On the whole, this spot configuration is very similar to the
one seen in the earlier published 1997/1998 data.
And binary. The spots are located in the equatorial
region, and the main concentration of spots is seen around phase 0.75,
i.e., 0.25 in phase from the secondary. Another weaker cool region spans the
phases 0.0-0.4, again around the equator. There are also indications of a
cool polar cap. On the whole, this spot configuration is very similar to the
one seen in the earlier published 1997/1998 data.
- 5.
- Long-term photometric observations indicate an activity cycle, but more measurements are needed to confirm this and its period. The investigation of the Doppler maps obtained January 1998 and September 2008 also hint at an activity cycle.
- 6.
- The chromospheric activity, investigated from the H
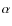 -line,
shows evidence of both prominences and cool clouds. The prominences do
not seem to show any strong evidence of occurring at certain locations in
the binary reference frame, nor are they associated with the coolest
spot seen on the surface. On the other hand, one of the detected
prominences seems to be related to the group of weaker cool spots located at
phases 0.0-0.4.
-line,
shows evidence of both prominences and cool clouds. The prominences do
not seem to show any strong evidence of occurring at certain locations in
the binary reference frame, nor are they associated with the coolest
spot seen on the surface. On the other hand, one of the detected
prominences seems to be related to the group of weaker cool spots located at
phases 0.0-0.4.
Zs.K. is a grantee of the Bolyai János Fellowship of the Hungarian Academy of Sciences. We also thank the ESO Scientific Visitor Programme for enabling Zs.K. to visit Garching during the preparation of this paper. This work has made use of the Smithsonian/NASA Astrophysics Data System (ADS) and of the Centre de Donnees astronomiques de Strasbourg (CDS), and the services from the NASA Exoplanet Science Institute, California Institute of Technology, http://nexsci.caltech.edu.
References
- Bordé, P., Coudé du Foresto, V., Chagnon, G., & Perrin, G. 2002, A&A, 393, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campbell, W. W. 1911, Lick Obs. Bull., 6, 140 [Google Scholar]
- Cannon, J. B. 1915, Publ. Dominion Obs. Ottawa, II, 141 [Google Scholar]
- Cohen, M., Walker, R. G., Carter, B., et al. 1999, AJ, 117, 1864 [NASA ADS] [CrossRef] [Google Scholar]
- Dekker, H., D'Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, SPIE, 4008, 534 [Google Scholar]
- Glindemann, A., Algomedo, J., Amestica, R., et al. 2003, Proc. SPIE, 4838, 89 [Google Scholar]
- Gray, R. O., & Corbally, C. J. 1994, AJ, 107, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Granzer, T., Reegen, P., & Strassmeier, K. G. 2001, AN, 322, 325 [Google Scholar]
- Hackman, T., Jetsu, L., & Tuominen, I. 2001, A&A, 374, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hussain, G. A. J. 2002, AN, 323, 349 [Google Scholar]
- Kovári Zs., Bartus, J., Strassmeier K. G., et al. 2007, A&A, 463, 1071 (Paper I) [Google Scholar]
- Kurucz, R. L. 1993, Kurucz CD No. 13 [Google Scholar]
- Le Bouquin, J.-B., Abuter, R., Bauvir, B., et al. 2008, Proc. SPIE, 7013, 701318 [CrossRef] [Google Scholar]
- Le Bouquin, J.-B., Absil, O., Benisty, M., et al. 2009, A&A, 498, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mérand, A., Bordé, P., & Coudé Du Foresto, V. 2006, A&A, 447, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millour, F., Valat, B., Petrov, R. G., & Vannier, M. 2008, Proc. SPIE, 7013, 701349 [CrossRef] [Google Scholar]
- Mozurkewich, D., Armstrong, J. T., Hindsley, R. B., et al. 2003, AJ, 126, 2502 [NASA ADS] [CrossRef] [Google Scholar]
- Nordgren, T. E., Sudol, J. J., & Mozurkewich, D. 2001, AJ, 122, 2707 [NASA ADS] [CrossRef] [Google Scholar]
- Oláh, K., Kolláth, Z., Granzer, T., et al. 2009, A&A, 501, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrov, R. G., Malbet, F., Weigelt, G., et al. 2007, A&A, 464, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piskunov, N. E., Tuominen, I., & Vilhu, O. 1990, A&A, 230, 363 [NASA ADS] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, in Numerical Recipes in FORTRAN - The Art of Scientific Computing, second edition (New York, USA: Cambridge University Press), 569 [Google Scholar]
- Rice, J. B. 2002, AN, 323, 220 [Google Scholar]
- Rice, J. B., & Strassmeier, K. G. 1996, A&A, 316, 164 [NASA ADS] [Google Scholar]
- Rice, J. B., Wehlau, W. H., & Khokhlova, V. L. 1989, A&A, 208, 179 [NASA ADS] [Google Scholar]
- Rüdiger G., Elstner, D., & Ossendrijver, M. 2003, A&A, 406, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G. 1999, A&A, 347, 225 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., Hall, D. S., Fekel, F. C., & Scheck, M. 1993, A&AS, 100, 173 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., Bartus, J., Cutispoto, G., & Rodonò, M. 1997, A&AS, 125, 11 [Google Scholar]
- Tatulli, E., Millour, F., Chelli, A., et al. 2007, A&A, 464, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittkowski, M., Boboltz, D. A., Driebe, T., et al. 2008, A&A, 479, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ... interferometry
![[*]](/icons/foot_motif.png)
- Based on observations collected at the European Southern Observatory, Chile (Prg. 081.D-0216(AB)); and with the Vienna automatic photometric telescopes Wolfgang and Amadeus, Arizona, USA.
All Tables
Table 1: Log of the VLTI/AMBER observations.
Table 2: The high-resolution spectroscopy with UVES at VLT.
Table 3: Uniform disk fit results for the VLTI/AMBER data.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13736fg1a.ps} \includegraphics[width=8cm,clip]{13736fg1b.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg31.png)
|
Figure 1:
VLTI/AMBER visibility data of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.7cm,clip]{13736fg2a.ps}\hspace*{2mm}...
...m}
\includegraphics[width=5.7cm,clip]{13736fg2f.ps}\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg46.png)
|
Figure 2:
Doppler imaging results of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13736fg3.ps}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg56.png)
|
Figure 3: Average map produced from all the maps shown in Fig. 2. |
| Open with DEXTER | |
| In the text | |
| |
Figure 4:
Temperature map of |
| Open with DEXTER | |
| In the text | |
| |
Figure 5:
Observed V magnitude of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{13736fg6.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg61.png)
|
Figure 6:
Variations in the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13736fg7.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg62.png)
|
Figure 7:
Dynamic spectrum of the H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13736fg8.eps}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg63.png)
|
Figure 8:
All the differential V and y magnitudes of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13736fg9.eps}\vspace*{-1mm}
\vspace*{-2mm}
\end{figure}](/articles/aa/full_html/2010/07/aa13736-09/Timg64.png)
|
Figure 9: All the differential V and y magnitudes plotted against the heliocentric Julian date. The large crosses show the mean magnitudes for that time. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.