EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 515 (June 2010) A&A, 515 (2010) A37 Full HTML
Free Access
Issue
A&A
Volume 515, June 2010
Article Number A37
Number of page(s) 5
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/200912545
Published online 08 June 2010
A&A 515, A37 (2010)

Binaries discovered by the SPY project

V. GD 687 - a massive double degenerate binary progenitor that will merge within a Hubble time[*]

S. Geier1 - U. Heber1 - T. Kupfer1 - R. Napiwotzki2

1 - Dr. Karl Remeis-Observatory & ECAP, Astronomical Institute, Friedrich-Alexander University Erlangen Nuremberg, Sternwartstr. 7, 96049 Bamberg, Germany
2 - Centre of Astrophysics Research, University of Hertfordshire, College Lane, Hatfield AL10 9AB, UK

Received 20 May 2009 / Accepted 18 March 2010

Abstract
Aims. The ESO SN Ia Progenitor Survey (SPY) aims at finding merging double degenerate binaries as candidates for supernova type Ia (SN Ia) explosions. A white dwarf merger has also been suggested to explain the formation of rare types of stars like R CrB, extreme helium or He sdO stars. Here we present the hot subdwarf B binary GD 687, which will merge in less than a Hubble time.
Methods. The orbital parameters of the close binary have been determined from time resolved spectroscopy. Since GD 687 is a single-lined binary, the spectra contain only information about the subdwarf primary and its orbit. From high resolution spectra the projected rotational velocity was derived. Assuming orbital synchronisation, the inclination of the system and the mass of the unseen companion were constrained.
Results. The derived inclination is $i=39.3^{+6.2}_{-5.6}~^{\circ}$. The mass $M_{\rm 2}=0.71_{-0.21}^{+0.22}~M_{\rm\odot}$ indicates that the companion must be a white dwarf, most likely of C/O composition. This is only the fourth case that an sdB companion has been proven to be a white dwarf unambiguously. Its mass is somewhat larger than the average white dwarf mass, but may be as high as $0.93~M_{\rm\odot}$ in which case the total mass of the system comes close to the Chandrasekhar limit.
Conclusions. GD 687 will evolve into a double degenerate system and merge to form a rare supermassive white dwarf with a mass in excess of solar. A death in a sub-Chandrasekhar supernova is also conceivable.

Key words: binaries: spectroscopic - subdwarfs - stars: individual: GD 687 - stars: rotation - supernovae: general

1 Introduction

Double degenerate (DD) binaries consisting of two white dwarf (WD) stars experience a shrinkage of their orbits caused by gravitational wave radiation. Sufficiently close binaries with orbital periods of less than half a day will eventually merge within less than a Hubble time. The outcome of such a merger can be a single compact object like a white dwarf or a neutron star. But the merger event may also lead to the ignition of nuclear burning and trigger the formation of rare objects such as extreme helium stars (Saio & Jeffery 2002), R CrB stars (Webbink 1984) or He sdO stars (Heber 2008; Napiwotzki 2008). The merger of two sufficiently massive C/O white dwarfs may lead to a Supernova of type Ia (SN Ia, Webbink 1984).

SN Ia play a key role in the study of cosmic evolution. They are utilised as standard candles for determining the cosmological parameters (e.g. Riess et al. 1998; Leibundgut 2001; Perlmutter et al. 1999). There is general consensus that the thermonuclear explosion of a white dwarf of Chandrasekhar mass causes a SN Ia. The DD merger (Iben & Tutukov 1984) is one of two main scenarios to feed a white dwarf to the Chandrasekhar mass. Progenitor candidates for the DD scenario have to merge in less than a Hubble time and the total binary mass must exceed the Chandrasekhar limit.

In general, DD candidates are assumed to consist of two white dwarfs. The discovery of the sdB+WD binary KPD 1930+2752, however, has highlighted the importance of such systems as SN Ia progenitor candidates (Billères et al. 2000; Maxted et al. 2000; Geier et al. 2007). Hot subdwarf stars (sdBs) are core helium-burning stars situated at the hot end of the horizontal branch with masses around $0.5~M_{\rm\odot}$ (Heber 1986). Although the formation of these objects is still under debate, it is general consensus that they must lose most of their envelope at the tip of the RGB and evolve directly from the EHB to the WD cooling tracks without ascending the AGB (see Heber 2009, for a review).

Since a high fraction of sdBs resides in close binaries with unseen companions (Maxted et al. 2001; Napiwotzki et al. 2004b), such systems can qualify as SN Ia progenitors, if the companion is a white dwarf and the lifetime of the sdB is shorter than the merging time of the binary. This is the case for the sdB+WD binary KPD 1930+2752, which is the best known DD progenitor candidate for SN Ia (Maxted et al. 2000; Geier et al. 2007).

Systematic radial velocity (RV) searches for DDs have been undertaken (e.g. Napiwotzki 2003, and references therein). The largest of these projects was the ESO SN Ia Progenitor Survey (SPY). More than 1000 WDs were checked for RV-variations (Napiwotzki et al. 2001a, 2003). SPY detected $\sim $100 new DDs (only 18 were known before). One of them may fulfil the criteria for SN Ia progenitor candidates (Napiwotzki et al. 2007).

This sample includes about two dozen radial velocity variable sdB stars with invisible companions. As the sdB stars are intrinsically brighter than the white dwarfs, the nature of the companion is not so easily revealed.

Most sdBs in close binary systems are single-lined and no features of the companions are visible in their spectra. In this case the nature of the unseen companion is hard to constrain since only lower limits can be derived for the companion masses. Given the fact that sdBs are subluminous stars, main sequence companions earlier than K-type can easily be excluded. But if the derived lower limit for the companion mass is lower than about half a solar mass it is in general not possible to distinguish between a main sequence companion and a compact object like a white dwarf. Despite the fact that the catalogue of Ritter & Kolb (2009) lists more than 80 sdB binaries, the nature of their companions can only be constrained in special cases (e.g. For et al. 2010; Geier et al. 2008), in particular from photometric variations due to eclipses, reflection effects or ellipsoidal deformations.

Results for eight DD systems discovered in the SPY survey have been presented in Papers I-IV (Napiwotzki et al. 2001; Napiwotzki et al. 2002; Karl et al. 2003; Nelemans et al. 2005). Here we study the sdB binary GD 687, a DD progenitor system which will merge in less than a Hubble time.

2 Binary parameters

2.1 Observations and radial velocity curve

GD 687 ( $\alpha_{2000}=01^{\rm h}10^{\rm m}18{\stackrel{\rm s}{\displaystyle .}}5$, $\delta_{2000}=-34^{\rm\circ}00'26''$) was included in the SPY survey, because it was misclassified as DA3 white dwarf (McCook & Sion 1999). GD 687 was observed twice in the course of the SPY project with the high resolution echelle spectrograph UVES at the ESO VLT. The spectra have a resolution of $R\approx37~000$ and cover $3200{-}6650~{\rm\AA}$ with two small gaps at $4580~{\rm\AA}$ and $5640~{\rm\AA}$.

Follow-up medium resolution spectra were taken with the EMMI ( $R\approx3400,\lambda=3880{-}4380~{\rm\AA}$) and the EFOSC2 ( $R\approx2200,\lambda=4450{-}5110~{\rm\AA}$) spectrographs mounted at the ESO NTT. Reduction was done with the ESO-MIDAS package. The radial velocities (RV) were measured by fitting a set of mathematical functions (Gaussians, Lorentzians and polynomials) to the hydrogen Balmer lines using the FITSB2 routine (Napiwotzki et al. 2004a). The measured RVs are given in Table 1.

Table 1:   Radial velocities of GD 687.

\begin{figure} \par\includegraphics[width=9cm,clip]{12545fig1.eps} \end{figure} Figure 1:

In this power spectrum $-\log\chi^{2}$ of the best sine fit is plotted against the orbital periods. The region around the best solution is shown in the inlet. Confidence limits ($1\sigma $, $3\sigma $, $6\sigma $) are marked with horizontal lines (dotted, dashed, solid).

Open with DEXTER

Sine curves were fitted to the RV data points in fine steps over a range of test periods. For each period the $\chi^{2}$ of the best fitting sine curve was determined. The result is similar to a power spectrum with the lowest $\chi^{2}$ indicating the most likely period (see Fig. 1). The plot shows two very closely spaced peaks. We performed a Monte Carlo simulation for the most likely periods. For each iteration a randomised set of RVs was drawn from Gaussian distributions with central value and width corresponding to the RV measurements and the analysis repeated.

The probability that the solution with the lowest $\chi^{2}$ and $P=0.37765~{\rm d}$ is the correct one is estimated to be $74\%$. The second best alias period ( $P=0.37828~{\rm d}$) has $\Delta\chi^{2}=9$ and a probability of $26\%$ to be the correct one (see Fig. 1 inlet). None of the 10 000 Monte Carlo iterations indicated a period different from the two discussed above. The probability that any other solution is the correct one is therefore less than $0.01\%$. Our analysis is based on the most likely solution.

In order to derive most conservative errors for the RV semi-amplitude K and the system velocity $\gamma$ we fixed the most likely period, created new RV datasets with a bootstrapping algorithm and calculated the orbital solution in each case. The standard deviation of these results was adopted as error estimate and is about three times higher than the $1\sigma $-error. The phase folded RV curve is shown in Fig. 2. Parameters are given in Table 2[*].

\begin{figure} \par\includegraphics[width=9cm,clip]{12545fig2.eps} \end{figure} Figure 2:

Radial velocities of the primary subdwarf plotted against orbital phase. The residuals are plotted below. Filled triangles mark RVs measured from UVES spectra, filled diamonds mark RVs obtained from EMMI spectra and filled circles RVs measured from EFOSC2 spectra.

Open with DEXTER

2.2 Gravity and projected rotational velocity

The atmospheric parameters of GD 687 were measured by fitting metal-line blanketed LTE models to the UVES spectra and are given in Lisker et al. (2005).

In order to derive $v_{\rm rot}~\sin{i}$ and the elemental abundances, we coadded the observed high resolution spectra after shifting them to rest wavelength. The spectrum was then compared with rotationally broadened, synthetic line profiles calculated with the LINFOR program (developed by Holweger, Steffen and Steenbock at Kiel university, modified by Lemke 1997).

Due to the wide slit used (2.1'') for the SPY survey (see Napiwotzki et al. 2001, for details) the resolution of the UVES spectra is seeing dependent in most cases. In order to measure $v_{\rm rot}~\sin{i}$ accurately, the instrumental profile has to be taken into account. We used the ESO archive to obtain the seeing conditions during the exposure times of the UVES spectra (DIMM seeing monitor, Sarazin & Roddier 1990), took the average ( $1.13~{\rm arcsec}$) and folded our models with the instrumental profile.

The projected rotational velocity was measured simultaneously with the elemental abundances to $v_{\rm rot}\sin{i}=21.2\pm2.0~{\rm km~s^{-1}}$ using the six strongest metal lines. In addition, an abundance and rotational broadening fit was done using two prominent helium lines (He  I 4472, 5876) and LTE model spectra (Heber et al. 2000). The resulting $v_{\rm rot}\sin{i}=19.8\pm2.2~{\rm km~s^{-1}}$ turned out to be perfectly consistent with the value measured from the metal lines. Since metal lines are more sensitive to rotational broadening we adopt the value derived from these lines for our analysis. The parameters are given in Table 2.

Our results depend very much on the accuracy of the $v_{\rm rot}\sin{i}$ and $\log{g}$ measurements. A thorough discussion of the error in surface gravity is given by Lisker et al. (2005). To quantify the $v_{\rm rot}\sin{i}$ error, we carried out numerical simulations. For this, synthetic spectra with fixed rotational broadening were computed and convolved with the instrumental profile. Random noise was added to mimic the observed spectra. The rotational broadening was measured in the way described above using a grid of synthetic spectra for various rotational and instrumental broadenings as well as S/N levels. Variations in the instrumental profile and the noise level were the dominant error sources. Behr (2003) used a similar method to measure the low $v_{\rm rot}\sin{i}$ of Blue Horizontal Branch stars from high resolution spectra. The errors given in that work are of the same order as the one given here for GD 687 ( $2.0~{\rm km~s^{-1}}$).

Table 2:   Orbital and atmospheric parameters of GD 687.

2.3 Analysis

The analysis strategy used is described only briefly. For details we refer the reader to Geier et al. (2007, 2008). Since the spectrum of GD 687 is single-lined, it contains no information about the orbital motion of the companion, and thus only the mass function $f_{\rm m} = {M_{\rm comp}^3 \sin^3i}/(M_{\rm comp} + M_{\rm sdB})^2 = P K^3/2 \pi G$ can be calculated. Although the RV semi-amplitude K and the period P are determined by the RV curve, $M_{\rm sdB}$, $M_{\rm comp}$ and $\sin^3i$ remain free parameters.

Nevertheless, the masses can be constrained by assuming tidal synchronisation (see also Napiwotzki et al. 2001b). Combining the orbital parameters with an estimate of the sdB mass and with the determination of its $v_{\rm rot}\sin{i}$ and surface gravity, allows the mass of the invisible companion to be constrained. The mass of the sdB primary is taken from the population synthesis models (Han et al. 2002, 2003) that predict a mass range of $M_{\rm sdB}=0.37$-0.48 $M_{\odot}$ for sdBs in binaries, which experienced a common envelope ejection. The mass distribution shows a sharp peak at a mass of about $0.47~{M_{\odot}}$ (see Fig. 22 of Han et al. 2003) ranging from 0.43 to 0.47 $M_{\odot}$. This theoretical mass distribution is consistent with analyses of close binary systems (e.g. Geier et al. 2007) as well as asteroseismic analyses of pulsating sdBs (see Charpinet et al. 2008 and references therein).

If the rotational period of the sdB primary is synchronised the rotational velocity $v_{\rm rot}= 2 \pi R_{\rm sdB}/P$ can be calculated. The radius of the primary is given by the mass radius relation $R = \sqrt{M_{\rm sdB}G/g}$. The measurement of the projected rotational velocity $v_{\rm rot}~\sin~i$ therefore allows us to constrain the inclination angle i. For the most likely sdB mass $M_{\rm sdB}=0.47~{M_{\odot}}$ the mass function can be solved, and both the inclination angle and the companion mass can be derived. The errors are calculated by chosing the most extreme values for the input parameters within their respective error limits. In order to account for the theoretical uncertainity in sdB mass, we adopted the predicted mass range for the sdB (0.43-0.47 $M_{\odot}$) and calculated the lower limit for the companion mass under the assumption that $M_{\rm sdB}=0.43~{M_{\odot}}$. The error budget is dominated by the uncertainties in the $v_{\rm rot}\sin{i}$ and $\log{g}$ measurements.

3 Nature of the unseen companion

The mass function provides a lower limit to the mass of the invisible companion of $0.35~{M_{\odot}}$. In the case of a white dwarf primary it is impossible to hide the contribution of a main sequence star even of the lowest mass in optical/NIR spectra since these are intrinsically faint. This is not the case for sdB stars. A main sequence companion with a mass lower than $0.45~{M_{\odot}}$ can not be excluded because its luminosity would be too low to be detectable in the spectra (Lisker et al. 2005). This is the reason why the companions' nature still remains unknown for most of the $\approx$80 sdB systems in the catalogue of Ritter & Kolb (2009). Additional information is needed.

No spectral features of a cool main sequence star are present in the optical spectra of GD 687. Furthermore, Farihi et al. (2005) included GD 687 in a near-infrared imaging survey to search for low-luminosity companions to white dwarfs and found no evidence for an infrared excess which could be caused by a cool main sequence companion.

As the lower limit for the mass of GD 687's companion derived from the mass function is lower than $0.45~{M_{\odot}}$, additional information is needed to clarify its nature. We made use of the gravity and projected rotational velocity to constrain the mass to $0.71_{-0.21}^{+0.22}~{M_{\odot}}$. The companion therefore can not be a main sequence star but has to be a white dwarf. Taking into account the possible mass range it is very likely to be of C/O composition. Its mass exceeds that of an average white dwarf.

GD 687 is only the fourth sdB star, for which the white dwarf nature of the companion could be shown unamibiguously. The others have been discovered by analysing ellipsoidal light variations (KPD 1930+2752, PG 0101+039) or eclipses (KPD 0422+5421, Orosz & Wade 1999). KPD 1930+2752 and PG 0101+039 have been confirmed with the method used here (Geier et al. 2007,2008).

\begin{figure} \par\includegraphics[width=9cm,clip]{12545fig3.eps} \end{figure} Figure 3:

$T_{\rm eff}$-$\log{g}$-diagram. The location of the EHB and the evolutionary tracks (dashed curves) are taken from Dorman et al. (1993).

Open with DEXTER

4 Discussion

The derived companion mass was calculated under the assumption of orbital synchronisation. Since theoretical synchronisation timescales for hot stars with radiative envelopes are not consistent (Zahn 1977; Tassoul & Tassoul 1992), empirical evidence for orbital sychronisation in sdB binaries is needed. Geier et al. (2008) found such evidence by detecting a variation in the lightcurve of the sdB+WD binary PG 0101+039, which could be identified as ellipsoidal deformation of the sdB. Since the orbital period of PG 0101+039 is $0.57~{\rm d}$, sdB binaries with shorter periods like GD 687 are very likely synchronised as well. Recently van Grootel et al. (2008) performed an asteroseismic analysis of the pulsating sdB binary Feige 48 and for the first time proved orbital sychronisation in this way. The orbital period of Feige 48 ( $0.36~{\rm d}$) is very similar to the one of GD 687. Furthermore, the atmospheric parameters of GD 687 ( $T_{\rm eff}=24~300~{\rm K}$, $\log{g}=5.32$) indicate that it has already evolved away from the ZAEHB (Zero Age Extreme Horizontal Branch) and should therefore, according to evolutionary calculations (e.g. Dorman et al. 1993), have a similar age as PG 0101+039 and Feige 48 (see Fig. 3). We thus conclude that the assumption of orbital sychronisation is fully justified in the case of GD 687.

In about $100~{\rm Myr}$ the helium-burning in the core of the sdB will come to an end. After a short period of helium-shell-burning this star will eventually become a white dwarf consisting of C and O. GD 687 is one of only a few known DD progenitor systems, where both components are C/O white dwarfs and which will merge in less than a Hubble time.

Compared to the sdB+WD binary KPD 1930+2752 ( $P\approx0.1~{\rm d}$, Maxted et al. 2000; Geier et al. 2007), which is the best known candidate for DD SN Ia progenitor, the orbital period of GD 687 is rather long. This leads to a merging time of $11.1~{\rm Gyr}$, which is just a little shorter than the Hubble time, compared to only $200~{\rm Myr}$ for KPD 1930+2752. With a total mass of $1.18_{-0.21}^{+0.22}~M_{\rm\odot}$ for the most likely subdwarf mass it may come close to the Chandrasekhar limit of $1.4~M_{\odot}$ and is therefore placed at the edge of the progenitor parameter space (see Fig. 4). In contrast to KPD 1930+2752, where the primary mass could be constrained by an additional analysis of the subdwarfs ellipsoidal deformation visible as variation in its lightcurve, no such constraint can be put on the primary mass of GD 687 yet.

Instead of exploding as SN Ia, the merger of the two white dwarfs will most likely lead to the formation of a supermassive white dwarf with O/Ne/Mg-core.

Up to now four binaries with total masses between about 1.2 and $1.4~M_{\odot}$ have been discovered. In two of them the visible component is an sdB. Since the sdB close binary fraction is much higher than the one of white dwarfs, it may be easier to find double-degenerate binary progenitors in the hot subdwarf population.

Two other massive DD systems, a central star of a planetary nebula (Tovmassian et al. 2004; Napiwotzki et al. 2005) and a white dwarf from the SDSS survey (Badenes et al. 2009; Marsh et al. 2010; Kulkarni & van Kerkwijk 2010), were discovered serendipitously.

Even though GD 687 does not qualify as SN Ia progenitor candidate, the discovery of a population of double degenerate binaries (and progenitor systems) with total masses close to the Chandrasekhar limit in the course of the SPY survey (see Fig. 4) provides evidence for a similar population exceeding this limit. The same binary evolution channel that produces the sub-Chandrasekhar systems will also produce super-Chandrasekhar systems with slight changes in the initial conditions only.

\begin{figure} \par\includegraphics[width=9cm,clip]{12545fig4.ps}\vspace*{1mm} \end{figure} Figure 4:

Total mass plotted against logarithmic period of double degenerate systems from the SPY survey. GD 687 is marked with the filled circle. For KPD 1930+2752 a mass range is given (Geier et al. 2007). The filled rectangles mark double-lined WDs, for which the absolute masses can be derived. The filled circle with arrow marks the lower mass limit derived for HE 1047-0436 (Napiwotzki et al. 2001), the filled diamond the lower mass limit derived for PN G 135.9+55.9 (Napiwotzki et al. 2005). The open symbols mark single-lined WDs, sdBs, and sdOs. The companion masses of the single-lined systems are derived for the expected average inclination angle ( $i=52^{\circ }$) (Napiwotzki et al. 2002; Karl et al. 2003; Karl 2004; Nelemans et al. 2005; Napiwotzki et al. 2007).

Open with DEXTER

Acknowledgements
S.G. is supported by the Deutsche Forschungsgemeinschaft under grant He1354/40-3.

References

  1. Badenes, C., Mullally, F., Thompson, S. E., & Lupton, R. H. 2009, ApJ, 707, 971 [NASA ADS] [CrossRef] [Google Scholar]
  2. Behr, B. 2003, ApJS, 149, 101 [NASA ADS] [CrossRef] [Google Scholar]
  3. Billères, M., Fontaine, G., Brassard, P., et al. 2000, ApJ, 530, 441 [NASA ADS] [CrossRef] [Google Scholar]
  4. Charpinet, S., van Grootel, V., Reese, D., et al. 2008, A&A, 489, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Dorman, B., Rood, R. T., & O'Connell, R. W. 1993, ApJ, 419, 596 [CrossRef] [Google Scholar]
  6. Ergma, E., Fedorova, A. V., & Yungelson, L. R. 2001, A&A, 376, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Farihi, J., Becklin, E. E., & Zuckerman, B. 2005, ApJ, 161, 394 [NASA ADS] [Google Scholar]
  8. For, B.-Q., Green, E. M., Fontaine, G., et al. 2010, ApJ, 708, 253 [NASA ADS] [CrossRef] [Google Scholar]
  9. Geier, S., Nesslinger, S., Heber, U., et al. 2007, A&A, 464, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Geier, S., Nesslinger, S., Heber, U., et al. 2008, A&A, 477, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Han Z., Podsiadlowski P., Maxted P. F. L., Marsh T. R., & Ivanova N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
  12. Han, Z., Podsiadlowski, P., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
  13. Heber, U. 1986, A&A, 155, 33 [NASA ADS] [Google Scholar]
  14. Heber, U. 2008, ASPCS, 391, 245 [NASA ADS] [Google Scholar]
  15. Heber, U. 2009, ARA&A, 47, 211 [NASA ADS] [CrossRef] [Google Scholar]
  16. Heber, U., Reid, I. N., & Werner, K. 2000, A&A, 363, 198 [NASA ADS] [Google Scholar]
  17. Iben, I. Jr., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
  18. Karl, C. 2004, Ph.D Thesis, Univ. Erlangen-Nürnberg [Google Scholar]
  19. Karl, C., Napiwotzki, R., Nelemans, G., et al. 2003, A&A, 410, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Kulkarni, S. R., & van Kerkwijk, M. H. 2010, ApJ, submitted[arXiv:1003.2169] [Google Scholar]
  21. Leibundgut, B. 2001, ARA&A, 39, 67 [NASA ADS] [CrossRef] [Google Scholar]
  22. Lemke, M. 1997, A&AS, 122, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Lisker, T., Heber, U., Napiwotzki, R., et al. 2005, A&A, 430, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Marsh, T. R., Gaensicke, B. T., Steeghs, D., et al. 2010, ApJL, submitted [arXiv:1002.4677] [Google Scholar]
  25. Maxted, P. F. L., Marsh, T. R., & North, R. C. 2000, MNRAS, 317, L41 [NASA ADS] [CrossRef] [Google Scholar]
  26. Maxted, P. F. L., Heber, U., Marsh, T. R., & North, R. C. 2001, MNRAS, 326, 139 [Google Scholar]
  27. McCook, G. P., & Sion, E. M. 1999, ApJS, 121, 1 [NASA ADS] [CrossRef] [Google Scholar]
  28. Nelemans, G., Napiwotzki, R., Karl, C., et al. 2005, A&A, 440, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Napiwotzki, R. 2008, ASPCS, 391, 257 [NASA ADS] [Google Scholar]
  30. Napiwotzki, R., Christlieb, N., Drechsel, H., et al. 2001a, AN, 322, 411 [Google Scholar]
  31. Napiwotzki, R., Edelmann H., Heber U., et al. 2001b, A&A 378, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Napiwotzki, R., Koester, D., Nelemans, G., et al. 2002, A&A, 386, 957 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Napiwotzki, R., Christlieb, N., Drechsel, H., et al. 2003, ESO Msngr, 112, 25 [Google Scholar]
  34. Napiwotzki, R., Karl, C., Lisker, T., et al. 2004a, Ap&SS, 291, 321 [NASA ADS] [CrossRef] [Google Scholar]
  35. Napiwotzki, R., Yungelson, L., Nelemans, G., et al. 2004b, ASPCS, 318, 402 [Google Scholar]
  36. Napiwotzki, R., Tovmassian, G., Richer, M. G., et al. 2005, AIP Conf. Ser., 804, 173 [NASA ADS] [CrossRef] [Google Scholar]
  37. Napiwotzki, R., Karl, C., Nelemans, G., et al. 2007, ASPCS, 372, 387 [Google Scholar]
  38. Orosz, J. A., & Wade, R. A. 1999, MNRAS, 310, 773 [NASA ADS] [CrossRef] [Google Scholar]
  39. Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
  40. Riess, A. G., Fillipenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  41. Ritter, H., & Kolb, U. 2009, VizieR Online Data Catalog, 1, 2018 [Google Scholar]
  42. Saio, H., & Jeffery, C. S. 2002, MNRAS, 333, 121 [NASA ADS] [CrossRef] [Google Scholar]
  43. Sarazin, M., & Roddier, F. 1990, A&A, 227, 294 [NASA ADS] [Google Scholar]
  44. Tassoul, J.-L., & Tassoul, M. 1992, ApJ, 395, 259 [NASA ADS] [CrossRef] [Google Scholar]
  45. Tovmassian, G. H., Napiwotzki, R., Richer, M. G., et al. 2004, ApJ, 616, 485 [NASA ADS] [CrossRef] [Google Scholar]
  46. van Grootel, V., Charpinet, S., Fontaine, G., & Brassard, P. 2008, A&A, 483, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
  48. Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]

Footnotes

... time[*]
Based on observations at the Paranal Observatory of the European Southern Observatory for programme No. 165.H-0588(A). Based on observations at the La Silla Observatory of the European Southern Observatory for programmes No. 072.D-0510(B), 079.D-0288(A), 080.D-0685(A) and 084.D-0348(A).
...[*]
Adopting the second best solution only leads to small changes in the derived parameters ( 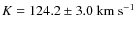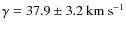$K=124.2\pm3.0~{\rm km~s^{-1}}$, $\gamma=37.9\pm3.2~{\rm km~s^{-1}}$) and has no significant impact on the qualitative discussion of our results.

All Tables

Table 1:   Radial velocities of GD 687.

Table 2:   Orbital and atmospheric parameters of GD 687.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{12545fig1.eps} \end{figure} Figure 1:

In this power spectrum $-\log\chi^{2}$ of the best sine fit is plotted against the orbital periods. The region around the best solution is shown in the inlet. Confidence limits ($1\sigma $, $3\sigma $, $6\sigma $) are marked with horizontal lines (dotted, dashed, solid).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{12545fig2.eps} \end{figure} Figure 2:

Radial velocities of the primary subdwarf plotted against orbital phase. The residuals are plotted below. Filled triangles mark RVs measured from UVES spectra, filled diamonds mark RVs obtained from EMMI spectra and filled circles RVs measured from EFOSC2 spectra.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{12545fig3.eps} \end{figure} Figure 3:

$T_{\rm eff}$-$\log{g}$-diagram. The location of the EHB and the evolutionary tracks (dashed curves) are taken from Dorman et al. (1993).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{12545fig4.ps}\vspace*{1mm} \end{figure} Figure 4:

Total mass plotted against logarithmic period of double degenerate systems from the SPY survey. GD 687 is marked with the filled circle. For KPD 1930+2752 a mass range is given (Geier et al. 2007). The filled rectangles mark double-lined WDs, for which the absolute masses can be derived. The filled circle with arrow marks the lower mass limit derived for HE 1047-0436 (Napiwotzki et al. 2001), the filled diamond the lower mass limit derived for PN G 135.9+55.9 (Napiwotzki et al. 2005). The open symbols mark single-lined WDs, sdBs, and sdOs. The companion masses of the single-lined systems are derived for the expected average inclination angle ( $i=52^{\circ }$) (Napiwotzki et al. 2002; Karl et al. 2003; Karl 2004; Nelemans et al. 2005; Napiwotzki et al. 2007).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.