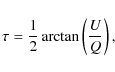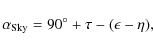EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 514 (May 2010) A&A, 514 (2010) A70 Full HTML
Free Access
Issue
A&A
Volume 514, May 2010
Article Number A70
Number of page(s) 8
Section Astronomical instrumentation
DOI https://doi.org/10.1051/0004-6361/200913834
Published online 21 May 2010
A&A 514, A70 (2010)

Measurement of the Crab nebula polarization at 90 GHz as a calibrator for CMB experiments

J. Aumont1,8 - L. Conversi2 - C. Thum3 - H. Wiesemeyer4 - E. Falgarone5 - J. F. Macías-Pérez6 - F. Piacentini7 - E. Pointecouteau8 - N. Ponthieu1 - J. L. Puget1 - C. Rosset9 - J. A. Tauber10 - M. Tristram11

1 - Institut d'Astrophysique Spatiale, Centre Universitaire d'Orsay, Bât. 121, 91405 Orsay Cedex, France
2 - European Space Astronomy Center, PO Box 78, 28691 Villanueva de la Cañada, Madrid, Spain
3 - IRAM - Institut de Radioastronomie Millimétrique, 300 rue de la Piscine, 38406 Saint-Martin d'Hères, France
4 - IRAM - Institut de Radioastronomie Millimétrique, Avenida Divina Pastora 7, Núcleo Central, 18012 Granada, Spain
5 - LERMA/LRA, CNRS UMR 8112, École Normale Supérieure and Observatoire de Paris, 24 rue Lhomond, 75231 Paris Cedex 05, France
6 - Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier Grenoble 1, CNRS/IN2P3, Institut National Polytechnique de Grenoble, 53 avenue des Martyrs, 38026 Grenoble, France
7 - Dipartimento di Fisica, Università di Roma ``La Sapienza'', Rome, Italy
8 - Centre d'Étude Spatiale des Rayonnements, Université de Toulouse, CNRS, 9 Av. du Colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
9 - APC, Université Denis Diderot-Paris 7, CNRS/IN2P3, CEA, Observatoire de Paris, 10 rue A. Domon & L. Duquet, Paris, France
10 - European Space Agency, Astrophysics Division, Keplerlaan 1, 2201AZ Noordwijk, The Netherlands
11 - LAL - Laboratoire de l'Accélérateur Linéaire, Université Paris-Sud 11, CNRS/IN2P3, Bât. 200, 91898 Orsay Cedex, France

Received 9 December 2009 / Accepted 16 February 2010

Abstract
Context. CMB experiments aiming at a precise measurement of the CMB polarization, such as the Planck satellite, need a strong polarized absolute calibrator on the sky to accurately set the detectors polarization angle and the cross-polarization leakage. As the most intense polarized source in the microwave sky at angular scales of few arcminutes, the Crab nebula will be used for this purpose.
Aims. Our goal was to measure the Crab nebula polarization characteristics at 90 GHz with unprecedented precision.
Methods. The observations were carried out with the IRAM 30 m telescope employing the correlation polarimeter XPOL and using two orthogonally polarized receivers.
Results. We processed the Stokes I, Q, and U maps from our observations in order to compute the polarization angle and linear polarization fraction. The first is almost constant in the region of maximum emission in polarization with a mean value of $\alpha_{\rm Sky}=152.1\pm 0.3^\circ$ in equatorial coordinates, and the second is found to reach a maximum of $\Pi=30$% for the most polarized pixels. We find that a CMB experiment having a 5 arcmin circular beam will see a mean polarization angle of $\alpha_{\rm Sky}=149.9\pm0.2^\circ$ and a mean polarization fraction of $\Pi=8.8\pm0.2$%.

Key words: ISM: supernova remnants - polarization - cosmology: cosmic background radiation

1 Introduction

The Crab nebula (Tau A, M1 or NGC 1952, at coordinates $\alpha = 5^{\rm h} 34^{\rm m} 32^{\rm s}$ and $\delta = 22^\circ 0\hbox{$^\prime$ }52\hbox{$^{\prime\prime}$ }$, J2000) is a supernova remnant that emits a highly polarized signal due to both the synchrotron emission of the central pulsar and its interaction with the surrounding gas (see e.g. Hester 2008). In this paper, we present the measurements of intensity and polarization of the Crab nebula at 90 GHz (3.3 mm) performed at the IRAM 30 m telescope using the XPOL instrument (Thum et al. 2008). The strength of this instrument is the precision in the angle of polarization with respect to the sky reference frame, which highly improves previous measurements. This precision is needed in particular to use the Crab nebula as an absolute polarization calibrator for cosmic microwave background (CMB) experiments, such as the Planck ESA mission. The results for circular polarization are irrelevant for current CMB polarimetry experiments and will be published elsewhere (Wiesemeyer et al., in prep.).

The last Thomson scattering of cosmological photons by free electrons at the time of decoupling between matter and radiation at $z_{\rm dec}=1088.2\pm 1.1$ (Dunkley et al. 2009) have led to a linearly polarized CMB radiation at a level of a few percent. The linear polarization pattern on the sky can be decomposed into a scalar and a pseudo-scalar field, respectively called E- and B-modes, which have the advantage of being independent of the reference frame (Zaldarriaga 2001; Zaldarriaga & Seljak 1997). This decomposition is particularly useful because primordial density fluctuations (scalar perturbations) can only produce E polarization, while B can only be produced by lensing effects, exotic phenomena such as cosmological birefringence (Carroll et al. 1990) and by the stochastic background of gravity waves arising from the inflation epoch (tensor perturbations). The detection of the latter would improve the constraints on the inflationary model parameters in an invaluable manner and constitutes one of the most ambitious goals of observational cosmology.

The first measurement of the CMB E polarization was made by the 30 GHz radio interferometer, DASI, in 2002 (Kovac et al. 2002). Since then, in addition to a further measurement by the DASI experiment (Leitch et al. 2005), E modes measurements have been made with the CBI (Readhead et al. 2004), CAPMAP (Bischoff et al. 2008), BOOMERanG (Montroy et al. 2006), Wmap (Page et al. 2007), MAXIPol (Wu et al. 2007), QUaD (Ade et al. 2008) and Bicep (Chiang et al. 2010). With these measurements, the $C_\ell^{\it EE}$ angular power spectrum has now been detected over a wide range of angular scales ( $30\lesssim\ell\lesssim1000$). Additionally, the Wmap satellite has given a very precise measurement of the temperature-E polarization correlation, the $C_\ell^{\it TE}$ angular cross power spectrum, at large scales up to multipoles $\ell\simeq500$ (Nolta et al. 2009). To date, no detection of non-zero $C_\ell^{BB}$ angular power spectrum has been reported and only upper limits on the effect of gravity waves from other spectra can be inferred. The best indirect limit to date on the tensor to scalar ratio r, given by Wmap data and other cosmological observables together is r<0.2 (95% C.L.) (Komatsu et al. 2009).

Upcoming experiments target the detection of lower values of the tensor-to-scalar ratio. The low signal of the B-modes compared to the temperature and E-modes signals will require a high control of systematics and good knowledge of the instrument. In particular, the knowledge of its polarization characteristics will require a highly and well known polarized source.

The Crab nebula represents the most suitable candidate as absolute calibrator for the polarization angle and the linear polarization degree, given that it is the most intense polarized source in the microwave sky at angular scales of few arcminutes (Flett & Henderson 1983,1981,1979).

The paper is organized as follows: in Sect. 2 we describe the required calibration accuracy for a CMB experiment aiming at the detection of the B-modes; in Sect. 3 we briefly describe the XPOL instrument; Sect. 4 reports the observations, data reduction and systematic error analysis; in Sect. 5 we give our results; we discuss the extension of our measurements to other frequencies in Sect. 6 and summarize our results in Sect. 7.

2 Required calibration accuracy

The expected primordial B-mode level at large angular scale, for r=0.01, is typically 1% of the E-mode level. More precisely, for $\ell < 20$, the E-mode is on the order of $0.07~\mu\mbox{K}^2$ (from the WMAP best-fit model, see Nolta et al. 2009), while the B-mode is expected at $10^{-4}~\mu\mbox{K}^2$. For comparison, the temperature anisotropies are at the level $1000~\mu\mbox{K}^2$ at large scale. The Planck High Frequency Instrument, for example, has the potential to detect or constrain the tensor-to-scalar ratio down to $r\simeq 0.03$ (Efstathiou & Gratton 2009). However, such a low level will be reachable only if the systematics are well controlled, otherwise, given the hierarchy of signal levels, $T\gg E\gg B$, we may expect leakage from temperature to polarization and a leakage of E-mode to B-mode.

Various instrument parameters, if not precisely known, will induce systematic effects. In the case of the Planck HFI polarization sensitive bolometers, the detectors are sensitive to the power carried by the electric field aligned with the detector's grid. The signal smeasured by a detector can be written (Rosset et al. 2010)

                        s = 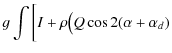$\displaystyle g\int \bigg[ I + \rho \big( Q \cos 2(\alpha+\alpha_d)$  
    $\displaystyle +U\sin 2(\alpha+\alpha_d)\big) \bigg] A(\vec{n}) {\rm d}\vec{n},$ (1)

where I, Q and U are the Stokes parameters of the sky signal (intensity and linear polarization in the sky reference frame), g is the detector gain, A is the instrument beam, $\rho$ is the detector polarization efficiency, $\alpha $is the angle between the telescope reference frame and the local meridian in the sky, $\alpha_d$ is the angle at which the polarimeter is maximally sensitive to polarized radiation, in the telescope reference frame (here, we have made the simplification that the beam for polarization is identical to the intensity beam, only modulated by the sine and cosine of the detector orientation) and $\vec{n}$ is a direction on the sky. In this simplified model, g and A are measurable with unpolarized light (cosmological and orbital dipole, planets). Only the polarization specific parameters, $\alpha $ and $\rho$, require a known polarized signal to be calibrated. Measuring with precision these properties in laboratory or with an artifical source can be difficult (see e.g. Takahashi et al. 2010; Rosset et al. 2010), so measuring them with a known astrophysical source allows cross-checking or even a better calibration. In any case, the best limit on the precision of the polarization efficiency and the orientation of detectors will be set by the precision on the polarization fraction and polarization orientation of the source.

In the case of a unique detector scanning the sky, it has been shown (Rosset et al. 2010; O'Dea et al. 2007) that the error on the B-mode power spectrum due to an error $\Delta\alpha$ in the polarization orientation and an error $\Delta\rho$ on the polarization efficiency is given by:

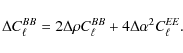
\begin{displaymath}\Delta C^{BB}_\ell = 2\Delta\rho C^{BB}_\ell + 4\Delta\alpha^2 C^{\it EE}_\ell. \end{displaymath} (2)

For example, an experiment targeting a tensor-to-scalar ratio measurement of r=0.01, using the large angular scale B-mode (at $\ell < 20$), will require the polarization orientation and the polarization efficiency to be known with a precision of:

\begin{displaymath}\Delta\alpha < 0.9^\circ,\qquad \Delta\rho<0.05, \end{displaymath} (3)

in order to have a leakage from E to B-modes lower than one tenth of the expected $C_\ell^{BB}$.

These tolerances set the precision needed for the calibrator, and define our goal for the Crab nebula observations presented in this paper.

3 Instrumental setup

3.1 General

For the observation of the Crab nebula, we used the IRAM 30 m telescope at 89.189 GHz, the frequency of the HCO+(1-0) transition, where the angular resolution (the full width at half power of the near-Gaussian beam) is $27^{\prime\prime}$. We used the following IRAM receivers: A100 cryostat (vertical linear polarization with respect to Nasmyth reference frame) and B100 cryostat (horizontal linear polarization). The mean system temperatures were 87 K (A100) and 113 K (B100) while mean receiver temperatures (single-sideband) were 67 K (A100) and 59 K (B100). The effective cold loads used for temperature calibration had a mean temperature of 87 K (A100) and 98 K (B100). We used the VESPA backends in XPOL mode (see Sect. 3.2), with a 500 MHz bandwith (200 channels spaced by 2.5 MHz). Finally, the conversion factor from antenna temperature outside atmosphere to flux density was 1 K = 6.0 Jy and the mean zenith opacity was $\tau_z=0.06$ at our observing frequency.

3.2 XPOL

The signals from the two orthogonal linearly polarized heterodyne receivers were detected in auto- and cross-correlation, from which the four Stokes parameters were derived as described in detail by Thum et al. (2008). This procedure, designated XPOL, employs a precise calibration of the phase between the two receivers, resulting in a phase error ${<}1^\circ$ per channel of 2.5 MHz, across the 500 MHz bandwidth.

Particular care was taken in the absolute calibration of the polarization angle $\tau$. This angle was re-measured, for the purpose of this experiment in the Nasmyth cabin, with respect to its horizontal axis, where the receivers are stationary, as

\begin{displaymath}\tau = \frac{1}{2} \arctan \left (\frac{U}{Q}\right ), \end{displaymath} (4)

where Q and U refer to the quantities measured in the Nasmyth reference frame. The precision with which the receivers, labelled H and V, actually measure horizontally and vertically polarized power is determined by the orientation of the grid (G3 in Fig. 1 of Thum et al. 2008) which splits the incoming beam into a transmitted fraction which is horizontally polarized, and a reflected fraction which is vertically polarized. The horizontality of the incoming beam, and thus also that of the H-fraction rests on the correct alignment of the telescope Nasmyth mirror M3, the subreflector, and the validity of the implemented homology corrections and the pointing model. Their combined error is less than 1 arcmin. The verticality of the V-fraction additionally depends on the orientation of G3 whose normal should make an angle of 45$^\circ$ with respect to the local vertical. The mounting frame of G3 has a typical mechanical precision of ${\la} 1$ mm over the length of 25 cm of the grid support frame. This corresponds to an angular precision of ${\sim} 0.3^\circ$ which was confirmed by a direct measurement with an electronic angle gauge in contact with the grid's frame.

Equation (4) shows that the precision of the $\tau$measurement further depends on the correct relative calibration of Stokes U and Q. Since XPOL measures Q as the power difference between the H and V receivers, but derives Stokes U from their correlation, we need to make a precise measurement of the inevitable correlation losses. This is done as a by-product of the frequent phase calibration measurements where a wire grid of precisely known orientation is observed against hot and cold loads. Due to the high signal-to-noise of these calibrations, the correlation losses can be determined with an rms error of ${\sim} 1$%, resulting in an rms error of $\tau$ of ${\sim} 0.3^\circ$.

The transfer of $\tau$ to the polarization angle $\alpha _{\rm Sky}$ as measured from north to east in the equatorial system is made through

\begin{displaymath}\alpha_{\rm Sky} = 90^\circ + \tau - (\epsilon - \eta), \end{displaymath} (5)

where the elevation $\epsilon$ and the parallactic rotation angle $\eta$do not introduce any additional error. We therefore estimate that our polarization angles have an absolute precision on the order of 0.5$^\circ$ or slightly better.

4 Observations and data reduction

4.1 Mapping strategy

The Stokes maps of the Crab nebula were taken in the on-the-fly mode (hereafter OTF), allowing us to map a large area on the sky within a reasonable time interval. The telescope was scanning the source while XPOL dumped twice per second the total power from the orthogonally polarized receivers, and the complex cross-correlation. The Stokes maps were subsequently derived from these quantities. Throughout the paper, Q and U will refer to the quantities measured in the Nasmyth system and then rotated in equatorial coordinates according to Eq. (5). The Crab nebula was scanned along the projections of latitude and longitude onto the local tangential plane (hereafter respectively $\alpha $and $\delta$ scanning directions). Such a scanning strategy is indispensable if artifacts due to the variations of the atmospheric emission, leading to stripes in the maps, are to be removed (see Sect. 4.2). The maps scanned along the $\alpha $ direction are $8.8' \times 6.4'$ large, those scanned along the $\delta$ direction $10.2' \times 5.5'$. The differences in size are due to slightly different system overheads coming from the acceleration and deceleration of the antenna mount drive before and after scanning an OTF stripe. The scanning speed was 16''/s, leading to a smearing of the 27'' wide beam (FWHM) by 8''. A pair of maps scanned in the orthogonal directions took 22 min, including regular temperature and phase calibrations. All the maps were projected on the same $51\times 41$ pixels frame with square pixels of size 13.7''.

4.2 Raw data reduction

The conversion from backend count rates to antenna temperatures follows the standard method applied at the IRAM 30 m observatory, involving total power measurements of the sky, a hot load, and a cold load. These calibration measurements are combined with the phase calibration measurements, namely an on-off between a fully linearly polarized signal at cold load temperature, and the unpolarized hot load signal at ambient temperature (Sect. 3). The calibrations were derived and applied to the data with the MIRA software (see Wiesemeyer 2009).

Since the continuum emission from the Supernova remnant has a well-defined outer boundary, there is no need to observe a separate emission-free reference position. The atmosphere emission was rather removed by subtracting, from each OTF subscan observed along a given direction, a linear baseline defined by the Crab nebula emission-free map boundary. Subtracting only a zero order spatial baseline would leave ``stripes'' in the maps along the scanning direction, which could be removed in Fourier space with the PLAIT algorithm (Emerson & Graeve 1988). Both methods were shown to yield equivalent results. In fact, they are both limited by the uncertainty of the absolute reference flux if the source boundary is not precisely known. In the image plane approach, the source and sky emission cannot be clearly separated from each other, in the Fourier plane technique case, the PLAIT algorithm does not work close to zero spatial frequency (whose Fourier component is the total flux density contained in the map).

\begin{figure} \par\includegraphics[width=8.3cm,clip]{13834fig1a.ps}\hspace*{1mm... ...s}\hspace*{1mm} \includegraphics[width=8.3cm,clip]{13834fig1d.ps} \end{figure} Figure 1:

Standard deviation maps for the Crab nebula intensity $\sigma (I)$ (top row) and polarized intensity $\sigma (P)$ (bottom row), in antenna temperature (K). $\sigma (I)$ and $\sigma (P)$ maps were computed using the 2CC and 2CX (see text) 39 maps (left column) and using the 28 2CC maps only (right panel). I and respectively P contours computed with the 28 2CC maps are overploted. We can see that when maps scanned along the $\alpha $ direction are added to the data set the standard deviation is higher and shows some features indicating an uncontrolled systematic effect.

Open with DEXTER

Since for XPOL the signal is downconverted into eight adjacent spectral basebands of 62.5 MHz width each, total power variations between the sky/hot/cold scan and the OTF record result in calibration mismatches among the basebands that introduce platforms in the autocorrelation spectra. In an attempt to correct for this undesired effect, one may naively think of using the data from a filterbank, connected in parallel and with a monolithic spectral band, such that they are not affected by platforming. However, in the subsequent data processing step (rotation from the Nasmyth to equatorial reference frame, for getting a stationary astronomical polarization), the spectra will be linearly combined with the real part of XPOL's cross correlation (which is, after phase calibration, Stokes U in the telescope's Nasmyth reference frame). The small calibration differences observed between XPOL and the filterbank are believed to be caused by non-linearities when the backends operate close to the saturation limit. Mixing these data would thus lead to an inconsistent calibration and hence an error in the polarization angle map of the Crab nebula. Therefore, another strategy was used:

  • for each autocorrelation spectrum (i.e. each record of an OTF map), the median across the whole band, with concatenated basebands, has been calculated;
  • for each of the eight basebands of a given spectrum, the mean continuum flux and noise has been determined;
  • when the absolute difference between the mean baseband signal and the median signal is greater than twice the baseband noise, the offset of the baseband signal has been corrected by the difference between the median and the baseband mean.
The result is a spectrum that looks ``flat''. The remaining calibration mismatches lead to stripes in the maps, as do fluctuations of atmospheric origin, and gain fluctuations owing to receiver instabilities. As a matter of fact, stripes are also present in filterbank spectra, which do not suffer from platforming.

It should be noted here that the cross-correlation spectra (Stokes U in the Nasmyth reference frame, and Stokes V) do not suffer from platforming either. This derives from the fact that the clipping voltage of a sampler is adjusted with respect to the signal's noise level, which may change when a given interval of the time series is measured. The zero time lag channel measures the total power (Parseval's theorem), which is positive definite. After the FFT, this shows as an offset to the spectral baseline. A cross-correlator analyses the signals from two independent samplers. Variations in the noise power of the signals coming from the samplers are largely uncorrelated, and therefore cancel out in the spectral cross-power (which is not a positive definite quantity anymore).

The data were gridded at Nyquist sampling. Because of the slightly different values of the start or end scanning coordinate between different subscans, the sampling is irregular. Therefore the data had to be resampled to a regular grid. This has been done by applying a Gaussian convolution kernel with a FWHM of one-third the telescope's half-power beam width. The kernel is truncated at three FWHM.

4.3 Description of the data sets

We performed two observation campaigns of the Crab Nebula, respectively from September 5 to 10, 2007, and from January 9 to 12, 2009.

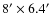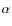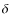  • First campaign: Observations were made during 6 intervals, under varying astmospheric opacity and stability conditions. Most of the maps were affected by a substantial atmospheric contamination, showing as strong linear stripes in the scanning direction. We obtained 66 I, Q, U and V maps resulting in $8' \times 6.4'$ maps after coadding $\alpha $-scanned and $\delta$-scanned maps. 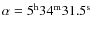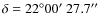These maps were centered on the reference point we called crabxpol having equatorial coordinates $\alpha = 5^{\rm h} 34^{\rm m} 31.5^{\rm s}$ and $\delta = 22^\circ 00\hbox{$^\prime$ }27.7\hbox{$^{\prime\prime}$ }$ (J2000). The centering and the size of these maps made the destriping delicate because the extension of the source emission was larger than the observed area and thus, strong mix-up with atmospheric contamination arose on maps' edges leading to uncontrolled systematics.
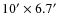  • Second campaign: Observations were made during 4 nights during which we experienced stable atmospheric conditions. As a consequence of the first observation campaign, we increased the coaddition of the $\alpha $-scanned and $\delta$-scanned maps to a size of $10' \times 6.7'$ in order to be able to characterize the atmospheric stripes outside the source. 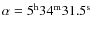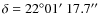11 maps of I, Q, U and V were observed centered on the same reference point as in the first campaign, namely crabxpol, and then we changed to a new reference point for center, called crabcenter and having equatorial coordinates $\alpha = 5^{\rm h} 34^{\rm m} 31.5^{\rm s}$ and $\delta = 22^\circ 01\hbox{$^\prime$ } 17.7\hbox{$^{\prime\prime}$ }$ (J2000), on which the next 28 maps were observed. This choice was made to have a better centering of the source extent in the north-south direction, allowing better destriping. The 11 first maps centered on crabxpol have a significantly higher noise level than the 28 centered on crabcenter due to worse weather condition at the beginning of the campaign.
These data sets thus gather 105 individual I, Q, U and Vmaps, divided in three subsets: first campaign maps centered on crabxpol (hereafter 1CX), second campaign maps centered on crabxpol (hereafter 2CX) and second campaign maps centered on crabcenter (hereafter 2CC). Because in the two first subsets the source extends over an area larger than the mapped one, the destriping is delicate and thus may lead to uncontrolled systematics. For each subsets and for combinations of different subsets we computed, for each Stokes parameter, mean and dispersion for each pixel among the whole data set. As the pixels are small with respect to the beam, the computed dispersion does not suffer from bias. Dispersion maps, in the case of the first and second subsets, present specific high-dispersion features arising from the confusion between stripes and source emission on the borders during the destriping procedure. This can be seen on Figure 1 where the combination of subsets 2CX and 2CC, for the intensity, shows a higher standard deviation feature than the 2CC alone. For consistency, we also checked the behavior of the polarized intensity standard deviation which slightly decreases when using only 2CC maps.

Thus, using only the 28 maps from 2CC provides the best results and any addition of 2CX maps, only 2CX maps scanned in $\alpha $ direction (direction in which the borders of the maps are off-source) and 1CX lead to worse results in terms of noise homogeneity and of signal-to-noise ratio, both in intensity and polarization. Consequently, our analysis will use only the 28 maps of the second campaign centered on the crabcenter reference point.

4.4 Systematic effects analysis

In order to check for residual systematic effects in the maps, we performed jack-knife tests dividing the 28 maps in several subsets using three criteria, i.e.: randomly, between maps scanned in $\alpha $ and $\delta$direction and between the three observation nights during which these 28 maps were taken. We also divided the data in two with respect to the position angle of the Nasmyth reference frame projected onto the sky, $\chi_0$, in order to check for sidelobe polarization effects (Forbrich et al. 2008), which may show whether the difference between the $\chi_0$ of subsets is close to 90$^\circ$.

Table 1:   Polarization angle $\alpha _{\rm Sky}$ and polarized fraction $\Pi $ computed for different divisions of the data set.

\begin{figure} \par\includegraphics[width=8.3cm,clip]{13834fig2a.ps}\hspace*{1mm... ...s}\hspace*{1mm} \includegraphics[width=8.5cm,clip]{13834fig2d.ps} \end{figure} Figure 2:

Maps of the Crab nebula at 89.189 GHz in antenna temperature (K) for intensity I (top-left), Q polarization (top-right), U polarization (bottom-left) and polarized intensity P (bottom-right). The position of the Crab nebula pulsar is indicated by the black cross.

Open with DEXTER

The mean and dispersion of the 28 observations allow us to derive a signal-to-noise map for I, Q, U and $P\equiv(Q^2+U^2)^{1/2}$. For the residual systematic effects analysis, we have chosen a region corresponding to S/N(P)>10 that includes 19 pixels. For these pixels, we compute the mean polarization angle $\alpha_{{\rm Sky},j}\equiv0.5\cdot\langle\arctan(U_j/Q_j)\rangle$ and the mean polarization fraction $\Pi_j\equiv\langle P_j/I_j\rangle$ for each map j. Then, $\alpha_{{\rm Sky},j}$ and $\Pi_j$ are averaged for each subset to give the mean $\alpha _{\rm Sky}$ and $\Pi $ and the error on the mean is given by the standard deviation over the subset of maps, preventing correlations between Q and U, or among pixels.

Results are displayed in Table 1. Values are stable against the selection of different data subsets. For the polarization angle, for each subset selection criteria, the values are compatible at less than two $\sigma$, showing no clue to residual systematic effects in the data. We observe a similar behavior for the polarization fraction, where only the subset corresponding to $\alpha $and $\delta$ scans shows a departure of slightly more than two $\sigma$. This systematic behavior is due to a percent-level difference in the intensity maps corresponding to each type of scan, caused by residual errors in the destriping which is less precise for $\delta$-scanned maps due to the limited number of off-source pixels in this case and leading to an overestimation of the intensity.

\begin{figure} \par\includegraphics[width=8cm,clip]{13834fig3a.ps}\hspace*{1mm} \includegraphics[width=9cm,clip]{13834fig3b.ps} \end{figure} Figure 3:

(Left) Map of the polarization angle $\alpha _{\rm Sky}$ in degree on which contours of the polarized intensity P for 0.04, 0.08 and 0.16 K have been overploted. (Right) Map of the polarization fraction $\Pi $ on which has been displayed the intensity contour for 0.15, 0.30 and 0.45 K.

Open with DEXTER

5 Results

After the raw data reduction, including atmospheric decontamination by linear baselines subtraction, we obtained a set of 28 systematic-reduced individual maps with which we compute average and standard deviation maps for I, Q, U, $P\equiv(Q^2+U^2)^{1/2}$, $\alpha_{\rm Sky}\equiv0.5\cdot\arctan(U/Q)$and $\Pi\equiv P/I$.

The Crab nebula intensity I map is displayed on top-left panel of Fig. 2, in antenna temperature, showing a maximum 0.91 K emission half an arcmin south from the pulsar position. The flux density integrated over the source and its error bar derived from the pixel-to-pixel standard deviation are measured as $S(I)=195.5\pm11.0$ Jy. This value is compatible within 3$\sigma$ with the value given by the WMAP satellite at 92.9 GHz of $S(I)=229\pm11$ Jy (Page et al. 2007).

The Q and U maps of the Crab nebula are displayed on top-right and bottom-left panel of Fig. 2, in antenna temperature (K). Q map is showing a roughly positive value, up to 0.16 K while U is showing a negative one down to -0.20 K.

The polarized intensity P map is displayed on bottom-right panel of Fig. 2, in antenna temperature, showing a maximum of 0.25 K half an arcmin south from the pulsar position. We can see that the Crab nebula is less extended in polarized intensity than in Stokes I. The polarized flux density is measured as $S(P)=14.5\pm3.2$ Jy, leading to a mean polarization fraction for the whole Crab nebula source of $\Pi=7.4\pm0.7$%. This value is compatible with the value measured by WMAP of $7.6\pm2.0$% (Page et al. 2007).

The $\alpha _{\rm Sky}$ map is displayed on the left panel of Fig. 3. It is worth noting that $\alpha _{\rm Sky}$ is almost constant around 150$^\circ$ in the region of maximum polarized intensity (P>0.05 K). This region corresponds to the region where each pixel's standard deviation $\sigma(\alpha_{\rm Sky})$ is the lowest ( ${\le} 30^\circ$), going down to $\sigma(\alpha_{\rm Sky})\lesssim3^\circ$ for the most intensely polarized pixels. The value of the angle we measured at the flux peak, $\alpha_{\rm Sky}=149.0\pm 1.4^\circ$, is in very good agreement with previous measurements at 1350 and 1100 $\mu$m (Flett & Murray 1991; Greaves et al. 2003). On the map edges, $\alpha _{\rm Sky}$ pixel-to-pixel deviation is high, except for the northern region where the average angle is around 230$^\circ$. When looking at the $\sigma(\alpha_{\rm Sky})$ map, we can see that pixels on the edges have an undetermined value ( $\sigma(\alpha_{\rm Sky})\simeq90^\circ$), whereas in the northern region they have $30^\circ\le\sigma(\alpha_{\rm Sky})\le50^\circ$, indicating a polarization angle there that is significantly different from that near the center of the nebula.

\begin{figure} \par\includegraphics[width=12cm,clip]{13834fig4.ps} \vspace*{-3mm} \end{figure} Figure 4:

Map of the Crab nebula polarized intensity P at 89.189 GHz in antenna temperature on which polarization vectors have been overpolted. Intensity contours at 0.15, 0.30 and 0.45 K are also displayed.

Open with DEXTER

The polarization fraction $\Pi $ map is displayed on the right panel of Fig. 3. We have set to 0 the pixels for which intensity is lower than 0.02 K in order to avoid the divergence of $\Pi $. Maximum polarization fraction is found to be spatially correlated with maximum polarized intensity region, with a polarization fraction reaching 30% for few pixels. A 1.5 arcmin circular region around the maximum polarization fraction has a significant $\Pi\sim20$%.

To summarize all these results, we display in Fig. 4 the polarized flux density P and the orientation of the polarization vectors associated with each map pixel. The polarization vectors pattern is compatible with 9 mm (Flett & Henderson 1979) and 850 $\mu$m (Greaves et al. 2003) observations.

We finally computed several values of the polarization angle $\alpha _{\rm Sky}$ and of the polarization fraction $\Pi $ for different regions, displayed in Table 2. We selected the pulsar position and high signal-to-noise ratio regions for the polarized intensity ( S/N(P)>3, corresponding roughly to the source's polarized emission extent and S/N(P)>10). Furthermore, we convolved each individual map by a circular Gaussian beams of 5 arcmin and 10 arcmin of FWHM before computing the mean polarization angle and fraction. These beams mimic the Planck satellite's beams (10' for the 100 GHz and 5'for the 217 and 353 GHz channels) and give an estimation on how a generic CMB experiment having Planck-like characteristic would see the Crab nebula's polarization. For each of these cases, the mean value and its associated error were computed similarly to Sect. 4.4.

6 Extension to other frequencies

The total intensity emission of the Crab nebula from 1 to 106 GHz is dominated by the well known synchrotron radiation observed at radio wavelengths with only one extra dust component in the far infrared (Macías-Pérez et al. 2010). This synchrotron emission shows a decrease of flux with increasing frequency which can be represented by a power law of spectral index $\beta = -0.296 \pm 0.06$(Baars et al. 1977; Macías-Pérez et al. 2010) from the radio to the submillimeter domains. The flux is also decreasing with time at a rate of $\alpha = 0.167 \pm 0.015$% yr-1 (Aller & Reynolds 1985). Moreover, from the visible to the X-rays the synchrotron emission evolves towards a much harder spectrum represented by a power law of spectral index $\beta = -0.698 \pm 0.018$(Macías-Pérez et al. 2010).

These statements allow us to postulate that where the synchrotron dominates, the emission at different wavelengths is produced by particles accelerated by the same magnetic field. The direction of polarization is thus expected to be constant while the polarization fraction may vary. Nevertheless, we expect values for both the polarization angle and the polarization fraction, at low-resolution, to be similar in the millimeter and submillimeter where the emission is produced by the same electron population.

Table 2:   Values of the polarization angle $\alpha _{\rm Sky}$ and of the polarization fraction $\Pi $.

Values of the polarization angle of the Crab nebula source have been reported over this wide range of wavelengths from the radio (e.g. at 9 mm, $\alpha_{\rm Sky}=154.8\pm2.0$, Flett & Henderson 1979) to the millimeter (at 3.3 mm, $\alpha_{\rm Sky}=153.7\pm0.4$, this paper) and to the X-rays (at 240 pm, $\alpha_{\rm Sky}=155.8\pm1.4$, Weisskopf et al. 1978). We can see that the value of the polarization angle is strikingly constant over nearly ten decades of wavelength. Furthermore, the value measured in the X-ray, similar to the one we measured at 90 GHz, indicates that we are probably dominated by synchrotron emission for the same regions in both cases and that an extrapolation up to 353 GHz, where present and future CMB experiments such as the Planck satellite are observing the sky, is rather safe.

The polarization fraction can be compared to other measurements too, keeping in mind that it is a quantity which changes inside the source rapidly and that shall be compared only for experiments observing with a comparable beam size. The comparison of our value of $\Pi=15.6\pm0.2$% to radio observations at 9 mm giving $\Pi=16\pm1$% (Flett & Henderson 1979) and the value we obtain when our maps were convolved by a 10' beam of $7.7\pm0.2$% to the WMAP experiment ($7.6\pm2.0$%, Page et al. 2007) indicates that those measurements are coherent with an emission coming from the same electron population wich leads to a constant polarization fraction over the CMB frequency range.

7 Summary

We mapped the polarized emission of the Crab nebula using the IRAM 30 m telescope at 89.189 GHz with an angular resolution of 27'', with two orthogonally linearly polarized heterodyne receivers. The Stokes parameters were derived from the auto- and cross-correlations using the XPOL procedure (Thum et al. 2008).

Observations have been undertaken during two campains, leading to a set of 105 individual I, Q and U maps having changing weather conditions, sizes and centering. Particular care has been taken in choosing the set of individual maps leading to the lower level of systematics in the final products. Additionnaly, jack-knife tests have been carried out in order to demonstrate the robustness of the data. As a result, we constructed 10 $'\times6.7'$ I, Q and U coaddition maps of these observations centered on the Crab nebula.

From these maps we have computed the polarized intensity $P=\sqrt{Q^2+U^2}$, the polarization angle $\alpha_{\rm Sky}\equiv0.5$  $\cdot\langle\arctan(U/Q)\rangle$and the polarization fraction $\Pi\equiv\langle P/I\rangle$. We derived our results on the polarization characteristics of the Crab nebula with these maps:

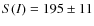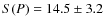  • The measured flux density is $S(I)=195\pm11$ Jy and the polarized flux density is $S(P)=14.5\pm3.2$ Jy.
  • The polarization angle is almost constant in the region of maximum emission in polarization with a mean value of 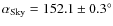$\alpha_{\rm Sky}=152.1\pm 0.3^\circ$. A region north to the pulsar is seen with an average angle of $\sim$230 $^{\rm\circ}$, but it does not correspond to a strongly polarized emission region. 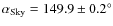When seen by a 5 arcmin beam, the mean polarization angle of the whole source as a value of $\alpha_{\rm Sky}=149.9\pm0.2^\circ$, in good agreement with the other measurements at radio, millimeter and X-rays wavelengths.
  • The polarization fraction shows a maximum in a region south from the pulsar position, reaching 30%. When averaged by a 5 arcmin beam, the measured mean value of the polarization fraction is 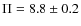$\Pi=8.8\pm0.2$%. This value is in very good agreement with the WMAP measurements at 94 GHz.
With a precision of a few tenths of degree on the polarization angle and of a few tenths of percent on the polarization fraction, these measurements will be especially interesting in the purpose of absolute calibration of the polarization angle and the cross-polarization leakage for present and future polarized CMB experiments, such as the Planck mission, in order to accurately disentangle instrumental and systematic B-modes polarization from the primordial one.

Acknowledgements
We gratefully acknowledge the support of IRAM to this program including the grant of discretion time by its director P. Cox. J. Aumont has been partly supported in this work by a post-doctoral position from CNES. E. Pointecouteau was supported by grant ANR-06-JCJC-01142.

References

  1. Ade, P., Bock, J., Bowden, M., et al. 2008, ApJ, 674, 22 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aller, H. D., & Reynolds, S. P. 1985, ApJ, 293, L73 [Google Scholar]
  3. Baars, J. W. M., Genzel, R., Pauliny-Toth, I. I. K., & Witzel, A. 1977, A&A, 61, 99 [NASA ADS] [Google Scholar]
  4. Bischoff, C., Hyatt, L., McMahon, J. J., et al. 2008, ApJ, 684, 771 [NASA ADS] [CrossRef] [Google Scholar]
  5. Carroll, S. M., Field, G. B., & Jackiw, R. 1990, Phys. Rev. D, 41, 1231 [NASA ADS] [CrossRef] [Google Scholar]
  6. Chiang, H. C., Ade, P. A. R., Barkats, D., et al. 2010, ApJ, 711, 1123 [NASA ADS] [CrossRef] [Google Scholar]
  7. Dunkley, J., Komatsu, E., Nolta, M. R., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef] [Google Scholar]
  8. Efstathiou, G., & Gratton, S. 2009, ICAP, 06, 011 [Google Scholar]
  9. Emerson, D. T., & Graeve, R. 1988, A&A, 190, 353 [NASA ADS] [Google Scholar]
  10. Flett, A. M., & Henderson, C. 1979, MNRAS, 189, 867 [NASA ADS] [Google Scholar]
  11. Flett, A. M., & Henderson, C. 1981, MNRAS, 194, 961 [NASA ADS] [Google Scholar]
  12. Flett, A. M., & Henderson, C. 1983, MNRAS, 204, 1285 [NASA ADS] [Google Scholar]
  13. Flett, A. M., & Murray, A. G. 1991, MNRAS, 249, 4P [NASA ADS] [CrossRef] [Google Scholar]
  14. Forbrich, J., Wiesemeyer, H., Thum, C., Belloche, A., & Menten, K. M. 2008, A&A, 492, 757 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Greaves, J. S., Holland, W. S., Jenness, T., et al. 2003, MNRAS, 340, 353 [NASA ADS] [CrossRef] [Google Scholar]
  16. Hester, J. J. 2008, ARA&A, 46, 127 [Google Scholar]
  17. Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
  18. Kovac, J. M., Leitch, E. M., Pryke, C., et al. 2002, Nature, 420, 772 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  19. Leitch, E. M., Kovac, J. M., Halverson, N. W., et al. 2005, ApJ, 624, 10 [NASA ADS] [CrossRef] [Google Scholar]
  20. Macías-Pérez, J. F., Mayet, F., Aumont, J., & Désert, F. 2010, ApJ, 711, 417 [NASA ADS] [CrossRef] [Google Scholar]
  21. Montroy, T. E., Ade, P. A. R., Bock, J. J., et al. 2006, ApJ, 647, 813 [NASA ADS] [CrossRef] [Google Scholar]
  22. Nolta, M. R., Dunkley, J., Hill, R. S., et al. 2009, ApJS, 180, 296 [NASA ADS] [CrossRef] [Google Scholar]
  23. O'Dea, D., Challinor, A., & Johnson, B. R. 2007, MNRAS, 376, 1767 [NASA ADS] [CrossRef] [Google Scholar]
  24. Page, L., Hinshaw, G., Komatsu, E., et al. 2007, ApJS, 170, 335 [NASA ADS] [CrossRef] [Google Scholar]
  25. Readhead, A. C. S., Myers, S. T., Pearson, T. J., et al. 2004, Science, 306, 836 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  26. Rosset, C., Ponthieu, N., Tristram, M., et al. 2010, A&A, accepted [Google Scholar]
  27. Takahashi, Y. D., Ade, P. A. R., Barkats, D., et al. 2010, ApJ, 711, 1141 [NASA ADS] [CrossRef] [Google Scholar]
  28. Thum, C., Wiesemeyer, H., Paubert, G., Navarro, S., & Morris, D. 2008, PASP, 120, 777 [NASA ADS] [CrossRef] [Google Scholar]
  29. Weisskopf, M. C., Silver, E. H., Kestenbaum, H. L., Long, K. S., & Novick, R. 1978, ApJ, 220, L117 [NASA ADS] [CrossRef] [Google Scholar]
  30. Wiesemeyer, H. 2009, http://www.iram.fr/IRAMES/otherDocuments/manuals/index.html [Google Scholar]
  31. Wu, J. H. P., Zuntz, J., Abroe, M. E., et al. 2007, ApJ, 665, 55 [Google Scholar]
  32. Zaldarriaga, M. 2001, Phys. Rev. D, 64, 103001 [NASA ADS] [CrossRef] [Google Scholar]
  33. Zaldarriaga, M., & Seljak, U. 1997, Phys. Rev. D, 55, 1830 [Google Scholar]

All Tables

Table 1:   Polarization angle $\alpha _{\rm Sky}$ and polarized fraction $\Pi $ computed for different divisions of the data set.

Table 2:   Values of the polarization angle $\alpha _{\rm Sky}$ and of the polarization fraction $\Pi $.

All Figures

  \begin{figure} \par\includegraphics[width=8.3cm,clip]{13834fig1a.ps}\hspace*{1mm... ...s}\hspace*{1mm} \includegraphics[width=8.3cm,clip]{13834fig1d.ps} \end{figure} Figure 1:

Standard deviation maps for the Crab nebula intensity $\sigma (I)$ (top row) and polarized intensity $\sigma (P)$ (bottom row), in antenna temperature (K). $\sigma (I)$ and $\sigma (P)$ maps were computed using the 2CC and 2CX (see text) 39 maps (left column) and using the 28 2CC maps only (right panel). I and respectively P contours computed with the 28 2CC maps are overploted. We can see that when maps scanned along the $\alpha $ direction are added to the data set the standard deviation is higher and shows some features indicating an uncontrolled systematic effect.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.3cm,clip]{13834fig2a.ps}\hspace*{1mm... ...s}\hspace*{1mm} \includegraphics[width=8.5cm,clip]{13834fig2d.ps} \end{figure} Figure 2:

Maps of the Crab nebula at 89.189 GHz in antenna temperature (K) for intensity I (top-left), Q polarization (top-right), U polarization (bottom-left) and polarized intensity P (bottom-right). The position of the Crab nebula pulsar is indicated by the black cross.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13834fig3a.ps}\hspace*{1mm} \includegraphics[width=9cm,clip]{13834fig3b.ps} \end{figure} Figure 3:

(Left) Map of the polarization angle $\alpha _{\rm Sky}$ in degree on which contours of the polarized intensity P for 0.04, 0.08 and 0.16 K have been overploted. (Right) Map of the polarization fraction $\Pi $ on which has been displayed the intensity contour for 0.15, 0.30 and 0.45 K.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{13834fig4.ps} \vspace*{-3mm} \end{figure} Figure 4:

Map of the Crab nebula polarized intensity P at 89.189 GHz in antenna temperature on which polarization vectors have been overpolted. Intensity contours at 0.15, 0.30 and 0.45 K are also displayed.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.