TYC 2675-663-1: a newly discovered W UMa system in an active state

M. D. Caballero-García; G. Torres; I. Ribas; D. Rísquez; B. Montesinos; J. M. Mas-Hesse; A. Domingo

doi:10.1051/0004-6361/200913602

Home

All issues

Volume 514 (May 2010)

A&A, 514 (2010) A36

Full HTML

Free Access

Issue		A&A Volume 514, May 2010


Article Number		A36
Number of page(s)		10
Section		Stellar structure and evolution
DOI		https://doi.org/10.1051/0004-6361/200913602
Published online		07 May 2010

A&A 514, A36 (2010)

TYC 2675-663-1: a newly discovered W UMa system in an active state

M. D. Caballero-García¹ - G. Torres² - I. Ribas³ - D. Rísquez⁴ - B. Montesinos⁵ - J. M. Mas-Hesse⁵ - A. Domingo⁵

1 - University of Cambridge, Institute of Astronomy, Cambridge CB3 0HA, UK
2 - Harvard-Smithsonian Center for Astrophysics, 60 Garden St., Cambridge, MA 02138, USA
3 - IEEC (Institut d'Estudis Espacials de Catalunya), Edif. Nexus-104, Gran Capità 2-4, 08034 Barcelona, Spain
4 - Leiden Observatory, PO Box 9513, 2300 RA Leiden, The Netherlands
5 - CAB-LAEX (CSIC-INTA), ESAC Campus, PO Box 78, 28691 Villanueva de la Cañada, Madrid, Spain

Received 4 November 2009 / Accepted 27 January 2010

Abstract
Aims. The recently discovered eclipsing binary system TYC 2675-663-1 is an X-ray source and shows properties in the optical that are similar to the W UMa systems, but are somewhat unusual compared to what is seen in other contact binary systems. The goal of this work is to characterize its properties and investigate its nature by means of detailed photometric and spectroscopic observations.
Methods. We have performed extensive V-band photometric measurements with the INTEGRAL satellite along with ground-based multi-band photometric observations, as well as high-resolution spectroscopic monitoring, from which we have measured the radial velocities of the components. These data have been analyzed to determine the stellar properties, including the absolute masses and radii. Additional low-resolution spectroscopy was obtained to investigate spectral features.
Results. From the measured eclipse timings we determine an orbital period for the binary of $P = 0.4223576 \pm 0.0000009$ days. The light-curve and spectroscopic analyses reveal the observations to be well represented by a model of an overcontact system composed of main-sequence F5 and G7 stars (temperature difference of nearly 1000 K), with the possible presence of a third star. Low-resolution optical spectroscopy reveals a complex H $_{\alpha }$ emission and other features that are not yet understood. The unusually high mass ratio of $q=0.81 \pm 0.05$ places it in the rare ``H'' (high mass ratio) subclass of the W UMa systems, which are presumably on their way to coalescence.

Key words: binaries: close - stars: fundamental parameters - X-rays: stars

1 Introduction

The star TYC 2675-663-1 (Tycho-2 catalog designation; Høg et al. 2000), with coordinates $\alpha = 20^{\rm h} 09^{\rm m} 11.2^{\rm s}$ , ${\delta}=+32^{\circ} 33\hbox{$^\prime$ }53\hbox{$^{\prime\prime}$ }$ (J2000), was observed during 2002-2005 in the Johnson V filter with the Optical Monitoring Camera (OMC) on board the INTEGRAL satellite (Mas-Hesse et al. 2003), as a part of a serendipitous program to monitor optical counterparts of ROSAT sources as potential variable objects. By cross-correlating the list of variable sources detected with the OMC during the first few months of operation with the ROSAT catalogs, five were found that were potential optical counterparts of X-ray sources (i.e., which were inside the ROSAT 3 $\sigma$ position error radius; Caballero-García et al. 2006; Caballero 2004). Three of them showed optical variability with modulations characteristic of binary systems (periodic variations, with regular periods and amplitudes larger than 0.1 mag). TYC 2675-663-1 showed the most striking variability pattern, with very irregular and variable behavior.

The source, which has received the designation IOMC 2675000078 in the OMC Input Catalog (Domingo et al. 2003) displays a color index of $B - V \approx 0.7$ (Høg et al. 2000), corresponding roughly to spectral type G and shows variability typical of a close eclipsing binary system. Little further information is available for this star, aside from entries in various astrometric catalogs, so we undertook photometric and spectroscopic observations in order to ascertain the nature of the object and identify the origin of its X-ray emission.

We present a detailed study of TYC 2675-663-1. The photometric and spectroscopic observations are presented in Sect. 2, with a description of the data reduction procedures. Section 3 contains the analysis of these observations, including the determination of the ephemeris, the stellar parameters and distance to the system and a discussion of the peculiar H $_{\alpha }$ emission we detected. Finally, in Sect. 4 we discuss the results and the nature of the system.

2 Observations and data reduction

2.1 Photometry

2.1.1 INTEGRAL/OMC photometry

The Optical Monitoring Camera (OMC) is a 50 mm aperture refractor telescope, co-aligned with the high-energy instruments on board the ESA INTEGRAL gamma-ray observatory (Mas-Hesse et al. 2003). The OMC provides continuous monitoring of up to 100 sources in the Johnson V band over its $5^\circ \times 5^\circ$ field of view. Telemetry constraints do not permit downloading of the entire OMC image. For this reason, windows were selected around the proposed X-ray/ $\gamma$ -ray targets as well as other targets of interest in the same field of view. The position of these windows is computed automatically, based on the sources compiled in the OMC Input Catalog (Domingo et al. 2003), which contains around 500 000 targets selected for being potentially variable in the optical. Only sub-windows of the CCD containing those objects, with a size of $11 \times 11$ pixels ( $3.2\hbox{$^\prime$ }\times 3.2\hbox{$^\prime$ }$ ), are transmitted to the ground. TYC 2675-663-1 is located at only 14 $\hbox{$^{\prime\prime}$ }$ from the ROSAT source 1RXS J200912.0+323344 (contained in the ROSAT All-Sky Survey Bright Source Catalog, Voges et al. (1999), with a catalog 1 $\sigma$ position error of 8 $^{\prime\prime}$ ) and this allowed us to monitor it as a potential optical counterpart.

At each INTEGRAL pointing the OMC collects a set of images with several different integration times, typically in the range of 10 s to 200 s (currently 10, 50 and 200 s), for the purpose of optimizing the dynamic range and also to minimize noise and cosmic-ray effects. For the analysis of TYC 2675-663-1 we used only the images with exposures of 100 s and 200 s to secure an adequate signal-to-noise ratio for the observations. The brightness measurements used here were obtained with the Off-line Scientific Analysis software. We used a photometric aperture of $5\times 5$ pixels, since contamination by nearby sources was not significant (see Fig. 1). The complete folded light curve is shown in Fig. 2.

$\begin{figure} \par\includegraphics[width=8.7cm,clip]{13602f1.eps} \end{figure}$	Figure 1: Field of view of the INTEGRAL/OMC target TYC 2675-663-1 (red point) and the ROSAT source 1RXS J200912.0+323344 (blue circle) at its nominal catalog position.
Open with DEXTER

Table 1: Log of the observations used in this work.

$\begin{figure} \par\includegraphics[width=8.7cm,clip]{13602f2.eps} \end{figure}$	Figure 2: Complete INTEGRAL/OMC light curve folded with the period of $P = 0.4223576 \pm 0.0000009$ d and reference epoch T₀ = 2 453 080.0249 (time of inferior conjunction of the secondary).
Open with DEXTER

2.1.2 Photometry from the Centro de Astrobiología (CAB) 0.5 m telescope

Ground-based photometric observations were collected with the 0.5 m Giordano Bruno robotic telescope of the Centro de Astrobiología (hereafter CAB), located at Calar Alto, Spain. This telescope is equipped with a Finger Lakes Instrumentation IMG1024S $1024 \times 1024$ back-illuminated CCD and Johnson B and V filters. The camera has an image scale of 0.97 arcsec pixel^-1, which results in a field of view of $16\hbox{$^\prime$ }\times 16\hbox{$^\prime$ }$ . The exposure times were 30 s and 20 s for the B and V filters, respectively. All images were corrected for bias current and flat field. We derived differential photometry with respect to three comparison stars in the V filter (USNO B1 1224-0557970, 1224-0558767 and 1223-0560307) and an additional fourth comparison star in B (USNO B1 1224-0558836). This allowed us to obtain differential photometry for the source with errors less than 0.02 mag for both B and V.

Table 2: Measured times of mid-eclipse for TYC 2675-663-1, listed with their errors ( $\sigma$ ), cycle number (E) and O -C residuals from the adopted ephemeris.

Table 3: Radial velocities obtained for the primary (1) and the secondary components (2).

Table 4: Spectroscopic orbital parameters of TYC 2675-663-1.

2.1.3 Photometry from the Observatorio Astronómico Nacional (OAN) 1.52 m telescope

In order to obtain better photometric precision we carried out additional observations with the 1.52 m telescope at the Observatorio Astronómico Nacional, also located at Calar Alto (hereafter OAN). This telescope was equipped with a Photometrics Series 200 back-illuminated CCD and Johnson B, V and I filters. The camera has a scale of 0.4 arcsec pixel^-1, with a field of view of $6.9\hbox{$^\prime$ }\times 6.9\hbox{$^\prime$ }$ . The exposure times were 90, 60 and 30 s for the B, V and I filters, respectively. We applied standard bias and flat field corrections. Differential photometry was derived with respect to three comparison stars, selected from objects in the field with B -V indices similar to the target. These stars were USNO-B1 1225-0549546, 1225-0549756 and 1225-0549576, with magnitudes of B = 14.1, 15.5, 19.3, V = 13.45, 14.65, 18.0 and I = 12.7, 13.7, 16.8, respectively. We used a photometric aperture radius of 7'' for the target. The closest star to the target is located at 11'' (USNO B1 1225-0549559) and is fainter, thus its contribution to the flux of the target is expected to be negligible.

2.2 Spectroscopy

2.2.1 High-resolution spectroscopy

TYC 2675-663-1 was observed for this project with the CfA Digital Speedometer (Latham 1992) on the 1.5 m Tillinghast reflector at the Fred L. Whipple Observatory on Mount Hopkins, Arizona (USA). This echelle spectrograph coupled with its intensified photon-counting Reticon detector delivers a single echelle order 45 Å wide centered at a wavelength near 5187 Å and a resolving power of $R \approx 35~000$ . The main features in this spectral window are the lines of the Mg I b triplet. A total of 18 spectra were gathered between 23 Sep. 2004 and 5 Nov. 2006, with signal-to-noise ratios ranging from 14 to 30 per resolution element of 8.5 km s^-1. ThAr exposures were taken before and after each stellar exposure for wavelength calibration. The velocity zero-point was monitored by means of sky exposures taken at dusk and dawn.

2.2.2 Low-resolution spectroscopy

For a more detailed spectral coverage and to better study the spectral properties of the object, a three-hour sequence of observations of TYC 2675-663-1 was gathered also with the 3.5 m telescope at Calar Alto with the double-beam spectrograph TWIN, on 25 Jul. 2007 from 22:02:06 (UTC) to 26 Jul. 01:02:24 (UTC). The wavelength coverage is $\sim$ 4400 Å to 5500 Å and $\sim$ 6000 Å to 7100 Å for the blue and red channels, respectively. The spectral resolution of these observations is 0.54 Å pix^-1, or $\sim$ 25 and 32 km s^-1 in the blue and red channels, respectively. The exposure time for each spectrum was 600 s (resolution of 50 phase bins per orbital cycle). The median seeing was about 2 $\hbox{$^{\prime\prime}$ }$ . Dome flat fields and bias images were taken at the beginning of the night and comparison HeAr lamp spectra were taken regularly for wavelength calibration.

3 Data analysis

3.1 Ephemeris

An initial value of the period of TYC 2675-663-1 was derived with a method based on the Phase Dispersion Minimization algorithm of Stellingwerf (1978). In order to refine this period, we determined individual times of minimum from all our photometry data (INTEGRAL/OMC, CAB 0.5 m and OAN 1.52 m) by fitting each eclipse with a fourth degree polynomial. A total of 59 timings were obtained (21 primary eclipses and 38 secondary eclipses), which are listed in Table 2. These were then used to establish the final period and reference epoch by solving for a linear ephemeris using standard weighted least-squares techniques. Primary and secondary minima were adjusted simultaneously and the orbit was assumed to be circular. Given the asymmetry of the eclipses, realistic uncertainties for the individual timings are a bit difficult to determine. Instead, we assigned reasonable initial uncertainties by telescope and then adjusted them by iterations so as to achieve reduced $\chi^2$ values near unity separately for the minima from each data set. In this way we established realistic timing errors of 0.011 days, 0.012 days and 0.006 days for the INTEGRAL/OMC and the 0.5 m and 1.52 m telescopes, respectively. The resulting period and epoch are given by

P	=	$\displaystyle 0.4223576 \pm 0.0000009~{\rm days}$	(1)
T₀	=	$\displaystyle 2~453~080.0249 \pm 0.0014~({\rm HJD}),$	(2)

where the reference epoch T₀ was chosen to be close to the mean value of all the timings. We detected no sign of period changes over the 3.7-year interval and we adopt this ephemeris for the remainder of the paper.

3.2 Radial velocities and spectroscopic orbit

Radial velocities from our high-resolution spectra were determined with the two-dimensional cross-correlation algorithm TODCOR (Zucker & Mazeh 1994), with templates for each star selected from a library of synthetic spectra based on Kurucz (1992) model atmospheres. Template parameters (effective temperature, surface gravity, rotational velocity) were chosen to match the properties determined for the components in the following sections and solar metallicity was assumed throughout. Although the typical precision for the radial velocities of single sharp-lined stars with this instrumentation is about 0.5 km s^-1, in this case the performance is significantly degraded because of the very large broadening of the spectral lines (which we attribute to rotation) coupled with the narrow wavelength range (single echelle order) and the double-lined nature of the object, which combined introduce considerable line blending. We estimated individual errors around 25 km s^-1 for our measurements of the velocities of the primary and secondary components, which are however much smaller than the large variations we detected. These measurements are listed in Table 3. A circular Keplerian orbit was fit to these velocities, holding the period and epoch of primary eclipse fixed at the values determined earlier. The fit does not include proximity effects, given that the observations were obtained mostly at the quadratures where those effects are expected to be small (especially when compared to the observational errors). We adopted these elements to compute the absolute dimensions of the components. The resulting orbital parameters are given in Table 4 and the observations along with our best fit are depicted in Fig. 3.

3.3 Light curve fitting

In order to characterize the system and determine its physical properties, we analyzed the light curves, taking into account the information obtained from the spectroscopic solution just described. Modelling of the photometry was performed with the PHOEBE package (Prsa & Zwitter 2005) (version 29c), based on the Wilson-Devinney model (Wilson & Devinney 1971). The main adjustable parameters in this model are typically the inclination of the orbit (i), the (pseudo-)potentials ( $\Omega_1$ , $\Omega_2$ ), the luminosity of the primary (L₁) in each passband, the temperature of the secondary ( $T_{\rm eff,2}$ ) and a phase shift. The light curves alone do not provide any constraint on the absolute temperatures, but only on the temperature ratio through the depth of the eclipses. Therefore, the primary value $T_{\rm eff,1}$ was held fixed. We estimated the temperature of the primary star from the combined (V-K)color and estimates of the magnitude difference between the components derived from the light curves in an iterative way. The result is $T_{\rm eff,1} = 6480 \pm 180$ K, where the error is a conservative estimate based on the scatter of values found from the color in the iterative process of fitting the OAN light curves.

Limb-darkening coefficients were interpolated from the tables by van Hamme (1993) using the square-root law. The gravity brightening exponents (0.3 for both stars) and bolometric albedos (0.5) were fixed at the values appropriate for stars with convective envelopes (Lucy 1968). The mass ratio q and projected semimajor axis $a \sin i$ were adopted from the spectroscopy. Because of the higher quality of the BVI photometry from the 1.52 m OAN compared to that from the 0.5 m CAB and the relatively short time span of the OAN observations that makes them less vulnerable than the INTEGRAL/OMC photometry to variability in the light curve, as described below, we used only the OAN data in the following to determine the light curve parameters. The three passbands were fitted simultaneously. The INTEGRAL/OMC measurements were used as a consistency check.

It is obvious from the light curves (Fig. 4) that the shape of the modulation changes continuously with phase, as in the classical W UMa systems, with no clear beginning or ending of the eclipses. This strongly suggests significant deformation of the components and perhaps some degree of contact. Consequently, we performed fits in both the semidetached mode (mode 4 in the Wilson-Devinney nomenclature, with the primary filling its Roche lobe) and also in the overcontact mode (mode 3), which is appropriate for W UMa-type systems and overcontact systems that are not in thermal contact. In the former case the potential of the primary was set to the value of its Roche lobe potential for the adopted mass ratio ( $q=0.81 \pm 0.05$ ): $\Omega_1 = 3.43 \pm 0.08$ . In the overcontact mode the potentials were constrained to be the same, but we did not force thermal contact, in other words, the surface brightness of the two stars can be different even though they might be in geometrical contact.

Initial solutions indicated a secondary temperature $T_{\rm eff,2}$ in the range of 5100-5700 K, but also gave rather low values of the inclination angle ( $\approx$ 57 deg) as a result of the relatively shallow eclipses, leading to absolute masses of $M_1 \approx 1.62~M_{\odot}$ and $M_2 \approx 1.31~M_{\odot}$ . Such large masses, which are typical of late A- and mid F-type stars, respectively, would imply temperatures that are considerably higher than we estimate based on the colors (see above). Experiments in which we included third light ( $\ell_3$ ) in our solutions revealed that it is statistically different from zero (> $3\sigma$ ), providing a plausible explanation. We obtained $\ell_3$ values of 2-3% in B, 3-4% in V and 4-5% in I, which suggests a red object contaminating the photometry. These solutions yielded considerably higher inclinations, as expected, by about 5-9 $^{\circ}$ . We did not see any clear evidence of a third star in our CfA or TWIN spectra, although the spectroscopic material is inadequate to detect such faint signatures, so it does not rule them out. Below we chose to include third light in our light curve modelling, on the basis that it is statistically significant and provides for a more consistent overall solution.

$\begin{figure} \par\includegraphics[width=8cm,clip]{13602f3.eps} \end{figure}$	Figure 3: CfA radial velocity measurements of TYC 2675-663-1 along with our best-fit model, folded with the period $P = 0.4223576 \pm 0.0000009$ d and $T_0~{\rm (HJD)} = 2~453~080.0249 \pm 0.0014$ (corresponding to phase 0.0).
Open with DEXTER

There are abundant signs of chromospheric activity in TYC 2675-663-1, manifested in the form of an occasional O'Connell effect, irregular shapes of the minima and occasional flares (see Fig. 4). There is also significant variability in the shape of the light curves, on typical timescales of a few weeks. The O'Connell effect is apparent in the different light levels at the quadratures ( $\Delta V$ , $\Delta B \approx 0.1$ mag) and its reality is demonstrated by the fact that it is seen in the light curves from the 0.5 m CAB telescope (not shown) during one of the same time intervals covered by the INTEGRAL/OMC photometry (Fig. 4), thus ruling out instrumental errors. This strongly suggests spottedness in one or both stars, which must be considered in order to avoid biases in the geometric elements. PHOEBE allows the spot effects to be modelled by assuming one or more uniform-temperature circular features parametrized by four additional adjustable variables: the longitude, colatitude, angular size and temperature contrast factor ( $T_{\rm spot}/T_{\rm star}$ ). However, because of well-known degeneracies in fitting for spot parameters from light curves (see, e.g., Eker 1999,1996) and the poor quality of our observations, it is impossible to discern precisely and unambiguously where the spots are in this system. For this work we arbitrarily chose to place a single spot on the secondary star, and we chose its location to be near the pole (colatitude $b = 20^{\circ}$ ), on the grounds that similar locations are often seen in other active and rapidly-rotating stars studied, e.g., with Doppler imaging techniques (see, e.g. Strassmeier 2009 and references therein). We also fixed the temperature contrast factor to $T_{\rm spot}/T_{\rm star} = 0.80$ , a value similar to that used in other studies. Experiments with a spot location near the equator produced fits of about the same quality and also gave similar values for all geometric and radiative quantities, within the errors. The fits converged to a large spot covering $\sim$ 20% of the surface of the secondary star.

Solutions with third light and spots using the OAN photometry were carried out both in the semi-detached mode and in the overcontact mode. The fits consistently indicated contact between the components and a slight preference for the overcontact configuration, but gave otherwise very similar results for all parameters, the differences being well within the errors. As seen in Table 5 the potentials of the two components in the semi-detached solution appear nearly identical (within the errors) and are equal to those from the overcontact solution. This agrees with the definition of the overcontact mode, in which the components have the same potentials. Therefore we adopted in the following the overcontact results. These solutions are presented in Table 5 and are shown in Fig. 5 together with the OAN photometry. The values of the parameters correspond to the results from simultaneously fitting the B, V and I light curves and the errors represent the dispersion of the solution with respect those from fits of the monochromatic light curves. A graphical representation of the configuration of the system and the location of the spot is shown in Fig. 6.

As a consistency check, we produced an additional fit with the INTEGRAL/OMC data in the adopted overcontact mode. However, because of the longer time coverage of these data compared to the OAN light curves and the significant spot variability on relatively short timescales, we did not consider spots in this solution (i.e., this is not an optimized fit and not our adopted fit). For the purpose of comparison, we fitted the same spotless model to the OAN light curves, and the results are listed in Table 6. There is very good agreement between the two data sets despite the simplified modelling. This solution is over-plotted with the INTEGRAL/OMC data in Fig. 4. A comparison for the OAN data between the spotted model in Table 5 and the unspotted model in Table 6 shows that the differences are rather small and that thus the absolute dimensions of TYC 2675-663-1 are unlikely to be much affected by the uncertainties in the spot modelling.

$\begin{figure} \par\mbox{\includegraphics[width=7.2cm,clip]{13602f4.eps}\hspace... ...s}\hspace{1mm} \includegraphics[width=7.2cm,clip]{13602f11.eps} }\end{figure}$	Figure 4: INTEGRAL/OMC light curve of TYC 2675-663-1 in the Johnson V band, folded with the adopted ephemeris. Separate time intervals are shown to illustrate the changes in shape due to activity ( from upper-left to lower-right). The superimposed curves (red) represent a fit without accounting for spots (see text), shown here only for reference.
Open with DEXTER

Table 5: Light curve solutions based on the OAN photometry, for an overcontact and semi-detached configuration.

$\begin{figure} \par\includegraphics[width=8cm,clip]{13602f12.eps} \includegrap... ...ip]{13602f13.eps} \includegraphics[width=8cm,clip]{13602f14.eps} \end{figure}$	Figure 5: Light curves of TYC 2675-663-1 obtained with the OAN telescope in the V, B and I bands ( top to bottom), folded according to the adopted ephemeris. This photometry is strictly differential (magnitudes shown have an arbitrary zero point). The curves represent our best-fit solution for an overcontact configuration, including the effect of spots.
Open with DEXTER

$\begin{figure} \vspace*{-1.5cm} \includegraphics[width=8cm,clip]{13602f15.eps} ... ...ip]{13602f16.eps} \includegraphics[width=8cm,clip]{13602f17.eps} \end{figure}$	Figure 6: Configuration of the system at different phases, showing the location of the spot on the secondary. From top to bottom, the phases are approximately 0.00, 0.25 and 0.75. The size and separation of the stars are rendered to scale.
Open with DEXTER

Table 6: Light curve solutions without accounting for spot effects, based on the INTEGRAL/OMC and OAN photometry.

Table 7: Absolute dimensions of TYC 2675-663-1.

3.4 Absolute dimensions

The combination of the light curve and spectroscopic parameters leads to the physical properties of the system presented in Table 7. The temperature difference between the stars is $\sim$ 940 K and the individual values correspond to spectral types of approximately F5 and G7 for the primary and secondary, respectively. Using these individual temperatures, we inferred bolometric corrections BC_V of -0.032^+0.009_-0.019 and -0.149^+0.080_-0.005 for the primary and secondary stars, respectively, based on the tabulations by Masana et al. (2006). The errors were propagated from the temperature uncertainties. With the bolometric magnitudes that follow from the temperatures and radii, we derive absolute visual magnitudes M_V of 3.84^+0.20_-0.22and 4.84_-0.60^+0.08. The magnitude difference agrees well with the value inferred from the flux ratio between the components from the fits (i.e., $M_{V~2} - M_{V~1} = 2.5 \log(L_{1}/L_{2}) = 0.96^{+0.16}_{-0.15}$ ; see Table 5).

The apparent visual magnitudes of the primary and secondary follow from the out-of-eclipse brightness and the light ratio and are $11.80 \pm 0.08$ and $12.80 \pm 0.08$ , respectively. With a visual extinction estimate of A(V) = 0.2 from Drimmel et al. (2003) and the absolute magnitudes given above, we infer a distance to the binary system of D = 360⁺¹³⁰_-50 pc.

3.5 X-ray emission

The sky position of the optical source TYC 2675-663-1 is 14 $^{\prime\prime}$ far from the ROSAT source 1RXS J200912.0+323344, which has a 1 $\sigma$ positional uncertainty of 8 $^{\prime\prime}$ (Voges et al. 1999). This implies a formal coincidence likelihood between the optical and the X-ray locations of <13%. The reality of this X-ray source is confirmed by its detection by the XMM-Newton satellite (under the designation XMMSL1 J200910.0+323358) at similar coordinates as the ROSAT source (Freyberg et al. 2006) and with a similar positional uncertainty. The count rate and hardness ratio of the source measured by ROSAT are $0.123 \pm 0.016$ counts s^-1 and $0.82 \pm 0.08$ , respectively. This translates to an integrated flux of $1.56 \times 10^{-12}$ erg s^-1cm^-2 in the 0.1-2.4 keV energy band (Schmitt et al. 1995). Assuming a distance to the source of D=360_-50⁺¹³⁰ pc then gives an intrinsic luminosity of $L_{X} = (2.4_{-0.6}^{+2.1}) \times 10^{31}$ erg s^-1. Considering the bolometric luminosities of the components of $L_{\rm bol} = 2.4^{+0.5}_{-0.4}$ $L_{\odot}$ and $1.04^{+0.6}_{-0.07}~L_{\odot}$ for the primary and the secondary, we derived an X-ray to total luminosity ratio of $\log L_X/L_{\rm bol} = -2.74^{+0.24}_{-0.40}$ , which is typical of binary systems with rotationally induced activity (see, e.g., Messina et al. 2003).

3.6 Analysis of spectroscopic features

Figures 7 and 8 display the sequence of 14 normalized low-resolution spectra from the TWIN spectrograph in the range from 4800 to 4950 Å and from 6400 to 6700 Å, showing the most interesting features. Among the most prominent are the strong Balmer lines in emission (H $_{\alpha }$ and H $_\beta$ at $\lambda = 6563$ Å and 4861 Å, respectively) and the He I line centered at 6680 Å. The H $_{\alpha }$ emission is complex and is discussed below.

In the red spectra (Fig. 8) there is a clear absorption feature at around 6490 Å. If this has a photospheric origin, it is likely to be a blend composed mainly of Ti II, Ca I, Fe I and Ba II lines, which are the ones with the largest oscillator strengths in this spectral range. To illustrate this we show in Fig. 9 the synthetic spectrum of a star similar to the primary component of TYC 2675-663-1 ( $T_{\rm eff} \sim 6000$ K, $\log g = 4.0$ , $v \sin i = 0$ km s^-1 and an assumed [M/H] = 0.0), together with the result of applying a rotational broadening of 144 km s^-1, which is our estimate for the primary star assuming spin-orbit synchronization. This washes out the narrow lines, producing a single broad feature, as observed. The steady character of this broad absorption suggests its origin in a third star, perhaps a distant companion to the binary system. This may perhaps explain the third light contribution inferred from the fits of the light curves in Sect. 3.3. Nevertheless, more complete spectroscopic observations are needed to confirm the likely stellar origin of this absorption complex.

$\begin{figure} \par\includegraphics[width=8cm,clip]{13602f18.eps} \end{figure}$	Figure 7: Blue spectra of TYC 2675-663-1 obtained with the TWIN spectrograph (4800-4950 Å) showing the H $_\beta$ emission complex centered at $\lambda _0 = 4861$ Å. Orbital phases for each spectrum are as indicated in Fig. 8.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{13602f19.eps} \end{figure}$	Figure 8: Red spectra of TYC 2675-663-1 obtained with the TWIN spectrograph (6400-6700 Å) showing the prominent H $_{\alpha }$ and He I emission features centered at $\lambda _0 = 6563$ Å and $\lambda _0 = 6680$ Å, respectively. In this figure the wavelength shift due to the orbital motion of the components is approximately 4 Å. Orbital phases are labelled.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{13602f20.eps} \end{figure}$	Figure 9: Synthetic spectrum corresponding to a star similar to the primary of TYC 2675-663-1, with $T_{\rm eff} \approx 6000$ K, $\log g = 4.0$ , [M/H] = 0.0, and no rotational broadening (red line). Superimposed is the same spectrum broadened with a rotation profile of 144 km s^-1 (black line), estimated for the primary in TYC 2675-663-1.
Open with DEXTER

3.6.1 The H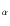 $_{\alpha }$ emission line

Very broad H $_{\alpha }$ emission ( ${\Delta v} \approx 1200$ km s^-1) is detected in the spectra of this binary system. Phenomenologically, the H $_{\alpha }$ complex can be described by the presence of what appear to be two broad and asymmetric emission lines centered at 6553 Å and 6568 Å, plus a steady absorption dip between them (P-Cygni profile). This emission has a complicated structure with several components that seem to be moving with orbital phase. In order to better understand this complex evolution with phase we fitted the profile with additional components. After trying a number of different combinations, we found that the behavior of the H $_{\alpha }$ region of the spectrum can be adequately described with five components (see Figs. 10 and 11): one in absorption and four in emission. The absorption line (line 5) is steady, with a radial velocity of $RV \approx -200$ km s^-1.

Similar outflows were associated with stellar winds in high mass or post-AGB stars (Varricatt et al. 2004; Chaty & Filliatre 2005), with velocities similar to those we found (e.g., -105 km s^-1; Smolinski et al. 1993). However, for the present binary system TYC 2675-663-1, which is composed of two main sequence stars of late spectral type (and likely a third star of similar or later spectral type), the absorption is unlikely to be due to stellar winds. Its nature is presently unclear.

In Fig. 11 two of the Gaussian components (lines 3 and 4) appear to follow the orbital motion of the primary star, with a maximum velocity excursion at quadrature ( $\phi = 0.25$ ). The velocities at quadrature are $RV \approx 150$ km s^-1 and $RV \approx 575$ km s^-1, respectively. Given the previously measured orbital semiamplitudes of $153 \pm 6$ km s^-1 and $189 \pm 7$ km s^-1 for the primary and secondary, respectively, we tentatively identify line 3 with the surface of the primary star. The emission represented by line 4 comes from a region that is moving three to four times faster. Elucidating the origin of these wings and the absorption feature of the H $_{\alpha }$ complex will most likely require further spectroscopic observations that are beyond the scope of the present work, to obtain complete phase coverage over a full orbital cycle.

$\begin{figure} \par\includegraphics[width=8cm,clip]{13602f21.eps} \end{figure}$	Figure 10: Enlarged view of the H $_{\alpha }$ complex from Fig. 8, with our 5-component fits (one absorption component and four emission components; see text). Orbital phases are labelled.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{13602f22.eps} \end{figure}$	Figure 11: Radial velocity variation of each line component fitted to the H $_{\alpha }$ complex in Fig. 10 as a function of orbital phase. The red line represents the absorption component and the other four lines are in emission (see text).
Open with DEXTER

4 Discussion

Our analysis of the close eclipsing binary TYC 2675-663-1 revealed properties similar in many respects to those of the W UMa systems, which are characterized by having short orbital periods (0.2-0.8 d) and an overcontact configuration and are composed of F-K stars sharing a common envelope that thermalizes the stars. This leads to near equal depths for the eclipses. TYC 2675-663-1 displays eclipses with clearly different depths, which would imply non-thermal equilibrium. Nevertheless, the stars have spectral types of F5 and G7 in the typical range of W UMa class and appear to be in geometrical contact despite the temperatures being different by approximately 940 K. The high mass ratio we derive, $q \equiv M_2/M_1 = 0.81 \pm 0.05$ , identifies the object as an H-type W UMa variable (``H'' for high mass ratio), a subgroup first proposed by Csizmadia et al. (2004). In these objects the energy transfer rate appears to be less efficient than in other types of contact binaries. They also show excess angular momentum, which can be understood as resulting from the first stages of the interaction between the components (see Li et al. 2004, and references therein). The overall properties of TYC 2675-663-1 suggest a system at or near contact and perhaps in the early stages of evolution toward a state of full geometrical and thermal contact (coalescence).

W UMa systems such as the binary studied here typically show increased chromospheric activity due to the rapid rotation of the components (Applegate 1992) and this is usually accompanied by soft X-ray emission (Messina et al. 2003). This chromospheric activity is manifested by the unequal brightness at quadratures, asymmetrical minima and erratic flares shown in the light curves, which are collectively referred to as the O'Connell effect. TYC 2675-663-1 shows clear evidence of each of these, including the X-ray emission. The presence of the He I $\lambda 6680$ Å emission line, as we see in the spectra ofTYC 2675-663-1, is often interpreted as evidence of the interaction between the components of the binary system, in the form of winds or streams of matter (Graham 1992; Scholz & Jayawardhana 2006; Greeley et al. 1999; Takami et al. 2001). The H $_{\alpha }$ region of the spectrum is complex, with emission and absorption components that are not yet fully understood.

Our spectroscopic and photometric observations of TYC 2675-663-1 provided a first picture of this close binary system, in which the two stars differ greatly in temperature, but are in a near-contact configuration, perhaps leading to coalescence. It appears to be a rare example of this class of W UMa objects. There is circumstantial evidence for a third star in the system. We hope that this study will be helpful in the development of theories to understand the early behavior and evolution of W UMa systems.

Acknowledgements

We are grateful to the referee, A. Prsa, for very helpful comments. M.C.G. thanks K. Yakut for very useful discussions and F. Vilardell for providing the table of the critical potentials. OMC has been funded by the Spanish MCyT under grants ESP95-0389-C02-02, ESP2002-04124-C03-01, ESP2005-07714-C03-03 and AYA2008-03467/ESP. We thank David Galadi and Teresa Eibe for the data taken at the CAB Giordano Bruno telescope. This research was partially supported by the MCyT under grant PNE2003-04352. This work is based on observations made with INTEGRAL, an ESA science mission with instruments and science data center funded by ESA member states and with the participation of Russia and the USA. We are grateful to the Calar Alto Observatory for allocation of Director's discretionary time to this program.

References

Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
Caballero, M. D. 2004, Proceedings to the 5th INTEGRAL Workshop on the INTEGRAL Universe, ed. V. Schoenfelder, G. Lichti, & C. Winkler, ESA SP 552, 875 [Google Scholar]
Caballero-García, M. D., Domingo, A., Rísquez, D., et al. 2006 Proceedings to the The X-ray Universe 2005, ed. A. Wilson, 604, 249 [Google Scholar]
Csizmadia, S., & Klagyivik, P. 2004, A&A, 426, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, The IRSA 2MASS All-Sky Point Source Catalog, NASA/IPAC Infrared Science Archive [Google Scholar]
Domingo, A., Caballero, M. D., Figueras, F., et al. 2003, A&A, 411, L281D [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Drimmel, R., Cabrera-Lavers, A., & López-Corredoira, M. 2003, A&A, 409, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Eker, Z. 1996, ApJ, 473, 388 [NASA ADS] [CrossRef] [Google Scholar]
Eker, Z. 1999, ApJ, 512, 386 [NASA ADS] [CrossRef] [Google Scholar]
Chaty, S., & Filliatre, P. 2005, Ap&SS, 297, 235C [NASA ADS] [CrossRef] [Google Scholar]
Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
Freyberg, M. J., Altieri, B., Bermejo, D., et al. 2006, Proceedings to the The X-ray Universe 2005, ed. A. Wilson, 604, 913 [Google Scholar]
Graham, J. A. 1992, PASP, 104, 479G [NASA ADS] [CrossRef] [Google Scholar]
Greeley, B. W., Blair, W. P., Long, K. S., et al. 1999, ApJ, 513, 491 [NASA ADS] [CrossRef] [Google Scholar]
Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
Li, L., Han, Z., & Zhang, F. 2004, MNRAS, 355, 1383 [Google Scholar]
Latham, D. W. 1992, in Complementary Approaches to Double and Multiple Star Research, IAU Coll. 135, ed. H. A. McAlister, & W. I. Harkopf (San Francisco: ASP), ASP Conf. Ser., 32, 110 [Google Scholar]
Lucy, L. B. 1968, ApJ, 153, 877 [NASA ADS] [CrossRef] [Google Scholar]
Masana, E., Jordi, C., & Ribas, I. 2006, A&A, 450, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mas-Hesse, J. M., Giménez, A., Culhane, J. L., et al. 2003, A&A, 411, L261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Messina, S., Pizzolato, N., Guinan, E. F., et al. 2003, A&A, 410, 671M [CrossRef] [EDP Sciences] [Google Scholar]
Prsa, A., & Zwitter, T. 2005, ApJ, 628, 426 [NASA ADS] [CrossRef] [Google Scholar]
Scholz, A., & Jayawardhana, R. 2006, ApJ, 638, 1056 [NASA ADS] [CrossRef] [Google Scholar]
Schmitt, J. H. M. M., Fleming, T. A., & Giampapa, M. S. 1995, ApJ, 450, 392 [NASA ADS] [CrossRef] [Google Scholar]
Smolinski, J., Climenhaga, J. L., Huang, Y., et al. 1993, Space Sci. Rev., 66, 231 [NASA ADS] [CrossRef] [Google Scholar]
Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]
Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
Takami, M., Bailey, J., Gledhill, T. M., Chrysostomou, A., & Hough, J. H. 2001, MNRAS, 323, 177 [NASA ADS] [CrossRef] [Google Scholar]
van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] [Google Scholar]
Varricatt, W. P., Williams, P. M., Ashok, N. M., et al. 2004, MNRAS, 351, 1307 [NASA ADS] [CrossRef] [Google Scholar]
Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
Zucker, S., & Mazeh, T. 1994, ApJ, 420, 806 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]

Footnotes

... software: Available in the web: http://isdc.unige.ch/?Soft+download
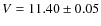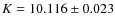...)color: We adopted $V = 11.40 \pm 0.05$ and $K = 10.116 \pm 0.023$ , where V comes from the mean INTEGRAL/OMC standard magnitude out of eclipse (similar to the Johnson V magnitude). The corresponding uncertainty is a conservative estimate based on the short period variations of the light curve over timescales of a few weeks (less affected by stellar activity, although those effects are still present, as seen in Fig. 4). The K magnitude is taken from the 2MASS catalog (Cutri et al. 2003). We also adopted reddening corrections of E(V - K) = 0.16 and E(B - V) = 0.065, as well as A(V) = 0.2 (Fitzpatrick 1999). 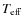The temperature is based on the (V-K)- $T_{\rm eff}$ relationship from Masana et al. (2006).
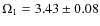
... $\Omega_1 = 3.43 \pm 0.08$: The corresponding secondary Roche lobe potential is 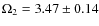$\Omega_2 = 3.47 \pm 0.14$ , assuming synchronous rotation.
... uncertainty: The quoted positions in the slew catalog have a 1 sigma error of 8 $\hbox{$^{\prime\prime}$ }$ , which for point sources is dominated by the accuracy of the attitude reconstruction during the slews. The statistical position error quoted in the catalog has a mean of $\sim$ 4 $\hbox{$^{\prime\prime}$ }$ (1 image pixel) for non-extended sources.

Copyright ESO 2010

All Tables