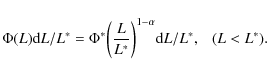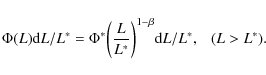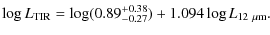EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 514 (May 2010) A&A, 514 (2010) A6 Full HTML
Science with AKARI
Free Access
Issue
A&A
Volume 514, May 2010
Science with AKARI
Article Number A6
Number of page(s) 12
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/200913182
Published online 03 May 2010
A&A 514, A6 (2010)

Science with AKARI

Evolution of infrared luminosity functions of galaxies in the AKARI NEP-deep field

Revealing the cosmic star formation history hidden by dust[*],[*]

T. Goto1,2,[*] - T. Takagi3 - H. Matsuhara3 - T. T. Takeuchi4 - C. Pearson5,6,7 - T. Wada3 - T. Nakagawa3 - O. Ilbert8 - E. Le Floc'h9 - S. Oyabu3 - Y. Ohyama10 - M. Malkan11 - H. M. Lee12 - M. G. Lee12 - H. Inami3,13,14 - N. Hwang2 - H. Hanami15 - M. Im12 - K. Imai16 - T. Ishigaki17 - S. Serjeant7 - H. Shim12

1 - Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI, 96822, USA
2 - National Astronomical Observatory, 2-21-1 Osawa, Mitaka, Tokyo, 181-8588, Japan
3 - Institute of Space and Astronautical Science, Japan Aerospace Exploration Agency, Sagamihara, Kanagawa 229-8510, Japan
4 - Institute for Advanced Research, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8601, Japan
5 - Rutherford Appleton Laboratory, Chilton, Didcot, Oxfordshire OX11 0QX, UK
6 - Department of Physics, University of Lethbridge, 4401 University Drive,Lethbridge, Alberta T1J 1B1, Canada
7 - Astrophysics Group, Department of Physics, The Open University, Milton Keynes, MK7 6AA, UK
8 - Laboratoire d'Astrophysique de Marseille, BP 8, Traverse du Siphon, 13376 Marseille Cedex 12, France
9 - CEA-Saclay, Service d'Astrophysique, France
10 - Academia Sinica, Institute of Astronomy and Astrophysics, Taiwan
11 - Department of Physics and Astronomy, UCLA, Los Angeles, CA, 90095-1547, USA
12 - Department of Physics & Astronomy, FPRD, Seoul National University, Shillim-Dong, Kwanak-Gu, Seoul 151-742, Korea
13 - Spitzer Science Center, California Institute of Technology, Pasadena, CA 91125, USA
14 - Department of Astronomical Science, The Graduate University for Advanced Studies, Hayama, Miura, Kanagawa, 240-0193, Japan
15 - Physics Section, Faculty of Humanities and Social Sciences, Iwate University, Morioka, 020-8550, Japan
16 - TOME R&D Inc. Kawasaki, Kanagawa 213 0012, Japan
17 - Asahikawa National College of Technology, 2-1-6 2-jo Shunkohdai, Asahikawa-shi, Hokkaido 071-8142, Japan

Received 26 August 2009 / Accepted 23 December 2009

Abstract
Aims. Dust-obscured star-formation increases with increasing intensity and increasing redshift. We aim to reveal the cosmic star-formation history obscured by dust using deep infrared observation with AKARI.
Methods. We constructed restframe 8 ${\mu }$m, 12 ${\mu }$m, and total infrared (TIR) luminosity functions (LFs) at 0.15<z<2.2 using 4128 infrared sources in the AKARI NEP-deep field. A continuous filter coverage in the mid-IR wavelength (2.4, 3.2, 4.1, 7, 9, 11, 15, 18, and 24 ${\mu }$m) by the AKARI satellite allowed us to estimate restframe 8 ${\mu }$m and 12 ${\mu }$m luminosities without using a large extrapolation based on an SED fit, which was the largest uncertainty in previous work.
Results. We find that all 8 ${\mu }$m ( 0.38<z<2.2), 12 ${\mu }$m ( 0.15<z<1.16), and TIR LFs (0.2<z<1.6) show continuous and strong evolution toward higher redshift. Our direct estimate of 8 ${\mu }$m LFs is useful since previous work often had to use a large extrapolation from the Spitzer 24 ${\mu }$m to 8 ${\mu }$m, where SED modeling is more difficult because of the PAH emissions. In terms of cosmic infrared luminosity density ( $\Omega_{\rm IR}$), which was obtained by integrating analytic fits to the LFs, we find good agreement with previous work at z<1.2. We find the $\Omega_{\rm IR}$ evolves as  ${\propto}(1+z)^{4.4\pm 1.0}$. When we separate contributions to  $\Omega_{\rm IR}$by LIRGs and ULIRGs, we found more IR luminous sources are increasingly more important at higher redshift. We find that the ULIRG (LIRG) contribution increases by a factor of 10 (1.8) from z = 0.35 to z = 1.4.

Key words: infrared: galaxies - galaxies: luminosity function, mass function - galaxies: evolution - galaxies: high-redshift - galaxies: formation - galaxies: starburst

1 Introduction

Studies of the extragalactic background suggest at least half the luminous energy generated by stars has been reprocessed into the infrared (IR) by dust (Franceschini et al. 2008; Lagache et al. 1999; Puget et al. 1996), suggesting that dust-obscured star formation was much greater at higher redshifts than today.

Bell et al. (2005) estimate that IR luminosity density is 7 times higher than the UV luminosity density at z $\sim$ 0.7 than locally. Takeuchi et al. (2005) report that UV-to-IR luminosity density ratio, $\rho_{L({\rm UV})}/\rho_{L({\rm dust})}$, evolves from 3.75 (z=0) to 15.1 by z=1.0 with careful treatment of the sample selection effect and that 70% of star formation activity is obscured by dust at 0.5<z<1.2. Both works highlight the importance of probing cosmic star formation activity at high redshift in the infrared bands. Several works have found that most extreme star-forming (SF) galaxies, which are increasingly important at higher redshifts, are also more heavily obscured by dust (Hopkins et al. 2001; Sullivan et al. 2001; Buat et al. 2007).

Despite the value of infrared observations, studies of infrared galaxies by the IRAS and the ISO were restricted to bright sources because of limited sensitivity (Takeuchi et al. 2003; Rowan-Robinson et al. 1997; Takeuchi et al. 2006; Serjeant et al. 2004; Saunders et al. 1990; Flores et al. 1999), until the recent launch of the Spitzer and the AKARI satellites. Their enormously improved sensitivities have revolutionized the field, as seen in the following.

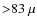  • Le Floc'h et al. (2005) analyzed the evolution of the total and 15 ${\mu }$m IR luminosity functions (LFs) at 0<z<1 based on the the Spitzer MIPS 24 ${\mu }$m data (${>}83~\mu$Jy and R<24) in the CDF-S, and find a positive evolution in both luminosity and density, suggesting the increasing importance of the LIRG and ULIRG populations at higher redshifts.

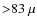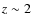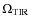  • Pérez-González et al. (2005) use MIPS 24 ${\mu }$m observations of the CDF-S and HDF-N (${>}83~\mu$Jy) to find that L* steadily increases by an order of magnitude to $z\sim 2$, suggesting that the luminosity evolution is stronger than the density evolution. The  $\Omega _{\rm TIR}$ scales as (1+z) 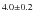$^{4.0\pm 0.2}$ from z=0 to 0.8.

  • Babbedge et al. (2006) construct LFs at 3.6, 4.5, 5.8, 8, and 24 ${\mu }$m over 0<z<2 using the data from the Spitzer wide-area infrared extragalactic (SWIRE) survey in a 6.5 deg2 ( 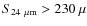$S_{24~\mu{\rm m}}>230~\mu$Jy). They find a clear luminosity evolution in all the bands, but the evolution is more pronounced at longer wavelength. Extrapolating from 24 ${\mu }$m, they inferred that 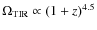$\Omega_{\rm TIR}\propto (1+z)^{4.5}$. They constructed separate LFs for three different galaxy spectral energy distribution (SED) types and type 1 AGN, finding that starburst and late-type galaxies showed stronger evolution. Comparison of 3.6 and 4.5 ${\mu }$m LFs with semi-analytic and spectrophotometric models suggests that the IMF is skewed towards higher mass star formation in more intense starbursts.

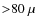  • Caputi et al. (2007) estimate restframe 8 ${\mu }$m LFs of galaxies over 0.08 deg2 in the GOODS fields based on Spitzer 24 ${\mu }$m (${>}80~\mu$Jy) at z=1 and 2. They find a continuous and strong positive luminosity evolution from z=0 to z=1, and to z=2. However, they also find that the number density of SF galaxies with 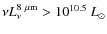$\nu L_{\nu}^{8~\mu{\rm m}}>10^{10.5}~L_{\odot}$ (AGNs are excluded) increases by a factor of 20 from z=0 to 1, but decreases by half from z=1 to 2 mainly from the decrease in LIRGs.

  • Magnelli et al. (2009) investigated restframe 15 ${\mu }$m, 35 ${\mu }$m, and total infrared (TIR) LFs using deep 70 ${\mu }$m observations ($\sim$300 ${\mu }$Jy) in the Spitzer GOODS and FIDEL (Far Infrared Deep Extragalactic Legacy Survey) fields (0.22 deg2 in total) at z<1.3. They stacked 70 ${\mu }$m flux at the positions of 24 ${\mu }$m sources when sources are not detected in 70 ${\mu }$m. 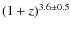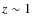They find no change in the shape of the LFs, but find a pure luminosity evolution proportional to $(1+z)^{3.6\pm 0.5}$, and find that LIRGs and ULIRGs have increased by a factor of 40 and 100 in number density by $z\sim 1$.

    Also, see Dai et al. (2009) for 3.6-8.0 ${\mu }$m LFs based on the IRAC photometry in the NOAO deep wide-field survey Bootes field.

However, most of the Spitzer work has relied on a large extrapolation from 24 ${\mu }$m flux to estimate the 8, 12 ${\mu }$m, or TIR luminosity. Consequently, Spitzer results heavily depended on the assumed IR SED library (Dale & Helou 2002; Lagache et al. 2003; Chary & Elbaz 2001). Indeed many authors point out that the largest uncertainty in these previous IR LFs comes from SED models, especially when one computes TIR luminosity solely from observed 24 ${\mu }$m flux (e.g., see Fig. 5 of Caputi et al. 2007).

AKARI, the first Japanese IR dedicated satellite, has continuous filter coverage across the mid-IR wavelengths, allowing us to estimate mid-infrared (MIR)-luminosity without using a large k-correction based on the SED models, therefore eliminating the largest uncertainty in previous work. By taking advantage of this, we present the restframe 8, 12 ${\mu }$m, and TIR LFs using the AKARI NEP-deep data in this work.

Restframe 8 ${\mu }$m luminosity in particular is relevant for SF galaxies, as it includes polycyclic aromatic hydrocarbon (PAH) emission. PAH molecules characterize SF regions (Desert et al. 1990), and the associated emission lines between 3.3 and 17 ${\mu }$m dominate the SED of SF galaxies with a main bump located around 7.7 ${\mu }$m. Restframe 8 ${\mu }$m luminosities have been confirmed as good indicators of knots of star formation (Calzetti et al. 2005) and of the overall star formation activity of SF galaxies (Wu et al. 2005). At z = 0.375, 0.875, 1.25 and 2, the restframe 8 ${\mu }$m is covered by the AKARI S11, L15,L18W and L24 filters. We present the restframe 8 ${\mu }$m LFs at these redshifts at Sect. 3.1.

Restframe 12 ${\mu }$m luminosity functions have also been studied extensively (Pérez-González et al. 2005; Rush et al. 1993). At z = 0.25, 0.5 and 1, the restframe 12 ${\mu }$m is covered by the AKARI L15,L18W and L24 filters. We present the restframe 12 ${\mu }$m LFs at these redshifts in Sect. 3.3. We also estimate TIR LFs through the SED fit using all the mid-IR bands of the AKARI. The results are presented in Sect. 3.5.

Unless otherwise stated, we adopt a cosmology with $(h,\Omega_{\rm m},\Omega_\Lambda) = (0.7,0.3,0.7)$ (Komatsu et al. 2009).

2 Data and analysis

2.1 Multi-wavelength data in the AKARI NEP-deep field

AKARI performed deep imaging in the north ecliptic pole (NEP) from 2-24 ${\mu }$m, with 4 pointings in each field over 0.4 deg2 (Matsuhara et al. 2007,2006; Wada et al. 2008). Due to the solar synchronous orbit of the AKARI, the NEP is the only AKARI field with very deep imaging at these wavelengths. The 5$\sigma$ sensitivity in the AKARI IR filters ( N2,N3,N4,S7,S9W,S11,L15,L18W, and L24) are 14.2, 11.0, 8.0, 48, 58, 71, 117, 121, and 275 ${\mu }$Jy (Wada et al. 2008). These filters provide us with a unique continuous wavelength coverage at 2-24 ${\mu }$m, where there is a gap between the Spitzer IRAC and MIPS and between the ISO LW2 and LW3. Please consult Pearson et al. (2009); Wada et al. (2007); Pearson et al. (2010); Wada et al. (2008) for data verification and a completeness estimate at these fluxes. The PSF sizes are 4.4, 5.1, and 5.4'' in 2-4, 7-11, $15{-}24~\mu$m bands. The depths of near-IR bands are limited by source confusion, but those of mid-IR bands are by sky noise.

In analyzing these observations, we first combined the three images of the MIR channels, i.e. MIR-S (S7,S9W, and S11) and MIR-L (L15,L18W, and L24), to obtain two high-quality images. In the resulting MIR-S and MIR-L images, the residual sky has been reduced significantly, which helps us obtain more reliable source catalogs. For both the MIR-S and MIR-L channels, we used SExtractor for the combined images to determine initial source positions. We followeds Takagi et al. (2007) procedures for photometry and band-merging of IRC sources. But this time, to maximize the number of MIR sources, we made two IRC band-merged catalogues based on the combined MIR-S and MIR-L images, and then concatenated these catalogs, eliminating duplicates.

In the band-merging process, the source centroid in each IRC image was determined, starting from the source position in the combined images as the initial guess. If the centroid determined in this way is shifted from the original position by >3'', we reject such a source as the counterpart. This band-merging method is used only for IRC bands. We compared raw number counts with previous work based on the same data but with different source extraction methods (Pearson et al. 2009,2010; Wada et al. 2008) and found good agreement.

A subregion of the NEP-deep field was observed in the $\it BVRi'z'$-bands with the Subaru telescope (Imai et al. 2007; Wada et al. 2008), reaching limiting magnitudes of zAB=26 in one field of view of the Suprime-Cam. We restricted our analysis to the data in this Suprime-Cam field (0.25 deg2), where we had enough UV-opical-NIR coverage to estimate good photometric redshifts. The u'-band photometry in this area is provided by the CFHT (Serjeant et al., in prep.). The same field was also observed with the KPNO2m/FLAMINGOs in J and Ks to the depth of $K{\rm s}_{\rm Vega}<20$ (Imai et al. 2007). GALEX covered the entire field to depths of FUV<25 and NUV<25 (Malkan et al., in prep.). In the Suprime-Cam field of the AKARI NEP-deep field, there are a total of 4128 infrared sources down to $\sim$100 ${\mu }$Jy in the L18W filter. All magnitudes are given in AB system in this paper.

For the optical identification of MIR sources, we adopted the likelihood ratio (LR) method (Sutherland & Saunders 1992). For the probability distribution functions of magnitude and angular separation based on correct optical counterparts (and for this purpose only), we used a subset of IRC sources, which are detected in all IRC bands. For this subset of 1100 all-band-detected sources, the optical counterparts were all visually inspected and ambiguous cases excluded. There are multiple optical counterparts for 35% of MIR sources within <3''. If we adopted the nearest-neighbor approach for the optical identification, the optical counterparts differ from that of the LR method for 20% of the sources with multiple optical counterparts. Thus, in total we estimate that fewer than 15% of MIR sources suffer from serious problems of optical identification.

2.2 Photometric redshift estimation

For these infrared sources, we computed photometric redshift using a publicly available code, LePhare[*] (Ilbert et al. 2009; Arnouts et al. 2007; Ilbert et al. 2006). The input magnitudes are FUV,NUV(GALEX), u(CFHT), B,V,R,i',z'(Subaru), J, and K(KPNO2m). We summarize the filters used in Table 1.

Table 1:   Summary of filters used.

\begin{figure} \par\includegraphics[width=6.5cm,clip]{13182fig1.ps} \end{figure} Figure 1:

Photometric redshift estimates with LePhare (Ilbert et al. 2009; Arnouts et al. 2007; Ilbert et al. 2006) for spectroscopically observed galaxies with Keck/DEIMOS (Takagi et al., in prep.). Red squares show objects where AGN templates were better fit. Errors of the photozs are $\frac{\Delta z}{1+z}$ = 0.036 for $z\leq 0.8$, but becomes worse at z> 0.8 to be $\frac{\Delta z}{1+z}$ = 0.10 mainly because of the relatively shallow near-IR data.

Open with DEXTER

Among various templates and fitting parameters we tried, we found the best results with the modified CWW (Coleman et al. 1980) and QSO templates. These CWW templates are interpolated and adjusted to match VVDS spectra better (Arnouts et al. 2007). We included strong emission lines in computing colors. We used the Calzetti extinction law. More details in training LePhare is given in Ilbert et al. (2006).

The resulting photometric redshift estimates agree reasonably well with 293 galaxies (R<24) with spectroscopic redshifts taken with Keck/DEIMOS in the NEP field (Takagi et al., in prep.). The measured errors on the photo-z are $\frac{\Delta z}{1+z}$ = 0.036 for $z\leq 0.8$ and $\frac{\Delta z}{1+z}$ = 0.10 for z>0.8. The $\frac{\Delta z}{1+z}$ becomes significantly larger at z>0.8, where we suffer from relative shallowness of our near-IR data. The rate of catastrophic failures is 4% ( $\frac{\Delta z}{1+z}>0.2$) in the spectroscopic sample.

In Fig. 1, we compare spectroscopic redshifts from Keck/DEIMOS (Takagi et al.) and our photometric redshift estimation. We remove those red square objects ($\sim$2% of the sample) from the LFs presented below. We caution that this can only remove extreme type-1 AGNs, so that fainter, type-2 AGN that could be removed by X-rays or optical spectroscopy still remain in the sample.

Figure 2 shows the distribution of photometric redshift. The distribution has several peaks, which correspond to galaxy clusters in the field (Goto et al. 2008). We had 12% of sources that do not have a good SED fit to obtain a reliable photometric redshift estimation. We applied this photo-z completeness correction to the LFs we obtain. Readers are referred to Negrello et al. (2009), who estimated photometric redshifts using only the AKARI filters to obtain 10% accuracy.

\begin{figure} \par\includegraphics[width=7cm,clip]{13182fig2.ps} \end{figure} Figure 2:

Photometric redshift distribution.

Open with DEXTER

2.3 The 1/Vmax method

We computed LFs with the 1/$V_{\max}$ method (Schmidt 1968). The advantage of their method is that it allows us to compute an LF directly from data, with no parameter dependence or an assumed model. A drawback is that it assumes a homogeneous galaxy distribution, and is thus vulnerable to local over-/under-densities (Takeuchi et al. 2000).

A comoving volume associated with any source of a given luminosity is defined as $V_{\max}=V_{z_{\max}}-V_{z_{\min}}$, where $z_{\min}$ is the lower limit of the redshift bin, and $z_{\max}$ is the maximum redshift at which the object could be seen given the flux limit of the survey, with a maximum value corresponding to the upper redshift of the redshift bin. More precisely,

$\displaystyle % z_{\max} = \min(z_{\max}~{\rm of~the~bin},~ z_{\max}~{\rm from~ the ~flux~limit}).$     (1)

We used the SED templates (Lagache et al. 2003) for k-corrections to obtain the maximum observable redshift from the flux limit.

For each luminosity bin then, the LF is derived as

$\displaystyle % \phi =\frac{1}{\Delta L}\sum_{i} \frac{1}{V_{\max,i}}w_i,$   (2)

where $V_{\max}$ is a comoving volume over which the ith galaxy could be observed, $\Delta L$ the size of the luminosity bin (0.2 dex), and wi the completeness correction factor of the ith galaxy. We used completeness correction measured by Wada et al. (2008) for 11 and 24 ${\mu }$m and Pearson et al. (2009,2010) for 15 and 18 ${\mu }$m. This correction is 25% at maximum, since we only use the sample where the completeness is greater than 80%.

2.4 Monte Carlo simulation

Uncertainties of the LF values stem from various factors such as fluctuations in the number of sources in each luminosity bin, the photometric redshift uncertainties, the k-correction uncertainties, and the flux errors. To compute these errors we performed Monte Carlo simulations by creating 1000 simulated catalogs, where each catalog contains the same number of sources, but we assigned a new redshift to each source following a Gaussian distribution centered on the photometric redshift with the measured dispersion of $\Delta z/(1+z)$ = 0.036 for $z\leq 0.8$ and $\Delta z/(1+z)$ = 0.10 for z>0.8 (Fig. 1). The flux of each source is also allowed to vary according to the measured flux error following a Gaussian distribution. For 8 ${\mu }$m and 12 ${\mu }$m LFs, we can ignore the errors due to the k-correction thanks to the AKARI MIR filter coverage. For TIR LFs, we added 0.05 dex of error for the uncertainty in the SED fitting following the discussion in Magnelli et al. (2009). We did not consider the uncertainty on the cosmic variance here since the AKARI NEP field covers a large volume and has comparable number counts to other general fields (Imai et al. 2008,2007). Each redshift bin we use covers ${\sim}10^6$ Mpc3 of volume. See Matsuhara et al. (2006) for more discussion of the cosmic variance in the NEP field. These estimated errors were added to the Poisson errors in each LF bin in quadrature.

3 Results

3.1 8 ${\mu }$m LF

Monochromatic 8 ${\mu }$m luminosity ( $L_{8~\mu{\rm m}}$) is known to correlate well with the TIR luminosity (Huang et al. 2007; Babbedge et al. 2006), especially for SF galaxies because the rest-frame 8 ${\mu }$m flux are dominated by prominent PAH features such as at 6.2, 7.7 and 8.6 ${\mu }$m. Since the AKARI has continuous coverage in the mid-IR wavelength range, the restframe 8 ${\mu }$m luminosity can be obtained without a large uncertainty in k-correction at a corresponding redshift and filter. For example, at z = 0.375, restframe 8 ${\mu }$m is redshifted into the S11 filter. Similarly, L15,L18W, and L24 cover restframe 8 ${\mu }$m at z = 0.875, 1.25, and 2. This continuous filter coverage is an advantage to AKARI data. Often SED models are used to extrapolate from Spitzer 24 ${\mu }$m flux in previous work, producing a source of the largest uncertainty. We summarize the filters used in Table 1.

To obtain restframe 8 ${\mu }$m LF, we applied a flux limit of F(S11) < 70.9, F(L15) < 117, F(L18W) < 121.4, and F(L24) < 275.8 ${\mu }$Jy at z = 0.38-0.58, z = 0.65-0.90, z = 1.1-1.4 and z = 1.8-2.2, respectively. These are the 5$\sigma$ limits measured in Wada et al. (2008). We excluded those galaxies whose SEDs are better fit with QSO templates (Sect. 2).

We used the completeness curve presented in Wada et al. (2008) and Pearson et al. (2009,2010) to correct for the incompleteness of the detection. However, this correction is 25% at maximum since the sample is 80% complete at the 5$\sigma$ limit. Our main conclusions are not affected by this incompleteness correction. To compensate for the increasing uncertainty in increasing z, we used redshift binsize of 0.38 < z < 0.58, 0.65 < z < 0.90, 1.1 < z < 1.4, and 1.8 < z < 2.2. We show the $L_{8~\mu{\rm m}}$ distribution in each redshift range in Fig. 3. Within each redshift bin, we used the 1/$V_{\max}$ method to compensate for the flux limit in each filter.

We show the computed restframe 8 ${\mu }$m LF in Fig. 4. The 8 ${\mu }$m luminosities corresponding to the flux limits at the central redshift in each redshift bin are indicated by arrows. Errorbars on each point are based on the Monte Carlo simulation (Sect. 2.3).

For a comparison, we also show the 8 ${\mu }$m LF of SF galaxies at 0<z<0.3 by Huang et al. (2007), using the 1/$V_{\max}$ method applied to the IRAC 8 ${\mu }$m GTO data. Compared to the local LF, our 8 ${\mu }$m LFs show strong evolution in luminosity. In the range of 0.48<z<2, $L^*_{8~\mu{\rm m}}$ evolves as  ${\propto}(1+z)^{1.6\pm0.2}$. Detailed comparison with the literature will be presented in Sect. 4.

\begin{figure} \par\includegraphics[width=7cm,clip]{13182fig3.ps} \end{figure} Figure 3:

8 ${\mu }$m luminosity distributions of samples used to compute restframe 8 ${\mu }$m LFs. From low redshift, 533, 466, 236, and 59 galaxies are in each redshift bin.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7cm,clip]{13182fig4.ps} \end{figure} Figure 4:

Restframe 8 ${\mu }$m LFs based on the AKARI NEP-deep field. The blue diamons, purple triangles, red squares, and orange crosses show the 8 ${\mu }$m LFs at 0.38<z<0.58, 0.65<z<0.90, 1.1<z<1.4, and 1.8<z<2.2, respectively. AKARI's MIR filters can observe restframe 8 ${\mu }$m at these redshifts in a corresponding filter. Errorbars are from the Monte Carlo simulations (Sect. 2.4). The dotted lines show analytical fits with a double-power law. Vertical arrows show the 8 ${\mu }$m luminosity corresponding to the flux limit at the central redshift in each redshift bin. Overplotted are Babbedge et al. (2006) in the pink dash-dotted lines, Caputi et al. (2007) in the cyan dash-dotted lines, and Huang et al. (2007) in the green dash-dotted lines. AGNs are excluded from the sample (Sect. 2.2).

Open with DEXTER

3.2 Bolometric IR luminosity density based on the 8 ${\mu }$m LF

Constraining the star formation history of galaxies as a function of redshift is a key to understanding galaxy formation in the Universe. One of the primary purposes in computing IR LFs is to estimate the IR luminosity density, which in turn is a good estimator of the dust-hidden cosmic star formation density (Kennicutt 1998). Since dust obscuration is more important for more actively SF galaxies at higher redshift, and such star formation cannot be observed in UV light, it is important to obtain IR-based estimate in order to fully understand the cosmic star formation history of the Universe.

We can estimate the total infrared luminosity density by integrating the LF weighted by the luminosity. First, we need to convert $L_{8~\mu{\rm m}}$ to the bolometric infrared luminosity. The bolometric IR luminosity of a galaxy is produced by the thermal emission of its interstellar matter. In SF galaxies, the UV radiation produced by young stars heats the interstellar dust, and the reprocessed light is emitted in the IR. For this reason, in SF galaxies, the bolometric IR luminosity is a good estimator of the current star formation rate (SFR) of the galaxy. Bavouzet et al. (2008) shows a strong correlation between $L_{8~\mu{\rm m}}$ and total infrared luminosity ( $L_{\rm TIR}$) for 372 local SF galaxies. The conversion given by Bavouzet et al. (2008) is

$\displaystyle % L_{\rm TIR}=377.9\times (\nu L_\nu)^{0.83}_{\rm rest~8~\mu m} (\pm37\%).$     (3)

Caputi et al. (2007) further constrained the sample to luminous, high S/N galaxies ( $\nu L_{\nu}^{8~\mu{\rm m}}>10^{10}~L_{\odot}$ and S/N > 3 in all MIPS bands) in order to match their sample better, and derived the following equation.
$\displaystyle % L_{\rm TIR}=1.91\times (\nu L_\nu)^{1.06}_{\rm rest~8~\mu m} (\pm 55\%).$     (4)

Since ours is also a sample of bright galaxies, we use this equation to convert $L_{8~\mu{\rm m}}$ to  $L_{\rm TIR}$. Because the conversion is based on local SF galaxies, it is a concern if it holds at higher redshift or not. Bavouzet et al. (2008) check this by stacking 24 ${\mu }$m sources at 1.3<z<2.3 in the GOODS fields to find the stacked sources are consistent with the local relation. They concluded that Eq. (3) is valid to link $L_{8~\mu{\rm m}}$ and  $L_{\rm TIR}$ at 1.3<z<2.3. Takagi et al. (2010) also show that local $L_{7.7~\mu{\rm m}}$ vs. $L_{\rm TIR}$ relation holds true for IR galaxies at z $\sim$ 1 (see their Fig. 10). Pope et al. (2008) show that $z\sim 2$ sub-millimeter galaxies lie on the relation between $L_{\rm TIR}$ and  $L_{\rm PAH,7.7}$ that has been established for local starburst galaxies. The  S70/S24 ratios of 70 ${\mu }$m sources in Papovich et al. (2007) are also consistent with local SED templates. These results suggest it is reasonable to use Eq. (4) for our sample.

The conversion, however, has been the largest source of error in estimating  $L_{\rm TIR}$ from  $L_{8~\mu{\rm m}}$. Bavouzet et al. (2008) themselves quote 37% of uncertainty, and Caputi et al. (2007) report 55% of dispersion around the relation. It should be kept in mind that the restframe $8~\mu$m is sensitive to the star-formation activity, but at the same time, it is where the SED models have strongest discrepancies due to the complicated PAH emission lines. A detailed comparison of different conversions is presented in Fig. 12 of Caputi et al. (2007), who report a factor of $\sim$5 differences among various models.

Then the 8 ${\mu }$m LF is weighted by the $L_{\rm TIR}$ and integrated to obtain TIR density. For integration, we first fit an analytical function to the LFs. In the literature, IR LFs were fit better by a double-power law (Babbedge et al. 2006) or a double-exponential (Le Floc'h et al. 2005; Takeuchi et al. 2006; Saunders et al. 1990; Pozzi et al. 2004) than a Schechter function, which declines too suddenly at the high luminosity, underestimating the number of bright galaxies. In this work, we fit the 8 ${\mu }$m LFs using a double-power law (Babbedge et al. 2006) as

\begin{displaymath}% \Phi(L){\rm d}L/L^{*} = \Phi^{*}\bigg(\frac {L}{L^{*}}\bigg)^{1-\alpha}{\rm d}L/L^{*}, ~~~ (L<L^{*}). \end{displaymath} (5)

\begin{displaymath}% \Phi(L){\rm d}L/L^{*} = \Phi^{*}\bigg(\frac {L}{L^{*}}\bigg)^{1-\beta}{\rm d}L/L^{*}, ~~~ (L>L^{*}). \end{displaymath} (6)

First, the double-power law is fitted to the lowest redshift LF at 0.38 < z < 0.58 to determine the normalization ($\Phi^{*}$) and slopes ( $\alpha,\beta$). For higher redshifts we did not have enough statistics to simultaneously fit 4 parameters ($\Phi^{*}$, L*, $\alpha$, and $\beta$). Therefore, we fixed the slopes and normalization at the local values and varied only L* at for the higher-redshift LFs. Fixing the faint-end slope is a common procedure with the depth of current IR satellite surveys (Babbedge et al. 2006; Caputi et al. 2007). The stronger evolution in luminosity than in density found by previous work (Le Floc'h et al. 2005; Pérez-González et al. 2005) also justifies this parametrization. Best-fit parameters are presented in Table 2. Once the best-fit parameters are found, we integrated the double power law outside the luminosity range in which we have data to obtain estimates of the total infrared luminosity density,  $\Omega _{\rm TIR}$.

Table 2:   Best-fit parameters for 8, 12 ${\mu }$m, and TIR LFs.

The resulting total luminosity density ( $\Omega_{\rm IR}$) is shown in Fig. 5 as a function of redshift. Errors are estimated by varying the fit within 1$\sigma$ of uncertainty in LFs, after which, errors in conversion from $L_{8~\mu{\rm m}}$ to  $L_{\rm TIR}$ are added. The latter is by far the larger source of uncertainty. Simply switching from Eqs. (3) to (4) (red solid line) produces a $\sim$50% difference. Results from Le Floc'h et al. (2005) are also shown for a comparision. The lowest redshift point was corrected following Magnelli et al. (2009).

We also show the evolution of monochromatic 8 ${\mu }$m luminosity ( $L_{8~\mu{\rm m}}$), which is obtained by integrating the fits, but without converting to  $L_{\rm TIR}$ in Fig. 6. The  $\Omega_{8~\mu{\rm m}}$ evolves as  ${\propto}(1+z)^{1.9\pm0.7}$. The SFR and  $L_{\rm TIR}$ are related by the following equation for a Salpeter IMF, $\phi~(m)$ $\propto$ m-2.35 between $0.1{-}100~M_{\odot}$ (Kennicutt 1998).

$\displaystyle % SFR (M_{\odot}~{\rm yr}^{-1}) =1.72 \times 10^{-10}~L_{\rm TIR} (L_{\odot})$     (7)

The right ticks of Fig. 5 shows the star formation density scale, converted from  $\Omega_{\rm IR}$ using the above equation.

In Fig. 5, $\Omega_{\rm IR}$ monotonically increases toward higher z. Compared with z=0, $\Omega_{\rm IR}$ is $\sim$10 times larger at z=1. The evolution between z=0.5 and z=1.2 is a little flatter, but this is perhaps because of a more irregular shape of LFs at 0.65 < z < 0.90, and so we do not consider it significant. The results here agree with previous work (e.g., Le Floc'h et al. 2005) within the errors. We compare the results with previous work in more detail in Sect. 4.

\begin{figure} \par\includegraphics[width=8cm,clip]{13182fig5.ps} \end{figure} Figure 5:

Evolution of TIR luminosity density computed by integrating the 8 ${\mu }$m LFs in Fig. 4.The red solid lines use the conversion in Eq. (4). The orange dashed lines use Eq. (3). Results from Le Floc'h et al. (2005) are shown with the cyan dotted lines.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7cm,clip]{13182fig6.ps} \end{figure} Figure 6:

Evolution of 8 ${\mu }$m IR luminosity density computed by integrating the 8 ${\mu }$m LFs in Fig. 4. The lowest redshift point is from Huang et al. (2007).

Open with DEXTER

3.3 12 ${\mu }$m LF

\begin{figure} \par\includegraphics[width=7cm,clip]{13182fig7.ps} \end{figure} Figure 7:

12 ${\mu }$m luminosity distributions of samples used to compute restframe 12 ${\mu }$m LFs. From low redshift, 335, 573, and 213 galaxies are in each redshift bin.

Open with DEXTER

In this section we estimate restframe 12 ${\mu }$m LFs based on the AKARI NEP-deep data. 12 ${\mu }$m luminosity ( $L_{12~\mu{\rm m}}$) has been studied well through ISO and IRAS, and is known to correlate closely with TIR luminosity (Spinoglio et al. 1995; Pérez-González et al. 2005).

As was the case for the 8 ${\mu }$m LF, it is advantageous that AKARI's continuous filters in the mid-IR allow us to estimate restframe 12 ${\mu }$m luminosity without much extrapolation based on SED models. Targeted redshifts are z = 0.25, 0.5 and 1 where L15,L18W and L24 filters cover the restframe 12 ${\mu }$m, respectively. We summarize the filters in Table 1. The methodology is the same as for the 8 ${\mu }$m LF. We used the sample to the 5$\sigma$ limit, corrected for the completeness, then used the 1/$V_{\max}$ method to compute LF in each redshift bin. The histogram of $L_{12~\mu{\rm m}}$ distribution is presented in Fig. 7. The resulting 12 ${\mu }$m LF is shown in Fig. 8. Compared with Rush et al. (1993)'s z=0 LF based on IRAS Faint Source Catalog, the 12 ${\mu }$m LFs show steady evolution with increasing redshift. In the range of 0.25<z<1, $L^*_{12~\mu{\rm m}}$ evolves as  ${\propto}(1+z)^{1.5\pm0.4}$.

\begin{figure} \par\includegraphics[width=7cm,clip]{13182fig8.ps} \end{figure} Figure 8:

Restframe 12 ${\mu }$m LFs based on the AKARI NEP-deep field. The blue diamonds, purple triangles, and red squares show the 12 ${\mu }$m LFs at 0.15<z<0.35, 0.38<z<0.62, and 0.84<z<1.16, respectively. Vertical arrows show the 12 ${\mu }$m luminosity corresponding to the flux limit at the central redshift in each redshift bin. Overplotted are Pérez-González et al. (2005) at z = 0.3, 0.5 and 0.9 in the cyan dash-dotted lines, and Rush et al. (1993) at z = 0 in the green dash-dotted lines. AGNs are excluded from the sample (Sect. 2.2).

Open with DEXTER

3.4 Bolometric IR luminosity density based on the 12 ${\mu }$m LF

One of the most frequently used monochromatic fluxes to estimate $L_{\rm TIR}$ is 12 ${\mu }$m. The total infrared luminosity is computed from the  $L_{12~\mu{\rm m}}$ using the conversion in Chary & Elbaz (2001), and Pérez-González et al. (2005):

$\displaystyle % \log L_{\rm TIR}=\log (0.89^{+0.38}_{-0.27})+1.094 \log L_{12~\mu{\rm m}}.$   (8)

Takeuchi et al. (2005) independently estimated the relation to be
$\displaystyle % \log L_{\rm TIR}=1.02+0.972 \log L_{12~\mu{\rm m}},$   (9)

which we also used to check our conversion. As both authors state, these conversions contain an error of factor of 2-3. Therefore, we should avoid conclusions that could be affected by such errors.

Then the 12 ${\mu }$m LF is weighted by the $L_{\rm TIR}$ and integrated to obtain TIR density. Errors are estimated by varying the fit within 1$\sigma$ of uncertainty in LFs, and errors in converting from $L_{12~\mu{\rm m}}$ to  $L_{\rm TIR}$ are added. The latter is by far the largest source of uncertainty. Best-fit parameters are presented in Table 2. In Fig. 10, we show total luminosity density based on the 12 ${\mu }$m LF presented in Fig. 8. The results show a rapid increase in  $\Omega_{\rm IR}$, agreeing with previous work (Le Floc'h et al. 2005) within the errors.

We also integrated monochromatic $L_{12~\mu{\rm m}}$ over the LFs (without converting to  $L_{\rm TIR}$) to derive the evolution of total $12~\mu{\rm m}$ monochromatic luminosity density, $\Omega_{12~\mu{\rm m}}$. The results are shown in Fig. 9, which shows a strong evolution of $\Omega_{12~\mu{\rm m}} \propto (1+z)^{1.4\pm1.4}$. It is interesting to compare this to $\Omega_{8~\mu{\rm m}}$ $\propto$ $(1+z)^{1.9\pm0.7}$ obtained in Sect. 3.2. Although errors are significant on both estimates, $\Omega_{12~\mu{\rm m}}$ and $\Omega_{8~\mu{\rm m}}$show a possibly different evolution, suggesting that the cosmic infrared spectrum changes its SED shape. Whether this is due to evolution in dust or to dusty AGN contribution is an interesting subject for future work.

\begin{figure} \par\includegraphics[width=7cm,clip]{13182fig9.ps} \end{figure} Figure 9:

Evolution of 12 ${\mu }$m IR luminosity density computed by integrating the 12 ${\mu }$m LFs in Fig. 8.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13182fig10.ps} \end{figure} Figure 10:

TIR luminosity density computed by integrating the 12 ${\mu }$m LFs in Fig. 8.

Open with DEXTER

3.5 TIR LF

AKARI's continuous mid-IR coverage is also superior for SED-fitting to estimate  $L_{\rm TIR}$, since for SF galaxies, the mid-IR part of the IR SED is dominated by the PAH emissions that reflect the SFR of galaxies, so it correlates well with  $L_{\rm TIR}$, which is also a good indicator of the galaxy SFR. The AKARI's continuous MIR coverage helps us to estimate  $L_{\rm TIR}$.

After photometric redshifts are estimated using the UV-optical-NIR photometry, we fix the redshift at the photo-z, then use the same LePhare code to fit the infrared part of the SED to estimate TIR luminosity. We used Lagache et al. (2003)'s SED templates to fit the photometry using the AKARI bands at >6 ${\mu }$m ( S7,S9W,S11,L15,L18W, and L24). We show an example of the SED fit in Fig. 11, where shown are the best-fit SEDs for the UV-optical-NIR and IR SED at $\lambda>6~\mu$m. The obtained total infrared luminosity ( $L_{\rm TIR}$) is shown as a function of redshift in Fig. 12, with spectroscopic galaxies in large triangles. The figure shows that the AKARI can detect LIRGs ( $L_{\rm TIR}>10^{11}~L_{\odot}$) up to z=1 and ULIRGs ( $L_{\rm TIR}>10^{12}~L_{\odot}$) to z=2. We also checked that using different SED models (Dale & Helou 2002; Chary & Elbaz 2001) does not change our essential results.

\begin{figure} \par\includegraphics[width=7cm,clip]{13182fig11.ps} \end{figure} Figure 11:

An example of the SED fit. The red dashed line shows the best-fit SED for the UV-optical-NIR SED, mainly to estimate photometric redshift. The blue solid line shows the best-fit model for the IR SED at $\lambda>6~\mu$m, to estimate  $L_{\rm TIR}$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7cm,clip]{13182fig12.ps} \end{figure} Figure 12:

TIR luminosity is shown as a function of photometric redshift. The photo-z is estimated using UV-optical-NIR photometry. $L_{\rm TIR}$ isobtained through SED fit in 7-24 ${\mu }$m.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7cm,clip]{13182fig13.ps} \end{figure} Figure 13:

A histogram of TIR luminosity. From low-redshift, 144, 192, 394, and 222 galaxies are in 0.2 < z < 0.5, 0.5 < z < 0.8, 0.8 < z < 1.2, and  1.2 < z < 1.6, respectively.

Open with DEXTER

Galaxies in the targeted redshift range are best sampled in the 18 ${\mu }$m band due to the wide bandpass of the L18W filter (Matsuhara et al. 2006). In fact, in a single-band detection, the 18 ${\mu }$m image returns the largest number of sources. Therefore, we applied the 1/$V_{\max}$ method using the detection limit at L18W. We also checked that using the L15 flux limit does not change our main results. The same Lagache et al. (2003) models are also used for the k-corrections necessary for computing $V_{\max}$ and $V_{\min}$. The redshift bins used are 0.2 < z < 0.5, 0.5 < z < 0.8, 0.8 < z < 1.2, and 1.2 < z < 1.6. A distribution of  $L_{\rm TIR}$ in each redshift bin is shown in Fig. 13.

The obtained $L_{\rm TIR}$ LFs are shown in Fig. 14. The uncertainties are estimated through the Monte Carlo simulations (Sect. 2.4). For a local benchmark, we overplot Sanders et al. (2003), who derived LFs from the analytical fit to the IRAS Revised Bright Galaxy Sample, i.e., $\phi \propto L^{-0.6}$ for L<L* and $\phi \propto L^{-2.2}$ for L>L* with $L^*=10^{10.5}~L_{\odot}$. The TIR LFs show a strong evolution compared to local LFs. At  0.25<z<1.3, $L^*_{\rm TIR}$ evolves as ${\propto}(1+z)^{4.1\pm0.4}$. We go on to compare LFs to the previous work in Sect. 4.

3.6 Bolometric IR luminosity density based on the TIR LF

Using the same methodology as in previous sections, we integrated  $L_{\rm TIR}$ LFs in Fig. 14 through a double-power law fit (Eqs. (5) and (6)). The resulting evolution of the TIR density is shown in Fig. 15, which is in good agreement with Le Floc'h et al. (2005) within the errors. Errors are estimated by varying the fit within 1$\sigma$ of uncertainty in LFs. For uncertainty in the SED fit, we added 0.15 dex of error. Best-fit parameters are presented in Table 2. In Fig. 15, we also show the contributions to  $\Omega _{\rm TIR}$ from LIRGs and ULIRGs. We also discuss the evolution of  $\Omega _{\rm TIR}$ in Sect. 4.

\begin{figure} \par\includegraphics[width=7cm,clip]{13182fig14.ps} \end{figure} Figure 14:

TIR LFs. Vertical lines show the luminosity corresponding to the flux limit at the central redshift in each redshift bin. AGNs areexcluded from the sample (Sect. 2.2).

Open with DEXTER

4 Discussion

4.1 Comparison with previous work

In this section, we compare our results to previous work, especially those based on the Spitzer data. Comparisons are best done in the same wavelengths, since the conversion from either $L_{8~\mu{\rm m}}$ or  $L_{12~\mu{\rm m}}$ to  $L_{\rm TIR}$ involves the largest uncertainty. Hubble parameters in the previous work are converted to h=0.7 for comparison.

4.1.1 8 ${\mu }$m LFs

Recently, using the Spitzer space telescope, restframe 8 ${\mu }$m LFs of $z\sim 1$ galaxies have been computed in detail by Caputi et al. (2007) in the GOODS fields and by Babbedge et al. (2006) in the SWIRE field. In this section, we compare our restframe 8 ${\mu }$m LFs (Fig. 4) to these and discuss possible differences.

In Fig. 4, we overplot Caputi et al. (2007)'s LFs at z=1 and z=2. Their z=2 LF is in good agreement with our LF at 1.8 < z < 2.2. However, their z=1 LF is larger than ours by a factor of 3-5 at $\log L>11.2$. The brightest ends ( $\log L\sim 11.4$) are consistent with each other to within 1$\sigma$. They excluded AGN using optical-to-X-ray flux ratio, and we also excluded AGN through the optical SED fit. Therefore, especially at the faint end, the contamination from AGN is not likely to be the main cause of differences. Since Caputi et al. (2007) uses GOODS fields, cosmic variance may play a role here. The exact reason for the difference is unknown, but we point out that their $\Omega_{\rm IR}$ estimate at z=1 is also higher than other estimates by a small factor (see their Fig. 15). In  $L_{\rm TIR}$, Magnelli et al. (2009) also report Caputi et al. (2007)'s z=1 LF is higher than their estimate based on 70 ${\mu }$m by several factors (see their Fig. 12). They concluded that the difference comes from the different SED models used, since their LF matched with that of Caputi et al. (2007)'s once the same SED models were used. We compare our total LFs to those in the literature below.

\begin{figure} \par\includegraphics[width=8cm,clip]{13182fig15.ps} \end{figure} Figure 15:

TIR luminosity density (red diamonds) computed by integrating the total LF in Fig. 14. The blue squares and orange triangles are only for LIRG and ULIRGs.

Open with DEXTER

Babbedge et al. (2006) also computed restframe 8 ${\mu }$m LFs using the Spitzer/SWIRE data. We overplot their results at 0.25<z<0.5 and 0.5<z<1 in Fig. 4. In both redshift ranges, good agreement is found at higher luminosity bins ( $L_{8~\mu{\rm m}}>10^{10.5}~L_{\odot}$). However, at all redshift ranges including the ones not shown here, Babbedge et al. (2006) tends to show a flatter faint-end tail than ours, and a smaller $\phi$ by a factor of $\sim$3. Although the exact reason is unknown, the deviation starts toward the fainter end, where both works approach the flux limits of the surveys. Therefore, the possibly incomplete sampling may be one of the reasons. It is also reported that the faint end of IR LFs depends on the environment, in the sense that higher density environment has a steeper faint-end tail (Goto et al. 2010). At z=1, Babbedge et al. (2006)'s LF deviates from that by Caputi et al. (2007) by almost a magnitude. Our 8 ${\mu }$m LFs are between these works.

These comparisons suggest that, even with the current generation of satellites and state-of-the-art SED models, factor-of-several uncertainties still remain in estimating the 8 ${\mu }$m LFs at $z\sim 1$. More accurate determination has to await a broader and deeper survey by next generation IR satellites such as Herschel and WISE.

To summarize, our 8 ${\mu }$m LFs are between those by Babbedge et al. (2006) and Caputi et al. (2007). Both of the previous works had to rely on SED models to estimate $L_{8~\mu{\rm m}}$ from the Spitzer $S_{24~\mu{\rm m}}$ in the MIR wavelengths where SED modeling is difficult. Here, AKARI's mid-IR bands are advantageous in directly observing redshifted, restframe 8 ${\mu }$m flux in one of the AKARI's filters, leading to more reliable measurement of 8 ${\mu }$m LFs without uncertainty from the SED modeling.

4.1.2 12 ${\mu }$m LFs

Pérez-González et al. (2005) investigated the evolution of restframe 12 ${\mu }$m LFs using the Spitzer CDF-S and HDF-N data. We overplot their results in similar redshift ranges in Fig. 8. Considering both LFs have significant error bars, these LFs agree with our LFs, and show significant evolution in the 12 ${\mu }$m LFs compared with the z=0 12 ${\mu }$m LF by Rush et al. (1993). The agreement is in stark contrast to the comparison in 8 ${\mu }$m LFs in Sect. 4.1.1, where we suffered from several differences. A possible reason for this is that 12 ${\mu }$m is redder than 8 ${\mu }$m enough that it is easier to be extrapolated from $S_{24~\mu{\rm m}}$ in the Spitzer work. In fact, at z=1, both the Spitzer 24 ${\mu }$m band and AKARI L24 observe the restframe 12 ${\mu }$m directly. In additon, mid-IR SEDs around 12 ${\mu }$m are flatter than at 8 ${\mu }$m, where PAH emissions are prominent. Therefore, SED models can predict the flux more accurately. In fact, this is part of the reason Pérez-González et al. (2005) chose to investigate 12 ${\mu }$m LFs. Pérez-González et al. (2005) used Chary & Elbaz (2001) SED to extrapolate $S_{24~\mu{\rm m}}$, and yet they agree with AKARI results, which are derived from filters that cover the restframe 12 ${\mu }$m. However, in other words, the discrepancy in 8 ${\mu }$m LFs highlights that the SED models are perhaps still imperfect in the 8 ${\mu }$m wavelength range; as a result, MIR-spectroscopic data that covers wider luminosity and redshift ranges will be needed to refine SED models in the mid-IR. AKARI's mid-IR slitless spectroscopy survey (Wada 2008) may help in this regard.

4.1.3 TIR LFs

Lastly, we compare our TIR LFs (Fig. 14) with those in the literature. Although the TIR LFs can also be obtained by converting 8 ${\mu }$m LFs or 12 ${\mu }$m LFs, we already compared our results in these wavelengths in the last sections. Here, we compare our TIR LFs to Le Floc'h et al. (2005) and Magnelli et al. (2009).

Le Floc'h et al. (2005) obtain TIR LFs using the Spitzer CDF-S data. They used the best-fit SED among various templates to estimate  $L_{\rm TIR}$. We overplot their total LFs in Fig. 14. Only LFs that overlap our redshift ranges are shown. The agreement at 0.3<z<0.45 and 0.6<z<0.8 is reasonable, considering the error bars on both sides. However, in all three redshift ranges, their LFs are higher than ours, especially for 1.0<z<1.2.

We also overplot TIR LFs by Magnelli et al. (2009), who used Spitzer 70 ${\mu }$m flux and Chary & Elbaz (2001) model to estimate  $L_{\rm TIR}$. In the two bins (centered on z=0.55 and z=0.85) that closely overlap with our redshift bins, excellent agreement is found. We also plot Huynh et al. (2007)'s LF at 0.6<z<0.9, which was computed from Spitzer $70~\mu$m imaging in the GOODS-N, and this also agrees closely with ours. These LFs are on top of each other within the error bars, despite the different data sets using different analyses.

This means that Le Floc'h et al. (2005)'s LFs are also higher than Magnelli et al. (2009)'s, in addition to ours. A possible reason is that both of us removed AGN (at least bright ones), whereas Le Floc'h et al. (2005) include them. This is also consistent with the difference being larger at 1.0<z<1.2 where both surveys are only sensitive to luminous IR galaxies, which are dominated by AGN. Another possible source of uncertainty is that we both used a single SED library, while Le Floc'h et al. (2005) picked the best SED template among several libraries for each galaxy.

4.2 Evolution of ${\Omega _{IR}}$

\begin{figure} \par\includegraphics[width=13.5cm,clip]{13182fig16.ps} \end{figure} Figure 16:

Evolution of TIR luminosity density based on TIR LFs (red circles), 8 ${\mu }$m LFs (stars), and 12 ${\mu }$m LFs (filled triangles). The blue open squares and orange filled squares are for only LIRG and ULIRGs, also based on our $L_{\rm TIR}$ LFs. Overplotted dot-dashed lines are estimates from the literature: Le Floc'h et al. (2005), Magnelli et al. (2009), Pérez-González et al. (2005), Caputi et al. (2007), and Babbedge et al. (2006) are in cyan, yellow, green, navy, and pink, respectively. The purple dash-dotted line shows UV estimate by Schiminovich et al. (2005). The pink dashed line shows the total estimate of IR (TIR LF) and UV (Schiminovich et al. 2005).

Open with DEXTER

In this section, we compare the evolution of $\Omega_{\rm IR}$ as a function of redshift. In Fig. 16, we plot  $\Omega_{\rm IR}$ estimated from TIR LFs, 8 ${\mu }$m LFs, and 12 ${\mu }$m LFs, as a function of redshift. Estimates based on 12 ${\mu }$m LFs and TIR LFs agree each other, while those from 8 ${\mu }$m LFs show a slightly higher value than others. This perhaps reflects that 8 ${\mu }$m is a more difficult part of the SED to be modeled, as we had poorer agreement among papers in the literature in 8 ${\mu }$m LFs. The bright-end slope of the double-power law was  3.5+0.2-0.4 in Table 2. This is flatter than a Schechter fit by Babbedge et al. (2006) and a double-exponential fit by Caputi et al. (2007). This is perhaps why we obtained higher  $\Omega_{\rm IR}$ in 8 ${\mu }$m.

We overplot estimates from various papers in the literature (Le Floc'h et al. 2005; Pérez-González et al. 2005; Babbedge et al. 2006; Caputi et al. 2007; Magnelli et al. 2009). Our  $\Omega_{\rm IR}$ has very good agreement with these at 0<z<1.2, with almost all other results lying within our error bars of  $\Omega_{\rm IR}$ from  $L_{\rm TIR}$ and 12 ${\mu }$m LFs. This is perhaps because an estimate of an integrated value such as  $\Omega_{\rm IR}$ is more reliable than estimates of LFs.

At z>1.2, our $\Omega_{\rm IR}$ shows a hint of continuous increase, while Caputi et al. (2007) and Babbedge et al. (2006) observe a slight decline at z>1. However, as both authors also point out, at this high-redshift range, both the AKARI and Spitzer satellites are only sensitive to LIRGs and ULIRGs, and thus the extrapolation to fainter luminosities assumes the faint-end slope of the LFs, which could be uncertain. In addition, this work has a poorer photo-z estimate at z>0.8 ( $\frac{\Delta z}{1+z}$ = 0.10) because of the relatively shallow near-IR data. Several authors tried to overcome this problem by stacking undetected sources. However, if an undetected source is also not detected at shorter wavelengths where positions for stacking are obtained, it would not be included in the stacking either. Next-generation satellite such as Herschel, WISE, and SPICA (Nakagawa 2008) will determine the faint-end slope at z>1 more precisely.

We parameterize the evolution of $\Omega_{\rm IR}$ using

\begin{displaymath}% \Omega_{\rm IR}(z) \propto (1+z)^{\gamma}. \end{displaymath} (10)

By fitting this to the $\Omega_{\rm IR}$ from TIR LFs, we obtained $\gamma = 4.4$ $\pm$ 1.0. This is consistent with most earlier works. For example, Le Floc'h et al. (2005) obtained $\gamma = 3.9$ $\pm$ 0.4, Pérez-González et al. (2005) obtained $\gamma = 4.0$ $\pm$ 0.2, Babbedge et al. (2006) obtained $\gamma = 4.5^{+0.7}_{-0.6}$, Magnelli et al. (2009) obtained $\gamma = 3.6$ $\pm$ 0.4. The agreement was expected from Fig. 16, but confirms a strong evolution of  $\Omega_{\rm IR}$.

4.3 Differential evolution among ULIRG, LIRG, normal galaxies

In Fig. 15, we also plot the contributions to  $\Omega_{\rm IR}$ from LIRGs and ULIRGs (measured from TIR LFs). Both LIRGs and ULIRGs show strong evolution, as has been seen for total  $\Omega_{\rm IR}$. Normal galaxies ( $L_{\rm TIR}<10^{11}~L_{\odot}$) are still dominant, but decrease their contribution toward higher redshifts. In contrast, ULIRGs continue to increase their contribution. From z = 0.35 to z = 1.4, $\Omega_{\rm IR}$ by LIRGs increases by a factor of $\sim$1.6, and  $\Omega_{\rm IR}$ by ULIRGs increases by a factor of $\sim$10. The physical origin of ULIRGs in the local Universe is often merger/interaction (Sanders & Mirabel 1996; Taniguchi & Shioya 1998; Goto 2005). It would be interesting to investigate whether the merger rate also increases in proportion to the ULIRG fraction or if different mechanisms can also produce ULIRGs at higher redshift.

4.4 Comparison to the UV estimate

\begin{figure} \par\includegraphics[width=6.8cm,clip]{13182fig17.ps} \end{figure} Figure 17:

Contribution of $\Omega _{\rm TIR}$ to $\Omega _{\rm total}=\Omega _{\rm UV}+\Omega _{\rm TIR}$ is shown as a function of redshift.

Open with DEXTER

We have been emphasizing the importance of IR probes of the total SFRD of the Universe. However, the IR estimates do not take the contribution of the unabsorbed UV light produced by the young stars into account. Therefore, it is important to estimate how significant this UV contribution is.

Schiminovich et al. (2005) find that the energy density measured at 1500 Å evolves as ${\propto}(1+z)^{2.5\pm0.7}$ at 0<z<1 and ${\propto}(1+z)^{0.5\pm0.4}$ at z>1, using the GALEX data supplemented by the VVDS spectroscopic redshifts. We overplot their UV estimate of  $\rho_{\rm SFR}$ in Fig. 16. The UV estimate is almost a factor of 10 smaller than the IR estimate at most of the redshifts, confirming the importance of IR probes when investing the evolution of the total cosmic star formation density. In Fig. 16 we also plot total SFD (or  $\Omega_{\rm total}$) by adding  $\Omega_{\rm UV}$ and  $\Omega _{\rm TIR}$. In Fig. 17, we show the ratio of the IR contribution to the total SFRD of the Universe ( $\Omega _{\rm TIR}$/ $\Omega_{\rm TIR}+\Omega_{\rm UV}$) as a function of redshift. Although the errors are large, Fig. 17 agrees with Takeuchi et al. (2005), and suggests that  $\Omega _{\rm TIR}$ explains 70% of  $\Omega_{\rm total}$ at z = 0.25, and that by z = 1.3, 90% of the cosmic SFD is explained by the infrared. This implies that  $\Omega _{\rm TIR}$ provides good approximation of the  $\Omega_{\rm total}$ at z>1.

5 Summary

We estimated restframe 8 ${\mu }$m, 12 ${\mu }$m, and total infrared luminosity functions using the AKARI NEP-deep data. Our advantage over previous work is AKARI's continuous filter coverage in the mid-IR wavelengths (2.4, 3.2, 4.1, 7, 9, 11, 15, 18, and 24 ${\mu }$m), which allow us to estimate mid-IR luminosity without a large extrapolation based on SED models, which were the largest uncertainty in previous work. Even for  $L_{\rm TIR}$, the SED fitting is much more reliable thanks to this continuous coverage of mid-IR filters.

Our findings follow.

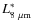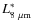
  • The 8 ${\mu }$m LFs show a strong and continuous evolution from z = 0.35 to z = 2.2. Our LFs are larger than those of Babbedge et al. (2006), but smaller than Caputi et al. (2007). The difference perhaps stems from the different SED models, highlighting a difficulty in SED modeling at wavelengths crowded by strong PAH emissions. $L^*_{8~\mu{\rm m}}$ shows a continuous evolution as  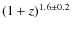$L^*_{8~\mu{\rm m}}$ $\propto$ $(1+z)^{1.6\pm0.2}$ in the range of 0.48<z<2.

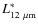
  • The 12 ${\mu }$m LFs show a strong and continuous evolution from z = 0.15 to z = 1.16 with 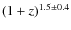$L^*_{12~\mu{\rm m}}$ $\propto$ $(1+z)^{1.5\pm0.4}$. This agrees well with Pérez-González et al. (2005), including a flatter faint-end slope. Better agreement than with 8 ${\mu }$m LFs was obtained, perhaps because of smaller uncertainty in modeling the 12 ${\mu }$m SED, and less extrapolation needed in Spitzer 24 ${\mu }$m observations.

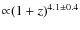  • The TIR LFs show good agreement with Magnelli et al. (2009), but are smaller than in Le Floc'h et al. (2005). At  0.25<z<1.3, $L^*_{\rm TIR}$ evolves as  ${\propto}(1+z)^{4.1\pm0.4}$. Possible causes of the disagreement include different treatments of SED models in estimating  $L_{\rm TIR}$ and AGN contamination.

  • TIR densities estimated from 12 ${\mu }$m and TIR LFs show a strong evolution as a function of redshift, with 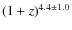$\Omega_{\rm IR}$ $\propto$  $(1+z)^{4.4\pm 1.0}$, which closely agrees with previous work at z < 1.2.

  • We investigated the differential contribution to  $\Omega_{\rm IR}$ by ULIRGs and LIRGs. We found that the ULIRG (LIRG) contribution increases by a factor of 10 (1.8) from z = 0.35 to z = 1.4, suggesting that IR galaxies are more dominant source of  $\Omega_{\rm IR}$ at higher redshift.

  • We estimated that $\Omega_{\rm IR}$ captures 80% of the cosmic star formation at redshifts less than 1, and virtually all of it at higher redshift. Thus adding the unobscured star formation detected at UV wavelengths would not change SFRD estimates significantly.

Acknowledgements
We are grateful to S.Arnouts for providing the LePhare code and kindly helping us in using the code. We thank the anonymous referee for many insightful comments, that significantly improved the paper. T.G. and H.I. acknowledge financial support from the Japan Society for the Promotion of Science (JSPS) through JSPS Research Fellowships for Young Scientists. H.M.L. acknowledges the support from KASI through its cooperative fund in 2008. T.T.T. has been supported by Program for Improvement of Research Environment for Young Researchers from Special Coordination Funds for Promoting Science and Technology and the Grant-in-Aid for the Scientific Research Fund (20740105) commissioned by the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan. T.T.T. has also been partially supported from the Grand-in-Aid for the Global COE Program ``Quest for Fundamental Principles in the Universe: from Particles to the Solar System and the Cosmos'' from the MEXT. This research is based on the observations with AKARI, a JAXA project with the participation of ESA. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this sacred mountain.

References

  1. Arnouts, S., Walcher, C. J., Le Fèvre, O., et al. 2007, A&A, 476, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Babbedge, T. S. R., Rowan-Robinson, M., Vaccari, M., et al. 2006, MNRAS, 370, 1159 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bavouzet, N., Dole, H., Le Floc'h, E., et al. 2008, A&A, 479, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bell, E. F., Papovich, C., Wolf, C., et al. 2005, ApJ, 625, 23 [NASA ADS] [CrossRef] [Google Scholar]
  5. Buat, V., Takeuchi, T. T., Iglesias-Páramo, J., et al. 2007, ApJS, 173, 404 [NASA ADS] [CrossRef] [Google Scholar]
  6. Calzetti D., Kennicutt, R. C., Jr., Bianchi, L., et al. 2005, ApJ, 633, 871 [NASA ADS] [CrossRef] [Google Scholar]
  7. Caputi, K. I., Lagache, G., Yan, L., et al. 2007, ApJ, 660, 97 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chary, R., & Elbaz, D. 2001, ApJ, 556, 562 [NASA ADS] [CrossRef] [Google Scholar]
  9. Coleman, G. D., Wu, C.-C., & Weedman, D. W. 1980, ApJS, 43, 393 [NASA ADS] [CrossRef] [Google Scholar]
  10. Dai, X., Assef, R. J., Kochanek, C. S., et al. 2009, ApJ, 697, 506 [NASA ADS] [CrossRef] [Google Scholar]
  11. Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]
  12. Desert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
  13. Flores, H., Hammer, F., Thuan, T. X., et al. 1999, ApJ, 517, 148 [NASA ADS] [CrossRef] [Google Scholar]
  14. Franceschini, A., Rodighiero, G., & Vaccari, M. 2008, A&A, 487, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Goto, T. 2005, MNRAS, 360, 322 [NASA ADS] [CrossRef] [Google Scholar]
  16. Goto, T., Hanami, H., Im, M., et al. 2008, PASJ, 60, 531 [Google Scholar]
  17. Goto, T., Koyama, Y., Wada, T., et al. 2010, A&A, 514, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Hopkins, A. M., Connolly, A. J., Haarsma, D. B., & Cram, L. E. 2001, AJ, 122, 288 [NASA ADS] [CrossRef] [Google Scholar]
  19. Huang, J.-S., Ashby, M. L. N., Barmby, P., et al. 2007, ApJ, 664, 840 [NASA ADS] [CrossRef] [Google Scholar]
  20. Huynh, M. T., Frayer, D. T., Mobasher, B., et al. 2007, ApJ, 667, L9 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
  23. Imai, K., Matsuhara, H., Oyabu, S., et al. 2007, AJ, 133, 2418 [NASA ADS] [CrossRef] [Google Scholar]
  24. Imai, K., Pearson, C. P., Matsuhara, H., et al. 2008, ApJ, 683, 45 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kennicutt, R. C., Jr. 1998, ARA&A, 36, 189 [Google Scholar]
  26. Lagache, G., Abergel, A., Boulanger, F., Désert, F. X., & Puget, J.-L. 1999, A&A, 344, 322 [NASA ADS] [Google Scholar]
  27. Lagache, G., Dole, H., & Puget, J.-L. 2003, MNRAS, 338, 555 [NASA ADS] [CrossRef] [Google Scholar]
  28. Le Floc'h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [NASA ADS] [CrossRef] [Google Scholar]
  29. Negrello, M., Serjeant, S., Pearson, C., et al. 2009, MNRAS, 394, 375 [NASA ADS] [CrossRef] [Google Scholar]
  30. Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
  31. Magnelli, B., Elbaz, D., Chary, R. R., et al. 2009, A&A, 496, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Matsuhara, H., Wada, T., Matsuura, S., et al. 2006, PASJ, 58, 673 [NASA ADS] [Google Scholar]
  33. Matsuhara, H., Wada, T., Pearson, C. P., et al. 2007, PASJ, 59, 543 [NASA ADS] [Google Scholar]
  34. Murakami, H., Baba, H., Barthel, P., et al. 2007, PASJ, 59, 369 [Google Scholar]
  35. Nakagawa, T. 2008, SPIE, 7010, [Google Scholar]
  36. Papovich, C., Rudnick, G., Le Floc'h, E., et al. 2007, ApJ, 668, 45 [NASA ADS] [CrossRef] [Google Scholar]
  37. Pérez-González, P. G., Rieke, G. H., Egami, E., et al. 2005, ApJ, 630, 82 [NASA ADS] [CrossRef] [Google Scholar]
  38. Pearson, C., et al. 2009, MNRAS, submitted [Google Scholar]
  39. Pearson, C., Oyabu, S., Wada, T., et al. 2010, A&A, 514, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Pope, A., Chary, R.-R., Alexander, D. M., et al. 2008, ApJ, 675, 1171 [Google Scholar]
  41. Pozzi, F., Gruppioni, C., Oliver, S., et al. 2004, ApJ, 609, 122 [NASA ADS] [CrossRef] [Google Scholar]
  42. Puget, J.-L., Abergel, A., Bernard, J.-P., et al. 1996, A&A, 308, L5 [NASA ADS] [Google Scholar]
  43. Rowan-Robinson, M., Mann, R. G., Oliver, S. J., et al., 1997, MNRAS, 289, 490 [NASA ADS] [CrossRef] [Google Scholar]
  44. Spinoglio, L., Malkan, M. A., Rush, B., Carrasco, L., & Recillas-Cruz, E. 1995, ApJ, 453, 616 [NASA ADS] [CrossRef] [Google Scholar]
  45. Rush, B., Malkan, M. A., & Spinoglio, L. 1993, ApJS, 89, 1 [NASA ADS] [CrossRef] [Google Scholar]
  46. Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] [Google Scholar]
  47. Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
  48. Saunders, W., Rowan-Robinson, M., Lawrence, A., et al. 1990, MNRAS, 242, 318 [NASA ADS] [CrossRef] [Google Scholar]
  49. Schiminovich, D., Ilbert, O., Arnouts, S., et al. 2005, ApJ, 619, L47 [NASA ADS] [CrossRef] [Google Scholar]
  50. Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef] [Google Scholar]
  51. Serjeant, S., Carramiñana, A., Gonzáles-Solares, E., et al. 2004, MNRAS, 355, 813 [NASA ADS] [CrossRef] [Google Scholar]
  52. Sullivan, M., Mobasher, B., Chan, B., et al. 2001, ApJ, 558, 72 [NASA ADS] [CrossRef] [Google Scholar]
  53. Sutherland, W., & Saunders, W. 1992, MNRAS, 259, 413 [NASA ADS] [CrossRef] [Google Scholar]
  54. Takagi, T., Matsuhara, H., Wada, T., et al. 2007, PASJ, 59, 557 [Google Scholar]
  55. Takagi, T., Ohyama, Y., Goto, T., et al. 2010, A&A, 514, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Takeuchi, T. T., Yoshikawa, K., & Ishii, T. T. 2000, ApJS, 129, 1 [Google Scholar]
  57. Takeuchi, T. T., Yoshikawa, K., & Ishii, T. T. 2003, ApJ, 587, L89 [NASA ADS] [CrossRef] [Google Scholar]
  58. Takeuchi, T. T., Buat, V., Iglesias-Páramo, J., Boselli, A., & Burgarella, D. 2005, A&A, 432, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Takeuchi, T. T., Buat, V., & Burgarella, D. 2005, A&A, 440, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Takeuchi, T. T., Ishii, T. T., Dole, H., et al. 2006, A&A, 448, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Taniguchi, Y., & Shioya, Y. 1998, ApJ, 501, L167 [NASA ADS] [CrossRef] [Google Scholar]
  62. Teplitz, H. I., Charmandaris, V., Chary, R., et al. 2005, ApJ, 634, 128 [NASA ADS] [CrossRef] [Google Scholar]
  63. Wada, T. 2008, cosp, 37, 3370 [Google Scholar]
  64. Wada, T., Oyabu, S., Ita, Y., et al. 2007, PASJ, 59, 515 [NASA ADS] [Google Scholar]
  65. Wada, T., Matsuhara, H., Oyabu, S., et al. 2008, PASJ, 60, 517 [NASA ADS] [Google Scholar]
  66. Wu, H., Cao, C., Hao, C.-N., et al. 2005, ApJ, 632, L79 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... dust[*]
This research is based on the observations with AKARI, a JAXA project with the participation of ESA.
...[*]
Based on data collected at Subaru Telescope, which is operated by the National Astronomical Observatory of Japan.
...[*]
JSPS SPD fellow.
... LePhare[*]
http://www.cfht.hawaii.edu/ arnouts/lephare.html

All Tables

Table 1:   Summary of filters used.

Table 2:   Best-fit parameters for 8, 12 ${\mu }$m, and TIR LFs.

All Figures

  \begin{figure} \par\includegraphics[width=6.5cm,clip]{13182fig1.ps} \end{figure} Figure 1:

Photometric redshift estimates with LePhare (Ilbert et al. 2009; Arnouts et al. 2007; Ilbert et al. 2006) for spectroscopically observed galaxies with Keck/DEIMOS (Takagi et al., in prep.). Red squares show objects where AGN templates were better fit. Errors of the photozs are $\frac{\Delta z}{1+z}$ = 0.036 for $z\leq 0.8$, but becomes worse at z> 0.8 to be $\frac{\Delta z}{1+z}$ = 0.10 mainly because of the relatively shallow near-IR data.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13182fig2.ps} \end{figure} Figure 2:

Photometric redshift distribution.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13182fig3.ps} \end{figure} Figure 3:

8 ${\mu }$m luminosity distributions of samples used to compute restframe 8 ${\mu }$m LFs. From low redshift, 533, 466, 236, and 59 galaxies are in each redshift bin.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13182fig4.ps} \end{figure} Figure 4:

Restframe 8 ${\mu }$m LFs based on the AKARI NEP-deep field. The blue diamons, purple triangles, red squares, and orange crosses show the 8 ${\mu }$m LFs at 0.38<z<0.58, 0.65<z<0.90, 1.1<z<1.4, and 1.8<z<2.2, respectively. AKARI's MIR filters can observe restframe 8 ${\mu }$m at these redshifts in a corresponding filter. Errorbars are from the Monte Carlo simulations (Sect. 2.4). The dotted lines show analytical fits with a double-power law. Vertical arrows show the 8 ${\mu }$m luminosity corresponding to the flux limit at the central redshift in each redshift bin. Overplotted are Babbedge et al. (2006) in the pink dash-dotted lines, Caputi et al. (2007) in the cyan dash-dotted lines, and Huang et al. (2007) in the green dash-dotted lines. AGNs are excluded from the sample (Sect. 2.2).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13182fig5.ps} \end{figure} Figure 5:

Evolution of TIR luminosity density computed by integrating the 8 ${\mu }$m LFs in Fig. 4.The red solid lines use the conversion in Eq. (4). The orange dashed lines use Eq. (3). Results from Le Floc'h et al. (2005) are shown with the cyan dotted lines.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13182fig6.ps} \end{figure} Figure 6:

Evolution of 8 ${\mu }$m IR luminosity density computed by integrating the 8 ${\mu }$m LFs in Fig. 4. The lowest redshift point is from Huang et al. (2007).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13182fig7.ps} \end{figure} Figure 7:

12 ${\mu }$m luminosity distributions of samples used to compute restframe 12 ${\mu }$m LFs. From low redshift, 335, 573, and 213 galaxies are in each redshift bin.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13182fig8.ps} \end{figure} Figure 8:

Restframe 12 ${\mu }$m LFs based on the AKARI NEP-deep field. The blue diamonds, purple triangles, and red squares show the 12 ${\mu }$m LFs at 0.15<z<0.35, 0.38<z<0.62, and 0.84<z<1.16, respectively. Vertical arrows show the 12 ${\mu }$m luminosity corresponding to the flux limit at the central redshift in each redshift bin. Overplotted are Pérez-González et al. (2005) at z = 0.3, 0.5 and 0.9 in the cyan dash-dotted lines, and Rush et al. (1993) at z = 0 in the green dash-dotted lines. AGNs are excluded from the sample (Sect. 2.2).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13182fig9.ps} \end{figure} Figure 9:

Evolution of 12 ${\mu }$m IR luminosity density computed by integrating the 12 ${\mu }$m LFs in Fig. 8.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13182fig10.ps} \end{figure} Figure 10:

TIR luminosity density computed by integrating the 12 ${\mu }$m LFs in Fig. 8.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13182fig11.ps} \end{figure} Figure 11:

An example of the SED fit. The red dashed line shows the best-fit SED for the UV-optical-NIR SED, mainly to estimate photometric redshift. The blue solid line shows the best-fit model for the IR SED at $\lambda>6~\mu$m, to estimate  $L_{\rm TIR}$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13182fig12.ps} \end{figure} Figure 12:

TIR luminosity is shown as a function of photometric redshift. The photo-z is estimated using UV-optical-NIR photometry. $L_{\rm TIR}$ isobtained through SED fit in 7-24 ${\mu }$m.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13182fig13.ps} \end{figure} Figure 13:

A histogram of TIR luminosity. From low-redshift, 144, 192, 394, and 222 galaxies are in 0.2 < z < 0.5, 0.5 < z < 0.8, 0.8 < z < 1.2, and  1.2 < z < 1.6, respectively.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13182fig14.ps} \end{figure} Figure 14:

TIR LFs. Vertical lines show the luminosity corresponding to the flux limit at the central redshift in each redshift bin. AGNs areexcluded from the sample (Sect. 2.2).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13182fig15.ps} \end{figure} Figure 15:

TIR luminosity density (red diamonds) computed by integrating the total LF in Fig. 14. The blue squares and orange triangles are only for LIRG and ULIRGs.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=13.5cm,clip]{13182fig16.ps} \end{figure} Figure 16:

Evolution of TIR luminosity density based on TIR LFs (red circles), 8 ${\mu }$m LFs (stars), and 12 ${\mu }$m LFs (filled triangles). The blue open squares and orange filled squares are for only LIRG and ULIRGs, also based on our $L_{\rm TIR}$ LFs. Overplotted dot-dashed lines are estimates from the literature: Le Floc'h et al. (2005), Magnelli et al. (2009), Pérez-González et al. (2005), Caputi et al. (2007), and Babbedge et al. (2006) are in cyan, yellow, green, navy, and pink, respectively. The purple dash-dotted line shows UV estimate by Schiminovich et al. (2005). The pink dashed line shows the total estimate of IR (TIR LF) and UV (Schiminovich et al. 2005).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=6.8cm,clip]{13182fig17.ps} \end{figure} Figure 17:

Contribution of $\Omega _{\rm TIR}$ to $\Omega _{\rm total}=\Omega _{\rm UV}+\Omega _{\rm TIR}$ is shown as a function of redshift.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.