EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 513 (April 2010) A&A, 513 (2010) A35 Full HTML
Free Access
Issue
A&A
Volume 513, April 2010
Article Number A35
Number of page(s) 17
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/200913444
Published online 21 April 2010
A&A 513, A35 (2010)

Chemical similarities between Galactic bulge and local thick disk red giants: O, Na, Mg, Al, Si, Ca, and Ti[*]

A. Alves-Brito1,2 - J. Meléndez3 - M. Asplund4 - I. Ramírez4 - D. Yong5

1 - Universidade de São Paulo, IAG, Rua do Matão 1226, Cidade Universitária, São Paulo 05508-900, Brazil
2 - Centre for Astrophysics and Supercomputing, Swinburne University of Technology, Hawthorn, Victoria 3122, Australia
3 - Centro de Astrofísica da Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
4 - Max Planck Institut für Astrophysik, Postfach 1317, 85741 Garching, Germany
5 - Research School of Astronomy and Astrophysics, The Australian National University, Cotter Road, Weston, ACT 2611, Australia

Received 9 October 2009 / Accepted 13 January 2010

Abstract
Context. The formation and evolution of the Galactic bulge and its relationship with the other Galactic populations is still poorly understood.
Aims. To establish the chemical differences and similarities between the bulge and other stellar populations, we performed an elemental abundance analysis of $\alpha $- (O, Mg, Si, Ca, and Ti) and Z-odd (Na and Al) elements of red giant stars in the bulge as well as of local thin disk, thick disk and halo giants.
Methods. We use high-resolution optical spectra of 25 bulge giants in Baade's window and 55 comparison giants (4 halo, 29 thin disk and 22 thick disk giants) in the solar neighborhood. All stars have similar stellar parameters but cover a broad range in metallicity ( $-1.5 <\rm [Fe/H] < +0.5$). A standard 1D local thermodynamic equilibrium analysis using both Kurucz and MARCS models yielded the abundances of O, Na, Mg, Al, Si, Ca, Ti and Fe. Our homogeneous and differential analysis of the Galactic stellar populations ensured that systematic errors were minimized.
Results. We confirm the well-established differences for [$\alpha $/Fe] at a given metallicity between the local thin and thick disks. For all the elements investigated, we find no chemical distinction between the bulge and the local thick disk, in agreement with our previous study of C, N and O but in contrast to other groups relying on literature values for nearby disk dwarf stars. For $-1.5 <\rm [Fe/H] < -0.3$ exactly the same trend is followed by both the bulge and thick disk stars, with a star-to-star scatter of only 0.03 dex. Furthermore, both populations share the location of the knee in the [$\alpha $/Fe] vs. [Fe/H] diagram. It still remains to be confirmed that the local thick disk extends to super-solar metallicities as is the case for the bulge. These are the most stringent constraints to date on the chemical similarity of these stellar populations.
Conclusions. Our findings suggest that the bulge and local thick disk stars experienced similar formation timescales, star formation rates and initial mass functions, confirming thus the main outcomes of our previous homogeneous analysis of [O/Fe] from infrared spectra for nearly the same sample. The identical $\alpha $-enhancements of thick disk and bulge stars may reflect a rapid chemical evolution taking place before the bulge and thick disk structures we see today were formed, or it may reflect Galactic orbital migration of inner disk/bulge stars resulting in stars in the solar neighborhood with thick-disk kinematics.

Key words: stars: abundances - Galaxy: abundances - Galaxy: bulge - Galaxy: disk - Galaxy: evolution

1 Introduction

The Galactic bulge is the least understood stellar population in the Milky Way, as even its classification (classical or pseudo-bulge; Kormendy & Kennicutt 2004) seems unclear. The Galactic bulge has signatures of an old (Ortolani et al. 1995; Zoccali et al. 2003) classical bulge formed rapidly during intensive star formation as reflected in the enhancement of $\alpha $-elements (e.g. McWilliam & Rich 1994; Cunha & Smith 2006; Zoccali et al. 2006; Lecureur et al. 2007; Fulbright et al. 2007; Meléndez et al. 2008; Ryde et al. 2009, 2010). On the other hand its boxy shape is consistent with a pseudo-bulge indicative of formation by secular evolution through dynamical instability of an already established inner disk.

Recently, Elmegreen et al. (2008) have shown that bulges formed by coalescence of giant clumps can have properties of both classical and pseudo-bulges, because secular evolution can take place in a very short timescale (<1 Gyr). They suggest that our Galactic bulge (and many $z \sim 2$ early disk galaxies; Genzel et al. 2008) formed this way, and that the bulge and thick disk may have formed at the same time. Thus, the nature of our Galactic bulge can be unveiled by detailed chemical composition analysis and by careful comparisons with the thick disk.

Although all recent works agree in enhancements of the $\alpha $-elements relative to solar abundances in bulge field K giants, the level of enhancement is currently under debate. Based on a comparison of bulge giant stars with thick disk dwarf stars, Zoccali et al. (2006), Lecureur et al. (2007) and Fulbright et al. (2007) suggested that the bulge and the thick disk have different chemical composition patterns, and that the $\alpha $-elements are overabundant in the bulge compared with the thick disk. Therefore, they argued for a shorter formation timescale and higher star formation rate for the Galactic bulge than that for the thick disk. Ballero et al. (2007) also concluded that the initial mass functions must have been different between the two populations based on both the high [Mg/Fe] and metallicity distribution of the bulge (see also Cescutti et al. 2009). Nevertheless, those comparisons should be taken with care as systematic errors may be present due to the very different stellar parameters, model atmospheres, and NLTE effects of dwarf and giant stars. Indeed, in our consistent analysis of high resolution infrared spectra of both bulge and thick disk giants with similar stellar parameters (Meléndez et al. 2008), we have shown that the bulge is in fact chemically very similar to the thick disk in [C/Fe], [N/Fe] and [O/Fe]. Here, we extend this work to other $\alpha $-elements (Mg, Si, Ti, Ca), and show that all the $\alpha $-elements in bulge and local thick disk giants have essentially identical chemical abundance patterns.

\begin{figure} \par\includegraphics[width=8cm,clip]{13444fg1.ps} \end{figure} Figure 1:

A $T_{\rm eff}-\log g$ diagram showing our program stars. The symbols are described in the plot. The two most luminous stars (filled triangles enclosed by circles) are bulge giants which show abundance anomalies like O-deficiency and Na-enhancement similar to those observed in some globular cluster stars. A typical error bar in $T_{\rm eff}$ and $\log g$ is shown.

Open with DEXTER

2 Observations

The sample consists of 80 cool giant stars (Fig. 1) with effective temperatures $3800 \le T_{\rm eff} \le 5000$ K, surface gravities $0.5 \le \log g \le 3.5$, and metallicities $-1.5 <\rm [Fe/H] < +0.5$. Similar number of thin disk (29), thick disk (22) and bulge (25) giants were selected, and a few (4) metal-rich halo giants were also included.

All of our bulge giants are located in Baade's window and are taken from Fulbright et al. (2006), who have cleaned the sample from nonbulge giants. For these bulge stars, we have already published an abundance analysis of C, N, O and Fe based on IR spectra (Meléndez et al. 2008). For the present study we make use of the equivalent widths measured in optical spectra using the HIRES spectrograph (at R = 45 000 or 67 000) on the Keck-I 10 m telescope by Fulbright et al. (2006, 2007).

To enable a proper comparison we have compiled a sample of thin disk, thick disk and halo stars for which we have obtained our own optical spectra. The assignment of population membership was based on UVW velocities (Bensby et al. 2004; Reddy et al. 2006). The sample selection was based on evaluating population membership in more than 1500 giant stars from the literature, in particular an updated version of the Cayrel de Strobel (2001) catalog (see Ramírez & Meléndez 2005a), the analysis of $\sim$180 clump giants by Mishenina et al. (2006), the study of $\sim$300 nearby giants by Luck & Heiter (2007), the survey of $\sim$380 giants by Hekker & Meléndez (2007), and the analysis of $\sim$320 giants by Takeda et al. (2008). Furthermore, the UVES library of stellar spectra (Bagnulo et al. 2003) was searched for suitable disk and halo giants.

Our analysis of thin disk, thick disk and halo stars is based mostly on high-resolution (R= 65 000) optical spectra taken in April 2007 with the MIKE spectrograph (Bernstein et al. 2003) on the Clay 6.5 m Magellan telescope, and complemented with observations using the 2dcoudé spectrograph (Tull et al. 1995, R = 60 000) on the 2.7 m Harlan J. Smith telescope at McDonald Observatory, the upgraded HIRES spectrograph (Vogt et al. 1994, R = 100 000) on the Keck I 10 m telescope, the UVES library[*] (Bagnulo et al. 2003, R = 80 000), and the ELODIE archive[*] (Moultaka et al. 2004, R = 42 000). The magnitudes, population membership and instrumentation used for the disk/halo sample are shown in Table 1.

The data were reduced with IRAF employing standard procedures: correction for bias, flat field, cosmic rays and background light, then optimal extraction of the spectra (using a bright star to trace the orders), wavelength calibration, barycentric and Doppler correction, and continuum normalization. In some cases, as described below, a variation to the reduction procedure was necessary. The tilt of the lines in the MIKE data is severe and varies across the CCD (e.g. Yong et al. 2006), therefore it must be carefully corrected to avoid degradation of the spectral resolution. The tilt was corrected using MTOOLS[*], specifically developed by J. Baldwin to account for the tilted slits in MIKE spectra. On the other hand, our HIRES spectra were extracted with a new version of MAKEE[*], an optimal extraction package developed by T. Barlow specifically for data reduction of the improved HIRES spectrograph. MAKEE also performs an automatic wavelength calibration cross-correlating the extracted ThAr spectra with a database of wavelength calibration solutions. Both the UVES and ELODIE archive data were already extracted and wavelength calibrated. The extracted spectra were shifted to the rest frame and continuum normalized using IRAF. The signal-to-noise ratio (S/N) per pixel of the reduced spectra ranges from $S/N \sim 45{-}100$ for the bulge giants (Fulbright et al. 2006), whereas for the disk and halo giants the S/N is typically $\sim$200 per pixel, ranging from $\sim$150 (2dCoude/McDonald) to $\sim$200 (MIKE/Magellan, ELODIE/OHP) to $\sim$250 (HIRES/Keck, UVES/VLT), as estimated from relatively line-free regions of the spectra.

Table 1:   Program stars data.

3 Abundance analysis

We have homogeneously performed all the equivalent width (EW) measurements for the disk and halo sample. In order to check that the EW measurements of the bulge giants by Fulbright et al. (2006, 2007) are consistent with our system for the disk and halo giants, we have observed one bulge star (IV-203) with the MIKE spectrograph and compared the EW measured by us with those obtained by Fulbright et al. (2006, 2007). The agreement is satisfactory, with a mean difference (this work - Fulbright et al. 2006, 2007) of -2.0 mÅ and a line-to-line scatter of $\sigma_{\rm QD}\footnote{We use here a robust standard deviation based on the ... ...= QD/1.349; see for example Abu-Shawiesh et~al. (\cite{AbuShawiesh09}).} = 5.5$ mÅ (Fig. 2a). Additionally, A. McWilliam has kindly made available to us the HIRES/Keck spectrum of another bulge giant (I-322) for comparison purposes. Again, the agreement is good with a difference (this work - Fulbright et al. 2006, 2007) of +2.2 m$\rm\AA$ and $\sigma_{\rm QD} = 5.5$ mÅ (Fig. 2b). Since most of the employed lines are relatively strong, the typical impact on abundances from these EW differences is negligible. Thus, the analysis of the faint bulge giants, the bright disk and the halo giants, is essentially in the same system.

\begin{figure} \par\includegraphics[width=8cm,clip]{13444fg2.ps} \end{figure} Figure 2:

Comparison of our equivalent width measurements with lines in common with Fulbright et al. (2006, 2007) for two bulge giant stars: a) IV-203 and b) I-322. The median (solid lines) and a robust proxy of standard deviation ( $\sigma _{\rm QD}$; dashed lines) are also displayed.

Open with DEXTER

Photometric temperatures were obtained using optical and infrared colors and the infrared flux method $T_{\rm eff}$-scale of Ramírez & Meléndez (2005b). We note that the new improved IRFM calibration of Casagrande et al. (2010) only applies to dwarf and subgiant stars and thus cannot be applied to our sample of giants. However, we do not expect any significant differences with respect to Ramírez & Meléndez (2005b) for the relevant stellar parameters, except perhaps for a small ($\sim$1%) zero-point offset in the $T_{\rm eff}$ scale, which is irrelevant here since we are performing a differential study.

Reddening for the bulge stars was estimated from extinction maps (Stanek 1996), while for the comparison sample both extinction maps (Meléndez et al. 2006b) and Na  I D ISM absorption lines were used. The E(B-V) values based on the D lines were obtained as follows. In the optical thin case the relation between column density N (units cm-2) and equivalent width EW (units mÅ) is

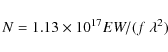
\begin{displaymath}N = 1.13 \times 10^{17} EW / (f ~ \lambda^2 ) \end{displaymath} (1)

(Spitzer 1968). The f values are 0.64 and 0.32, respectively, for the 5889.950 and 5895.924 Å lines (NIST database[*]). Note that the above relation between N(Na I) and equivalent width holds only for lines on the linear part of the curve of growth, i.e., for small values of E(B-V); for reddening larger than a few 0.01 mag the interstellar lines must be modeled in detail (e.g. Welty et al. 1994) to avoid underestimation of the column densities. In particular we use the profile fitting program FITS6P (Welty et al. 1994).

The N(Na I) density was transformed to N(H) with the relation found by Ferlet et al. (1985):

\begin{displaymath}{\rm log} N({\rm H I + H_2}) = ({\rm log} N({\rm Na I}) + 9.09) / 1.04, \end{displaymath} (2)

where both N(Na I) and N(H) are in cm-2. Finally, E(B-V) was computed from the total hydrogen density (Bohlin et al. 1978)

\begin{displaymath}E(B-V) = N({\rm H I + H_2}) / 5.8 \times 10^{21}, \end{displaymath} (3)

where N(H) is in cm-2 and E(B-V) in magnitudes. Although this relation seems not well established for E(B-V)<0.1, Ramirez et al. (2006) have shown it to be very accurate for a E(B-V)=0.01 star.

Albeit not used in the present work, we should mention for completeness that in addition to reddening maps and Na D interstellar lines, E(B-V) can also be estimated from other interstellar features such as the diffuse interstellar band at 862 nm (Munari et al. 2008), as well as multicolor photometry (e.g. Sect. 4.2 of Meléndez et al. 2006b; Ramírez et al. 2006) and polarization (e.g. Fosalba et al. 2002).

The stellar surface gravities were derived from improved Hipparcos parallaxes (Sneden 1973) for the sample of nearby giant stars and assuming a distance of 8 kpc for the bulge giants. In addition, Yonsei-Yale (Y2; Demarque et al. 2004) and Padova isochrones (da Silva et al. 2006) were employed to determine evolutionary gravities, as well as the input masses that were adopted for the trigonometric gravities. In order to estimate the Y2 gravities, we generated a fine grid of isochrones, assuming [$\alpha $/Fe] = 0 and +0.3 for $\rm [Fe/H] > 0$ and $\rm [Fe/H] < -1$, respectively, and linearly interpolated in between. All solutions allowed by the error bars were searched for, adopting as final result the median values. The Padova gravities were obtained using the Bayesian tool PARAM[*]. As shown in Fig. 3, both (Y2, Padova) evolutionary gravities agree excellently with the trigonometric gravities of our nearby giants with reliable (uncertainties $\le$10%) Hipparcos parallaxes. The evolutionary $\log g$ values required small zero-point corrections of -0.04 (Y2) and +0.07 dex (Padova), to be on the same scale as the Hipparcos-based results for our sample giant stars (Fig. 3). Bolometric corrections from Alonso et al. (1999) were adopted.

We used iron lines to check our $T_{\rm eff}$ and log g, but did not assume a priori that our adopted effective temperatures, surface gravities, 1D model atmospheres, gf-values, selection of lines, equivalent width measurements and LTE line formation, would result in absolute excitation (zero slope of Fe  I abundances vs. excitation potential) and ionization ( $A_{\rm FeI} = A_{\rm FeII}$) equilibria. We used the nearby disk/halo giants to determine the slopes (d $(A_{\rm FeI}) / {\rm d}(\chi_{\rm exc})$) and differences between Fe  I and Fe  II, followed by most stars. Our tests of the ionization and excitation balances of Fe  I and Fe  II lines revealed that most of the sample giants (58 stars) satisfy our relative spectroscopic equilibrium of iron lines within the uncertainties, therefore the overall agreement is encouraging. Nevertheless, the photometric stellar parameters of 22 stars (8 thin disk, 5 thick disk, 1 halo, and 8 bulge stars) required some adjustments to be on our relative spectroscopic equilibrium scale. The corrections based on the trend followed by the bright disk/halo giants, for which the photometric stellar parameters (and stellar spectra) were more reliable than for the bulge sample, is

\begin{displaymath}{\rm d}(A_{\rm FeI}) / {\rm d}(\chi_{\rm exc}) = 0.008 ~ {\rm dex \; eV^{-1} \;(Kurucz \; overshooting),} \end{displaymath} (4)

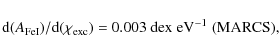
\begin{displaymath}{\rm d}(A_{\rm FeI}) / {\rm d}(\chi_{\rm exc}) = 0.003 ~ {\rm dex \; eV^{-1} \; (MARCS),} \end{displaymath} (5)

stars within 2-$\sigma$ ( $\sigma = 0.011$ dex eV-1) were considered to fulfill our relative excitation equilibrium. Ionization balance was achieved if

\begin{displaymath}A(Fe {\sc II}) - A(Fe {\sc I}) = 0.08 ~ {\rm dex \;(Kurucz \; overshooting),} \end{displaymath} (6)

\begin{displaymath}A(Fe {\sc II}) - A(Fe {\sc I}) = 0.00 ~ {\rm dex \;(MARCS),} \end{displaymath} (7)

and stars within $\pm 0.07$ dex were considered to fulfill our relative ionization equilibrium. After these corrections were performed the deviating thin disk, thick disk, halo and bulge stars have stellar parameters in the same system, i.e. in the Ramírez & Meléndez (2005b) temperature scale and $\log g$ in the Hipparcos scale.
\begin{figure} \par\includegraphics[width=8cm,clip]{13444fg3.ps} \end{figure} Figure 3:

Comparison between evolutionary gravities from Y2 (filled circles) and Padova (open circles) isochrones, and trigonometric gravities for giant stars with good ( $\sigma (\pi )/\pi \le 10$%) Hipparcos parallaxes. The solid and dashed lines depict perfect agreement and variations of $\pm $0.1 dex, respectively.

Open with DEXTER

The microturbulence was obtained by flattening any trend in the [FeI/H] versus reduced equivalent width diagram. The microturbulence follow tight relations with temperature and $\log g$(Fig. 4), with a scatter of only 0.20 km s-1:

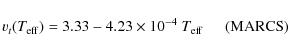
\begin{displaymath}v_t(T_{\rm eff}) = 3.33 - 4.23 \times 10^{-4} ~T_{\rm eff} \hspace*{5mm} {\rm (MARCS)} \end{displaymath} (8)

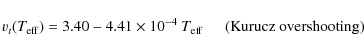
\begin{displaymath}v_t(T_{\rm eff}) = 3.40 - 4.41 \times 10^{-4} ~T_{\rm eff} \hspace*{5mm} {\rm (Kurucz \; overshooting)} \end{displaymath} (9)

\begin{displaymath}v_t({\rm log} ~ g) = 1.82 -0.186 \log g \hspace*{5mm} {\rm (MARCS)} \end{displaymath} (10)

\begin{displaymath}v_t({\rm log} ~ g) = 1.84 -0.202 \log g \hspace*{5mm} {\rm (Kurucz \; overshooting)}. \end{displaymath} (11)

The lines used for analysis (presented as online material) have been carefully selected to minimize the impact of blends. Completely avoiding blends is almost an impossible task in cool, relatively metal-rich giants as in our sample, since their spectra are heavily blended with many atomic and molecular lines (e.g. Coelho et al. 2005), in particular due to CN. We have tried to avoid blending by performing spectral synthesis of CN (using the line list of Meléndez & Barbuy 1999) and discarding the atomic lines whose equivalent widths are contaminated by more than 10% by CN. The cool giant Arcturus (Hinkle et al. 2000) was also carefully inspected to discard lines that are severely contaminated with other features. In some cases even lines which are blended by more than 10% have to be included, especially for elements other than iron because only a few useful lines were available. For heavily blended lines we have performed the measurements by fitting only the unblended part of the profile, or deblending the feature using two or more components. A preliminary version of our line list (Hekker & Meléndez 2007) has been tested in $\sim$380 field (Hekker & Meléndez 2007) and 39 open cluster (Santos et al. 2009) giants, and the final list has been already used in field bulge (Ryde et al. 2010) and globular cluster (Meléndez & Cohen 2009) giants.
\begin{figure} \par\includegraphics[width=8cm,clip]{13444fg4.ps} \end{figure} Figure 4:

Microturbulent velocity as a function of effective temperature ( upper panel) and log g ( lower panel). Giant stars with [Fe/H] < -0.70 and [Fe/H] $\geq $ -0.70 are, respectively, represented by filled and open circles. The solid line is a linear least squares fit to the data, whose results are labeled in the figure.

Open with DEXTER

Table 2:   Sensitivities in the abundance ratios by employing the Kurucz models (Castelli et al. 1997). The total internal uncertainties* are given in the last column.

The stellar chemical abundances were obtained from an equivalent width analysis using the 2002 version of MOOG (Sneden 1973). The same transition probabilities were applied to both the bulge and comparison samples. In the present work, we employed both Kurucz models with convective overshooting (Castelli et al. 1997) and specially calculated MARCS (Gustafsson et al. 2008) 1D hydrostatic model atmospheres. For the MARCS models, both $\alpha $-enhanced ( $[\alpha/{\rm Fe}]=+0.2$ and +0.4) and scaled-solar abundances models were constructed; for the Kurucz models, adjustments of [Fe/H] were applied to simulate the effects of $\alpha $-enhancement on the model atmospheres (Salaris et al. 1993):

\begin{displaymath}\Delta [{\rm Fe/H}] = \log \left(0.64 \times 10^{[\alpha/{\rm Fe}]} + 0.36\right). \end{displaymath} (12)

The effects of failing to account for the variations in $[\alpha/{\rm Fe}]$ are relatively small for a difference of $[\alpha/{\rm Fe}] = +0.1$ dex (Table 2), but could be important ($\sim$0.1 dex) for the typical enhancement of $[\alpha/{\rm Fe}]$ $\sim$+0.3-0.4 seen in thick disk, halo and bulge stars.

We estimate that our stellar parameters have typical uncertainties of $\Delta T_{\rm eff} \approx \pm 75$ K, $\Delta \log g \approx \pm 0.3$ dex and $\Delta v_{\rm t} \approx 0.2$ km s-1. The impact of these uncertainties on the abundance ratios, as well as the total abundance errors due to uncertainties in $T_{\rm eff}$, $\log g$, $v_{\rm t}$ and [$\alpha $/Fe] added in quadrature, are shown in Table 2, but note that some uncertainties are likely to be correlated to some degree (see, e.g., Fulbright et al. 2007). The uncertainties given in Table 2 are probably conservative in some cases, as shown by the relatively low scatter (as a function of metallicity) of our abundance ratios; the uncertainties in the abundance ratios [X/Fe] are probably $\leq$0.10 dex.

The uncertainty of $\pm $75 K in $T_{\rm eff}$ is the based on the upper and lower envelopes (excluding outliers) of the differences between the slopes of iron abundance vs. excitation potential ( ${\rm d}(A_{\rm FeI}) / {\rm d}(\chi_{\rm exc})$) of the initial photometric temperatures and the adopted zero-points (relations 4 and 5). Note that these differences are due not only to errors in the temperature calibrations, photometric errors and the quality of the spectra, but also to errors in E(B-V), which although low for the nearby giants, may be higher for the bulge giants. Nevertheless, since we corrected all outliers from our adopted zero-points (which in some cases may be due to incorrect reddenings), we are inmune to large errors in E(B-V). Our error of 0.3 dex in log g is based on the differences between FeII and FeI from the initial trigonometric log g and the adopted zero point in FeII-FeI (relations 6 and 7). Note that since we are basing our uncertainties on the upper and lower discrepancies of the initial input stellar parameters and the adopted zero-points, our uncertainties in $T_{\rm eff}$ and log g are conservative. For the bright disk/halo stars internal errors of 50 K in $T_{\rm eff}$ and 0.2 dex in log g may be more adequate. Ryde et al. (2010) suggested that the uncertainties adopted in the stellar parameters of our method (which was used to determine the atmospheric parameters in their sample) are sound for their bulge giants. In particular, uncertainties in $T_{\rm eff}$ higher than $\sim$75 K are excluded based on the relatively low star-to-star scatter of their [O/Fe] ratios.

No predictions of the effects of 3D hydrodynamical models instead of classical 1D models used here are available as yet for the exact stellar parameters of our targets (Asplund 2005). Collet et al. (2007) have performed such calculations for slightly less evolved red giants ( $T_{\rm eff} \approx 4700$ and $\log g \approx 2$) and found that the the 3D abundance corrections for the species considered herein are expected to be modest: $\vert\Delta \log \epsilon\vert \la 0.1$ dex at $[{\rm Fe/H}] \sim 0$. At lower metallicity the 3D effects become more severe so that at $\rm [Fe/H]=-1$ our 1D-based abundances could be in error by $\la $0.2 dex. However, given the similarity in parameters between the bulge and disk giants, the relative abundance ratio differences - which we are primarily interested in here - will be significantly smaller and thus inconsequential for our conclusions.

Of particular importance to our work are the adopted zero-points of our abundance scale. Most works use the Sun to define the zero-point of the thin disk at [Fe/H] = 0.0, but due to the differences between dwarfs and giants, this approach may introduce systematic errors. Instead, in the present work we use seven thin disk giants with $-0.1 <\rm [Fe/H] <+0.1$ dex (HD 29503, HD 45415, HD 99648, HD 100920, HD 115478, HD 186378, HD 214376) to define our zero points, which are shown in Table 3 for both the Kurucz and MARCS models. In Table 3 we also show for comparison a different abundance analysis of the Sun. As can be seen, our zero-points for Fe, Na and Ca agree with the solar abundances, but for O, Mg, and Si the giants show a higher zero-point by $\sim$+0.1 dex, and for Al differences as high as +0.15 are found. On the other hand, Ti is lower by $\sim$0.1 dex. These zero-point offsets of -0.1 to +0.15 dex show that it is not straightforward to compare abundances obtained in giants with those found in dwarfs.

These zero points we have found for giants are internal for our particular set of gf-values and analysis techniques. For comparison with chemical evolution models, the absolute zero-points should be adopted from an analysis of the Sun (Asplund et al. 2009), which represents well the local thin disk at [Fe/H] = 0.0, except for small peculiarities of a few 0.01 dex (Meléndez et al. 2009; Ramírez et al. 2009).

The final stellar parameters are given in Tables 4 and 5 for the MARCS and the Kurucz models, respectively, while the abundance ratios are given in Tables 6 and 7. The equivalent width measurements are given in Tables 8-15, which are only available in electronic form at the CDS.

Table 3:   Internal zero-point abundances adopted for our giant stars using MARCS and Kurucz models.

Table 4:   Final atmospheric parameters using the MARCS models.

Table 5:   Final atmospheric parameters using the Kurucz models.

 

Table 6:   Abundance ratios using the MARCS models.

 

Table 7:   Abundance ratios using the Kurucz models.

4 Results

In Fig. 5 we show the [O/Fe] ratios obtained in this work for both MARCS and Kurucz overshooting model atmospheres. As can be seen, there is a good overall agreement between MARCS and Kurucz models. In particular, the difference in iron abundance (MARCS - Kurucz) is only -0.02 dex ( $\sigma = 0.03$ dex). Thus we present results based on the MARCS models only in the following figures. Even though both sets of models give similar chemical abundance ratios (see Tables 6 and 7), for comparison with chemical evolution models we suggest to adopt the MARCS results, since they were computed with the correct [$\alpha $/Fe] ratio. Our disk/halo comparison sample shows that the oxygen abundances obtained here from the [O  I] 630 and 636 nm lines and in Meléndez et al. (2008) from infrared OH lines are in excellent agreement. The mean difference is only -0.04 dex (OH - [O  I]) with a scatter of 0.10 dex. Since this is identical to the estimated error in [O/Fe] from OH found in Meléndez et al. (2008), the uncertainties in our stellar parameters are likely somewhat overestimated, as already discussed above. Although the oxygen abundances obtained from [O  I] and OH lines agree well, the results obtained from OH lines have less scatter, possibly because several OH lines were used instead of relying on only one or two forbidden lines. Therefore, for comparisons of oxygen abundances with detailed chemical evolution models of the thin disk, thick disk and bulge, we believe that the OH lines are preferable (Meléndez et al. 2008; Ryde et al. 2009, 2010). The [O  I]-based oxygen abundances confirm the similarity between the bulge and the local thick disk, which we previously demonstrated based on OH lines. This is in contrast to some previous works on the topic (Zoccali et al. 2006; Fulbright et al. 2007; Lecureur et al. 2007), which argue that [O/Fe] in the bulge is higher than in the thick disk based on a comparison to disk dwarf stars.

\begin{figure} \par\includegraphics[width=8cm,clip]{13444fg5.ps} \vspace*{-3mm}\end{figure} Figure 5:

[O/Fe] vs. [Fe/H] for the sample stars employing MARCS ( top) and Kurucz ( bottom) model atmospheres. Symbols are as explained in the figure. Note however that hereafter the bulge stars I-264 and IV-203 are omitted from all figures (refer to the text for detail).

Open with DEXTER
\begin{figure} \par\includegraphics[width=8cm,clip]{13444fg6.ps} \end{figure} Figure 6:

[Mg/Fe] as a function of [Fe/H] for MARCS model atmospheres. Symbols as explained in the figure.

Open with DEXTER

As pointed out by Fulbright et al. (2007), two O-deficient stars (I-264 and IV-203) at $[{\rm Fe/H}] \approx -1.25$ have peculiar abundances similar to the O-Na anti-correlation seen in globular clusters (e.g. Gratton et al. 2004; Cohen & Meléndez 2005; Yong et al. 2005; Carretta et al. 2009). Fulbright et al. (2007) found that these two giants have high Na and Al abundances reminiscent of the abundance anomalies seen in globular clusters, which we confirm. Thus, the oxygen abundances of these two stars most likely do not reflect the typical bulge composition.

The results for the other $\alpha $-elements (Mg, Si, Ca, Ti) studied here are shown in Figs. 6-9. As can be clearly seen, the chemical patterns of the bulge and thick disk are indistinguishable also for those elements, reinforcing our previous findings based on oxygen abundances. The average of our Mg abundances for the seven stars with [Fe/H] $\ge$ 0 is [Mg/Fe] = 0.1 $\pm $ 0.1, in good agreement with the results from microlensed bulge dwarfs, which typically have $\rm [Mg/Fe]\approx +0.1$(Cohen et al. 2008, 2009; Johnson et al. 2008; Bensby et al. 2009). The latest preliminary results based on microlensed bulge dwarf stars (Bensby et al. 2010) also indicate similarities between the bulge and thick disk for Ti and Mg at all probed metallicities ( $-0.8 <\rm [Fe/H] < +0.5$).

\begin{figure} \par\includegraphics[width=8cm,clip]{13444fg7.ps} \end{figure} Figure 7:

[Si/Fe] vs. [Fe/H] for MARCS model atmospheres. Symbols as explained in the figure.

Open with DEXTER

Even clearer results were found when we combined the results for all $\alpha $-elements, as shown in Fig. 10. It is clear that the chemical patterns of the bulge and thick disk are indistinguishable in their abundance patterns up to the metallicity range where the thick disk is unambiguously identified, i.e., up to $[{\rm Fe/H}]\approx -0.3$. Bensby et al. (2003, 2004) reported the existence of a knee connecting thick-disk stars from $\rm [Fe/H]\approx -0.3$ and high [$\alpha $/Fe] to [Fe/H] > 0.0 and low [$\alpha/$Fe], but Reddy et al. (2006) and Ramírez et al. (2007) did not find any evidence of such a knee. A re-examination of the latter results including new observations of kinematically selected thick-disk metal-rich objects is underway (Reddy et al., in preparation) and will address this discrepancy. The problem is that at high [Fe/H] there is a significant number of thick-disk candidates that follow the thin disk abundance pattern. This suggests that hot kinematics alone cannot be used to separate the thin from the thick disk, especially at high [Fe/H]. At super-solar metallicities the problem may be unsolvable because the abundance patterns of both disks merge. Interestingly, the chemical similarities between the Galactic bulge and the local thick disk giant stars we find in this work in fact extend to super-solar metallicities. Yet, as explained above, it remains to be demonstrated that the few selected thick disk stars are bona fide thick disk members rather than kinematically heated thin disk stars.

From Table 1 we see that three giants, which are kinematically classified as thick disk (HD 77236, HD 107328) and thin disk (HD 30608) members, present ambiguous kinematical population. The star HD 77236 could be either a thick disk/halo star, while the stars HD 107328 and HD 30608 both have similar likelihood of belonging to the thin or thick disk populations. These stars have [Fe/H] = (-0.67, -0.43, -0.28) and [$\alpha $/Fe] = (+0.33, +0.30, +0.08), respectively, which means that both HD 77236 and HD 107328 could indeed be thick disk stars, while the star HD 30608 has an abundance pattern consistent with a thin disk star at [Fe/H] $\sim$ -0.3.

\begin{figure} \par\includegraphics[width=8cm,clip]{13444fg8.ps} \end{figure} Figure 8:

[Ca/Fe] vs. [Fe/H] for MARCS model atmospheres. Symbols as explained in the figure.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.3cm,clip]{13444fg9.ps} \end{figure} Figure 9:

Plot of [Ti/Fe] against [Fe/H] for the sample stars employing MARCS model atmospheres. Symbols are as explained in the figure.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.3cm,clip]{13444fg10.ps} \end{figure} Figure 10:

Mean $\alpha $-elements abundance ratio ([(O, Mg, Si, Ca, Ti)/Fe]) as a function of [Fe/H] for MARCS model atmospheres. Symbols as explained in the figure.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.3cm,clip]{13444fg11.ps} \vspace*{-4mm} \end{figure} Figure 11:

Fit of [$\alpha $/Fe] vs. [Fe/H] for metal-poor ( $\rm [Fe/H] < -0.5$) and metal-rich ( $\rm [Fe/H] \ge -0.5$) bulge ( top), thick disk (center) and both bulge and thick disk (bottom) stars. Both stellar populations can be fitted by similar relations, with a scatter as low as $\sigma = 0.03$ dex.

Open with DEXTER

Linear fits of both the bulge and the thick disk [$\alpha $/Fe] vs. [Fe/H] relations up to [Fe/H] = -0.3, show that both populations follow identical patterns, with a star-to-star scatter of only $\sigma = 0.03$ dex. We thus set the most stringent constraints to date on the chemical similarity of bulge and local thick disk stars. The metallicity of the bulge extends to significantly higher [Fe/H] than that, which remains to be convincingly demonstrated for the thick disk, as previously discussed.

In order to quantify how similar the bulge and the thick disk are at all metallicities, we divided the stars in a metal-poor and a metal-rich sample with the division set somewhat arbitrarily at $\rm [Fe/H] = -0.5$, and we performed linear fits of [$\alpha $/Fe] vs. [Fe/H]. We found that the metal-poor part of both stellar populations can be fitted by essentially identical relations (Fig. 11): [$\alpha $/Fe] = 0.22- $0.10 \times\rm [Fe/H]$for the bulge ( $\sigma = 0.03$ dex) and [$\alpha $/Fe] = 0.27- $0.07 \times \rm [Fe/H]$ for the thick disk ( $\sigma = 0.03$ dex). These relations are identical to within $\pm $0.01 dex at [Fe/H] = -1.5and to within $\pm $0.02 dex at $\rm [Fe/H] = -0.5$, hence both datasets can be fitted by a single relation followed by both stellar populations:

\begin{displaymath}{\rm [\alpha/Fe] = 0.268 -0.065 \times [Fe/H] \; \; ([Fe/H] < -0.5)}, \end{displaymath} (13)

with a very low star-to-star scatter of only 0.03 dex (Fig. 11).

A similar exercise for the most metal-rich bulge and thick disk stars with $\rm [Fe/H] \geq -0.5$ results in a single relation followed by both stellar populations (Fig. 11):

\begin{displaymath}{\rm [\alpha/Fe] = 0.104 -0.381 \times [Fe/H] \; \; ([Fe/H] \geq -0.5)}, \end{displaymath} (14)

with a low star-to-star scatter of only 0.06 dex (Fig. 11). This scatter is higher than for the more metal-poor stars ( $\sigma = 0.03$ dex), but fully explained by the higher uncertainties in the analysis of the more crowded spectra of the metal-rich stars. Nevertheless, we do not discard that there may be some contamination in the metal-rich samples. We demonstrate thus that at all probed metallicities ( $-1.5 <\rm [Fe/H] < +0.5$) of both the bulge and thick disk stellar populations have a striking chemical similarity.

The Al abundances of the most metal-rich bulge stars ([Fe/H] $\gtrsim$ 0) seem enhanced ([Al/Fe] $\sim$ +0.25), but Na seems solar (although with a large scatter) at these metallicities, as illustrated in Figs. 12, 13. Thus, the enhancement in Al in metal-rich bulge giants is probably not related to the Al-Na correlation seen in globular clusters, but is most likely due to the fact that the two Al  I lines employed are blended and are more difficultto deblend in the relatively moderate S/N spectra of the metal-rich bulge giants. This is reinforced by recent studies of metal-rich bulge dwarfs through microlensing (Cohen et al. 2008; Johnson et al. 2008; Bensby et al. 2009), which find [Al/Fe] $\sim$ +0.10 dex. Thus, our Al abundances for bulge stars with [Fe/H] $\gtrsim$ 0 are likely affected by systematic errors, which should be borne in mind in comparisons with chemical evolution models.

\begin{figure} \par\includegraphics[width=7.3cm,clip]{13444fg12.ps} \end{figure} Figure 12:

[Na/Fe] vs. [Fe/H] for MARCS model atmospheres. Symbols as explained in the figure.

Open with DEXTER

\begin{figure} \par\includegraphics[width=7.3cm,clip]{13444fg13.ps} \end{figure} Figure 13:

[Al/Fe] vs. [Fe/H] for MARCS model atmospheres. Symbols as explained in the figure.

Open with DEXTER

5 Discussion

Our previous homogeneous abundance analysis of OH lines in high resolution infrared Gemini+Phoenix spectra was the first to show that the Galactic bulge and the local thick disk have indistinguishable [O/Fe] trends up to at least metallicities $\rm [Fe/H]\approx -0.3$ where the thick disk is unambiguously identified (Meléndez et al. 2008). In the present work we analyzed the forbidden oxygen lines and demonstrated that those indeed give consistent results with the OH lines. Importantly, we also extended the conclusions of Meléndez et al. (2008) to other $\alpha $-elements (Mg, Si, Ca, Ti). The $\alpha $-elements in the bulge and local thick disk stars are the same in the range $-1.5 <\rm [Fe/H] < -0.3$, showing a very low star-to-star scatter in [$\alpha $/Fe] of only 0.03 dex. Similarly, the [Na/Fe] and [Al/Fe] trends agree well for the bulge and the local thick disk, although this is not too surprising given that there is no obvious offset between the thick and thin disk for those two elements.

Previous works (Fulbright et al. 2007; Lecureur et al. 2007) have found high [Mg/Fe] ratios in bulge stars, as well as high [X/Fe] ratios in other elements with respect to the thick disk. It may seem surprising that using the same equivalent widths as Fulbright et al. (2007) we find significantly lower [Mg/Fe] in bulge giants at all metallicities. However, as mentioned in Sect. 3, the zero-points we use in our analysis are based on seven thin disk solar metallicity giants, which, as shown in Table 3, are not the same as the zero-points based on the Sun, which is $\sim$1400 K hotter and has a surface gravity $\sim$300 times higher than our giants. The differences shown in Table 3 between the Sun and our giants could be due to the different impact of 3D and non-LTE effects on giant and dwarfs, as well as to problems with line blending in giants. Furthermore, since we compare bulge giants to thick disk giants, our conclusions on the similarity of the bulge and thick disk is independent of the adopted zero-point, unlike the comparisons of Zoccali et al. (2006), Fulbright et al. (2007) and Lecureur et al. (2007), who compared bulge giants to disk dwarfs. Although both Fulbright et al. (2007) and Lecureur et al. (2007) used the giants Arcturus ( $\rm [Fe/H] \sim -0.5$) and $\mu$ Leo ( $\rm [Fe/H] \sim+0.3$) as reference stars, their zero-points are ultimately based on the Sun[*], which as shown in Table 3, may be inadequate for the study of giants. It is important to mention that Fulbright et al. (2007) also included 17 nearby disk giants (mostly from the thin disk) to check whether they follow the same abundance pattern as disk dwarfs, but most of their giants were observed at a lower resolving power, $R \sim 30~000$, implying higher errors in the abundances obtained from the crowded spectra of metal-rich giant stars. Furthermore, their comparison sample of disk dwarfs included several studies which may have different systematic offsets between them. For example the study by Reddy et al. (2003) used Strömgren photometry to estimate effective temperatures using the (b-y) calibration by Alonso et al. (1996). However, as recently shown by Meléndez et al. (2010, in preparation) using uvby-$\beta$ photometry of solar twins, this calibration has a zero-point error of 130 K. In turn, this implies abundance variations ($\Delta$[X/H]) from -0.12 dex (O based on OI triplet, which was the main abundance indicator used by Reddy et al. 2003) to +0.13 dex (Ti). Yet, due to a compensating change in iron, for most elements studied here (except for [O/Fe] that is affected by -0.22 dex; based on the OI triplet), the $\Delta$[X/Fe] ranges from -0.08 dex ([Si/Fe]) to +0.03 dex ([Ti/Fe]). On the other hand, Bensby et al. (2003, 2004) adopted spectroscopic temperatures, therefore not only their Teff but also their [X/Fe] abundance ratios are likely more accurate for comparison of these reddened bulge regions.

Thus, the main reason why our conclusions regarding the abundance trends in the bulge in comparison with the thick and thin disk differ from the findings of previous studies (e.g. Zoccali et al. 2006; Fulbright et al. 2007; Lecureur et al. 2007) is that we perform a strictly differential analysis of red giants with very similar parameters for all populations rather than relying on either literature data or using dwarf stars for the disk samples. We therefore bypass several potential systematic errors that can scupper any analysis (e.g. 3D, non-LTE, stellar parameters, gf-values, see discussion in Asplund 2005). It is also worth noting that Bensby et al. (2010) have shown that microlensed dwarfs in the Galactic bulge present [$\alpha $/Fe] abundance ratios similar to those of dwarfs in the Galactic thick disk, which agrees with our results for giant stars.

\begin{figure} \par\includegraphics[width=7.3cm,clip]{13444fg14.ps} \end{figure} Figure 14:

[C/O] vs. [O/H] for the bulge ( triangles), thick disk ( filled circles) and thin disk ( open circles) with data taken from Meléndez et al. (2008) and Ryde et al. (2010). The original (undepleted) C abundances were estimated from C+N (refer to the text). Overplotted we show model predictions as given in Cescutti et al. (2009, cf. their Fig. 5).

Open with DEXTER

The identical enhancement of the $\alpha $-elements in the bulge and the local thick disk - including the location of the knee that canonically is supposed to reflect the start of significant contribution of Fe production from SNe Ia - argues that the two stellar populations not only shared a similar star formation rate but also initial mass function, in contrast to the conclusions of some recent studies (e.g. Ballero et al. 2007; McWilliam et al. 2008; Cescutti et al. 2009). We emphasize that this similarity does not automatically imply a casual connection between the bulge and the local thick disk, but it would be worthwhile to explore this possibility further, in particular since such a relationship has been proposed for other spiral galaxies (e.g. van der Kruit & Searle 1981). A rewarding avenue to pursue would be the effects of Galactic radial migration (e.g. Sellwood & Binney 2002; Haywood 2008; Roskar et al. 2008; Schönrich & Binney 2009a,b). We note especially the hypothesis by Schönrich & Binney (2009b) that the thick disk is a natural consequence of radial mixing, i.e. the thick disk stars in the solar neighborhood originated in the inner part of the Galaxy. It would therefore be particularly interesting to carry out a detailed chemical analysis of a sample of in-situ inner disk stars to investigate any chemical similarities with the bulge and the local thick disk giants studied herein.

\begin{figure} \par\includegraphics[width=8cm,clip]{13444fg15.ps} \end{figure} Figure 15:

[O/Mg] as a function of [Fe/H] ( top panel) and [Mg/H] ( bottom panel). Symbols as explained in the figure.

Open with DEXTER

McWilliam et al. (2008) have argued that their observed steadily declining [O/Mg] vs. [Mg/H] trends for both the bulge and the solar vicinity are the result of metallicity-dependent O yields due to mass-loss in massive stars, possibly augmented by stellar rotation (e.g. Maeder 1992; Meynet & Maeder 2002). Since these stellar winds remove C that would otherwise be converted to O, the decreasing O production should be accompanied by enhanced C yields. Cescutti et al. (2009) have extended the chemical modeling of McWilliam et al. by investigating the resulting [C/O] trends. Although neither of their models match the observed [C/O] vs. [O/H] ratios for the bulge or disk in detail, they argue that the observations support the metallicity-dependent yields of massive stars.

In Fig. 14 we plot the [C/O] vs. [O/H] ratios of bulge and disk stars based on Melendez et al. (2008) and Ryde et al. (2010), which are both in similar abundance scales. As in Cescutti et al. (2009), the primordial C abundances were estimated by adding C+N and subtracting a ``primordial'' N abundance assuming [N/Fe] = 0. As can be seen, none of the Cescutti et al. models provide a good fit to the data. As mentioned by them, adopting an IMF not as skewed to massive stars as that adopted by Ballero et al. (2007) may help to alleviate the discrepancy, but on the other hand it may ruin their fit to the bulge metallicity distribution.

Regarding the [O/Mg] ratios, our own observational data paint a somewhat different picture than the one presented by McWilliam et al. (2008) and Cescutti et al. (2009). Figure 15 shows our [O/Mg] results against both [Fe/H] and [Mg/H]. All three populations - bulge, thick and thin disk - are similar up to at least solar metallicity and follow an essentially flat trend with $\rm [O/Mg]\approx 0.0{-}0.1$. The similarities between the thick and thin disks extend even further provided the few stars with $\rm [Fe/H] > 0$ classified as belonging to the thick disk kinematically are truly bona-fide members. There is some indication that for the bulge [O/Mg] becomes negative for super-solar metallicities in line with the findings of Lecureur et al. (2007) and McWilliam et al. (2008). They claim however an essentially continuous downward trend over the entire metallicity span of their sample while we find a flat trend with a possible break around solar [Fe/H]. Nevertheless, a comparison between Fulbright et al. (2007) and our [O/Mg] ratios for bulge giants (Fig. 16), shows that their [O/Mg] ratios actually do not have a continuous downward trend, but instead their data show a shallow trend up to $\rm [Fe/H] \sim +0.1$, and then a steep decrease for higher metallicities. Thus, both Fulbright et al. (2006, 2007) and our own analysis shows that there may be a break around solar metallicity in the [O/Mg] ratios. However, none of the models presented in Cescutti et al. (2009) shows the sharp break around solar metallicity indicated by the bulge giants (Fig. 16). The existence of this break would have to be confirmed by a significantly larger bulge sample than we have access to here; adding the most metal-rich stars from the Lecureur et al. study would be worthwhile in this respect (as mentioned earlier, our bulge sample consists of the stars observed by Fulbright et al. 2006, 2007). If real, the downward trend could be a manifestation of metallicity-dependent O yields due to mass-loss in massive stars.

\begin{figure} \par\includegraphics[width=8cm,clip]{13444fg16.ps}\vspace*{-2mm} \end{figure} Figure 16:

[O/Mg] as a function of [Fe/H] for bulge giants according to Fulbright et al. (2007) (open triangles) and our work (filled triangles). Both studies show a shallow trend up to about solar metallicity and a step decrease in [O/Mg] for higher metallicities. Recent predictions by Cescutti et al. (2009) are shown as solid (WW95 model), short dashed (WW95+M92), long dashed (WW95+MM02) and dot-short dashed (MM02) lines. All models have been shifted by -0.2 dex in [O/Mg] (see Cescutti et al. 2009, for a description of the models and an explanation of the empirical offset).

Open with DEXTER

Acknowledgements
AAB acknowledges CAPES for financial support 4685-06-7 (PDE) and a FAPESP fellowship No. 04/00287-9. We would like to thank the anonymous referee for helpful constructive comments on the paper. Likewise, we are grateful to A. McWilliam for sharing the Keck spectrum of one bulge star used for comparison purposes, and G. Cescutti for sending the models shown in Figs. 14 and 16. This work has been supported by the Australian Research Council (DP0588836), ANSTO (06/07-0-11), National Science Foundation (AST 06-46790), and the Portuguese FCT/MCTES (project PTDC/CTE-AST/65971/2006). J.M. is supported by a Ciencia 2007 contract funded by FCT/MCTES (Portugal) and POPH/FSE (EC). Based partly on observations obtained at the Las Campanas Magellan telescopes (through Australian time with travel support provided by the Australian Access to Major Facilities Programme 06/07-O-11), Keck Observatory (operated jointly by the California Institute of Technology, the University of California and the National Aeronautics and Space Administration) and McDonald Observatory.


References

  1. Abu-Shawiesh, M. O., Al-Athari, F. M., & Kittani, H. F. 2009, J. Appl. Sci., 9, 2835 [CrossRef] [Google Scholar]
  2. Alonso, A., Arribas, S., & Martínez-Roger, C. 1996, A&AS, 313, 873 [Google Scholar]
  3. Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
  5. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bagnulo, S., Jehin, E., Ledoux, C., et al. 2003, The Messenger, 114, 10 [NASA ADS] [Google Scholar]
  7. Ballero, S. K., Matteucci, F., Origlia, L., & Rich, R. M. 2007, A&A, 467, 123 [Google Scholar]
  8. Bensby, T., Feltzing, S., & Lundström, I. 2003, A&A, 410, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bensby, T., Feltzing, S., & Lundström, I. 2004, A&A, 415, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bensby, T., Johnson, J. A., Cohen, J., et al. 2009, A&A, 499, 737 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bensby, T., Feltzing, S., Johnson, J. A., et al. 2010, A&A, 512, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bernstein, R., Shectman, S. A., Gunnels, S. M., Mochnacki, S., & Athey, A. E. 2003, Proc. SPIE, 4841, 1694 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
  14. Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 [NASA ADS] [Google Scholar]
  17. Cayrel de Strobel, G., Soubiran, C., & Ralite, N. 2001, A&A, 373, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Cescutti, G., Matteucci, F., McWilliam, A., & Chiappini, C. 2009, A&A, 505, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Coelho, P., Barbuy, B., Meléndez, J., Schiavon, R. P., & Castilho, B. V. 2005, A&A, 443, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Cohen, J. G., & Meléndez, J. 2005, AJ, 129, 303 [NASA ADS] [CrossRef] [Google Scholar]
  21. Cohen, J. G., Huang, W., Udalski, A., Gould, A., & Johnson, J. A. 2008, ApJ, 682, 1029 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cohen, J. G., Thompson, I. B., Sumi, T., et al. 2009, ApJ, 699, 66 [NASA ADS] [CrossRef] [Google Scholar]
  23. Collet, R., Asplund, M., & Trampedach, R. 2007, A&A, 469, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Cunha, K., & Smith, V. V. 2006, ApJ, 651, 491 [NASA ADS] [CrossRef] [Google Scholar]
  25. da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Demarque, P., Woo, J.-H., Kim, Y.-C., & Yi, S. K. 2004, ApJS, 155, 667 [NASA ADS] [CrossRef] [Google Scholar]
  27. Elmegreen, B. G., Bournaud, F., & Elmegreen, D. M. 2008, ApJ, 688, 67 [NASA ADS] [CrossRef] [Google Scholar]
  28. Ferlet, R., Vidal-Madjar, A., & Gry, C. 1985, ApJ, 298, 838 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fosalba, P., Lazarian, A., Prunet, S., & Tauber, J. A. 2002, ApJ, 564, 762 [NASA ADS] [CrossRef] [Google Scholar]
  30. Fulbright, J. P., McWilliam, A., & Rich, R. M. 2006, ApJ, 636, 821 [NASA ADS] [CrossRef] [Google Scholar]
  31. Fulbright, J. P., McWilliam, A., & Rich, R. M. 2007, ApJ, 661, 1152 [NASA ADS] [CrossRef] [Google Scholar]
  32. Genzel, R., Burkert, A., Bouché, N., et al. 2008, ApJ, 687, 59 [NASA ADS] [CrossRef] [Google Scholar]
  33. Gratton, R. G., & Sneden, C. 1990, A&A, 234, 366 [NASA ADS] [Google Scholar]
  34. Gratton, R., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
  35. Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
  36. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Haywood, M. 2008, MNRAS, 388, 1175 [NASA ADS] [CrossRef] [Google Scholar]
  38. Hekker, S., & Meléndez, J. 2007, A&A, 475, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Hinkle, K., Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near Infrared Atlas of the Arcturus Spectrum 3727-9300 A, ed. K. Hinkle, L. Wallace, J. Valenti, & D. Harmer (San Francisco: ASP) [Google Scholar]
  40. Kormendy, J., & Kennicutt, Jr., R. C. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
  41. Johnson, J. A., Gaudi, B. S., Sumi, T., Bond, I. A., & Gould, A. 2008, ApJ, 685, 508 [NASA ADS] [CrossRef] [Google Scholar]
  42. Lecureur, A., Hill, V., Zoccali, M., et al. 2007, A&A, 465, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Luck, R. E., & Heiter, U. 2007, AJ, 133, 2464 [NASA ADS] [CrossRef] [Google Scholar]
  44. Maeder, A. 1992, A&A, 264, 105 [NASA ADS] [Google Scholar]
  45. McWilliam, A., & Rich, R. M. 1994, ApJS, 91, 749 [NASA ADS] [CrossRef] [Google Scholar]
  46. McWilliam, A., Matteucci, F., Ballero, S., et al. 2008, AJ, 136, 367 [NASA ADS] [CrossRef] [Google Scholar]
  47. Meléndez, J., & Barbuy, B. 1999, ApJS, 124, 527 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  48. Meléndez, J., & Ramírez, I. 2007, ApJ, 669, L89 [NASA ADS] [CrossRef] [Google Scholar]
  49. Meléndez, J., & Cohen, J. G. 2009, ApJ, 699, 2017 [NASA ADS] [CrossRef] [Google Scholar]
  50. Meléndez, J., Dodds-Eden, K., & Robles, J. A. 2006a, ApJ, 641, L133 [NASA ADS] [CrossRef] [Google Scholar]
  51. Meléndez, J., Shchukina, N. G., Vasiljeva, I. E., & Ramírez, I. 2006b, ApJ, 642, 1082 [NASA ADS] [CrossRef] [Google Scholar]
  52. Meléndez, J., Asplund, M., Alves-Brito, A., et al. 2008, A&A, 484, L21 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  53. Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, ApJ, 704, L66 [NASA ADS] [CrossRef] [Google Scholar]
  54. Meynet, G., & Maeder, A. 2002, A&A, 390, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Mishenina, T. V., Bienaymé, O., Gorbaneva, T. I., et al. 2006, A&A, 456, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Moultaka, J., Ilovaisky, S. A., Prugniel, P., & Soubiran, C. 2004, PASP, 116, 693 [NASA ADS] [CrossRef] [Google Scholar]
  57. Munari, U., Tomasella, L., Fiorucci, M., et al. 2008, A&A, 488, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Ortolani, S., Renzini, A., Gilmozzi, R., et al. 1995, Nature, 377, 701 [NASA ADS] [CrossRef] [Google Scholar]
  59. Ramírez, I., & Meléndez, J. 2005a, ApJ, 626, 446 [Google Scholar]
  60. Ramírez, I., & Meléndez, J. 2005b, ApJ, 626, 465 [Google Scholar]
  61. Ramírez, I., Allende Prieto, C., Redfield, S., & Lambert, D. L. 2006, A&A, 459, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Ramírez, I., Allende Prieto, C., & Lambert, D. L. 2007, A&A, 465, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Reddy, B. E., Lambert, D. L., & Allende Prieto, C. 2006, MNRAS, 367, 1329 [NASA ADS] [CrossRef] [Google Scholar]
  65. Roskar, R., Debattista, V. P., Quinn, T. R., Stinson, G. S., & Wadsley, J. 2008, ApJ, 684 [Google Scholar]
  66. Ryde, N., Edvardsson, B., Gustafsson, B., et al. 2009, A&A, 496, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Ryde, N., Gustafsson, B., Edvardsson, B., et al. 2010, A&A, 509, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Salaris, M., Chieffi, A., & Straniero, O. 1993, ApJ, 414, 580 [NASA ADS] [CrossRef] [Google Scholar]
  69. Santos, N. C., Lovis, C., Pace, G., Melendez, J., & Naef, D. 2009, A&A, 493, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Schonrich, R., & Binney, J. 2009a, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
  71. Schonrich, R., & Binney, J. 2009b, MNRAStmp, 1255S [Google Scholar]
  72. Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
  73. Sneden, C. A. 1973, Ph.D. Thesis, Univ. of Texas, Austin [Google Scholar]
  74. Spitzer, L. 1968, Diffuse matter in space (New York: Interscience Publication) [Google Scholar]
  75. Stanek, K. Z. 1996, ApJ, 460, L37 [NASA ADS] [CrossRef] [Google Scholar]
  76. Takeda, Y., Sato, B., & Murata, D. 2008, PASJ, 60, 781 [NASA ADS] [CrossRef] [Google Scholar]
  77. Tull, R. G., MacQueen, P. J., Sneden, C., & Lambert, D. L. 1995, PASP, 107, 251 [NASA ADS] [CrossRef] [Google Scholar]
  78. van der Kruit, P. C., & Searle, L. 1981, A&A, 95, 105 [NASA ADS] [Google Scholar]
  79. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, Proc. SPIE, 2198, 362 [Google Scholar]
  81. Welty, D. E., Hobbs, L. M., & Kulkarni, V. P. 1994, ApJ, 436, 152 [NASA ADS] [CrossRef] [Google Scholar]
  82. Yong, D., Grundahl, F., Nissen, P. E., Jensen, H. R., & Lambert, D. L. 2005, A&A, 438, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Yong, D., Aoki, W., Lambert, D. L., & Paulson, D. B. 2006, ApJ, 639, 918 [NASA ADS] [CrossRef] [Google Scholar]
  84. Zoccali, M., Renzini, A., Ortolani, S., et al. 2003, A&A, 399, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Zoccali, M., Lecureur, A., Barbuy, B., et al. 2006, A&A, 457, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Footnotes

... Ti[*]
Tables 8-15 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/513/A35
... library[*]
http://www.sc.eso.org/santiago/uvespop/
... archive[*]
http://atlas.obs-hp.fr/elodie/
... MTOOLS[*]
http://www.lco.cl/telescopes-information/magellan/instruments-1/mike/IRAF_tools/iraf-mtools-package/
... MAKEE[*]
http://www2.keck.hawaii.edu/inst/hires/hires.html
... database[*]
http://physics.nist.gov/PhysRefData/ASD/lines_form.html
... PARAM[*]
http://stev.oapd.inaf.it/cgi-bin/param
... Sun[*]
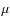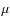Similar problems were already recognized by Gratton & Sneden (1990) in their abundance analysis of $\mu$ Leo, which was ultimately relative to the Sun since they used solar gf-values. They remark that their procedure might introduce inconsistencies due to the different atmospheric structures of $\mu$ Leo and the Sun. Furthermore, independently of the adopted gf-values, by definition the solar abundances are needed to obtain [X/Fe].

All Tables

Table 1:   Program stars data.

Table 2:   Sensitivities in the abundance ratios by employing the Kurucz models (Castelli et al. 1997). The total internal uncertainties* are given in the last column.

Table 3:   Internal zero-point abundances adopted for our giant stars using MARCS and Kurucz models.

Table 4:   Final atmospheric parameters using the MARCS models.

Table 5:   Final atmospheric parameters using the Kurucz models.

Table 6:   Abundance ratios using the MARCS models.

Table 7:   Abundance ratios using the Kurucz models.

All Figures

  \begin{figure} \par\includegraphics[width=8cm,clip]{13444fg1.ps} \end{figure} Figure 1:

A $T_{\rm eff}-\log g$ diagram showing our program stars. The symbols are described in the plot. The two most luminous stars (filled triangles enclosed by circles) are bulge giants which show abundance anomalies like O-deficiency and Na-enhancement similar to those observed in some globular cluster stars. A typical error bar in $T_{\rm eff}$ and $\log g$ is shown.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13444fg2.ps} \end{figure} Figure 2:

Comparison of our equivalent width measurements with lines in common with Fulbright et al. (2006, 2007) for two bulge giant stars: a) IV-203 and b) I-322. The median (solid lines) and a robust proxy of standard deviation ( $\sigma _{\rm QD}$; dashed lines) are also displayed.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13444fg3.ps} \end{figure} Figure 3:

Comparison between evolutionary gravities from Y2 (filled circles) and Padova (open circles) isochrones, and trigonometric gravities for giant stars with good ( $\sigma (\pi )/\pi \le 10$%) Hipparcos parallaxes. The solid and dashed lines depict perfect agreement and variations of $\pm $0.1 dex, respectively.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13444fg4.ps} \end{figure} Figure 4:

Microturbulent velocity as a function of effective temperature ( upper panel) and log g ( lower panel). Giant stars with [Fe/H] < -0.70 and [Fe/H] $\geq $ -0.70 are, respectively, represented by filled and open circles. The solid line is a linear least squares fit to the data, whose results are labeled in the figure.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13444fg5.ps} \vspace*{-3mm}\end{figure} Figure 5:

[O/Fe] vs. [Fe/H] for the sample stars employing MARCS ( top) and Kurucz ( bottom) model atmospheres. Symbols are as explained in the figure. Note however that hereafter the bulge stars I-264 and IV-203 are omitted from all figures (refer to the text for detail).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13444fg6.ps} \end{figure} Figure 6:

[Mg/Fe] as a function of [Fe/H] for MARCS model atmospheres. Symbols as explained in the figure.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13444fg7.ps} \end{figure} Figure 7:

[Si/Fe] vs. [Fe/H] for MARCS model atmospheres. Symbols as explained in the figure.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13444fg8.ps} \end{figure} Figure 8:

[Ca/Fe] vs. [Fe/H] for MARCS model atmospheres. Symbols as explained in the figure.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.3cm,clip]{13444fg9.ps} \end{figure} Figure 9:

Plot of [Ti/Fe] against [Fe/H] for the sample stars employing MARCS model atmospheres. Symbols are as explained in the figure.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.3cm,clip]{13444fg10.ps} \end{figure} Figure 10:

Mean $\alpha $-elements abundance ratio ([(O, Mg, Si, Ca, Ti)/Fe]) as a function of [Fe/H] for MARCS model atmospheres. Symbols as explained in the figure.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.3cm,clip]{13444fg11.ps} \vspace*{-4mm} \end{figure} Figure 11:

Fit of [$\alpha $/Fe] vs. [Fe/H] for metal-poor ( $\rm [Fe/H] < -0.5$) and metal-rich ( $\rm [Fe/H] \ge -0.5$) bulge ( top), thick disk (center) and both bulge and thick disk (bottom) stars. Both stellar populations can be fitted by similar relations, with a scatter as low as $\sigma = 0.03$ dex.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.3cm,clip]{13444fg12.ps} \end{figure} Figure 12:

[Na/Fe] vs. [Fe/H] for MARCS model atmospheres. Symbols as explained in the figure.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.3cm,clip]{13444fg13.ps} \end{figure} Figure 13:

[Al/Fe] vs. [Fe/H] for MARCS model atmospheres. Symbols as explained in the figure.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.3cm,clip]{13444fg14.ps} \end{figure} Figure 14:

[C/O] vs. [O/H] for the bulge ( triangles), thick disk ( filled circles) and thin disk ( open circles) with data taken from Meléndez et al. (2008) and Ryde et al. (2010). The original (undepleted) C abundances were estimated from C+N (refer to the text). Overplotted we show model predictions as given in Cescutti et al. (2009, cf. their Fig. 5).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13444fg15.ps} \end{figure} Figure 15:

[O/Mg] as a function of [Fe/H] ( top panel) and [Mg/H] ( bottom panel). Symbols as explained in the figure.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13444fg16.ps}\vspace*{-2mm} \end{figure} Figure 16:

[O/Mg] as a function of [Fe/H] for bulge giants according to Fulbright et al. (2007) (open triangles) and our work (filled triangles). Both studies show a shallow trend up to about solar metallicity and a step decrease in [O/Mg] for higher metallicities. Recent predictions by Cescutti et al. (2009) are shown as solid (WW95 model), short dashed (WW95+M92), long dashed (WW95+MM02) and dot-short dashed (MM02) lines. All models have been shifted by -0.2 dex in [O/Mg] (see Cescutti et al. 2009, for a description of the models and an explanation of the empirical offset).

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.