| Issue |
A&A
Volume 513, April 2010
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 20 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913200 | |
| Published online | 22 April 2010 | |
Nitrogen chemistry and depletion in
starless cores![[*]](/icons/foot_motif.png)
P. Hily-Blant1 - M. Walmsley2 - G. Pineau des Forêts3,4 - D. Flower5
1 - LAOG (UMR 5571) Observatoire de Grenoble, BP 53, 38041 Grenoble
Cedex 9, France
2 - INAF, Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5,
50125 Firenze, Italy
3 - IAS (UMR 8617), Université de Paris-Sud, 91405 Orsay, France
4 - LERMA (UMR 8112), Observatoire de Paris, 61 Avenue de
l'Observatoire, 75014 Paris, France
5 - Physics Department, The University, Durham DH1 3LE, UK
Received 28 August 2009 / Accepted 30 November 2009
Abstract
Aims. We investigated the chemistry of
nitrogen-containing species, principally isotopologues of CN, HCN, and
HNC, in a sample of pre-protostellar cores.
Methods. We used the IRAM 30 m telescope to
measure the emission in rotational and hyperfine transitions of CN,
HCN, , H, HN, and HC in L 1544, L 183,
Oph D, L 1517B, L 310. The observations were
made along axial cuts through the dust emission peak, at a number of
regularly-spaced offset positions. The observations were reduced and
analyzed to obtain the column densities, using the measurements of the
less abundant isotopic variants in order to minimize the consequences
of finite optical depths in the lines. The observations were compared
with the predictions of a free-fall gravitational collapse model, which
incorporates a non-equilibrium treatment of the relevant chemistry.
Results. We found that CN, HCN, and HNC remain
present in the gas phase at densities well above that at which
CO depletes on to grains. The CN:HCN and the HNC:HCN abundance
ratios are larger than unity in all the objects of our sample.
Furthermore, there is no observational evidence for large variations of
these ratios with increasing offset from the dust emission peak and
hence with density. Whilst the differential freeze-out of CN and CO can
be understood in terms of the current chemistry, the behaviour of the
CN:HCN ratio is more difficult to explain. Models suggest that most
nitrogen is not in the gas phase but may be locked in ices. Unambiguous
conclusions require measurements of the rate coefficients of the key
neutral-neutral reactions at low temperatures.
Key words: ISM: abundances - ISM: molecules - ISM: clouds
1 Introduction
Table 1:
The sample of cores observed. Note that ![]() Oph D is also known
as L 1696A.
Oph D is also known
as L 1696A.
Observations of rotational transitions of molecules and radicals play a key role in deriving information on solar-mass objects in the early stages of gravitational collapse. The variation of the intensities of the emission lines can be interpreted in terms of the chemical reactions and gas-grain interactions occurring in the medium, and the line profiles and frequency shifts in terms of the kinematics of the collapsing gaseous material. Indeed, apart from infrared observations of dust continuum emission, which yield no chemical or kinematical information, measurements of radio transitions of molecules provide the only means of probing the evolution of pre-protostellar cores.
An obstacle to the use of molecular line emission to study the
early
stages of star formation is the propensity of some molecules to freeze
on to the grains at the low temperatures,
![]() K,
which
prevail. Observations of prestellar cores have shown that the
fractional abundances of the carbon-containing species, CO
and CS,
decrease strongly towards the core centres, whereas the fractions of
the nitrogen-containing species, and NH3, either
remain
constant or even increase towards the centre, where the density is
highest (Tafalla et al.
2002). Differential freeze-out of the C- and
N-containing species on to the grains was the generally-accepted
explanation of these observational results. However, recent
observations of the NO radical have demonstrated that the real
situation is more complicated. A comparison of the profiles of NO and
along cuts through the prestellar cores L 1544 and
L 183
(Akyilmaz et al. 2007,
hereafter A07) has shown that the fractional
abundance of NO, unlike that of , decreases towards
the
centres of these cores (their centres being identified with the peak
of the dust emission). Thus, not all nitrogen-containing species
remain in the gas phase at densities
K,
which
prevail. Observations of prestellar cores have shown that the
fractional abundances of the carbon-containing species, CO
and CS,
decrease strongly towards the core centres, whereas the fractions of
the nitrogen-containing species, and NH3, either
remain
constant or even increase towards the centre, where the density is
highest (Tafalla et al.
2002). Differential freeze-out of the C- and
N-containing species on to the grains was the generally-accepted
explanation of these observational results. However, recent
observations of the NO radical have demonstrated that the real
situation is more complicated. A comparison of the profiles of NO and
along cuts through the prestellar cores L 1544 and
L 183
(Akyilmaz et al. 2007,
hereafter A07) has shown that the fractional
abundance of NO, unlike that of , decreases towards
the
centres of these cores (their centres being identified with the peak
of the dust emission). Thus, not all nitrogen-containing species
remain in the gas phase at densities ![]()
![]() ,
which
prevail in the central regions. On the other hand, still more recent
observations of CN (Hily-Blant
et al. 2008) have shown that the
emission of this radical follows closely the dust emission in both
L 1544 and L 183. In so far as these two objects are
representative of
their class, it appears that the adsorption process must somehow
differentiate between nitrogen-bearing species.
,
which
prevail in the central regions. On the other hand, still more recent
observations of CN (Hily-Blant
et al. 2008) have shown that the
emission of this radical follows closely the dust emission in both
L 1544 and L 183. In so far as these two objects are
representative of
their class, it appears that the adsorption process must somehow
differentiate between nitrogen-bearing species.
In the present work, we extended our observations of nitrogen-containing species to include isotopologues of HCN. In addition to L 1544 and L 183, we have studied Oph D, L 1517B, and L 310. The observations are described and analyzed in Sect. 2. Sections 3 and 4 describe the observations and present estimates of N-bearing species abundances. In Sect. 5, we consider the chemical processes, including freeze-out on to the grains, which determine the gas-phase abundances of key N- and also C- and O-containing species in prestellar cores. Section 6 summarizes the model that has been adopted of the early stages of the collapse of the representative prestellar core L 1544. The fractional chemical abundances predicted by the model are presented and the corresponding column density profiles are compared with the observations. Finally, in Sect. 7, we make our concluding remarks.
2 Observational procedures and data reduction
The observations were performed at the IRAM 30 m
telescope in January
2008. The data have been reduced and anlayzed using the CLASS90
software (Hily-Blant
et al. 2005). The instrumental setup was
identical to that used by Hily-Blant
et al. (2008): frequency-switching
spectra, with a frequency-throw of 7.8 MHz, were recorded by
the VESPA
facility, with 20 kHz spectral resolution and 20 to
80 MHz
bandwidth. The half-power beam-width is calculated as
HPBW
![]() ,
that is 28
,
that is 28
![]() at 87 GHz
and 22
at 87 GHz
and 22
![]() at 113 GHz.
Cross-like patterns with 20
at 113 GHz.
Cross-like patterns with 20
![]() spacing
were observed towards each source. The crosses were centered on the
dust emission peak, as determined from published continuum maps; all
offsets quoted in the present paper refer to the central positions
listed in Table 1.
Table C.1
summarizes
the lines observed for each object. The amplitude calibration was
checked every 10 min, the pointing every hour, and the focus
every two
hours, typically. Instrumental spectral effects were compensated by
subtracting polynomial baselines from each spectrum before
folding. More details on the data reduction procedures can be found in
Appendix B.
All results (unless explicitly stated) have been
translated from the antenna temperature scale () to the main-beam
temperature scale
spacing
were observed towards each source. The crosses were centered on the
dust emission peak, as determined from published continuum maps; all
offsets quoted in the present paper refer to the central positions
listed in Table 1.
Table C.1
summarizes
the lines observed for each object. The amplitude calibration was
checked every 10 min, the pointing every hour, and the focus
every two
hours, typically. Instrumental spectral effects were compensated by
subtracting polynomial baselines from each spectrum before
folding. More details on the data reduction procedures can be found in
Appendix B.
All results (unless explicitly stated) have been
translated from the antenna temperature scale () to the main-beam
temperature scale
![]() ,
with the values of listed in Table C.1; is the
forward
efficiency, and is the beam efficiency.
,
with the values of listed in Table C.1; is the
forward
efficiency, and is the beam efficiency.
![\begin{figure*}
\par\mbox {\includegraphics[angle=-90,width=5cm,clip]{13200_1.ep...
...8cm}
\includegraphics[angle=-90,width=5cm,clip]{13200_5.eps} }
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg48.png)
|
Figure 1: Continuum emission () at 1.2 mm with the locations of the line integrations (crosses). The HPBW at 1.2 mm and at the 3 mm frequencies discussed in this paper are indicated. A linear scale of 0.05 pc is also shown, assuming a distance of 150 pc for all cores except L 183 (110 pc). Continuum maps for L 1544, Oph D, L 183, L 1517B and L 310 are taken from Ward-Thompson et al. (1999), Pagani et al. (2003), Tafalla et al. (2004) and Bacmann et al. (2000) respectively. |
| Open with DEXTER | |
3 Observational results
All objects in our sample are pre-stellar, in the sense that none
shows signposts of embedded stellar objects. Their peak particle number
densities span more
than an order of magnitude (see Table 1): the peak
densities decrease from approximately ![]() (L 183,
L 1544)
to
(L 183,
L 1544)
to ![]() in L 310.
All the objects have been extensively
observed, both in their lines and continuum (see
Fig. 1).
Our observations focused on the
nitrogen-bearing species CN, HCN, , H, HN, and
HC. All these molecules present hyperfine structure
(HFS). However, in the cases of HN and HC, the hyperfine
structures were not resolved in our 20 kHz resolution spectra.
All
transitions are in the 3 mm band; the CN line was observed in
parallel at 1.3 mm (see Table A.1).
in L 310.
All the objects have been extensively
observed, both in their lines and continuum (see
Fig. 1).
Our observations focused on the
nitrogen-bearing species CN, HCN, , H, HN, and
HC. All these molecules present hyperfine structure
(HFS). However, in the cases of HN and HC, the hyperfine
structures were not resolved in our 20 kHz resolution spectra.
All
transitions are in the 3 mm band; the CN line was observed in
parallel at 1.3 mm (see Table A.1).
3.1 Line properties
All lines were observed successfully towards the three most centrally peaked cores, L 183, L 1544, and Oph D; the emission lines are shown in Fig. 2. For CN and , only the weakest HFS components (at 113520.4315 MHz and 93176.2650 MHz) are shown. For each of the other lines, the strongest HFS component is considered instead: 108780.2010 MHz, 86340.1840 MHz, 87090.8590 MHz, and 86054.9664 MHz for , H, HN and respectively. The HN hyperfine structure is not fully resolved and the two hyperfine transitions of are not resolved. The line is detected in the four densest objects, L 183, L 1544, Oph D and L 1517B.
Tables D.1-D.5 give the
properties of all lines
towards all the positions in each source. The integrated intensities,
W, were derived from Gaussian fitting of a given HFS
component (see
above). Several Gaussian components were fitted in some cases, for the
known hyperfine structure of HN, and also in the
obvious cases of multiple-component line profiles (L 1544). In
such
cases, W is the sum of the integrated intensities
of each velocity
component. The peak temperature
![]() is
the maximum intensity over
the line. Given that the lines are, in general, not Gaussian, the
linewidth is estimated as the equivalent width,
is
the maximum intensity over
the line. Given that the lines are, in general, not Gaussian, the
linewidth is estimated as the equivalent width,
![]() and
the statistical uncertainty is obtained by propagating the errors. For
non-detections, upper limits on the integrated intensity were obtained
by fitting a Gaussian at a fixed position. Upper limits on the
intensity are at the 3
and
the statistical uncertainty is obtained by propagating the errors. For
non-detections, upper limits on the integrated intensity were obtained
by fitting a Gaussian at a fixed position. Upper limits on the
intensity are at the 3![]() level
while those on the integrated
intensity are at the 5
level
while those on the integrated
intensity are at the 5![]() level.
level.
Towards L 1544, all resolved lines show two clear peaks, with a dip centred at 7.20 . These two peaks are seen in several tracers including by Hirota et al. (2003) who concluded that there are two distinct velocity components along the line of sight (Tafalla et al. 1998). Owing to their double-peak profiles, lines towards L 1544 have the largest integrated intensities of all the lines that we observed.
The comparison of the linewidths shows that the lines towards
L 183 are the narrowest with full widths at half maximum
![]() .
The H line in this source exhibits a
blue wing and the profile can be well fitted by two Gaussian
components with FWHM of 0.38 and
0.85 ; this blue wing is not
evident in any other tracer. Towards Oph D and
L 1517B, the linewidth
is larger by a factor of 2 to 3, although the
comparison with L 1544
is rendered difficult by the double-peak line profiles. In several
tracers, H, L 310 displays the largest linewidth
(<0.8 ) but small integrated intensities. In all the
sources, has been detected, and the properties of the line, averaged
over all offset positions, are listed in Table 2. The
peak and integrated intensities decrease as the peak density
decreases. Again, L 1544 seems to be an exception, owing to
the
double-peak line profile. The FWHM are comparable (
.
The H line in this source exhibits a
blue wing and the profile can be well fitted by two Gaussian
components with FWHM of 0.38 and
0.85 ; this blue wing is not
evident in any other tracer. Towards Oph D and
L 1517B, the linewidth
is larger by a factor of 2 to 3, although the
comparison with L 1544
is rendered difficult by the double-peak line profiles. In several
tracers, H, L 310 displays the largest linewidth
(<0.8 ) but small integrated intensities. In all the
sources, has been detected, and the properties of the line, averaged
over all offset positions, are listed in Table 2. The
peak and integrated intensities decrease as the peak density
decreases. Again, L 1544 seems to be an exception, owing to
the
double-peak line profile. The FWHM are comparable (![]()
![]() )
for all sources; but, once again, the FWHM is
significantly larger (by
a factor 2) in L 310 than in the other sources.
)
for all sources; but, once again, the FWHM is
significantly larger (by
a factor 2) in L 310 than in the other sources.
Table 2: Properties of the average profiles and average fractional abundance towards the observed cores (main beam temperature scale).
![\begin{figure*}
\mbox {\includegraphics[width=6cm,clip]{13200_6.eps}\hspace*{3m...
...
\includegraphics[width=6cm,clip]{13200_10.eps}\hspace*{6.3cm}
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg63.png)
|
Figure 2:
Comparison of the line profiles of different tracers; the spectra have
been shifted vertically for clarity. For CN, , and , the weakest HFS
components (at 113520.4315, 226887.3520 and 93176.2650 MHz
respectively) are shown. For each of the other lines, the strongest HFS
component is considered: 108780.2010, 86340.1840, 87090.8590, and
86054.9664 MHz for , H, HN and respectively. The spectrum is
taken from A07. The spectra are for zero offset (cf. Table 1). Towards
L 1517B, the CN spectrum is replaced by CN and the spectrum is
taken from Tafalla et al.
(2002). Towards Oph D, the spectrum at offset (0
|
| Open with DEXTER | |
3.2 Line ratios
The ratios of total integrated intensities
![]() for
some line
combinations in each source, are shown in
Fig. C.1.
Under the optically thin assumption,
these ratios reflect the relative abundances. The ratios CN/HCN or
/H are constant to within a factor of 2 across all the
cores and vary between about 0.5 to 5 from source to
source. Towards
L 1517B, the /H ratio appears to decrease towards the
centre. Significant also is the fact that the H/HN is
constant and of similar magnitude (0.2-0.8) in all sources,
independent of the central density.
for
some line
combinations in each source, are shown in
Fig. C.1.
Under the optically thin assumption,
these ratios reflect the relative abundances. The ratios CN/HCN or
/H are constant to within a factor of 2 across all the
cores and vary between about 0.5 to 5 from source to
source. Towards
L 1517B, the /H ratio appears to decrease towards the
centre. Significant also is the fact that the H/HN is
constant and of similar magnitude (0.2-0.8) in all sources,
independent of the central density.
Table 3: Fractional abundances of CN, HCN, HNC and relative to H towards the dust emission peaks of our source sample. Tables D.1-D.5 give the fractional abundances toward all the observed positions.
![\begin{figure*}
\par\includegraphics[angle=-90,width=3.3cm,clip]{13200_11.eps}\h...
...8cm}
\includegraphics[angle=-90,width=3.3cm,clip]{13200_14.eps}
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg67.png)
|
Figure 3: Relative integrated intensity of each HFS component for several species, at the central position for each source. In each panel, the dashed line indicates the relative intensities in LTE for optically thin emission. The thick line shows the optically thick limit. The abscissa is the rest line frequency. |
| Open with DEXTER | |
Most of the lines that have been observed are split by the hyperfine interaction, and the relative intensities of the hyperfine components can be used as a measure of optical depth. It is generally assumed that the level populations of hyperfine states are in LTE and hence proportional to the statistical weights, within a given rotational level. However, it has been known for some time that this assumption is often invalid (see, for example, the discussion of Walmsley et al. 1982), and this is confirmed by our data. When the populations are in LTE, one expects the satellite line intensity ratios to lie between the ratios of the line strengths, in the optically thin limit, and unity for high optical depths. As may be seen from Fig. 3, this is usually but not always the case. For example, it is clear that the CN ratios towards L 183 are inconsistent with this expectation, whereas the ratios observed towards other sources suggest high optical depths and are broadly consistent with equal excitation temperatures in the different components. The observed ratios show clear signs of deviations from LTE, but the effects are much less drastic than in the more abundant isotopologue, and we suspect that optical depths are low. In the case of H, departures from LTE appear to be minor.
The reasons for departures from LTE such as seen in Fig. 3 are presently unknown and need to be established. Such an investigation would require calculations of the collisional rate coefficients, analogous to those of Monteiro & Stutzki (1986), as well as a treatment of the radiative transfer; this is beyond the scope of the current study. For the present, we use low abundance isotopologues such as and H to trace abundance gradients, neglecting collisional excitation and the possibility of fractionation of the 13C and 15N isotopologues.
![\begin{figure*}
\par\includegraphics[angle=-90,width=14cm,clip]{13200_15.eps}\vs...
...5cm}
\includegraphics[angle=-90,width=14cm,clip]{13200_18.eps}
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg69.png)
|
Figure 4:
Derived column densities towards each source. From top to
bottom: L 1544, L 183, Oph D, and
L 1517B. The column densities are plotted as a function of the
distance from the dust emission peak, along both cuts. Also plotted is
the H2 column density (grey histogram, right
scale), as derived from the dust emission (assuming |
| Open with DEXTER | |
![\begin{figure*}
\par\includegraphics[angle=-90,width=14cm,clip]{13200_19.eps}\vs...
...cm}
\includegraphics[angle=-90,width=14cm,clip]{13200_22.eps}
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg70.png)
|
Figure 5: Same as Fig. 4 for the derived fractional abundances. |
| Open with DEXTER | |
4 Column densities and abundance ratios
We determine column densities using the standard formalism described
in Appendix C
(Eqs. (C.1)
and (C.2))
and
assume the local (solar neighbourhood)
![]() C=
68ratio.
It is instructive to consider also the abundance variations
from source to source. Converting column densities into relative
abundances requires the molecular hydrogen column density, ,
which we have determined (indirectly) from measurements of the dust
emission, using bolometer maps available in the literature
(Tafalla
et al. 2004; Pagani et al. 2003; Ward-Thompson
et al. 1999; Bacmann et al. 2000)
and smoothing
where necessary to a 20
C=
68ratio.
It is instructive to consider also the abundance variations
from source to source. Converting column densities into relative
abundances requires the molecular hydrogen column density, ,
which we have determined (indirectly) from measurements of the dust
emission, using bolometer maps available in the literature
(Tafalla
et al. 2004; Pagani et al. 2003; Ward-Thompson
et al. 1999; Bacmann et al. 2000)
and smoothing
where necessary to a 20
![]() beam. We assumed a dust
temperature of
8 K and a 1.3 mm absorption coefficient of
beam. We assumed a dust
temperature of
8 K and a 1.3 mm absorption coefficient of
![]() (see
HWFP08). The results are shown in
Fig. 5
for L1544, L 183, Oph D, and L 1517B.
(see
HWFP08). The results are shown in
Fig. 5
for L1544, L 183, Oph D, and L 1517B.
We remark first that, towards L 1544, the column densities of , H, and are all roughly proportional to the hydrogen column density, as inferred from dust emission (see Fig. 4); this has been noted already by HWPF08 for the case of . The derived abundances do not change appreciably towards the dust peak, in spite of a variation of almost an order of magnitude in the hydrogen column density. Thus, in this source, and with the current resolution, the CN-containing species do not appear to be significantly depleted at high densities. On the other hand, the abundances tend to increase to the NW of the dust emission peak (see the SE-NW cut); we assume that this is related to asymmetry of the source. It is interesting that behaves in similar fashion. Important for the later discussion is the fact that the abundance ratios :H and :H are approximately equal to 2 (with variations of up to a factor of 2); we assume that this reflects the ratios HNC:HCN and CN:HCN, respectively.
However, L 1544 is not typical. Towards
L 183, for example (see the EW
cuts in Fig. 4),
the peak H and column
densities are offset to the east, relative to the dust emission,
whereas and appear to follow the dust emission. The
situation is similar in Oph D although we did not observe in
this source. Towards L 1517B, correlates reasonably well with
![]() but this is
not the case of nor, probably, of
H. Bearing in mind the inaccuracy of the abundance
determinations, and the possibility of 13C
fractionation, we
conclude conservatively that there is no evidence for an order of
magnitude variation in the CN:HCN nor the HNC:HCN abundance ratios
between the dust emission peak and offset positions.
but this is
not the case of nor, probably, of
H. Bearing in mind the inaccuracy of the abundance
determinations, and the possibility of 13C
fractionation, we
conclude conservatively that there is no evidence for an order of
magnitude variation in the CN:HCN nor the HNC:HCN abundance ratios
between the dust emission peak and offset positions.
We give also in Table 3 our estimates
of the fractional
abundances, relative to H, of CN, HCN, and HNC towards the
dust
emission peaks of our sample of sources; these abundances have been
derived assuming the local value of 68 for the 12C:13C
ratio. All the relative abundances are of order ![]() ,
with CN
and HNC being more abundant than HCN by a factor of about 2.
This
value is close to the ratio determined by Irvine
& Schloerb (1984) toward
TMC-1. Values larger than 1 for the HNC:HCN abundance ratio
were found towards a sample of 19 dark clouds by Hirota et al. (1998)
with an average ratio of
,
with CN
and HNC being more abundant than HCN by a factor of about 2.
This
value is close to the ratio determined by Irvine
& Schloerb (1984) toward
TMC-1. Values larger than 1 for the HNC:HCN abundance ratio
were found towards a sample of 19 dark clouds by Hirota et al. (1998)
with an average ratio of ![]() .
We do not see indications of
significant abundance differences between cores of high central
density (L 1544 and L 183) and cores of lower central
density
(L 1517B, Oph D). Whilst the complexities of the
source structure and
of radiation transfer prevent our establishing the existence of small
abundance differences, we may conclude that there remain appreciable
amounts of CN, HCN, and HNC at densities above the typical density
(34 ) at which CO depletes on to grains. Not surprisingly,
this effect is seen most readily in sources of high central column
density, like L 1544, in which emission from the low density
envelope
is less important.
.
We do not see indications of
significant abundance differences between cores of high central
density (L 1544 and L 183) and cores of lower central
density
(L 1517B, Oph D). Whilst the complexities of the
source structure and
of radiation transfer prevent our establishing the existence of small
abundance differences, we may conclude that there remain appreciable
amounts of CN, HCN, and HNC at densities above the typical density
(34 ) at which CO depletes on to grains. Not surprisingly,
this effect is seen most readily in sources of high central column
density, like L 1544, in which emission from the low density
envelope
is less important.
5 Chemical considerations
In this Section, we seek to update and extend previous studies of the interstellar chemistry of N-containing species Schilke et al. (1992); Pineau des Forêts et al. (1990), with a view to providing a framework for the interpretation of our observations of prestellar cores. We shall show that it is possible to derive a simple expression for the CN:HCN abundance ratio, in particular, by identifying the principal reactions involved in the formation and destruction of these species.
5.1 Main chemical reactions
The fractional abundances of gas-phase species in prestellar cores are determined by:
- the initial composition of the molecular gas which undergoes gravitational collapse;
- variations of the density with time;
- the rates of gas-phase reactions at the low temperatures (
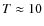 K) of the cores;
K) of the cores;
- the rates of adsorption of the constituents of the gas on to grains.
The conversion of atomic into molecular nitrogen in the gas
phase is
believed to occur in the reactions
and
The reactions
can also destroy NO, producing CN in the case of (5), and
can destroy CN.
From the above, we see that NO forms from the reaction of N with OH, whereas CN forms from N and CH. It follows that the ratio of carbon to oxygen in the gas phase is a factor determining the relative abundance of NO and CN. The NO:CN abundance ratio will be lower in gas which is depleted of oxygen, either because of an intrinsically high C:O elemental abundance ratio, or due to the differential freeze-out of O and C on to the grains, where the oxygen is incorporated mainly as water ice.
Once N2 has formed, in (2) and (4), N2H+
is
produced in the protonation reaction
Dissociative ionization of N2 by He+ results in the production of N+:
Whilst the reaction of N+ with para-H2 (in its ground rotational state) is endothermic, by approximately 168 K, its reaction with ortho-H2 is slightly exothermic and occurs even at low temperatures Le Bourlot (1991). Subsequent hydrogenation reactions with H2 lead to NH4+, which can dissociatively recombine to produce NH3. Thus, N2 is a progenitor of both N2H+ and NH3, whilst NO and CN are intermediaries in the formation of N2.
HCN and HNC are produced principally in the reactions
in which the products have so much excess energy that rapid isomerization is expected to yield practically equal amounts of HCN and HNC (Herbst et al. 2000). As CH and CH2 are produced through the dissociative recombination of hydrocarbon ions, notably CH3+, they are expected to coexist in the medium. It follows that CN, HCN and HNC should coexist also. HNC converts to HCN in the reaction
The reverse reaction is endothermic and proceeds at a negligible rate at low temperatures. HCN is destroyed principally in the charge transfer reaction with H+ and in the proton transfer reaction with H3+
HCN+ reacts rapidly with H2, producing H2CN+, which dissociatively recombines with electrons, producing HCN and HNC; but there exists a branch to CN
for which the branching ratio
Because CN but not HCN (nor HNC) is destroyed by O, the abundance ratio CN:HCN increases as the C:O ratio increases. The chemical network is summarized in Fig. 6.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13200_23.eps}
\end{figure}](/articles/aa/full_html/2010/05/aa13200-09/Timg91.png)
|
Figure 6: The principal reactions involved in the low-temperature chemistry of nitrogen-containing species, and specifically of CN, HCN and HNC. |
| Open with DEXTER | |
5.2 Simplified analysis of the chemistry
We show now that an analysis of the principal reactions leading to the
formation and destruction of CN and HCN leads to a simple analytical
formula for the CN:HCN abundance ratio. When
reactions (3) and
(4) determine the
abundance of
CN,
with the adopted values of the rate coefficients for these reactions at T = 10 K.
We have seen already that HCN is formed in reaction (10), with a
rate coefficient
![]() ,
and it
is removed principally by H+ and H3+,
forming H2CN+(reactions 13 and 14). It follows
that
,
and it
is removed principally by H+ and H3+,
forming H2CN+(reactions 13 and 14). It follows
that
![\begin{displaymath}k_{10}n({\rm CH}_2)n({\rm N}) = k_{\rm L}n({\rm
HCN})[n({\rm H}^+)+n({\rm H}_3^+)]f_{\rm CN},\end{displaymath}](/articles/aa/full_html/2010/05/aa13200-09/img94.png)
where
Under the above assumptions, the CN:HCN ratio is proportional to the
CH:CH2 ratio:
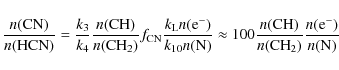
where we have assumed that
CH has its chemical origin in the reaction
of He+ with CO
for which the adopted value of the rate coefficient is
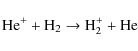
Most of the C+ ions produced in
reaction (16)
combine
radiatively with H2 to form CH2+,
which reacts rapidly with
H2, forming CH3+
which then recombines dissociatively with
electrons, yielding CH
but also C and CH2. The ratio
and
forming CO, and hence the elemental C:O ratio is, once again, a pertinent parameter for the CN:HCN ratio. So too are the rate coefficients for reactions (20), (21) and (22). We adopted the (temperature-independent) values of these rate coefficients in the NIST chemical kinetics database
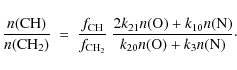
It follows that
5.3 The abundance of atomic nitrogen in cores
Atomic abundances in prestellar cores are notoriously difficult to determine. Although the atomic fine structure transitions are, in principle, observable, it is difficult, in practice, to distinguish a component corresponding to dense, cold molecular material from emission arising from low density, hotter layers along the line of sight. The emission from photon dominated regions (PDRs), for example, tends to be stronger than that from cores.
The analysis in Sect. 5.2 suggests that
the CH:CH2ratio is dependent on the abundances
of atomic oxygen and
nitrogen. Combining the expressions for the CH:CH2
and the CN:HCN
ratios, there
follows the inequality
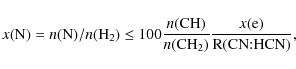
where
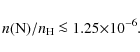
This value is considerably less than the cosmic nitrogen abundance (
An analogous inequality, in terms of the measured CN:HCN
ratio, can be
derived for the fractional abundance of atomic oxygen,
![]() .
However, it is a much weaker constraint than the limit on
.
However, it is a much weaker constraint than the limit on
![]() .
Other observables, such as NO, provide stronger
constraints on the fractional abundance of atomic oxygen
(see A07).
.
Other observables, such as NO, provide stronger
constraints on the fractional abundance of atomic oxygen
(see A07).
6 Models
6.1 Steady state
![\begin{figure}
\par\includegraphics[width=6cm,clip]{13200_24.eps}
\end{figure}](/articles/aa/full_html/2010/05/aa13200-09/Timg132.png)
|
Figure 7:
Steady-state fractional abundances of nitrogen-containing species for a
density |
| Open with DEXTER | |
The timescale for the nitrogen chemistry to reach steady state is
known to be large, relative to the free-fall time in a prestellar
core, owing to the slow conversion of N to N2
(see, for example, Flower
et al. 2006). Our model calculations show that, with
a
cosmic ray ionization rate
![]() s-1,
this timescale
is of the order of 106 yr. As a
consequence, the results of the
time-dependent models of gravitational collapse depend on the initial
composition which is adopted and the rate of dynamical evolution.
s-1,
this timescale
is of the order of 106 yr. As a
consequence, the results of the
time-dependent models of gravitational collapse depend on the initial
composition which is adopted and the rate of dynamical evolution.
Following the discussion in Sect. 5, it is nevertheless instructive to examine the results of steady-state calculations (that is to say time independent and only in the gas phase), as functions of the fractions of elemental oxygen and nitrogen in the gas phase. In this way, an impression may be obtained of the dependence of the observables on the degrees of depletion, without the complications of the time dependence, which is considered in Sect. 6.2.
In the upper panel of Fig. 7, we present the
fractional
abundances of nitrogen-containing species in steady state for a
density ![]() ,
a kinetic temperature T = 10 K, and a
cosmic ray ionization rate of
,
a kinetic temperature T = 10 K, and a
cosmic ray ionization rate of
![]() s-1.
For reaction (7),
we adopted a temperature-independent rate coefficient
s-1.
For reaction (7),
we adopted a temperature-independent rate coefficient![]() (
(
![]() )
although we note that there is some theoretical evidence that the rate
of this reaction may decrease with temperature (Andersson & Markovi 2003).
The fraction of elemental
nitrogen in the gas phase varies from 0.017 to 1. We
assume implicitly
that the ``missing'' nitrogen is in solid form. Following A07,
we adopt
a relative abundance of elemental carbon to oxygen in the gas phase
)
although we note that there is some theoretical evidence that the rate
of this reaction may decrease with temperature (Andersson & Markovi 2003).
The fraction of elemental
nitrogen in the gas phase varies from 0.017 to 1. We
assume implicitly
that the ``missing'' nitrogen is in solid form. Following A07,
we adopt
a relative abundance of elemental carbon to oxygen in the gas phase
![]() .
In the lower panel, the fractional abundance of
elemental nitrogen in the gas phase is held constant at
.
In the lower panel, the fractional abundance of
elemental nitrogen in the gas phase is held constant at
![]() and
the C:O ratio is varied by changing the fractional
abundance of oxygen in the gas phase
and
the C:O ratio is varied by changing the fractional
abundance of oxygen in the gas phase
![]() .
.
We see from Fig. 7 that, in steady state, there tends to be somewhat more molecular than atomic nitrogen in the gas phase. Species such as NH3 and have abundances which are roughly proportional to N2. The HCN abundance is relatively insensitive to changes in the gas phase C:O ratio but follows the gas-phase nitrogen abundance. On the other hand, CN and NO are sensitive to the C:O ratio. The net effect is that CN:HCN increases with C:O and decreases with the fraction of nitrogen in the gas phase.
![\begin{figure*}
\par\mbox{\includegraphics[width=8cm,clip]{13200_25.eps}\hspace*...
...}
\includegraphics[width=8cm,clip]{13200_28.eps} }
\vspace{4mm}
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg137.png)
|
Figure 8:
The fractional abundances computed by the gravitational collapse model.
We show in panel a) results for the HCN
abundance as a function of the CN:HCN ratio. In panel
b) we show the HCN abundance as a function of the N2H+
abundance. In panel c) the HCN abundance
as a function of the NO abundance. The initial C:O ratio is assumed to
be 0.97. Each point is labeled with the initial gas phase
nitrogen abundance from -6 to 6.4-5. The initial steady state values
(filled squares, green) are shown for comparison. Results for a density
of 105 are given as blue open circles
and for 106 as filled red circles.
Data points are shown with black error bars. Data for N2H+ towards
Oph D and L 1517B are taken from Crapsi et al. (2005).
In panel d) we show the HCN:CO abundance
ratio as a function of the CO fractional abundance, for different
initial gas phase nitrogen abundances. For a given
|
| Open with DEXTER | |
6.2 Gravitational collapse
A more satisfactory approach to comparing observational results with
models is through a simulation of a gravitational collapse. In
Fig. 8,
we compare the observed values of the HCN
abundance and the CN:HCN ratio with the predictions of models in which
the density and the chemistry evolve following free-fall
gravitational collapse. All neutral species are assumed to adsorb on to
dust grains (of radius 0.5 ) with a sticking coefficient of
unity and are desorbed by cosmic ray impacts (Flower
et al. 2006). We assume that, initially, the
chemical
composition of the gas has attained steady state at a density
![]() .
We make various assumptions concerning the amount of
nitrogen initially in the gas phase (or, equivalently, the fraction
which is initially in the form of nitrogen-containing ices on grain
surfaces).
.
We make various assumptions concerning the amount of
nitrogen initially in the gas phase (or, equivalently, the fraction
which is initially in the form of nitrogen-containing ices on grain
surfaces).
The fraction of elemental nitrogen in the ambient molecular
medium
which is in solid form is poorly known. There is evidence for ammonia
ice in spectral profiles observed towards some young YSOs, with
perhaps 15% of the abundance of water ice (Gibb et al. 2000), but
no
such evidence exists towards background stars; there is perhaps a
substantial fraction of the nitrogen in the form of N2
ice also. In
prestellar cores, the abundance of places lower limits on the
amount of gas-phase nitrogen, which we estimate conservatively to be
about 10-6. Accordingly, we have varied the
initial gas phase
nitrogen abundance in our models in the range
![]() ,
where the upper limit
corresponds to the value observed in diffuse interstellar gas
(Sofia & Meyer 2001).
Figure 8
displays the fractional
abundances computed in the course of the collapse, at densities
,
where the upper limit
corresponds to the value observed in diffuse interstellar gas
(Sofia & Meyer 2001).
Figure 8
displays the fractional
abundances computed in the course of the collapse, at densities
![]() and
and ![]() . We show also, for
comparison, the
initial (steady state) values.
. We show also, for
comparison, the
initial (steady state) values.
It may be seen from Fig. 8 that, at a density of 105 which is the more relevant value for the purpose of comparing with observations, reasonable agreement is obtained only for initial gas-phase nitrogen abundances close to 10-6 - in other words, close to the lower limit. Even so, the computed abundances do not fit well the observations of L 183 and Oph D; but we note that the density at the dust peak in L 183 approaches 106 . Our model results are dependent also on the fraction of oxygen locked in ices, or, equivalently, on the initial gas-phase C:O ratio. It is possible that this ratio varies considerably from source to source, resulting in discrepancies when we compare observations with model predictions.
Figure 8
(bottom right panel) shows the HCN:CO abundance
ratio as a function of the CO fractional abundance. For a given
initial abundance of gaseous nitrogen
![]() (=
(=
![]() ),the abundance ratio is
followed along the collapse
and values are shown at densities
),the abundance ratio is
followed along the collapse
and values are shown at densities ![]() ,
45 and
6 . The differential freeze-out of HCN and CO is evident. In
all these models, CO depletes by two orders of magnitude. The
behaviour of HCN regarding depletion is different in that it depends
on the initial
,
45 and
6 . The differential freeze-out of HCN and CO is evident. In
all these models, CO depletes by two orders of magnitude. The
behaviour of HCN regarding depletion is different in that it depends
on the initial ![]() .
For a large initial
.
For a large initial
![]() ,
HCN depletes only a factor of 3 less than
CO. However, at the other extreme value (
,
HCN depletes only a factor of 3 less than
CO. However, at the other extreme value (
![]() ),
HCN depletes 10 times less than CO. Observational
values towards
L 1544 (Caselli
et al. 1999) and L 1517B (Tafalla et al. 2002)
favour
differential freeze-out between HCN and CO and thus low
initial
),
HCN depletes 10 times less than CO. Observational
values towards
L 1544 (Caselli
et al. 1999) and L 1517B (Tafalla et al. 2002)
favour
differential freeze-out between HCN and CO and thus low
initial ![]() .
.
We conclude from Fig. 8 that the models fail to explain the observations. One possible reason for this failure is our neglect of line-of-sight effects in the models used to construct Fig. 8. The observed quantities are column densities, which are integrals along the line of sight over a range of densities; our analysis neglects this effect. However, trial calculations for one source (L 1544; see Appendix D) suggest that including line-of-sight integration can reduce but not eliminate the discrepancies between model predictions and observations. Another possibility might be that the duration of the collapse is longer that the free-fall time. However, if this time is significantly increased, the abundance of gaseous CO drops too rapidly with increasing density (Flower et al. 2005). More important may be errors in the rate coefficients that we have used for some of the key reactions, discussed in Sect. 5. It is clear, for example, that our predictions relating to CN are sensitive to the rates of reactions (3), (4), and (10) at temperatures of the order of 10 K. Further progress in this field will require reliable determinations of the rate coefficients of these reactions at low temperatures.
We find that the values of the CN:HCN ratio observed in
prestellar
cores indicate that the fraction of nitrogen in the gas phase is
likely to be considerably lower than the diffuse-gas value of
![]() .
Nitrogen (like oxygen) may deplete on to grain
surfaces at relatively low densities. Confirmation will require the
identification of nitrogen-containing ices and estimates of their
relative abundances. A rather similar conclusion has been reached by
Maret et al. (2006)
in a study of B68.
.
Nitrogen (like oxygen) may deplete on to grain
surfaces at relatively low densities. Confirmation will require the
identification of nitrogen-containing ices and estimates of their
relative abundances. A rather similar conclusion has been reached by
Maret et al. (2006)
in a study of B68.
We finally note that our observations show HNC:HCN ![]() 2,
whereas the exhaustive theoretical study of Herbst
et al. (2000)
predicted HNC:HCN
2,
whereas the exhaustive theoretical study of Herbst
et al. (2000)
predicted HNC:HCN ![]() 1. It is possible
that enhanced line
trapping in HNC, relative to HCN, results in our deriving an
anomalously high HNC:HCN abundance ratio; but it is unlikely that this
effect can explain fully the discrepancies with the model
predictions. Maybe more relevant is the apparent correlation between
the HNC:HCN ratio and freeze-out, as suggested by the results from Hirota et al. (1998)
who show that the largest (resp. smallest) ratio is observed toward a
strongly depleted core (resp. undepleted).
1. It is possible
that enhanced line
trapping in HNC, relative to HCN, results in our deriving an
anomalously high HNC:HCN abundance ratio; but it is unlikely that this
effect can explain fully the discrepancies with the model
predictions. Maybe more relevant is the apparent correlation between
the HNC:HCN ratio and freeze-out, as suggested by the results from Hirota et al. (1998)
who show that the largest (resp. smallest) ratio is observed toward a
strongly depleted core (resp. undepleted).
7 Concluding remarks
We have studied the behaviour of nitrogen-containing species, principally CN, HCN, and HNC, in the pre-protostellar cores L 183, L 1544, Oph D, L 1517B, and L 310. Our main conclusions are as follows.
- We observe that CN, HCN, and HNC remain present in the gas phase at densities above the typical density (34 ) at which CO depletes on to grains.
- The CN:HCN and HNC:HCN ratios are larger than unity in all objects and do not vary much within in each core. Whilst the differential freeze-out of CN and CO can be understood, the approximate constancy of the CN:HCN ratio cannot.
- The CN:HCN ratio puts upper limits on the abundance of atomic nitrogen in the gas phase, and the NO:HCN ratio constrains the C:O ratio. Though uncertain, the comparison between observations and models indicates that most of the nitrogen is locked into ices, even at densities probably as low as 4 .
We thank M. Tafalla for providing us with the spectra towards L 1517B and for his helpfull referee report. We also thank Holger Müller of the CDMS for helpful comments on the spectroscopy. This work has been been partially supported by the EC Marie-Curie Research Training Network ``The Molecular Universe'' (MRTN-CT-2004-512302).
Appendix A: Spectroscopic data
Table A.1:
Hyperfine structure in CN (
![]() );
from Skatrud et al. (1983).
);
from Skatrud et al. (1983).
Appendix B: Data reduction
Data reduction was done with the CLASS90 software from the GILDAS
program suite![]() .
We summarize here the reduction
of the frequency-switched spectra obtained with the VESPA
autocorrelator facility at the IRAM 30 m radio
telescope.
.
We summarize here the reduction
of the frequency-switched spectra obtained with the VESPA
autocorrelator facility at the IRAM 30 m radio
telescope.
All spectra were corrected first from the instrumental spectral transfer function. The resulting spectra were then folded and averaged (each folded spectrum being weighted by the effective rms of the residuals after baseline subtraction). A zero-order polynomial was fitted to the resulting spectrum to compute the final rms. Whenever platforming was present in the data, the spectrum was split into as many parts as needed, and each part was treated individually with a first-order polynomial in order to adjust the continuum level. The concatenated sub-parts were then treated as a single spectrum. This method proved to be robust. In some cases, the amplitude of ripples was large enough to require special treatment. Ripples were subtracted by fitting a sine wave to the spectrum, using an improved version of sine fitting, as compared with the default CLASS90 procedure. In the case of a spectrum presenting ripples, channels in the spectral windows (where there is presumably some line emission) were replaced by a sine wave, determined by the first-guess parameters (amplitude, period and phase). As the critical parameter in the sine wave minimization proved to be the period, the minimization was repeated for several values of the period. In all cases, this algorithm converged to an acceptable solution, as indicated by the residuals and inspection by eye.
Appendix C: Column density derivation
![\begin{figure*}
\par\includegraphics[angle=-90,width=11cm,clip]{13200_29.eps}\vs...
...degraphics[angle=-90,width=11cm,clip]{13200_33.eps} \vspace{10mm}
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg148.png)
|
Figure C.1:
Ratio of the total integrated intensities
|
| Open with DEXTER | |
Table C.1:
Conversion factor, N0 (in
12/()), at an excitation temperature
![]() K
(see Eq. (C.2)).
K
(see Eq. (C.2)).
All column densities are derived assuming optically thin
emission with
levels populated in LTE at the excitation temperature T_ex. Under
these assumptions, the column density is directly proportional to the
integrated flux in the line
![]() .
From a transition
.
From a transition
![]() between
energy levels
between
energy levels ![]() and
and ![]() (corresponding to an energy
(corresponding to an energy
![]() ),
one can compute the total column density of the molecule as
),
one can compute the total column density of the molecule as
in SI units, where
with
Appendix D: Modelling of the prestellar core L 1544
In order to interpret our observations of L 1544, we make use
of the
model of one-dimensional, free-fall gravitational collapse used in
our previous study (A07). This model incorporates dust grain
coagulation and a time-dependent chemistry, including the reactions
listed in Sect. 5
above, which are directly relevant
to the present work. We assume a constant kinetic temperature, T
=
10 K, and a cosmic ray ionization rate,
![]() s-1.
Further information on the model may be found in
Flower et al. (2005).
s-1.
Further information on the model may be found in
Flower et al. (2005).
An important aspect of the interpretation is to connect, as
realistically as possible, the abundance profiles ( the number
density of species X, n(X) as a function
of the total density,
![]() ),
which are the output of the
model, to the observed variations in L 1544 of column
densities,
N(X), with impact parameter r.
In order to make this connection,
we proceed as follows:
),
which are the output of the
model, to the observed variations in L 1544 of column
densities,
N(X), with impact parameter r.
In order to make this connection,
we proceed as follows:
- we relate the gas density at r to the
central density by means of the relation
![\begin{displaymath}\nh(r) = \nh(0)/[1+(r/r_2)^{\alpha }]\end{displaymath}](/articles/aa/full_html/2010/05/aa13200-09/img170.png)
Tafalla et al. (2002), where r is the offset from centre, r = 0, and r2 is the radial distance over which the density decreases to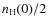 .
Following Tafalla et al.
(2002), we adopt r2
= 20
.
Following Tafalla et al.
(2002), we adopt r2
= 20
 (equivalent to
0.014 pc at the distance of L 1544)
and
(equivalent to
0.014 pc at the distance of L 1544)
and 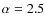 ;
the central density
;
the central density 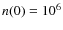 (A07), which is somewhat smaller than the value reported in
Table 1
for this object but within the probable uncertainties of its
determination;
(A07), which is somewhat smaller than the value reported in
Table 1
for this object but within the probable uncertainties of its
determination;
- using the computed values of n(X) , we
calculate the corresponding column density, N(X),
by integrating along the line of sight for any given value of r
in the adopted range
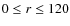 arcsec,
over which the density
arcsec,
over which the density 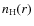 decreases from 6 to
decreases from 6 to 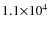 ;
;
- finally, the column densities are convolved with a Gaussian
profile with a (1/e) radius of 15
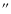 ,
corresponding to a HPBW
of 25
,
corresponding to a HPBW
of 25
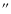 ,
in order to simulate approximately the IRAM 30 m
telescope beam at 100 GHz.
,
in order to simulate approximately the IRAM 30 m
telescope beam at 100 GHz.
We consider first the predictions of the chemical model, and specifically the abundances of nitrogen-containing species. We turn our attention then to the Gaussian-beam averaged column densities, and their comparison with the observations.
D.1 Abundance profiles
In Fig. D.1
are plotted the fractional abundance profiles of
CN, HCN, NO and N2H+;
note that the x-axis has been reversed
in order to facilitate the comparison with later Figures, in which the
x-coordinate is the offset from the centre, where
the density of the
medium is highest. We see from Fig. D.1 that, at low
densities, the fractional abundance of HCN exceeds that of CN, by a
factor which approaches two orders of magnitude when
![]() .
The fractional abundance of HCN decreases towards the
maximum density of 6 , where
.
The fractional abundance of HCN decreases towards the
maximum density of 6 , where
![]() .
This behaviour can be understood by reference to the
discussion in Sect. 5
above: CN is formed and
destroyed in reactions (3, 4) which involve
atomic
nitrogen; HCN, on the other hand, is formed in reaction (10)
with N but destroyed in reactions with H+ and H3+
that
ultimately lead to CN. Consequently, as the density of the medium
increases, and neutral species begin to freeze on to the grains, the
fractional abundance of HCN falls, whereas the fractional abundance of
CN remains roughly constant until, finally, CN too freezes on to the
grains.
.
This behaviour can be understood by reference to the
discussion in Sect. 5
above: CN is formed and
destroyed in reactions (3, 4) which involve
atomic
nitrogen; HCN, on the other hand, is formed in reaction (10)
with N but destroyed in reactions with H+ and H3+
that
ultimately lead to CN. Consequently, as the density of the medium
increases, and neutral species begin to freeze on to the grains, the
fractional abundance of HCN falls, whereas the fractional abundance of
CN remains roughly constant until, finally, CN too freezes on to the
grains.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{13200_34.eps}
\includegraphics[width=6.5cm,clip]{13200_35.eps}
\end{figure}](/articles/aa/full_html/2010/05/aa13200-09/Timg179.png)
|
Figure D.1:
The number densities of CN, HCN, NO and N2H+,
relative to
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{13200_36.eps}
\includegraphics[width=6.5cm,clip]{13200_37.eps}
\end{figure}](/articles/aa/full_html/2010/05/aa13200-09/Timg180.png)
|
Figure D.2: The column densities of CN, HCN, NO and N2H+, relative to H2, as predicted by the model described in Sect. D. The lower panel illustrates the effects of introducing a barrier of 25 K to both reaction (2) and reaction (4). |
| Open with DEXTER | |
Small barriers can arise when the potential energy curves
involved in
the atom-molecule reaction exhibit (much larger) barriers for certain
angles of approach but no barrier for others. In order to determine
the thermal rate coefficient, the probability of the reaction must be
averaged over the relative collision angle. If the rate coefficient is
then fitted to an Arrhenius form,
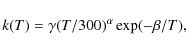
small, positive values of
It is clear from Fig. D.1
that the small reaction barrier
has the effect of enhancing the fractional abundance of CN and
reducing the amplitude of the variation in the ratio
![]() .
We shall see in the following
Sect. D.2
that this variation is damped further when the
ratio of the corresponding Gaussian-beam averaged column densities is
considered.
.
We shall see in the following
Sect. D.2
that this variation is damped further when the
ratio of the corresponding Gaussian-beam averaged column densities is
considered.
The results in Fig. D.1 have been
obtained assuming that the
grain-sticking probability was unity for all species, and that the
elemental abundance ratio
![]() ,
i.e. a
marginally oxygen-rich medium. This value of the C:O ratio was an
outcome of the modelling by A07 of observations of NO and N2H+
in
L 1544. These authors investigated also the consequences of
varying
the values of the sticking coefficient for atomic C, N
and O, and the
initial value of the N:N2 abundance ratio. We
recall that
increasing the elemental C:O abundance ratio further has the
consequence of reducing the HCN:CN ratio, thereby improving the
agreement with the observations. On the other hand, the CN:NO ratio
also rises, and the values of this ratio in Fig. D.1, where
,
i.e. a
marginally oxygen-rich medium. This value of the C:O ratio was an
outcome of the modelling by A07 of observations of NO and N2H+
in
L 1544. These authors investigated also the consequences of
varying
the values of the sticking coefficient for atomic C, N
and O, and the
initial value of the N:N2 abundance ratio. We
recall that
increasing the elemental C:O abundance ratio further has the
consequence of reducing the HCN:CN ratio, thereby improving the
agreement with the observations. On the other hand, the CN:NO ratio
also rises, and the values of this ratio in Fig. D.1, where
![]() ,
already exceed the values of the
corresponding column density ratio, observed in L 1544, where
,
already exceed the values of the
corresponding column density ratio, observed in L 1544, where
![]() by
typically an order of magnitude. It is
possible that selective variations in the values of the sticking
probability, or in the initial N:N2 abundance
ratio
by
typically an order of magnitude. It is
possible that selective variations in the values of the sticking
probability, or in the initial N:N2 abundance
ratio![]() , might alleviate some
of these discrepancies. However, whilst there remain such large
uncertainties in the values of the rate coefficients for the key
neutral-neutral reactions, discussed in Sect. 5, it
would perhaps be premature to investigate further the consequences of
modifying the values of other (and equally uncertain) parameters, in
an attempt to improve the agreement between the models and the
observations. Our aim here is to point to the discrepancies and
highlight the uncertainties; and it seems unlikely that further
progress can be made until the rates of at least some of the key
reactions have been measured at low temperatures.
, might alleviate some
of these discrepancies. However, whilst there remain such large
uncertainties in the values of the rate coefficients for the key
neutral-neutral reactions, discussed in Sect. 5, it
would perhaps be premature to investigate further the consequences of
modifying the values of other (and equally uncertain) parameters, in
an attempt to improve the agreement between the models and the
observations. Our aim here is to point to the discrepancies and
highlight the uncertainties; and it seems unlikely that further
progress can be made until the rates of at least some of the key
reactions have been measured at low temperatures.
Table D.1: Line properties (main beam temperature scale) and total column densities derived towards L 183. Numbers in parentheses are powers of 10.
Table D.2: As Table D.1 but for lines observed towards L 1544.
Table D.3: As Table D.1 but for lines observed towards Oph D.
Table D.4: As Table D.1 but for lines observed towards L 1517B.
Table D.5:
As Table D.3
but for lines observed towards L 310. The dust and thus column
densities are only the 3![]() level.
level.
D.2 Column densities
In Fig. D.2
are shown the computed column densities of CN,
HCN, NO and , relative to the column density of . The
fractional abundances of these species, relative to ![]() ,
derive from
the models discussed in the previous Sect. D.1.
,
derive from
the models discussed in the previous Sect. D.1.
At zero offset, the line of sight passes through regions with
densities covering the entire range of the model,
![]() .
Consequently, the column density ratio,
.
Consequently, the column density ratio,
![]() ,
evaluated at the
peak density
,
evaluated at the
peak density ![]() ;
further smoothing is introduced by
the Gaussian-beam averaging. The overall effect of the
line-of-sight and Gaussian-beam averaging is a flattening of the
column density profiles (Fig. D.2), compared with
the
fractional abundance profiles (Fig. D.1). Comparing the
two
panels of Fig. D.2,
we see that the introduction of the
small barriers to the reactions of CN and NO with N reduces
substantially the
;
further smoothing is introduced by
the Gaussian-beam averaging. The overall effect of the
line-of-sight and Gaussian-beam averaging is a flattening of the
column density profiles (Fig. D.2), compared with
the
fractional abundance profiles (Fig. D.1). Comparing the
two
panels of Fig. D.2,
we see that the introduction of the
small barriers to the reactions of CN and NO with N reduces
substantially the
![]() column
density
ratio. Although they do not attain the observed value, of the order
of 1, the computed values of
column
density
ratio. Although they do not attain the observed value, of the order
of 1, the computed values of
![]() in
the lower
panel of Fig. D.2
are clearly more compatible with the
observations of L 1544 than are those in the upper panel.
in
the lower
panel of Fig. D.2
are clearly more compatible with the
observations of L 1544 than are those in the upper panel.
References
- Akyilmaz, M., Flower, D. R., Hily-Blant, P., Pineau des Forêts, G., & Walmsley, C. M. 2007, A&A, 462, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Andersson, S. & Markovi, N., & Nyman, G. 2003, J. Phys. Chem. A, 107, 5439 [CrossRef] [Google Scholar]
- Bacmann, A., André, P., Puget, J.-L., et al. 2000, A&A, 361, 555 [NASA ADS] [Google Scholar]
- Bacmann, A., Lefloch, B., Ceccarelli, C., et al. 2002, A&A, 389, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, M. C., & Tafalla, M. 2007, A&A, 470, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2005, A&A, 436, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2006, A&A, 456, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Schutte, W. A., et al. 2000, ApJ, 536, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Harju, J., Juvela, M., Schlemmer, S., et al. 2008, A&A, 482, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, E., Terzieva, R., & Talbi, D. 2000, MNRAS, 311, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Pety, J., & Guilloteau, S. 2005, CLASS evolution: I. Improved OTF support, Tech. rep., IRAM [Google Scholar]
- Hily-Blant, P., Walmsley, M., Pineau des Forêts, G., & Flower, D. 2008, A&A, 480, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirota, T., Yamamoto, S., Mikami, H., & Ohishi, M. 1998, ApJ, 503, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Hirota, T., Ikeda, M., & Yamamoto, S. 2003, ApJ, 594, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Irvine, W. M., & Schloerb, F. P. 1984, ApJ, 282, 516 [Google Scholar]
- Le Bourlot, J. 1991, A&A, 242, 235 [NASA ADS] [Google Scholar]
- Maret, S., Bergin, E. A., & Lada, C. J. 2006, Nature, 442, 425 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Monteiro, T. S., & Stutzki, J. 1986, MNRAS, 221, 33P [NASA ADS] [CrossRef] [Google Scholar]
- Pagani, L., Lagache, G., Bacmann, A., et al. 2003, A&A, 406, L59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Bacmann, A., Motte, F., et al. 2004, A&A, 417, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Bacmann, A., Cabrit, S., & Vastel, C. 2007, A&A, 467, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineau des Forêts, G., Roueff, E., & Flower, D. R. 1990, MNRAS, 244, 668 [NASA ADS] [Google Scholar]
- Schauer, M. M., Jefferts, S. R., Barlow, S. E., & Dunn, G. H. 1989, J. Chem. Phys., 91, 4593 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Walmsley, C. M., Pineau des Forêts, G., et al. 1992, A&A, 256, 595 [NASA ADS] [Google Scholar]
- Skatrud, D. D., de Lucia, F. C., Blake, G. A., & Sastry, K. V. L. N. 1983, J. Mol. Spec., 99, 35 [Google Scholar]
- Sofia, U. J., & Meyer, D. M. 2001, ApJ, 554, L221 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Mardones, D., Myers, P. C., et al. 1998, ApJ, 504, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., Santiago-García, J., Myers, P. C., et al. 2006, A&A, 455, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walmsley, C. M., Churchwell, E., Nash, A., & Fitzpatrick, E. 1982, ApJ, 258, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, A&A, 418, 1035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ward-Thompson, D., Motte, F., & André, P. 1999, MNRAS, 305, 143 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... cores
![[*]](/icons/foot_motif.png)
- Based partly on observations carried out with the IRAM 30 m telescope. IRAM is supported by INSU-CNRS/MPG/IGN.
- ...
database
![[*]](/icons/foot_motif.png)
- http://kinetics.nist.gov/kinetics/
- ... coefficient
![[*]](/icons/foot_motif.png)
- From the osu_03_2008 rates of Eric Herbst's group (http://www.physics.ohio-state.edu/ eric)
- ... suite
![[*]](/icons/foot_motif.png)
- Available at http://www.iram.fr/GILDAS
- ... ratio
![[*]](/icons/foot_motif.png)
- The
equilibrium value of the N:N2 ratio, adopted in the present
models, is
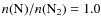 ,
as compared with the
(non-equilibrium) value of 18 adopted by A07.
,
as compared with the
(non-equilibrium) value of 18 adopted by A07.
All Tables
Table 1:
The sample of cores observed. Note that ![]() Oph D is also known
as L 1696A.
Oph D is also known
as L 1696A.
Table 2: Properties of the average profiles and average fractional abundance towards the observed cores (main beam temperature scale).
Table 3: Fractional abundances of CN, HCN, HNC and relative to H towards the dust emission peaks of our source sample. Tables D.1-D.5 give the fractional abundances toward all the observed positions.
Table A.1:
Hyperfine structure in CN (
![]() );
from Skatrud et al. (1983).
);
from Skatrud et al. (1983).
Table C.1:
Conversion factor, N0 (in
12/()), at an excitation temperature
![]() K
(see Eq. (C.2)).
K
(see Eq. (C.2)).
Table D.1: Line properties (main beam temperature scale) and total column densities derived towards L 183. Numbers in parentheses are powers of 10.
Table D.2: As Table D.1 but for lines observed towards L 1544.
Table D.3: As Table D.1 but for lines observed towards Oph D.
Table D.4: As Table D.1 but for lines observed towards L 1517B.
Table D.5:
As Table D.3
but for lines observed towards L 310. The dust and thus column
densities are only the 3![]() level.
level.
All Figures
![\begin{figure*}
\par\mbox {\includegraphics[angle=-90,width=5cm,clip]{13200_1.ep...
...8cm}
\includegraphics[angle=-90,width=5cm,clip]{13200_5.eps} }
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg48.png)
|
Figure 1: Continuum emission () at 1.2 mm with the locations of the line integrations (crosses). The HPBW at 1.2 mm and at the 3 mm frequencies discussed in this paper are indicated. A linear scale of 0.05 pc is also shown, assuming a distance of 150 pc for all cores except L 183 (110 pc). Continuum maps for L 1544, Oph D, L 183, L 1517B and L 310 are taken from Ward-Thompson et al. (1999), Pagani et al. (2003), Tafalla et al. (2004) and Bacmann et al. (2000) respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure*}
\mbox {\includegraphics[width=6cm,clip]{13200_6.eps}\hspace*{3m...
...
\includegraphics[width=6cm,clip]{13200_10.eps}\hspace*{6.3cm}
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg63.png)
|
Figure 2:
Comparison of the line profiles of different tracers; the spectra have
been shifted vertically for clarity. For CN, , and , the weakest HFS
components (at 113520.4315, 226887.3520 and 93176.2650 MHz
respectively) are shown. For each of the other lines, the strongest HFS
component is considered: 108780.2010, 86340.1840, 87090.8590, and
86054.9664 MHz for , H, HN and respectively. The spectrum is
taken from A07. The spectra are for zero offset (cf. Table 1). Towards
L 1517B, the CN spectrum is replaced by CN and the spectrum is
taken from Tafalla et al.
(2002). Towards Oph D, the spectrum at offset (0
|
| Open with DEXTER | |
| In the text | |
![\begin{figure*}
\par\includegraphics[angle=-90,width=3.3cm,clip]{13200_11.eps}\h...
...8cm}
\includegraphics[angle=-90,width=3.3cm,clip]{13200_14.eps}
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg67.png)
|
Figure 3: Relative integrated intensity of each HFS component for several species, at the central position for each source. In each panel, the dashed line indicates the relative intensities in LTE for optically thin emission. The thick line shows the optically thick limit. The abscissa is the rest line frequency. |
| Open with DEXTER | |
| In the text | |
![\begin{figure*}
\par\includegraphics[angle=-90,width=14cm,clip]{13200_15.eps}\vs...
...5cm}
\includegraphics[angle=-90,width=14cm,clip]{13200_18.eps}
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg69.png)
|
Figure 4:
Derived column densities towards each source. From top to
bottom: L 1544, L 183, Oph D, and
L 1517B. The column densities are plotted as a function of the
distance from the dust emission peak, along both cuts. Also plotted is
the H2 column density (grey histogram, right
scale), as derived from the dust emission (assuming |
| Open with DEXTER | |
| In the text | |
![\begin{figure*}
\par\includegraphics[angle=-90,width=14cm,clip]{13200_19.eps}\vs...
...cm}
\includegraphics[angle=-90,width=14cm,clip]{13200_22.eps}
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg70.png)
|
Figure 5: Same as Fig. 4 for the derived fractional abundances. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{13200_23.eps}
\end{figure}](/articles/aa/full_html/2010/05/aa13200-09/Timg91.png)
|
Figure 6: The principal reactions involved in the low-temperature chemistry of nitrogen-containing species, and specifically of CN, HCN and HNC. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{13200_24.eps}
\end{figure}](/articles/aa/full_html/2010/05/aa13200-09/Timg132.png)
|
Figure 7:
Steady-state fractional abundances of nitrogen-containing species for a
density |
| Open with DEXTER | |
| In the text | |
![\begin{figure*}
\par\mbox{\includegraphics[width=8cm,clip]{13200_25.eps}\hspace*...
...}
\includegraphics[width=8cm,clip]{13200_28.eps} }
\vspace{4mm}
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg137.png)
|
Figure 8:
The fractional abundances computed by the gravitational collapse model.
We show in panel a) results for the HCN
abundance as a function of the CN:HCN ratio. In panel
b) we show the HCN abundance as a function of the N2H+
abundance. In panel c) the HCN abundance
as a function of the NO abundance. The initial C:O ratio is assumed to
be 0.97. Each point is labeled with the initial gas phase
nitrogen abundance from -6 to 6.4-5. The initial steady state values
(filled squares, green) are shown for comparison. Results for a density
of 105 are given as blue open circles
and for 106 as filled red circles.
Data points are shown with black error bars. Data for N2H+ towards
Oph D and L 1517B are taken from Crapsi et al. (2005).
In panel d) we show the HCN:CO abundance
ratio as a function of the CO fractional abundance, for different
initial gas phase nitrogen abundances. For a given
|
| Open with DEXTER | |
| In the text | |
![\begin{figure*}
\par\includegraphics[angle=-90,width=11cm,clip]{13200_29.eps}\vs...
...degraphics[angle=-90,width=11cm,clip]{13200_33.eps} \vspace{10mm}
\end{figure*}](/articles/aa/full_html/2010/05/aa13200-09/Timg148.png)
|
Figure C.1:
Ratio of the total integrated intensities
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{13200_34.eps}
\includegraphics[width=6.5cm,clip]{13200_35.eps}
\end{figure}](/articles/aa/full_html/2010/05/aa13200-09/Timg179.png)
|
Figure D.1:
The number densities of CN, HCN, NO and N2H+,
relative to
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{13200_36.eps}
\includegraphics[width=6.5cm,clip]{13200_37.eps}
\end{figure}](/articles/aa/full_html/2010/05/aa13200-09/Timg180.png)
|
Figure D.2: The column densities of CN, HCN, NO and N2H+, relative to H2, as predicted by the model described in Sect. D. The lower panel illustrates the effects of introducing a barrier of 25 K to both reaction (2) and reaction (4). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



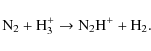
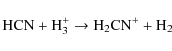
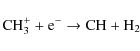
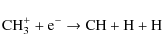
![\begin{displaymath}N_{\rm tot} = \frac{3\epsilon_0h}{2\pi^2}~\frac{1}{\ensuremat...
...W_{\rm tot}} }{\Delta J_\nu [1-\exp(-\frac{T_0}{T_{\rm ex}})]}
\end{displaymath}](/articles/aa/full_html/2010/05/aa13200-09/img162.png)
![\begin{displaymath}N_{\rm tot} = \frac{8\tdix{12}}{\ensuremath{J_{\rm u}}\mu_{\r...
...T_0}{T_{\rm ex}})]} = N_0(T_{\rm ex}) ~\ensuremath{W_{\rm tot}}\end{displaymath}](/articles/aa/full_html/2010/05/aa13200-09/img166.png)