EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 513 (April 2010) A&A, 513 (2010) A65 Full HTML
Free Access
Issue
A&A
Volume 513, April 2010
Article Number A65
Number of page(s) 14
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200911803
Published online 30 April 2010
A&A 513, A65 (2010)

The large-scale magnetic field in the fourth Galactic quadrant

T. Nota - P. Katgert

Leiden Observatory, Leiden University, Niels Bohrweg 2, Leiden, The Netherlands

Received 5 February 2009 / Accepted 28 November 2009

Abstract
Context. Aims. We have re-examined the published rotation measures (RMs) of extragalactic point sources and pulsars with $\vert b\vert < 3\hbox{$^\circ$ }$ to study the magnetic field in the fourth Galactic quadrant.
Methods. We reduced the influence of structure in electron density as much as possible by excluding objects for which H$\alpha$-data indicate large fluctuations in $n_{\rm e}$ somewhere along the line of sight. We also excluded objects for which the RM may have been significantly ``corrupted'' by an intervening supernova remnant. We modeled RM(l), the longitude dependence of RM of the unaffected extragalactic sources and pulsars. We assumed several geometries for the large-scale field. All but one of those are based on logarithmic spiral arms (with various pitch angles and widths), while one has circular symmetry. We also made different assumptions about the large-scale $n_{\rm e}$-distribution.
Results. The data suggest the following generic behaviour of the large-scale field in the 4th Galactic quadrant. The field is most likely organized along logarithmic spiral arms and shows two significant reversals: from the Norma arm (CCW field) to the Norma-Crux interarm region (CW field), and from the Norma-Crux interarm region to the Crux arm (CCW field). The present data do not constrain the field in and beyond the Crux-Carina interarm region. Although the models give a good description of the global character of RM(l), individual RM-estimates deviate by typically 15 times their measurement errors. We argue that these large deviations are most likely due to the ``small-scale'' field that dominates on scales of up to several hundred pc.
Conclusions. The picture that emerges is thus of a field that has significant structure on smaller scales, but for which the average values in arms and interarm regions are nevertheless well-defined. In addition, this smaller-amplitude large-scale field appears to reverse at each arm-interarm boundary that we can study with the present data. We briefly discuss the link between these results and theoretical predictions.

Key words: Galaxy: structure - ISM: magnetic fields

1 Introduction

In nearby galaxies, the large-scale magnetic field can be mapped fairly well (e.g., Beck 2007). However, because the observations in general still have fairly low linear resolution, structure on scales below a (few) hundred pc is not resolved, and any smaller-scale structure in the magnetic field is averaged out. In the Galaxy, on the other hand, observations of the magnetic field can have much higher linear resolution, but it has proven difficult to construct an unambiguous picture of the large-scale magnetic field in our Galaxy ``from within''. The small-scale field may be comparable to the large-scale field, and this makes it even more difficult to obtain unbiased estimates of the large-scale field in the Galaxy.

Notwithstanding these difficulties, several groups have tried to map the large-scale Galactic field, using observations of the rotation measures (RM) of pulsars (e.g., Men et al. 2008; Weisberg et al. 2004; Han et al. 2006; Vallée 2008a; Noutsos et al. 2008) and/or extragalactic radio sources (Brown et al. 2007). An intrinsic problem in the use of RM is that its information on the l.o.s.-component of the magnetic field, $B_{\Vert}$, is coupled with the density of free electrons $n_{\rm e}$, since

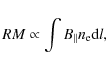
\begin{displaymath}RM \propto \int B_{\Vert} n_{\rm e} {\rm d}l,\end{displaymath}

(where the integral extends from source to observer). Beck et al. (2003) pointed out that all estimates of the strength of the large-scale magnetic field $\overline{B}$ from RM-data therefore involve assumptions about possible correlations between $n_{\rm e}$ and the magnetic field. Only if there is no correlation does $\langle B_{\Vert}\rangle_{n_{\rm e}}$ provide an unbiased estimate of $\overline{B}$. Beck et al. (2003) estimate that in the Galactic ISM the conditions are such that $\overline{B}$ is under- or overestimated by at most a factor of about 2.

For pulsars, the dispersion measure, DM, can be obtained, which gives the integral of $n_{\rm e}$, and the $n_{\rm e}$-weighted average value of $B_{\Vert}$ between observer and pulsar follows as $\langle B_{\Vert}\rangle_{n_{\rm e}} = 1.232 RM/DM$. However, most pulsars do not have parallactic distances, and the uncertainty in the model of the Galactic $n_{\rm e}$-distribution then limits the precision with which the distance can be derived from DM. This in turn limits the quality of the mapping of the large-scale field. For extragalactic sources, the distances are well known (effectively infinite compared to Galactic scales) but one must again resort to a model of the Galactic $n_{\rm e}$-distribution to obtain an estimate of the $n_{\rm e}$-averaged value of the Galactic $B_{\Vert}$. In principle, RM estimates of extragalactic sources might include an intergalactic contribution but due to lack of information this is generally ignored, and we follow that custom.

The various analyses of the large-scale Galactic magnetic field are often based on identical or very similar datasets. Still, they have led to different or even contradictory conclusions. Using RMs of 554 southern pulsars mostly in the first and fourth Galactic quadrants, Han et al. (2006) conclude that the field in the spiral arms interior to the Sun is counterclockwise (CCW) as viewed from the Galactic North Pole (a convention that we follow), while the field in the interarm regions is most likely clockwise (CW). Brown et al. (2007) used RMs of 148 EGS close to the Galactic plane ( $\vert b\vert \le 1.5\hbox{$^\circ$ }$) in the fourth Galactic quadrant, in combination with RMs of 120 pulsars in the same region. They concluded that the best-fit model to those data has a CW field everywhere, except in the Crux-Scutum arm and in the Molecular Ring. This picture is confirmed, to a large extent, by Vallée (2008a), who concludes in addition that the magnetic field does not follow the arms (with an approximate pitch angle of about -10$^\circ$) but instead has circular symmetry.

Noutsos et al. (2008) compared their pulsar data with predictions from four analytical models, and found that none of the models provide an acceptable description of the data. Using 482 pulsars with $\vert b\vert < 10 \hbox{$^\circ$ }$, Men et al. (2008) concluded that the three most widely used theoretical models are all ruled out by the data, and at similar confidence levels. They attribute this to the large-scale field in the Galactic disk having a more complex pattern than just circular, axisymmetric, or bisymmetric.

In this paper, we use published RM data of pulsars and extragalactic sources in the fourth Galactic quadrant with $\vert b\vert \le 3\hbox{$^\circ$ }$ in an attempt to understand the reasons for these (at least partly) conflicting results. A crucial step in our analysis is the assessment of the reliability (as opposed to the uncertainty) of each RMestimate. As was first stressed by Mitra et al. (2003), RM estimates of pulsars may be biased when the pulsar lies behind an HII region, and we extend this idea to the more general case of unusually large variations in the electron density $n_{\rm e}$ along the line of sight to the pulsar or EGS. In addition, we also consider the potential bias in RM introduced when the line of sight to the pulsar or EGS is intercepted by a supernova remnant.

In Sect. 2, we summarize the data that we used. In Sect. 3, we describe our analysis of the reliability of individual RM estimates, and in Sect. 4 we present the results of the reliability analysis, as well as the longitude dependence of the reliable RMs. In Sect. 5, we present the properties of the models that we fit to the data. In Sect. 6, we discuss the information about the large-scale field that emerges from the model fitting. In Sect. 7, we discuss the source of the large spread of the data about the best-fit models, and in Sect. 8 we summarize and discuss our results.

2 The data

We limited ourselves to the fourth Galactic quadrant, for which homogeneous samples of RMs of low-latitude extragalactic sources (henceforth EGS) and pulsars (PSR) are available in the literature. Our discussion is therefore restricted to the magnetic field in the Galactic midplane.

We used the 148 EGS observed and used by Brown et al. (2007) in the Galactic longitude range $253\hbox {$^\circ $ }\le l \le 358\hbox {$^\circ $ }$ and with Galactic latitudes $\vert b\vert \le 1\hbox{$.\!\!^\circ$ }5$ to which we added 12 sources from Gaensler et al. (2001), one from Broten et al. (1988), and one from Clegg et al. (1992) in the same longitude range but with $1\hbox{$.\!\!^\circ$ }5 < \vert b\vert \le 3\hbox{$.\!\!^\circ$ }0$. Thus, the total number of EGS is 162, and details of these are given in Tables 2 and 4. The effective latitude limit of $1\hbox{$.\!\!^\circ$ }5$ implies a maximum vertical distance from the midplane (z) of about 500 pc for a line-of-sight 20 kpc long.

We used 180 PSR with $253\hbox {$^\circ $ }\le l \le 358\hbox {$^\circ $ }$ and $\vert b\vert \le 3\hbox{$.\!\!^\circ$ }0$. The data were taken from Han et al. (1999), Taylor et al. (2000), Han et al. (2006), and from the ATNF pulsar catalogue[*]. For the average estimated distance of the PSR of about 5 kpc our latitude limit corresponds to a maximum vertical distance |z| of about 250 pc. We chose not to apply a limit in |z|. First, such a limit would be ill-defined in view of the considerable uncertainties in the pulsar distances, which are almost all based on dispersion measures and thus rely heavily on assumptions about the $n_{\rm e}$-distribution. Secondly, PSR at higher latitudes with $\vert z\vert < z_{\rm max}$ have, on average, shorter distances and do not provide much extra information about the horizontal component of the large-scale field due to projection.

Noutsos et al. (2008) published new and revised RM estimates for many PSR. In the majority of cases, the differences between the new and old values are within the quoted errors, although some objects show a disagreement of up to 10 rad m-2. However, only very rarely are the two RM-values highly discrepant. Where applicable, we adopted the values from Noutsos et al. (2008). The details of the 180 PSR are given in Tables 3 and 5. The RM estimates and their estimated errors were taken from the various papers; the estimated errors generally range from a few to a few tens of rad m-2.

In Fig. 1, we show all data for EGS (upper panel) and PSR (lower panel) versus Galactic longitude. We show only the RMestimates, because for the large majority of objects the symbols encompass the estimated errors. In other words, the large spread in RM in both panels is not due to errors in the RM estimates.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{11803fg1a.ps}\par\vspace*{2mm} \includegraphics[width=8.5cm,clip]{11803fg1b.ps} \end{figure} Figure 1:

The RM estimates from the literature for EGS ( upper panel) and PSR ( lower panel), versus Galactic longitude; there are 162 EGS and 180 PSR with $253\hbox {$^\circ $ }\le l \le 358\hbox {$^\circ $ }$ and $\vert b\vert \le 3\hbox{$.\!\!^\circ$ }0$. The coding of the RM estimates reflects our judgement of their reliability, where the open symbols indicate the unreliable estimates (see Sects. 3 and 4 for details).

Open with DEXTER

3 The reliability of the RM estimates

As was shown by Noutsos et al. (2008), the large spread in RM in Fig. 1 can neither be due to measurement errors nor to 180 $\hbox{$^\circ$ }$ ambiguities in the polarization angles; the latter are essentially under control in ``modern'' closely-spaced multi-frequency polarization data. The large spread in RM is most apparent in the $\Delta RM$ of close pairs (with angular distances of at most a few degrees) which can be as large as several hundreds or even 1000 rad m-2. These $\Delta RM$ values most likely have their origin in structure in the Galactic interstellar medium (ISM), which manifests itself in the small-scale magnetic field and in inhomogeneities in the electron density.

One aspect of the latter is the effect of HII regions on RM values of EGS and PSR. This was first discussed by Mitra et al. (2003), following earlier work on the effect of HII regions and OB stars on the dispersion measure (DM) of PSR by Prentice & Ter Haar (1969), Grewing & Walmsley (1971), and in an earlier paper by Mitra & Ramachandran (2001). Several discussions of such observed or suspected RM anomalies can be found in the literature (see e.g., Brown & Taylor 2001; Rand & Kulkarni 1989; Han et al. 1999). Another aspect of the effect of structure in the ISM on RM estimates is that produced by Supernova Remnants (SNR); this has been discussed by Mitra et al. (2003), Haverkorn et al. (2008), and Whiting et al. (2009).

Somewhat surprisingly, these two effects have never been fully taken into account in discussions of the large-scale component of the Galactic magnetic field based on RM estimates of PSR and/or EGS (see e.g., Rand & Kulkarni 1989; Rand & Lyne 1994; Indrani & Deshpande 1999; Han et al. 1999; Frick et al. 2001; Han et al. 2006; Brown et al. 2007; Men et al. 2008; Vallée 2008a). From time to time, one finds references to unexpected deviations from smoothness in the RM-distributions, as e.g., in the so-called ``Carina-anomaly'' mentioned by Han et al. (2006). However we are not aware of any systematic identification of unreliable RM estimates except in the analysis of Haverkorn et al. (2008), but their focus was not on the large-scale Galactic magnetic field.

Yet, the ``corruption'' of RMs due to structure in the ISM was demonstrated to be potentially severe by Mitra et al. (2003). These authors estimated that an HII region with angular size of 2 $\hbox{$^\circ$ }$ and a linear diameter of 30 pc could produce a $\Delta RM$ of 250 rad m-2, and that would make the estimated magnetic field strength very unreliable, if not unusable. In the following subsections, we describe how we judged the (un-)reliability of the individual RMestimates of EGS and PSR. The other aspect of structure in the Galactic ISM, namely variations of the magnetic field on small scales, and its effect on RM values of EGS and PSR will be discussed in Sect. 7.

3.1 RM ``corruption'' by significant structure in n$_{\rm e}$

When using a measured RM estimate as an indicator of the $n_{\rm e}$-averaged strength of the magnetic field, it is advisable to eliminate data for which there is evidence that the $n_{\rm e}$-distribution is very non-uniform. This is because a very non-uniform weighting of the line-of-sight component of the field may enhance local structure in the field, which can rob the concept of large-scale field of its meaning. That is particularly relevant when the small-scale field is comparable to or stronger than the large-scale field, as is thought to be the case in the spiral arms (e.g., Haverkorn et al. 2008; Beck 2007). This problem is exacerbated by field reversals, because a very uneven weighting of positive and negative field contributions may even lead to incorrect conclusions about the direction of the mean field.

Berkhuijsen et al. (2006) determined the degree of non-uniformity in the $n_{\rm e}$-distribution along lines of sight towards 157 PSR, at Galactic latitudes $\vert b\vert > 5\hbox{$^\circ$ }$ and within about 3 kpc from the Sun. They quantify the degree of non-uniformity by the volume filling factor, $f_{\rm v}$ ($\approx$ $DM^2/[EM_{\rm p} D])$, where $EM_{\rm p}$ is the emission measure produced in front of the PSR and D its physical distance. They find that $f_{\rm v}$ ranges from about 1 to 50%, with a median value of about 10%.

To be able to eliminate lines of sight with very non-uniform $n_{\rm e}$-distributions, we must have a way of selecting against low values of $f_{\rm v}$. However, since we do not have DM estimates for the EGS, we cannot use $f_{\rm v}$ as an indicator of unreliable estimates of RM for EGS and PSR alike. In principle, we could have inferred $f_{\rm v}$for our PSR directly from EM and DM, if at these low latitudes a reliable correction for extinction was possible, and if the estimation of $EM_{\rm p}$ would not be as problematic as it is at low latitudes.

From the above expression for $f_{\rm v}$, it can be seen that large values of EM correspond in general to low values of $f_{\rm v}$. However, a large value of EM by itself does not guarantee a low value of $f_{\rm v}$, but one can compare the EM value for the line of sight of interest with EM values for neighbouring lines of sight. More precisely: one can estimate the probability that the observed EM for the line of sight in question will be exceeded in a random draw from the collection of EM values observed for neighbouring lines of sight. If this probability is below a certain threshold value, the RM estimate for the particular line of sight is suspect because the EM value is uncharacteristically high for its surroundings.

We used the Southern H$\alpha$ Sky Survey Atlas (SHASSA, Gaustad et al. 2001) to investigate whether the EM values for the lines of sight to our EGS and PSR are uncharacteristically high for their surroundings. We used the H$\alpha$ intensities straight from the survey, without translation into EM (the ratio of the two is constant and depends only on temperature), and without correction for interstellar reddening (as reddening corrections cannot be usefully applied for $\vert b\vert < 5 \hbox{$^\circ$ }$; see e.g. Berkhuijsen et al. 2006). For PSR, we did not attempt to correct the observed EM to $EM_{\rm p}$. It is therefore possible that we erroneously reject a PSR RM because of a highly non-uniform $n_{\rm e}$-distribution beyond the PSR, but then at least we do not retain unreliable RMs that should have been rejected.

We compared the H$\alpha$ intensity observed towards each object with the distributions of the H$\alpha$ intensities in 3 ``concentric'' squares centered on the object, with sides of $0\hbox{$.\!\!^\circ$ }67$, $1\hbox{$.\!\!^\circ$ }33$ and  $2\hbox{$.\!\!^\circ$ }67$. If the H$\alpha$ intensity towards the object exceeds a certain threshold in at least one of the square areas, its RMestimate is considered to be unreliable. We gauged the effect of the value of the threshold on the results by considering thresholds corresponding to the 97.5th, 95th, 90th, 80th, and 60th percentiles in the $I_{\rm H\alpha}$-distributions. It appears that the estimates of the large-scale magnetic field are quite insensitive to the exact value of the threshold, although for the 60th-percentile threshold the statistics are significantly reduced. Even though the spread in the observed RM values about the model solutions (see Sect. 6) varies by at most 10% from the 80th percentile upwards, we used the 95th-percentile threshold for the model fits discussed in Sect. 6, because $\langle \vert\Delta RM\vert\rangle$ is smallest for that value.

We guarded against H$\alpha$ intensities that are exceptional on a small but not on a larger angular scale by rescinding the verdict ``unreliable'' if the H$\alpha$ intensity towards the object was exceeded by more than 10% of the H$\alpha$ intensities in (one of) the larger square(s). Clearly, the verdict ``unreliable'' cannot be rescinded when based on the data in the largest square. This procedure finds sources that are at a significant local maximum within a rather uniform H$\alpha$ intensity, or near mostly (but not exclusively) small HII regions (step 1).

To identify sources close to a local maximum on a strong H$\alpha$-intensity gradient (say, towards the edge of an HII region), we divided each of the 3 rectangular areas centered on the object in 4 quadrants and applied the above test to the 4 subareas. If this showed the object to be at a local maximum on an H$\alpha$-intensity gradient, we checked that the gradient was likely to be caused by a nearby (< $0\hbox{$.\!\!^\circ$ }5$) HII region (step 2). Finally, we also checked whether the object was in the direction of a known large HII region (e.g., from the RCW catalogue, Rodgers et al. 1960), which might not have been evident from either of the above tests (step 3).

While EGS at a maximum in the H$\alpha$ intensity are always beyond the structure that causes the maximum, this is not necessarily true for PSR. The distance of the PSR must therefore be compared with the estimated distance of the HII region (from stellar distances or kinematical distances from e.g., CO velocities) to decide whether the RM of the PSR is unreliable. As is commonly done, we estimated the PSR distances from the observed DM with the $n_{\rm e}$-model of Cordes & Lazio (2002) (which we will refer to as CL02), but it must be remembered that in general these estimates are quite uncertain. In the latter comparison we adopt a 20% uncertainty in the PSR distance obtained from the observed DM in combination with CL02, i.e., the HII region must be closer than 80% of the estimated PSR distance for the RM estimate to be rejected.

3.2 RM corruption by supernova remnants

If the line of sight towards a target is intercepted by (part of) a SNR shell, the RM of the target may be significantly biased,as significant variations of RM, of up to 100 rad m-2, have been observed across individual SNR (see e.g. Mitra et al. 2003, and references therein). We used the SNR catalogue produced from observations at 843 MHz with the Molonglo Observatory Synthesis Telescope by Whiteoak & Green (1996), and its updates, to identify targets for which the RM estimate is likely to be biased. Since not all sources rejected by Haverkorn et al. (2008) were identified in this way, we also inspected the 2.4 GHz Stokes I maps from Parkes (Duncan et al. 1995b), to ensure consistency with Haverkorn et al.

As before, we need to ascertain that the SNR is in front of the PSR before we can reject a PSR RM estimate as being unreliable. Distances of SNR are generally not very well known, as they are mostly based on observed average surface brightness in combination with evolutionary models (see e.g., Green 2004). We again adopted a 20% uncertainty in the PSR distance implied by the observed DM, in combination with CL02. For several PSR, it was likely that the RMis corrupted by an intervening SNR. In addition, for some PSR a physical association with the SNR is very likely.

4 Application of the tests for RM reliability

4.1 Rejected PSR and extragalactic sources

The objects that were rejected as a result of the procedures described above (with 95%-percentile $I_{\rm H\alpha}$-threshold), are listed in Tables 2 and 3. PSR are listed with their estimated rotation measure (RM), dispersion measure (DM), distance (from the observed DM and the CL02 model), and H$\alpha$ intensity. For objects that were rejected by the H$\alpha$/HII-region test we indicate the reason for the rejection (``H$\alpha$ step''). We also give distance estimates of the HII-regions that are likely to be responsible for the enhanced emission, as well as references to the source of this distance estimate. For PSR that are omitted because the line of sight appears to be intercepted by a supernova remnant, we give the name of the remnant and its distance estimate, again with a reference to the source of the distance estimate. As mentioned before, for the EGS there is no need to give distance estimates of either HII regions or supernova remnants.

It is remarkable that the H$\alpha$/HII-region test has a relatively large effect on lines of sight with large values of RM. This is evident from Fig. 1 where the open symbols indicate the unreliable RM estimates. About half (31 of 60) of the lines of sight with |RM| > 500 rad m-2 are rejected and this fraction is the same for PSR (14 of 27) and EGS (17 of 33). Since the values of RM do not enter the tests at all, this provides support for the assumption that a significant part of the large spread in Fig. 1 is indeed due to structure in $n_{\rm e}$. Additional support is provided by the results of the modeling described in Sect. 6.

The SNR test leads to the rejection of 10 RM estimates of PSR and 23 of EGS. Of these 33 objects, 9 have |RM| > 500 rad m-2.

The slightly different rejection statistics of EGS and PSR (21 against 25%) probably reflects the fact that PSR are concentrated in the spiral arms, where the HII regions occur predominantly, while the relation between spiral arms and SNR is probably less tight.

4.2 The reliable data

The EGS and PSR with reliable RMs are listed in Tables 4 and 5. Ten of the PSR in Table 5 would have been rejected by the H$\alpha$/HII-region test, if the HII-region had not been either clearly beyond the PSR or at least not clearly in front of it, taking account of the error margins. These PSR and HII-regions are: J0837-4135 (RCW27), J1015-5719 (RCW49), J1020-5921 (RCW47), J1038-5831 (RCW53), J1046-5813 (RCW53), J1048-5832 (RCW53), J1056-6258 (RCW55), J1123-6102 (RCW57B), J1126-6054 (RCW57B), and J1718-3825 (RCW123).

\begin{figure} \par\includegraphics[width=8.5cm,clip]{11803fg2a.ps}\par\vspace*{2mm} \includegraphics[width=8.5cm,clip]{11803fg2b.ps} \end{figure} Figure 2:

The dependence on Galactic longitude l of the reliable RM values. In the upper panel, the PSR are shown, coded according to distance (open symbols: PSR within 5 kpc; filled symbols: PSR beyond 5 kpc). In the lower panel, the distant PSR (filled squares) and extragalactic sources (open circles) are shown together; in this panel, the lower limit to PSR distance is 6 kpc for $l > 325\hbox {$^\circ $ }$.

Open with DEXTER
The results are also shown in the plots of RM versus l, in Fig. 2. In the upper panel we show the PSR, coded according to distance; the open symbols indicate PSR with estimated distance within 5 kpc, and the filled symbols those with larger distances. This minimum distance corresponds to the distance of the tangent point of the Crux spiral arm (see Sect. 5.2). It is clear that the PSR closer than 5 kpc show little evidence of coherent structure in the RM(l)-distribution. This is understandable because the spiral structure manifests itself clearly only for distances that are at least as large as the distance of the tangent points of the Crux or Norma arms. In the lower panel of Fig. 2 we show the large-distance PSR as well as the EGS. Note that in this panel we have increased the PSR distance limit to 6 kpc for $l > 325\hbox {$^\circ $ }$. At these longitudes, we thus select the PSR close to the tangent point of the Norma- arm-cum-Molecular-Ring (see Sect. 5.2).

Figure 2 shows that application of the two rejection criteria has turned Fig. 1 into a unexpectedly clean picture, especially for $l \la 330\hbox{$^\circ$ }$. The data in the lower panel indicate three clear changes of the sign of RM, namely at $l \sim 306\hbox{$^\circ$ }$, $l \sim 315\hbox{$^\circ$ }$, and $l \sim 323\hbox{$^\circ$ }$. The change of sign at $l \sim 306\hbox{$^\circ$ }$ is well-documented, and it is also clearly visible in the total dataset (see, in particular, the upper panel of Fig. 1). The other changes of sign rely very much on the predominantly (but admittedly not exclusively) positive RM-values around $l \sim 320\hbox{$^\circ$ }$. These carried little weight in the analyses of Brown et al. (2007) and Vallée (2008a); however, most of those RM estimates survived the two tests that we described in Sect. 3.

Another remarkable result in Fig. 2 is that the RM(l)distributions of EGS and ``distant'' PSR are quite similar. The similarity is most apparent in the longitudes at which RM appears to change sign, but it also manifests itself in the global magnitudes of the RM estimates. We note that most of the data in the longitude range $280\hbox{$^\circ$ }\la l \la 295\hbox{$^\circ$ }$ (except for small-distance PSR) was found to be unreliable, because they mostly failed the H$\alpha$/HII-region test. This means that all results that rely heavily or exclusively on data in that longitude range (where the Carina arm dominates) must be regarded with caution.

5 Model predictions of RM(l)

To go beyond the general conclusions in the last paragraphs of Sect. 4.2, and to obtain information about the large-scale Galactic magnetic field and its possible reversals, we compared the observed RM(l) with model predictions. Such predictions require at least the following ingredients: 1) a model of the $n_{\rm e}$-distribution; and 2) a definition of the global geometry of the large-scale field. The latter involves the demarcation of the regions in which we will assume the field to have the same strength and handedness.

5.1 Electron-density model

We used two models for the Galactic $n_{\rm e}$-distribution: one derived by Cordes & Lazio (2002) from the measured dispersion measures of 1143 PSR and one with a uniform density. The model by Cordes & Lazio (CL02) consists of several components: thin and thick disks, spiral arms, and a Galactic center component. The code NE2001-1.0, which allows the calculation of $n_{\rm e}$ according to CL02 at arbitrary positions within the Galaxy, is publicly available[*]. The CL02 model is based on data for 1143 PSR, but only a very small fraction of those have accurate distances. Since this model became available, new estimates have been made of the scale-height of the thick-disk component (Berkhuijsen & Müller 2008; Gaensler et al. 2008); and new information about the small-scale structure of the warm ionized medium, such as the volume filling-factor (Berkhuijsen et al. 2006; Berkhuijsen & Müller 2008), was obtained. However, these new insights have not yet led to an improved overall model. As Gaensler et al. (2008) noted, the new insights are probably less relevant at low latitudes, and the by now well-documented underestimation of PSR distances by the CL02 model is most severe at high latitudes.

Since many of the details of the $n_{\rm e}$-model have yet to be confirmed and/or updated, we have also used a model with constant $n_{\rm e}$. From 81 low-latitude PSR with reliable RM, we derived the constant value of $n_{\rm e}$ that on average would produce the CL02 PSR distances, to be $n_{\rm e} = 0.06$ cm-3. It must be noted that this is just an estimate of the smeared-out density in the CL02 model, which may therefore still be an overestimate. It is certainly much higher than recent estimates of the midplane density of the thick disk. Berkhuijsen & Müller (2008) find 0.023 cm-3, but Gaensler et al. (2008) find 0.03 cm-3, at least when they include the low-latitude PSR. To this, the contributions of the thin disk and the smoothed spiral arms must be added but neither contribution is known very well. Cordes & Lazio (2002) give a density of the thin disk at z=0 of 0.09 cm-3 but the error in this is probably quite substantial, while in their model the thin-disk density has already dropped to 0.01 cm-3 at $z \sim 250$ pc. Given all these uncertainties, we decided to use, somewhat arbitrarily, a constant value of $n_{\rm e} = 0.04$ cm-3.

5.2 The geometry of the large-scale magnetic field

\begin{figure} \par\includegraphics[width=8.5cm,clip]{11803fg3.ps} \end{figure} Figure 3:

The regions with constant-amplitude field in our modeling of the large-scale magnetic field in the fourth Galactic quadrant. The definition of these regions is superimposed on a logarithmic greyscale representation of CL02 for z = 0. The Sun is at x = 0, y = 8.5. In the left panel, we show the definition for $p=12\hbox{$.\!\!^\circ$ }5$ and d=1.0 kpc. The arm regions are color-coded with central line and boundaries. The coding is: red - Norma arm, blue - Crux arm, green - Carina arm, yellow - Perseus arm. In the right panel, we illustrate the ring model championed by Vallée for a ringwidth of 1-kpc.

Open with DEXTER

It is widely assumed that the large-scale Galactic magnetic field follows the spiral arms. The main reason for that assumption is the orientation w.r.t. the optical spiral arms of the radio polarization angles in external galaxies. In our analysis, we thus mostly assume that the large-scale magnetic field can be fully described by its strength and handedness in arm and interarm regions. This requires a definition of the extent of these regions, so that we can assign each position on a given line of sight (i.e., for each (l,b)-pair) to one of these regions.

To define the spiral arms, we used the six observed longitudes in the 1st and 4th quadrants where the arms are seen tangentially, as derived by Vallée (2008b) from a host of observations using various tracers. These longitudes are: $31\hbox{$^\circ$ }\pm3\hbox{$^\circ$ }$ and $51\hbox{$^\circ$ }\pm4\hbox{$^\circ$ }$ in the 1st quadrant and $284\hbox{$^\circ$ }\pm2\hbox{$^\circ$ }$, $310\hbox{$^\circ$ }\pm3\hbox{$^\circ$ }$, $327\hbox{$^\circ$ }\pm3\hbox{$^\circ$ }$, and $339\hbox{$^\circ$ }\pm2\hbox{$^\circ$ }$ in the 4th quadrant. To these values, we fitted four-armed logarithmic spirals with various pitch angles p. The rms deviations between the observed and predicted longitudes were used, together with the Carina-Perseus interarm distance (along the direction from the Galactic center to the Sun), and the accurate distance to the W3OH complex in the Perseus arm, to estimate the allowed range of pitch angles.

We used $2.8 \pm 0.3$ kpc for the interarm distance and $1.95\pm0.04$ kpc for the W3OH distance (where $R_{\rm GC,Sun} = 8.5$ kpc, in line with CL02). We conclude that the allowed range of p is approximately $12\hbox{$.\!\!^\circ$ }5\pm1\hbox{$.\!\!^\circ$ }5$, and we derived solutions for $p=[11\hbox{$.\!\!^\circ$ }0,12\hbox{$.\!\!^\circ$ }5,14\hbox{$.\!\!^\circ$ }0$]. These values are consistent with previous estimates by e.g., Vallée (2005b), but we note that the estimate of the pitch angle by Heiles (1996) from starlight polarization data is not consistent with these values.

For the definition of the various arm and interarm regions, we assume that all arm regions have the same constant width d about the defining logarithmic spirals, and we have chosen d = 0.8(0.2)1.4 kpc. Since the interarm regions complement the arm regions, they do not have constant widths, but open up outwardly (see e.g., the left panel of Fig. 3). With the 12 (p,d)-pairs, we attempt to mimic that in reality spiral arms have neither constant pitch angle nor constant arm width.

The model thus has 7 regions (4 arm and 3 interarm regions), in each of which we assume the magnetic field to have the same strength (where we ignore the details of the jump conditions of the field at the interfaces between neighbouring regions with different field strengths). The field direction at each point is identical to that at the nearest point on the central line of the arm or interarm region (midpoint between neighbouring arms) to which it belongs. At each position, this defines the angle between the magnetic field and the line of sight, and thus the projection factor required to derive the line-of-sight component of the field. We assume that the definition of arm and interarm regions is identical for all vertical heights z of interest because we limit ourselves to $\vert b\vert \le 3\hbox{$^\circ$ }$(i.e., $\vert z\vert \la 700$ pc). We also assume that the field strength does not depend on the vertical distance z from the plane (at least for the distances in question) and that the field vector is parallel to that at the footpoint in the plane.

Our definition of arms and interarm regions in the Galactic plane for $p=12\hbox{$.\!\!^\circ$ }5$ and d=1.0 kpc is shown in the left panel of Fig. 3, superimposed on a logarithmic grey-scale representation of the CL02 model at z=0. The arms represented in our models correspond approximately to the Perseus, Carina, Crux, and Norma arms. It is clear that the arms in the CL02 $n_{\rm e}$-model are not perfectly consistent with an m=4 logarithmic spiral. In particular, the Crux arm is not reproduced very well in the logarithmic-spiral model. However, we refrained from tweaking the spiral model, in view of the uncertainties in the CL02 model.

For the Galaxy, the assumption of a spiral-arm related field was challenged by Vallée (2005a) who, in a study of RM estimates of over 350 PSR in all 4 quadrants, assumed that the field has circular symmetry, which he claimed provides the best fit to the data. In his most recent analysis (Vallée 2008a), he finds that the field is clockwise (CW) everywhere except in a 2 kpc wide annulus between 5 and 7 kpc (with $R_{\rm GC,Sun} = 7.6$ kpc), where it is counterclockwise (CCW). Men et al. (2008) also compare the PSR data with a ring model, and find that this model does not provide a good fit to the data. However, it is not clear to us how robust these conclusions are, because in these analyses unreliable RM estimates were not identified and rejected. Below (see Sect. 6), we investigate this point further, and therefore we show, in the right panel of Fig. 3, a ring model with ringwidth of 1 kpc. With a radial range from 4 to 12 kpc, this model has a number of unknowns (field strenghths) that is comparable to that in the model shown in the left panel.

5.3 Combining n$_{\rm e}$ with the model for the large-scale field

\begin{figure} \par\includegraphics[width=17cm,clip]{11803fg4.ps} \end{figure} Figure 4:

The results of the model fits of RM(l) for the spiral-arm related large-scale field, for EGS and PSR with CL02 $n_{\rm e}$, and $n_{\rm e} = 0.04$ cm-3. Each subpanel contains 12 field strengths with their bootstrap errors. These are arranged ( from left to right) in three groups of pitch angle ( $11\hbox{$.\!\!^\circ$ }0$, $12\hbox{$.\!\!^\circ$ }5$, $14\hbox{$.\!\!^\circ$ }0$), and each group contains the solutions for the four arm widths (0.8 kpc, 1 kpc, 1.2 kpc, 1.4 kpc), also ordered from left to right. In the fourth Galactic quadrant, positive field strengths correspond to CW fields. Arrows indicate solutions outside the plotted range with S/N-ratio >1.

Open with DEXTER

A model prediction of RM at a particular l and b can be regarded as the sum of several $\Delta RM$ contributions, one $\Delta RM$ for each of the arm/interarm regions, or for each of the concentric rings. Each term is equal to the field strength in the region |Bi|multiplied by a weight Wi, or

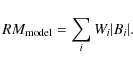
\begin{displaymath}RM_{\rm model} = \sum_i W_i \vert B_i\vert.\end{displaymath}

The weight Wi converts field strength into $\Delta RM$, and takes into account the distribution of $n_{\rm e}$ along the particular line of sight, as well as the projection angle between the line-of-sight direction and the field vector. Thus,

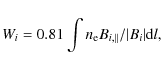
\begin{displaymath}W_i = 0.81 \int n_{\rm e}B_{i,\Vert}/\vert B_i\vert {\rm d}l,\end{displaymath}

where the integral extends over the part(s) of the line of sight that belong to region i, and where $B_{i,\Vert}/\vert B_i\vert$ is the cosine of the projection angle. For each line of sight, the N values of Wi are uniquely defined by the model assumptions discussed in Sect. 5.

The values of Wi were calculated by numerical integration using a 50-pc grid of $n_{\rm e}$, for the (l,b)-combinations of all objects with a reliable RM estimate in the longitude range $270\hbox{$^\circ$ }< l \le 330\hbox{$^\circ$ }$. For the EGS, the integration was performed out to the boundary of the $n_{\rm e}$-grid (corresponding to $R_{\rm GC} = 17.5$ kpc) because $n_{\rm e}$ is not defined in CL02 beyond that distance. For the PSR, the integration was performed out to the distance of the PSR.

Note that the PSR distances in Tables 3 and 5 were taken from the literature (and those follow from the CL02 web-interface). In the modeling (with CL02), we performed a direct integration of $n_{\rm e}$ up to the measured DM to obtain the PSR distance, as recommended by Cordes (private communication). The effect of the distance errors cannot be taken into account in the modeling, because a redistribution of all PSR according to their distance errors produces a pseudo-observation that is equivalent to the original one. Therefore, no information about the effect of the distance errors can be obtained.

6 The large-scale field in the 4th Galactic quadrant

We derived the best-fit values of Bi for pitch angles $p = 11\hbox{$.\!\!^\circ$ }0, 12\hbox{$.\!\!^\circ$ }5$, and $14\hbox{$.\!\!^\circ$ }0$ and for armwidths d = 0.8, 1.0, 1.2, and 1.4 kpc, from least-squares fits to the observed RM(l) values. We did not weight the observations with the inverse of the square of the estimated error of the measured RM, because the residuals between data and model are typically 15-30 larger than the measurement errors of $\sim$10-20 rad m-2. We regard this as an indication that the differences between data and model are not due to measurement errors. As we will discuss in Sect. 7 it is likely that these differences are primarily due to the small-scale component of the magnetic field. In spite of the large spread about the best-fit solutions, the significance of several of the derived Bi-values is quite high (up to 7$\sigma$). The values of $\sigma_{B_i}$ were derived from 10 000 bootstraps with residual resampling. The histograms of the 10 000 values of Bi are all very close to being Gaussian, and thus yield $\sigma_{B_i}$.

We derived separate solutions for EGS and PSR. We used all PSR with reliable RM estimates (i.e., those displayed in the upper panel of Fig. 2) and not just those beyond 5 or 6 kpc, which are shown in the lower panel of the same figure. The results are displayed in Fig. 4 for both EGS and PSR, and for 2 $n_{\rm e}$ models (CL02, and $n_{\rm e} = 0.04$ cm-3). Each subpanel contains 12 field strengths with their bootstrap errors. These are arranged (from left to right) in three groups of pitch angle ( $11\hbox{$.\!\!^\circ$ }0$, $12\hbox{$.\!\!^\circ$ }5$, $14\hbox{$.\!\!^\circ$ }0$), and each group contains the solutions for the four arm widths (0.8 kpc, 1 kpc, 1.2 kpc, 1.4 kpc), also ordered from left to right.

The most remarkable result in Fig. 4 is that the character of the solutions depends relatively little on the geometric details of the model (i.e., pitch angle and armwidth). In other words, the data that we used appear to define a generic solution. The three field strengths that are determined at $\ga$$3\sigma$ (for the Norma and Crux arms, and for the Norma-Crux interarm region) always show very convincing evidence for reversals. Because the relative contributions of arm and interarm regions vary with assumed arm width, the inferred field strengths in arms are lower for larger arm widths, while in interarm regions the opposite is true. However, the effects are not large and the handedness is not affected.

The dependence of the solution on the $n_{\rm e}$-model is slightly different for EGS and PSR. For the EGS, the field strengths scale more or less with the inverse of $\langle n_{\rm e}\rangle$. However, the details in the CL02 model produce deviations from strict inverse proportionality, and change the significance of the Bi-values. In contrast, the field strengths derived from the PSR appear to scale more weakly with $\langle n_{\rm e}\rangle$. This relative independence from the assumed $n_{\rm e}$-model is not unexpected. Although the PSR distances differ on average by a factor of 1.5 (see Sect. 5.1) between the two models, about 60% of the PSR assigments are unchanged. The field strengths implied by the PSR with unchanged assignment hardly change because the product of $n_{\rm e}$ and distance (i.e., DM) is unchanged. Only for the Norma arm does Bi differ significantly between the two $n_{\rm e}$-models, because very few PSR are assigned to that arm in the CL02 model.

Table 1:   The field strengths in the best-fit model in which the field has circular symmetry.

The significant reversals that we find in the inner Galaxy were, to some extent, already hinted at in Han et al. (2006) and Brown et al. (2007), although in the latter analysis the location of, in particular, the Norma arm differs substantially from ours. However, in neither of these studies was the significance and robustness of the result discussed. Our analysis shows that the field beyond the Crux arm is not constrained by the present data for EGS or PSR. Therefore, we attribute the apparent discrepancy between the results of Han et al. (2006) and Brown et al. (2007) for, in particular, the Carina arm to structure in $n_{\rm e}$ that was not accounted for. Similarly, the conclusion by Noutsos et al. (2008) that there is a reversal between the Crux and Carina arms would seem unwarranted.

Incidentally, the field strenghths and directions implied by EGS and PSR for the Norma and Crux arms and the Norma-Crux interarm region agree quite well. This is probably a manifestation of the fact that the projection of the field (as a result of the angle between field vector and line-of-sight) reduces the contribution to RM from the nearer and more distant parts of the line-of-sight. In other words, the sections of the line-of-sight closest to the tangent point of an arm c.q. interarm region contribute most to the integral of the product of $n_{\rm e}$ and $B_{\Vert}$. This argument appears to apply equally to EGS and PSR, in spite of the considerable uncertainties in the PSR distances.

A general feature of all solutions is the absence of clear systematic trends in $\Delta RM(l)$ (the difference between data and model) and this supports the evidence from the bootstrap errors. However, the large values of $\Delta RM$ clearly indicate that the model is oversimplified. This is evident from $\langle \vert\Delta RM\vert\rangle$, which, for the 24 model fits, is $208 \pm 12$ rad m-2 for the EGS and $167 \pm 7$ rad m-2 for the PSR. The very small dispersions in $\vert\Delta RM\vert$ of $\sim$10 rad m-2 around their mean values imply that it is not sensible to announce a best-fit model. The uncertainty in the $n_{\rm e}$-model and the use of two types of tracers (EGS and PSR), combined with the very uniform fit quality, preclude the choice of a true best-fit model for the large-scale field. We note that the $\langle \vert\Delta RM\vert\rangle$ of the EGS is somewhat, but significantly, larger than that of the PSR. One explanation for this could be the non-negligible intrinsic RMs of the EGS.

It is interesting to see how the four solutions that formally provide the best fit to the data reproduce the character of the observed RM(l). This is shown in Fig. 5. It is clear, especially from the left panels, that the global trends, and in particular the changes of sign, are reproduced quite well by the models. At the same time, it is also clear that the limitations of the models (with fixed pitch angle and armwidth) results in less-than-perfect agreement. However, it is remarkable that the large values of $\langle \vert\Delta RM\vert\rangle$, which quantify the mismatch between data and model, are essentially identical for all models. In Sect. 7, we argue that this spread can (and most probably must) be attributed primarily to small-scale structure in the magnetic field, which acts as ``noise'' in the solutions for the large-scale field.

\begin{figure} \par\includegraphics[width=8.8cm,clip]{11803fg5.ps} \end{figure} Figure 5:

A comparison of the observed RM values (filled symbols) used in the solutions ( left: EGS, right: PSR; top $n_{\rm e}$ = cst., bottom: $n_{\rm e}$ = CL02) with the predictions from the best-fit models (open symbols). Note that the best solutions are for different pitch-angle armwidth combinations; top-left: ( $11\hbox{$.\!\!^\circ$ }0$, 1.4), bottom left: ( $14\hbox{$.\!\!^\circ$ }0$, 0.8), top-right: ( $12\hbox{$.\!\!^\circ$ }5$, 1.4) and bottom-right: ( $11\hbox{$.\!\!^\circ$ }0$, 1.4).

Open with DEXTER

Although we argued that unreliable values of RM should not be used, we did derive solutions in which we used all data, to understand how the inclusion of unreliable RMs may have affected earlier work. For the EGS, the significance of the field strength determinations is more or less unchanged, but for the PSR the significance is reduced. The inclusion of the ``rejected'' data causes the field in the Carina arm to become moderately significant ( $2{-}3\sigma$ according to the EGS and $\sim$$2\sigma$ according to the PSR) with a strength of $\sim$$1~\mu$G and CW handedness. It is interesting that the $\langle \vert\Delta RM\vert\rangle$ of the rejected data w.r.t. the solutions based on the reliable data are $312 \pm 11$ (EGS) and $455 \pm 27$ (PSR). Comparison of these values with $\langle \vert\Delta RM\vert\rangle$ of the reliable data indicates that we have removed a large part of the effect of $n_{\rm e}$-structure by excluding the unreliable RM-values. It is interesting that the difference is larger for PSR than for EGS.

For completeness, we also fitted a ring model to the reliable data for EGS and PSR, even though circular fields require large-scale electrical currents that cannot be maintained. We used 8 rings between 4 and 12 kpc with widths of 1 kpc, so that the number of unknown field strengths is essentially identical to that in the solutions for the spiral-arm-related field. This ring width is also very close to that used by Vallée (2008a). The model fits the data with a spread that is very comparable to that of the models with a spiral-arm related field, as is evident from the very similar values of $\langle \vert\Delta RM\vert\rangle$ and bootstrap errors, at least within 9 kpc. As with the spiral-arm models, there are no systematic trends in  $\Delta RM(l)$.

The result is shown in Table 1. The agreement between EGS and PSR is not as good as in the previous solutions (see Fig. 4). The inner three rings show a field reversal, which is significant in the models with constant $n_{\rm e}$, but far less so for the CL02 $n_{\rm e}$-model. In all other rings, the results are either not significant or not concordant between EGS and PSR.

Using 554 PSR in all 4 Galactic quadrants, Vallée finds that the Galaxy has a large-scale CW field (i.e. B>0), but the ring between $\sim$5 and $\sim$8 kpc has a CCW field. It is not clear if a comparison between our solution and that obtained by Vallée (2008a) is meaningful because the latitude selection of that sample is unclear. However, if we assume this comparison to be sensible, we must conclude that there is a disagreement between Vallée's ring model fit and ours. Between 4 and 5 kpc, the EGS indicate a field that is CCW, in contrast to the result of Vallée. The PSR data in this radial range are consistent with the EGS data, and one would expect Vallée's larger PSR sample to also show this reversal. This disagreement, combined with the rather poor agreement between our EGS and PSR ring model solutions, throws serious observational doubt on the reality of the ring model.

7 The small-scale magnetic field as the primary source of $\langle \vert\Delta \textit{RM}\vert\rangle$

Men et al. (2008) concluded that the three theoretical models of the large-scale field that they used are ruled out almost equally by the data. The reason is that, while in some regions in the disk the value of $\chi_{\rm red}^{2}$ indicates that a particular model is acceptable, there are always several regions where $\chi_{\rm red}^{2} \gg 1$. The large spreads around our best-fit solutions are probably a manifestation of the same problem, even though our analysis is limited to the 4th quadrant. Yet, as we argue below, the large values of $\chi_{\rm red}^{2}$ and $\langle \vert\Delta RM\vert\rangle$ do not invalidate the concept of a large-scale field.

In our attempt to eliminate the influence of significant structure in $n_{\rm e}$, we used a threshold in the $I_{\rm H\alpha}$-distribution around the object corresponding to the 95th percentile (see Sect. 3.1). We made this choice because the sample defined by that threshold yields the smallest value of $\langle \vert\Delta RM\vert\rangle$. Although it is likely that most of the high-amplitude structure in $n_{\rm e}$ has been eliminated, it is not possible to quantify the extent to which the accepted data are still affected by low-amplitude $n_{\rm e}$-structure. Even so, we consider it very likely that the large values of $\langle \vert\Delta RM\vert\rangle$ for the reliable data are primarily due to small-scale field structure superimposed on the large-scale magnetic field.

The amplitude of the small-scale magnetic field can, and has been, estimated from PSR pairs. For each PSR pair with sufficiently small angular distance that the spatial separation is mainly in the l.o.s.-direction, one can derive $\vert\Delta B_{\Vert}\vert$ from the observed RM and DM-values as $ 1.232 \vert\Delta RM/ \Delta DM\vert$. This was previously done by Ohno & Shibata (1993) and Rand & Kulkarni (1989), following Ruzmaikin et al. (1988). In Fig. 6, we show the result for our ``reliable'' PSR, for pairs in arm regions (left panel) and interarm regions (right panel). The assignment of the PSR uses arms with a pitch angle $p=12\hbox{$.\!\!^\circ$ }5$, width d = 1.0 kpc, and $n_{\rm e} = 0.04$ cm-3. We mention in passing that there may be a small difference between arm and interarm regions in the expected sense (smaller $\vert\Delta B_{\Vert}\vert$ in interarm regions). However, in view of the distance uncertainties of the PSR and the associated uncertainty in the assignment to arms and interarm regions, it is not possible to estimate its significance.

\begin{figure} \par\includegraphics[width=8.9cm,clip]{11803fg6.ps} \end{figure} Figure 6:

$\vert\Delta B_{\Vert}(\Delta DM)\vert$, as derived from RM and DM estimates of pairs of PSR with small angular separation, for $p=12\hbox{$.\!\!^\circ$ }5$, d = 1.0 kpc. Pairs are only between PSR in the same arm or interarm region (we used $n_{\rm e} = 0.04$ cm-3 for the assignment); each region is indicated by a different symbol. In the left panel the coding is: open squares - pairs in the Norma arm, filled circles - pairs in the Crux arm, and open circles - pairs in the Carina arm. In the right panel the coding is: open squares - Norma-Crux interarm region, open circles - Crux-Carina interarm region, and filled circles - Carina-Perseus interarm region.

Open with DEXTER

The result in Fig. 6 is very similar to that obtained by Ohno & Shibata (1993), who used a sample of 182 Galactic PSR in all 4 quadrants. They also found that $\vert\Delta B_{\Vert}\vert$ shows a global inverse dependence on $\Delta DM$, with a maximum value of $\sim$$100~\mu$G for $\Delta DM \sim 1$ cm-3 pc, while at each value of $\Delta DM$, $\vert\Delta B_{\Vert}\vert$ exhibits a range of up to 2 decades. For that reason, we refrain from a detailed analysis of the result in Fig. 6, but instead we reiterate the main conclusions of their analysis.

On the assumption that all cells have the same size, Ohno & Shibata (1993) derive the strength of the random field, $\delta B$, that reproduces the observed global slope of the upper envelope of $\vert\Delta B_{\Vert}\vert$as a function of assumed cell size L. Although the stochastic nature of the model produces a spread in $\vert\Delta B_{\Vert}\vert$, the latter is generally smaller than observed. Therefore, they conclude that the observed spread also implies a significant spread in $n_{\rm e}$. It appears that the data can be represented fairly well for a range of assumed cell sizes and $n_{\rm e}$-fluctuations. They estimate $\delta B$ to be 4-6 $\mu$G (which should be compared to their estimate of 1-2 $\mu$G for the regular field), essentially independent of assumed cell size and spread in $n_{\rm e}$.

It seems plausible that the significant spread in $n_{\rm e}$, required in the analysis of Ohno & Shibata (1993) to match the data, is partly a result of the assumption of fixed cell size. A more realistic assumption of a spectrum of linear scales for $\delta B$ will produce a spread in $\vert\Delta B_{\Vert}\vert$ for fixed $\Delta DM$, which reduces the spread in $n_{\rm e}$ required by the single cell size analysis. This may be the reason why our data do not show a smaller range of $\vert\Delta B_{\Vert}\vert$, even though we excluded lines of sight with abundant $n_{\rm e}$-structure. However, the main conclusion remains that a $\delta B$ of 4-6 $\mu$G is required to produce the observed maximum values of $\vert\Delta B_{\Vert}\vert$ at each $\Delta DM$.

By implication, the small-scale field is an important (if not the) contributor to the $\langle \vert\Delta RM\vert\rangle$ of the reliable RM-values around the best-fit models. This means that the $\chi_{\rm red}^{2}$values obtained e.g., by Men et al. (2008) will be significantly reduced when the small-scale field is included in the prediction of the uncertainty in the observed RM-estimates. Any model of the (spectrum of the) small-scale field should reproduce the observed $\vert\Delta B_{\Vert}(\Delta DM)\vert$ of the PSR pairs. Therefore, one would predict the value of $\langle \vert\Delta RM\vert\rangle$ to be very close to $ 1/\surd2 \times \langle\vert\Delta B_{\Vert} \times \Delta DM\vert\rangle$, especially because we significantly suppressed the contribution to $\langle \vert\Delta RM\vert\rangle$ by $n_{\rm e}$-structure in our sample. The value of $\langle \vert\Delta RM\vert\rangle$ predicted from the observed $\vert\Delta B_{\Vert}\vert$ values of the PSR pairs is 162 rad m-2 (the average for all 24 models), which should be compared to the observed value of $167 \pm 7$ rad m-2. As a result, the predicted values of $\chi^2$ are close to unity for all models that we considered.

Table 2:   The rejected extragalactic sources.

Table 3:   The rejected PSR.

Table 4:   The extragalactic sources with reliable RM estimates

Table 5:   The PSR with reliable RM estimates.

8 Summary and discussion

We have used published rotation-measure (RM) data for low-latitude pulsars (PSR) and extragalactic sources (EGS) to study the large-scale magnetic field in the fourth Galactic quadrant. Because RM is the integral of the product of the l.o.s. component of the field and the electron density, one must take special care to obtain a ``view'' of the field that is as unaffected as possible by structure in the electron density. We therefore identified and rejected RM estimates of objects for which the emission measure (EM) indicates a high probability of a large amount of $n_{\rm e}$-structure somewhere along the line of sight.

The need for this cleaning of the data is evident from the finding that the lines of sight with a high probability of strong $n_{\rm e}$-structure turn out to be preferentially those with large RMvalues. Because the average $n_{\rm e}$ did not enter the selection, this confirms our presumption that the RM values corresponding to uncharacteristically large EM-values are indeed less reliable. Not surprisingly, the spread of the rejected data about the model that we fit to the accepted data appears to be about twice as large as that of the accepted data around the solution that they define. We have also identified and rejected RM estimates that are likely to be unreliable because the line of sight towards the object appears to be intercepted by a supernova remnant.

We have modeled the dependence of RM on Galactic longitude, RM(l), of the objects with ``reliable'' RM values, for EGS and PSR, by making least-squares fits to the observed RM(l). We used the $n_{\rm e}$-distribution from Cordes and Lazio as well as a constant $n_{\rm e}$-value (of 0.04 cm-3), combined with several models of the arm-interarm structure of the large-scale field. The arms were mostly assumed to be logarithmic spirals, and their pitch angle and width were varied. We also considered a model in which the field has circular symmetry.

The most remarkable result for a field with logarithmic-spiral structure is that the details of the spiral-arm model (pitch angle, armwidth) and $n_{\rm e}$-distribution hardly affect the character of the solution. The data that we used thus appear to define a generic solution, with well-defined field strengths of a few $\mu$G for the Norma and Crux arms and for the Norma-Crux interarm region, and these always show convincing evidence for reversals. For the well-defined field strengths, there is good agreement between the evidence from EGS and from PSR. Beyond the Crux arm, the present data do not constrain the large-scale field, and that probably explains previous contradictory results for, in particular, the Carina arm.

In their modeling, Brown et al. (2007) assumed that the strength of the large-scale field decreases with Galactocentric radius, following results by Heiles (1996), Beck (2001), and Brown et al. (2003). However, we do not find strong evidence for a systematic variation with galactocentric radius of the strength of the large-scale field. This is not inconsistent with the global assertion in the literature that models of the Galactic synchrotron emission require a larger field strength in the central regions of the Galaxy because that does not specifically refer to the regular field.

We argue that the model in which the field has circular symmetry is less likely to be correct. This is because our 4th-quadrant solution for an axially symmetric field does not agree with that obtained by Vallée, who used PSR in all four quadrants. In addition, the evidence from EGS and PSR is less concordant for the circularly symmetric model than for the spiral-arm models. Incidentally, the solutions based on PSR data involve distance estimates that are mostly based on dispersion measures and that are therefore quite uncertain.

We are thus led to a picture in which the magnetic field of the Galaxy has a clear large-scale structure that is related to the spiral arms. This large-scale field, of rather modest amplitude, shows clear reversals at each arm-interarm interface where our data have sufficient weight. It has been suggested that the reversals of the Galactic magnetic field must be suspect, because only very few external galaxies show evidence for field reversals. In addition, the reversals that are observed seem to have a different character from those in the Galaxy (see, e.g., Beck 2009). However, only future studies of the distribution of rotation measures of extragalactic background sources observed through the disk of inclined nearby, well-resolved spiral galaxies, as discussed e.g., by Stepanov et al. (2008), can tell whether the Galaxy is indeed exceptional as far as the large-scale magnetic field is concerned.

Superimposed on this large-scale field is a small-scale field, which, on the basis of evidence from PSR pairs, is estimated to be at least as strong as the large-scale field on scales below $\sim$1 kpc. That external galaxies have not yet shown the kind of small-scale field that is evident in the Galaxy is probably mostly due to limited resolution. It must be realized that the small-scale field that produces the measured $\vert\Delta B_{\Vert}(\Delta DM)\vert$ shown in Fig. 6 is, by construction, mostly directed along the arm. Unfortunately, the present data do not allow a study of the small-scale structure of the field perpendicular to the arms in the Galactic plane.

Our study is restricted to the midplane in the fourth Galactic quadrant, which precludes conclusions about the overall structure of the field. Nevertheless, it is interesting to confront the observed field reversals in the fourth quadrant to models of the large-scale field discussed in the literature. Our best-fit model of the large-scale field seems to resemble most closely the quadrisymmetric (QSS) spiral model illustrated, e.g., in Fig. 2 of Stepanov et al. (2008). How a field with such a configuration, i.e., with many reversals, is formed is a question that still needs to be answered, in spite of the general opinion that a dynamo is involved. A possible clue to the source of the reversals may be the connection between the velocity profile (across pressure maxima and minima in a galactic disc) and the direction of the field, found in numerical MHD calculations by Dziourkevitch et al. (2004) and Johansen et al. (2009).

An equally interesting question is how the modest large-scale field can coexist with the larger-amplitude small-scale field, which dominates on scales below $\sim$1 kpc. The small-scale field is probably generated by local injections of kinetic energy (from supernova explosions), which produce currents that generate local amplification of the field on the relevant scales. In dynamo theory, the coexistence of the large- and small-scale fields is a natural consequence of the feeding of the large-scale field from the small-scale field (see, e.g., Arshakian et al. 2009). This phenomenon (``inverse cascade'') is seen in direct numerical simulations, e.g., by Brandenburg (2001), where a robust and well-defined average field (which was not imposed) coexists with a small-scale field that has a dispersion $\sim$3 times larger than this average field. Simulations of the Parker instability in a strongly magnetised medium have shown that a large-scale radial field arises, with several reversals above and below the mid-plane of the disc (Hanasz et al. 2002; Johansen & Levin 2008). Calculations in which supernovae provide most of the energy input show the creation of a similar large-scale magnetic field that exhibits reversals in time (Gressel et al. 2008).

Acknowledgements
We thank the referee, Rainer Beck, for probing questions that triggered a broadening of our discussion, as a result of which the conclusions have become more generic. We thank Dominic Schnitzeler for useful discussions and help with the use of the CL02 model, and Marijke Haverkorn for helpful comments. We especially appreciate discussions with Anders Johansen about possible links between the observational results and state-of-the-art MHD modeling.

References

  1. Arnal, E. M., May, J., & Romero, G. A. 2003, A&A, 412, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Arshakian, T. G., Beck, R., Krause, M., & Sokoloff, D. 2009, A&A, 494, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Avedisova, V. S., & Palous, J. 1989, Bull. Astron. Inst. Czechoslovakia, 40, 42 [Google Scholar]
  4. Beck, R. 2001, Space Sci. Rev., 99, 243 [NASA ADS] [CrossRef] [Google Scholar]
  5. Beck, R. 2007, in EAS Publ. Ser., 23, 19 [Google Scholar]
  6. Beck, R. 2009, Rev. Mex. Astron. Astrofis. Conf. Ser., 36, 1 [NASA ADS] [Google Scholar]
  7. Beck, R., Shukurov, A., Sokoloff, D., & Wielebinski, R. 2003, A&A, 411, 99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Benaglia, P., & Cappa, C. E. 1999, A&A, 346, 979 [NASA ADS] [Google Scholar]
  9. Berkhuijsen, E. M., & Müller, P. 2008, A&A, 490, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Berkhuijsen, E. M., Mitra, D., & Mueller, P. 2006, Astron. Nachr., 327, 82 [NASA ADS] [CrossRef] [Google Scholar]
  11. Blitz, L., Fich, M., & Stark, A. A. 1982, ApJS, 49, 183 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bocchino, F., Parmar, A. N., Mereghetti, S., et al. 2001, A&A, 367, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Brandenburg, A. 2001, ApJ, 550, 824 [NASA ADS] [CrossRef] [Google Scholar]
  14. Broten, N. W., MacLeod, J. M., & Vallee, J. P. 1988, Ap&SS, 141, 303 [NASA ADS] [CrossRef] [Google Scholar]
  15. Brown, J. C., & Taylor, A. R. 2001, ApJ, 563, L31 [NASA ADS] [CrossRef] [Google Scholar]
  16. Brown, J. C., Taylor, A. R., Wielebinski, R., & Mueller, P. 2003, ApJ, 592, L29 [NASA ADS] [CrossRef] [Google Scholar]
  17. Brown, J. C., Haverkorn, M., Gaensler, B. M., et al. 2007, ApJ, 663, 258 [NASA ADS] [CrossRef] [Google Scholar]
  18. Caraveo, P. A., De Luca, A., Mignani, R. P., & Bignami, G. F. 2001, ApJ, 561, 930 [NASA ADS] [CrossRef] [Google Scholar]
  19. Caswell, J. L., McClure-Griffiths, N. M., & Cheung, M. C. M. 2004, MNRAS, 352, 1405 [NASA ADS] [CrossRef] [Google Scholar]
  20. Cha, A. N., Sembach, K. R., & Danks, A. C. 1999, ApJ, 515, L25 [NASA ADS] [CrossRef] [Google Scholar]
  21. Clegg, A. W., Cordes, J. M., Simonetti, J. M., & Kulkarni, S. R. 1992, ApJ, 386, 143 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cordes, J. M., & Lazio, T. J. W. 2002 [arXiv:astro-ph/0207156] [Google Scholar]
  23. Cordes, J. M., & Lazio, T. J. W. 2003 [arXiv:astro-ph/0301598] [Google Scholar]
  24. Dodson, R., & Golap, K. 2002, MNRAS, 334, L1 [NASA ADS] [CrossRef] [Google Scholar]
  25. Duncan, A. R., Haynes, R. F., Stewart, R. T., & Jones, K. L. 1995a, MNRAS, 277, 319 [NASA ADS] [Google Scholar]
  26. Duncan, A. R., Stewart, R. T., Haynes, R. F., & Jones, K. L. 1995b, MNRAS, 277, 36 [NASA ADS] [Google Scholar]
  27. Dziourkevitch, N., Elstner, D., & Rüdiger, G. 2004, A&A, 423, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Frick, P., Stepanov, R., Shukurov, A., & Sokoloff, D. 2001, MNRAS, 325, 649 [NASA ADS] [CrossRef] [Google Scholar]
  29. Gaensler, B. M., Dickey, J. M., McClure-Griffiths, N. M., et al. 2001, ApJ, 549, 959 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gaensler, B. M., Madsen, G. J., Chatterjee, S., & Mao, S. A. 2008, PASA, 25, 184 [NASA ADS] [CrossRef] [Google Scholar]
  31. Gaustad, J. E., McCullough, P. R., Rosing, W., & Van Buren, D. 2001, PASP, 113, 1326 [NASA ADS] [CrossRef] [Google Scholar]
  32. Georgelin, Y. M., Boulesteix, J., Georgelin, Y. P., Laval, A., & Marcelin, M. 1987, A&A, 174, 257 [NASA ADS] [Google Scholar]
  33. Georgelin, Y. M., Boulesteix, J., Georgelin, Y. P., Le Coarer, E., & Marcelin, M. 1988, A&A, 205, 95 [NASA ADS] [Google Scholar]
  34. Georgelin, Y. M., Russeil, D., Marcelin, M., et al. 1996, A&AS, 120, 41 [Google Scholar]
  35. Georgelin, Y. M., Russeil, D., Amram, P., et al. 2000, A&A, 357, 308 [NASA ADS] [Google Scholar]
  36. Giacani, E. B., Frail, D. A., Goss, W. M., & Vieytes, M. 2001, AJ, 121, 3133 [NASA ADS] [CrossRef] [Google Scholar]
  37. Green, D. A. 2004, Bull. Astron. Soc. India, 32, 335 [NASA ADS] [Google Scholar]
  38. Gressel, O., Elstner, D., Ziegler, U., & Rüdiger, G. 2008, A&A, 486, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Grewing, M., & Walmsley, M. 1971, A&A, 11, 65 [NASA ADS] [Google Scholar]
  40. Han, J. L., Manchester, R. N., & Qiao, G. J. 1999, MNRAS, 306, 371 [NASA ADS] [CrossRef] [Google Scholar]
  41. Han, J. L., Manchester, R. N., Lyne, A. G., Qiao, G. J., & van Straten, W. 2006, ApJ, 642, 868 [NASA ADS] [CrossRef] [Google Scholar]
  42. Hanasz, M., Otmianowska-Mazur, K., & Lesch, H. 2002, A&A, 386, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Haverkorn, M., Brown, J. C., Gaensler, B. M., & McClure-Griffiths, N. M. 2008, ApJ, 680, 362 [NASA ADS] [CrossRef] [Google Scholar]
  44. Heiles, C. 1996, in Polarimetry of the Interstellar Medium, ed. W. G. Roberge, & D. C. B. Whittet, ASP Conf. Ser., 97, 457 [Google Scholar]
  45. Indrani, C., & Deshpande, A. A. 1999, New Astron., 4, 33 [NASA ADS] [CrossRef] [Google Scholar]
  46. Johansen, A., & Levin, Y. 2008, A&A, 490, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Johansen, A., Youdin, A., & Klahr, H. 2009, ApJ, 697, 1269 [NASA ADS] [CrossRef] [Google Scholar]
  48. Kaspi, V. M., Manchester, R. N., Johnston, S., Lyne, A. G., & D'Amico, N. 1992, ApJ, 399, L155 [NASA ADS] [CrossRef] [Google Scholar]
  49. Men, H., Ferrière, K., & Han, J. L. 2008, A&A, 486, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Mitra, D., & Ramachandran, R. 2001, A&A, 370, 586 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Mitra, D., Wielebinski, R., Kramer, M., & Jessner, A. 2003, A&A, 398, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Noutsos, A., Johnston, S., Kramer, M., & Karastergiou, A. 2008, MNRAS, 386, 1881 [NASA ADS] [CrossRef] [Google Scholar]
  53. Ohno, H., & Shibata, S. 1993, MNRAS, 262, 953 [NASA ADS] [Google Scholar]
  54. Prentice, A. J. R., & Ter Haar, D. 1969, MNRAS, 146, 423 [NASA ADS] [CrossRef] [Google Scholar]
  55. Rand, R. J., & Kulkarni, S. R. 1989, ApJ, 343, 760 [NASA ADS] [CrossRef] [Google Scholar]
  56. Rand, R. J., & Lyne, A. G. 1994, MNRAS, 268, 497 [NASA ADS] [CrossRef] [Google Scholar]
  57. Rizzo, J. R., & Arnal, E. M. 1998, A&A, 332, 1025 [Google Scholar]
  58. Rodgers, A. W., Campbell, C. T., & Whiteoak, J. B. 1960, MNRAS, 121, 103 [NASA ADS] [CrossRef] [Google Scholar]
  59. Russeil, D. 2003, A&A, 397, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Ruzmaikin, A. A., Sokolov, D. D., & Shukurov, A. M., 1988, in Magnetic fields of galaxies, Ap&SS Library, 133 [Google Scholar]
  61. Sahu, M. S. 1992, Ph.D. Thesis, AA (Kapteyn Institute, Groningen, The Netherlands) [Google Scholar]
  62. Stepanov, R., Arshakian, T. G., Beck, R., Frick, P., & Krause, M. 2008, A&A, 480, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Tapia, M., Roth, M., Vázquez, R. A., & Persi, P. 2004, in Rev. Mex. Astron. Astrofis. Conf. Ser. 22, ed. G. Garcia-Segura, G. Tenorio-Tagle, J. Franco, & H. W. Yorke, 73 [Google Scholar]
  64. Taylor, J. H., Manchester, R. N., & Lyne, A. G. 2000, VizieR Online Data Catalog, 7189, 0 [Google Scholar]
  65. Vallée, J. P. 2005a, ApJ, 619, 297 [NASA ADS] [CrossRef] [Google Scholar]
  66. Vallée, J. P. 2005b, AJ, 130, 569 [NASA ADS] [CrossRef] [Google Scholar]
  67. Vallée, J. P. 2008a, ApJ, 681, 303 [NASA ADS] [CrossRef] [Google Scholar]
  68. Vallée, J. P. 2008b, AJ, 135, 1301 [NASA ADS] [CrossRef] [Google Scholar]
  69. Vazquez, R. A., & Baume, G. 2001, VizieR Online Data Catalog, 337, 10908 [NASA ADS] [Google Scholar]
  70. Weisberg, J. M., Cordes, J. M., Kuan, B., et al. 2004, ApJS, 150, 317 [NASA ADS] [CrossRef] [Google Scholar]
  71. Whiteoak, J. B. Z., & Green, A. J. 1996, A&AS, 118, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Whiting, C. A., Spangler, S. R., Ingleby, L. D., & Haffner, L. M. 2009, ApJ, 694, 1452 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... catalogue[*]
http://www.atnf.csiro.au/research/pulsar/psrcat
... available[*]
http://www.astro.cornell.edu/ cordes/CL02/

All Tables

Table 1:   The field strengths in the best-fit model in which the field has circular symmetry.

Table 2:   The rejected extragalactic sources.

Table 3:   The rejected PSR.

Table 4:   The extragalactic sources with reliable RM estimates

Table 5:   The PSR with reliable RM estimates.

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{11803fg1a.ps}\par\vspace*{2mm} \includegraphics[width=8.5cm,clip]{11803fg1b.ps} \end{figure} Figure 1:

The RM estimates from the literature for EGS ( upper panel) and PSR ( lower panel), versus Galactic longitude; there are 162 EGS and 180 PSR with $253\hbox {$^\circ $ }\le l \le 358\hbox {$^\circ $ }$ and $\vert b\vert \le 3\hbox{$.\!\!^\circ$ }0$. The coding of the RM estimates reflects our judgement of their reliability, where the open symbols indicate the unreliable estimates (see Sects. 3 and 4 for details).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{11803fg2a.ps}\par\vspace*{2mm} \includegraphics[width=8.5cm,clip]{11803fg2b.ps} \end{figure} Figure 2:

The dependence on Galactic longitude l of the reliable RM values. In the upper panel, the PSR are shown, coded according to distance (open symbols: PSR within 5 kpc; filled symbols: PSR beyond 5 kpc). In the lower panel, the distant PSR (filled squares) and extragalactic sources (open circles) are shown together; in this panel, the lower limit to PSR distance is 6 kpc for $l > 325\hbox {$^\circ $ }$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{11803fg3.ps} \end{figure} Figure 3:

The regions with constant-amplitude field in our modeling of the large-scale magnetic field in the fourth Galactic quadrant. The definition of these regions is superimposed on a logarithmic greyscale representation of CL02 for z = 0. The Sun is at x = 0, y = 8.5. In the left panel, we show the definition for $p=12\hbox{$.\!\!^\circ$ }5$ and d=1.0 kpc. The arm regions are color-coded with central line and boundaries. The coding is: red - Norma arm, blue - Crux arm, green - Carina arm, yellow - Perseus arm. In the right panel, we illustrate the ring model championed by Vallée for a ringwidth of 1-kpc.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{11803fg4.ps} \end{figure} Figure 4:

The results of the model fits of RM(l) for the spiral-arm related large-scale field, for EGS and PSR with CL02 $n_{\rm e}$, and $n_{\rm e} = 0.04$ cm-3. Each subpanel contains 12 field strengths with their bootstrap errors. These are arranged ( from left to right) in three groups of pitch angle ( $11\hbox{$.\!\!^\circ$ }0$, $12\hbox{$.\!\!^\circ$ }5$, $14\hbox{$.\!\!^\circ$ }0$), and each group contains the solutions for the four arm widths (0.8 kpc, 1 kpc, 1.2 kpc, 1.4 kpc), also ordered from left to right. In the fourth Galactic quadrant, positive field strengths correspond to CW fields. Arrows indicate solutions outside the plotted range with S/N-ratio >1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{11803fg5.ps} \end{figure} Figure 5:

A comparison of the observed RM values (filled symbols) used in the solutions ( left: EGS, right: PSR; top $n_{\rm e}$ = cst., bottom: $n_{\rm e}$ = CL02) with the predictions from the best-fit models (open symbols). Note that the best solutions are for different pitch-angle armwidth combinations; top-left: ( $11\hbox{$.\!\!^\circ$ }0$, 1.4), bottom left: ( $14\hbox{$.\!\!^\circ$ }0$, 0.8), top-right: ( $12\hbox{$.\!\!^\circ$ }5$, 1.4) and bottom-right: ( $11\hbox{$.\!\!^\circ$ }0$, 1.4).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.9cm,clip]{11803fg6.ps} \end{figure} Figure 6:

$\vert\Delta B_{\Vert}(\Delta DM)\vert$, as derived from RM and DM estimates of pairs of PSR with small angular separation, for $p=12\hbox{$.\!\!^\circ$ }5$, d = 1.0 kpc. Pairs are only between PSR in the same arm or interarm region (we used $n_{\rm e} = 0.04$ cm-3 for the assignment); each region is indicated by a different symbol. In the left panel the coding is: open squares - pairs in the Norma arm, filled circles - pairs in the Crux arm, and open circles - pairs in the Carina arm. In the right panel the coding is: open squares - Norma-Crux interarm region, open circles - Crux-Carina interarm region, and filled circles - Carina-Perseus interarm region.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.