| Issue |
A&A
Volume 512, March-April 2010
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913298 | |
| Published online | 25 March 2010 | |
The X-ray to optical-UV luminosity ratio
of X-ray selected type 1 AGN in XMM-COSMOS![[*]](/icons/foot_motif.png)
E. Lusso1,2 - A. Comastri2 - C. Vignali1,2 - G. Zamorani2 - M. Brusa3 - R. Gilli2 - K. Iwasawa2 - M. Salvato4 - F. Civano5 - M. Elvis5 - A. Merloni3,6 - A. Bongiorno3 - J. R. Trump7 - A. M. Koekemoer8 - E. Schinnerer9 - E. Le Floc'h10 - N. Cappelluti3 - K. Jahnke9 - M. Sargent11 - J. Silverman11 - V. Mainieri3,12 - F. Fiore13 - M. Bolzonella2 - O. Le Fèvre14 - B. Garilli15 - A. Iovino16 - J. P. Kneib14 - F. Lamareille17 - S. Lilly11 - M. Mignoli2 - M. Scodeggio15 - D. Vergani1,2
1 - Dipartimento di Astronomia, Università di Bologna, via Ranzani 1,
40127 Bologna, Italy
2 - INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127
Bologna, Italy
3 - Max Planck Institut für extraterrestische Physik,
Giessenbachstrasse 1, 85748 Garching, Germany
4 - California Institute of Technology, MC 105-24, 1200 East California
Boulevard, Pasadena, CA 91125, USA
5 - Harvard-Smithsonian Center for Astrophysics, 60 Garden Street,
Cambridge, MA 02138, USA
6 - Excellence Cluster Universe, Boltzmannstr. 2, 85748 Garching,
Germany
7 - Steward Observatory, University of Arizona, 933 N Cherry Ave,
Tucson, AZ 85721, USA
8 - Space Telescope Science Institute, 3700 San Martin Drive,
Baltimore, MD 21218, USA
9 - Max Planck Institut für Astronomie, Königstuhl 17, 69117
Heidelberg, Germany
10 - Institute for Astronomy, University of Hawaii, 2680 Woodlawn
Drive, Honolulu, HI 96822-1839, USA
11 - Department of Physics, ETH Zurich, 8093 Zurich, Switzerland
12 - ESO, Karl-Schwarschild-Strasse 2, 85748 Garching, Germany
13 - INAF - Osservatorio Astronomico di Roma, via Frascati 33,
Monteporzio (Rm) 00040, Italy
14 - Laboratoire d'Astrophysique de Marseille, OAMP, CNRS-Université
Aix-Marseille, 38 rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13,
France
15 - INAF - IASF, via Bassini 15, 20133 Milano, Italy
16 - INAF - Osservatorio Astronomico di Brera, via Brera 28, 20121
Milan, Italy
17 - Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de
Toulouse, CNRS, 14 avenue Edouard Belin, 31400 Toulouse, France
Received 15 September 2009 / Accepted 4 January 2010
Abstract
We present a study of the X-ray to optical properties of a sample of
545 X-ray selected type 1 AGN, from the XMM-COSMOS
survey, over a wide range of redshifts (
0.04<z<4.25)
and X-ray luminosities (
![]() ).
About 60% of them are spectroscopically identified type 1 AGN,
while the others have a reliable photometric redshift and are
classified as type 1 AGN on the basis of their multi-band
Spectral Energy Distributions. We discuss the relationship between UV
and X-ray luminosity, as parameterized by the
).
About 60% of them are spectroscopically identified type 1 AGN,
while the others have a reliable photometric redshift and are
classified as type 1 AGN on the basis of their multi-band
Spectral Energy Distributions. We discuss the relationship between UV
and X-ray luminosity, as parameterized by the ![]() spectral
slope, and its dependence on redshift and luminosity. We compare our
findings with previous investigations of optically selected broad-line
AGN (mostly from SDSS). A highly significant correlation
between
spectral
slope, and its dependence on redshift and luminosity. We compare our
findings with previous investigations of optically selected broad-line
AGN (mostly from SDSS). A highly significant correlation
between ![]() and
and ![]() is found, in agreement with previous investigations of optically
selected samples. We calculate bolometric corrections,
is found, in agreement with previous investigations of optically
selected samples. We calculate bolometric corrections, ![]() ,
for the whole sample using hard X-ray luminosities (
,
for the whole sample using hard X-ray luminosities (
![]() ),
and the Eddington ratios for a subsample of 150 objects for
which black hole mass estimates are available. We confirm the trend of
increasing bolometric correction with increasing Eddington ratio as
proposed in previous works. A tight correlation is found
between
),
and the Eddington ratios for a subsample of 150 objects for
which black hole mass estimates are available. We confirm the trend of
increasing bolometric correction with increasing Eddington ratio as
proposed in previous works. A tight correlation is found
between
![]() and
and
![]() ,
which can be used to estimate accurate bolometric corrections using
only optical and X-ray data. We find a significant correlation between
,
which can be used to estimate accurate bolometric corrections using
only optical and X-ray data. We find a significant correlation between ![]() and Eddington ratio, in which the ratio between X-ray and optical flux
decreases with increasing Eddington ratio.
and Eddington ratio, in which the ratio between X-ray and optical flux
decreases with increasing Eddington ratio.
Key words: galaxies: active - Galaxy: evolution - quasars: general - methods: statistical
1 Introduction
The distribution of X-ray to optical-UV ratio in quasars, as a
function of optical and X-ray luminosity and redshift, has been the
subject of active investigations for more than 30 years (Tananbaum et al. 1979).
The ratio is parameterized by the optical to X-ray spectral
index (
![]() )
defined as:
)
defined as:
In the past, it was widely adopted to compute the QSO contribution to the X-ray background and estimate the X-ray luminosity function from optical counts (e.g., Zamorani et al. 1981; Avni & Tananbaum 1986; Silverman et al. 2005). These studies, based on Einstein observations, found a mean value of
These studies could not properly address the effect of a
source selection in a different band (i.e. X-rays). The
availability of large samples of X-ray selected QSOs with a high
quality photometric and spectroscopic coverage in the optical now opens
the possibility for an extended investigation of the ![]() distribution
and its evolution.
distribution
and its evolution.
Understanding how ![]() evolves with luminosity and redshift may provide a first hint about the
nature of the energy generation mechanism in AGN. It is also a
first step towards an estimate of the AGN bolometric
luminosity function (Hopkins
et al. 2007) and the mass function of Supermassive
Black Holes (SMBHs) (e.g. Marconi
et al. 2004), and towards the understanding of the
structure of the AGN accretion disk and X-ray corona. While the
calculation of the bolometric luminosity requires good-quality data
over a large portion of the electromagnetic spectrum, it is
relatively easy to compute
evolves with luminosity and redshift may provide a first hint about the
nature of the energy generation mechanism in AGN. It is also a
first step towards an estimate of the AGN bolometric
luminosity function (Hopkins
et al. 2007) and the mass function of Supermassive
Black Holes (SMBHs) (e.g. Marconi
et al. 2004), and towards the understanding of the
structure of the AGN accretion disk and X-ray corona. While the
calculation of the bolometric luminosity requires good-quality data
over a large portion of the electromagnetic spectrum, it is
relatively easy to compute ![]() for sizable samples of objects up to high redshift.
for sizable samples of objects up to high redshift.
We analyze the dependence of ![]() upon redshift, optical and X-ray luminosities using a large X-ray
selected sample of type 1 AGN in the Cosmic Evolution Survey
(COSMOS) field (Scoville
et al. 2007). The COSMOS field is a so far unique
area for deep and wide comprehensive multi-wavelength coverage: radio
with the VLA, infrared with Spitzer, optical bands
with Hubble, Subaru, SDSS and
other ground-based telescopes, near- and far-ultraviolet bands with the
Galaxy Evolution Explorer (GALEX) and X-rays with
XMM-Newton and Chandra. The
spectroscopic coverage with VIMOS/VLT and IMACS/Magellan, coupled with
the reliable photometric redshifts derived from multiband fitting,
allows us to build a large and homogeneous sample of QSOs with a well
sampled spectral coverage and to keep selection effects under control.
upon redshift, optical and X-ray luminosities using a large X-ray
selected sample of type 1 AGN in the Cosmic Evolution Survey
(COSMOS) field (Scoville
et al. 2007). The COSMOS field is a so far unique
area for deep and wide comprehensive multi-wavelength coverage: radio
with the VLA, infrared with Spitzer, optical bands
with Hubble, Subaru, SDSS and
other ground-based telescopes, near- and far-ultraviolet bands with the
Galaxy Evolution Explorer (GALEX) and X-rays with
XMM-Newton and Chandra. The
spectroscopic coverage with VIMOS/VLT and IMACS/Magellan, coupled with
the reliable photometric redshifts derived from multiband fitting,
allows us to build a large and homogeneous sample of QSOs with a well
sampled spectral coverage and to keep selection effects under control.
The broad-band information contained in the COSMOS database is
well suited for a detailed study of AGN spectral energy
distributions (SEDs), bolometric luminosities (
![]() )
and bolometric corrections, in particular the one from the X-rays,
defined as:
)
and bolometric corrections, in particular the one from the X-rays,
defined as:
![\begin{displaymath}%
k_{\rm bol}=L_{\rm bol}/{L_{[2-10]~{\rm keV}}}.
\end{displaymath}](/articles/aa/full_html/2010/04/aa13298-09/img36.png)
|
(2) |
If the black hole mass is available (
This paper is organized as follows. In Sect. 2 we describe
the selection criteria for the sample used in this work.
Section 3
presents the data and the method by which we construct SEDs. Data
analysis and results are given in Sect. 4. In
Sect. 5
we estimate the possible effects of reddening and host-galaxy light
contribution on our main results. The discussion of our findings is
given in Sect. 6
and a summary of the results is given in Sect. 7.
We adopted a flat model of the universe with a Hubble constant ![]() ,
,
![]() ,
,
![]() (Komatsu et al. 2009).
(Komatsu et al. 2009).
2 The data set
2.1 The parent sample
The XMM-COSMOS catalog comprises 1822 point-like X-ray sources detected
by XMM-Newton over an area of 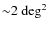 for a total of
for a total of 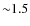 Ms
at a fairly homogeneous depth of
Ms
at a fairly homogeneous depth of 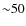 ks (Hasinger et al. 2007; Cappelluti et al. 2009).
Following Brusa et al. (2009b),
we excluded 24 sources which turned out to be a blend of two Chandra
sources leading to a total of 1798 X-ray selected point-like
sources.
ks (Hasinger et al. 2007; Cappelluti et al. 2009).
Following Brusa et al. (2009b),
we excluded 24 sources which turned out to be a blend of two Chandra
sources leading to a total of 1798 X-ray selected point-like
sources.
Spectroscopic redshifts for the proposed counterparts are
compiled by Brusa et al.
(2009b) from the Magellan/IMACS and MMT observation
campaigns (![]() objects,
Trump et al. 2009),
from the zCOSMOS project (
objects,
Trump et al. 2009),
from the zCOSMOS project (![]() objects, Lilly et al. 2007), or
were already present either in the SDSS survey catalog (
objects, Lilly et al. 2007), or
were already present either in the SDSS survey catalog (![]() objects,
Adelman-McCarthy
et al. 2005; Kauffmann
et al. 2003
objects,
Adelman-McCarthy
et al. 2005; Kauffmann
et al. 2003![]() ),
or in the literature (
),
or in the literature (![]() objects, Prescott et al. 2006).
In summary, good-quality spectroscopic redshifts are available
for 738 sources, corresponding to a substantial fraction (
objects, Prescott et al. 2006).
In summary, good-quality spectroscopic redshifts are available
for 738 sources, corresponding to a substantial fraction (![]() %) of the
entire XMM-Newton sample.
%) of the
entire XMM-Newton sample.
Photometric redshifts for almost all XMM-COSMOS sources have
been obtained exploiting the COSMOS multi-wavelength database and are
presented in Salvato et al.
(2009,
hereafter S09). Since the large majority of the XMM-COSMOS
sources are AGN, in addition to the standard photometric
redshift treatments for normal galaxies, a new set of SED templates has
been adopted, together with a correction for long-term variability and
luminosity priors for point-like sources (see below and S09
for further details). The availability of the intermediate band Subaru
filters (Taniguchi et al.
2007) is crucial in picking up emission lines
(see also Wolf et al.
2004). This led, for the first time for an
AGN sample, to a photometric redshift
accuracy comparable to that achieved for inactive galaxies (
![]() and
and ![]() outliers)
down to
outliers)
down to ![]() .
At fainter magnitudes (
22.5 <i<24.5),
the dispersion increases to
.
At fainter magnitudes (
22.5 <i<24.5),
the dispersion increases to ![]() with
with ![]() outliers, still
remarkably good for an AGN sample. A photometric
redshift is available for all but 32 objects out
of 1798.
outliers, still
remarkably good for an AGN sample. A photometric
redshift is available for all but 32 objects out
of 1798.
In addition to the photometric redshifts, S09 provide also a photometric classification based on the best-fit broad-band SED template. Briefly, each AGN SED has been fitted with a total of 30 different templates which include both normal galaxies (early type, late type and ULIRG galaxies), low-and-high luminosity QSOs (both type 1 and 2) and hybrids created assuming a varying ratio between the AGN and a galaxy templates (90:10, 80:20,..., 10:90; see S09 for details and Polletta et al. 2007). About 40% of the sources are best-fitted by AGN-dominated SED, while the remaining sources are reproduced by host galaxy-dominated SED. The photometric classification is also confirmed a posteriori (see Fig. 10 in S09) with the distribution of the XMM sources in the X-ray hardness ratio plane (Cappelluti et al. 2009; Hasinger et al. 2007).
We restricted the analysis to the X-ray sources detected in
the soft band at a flux larger than ![]() (Cappelluti et al. 2009).
Given that objects for which no secure optical counterpart could be
assigned, are usually affected by severe blending problems, making the
photo-z estimate unreliable, our parent
sample consists of 1312 sources (hereafter
(Cappelluti et al. 2009).
Given that objects for which no secure optical counterpart could be
assigned, are usually affected by severe blending problems, making the
photo-z estimate unreliable, our parent
sample consists of 1312 sources (hereafter
![]() )
for which a secure optical counterpart can be associated
(see discussion in Brusa et al. 2009a,b).
)
for which a secure optical counterpart can be associated
(see discussion in Brusa et al. 2009a,b).
2.2 Type 1 AGN sample
From the ![]() catalog we have selected 361 spectroscopically classified broad-line AGN
catalog we have selected 361 spectroscopically classified broad-line AGN![]() on the basis of broad
emission lines (
on the basis of broad
emission lines (
![]() )
in their optical spectra. We will refer to this sample as the ``spectro-z''
sample. As a comparison, in the
)
in their optical spectra. We will refer to this sample as the ``spectro-z''
sample. As a comparison, in the ![]() catalog
there are 241 objects spectroscopically classified as not
broad-line AGN (type 2 or emission-line or absorption-line
galaxies).
catalog
there are 241 objects spectroscopically classified as not
broad-line AGN (type 2 or emission-line or absorption-line
galaxies).
The spectroscopic completeness of the X-ray selected sample quickly decreases towards faint optical magnitudes. A sizable fraction of type 1 AGN may be present among optically faint X-ray sources; not to use them in our analysis would significantly bias the distribution of X-ray to optical flux ratios. In order to extend our type 1 AGN sample to fainter magnitude, we proceed as follows.
First, we looked at the distribution of the best-fit
photometric classifications for the spectroscopically identified
sample. Figure 1
shows the distribution separately for the
361 spectroscopically identified type 1 AGN (hatched
histogram) and for the 241 sources which are not
broad-line AGN (filled histogram). The dashed line
at the SED type = 19 marks the division between
galaxy-dominated and AGN-dominated SED (see Table 2 in S09 for
details). The large majority of the broad emission line AGN in the
spectro-z sample (>90%) are classified as
type 1 AGN by the SED fitting. The distribution of
the 241 not broad-line sources is in agreement with the SED-based
classification (![]() 83%
have Class < 19), and the number of
not-type 1 which have Class
83%
have Class < 19), and the number of
not-type 1 which have Class ![]() 19 is relatively
small (42 sources, about 17%). Then, we consider the
remaining 613 X-ray sources in the
19 is relatively
small (42 sources, about 17%). Then, we consider the
remaining 613 X-ray sources in the ![]() sample
for which only a photometric redshift is available from S09, and
exclude all the sources which are best-fitted with a stellar template.
The distribution of the best-fit templates for this photometric sample
is also shown in Fig. 1
(open histogram). In the following, we
assume that the 236 X-ray sources, classified by the SED
fitting with an AGN-dominated SED are type 1 AGN. We
will refer to this sample as the ``photo-z'' sample.
sample
for which only a photometric redshift is available from S09, and
exclude all the sources which are best-fitted with a stellar template.
The distribution of the best-fit templates for this photometric sample
is also shown in Fig. 1
(open histogram). In the following, we
assume that the 236 X-ray sources, classified by the SED
fitting with an AGN-dominated SED are type 1 AGN. We
will refer to this sample as the ``photo-z'' sample.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig1.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg61.png)
|
Figure 1: Distribution of the photometric classification (see Table 2 in Salvato et al. 2009) for the spectroscopically identified type 1 AGN sample (hatched histogram), for the photometric sample (open histogram) and for the not-type 1 AGN sample (filled histogram). The dashed line at SED type = 19 marks our adopted separation between sources with photometric redshift that we define as type 1 AGN (236 sources on the right) and not-type 1 (377 sources on the left) on the basis of the best-fitting SED template. |
| Open with DEXTER | |
In Fig. 2
we plot the soft X-ray flux as a function of i* CFHT magnitude.
Points and crosses represent sources in the spectro-z
and photo-z sample, respectively. The
dashed lines delimit the region typically occupied by AGN along the
X-ray to optical flux ratio ![]()
![]() . The 236 sources
in the photo-z sample increase the completeness of
the data-set at fainter magnitudes. While some
type 1 AGN may have been missed (about
. The 236 sources
in the photo-z sample increase the completeness of
the data-set at fainter magnitudes. While some
type 1 AGN may have been missed (about ![]() ,
with SED type < 19 in Fig. 1), we are
confident that the described choice minimizes the selection bias
against optically faint type 1 AGN.
We only include sources that have optical-UV data in order to compute
monochromatic luminosities at
,
with SED type < 19 in Fig. 1), we are
confident that the described choice minimizes the selection bias
against optically faint type 1 AGN.
We only include sources that have optical-UV data in order to compute
monochromatic luminosities at ![]() and the SED. This selection criterium only excludes the photometric
source with XID = 5120.
and the SED. This selection criterium only excludes the photometric
source with XID = 5120.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig2.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg66.png)
|
Figure 2:
Plot of the [0.5-2] keV flux versus the total i*
CFHT magnitude for the spectroscopically identified (black
points) and the photo-z classified (red
crosses) broad line AGN. The dashed lines represent the
constant X-ray to optical flux ratio |
| Open with DEXTER | |
It is well known that radio-loud AGN have an enhanced X-ray emission
mechanism linked to the jets, which can provide an increment in the
X-ray emission with respect to radio-quiet AGN with similar optical
luminosities (e.g., Zamorani
et al. 1981; Wilkes
& Elvis 1987; Cappi
et al. 1997). We exclude RL AGN from the
total sample using the ``standard'' definition of radio-loudness, ![]() (Kellermann et al. 1989)
(Kellermann et al. 1989)![]() . We converted the
monochromatic flux at
. We converted the
monochromatic flux at ![]() ,
reported in the final catalog of the VLA-COSMOS Deep project
(see for more detail Schinnerer et al. 2009,
submitted; and Bondi et al.
2008) to
,
reported in the final catalog of the VLA-COSMOS Deep project
(see for more detail Schinnerer et al. 2009,
submitted; and Bondi et al.
2008) to ![]() assuming
assuming ![]() with
with ![]() .
We excluded from the sample 51 radio-loud
type 1 AGN (39 AGN from the spectroscopic
sample and 12 sources with photometric redshift) with a value
of radio-loudness
.
We excluded from the sample 51 radio-loud
type 1 AGN (39 AGN from the spectroscopic
sample and 12 sources with photometric redshift) with a value
of radio-loudness ![]() .
.
The final type 1 AGN sample used in our analysis, therefore,
comprises 545 X-ray selected AGN (322 from the
spectro-z sample and 223 from the photo-z
sample) spanning a wide range of redshifts (
0.04<z<4.25)
and X-ray luminosities (
![]() ).
The selection criteria are summarized in Table 1.
).
The selection criteria are summarized in Table 1.
Assuming that the fraction of misclassificated sources in the spectro-z sample (17%) and the fraction of missing type 1 sources (10%) could be applied to the photometric sample, we are able to estimate the uncertainties associated to the photo-z sample. If this were the case, the incompleteness and the contamination on the total sample are very low, namely about 4% and 7%, respectively.
The redshift distributions of the total, spectroscopic and photometric samples are presented in Fig. 3. The median redshift of the total sample is 1.57 (the mean redshift is 1.66, with a dispersion of 0.75). The median redshift of the spectro-z sample is 1.54, while the median of the photo-z sample is 1.66.
Table 1:
Selection criteria from ![]() catalog.
catalog.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig3.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg79.png)
|
Figure 3: Redshift distribution of the 545 type 1 AGN considered in this work (open histogram). The filled histogram shows the redshift distribution for the sample of 322 spectroscopically identified sources, while the hatched histogram is the redshift distribution for the 223 sources without spectroscopic redshift. |
| Open with DEXTER | |
3 Rest-frame monochromatic fluxes and spectral energy distributions
To obtain rest-frame monochromatic luminosities at 2 keV and ![]() and estimate bolometric luminosities, we used all the multi-color
information as compiled by Brusa
et al. (2009b). The catalog includes
multi-wavelength data from mid infrared to hard X-rays: MIPS
24
and estimate bolometric luminosities, we used all the multi-color
information as compiled by Brusa
et al. (2009b). The catalog includes
multi-wavelength data from mid infrared to hard X-rays: MIPS
24 ![]() m
GO3 data (Le Floc'h et al. 2009, ApJ, submitted),
IRAC flux densities (Sanders
et al. 2007), near-infrared CFHT/K-band
data (McCracken et al. 2008),
HST/ACS F814W imaging of the COSMOS field (Koekemoer et al. 2007),
optical multiband photometry (SDSS, Subaru, Capak
et al. 2007) and near- and far-ultraviolet bands
with GALEX (Zamojski
et al. 2007).
m
GO3 data (Le Floc'h et al. 2009, ApJ, submitted),
IRAC flux densities (Sanders
et al. 2007), near-infrared CFHT/K-band
data (McCracken et al. 2008),
HST/ACS F814W imaging of the COSMOS field (Koekemoer et al. 2007),
optical multiband photometry (SDSS, Subaru, Capak
et al. 2007) and near- and far-ultraviolet bands
with GALEX (Zamojski
et al. 2007).
Table 2: Optical and X-ray properties of the total sample.
More specifically, the number of detections at ![]() m
is 472; for the 73 undetected sources, we consider 5
m
is 472; for the 73 undetected sources, we consider 5![]() upper
limits of
upper
limits of ![]() .
Most of the sources are detected by IRAC: 545, 543, 544 and 543 at
.
Most of the sources are detected by IRAC: 545, 543, 544 and 543 at ![]() ,
,
![]() ,
,
![]() and
and ![]() band, respectively (all type 1 AGN were
detected in the 3.6
band, respectively (all type 1 AGN were
detected in the 3.6
![]() IRAC band). For the undetected sources we consider 5
IRAC band). For the undetected sources we consider 5![]() upper
limits of
upper
limits of ![]() ,
,
![]() and
and ![]() at
at ![]() ,
,
![]() and
and ![]() ,
respectively (see Table 3 of Sanders et al. 2007).
Only very faint objects went undetected in the optical and near
infrared bands: only 2 upper limits in the z+ band;
1 upper limit in the BJ,
VJ and
r+ bands;
8 upper limits in both i*
and u* CFHT bands;
9 in the
,
respectively (see Table 3 of Sanders et al. 2007).
Only very faint objects went undetected in the optical and near
infrared bands: only 2 upper limits in the z+ band;
1 upper limit in the BJ,
VJ and
r+ bands;
8 upper limits in both i*
and u* CFHT bands;
9 in the ![]() CFHT band
and 31 in the J UKIRT band.
The observations are not simultaneous, as they span a time
interval of about 5 years: 2001 (SDSS),
2004 (Subaru and CFHT) and 2006 (IRAC).
In order to reduce variability effect, we selected the bands
closest in time to the IRAC observations (i.e., we excluded
SDSS data). In Table 2 we list the main
X-ray and optical properties of the sample. The data for the
SED computation were blueshifted to the rest-frame and no K-correction
has been applied. Galactic reddening has been taken into account:
we used the selective attenuation of the stellar
continuum
CFHT band
and 31 in the J UKIRT band.
The observations are not simultaneous, as they span a time
interval of about 5 years: 2001 (SDSS),
2004 (Subaru and CFHT) and 2006 (IRAC).
In order to reduce variability effect, we selected the bands
closest in time to the IRAC observations (i.e., we excluded
SDSS data). In Table 2 we list the main
X-ray and optical properties of the sample. The data for the
SED computation were blueshifted to the rest-frame and no K-correction
has been applied. Galactic reddening has been taken into account:
we used the selective attenuation of the stellar
continuum
![]() taken from Table 11 of Capak
et al. (2007). Galactic extinction is estimated from
Schlegel et al. (1998)
for each object in the
taken from Table 11 of Capak
et al. (2007). Galactic extinction is estimated from
Schlegel et al. (1998)
for each object in the ![]() catalog.
Count rates in the 0.5-2 keV and 2-10 keV are
converted into monochromatic X-ray fluxes in the observed frame
at 1 and 4 keV, respectively, using a Galactic column
density
catalog.
Count rates in the 0.5-2 keV and 2-10 keV are
converted into monochromatic X-ray fluxes in the observed frame
at 1 and 4 keV, respectively, using a Galactic column
density ![]()
![]()
![]() (see Cappelluti
et al. 2009), and assuming a photon index
(see Cappelluti
et al. 2009), and assuming a photon index ![]() and
and ![]() ,
for the soft and hard band, respectively.
,
for the soft and hard band, respectively.
3.1 The SED computation
With a procedure similar to that adopted by Elvis et al.
(2010, in prep.), we assembled SEDs for the
545 type 1 AGN. First of all, we plotted the
information of all the sources, from ![]() to the hard X-ray band (the few upper limits in the optical
and near-infrared are not considered), in the
to the hard X-ray band (the few upper limits in the optical
and near-infrared are not considered), in the ![]() rest-frame
plane. For each source we consider the rest-frame luminosity and
corresponding frequency in each of the available bands. We determine a
first order polynomial between two adjacent points, and the resulting
function is then sampled with a step of
rest-frame
plane. For each source we consider the rest-frame luminosity and
corresponding frequency in each of the available bands. We determine a
first order polynomial between two adjacent points, and the resulting
function is then sampled with a step of ![]() .
In this way a ``first order'' SED, where every point
is separated by 0.085 in log frequency,
is created. The resulting SED is ``smoothed'' using a fourth
order polynomial interpolation and re-sampled with a step of
.
In this way a ``first order'' SED, where every point
is separated by 0.085 in log frequency,
is created. The resulting SED is ``smoothed'' using a fourth
order polynomial interpolation and re-sampled with a step of ![]() .
This choice is motivated by the fact that a single interpolation with a
high-order polynomium could introduce spurious features in the final
SED. This procedure allows us to build densely sampled SEDs at all
frequencies, to extract accurate
.
This choice is motivated by the fact that a single interpolation with a
high-order polynomium could introduce spurious features in the final
SED. This procedure allows us to build densely sampled SEDs at all
frequencies, to extract accurate ![]() and 2 keV rest-frame monochromatic luminosities at all
redshifts, to estimate bolometric luminosities and bolometric
corrections.
and 2 keV rest-frame monochromatic luminosities at all
redshifts, to estimate bolometric luminosities and bolometric
corrections.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig4.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg119.png)
|
Figure 4:
The SED of a spectroscopically identified QSO at z=1.8
(XID = 2046, black line),
compared with the mean SED of Elvis et al. (1994, blue
line). The rest-frame data, used to construct the SED of
XID = 2046 are, from left to right: black triangle, |
| Open with DEXTER | |
For the computation of the bolometric luminosity we need to extrapolate
the data in the UV to X-ray gap and at high X-ray energies. From the
rest-frame UV luminosity data point at the highest frequency
in each SED, we assume a power law spectrum to 500 ![]() ,
as measured by HST observations for radio-quiet AGN (
,
as measured by HST observations for radio-quiet AGN (
![]() ,
see Zheng et al. 1997).
We then linearly connect the UV luminosity at 500
,
see Zheng et al. 1997).
We then linearly connect the UV luminosity at 500 ![]() to the luminosity corresponding to the frequency of 1 keV. We
extrapolate from the X-ray data point to the luminosity at
1 keV computing the slope,
to the luminosity corresponding to the frequency of 1 keV. We
extrapolate from the X-ray data point to the luminosity at
1 keV computing the slope, ![]() (
(
![]() ).
Finally, the X-ray spectrum is extrapolated at higher energies using
the observed slope
).
Finally, the X-ray spectrum is extrapolated at higher energies using
the observed slope
![]() ,
and introducing an exponential cut-off at 200 keV,
,
and introducing an exponential cut-off at 200 keV, ![]() (Gilli et al. 2007).
Hence, the bolometric luminosity is computed integrating the
extrapolated SED in the
(Gilli et al. 2007).
Hence, the bolometric luminosity is computed integrating the
extrapolated SED in the ![]() rest-frame
plane. Our bolometric luminosities are in agreement with those computed
by Elvis et al. (2010, in prep.). In Figs. 4 and 5 we show two
examples of SED used for the calculation of the bolometric luminosities
and the rest-frame monochromatic luminosities of the type 1
AGN sample. Given the selection criteria, the SEDs of the
objects in our sample are quite different, ranging from blue QSO with
an SED close to that reported by Elvis
et al. (1994) for radio-quiet AGN, to objects with
red SED possibly due to intrinsic absorption and/or host-galaxy
contamination. We will discuss in Sects. 5.1
and 5.2
how we take the possible effects of reddening and host-galaxy
contamination into account in our analysis. A complete
type 1 AGN SED atlas will be presented in Elvis
et al. (2010, in prep.).
rest-frame
plane. Our bolometric luminosities are in agreement with those computed
by Elvis et al. (2010, in prep.). In Figs. 4 and 5 we show two
examples of SED used for the calculation of the bolometric luminosities
and the rest-frame monochromatic luminosities of the type 1
AGN sample. Given the selection criteria, the SEDs of the
objects in our sample are quite different, ranging from blue QSO with
an SED close to that reported by Elvis
et al. (1994) for radio-quiet AGN, to objects with
red SED possibly due to intrinsic absorption and/or host-galaxy
contamination. We will discuss in Sects. 5.1
and 5.2
how we take the possible effects of reddening and host-galaxy
contamination into account in our analysis. A complete
type 1 AGN SED atlas will be presented in Elvis
et al. (2010, in prep.).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig5.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg125.png)
|
Figure 5: The SED of a spectroscopically identified QSO at z=1.161 (XID = 265, black line). Keys are as in Fig. 4. |
| Open with DEXTER | |
4 Statistical analysis
To study the possible correlations between ![]() ,
,
![]() ,
,
![]() and redshift, we used the Astronomy Survival Analysis software package
(ASURV rev. 1.2; Isobe
et al. 1990; Lavalley
et al. 1992). ASURV implements the bivariate
data-analysis methods and also properly treats censored data using the
survival analysis methods (Feigelson
& Nelson 1985; Isobe
et al. 1986). We have employed both full parametric
estimate and maximized (EM) regression algorithm and semiparametric
Buckley-James regression algorithm (Buckley & James 1979) to
perform the linear regression of the data. The EM regression
algorithm is based on the ordinary least-squares regression of the
dependent variable Y against the
independent variable X (OLS[Y|X]).
The regression line is defined in such a way that it minimizes the sum
of the squares of the Y residuals. Since
in our analysis the choice of the independent variable is not
straightforward, we have also used the inverse of OLS(Y|X)
(OLS[X|Y]) and we then calculated
the bisector of the two regression lines (see Isobe et al. 1990). We
only present the findings from the EM regression algorithm,
since in all cases the results from the Buckley-James regression
algorithm agreed within the errors; we also report the findings from
OLS bisector. Moreover, we used the partial-correlation
analysis method to compute the correlation between two variables,
checking the effect of an additional parameter which the two variables
depend on. This method is implemented in the FORTRAN program
PARTIAL_TAU, available from the Penn State Center of Astrostatistics,
and uses the methodology presented in Akritas
& Siebert (1996). The procedure is based on Kendall
and redshift, we used the Astronomy Survival Analysis software package
(ASURV rev. 1.2; Isobe
et al. 1990; Lavalley
et al. 1992). ASURV implements the bivariate
data-analysis methods and also properly treats censored data using the
survival analysis methods (Feigelson
& Nelson 1985; Isobe
et al. 1986). We have employed both full parametric
estimate and maximized (EM) regression algorithm and semiparametric
Buckley-James regression algorithm (Buckley & James 1979) to
perform the linear regression of the data. The EM regression
algorithm is based on the ordinary least-squares regression of the
dependent variable Y against the
independent variable X (OLS[Y|X]).
The regression line is defined in such a way that it minimizes the sum
of the squares of the Y residuals. Since
in our analysis the choice of the independent variable is not
straightforward, we have also used the inverse of OLS(Y|X)
(OLS[X|Y]) and we then calculated
the bisector of the two regression lines (see Isobe et al. 1990). We
only present the findings from the EM regression algorithm,
since in all cases the results from the Buckley-James regression
algorithm agreed within the errors; we also report the findings from
OLS bisector. Moreover, we used the partial-correlation
analysis method to compute the correlation between two variables,
checking the effect of an additional parameter which the two variables
depend on. This method is implemented in the FORTRAN program
PARTIAL_TAU, available from the Penn State Center of Astrostatistics,
and uses the methodology presented in Akritas
& Siebert (1996). The procedure is based on Kendall ![]() -statistic
that properly handles censored data.
-statistic
that properly handles censored data.
We summarize the results for partial-correlation analysis in Table 3.
Table 3:
Correlations and their significance from Kendall-![]() statistics (K-
statistics (K-![]() )
and from Partial Kendall-
)
and from Partial Kendall-![]() .
.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{13298fig6.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg131.png)
|
Figure 6:
Values of the rest-frame monochromatic luminosity
|
| Open with DEXTER | |
4.1
L
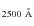 vs. L
2 keV
vs. L
2 keV
Previous studies on optically selected AGN reported a relationship
between ![]() and
and ![]() in the form
in the form ![]() ,
with the best-fit values of the exponent between
,
with the best-fit values of the exponent between ![]() (e.g. Avni &
Tananbaum 1982, 1986; Chanan
1983; Kriss
& Canizares 1985; Anderson
& Margon 1987; Wilkes
et al. 1994; Yuan
et al. 1998;Vignali
et al. 2003; Strateva
et al. 2005; S06; J07; see also La Franca et al. 1995,
who found
(e.g. Avni &
Tananbaum 1982, 1986; Chanan
1983; Kriss
& Canizares 1985; Anderson
& Margon 1987; Wilkes
et al. 1994; Yuan
et al. 1998;Vignali
et al. 2003; Strateva
et al. 2005; S06; J07; see also La Franca et al. 1995,
who found ![]() ). For the
best-fit parameters using OLS(Y|X)
(i.e. treating
). For the
best-fit parameters using OLS(Y|X)
(i.e. treating ![]() as the independent variable) we find
as the independent variable) we find
while treating
We then compute the bisector of the two regression lines as described by Isobe et al. (1990) and find
with a dispersion of 0.37. The difference of the best-fit
4.2
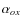 vs.
L
vs.
L
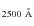
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig7.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg150.png)
|
Figure 7:
Plot of the |
| Open with DEXTER | |
Previous X-ray studies of AGN using optically selected samples (e.g., Vignali et al. 2003; Strateva et al. 2005;
S06; J07) revealed a highly significant correlation between ![]() and the
and the ![]() monochromatic luminosity, with a slope of
monochromatic luminosity, with a slope of ![]() .
We apply EM regression to our X-ray selected type 1
sample and confirm the
.
We apply EM regression to our X-ray selected type 1
sample and confirm the ![]() correlation
at the
correlation
at the ![]() significance
level. The correlation becomes stronger when taking into account the
effect of redshift using Kendall-
significance
level. The correlation becomes stronger when taking into account the
effect of redshift using Kendall-![]() partial-correlation analysis (
partial-correlation analysis (
![]() ). The best-fit relation for
). The best-fit relation for ![]() ,
using OLS(Y|X)
(i.e. treating
,
using OLS(Y|X)
(i.e. treating ![]() as the independent variable), is
as the independent variable), is
with a dispersion of 0.18. For the spectro-z sample, we found a slope of 0.166

|
(8) |
where
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig8.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg159.png)
|
Figure 8:
Plot of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig9.ps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg160.png)
|
Figure 9:
Plot of |
| Open with DEXTER | |
4.3
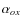 vs.
L
2 keV
and vs. redshift
vs.
L
2 keV
and vs. redshift
We find no significant correlation between ![]() and
and ![]() (e.g.; Kriss &
Canizares 1985; Avni
& Tananbaum 1986; Wilkes
et al. 1994 and Yuan
et al. 1998). For comparison with S06 and J07, we
perform the EM regression method and the best-fit parameters
for the
(e.g.; Kriss &
Canizares 1985; Avni
& Tananbaum 1986; Wilkes
et al. 1994 and Yuan
et al. 1998). For comparison with S06 and J07, we
perform the EM regression method and the best-fit parameters
for the ![]() relation
(i.e. treating
relation
(i.e. treating
![]() as the independent variable) are
as the independent variable) are
For the spectro-z sample the slope is 0.012
The significance of the correlation between
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig10.ps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg168.png)
|
Figure 10:
Plot of the hard X-ray bolometric corrections against |
| Open with DEXTER | |
4.4 Bolometric corrections vs. Eddington ratio
In Fig. 10
we plot ![]() vs.
vs. ![]() .
In order to better estimate the bolometric correction values we select
a subsample of 343 AGN with detections in both soft and hard
bands.
The best-fit relation is computed using a second-degree polynomial:
.
In order to better estimate the bolometric correction values we select
a subsample of 343 AGN with detections in both soft and hard
bands.
The best-fit relation is computed using a second-degree polynomial:
We quantify the
The bolometric luminosity which enters in the calculation of
the Eddington ratio,
![]() ,
is computed by integrating the individual SEDs from
,
is computed by integrating the individual SEDs from ![]() to 200 keV (see Sect. 3.1).
By neglecting the IR bump we avoid counting twice the
UV emission reprocessed by dust. The hard X-ray bolometric
correction,
to 200 keV (see Sect. 3.1).
By neglecting the IR bump we avoid counting twice the
UV emission reprocessed by dust. The hard X-ray bolometric
correction, ![]() , is
computed as the ratio between
, is
computed as the ratio between ![]() and the X-ray luminosity,
and the X-ray luminosity,
![]() .
.
A remarkably good correlation is found between ![]() and the Eddington ratio. Since the choice of the independent or
dependent variable is not straightforward, we here computed the
OLS bisector for the
and the Eddington ratio. Since the choice of the independent or
dependent variable is not straightforward, we here computed the
OLS bisector for the ![]() relation
as already done for the
relation
as already done for the ![]() relation.
We found that the best-fit parameters for the
relation.
We found that the best-fit parameters for the ![]() relation
using OLS(Y|X)
(i.e. treating
relation
using OLS(Y|X)
(i.e. treating ![]() as the independent variable) are
as the independent variable) are
while the relation using OLS(X|Y) is
We then compute the bisector of the two regression lines and we find
The absence of a correlation is excluded at the
Figure 11
shows ![]() as a function of
as a function of ![]() for our sub-sample of type 1 AGN and for the sample of local
Seyferts by VF09, where radio-loud objects and low X-ray flux
observations are removed. Points with error bars are obtained averaging
the values of bolometric correction in each bin of
for our sub-sample of type 1 AGN and for the sample of local
Seyferts by VF09, where radio-loud objects and low X-ray flux
observations are removed. Points with error bars are obtained averaging
the values of bolometric correction in each bin of ![]() ,
and standard errors at
,
and standard errors at ![]() are plotted for comparison (see Sect. 4.3 of VF09 for
details). The VF09 sample contains AGN with simultaneous
optical, UV and X-ray data retrieved from the XMM-Newton
EPIC-pn and Optical Monitor (OM) archives, while the virial
are plotted for comparison (see Sect. 4.3 of VF09 for
details). The VF09 sample contains AGN with simultaneous
optical, UV and X-ray data retrieved from the XMM-Newton
EPIC-pn and Optical Monitor (OM) archives, while the virial
![]() is estimated using the reverberation mapping method (Peterson et al. 2004).
It is worth noting that, although the methods to construct the
SEDs and measure
is estimated using the reverberation mapping method (Peterson et al. 2004).
It is worth noting that, although the methods to construct the
SEDs and measure ![]() are completely different from those adopted by VF09, the trend
of increasing bolometric correction with Eddington ratio is confirmed,
with mean
are completely different from those adopted by VF09, the trend
of increasing bolometric correction with Eddington ratio is confirmed,
with mean ![]() for
for ![]() ,
,
![]() for
for ![]() and
and ![]() for
for ![]() .
.
Equation (12) is in agreement, within the errors, with the VF09 results, which are shown in Fig. 11. The Eq. (12), represented by the orange dashed line, and red bins are directly comparable, because of the treatment of the independent variable.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig11.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg191.png)
|
Figure 11: Hard X-ray bolometric correction versus Eddington ratio for the 150 type 1 AGN with BH mass estimate. The solid black line shows the best-fit relation that we found using the OLS bisector algorithm (see Eq. (14)), while the orange and the green dashed lines represent Eqs. (12) and (13), respectively. Red open circles represent the sample by VF09 (25 sources, see their Fig. 6 for details) and the corresponding bins with error bars. |
| Open with DEXTER | |
Differently from VF09, we found a correlation also between ![]() and the Eddington ratio. In the same interval of
and the Eddington ratio. In the same interval of ![]() we have a larger number of sources, hence the presence of the
correlation could be simply due to the better statistic, although the
dispersion is rather large. In Fig. 12 we present
we have a larger number of sources, hence the presence of the
correlation could be simply due to the better statistic, although the
dispersion is rather large. In Fig. 12 we present ![]() against
against ![]() ,
where the best-fit relation using OLS(Y|X) is
,
where the best-fit relation using OLS(Y|X) is
while the best-fit relation using OLS(X|Y) is
Finally, the bisector of the two regression lines is
The absence of a correlation is excluded at
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig12.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg196.png)
|
Figure 12:
Plot of |
| Open with DEXTER | |
5 Effects of reddening and host-galaxy light
As mentioned in Sect. 3.1 and
discussed at length in Elvis et al. (2010, in prep.),
the objects used in this analysis show a large variety of SEDs.
In addiction to objects with a ``typical'' type 1 AGN
SED (see Fig. 4),
there is also a not negligible number of objects which show a red
optical-UV SED (see Fig. 5). While some
of them may be intrinsically red AGN, it is likely that for most of
them this red optical-UV SED is due either to intrinsic absorption or
to a significant contribution of emission from the host-galaxy, or both
(see Richards
et al. 2003, hereafter R03). In the
analysis presented in the previous sections, we used the
``observed''
![]() .
If intrinsic absorption or contribution from the host-galaxy
are not negligible, the used
.
If intrinsic absorption or contribution from the host-galaxy
are not negligible, the used
![]() would be biased. In particular, the intrinsic
would be biased. In particular, the intrinsic
![]() would be higher in presence of reddening, while it would be smaller in
presence of a significant contribution from the host-galaxy. In the
following we try to estimate the size of the effect of extinction
and/or host-galaxy contribution to the relations between
would be higher in presence of reddening, while it would be smaller in
presence of a significant contribution from the host-galaxy. In the
following we try to estimate the size of the effect of extinction
and/or host-galaxy contribution to the relations between ![]() and
and ![]() discussed in Sects. 4.1
and 4.2.
discussed in Sects. 4.1
and 4.2.
5.1 Intrinsic extinction
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig13.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg197.png)
|
Figure 13:
Distribution of redshifts versus the relative |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig14.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg198.png)
|
Figure 14:
Distribution of |
| Open with DEXTER | |
Following the procedure described in R03, we estimate the
underlying continuum color by subtracting the median colors of AGN in
redshift bins of ![]() from the observed color of each source in that bin. We refer to
from the observed color of each source in that bin. We refer to ![]() as the relative color (see Richards
et al. 2001), where the average
as the relative color (see Richards
et al. 2001), where the average
![]() is computed in each redshift bin. All sources have been detected in the
Subaru g+ band,
only 8 sources do not have i* CFHT magnitude.
For these AGN we consider the detection in the i+ Subaru band.
In Fig. 13
we plot the redshift of the sources as a function of their relative
color (see Fig. 6
in R03). The
is computed in each redshift bin. All sources have been detected in the
Subaru g+ band,
only 8 sources do not have i* CFHT magnitude.
For these AGN we consider the detection in the i+ Subaru band.
In Fig. 13
we plot the redshift of the sources as a function of their relative
color (see Fig. 6
in R03). The ![]() distribution
shows a large scatter with respect to the SDSS sample
in R03. Given the quality of the COSMOS photometric
data, this is not due to photometric errors, but likely to the
different selection criteria: SDSS quasar candidates are
selected using optical color-color selection, so the scatter
in
distribution
shows a large scatter with respect to the SDSS sample
in R03. Given the quality of the COSMOS photometric
data, this is not due to photometric errors, but likely to the
different selection criteria: SDSS quasar candidates are
selected using optical color-color selection, so the scatter
in
![]() is smaller than in our X-ray selected sample. However, we can still use
the same plot in order to identify possibly reddened sources. Under the
assumption that all type 1 AGN have the same
continuum shape, the dashed lines show the expected change in relative
color as a function of redshift for an SMC reddening law (Prevot et al. 1984) with
E(B-V) = 0.04,
0.12 and 0.20 moving from left to right in the
is smaller than in our X-ray selected sample. However, we can still use
the same plot in order to identify possibly reddened sources. Under the
assumption that all type 1 AGN have the same
continuum shape, the dashed lines show the expected change in relative
color as a function of redshift for an SMC reddening law (Prevot et al. 1984) with
E(B-V) = 0.04,
0.12 and 0.20 moving from left to right in the ![]() axis.
Following R03, we define dust-reddened
type 1 AGN all the sources that lie to the right of
the dashed line at E(B-V) =
0.12. Using this definition, about 10% of the total sample is
affected by intrinsic absorption. For about 80% of the sample,
reddening is negligible, with E(B-V)
less than 0.04. The 53 reddened
type 1 AGN have been divided in 4 subsamples
which correspond to an average E(B-V) value
of about 0.12, 0.16, 0.20 and 0.24 (see caption in
Fig. 13).
Monochromatic luminosities at
axis.
Following R03, we define dust-reddened
type 1 AGN all the sources that lie to the right of
the dashed line at E(B-V) =
0.12. Using this definition, about 10% of the total sample is
affected by intrinsic absorption. For about 80% of the sample,
reddening is negligible, with E(B-V)
less than 0.04. The 53 reddened
type 1 AGN have been divided in 4 subsamples
which correspond to an average E(B-V) value
of about 0.12, 0.16, 0.20 and 0.24 (see caption in
Fig. 13).
Monochromatic luminosities at
![]() of these objects were corrected using the SMC reddening law
and the corresponding average value of E(B-V)
in each bin. Figure 14 shows the
distribution of the optical luminosities before and after de-reddening.
The
of these objects were corrected using the SMC reddening law
and the corresponding average value of E(B-V)
in each bin. Figure 14 shows the
distribution of the optical luminosities before and after de-reddening.
The ![]() distribution
of the reddened AGN is significantly different (i.e. lower
luminosity) from that of the total sample. This would suggest that
extinction is more important for lower luminosity AGN
(see Gaskell
et al. 2004). The average shift induced by the
correction for the intrinsic extinction in the 10% of the
total sample is
distribution
of the reddened AGN is significantly different (i.e. lower
luminosity) from that of the total sample. This would suggest that
extinction is more important for lower luminosity AGN
(see Gaskell
et al. 2004). The average shift induced by the
correction for the intrinsic extinction in the 10% of the
total sample is ![]()
![]() 0.07.
0.07.
X-ray absorption is generally negligible in
type 1 AGN; however, it is known that a
fraction of the order of 10% of broad-line AGN may be obscured
by column densities up to 1022 cm-2
(see Mainieri
et al. 2007). Unabsorbed X-ray fluxes can be
computed if the absorption column density (![]() )
is known, which is not the case for most of the sources in our
sample. Hardness ratios may be used instead, but they are almost
insensitive to column densities of the order of 1022 cm-2
or slightly higher at the average redshifts of the XMM-COSMOS sources,
and they tend to over-estimate
)
is known, which is not the case for most of the sources in our
sample. Hardness ratios may be used instead, but they are almost
insensitive to column densities of the order of 1022 cm-2
or slightly higher at the average redshifts of the XMM-COSMOS sources,
and they tend to over-estimate ![]() (e.g. Perola
et al. 2004). In order to quantify the
average impact of X-ray absorption on the
(e.g. Perola
et al. 2004). In order to quantify the
average impact of X-ray absorption on the ![]() distribution
and bolometric corrections, we have assumed that 10% of the
sources in our sample are obscured by a column density of 1022 cm-2.
We note that this assumption is likely to overestimate X-ray absorption
in type 1 AGN (see Fig. 13 in Mainieri et al. 2007).
By correcting X-ray monocromatic fluxes at 2 keV for
randomly chosen 10% of the sources, the unobscured X-ray
fluxes are 10% higher. The shift induced by this correction in
the 10% of the total sample is
distribution
and bolometric corrections, we have assumed that 10% of the
sources in our sample are obscured by a column density of 1022 cm-2.
We note that this assumption is likely to overestimate X-ray absorption
in type 1 AGN (see Fig. 13 in Mainieri et al. 2007).
By correcting X-ray monocromatic fluxes at 2 keV for
randomly chosen 10% of the sources, the unobscured X-ray
fluxes are 10% higher. The shift induced by this correction in
the 10% of the total sample is ![]() .
.
Broad absorption-line quasars (BAL QSOs) are known to be X-ray
obscured (e.g., Green
et al. 1995; Gallagher
et al. 1999; Brandt
et al. 2000), and are not included in previous
studies of optically selected samples because they can cause an
artificial steepening of the ![]() and
and ![]() correlations.
Due to the lack of a systematic analysis of the optical
spectra of broad-line AGN in the zCOSMOS and IMACS spectroscopic
surveys and the inclusion of photometric type 1 AGN,
we do not have an estimate of the BAL fraction in our sample.
Assuming they constitute about 10-15% of the entire quasar population
(e.g. R03, Hewett
& Foltz 2003), BAL QSO may be numerous among
red sources in Fig. 14
and/or X-ray obscured AGN. Therefore, we expect that the effects of
dust reddening and X-ray absorption considered and quantified in the
previous paragraphs take into account, at least in a
statistical sense, the BAL QSO contamination.
Moreover, the considered fraction of BAL QSOs comes from
optically selected samples, so that the same fraction should
be smaller (and possibly redshift dependent) for soft X-ray
selected samples.
correlations.
Due to the lack of a systematic analysis of the optical
spectra of broad-line AGN in the zCOSMOS and IMACS spectroscopic
surveys and the inclusion of photometric type 1 AGN,
we do not have an estimate of the BAL fraction in our sample.
Assuming they constitute about 10-15% of the entire quasar population
(e.g. R03, Hewett
& Foltz 2003), BAL QSO may be numerous among
red sources in Fig. 14
and/or X-ray obscured AGN. Therefore, we expect that the effects of
dust reddening and X-ray absorption considered and quantified in the
previous paragraphs take into account, at least in a
statistical sense, the BAL QSO contamination.
Moreover, the considered fraction of BAL QSOs comes from
optically selected samples, so that the same fraction should
be smaller (and possibly redshift dependent) for soft X-ray
selected samples.
Applying these corrections for absorption in the optical and
in the X-ray, we find that the slopes of the ![]() and
and ![]() relations
become
relations
become ![]()
![]() 0.021 (OLS bisector algorithm) and 0.147
0.021 (OLS bisector algorithm) and 0.147 ![]() 0.008. Both these ``corrected'' slopes are within one sigma from those
derived with no correction for absorption (see Eqs. (6)
and (7)).
The slight steepening of the
0.008. Both these ``corrected'' slopes are within one sigma from those
derived with no correction for absorption (see Eqs. (6)
and (7)).
The slight steepening of the ![]() relation
is due to the fact that the fraction of optically extincted AGN is
higher at lower optical luminosity (see Fig. 14). The
corrections for absorption increase the mean value of
relation
is due to the fact that the fraction of optically extincted AGN is
higher at lower optical luminosity (see Fig. 14). The
corrections for absorption increase the mean value of
![]() by only 0.01. We therefore conclude that the absorption
corrections do not change significantly our overall results.
by only 0.01. We therefore conclude that the absorption
corrections do not change significantly our overall results.
5.2 Host-galaxy contamination
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig15.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg206.png)
|
Figure 15: Distribution of the optical index for the total sample (open histogram), for the 145 AGN which have a host-galaxy contribution less than 10% (filled histogram) and for the 96 AGN which have a host-galaxy contribution greater than 10% (hatched histogram). |
| Open with DEXTER | |
In order to estimate the possible effect of the contribution
of the host-galaxy stellar light to the ![]() luminosity,
we have considered a subsample of 241 sources for which we
have a host-galaxy contribution computed subtracting a
point-spread-function scaled to a central 4 pixel aperture,
and measuring the extended flux in ACS F814W
(Jahnke et al. 2004;
Jahnke et al. 2009):
145 sources have an extended host-galaxy contribution of less
than 10%, while for 96 AGN the contamination of the
host-galaxy light is greater than 10%. This is a robust, model
independent measure to determine whether substantial extended flux is
present or not. A useful parameter that we can compute for the
total sample is the optical spectral index,
luminosity,
we have considered a subsample of 241 sources for which we
have a host-galaxy contribution computed subtracting a
point-spread-function scaled to a central 4 pixel aperture,
and measuring the extended flux in ACS F814W
(Jahnke et al. 2004;
Jahnke et al. 2009):
145 sources have an extended host-galaxy contribution of less
than 10%, while for 96 AGN the contamination of the
host-galaxy light is greater than 10%. This is a robust, model
independent measure to determine whether substantial extended flux is
present or not. A useful parameter that we can compute for the
total sample is the optical spectral index,
![]() .
By linking it with the morphological information we can try to
quantify the host-galaxy contribution for each AGN.
.
By linking it with the morphological information we can try to
quantify the host-galaxy contribution for each AGN.
Following Vanden Berk
et al. (2001), we compute the optical spectral index
using the monochromatic luminosities at ![]() and
and ![]()
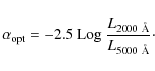
|
(18) |
Figure 15 shows the distribution of
We then tried to estimate the fraction of galaxy light at ![]() assuming a typical slope
assuming a typical slope ![]() for the nucleus component and
for the nucleus component and ![]() for the galaxies. We further assume that the monochromatic luminosity
in the range
for the galaxies. We further assume that the monochromatic luminosity
in the range ![]() is due to the contribution of two power laws:
is due to the contribution of two power laws:
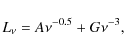
|
(19) |
where A and G are the normalization constants we want to estimate. With this assumption the observed
Applying this correction, we find that the slopes of the ![]() and
and ![]() become 0.660
become 0.660 ![]() 0.022 (OLS bisector algorithm) and 0.197
0.022 (OLS bisector algorithm) and 0.197 ![]() 0.011, respectively. Both these slopes corrected for the possible
host-galaxy contribution are different at about
0.011, respectively. Both these slopes corrected for the possible
host-galaxy contribution are different at about ![]() from those derived with no correction (see Eqs. (6)
and (7)).
In this case, the flattening of the
from those derived with no correction (see Eqs. (6)
and (7)).
In this case, the flattening of the ![]() relation
is due to the fact that
relation
is due to the fact that ![]() tends to be steeper (i.e. with a possibly higher contribution
from the host-galaxy) for lower luminosity AGN. This
correction decreases the mean value of
tends to be steeper (i.e. with a possibly higher contribution
from the host-galaxy) for lower luminosity AGN. This
correction decreases the mean value of ![]() by
by
![]() .
.
At face value, the possible effects of host-galaxy
contribution estimated above are not negligible. However, we stress
that these estimates have to be taken as upper limits, for at least two
reasons. First, in our derivation of the constants A
and G we have assumed that all AGN have the
same intrinsic
![]() ;
in presence of a dispersion of
;
in presence of a dispersion of ![]() distribution
of AGN, the contribution from the host-galaxy would be smaller than
that we have derived. Secondly, the same would happen also if,
as it is likely to be the case, both effects (extinction and
host-galaxy contribution) are at work at the same time.
distribution
of AGN, the contribution from the host-galaxy would be smaller than
that we have derived. Secondly, the same would happen also if,
as it is likely to be the case, both effects (extinction and
host-galaxy contribution) are at work at the same time.
6 Discussion
6.1 Sample biases and systematics
We used the COSMOS multi-wavelength database to build a large X-ray
selected sample of type 1 AGN and study their optical
to X-ray properties. The sample size is comparable to that of optically
selected samples previously reported in the literature (e.g., Gibson et al. 2008),
but to our knowledge this is the largest complete X-ray selected sample
for which the study of the ![]() distribution
is performed. In order to keep the selection criteria as clean
as possible and to cope with the lack of spectroscopic information at
faint optical magnitudes, the type 1 classification is based
on both spectroscopic and photometric redshifts. This choice guarantees
a well defined and relatively simple selection function,
but it is not completely free from other biases.
In particular, contamination from photometrically
misclassified type 1 AGN cannot be excluded
(see Sect. 2.2).
Other possible biases and systematics include the contribution of the
effect of dust reddening and gas absorption at UV and X-ray frequencies
and the host-galaxy light to the
distribution
is performed. In order to keep the selection criteria as clean
as possible and to cope with the lack of spectroscopic information at
faint optical magnitudes, the type 1 classification is based
on both spectroscopic and photometric redshifts. This choice guarantees
a well defined and relatively simple selection function,
but it is not completely free from other biases.
In particular, contamination from photometrically
misclassified type 1 AGN cannot be excluded
(see Sect. 2.2).
Other possible biases and systematics include the contribution of the
effect of dust reddening and gas absorption at UV and X-ray frequencies
and the host-galaxy light to the ![]() nuclear
flux. Even though we tried to estimate and quantify the impact of the
above mentioned biases (see Sects. 5.1
and 5.2),
some residual contamination due to either one or more of these biases
cannot be completely excluded. However, we are confident that the most
important results of our analysis, and especially those concerning the
average properties of the total sample, are not significantly affected.
nuclear
flux. Even though we tried to estimate and quantify the impact of the
above mentioned biases (see Sects. 5.1
and 5.2),
some residual contamination due to either one or more of these biases
cannot be completely excluded. However, we are confident that the most
important results of our analysis, and especially those concerning the
average properties of the total sample, are not significantly affected.
The correlations between optical and X-ray luminosities obtained from the analysis of the spectroscopic sample are recovered, if only photo-z are considered. Even though the best fit parameters of the correlations are slightly different, the inclusion of photo-z sources allow us to extend the study of optical and X-ray properties to much lower luminosities.
6.2 Constraints on the X-ray emission models
The optical to X-ray spectral index ![]() connects the two portions of the AGN broad-band spectrum dominated by
the accretion power and thus it is expected to be a reliable tracer of
the accretion properties and, in particular, of the relation
between disk emission, peaking in the UV, and coronal X-ray emission.
Previous studies have shown a non linear dependence of the X-ray versus
UV luminosity, which implies a correlation between the
optical-UV to X-ray luminosity ratio on monochromatic luminosity and/or
redshift. Based on extensive analysis of large samples of optically
selected AGN (i.e. Vignali
et al. 2003; Strateva
et al. 2005, S06, J07) it is concluded that
connects the two portions of the AGN broad-band spectrum dominated by
the accretion power and thus it is expected to be a reliable tracer of
the accretion properties and, in particular, of the relation
between disk emission, peaking in the UV, and coronal X-ray emission.
Previous studies have shown a non linear dependence of the X-ray versus
UV luminosity, which implies a correlation between the
optical-UV to X-ray luminosity ratio on monochromatic luminosity and/or
redshift. Based on extensive analysis of large samples of optically
selected AGN (i.e. Vignali
et al. 2003; Strateva
et al. 2005, S06, J07) it is concluded that ![]() is primary dependent on optical luminosity at
is primary dependent on optical luminosity at
![]() .
The results presented in this paper confirm and extend the previous
findings to a large sample of X-ray selected AGN, suggesting that band
selection does not significantly modify the current observational
picture. The observed
.
The results presented in this paper confirm and extend the previous
findings to a large sample of X-ray selected AGN, suggesting that band
selection does not significantly modify the current observational
picture. The observed ![]() (or
(or
![]() )
correlation implies that more optical luminous AGN emit less X-rays per
unit UV luminosity than less luminous AGN. The
predicted UV to X-ray luminosity ratio depends on the hot corona
covering factor, optical depth and electron temperatures. The
optical-UV and X-ray emission of radio-quiet AGN can be explained by
the interplay between hot electrons in a coronal gas and a colder
accretion flow. Soft photons from the accretion disk are Comptonized by
hot electrons and lead to the formation of a power law
spectrum in the hard X-rays accompanied by a high energy cut-off at the
electrons' temperature (Haardt & Maraschi 1991,1993).
If only a fraction of the accretion power is released in the
hot phase, as in the patchy corona model (Haardt et al. 1994),
the
)
correlation implies that more optical luminous AGN emit less X-rays per
unit UV luminosity than less luminous AGN. The
predicted UV to X-ray luminosity ratio depends on the hot corona
covering factor, optical depth and electron temperatures. The
optical-UV and X-ray emission of radio-quiet AGN can be explained by
the interplay between hot electrons in a coronal gas and a colder
accretion flow. Soft photons from the accretion disk are Comptonized by
hot electrons and lead to the formation of a power law
spectrum in the hard X-rays accompanied by a high energy cut-off at the
electrons' temperature (Haardt & Maraschi 1991,1993).
If only a fraction of the accretion power is released in the
hot phase, as in the patchy corona model (Haardt et al. 1994),
the ![]() ratio
is higher than the value computed using a model with more uniform
corona. The observed correlation suggest that disk-corona parameters
are depending on UV luminosity.
ratio
is higher than the value computed using a model with more uniform
corona. The observed correlation suggest that disk-corona parameters
are depending on UV luminosity.
6.3 Using  as a bolometric correction estimator
as a bolometric correction estimator
An accurate determination of bolometric quantities is essential to compute AGN accretion rates and, more in general, to all the arguments related to the accretion onto SMBH at large. These parameters require to sample the AGN SED over a broad range of wavelengths from near-infrared to hard X-rays. Owing to the excellent quality of the multi-wavelength COSMOS database, this is becoming possible for large AGN samples (Elvis et al. 2010, in prep.). Because the optical-UV to X-ray portion of the spectrum contains about 60% of the total bolometric luminosity, we have investigated to what extent the UV to X-ray luminosity ratio can be considered a reliable proxy of the bolometric correction.
We computed bolometric corrections from the 2-10 keV
energy range for all the objects in our sample with detection in both
soft and hard bands. Given the strong luminosity dependence
of
![]() upon UV luminosity which is close to the SED maximum,
it is not surprising to find a significant correlation between
upon UV luminosity which is close to the SED maximum,
it is not surprising to find a significant correlation between
![]() and
and
![]() .
However, it is important to note that the correlation,
best-fitted by a second order polynomial, has a small dispersion around
the best-fit (see Fig. 10). The existence
of such a tight relation between these two parameters suggests that the
AGN bolometric output is well traced by
.
However, it is important to note that the correlation,
best-fitted by a second order polynomial, has a small dispersion around
the best-fit (see Fig. 10). The existence
of such a tight relation between these two parameters suggests that the
AGN bolometric output is well traced by ![]() over a broad range of redshifts and luminosities. Moreover,
it offers the opportunity to estimate reliable bolometric
corrections, for large AGN samples, provided that rest-frame
over a broad range of redshifts and luminosities. Moreover,
it offers the opportunity to estimate reliable bolometric
corrections, for large AGN samples, provided that rest-frame ![]() and 2 keV luminosities are known.
and 2 keV luminosities are known.
6.4 Bolometric corrections and Eddington ratios
Accretion rates are then estimated using the previously computed
bolometric corrections. A correlation is found between the
2-10 keV bolometric correction and the Eddington ratio for a
sizable subsample of 150 objects (see Fig. 11), for which
black hole masses are computed from the broad emission lines FWHM
(see Merloni et al. 2009; Trump
et al. 2009, for a detailed discussion). The
presence of this correlation was originally suggested by Vasudevan & Fabian (2007)
using broad-band observations of nearby Seyfert galaxies and confirmed
in a subsequent paper (VF09) using simultaneous optical-UV and X-ray
data. A similar trend is reported by Bianchi
et al. (2009) from a multi-wavelength analysis of
archival XMM-Newton observations.
Although we do not have simultaneous data or ![]() estimate from reverberation mapping, our findings are consistent with
the
estimate from reverberation mapping, our findings are consistent with
the ![]() relation
by VF09. This correlation may, in principle, be
induced by the fact that both parameters depend on the bolometric
luminosity. However, if we look for the effect of the
bolometric luminosity using the Kendall-
relation
by VF09. This correlation may, in principle, be
induced by the fact that both parameters depend on the bolometric
luminosity. However, if we look for the effect of the
bolometric luminosity using the Kendall-![]() partial correlation analysis, we found that the correlation is still
significant. This suggests that the systematic effects introduced by
the presence of bolometric luminosity on both axes are not relevant
(see also Sect. 5.1.4 in VF07).
partial correlation analysis, we found that the correlation is still
significant. This suggests that the systematic effects introduced by
the presence of bolometric luminosity on both axes are not relevant
(see also Sect. 5.1.4 in VF07).
A fairly significant correlation, albeit with a large scatter,
is also found between ![]() and the Eddington ratio. In the framework of the disk-corona
models discussed above, sources with steep
and the Eddington ratio. In the framework of the disk-corona
models discussed above, sources with steep ![]() are explained by a patchy corona where the number of blobs or their
covering factor decreases for increasing values of
are explained by a patchy corona where the number of blobs or their
covering factor decreases for increasing values of
![]() .
For a given BH mass, bright UV emission is due to a
high accretion rate. If in highly accreting sources most of
the power is dissipated in the disk, rather than in the hot corona,
then a correlation between
.
For a given BH mass, bright UV emission is due to a
high accretion rate. If in highly accreting sources most of
the power is dissipated in the disk, rather than in the hot corona,
then a correlation between ![]() and Eddington ratio is expected.
and Eddington ratio is expected.
7 Summary and conclusions
In this paper we have presented the analysis of the UV to X-ray
properties of 545 radio-quiet X-ray selected
type 1 AGN, in the multi-wavelength COSMOS
survey. The full data-set covers a large range of redshifts (
0.04<z<4.25)
and X-ray luminosities (
![]() ).
It is mostly composed by spectroscopically selected
type 1 AGN (322 sources,
).
It is mostly composed by spectroscopically selected
type 1 AGN (322 sources, ![]() of the total sample), with the addition of
223 type 1 AGN classified on the basis of
the best-fitting SED procedure provided by S09. We constructed
single SEDs for the full sample and, from these, we computed optical
and X-ray rest-frame luminosities at
of the total sample), with the addition of
223 type 1 AGN classified on the basis of
the best-fitting SED procedure provided by S09. We constructed
single SEDs for the full sample and, from these, we computed optical
and X-ray rest-frame luminosities at ![]() and 2 keV, respectively; we also investigated the dependence
of
and 2 keV, respectively; we also investigated the dependence
of ![]() upon redshift,
upon redshift, ![]() and
and ![]() using the fully parametric EM (estimated and maximized) regression
algorithm and Kendall-
using the fully parametric EM (estimated and maximized) regression
algorithm and Kendall-![]() partial correlation analysis. Moreover, we estimated bolometric
correction and bolometric luminosities for a subsample of
343 AGN for which we have detections in both soft and hard
bands. Our principal results are the following:
partial correlation analysis. Moreover, we estimated bolometric
correction and bolometric luminosities for a subsample of
343 AGN for which we have detections in both soft and hard
bands. Our principal results are the following:
- 1.
- We confirm the
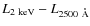 correlation parametrized by
correlation parametrized by 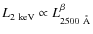 ,
where
,
where 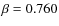
 0.022. The best-fit slope agrees with previous studies based on
optically selected samples, which found a value of
0.022. The best-fit slope agrees with previous studies based on
optically selected samples, which found a value of  inconsistent with unity.
inconsistent with unity.
- 2.
- The mean value of
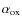 for the full X-ray selected sample is
for the full X-ray selected sample is 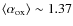
 0.01 with a dispersion around the mean of 0.18. We confirm the
correlation between
0.01 with a dispersion around the mean of 0.18. We confirm the
correlation between  and
and 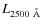 at the
at the 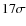 significance
level. The correlation becomes stronger if we take into account the
effect of redshift using the partial correlation analysis (
significance
level. The correlation becomes stronger if we take into account the
effect of redshift using the partial correlation analysis (
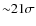 ). The slope of our the
best-fit relation between
). The slope of our the
best-fit relation between 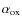 and
and 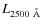 is consistent at least within
is consistent at least within 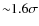 with that obtained for an optically selected sample.
with that obtained for an optically selected sample.
- 3.
- From the EM regression method, we find a weak correlation
between
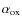 and redshift; if the effect of
and redshift; if the effect of 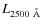 is taken into account, the correlation disappears.
is taken into account, the correlation disappears.
- 4.
- We do not find any significant correlation between
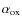 and
and 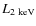 (
(
 significance level if we take into account the effect of the optical
luminosity).
significance level if we take into account the effect of the optical
luminosity).
- 5.
- We found a tight correlation between the
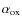 values and the hard X-ray bolometric correction values. The
values and the hard X-ray bolometric correction values. The 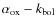 relation
could be used as a practical tool to provide an accurate estimate (
relation
could be used as a practical tool to provide an accurate estimate (
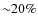 at
at  )
of the bolometric correction using only the
)
of the bolometric correction using only the 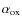 value.
value.
- 6.
- We found a correlation for both
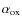 and
and 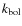 with Eddington ratio. Our results for the
with Eddington ratio. Our results for the 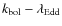 relation
and for
relation
and for 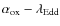 suggest that there is a connection between the broad-band emission,
mostly in the UV, and the Eddington ratio, which is directly linked to
the ratio between mass accretion rate,
suggest that there is a connection between the broad-band emission,
mostly in the UV, and the Eddington ratio, which is directly linked to
the ratio between mass accretion rate,
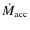 ,
and Eddington accretion rate,
,
and Eddington accretion rate,
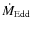 .
.
- 7.
- We have estimated the possible effects of intrinsic
absorption and/or contribution of the host-galaxy on the
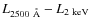 and
and 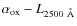 relations.
If the main reason for the red optical-UV SEDs in our sample were
intrinsic extinction, the resulting
relations.
If the main reason for the red optical-UV SEDs in our sample were
intrinsic extinction, the resulting 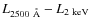 relation
would be slightly steeper (
relation
would be slightly steeper (
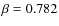
 0.021); if, instead, the host-galaxy contribution were
important in determining the red optical-UV SEDs, the resulting
0.021); if, instead, the host-galaxy contribution were
important in determining the red optical-UV SEDs, the resulting 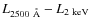 relation
would be flatter (
relation
would be flatter (
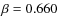
 0.022). Neither effect can produce a linear correlation (
0.022). Neither effect can produce a linear correlation (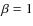 ).
).
In Italy, the XMM-COSMOS project is supported by PRIN/MIUR under grant 2006-02-5203, ASI-INAF grants I/023/05/00, I/088/06 and ASI/COFIS/WP3110 I/026/07/0. In Germany the XMM-Newton project is supported by the Bundesministerium für Wirtshaft und Techologie/Deutsches Zentrum für Luft und Raumfahrt and the Max-Planck society. The entire COSMOS collaboration is gratefully acknowledged.
References
- Adelman-McCarthy, J. K., et al. 2005, VizieR Online Data Catalog, 2267, 0 [Google Scholar]
- Akritas, M. G., & Siebert, J. 1996, MNRAS, 278, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, S. F., & Margon, B. 1987, ApJ, 314, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Avni, Y., & Tananbaum, H. 1982, ApJ, 262, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Avni, Y., & Tananbaum, H. 1986, ApJ, 305, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Bechtold, J., Siemiginowska, A., Shields, J., et al. 2003, ApJ, 588, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., Fonseca Bonilla, N., Guainazzi, M., Matt, G., & Ponti, G. 2009, A&A, 501, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bondi, M., Ciliegi, P., Schinnerer, E., et al. 2008, ApJ, 681, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, W. N., Laor, A., & Wills, B. J. 2000, ApJ, 528, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Brusa, M., Civano, F., & Comastri, A. 2009a, ApJ, submitted [Google Scholar]
- Brusa, M., Comastri, A., Gilli, R., et al. 2009b, ApJ, 693, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Cappelluti, N., Brusa, M., Hasinger, G., et al. 2009, A&A, 497, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cappi, M., Matsuoka, M., Comastri, A., et al. 1997, ApJ, 478, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Chanan, G. A. 1983, ApJ, 275, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Wilkes, B. J., McDowell, J. C., et al. 1994, ApJS, 95, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, S. C., Brandt, W. N., Sambruna, R. M., Mathur, S., & Yamasaki, N. 1999, ApJ, 519, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C., Goosmann, R., Antonucci, R., & Whysong, D. 2004, in AGN Physics with the Sloan Digital Sky Survey, ed. G. T. Richards, & P. B. Hall, ASP Conf. Ser., 311, 61 [Google Scholar]
- Gibson, R. R., Brandt, W. N., & Schneider, D. P. 2008, ApJ, 685, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, P. J., Schartel, N., Anderson, S. F., et al. 1995, ApJ, 450, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Green, P. J., Aldcroft, T. L., Richards, G. T., et al. 2009, ApJ, 690, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Haardt, F., Maraschi, L., & Ghisellini, G. 1994, ApJ, 432, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G., Cappelluti, N., Brunner, H., et al. 2007, ApJS, 172, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Hewett, P. C., & Foltz, C. B. 2003, AJ, 125, 1784 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Richards, G. T., & Hernquist, L. 2007, ApJ, 654, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, T., Feigelson, E. D., & Nelson, P. I. 1986, ApJ, 306, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jahnke, K., Sánchez, S. F., Wisotzki, L., et al. 2004, ApJ, 614, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Jahnke, K., Bongiorno, A., Brusa, M., et al. 2009, ApJ, 706, L215 [NASA ADS] [CrossRef] [Google Scholar]
- Just, D. W., Brandt, W. N., Shemmer, O., et al. 2007, ApJ, 665, 1004 [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kellermann, K. I., Sramek, R., Schmidt, M., Shaffer, D. B., & Green, R. 1989, AJ, 98, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C., Bechtold, J., Trump, J. R., Vestergaard, M., & Siemiginowska, A. 2008, ApJS, 176, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Kriss, G. A., & Canizares, C. R. 1985, ApJ, 297, 177 [NASA ADS] [CrossRef] [Google Scholar]
- La Franca, F., Franceschini, A., Cristiani, S., & Vio, R. 1995, A&A, 299, 19 [NASA ADS] [Google Scholar]
- Lavalley, M., Isobe, T., & Feigelson, E. 1992, in Astronomical Data Analysis Software and Systems I, ed. D. M. Worrall, C. Biemesderfer, & J. Barnes, ASP Conf. Ser., 25, 245 [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Mainieri, V., Hasinger, G., Cappelluti, N., et al. 2007, ApJS, 172, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Radovich, M., Iovino, A., et al. 2008, VizieR Online Data Catalog, 2286, 0 [Google Scholar]
- Merloni, A., Bongiorno, A., Bolzonella, M, et al. 2010, ApJ, 708, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Perola, G. C., Puccetti, S., Fiore, F., et al. 2004, A&A, 421, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Polletta, M., Tajer, M., Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Prescott, M. K. M., Impey, C. D., Cool, R. J., & Scoville, N. Z. 2006, ApJ, 644, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Prevot, M. L., Lequeux, J., Prevot, L., Maurice, E., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [NASA ADS] [Google Scholar]
- Richards, G. T., Fan, X., Schneider, D. P., et al. 2001, AJ, 121, 2308 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Hall, P. B., Vanden Berk, D. E., et al. 2003, AJ, 126, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Salvato, M., Hasinger, G., Ilbert, O., et al. 2009, ApJ, 690, 1250 [CrossRef] [Google Scholar]
- Sanders, D. B., Salvato, M., Aussel, H., et al. 2007, ApJS, 172, 86 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Aussel, H., Benson, A., et al. 2007, ApJS, 172, 150 [Google Scholar]
- Shemmer, O., Brandt, W. N., Schneider, D. P., et al. 2006, ApJ, 644, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. D., Green, P. J., Barkhouse, W. A., et al. 2005, ApJ, 618, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Stalin, C. S., Petitjean, P., Srianand, R., et al. 2009, MNRAS, accepted [arXiv:0909.0464] [Google Scholar]
- Steffen, A. T., Strateva, I., Brandt, W. N., et al. 2006, AJ, 131, 2826 [NASA ADS] [CrossRef] [Google Scholar]
- Strateva, I. V., Brandt, W. N., Schneider, D. P., Vanden Berk, D. G., & Vignali, C. 2005, AJ, 130, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Tananbaum, H., Avni, Y., Branduardi, G., et al. 1979, ApJ, 234, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, Y., Scoville, N., Murayama, T., et al. 2007, ApJS, 172, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Trump, J. R., Impey, C. D., Gabor, J. M., et al. 2007, in The Central Engine of Active Galactic Nuclei, ed. L. C. Ho, & J.-W. Wang, ASP Conf. Ser., 373, 726 [Google Scholar]
- Trump, J. R., Impey, C. D., Elvis, M., et al. 2009, ApJ, 696, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Vanden Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., & Fabian, A. C. 2007, MNRAS, 381, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., & Fabian, A. C. 2009, MNRAS, 392, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Brandt, W. N., & Schneider, D. P. 2003, AJ, 125, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkes, B. J. & Elvis, M. 1987, ApJ, 323, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkes, B. J., Tananbaum, H., Worrall, D. M., et al. 1994, ApJS, 92, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C., Meisenheimer, K., Kleinheinrich, M., et al. 2004, A&A, 421, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Young, M., Elvis, M., & Risaliti, G. 2009, ApJS, 183, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, W., Siebert, J., & Brinkmann, W. 1998, A&A, 334, 498 [NASA ADS] [Google Scholar]
- Zamojski, M. A., Schiminovich, D., Rich, R. M., et al. 2007, ApJS, 172, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Zamorani, G., Henry, J. P., Maccacaro, T., et al. 1981, ApJ, 245, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W., Kriss, G. A., Telfer, R. C., Grimes, J. P., & Davidsen, A. F. 1997, ApJ, 475, 469 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... XMM-COSMOS
![[*]](/icons/foot_motif.png)
- Full Table 2 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/512/A34
- ...Kauffmann et al. 2003
![[*]](/icons/foot_motif.png)
- These sources have been retrieved from the Nasa Extragalactic Database (NED) and from the SDSS archive.
- ... AGN
![[*]](/icons/foot_motif.png)
- The origin of spectroscopic redshifts for the 361 sources is as follows: 63 objects from the SDSS archive, 75 from MMT observations (Prescott et al. 2006), 112 from the IMACS observation campaign (Trump et al. 2007), 93 from the zCOSMOS bright 10 k sample (see Lilly et al. 2007) and 18 from the zCOSMOS faint catalog.
- ...
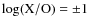
![[*]](/icons/foot_motif.png)
-
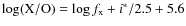 .
.
- ...Kellermann et al. 1989)
![[*]](/icons/foot_motif.png)
- Radio-loudness is defined as
where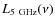 and
and 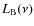 are the rest-frame monochromatic luminosities at
are the rest-frame monochromatic luminosities at  and in the optical B band, respectively.
and in the optical B band, respectively.
All Tables
Table 1:
Selection criteria from ![]() catalog.
catalog.
Table 2: Optical and X-ray properties of the total sample.
Table 3:
Correlations and their significance from Kendall-![]() statistics (K-
statistics (K-![]() )
and from Partial Kendall-
)
and from Partial Kendall-![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig1.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg61.png)
|
Figure 1: Distribution of the photometric classification (see Table 2 in Salvato et al. 2009) for the spectroscopically identified type 1 AGN sample (hatched histogram), for the photometric sample (open histogram) and for the not-type 1 AGN sample (filled histogram). The dashed line at SED type = 19 marks our adopted separation between sources with photometric redshift that we define as type 1 AGN (236 sources on the right) and not-type 1 (377 sources on the left) on the basis of the best-fitting SED template. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig2.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg66.png)
|
Figure 2:
Plot of the [0.5-2] keV flux versus the total i*
CFHT magnitude for the spectroscopically identified (black
points) and the photo-z classified (red
crosses) broad line AGN. The dashed lines represent the
constant X-ray to optical flux ratio |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig3.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg79.png)
|
Figure 3: Redshift distribution of the 545 type 1 AGN considered in this work (open histogram). The filled histogram shows the redshift distribution for the sample of 322 spectroscopically identified sources, while the hatched histogram is the redshift distribution for the 223 sources without spectroscopic redshift. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig4.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg119.png)
|
Figure 4:
The SED of a spectroscopically identified QSO at z=1.8
(XID = 2046, black line),
compared with the mean SED of Elvis et al. (1994, blue
line). The rest-frame data, used to construct the SED of
XID = 2046 are, from left to right: black triangle, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig5.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg125.png)
|
Figure 5: The SED of a spectroscopically identified QSO at z=1.161 (XID = 265, black line). Keys are as in Fig. 4. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{13298fig6.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg131.png)
|
Figure 6:
Values of the rest-frame monochromatic luminosity
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig7.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg150.png)
|
Figure 7:
Plot of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig8.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg159.png)
|
Figure 8:
Plot of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig9.ps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg160.png)
|
Figure 9:
Plot of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig10.ps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg168.png)
|
Figure 10:
Plot of the hard X-ray bolometric corrections against |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig11.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg191.png)
|
Figure 11: Hard X-ray bolometric correction versus Eddington ratio for the 150 type 1 AGN with BH mass estimate. The solid black line shows the best-fit relation that we found using the OLS bisector algorithm (see Eq. (14)), while the orange and the green dashed lines represent Eqs. (12) and (13), respectively. Red open circles represent the sample by VF09 (25 sources, see their Fig. 6 for details) and the corresponding bins with error bars. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig12.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg196.png)
|
Figure 12:
Plot of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig13.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg197.png)
|
Figure 13:
Distribution of redshifts versus the relative |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig14.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg198.png)
|
Figure 14:
Distribution of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13298fig15.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa13298-09/Timg206.png)
|
Figure 15: Distribution of the optical index for the total sample (open histogram), for the 145 AGN which have a host-galaxy contribution less than 10% (filled histogram) and for the 96 AGN which have a host-galaxy contribution greater than 10% (hatched histogram). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}%
\alpha_{\rm ox}=-\frac{{\rm Log}~[L_{2~{\rm keV}}/L_{2500~{\rm\AA}}]}{2.605}\cdot
\end{displaymath}](/articles/aa/full_html/2010/04/aa13298-09/img30.png)
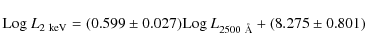
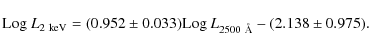
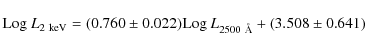
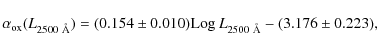
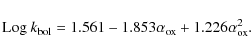
![\begin{displaymath}%
R=\left[\frac{L_{5~{\rm GHz}}(\nu)}{L_{{\rm B}}(\nu)}\right],
\end{displaymath}](/articles/aa/full_html/2010/04/aa13298-09/img68.png)