| Issue |
A&A
Volume 512, March-April 2010
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200912726 | |
| Published online | 24 March 2010 | |
Infrared properties of the SDSS-maxBCG galaxy clusters
M. Roncarelli1 - E. Pointecouteau1 - M. Giard1 - L. Montier1 - R. Pello 2
1 - Centre d'Etude Spatiale des Rayonnements, CNRS/Université de
Toulouse, 9 Avenue du Colonel Roche, BP 44346, 31028 Toulouse
Cedex 04, France
2 -
Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de
Toulouse, CNRS, 14 Av. Edouard Belin, 31400 Toulouse, France
Received 19 June 2009 / Accepted 5 January 2010
Abstract
Context. The physics of galaxy clusters has proven to be
influenced by several processes connected with their galactic component
which pollutes the intracluster medium (ICM) with metals, stars and
dust. However, it is not clear whether the presence of diffuse
dust can play a role in clusters physics since a characterisation of
the infrared (IR) properties of galaxy clusters is very challenging and
yet to be completely achieved.
Aims. In our study we focus on the recent work of Giard
et al. (2008, A&A, 490, 547) who performed a stacking analysis
of the IRAS data in the direction of several thousands of galaxy
clusters, providing a statistical characterisation of their
IR luminosity and redshift evolution. We model the
IR properties of the galactic population of the
SDSS-maxBCG clusters (0.1<z<0.3) in order to check if
it accounts for the entire observed signal and to constrain the
possible presence of other components, like dust in the ICM.
Methods. Starting from the optical properties of the galaxies of
the SDSS-maxBCG clusters, we estimate their emission in the 60 and
100 ![]() m
IRAS bands making use of modeled spectral energy distributions of
different spectral types (E/S0, Sa, Sb, Sc and starburst). We also
consider the evolution of the galactic population/luminosity with
redshift.
m
IRAS bands making use of modeled spectral energy distributions of
different spectral types (E/S0, Sa, Sb, Sc and starburst). We also
consider the evolution of the galactic population/luminosity with
redshift.
Results. The total galactic emission, which is dominated by the
contribution of star-forming late-type galaxies, is consistent
with the observed signal. In fact, our galactic emission model
slightly overestimates the observed fluxes, with the excess being
concentrated in low-redshift clusters (
![]() ).
).
Conclusions. Our results indicate that, if present, the IR
emission from intracluster dust must be very small compared to the one
associated to the galaxy members. This translates into an upper limit
on the dust-to-gas mass ratio in the ICM of
![]()
![]() 10-5.
The excess in luminosity obtained at low redshift constitutes an
indication that the cluster environment is driving a process of
star-formation quenching on its galaxy members.
10-5.
The excess in luminosity obtained at low redshift constitutes an
indication that the cluster environment is driving a process of
star-formation quenching on its galaxy members.
Key words: large scale structure of Universe - galaxies: clusters: general - intergalactic medium - infrared: galaxies
1 Introduction
Clusters of galaxies form in correspondence of the peaks of the
primordial matter density field as a result of the gravitational
collapse of both dark matter and baryons. In the framework of the
standard ![]() CDM cosmological model and the hierarchical clustering of the large scale structure
formation they constitute both the most recent and the largest virialised objects of the Universe.
CDM cosmological model and the hierarchical clustering of the large scale structure
formation they constitute both the most recent and the largest virialised objects of the Universe.
Nowadays, it is clear that gravitation is not the only process that influences the physics of the intracluster medium (ICM, hereafter). The electrons of the ionized plasma emit via free-free interaction with the protons, making clusters bright X-ray sources and allowing the gas to cool efficiently, particularly in the central regions. During the last decade, the observations of the XMM-Newton and Chandra X-ray satellites highlighted the presence of several interaction mechanisms between the galactic component and the ICM, showing that the evolution of the two is intimately tied. For instance, the accretion of cold gas onto the brightest cluster galaxies (BCGs) at the cluster center is strongly suspected to fuel the super-massive blackholes they host. This process is able to trigger star-formation within the BCGs (O'Dea et al. 2008; Pipino et al. 2009) and power episodic violent outbursts of their central active galactic nuclei (AGNs), whose energy injection into the ICM prevents the overcooling of the gas (Fabian et al. 2006; McNamara & Nulsen 2007). AGNs feedback and other non-gravitational processes, such as supernovae (SNe) powered galactic winds (Kapferer et al. 2006; Schindler & Diaferio 2008; Sijacki & Springel 2006), preheating of the ICM (see e.g. Fang & Haiman 2008), together with gravitational ones (i.e. galaxy-galaxy interactions, ram-pressure stripping, galaxy mergers) induce energy and matter exchanges between the galactic medium and the ICM. To date these complex physical processes and their impact on the statistical cluster properties, thus on our understanding of structure formation (Voit 2005) and use of the cluster population in cosmological studies (Mantz et al. 2009,2008; Vikhlinin et al. 2009), are under scrutinous observational and theoretical investigations (see, e.g., Arnaud 2005; Borgani 2008, and references therein).
The presence of heavy elements in the ICM is the most direct evidence
and consequence of the ejection of galactic material. Within clusters
their abundance has been widely measured making use of X-ray
observations (see the reviews by Arnaud 2005; Sarazin 1988; Werner et al. 2008) with a typical abundance of 0.3 ![]() .
Stars and SNe constitute the most efficient way to produce and
disperse metals. Heavy elements in the ICM originate from different processes: early enrichment
(Aguirre & Schaye 2007),
continuous injection from galaxy members and in situ production by
intra-cluster stars (sources of the intra-cluster light, see Arnaboldi 2004; Dolag et al. 2010; Murante et al. 2007; Krick & Bernstein 2007; Conroy et al. 2007).
The aforementioned processes do not discriminate between the natures of
the ejected galactic material, therefore these enrichments are
unambiguously linked also to the ejection of neutral gas and dust in
the ICM.
.
Stars and SNe constitute the most efficient way to produce and
disperse metals. Heavy elements in the ICM originate from different processes: early enrichment
(Aguirre & Schaye 2007),
continuous injection from galaxy members and in situ production by
intra-cluster stars (sources of the intra-cluster light, see Arnaboldi 2004; Dolag et al. 2010; Murante et al. 2007; Krick & Bernstein 2007; Conroy et al. 2007).
The aforementioned processes do not discriminate between the natures of
the ejected galactic material, therefore these enrichments are
unambiguously linked also to the ejection of neutral gas and dust in
the ICM.
Observations indicate that in galactic environments dust is a minor component, with dust-to-gas ratio
![]() (Mathis et al. 1977) and it could be as low as
(Mathis et al. 1977) and it could be as low as
![]() in the ICM (Popescu et al. 2000; Aguirre et al. 2001).
Nonetheless, dust particles have lifetimes long enough to be heated by
collisions with the hot electrons and re-emit at the infrared (IR)
wavelengths. In this way they can constitute an additional cooling
agent of the gas (Montier & Giard 2004) which
might play an important role in ICM physics, as seen with the
implementation of dust cooling in hydrodynamical simulations (da Silva et al. 2009).
in the ICM (Popescu et al. 2000; Aguirre et al. 2001).
Nonetheless, dust particles have lifetimes long enough to be heated by
collisions with the hot electrons and re-emit at the infrared (IR)
wavelengths. In this way they can constitute an additional cooling
agent of the gas (Montier & Giard 2004) which
might play an important role in ICM physics, as seen with the
implementation of dust cooling in hydrodynamical simulations (da Silva et al. 2009).
However obtaining observational constraints on the possible
IR signal coming from intracluster dust is a very challenging
issue, since the average sky fluctuations caused by background galaxies
and galactic cirrus clouds are comparable or even higher than the
overall flux coming from a single cluster, which is anyway expected to
be dominated by the dust emission from star-forming galaxies.
In fact, nowadays the only claimed (and still controversial)
detection of this IR emission comes from the studies on the Coma
cluster of Stickel et al. (1998,2002), who measured a diffuse dust mass of
![]() ,
while other attempts resulted in non detections (see, e.g., Bai et al. 2007).
,
while other attempts resulted in non detections (see, e.g., Bai et al. 2007).
If studies on single objects appear very problematic, the low
signal-to-noise problem can be overcome by adopting a statistical
approach, taking advantage of the high number of clusters detected
mainly with optical surveys (see Biviano 2008, for a review). This concept was first used at IR wavelengths by Montier & Giard (2005) who performed a stacking analysis of the Infra Red Astronomical Satellite
(IRAS) survey in the direction of more than 11 000 known
galaxy clusters and groups and obtained a statistical detection of the
overall clusters signal at 12, 25, 60 and 100 ![]() m. Starting from this result, Giard et al. (2008)
characterised the IR luminosity evolution of the stacked sample,
analysing also its correlation with their X-ray luminosities. These
works constitute a first important result on the global
IR properties of galaxy clusters. However, since the clusters
IR emission could be dominated by star-forming galaxies,
it becomes crucial to disentangle the galactic signal from a
possible diffuse component in order to quantify its implications on
cluster physics. On the other side, understanding the
IR properties of the cluster galaxies could provide hints on the
environmental effects over their star-formation, which are nowadays
objects of studies at different wavelengths, from the radio to the
ultraviolet (UV, see Boselli & Gavazzi 2006, for a review).
m. Starting from this result, Giard et al. (2008)
characterised the IR luminosity evolution of the stacked sample,
analysing also its correlation with their X-ray luminosities. These
works constitute a first important result on the global
IR properties of galaxy clusters. However, since the clusters
IR emission could be dominated by star-forming galaxies,
it becomes crucial to disentangle the galactic signal from a
possible diffuse component in order to quantify its implications on
cluster physics. On the other side, understanding the
IR properties of the cluster galaxies could provide hints on the
environmental effects over their star-formation, which are nowadays
objects of studies at different wavelengths, from the radio to the
ultraviolet (UV, see Boselli & Gavazzi 2006, for a review).
In this work we attempt to reconstruct the observed stacked IR emission measured in the direction of galaxy clusters in the IRAS whole sky survey. We model in details the contribution of cluster galaxies to the total IR emission in order to understand whether this contribution is sufficient to explain the fluxes and luminosities derived by Montier & Giard (2005) and Giard et al. (2008) or if, on the contrary, there is an indication of a non-galactic component, possibly associated to intracluster dust. Since for our modelisation we make use of the known spectral properties of galaxies as observed mainly in the field, the comparison between our results and observed data can be useful also to highlight possible differences between cluster and field galaxies.
This paper is organised as follows. In the next section we briefly present the statistical detection of the clusters IR emission of Montier & Giard (2005) and Giard et al. (2008) and we focus in particular on the subsample of the SDSS-maxBCG catalogue. In Sect. 3 we describe the details of our modelisation for the IR luminosity of cluster galaxies and discuss the possible presence of other galactic components in Sect. 4. In Sect. 5 we apply our model to estimate the IRAS fluxes, then our results are discussed in Sect. 6. Finally, we present our conclusions in Sect. 7.
Throughout this paper we assume a flat ![]() CDM cosmological model with
CDM cosmological model with
![]() .
.
2 The statistical IR emission of clusters
Working on a list of 11 507 groups and clusters selected from 14 publicly available catalogues![]() , Montier & Giard (2005)
performed a clear statistical detection of the IR flux in the
direction of galaxy clusters by stacking their corresponding fields
(within 10' from the cluster center) in the IRAS all sky survey.
After dealing carefully with the point sources contamination,
foreground/background subtraction and other various systematic effects,
they measured
stacked fluxes at 60 and 100
, Montier & Giard (2005)
performed a clear statistical detection of the IR flux in the
direction of galaxy clusters by stacking their corresponding fields
(within 10' from the cluster center) in the IRAS all sky survey.
After dealing carefully with the point sources contamination,
foreground/background subtraction and other various systematic effects,
they measured
stacked fluxes at 60 and 100 ![]() m
with signal-to-noise ratio of 57 and 43 respectively. Over
the four IRAS wavelengths this emission proves to be consistent
with the spectral signature of galactic IR emission.
m
with signal-to-noise ratio of 57 and 43 respectively. Over
the four IRAS wavelengths this emission proves to be consistent
with the spectral signature of galactic IR emission.
More recently, on the basis of Montier & Giard (2005) results, Giard et al. (2008)
performed a statistical analysis in redshift, presenting for the first
time the evolution of the IR luminosity of galaxy clusters. In
addition to Montier & Giard (2005) original list of 11 507 clusters, Giard et al. (2008) backed-up their analysis on two standalone catalogues - i.e. the ``Northern Sky Optical Cluster Survey'' (NSC, Gal et al. 2003), and the SDSS-maxBCG catalogue (Koester et al. 2007) - for which a richness information was available. They extended their IRAS stacking analysis to the Rosat All Sky Survey (RASS, Voges 1992)
in order to compare the evolution in redshifts of the IR and X-ray
luminosity. They showed that the stacked IR luminosities are on
average 20 times higher than the X-ray luminosities. They also
found that the IR luminosity is evolving rapidly as (1+z)5 in the
0.1 < z < 1 interval. Giard et al. (2008)
also made use of the richness information (i.e. correlated to the
halo occupation number), contained in the SDSS-maxBCG and
NSC catalogues, to constrain the dependence of the
IR luminosities with cluster richness. They derived a correlation
following
![]() .
.
In order to understand the aforementioned results at 60 and 100 ![]() m,
in this work we focus on the modelisation of the
IR luminosity and fluxes of galaxy clusters.
The IR spectrum of galaxies, which is dominated by dust
emission (Lagache et al. 2005; Soifer et al. 2008), is expected to make a major contribution
to the IR emission detected in the direction of clusters (Giard et al. 2008).
Therefore, a careful modeling of the IR emission of member
galaxies is needed in order to understand the global properties of
clusters in the IR, and in particular to disentangle between the
relative contribution
of galaxies and intracluster dust. Given the inhomogeneity of the main
dataset used by Montier & Giard (2005) and Giard et al. (2008)
(i.e. the 11 507 groups and clusters) in terms of
cluster size and detection method, it becomes very difficult to
define a global selection function of such sample, that would be
necessary in order to have a suitable starting base for our work.
In order to overcome these difficulties we decided to base our
modelisation on a restricted and well defined cluster sample by
considering a single catalogue. For the purpose of our calculations we
chose the SDSS-maxBCG catalogue.
m,
in this work we focus on the modelisation of the
IR luminosity and fluxes of galaxy clusters.
The IR spectrum of galaxies, which is dominated by dust
emission (Lagache et al. 2005; Soifer et al. 2008), is expected to make a major contribution
to the IR emission detected in the direction of clusters (Giard et al. 2008).
Therefore, a careful modeling of the IR emission of member
galaxies is needed in order to understand the global properties of
clusters in the IR, and in particular to disentangle between the
relative contribution
of galaxies and intracluster dust. Given the inhomogeneity of the main
dataset used by Montier & Giard (2005) and Giard et al. (2008)
(i.e. the 11 507 groups and clusters) in terms of
cluster size and detection method, it becomes very difficult to
define a global selection function of such sample, that would be
necessary in order to have a suitable starting base for our work.
In order to overcome these difficulties we decided to base our
modelisation on a restricted and well defined cluster sample by
considering a single catalogue. For the purpose of our calculations we
chose the SDSS-maxBCG catalogue.
2.1 The SDSS-maxBCG catalogue
Since we want to reconstruct the total IR luminosity and flux due to cluster galaxies, we require an information on the halo occupation number (i.e. the number of galaxies within the cluster potential well). In this view the SDSS-maxBCG catalogue (Koester et al. 2007) is the most fitted to our needs. Indeed, since the SDSS-maxBCG catalogue is created by identifying overdensities in the galaxy distribution, it contains information about the richness of the cluster itself that we can use directly without having to deal with the uncertainties connected with the N-M and LX-M relations, that would be necessary, for instance, in case of X-ray selected clusters. Moreover, the number of objects contained in the SDSS-maxBCG catalogue is the highest among all the others (i.e. 13 807 groups and clusters), thus providing a good statistics which is needed to assess the robustness of our results. Finally, Koester et al. (2007) provide also the total luminosity in the r and i-band of the identified cluster members which also have a well defined spectral type (E/S0 galaxies). We will make use of this information to obtain an estimate of their flux in the IRAS bands (see Sect. 3).The SDSS-maxBCG catalogue has been obtained by analysing the clustering
properties of more than 500 000 SDSS galaxies in an area
of ![]() 7500 deg2 in the redshift range 0.1<z<0.3. For each cluster the catalogue contains a photometric redshift and an indication of the cluster richness,
7500 deg2 in the redshift range 0.1<z<0.3. For each cluster the catalogue contains a photometric redshift and an indication of the cluster richness,
![]() .
This quantity corresponds to the number of early-type galaxy members at a distance lower than R200 from the central BCG. The adopted definition of R200 is the radius at which the deprojected galactic density is 200
.
This quantity corresponds to the number of early-type galaxy members at a distance lower than R200 from the central BCG. The adopted definition of R200 is the radius at which the deprojected galactic density is 200
![]() -1
times the average galactic density on the large scale: in the
approximation of galaxies following the matter distribution,
this is equivalent to the usual cosmological definition of R200 as the radius enclosing a density 200 times larger than the critical density of the Universe (see the discussion in Hansen et al. 2005, for details).
-1
times the average galactic density on the large scale: in the
approximation of galaxies following the matter distribution,
this is equivalent to the usual cosmological definition of R200 as the radius enclosing a density 200 times larger than the critical density of the Universe (see the discussion in Hansen et al. 2005, for details).
It is important to note that
![]() does not
represent the total cluster richness because it does not include spiral
galaxies: in fact, the cluster members candidates have been
selected for having colors matching the E/S0 ridgeline (Bower et al. 1992) and Mr<-16. We will explain in the detail our definition of the cluster richness in Sect. 3.2.
does not
represent the total cluster richness because it does not include spiral
galaxies: in fact, the cluster members candidates have been
selected for having colors matching the E/S0 ridgeline (Bower et al. 1992) and Mr<-16. We will explain in the detail our definition of the cluster richness in Sect. 3.2.
The SDSS-maxBCG catalogue includes 13 823 groups and clusters with
![]()
![]() 10 and it is widely dominated by the presence of groups and small clusters (
10 and it is widely dominated by the presence of groups and small clusters (
![]()
![]() 10-15). As a reference, when computing their corresponding M200 with the relation of Rykoff et al. (2008), the median of the mass distribution is 4.5
10-15). As a reference, when computing their corresponding M200 with the relation of Rykoff et al. (2008), the median of the mass distribution is 4.5 ![]()
![]() .
In this work, we adopted the trimming done by Giard et al. (2008)
on the SDSS-maxBCG catalogue of objects located in regions of the sky
not covered by the IRAS data, with noisy images, or whose
fields contain strong IR sources. This selection process ended up
in a sample of 7476 clusters, corresponding to a total of
121 318 E/S0 galaxy members, that will be the object of
our analysis.
.
In this work, we adopted the trimming done by Giard et al. (2008)
on the SDSS-maxBCG catalogue of objects located in regions of the sky
not covered by the IRAS data, with noisy images, or whose
fields contain strong IR sources. This selection process ended up
in a sample of 7476 clusters, corresponding to a total of
121 318 E/S0 galaxy members, that will be the object of
our analysis.
3 Modeling galaxy luminosities
The main source of the IR radiation of galaxy clusters is expected
to be the thermal emission due to the dust reprocessing the
UV photons emitted by stars inside cluster galaxies. Since we are
basing our work on galaxies observed in the optical band, we need to
construct a valid model that is able to connect their galactic r band emission to the corresponding dust emission in the IR. In particular, we will focus on the 60 ![]() m and 100
m and 100 ![]() m IRAS bands fluxes, in order to compare our results with the most relevant measurements of Giard et al. (2008).
The characteristics of the galactic IR emission depend on the
amount of dust present in the galaxies and are strictly connected with
their star-formation rate (SFR) and, therefore, their
spectral type.
m IRAS bands fluxes, in order to compare our results with the most relevant measurements of Giard et al. (2008).
The characteristics of the galactic IR emission depend on the
amount of dust present in the galaxies and are strictly connected with
their star-formation rate (SFR) and, therefore, their
spectral type.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12726fg1.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12726-09/Timg22.png)
|
Figure 1:
SEDs as a function of wavelength for the 5 GRASIL (Silva et al. 1998)
templates used in this work. The red line shows our reference model for
E/S0 galaxies, the three blue lines represent normal spiral
galaxies Sa, Sb, Sc (light blue, average, dark blue, respectively)
and the green line represents our starburst galaxy model, corresponding
to M 82. All of the templates have been arbitrarily normalized to
the same integrated luminosity of 1030 erg s-1 in the band 8-1000 |
| Open with DEXTER | |
Spectral energy distribution (SED) templates obtained with the spectral synthesis code GRASIL (Silva et al. 1998) were used in order to represent the typical emission of galaxies in the local universe. GRASIL SEDs extend from UV to radio wavelengths, including dust reprocessing and nebular line emission. We used four templates for normal galaxies, with Salpeter's initial mass function and age 13 Gyr, namely an elliptical galaxy and three different spiral galaxies (Sa, Sb and Sc). We also included the GRASIL model fit to multi-wavelength observations of M 82 as a semi-empirical template to represent the typical SED of local starburst galaxies (Silva et al. 1998). For spiral galaxies, the SEDs correspond to a weighted average over the different lines of sight, from face-on to edge-on, in order to statistically account for the mean spatial orientations of cluster galaxies. The five templates are displayed in Fig. 1.
The SED models described above were used to derive the expected
IR luminosities from observed fluxes and corresponding
luminosities in the r band. For a given template, the luminosity in the r band is given by
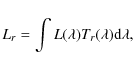
|
(1) |
where
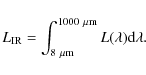
|
(2) |
Therefore, for each template SED, the scaling ratio can be defined as follows
Table 1 summarizes the
Table 1: Reference spectral types and galactic population models used in this work.
3.1 Early-type galaxies
Early-type galaxies are characterized by an old stellar population
and a star-formation history which is essentially compatible with
passive evolution: for this reason they are not expected to
dominate the emission in the IRAS bands. In fact, for a fixed
![]() ,
the amount of energy emitted at wavelengths
,
the amount of energy emitted at wavelengths
![]()
![]() m is one order of magnitude lower with respect to normal spirals (see Fig. 1).
However, it is known that in dense environments elliptical
galaxies largely dominate the galactic population, being about
4 times more frequent than spirals (see, e.g., Dressler 1980; Dressler et al. 1997). Moreover red galaxies are usually more massive and more luminous in the r band than blue ones. For these reasons their total contribution on the clusters IR signal may be non-negligible.
m is one order of magnitude lower with respect to normal spirals (see Fig. 1).
However, it is known that in dense environments elliptical
galaxies largely dominate the galactic population, being about
4 times more frequent than spirals (see, e.g., Dressler 1980; Dressler et al. 1997). Moreover red galaxies are usually more massive and more luminous in the r band than blue ones. For these reasons their total contribution on the clusters IR signal may be non-negligible.
As mentioned in Sect. 2.1, Koester et al. (2007) identified the number
![]() of E/S0 galaxies (Mr<-16) inside R200 of each of the 7476 clusters of our sample. For each cluster, the authors provide the luminosity, k-corrected at z = 0.25, in the r band
of the BCG
and of the other E/S0 members as a whole. We corrected these
luminosities into rest-frame luminosities by using the
LRG template of KCORRECT (Blanton & Roweis 2007): we refer to
of E/S0 galaxies (Mr<-16) inside R200 of each of the 7476 clusters of our sample. For each cluster, the authors provide the luminosity, k-corrected at z = 0.25, in the r band
of the BCG
and of the other E/S0 members as a whole. We corrected these
luminosities into rest-frame luminosities by using the
LRG template of KCORRECT (Blanton & Roweis 2007): we refer to
![]() and
and
![]() for the luminosity of the BCG and of the cluster as a
whole, respectively, after this correction. Given the uniform
properties of early-type galaxies, and the high number of such objects
in our sample, their typical SED should be well represented by the
E/S0 template described above. In fact, although the
IR signal of every single galaxy is lost in the stacking process,
the E/S0 template still represents the average behavior of the
early-type population of galaxies.
for the luminosity of the BCG and of the cluster as a
whole, respectively, after this correction. Given the uniform
properties of early-type galaxies, and the high number of such objects
in our sample, their typical SED should be well represented by the
E/S0 template described above. In fact, although the
IR signal of every single galaxy is lost in the stacking process,
the E/S0 template still represents the average behavior of the
early-type population of galaxies.
For every cluster we assign a r-band luminosity to all
of its early-type members contained in the SDSS-maxBCG catalogue.
For the BCG we use the value of
![]() ,
while for the other galaxies we use the average luminosity of the non-BCG E/S0 galaxies, determined as
,
while for the other galaxies we use the average luminosity of the non-BCG E/S0 galaxies, determined as
From Eq. (3), we translated these r-band luminosities into IR luminosities:
3.2 Contribution of late-type galaxies
Although the majority of optically bright galaxies in clusters environment are elliptical, and despite spiral galaxies in dense environments tend to be quickly stripped of their gas and have their star-formation quenched, they are still expected to provide a dominant contribution to the IR emission, due to their higher SFRs. Therefore, the contribution of late-type galaxies to the IR emission is crucial for our purposes and should be carefully estimated. Given the fact that late-type galaxies are not considered in the SDSS-maxBCG catalogue, their contribution was computed based on available modelings of galaxy populations, in particular the distribution of galaxies as a function of spectral type and luminosity. Since our sample goes from galaxy groups to rich clusters, we have included the environment dependence of these variables.
We based our model on the known properties of galaxies in the local universe as given by Balogh et al. (2004) who analysed the bimodal distribution of galaxies in a local (z<0.08) sample
of SDSS galaxies (DR1). These authors performed a detailed study
on the color and luminosity distribution of galaxies as a function of
their environment for both early and late-type galaxies. For each
galaxy they define a density estimator ![]() which represents the local projected galaxy density (Mr<-20) in Mpc-2 and they use it to classify the different environmental
regimes. Beside
which represents the local projected galaxy density (Mr<-20) in Mpc-2 and they use it to classify the different environmental
regimes. Beside
![]() mentioned before (see Sect. 2.1), the SDSS-maxBCG dataset contains also information about the number of galaxies
mentioned before (see Sect. 2.1), the SDSS-maxBCG dataset contains also information about the number of galaxies
![]() projected within a distance lower than 1 h-1 Mpc from the BCG, with the magnitude limit of Mr<-16. Therefore for each cluster we can assume a unique value of
projected within a distance lower than 1 h-1 Mpc from the BCG, with the magnitude limit of Mr<-16. Therefore for each cluster we can assume a unique value of ![]() for all of its members by establishing a relation with
for all of its members by establishing a relation with
![]() and, finally, with the properties of the population of late-type galaxies present.
and, finally, with the properties of the population of late-type galaxies present.
We proceed as follows.
- i)
- First of all, we integrate the double gaussian distributions of red and blue galaxies
(Fig. 1 of Balogh et al. 2004) obtaining a ratio of red and blue galaxies for the 5 values of
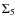 considered: for our work, we only need the three density bins
corresponding to dense environments (i.e. groups and clusters,
considered: for our work, we only need the three density bins
corresponding to dense environments (i.e. groups and clusters,
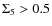 ). In these bins the resulting spiral fractions are
). In these bins the resulting spiral fractions are
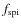 = 0.597, 0.478 and 0.286, in order of increasing density.
= 0.597, 0.478 and 0.286, in order of increasing density.
- ii)
- In order to use these values for our calculations we need, at first, to correct the value of
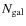 .
The galaxy samples of Koester et al. (2007), in fact, has a magnitude limit Mr < -16 while the definition of
.
The galaxy samples of Koester et al. (2007), in fact, has a magnitude limit Mr < -16 while the definition of 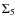 includes only galaxies with Mr < -20: for this reason we use the red galaxies luminosity function (LF) given by Baldry et al. (2004) to calculate the number of expected galaxy members with Mr < -20. We obtained
includes only galaxies with Mr < -20: for this reason we use the red galaxies luminosity function (LF) given by Baldry et al. (2004) to calculate the number of expected galaxy members with Mr < -20. We obtained
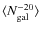 =
=
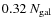 .
As for Balogh et al. (2004), the sample of Baldry et al. (2004)
is constituted by local SDSS galaxies, with the difference that it
contains no density distinction (e.g. field galaxies). Therefore,
by using the LF of Baldry et al. (2004)
for this calculation we neglect the effect of environmental properties;
anyway, since red galaxies are mostly present in galaxy clusters, we do
not expect this to change significantly our results.
.
As for Balogh et al. (2004), the sample of Baldry et al. (2004)
is constituted by local SDSS galaxies, with the difference that it
contains no density distinction (e.g. field galaxies). Therefore,
by using the LF of Baldry et al. (2004)
for this calculation we neglect the effect of environmental properties;
anyway, since red galaxies are mostly present in galaxy clusters, we do
not expect this to change significantly our results.
- iii)
- We are now able to obtain a first estimation of the density parameter associated to every cluster with the formula
where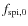 is the fraction of spiral galaxy (with Mr < -20) that for this calculation we fix arbitrarily to the initial value to
is the fraction of spiral galaxy (with Mr < -20) that for this calculation we fix arbitrarily to the initial value to
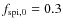 .
.
- iv)
- Using the value of
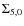 we calculate a new estimate
we calculate a new estimate
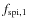 of the spiral fraction by interpolating between the values of
of the spiral fraction by interpolating between the values of
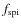 obtained by Balogh et al. (2004); this allows the calculation of a new value
obtained by Balogh et al. (2004); this allows the calculation of a new value
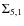 of the galaxy density with Eq. (5).
of the galaxy density with Eq. (5).
- v)
- We repeat this procedure until
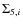 and
and
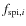 converge to definite values and check that the result does not depend on the initial choice of
converge to definite values and check that the result does not depend on the initial choice of
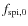 ,
thus obtaining the expected number of spiral galaxies with Mr < -20
,
thus obtaining the expected number of spiral galaxies with Mr < -20
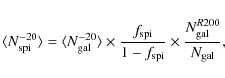
(6)
where the factor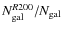 accounts for the ratio between the galaxies inside R200 and 1 h-1 Mpc.
accounts for the ratio between the galaxies inside R200 and 1 h-1 Mpc.
- vi)
- Finally, we add the expected number of spiral galaxies in the magnitude range
-20 < Mr < -18 by referring again to the galaxy distributions of Balogh et al. (2004), thus obtaining for every cluster the estimated value of the number of spiral members with Mr < -18,
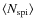 .
This value is then used as the average of a poissonian distribution,
that we assumed to assign a randomised number of spiral
.
This value is then used as the average of a poissonian distribution,
that we assumed to assign a randomised number of spiral
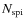 to each cluster, thus to determine the total cluster galaxies:
to each cluster, thus to determine the total cluster galaxies:
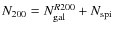 .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12726fg2.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12726-09/Timg52.png)
|
Figure 2:
Fraction of spiral galaxies within R200 (see Sect. 2.1 for the definition of R200) as a function of
|
| Open with DEXTER | |
This formalism led us to derive an average fraction of about
30% spiral galaxies in our sample of SDSS-maxBCG clusters
(see Table 1). The relation between
![]() and the fraction of spiral galaxies inside the whole cluster is shown in Fig. 2.
When considering galaxies with the same magnitude limit (dashed line),
the spiral fraction can be higher than 0.5 for groups and small
clusters, and then lessens with increasing
and the fraction of spiral galaxies inside the whole cluster is shown in Fig. 2.
When considering galaxies with the same magnitude limit (dashed line),
the spiral fraction can be higher than 0.5 for groups and small
clusters, and then lessens with increasing
![]() down to
down to ![]() 0.4 for
0.4 for
![]() = 70. When considering all the galaxies included in our model (i.e. Mr<-16 for early-type and Mr < -18 for late-type, solid line) the spiral fraction becomes lower by about 0.2.
= 70. When considering all the galaxies included in our model (i.e. Mr<-16 for early-type and Mr < -18 for late-type, solid line) the spiral fraction becomes lower by about 0.2.
The morphology-density study of Balogh et al. (2004) becomes useful also to assign a magnitude and a color to each spiral galaxy. For a given value of ![]() it is possible to construct a probability distribution
it is possible to construct a probability distribution
![]() for a late-type galaxy to have a given magnitude Mr and a given intrinsic color u-r. The former value is used to determine the luminosity Lr in the r-band as
for a late-type galaxy to have a given magnitude Mr and a given intrinsic color u-r. The former value is used to determine the luminosity Lr in the r-band as
where L0,r = 2.15
3.3 Evolution with redshift of spiral galaxies
Despite being the SDSS-maxBCG a catalogue of relatively nearby groups and clusters (0.1<z<0.3),
it is necessary to take into account the evolution with redshift
of the late-type galaxies properties with respect to the results of Balogh et al. (2004) which are derived from a local (i.e. z<0.08) sample of SDSS galaxies. For the purpose of our modelisation we consider the sample of Balogh et al. (2004) as representative of the galaxy population at
![]() ,
the central value of the interval, and apply two independent evolution effects.
,
the central value of the interval, and apply two independent evolution effects.
Spiral fraction evolution.
It is generally accepted that in a hierarchical structure formation scenario spiral galaxies tend to evolve towards S0 or ellipticals. This can happen either passively, with the consumption of the gas reservoir and its ejection with SNe explosions, or it can also be triggered by environmental interactions with other galaxies and with the ICM (see Boselli & Gavazzi 2006, for a review): it is therefore expected that the fraction of late-type galaxies increases with redshift (the so called Butcher-Oemler effect, Butcher & Oemler 1984). In fact, Laganá et al. (2009) find a change from about 0.1 to 0.3 in the spiral fraction of 20 galaxy clusters in the interval 0<z<0.25. Fitting the data on the fraction of star-forming galaxies of these clusters, they quantify its redshift evolution as:![\begin{displaymath}%
\langle N_{\rm spi}(z) \rangle = [1+1.3 ~ (z-z_{\rm B})]<N_{\rm spi}>_{z=0}.
\end{displaymath}](/articles/aa/full_html/2010/04/aa12726-09/img61.png)
|
(8) |
Including this effect in our modelisation raises the global spiral fraction of our sample from 30% to 35%, as shown in Table 1. Although this number may seem high for clusters (see e.g. Bai et al. 2006, for the Coma cluster) we must consider that the SDSS-maxBCG catalogue is dominated by groups and small clusters, as mentioned in Sect. 2.1. However, when applying our model to the case of MS 1054-03 as observed by Bai et al. (2007) (z=0.83, N200=144), we obtain
Luminosity evolution.
The current hierarchical structure formation scenario predicts that the peak of the star-formation is to be placed at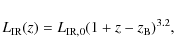
|
(9) |
where
We do not include any specific effect of spiral population evolution towards bluer types with increasing redshift. In fact, the fraction of the different spectral types of spirals in the redshift range we are interested in is not expected to differ significantly with respect to the local galaxies inside galaxy clusters (see e.g. De Lucia et al. 2007). Moreover the consequent effect of slightly increased global luminosity is anyway partially included when assuming the luminosity evolution with redshift aforementioned.
3.4 Uncertainties on the model parameters
The choice of the values of the different parameters introduces a
degree of uncertainty in our modelisation, the most important of
which are connected with the choice of the redshift evolution
parameters and the u-r color intervals used to define the spiral types (see Table 1).
In order to quantify these uncertainties, we introduce two other
sets of parameters to define a conservative and an extreme scenario and
we will use the values of the
fluxes estimated with these models to define the degree of confidence
of our results. More precisely, for what concerns the redshift
evolution we adopt the
![]() values for
values for
![]() and
and
![]() ,
as measured by Laganá et al. (2009) and Le Floc'h et al. (2005), respectively. Moreover, we also artificially add a shift in the u-r color intervals of
,
as measured by Laganá et al. (2009) and Le Floc'h et al. (2005), respectively. Moreover, we also artificially add a shift in the u-r color intervals of ![]() in order to obtain a redder (conservative scenario) and a bluer
(extreme) spiral population. Anyway, these changes introduce only minor
modifications in the galaxy population: the difference in the global
spiral fraction is of
in order to obtain a redder (conservative scenario) and a bluer
(extreme) spiral population. Anyway, these changes introduce only minor
modifications in the galaxy population: the difference in the global
spiral fraction is of ![]() %,
while the only significant change is in the fraction of starburst
galaxies that goes from 0.2% in the conservative model
to 1.1% in the extreme one. On the whole, the difference in the
final fluxes is mainly introduced by the modified luminosity evolution.
The results on the galaxy population for the conservative model are
also shown in Table 1.
%,
while the only significant change is in the fraction of starburst
galaxies that goes from 0.2% in the conservative model
to 1.1% in the extreme one. On the whole, the difference in the
final fluxes is mainly introduced by the modified luminosity evolution.
The results on the galaxy population for the conservative model are
also shown in Table 1.
3.5 The IR luminosity function of the SDSS-maxBCG galaxies
We show in Fig. 3
the luminosity function of the galaxies included in our reference
model, for the different spectral types. The luminosity considered is
given in the rest-frame 60 ![]() m IRAS band.
m IRAS band.
The luminosities go from a minimum of
![]()
![]() for the fainter E/S0 galaxies up to a maximum of some 1011
for the fainter E/S0 galaxies up to a maximum of some 1011 ![]() for the brightest spirals. Each type of spiral has a luminosity range
of about 2 orders of magnitudes: this is a consequence of our
method (see Sect. 3.2), that held the spiral magnitudes within the interval
-23<Mr<-18 which corresponds to a factor of
for the brightest spirals. Each type of spiral has a luminosity range
of about 2 orders of magnitudes: this is a consequence of our
method (see Sect. 3.2), that held the spiral magnitudes within the interval
-23<Mr<-18 which corresponds to a factor of
![]() in luminosity with the only possible modification introduced by the
redshift evolution. Anyway, we don't expect this limitation to affect
significantly our results. In fact, this limit range is wider than
the one covered by the distribution of the BCGs, which are the only
galaxies for which we have direct observational constraints. On the
contrary the E/S0 curve appears narrower because we considered the
average luminosity of the E/S0 galaxies inside each cluster, thus
limiting the dispersion of the E/S0 galaxies to the dispersion of
the cluster luminosities.
in luminosity with the only possible modification introduced by the
redshift evolution. Anyway, we don't expect this limitation to affect
significantly our results. In fact, this limit range is wider than
the one covered by the distribution of the BCGs, which are the only
galaxies for which we have direct observational constraints. On the
contrary the E/S0 curve appears narrower because we considered the
average luminosity of the E/S0 galaxies inside each cluster, thus
limiting the dispersion of the E/S0 galaxies to the dispersion of
the cluster luminosities.
When considering the luminosity function in the 100 ![]() m IRAS band the range and shape is similar for all the spectral types. Only starbursts are a factor
m IRAS band the range and shape is similar for all the spectral types. Only starbursts are a factor ![]() 3 fainter in this band due to the drop in luminosity (see Fig. 1) which is due to an average higher galactic dust temperature compared to non-starburst.
3 fainter in this band due to the drop in luminosity (see Fig. 1) which is due to an average higher galactic dust temperature compared to non-starburst.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12726fg3.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12726-09/Timg79.png)
|
Figure 3:
Luminosity functions of each spectral type implemented in our model in the IRAS 60 |
| Open with DEXTER | |
4 Other galactic components
In this section we try to put some constraints on the impact of three components of galactic origin which are not included in our modelisation of the IR emission of cluster galaxies: a missed population of faint galaxies, the possible presence of dust-embedded AGNs and the IR emission coming from heavily obscured star-forming galaxies. In all of these cases we conclude that their impact on our final results is probably very small, if not completely negligible.
4.1 Faint galaxy population
As mentioned in Sect. 3, our modelisation includes red galaxies with Mr < -16 (the limit of the SDSS-maxBCG catalogue) and blue galaxies with Mr < -18, thus neglecting the signal of fainter objects, that may not be identified by the SDSS observations although present inside the cluster. We try to obtain a rough estimation of the impact of these objects on the total emission by referring to the luminosity functions obtained by Baldry et al. (2004, see their Fig. 7).
For what concerns early-type galaxies, the faint-end of the LF (
M*=-21.49,
![]() in the Schecter function parameterisation) has a negative slope,
so the number of galaxies is expected to diminish at higher
magnitudes. For this reason no significant impact can be associated to
these objects.
in the Schecter function parameterisation) has a negative slope,
so the number of galaxies is expected to diminish at higher
magnitudes. For this reason no significant impact can be associated to
these objects.
On the other side, the faint-end of the blue galaxies LF (
M*=-20.60,
![]() )
has a positive slope, so an increasing number of galaxies is
expected with lower luminosities. For simplicity, we consider the
assumption that all galaxies with Mr < -18 have been included in our
modelisation, then we integrate the late-type LF
)
has a positive slope, so an increasing number of galaxies is
expected with lower luminosities. For simplicity, we consider the
assumption that all galaxies with Mr < -18 have been included in our
modelisation, then we integrate the late-type LF
![]() of Baldry et al. (2004) splitting it in two at this magnitude limit. We obtain
of Baldry et al. (2004) splitting it in two at this magnitude limit. We obtain
where L(Mr) is the luminosity as a function of the magnitude Mr, thus indicating that the emission of the faint galaxy population is marginal with respect to the bright one.
Moreover, since the LF of Baldry et al. (2004) is obtained with the observation of field galaxies, it is reasonable to expect that in cluster environments the faint-end of the LF would be shallower, if not even negative, due to the processes of merging that affect particularly the smaller objects. Therefore the ratio of 0.13 obtained in Eq. (10) can be safely considered an upper limit of the true value. For these reasons, and considering the assumption of the connection between the luminosity in the optical and IR bands used throughout this work, we can conclude that even if we can not exclude the presence of the signal of a population of faint (Mr > -18) unresolved galaxies, we expect that the contribution of faint star-forming galaxies to be marginal.
4.2 Dusty AGNs
When estimating the total IR luminosities of the galaxies of our sample, we do not take into account what could be the contribution of AGN deeply embedded in dusty cocoons within cluster galaxies.
In fact, recent results indicate the existence of a population of heavily absorbed AGNs in the field (see e.g. Lanzuisi et al. 2009; Fiore et al. 2009):
these objects are detectable at IR wavelengths. Although optical
observations indicate a very small fraction of cluster galaxies with
detected AGNs (![]() %, see e.g. Dressler et al. 1999), some X-ray observations have detected an excess
of point sources associated to AGNs in cluster fields. For example, Martini et al. (2006) observed with Chandra a sample of 8 low redshift (
%, see e.g. Dressler et al. 1999), some X-ray observations have detected an excess
of point sources associated to AGNs in cluster fields. For example, Martini et al. (2006) observed with Chandra a sample of 8 low redshift (![]() )
clusters, finding
)
clusters, finding ![]() 5%
of their galaxy members hosting an AGN, most of which are not detected
with optical surveys. These AGNs are also present in
E/S0 galaxies, and whilst they are obscured in the optical (their
emission being heavily
absorbed), they could be bright in the IR. Therefore, they could
contribute to the total IR cluster emission.
5%
of their galaxy members hosting an AGN, most of which are not detected
with optical surveys. These AGNs are also present in
E/S0 galaxies, and whilst they are obscured in the optical (their
emission being heavily
absorbed), they could be bright in the IR. Therefore, they could
contribute to the total IR cluster emission.
It is difficult to quantify with precision the impact on the total IR signal of these kinds of objects. We take as a reference the work done by Bai et al. (2007), who studied the IR properties of the galaxies of MS 1054-03 (z=0.83) with the Spitzer satellite. They identified eight point sources with X-ray and radio observations that could be associated with AGNs: anyway, only three of these objects have an IR counterpart over the 144 IR-detected cluster members, and only one of these is associated with a bright star-forming object. For these reasons the authors conclude that the contamination from AGNs is negligible. Similar conclusions have been drawn by Bai et al. (2006) in their study of the Coma cluster (z=0.023).
Even if they are based on single cluster studies, these results, which have been obtained both at redshift higher and lower than our cluster sample, indicate that the impact of AGN contamination in the observations of Giard et al. (2008) is probably very small.
4.3 Heavily obscured star-forming galaxies
Optical observations have highlighted the fact that some galaxy clusters host heavily obscured star-forming galaxies. In the framework of our modelisation, the presence of these objects would lead to an underestimate of their IR emission based on the optical one (see Metcalfe et al. 2005, for a review). In particular, IR observations on A1689 (Duc et al. 2002), J1888.16CL (Duc et al. 2004), CL0024+1654 (Coia et al. 2005) and, more recently, on A1758 (Haines et al. 2009) have revealed galaxies with much higher SFRs with respect to what is expected from optical diagnostics (e.g. [O II]). However, all of these clusters show clear signs of recent dynamical activities, like major mergers and significant accretion of galaxies from the field, thus suggesting that these phenomena are responsible of the star-formation triggering. Since our cluster sample is at a relatively low redshift, we do not expect it to contain a high fraction of dynamically active haloes and, therefore, to be significantly affected by the presence of heavily obscured star-formation.
5 Reconstructing the stacked IR flux
As mentioned before the main objective of this work is to explain
the origin of the IR emission observed in the direction of galaxy
clusters by Montier & Giard (2005) and Giard et al. (2008). Therefore,
we want to compare the flux expected out of our model from the galactic emission in the 60 ![]() m and 100
m and 100 ![]() m IRAS bands with the one measured by Giard et al. (2008).
In order to do so, we need to compute for every single cluster the
expected flux taking into account the instrumental beam and the
spectral band pass of the IRAS satellite.
m IRAS bands with the one measured by Giard et al. (2008).
In order to do so, we need to compute for every single cluster the
expected flux taking into account the instrumental beam and the
spectral band pass of the IRAS satellite.
We assume that every galaxy is placed at the redshift z of the cluster to which it belongs and we compute its flux
![]()
![]() in a given band
in a given band

|
(11) |
where
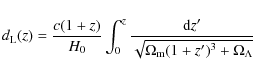
|
(12) |
is the luminosity distance of the cluster (H0
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{12726fg4.ps}\vspace{-2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa12726-09/Timg95.png)
|
Figure 4: Distribution of the angular sizes of R200 for the cluster sample in 4 redshift intervals chosen in order to contain the same number of clusters (i.e. 1869). The bin size of each histogram is 0.5 arcmin. |
| Open with DEXTER | |
The stacked signals by Giard et al. (2008) are integrated fluxes over an angular area of 10' of radius centered on the cluster (see Sect. 2 for details). Since the IRAS FWHM beams are 4' and 4.5' at 60 and 100 ![]() m
respectively, thus comparable to the size of the observed field, we
need to take into account the possible loss of signal from galaxies
distant from the cluster center due to the convolution with the
instrumental beam. In order to model this effect, we
have to distribute the cluster galaxies in the cluster potential well.
We thus randomly assign to every galaxy a distance from the BCG
(considered to be at the cluster center, thus at the center of the
10' field) by assuming that their spatial distribution follows
a NFW profile (Navarro et al. 1997). The two parameters needed to characterise the NFW profile are R200 and the concentration c. They were obtained from the richness
m
respectively, thus comparable to the size of the observed field, we
need to take into account the possible loss of signal from galaxies
distant from the cluster center due to the convolution with the
instrumental beam. In order to model this effect, we
have to distribute the cluster galaxies in the cluster potential well.
We thus randomly assign to every galaxy a distance from the BCG
(considered to be at the cluster center, thus at the center of the
10' field) by assuming that their spatial distribution follows
a NFW profile (Navarro et al. 1997). The two parameters needed to characterise the NFW profile are R200 and the concentration c. They were obtained from the richness
![]() of each halo (see Sect. 2.1) and by adopting the N - M scaling relation of Rykoff et al. (2008) derived from the SDSS-maxBCG, and the (M,z)-c relation of Dolag et al. (2004)
derived from numerical simulations. Then for every galaxy we compute
the fraction of the signal that falls inside the observed region in the
two bands. This effect proves to be completely negligible as globally
less than one per cent of the signal falls outside the field in both
bands. Since galaxies of later spectral types are expected to be more
spread than ellipticals, as a result of their recent accretion into the
cluster (see, e.g., the discussion in Popesso et al. 2005), we repeated our estimation on the possible lost signal by assuming that late-type galaxies are distributed
uniformly in a sphere of radius R200:
even with this extreme hypothesis the amount of signal that is expected
to fall outside the field remains negligible (about 3% of the
total). The low impact of this effect on the global results can also be
seen from the distributions of the angular sizes of R200 obtained with this method shown in Fig. 4
for different redshift bins. More than 70% of the clusters have
angular sizes lower than 5' and only in the lowest redshift bin
some objects (43) exceed the 10' aperture.
of each halo (see Sect. 2.1) and by adopting the N - M scaling relation of Rykoff et al. (2008) derived from the SDSS-maxBCG, and the (M,z)-c relation of Dolag et al. (2004)
derived from numerical simulations. Then for every galaxy we compute
the fraction of the signal that falls inside the observed region in the
two bands. This effect proves to be completely negligible as globally
less than one per cent of the signal falls outside the field in both
bands. Since galaxies of later spectral types are expected to be more
spread than ellipticals, as a result of their recent accretion into the
cluster (see, e.g., the discussion in Popesso et al. 2005), we repeated our estimation on the possible lost signal by assuming that late-type galaxies are distributed
uniformly in a sphere of radius R200:
even with this extreme hypothesis the amount of signal that is expected
to fall outside the field remains negligible (about 3% of the
total). The low impact of this effect on the global results can also be
seen from the distributions of the angular sizes of R200 obtained with this method shown in Fig. 4
for different redshift bins. More than 70% of the clusters have
angular sizes lower than 5' and only in the lowest redshift bin
some objects (43) exceed the 10' aperture.
With the stacking technique adopted by Giard et al. (2008), it is clear that also the signal coming from foreground/background objects is present in the observed fields. Anyway, as said in Sect. 2, the authors adopted a background subtraction based on the signal in the fields adjacent to every map, relying on the high statistical robustness of their sample. For this reason we can safely conclude that the emission of foreground/background objects has been successfully subtracted, thus we do not need to include it in our modelisation.
6 Results and discussion
6.1 Predicted and observed IR fluxes
Our estimations of the 60 and 100 ![]() m fluxes from cluster galaxies are reported in Table 2, associated to the emission calculated with our model for the different galaxy populations.
m fluxes from cluster galaxies are reported in Table 2, associated to the emission calculated with our model for the different galaxy populations.
Table 2:
Estimated fluxes in the 60 ![]() m and 100
m and 100 ![]() m IRAS bands from the galaxy population of the SDSS-maxBCG clusters.
m IRAS bands from the galaxy population of the SDSS-maxBCG clusters.
The total flux due to the early-type galaxies estimated with our model is 39.3 Jy at 60 ![]() m band and 79.4 Jy in the 100
m band and 79.4 Jy in the 100 ![]() m band, accounting for about 7% of and 6%, respectively, of the fluxes measured in the same bands by Giard et al. (2008). In both bands about 20% of the E/S0 signal comes from the BCGs.
m band, accounting for about 7% of and 6%, respectively, of the fluxes measured in the same bands by Giard et al. (2008). In both bands about 20% of the E/S0 signal comes from the BCGs.
As expected, late-type galaxies constitute by far the most significant
contribution to the IR emission. According to our reference model
they contribute to 645.2 Jy at 60 ![]() m and
1904.8 Jy at 100
m and
1904.8 Jy at 100 ![]() m
thus accounting for about 95% of the total galactic emission. This
contribution comes mostly from the Sb and Sc population, with the
Sc being widely dominant in the 100
m
thus accounting for about 95% of the total galactic emission. This
contribution comes mostly from the Sb and Sc population, with the
Sc being widely dominant in the 100 ![]() m band.
m band.
Despite their high luminosities, we predict that starburst galaxies do
not provide a significant contribution to the IR emission, due to
their low expected number. We obtain a contribution of
15.4 Jy at 60 ![]() m and 12.1 Jy at 100
m and 12.1 Jy at 100 ![]() m
corresponding respectively to about 2% and 0.5% of total
predicted signal. Only in our extreme scenario their contribution
becomes non-negligible in the 60
m
corresponding respectively to about 2% and 0.5% of total
predicted signal. Only in our extreme scenario their contribution
becomes non-negligible in the 60 ![]() m
band, reaching the 5% of the total predicted flux. This low
contribution agrees with the low rate of starburst galaxies as found in
the field by Le Floc'h et al. (2005) at the redshift range of the SDSS-maxBCG catalogue (i.e. 0.1<z<0.3).
m
band, reaching the 5% of the total predicted flux. This low
contribution agrees with the low rate of starburst galaxies as found in
the field by Le Floc'h et al. (2005) at the redshift range of the SDSS-maxBCG catalogue (i.e. 0.1<z<0.3).
The total fluxes associated to the galactic emission predicted by our reference model are
![]() Jy at 60
Jy at 60 ![]() m and
m and
![]() Jy at 100
Jy at 100 ![]() m (the bracketed interval indicate the values derived from our conservative and extreme models, see Sect. 3.4).
It appears that the reconstructed IR emission due to the
galactic dust emission of the cluster members can explain the entire
signal measured by Giard et al. (2008), with an
indication that our reference model overestimates the total flux, particularly at 100
m (the bracketed interval indicate the values derived from our conservative and extreme models, see Sect. 3.4).
It appears that the reconstructed IR emission due to the
galactic dust emission of the cluster members can explain the entire
signal measured by Giard et al. (2008), with an
indication that our reference model overestimates the total flux, particularly at 100 ![]() m. Indeed, these authors obtained 570.1
m. Indeed, these authors obtained 570.1 ![]() 36.1 Jy and 1359.9
36.1 Jy and 1359.9 ![]() 249.1 Jy at 60
249.1 Jy at 60 ![]() m and 100
m and 100 ![]() m,
respectively. We will propose an explanation of this discrepancy in the
next sections. However, when considering our conservative scenario, the
predicted emission is in good agreement with the total measured signal
in both bands.
m,
respectively. We will propose an explanation of this discrepancy in the
next sections. However, when considering our conservative scenario, the
predicted emission is in good agreement with the total measured signal
in both bands.
Given these results, modulo the uncertainties of our modelisation, we obtain that the IR emission of the galaxy members is consistent with the total observed emission of our clusters sample, leaving little space to the possible presence of other components like intracluster dust.
6.2 Redshift evolution
In this section we characterise the redshift evolution of the average clusters luminosity. Following Desert et al. (1990), we define the total luminosity in the 60 and 100 ![]() m IRAS bands as
m IRAS bands as
where
We show in Fig. 5 the average luminosity as obtained from Eq. (13) for the clusters at different redshifts, both as predicted by our model and as observed by Giard et al. (2008).
Our 4 bins are defined in order to contain the same number of
clusters (i.e. 1869).
This analysis shows clearly that the discrepancy between our reference
model with respect to the observed fluxes is due to the low-redshift
clusters only, which are responsible for most of the predicted flux.
In fact, while our reference model is compatible within ![]() with the results of Giard et al. (2008) in the 3 high-redshift bins, in the first bin (
0.10<z<0.17) the predicted
luminosity is higher at
with the results of Giard et al. (2008) in the 3 high-redshift bins, in the first bin (
0.10<z<0.17) the predicted
luminosity is higher at ![]() confidence. Our conservative scenario is also compatible with observed luminosities at z>0.17, while the discrepancy for the low-redshift clusters persists at
more than
confidence. Our conservative scenario is also compatible with observed luminosities at z>0.17, while the discrepancy for the low-redshift clusters persists at
more than ![]() .
On the contrary, our extreme model is excluded by the results of Giard et al. (2008) through all the redshift range.
.
On the contrary, our extreme model is excluded by the results of Giard et al. (2008) through all the redshift range.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12726fg5.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12726-09/Timg105.png)
|
Figure 5:
Average cluster luminosities (see Eq. (13)) as a function of redshift. Diamonds represent the measurements and associated |
| Open with DEXTER | |
6.3 Selection bias
Our results indicate that although our model well describes the global
IR emission of the SDSS-maxBCG galaxy clusters at
![]() ,
the predicted galactic emission at low redshift clearly exceeds the
measured stacked signal. The strong decrease in the IR luminosity
is present also in the NED and NSC clusters samples analysed by Giard et al. (2008)
and, as discussed in their work, it can be interpreted as a
selection effect which biases towards rich and massive clusters at high
redshift as it is evident for the NSC sample (see their
Fig. 6). However, this is not the case for the clusters object of our analysis. In Fig. 6 we show the average cluster richness in the same redshift bins both for the values of
,
the predicted galactic emission at low redshift clearly exceeds the
measured stacked signal. The strong decrease in the IR luminosity
is present also in the NED and NSC clusters samples analysed by Giard et al. (2008)
and, as discussed in their work, it can be interpreted as a
selection effect which biases towards rich and massive clusters at high
redshift as it is evident for the NSC sample (see their
Fig. 6). However, this is not the case for the clusters object of our analysis. In Fig. 6 we show the average cluster richness in the same redshift bins both for the values of
![]() ,
directly obtained from the SDSS-maxBCG catalogue, and N200 which includes late-type galaxies, as described in Sect. 3.2.
It is clear that no selection bias is present in our clusters
sample: on the contrary low-redshift clusters show slightly higher
values of
,
directly obtained from the SDSS-maxBCG catalogue, and N200 which includes late-type galaxies, as described in Sect. 3.2.
It is clear that no selection bias is present in our clusters
sample: on the contrary low-redshift clusters show slightly higher
values of
![]() .
Even when including late-type galaxies this trend does not change significantly.
.
Even when including late-type galaxies this trend does not change significantly.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12726fg6.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12726-09/Timg107.png)
|
Figure 6:
Average richness as a function of redshift. Diamonds represent the average values of
|
| Open with DEXTER | |
6.4 Effect of the cluster environment
These considerations indicate that the discrepancy between our model
and the decrease of luminosity towards lower redshift must be connected
with an evolution of the galaxy IR luminosity driven by the
cluster environment, associated to gas and/or dust removal and
consequent star-formation quenching. This can happen via ram-pressure
stripping and tidal interaction. This picture is in agreement with the
low number of high IR-to-optical galaxies observed in local galaxy
clusters (see, e.g., Bicay & Giovanelli 1987). A similar phenomenon is also seen in the observed properties of the galaxies of the Virgo cluster. In fact, Boselli et al. (2006) observed a truncation in the disk of NGC 4569 both in the UV and in the IR (8-70 ![]() m) that they associate to a ram-pressure stripping of the external regions. More in general, Gavazzi et al. (2006) observe a consistent
m) that they associate to a ram-pressure stripping of the external regions. More in general, Gavazzi et al. (2006) observe a consistent
![]() deficiency in Virgo galaxies which indicates a low SFR and diminished dust heating/emission (see also the
discussion in Boselli & Gavazzi 2006).
In this scenario, once the star-formation quenching happens, the
SEDs of the galaxy members would be consistently modified at the IR and
UV wavelengths, being not compatible anymore with field galaxies,
thus explaining the excess predicted by our model. However, we must
point out that the environmental effects on the Virgo cluster are
likely to be much stronger than what is expected for the population of
clusters considered in our analysis. In fact, the
Virgo cluster is about one order of magnitude more massive than
the majority of the SDSS-maxBCG galaxy clusters and it shows
several evidences of recent dynamical activity. On the contrary, being
the SDSS-maxBCG cluster sample mainly constituted by small haloes
(see Sect. 2.1),
in the context of the hierarchical structure formation scenario it
is reasonable to expect that they correspond to relaxed and dynamically
old systems (see, for instance, the results on the concentration-mass
relation of Buote et al. 2007; Dolag et al. 2004).
deficiency in Virgo galaxies which indicates a low SFR and diminished dust heating/emission (see also the
discussion in Boselli & Gavazzi 2006).
In this scenario, once the star-formation quenching happens, the
SEDs of the galaxy members would be consistently modified at the IR and
UV wavelengths, being not compatible anymore with field galaxies,
thus explaining the excess predicted by our model. However, we must
point out that the environmental effects on the Virgo cluster are
likely to be much stronger than what is expected for the population of
clusters considered in our analysis. In fact, the
Virgo cluster is about one order of magnitude more massive than
the majority of the SDSS-maxBCG galaxy clusters and it shows
several evidences of recent dynamical activity. On the contrary, being
the SDSS-maxBCG cluster sample mainly constituted by small haloes
(see Sect. 2.1),
in the context of the hierarchical structure formation scenario it
is reasonable to expect that they correspond to relaxed and dynamically
old systems (see, for instance, the results on the concentration-mass
relation of Buote et al. 2007; Dolag et al. 2004).
6.5 Constraints on intracluster dust
If we take as a reference our conservative scenario and compare its
results with the average observed luminosity in the three high-redshift
bins, we can estimate an upper limit on the possible emission due to
extragalactic dust of about 10% of the total luminosity, which
translates into a dust-to-gas mass abundance of
![]()
![]() 10-5 (see the discussion in Giard et al. 2008). This figure is in agreement with the expectations from theoretical models (Popescu et al. 2000; Aguirre et al. 2001) and with current observational upper limits on the dust abundance.
Chelouche et al. (2007) analysed the
reddening of a sample of quasars in the direction of the clusters of
the SDSS-maxBCG catalogue, obtaining an estimate of
10-5 (see the discussion in Giard et al. 2008). This figure is in agreement with the expectations from theoretical models (Popescu et al. 2000; Aguirre et al. 2001) and with current observational upper limits on the dust abundance.
Chelouche et al. (2007) analysed the
reddening of a sample of quasars in the direction of the clusters of
the SDSS-maxBCG catalogue, obtaining an estimate of
![]() .
A similar result has also been obtained by Bovy et al. (2008) by measuring the dust absorption on the spectra of galaxies located behind local (
.
A similar result has also been obtained by Bovy et al. (2008) by measuring the dust absorption on the spectra of galaxies located behind local (
![]() )
galaxy clusters.
)
galaxy clusters.
If on one side we do not see an evidence of intracluster dust emission in our sample, these last considerations leave an open question of how much dust has been lost by cluster galaxies polluting the ICM and if it can live enough to produce a significant diffuse IR emission. According to Popescu et al. (2000), the dust stripped from infalling galaxies will probably remain localised close to their parent galaxies without diffusing efficiently into the ICM. In any case, the strong decrease in the total cluster luminosity observed by Giard et al. (2008) compared to our results, suggests that, if present, the signal of intracluster dust should be very small.
7 Summary and conclusions
In this work we performed, for the first time, a thorough
modelisation of the overall IR emission of galaxy clusters due to
cluster galaxies IR emission. We tested the results of our model
against the statistical stacking measurements of clusters
IR emission in the 60 and 100 ![]() m IRAS bands by Giard et al. (2008), making use of the SDSS-maxBCG catalogue of groups and clusters (Koester et al. 2007).
m IRAS bands by Giard et al. (2008), making use of the SDSS-maxBCG catalogue of groups and clusters (Koester et al. 2007).
We used the available SDSS-maxBCG data on the luminosity in the r-band of the cluster early-type members, and converted them into IR luminosities by adopting the model templates of the GRASIL code (Silva et al. 1998). Since the SDSS-maxBCG catalogue does not contain information on the late-type galaxies component, we used the results on the morphology-density relation obtained by Balogh et al. (2004) on a local SDSS galaxy sample to construct a model to statistically associate to every cluster its spiral galaxy population, namely the number of spiral members, their spectral type and their Mr. Again, this information on the optical properties has been used to obtain the corresponding IR emission by making use of 4 other GRASIL templates to represent normal late-type (Sa, Sb and Sc) and starburst galaxies. We also included in our model the expected redshift evolution of the spiral fraction and the IR luminosity by using results on observed galaxies in order to account for the possible difference in the spiral galaxy population of the SDSS-maxBCG catalogue (0.1<z<0.3) and the more local objects of the Balogh et al. (2004) sample (z<0.08).
Finally, we used our predictions to calculate the total expected galactic flux, by considering also the possible loss of signal due to the IRAS beam smoothing and the IRAS response function, and compared it with the measurements of Giard et al. (2008).
Our main results can be summarized as follows.
- i)
- According to our model, late-type galaxies represent about
 % of the galaxy population in nearby groups and clusters (i.e. z<0.3). This figure is coherent with the fact that this sample is dominated by groups and small clusters (
% of the galaxy population in nearby groups and clusters (i.e. z<0.3). This figure is coherent with the fact that this sample is dominated by groups and small clusters (
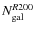 = 10-20), thus letting this fraction of late-types falling between the field (
= 10-20), thus letting this fraction of late-types falling between the field (
 )
and the rich cluster (
)
and the rich cluster (
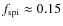 ) regime.
) regime.
- ii)
- As expected, normal late-type galaxies constitute the most
important contribution to the total IR luminosity at 60 and
100
 m accounting for
m accounting for 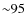 % of the total galactic emission. Oppositely, the impact of starburst galaxies is marginal.
% of the total galactic emission. Oppositely, the impact of starburst galaxies is marginal.
- iii)
- Early-type galaxies dominate the faint end of the LF in the IR and they account for the remaining
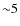 % of the galactic contribution of the cluster IR emission.
% of the galactic contribution of the cluster IR emission.
- iv)
- Our model shows that the total flux estimated from the galaxy
accounts, within uncertainties, for the entire stacked signal measured
by Giard et al. (2008). With our reference model we obtain 684.5 Jy at 60
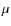 m and 1904.8 Jy at 100
m and 1904.8 Jy at 100 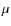 m, which exceeds the stacked fluxes measured by Giard et al. (2008).
However, when considering the uncertainties in our parameters, we
showed that in a conservative scenario this discrepancy disappears.
m, which exceeds the stacked fluxes measured by Giard et al. (2008).
However, when considering the uncertainties in our parameters, we
showed that in a conservative scenario this discrepancy disappears.
- v)
- We compared the redshift distribution of the IR emission predicted by our model to the measurements of Giard et al. (2008) and found that the excess flux is present only in the clusters at lower redshift (
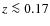 ).
).
The lack of diffuse dust, however, does not mean that the environment
is not influencing the IR properties of its galaxy members. The
fact that the predicted excess emission is concentrated in the lowest
redshift objects indicates that the IR emission of late-type
galaxies in local clusters is not completely compatible with their
field equivalents. This result is in agreement with the lack of bright
IR galaxies observed in several local clusters (see Boselli & Gavazzi 2006,
and references therein) and it is likely connected to the quenching of
the star-forming activity driven by the cluster environment on its
galaxy members, due to gas or dust removal: in this last case, the
dust injected in the ICM is probably quickly depleted via sputtering
processes. However, it is not clear why this could act
significantly only at ![]() when most of the large-scale structures are already formed. For this
reason, and given the limited redshift range of the
SDSS-maxBCG catalogue, it would be interesting to extend our
analysis to higher redshifts, where the SFR is expected to be higher
and more dynamical activity is expected at cluster scales.
when most of the large-scale structures are already formed. For this
reason, and given the limited redshift range of the
SDSS-maxBCG catalogue, it would be interesting to extend our
analysis to higher redshifts, where the SFR is expected to be higher
and more dynamical activity is expected at cluster scales.
We thank an anonymous referee who helped improving the presentation of our results. We are grateful to L. Silva for publishing some GRASIL templates in her webpage. We thank M. Balogh and T. F. Laganá for providing some additional data not published in their papers. We acknowledge useful discussions with S. Bardelli, J.-P. Bernard, A. Boselli, J. Lanoux, L. Pozzetti, F. Pozzi and C. Tonini. We are particularly grateful to A. Bongiorno for the help provided in the treatment of optical data. The authors L. Montier, E. Pointecouteau and M. Roncarelli acknowledge the support of grant ANR-06-JCJC-0141.
References
- Abell, G. O., Corwin, Jr., H. G., & Olowin, R. P. 1989, ApJS, 70, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguirre, A., & Schaye, J. 2007, in EAS Publ. Ser. 24, ed. E. Emsellem, H. Wozniak, G. Massacrier, J.-F. Gonzalez, J. Devriendt, & N. Champavert, 165 [Google Scholar]
- Aguirre, A., Hernquist, L., Schaye, J., et al. 2001, ApJ, 561, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M. 2004, in Baryons in Dark Matter Halos, ed. R. Dettmar, U. Klein, & P. Salucci [Google Scholar]
- Arnaud, M. 2005, in Background Microwave Radiation and Intracluster Cosmology, ed. F. Melchiorri, & Y. Rephaeli, 77 [Google Scholar]
- Bai, L., Rieke, G. H., Rieke, M. J., et al. 2006, ApJ, 639, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, L., Rieke, G. H., & Rieke, M. J. 2007, ApJ, 668, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Glazebrook, K., Brinkmann, J., et al. 2004, ApJ, 600, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M. L., Baldry, I. K., Nichol, R., et al. 2004, ApJ, 615, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Bicay, M. D., & Giovanelli, R. 1987, ApJ, 321, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A. 2008, Lectures of the International School of Physics Enrico Fermi, Varenna, July 2008 [arXiv:0811.3535] [Google Scholar]
- Blanton, M. R., & Roweis, S. 2007, AJ, 133, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Borgani, S. 2008, in A Pan-Chromatic View of Clusters of Galaxies and the Large-Scale Structure, ed. M. Plionis, O. López-Cruz, & D. Hughes (Berlin: Springer Verlag), Lecture Notes in Physics, 740, 287 [Google Scholar]
- Boselli, A., & Gavazzi, G. 2006, PASP, 118, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Boissier, S., Cortese, L., et al. 2006, ApJ, 651, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Hogg, D. W., & Moustakas, J. 2008, ApJ, 688, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Lucey, J. R., & Ellis, R. S. 1992, MNRAS, 254, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Buote, D. A., Gastaldello, F., Humphrey, P. J., et al. 2007, ApJ, 664, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Butcher, H., & Oemler, Jr., A. 1984, ApJ, 285, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Chelouche, D., Koester, B. P., & Bowen, D. V. 2007, ApJ, 671, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Coia, D., McBreen, B., Metcalfe, L., et al. 2005, A&A, 431, 433 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conroy, C., Wechsler, R. H., & Kravtsov, A. V. 2007, ApJ, 668, 826 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, A. C., Catalano, A., Montier, L., et al. 2009, MNRAS, 396, 849 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Poggianti, B. M., Aragón-Salamanca, A., et al. 2007, MNRAS, 374, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Desert, F.-X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
- Dolag, K., Bartelmann, M., Perrotta, F., et al. 2004, A&A, 416, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dolag, K., Murante, G., & Borgani, S. 2010, MNRAS, in press,[arXiv:0911.1129] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Oemler, A. J., Couch, W. J., et al. 1997, ApJ, 490, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Smail, I., Poggianti, B. M., et al. 1999, ApJS, 122, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Duc, P.-A., Fadda, D., Poggianti, B., et al. 2004, 347 [Google Scholar]
- Duc, P.-A., Poggianti, B. M., Fadda, D., et al. 2002, A&A, 382, 60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Sanders, J. S., Taylor, G. B., et al. 2006, MNRAS, 366, 417 [Google Scholar]
- Fang, W., & Haiman, Z. 2008, ApJ, 680, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Fiore, F., Puccetti, S., Brusa, M., et al. 2009, ApJ, 693, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Shimasaku, K., & Ichikawa, T. 1995, PASP, 107, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Gal, R. R., de Carvalho, R. R., Lopes, P. A. A., et al. 2003, AJ, 125, 2064 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., Boselli, A., Cortese, L., et al. 2006, A&A, 446, 839 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giard, M., Montier, L., Pointecouteau, E., & Simmat, E. 2008, A&A, 490, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haines, C. P., Smith, G. P., Egami, E., et al. 2009, MNRAS, 396, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, S. M., McKay, T. A., Wechsler, R. H., et al. 2005, ApJ, 633, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Kapferer, W., Ferrari, C., Domainko, W., et al. 2006, A&A, 447, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Krick, J. E., & Bernstein, R. A. 2007, AJ, 134, 466 [Google Scholar]
- Lagache, G., Puget, J.-L., & Dole, H. 2005, ARA&A, 43, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Laganá, T. F., Dupke, R. A., Sodré, Jr., L., Lima Neto, G. B., & Durret, F. 2009, MNRAS, 394, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzuisi, G., Piconcelli, E., Fiore, F., et al. 2009, A&A, 498, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Floc'h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A., Allen, S. W., Ebeling, H., & Rapetti, D. 2008, MNRAS, 387, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A., Allen, S. W., Rapetti, D., & Ebeling, H. 2009, MNRAS, submitted, [arXiv:0909.3098] [Google Scholar]
- Martini, P., Kelson, D. D., Kim, E., Mulchaey, J. S., & Athey, A. A. 2006, ApJ, 644, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Metcalfe, L., Fadda, D., & Biviano, A. 2005, Space Sci. Rev., 119, 425 [Google Scholar]
- Montier, L. A., & Giard, M. 2004, A&A, 417, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montier, L. A., & Giard, M. 2005, A&A, 439, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murante, G., Giovalli, M., Gerhard, O., et al. 2007, MNRAS, 377, 2 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- O'Dea, C. P., Baum, S. A., Privon, G., et al. 2008, ApJ, 681, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Pipino, A., Kaviraj, S., Bildfell, C., et al. 2009, MNRAS, 395, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Popescu, C. C., Tuffs, R. J., Fischera, J., & Völk, H. 2000, A&A, 354, 480 [NASA ADS] [Google Scholar]
- Popesso, P., Biviano, A., Böhringer, H., Romaniello, M., & Voges, W. 2005, A&A, 433, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rykoff, E. S., McKay, T. A., Becker, M. R., et al. 2008, ApJ, 675, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1988, X-ray emission from clusters of galaxies (Cambridge: Cambridge University Press), Cambridge Astrophys. Ser. [Google Scholar]
- Schindler, S., & Diaferio, A. 2008, Space Sci. Rev., 134, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Sijacki, D., & Springel, V. 2006, MNRAS, 366, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, L., Granato, G. L., Bressan, A., & Danese, L. 1998, ApJ, 509, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Soifer, B. T., Helou, G., & Werner, M. 2008, ARA&A, 46, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Stickel, M., Lemke, D., Mattila, K., Haikala, L. K., & Haas, M. 1998, A&A, 329, 55 [NASA ADS] [Google Scholar]
- Stickel, M., Klaas, U., Lemke, D., & Mattila, K. 2002, A&A, 383, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W. 1992, The ROSAT all-sky X ray survey, Tech. rep. [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, N., Durret, F., Ohashi, T., Schindler, S., & Wiersma, R. P. C. 2008, Space Sci. Rev., 134, 337 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... catalogues
![[*]](/icons/foot_motif.png)
- The list was build making use of the SIMBAD database, operated at CDS, Strasbourg, France (http://simbad.u-strasbg.fr/simbad/) and NASA/IPAC Extragalactic Database (NED), operated by the JPL/Caltech (http://nedwww.ipac.caltech.edu), among which the ABELL catalogue (Abell et al. 1989) and the ``Northern Sky Optical Cluster Survey'' (NSC, Gal et al. 2003).
- ... system
![[*]](/icons/foot_motif.png)
- Referring to their Table 3, they obtain u-r colors of 2.26 for Sab and 1.68 for Sbc, thus close to our assumptions for the Sa/Sb and Sb/Sc limits, respectively.
- ...
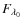
![[*]](/icons/foot_motif.png)
- This quantity corresponds to a flux per unit frequency
(e.g. Jy). Anyway we prefer to use the notation
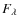 ,
rather than
,
rather than 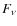 ,
to refer directly to the fluxes F60
and F100 in
the 60 and 100
,
to refer directly to the fluxes F60
and F100 in
the 60 and 100 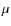 m bands, respectively.
m bands, respectively.
- ... convolved
![[*]](/icons/foot_motif.png)
- For these calculations we used the tools of the DUSTEM code, an updated version of the emission model of Desert et al. (1990), which contains details on the IRAS response functions in the different bands.
All Tables
Table 1: Reference spectral types and galactic population models used in this work.
Table 2:
Estimated fluxes in the 60 ![]() m and 100
m and 100 ![]() m IRAS bands from the galaxy population of the SDSS-maxBCG clusters.
m IRAS bands from the galaxy population of the SDSS-maxBCG clusters.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12726fg1.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12726-09/Timg22.png)
|
Figure 1:
SEDs as a function of wavelength for the 5 GRASIL (Silva et al. 1998)
templates used in this work. The red line shows our reference model for
E/S0 galaxies, the three blue lines represent normal spiral
galaxies Sa, Sb, Sc (light blue, average, dark blue, respectively)
and the green line represents our starburst galaxy model, corresponding
to M 82. All of the templates have been arbitrarily normalized to
the same integrated luminosity of 1030 erg s-1 in the band 8-1000 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12726fg2.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12726-09/Timg52.png)
|
Figure 2:
Fraction of spiral galaxies within R200 (see Sect. 2.1 for the definition of R200) as a function of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12726fg3.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12726-09/Timg79.png)
|
Figure 3:
Luminosity functions of each spectral type implemented in our model in the IRAS 60 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{12726fg4.ps}\vspace{-2mm}
\end{figure}](/articles/aa/full_html/2010/04/aa12726-09/Timg95.png)
|
Figure 4: Distribution of the angular sizes of R200 for the cluster sample in 4 redshift intervals chosen in order to contain the same number of clusters (i.e. 1869). The bin size of each histogram is 0.5 arcmin. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12726fg5.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12726-09/Timg105.png)
|
Figure 5:
Average cluster luminosities (see Eq. (13)) as a function of redshift. Diamonds represent the measurements and associated |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12726fg6.ps}
\end{figure}](/articles/aa/full_html/2010/04/aa12726-09/Timg107.png)
|
Figure 6:
Average richness as a function of redshift. Diamonds represent the average values of
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



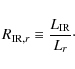
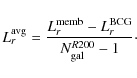
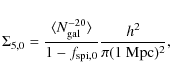
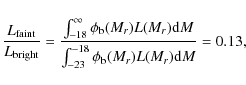
![\begin{displaymath}%
L_{60+100} \equiv 4 \pi d_{\rm L}^2 \times \left[ \lambda \...
...Delta \nu}{\Delta \lambda} F_\lambda(100~\mu {\rm m}) \right],
\end{displaymath}](/articles/aa/full_html/2010/04/aa12726-09/img100.png)