| Issue |
A&A
Volume 512, March-April 2010
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 22 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200809900 | |
| Published online | 07 April 2010 | |
Heavy coronal ions in the heliosphere
I. Global distribution of charge-states of C, N, O, Mg, Si, and S![[*]](/icons/foot_motif.png)
S. Grzedzielski1 - M. E. Wachowicz1 - M. Bzowski1 - V. Izmodenov2
1 - Space Research Centre, Polish Academy of Sciences, Bartycka 18A, 00-716 Warsaw, Poland
2 - Lomonosov Moscow State University, Department of Mechanics and
Mathematics & Space Research Institute (IKI) Russian Academy of
Sciences, Moscow, Russia
Received 3 April 2008 / Accepted 2 December 2009
Abstract
Aims. Our aim is to investigate and study the de-charging of
the elements C, N, O, Mg, Si and S-ions, and assess the fluxes of
the resulting ENA in the heliosphere.
Methods. The model treats the heavy ions as test particles
convected by (and in a particular case also diffusing through) a
hydrodynamically calculated background plasma flow from 1 AU to
the termination shock (TS), the heliosheath (HS) and finally the
heliospheric tail (HT). The ions undergo radiative and dielectronic
recombinations, charge exchanges, photo- and electron impact
ionizations with plasma particles, interstellar neutral atoms
(calculated in a Monte-Carlo model) and solar photons.
Results. Highly-charged heavy coronal ions flowing with the
solar wind undergo successive de-ionizations, mainly in the
heliosheath, which leads to charge-states much lower than in the
supersonic solar wind. If Coulomb scattering is the main ion
energy-loss mechanism, the end product of these deionizations are
fluxes of ENA of ![]() 1 keV/nucleon
originating in the upwind heliosheath that for C, Mg, Si and S may
constitute sources of pickup ions (PUI), significantly exceeding the
interstellar supply.
1 keV/nucleon
originating in the upwind heliosheath that for C, Mg, Si and S may
constitute sources of pickup ions (PUI), significantly exceeding the
interstellar supply.
Conclusions. Discussed processes result in (i) distinct difference of the ion charge q in the supersonic solar wind (approximately
![]() ,
Z = atomic number) compared to that in the HS (approximately
,
Z = atomic number) compared to that in the HS (approximately
![]() ); (ii) probable concentration of singly ionized atoms (q
= +1) in the heliosheath towards the heliopause (HP) and in the HT;
(iii) possible significant production of ENA in the HS offering natural
explanation for production of PUI, and - after acceleration at the TS -
anomalous cosmic rays (ACR) of species (like C, Mg, Si, S) unable to
enter the heliospheric cavity from outside because of their total
ionization in the local interstellar medium.
); (ii) probable concentration of singly ionized atoms (q
= +1) in the heliosheath towards the heliopause (HP) and in the HT;
(iii) possible significant production of ENA in the HS offering natural
explanation for production of PUI, and - after acceleration at the TS -
anomalous cosmic rays (ACR) of species (like C, Mg, Si, S) unable to
enter the heliospheric cavity from outside because of their total
ionization in the local interstellar medium.
Key words: Sun: abundances - solar wind - interplanetary medium - ISM: abundances - cosmic rays - atomic processes
1 Introduction
The ions of C, N, O, Mg, Si and S leave the Sun multiply ionized; typically more than 99% of them have charge-states q > +4 (von Steiger et al. 2000; Gloeckler et al. 1998), resulting from very high ionization rates in the corona. These q-values are usually taken as ``frozen'' over the solar wind ride through the inner heliosphere. However, freezing must evidently fail in the case of long residence times, i.e. for ions in the heliosheath (HS) and heliospheric tail (HT), the regions that constitute the main reservoir of heavy ions in the heliosphere.In the present paper (Paper I) we examine the situation in detail
by developing a global model of the time evolution of charge-states
of C, N, O, Mg, Si and S ions as the solar plasma flows from the
corona to the termination shock (TS), the HS, and finally the HT. We
show that when successive solar wind plasma elements fill out the
heliosheath, the ions undergo - mostly by electron capture from neutral
interstellar H and He atoms - a significant reshuffling of
charge-states, while possibly retaining their initial energies of ![]() 1 keV/n.
This leads to a number of as yet unexplored consequences, like distinct
differences in prevailing ionic charge-states between the supersonic
solar wind and the heliosheath (Sect. 3.1, Table 2),
dependence of spatial distribution of charge-states on the rate of
thermalization of heavy ions in heliosheath plasmas (Sect. 3.2),
concentration of singly ionized atoms towards the heliopause
(Sect. 3.1, Fig. 2), and probable production in this layer of significant fluxes of ENA of
1 keV/n.
This leads to a number of as yet unexplored consequences, like distinct
differences in prevailing ionic charge-states between the supersonic
solar wind and the heliosheath (Sect. 3.1, Table 2),
dependence of spatial distribution of charge-states on the rate of
thermalization of heavy ions in heliosheath plasmas (Sect. 3.2),
concentration of singly ionized atoms towards the heliopause
(Sect. 3.1, Fig. 2), and probable production in this layer of significant fluxes of ENA of ![]() 1 keV/nucleon
(Sect. 5, Fig. 5).
1 keV/nucleon
(Sect. 5, Fig. 5).
An interesting paper addressing related issues was recently published by Koutroumpa et al. (2007). In this paper expected charge-exchange induced soft X-ray and EUV emissions of the solar wind heavy ions were examined, taking into account detailed space- and time-dependent variability. However, the authors discuss essentially emissions due to ions in charge-states as they emerge from the solar corona (``primary'' ions, as they call them). While being justified in the supersonic solar wind, their approach does not describe the deep ``reworking'' of ion charge-states in the heliosheath, which is the central topic of our paper and which - as we show - bears both on heavy neutral atoms and PUI (pickup ion) populations (and plausibly X- and EUV- emissions).
In a follow-up paper (Paper II) we discuss the consequences of our modeling for heliospheric physics, concerning the experimental/observational detection of the predicted effects in XUV as well as in the form of fluxes of ENA, the possibility of diagnosing the overall structure of the heliosheath, and the question of supplying seed ions (PUI) for the ACR populations of species with low-FIP (First Ionization Potential).
2 The physical model
2.1 Test particle description of heavy ions
We treat heavy ions as test particles carried by the general flow of interplanetary plasma that undergo (binary) interactions with solar wind electrons, protons, with solar ionizing photons and with neutral atoms coming from interstellar space. We take into account radiative and dielectronic recombinations, impact ionizations, photoionizations and charge exchanges. A single interaction is assumed to alter the ionic charge q byTo clarify the details of processes taken into account we give here as an example the expanded form of Eq. (1) written for the doubly-charged ion of carbon (C+2):
In the above equation
Analogous equations were used for all ionic charge-states for all six elements taken into consideration. It should be stressed that in the whole set of type (2) equations a number of numerically unimportant binary processes were omitted, like proton and electron impact ionization, as well as photoionization for charge-states >+2, etc.
2.2 Flow of background plasma and neutral atoms
The background flow of solar plasma and neutral hydrogen atoms in
supersonic solar wind, inner heliosheath and distant heliospheric tail
was calculated based on the time-independent, single-fluid,
non-magnetic, gas-dynamical model for heliospheric proton-electron
plasma coupled by mass, momentum and energy exchange with neutral
interstellar hydrogen atoms as developed by Izmodenov & Alexashov (2003).
In this self-consistent treatment the neutral H distribution was
calculated kinetically (Monte-Carlo approach). The Sun as the source of
solar wind and ionizing photons is assumed to be spherically symmetric,
with the wind speed of 450 km s-1, Mach number 10 and
![]() cm-3 at Earth orbit. At infinity, a uniform interstellar flow of 25 km s-1, with the neutral hydrogen density
cm-3 at Earth orbit. At infinity, a uniform interstellar flow of 25 km s-1, with the neutral hydrogen density
![]() cm-3, proton density
cm-3, proton density
![]() cm-3 (=electron
density) and temperature 6000 K was assumed. To account for the
presence of helium we took a simple model of a uniform He I
substratum with the atom density
cm-3 (=electron
density) and temperature 6000 K was assumed. To account for the
presence of helium we took a simple model of a uniform He I
substratum with the atom density
![]() at./cm3 (Gloeckler et al. 2004), flowing with a velocity of 26.4 km s-1 (Witte 2004).
Therefore our model disregards small scale features like the He I
cavity and helium cone, which are anyway of little consequence for the
situation in the heliosheath.
at./cm3 (Gloeckler et al. 2004), flowing with a velocity of 26.4 km s-1 (Witte 2004).
Therefore our model disregards small scale features like the He I
cavity and helium cone, which are anyway of little consequence for the
situation in the heliosheath.
Because of axial symmetry, all variables depend on the radial distance r from the Sun and the angle ![]() from
the apex direction (i.e. the direction of inflow of the local
interstellar gas in the heliocentric frame). The evolution of spatial
density of all charge-states for a species of atomic number Z was calculated by numerical integration of a set of Z+1
coupled ordinary, linear differential equations of type (1), in
which the dependence of coefficients on the spatial coordinate along
the flowline was given by the solutions of the combined hydrodynamic +
Monte Carlo model mentioned above. The integration was carried along
180 flow lines, corresponding to initial (at Earth orbit) values
of the angle
from
the apex direction (i.e. the direction of inflow of the local
interstellar gas in the heliocentric frame). The evolution of spatial
density of all charge-states for a species of atomic number Z was calculated by numerical integration of a set of Z+1
coupled ordinary, linear differential equations of type (1), in
which the dependence of coefficients on the spatial coordinate along
the flowline was given by the solutions of the combined hydrodynamic +
Monte Carlo model mentioned above. The integration was carried along
180 flow lines, corresponding to initial (at Earth orbit) values
of the angle ![]() counted from the apex direction equal to 1, 2...180
counted from the apex direction equal to 1, 2...180![]() .
Using
.
Using
![]() ,
the time integration can be transformed into a space integration along the curvilinear coordinate s
running along each of the flow lines. Such a procedure was performed
for each of the species separately. In this way a complete spatial
distribution of all
N(Z,A)+i for every considered species could be obtained.
,
the time integration can be transformed into a space integration along the curvilinear coordinate s
running along each of the flow lines. Such a procedure was performed
for each of the species separately. In this way a complete spatial
distribution of all
N(Z,A)+i for every considered species could be obtained.
As long as the solar wind parcel moves supersonically between the Sun
and the termination shock, the heavy ions can be thought to cool
adiabatically like the background plasma and therefore stay in
approximate thermal equilibrium with the local plasma environment. In
this case
![]() for
all interactions with electrons (radiative and dielectronic
recombination, ionizing impacts) and for charge exchange reactions with
protons was calculated assuming particle velocity distributions to be
maxwellians corresponding to local (single-fluid) temperature. For
heavy ion-neutral atom interactions
for
all interactions with electrons (radiative and dielectronic
recombination, ionizing impacts) and for charge exchange reactions with
protons was calculated assuming particle velocity distributions to be
maxwellians corresponding to local (single-fluid) temperature. For
heavy ion-neutral atom interactions
![]() = solar wind bulk speed = 500 km s-1 was taken, as a rough compromise between the slow
(
= solar wind bulk speed = 500 km s-1 was taken, as a rough compromise between the slow
(![]() near equatorial) and fast (
near equatorial) and fast (![]() high latitudes) solar wind streams.
high latitudes) solar wind streams.
Upon crossing the termination shock the proton-electron plasma on a single-fluid model heats up to about ![]() 106 K
. However, there is no reason to assume the same single-fluid
temperature applies to heavy ions. Even for relatively light ions like
protons, about one-fifth of their total population flows downstream at
quasi-perpendicular shocks in the form of a ring distribution in
velocity space that is immediately formed in the shock ramp (Möbius
et al. 2001)
and so is unaffected by particle-wave coupling. Such tendency is even
more plausible for various heavy ions that have no particular reason to
be in resonance with the wave-field excited by the majority proton
population. Rather, the downstream heavy ions may on average
approximately retain their range of upstream kinetic energies (about
0.5-3 keV/n for velocities 300-750 km s-1),
while undergoing pitch-angle scattering/reflection on shock structures
and - for a small fraction - acceleration to energies much higher than
in the upstream (Kucharek et al. 2006; Louarn et al. 2003).
For strong shocks such behavior should lead to the often considered
assumption that the downstream effective temperature of the heavy ions
is proportional to the ion mass. This is suggested by direct
experimental evidence (Berdichevsky et al. 1997)
from the Ulysses data on interplanetary shock crossings, when
downstream of the shock regions, which are characterized by a
quasisteady plasma flux, values of T(4He2+)/T(H+) and T(O6+)/T(H+)
are observed in the range of 4.6 to 10.8 and 19 to 48,
respectively (i.e. heating is even more than mass proportional). A less
clear-cut conclusion was recently drawn from a study of interplanetary
shocks driven by the coronal mass ejections (SWICS spectrometer on the
ACE spacecraft), (Korreck 2005; Korreck et al. 2007). Though heating seems to depend on several parameters like magnetic field angle, Mach number, plasma-
106 K
. However, there is no reason to assume the same single-fluid
temperature applies to heavy ions. Even for relatively light ions like
protons, about one-fifth of their total population flows downstream at
quasi-perpendicular shocks in the form of a ring distribution in
velocity space that is immediately formed in the shock ramp (Möbius
et al. 2001)
and so is unaffected by particle-wave coupling. Such tendency is even
more plausible for various heavy ions that have no particular reason to
be in resonance with the wave-field excited by the majority proton
population. Rather, the downstream heavy ions may on average
approximately retain their range of upstream kinetic energies (about
0.5-3 keV/n for velocities 300-750 km s-1),
while undergoing pitch-angle scattering/reflection on shock structures
and - for a small fraction - acceleration to energies much higher than
in the upstream (Kucharek et al. 2006; Louarn et al. 2003).
For strong shocks such behavior should lead to the often considered
assumption that the downstream effective temperature of the heavy ions
is proportional to the ion mass. This is suggested by direct
experimental evidence (Berdichevsky et al. 1997)
from the Ulysses data on interplanetary shock crossings, when
downstream of the shock regions, which are characterized by a
quasisteady plasma flux, values of T(4He2+)/T(H+) and T(O6+)/T(H+)
are observed in the range of 4.6 to 10.8 and 19 to 48,
respectively (i.e. heating is even more than mass proportional). A less
clear-cut conclusion was recently drawn from a study of interplanetary
shocks driven by the coronal mass ejections (SWICS spectrometer on the
ACE spacecraft), (Korreck 2005; Korreck et al. 2007). Though heating seems to depend on several parameters like magnetic field angle, Mach number, plasma- ![]() and ion mass-to-charge, it appears however to be more efficient for
strong perpendicular shocks (estimates of possible effects resulting
from seemingly much ``milder'' termination shock transitions observed
by the Voyager spacecraft as compared with expectations are presented
in Sect. 6).
and ion mass-to-charge, it appears however to be more efficient for
strong perpendicular shocks (estimates of possible effects resulting
from seemingly much ``milder'' termination shock transitions observed
by the Voyager spacecraft as compared with expectations are presented
in Sect. 6).
2.3 Isotropization versus thermalization
Based on these arguments we explore in the present model two limiting cases of heavy ion behavior in the heliosheath, which depend on the assumed efficiency of coupling to the background plasma:
- (i)
- Isotropization. This is our term for the pitch-angle
scattering of the ions into a velocity shell distribution by
low-frequency electromagnetic waves that are excited by the initial
velocity ring distribution, combined with scattering on a ``soup'' of
coherent structures resulting from the shock transition (Alexandrova
et al. 2004, 2006).
The heavy ions isotropize momentum while preserving energy. Then, on a
Coulomb time scale of energy exchange with background heliosheath
plasma (and aided by inelastic collisions with neutral H), the
heavy ions cool down to the level of the background temperatures.
However, the typical time scale for Coulomb cooling of a
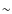 1 keV/n ion on protons is 1011 s for O+8, and longer for lesser charges and higher masses. It is therefore much longer than the upwind heliosheath flow times of
1 keV/n ion on protons is 1011 s for O+8, and longer for lesser charges and higher masses. It is therefore much longer than the upwind heliosheath flow times of
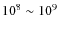 s.
As a consequence, the heliosheath plasma flowing along the flow lines
should carry in its mist a (minor) population of heavy ions endowed
with energies on the order of
s.
As a consequence, the heliosheath plasma flowing along the flow lines
should carry in its mist a (minor) population of heavy ions endowed
with energies on the order of 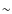 1 keV/n.
These particles undergo, as the most important process, electron
capture collisions with neutral H and He. On top of that the
heavy ions undergo all other mentioned binary processes, with rates
(for electronic processes) corresponding to local ``hot'' maxwellian
velocity distributions as governed by the temperature of the
hydrodynamic single-fluid post-shock solution. We consider
isotropization to be the most probable case for at least the bulk of
the upwind heliosheath. Most of the results presented below pertain to
this situation (cf. Sect. 3.1);
1 keV/n.
These particles undergo, as the most important process, electron
capture collisions with neutral H and He. On top of that the
heavy ions undergo all other mentioned binary processes, with rates
(for electronic processes) corresponding to local ``hot'' maxwellian
velocity distributions as governed by the temperature of the
hydrodynamic single-fluid post-shock solution. We consider
isotropization to be the most probable case for at least the bulk of
the upwind heliosheath. Most of the results presented below pertain to
this situation (cf. Sect. 3.1);
- (ii)
- thermalization. By this we understand the other extreme, in
which upon the TS crossing the heavy ions adjust very quickly (say,
within a time of
 s)
their temperature to the temperature of the background plasma. This
requires a very high rate of energy exchange between the heavy ions and
protons, possibly by heavy ion resonant wave proton interactions. As
the energy density Ww of waves induced by the heavy ions cannot exceed (Winske & Gary 1986)
s)
their temperature to the temperature of the background plasma. This
requires a very high rate of energy exchange between the heavy ions and
protons, possibly by heavy ion resonant wave proton interactions. As
the energy density Ww of waves induced by the heavy ions cannot exceed (Winske & Gary 1986) 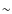 one-half of energy density of the heavy ions themselves
(<0.0005 of the post-shock background energy density Wb), the shortest time
one-half of energy density of the heavy ions themselves
(<0.0005 of the post-shock background energy density Wb), the shortest time 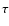 behind the TS would be on the order of (Gary 1991):
behind the TS would be on the order of (Gary 1991):
for the extreme case of a saturated cyclotron turbulence peaked exactly at the gyrofrequencies of the dominant (at TS) O+6 and O+5 ions. In this estimate a post-shock magnetic field of 0.1 nT was assumed (Burlaga et al. 2005). There are no indications that such a turbulence does indeed prevail behind the TS and even if it did, other heavy ions with different mass-to-charge ratios might miss the peak of gyrofrequencies. We thus consider the ``thermalization'' case as rather less likely. However, for comparison and to get a better feeling of the situation calculations of such cases were also performed (cf. Sect. 3.2). The truth, probably, lies somewhere between (i) and (ii), plausibly more close to (i).
2.4 Cross sections and rates for relevant binary processes
To describe the rates of binary processes affecting charge-states of heavy ions we tried to use the most reliable data. In particular radiative recombination rates were taken from Aldrovandi & Pequignot (1973), Verner et al. (1996), Zatsarinny et al. (2003) and the dielectronic recombination rates following Mazzotta et al. (1998), Zatsarinny et al. (2003, 2004). Electron impact ionization rates were taken into account for all charge-states of considered species from the AMDIS data base and the photoionization rates for neutral and singly ionized ions, based on compilations corresponding to average Sun data. A significant effort was made to collect adequate cross sections for heavy ion electron capture from neutral H and He (Stancil et al. 1998, 1999; Kingdon et al. 1996; Lin et al. 2005; Wang et al. 2003).
2.5 Initial values for heavy ion charge-states
Integrations of Eqs. (1) for all six species were performed for various initial values of
N(Z,A)+i based on
in-situ measurements by the instruments MTOF/Celias on SOHO, SWICS on
Ulysses, and SWIMS on ACE (Bochsler et al. 2000; von Steiger et al. 2000; Raines et al. 2005). Values either taken at or reduced to Earth orbit (assuming 1/r2 dependence on heliocentric distance) were used. The presented final results are based on sets of relative initial
N(Z,A)+i values averaged over the solar cycle resulting from the SWICS measurements (Table 1). The abundance data below 10-3 (empty fields in Table 1)
were confronted with independent data gathered in the MTOF/Celias
experiment. In effective calculations the initial ratios of total
number density of ions of a given species to solar wind proton density
were taken from Raines et al. (2005) and
von Steiger et al. (2000; Plate 2). The numerical values are as follows:
O/H ratio =
![]() ,
C/O = 0.67, N/O = 0.077,
Mg/O = 0.145, Si/O = 0.146, S/O = 0.05.
,
C/O = 0.67, N/O = 0.077,
Mg/O = 0.145, Si/O = 0.146, S/O = 0.05.
Table 1: Initial (1 AU) relative abundances of charge-states of heavy ions.
The relative abundances corresponding to experimentally undetectable levels of particular charge-states (empty fields in Table 1) were assumed to be either 10-7 or 10-3. It was verified that results for charge-states that become dominant beyond the TS do not depend on these undetected values. On the whole it was found that results in the distant solar wind and heliosheath are only weakly sensitive to changes in the initial N(Z,A)+i values. The most important physical factor in the whole process turned out to be consecutive deionizations of heavy ions due to electron capture from neutral atoms.
3 Distribution of heavy ion charge-states in the heliosphere
3.1 Case isotropization
The spatial distribution of all charge-states of C , N, O, Mg, Si, and
S ions is constructed out of a grid of 180 solutions of Eq. (1) for each species, corresponding to individual flow lines starting at
![]() as described above. Each solution describes the time evolution (and,
consequently, the spatial variability along the streamline) of the
charge-states of the considered elements. The typical behavior is shown
in Fig. 1. This case corresponds to isotropization. Decreasing
size of black dots corresponds to decreasing ion charge (largest O+8, smallest O+2, grey line denotes O+1). We call attention to the increasing importance of low charge-states O-ions (
q = +1, +2, +3) as plasma crosses the TS and approaches the
cross wind (CW) direction. This is due to much longer plasma residence
times in this region, about
as described above. Each solution describes the time evolution (and,
consequently, the spatial variability along the streamline) of the
charge-states of the considered elements. The typical behavior is shown
in Fig. 1. This case corresponds to isotropization. Decreasing
size of black dots corresponds to decreasing ion charge (largest O+8, smallest O+2, grey line denotes O+1). We call attention to the increasing importance of low charge-states O-ions (
q = +1, +2, +3) as plasma crosses the TS and approaches the
cross wind (CW) direction. This is due to much longer plasma residence
times in this region, about ![]() 101 yr as compared to
101 yr as compared to ![]() 1 year in the supersonic region. This acts in favor of electron capture processes, as reionization is very improbable for q > +1. About 70 yr after leaving the Sun the bulk of oxygen ions is in the form of O+1. The section of the considered flow line for which O+1 starts to dominate is indicated as black dots in the left panel.
1 year in the supersonic region. This acts in favor of electron capture processes, as reionization is very improbable for q > +1. About 70 yr after leaving the Sun the bulk of oxygen ions is in the form of O+1. The section of the considered flow line for which O+1 starts to dominate is indicated as black dots in the left panel.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{09900f01.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg58.png)
|
Figure 1:
The geometry of selected 30 (out of 180) flow lines in the upwind and near tail heliosphere ( left panel). Black dots indicate the region where O1 dominates (see text). As an example ( right panel) the time evolution of relative abundances is shown for all charge-states of oxygen (i.e.
N(8,16)+i divided by the total number of O-ions per unit solarwind mass) along a flow line that starts
|
| Open with DEXTER | |
One obtains qualitatively similar behavior for other flow lines
starting into the upwind heliosphere. Note however that the flow time
scales from the TS to CW vary very significantly with ![]() :
from 70 years for
:
from 70 years for
![]() to 1.6 years for
to 1.6 years for
![]() .
This means that the closer to the apex direction a flow line starts, the sooner it will be dominated by the O+1 ions. This tendency, combined with the topology of flow lines as shown in the left panel of Fig. 1, means that the relative abundance of O+1 will increase towards the heliopause all over the upwind heliosphere. The described behavior is illustrated in Fig. 2, which shows heliospheric maps of density distributions (ions/cm3) of oxygen ions in various ionization states. Consecutive rows describe (left to right): O+8 - O+7, O+6 - O+5, O+4 - O+3, O+2 - O+1 with common color coding for ion density (in cm-3). Note a high density ridge appears for O+3 beyond the termination shock. Finally, one obtains for O+1 a strong density enhancement towards the heliopause.
.
This means that the closer to the apex direction a flow line starts, the sooner it will be dominated by the O+1 ions. This tendency, combined with the topology of flow lines as shown in the left panel of Fig. 1, means that the relative abundance of O+1 will increase towards the heliopause all over the upwind heliosphere. The described behavior is illustrated in Fig. 2, which shows heliospheric maps of density distributions (ions/cm3) of oxygen ions in various ionization states. Consecutive rows describe (left to right): O+8 - O+7, O+6 - O+5, O+4 - O+3, O+2 - O+1 with common color coding for ion density (in cm-3). Note a high density ridge appears for O+3 beyond the termination shock. Finally, one obtains for O+1 a strong density enhancement towards the heliopause.
![\begin{figure}
\par\includegraphics[width=11.2cm,clip]{09900f02.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg62.png)
|
Figure 2:
Heliospheric maps of density distributions (ions/cm3)
of oxygen ions in various ionization states under isotropization
condition. The color coding in the right bottom corner corresponds to
|
| Open with DEXTER | |
Similar maps were obtained for all considered species, as shown in the online material. Two basic features are clearly prominent in all heavy ion distribution maps of the heliosphere:
- (1)
- For all considered ions there is a definite difference in the charge-states q in the supersonic solar wind as compared with the charge-states q in the heliosheath. For atoms of the atomic number Z the divide lies around q = +Z/2. Typically,
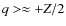 in the supersonic solar wind, while in the HS
in the supersonic solar wind, while in the HS
 .
Table 2 shows the situation in detail;
.
Table 2 shows the situation in detail;
- (2)
- Preferential concentration of singly-charged ions (q=+1) in certain regions of the heliosphere. Ions like C+1, N+1, O+1, Si+1 are most abundant on the upwind flanks of the heliosheath close to the HP, while Mg+1 and S+1 can be found on the distant flanks and in the heliotail.
The typical density contrast between the maximum in q=+1 layer (which in most cases is lining up the heliopause) and the region adjacent to the termination shock is on the order of ![]() 103,
103, ![]()
![]() ,
,
![]() 105,
105, ![]() 105,
105, ![]() 106, for C+1, N+1, O+1, Mg+1, Si+1. For O+1 and Mg+1 the q=+1 layer virtually lines up the heliopause; however, for C+1, N+1 and Si+1 the maximum density in that layer is attained at distances correspondingly of
106, for C+1, N+1, O+1, Mg+1, Si+1. For O+1 and Mg+1 the q=+1 layer virtually lines up the heliopause; however, for C+1, N+1 and Si+1 the maximum density in that layer is attained at distances correspondingly of ![]() 2, 7 and 3 AU from the heliopause (at
2, 7 and 3 AU from the heliopause (at
![]() off the apex direction). Existence of this relatively high density
layer for singly ionized species is a direct consequence of the fact
that heliosheath flow time scales are longest for the flow lines
closest to the heliopause: this provides the ions with more chance for
electron capture from neutrals. Differences between the positions of
relative values of maxima for different species reflect particularities
of individual cross sections. For instance, as can be seen from the
maps, the regions of high density of Si+1 and S+1 are shifted towards the HT compared to the O+1
density distribution. An overview of the heliospheric density
distribution in the isotropization case for all charge-states of all
considered species can be seen in the online material (Figs. 6-10). The format of these figures follows the format of Fig. 2.
off the apex direction). Existence of this relatively high density
layer for singly ionized species is a direct consequence of the fact
that heliosheath flow time scales are longest for the flow lines
closest to the heliopause: this provides the ions with more chance for
electron capture from neutrals. Differences between the positions of
relative values of maxima for different species reflect particularities
of individual cross sections. For instance, as can be seen from the
maps, the regions of high density of Si+1 and S+1 are shifted towards the HT compared to the O+1
density distribution. An overview of the heliospheric density
distribution in the isotropization case for all charge-states of all
considered species can be seen in the online material (Figs. 6-10). The format of these figures follows the format of Fig. 2.
Table 2: Prevailing charge-states of heavy ions in the supersonic solar wind and heliosheath.
3.2 Case thermalization
The spatial distribution of all charge-states of C, N, O, Mg, Si, and
S ions is obtained in a similar way as for the case of
``isotropization'' (cf. Sect. 3.1). The main difference consists
in different effective values for the relevant reaction rates, i.e.
products of collision speed
![]() (=
(=
![]() in Eq. (2)) times corresponding collision cross section
in Eq. (2)) times corresponding collision cross section
![]() for heavy ion interactions with neutral atoms and other plasma constituents.
for heavy ion interactions with neutral atoms and other plasma constituents.
![]() is now determined mainly by the local single-fluid temperature as given
by the hydrodynamic solution. As a consequence, for ion-neutral
collisions instead of
is now determined mainly by the local single-fluid temperature as given
by the hydrodynamic solution. As a consequence, for ion-neutral
collisions instead of
![]() km s-1, as in the case of isotropization, we have now values of tens of
km s-1 only. For instance, for C-ions the typical
km s-1, as in the case of isotropization, we have now values of tens of
km s-1 only. For instance, for C-ions the typical
![]() values in the relatively dense,
values in the relatively dense, ![]() 50 AU wide heliosheath layer adjacent to the heliopause amount now to 30-50 km s-1 in the heliosheath nose region
50 AU wide heliosheath layer adjacent to the heliopause amount now to 30-50 km s-1 in the heliosheath nose region
![]() and to
and to ![]() 20-30 km s-1 in the CW direction (
20-30 km s-1 in the CW direction (
![]() ).
As a result, the evolution of species by binary interactions is much
slowed down compared to isotropization, while the hydrodynamic flow
time scale remains unchanged. Because of this, the evolution of heavy
ion charge-states along each of the flow lines is now significantly
retarded, i.e. successive de-ionizations of heavy ions occur much
farther down the streamline. This translates into a very different
spatial distribution of particular charge-states when compared with
isotropization.
).
As a result, the evolution of species by binary interactions is much
slowed down compared to isotropization, while the hydrodynamic flow
time scale remains unchanged. Because of this, the evolution of heavy
ion charge-states along each of the flow lines is now significantly
retarded, i.e. successive de-ionizations of heavy ions occur much
farther down the streamline. This translates into a very different
spatial distribution of particular charge-states when compared with
isotropization.
To illustrate this effect we show in Fig. 3 the density maps for O-ions in the case of thermalization in exactly the same format as for the case of isotropization in Fig. 2. The maps show the density distributions (ions/cm3) of oxygen ions in various ionization states. Consecutive rows describe (left to right): O+8 - O+7, O+6 - O+5, O+4 - O+3, O+2 - O+1 with common color coding for ion density (in cm-3).
![\begin{figure}
\par\includegraphics[width=12cm,clip]{09900f03.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg72.png)
|
Figure 3: Heliospheric maps of density distributions (ions/cm3) of oxygen ions in various ionization states under thermalization condition (density coding as in Fig. 2). (Scale in AU on both axes). |
| Open with DEXTER | |
One immediately notes important differences between the present ``thermalization'' case and the ``isotropization'' case shown in Fig. 2. For instance, such a high-charge state like O+6 is now still very much present over the upwind heliosheath, and O+5, O+4 extend even well into the heliosheath tail area, while under isotropization these charge states were virtually absent. A striking difference is also visible in the distributions of O+3 ions. While under ``isotropization'' the density of these ions decreased sharply towards the heliopause, in the case of ``thermalization'' the reverse is true: the density attains maximum at the heliopause. Finally, concerning O+1, one immediately recognizes that the amount of oxygen that was able to reach this charge-state in the upwind heliosheath under thermalization is a tiny fraction of the corresponding amount converted to O+1 under isotropization.
One obtains qualitatively similar differences between cases of isotropization and thermalization for all other considered ions. Maps of distribution for most of the charge-states for all considered ions can be found in the online material (Figs. 11-15). The format of these figures follows the format of Fig. 2. On the whole, it can be stated that in the case when isotropization holds, the upwind heliosheath will be predominantly populated by the low charge-states while, when fast thermalization of heavy ions prevails, the ions will be in the high charge-states. This resembles the divide present in the isotropization case between the heavy ions in the supersonic solar wind and heliosheath (cf. Table 2, Sect. 3.1). The precise meaning of low and high charge-states depends in this context on the species in question, in the function of the interplay between various reaction rates. It goes without saying that no higher charge-states should appear in the heliosheath than those that are present in the solar corona. This follows from a vanishingly low probability of ionizing an already highly charged heavy ion.
The important conclusion one can infer from the comparison of the``isotropization'' and ``thermalization'' cases is that observational determination of the prevailing charge-states in the upwind heliosheath should be indicative of the relative importance of plasma ``collective'' (i.e. waves, turbulence, etc.) thermalization processes in the heliosheath versus cooling by Coulomb scattering on background plasma and binary collisions with neutral atoms. Should low charge-states dominate, as we in fact expect, then collective effects would be of little importance and the heavy ions should stay hot well into the heliospheric tail.
4 Spatial diffusion
A physical process, not mentioned hitherto, that may in principle
affect the distribution of heavy ions in the heliosphere is spatial
diffusion. Its effect over solar wind fast ride to the TS is obviously
small, because of the short time scale and heavy ion low energy as seen
in the co-moving plasma frame. However, diffusion may carry ions away
from the parent parcel of solar wind as the plasma moves relatively
slowly along hydrodynamic flow lines in the heliosheath and, in
addition, ions are hotter after the TS crossing. The distance in
coordinates co-moving with the fluid, covered in Brownian motion, is on
the order of
![]() ,
where
,
where
![]() is the diffusion coefficient for the heavy ions and
is the diffusion coefficient for the heavy ions and
![]() is the hydrodynamic flow time scale, counted from the TS.
Obviously, diffusion is more important for faster thermal motion, i.e.
it may be primarily of importance forthe case of ``isotropization''.
Unfortunately there are no direct data on diffusion in the heliosheath
of ions of tens of keV energy. The Bohm diffusion coefficient for a
1 keV/n O+5 ion in a B = 0.1 nT heliosheath magnetic field is
is the hydrodynamic flow time scale, counted from the TS.
Obviously, diffusion is more important for faster thermal motion, i.e.
it may be primarily of importance forthe case of ``isotropization''.
Unfortunately there are no direct data on diffusion in the heliosheath
of ions of tens of keV energy. The Bohm diffusion coefficient for a
1 keV/n O+5 ion in a B = 0.1 nT heliosheath magnetic field is
![]() cm2 s-1.
The Bohm diffusion is often considered to be a generous value for
diffusion perpendicular to the magnetic field. Recently Zank
et al. (2006) provided
arguments for possibly lower values of the diffusion coefficient in the
heliosheath based on the idea that the effective mfp is mostly related
to gyroradii of low energy ions. As the main aim of this section is to
provide estimates for the ``worst case'' scenario when diffusion
effects could invalidate the ``hydrodynamical'' results of
Sects. 3.1 and 3.2, we develop below a diffusive model with
very fast diffusion. In particular we extrapolate the formula for the
parallel diffusion coefficient derived from global heliospheric
distribution and solar cycle modulation of
cm2 s-1.
The Bohm diffusion is often considered to be a generous value for
diffusion perpendicular to the magnetic field. Recently Zank
et al. (2006) provided
arguments for possibly lower values of the diffusion coefficient in the
heliosheath based on the idea that the effective mfp is mostly related
to gyroradii of low energy ions. As the main aim of this section is to
provide estimates for the ``worst case'' scenario when diffusion
effects could invalidate the ``hydrodynamical'' results of
Sects. 3.1 and 3.2, we develop below a diffusive model with
very fast diffusion. In particular we extrapolate the formula for the
parallel diffusion coefficient derived from global heliospheric
distribution and solar cycle modulation of ![]() 0.1-several GeV cosmic ray ions (Le Roux et al. 1996) to very low energies (
0.1-several GeV cosmic ray ions (Le Roux et al. 1996) to very low energies (![]()
![]() ):
):
In this formula
The resulting heavy ion diffusion off the hydrodynamic flow line is estimated below for O+2 both for ``isotropization' and ``thermalization''. In the latter case, for
![]() K
in the sub-heliopause plasma,
K
in the sub-heliopause plasma,
![]() AU
and is therefore rather small compared to heliosheath spatial scales.
This suggests that were ``thermalization'' the proper description of
heavy ions' thermodynamic state, a purely hydrodynamic model as
described in Sect. 3.2 would suffice.
AU
and is therefore rather small compared to heliosheath spatial scales.
This suggests that were ``thermalization'' the proper description of
heavy ions' thermodynamic state, a purely hydrodynamic model as
described in Sect. 3.2 would suffice.
However, in the case of ``isotropization'' ion energies in plasma frame are ![]() 1 keV/n and diffusion may no longer be negligible, especially at low
1 keV/n and diffusion may no longer be negligible, especially at low ![]() .
For the streamlines mentioned the diffusive displacement over the heliosheath flow time scale amounts to
.
For the streamlines mentioned the diffusive displacement over the heliosheath flow time scale amounts to
![]() 15-25 AU.
This means that details of solutions presented for ``isotropization''
(Sect. 3.1) in the upwind heliosphere may in reality become
smeared out. To qualitatively assess the magnitude of possible effects
we develop in the this section a simplified, time-independent,
spherically symmetric, convective-diffusive description of the heavy
ion flow. Results obtained with this approach suggest that even
diffusion as fast as the one extrapolated from cosmic ray studies will
not invalidate the main results obtained under the axisymmetric
hydrodynamical model used as basis in the present paper.
15-25 AU.
This means that details of solutions presented for ``isotropization''
(Sect. 3.1) in the upwind heliosphere may in reality become
smeared out. To qualitatively assess the magnitude of possible effects
we develop in the this section a simplified, time-independent,
spherically symmetric, convective-diffusive description of the heavy
ion flow. Results obtained with this approach suggest that even
diffusion as fast as the one extrapolated from cosmic ray studies will
not invalidate the main results obtained under the axisymmetric
hydrodynamical model used as basis in the present paper.
The heavy ions are again treated as test particles carried by
background plasma and interacting with a stream of neutral atoms
entering the heliosphere cavity through the heliopause. As before, the
ions undergo all binary processes as described by Eqs. (1). This time, however, they are also allowed to diffuse through plasma with a diffusion coefficient ![]() as given by Eq. (4). The situation is commonly described by a cosmic-ray-type transport equation (Jokipii 1987). In our case the cosmic ray particles are replaced by the heavy ions, and we consider only the total pressure
as given by Eq. (4). The situation is commonly described by a cosmic-ray-type transport equation (Jokipii 1987). In our case the cosmic ray particles are replaced by the heavy ions, and we consider only the total pressure
![]() of the heavy ion gas without attempting to describe the possible
evolution of the momentum distribution function (Drury & Voelk 1981). In spherical symmetry the transport equation for
of the heavy ion gas without attempting to describe the possible
evolution of the momentum distribution function (Drury & Voelk 1981). In spherical symmetry the transport equation for
![]() takes then the form (a separate equation for each ion):
takes then the form (a separate equation for each ion):
where
The background plasma is supposed to enter the HS through a spherical TS placed at heliocentric distance
![]() AU with a purely radial hydrodynamic speed
AU with a purely radial hydrodynamic speed
![]() km s-1 on the downstream side. From the TS the plasma flows radially outwards with the velocity v(r) given by:
km s-1 on the downstream side. From the TS the plasma flows radially outwards with the velocity v(r) given by:
where v is given in km s-1 and r in cm. The values of
Solutions of Eqs. (1) and (5) with the approximations given in Eqs. (4) and (6) yield the distribution of heavy ion population under assumed radial convection-diffusion. Appropriate equations for each species were effectively solved with the following boundary conditions:
- (1)
- the flux of heavy ions introduced into the (considered sector of) heliosheath at
 corresponds to the flux carried (on average) by the hydrodynamic flow;
corresponds to the flux carried (on average) by the hydrodynamic flow;
- (2)
- the heavy ion pressure at the HP vanishes (
 )
because of the free escape of the ions into the external medium due to the expected high value of
)
because of the free escape of the ions into the external medium due to the expected high value of 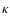 in
the local interstellar gas compared with the heliosphere values (an
increase by 2 or 3 orders of magnitude). The high external
values of
in
the local interstellar gas compared with the heliosphere values (an
increase by 2 or 3 orders of magnitude). The high external
values of 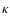 are suggested by appropriate formulae
for
are suggested by appropriate formulae
for 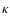 as a function of particle rigidity in the interstellar medium (Axford 1981;
Moskalenko et al. 2001), when extrapolated to the very low energy domain considered in the present context.
as a function of particle rigidity in the interstellar medium (Axford 1981;
Moskalenko et al. 2001), when extrapolated to the very low energy domain considered in the present context.
It is evident from Fig. 4 that the heavy ion density gradient (n-gradient) under the diffusive isotropization model is much less steep than for the hydrodynamical model. The density contrast between the midway maximum and the post-shock values ranges from 2.7 for C to 3.3 for Si. However, the total ENA production by neutralization of ions is much the same as in the purely hydrodynamic case (cf. Sect. 3.1).
![\begin{figure}
\par\includegraphics[width=8cm]{09900f04.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg103.png)
|
Figure 4:
Heavy ion densities (number per cm3) for diffusive, spherically symmetric solution. The left border of the diagram corresponds to the termination shock position
|
| Open with DEXTER | |
5 Production of energetic neutral atoms (ENA) in the heliosheath
5.1 Expected fluxes of ENA at 1 AU
Singly ionized ions produce neutral atoms by charge exchange with
interstellar H (and He). In the case of ``isotropization'' the
resulting neutral atoms will inherit the ![]() 1 keV/n energies (ENAs). The intensity I (in atoms cm-2 s-1 sr-1) of ENA fluxes for a particular species is given by an integral over the LOS (line-of-sight) of the source function:
1 keV/n energies (ENAs). The intensity I (in atoms cm-2 s-1 sr-1) of ENA fluxes for a particular species is given by an integral over the LOS (line-of-sight) of the source function:
where n+1 denotes the density of singly charged ions,
Table 3: Survival probabilities for the 1 keV/nucleon ENA flight from the heliopause to 1 AU.
These intensities are not corrected for the losses that ENA will
undergo during their flight from the heliosheath. We calculated the
losses for a more realistic situation where the observer is displaced
from the Sun by 1 AU along the LOS. The calculations include
photoionization losses assumed to vary ![]() 1/r2, charge exchange losses with the supersonic solar wind, varying also
1/r2, charge exchange losses with the supersonic solar wind, varying also ![]() 1/r2, losses induced by electron impact ionization in the supersonic solar wind for electron temperature
1/r2, losses induced by electron impact ionization in the supersonic solar wind for electron temperature ![]() varying as in Marsch et al. (1989),
charge exchange losses in the heliosheath for plasma density as
determined by the hydrodynamical model and electron impact ionization
losses in the heliosheath assuming
varying as in Marsch et al. (1989),
charge exchange losses in the heliosheath for plasma density as
determined by the hydrodynamical model and electron impact ionization
losses in the heliosheath assuming
![]() K
. The resulting correction factors (ENA survival probability over flight to 1 AU) to be applied to intensities
K
. The resulting correction factors (ENA survival probability over flight to 1 AU) to be applied to intensities ![]() shown in Fig. 5 are given in the Table 3.
shown in Fig. 5 are given in the Table 3.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{09900f05.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg112.png)
|
Figure 5: Logarithm of intensities of ENA (cm-2 s-1 sr-1) emitted by heliosheath plasma, as a function of the angular distance of the LOS from the apex direction (radians), seen from the Sun if no losses intervened. Curves from top to bottom (right side of diagram) correspond to: O, C, N, Si, Mg, S. |
| Open with DEXTER | |
The ENA intensities from Fig. 5 corrected for survival probabilities as in Table 3 suggest that in the case of ``isotropization'' the expected fluxes may attain 0.1 at./(cm2 s sr) for C and O and about ![]() 10-2 at./(cm2 s sr) for N and Mg. One may hope that fluxes of
10-2 at./(cm2 s sr) for N and Mg. One may hope that fluxes of ![]() 0.1 at./(cm2 s
sr) could be within the reach of a dedicated experiment such as the
NASA SMEX mission IBEX. If successful, such measurements would provide
a method to directly diagnose the velocity distribution function of
heavy ions in the heliosheath. Investigation of variation of ENA
intensities over the sky could inform about possible asymmetries in the
shape of the heliopause, whether it is due to external magnetic field
or to non-uniform distribution of the surrounding interstellar plasma.
We stress however that such interesting possibilities are very much
contingent on the fulfillment of the conditions for ``isotropization''.
0.1 at./(cm2 s
sr) could be within the reach of a dedicated experiment such as the
NASA SMEX mission IBEX. If successful, such measurements would provide
a method to directly diagnose the velocity distribution function of
heavy ions in the heliosheath. Investigation of variation of ENA
intensities over the sky could inform about possible asymmetries in the
shape of the heliopause, whether it is due to external magnetic field
or to non-uniform distribution of the surrounding interstellar plasma.
We stress however that such interesting possibilities are very much
contingent on the fulfillment of the conditions for ``isotropization''.
It is also important to note that were diffusion significant for isotropization (cf. Sect. 4), the overall intensity of ENA fluxes would not change much, though details of angular dependence as shown in Fig. 5 might look different. In the case of ``thermalization'', presence of measurable fluxes of neutral atoms from the heliosheath seems improbable on three accounts: very low particle energies, high losses over flight to 1 AU, displacement of sources from the upwind heliosheath to (more distant) tail regions. A more detailed discussion of the opportunities to use possible detection of ENA fluxes for the diagnostics of the strucuture of the heliosphere will be presented in Paper II.
5.2 Pickup ions from ENA as seed particles for anomalous cosmic rays
ENA entering the supersonic solar wind region between the Sun and TS constitute an additional source of pickup ions (PUI) compared to neutral interstellar atoms. The importance of this source relative to interstellar supply can be assessed by comparing the fraction of the total flux of ENA crossing the TS from downstream that become ionized in the supersonic solar wind, with the corresponding ionized fraction of the total (parallel) flux of interstellar neutral atoms. Such a comparison was made separately for each species, and we took into account the same loss processes as discussed in Sect. 5.1. Concerning the geometry, we assumed for simplicity a spherical configuration with the supersonic solar wind constituting for the neutral atoms a circular target with a radius equal to the TS radius (=106.9 AU) and all ENA sources, assumed equidistant from the Sun, contained within a narrow emitting layer of radius 178.9 AU lining up from inside the heliopause. Actually, we took only sources contained in the upwind-half of the heliosheath, as our modeling did not consistently include the tail section of the heliosphere. We recall that such a restriction of ENA sources to a narrow layer is typical in the ``isotropization'' case (cf. Sect. 3.1). Identical numerical values for both radii were taken as in Sect. 4. Note on the other hand that should diffusion be important (Sect. 4.), the sources of ENA would be distributed all over the heliosheath and the contribution of ENA to the production of PUI would increase due to larger geometrical factor of the solar wind target.
The flux of interstellar atoms impinging on the heliosphere was estimated based on results by Slavin & Frisch (2007)
(their model 26). In their modeling they undertook a detailed
analysis of ionization conditions and related abundances of various
species in the interstellar gas at solar location, taking into account
both local in-situ data on fluxes of interstellar atoms, column
densities of gas towards nearby stars and data on ionizing radiations
from stars and the Local Bubble. In particular Slavin and Frisch
analyzed issues related to the plausible significant ionization
gradient in the Local Interstellar Cloud (LIC), and reinterpreted the
interstellar abundances in this context. For instance, they infer that
local interstellar C seems to be overabundant compared to the solar
standard and that Mg and Si are highly depleted by deposition onto
interstellar grains. In our calculation we used the following values
for the neutral fractions of atoms of the six considered species, based
on model 26 in Table 6 of Slavin & Frisch (2007): C -
![]() ,
N - 0.720, O - 0.814, Mg -
,
N - 0.720, O - 0.814, Mg -
![]() ,
Si -
,
Si -
![]() ,
S -
,
S -
![]() .
For the purpose of our model we used [O]/[H] = 331 ppm,
with a hydrogen ionization degree of 0.224 (both values are also taken
from their Table 6) and an assumed interstellar neutral hydrogen
density at solar location equal to 0.15 at. cm-3.
.
For the purpose of our model we used [O]/[H] = 331 ppm,
with a hydrogen ionization degree of 0.224 (both values are also taken
from their Table 6) and an assumed interstellar neutral hydrogen
density at solar location equal to 0.15 at. cm-3.
The results of our calculations of the relative importance of PUI that are created by the ENA fluxes expected according to present modeling compared with the interstellar supply are shown in Table 4. It is evident that for species like N and O, which are thought to be largely neutral in the local interstellar gas, the relative contribution to PUI production in supersonic solar wind by heliospheric ENA is insignificant. However, for the low-FIP species like C, Mg, Si, S, which should be virtually totally ionized in front of the heliosphere (Slavin & Frisch 2007), the heliosheath PUI supply resulting from our modeling can be orders of magnitude more significant than the interstellar one. It is worth noting that our estimate of carbon PUI supply by deionization in the heliosheath exceeds the total carbon PUI supply from all other so-called ``inner'' and ``outer'' sources, like outgassing of comets, grain sputtering, solar wind neutralization on grains, that are invoked (Schwadron et al. 2002) to explain the PUI seed ions for the observed ACR carbon. As values in Table 4 indicate, the heliosheath ENA may constitute even more attractive candidates for PUI in the case of other low-FIP species accelerated to ACR energies. It is therefore tempting to speculate that deionization of heavy solar ions in the heliosheath, combined with a subsequent ENA drift into and ionization by the supersonic solar wind provides the necessary mechanism for production of seed particles for heliospheric ACR populations of most, if not all, low-FIP species present in ACR spectra. We will present a detailed discussion of this question in Paper II.
Table 4: Comparison of heliosheath supply of PUI with interstellar supply of PUI.
6 Influence on results of plasma state as observed at the Voyager-2 crossing of the termination shock
The plasma experiment on Voyager-2 revealed an unexpected effect at
the termination shock crossing in Aug./Sep. 2007. This was that the
post-shock temperature of the majority of the protons seems to be much
lower (![]() 105 K
) than expected from a simple hydrodynamic single-fluid shock transition model (
105 K
) than expected from a simple hydrodynamic single-fluid shock transition model (![]() 106 K
) (Richardson et al. 2008).
At the same time Voyager observed that the bulk flow velocity starts to
decrease well ahead of the shock. This results in a much smaller
effective velocity jump at the shock itself.
106 K
) (Richardson et al. 2008).
At the same time Voyager observed that the bulk flow velocity starts to
decrease well ahead of the shock. This results in a much smaller
effective velocity jump at the shock itself.
Such effects evidently may affect the post-shock behavior of
heavy ions. If one assumes that the momentaneous bulk speed of heavy
ions equals that of protons, then Figs. 2 and 3 in Richardson
et al. (2008) suggest that heavy ion bulk velocity jumps at the observed shock transitions could be on the order of ![]() 160 km s-1 for the transition TS-1 and
160 km s-1 for the transition TS-1 and ![]() 170 km s-1 for both TS-2 and TS-3.
170 km s-1 for both TS-2 and TS-3.
This means that in the isotropization case, for instance, the random
post-shock speed of heavy ions relative to the bulk plasma will be not
on the order of 500 km s-1, as assumed in Sect. 3.1, but perhaps only ![]() 170 km s-1.
Such velocity changes affect both the binary collision frequencies and
the values of cross section (rates) as specified in relevant equations
of type (2).
170 km s-1.
Such velocity changes affect both the binary collision frequencies and
the values of cross section (rates) as specified in relevant equations
of type (2).
In order to assess the magnitude of a possible influence of such a situation on the resulting spatial distribution of heavy ion charge-states we have calculated the distribution of all charge-states of carbon for post-shock heavy ion random speed in the heliosheath equal to 170 km s-1. (Shown in online material - Fig. 16).
The distribution of heliospheric of C-ion charge-states corresponding
to the ``isotropization'' case with heavy ion random speed of
170 km s-1 is shown in Fig. 16,
following the same format presentation as previously. It is evident
that again the lowest charge-states will concentrate towards the
heliopause, though the number of ions that succeeded to undergo a
series of consecutive de-charging by electron capture in the upwind
heliosheath is smaller in the present (170 km s-1)
``isotropization'' case than in the previous one (500 km s-1). Again, as previously, it is possible to calculate (Eq. (7)) the intensities (atoms cm-2 s-1 sr-1) of C ENA transcharged on the neutral H atom background and moving now with 170 km s-1 (which corresponds to ![]() 1.5 keV for C ENA). The resulting 170 km s-1-intensities are shown as a function of the angle
1.5 keV for C ENA). The resulting 170 km s-1-intensities are shown as a function of the angle ![]() from the apex in Table 5. Calculating the losses of C ENA starting with 170 km s-1 at the heliopause in the same way as in Sect. 5 one arrives at about
from the apex in Table 5. Calculating the losses of C ENA starting with 170 km s-1 at the heliopause in the same way as in Sect. 5 one arrives at about ![]() of C ENA surviving the ride to 1 AU, as compared with
of C ENA surviving the ride to 1 AU, as compared with ![]() for the 500 km s-1 C ENA (Table 3). The expected intensity of 170 km s-1 C ENA at Earth orbit is then from
for the 500 km s-1 C ENA (Table 3). The expected intensity of 170 km s-1 C ENA at Earth orbit is then from
![]() 0.03 (cm2 s sr)-1 at the apex direction to
0.03 (cm2 s sr)-1 at the apex direction to ![]() 0.06 (cm2 s sr)-1 at cross wind.
0.06 (cm2 s sr)-1 at cross wind.
Table 5: Expected C ENA intensities in (cm2 s sr)-1.
7 Final remarks and conclusions
The gist of the present paper lies in the observation that for the
presently estimated densities of neutral interstellar atoms at
heliosphere's peripheries, the time scale for complete deionization (by
electron capture from the neutrals) of heavy solar ions convected with
the solar wind may be comparable with the plasma flow time in the
heliosheath (![]() 108 - 109 s). The important proviso is that heavy ions lose their
108 - 109 s). The important proviso is that heavy ions lose their
![]() 1 keV/nucleon
energy slowly enough to secure high collision rates. This last
condition, in turn, is satisfied if the cooling of heavy ions is due
primarily to Coulomb scattering (time scale of
1 keV/nucleon
energy slowly enough to secure high collision rates. This last
condition, in turn, is satisfied if the cooling of heavy ions is due
primarily to Coulomb scattering (time scale of ![]() 1011 s)
on the relatively cold background (bulk) plasma, i.e. when no energy
equilibration by collective plasma processes is operative in the
post-termination shock solar wind (we call this case ``isotropization''
to stress that ions randomize their velocities while preserving
energies, Sect. 2.3). As we show in our modeling, the concurrence
of the above conditions would result in definite predictions concerning
the state of plasma populations in the outer heliosphere:
1011 s)
on the relatively cold background (bulk) plasma, i.e. when no energy
equilibration by collective plasma processes is operative in the
post-termination shock solar wind (we call this case ``isotropization''
to stress that ions randomize their velocities while preserving
energies, Sect. 2.3). As we show in our modeling, the concurrence
of the above conditions would result in definite predictions concerning
the state of plasma populations in the outer heliosphere:
- 1.
- the charge-states of heavy ions in the heliosheath should be much lower than in the supersonic solar wind, implying possible opportunities for detection by detailed analysis of soft X-ray and EUV emissions (Sect. 3.1) (this method could also be of interest for the study of astrospheres around the nearby stars). This issue is discussed for some simple cases in Paper II;
- 2.
- neutralization of singly-charged heavy ions concentrated
predominantly very close to the upwind flanks of the heliopause should
give rise to fluxes of ENA, that could - at least for carbon and oxygen
- be within reach of a dedicated instrument (
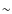 0.3 (cm2 s sr)-1,
Sects. 3.1 and 5.1). If the termination shock is much weaker,
as implied by the recent Voyager-2 crossings, calculations for C
indicate that C ENA would be less energetic (1.5 keV total
energy), but the intensities would decrease by no more than one order
of magnitude (Sect. 6) compared to values in Fig. 5 (Sect. 5);
0.3 (cm2 s sr)-1,
Sects. 3.1 and 5.1). If the termination shock is much weaker,
as implied by the recent Voyager-2 crossings, calculations for C
indicate that C ENA would be less energetic (1.5 keV total
energy), but the intensities would decrease by no more than one order
of magnitude (Sect. 6) compared to values in Fig. 5 (Sect. 5);
- 3.
- ENA produced in the vicinity of the heliopause will drift all over the heliosphere and upon the (re)entering the supersonic solar wind and (re)ionization therein will provide sources of PUI, which for the considered low-FIP species (C, Mg, Si, S) exceed other possible sources of ACR seed populations (Sect. 5.2, Table 4).
This research has been supported by the Polish MNiSW grants 1P03D00927, N522 002 31/0902, and N N203 4159 33.
References
- Aldrovandi, S. M. V., & Pequignot, D. 1973, A&A, 25,137 [NASA ADS] [Google Scholar]
- Alexandrova, O., & Mangeney, A. 2004, Proc. Probl. Geocosmos, 132 [Google Scholar]
- Alexandrova, O., Mangeney, A., & Maksimovic, M., et al. 2004, J. Geophys. Res., 109, 207 [CrossRef] [Google Scholar]
- Alexandrova, O., Mangeney, A., & Maksimovic, M., et al. 2006, J. Geophys. Res., 111, 208 [Google Scholar]
- Alexandrova, O., Mangeney, A., & Maksimovic, M. 2006, Proc. Probl. Geocosmos, 3 [Google Scholar]
- Axford, W. I. 1981, Proc. 17th ICRC Paris, 1981, 12, 155 [Google Scholar]
- Berdichevsky, D., Geiss, J., Gloeckler, G., & Mall, U. 1997, JGR, 102, 2623 [Google Scholar]
- Bochsler, P. 2000, Rev. Geophys. 38, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F., Ness, N. F., & Acuna, M. H., et al. 2005, Science, 309, 2027 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Burlaga, L. F., Ness, N. F., Acun, M. H., et al. 2008, Nature, 454, 75 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Drury, L. O., & Voelk, H. J. 1981, ApJ, 248, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Dubinin, E. M., Maksimovic, M., & Cornilleau-Wehrlin, N., et al. 2007, Ann. Geophys., 25, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, S. P. 1991, Space Sci. Rev., 56, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Gloeckler, G., Cain, J., Ipavich, F. M., Tums, E. O., & Bedini, P., et al. 1998, Space Sci. Rev., 86, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Gloeckler, G., Geiss J., & Balsiger H., et al. 1993, Science, 261, 70 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gloeckler, G., Möbius, E., Geiss, J., et al. 2004, A&A, 426, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izmodenov, V. V., & Alexashov, D. B. 2003, Astrophys. Lett., 29, 58 [Google Scholar]
- Jokipii, J. R. 1987, ApJ, 313, 842 [Google Scholar]
- Kingdon, J. B., & Ferland, G. J. 1996, ApJS, 106, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Korreck, K. E. 2005, Ph.D. Thesis, Univ. of Michigan [Google Scholar]
- Korreck, K. E., Zurbuchen, T. H, Lepri, S. T., & Raines, J. M. 2007, ApJ, 659, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Koutroumpa, D., Lallement, R., & Kharchenko, V., et al. 2006, A&A, 460, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kucharek, H., Möbius, E., & Scholer, M., et al. 2006, Proc. Cluster and Double Star Symposium, Noordwijk, The Netherlands [Google Scholar]
- Lee, L., & Wu, B. 2000, ApJ, 535, 1014 [NASA ADS] [CrossRef] [Google Scholar]
- le Roux, J. A., Potgieter, M. S., &. Ptuskin, V. S. 1996, J. Geophys. Res., 101, 4791 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C. Y., Stancil, P. C., Gu, J. P., Buenjer, R. J., & Kimura, M. 2005, Phys. Rev. A, 71, 062708 [NASA ADS] [CrossRef] [Google Scholar]
- Louarn, P., Budnik, E., Sauvaud, J. A., et al. 2003, Ann. Geophys., 21, 1483 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Thieme, K. M., Rosenbauer, H., & Pilipp, W. G. 1989, J. Geophys. Res., 94, 6893 [Google Scholar]
- Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moskalenko, I. V., Strong, A. W., Ormes, J. F., Potgieter, M. S., & Langner, U. W. 2001, Proc. 27th ICRC, 1868 [Google Scholar]
- Möbius, E., Kucharek, H., Mouikis, C., et al. 2001, Ann. Geophys., 19, 1411 [NASA ADS] [CrossRef] [Google Scholar]
- Raines, J., Lepi, S. T., & Zurbuchen, T. H., et al. 2005, Proc. Solar Wind 11, ed. B. Fleck, T. H. Zurbuchen, & H. Lacoste, ESA Publ. Div., ESTEC Netherlands, 539 [Google Scholar]
- Reames, D. V. 1998, Proc. ISSI Workshop, Bern, Switzerland, 327 [Google Scholar]
- Richardson, J. D., Kasper, J. C., Wang, C., Belcher, J. W., & Lazarus A. J. 2008, Nature, 454, 63 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schwadron, N. A., Combi, M., Huebner, W., & McComas, D. J. 2002, GRL, 29, 54 [NASA ADS] [Google Scholar]
- Slavin, J. D., & Frisch, P. C. 2007, Space Sci. Rev., 130, 409. [NASA ADS] [CrossRef] [Google Scholar]
- Stancil, P. C., Havener, C. C., Krstic, P. S., et al. 1998, ApJ, 502, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Stancil, P. C., Schultz, D. R., Kimura, M., et al. 1999, A&AS, 140, 225 [Google Scholar]
- Wang, C., & Richardson, J. D. 2005, Adv. Space Res., 35, 2102 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J. G., Stancil, P. C., Turner, A. R., & Cooper, D. L. 2003, Phys. Rev. A, 67, 12710 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Lin, R. P., Larson, D. E., & Luhmann, J. G. 2008, Nature, 454, 81 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Winske, D., & Gary, S. P. 1986, J. Geophys. Res., 91, 6825 [NASA ADS] [CrossRef] [Google Scholar]
- Witte, M. 2004, A&A, 426, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- von Steiger, R., Schwadron, N. A., Fisk, A., et al. 2000, J. Geophys. Res., 105, 27217 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P., Gang, Li, Florinski, V., et al. 2006, J. Geophys. Res., 111, 6108 [Google Scholar]
- Zatsarinny, O., Gorczyca, T. W., Korista, K. T., Badnell, N. R., & Savin, D. W. 2003, A&A, 412, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zatsarinny, O., Gorczyca, T. W., Korista, K. T., Badnell, N. R., & Savin, D. W. 2004, A&A, 417, 1173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Online Material
![\begin{figure}
\par\includegraphics[width=16cm,clip]{09900f06.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg133.png)
|
Figure 6: Heliospheric maps of density distributions (ions/cm3) of carbon ions in various ionization states under isotropization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{09900f07.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg134.png)
|
Figure 7: Heliospheric maps of density distributions (ions/cm3) of nitrogen ions in various ionization states under isotropization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{09900f08.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg135.png)
|
Figure 8: Heliospheric maps of density distributions (ions/cm3) of magnesium ions in various ionization states under isotropization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{09900f09.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg136.png)
|
Figure 9: Heliospheric maps of density distributions (ions/cm3) of silicon ions in various ionization states under isotropization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{09900f10.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg137.png)
|
Figure 10: Heliospheric maps of density distributions (ions/cm3) of sulfur ions in various ionization states under isotropization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{09900f11.eps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg138.png)
|
Figure 11: Heliospheric maps of density distributions (ions/cm3) of carbon ions in various ionization states under thermalization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{09900f12.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg139.png)
|
Figure 12: Heliospheric maps of density distributions (ions/cm3) of nitrogen ions in various ionization states under thermalization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{09900f13.eps}\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg140.png)
|
Figure 13: Heliospheric maps of density distributions (ions/cm3) of magnesium ions in various ionization states under thermalization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{09900f14.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg141.png)
|
Figure 14: Heliospheric maps of density distributions (ions/cm3) of silicon ions in various ionization states under thermalization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{09900f15.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg142.png)
|
Figure 15: Heliospheric maps of density distributions (ions/cm3) of sulfur ions in various ionization states under thermalization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{09900f16.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg143.png)
|
Figure 16: Heliospheric maps of density distributions (ions/cm3) of carbon ions in various ionization states of carbon for post-shock heavy ion random speed in the heliosheath equal to 170 km s-1 (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
Footnotes
- ... S
![[*]](/icons/foot_motif.png)
- Figures 6 to 16 are only available in electronic form at http://www.aanda.org
All Tables
Table 1: Initial (1 AU) relative abundances of charge-states of heavy ions.
Table 2: Prevailing charge-states of heavy ions in the supersonic solar wind and heliosheath.
Table 3: Survival probabilities for the 1 keV/nucleon ENA flight from the heliopause to 1 AU.
Table 4: Comparison of heliosheath supply of PUI with interstellar supply of PUI.
Table 5: Expected C ENA intensities in (cm2 s sr)-1.
All Figures
![\begin{figure}
\par\includegraphics[width=17cm,clip]{09900f01.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg58.png)
|
Figure 1:
The geometry of selected 30 (out of 180) flow lines in the upwind and near tail heliosphere ( left panel). Black dots indicate the region where O1 dominates (see text). As an example ( right panel) the time evolution of relative abundances is shown for all charge-states of oxygen (i.e.
N(8,16)+i divided by the total number of O-ions per unit solarwind mass) along a flow line that starts
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11.2cm,clip]{09900f02.eps}
\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg62.png)
|
Figure 2:
Heliospheric maps of density distributions (ions/cm3)
of oxygen ions in various ionization states under isotropization
condition. The color coding in the right bottom corner corresponds to
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{09900f03.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg72.png)
|
Figure 3: Heliospheric maps of density distributions (ions/cm3) of oxygen ions in various ionization states under thermalization condition (density coding as in Fig. 2). (Scale in AU on both axes). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{09900f04.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg103.png)
|
Figure 4:
Heavy ion densities (number per cm3) for diffusive, spherically symmetric solution. The left border of the diagram corresponds to the termination shock position
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{09900f05.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg112.png)
|
Figure 5: Logarithm of intensities of ENA (cm-2 s-1 sr-1) emitted by heliosheath plasma, as a function of the angular distance of the LOS from the apex direction (radians), seen from the Sun if no losses intervened. Curves from top to bottom (right side of diagram) correspond to: O, C, N, Si, Mg, S. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{09900f06.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg133.png)
|
Figure 6: Heliospheric maps of density distributions (ions/cm3) of carbon ions in various ionization states under isotropization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{09900f07.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg134.png)
|
Figure 7: Heliospheric maps of density distributions (ions/cm3) of nitrogen ions in various ionization states under isotropization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{09900f08.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg135.png)
|
Figure 8: Heliospheric maps of density distributions (ions/cm3) of magnesium ions in various ionization states under isotropization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{09900f09.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg136.png)
|
Figure 9: Heliospheric maps of density distributions (ions/cm3) of silicon ions in various ionization states under isotropization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{09900f10.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg137.png)
|
Figure 10: Heliospheric maps of density distributions (ions/cm3) of sulfur ions in various ionization states under isotropization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{09900f11.eps}\vspace*{3mm}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg138.png)
|
Figure 11: Heliospheric maps of density distributions (ions/cm3) of carbon ions in various ionization states under thermalization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{09900f12.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg139.png)
|
Figure 12: Heliospheric maps of density distributions (ions/cm3) of nitrogen ions in various ionization states under thermalization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{09900f13.eps}\vspace*{4mm}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg140.png)
|
Figure 13: Heliospheric maps of density distributions (ions/cm3) of magnesium ions in various ionization states under thermalization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{09900f14.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg141.png)
|
Figure 14: Heliospheric maps of density distributions (ions/cm3) of silicon ions in various ionization states under thermalization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{09900f15.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg142.png)
|
Figure 15: Heliospheric maps of density distributions (ions/cm3) of sulfur ions in various ionization states under thermalization condition (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{09900f16.eps}
\end{figure}](/articles/aa/full_html/2010/04/aa09900-08/Timg143.png)
|
Figure 16: Heliospheric maps of density distributions (ions/cm3) of carbon ions in various ionization states of carbon for post-shock heavy ion random speed in the heliosheath equal to 170 km s-1 (density coding as in Fig. 2). (Scale in AU on both axes.) |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




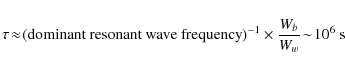

![\begin{displaymath}
\frac{1}{r^2} \frac{{\rm d}}{{\rm d}r} {\left[\frac{r^2}{\ga...
...}r}\right)\right]} - v \frac{{\rm d}p_{\rm hi}}{{\rm d}r} = Q,
\end{displaymath}](/articles/aa/full_html/2010/04/aa09900-08/img91.png)

