EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 511 (February 2010) A&A, 511 (2010) L8 Full HTML
Free Access

This article has an erratum: [https://doi.org/10.1051/0004-6361/200913670e]

Issue
A&A
Volume 511, February 2010
Article Number L8
Number of page(s) 6
Section Letters
DOI https://doi.org/10.1051/0004-6361/200913670
Published online 10 March 2010
A&A 511, L8 (2010)

LETTER TO THE EDITOR

A scenario of planet erosion by coronal radiation[*]

J. Sanz-Forcada1 - I. Ribas2 - G. Micela3 - A. M. T. Pollock4 - D. García-Álvarez5,6 - E. Solano1,7 - C. Eiroa8

1 - Laboratorio de Astrofísica Estelar y Exoplanetas, Centro de Astrobiología / CSIC-INTA, LAEFF Campus, PO Box 78, 28691 Villanueva de la Cañada, Madrid, Spain
2 - Institut de Ciènces de l'Espai (CSIC-IEEC), Campus UAB, Fac. de Ciències, Torre C5-parell-2 $^{\underline a}$ planta, 08193 Bellaterra, Spain
3 - INAF - Osservatorio Astronomico di Palermo G. S. Vaiana, Piazza del Parlamento, 1, 90134 Palermo, Italy
4 - XMM-Newton SOC, European Space Agency, ESAC, Apartado 78, 28691 Villanueva de la Cañada, Madrid, Spain
5 - Instituto de Astrofísica de Canarias, 38205 La Laguna, Spain
6 - Grantecan CALP, 38712 Breña Baja, La Palma, Spain
7 - Spanish Virtual Observatory, Centro de Astrobiología/CSIC-INTA, LAEFF Campus, Madrid, Spain
8 - Dpto. de Física Teórica, C-XI, Facultad de Ciencias, Universidad Autónoma de Madrid, Cantoblanco, 28049 Madrid, Spain

Received 14 November 2009 / Accepted 8 February 2010

Abstract
Context. According to theory, high-energy emission from the coronae of cool stars can severely erode the atmospheres of orbiting planets. No observational tests of the long-term erosion effects have been made yet.
Aims. We analyze the current distribution of planetary mass with X-ray irradiation of the atmospheres to make an observational assessment of the consequences of erosion by coronal radiation.
Methods. We studied a large sample of planet-hosting stars with XMM-Newton, Chandra, and ROSAT, carefully identified the X-ray counterparts, and fit their spectra to accurately measure the stellar X-ray flux.
Results. The distribution of the planetary masses with X-ray flux suggests that erosion has taken place. Most surviving massive planets ( $M_{\rm p} \sin i >1.5$ $M_{\rm J}$) have been exposed to lower accumulated irradiation. Heavy erosion during the initial stages of stellar evolution is followed by a phase of much weaker erosion. A line dividing these two phases could be present, showing a strong dependence on planet mass. Although a larger sample will be required to establish a well-defined erosion line, the distribution found is very suggestive.
Conclusions. The distribution of planetary mass with X-ray flux is consistent with a scenario in which planet atmospheres have suffered the effects of erosion by coronal X-ray and EUV emission. The erosion line is an observational constraint for models of atmospheric erosion.

Key words: planetary systems - stars: coronae - astrobiology - X-rays: stars

1 Introduction

The expected effects on the erosion of exoplanetary atmospheres by stellar radiation have been the subject of much theoretical work (Davis & Wheatley 2009; García Muñoz 2007; Cecchi-Pestellini et al. 2006; Erkaev et al. 2007; Cecchi-Pestellini et al. 2009; Baraffe et al. 2004; Hubbard et al. 2007; Yelle 2004; Penz et al. 2008; Lecavelier Des Etangs 2007; Ribas et al. 2005; Tian et al. 2005; Lammer et al. 2003; Penz & Micela 2008). In planets around late-type stars, stellar radiation in the X-ray ($\sim$1-100 Å) and EUV ($\sim$100-900 Å) ranges has the strongest effect on atmospheric evaporation. Late-type stars are copious emitters of X-ray and EUV radiation from high-temperature ($\sim$1-30 MK) material in coronae, whose development is favoured by fast rotation making it most important for young stars that retain much of the angular momentum of the parent cloud. Observations of stellar clusters have shown that X-ray emission decreases with age, as the rotation slows (cf. Favata & Micela 2003). The sample of known exoplanets is now large enough for an observational search to be made for the erosion effects on planet masses.

After planet formation and once the protoplanetary disk has dissipated, a planet is exposed to high levels of coronal emission from the rapidly rotating young host star, which is much stronger for closer-in planets. This emission is expected to progressively erode the planet atmosphere through evaporation (thermal losses) mediated by gravity. A planetary magnetic field should provide some protection against losses of ionized material, although little work has been done on these effects (e.g. Grießmeier et al. 2009, and references therein). Once the star slows down and becomes more X-ray and EUV quiet, the planet mass decreases at a lower rate. The relatively simple approach proposed by Watson et al. (1981) and subsequently modified by Lammer et al. (2003), Baraffe et al. (2004), and Erkaev et al. (2007) to account for the expansion radius of the atmosphere R1 ( $R_1 \ge R_{\rm p}$) and the filling of the Roche lobe (using the K parameter, with $K \le 1$) leads to the following expression for the thermal planetary mass-loss rate

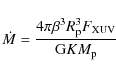
\begin{displaymath}% \dot M=\frac{4 \pi \beta^3 R_{\rm p}^3 F_{\rm XUV}}{{\rm G} K M_{\rm p}} \end{displaymath} (1)

where $\beta = R_1/R_{\rm p}$, $F_{\rm XUV}$ is the X-ray and EUV flux at the planet orbit, and G is the gravitational constant.

We have adopted the direct experimental approach of examining the dependence of planet mass on the X-ray flux it has received. In the long term the effects of erosion by atmospheric losses should result in an uneven distribution of planet masses with the X-ray flux at the planet orbit. We set up a database of X-ray and EUV emission of the stars hosting exoplanets (``X-exoplanets'', Sanz-Forcada et al. 2009) to facilitate analysis of the effects of coronal radiation on exoplanet atmospheres. In this work we present the results of a study with the whole sample of 59 non-giant stars hosting 75 exoplanets with masses up to 8 $M_{\rm J}$ that have been observed in X-rays with XMM-Newton, Chandra, or ROSAT, making what we consider to be the safe assumption that the X-ray flux is proportional to the entire evaporating flux, because both X-rays and EUV stem from similar processes in the corona of the star. Present-day telescopes give no access to stellar EUV observations, which would also be limited by absorption in the insterstellar medium. In Sect. 2 we describe the observations, data reduction, and results, before discussing their implications in Sect. 3, and finish with the conclusions in Sect. 4.

\begin{figure} \par\includegraphics[width=7cm,clip]{13670fg1.eps} \end{figure} Figure 1:

Distribution of planetary masses ( $M_{\rm p} \sin i$) with X-ray flux at the planet orbit. Filled symbols (squares for subgiants, circles for dwarfs) are XMM-Newton and Chandra data. Arrows indicate upper limits. Open symbols are ROSAT data without error bars. Diamonds represent Jupiter, Saturn, and the Earth. The dashed line marks the ``erosion line''. Dotted lines indicate the X-ray flux of the younger Sun at 1 au.

Open with DEXTER

2 Observations and results

The XMM-Newton and Chandra X-ray observations shown in Table 1 were reduced following standard procedures following corrections for proper motion. These corrections were particularly important in some cases for discarding erroneous detections reported in the literature. For 47 UMa, for example, we find $\log L_{\rm X}\sim25.45$ erg s-1 compared to the value of $\log L_{\rm X}=27.13$ erg s-1 estimated by Kashyap et al. (2008). The star was detected near its expected position $\alpha$ = 10:59:28.0, $\delta$ = 40:25:46 close to a brighter source $\alpha$ = 10:59:26.7, $\delta$ = 40:26:04: the instrumental spatial resolution is 6 $^{\prime\prime}$. Tentative evidence for detection of a Fe K$\alpha$ emission line suggests the brighter source may be a highly obscured AGN at $z\sim0.2$ (G. Miniutti, private comm.). In the same way as for HD 209458, we calculated an upper limit of $\log L_{\rm X}<26.12$ erg s-1, a value much lower than reported elsewhere by Kashyap et al. (2008) and Penz & Micela (2008), who might have confused the star with a nearby object.

Extracted spectra were fit using standard procedures with coronal models of 1 to 3 temperature components (see e.g., Sanz-Forcada et al. 2003b). The actual model used in the fit has little influence on the calculated X-ray (0.12-2.48 keV or 5-103 Å) flux shown in Table 1. More details on the data reduction and treatment will be given in Sanz-Forcada et al. 2010 (in prep.). Measurements with S/N < 3 were considered as upper limits. We complemented the sample with lower spatial resolution ROSAT measurements, excluding detections with low statistics (S/N < 3), and further marking as upper limits the objects with suspected X-ray bright companions. The sample of 75 exoplanets including XMM-Newton, Chandra, and ROSAT detections have been compared with the whole exoplanet database (417 objects to date) to check whether our sample is representative of the known exoplanets. We applied the Kolmogorov-Smirnov test to compare both samples, and they represent the same distributions in mass (99.7% probability) or period (92.8% probability) in single variable tests.

\begin{figure} \par\includegraphics[width=7cm,clip]{13670fg2.eps} \vspace*{-2mm} \end{figure} Figure 2:

Distribution of planetary masses ( $M_{\rm p} \sin i$) with the X-ray flux accumulated at the planet orbit since an age of 20 Myr to the present day (see text). Symbols as in Fig. 1.

Open with DEXTER

The stellar X-ray flux was converted into X-ray luminosity, $L_{\rm X}$, using the distances listed in Table 1. Also listed are some physical properties of the hosted exoplanets, collected from the exoplanets database (Schneider 1995, http://exoplanet.eu/). The X-ray flux received at the orbit of the planet is then given by $F_{\rm X}=L_{\rm X}/(4 \pi a_{\rm p}^2)$, where $a_{\rm p}$ is the semimajor axis. The mass-loss rate from atmospheric losses with $\beta=K=1$produced by X-rays simplifies to

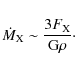
\begin{displaymath}% \dot M_{\rm X} \sim \frac{3 F_{\rm X}}{{\rm G} \rho}\cdot \end{displaymath} (2)

Table 1 includes this calculation for a density of $\rho$ = 1.0 g cm-3. As references Jupiter, HD 209458b, and HD 189733b have $\rho$ = 1.24, 0.37, and 0.95 g cm-3, respectively.

The distribution of $F_{\rm X}$ against the planet mass, $M_{\rm p} \sin i$, is plotted in Fig. 1. There is a separation that seems to be related to mass. We plotted a line that roughly follows this separation: $\log F_{\rm X}=3{-}0.5~ (M_{\rm p} \sin i)$, with $M_{\rm p}$ in Jovian masses and $F_{\rm X}$ in CGS units. This line is not based on any previous assumption or physical law. We also include the Solar System planets in the diagram by using current emission of the solar corona, which ranges $26\leq\log L_{\rm X}\leq27.7$ (Orlando et al. 2001), with the vertical segments indicating the variations over the solar cycle. In this context we can compare the radiation arriving at the Earth when life first appeared about $\sim$3.5 Gyr ago (see Cnossen et al. 2007, and references therein) and at an earlier stage, to see whether coronal erosion could have affected the Earth at that time. We use two stars considered proxies of the Sun at an early age (Ribas et al. 2005), $\kappa$ Cet ($\sim$1 Gyr, $\log L_{\rm X}=28.89$) and EK Dra ($\sim$0.1 Gyr, $\log L_{\rm X}=30.06$)[*]. Lines indicating their $F_{\rm X}$ received at 1 au are plotted in Fig. 1 to mimic the flux at the Earth's orbit in the past.

Since the effects of erosion accumulate over the planet's lifetime, we calculated the integrated X-ray flux that has arrived on the planet orbit between the age of 20 Myr, when most protoplanetary disks would have dissipated, and the present day. We need to know the stellar age and the X-ray luminosity evolution with time for each star in the sample. We can estimate both following Garcés et al. (2010, in prep.), who relate the average X-ray luminosity to the age of late F to early M dwarfs:

                      $\displaystyle % L_{\rm X}$ = $\displaystyle 6.3\times10^{-4}~ L_{\rm bol} \quad \qquad (\tau < \tau_i)$  
$\displaystyle L_{\rm X}$ = $\displaystyle 1.89\times10^{28}~ \tau^{-1.55} \qquad (\tau > \tau_i)$ (3)

with $\tau_i = 2.03$ $\times$ $10^{20}~ L_{\rm bol}^{-0.65}$. $L_{\rm X}$ and  $L_{\rm bol}$ are in erg s-1, and $\tau$is the age in Gyr. The relation was found with independent age indicators and/or wide binary coeval companions to X-ray sources. The $\tau_i$ parameter marks the typical change from saturation regime to an inverse proportionality between $L_{\rm X}/L_{\rm bol}$ and rotation period (e.g. Pizzolato et al. 2003). The calculation is taken as a first approximation of the stellar age (Table 1), considering also that there is an uncertainty of about an order of magnitude in the $L_{\rm X}$ levels of stars of the same spectral type and age (Penz et al. 2008; Penz & Micela 2008). The accumulated X-ray flux at the planet orbit is shown in Fig. 2. Subgiants are marked with different symbols since it is not known whether they follow the same relation. A hard limit of ${\sim}10^{21.76}$ erg cm-2 in 10 Gyr is found by combining the highest luminosity ( $L_{\rm bol}=10^{34.5}~{\rm erg}~{\rm s}^{-1}$) and the shortest distance to the star (0.02 au) of planets in the sample. No higher values are expected to be found in future observations of ``hot Jupiters''. Our highest flux is 10 21.05 erg cm-2.

The effects of erosion in the long term are also expected to have an effect on the density of the population of close-in planets. The valuable information regarding the density is provided in most cases by the transit technique, that favours detection of planets with short periods, hence short distances. Our sample only has four planets with known density (HD 209458 b, HD 189733 b, Gj 436 b, and 2M1207 b), but we can check the distribution of density with mass (Fig. 3). This distribution is not representative of the whole population of exoplanets, and its results should only apply to close-in planets since erosion effects might be relevant.

\begin{figure} \par\includegraphics[angle=90,width=7cm,clip]{13670fg3.ps} \vspace*{-2mm} \end{figure} Figure 3:

Density of the 66 planets of known radius (7 Jan. 2010) with $M_{\rm p} < 8~M_{\rm J}$ (filled circles). Diamonds represent the Solar System planets.

Open with DEXTER

3 Discussion

The observed sample seems to indicate an ``erosion line'' (Fig. 1) below which most planets are located. There are few planets above the erosion line, and they are probably at an early evolutionary stage and have spent less time exposed to high $F_{\rm X}$. The long-term accumulation effects are clearer in Fig. 2, which shows that only 3 out of 34 planets above 1.5 $M_{\rm J}$ have survived a flux of 1019 erg cm-2, although the determination of this flux could be wrong for two of them (see below). This plot partially removes the effect of age. Following dissipation of the protoplanetary disk, planets exposed to high radiation should suffer heavy erosion, until the X-ray flux decreases as stellar rotation slows or the planet has become small enough for gravity or magnetospheric trapping to halt erosion. The thermal losses (Eq. (2)) indicate that $F_{\rm X}$ and density control the mass loss rate. The dependence of the erosion line on mass, combined with the mass distribution observed in Fig. 2, confirms that $F_{\rm X}$ is the main variable, with few massive planets surviving exposure to high radiation as discussed below. The distribution of density with mass displayed in Fig. 3 is also consistent with the effects of erosion, since planets with higher densities would suffer less erosion, resulting in a population of massive planets in the long term that are denser than lower mass planets. Gaseous planets should not substantially increase their density, while being eroded above jovian-like masses. Note also that Eq. (2) is only valid for gaseous planets, and rocky planets should suffer little erosion from XUV radiation.

In addition to thermal evaporation, non-thermal losses, such as ion pick up and sputtering processes, could also be important following ionization of the outer atmosphere by the coronal radiation or high-energy particles mediated by any planetary magnetic field. Indeed, it is possible that the observations already reflect the relative weakness of magnetic fields in massive planets and the consequent inability to slow erosion. Low-mass planets, with a wide range of densities and distances in this sample, might have stronger fields that reduce erosion.

The planets $\tau$ Boo b, HD 195019 b, and Gl 86 b, seem to challenge this interpretation (Fig. 2), retaining high masses despite the high X-ray flux received. However, the fact that we see a young planet, $\tau$ Boo b (age $\sim$ 400 Myr, according to Eq. (3)), still suffering heavy erosion ( $\dot M_{\rm X}$ = 11 $M_{\rm J}$ Gyr-1 for $\rho$ = 1 g cm-3) reinforces our interpretation of the erosion line. The age and accumulated X-ray flux determination of HD 195019, a G3IV-V star, could be inaccurate, although it would have to be much younger for the accumulated X-ray flux to be substantially reduced. This object falls below the erosion line though. The third case, Gl 86, has a white dwarf at only $\sim$21 au (Mugrauer & Neuhäuser 2005; Els et al. 2001), and although its contribution to the X-ray flux should not be significant, we cannot discard that dynamical processes have changed the distance of the planet to the star over its lifetime (see also Lagrange et al. 2006). Finally, it is possible that these three planets have higher densities that have partly protected them against erosion.

No significant evaporation is currently underway in Solar System planets, consistent with their location in Figs. 1, 2. It is interesting to see that, when life appeared on Earth, the planet was well below the ``erosion line'', so probably suffering little or no erosion. Even 100 Myr after the Sun was born, the Earth was still below the the erosion line. By contrast, any atmosphere on Mercury, much nearer the Sun (0.47 au), would have been stripped away.

The sample of known exoplanets is by no means complete. Several selection effects could be present. (i) With the methods used in exoplanet surveys, it is easier to detect massive planets close to stars. This should bring more massive planets with high $F_{\rm X}$ into our sample, thereby yielding a positive relation of $F_{\rm X}$ with planet mass. This bias reinforces our conclusions, since we find the opposite effect: the more massive planets receive a lower $F_{\rm X}$. (ii) Initial conditions in the disk could yield to more massive planets placed at longer distances. The current sample of extrasolar planets has a deficit of massive planets at the shortest distances. We assume that initial conditions have little impact within this range of distances but we cannot exclude that the observed distribution is an effect of planet formation. (iii) X-ray luminous stars are easier to detect in X-rays surveys, so we should be biased towards planets with high $F_{\rm X}$ (very few present in our sample), independent of planet mass. On the other hand, the planet-hunting programs generally discard the active (young) stars. Among these stars, we would likely find more planets above the ``erosion line'', but the planet would still be under heavy erosion for a young star, in good agreement with our interpretation of the data. (iv) Finally, most of the planets in the sample have $M_{\rm p} \sin i < 2.5~M_{\rm J}$, with few planets above this mass, that would actually be the most useful objects for confirming our conclusions.

Our approach is an alternative to the one followed by Lecavelier Des Etangs (2007), who balance the potential energy of the planet with the EUV flux received from the star, based on a number of assumptions for estimating the present and past EUV flux (with no estimation of the age of each star), and the radius and composition of the planet. In particular, the EUV flux is estimated using the flux in the range 110-200 Å typical of each spectral type, and then scaled to the range 100-1200 Å based on the solar pattern, an approach discouraged by the differences seen in the few known EUV spectra in the literature (see, e.g., Sanz-Forcada et al. 2003a). Lecavelier Des Etangs (2007) extend this calculation for individual cases, most notably claiming that Gj 876 b must be dense to have survived the large estimated EUV flux. Our real measurements (close to the ROSAT value of $\log L_{\rm X}=26.5$) indicate that this planet receives less coronal radiation than others with low density, such as HD 189733 b. Davis & Wheatley (2009) instead balance the potential energy with the X-ray flux that would arrive just during the saturation period of stellar evolution, averaged according to spectral type. This would be a lower limit of the XUV flux, as the EUV band is missing. As a result they suggest there is a ``destruction limit'' below which only dense planets would survive. The present sample of exoplanets has at least three planets (GJ 1214 b, GJ 436 b, HAT-P-12 b) with low densities ($\rho=1.58$, 1.06, and 0.30 g cm-3, respectively) below this limit.

4 Conclusions

Among 75 extrasolar planets, only 3 out of 34 high-mass planets of $M_{\rm p} \sin i >1.5$ (one of them still young) have been exposed to the levels of radiation suffered by most of the low-mass planets in the sample. We suggest that this is a consequence of the long-term effects of erosion of gaseous planets by coronal radiation. We propose that the existence of an ``erosion line'' that depends on the planet mass for the mass range explored, indicating that erosion would have stronger effects for more massive planets. The heterogeneity of our sample makes it difficult to apply the thermal erosion models in the long term, but these models cannot explain the observed dependence on mass. More complex models are required that consider the chemical composition that could be very different among planets: different molecules and ionization stages have different responses to XUV radiation. Non-thermal losses should also be considered, against which the presence of a planetary magnetic field might provide protection. Planets above the erosion line, such as the young $\tau$ Boo b, would be good candidates to search for current effects of erosion by coronal radiation. Finally we cannot exclude that the observed distribution is not partly an effect of planetary formation processes that would result in massive planets on wider orbits. More observations of X-ray emission of planets with $M_{\rm p} \sin i \ga 2.5~M_{\rm J}$ are needed to confirm our conclusions.



Acknowledgements
J.S.F. and D.G.A. acknowledge support from the Spanish MICINN through grant AYA2008-02038 and the Ramón y Cajal Program ref. RYC-2005-000549. I.R. acknowledges support from the Spanish MICINN via grant AYA2006-15623-C02-01. This research has made use of the NASA's High Energy Astrophysics Science Archive Research Center (HEASARC) and the public archives of XMM-Newton and Chandra. We thank G. Miniutti for help with the extragalactic source near 47 UMa. We are grateful to the anonymous referee and to the editor, T. Guillot, for the careful reading of and useful comments on the manuscript.

References

  1. Baraffe, I., Selsis, F., Chabrier, G., et al. 2004, A&A, 419, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Cecchi-Pestellini, C., Ciaravella, A., & Micela, G. 2006, A&A, 458, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Cecchi-Pestellini, C., Ciaravella, A., Micela, G., & Penz, T. 2009, A&A, 496, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Cnossen, I., Sanz-Forcada, J., Favata, F., et al. 2007, J. Geophys. Res. (Planets), 112, E02008 [Google Scholar]
  5. Davis, T. A. & Wheatley, P. J. 2009, MNRAS, 396, 1012 [NASA ADS] [CrossRef] [Google Scholar]
  6. Els, S. G., Sterzik, M. F., Marchis, F., et al. 2001, A&A, 370, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Erkaev, N. V., Kulikov, Y. N., Lammer, H., et al. 2007, A&A, 472, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Favata, F. & Micela, G. 2003, Space Science Reviews, 108, 577 [Google Scholar]
  9. García Muñoz, A. 2007, Planet. Space Sci., 55, 1426 [NASA ADS] [CrossRef] [Google Scholar]
  10. Grießmeier, J., Stadelmann, A., Grenfell, J. L., Lammer, H., & Motschmann, U. 2009, Icarus, 199, 526 [NASA ADS] [CrossRef] [Google Scholar]
  11. Hubbard, W. B., Hattori, M. F., Burrows, A., Hubeny, I., & Sudarsky, D. 2007, Icarus, 187, 358 [NASA ADS] [CrossRef] [Google Scholar]
  12. Kashyap, V. L., Drake, J. J., & Saar, S. H. 2008, ApJ, 687, 1339 [NASA ADS] [CrossRef] [Google Scholar]
  13. Lagrange, A., Beust, H., Udry, S., Chauvin, G., & Mayor, M. 2006, A&A, 459, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [NASA ADS] [CrossRef] [Google Scholar]
  15. Lecavelier Des Etangs, A. 2007, A&A, 461, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Mugrauer, M. & Neuhäuser, R. 2005, MNRAS, 361, L15 [NASA ADS] [CrossRef] [Google Scholar]
  17. Orlando, S., Peres, G., & Reale, F. 2001, ApJ, 560, 499 [NASA ADS] [CrossRef] [Google Scholar]
  18. Penz, T. & Micela, G. 2008, A&A, 479, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Penz, T., Micela, G., & Lammer, H. 2008, A&A, 477, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Pizzolato, N., Maggio, A., Micela, G., Sciortino, S., & Ventura, P. 2003, A&A, 397, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Ribas, I., Guinan, E. F., Güdel, M., & Audard, M. 2005, ApJ, 622, 680 [NASA ADS] [CrossRef] [Google Scholar]
  22. Sanz-Forcada, J., Brickhouse, N. S., & Dupree, A. K. 2003a, ApJS, 145, 147 [NASA ADS] [CrossRef] [Google Scholar]
  23. Sanz-Forcada, J., Maggio, A., & Micela, G. 2003b, A&A, 408, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Sanz-Forcada, J., García-Álvarez, D., Velasco, A., et al. 2009, in Solar and Stellar Variability Impact on Earth and Planets; ed. by A. Kosavichenko, A. Andrei, and J.-P. Rozelot, IAU Symp., 264, in press [Google Scholar]
  25. Tian, F., Toon, O. B., Pavlov, A. A., & De Sterck, H. 2005, ApJ, 621, 1049 [NASA ADS] [CrossRef] [Google Scholar]
  26. Watson, A. J., Donahue, T. M., & Walker, J. C. G. 1981, Icarus, 48, 150 [NASA ADS] [CrossRef] [Google Scholar]
  27. Yelle, R. V. 2004, Icarus, 170, 167 [NASA ADS] [CrossRef] [Google Scholar]

Online Material

Table 1:   X-ray flux ( 0.12-2.48 keV) of stars with exoplanetsa.


Footnotes

... radiation[*]
Table 1 is only available in electronic form at http://www.aanda.org
...$\log L_{\rm X}=30.06$)[*]
$L_{\rm X}$ calculated from XMM-Newton data.

All Tables

Table 1:   X-ray flux ( 0.12-2.48 keV) of stars with exoplanetsa.

All Figures

  \begin{figure} \par\includegraphics[width=7cm,clip]{13670fg1.eps} \end{figure} Figure 1:

Distribution of planetary masses ( $M_{\rm p} \sin i$) with X-ray flux at the planet orbit. Filled symbols (squares for subgiants, circles for dwarfs) are XMM-Newton and Chandra data. Arrows indicate upper limits. Open symbols are ROSAT data without error bars. Diamonds represent Jupiter, Saturn, and the Earth. The dashed line marks the ``erosion line''. Dotted lines indicate the X-ray flux of the younger Sun at 1 au.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7cm,clip]{13670fg2.eps} \vspace*{-2mm} \end{figure} Figure 2:

Distribution of planetary masses ( $M_{\rm p} \sin i$) with the X-ray flux accumulated at the planet orbit since an age of 20 Myr to the present day (see text). Symbols as in Fig. 1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[angle=90,width=7cm,clip]{13670fg3.ps} \vspace*{-2mm} \end{figure} Figure 3:

Density of the 66 planets of known radius (7 Jan. 2010) with $M_{\rm p} < 8~M_{\rm J}$ (filled circles). Diamonds represent the Solar System planets.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.