| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200912405 | |
| Published online | 05 March 2010 | |
The chemical composition of TS 01, the most oxygen-deficient planetary nebula
AGB nucleosynthesis in a metal-poor binary star![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
G. Stasinska1 - C. Morisset2 - G. Tovmassian3 - T. Rauch4 - M. G. Richer3 - M. Peña2 - R. Szczerba5 - T. Decressin6 - C. Charbonnel7 - L. Yungelson8 - R. Napiwotzki9 - S. Simón-Díaz10 - L. Jamet1
1 - LUTH, Observatoire de Paris, CNRS, Université Paris Diderot, Place Jules Janssen, 92190 Meudon, France
2 -
Instituto de Astronomia, Universidad Nacional Autonoma de Mexico, Apdo. Postal 70264, Mexico D.F., 04510 Mexico
3 -
Instituto de Astronomia, Universidad Nacional Autonoma
de Mexico, Apdo. Postal 877, Ensenada, Baja California, 22800 Mexico
4 -
Institute for Astronomy and Astrophysics,
Kepler Center for Astro and Particle Physics,
Eberhard Karls University, Sand 1,
72076 Tübingen,
Germany
5 -
N. Copernicus Astronomical Center, Rabianska 8, 87-100 Torun, Poland
6 -
Argelander Institute for Astronomy (AIfA), Auf dem Hügel 71, 53121 Bonn,
Germany
7 - Geneva Observatory, University of Geneva, ch. des Maillettes
51, 1290 Sauverny, Switzerland and Laboratoire d'Astrophysique de
Toulouse-Tarbes, CNRS UMR 5572, Université de Toulouse, 14, Av.
E.Belin, 31400 Toulouse, France
8 -
Institute of Astronomy of the Russian Academy of Sciences, 48 Pyatniskaya Str., 119017 Moscow, Russia
9 -
Centre for Astrophysics Research, University of Hertfordshire, College Lane, Hatfield
AL109AB, UK
10 -
Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain
Received 30 April 2009 / Accepted 15 December 2009
Abstract
The planetary nebula TS 01 (also called
PN G 135.9+55.9 or SBS 1150+599A) with its
record-holding low oxygen abundance and its double degenerate close
binary core (period 3.9 h) is an exceptional object located in the
Galactic halo.
We have secured observational data in a complete wavelength
range to pin down the abundances of half a dozen elements in the
nebula. The abundances are obtained via detailed photoionization
modelling which takes into account all the observational constraints
(including geometry and aperture effects) using the pseudo-3D
photoionization code Cloudy_3D. The spectral energy distribution of the
ionizing radiation is taken from appropriate model atmospheres.
Incidentally we find from the new observational constraints that both
stellar components contribute to the ionization: the ``cool'' one
provides the bulk of hydrogen ionization, while the ``hot'' one is
responsible for the presence of the most highly charged ions, which
explains why previous attempts to model the nebula experienced
difficulties. The nebular abundances of C, N, O, and Ne are found to be
1/3.5, 1/4.2, 1/70, and 1/11 of the solar value respectively, with
uncertainties of a factor 2. Thus the extreme O deficiency of this
object is confirmed. The abundances of S and Ar are less than 1/30
of solar. The abundance of He relative to H is
![]() .
Standard models of stellar evolution and nucleosynthesis cannot explain
the abundance pattern observed in the nebula. To obtain an extreme
oxygen deficiency in a star whose progenitor has an initial mass of
about 1
.
Standard models of stellar evolution and nucleosynthesis cannot explain
the abundance pattern observed in the nebula. To obtain an extreme
oxygen deficiency in a star whose progenitor has an initial mass of
about 1 ![]() requires an additional mixing process, which can be induced by stellar
rotation and/or by the presence of the close companion. We have
computed a stellar model with an initial mass of 1
requires an additional mixing process, which can be induced by stellar
rotation and/or by the presence of the close companion. We have
computed a stellar model with an initial mass of 1 ![]() ,
appropriate metallicity, and initial rotation of 100 km s-1, and find that rotation greatly improves the agreement between the predicted and observed abundances.
,
appropriate metallicity, and initial rotation of 100 km s-1, and find that rotation greatly improves the agreement between the predicted and observed abundances.
Key words: planetary nebulae: individual: TS 01 - ISM: abundances - stars: AGB and post-AGB - binaries: general - nuclear reactions, nucleosynthesis, abundances
1 Introduction
SBS 1150+599A was discovered in the second Byurakan Sky Survey and first classified as a cataclysmic variable (Stepanian et al. 1999). Tovmassian et al. (2001) discussed in detail the nature of the object and arrived at the conclusion that it is in fact a planetary nebula (PN). The object was renamed PN G 135.9+55.9, following the nomenclature for Galactic PNe from the Strasbourg-ESO catalogue of Galactic Planetary Nebulae (Acker et al. 1992). For the sake of brevity we will refer to it as TS 01 in the rest of the paper. This PN is special in at least three important aspects. First of all, its oxygen abundance is very low, significantly lower than in any other PN known up to now (Richer et al. 2002; Péquignot & Tsamis 2005; Tovmassian et al. 2001; Jacoby et al. 2002). Second, its nucleus is a spectroscopic binary with a period of only a few hours (Tovmassian et al. 2004). Third, it appears from estimates of the nature and masses of the two stellar components, that TS 01 could turn into a double degenerate type Ia supernova (Tovmassian et al. 2004). Each of these aspects, even taken alone, makes TS 01 an exceptional object.
In this paper, we reexamine the chemical composition of TS 01.
Briefly, the story of the determination of the chemical composition of
this object is the following. Tovmassian et al. (2001) had optical
spectra of TS 01 in the range 3900-7000 Å obtained with
2 m class telescopes which showed no lines from heavy elements
except a very weak [O III] ![]() 5007, with an intensity a few percent of H
5007, with an intensity a few percent of H![]() .
A coarse photoionization analysis suggested an oxygen abundance smaller
than 1/100 solar. Note that standard empirical methods for abundance
determinations in PNe cannot be used for TS 01, since the electron
temperature cannot be determined directly from observations. To go
further in the abundance determination of TS 01 required an
estimate of the effective temperature of the central star. One way is
to obtain a good blue spectrum of the PN, and use the [Ne V]
.
A coarse photoionization analysis suggested an oxygen abundance smaller
than 1/100 solar. Note that standard empirical methods for abundance
determinations in PNe cannot be used for TS 01, since the electron
temperature cannot be determined directly from observations. To go
further in the abundance determination of TS 01 required an
estimate of the effective temperature of the central star. One way is
to obtain a good blue spectrum of the PN, and use the [Ne V] ![]() 3426/ [Ne III]
3426/ [Ne III] ![]() 3869 ratio (or a limit on it) as a constraint. Richer et al. (2002) at the Canada-France-Hawaii Telescope (CFHT) and Jacoby et al. (2002) at the Multiple Mirror Telescope (MMT) secured deep blue spectra to detect these lines. Jacoby et al. (2002) detected the [Ne V]
3869 ratio (or a limit on it) as a constraint. Richer et al. (2002) at the Canada-France-Hawaii Telescope (CFHT) and Jacoby et al. (2002) at the Multiple Mirror Telescope (MMT) secured deep blue spectra to detect these lines. Jacoby et al. (2002) detected the [Ne V] ![]() 3426 line at a level of 0.8 H
3426 line at a level of 0.8 H![]() .
Richer et al. (2002) found only an upper limit of 0.1 H
.
Richer et al. (2002) found only an upper limit of 0.1 H![]() ! Concerning the [Ne III]
! Concerning the [Ne III] ![]() 3869 line, Jacoby et al. (2002) measured an intensity about ten times higher than Richer et al. (2002).
The two papers appeared within a few days of each other on astro-ph,
revealing this big conflict in the observations. The two groups
conducted independent photoionization analyses, and both concluded that
the O/H ratio is less than 1/100 solar (the main reason for their
similar result for the oxygen abundance was the similar [Ne V]
3869 line, Jacoby et al. (2002) measured an intensity about ten times higher than Richer et al. (2002).
The two papers appeared within a few days of each other on astro-ph,
revealing this big conflict in the observations. The two groups
conducted independent photoionization analyses, and both concluded that
the O/H ratio is less than 1/100 solar (the main reason for their
similar result for the oxygen abundance was the similar [Ne V] ![]() 3426/[Ne III]
3426/[Ne III] ![]() 3869 ratio used by both studies). Péquignot & Tsamis (2005)
made a combination of the two observational data sets and conducted
their own photoionization analysis. They concluded that the O/H ratio
of TS 01 lies between 1/30-1/15 solar (still holding the record
for the most oxygen poor planetary nebula, but much higher than
previously published). However, Péquignot & Tsamis (2005) neglected to consider observations of TS 01 made with the Hubble Space Telescope (HST) and the Far Ultraviolet Spectroscopic Explorer
(FUSE). As a result, some of their ``predicted'' line intensities are
in conflict with what is actually observed in the UV. HST observations
were obtained in 2003 and presented in a short, preliminary version by Jacoby et al. (2006). Those authors quoted an oxygen abundance of 1/30-1/40 solar, and carbon and nitrogen abundances roughly 1/10 solar.
3869 ratio used by both studies). Péquignot & Tsamis (2005)
made a combination of the two observational data sets and conducted
their own photoionization analysis. They concluded that the O/H ratio
of TS 01 lies between 1/30-1/15 solar (still holding the record
for the most oxygen poor planetary nebula, but much higher than
previously published). However, Péquignot & Tsamis (2005) neglected to consider observations of TS 01 made with the Hubble Space Telescope (HST) and the Far Ultraviolet Spectroscopic Explorer
(FUSE). As a result, some of their ``predicted'' line intensities are
in conflict with what is actually observed in the UV. HST observations
were obtained in 2003 and presented in a short, preliminary version by Jacoby et al. (2006). Those authors quoted an oxygen abundance of 1/30-1/40 solar, and carbon and nitrogen abundances roughly 1/10 solar.
Before embarking on a new determination of abundances, we have chosen to gather the best possible observations at all wavelength ranges. These data provide many more constraints than were available in any previous study. In order to make the best use of the large amount of data obtained with different telescopes, we use a pseudo-3D photoionization code, Cloudy_3D, which is able to account for the nebular geometry as we see it now, and with which we can properly take into account the aperture effects. This code is based on CLOUDY (Ferland et al. 1998) and was written by Morisset (2006).
The paper is organized as follows. Section 2 presents the new observational material: several optical spectra, HST imaging and spectroscopy, infrared spectroscopy with the Spitzer Telescope, and mentions our X-ray observations with XMM. Section 3 summarizes other data that we used as constraints for the photoionization modelling. Section 4 describes our modelling strategy and presents our ``reference model''. Section 5 evaluates the error bars on the derived elemental abundances, taking into account observational uncertainties in emission-line fluxes, uncertainties in model input parameters and also uncertainties arising from an imperfect description of the physical processes included in the models. In Sect. 6, we compare the chemical composition of TS 01 with that of other PNe in the Galactic halo and discuss it in terms of stellar nucleosynthesis in the asymptotic giant branch (AGB) phase. Finally, Sect. 7 summarizes our main findings.
2 New observational data on emission lines
We present the observational data that we secured on TS 01 and its stellar core since the work presented in Tovmassian et al. (2004). Some of those data were already briefly reported in conference proceedings, but here we describe the acquisition and reduction processes in more detail. Note that the observations and reductions were done by different people and at different epochs, when our knowledge on the object was not the same. This explains the differences in the tactics employed to reduce the data, estimate the line fluxes and correct for reddening. We did not try to fully homogenize the data reduction process, since we felt it unnecessary for our purposes.
The log and characteristics of each set of observations are given in Table 1.
Table 1: Log and characteristics of the spectroscopic observations.
2.1 Imaging
We (M.P.) retrieved the data corresponding to the proposal ID 9466 from the HST archives and analyzed them. The observations were performed on May 5, 2003. Two types of data are available: direct imaging and spectroscopy.
Direct imaging was obtained with the Advanced Camera for Surveys (ACS).
The high resolution channel with a field of view of
![]() and a plate-scale of 0.027
and a plate-scale of 0.027
![]() per pixel, with filters around H
per pixel, with filters around H![]() (central wavelength
(central wavelength
![]() Å) and [Ne V]
Å) and [Ne V] ![]() 3426 (central wavelength
3426 (central wavelength
![]() Å) were used.
Å) were used.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f01.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg17.png)
|
Figure 1:
HST-ACS H |
| Open with DEXTER | |
Figure 1 shows the H![]() image
obtained by averaging the four calibrated frames j8do01021, j8do01022,
j8do01023, j8do01024 (870 s exposure time each; 58 min in
total), after aligning them with respect to j8do01021. The image is
roughly elliptical in shape with two brighter,
symmetrically-placed lobes at a position angle of about
image
obtained by averaging the four calibrated frames j8do01021, j8do01022,
j8do01023, j8do01024 (870 s exposure time each; 58 min in
total), after aligning them with respect to j8do01021. The image is
roughly elliptical in shape with two brighter,
symmetrically-placed lobes at a position angle of about
![]() that
extend the full major axis of the ellipse. The nebula is not perfectly
symmetric, with the outermost southern part much fainter. The size of
the nebular image is about 5
that
extend the full major axis of the ellipse. The nebula is not perfectly
symmetric, with the outermost southern part much fainter. The size of
the nebular image is about 5
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f02.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg19.png)
|
Figure 2:
HST-ACS H |
| Open with DEXTER | |
Figure 2 shows the same image as Fig. 1, with the different observing apertures indicated: continuous lines for Kitt Peak, dotted lines for HST STIS, circle for SDSS. For the CFHT 2003 observations, the slit was rotated before each of the seven exposures (see Sect. 2.2.1), so as to remain as close as possible to the parallactic angle. The position of the slit is not indicated in the figure for the sake of clarity, but was taken into account correctly when comparing the predicted line intensities with the observed ones (see Sect. 4.2).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f03.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg20.png)
|
Figure 3:
HST-ACS image of TS 01 in the [Ne V] |
| Open with DEXTER | |
Figure 3 shows an average of the [Ne V]![]() 3432 calibrated images
j8do01011, j8do01012, j8do01013 and j8do01014 (3000 s of exposure time each;
200 min in total). This image reveals a very faint, roughly spherical extended
nebulosity and an important emission in the centre, probably caused by
the stellar core. Some faint extensions are marginally detected in the directions of the
H
3432 calibrated images
j8do01011, j8do01012, j8do01013 and j8do01014 (3000 s of exposure time each;
200 min in total). This image reveals a very faint, roughly spherical extended
nebulosity and an important emission in the centre, probably caused by
the stellar core. Some faint extensions are marginally detected in the directions of the
H![]() lobes.
lobes.
2.2 Optical spectroscopy
2.2.1 CFHT data
CFHT 2003
TS 01 was reobserved at the CFHT by M.R. and G.S. on 1 May 2003 using the MOS spectrograph and a 1
![]() slit (Le Fèvre et al. 1994).
The U900 grism was used, giving a spectral range of 3400-5300 Å
and a spectral resolution of 3-3.5 Å (measured from arc lamp
spectra). Seven 1800 s exposures were obtained. During each
exposure, the slit was set to within 10
slit (Le Fèvre et al. 1994).
The U900 grism was used, giving a spectral range of 3400-5300 Å
and a spectral resolution of 3-3.5 Å (measured from arc lamp
spectra). Seven 1800 s exposures were obtained. During each
exposure, the slit was set to within 10![]() of the parallactic angle. Details of the reduction process of the
individual exposures are given in Tovmassian et al. (2004).
of the parallactic angle. Details of the reduction process of the
individual exposures are given in Tovmassian et al. (2004).
To obtain a high signal-to-noise spectrum of the nebular emission
lines, it is necessary to account for the stellar and nebular continuum
emission. These contributions were subtracted from the individual
exposures before summing the individual spectra. First, the observed
spectra were shifted in velocity so that the stellar absorption line
was at rest. Next, the H![]() intensity was measured and used to scale a model of the nebular continuum emission. Since the H
intensity was measured and used to scale a model of the nebular continuum emission. Since the H![]() flux is affected by stellar absorption, the stellar absorption was
assumed to have an equivalent width of 13 Å, a value typical for
the models used (see below). This scaled nebular continuum was then
subtracted from the observed spectrum. Then, a model stellar atmosphere
was scaled so as to match the observed continuum level and subtracted
from the observed spectrum. This procedure leaves a pure nebular
emission line spectrum, supposing that the model nebular and stellar
continua are representative of their real counterparts. It is unlikely
that subtracting the continua introduces significant uncertainty into
our final line intensities. Model stellar spectra with
flux is affected by stellar absorption, the stellar absorption was
assumed to have an equivalent width of 13 Å, a value typical for
the models used (see below). This scaled nebular continuum was then
subtracted from the observed spectrum. Then, a model stellar atmosphere
was scaled so as to match the observed continuum level and subtracted
from the observed spectrum. This procedure leaves a pure nebular
emission line spectrum, supposing that the model nebular and stellar
continua are representative of their real counterparts. It is unlikely
that subtracting the continua introduces significant uncertainty into
our final line intensities. Model stellar spectra with
![]() pairs of (90 kK, 5.05), (120 kK, 5.35), and (150 kK,
5.56) computed by R.N. (see Tovmassian et al. 2004) were
subtracted from our observed spectra and the differences in the
resulting line intensities were always smaller than the uncertainties
in the fits
pairs of (90 kK, 5.05), (120 kK, 5.35), and (150 kK,
5.56) computed by R.N. (see Tovmassian et al. 2004) were
subtracted from our observed spectra and the differences in the
resulting line intensities were always smaller than the uncertainties
in the fits![]() .
.
Once the stellar and nebular continua were subtracted, the individual
nebular spectra were shifted back to their original velocities and
summed. We measured the nebular emission line strengths from this final
spectrum. The line intensities were measured using INTENS, a
locally-implemented software package (McCall et al. 1985).
This software simultaneously fits a sampled Gaussian function to the
emission line(s) and a straight line to the continuum. It returns the
line strengths, line wavelengths, and uncertainties in these
quantities. The line intensities presented in Table 2 together with their uncertainties are those measured after subtracting the stellar spectrum for
![]() k K and
k K and
![]() .
The listed intensities are not corrected for reddening. In the case of no detection, two-sigma upper limits are given instead.
.
The listed intensities are not corrected for reddening. In the case of no detection, two-sigma upper limits are given instead.
We note that the [Ne V] ![]() 3426 line is present, and strong. Its intensity is of the same order as in the spectrum of Jacoby et al. (2002), and much higher than the upper limit given by Richer et al. (2002). The remaining lines have intensities roughly in agreement with those published by Richer et al. (2002) and Jacoby et al. (2002), except for the [Ne III] line which appeared on the top of a bump in Jacoby et al. (2002) and was attributed a high intensity in that paper.
3426 line is present, and strong. Its intensity is of the same order as in the spectrum of Jacoby et al. (2002), and much higher than the upper limit given by Richer et al. (2002). The remaining lines have intensities roughly in agreement with those published by Richer et al. (2002) and Jacoby et al. (2002), except for the [Ne III] line which appeared on the top of a bump in Jacoby et al. (2002) and was attributed a high intensity in that paper.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{12405f04.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg25.png)
|
Figure 4: Flux-calibrated CFHT spectra of TS 01. In blue is the CFHT 2003 spectrum with the nebular and stellar continua subtracted, in black the original CFHT 2001 spectrum, and in red the CFHT 2001 spectrum with the correct wavelength solution. |
| Open with DEXTER | |
CFHT 2001
Table 2:
Intensities of optical lines, corrected for stellar absorption, but not for reddening, with respect to H![]() .
.
In view of the important discrepancy with the Richer et al. (2002) data concerning the [Ne V] ![]() 3426
line, we decided to reanalyze the spectrum of TS 01 we had
obtained in March 2001 at the CFHT. First, though, we refer the
interested reader to Richer et al. (2002) for a discussion of the
details of these observations. The basic difficulty with these
observations was that the arc lamp spectra were taken with the same 5
3426
line, we decided to reanalyze the spectrum of TS 01 we had
obtained in March 2001 at the CFHT. First, though, we refer the
interested reader to Richer et al. (2002) for a discussion of the
details of these observations. The basic difficulty with these
observations was that the arc lamp spectra were taken with the same 5
![]() slit
used for the object observations, which resulted in an arc spectrum
with severely blended lines. After repeating the wavelength calibration
more carefully, we found that our previous solution had stretched out
the spectrum at the shortest wavelengths, leading us to not recognize
the [Ne V]
slit
used for the object observations, which resulted in an arc spectrum
with severely blended lines. After repeating the wavelength calibration
more carefully, we found that our previous solution had stretched out
the spectrum at the shortest wavelengths, leading us to not recognize
the [Ne V] ![]() 3426
line because of its low contrast with respect to the continuum and its
erroneous wavelength. The analysis of this spectrum was considerably
simpler given that the stellar features were not resolved. We simply
fit the continuum shape and removed it (INTENS assumes that the
continuum is a straight line), then measured the line intensities with
INTENS. The resulting line intensities are given in Table 2. The intensity we find now for [Ne V]
3426
line because of its low contrast with respect to the continuum and its
erroneous wavelength. The analysis of this spectrum was considerably
simpler given that the stellar features were not resolved. We simply
fit the continuum shape and removed it (INTENS assumes that the
continuum is a straight line), then measured the line intensities with
INTENS. The resulting line intensities are given in Table 2. The intensity we find now for [Ne V] ![]() 3426 agrees with the one given by Jacoby et al. (2002)
and is compatible within two sigmas with the one obtained with the CFHT
2003 data. Slit effects could perhaps explain the slight difference in
intensity between CFHT 2001 and CFHT 2003.
3426 agrees with the one given by Jacoby et al. (2002)
and is compatible within two sigmas with the one obtained with the CFHT
2003 data. Slit effects could perhaps explain the slight difference in
intensity between CFHT 2001 and CFHT 2003.
2.2.2 Kitt Peak data
TS 01 was observed at the 4 m telescope of Kitt Peak
National Observatory on 1 January 2003. The grating used was KPC-10A,
and the slit
![]() ,
with an orientation of
,
with an orientation of
![]() .
Two exposures of 600 s were obtained. The data were reduced by
L.J., employing the same procedure as for the SDSS spectrum, explained
below.
.
Two exposures of 600 s were obtained. The data were reduced by
L.J., employing the same procedure as for the SDSS spectrum, explained
below.
2.2.3 SDSS and Kitt Peak data
The spectrum of TS 01 appears in the data of the Sloan Digital Sky Survey SDSS (http://www.sdss.org) under the name 0953-52411-160![]() . We present its analysis performed by L.J.
. We present its analysis performed by L.J.
We separated the nebular emission from the stellar spectrum and
evaluated the reddening with as few free parameters as possible. We
assumed the stellar spectrum to be that of a single white dwarf (WD),
hence neglecting the possible contribution of the companion; we
considered three model WD spectra at temperatures of 90, 120
and 150 kK (the same as used for the CFHT 2003 spectrum). As
for the nebular continuum, we computed the free-free and free-bound
emissivities of H+ and He++ with the CHIANTI code (Landi et al. 2006), assuming an abundance ratio He++/H+=0.075 and an electronic temperature of 30 kK (Richer et al. 2002). We also retrieved the H![]() nebular emissivity at this temperature from Storey & Hummer (1995).
nebular emissivity at this temperature from Storey & Hummer (1995).
First, we computed a model of the total (stellar+nebular) spectrum around the H![]() line. In each of the WD spectral models, the H
line. In each of the WD spectral models, the H![]() line has a Voigt profile with a given equivalent width (EW)
line has a Voigt profile with a given equivalent width (EW)
![]() ,
Gaussian width
,
Gaussian width
![]() and Lorentzian width
and Lorentzian width
![]() .
As for the nebular emission, we computed the EW
.
As for the nebular emission, we computed the EW
![]() of the emission line with respect to the nebular continuum.
Furthermore, we assumed the real width of the nebular line to be much
smaller than the instrumental one, so its observed Gaussian and
Lorentzian widths, respectively
of the emission line with respect to the nebular continuum.
Furthermore, we assumed the real width of the nebular line to be much
smaller than the instrumental one, so its observed Gaussian and
Lorentzian widths, respectively
![]() and
and
![]() ,
are representative of the instrumental PSF. Consequently, the observed widths of the stellar line are
,
are representative of the instrumental PSF. Consequently, the observed widths of the stellar line are
![]() and
and
![]() .
We normalized the local stellar+nebular continuum with the fit of a
slope on either side of the line. Finally, we let the central
wavelengths of the stellar and nebular line, respectively
.
We normalized the local stellar+nebular continuum with the fit of a
slope on either side of the line. Finally, we let the central
wavelengths of the stellar and nebular line, respectively
![]() and
and
![]() ,
be independent from each other. Using the data and assumptions
gathered, we fitted a consistent model on the observed spectrum around
the line. Calling
,
be independent from each other. Using the data and assumptions
gathered, we fitted a consistent model on the observed spectrum around
the line. Calling
![]() the profile of the nebular line,
the profile of the nebular line,
![]() that of the star (both being normalized to an EW of unity), and C* the stellar contribution to the flux, the model can be written as
that of the star (both being normalized to an EW of unity), and C* the stellar contribution to the flux, the model can be written as
| |
= | ||
| (1) |
For all three WD model atmospheres, we obtained very good fits with no visible systematic residuals.
Given that the intrinsic H![]() /H
/H![]() nebular line ratio in TS 01 is not merely the case B recombination value, and given the additional problems with H
nebular line ratio in TS 01 is not merely the case B recombination value, and given the additional problems with H![]() (see Sect. 5.3.1),
we cannot use this ratio to evaluate the extinction. Hence, we used the
continuum to measure the latter. We first corrected the data for the
small foreground extinction (
E(B-V)=0.029) estimated by Schlegel et al. (1998).
Then, we removed most of the nebular or stellar lines from the
observations making use of a median filter. Finally, adopting the SMC
extinction law (Prévot et al. 1984; Bouchet et al. 1985)
and comparing the filtered spectrum with the theoretical continuum, we
evaluated the reddening and corrected the data for it. The choice of
the extinction law was motivated by the low metallicity of TS 01.
The reddening amounts obtained (additionally to the foreground one) are
E(B-V)=0.033, 0.044 and 0.050 for the 90, 120 and 150 kK WD models, respectively.
(see Sect. 5.3.1),
we cannot use this ratio to evaluate the extinction. Hence, we used the
continuum to measure the latter. We first corrected the data for the
small foreground extinction (
E(B-V)=0.029) estimated by Schlegel et al. (1998).
Then, we removed most of the nebular or stellar lines from the
observations making use of a median filter. Finally, adopting the SMC
extinction law (Prévot et al. 1984; Bouchet et al. 1985)
and comparing the filtered spectrum with the theoretical continuum, we
evaluated the reddening and corrected the data for it. The choice of
the extinction law was motivated by the low metallicity of TS 01.
The reddening amounts obtained (additionally to the foreground one) are
E(B-V)=0.033, 0.044 and 0.050 for the 90, 120 and 150 kK WD models, respectively.
The last processing of the data was the removal of the stellar and
nebular continua, to avoid the contamination of the nebular lines by
the underlying stellar features. We used the fit of the H![]() line to shift the theoretical stellar spectrum and nebular continuum
according to their evaluated radial velocities, convolved them by the
average instrumental PSF and subtracted them. Finally, we identified
visually the detectable lines and measured their fluxes. The fully
processed SDSS spectrum with the 90 kK WD model spectrum removed
is presented in Fig. 5, while Fig. 6
shows the result of the processing of the Kitt Peak spectrum. The
choice of the WD model had a moderate impact on the evaluation of the
line fluxes, of order of 2% for most of them and
line to shift the theoretical stellar spectrum and nebular continuum
according to their evaluated radial velocities, convolved them by the
average instrumental PSF and subtracted them. Finally, we identified
visually the detectable lines and measured their fluxes. The fully
processed SDSS spectrum with the 90 kK WD model spectrum removed
is presented in Fig. 5, while Fig. 6
shows the result of the processing of the Kitt Peak spectrum. The
choice of the WD model had a moderate impact on the evaluation of the
line fluxes, of order of 2% for most of them and ![]() in the worst case. The intensities of the SDSS spectrum and the Kitt Peak spectrum are listed in Table 2.
in the worst case. The intensities of the SDSS spectrum and the Kitt Peak spectrum are listed in Table 2.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f05.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg46.png)
|
Figure 5: Fully processed SDSS spectrum (dereddened, free of continuum and stellar lines). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f06.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg47.png)
|
Figure 6: Fully processed Kitt Peak spectrum (dereddened, free of continuum and stellar lines). |
| Open with DEXTER | |
2.3 Ultraviolet spectroscopy
2.3.1 HST STIS data
The HST STIS spectroscopic data correspond to the same proposal (ID 9466) as the imaging data.
A
![]() slit was used. It was oriented along
the bright jet-like emission of the nebula (PA 103
slit was used. It was oriented along
the bright jet-like emission of the nebula (PA 103![]() ), see Fig. 2.
), see Fig. 2.
Far UV observations
| Figure 7: 2D calibrated HST FUV spectrum of TS 01. |
|
| Open with DEXTER | |
The MAMA detector combined with a G140L grating provided 2D spectra
o8do03020,
o8do03030, o8do03040, o8do03050 and o8do03060, with 4675 s
exposure time each. The spectra cover a wavelength range from 1170
to 1700 Å, with a resolving power of 1190
at the central wavelength 1425 Å. The 2D spectra show a bright
blue stellar continuum and a few faint and extended
emission lines from the nebula. Calibrated 2D spectra were combined
(after
shifting because the spectroscopic observations were dithered) to
produce a 389.6 min spectrum. The resulting 2D spectrum is shown in
Fig. 7.
The stellar spectrum shows good signal-to-noise and stellar and
interstellar absorption are present. The analysis of the stellar
spectrum is presented in a companion paper (Tovmassian et al., in
prep.). Regarding nebular lines, the following ones are detected:
N V ![]() 1240, N IV]
1240, N IV] ![]() 1488, C IV]
1488, C IV] ![]() 1550 and He II]
1550 and He II] ![]() 1640. Selective absorption of resonance lines by the intervening interstellar medium is treated in Sect. 3.4.
1640. Selective absorption of resonance lines by the intervening interstellar medium is treated in Sect. 3.4.
From the combined 2D spectrum the nebular emission was extracted on both sides
of the central star, with an extraction window of 60 pixels, equivalent to
1.464
![]() .
Figure 8 is a combination of both nebular spectra. The line fluxes in each lobe and the combined values with respect He II]
.
Figure 8 is a combination of both nebular spectra. The line fluxes in each lobe and the combined values with respect He II] ![]() 1640 are listed in Table 3.
1640 are listed in Table 3.
Near UV observations
The MAMA detector combined with a G230LL grating provided 2D spectra
o8do02010,
o8do02020, o8do02030, o8do02040 and o8do02050, covering a wavelength
range
from about 1600 to 3150 Å. The calibrated 2D spectra were combined
(after
aligning) to produce a spectrum with a total exposure time
of 237.5 min. As for the FUV, the NUV stellar spectrum has
good signal-to-noise, and stellar and
interstellar absorption can be seen. However, no nebular lines are
detected. In particular, He II ![]() 1640, N III]
1640, N III] ![]() 1750, and C III]
1750, and C III] ![]() 1909 are not seen. Table 3 gives upper limits for the latter line intensities, with respect to He II
1909 are not seen. Table 3 gives upper limits for the latter line intensities, with respect to He II ![]() 1640, as seen in the FUV spectrum.
1640, as seen in the FUV spectrum.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12405f08.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg50.png)
|
Figure 8:
HST FUV nebular spectrum of TS 01, not corrected for reddening, showing the He II |
| Open with DEXTER | |
Table 3: Observed HST UV line fluxes, relative to He II 1640.
2.3.2 FUSE data
The observations of TS 01 with the Far Ultraviolet Spectroscopic Explorer (FUSE) and their reductions (done by G.T.) are described in Tovmassian et al. (2004). No emission lines were detected in the observed wavelength region between 900 and 1200 Å, except the H Ly![]() line. For the photoionization modelling of the nebula, it is important
to determine upper limits to the intensities of nebular lines expected
in this wavelength range. We proceeded in the following way. From a
previous model of TS 01 we took the computed nebular continuum. We
superimposed on it the lines C III
line. For the photoionization modelling of the nebula, it is important
to determine upper limits to the intensities of nebular lines expected
in this wavelength range. We proceeded in the following way. From a
previous model of TS 01 we took the computed nebular continuum. We
superimposed on it the lines C III ![]() 977.020, N III
977.020, N III ![]() 989.799 and He II
989.799 and He II ![]() 992.4
with FWHM of 0.1 Å (which corresponds to the measured expansion velocity of 30 km s-1, see Sect. 3.2). To this we added the central star model mentioned in Sect. 2.2.1.
The resulting spectrum was processed through the interstellar hydrogen
absorption simulator (http://violet.pha.jhu.edu/ gak/fwebsim.html) to be
compared with the observations.
It turned out that the corresponding lines start to be detectable in the
resulting spectrum when the line flux reaches approximately
992.4
with FWHM of 0.1 Å (which corresponds to the measured expansion velocity of 30 km s-1, see Sect. 3.2). To this we added the central star model mentioned in Sect. 2.2.1.
The resulting spectrum was processed through the interstellar hydrogen
absorption simulator (http://violet.pha.jhu.edu/ gak/fwebsim.html) to be
compared with the observations.
It turned out that the corresponding lines start to be detectable in the
resulting spectrum when the line flux reaches approximately
![]() erg cm-2 s-1.
Indeed, the wavelength region that we are exploiting here is very complicated.
Apart from the different interstellar absorptions and terrestrial airglow,
the lines in this region also lie at the edges of the detectors where they overlap, and
errors are much higher compared to other regions to the red.
erg cm-2 s-1.
Indeed, the wavelength region that we are exploiting here is very complicated.
Apart from the different interstellar absorptions and terrestrial airglow,
the lines in this region also lie at the edges of the detectors where they overlap, and
errors are much higher compared to other regions to the red.
2.4 Mid-infrared spectroscopy
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12405f09.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg52.png)
|
Figure 9:
LH infrared spectrum of TS 01 between 22 and 28 |
| Open with DEXTER | |
TS 01 was observed using the infrared spectrograph (IRS, Houck et al. 2004) on
board the Spitzer Space Telescope (Werner et al. 2004) on 22 April 2006
(program ![]() 20358). The observations used the short-high
(SH: 9.9-19.6
20358). The observations used the short-high
(SH: 9.9-19.6 ![]() m;
m;
![]() )
and long-high (LH:18.7-37.2
)
and long-high (LH:18.7-37.2 ![]() m;
m;
![]() )
modules. The aperture of the SH module is
)
modules. The aperture of the SH module is
![]() and of the
LH one is
and of the
LH one is
![]() ,
so the entire nebular flux was measured. The
details of the performed observations are shown in Table 1.
For LH we used four exposure cycles of 240 s each for on-source and off-source
observations, while for SH only on-source observations were performed with six exposure
cycles of 480 s each. The starting points for our interactive data reduction were the
co-added 2D flat-fielded BCD (basic calibrated DATA)
images (one for each node position; pipeline version 15.3 for
SH and 17.2 for LH). The rogue pixels were removed using the IRSCLEAN
tool
,
so the entire nebular flux was measured. The
details of the performed observations are shown in Table 1.
For LH we used four exposure cycles of 240 s each for on-source and off-source
observations, while for SH only on-source observations were performed with six exposure
cycles of 480 s each. The starting points for our interactive data reduction were the
co-added 2D flat-fielded BCD (basic calibrated DATA)
images (one for each node position; pipeline version 15.3 for
SH and 17.2 for LH). The rogue pixels were removed using the IRSCLEAN
tool![]() , with the aggressive parameter equal to 0.
Then the data were processed (full extraction, trimming, defringing and averaging over
cycles) into a single spectrum per node position using SMART
, with the aggressive parameter equal to 0.
Then the data were processed (full extraction, trimming, defringing and averaging over
cycles) into a single spectrum per node position using SMART![]() (Higdon et al. 2004).
A similar procedure has been applied
for LH off-source observations, and the obtained spectra have been
subtracted from the
on-source data for the corresponding node position, to cancel out the
sky background. The resulting spectrum between 22 and 28
(Higdon et al. 2004).
A similar procedure has been applied
for LH off-source observations, and the obtained spectra have been
subtracted from the
on-source data for the corresponding node position, to cancel out the
sky background. The resulting spectrum between 22 and 28 ![]() m is shown in Fig. 9.
For the high-resolution SH module no background subtraction was done since no sky
measurements were taken and the SH slit is too small for on-slit background subtraction.
Finally, the spectra obtained for both modules were averaged over two node positions, and
the detected nebular lines were measured within SMART.
m is shown in Fig. 9.
For the high-resolution SH module no background subtraction was done since no sky
measurements were taken and the SH slit is too small for on-slit background subtraction.
Finally, the spectra obtained for both modules were averaged over two node positions, and
the detected nebular lines were measured within SMART.
The resulting intensities are listed in Table 4 together with the estimated uncertainties. These uncertainties do not include possible calibration errors. It is generally considered that the absolute flux calibration has an accuracy of 20-30%. This will be taken into account in the modelling (see Sect. 4.2).
Table 4 also lists the blue-shifts of the lines. One can see that they are consistent with the optical measurements of Tovmassian et al. (2001).
2.5 XMM data
TS 01 has been also observed in the X-rays with XMM. The data acquisition and analysis is presented in Tovmassian et al. (in prep.).
3 What else do we know about TS 01 and its exciting star?
3.1 Extinction
TS 01 suffers only little extinction. Using the observed H![]() /H
/H![]() and H
and H![]() /H
/H![]() ratios, Richer et al. (2002) had found
ratios, Richer et al. (2002) had found
![]() mag.
However, this estimate was made without considering the underlying
stellar absorption in the Balmer lines. Due account for this effect
significantly reduces the estimated E(B-V), as
noted by Tovmassian et al. (2004). The extinction can also be
estimated by considering the spectral energy distribution of the
stellar core as observed in the far UV by FUSE. Assuming a temperature
of 120 kK for the central star, Tovmassian et al. (2004)
obtained a good fit to these observations for
E(B-V)=0.045 mag, when using a non-canonical value for RV of 2.3 and the interstellar reddening tables from Fitzpatrick (1999). Such a low value of RV
compared to the standard one of 3.1 was considered compatible with the
location of TS 01 well outside the galactic disk, since the
intervening dust is likely composed of smaller grains than in the
spiral arms. However, we now know that the temperature of the star
which dominates the UV continuum is much cooler (see Sect. 3.3
and Tovmassian et al., in prep.), implying that a steep reddening
law is not needed after all. In the remainder of the paper as well as
in Tovmassian et al. (in prep.) we use the Fitzpatrick (1999) reddening law parametrized with RV = 3.1, and take
E(B-V)=0.03 mag, which satisfactorily accounts for
the observed H and He line ratios as well as the observed continuum.
Note that the absence of an absorption dip at 2200 Å imposes an
upper limit of 0.06 for E(B-V).
mag.
However, this estimate was made without considering the underlying
stellar absorption in the Balmer lines. Due account for this effect
significantly reduces the estimated E(B-V), as
noted by Tovmassian et al. (2004). The extinction can also be
estimated by considering the spectral energy distribution of the
stellar core as observed in the far UV by FUSE. Assuming a temperature
of 120 kK for the central star, Tovmassian et al. (2004)
obtained a good fit to these observations for
E(B-V)=0.045 mag, when using a non-canonical value for RV of 2.3 and the interstellar reddening tables from Fitzpatrick (1999). Such a low value of RV
compared to the standard one of 3.1 was considered compatible with the
location of TS 01 well outside the galactic disk, since the
intervening dust is likely composed of smaller grains than in the
spiral arms. However, we now know that the temperature of the star
which dominates the UV continuum is much cooler (see Sect. 3.3
and Tovmassian et al., in prep.), implying that a steep reddening
law is not needed after all. In the remainder of the paper as well as
in Tovmassian et al. (in prep.) we use the Fitzpatrick (1999) reddening law parametrized with RV = 3.1, and take
E(B-V)=0.03 mag, which satisfactorily accounts for
the observed H and He line ratios as well as the observed continuum.
Note that the absence of an absorption dip at 2200 Å imposes an
upper limit of 0.06 for E(B-V).
3.2 Expansion velocity
Table 4: Observed mid IR line fluxes, in units of 10-21 W cm-2.
The expansion velocity of TS 01 has been measured by Richer et al. (2003).
This parameter is useful to estimate the expansion cooling in the
nebula. It also allows one to have an idea of the nebular dynamical
age. We adopt
![]() km s-1.
km s-1.
3.3 The stellar core
Our understanding of the stellar core of TS 01 has evolved
considerably since the first paper where it was suggested that
SBS 1150+599A is a high excitation planetary nebula (Tovmassian
et al. 2001) with a central star that has an effective temperature
above 100 000 K. Spectroscopic variations in the course of
one single night, reported in Tovmassian et al. (2004), indicated
the presence of a double system with a compact star. Photometric
observations then unambiguously determined a period of 3.92 h (Napiwotzki et al. 2005).
Analysis of the light curve indicated that the visible star is likely
an elongated ellipsoid irradiated by a source of higher energy. It also
supported the previous conclusion that the companion must be a (pre-?)
white dwarf or a neutron star. Finally, X-ray observations (Tovmassian et al. 2008,2007)
obtained with the XMM-Newton satellite directly revealed the light from
the companion, which turns out to be a hot compact star! Thus, as will
be shown later, the ``cool'' star is the one visible in the optical and
the UV and it provides most of the ionizing photons. But it is the
``hot'' star which gives rise to the high excitation lines observed in
the nebula. The best fit to the total spectral energy distribution of
the binary core indicates that the cool component has a temperature
![]() kK, while the hot component should have
kK, while the hot component should have
![]() kK. However, the determination of the temperature of the hot component is not very accurate.
Note that, in the scenario developped by Tovmassian et al. (in prep.), the hot component is an old white dwarf, which has a 170 kK temperature not
because it is still early on its cooling path, but because it was heated by nuclear burning of the
accreted material on its surface.
For the cool component Tovmassian et al. (in prep.) obtains the following:
kK. However, the determination of the temperature of the hot component is not very accurate.
Note that, in the scenario developped by Tovmassian et al. (in prep.), the hot component is an old white dwarf, which has a 170 kK temperature not
because it is still early on its cooling path, but because it was heated by nuclear burning of the
accreted material on its surface.
For the cool component Tovmassian et al. (in prep.) obtains the following:
![]() K,
K,
![]() .
The lower limit on the temperature is the intrinsic temperature of the
star, the upper limit corresponds to the zone heated by irradiation. It
is important to note that the cool component is not spherical and has
not only an inhomogeneous temperature distribution on its surface but
also an uneven gravitational acceleration. Its total luminosity is
estimated by Tovmassian et al. (in prep.) to be
.
The lower limit on the temperature is the intrinsic temperature of the
star, the upper limit corresponds to the zone heated by irradiation. It
is important to note that the cool component is not spherical and has
not only an inhomogeneous temperature distribution on its surface but
also an uneven gravitational acceleration. Its total luminosity is
estimated by Tovmassian et al. (in prep.) to be
![]()
![]() with about 30% uncertainty. Below we will consider for the sake of
simplicity that the cool star is sufficiently well represented by a
stellar model atmosphere with
with about 30% uncertainty. Below we will consider for the sake of
simplicity that the cool star is sufficiently well represented by a
stellar model atmosphere with
![]() kK and
kK and
![]() ,
with a total luminosity of 1700
,
with a total luminosity of 1700 ![]() .
.
The abundance analysis performed by T.R. on the cool star gives
![]() and
and
![]() ,
with an uncertainty of about 0.3 dex, and upper limits
,
with an uncertainty of about 0.3 dex, and upper limits
![]() and
and
![]() .
.
3.4 Interstellar absorption of nebular UV lines
In the course of his stellar atmosphere analysis, T.R. noted that the observed C IV ![]() 1550 Å and N V
1550 Å and N V ![]() 1240 Å
absorption lines were stronger than predicted by his best models. He
suggested that these lines are probably affected by interstellar
absorption. In that case, the intensities of the C IV
1240 Å
absorption lines were stronger than predicted by his best models. He
suggested that these lines are probably affected by interstellar
absorption. In that case, the intensities of the C IV ![]() 1550 Å and N V
1550 Å and N V ![]() 1240 Å
nebular lines are also affected by absorption. Since these lines are
crucial for the determination of the nebular abundances in TS 01,
we here explain how we corrected for this effect.
1240 Å
nebular lines are also affected by absorption. Since these lines are
crucial for the determination of the nebular abundances in TS 01,
we here explain how we corrected for this effect.
We use the following notations (all quantities are a function of wavelength):
![]() :
flux extracted at the position of the star;
:
flux extracted at the position of the star;
![]() :
flux extracted at the adjacent position in the nebula;
F*: real stellar flux;
:
flux extracted at the adjacent position in the nebula;
F*: real stellar flux;
![]() :
real nebular flux;
:
real nebular flux;
![]() :
sky emission and nebular continuum.
The optical depth due to interstellar absorption is denoted
:
sky emission and nebular continuum.
The optical depth due to interstellar absorption is denoted ![]() .
We have
.
We have
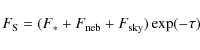
and
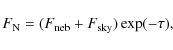
so that, in the spectrum analyzed by R.T., we have:
Concerning the C IV
Concerning the N V ![]() 1240 Å line, we find from Fig. 11
1240 Å line, we find from Fig. 11
![]() (red line in the figure),
(red line in the figure),
![]() (black line in the figure), leading to
(black line in the figure), leading to
![]() .
Therefore, if the measured nebular flux is
.
Therefore, if the measured nebular flux is
![]() (last column of Table 3), the nebular flux after correction for absorption is
(last column of Table 3), the nebular flux after correction for absorption is
![]() .
The uncertainty is larger here, since the line is weaker. We adopt 30%.
.
The uncertainty is larger here, since the line is weaker. We adopt 30%.
4 Photoionization modelling
4.1 Global strategy
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f10.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg88.png)
|
Figure 10: Stellar model atmosphere fitting of carbon lines in the stellar core of TS 01. Observation is in black. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f11.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg89.png)
|
Figure 11: Stellar model atmosphere fitting of nitrogen lines in the stellar core of TS 01. Observation is in black. |
| Open with DEXTER | |
| Figure 12:
Density structure of the nebula. Left: the chosen density structure of the model along the polar axis and along an axis perpendicular to it; middle: the resulting H |
|
| Open with DEXTER | |
We assume that the nebula is axisymmetric with its large axis in the
plane of the sky and that the lobes have a circular cross-section. By
trial and error, we choose a density structure to reproduce the
observed H![]() surface brightness distribution. The chosen density law along the polar
axis and along an axis perpendicular to it is shown in the left panel
of Fig. 12. The resulting H
surface brightness distribution. The chosen density law along the polar
axis and along an axis perpendicular to it is shown in the left panel
of Fig. 12. The resulting H![]() surface brightness distribution along the same axes is shown in the
middle panel of this figure (continuous lines) and is compared with the
observed distribution
surface brightness distribution along the same axes is shown in the
middle panel of this figure (continuous lines) and is compared with the
observed distribution![]() (dotted lines). The right panel shows the theoretical H
(dotted lines). The right panel shows the theoretical H![]() image, which can be compared with the observed image shown in Fig. 1,
especially as regards the width of the polar lobes. Note that the
density contrast between the lobes and the main body of the nebula is
very modest: only a factor of about 2.
The density distribution is parametrized by n0, the value of the density at the centre. For each run, we choose n0 in a way that, within a circle of a radius of 2.5
image, which can be compared with the observed image shown in Fig. 1,
especially as regards the width of the polar lobes. Note that the
density contrast between the lobes and the main body of the nebula is
very modest: only a factor of about 2.
The density distribution is parametrized by n0, the value of the density at the centre. For each run, we choose n0 in a way that, within a circle of a radius of 2.5
![]() ,
our model returns an HH
,
our model returns an HH![]() flux of
flux of
![]() erg cm-2 s-1, which corresponds to the observed extinction-corrected value from Richer et al. (2002)
erg cm-2 s-1, which corresponds to the observed extinction-corrected value from Richer et al. (2002)![]() . The value of n0 is thus dependent on the distance d for which the computations are made.
. The value of n0 is thus dependent on the distance d for which the computations are made.
The distance d in turn results from a fitting of the theoretical optical/UV continuum to the observed one (taking into account nebular continuum, aperture effects and reddening).
For the stars, we use model atmospheres computed by T.R. with the Tubingen NLTE model atmosphere package (TMAP). For the cool component, we use models tailored for our object. For the hot component, in absence of sufficient observational constraints, we chose among the complete flux tables for H-Ni models with halo composition (May 2001) downloaded from http://astro.uni-tuebingen.de/ rauch. Those models are described in Rauch (2003).
4.2 The ultraviolet, optical and infrared fluxes on the same scale
After a model has been run, the extinction-corrected line intensities are computed for each of the observing slits and are compared to the observations. This is the best way to deal with aperture corrections, in particular when combining UV and optical, or IR and optical data. Indeed, such a procedure accounts for the ionization structure of the object under study.
Absolute calibration of spectroscopic observations is
notoriously difficult. We intercalibrate the UV/optical data by forcing
the measured value of the He II ![]() 1640/He II
1640/He II ![]() 4686 ratio to the one predicted by our photoionization models in the corresponding slits. The value of
4686 ratio to the one predicted by our photoionization models in the corresponding slits. The value of
![]() ,
representing the factor by which the measured UV fluxes have to be multiplied for the He II
,
representing the factor by which the measured UV fluxes have to be multiplied for the He II ![]() 1640/He II
1640/He II ![]() 4686 ratio to be in agreement with the model, lies between 0.90 and 0.92 in our models. The value of
4686 ratio to be in agreement with the model, lies between 0.90 and 0.92 in our models. The value of
![]() is higher for models with higher electron temperature. To allow an
easier comparison between models and observations, we fix the value of
is higher for models with higher electron temperature. To allow an
easier comparison between models and observations, we fix the value of
![]() to 0.91.
to 0.91.
For Spitzer-IRS observations we multiply the observed fluxes by a factor
![]() which adjusts the observed values of [Ne V]
which adjusts the observed values of [Ne V] ![]() 24.3
24.3 ![]() m/[Ne V]
m/[Ne V] ![]() 3426 (after reddening correction) to the one predicted by the photoionization model in the corresponding slit. The values of
3426 (after reddening correction) to the one predicted by the photoionization model in the corresponding slit. The values of
![]() range between 0.87 and 0.95 for the models we considered. It might be
judged unreasonable to scale infrared fluxes using the [Ne V]
range between 0.87 and 0.95 for the models we considered. It might be
judged unreasonable to scale infrared fluxes using the [Ne V] ![]() 24.3
24.3 ![]() m/[Ne V]
m/[Ne V] ![]() 3426 ratio. However, in the electron temperature domain relevant for TS 01, this ratio does not vary very strongly (from
3426 ratio. However, in the electron temperature domain relevant for TS 01, this ratio does not vary very strongly (from
![]() kK to 40 kK, it decreases by only a factor of two). In any case, this is the only option we have to link the Spitzer line fluxes with the optical ones, since our Spitzer
data contain no H or He lines. Of course we bear this difficulty in
mind in the discussion. To remove the model dependance of the IR fluxes
correction, we fix the value of
kK to 40 kK, it decreases by only a factor of two). In any case, this is the only option we have to link the Spitzer line fluxes with the optical ones, since our Spitzer
data contain no H or He lines. Of course we bear this difficulty in
mind in the discussion. To remove the model dependance of the IR fluxes
correction, we fix the value of
![]() to 0.91.
to 0.91.
The fact that both
![]() and
and
![]() are found very close to unity is remarkable and means that the flux
calibration of the STIS and IRS LH spectra of TS 01 is excellent.
are found very close to unity is remarkable and means that the flux
calibration of the STIS and IRS LH spectra of TS 01 is excellent.
4.3 Judging a model
To judge a model it is convenient to divide the line ratios to be fitted into different categories:
- ratios of hydrogen lines or of helium lines: they probe the reddening law, the stellar underlying absorption, and the recombination line theory;
- ratios of two different ions of the same element, such as [O IV]
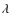 25.9
25.9 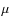 m/[O III]
m/[O III] 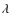 5007, N V
5007, N V 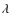 1240/[N IV]
1240/[N IV] 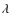 1486, [Ne V]
1486, [Ne V] 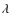 3426/[Ne III]
3426/[Ne III] 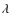 3869, and [Ne V]
3869, and [Ne V] 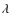 3426/[Ne IV]
3426/[Ne IV] 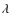 4720.
They basically test whether the ionization structure is well reproduced
by the model. In this category, we add the He II
4720.
They basically test whether the ionization structure is well reproduced
by the model. In this category, we add the He II 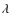 4686/HH
4686/HH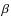 line ratio, which is more dependent on the ionization level of the nebula than on the abundance of helium;
line ratio, which is more dependent on the ionization level of the nebula than on the abundance of helium;
- ratios of lines used to determine the chemical composition: [O IV]
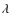 25.9
25.9 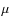 m/HH
m/HH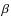 ,
C IV
,
C IV 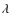 1549/HH
1549/HH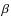 ,
N V
,
N V 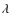 1240/HH
1240/HH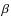 ,
and [Ne V]
,
and [Ne V] 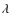 3426/HH
3426/HH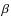 .
We also consider [O III]
.
We also consider [O III] 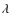 5007/HH
5007/HH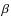 (although it is redundant with [O IV]
(although it is redundant with [O IV] 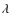 25.9
25.9 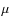 m/HH
m/HH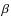 once the ionization structure is reproduced).
once the ionization structure is reproduced).
For all the observables considered (usually line ratios), we compute the value of
| (2) |
where
| (3) |
where
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12405f13.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg102.png)
|
Figure 13:
Graphic chart to compare the reference model with the measured line
ratios of TS 01. The numbers on the top of the panels indicate the
values of |
| Open with DEXTER | |
4.4 The reference model
Here we present our reference model, R. This is the model for which all the values of
![]() are as close as possible to zero, taking the following characteristics for the cool star:
are as close as possible to zero, taking the following characteristics for the cool star:
![]() kK,
kK,
![]() ,
,
![]()
![]() ,
and applying the extinction corrections with RV = 3.1 and
E(B-V)=0.03 mag as explained in Sect. 3.1.
The model contains graphite grains (as expected for a carbon-rich
planetary nebula, which is the case of TS 01 as seen below). The
grains have a standard size distribution and a total dust-to-gas mass
ratio of one tenth of the standard value. A larger abundance of grains
would bring the predicted continuum around 24
,
and applying the extinction corrections with RV = 3.1 and
E(B-V)=0.03 mag as explained in Sect. 3.1.
The model contains graphite grains (as expected for a carbon-rich
planetary nebula, which is the case of TS 01 as seen below). The
grains have a standard size distribution and a total dust-to-gas mass
ratio of one tenth of the standard value. A larger abundance of grains
would bring the predicted continuum around 24 ![]() m
into conflict with the observation. Below we explore deviations from
the reference model which still account for the observational data.
m
into conflict with the observation. Below we explore deviations from
the reference model which still account for the observational data.
The reference model has
![]() kK,
kK,
![]() ,
and a total luminosity
,
and a total luminosity
![]()
![]()
![]() ; n0=181 cm-3 and the following abundances, in units of
; n0=181 cm-3 and the following abundances, in units of
![]() X/H): H
X/H): H
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
The models and observations to which they are compared are presented in Table 5.
Column 1 of this table lists the line identifications, Col. 2
characterizes the observation using the following nomenclature: 0 for
CFHT 2003, 1 for STIS, 2 for FUSE, 3 for Spitzer, 4 for SDSS,
5 for CFHT 2001. For lines which belong to a wavelength range that was
not observed, the number 6 is attributed. Column 3 lists the
observed reddening-corrected line intensities (or their upper limits),
in units of HH![]() = 100 in the corresponding apertures. Column 4 lists the acceptable relative error
= 100 in the corresponding apertures. Column 4 lists the acceptable relative error ![]() O/O used to compute
O/O used to compute ![]() .
In the case of HST, FUSE and Spitzer data, we estimate the value of HH
.
In the case of HST, FUSE and Spitzer data, we estimate the value of HH![]() in the relevant aperture, based on our models (since, as explained in Sect. 4,
they deliver a smoothed version of the observed surface brightness
distribution). The top rows of Col. 5 of the table list the
characteristics of the reference model. The predicted line intensities
in the relevant aperture are given in the following rows in units of HH
in the relevant aperture, based on our models (since, as explained in Sect. 4,
they deliver a smoothed version of the observed surface brightness
distribution). The top rows of Col. 5 of the table list the
characteristics of the reference model. The predicted line intensities
in the relevant aperture are given in the following rows in units of HH![]() = 100
in the same aperture. For easier analysis, the next rows list a few
important line ratios, where the intensity of each line is measured
through the aperture corresponding to the observation. In order to
shorten the table, we do not list the lines for which the predictions
from all our models give values smaller than 0.001 of HH
= 100
in the same aperture. For easier analysis, the next rows list a few
important line ratios, where the intensity of each line is measured
through the aperture corresponding to the observation. In order to
shorten the table, we do not list the lines for which the predictions
from all our models give values smaller than 0.001 of HH![]() (we note that this is the case for all the recombination lines of
elements C, N, O). We list only the strongest H and He lines (we
checked that the weaker H I and He II lines always give
(we note that this is the case for all the recombination lines of
elements C, N, O). We list only the strongest H and He lines (we
checked that the weaker H I and He II lines always give
![]() in our models, implying that the correction for stellar absorption and reddening is satisfactory).
in our models, implying that the correction for stellar absorption and reddening is satisfactory).
The graphical representation of the line ratios predicted by model R and used to estimate the chemical composition of TS 01 is shown in Fig. 13. This is the kind of chart that was used in practice when judging the models that were run. A ``best model'' is one for which all the diamonds fall as close as possible to the ordinate 0. In any case, an acceptable model should have all line ratios represented by a diamond between the two horizontal lines, which represent a one-sigma deviation from the observed value. In addition, acceptable models should not return line intensities above the upper limits allowed by the observations.
Figure 14 shows
the monochromatic images of the reference model in various emission
lines. It reveals a few interesting features of the model: some lines,
such as [O III] ![]() 5007 and [Ne III]
5007 and [Ne III] ![]() 3869 arise mainly in the lobes. Other lines, such as C IV
3869 arise mainly in the lobes. Other lines, such as C IV ![]() 1549, N V
1549, N V ![]() 1240, and [Ne V]
1240, and [Ne V] ![]() 3426 line come from the entire nebula (in agreement with what Fig. 3 suggests for [Ne V]
3426 line come from the entire nebula (in agreement with what Fig. 3 suggests for [Ne V] ![]() 3426), while O VI
3426), while O VI ![]() 1032 and [Ne VI]
1032 and [Ne VI] ![]() 7.6
7.6![]() m (the latter not in the observed wavelength range) come from the innermost regions. We can also see that the two C III lines, C III]
m (the latter not in the observed wavelength range) come from the innermost regions. We can also see that the two C III lines, C III] ![]() 1909 and C III
1909 and C III ![]() 977, although produced by the same ion, come from different regions: C III
977, although produced by the same ion, come from different regions: C III ![]() 977 has an important component coming from the central main body (see Fig. 14), where the very high electron temperature allows for its excitation even if C++ is not very abundant there.
977 has an important component coming from the central main body (see Fig. 14), where the very high electron temperature allows for its excitation even if C++ is not very abundant there.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12405f14.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg121.png)
|
Figure 14:
Monochromatic images of the reference model in various lines (the
values of the wavelengths are in Å if they are larger than 900, and in |
| Open with DEXTER | |
Figure 15 compares the
observed energy distribution from TS 01 with the computed one. The
top panel shows the reddening-corrected flux computed for model R,
in erg cm-2 s-1 Å-1, in the wavelength range of 900 Å-40 ![]() m.
The observations are superimposed in various colours, as indicated in
the caption. One can see that the model reproduces the observed
spectral energy distribution quite well (except for the IRS SH
observations which could not be corrected for sky emission, as
explained in Sect. 2.4).
The bottom panel shows the energy distribution in the soft X-ray range:
the blue curve is the hot star, the green triangles are the XMM
observations. The flux from the star has been corrected for the nebular
absorption (computed by CLOUDY) and for the interstellar absorption,
taking a hydrogen column density of
m.
The observations are superimposed in various colours, as indicated in
the caption. One can see that the model reproduces the observed
spectral energy distribution quite well (except for the IRS SH
observations which could not be corrected for sky emission, as
explained in Sect. 2.4).
The bottom panel shows the energy distribution in the soft X-ray range:
the blue curve is the hot star, the green triangles are the XMM
observations. The flux from the star has been corrected for the nebular
absorption (computed by CLOUDY) and for the interstellar absorption,
taking a hydrogen column density of
![]() cm-2.
For each computed model we checked that the ionizing flux does not
violate the observed stellar emission up to 200 eV. At higher
energies, the observed emission may have another origin than the stars
we consider, but it does not affect our model fitting, since we have no
relevant observational constraints (the ion with the highest ionization
potential observed is Ne4+, which has an ionization potential of 97.1 eV).
cm-2.
For each computed model we checked that the ionizing flux does not
violate the observed stellar emission up to 200 eV. At higher
energies, the observed emission may have another origin than the stars
we consider, but it does not affect our model fitting, since we have no
relevant observational constraints (the ion with the highest ionization
potential observed is Ne4+, which has an ionization potential of 97.1 eV).
Figure 16 compares the energy distributions of the two stars considered in the modelling: the ``cool'' star is in red, the ``hot'' one is in blue. The sum of the two is in black. As mentioned in Sect. 3.3, the cool star dominates in the optical range (a few eV) and until about 20 eV, but it is the hot star which provides the photons with energies above 40-50 eV. Consequently it is the cool star which provides most of the H ionizing photons, but it is the hot star which provides the photons responsible for the presence of the He II, N V, [O IV], [Ne IV], [Ne V] and [Ar V] lines. This is a very uncommon situation, perhaps a unique case among planetary nebulae: TS 01 has two ionizing stars! This explains why our previous attempts to model the object were facing the difficulty that the nebula needed plenty of photons of energies above 54.4 eV, while the Balmer absorption lines in the stellar continuum indicated a moderate temperature.
From Figs. 13, 15, and Table 5 one can see that our reference model fits all the observational constraints very well. The only exception is that of C III] ![]() 1909,
whose intensity is slightly above the upper limit we gave to the STIS
observation. However, we consider this result to be still acceptable,
since upper limit fluxes for unobserved lines are difficult to estimate
accurately. The abundances of C, N, O, and Ne in the reference model
are, respectively, 1/3.5, 1/4.2, 1/70, and 1/11, and, for S and Ar <
1/30 of the solar values given by Asplund et al. (2005).
1909,
whose intensity is slightly above the upper limit we gave to the STIS
observation. However, we consider this result to be still acceptable,
since upper limit fluxes for unobserved lines are difficult to estimate
accurately. The abundances of C, N, O, and Ne in the reference model
are, respectively, 1/3.5, 1/4.2, 1/70, and 1/11, and, for S and Ar <
1/30 of the solar values given by Asplund et al. (2005).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12405f15.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg123.png)
|
Figure 15: Comparison of the reddened spectrum of the reference model with observations. Top: from the UV to the IR. The reddened model is in black. The colour code for the observations is as follows. Magenta: FUSE; blue: HST; green: SDSS ; red: Spitzer (the SH observations could not be sky-corrected). Bottom: X-ray domain. The model (with extinction applied) is in blue. The XMM observations are represented by triangles. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12405f16.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg124.png)
|
Figure 16: Spectral energy distribution (normalized to arbitrary units) of the radiation from the ionizing stars in the reference model. Red: the ``cold'' star; blue: the ``hot'' star; black: the sum of the two. |
| Open with DEXTER | |
5 The chemical composition of TS 01
5.1 Range of abundances for the reference model
Table 5:
Photoionization models versus observations. Line intensities are in units of H![]() in the corresponding aperture.
in the corresponding aperture.
We now investigate the error bars on abundances that are due only to
the uncertainties in the observed line intensities. Since C, N, O, and
Ne contribute very little to the energy budget, it is straightforward
to estimate from model R the minimum and maximum abundances
corresponding to the minimum and maximum values of [O IV] ![]() 25.9
25.9 ![]() m/HH
m/HH![]() ,
C IV
,
C IV ![]() 1549/HH
1549/HH![]() ,
N V
,
N V ![]() 1240/HH
1240/HH![]() ,
and [Ne V]
,
and [Ne V] ![]() 3426/HH
3426/HH![]() without changing the ionization structure of the nebula. However, one
has also to consider the error bars on line ratios that constrain the
ionization structure: [O IV]
without changing the ionization structure of the nebula. However, one
has also to consider the error bars on line ratios that constrain the
ionization structure: [O IV] ![]() 25.9
25.9 ![]() m/[O III]
m/[O III] ![]() 5007, N V
5007, N V ![]() 1240/[N IV]
1240/[N IV] ![]() 1486, [Ne V]
1486, [Ne V] ![]() 3426/[Ne III]
3426/[Ne III] ![]() 3869, and [Ne V]
3869, and [Ne V] ![]() 3426/[Ne IV]
3426/[Ne IV] ![]() 4720.
The minimum values of the C, N, O, and Ne abundances in TS 01 are
obtained by a model with the lowest ionization compatible with the
observations and the lower limits of [O IV]
4720.
The minimum values of the C, N, O, and Ne abundances in TS 01 are
obtained by a model with the lowest ionization compatible with the
observations and the lower limits of [O IV] ![]() 25.9
25.9 ![]() m/HH
m/HH![]() ,
C IV
,
C IV ![]() 1549/HH
1549/HH![]() ,
N V
,
N V ![]() 1240/HH
1240/HH![]() ,
and [Ne V]
,
and [Ne V] ![]() 3426/HH
3426/HH![]() .
Such a model, Mi, is reported in Col. 6 of Table 5. It is derived from the reference model R by lowering the values of
.
Such a model, Mi, is reported in Col. 6 of Table 5. It is derived from the reference model R by lowering the values of
![]() ,
and decreasing the values of the C, N, O, and Ne abundances. With
similar considerations, one can construct a model Ma, which will give
the maximum C, N, O, and Ne abundances. This model, with a higher
,
and decreasing the values of the C, N, O, and Ne abundances. With
similar considerations, one can construct a model Ma, which will give
the maximum C, N, O, and Ne abundances. This model, with a higher
![]() and same
and same
![]() is listed in Col. 7 of Table 5.
is listed in Col. 7 of Table 5.
The resulting limits on the abundances of C, N, O, and Ne in the gaseous phase![]() of TS 01 are thus:
of TS 01 are thus:
The limits on the C/O, N/O and Ne/O ratios are obtained by considering tailored models which reproduce the extreme values of the observed intensities of the C, N and Ne lines. They are:
To derive the lower limit on He/H, one must consider the model with the lowest ionization compatible with the observed [O IV]
5.2 Additional sources of abundance uncertainties
In this section, we discuss how reasonable variations of the parameters
that were so far fixed in the modelling procedure affect the derived
abundances. We also discuss some more general problems that may have an
influence on the estimated chemical composition of TS 01. To save
space, the models that were constructed to discuss these additional
uncertainties are not listed in the paper. We will only mention their
impact on the derived abundances. Note that all of those additional
models have the required angular size and total H![]() flux, and their abundances have been chosen to fit the observed emission line ratios.
flux, and their abundances have been chosen to fit the observed emission line ratios.
5.2.1 The effect of changing the description of the stars
So far, we have kept the parameters of the cool star fixed. Even if they are rather well determined, as explained in Sect. 3.3 and Tovmassian et al. (in prep.), it is important to see the effect that a change in those parameters implies on the derived chemical composition of the nebula. It turns out that an increase of 5 kK inWe then explored the effects of changing the parameters of the hot star. By increasing the temperature of the hot star by 10 kK, (implying a slight decrease of its luminosity to fit the observations) one decreases the C, N, O, Ne abundances of the fitted nebular model by about 0.2 dex.
We also explored the effect of changing the model atmosphere of the hot
star. One extreme case is to consider a model atmosphere composed only
of H and He, instead of the Galactic halo chemical composition.
Consequently, there are no absorption edges in the atmosphere above
54 eV. The model which fits the observations presents an intense
[Ne VI] ![]() 7.6
7.6![]() m
emission (unfortunately outside the wavelength range of our IRS
observations of TS 01). Its Ne abundance is higher by
0.15 dex than that of the reference model, while the abundances of
the remaining elements are almost unchanged.
m
emission (unfortunately outside the wavelength range of our IRS
observations of TS 01). Its Ne abundance is higher by
0.15 dex than that of the reference model, while the abundances of
the remaining elements are almost unchanged.
5.2.2 Dust issues
Concerning the extinction and reddening issues, a change of E(B-V) and RV within limits compatible with the observed Balmer decrement and the observed stellar energy distribution does not alter the abundances derived for TS 01 significantly.
Our reference model has a dust-to-gas mass ratio of 10-1 times the canonical value, with the canonical grain size distribution as stated in Sect. 4.4. The chemical composition of the grains - pure graphite - is dictated by the fact that the object is undoubtedly carbon-rich, as seen in Sects. 3.3 and 5.1. The total abundance of grains in the reference model is chosen in a way that the predicted infrared flux which arises from the heated grains does not exceed the observed IRS LH flux and that it produces no significant dip at 2200 Å, since this is not observed. The total amount of carbon locked in grains in the reference model is 0.4 times that of the abundance of carbon in the gas phase. This means that the total abundance of carbon in the nebula (gas plus grains) is larger by about 0.15 dex than given in Sect. 5.1.
5.2.3 The role of morphology
While constructing our reference model (and all the models described
before), we have chosen a geometry that reproduces the observed H![]() surface brightness, including the lobes. It is interesting to
experiment with a simpler model without any lobes, in which the
averaged surface brightness is the same as in the reference model. The
abundances in such a model differ insignificantly from those of the
reference model. We have to confess that we were somewhat surprised by
this result, since as shown in Fig. 14 the emission in such lines as [O III]
surface brightness, including the lobes. It is interesting to
experiment with a simpler model without any lobes, in which the
averaged surface brightness is the same as in the reference model. The
abundances in such a model differ insignificantly from those of the
reference model. We have to confess that we were somewhat surprised by
this result, since as shown in Fig. 14 the emission in such lines as [O III] ![]() 5007 or [Ne III]
5007 or [Ne III] ![]() 3869
traces the lobes very distinctly. On the other hand, one has to
remember that the density contrast between the lobes and the ambient
medium is only a factor of two, as seen in Fig. 12.
3869
traces the lobes very distinctly. On the other hand, one has to
remember that the density contrast between the lobes and the ambient
medium is only a factor of two, as seen in Fig. 12.
5.3 Caveats
5.3.1 The problem of H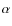
One of the intriguing problems in the observations of TS 01 is the behaviour of the H![]() line. As seen in Table 2, the observed H
line. As seen in Table 2, the observed H![]() /HH
/HH![]() ratio varies among data taken during different runs and at different
telescopes. Since the ratios of all the remaining hydrogen lines look
normal within the error bars, we are inclined to think that this H
ratio varies among data taken during different runs and at different
telescopes. Since the ratios of all the remaining hydrogen lines look
normal within the error bars, we are inclined to think that this H![]() problem has no influence on the derived chemical composition.
Nevertheless, we feel it important to try to understand the reason for
the observed values of H
problem has no influence on the derived chemical composition.
Nevertheless, we feel it important to try to understand the reason for
the observed values of H![]() /HH
/HH![]() .
.
In the present study, we have done the computations with the full
treatment of hydrogen as offered by CLOUDY (this, and not case B, is
actually the default option in CLOUDY). Under the physical conditions
in this nebula, one indeed does not expect the Balmer lines to be
emitted under case B, not even with the added effect of collisional
excitation. The ionization parameter of the emitting regions is high
and the nebula is optically thin, which renders it a good candidate for
case C as described by Baker & Menzel (1938) and reconsidered by Ferland (1999).
In such a case, absorption of Lyman photons from the star contributes
to the emission of the Balmer lines, and the Balmer decrement depends
on the number of respective Lyman line photons in the star. However, we
are far from reproducing the H![]() /HH
/HH![]() ratios observed in the various slits. Of course, the computed Balmer
decrement strongly depends on the fluxes at the wavelengths of the H
Lyman lines in the model atmosphere used. But the differences in the H
ratios observed in the various slits. Of course, the computed Balmer
decrement strongly depends on the fluxes at the wavelengths of the H
Lyman lines in the model atmosphere used. But the differences in the H![]() /HH
/HH![]() ratios in the different observing runs make it doubtful that simple stellar fluorescence can explain the observations.
ratios in the different observing runs make it doubtful that simple stellar fluorescence can explain the observations.
The reference model predicts a ratio of about 2.81.
The differences in the observed H![]() /HH
/HH![]() ratios cannot have a nebular origin since the associated time scales are far too long.
ratios cannot have a nebular origin since the associated time scales are far too long.
Water vapour absorption near H![]() is far too weak to explain the variations
is far too weak to explain the variations![]() .
Now that the nature of the binary central star is better known, we can also discard the possibility that much of the H
.
Now that the nature of the binary central star is better known, we can also discard the possibility that much of the H![]() emission comes from an accretion disc. Active mass transfer in the
system has ceased and, even if there is a stellar wind or weak remnant
of an accretion disc around the hot component, it cannot have a big
influence on emission lines, since we detect fairly symmetric
underlying absorption lines from the cool component at all orbital
phases. These symmetric lines also imply that extra emission from the
irradiated face of the cool component does not contribute any
significant H
emission comes from an accretion disc. Active mass transfer in the
system has ceased and, even if there is a stellar wind or weak remnant
of an accretion disc around the hot component, it cannot have a big
influence on emission lines, since we detect fairly symmetric
underlying absorption lines from the cool component at all orbital
phases. These symmetric lines also imply that extra emission from the
irradiated face of the cool component does not contribute any
significant H![]() emission.
emission.
The remaining option is atmospheric refraction (Filippenko 1982), since the slit was not oriented at the parallactic angle for many (though not all) of the spectra with H![]() /HH
/HH![]() ratios differing significantly from 2.81 (rather, usually east-west). What is odd
a priori,
if atmospheric refraction is responsible, is that the lines from H
ratios differing significantly from 2.81 (rather, usually east-west). What is odd
a priori,
if atmospheric refraction is responsible, is that the lines from H![]() to HH
to HH![]() are observed with constant intensity ratios.
Simulations in which we convolve the quantum efficiency of the slit camera used at SPM
are observed with constant intensity ratios.
Simulations in which we convolve the quantum efficiency of the slit camera used at SPM![]() with the object's very blue spectrum indicate that the effective
wavelength is between 4000 Å and 4500 Å. Thus, the effective
wavelength, which is what is used to centre the object in the slit, is
between the blue lines, so atmospheric refraction has very little
effect upon them. As a result, H
with the object's very blue spectrum indicate that the effective
wavelength is between 4000 Å and 4500 Å. Thus, the effective
wavelength, which is what is used to centre the object in the slit, is
between the blue lines, so atmospheric refraction has very little
effect upon them. As a result, H![]() should be the only optical line that may be significantly affected by
atmospheric refraction. Also, compared to the usual assumptions, the
wavelength baseline over which atmospheric refraction operates is
unusually large in this case, of the order of 2000 Å or more.
Tests using the SPM4 dataset (Richer et al. 2002),
in which this issue can be studied in greatest detail, clearly
implicate the effect of atmospheric refraction since the spectral shape
of the central star's continuum varies as a function of the difference
between the slit position angle and the parallactic angle. Therefore we
are inclined to attribute the variations observed in the H
should be the only optical line that may be significantly affected by
atmospheric refraction. Also, compared to the usual assumptions, the
wavelength baseline over which atmospheric refraction operates is
unusually large in this case, of the order of 2000 Å or more.
Tests using the SPM4 dataset (Richer et al. 2002),
in which this issue can be studied in greatest detail, clearly
implicate the effect of atmospheric refraction since the spectral shape
of the central star's continuum varies as a function of the difference
between the slit position angle and the parallactic angle. Therefore we
are inclined to attribute the variations observed in the H![]() /HH
/HH![]() ratio to atmospheric refraction.
ratio to atmospheric refraction.
5.3.2 Atomic data
As noted by Péquignot & Tsamis (2005), the atomic data on which photoionization models are built are not of perfect accuracy. All the models we have computed rely on CLOUDY c07.02.01. It is not excluded that future advances in atomic physics, especially in the calculation of recombination coefficients for highly ionized species, might affect the computed ionization structure. However, the fact that we now have observational data (or stringent upper limits) on several ions of each of the elements C, N, O and Ne in TS 01 makes us confident in the robustness of the chemical composition that we have derived. The relatively large error bars we obtain on the abundances (principally due to the lack of a direct measure of the electron temperature in the nebula) imply that the uncertainties in atomic data, including the collision strengths of the lines used for the diagnostics, should be negligible in the total error budget.
5.3.3 Dynamical effects
Schönberner et al. (2005) have
drawn attention to the possible importance of dynamical effects in the
thermal balance of nebulae. They make the point that the role of
dynamical expansion in the cooling budget increases as the metallicity
decreases. We have therefore included the effect of expansion cooling
in CLOUDY by introducing a wind cooling contribution in the routine ``cool\_eval.cpp'':
dynamics.dDensityDT = (float)(2.*fudge(0));with the user defined parameter ``fudge'' related to the expansion velocity and the outer radius of the nebula by
CoolHeavy.expans =
dense.pden*phycon.te*BOLTZMANN*dynamics.
dDensityDT;
All the models presented above have been computed with an expansion velocity of 30 km s-1, corresponding to the observed value (see Sect. 3.2). We have tried other values for
![]() in the equation above, but noted no significant changes in the output between 0 and 200 km s-1, the extreme values we tried.
This result is at variance with the finding by Schönberner et al. (2005)
that expansion cooling significantly reduces the temperature with
respect to a fully static model of the same density structure.
in the equation above, but noted no significant changes in the output between 0 and 200 km s-1, the extreme values we tried.
This result is at variance with the finding by Schönberner et al. (2005)
that expansion cooling significantly reduces the temperature with
respect to a fully static model of the same density structure.
In our models, the dominant cooling process is collisional excitation of H Ly![]() ,
and, at the ionization level predicted by the model, it is clear that
expansion cooling must be negligible, unless the velocity of the jet is
of the order of 1000 km s-1.
,
and, at the ionization level predicted by the model, it is clear that
expansion cooling must be negligible, unless the velocity of the jet is
of the order of 1000 km s-1.
Could it be that the lower temperature found by Schönberner et al. (2005)
in fully dynamical models with respect to hydrostatic ones, which they
attribute to expansion cooling, is actually the result of some other
process? The only idea that comes to mind is a departure from
ionization equilibrium. For an average temperature of 30 kK and an
average density of about 200 cm-3, the recombination time for hydrogen is about 103 yr.
From the apparent size, expansion velocity and distance to TS01, one can estimate an expansion time of ![]()
![]() yr. Therefore, the nebula should not be far from ionization equilibrium.
On the other hand, the dynamical model shown in Schönberner et al. (2005) was for a 0.595
yr. Therefore, the nebula should not be far from ionization equilibrium.
On the other hand, the dynamical model shown in Schönberner et al. (2005) was for a 0.595![]() star with an effective temperature of 100 kK, corresponding to an evolution time of
star with an effective temperature of 100 kK, corresponding to an evolution time of ![]()
![]() yr. The average density of the nebula in their simulation is then about 100 cm-3.
In such a situation, the nebula is farther from ionization equilibrium.
Since their star is in a phase where the number of ionizing photons
increases with time, the ionization level of the dynamical model should
be lower than that of the corresponding static model. Hence, Lyman
alpha cooling should be more important and the electron temperature
lower than in the hydrostatic model, which is indeed what their
dynamical model yields. In TS 01 the dynamical effects on the
ionization and temperature of the nebula should be much smaller than in
the case computed by Schönberner et al., if noticeable at all. In
their model, the temperature drop due to dynamical effects is about
10 kK. Given the argumentation above, we consider that any
dynamical effect on the electron temperature in TS 01 would be of
2-3 kK at most with respect to the temperature we compute in our
model. As an experiment, we computed a model where we use the CLOUDY
parameter ``cextra'' with a value of
10 -20.3 erg cm3 s-1
to simulate an extra cooling factor that reduces the average electron
temperature by about 3 kK with respect to the reference model. We
then adjusted the abundances to reproduce the observed line ratios. We
found that the abundances in this model are not very different from
those of model R. In particular, the abundance of O is not changed. The
reason is that the model must reproduce the [Ne V]
yr. The average density of the nebula in their simulation is then about 100 cm-3.
In such a situation, the nebula is farther from ionization equilibrium.
Since their star is in a phase where the number of ionizing photons
increases with time, the ionization level of the dynamical model should
be lower than that of the corresponding static model. Hence, Lyman
alpha cooling should be more important and the electron temperature
lower than in the hydrostatic model, which is indeed what their
dynamical model yields. In TS 01 the dynamical effects on the
ionization and temperature of the nebula should be much smaller than in
the case computed by Schönberner et al., if noticeable at all. In
their model, the temperature drop due to dynamical effects is about
10 kK. Given the argumentation above, we consider that any
dynamical effect on the electron temperature in TS 01 would be of
2-3 kK at most with respect to the temperature we compute in our
model. As an experiment, we computed a model where we use the CLOUDY
parameter ``cextra'' with a value of
10 -20.3 erg cm3 s-1
to simulate an extra cooling factor that reduces the average electron
temperature by about 3 kK with respect to the reference model. We
then adjusted the abundances to reproduce the observed line ratios. We
found that the abundances in this model are not very different from
those of model R. In particular, the abundance of O is not changed. The
reason is that the model must reproduce the [Ne V] ![]() 3426/[Ne III]
3426/[Ne III] ![]() 3869 ratio, which is nearly temperature-independent, and that ratios used to constrain the oxygen abundance ([O IV]
3869 ratio, which is nearly temperature-independent, and that ratios used to constrain the oxygen abundance ([O IV] ![]() 25.9
25.9 ![]() m/HH
m/HH![]() and [O III]
and [O III] ![]() 5007/HH
5007/HH![]() )
are not very sensitive to the temperature above 30 kK.
)
are not very sensitive to the temperature above 30 kK.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{12405f17.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg141.png)
|
Figure 17:
Comparison of TS 01 (filled red circle) with other Galactic PNe in
abundance ratios diagrams. The different black symbols represent: K648
(circle), DdDm-1 (square), PN006-41.9 (triangle), NGC 2242 (diamond),
NGC 4361 (plus sign), M2-29 (asterisk), H4-1 (star), PN 243.8-37.1
(filled triangle), and BoBn-1, which actually belongs to the
Sagittarius dwarf spheroidal galaxy ( |
| Open with DEXTER | |
5.4 Wrapping up
In summary, considering all the possible sources of uncertainties and adding in quadrature the various independent errors, we find that the elemental abundances in the gas phase of TS 01 are as listed in Table 6.
Table 6: Nebular abundances of TS 01, in various units.
An additional amount of carbon, about 40% of the total elemental
abundance, is locked up in dust grains. Allowance for this component
raises the carbon abundance in the nebula to
![]() .
.
The error bars on the derived abundances may seem large when compared to the typical error bars in other PNe. However, one must remember that the analysis of TS 01 is much more difficult, due to the absence of direct temperature diagnostics and to the weakness of the lines from metals.
The abundances derived for the nebula are consistent with those derived by T. R. for the atmosphere of the cool star, see Sect. 3.3, except for carbon whose abundance is larger by 0.8 dex in the nebula. This agreement is remarkable, given the difficulty of the analysis. Whether the discrepancy between the carbon stellar and nebular abundances is real should be examined in more detail.
6 Understanding the observed chemical composition
6.1 TS 01 compared to other Galactic halo PNe
Figure 17 shows the abundance pattern of TS 01 with respect to those of other PNe located in the Galactic halo as derived by Howard et al. (1997).
The panels in the top rows of this figure show the elemental abundances
with respect to oxygen as a function of O/H, a common way to display
abundances in PNe. As has been noted before, PNe belonging to the
Galactic halo display a large dispersion in their abundances relative
to oxygen![]() .
In this respect, TS 01 is not an exception. But it is extreme in
its value of O/H which is significantly lower than in other PNe of the
Galactic halo. On the other hand, the C/O, N/O, Ne/O ratios are similar
to the highest ones found in those objects. In the panels of the bottom
row, the abundance ratios are computed with respect to argon and
displayed as a function of 12 + log Ar/H. The reason for
doing this is that the abundance of Ar is not expected to be modified
with respect to the initial chemical composition out of which the
progenitor star was formed. Of course, the determination of the argon
abundance is much less accurate than that of oxygen. In the case of
TS 01, we even have only an upper limit. Yet, the bottom row of
Fig. 17 confirms the
impression that, regarding the chemical composition, TS 01 is
different from the remaining halo PNe especially because of its
remarkable low oxygen abundance. It may have the lowest Ar/H as well,
but we do not know, since we have only an upper limit on its abundance.
.
In this respect, TS 01 is not an exception. But it is extreme in
its value of O/H which is significantly lower than in other PNe of the
Galactic halo. On the other hand, the C/O, N/O, Ne/O ratios are similar
to the highest ones found in those objects. In the panels of the bottom
row, the abundance ratios are computed with respect to argon and
displayed as a function of 12 + log Ar/H. The reason for
doing this is that the abundance of Ar is not expected to be modified
with respect to the initial chemical composition out of which the
progenitor star was formed. Of course, the determination of the argon
abundance is much less accurate than that of oxygen. In the case of
TS 01, we even have only an upper limit. Yet, the bottom row of
Fig. 17 confirms the
impression that, regarding the chemical composition, TS 01 is
different from the remaining halo PNe especially because of its
remarkable low oxygen abundance. It may have the lowest Ar/H as well,
but we do not know, since we have only an upper limit on its abundance.
As can be seen from Fig. 17, the progenitors of many of the PNe belonging to the Galactic halo underwent considerable nuclear processing, which affected not only the helium, carbon and nitrogen abundances in the nebulae, but also the oxygen one. In such a situation, the metallicity of the progenitor - generally identified with the oxygen abundance in the nebula - cannot be easily determined. If one uses the sum of the mass-fraction abundances of C, N, O, Ne, S, and Ar as a proxy for the upper limit of the metallicity, we find that in solar units, TS 01 has a metallicity of at most 1/12 solar, well below the upper limits for the remaining halo PNe. If we take the argon abundance as a proxy for the metallicity, we find that the metallicity of TS 01 is less than 1/30 solar. The two other halo PNe with very low metallicity, using this criterion, are BoBn-1 (1/20 solar) and K 648, which holds the record from this point of view (1/300 solar).
6.2 What we know of the progenitor of TS 01
Let us first summarize the main features of a possible evolution of
the stellar core of TS 01 as explained in Tovmassian et al.
(2007, 2008, and in prep.). The total mass of the system is close to
1.4 ![]() .
The mass of the cool component is
(0.5-0.6)
.
The mass of the cool component is
(0.5-0.6) ![]() .
Then the mass of the hot component must be (0.8-0.9)
.
Then the mass of the hot component must be (0.8-0.9) ![]() .
For
.
For
![]() this implies that its progenitor had a mass of
this implies that its progenitor had a mass of
![]() 3
3 ![]() (Hurley et al. 2000). Star formation in the halo ceased at least 10 Gyr ago, see e.g. Marín-Franch et al. (2009).
Since the lifetime of a (2-3)
(Hurley et al. 2000). Star formation in the halo ceased at least 10 Gyr ago, see e.g. Marín-Franch et al. (2009).
Since the lifetime of a (2-3) ![]() star with
star with
![]() is
is ![]() 300 Myr,
the first Roche lobe overflow occurred at least 10 Gyr ago. It
resulted in a common envelope with inefficient accretion, hardly more
than
300 Myr,
the first Roche lobe overflow occurred at least 10 Gyr ago. It
resulted in a common envelope with inefficient accretion, hardly more
than ![]() 0.01
0.01 ![]() (Yungelson et al. 1995). The initially more massive star of the system turned into the currently hot component. Since we observe a PN now,
the companion of the hot component must have completed its evolution in
10 Gyr. The least massive star able to do this had a mass of about
0.9
(Yungelson et al. 1995). The initially more massive star of the system turned into the currently hot component. Since we observe a PN now,
the companion of the hot component must have completed its evolution in
10 Gyr. The least massive star able to do this had a mass of about
0.9 ![]() after the first common envelope stage.
When this low mass star evolved off the main sequence,
a symbiotic system formed. Mass transfer during this stage was
negligible as well. The symbiotic stage ended when the low mass star
filled its Roche lobe on the AGB. Again, a
common envelope formed, reducing the separation of the components and
diminishing the orbital period to 3.9 h. The nebula we observe now
is the remnant of this second common envelope.
after the first common envelope stage.
When this low mass star evolved off the main sequence,
a symbiotic system formed. Mass transfer during this stage was
negligible as well. The symbiotic stage ended when the low mass star
filled its Roche lobe on the AGB. Again, a
common envelope formed, reducing the separation of the components and
diminishing the orbital period to 3.9 h. The nebula we observe now
is the remnant of this second common envelope.
6.3 Can standard single AGB models explain the observed abundance pattern?
We consulted the available
yields from recent standard
evolution models for single stars at low metallicities
(see Karakas & Lattanzio 2003;
and Cristallo et al. 2009).
The corresponding nucleosynthetic predictions for low-mass AGBs show
the signature of recurring third dredge-up episodes that increase
the surface abundances of C as well as (but to a lower extent) that of
O and N. This is at odds with the abundance patterns determined in
TS 01, which exhibits an extreme O depletion.
As a matter of fact,
only massive AGB models (
![]()
![]() )
predict O depletion as a result of hot bottom burning (HBB)
during the thermal pulse AGB phase (TP-AGB). Besides being in conflict
with the binary analysis recalled above, these massive AGB models are
facing other difficulties. First,
they predict that carbon also should be depleted by the CNO-cycle
in the envelope.
Second, such massive AGB stars are predicted to
experience a deep second dredge-up
that increases the He abundance
well above the observed value (number ratio of
)
predict O depletion as a result of hot bottom burning (HBB)
during the thermal pulse AGB phase (TP-AGB). Besides being in conflict
with the binary analysis recalled above, these massive AGB models are
facing other difficulties. First,
they predict that carbon also should be depleted by the CNO-cycle
in the envelope.
Second, such massive AGB stars are predicted to
experience a deep second dredge-up
that increases the He abundance
well above the observed value (number ratio of
![]() ,
thus
,
thus
![]() in mass fraction).
in mass fraction).
6.4 Towards an explanation of the chemical composition of TS 01
We note however that those models use standard assumptions. In particular they do not account for rotation-induced mixing that is known to affect stellar evolution and nucleosynthesis (see Decressin et al. 2009b and references therein). Additionally, the rotational transport itself may have been strengthened by the stellar coupling in the binary system (see e.g. de Mink et al. 2009; Pols et al. 1997). Unfortunately binary stellar models which treat the effect of mixing on the nucleosynthesis of low-mass stars are not yet available, but we can use single rotating AGB models to infer the impact of mixing during the pre-AGB phase on the surface chemical composition.
We thus compare the abundance obtained for our nebula to standard and
rotating models of a 1 ![]() star computed with the code
STAREVOL (V2.92) (Siess 2006; Siess et al. 2000) from the pre-main
sequence to the end of the TP-AGB phase (for more details, see Decressin et al. 2009a). In the rotating model, an initial rotation of
100 km s-1 is assumed on the zero age main sequence. This is the mean value given by
Gaige (1993) for a star with the effective temperature
of our models near the ZAMS (
star computed with the code
STAREVOL (V2.92) (Siess 2006; Siess et al. 2000) from the pre-main
sequence to the end of the TP-AGB phase (for more details, see Decressin et al. 2009a). In the rotating model, an initial rotation of
100 km s-1 is assumed on the zero age main sequence. This is the mean value given by
Gaige (1993) for a star with the effective temperature
of our models near the ZAMS (![]() 7000 K).
This observational value is
obtained from stars in the Hyades, which are more metal-rich than our
model. If low-metallicity stars are born with the same amount of angular
momentum we could expect, due to their compactness, an even higher
initial velocity. Thus our model indicates the minimal chemical changes we
would obtain when rotation is taken into account.
7000 K).
This observational value is
obtained from stars in the Hyades, which are more metal-rich than our
model. If low-metallicity stars are born with the same amount of angular
momentum we could expect, due to their compactness, an even higher
initial velocity. Thus our model indicates the minimal chemical changes we
would obtain when rotation is taken into account.
The
transport of angular momentum and chemical species is driven by meridional
circulation and shear turbulence (Maeder & Zahn 1998; Zahn 1992). The metallicity
is set to
![]() (i.e.,
(i.e.,
![]() ), which
corresponds to the upper limit for the metallicity derived from the Ar
abundance in TS 01. The composition is scaled to the solar one according to the
Grevesse & Sauval (1998) mixture, and enhancement in
), which
corresponds to the upper limit for the metallicity derived from the Ar
abundance in TS 01. The composition is scaled to the solar one according to the
Grevesse & Sauval (1998) mixture, and enhancement in ![]() -elements
([
-elements
([![]() /Fe] = +0.3 dex) is accounted for. We use the OPAL opacity
tables (Iglesias & Rogers 1996) above a temperature of 8 kK that account for C and O
enrichments, and the Ferguson et al. (2005) data at lower
temperatures. We follow the evolution of 53 chemical species from 1H to
37Cl. We use the NACRE nuclear reaction rates
(Angulo et al. 1999) by default and those by
Caughlan & Fowler (1988) otherwise (see Siess & Arnould 2008). The
treatment of convection is based on the classical mixing length formalism
with
/Fe] = +0.3 dex) is accounted for. We use the OPAL opacity
tables (Iglesias & Rogers 1996) above a temperature of 8 kK that account for C and O
enrichments, and the Ferguson et al. (2005) data at lower
temperatures. We follow the evolution of 53 chemical species from 1H to
37Cl. We use the NACRE nuclear reaction rates
(Angulo et al. 1999) by default and those by
Caughlan & Fowler (1988) otherwise (see Siess & Arnould 2008). The
treatment of convection is based on the classical mixing length formalism
with
![]() ,
and
diffusive
overshoot is added below the
convective envelope according to Herwig (2000). The mass loss rate is
computed with the Reimers (1975) formula (with
,
and
diffusive
overshoot is added below the
convective envelope according to Herwig (2000). The mass loss rate is
computed with the Reimers (1975) formula (with
![]() )
for
the pre-AGB phase and then we use the Vassiliadis & Wood (1993) one during the AGB
phase. We also add diffusive overshoot following Herwig (2000) to allow for a
third-dredge up during the AGB phase.
)
for
the pre-AGB phase and then we use the Vassiliadis & Wood (1993) one during the AGB
phase. We also add diffusive overshoot following Herwig (2000) to allow for a
third-dredge up during the AGB phase.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{12405f18.eps}\vspace*{-1mm}
\vspace*{-1mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg166.png)
|
Figure 18:
Comparison of the chemical composition in TS 01 with the results
of stellar evolution models for a star with an initial mass 1 |
| Open with DEXTER | |
7 Conclusions
The planetary nebula PN G 135.9+55.9 (SBS 1150+599A), here referred to as TS 01, has been a source of many surprises. It is the most oxygen-poor planetary nebula known. Its stellar core consists of a close binary, whose period of approximately 3.9 h is the shortest known of any planetary nebula nucleus. The binary nucleus is the first known example of a double degenerate system in a planetary nebula. It is also the best candidate progenitor of a type Ia supernova. Here we consider the chemical composition of the nebular shell in detail. In a companion paper, Tovmassian et al. (in prep.) study the nature, history, and evolution of the binary system.We have obtained observational data in a complete wavelength range in order to pin down the abundances of half a dozen of elements in TS 01. The data consist of imaging and spectroscopy in the UV, optical and IR ranges. Optical data were obtained at different telescopes, resulting in high quality and reliable observational material for this object which exhibits an exceptionally line-poor optical spectrum.
We then defined a strategy to determine the abundances in TS 01. Since no direct electron temperature diagnostic is available, it was necessary to apply tailored photoionization modelling. We did this with much care, taking into account all the observational information at our disposal, in order to minimize the uncertainties in the derived abundances. The photoionization modelling was performed using the pseudo-3D photoionization code Cloudy_3D based on CLOUDY (version c07.02.01). Using CLOUDY, we took advantage of its detailed treatment of the hydrogen atom, which is crucial in this density-bounded nebula. Using the 3D features allowed us to take into account the apparent geometry of the nebula and the location, sizes and orientations of the observing slits, thus minimizing the errors linked to aperture effects. The spectral energy distribution of the ionizing radiation was obtained from appropriate model atmospheres.
One interesting feature of TS 01 is that both its stellar components contribute to its ionization: the ``cool'' one provides the bulk of hydrogen ionization, and the ``hot'' one is responsible for the presence of the most highly charged ions. Thus one can say that TS 01 has two ionizing stars. This is the first such case discovered among planetary nebulae!
The abundances of C, N, O, and Ne in the nebula are found to be
1/3.5, 1/4.2, 1/70, and 1/11 of the solar value, respectively, with
error bars of ![]() 0.3 dex.
For S and Ar, the abundances are less than 1/30 of solar. This makes of
TS 01 the planetary nebula with the most extreme composition known
so far. In particular, it is by far the most oxygen-deficient. The
abundance of helium is 12 + log He/H = 10.95, with an accuracy that is
not as high as one might have desired (
0.3 dex.
For S and Ar, the abundances are less than 1/30 of solar. This makes of
TS 01 the planetary nebula with the most extreme composition known
so far. In particular, it is by far the most oxygen-deficient. The
abundance of helium is 12 + log He/H = 10.95, with an accuracy that is
not as high as one might have desired (![]() 0.04 dex).
The nebular abundances in TS 01 are found to be consistent with
those in the atmosphere of the cool star, except for carbon which
appears higher by
0.04 dex).
The nebular abundances in TS 01 are found to be consistent with
those in the atmosphere of the cool star, except for carbon which
appears higher by ![]() 0.8 dex than in the star.
0.8 dex than in the star.
The observed properties of the stellar core allow us to put limits on
the
masses and age of the binary system, as explained in Tovmassian
et al. (in prep.) and recalled in the present paper. In
particular, the initial
mass of the progenitor of the present nebula was ![]() 0.9
0.9 ![]() .
We have computed state-of-the-art AGB models
with appropriate mass and metallicity to compare them with the chemical composition of TS 01.
While a non-rotating model cannot explain the observed abundance patterns, the introduction of a 100 km s-1 initial rotation in the model (which may be seen as a way to mimick the mixing due to the presence of the companion)
greatly improves the comparison. Rotation-induced mixing leads to low O and high N abundances already at the
end of the second dredge-up, whereas the C abundance increases afterwards
during each third dredge-up.
However, to fully reproduce the observed pattern requires the
binary interactions (and especially the first episode of mass transfer)
to spin up the star to produce a very efficient mixing. This conjecture
still needs to be verified by proper binary models.
.
We have computed state-of-the-art AGB models
with appropriate mass and metallicity to compare them with the chemical composition of TS 01.
While a non-rotating model cannot explain the observed abundance patterns, the introduction of a 100 km s-1 initial rotation in the model (which may be seen as a way to mimick the mixing due to the presence of the companion)
greatly improves the comparison. Rotation-induced mixing leads to low O and high N abundances already at the
end of the second dredge-up, whereas the C abundance increases afterwards
during each third dredge-up.
However, to fully reproduce the observed pattern requires the
binary interactions (and especially the first episode of mass transfer)
to spin up the star to produce a very efficient mixing. This conjecture
still needs to be verified by proper binary models.
One feature for which we have no explanation so far is the fact that the carbon abundance in the nebula seems to be much higher than in its progenitor. This fact would need to be confirmed with deeper observations in the optical and the UV though.
With respect to our first publication on TS 01 by Tovmassian et al. (2001), our understanding of the status and properties of this object has thus made enormous progress. While this object is unique when considering all its observed properties together, similar objects might be plentiful in the Galactic halo - although not necessarily in a stage exhibiting a detectable planetary nebula.
AcknowledgementsThis work, which extended over a period of more than seven years, could be accomplished thanks to extensive use of e-mail, short visits and informal meetings on the occasion of conferences. We thank Gary Ferland and his associates for having offered CLOUDY to the community. We are indebted to A. Weiss for providing unpublished evolutionary tracks. We are grateful to Yuri Izotov for sending the TS 01 spectrum he obtained at Kitt Peak and for drawing our attention to the existence of this object in the SDSS data base (he found it while examining by eye the hundreds of thousands of spectra from the main galaxy sample!). Funding for the Sloan Digital Sky Survey (SDSS) has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. G.S. and S.S.-D. acknowledge the hospitality and financial support of the Instituto de Astronomia of the UNAM in Mexico City and Ensenada during many visits. C.M. acknowledges the hospitality and support of the Observatoire de Paris and the grant CONACyT-49749. G.S., C.M., R.Sz, R.N., S.S.-D. acknowledge support from the European Associated Laboratory ``Astrophysics Poland-France''. G.T. acknowledges a grant from UC-MEXUS, which made his stay at CASS UCSD possible and continuous support from CONACyT. T.R. is supported by the German Federal Ministry of Education and Research (BMBF) grant 50 OR 0806. M.R. acknowledges the following grants: CONACyT 43121 and 82066, DGAPA-UNAM IN116908, 112103, 108506, and 108406. M.P. acknowledges financial support from UNAM-DGAPA grants IN118405 and IN112708 and from a CONACyT-CNRS 2008 project. R.Sz. acknowledge partial support from grant N203 393334 of MNiSW/Poland. C.C. and T.D. acknowledge financial support from the French Programme National de Physique Stellaire (PNPS) of CNRS/INSU, and from the Swiss National Science Foundation (FNS). L.Yu. acknowledges support from RFBR grant 07-02-00454 and Presidium of the Russian Academy of Sciences Program ``Origin, Evolution and Structure of the Universe Objects''. S.S.-D. acknowledges support from the Spanish Ministerio de Educación y Ciencia under the MEC/fulbright postdoctoral program.
Note added in proof.
Sandin et al. (arXiv:0912.5430)
recently derived the nebular abundances in PN G 135.9+55.9 using
hydrodynamical models, and claim that in this object, departure from
thermal equilibrium leads to lower electron temperatures and hence
weaker emission in collisionally excited lines. The abundances they
give, however, turn out to be similar to the ones we find within the
error bars that we provide (and which actually take into account the
uncertainty due to dynamical effects). The reason for this similarity
is partly fortuitous. Briefly, the observational constraints they
consider are not exactly the same as ours. In particular, these authors
do not correct the C IV ![]() 1549
line for absorption, nor do they consider depletion unto dust grains,
they do not take into account aperture effects, and they do not compare
their computed infrared line fluxes to observed ones. On the other
hand, the scenario they adopt for their hydrodynamical model (a single
star with mass 0.595
1549
line for absorption, nor do they consider depletion unto dust grains,
they do not take into account aperture effects, and they do not compare
their computed infrared line fluxes to observed ones. On the other
hand, the scenario they adopt for their hydrodynamical model (a single
star with mass 0.595![]() )
contradicts our observations of the stellar core (see Tovmassian et al.
2007, and Sects. 3 and 6 of our paper). As explained in Sect. 5.3
of our paper, the dynamical effects in PN G 135.9+55.9 must be less
important than they claim.
)
contradicts our observations of the stellar core (see Tovmassian et al.
2007, and Sects. 3 and 6 of our paper). As explained in Sect. 5.3
of our paper, the dynamical effects in PN G 135.9+55.9 must be less
important than they claim.
References
- Acker, A., Marcout, J., Ochsenbein, F., Stenholm, B., & Tylenda, R. 1992, Strasbourg - ESO catalogue of galactic planetary nebulae. Part 1; Part 2 (Garching: European Southern Observatory) [Google Scholar]
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2008, ApJS, 175, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nuclear Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. T. G. Barnes, III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Baker, J. G., & Menzel, D. H. 1938, ApJ, 88, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchet, P., Lequeux, J., Maurice, E., Prevot, L., & Prevot-Burnichon, M. L. 1985, A&A, 149, 330 [NASA ADS] [Google Scholar]
- Caughlan, G. R., & Fowler, W. A. 1988, Atomic Data and Nuclear Data Tables, 40, 283 [Google Scholar]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Cantiello, M., Langer, N., et al. 2009, A&A, 497, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decressin, T., Charbonnel, C., Siess, L., et al. 2009a, A&A, 505, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decressin, T., Mathis, S., Palacios, A., et al. 2009b, A&A, 495, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J. 1999, PASP, 111, 1524 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Filippenko, A. V. 1982, PASP, 94, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Gaige, Y. 1993, A&A, 269, 267 [NASA ADS] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Higdon, S. J. U., Devost, D., Higdon, J. L., et al. 2004, PASP, 116, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Houck, J. R., Roellig, T. L., van Cleve, J., et al. 2004, ApJS, 154, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, J. W., Henry, R. B. C., & McCartney, S. 1997, MNRAS, 284, 465 [NASA ADS] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., Feldmeier, J. J., Claver, C. F., et al. 2002, AJ, 124, 3340 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., Garnavich, P. M., Bond, H. E., et al. 2006, in Planetary Nebulae in our Galaxy and Beyond, ed. M. J. Barlow, & R. H. Méndez, IAU Symp., 234, 431 [Google Scholar]
- Karakas, A. I., & Lattanzio, J. C. 2003, PASA, 20, 279 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., et al. 2006, ApJS, 162, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Crampton, D., Felenbok, P., & Monnet, G. 1994, A&A, 282, 325 [NASA ADS] [Google Scholar]
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
- Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- McCall, M. L., Rybski, P. M., & Shields, G. A. 1985, ApJS, 57, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Morisset, C. 2006, in Planetary Nebulae in our Galaxy and Beyond, ed. M. J. Barlow, & R. H. Méndez, IAU Symp., 234, 467 [Google Scholar]
- Napiwotzki, R., Tovmassian, G., Richer, M. G., et al. 2005, in Planetary Nebulae as Astronomical Tools, ed. R. Szczerba, G. Stasinska, & S. K. Gorny, AIP Conf. Ser., 804, 173 [Google Scholar]
- Péquignot, D., & Tsamis, Y. G. 2005, A&A, 430, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pols, O. R., Tout, C. A., Schroder, K.-P., Eggleton, P. P., & Manners, J. 1997, MNRAS, 289, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Prévot, M. L., Lequeux, J., Prevot, L., Maurice, E., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [NASA ADS] [Google Scholar]
- Rauch, T. 2003, A&A, 403, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reimers, D. 1975, Circumstellar envelopes and mass loss of red giant stars (Problems in stellar atmospheres and envelopes), 229 [Google Scholar]
- Richer, M. G., López, J. A., Steffen, W., et al. 2003, A&A, 410, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richer, M. G., Tovmassian, G., Stasinska, G., et al. 2002, A&A, 395, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schönberner, D., Jacob, R., Steffen, M., & Roth, M. M. 2005, in Planetary Nebulae as Astronomical Tools, ed. R. Szczerba, G. Stasinska, & S. K. Gorny, AIP Conf. Ser., 804, 269 [Google Scholar]
- Siess, L. 2006, A&A, 448, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L., & Arnould, M. 2008, A&A, 489, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
- Stepanian, J. A., Chavushyan, V. H., Carrasco, L., Tovmassian, H. M., & Erastova, L. K. 1999, PASP, 111, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Storey, P. J., & Hummer, D. G. 1995, MNRAS, 272, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Tovmassian, G., Tomsick, J., Napiwotzki, R., et al. 2007 [arXiv:0709.4016] [Google Scholar]
- Tovmassian, G., Tomsick, J., Napiwotzki, R., et al. 2008, in Astrophysics of Compact Objects, ed. Y.-F. Yuan, X.-D. Li, & D. Lai, AIP Conf. Ser., 968, 62 [Google Scholar]
- Tovmassian, G. H., Stasinska, G., Chavushyan, V. H., et al. 2001, A&A, 370, 456 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tovmassian, G. H., Napiwotzki, R., Richer, M. G., et al. 2004, ApJ, 616, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
- Yungelson, L., Livio, M., Tutukov, A., & Kenyon, S. J. 1995, ApJ, 447, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
Footnotes
- ... star
![[*]](/icons/foot_motif.png)
- Based on observations obtained at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council of Canada, the Institut National des Sciences de l'Univers of the Centre National de la Recherche Scientifique of France, and the University of Hawaii.
- ...
![[*]](/icons/foot_motif.png)
- Based on observations with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555.
- ...
![[*]](/icons/foot_motif.png)
- Based on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under NASA contract 1407.
- ... fits
![[*]](/icons/foot_motif.png)
- This treatment was applied well before we had understood that the optical continuum was dominated by a star of 55 kK (see Sect. 3.3). In view of the fact that the lines we use for the dignostics discussed in the present paper are hardly affected by this correction, we decided not to redo the subtraction using more adequate model stellar spectra.
- ... 0953-52411-160
![[*]](/icons/foot_motif.png)
- The analysis by L.J. was done soon after our discovery of the spectrum in SDSS data release 2. In data release 6 (Adelman-McCarthy et al. 2008), SDSS spectra were recalibrated, resulting in an increase of about 30% of the fluxes of TS 01. Line ratios remained unchanged. Therefore, the analysis of L.J. remains valid. On the other hand, whenever we needed to consider the TS 01 continuum in this paper, we used the recalibrated spectrum.
- ...
tool
![[*]](/icons/foot_motif.png)
- This tool is available from the Spitzer Science Center website: http://ssc.spitzer.caltech.edu.
- ... SMART
![[*]](/icons/foot_motif.png)
- SMART was developed by the IRS Team at Cornell University and is available through the Spitzer Science Center at Caltech.
- ... distribution
![[*]](/icons/foot_motif.png)
- For comparison with the model, we have symmetrised the observed nebular surface brightness.
- ...Richer et al. (2002)
![[*]](/icons/foot_motif.png)
- Note that the models are not ionization bounded.
- ...
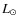
![[*]](/icons/foot_motif.png)
- The mass of the hot stellar component in the models depends
on the value assumed for the gravity, which is not well constrained.
For the photoionization modelling, what really matters is
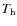 and
and 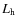 .
.
- ... phase
![[*]](/icons/foot_motif.png)
- The contribution of grains to the abundance of carbon is discussed in Sect. 5.2.2.
- ... variations
![[*]](/icons/foot_motif.png)
- http://www.astrossp.unam.mx/sitio/abs_telurica_english.htm
- ... SPM
![[*]](/icons/foot_motif.png)
- http://www.astrossp.unam.mx//Instruments/bchivens/camrend/manual-english.pdf
- ... oxygen
![[*]](/icons/foot_motif.png)
- The dispersion in S/O, however, is likely significantly affected by important errors in the sulfur abundances.
All Tables
Table 1: Log and characteristics of the spectroscopic observations.
Table 2:
Intensities of optical lines, corrected for stellar absorption, but not for reddening, with respect to H![]() .
.
Table 3: Observed HST UV line fluxes, relative to He II 1640.
Table 4: Observed mid IR line fluxes, in units of 10-21 W cm-2.
Table 5:
Photoionization models versus observations. Line intensities are in units of H![]() in the corresponding aperture.
in the corresponding aperture.
Table 6: Nebular abundances of TS 01, in various units.
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f01.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg17.png)
|
Figure 1:
HST-ACS H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f02.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg19.png)
|
Figure 2:
HST-ACS H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f03.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg20.png)
|
Figure 3:
HST-ACS image of TS 01 in the [Ne V] |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{12405f04.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg25.png)
|
Figure 4: Flux-calibrated CFHT spectra of TS 01. In blue is the CFHT 2003 spectrum with the nebular and stellar continua subtracted, in black the original CFHT 2001 spectrum, and in red the CFHT 2001 spectrum with the correct wavelength solution. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f05.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg46.png)
|
Figure 5: Fully processed SDSS spectrum (dereddened, free of continuum and stellar lines). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f06.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg47.png)
|
Figure 6: Fully processed Kitt Peak spectrum (dereddened, free of continuum and stellar lines). |
| Open with DEXTER | |
| In the text | |
| |
Figure 7: 2D calibrated HST FUV spectrum of TS 01. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12405f08.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg50.png)
|
Figure 8:
HST FUV nebular spectrum of TS 01, not corrected for reddening, showing the He II |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12405f09.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg52.png)
|
Figure 9:
LH infrared spectrum of TS 01 between 22 and 28 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f10.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg88.png)
|
Figure 10: Stellar model atmosphere fitting of carbon lines in the stellar core of TS 01. Observation is in black. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12405f11.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg89.png)
|
Figure 11: Stellar model atmosphere fitting of nitrogen lines in the stellar core of TS 01. Observation is in black. |
| Open with DEXTER | |
| In the text | |
| |
Figure 12:
Density structure of the nebula. Left: the chosen density structure of the model along the polar axis and along an axis perpendicular to it; middle: the resulting H |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12405f13.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg102.png)
|
Figure 13:
Graphic chart to compare the reference model with the measured line
ratios of TS 01. The numbers on the top of the panels indicate the
values of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12405f14.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg121.png)
|
Figure 14:
Monochromatic images of the reference model in various lines (the
values of the wavelengths are in Å if they are larger than 900, and in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12405f15.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg123.png)
|
Figure 15: Comparison of the reddened spectrum of the reference model with observations. Top: from the UV to the IR. The reddened model is in black. The colour code for the observations is as follows. Magenta: FUSE; blue: HST; green: SDSS ; red: Spitzer (the SH observations could not be sky-corrected). Bottom: X-ray domain. The model (with extinction applied) is in blue. The XMM observations are represented by triangles. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12405f16.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg124.png)
|
Figure 16: Spectral energy distribution (normalized to arbitrary units) of the radiation from the ionizing stars in the reference model. Red: the ``cold'' star; blue: the ``hot'' star; black: the sum of the two. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{12405f17.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg141.png)
|
Figure 17:
Comparison of TS 01 (filled red circle) with other Galactic PNe in
abundance ratios diagrams. The different black symbols represent: K648
(circle), DdDm-1 (square), PN006-41.9 (triangle), NGC 2242 (diamond),
NGC 4361 (plus sign), M2-29 (asterisk), H4-1 (star), PN 243.8-37.1
(filled triangle), and BoBn-1, which actually belongs to the
Sagittarius dwarf spheroidal galaxy ( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{12405f18.eps}\vspace*{-1mm}
\vspace*{-1mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12405-09/Timg166.png)
|
Figure 18:
Comparison of the chemical composition in TS 01 with the results
of stellar evolution models for a star with an initial mass 1 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


