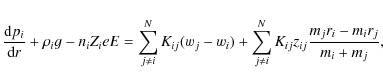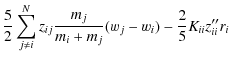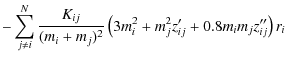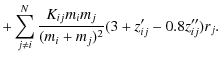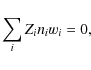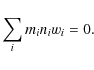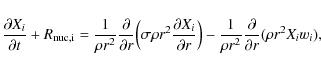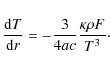| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200912290 | |
| Published online | 17 March 2010 | |
Gravitational settling in pulsating subdwarf B stars and their progenitors
Haili Hu1,2 - E. Glebbeek3 - A. A. Thoul4 - M.-A. Dupret4 - R. J. Stancliffe5 - G. Nelemans1 - C. Aerts1,2
1 - Department of Astrophysics, IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL, Nijmegen, The Netherlands
2 - Institute of Astronomy, Katholieke Universiteit Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
3 - Department of Physics and Astronomy, McMaster University, 1280 Main Street West, Hamilton, Ontario, Canada L8S 4M1, Canada
4 - Institute d'Astrophysique et Géophysique, Université de Liège, Belgium
5 - Centre for Stellar and Planetary Astrophysics, Monash University, PO Box 28M, Clayton VIC 3800, Australia
Received 6 April 2009 / Accepted 15 December 2009
Abstract
Context. Diffusion of atoms can be important during
quiescent phases of stellar evolution. Particularly in the very thin
inert envelopes of subdwarf B stars, diffusive movements will
considerably change the envelope structure and the surface abundances
on a short timescale. Also, the subdwarfs will inherit the effects of
diffusion in their direct progenitors, namely giants near the tip of
the red giant branch. This will influence the global evolution and the
pulsational properties of subdwarf B stars.
Aims. We investigate the impact of gravitational settling,
thermal diffusion and concentration diffusion on the evolution and
pulsations of subdwarf B stars. Although radiative levitation is not
explicitly calculated, we evaluate its effect by approximating the
resulting iron accumulation in the driving region. This allows us to
study the excitation of the pulsation modes, albeit in a parametric
fashion. Our diffusive stellar models are compared with models evolved
without diffusion.
Methods. We use a detailed stellar evolution code to solve
simultaneously the equations of stellar structure and evolution,
including the composition changes due to diffusion. The diffusion
calculations are performed for a multicomponent fluid using diffusion
coefficients derived from a screened Coulomb potential. We constructed
subdwarf B models with a mass of 0.465 ![]() from a 1
from a 1 ![]() and 3
and 3 ![]() zero-age main sequence progenitor. The low mass star ignited helium in
an energetic flash, while the intermediate mass star started helium
fusion gently. For each progenitor type we computed series with and
without atomic diffusion.
zero-age main sequence progenitor. The low mass star ignited helium in
an energetic flash, while the intermediate mass star started helium
fusion gently. For each progenitor type we computed series with and
without atomic diffusion.
Results. Atomic diffusion in red giants causes the helium core
mass at the onset of helium ignition to be larger. We find an increase
of 0.0015 ![]() for the 1
for the 1 ![]() model and 0.0036
model and 0.0036 ![]() for the 3
for the 3 ![]() model. The effects on the red giant surface abundances are small after
the first dredge up. The evolutionary tracks of the diffusive subdwarf
B models are shifted to lower surface gravities and effective
temperatures due to outward diffusion of hydrogen. This affects both
the frequencies of the excited modes and the overall frequency
spectrum. Especially the structure and pulsations of the
post-non-degenerate sdB star are drastically altered, proving that
atomic diffusion cannot be ignored in these stars. Sinking of metals
could to some extent increase the gravities and temperatures due to the
associated decrease in the stellar opacity. However, this effect should
be limited as it is counteracted by radiative levitation.
model. The effects on the red giant surface abundances are small after
the first dredge up. The evolutionary tracks of the diffusive subdwarf
B models are shifted to lower surface gravities and effective
temperatures due to outward diffusion of hydrogen. This affects both
the frequencies of the excited modes and the overall frequency
spectrum. Especially the structure and pulsations of the
post-non-degenerate sdB star are drastically altered, proving that
atomic diffusion cannot be ignored in these stars. Sinking of metals
could to some extent increase the gravities and temperatures due to the
associated decrease in the stellar opacity. However, this effect should
be limited as it is counteracted by radiative levitation.
Key words: diffusion - subdwarfs - stars: evolution - stars: oscillations - methods: numerical
1 Introduction
Atomic diffusion in stars can change the chemical abundances during
different evolutionary stages. For example, the chemically peculiar
subdwarf B (sdB) stars show surface abundance anomalies most
likely caused by diffusive processes (Fontaine & Chayer 1997). These stars, which are believed to be low mass (![]() 0.5
0.5 ![]() )
core-He-burning stars, have atmospheres typically dominated by H and deficient in He (Heber 1991). In addition, Michaud et al. (2007)
found significant differences between stellar models evolved with and
without diffusion on the Red Giant Branch (RGB) and the Horizontal
Branch (HB). Some of their results should also apply to sdB stars,
which are commonly believed to be Extreme Horizontal Branch (EHB) stars
and the descendants of red giants.
)
core-He-burning stars, have atmospheres typically dominated by H and deficient in He (Heber 1991). In addition, Michaud et al. (2007)
found significant differences between stellar models evolved with and
without diffusion on the Red Giant Branch (RGB) and the Horizontal
Branch (HB). Some of their results should also apply to sdB stars,
which are commonly believed to be Extreme Horizontal Branch (EHB) stars
and the descendants of red giants.
Some sdB stars show pulsations, and two types of pulsators are distinguished; the short-period variable EC 14026
stars (Kilkenny et al. 1997), and the long-period variable PG 1716stars
(Green et al. 2003). The rapid oscillations in EC 14026 stars are interpreted as low-order p-modes, driven by the
![]() -mechanism operating in the iron opacity bump (Charpinet et al. 1996). The same mechanism has been shown to excite long-period, high-order g-modes in models slightly cooler than the PG 1716 stars (Fontaine et al. 2003). This temperature discrepancy might be related to the stellar opacities (Jeffery & Saio 2006b). The local iron enhancement necessary in the driving region around
-mechanism operating in the iron opacity bump (Charpinet et al. 1996). The same mechanism has been shown to excite long-period, high-order g-modes in models slightly cooler than the PG 1716 stars (Fontaine et al. 2003). This temperature discrepancy might be related to the stellar opacities (Jeffery & Saio 2006b). The local iron enhancement necessary in the driving region around
![]() is caused by the competing diffusion processes of radiative levitation and gravitational settling.
is caused by the competing diffusion processes of radiative levitation and gravitational settling.
Despite the obvious importance of diffusion in these stars, sdB evolutionary models did not include this process consistently up to now. Instead, it was often assumed that, as a result of gravitational settling, the thin envelope is H-rich and the H-profile is arbitrarily steep. However, the envelope composition and the precise form of the He-H transition layer are important for the pulsation modes. Furthermore, the assumption of such a H-envelope is inappropriate for the newly proposed post-non-degenerate sdB stars by Han et al. (2002). Hu et al. (2008) showed that these stars have a broad He-H transition layer extending to deeper regions, where diffusion is not expected to work efficiently. This is in contrast to the canonical post-He-flash sdB models, that inherit a steep H-profile from their progenitors on the RGB.
While the inclusion of gravitational settling, thermal diffusion and concentration diffusion during stellar evolution is relatively straightforward as we show here, the implementation of radiative levitation is far more difficult. Still, radiative levitation has been treated consistently in some stellar evolutionary models, for example for Population I and II main sequence stars (Richard et al. 2002,2001) and HB stars (Michaud et al. 2007). These studies have led to important insights in the stellar structure, evolution and abundance anomalies, see Michaud & Richer (2008) for a review. Although it is eventually also our aim to include radiative accelerations in our sdB models, it is beyond the scope of this work.
In order to study the mode excitation in sdB stars
nevertheless, different approximations have been made in the
literature. One could simply enhance Fe uniformly through the entire
stellar envelope (Jeffery & Saio 2006a; Charpinet et al. 1996),
but then the stellar evolution and pulsations would be unrealistically
altered. A more sophisticated treatment assumes a diffusive equilibrium
profile of Fe, see Charpinet et al. (1997). These authors argued that the equilibrium state is reached on timescales much shorter than the sdB evolutionary timescale (![]() 105 compared to
105 compared to ![]() 108 years). Hu et al. (2008) approximated the equilibrium Fe profile with a Gaussian function centered around
108 years). Hu et al. (2008) approximated the equilibrium Fe profile with a Gaussian function centered around
![]() .
Such a parametric approach is convenient for the study of mode
excitation, because the exact shape of the non-uniform Fe profile does
not greatly affect the driving, as long as the resulting opacity bump
is large enough. Secondly, Fe is only enhanced in the driving region,
corresponding to a very thin mass-shell (
.
Such a parametric approach is convenient for the study of mode
excitation, because the exact shape of the non-uniform Fe profile does
not greatly affect the driving, as long as the resulting opacity bump
is large enough. Secondly, Fe is only enhanced in the driving region,
corresponding to a very thin mass-shell (![]()
![]() ).
Thus, such a parametric approach does not model the shape of the Fe
distribution in detail, but is more realistic than simply increasing
the metallicity in the entire envelope.
).
Thus, such a parametric approach does not model the shape of the Fe
distribution in detail, but is more realistic than simply increasing
the metallicity in the entire envelope.
In this study, we constructed sdB models with gravitational settling, temperature diffusion and concentration diffusion from the zero-age main sequence (ZAMS) to the EHB. Radiative accelerations were neglected, but in order to evaluate how our results might be affected, we enforced Fe enhancement in one series of calculations, in the same way as in Hu et al. (2008). For convenience, we will refer to the collective effects of gravitational settling, thermal and concentration diffusion as ``atomic diffusion'' in the rest of this paper. The work presented here should be considered as a necessary but intermediate step towards achieving our goal of improving the seismic models for sdB stars. A more detailed study, including the effects on sdB pulsations, will be presented in a future paper as we are currently implementing additional transport processes in our models (e.g., radiative levitation, thermohaline mixing, and turbulence). Here, we focus on the implementation of atomic diffusion and the qualitative effects on the evolution tracks and stability of the pulsation modes of sdB stars.
In the next section, we introduce the method followed in this work. In Sect. 2.1 we present the diffusion equations. In Sect. 2.2, we describe the stellar evolution code and the input physics. In Sect. 3, we show calibrated solar models as a test for the updated diffusion and evolution code. In Sect. 4, we examine the effects of atomic diffusion in red giants, which we used to build diffusive sdB models presented in Sect. 5. The conclusions are discussed in Sect. 6.
2 Method
2.1 The diffusion equations
The effects of diffusion are in general small, and this has led to various, sometimes unnecessary, approximations in its treatment, e.g. considering trace elements and binary mixtures. Also, the calculation of the diffusion coefficients is greatly simplified by describing the interaction between particles by a pure Coulomb potential with a long range cut-off. However, a screened Coulomb potential gives more accurate results, especially at high densities (Paquette et al. 1986). Here, we calculate the diffusion velocities due to gradients of pressure (i.e. gravitational settling), temperature, and concentration in a multicomponent fluid. We use the routine by Thoul et al. (1994) (hereafter TBL) to solve Burgers flow equations (Burgers 1969). The original TBL routine uses diffusion coefficients derived from a pure Coulomb potential with a cut-off at the Debye length. We have updated it to make use of more accurate diffusion coefficients derived from a screened Coulomb potential by Paquette et al. (1986).
For a review of the basic equations describing atomic diffusion in stars we refer to Thoul & Montalbán (2007). We briefly recall the most important ones. The Burgers diffusion equations are (N equations),
including the heat flow equation (N equations),
In addition, we have two constraints: current neutrality,
and local mass conservation,
In the above 2N+2 equations, pi,
A rigorous study requires the calculation of the degree of ionization, and the treatment of each ion as a separate species. As a simplification, one often uses the mean ionic charge. However, we found that this gives inconsistent results in regions where the degree of ionization changes rapidly. Also, difficulties arise in the case of neutral atoms, for TBL defined the concentrations with respect to electrons. Furthermore, we have not included diffusion coefficients of neutral atoms, which are due to atomic polarizability rather than Coulomb scattering. To avoid these complications, we simply assume full ionization for the calculation of the diffusion velocities, although we are aware that this might lead to a slight underestimation of the diffusion velocities (Turcotte et al. 1998; Schlattl 2002). For the equation of state the ionization of H, He, C, N, O and Ne are calculated using an approximate pressure ionization model (Pols et al. 1995).
The diffusion velocity can be expressed in terms of gradients of ion abundances, pressure and temperature,
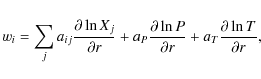
where the coefficients aij, aP and aT follow from the TBL procedure. Having calculated the diffusion velocities, we can now solve the equations for the composition changes,
where
2.2 The stellar evolution code and input physics
The stellar models are constructed with the stellar evolution code STARS developed by Eggleton (1972,1973,1971), and (). This code has been updated by Pols et al. (1995) to make use of an equation of state that includes pressure ionization and Coulomb interaction. Stancliffe & Glebbeek (2008) implemented gravitational settling in STARS by considering trace elements in a H background. Here, we solve the full set of Burgers equations as described in the previous section.
Stancliffe (2006) distinguishes three different methods for a stellar evolution code to solve the structure equations together with the equations for composition changes: the fully simultaneous, partially simultaneous and non-simultaneous approach. The STARS code follows the fully simultaneous approach, i.e. the composition equations are solved simultaneously with the structure (and the mesh-spacing). While the non-simultaneous and the partially simultaneous approach can encounter numerical instabilities if the diffusion timescale becomes short, the simultaneous approach is not hampered by this. The drawback, however, is that it is computationally expensive to follow a large number of nuclear species in this way. We therefore limit to the abundance changes of seven species: H, He, C, N, O, Ne, and a fictitious species gathering all the other ones. Thus, the heavy elements that are not explicitly followed are assumed to diffuse equally.
The code uses nuclear reaction rates from the NACRE compilation (Angulo et al. 1999) supplemented by reaction rates from Caughlan & Fowler (1988). The 14N(p,![]() )15O reaction rate is reduced to 0.64 times the NACRE value, as suggested by Herwig et al. (2006) and Formicola & LUNA Collaboration (2002). The neutrino loss rates are from Itoh et al. (1989,1992). The metal mixture is scaled to solar abundances (Grevesse & Noels 1993). Convection is treated with the mixing-length prescription of Böhm-Vitense (1958). We use a mixing-length parameter (the ratio of the mixing-length to the local pressure scale height) of
)15O reaction rate is reduced to 0.64 times the NACRE value, as suggested by Herwig et al. (2006) and Formicola & LUNA Collaboration (2002). The neutrino loss rates are from Itoh et al. (1989,1992). The metal mixture is scaled to solar abundances (Grevesse & Noels 1993). Convection is treated with the mixing-length prescription of Böhm-Vitense (1958). We use a mixing-length parameter (the ratio of the mixing-length to the local pressure scale height) of
![]() ,
which gives an excellent fit to the Sun with the input physics used here (see Sect. 3).
,
which gives an excellent fit to the Sun with the input physics used here (see Sect. 3).
Both convective and semi-convective mixing are treated as diffusion processes (see Eq. (5)). It is assumed that mixing occurs in regions where
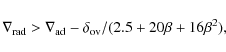
where
Mass-loss on the RGB is described by a version of Reimers' law (Reimers 1975) based on a physical approach by Schröder & Cuntz (2005):

with the parameter
Due to diffusion, the H-abundance in the outer stellar layers will exceed the initial value. If the envelope is radiative and mass-loss is limited, the outer layer will consist of almost pure H. The standard opacity tables in the STARS code (Chen & Tout 2007; Pols et al. 1995; Eldridge & Tout 2004) are not suitable here, because they only go up to X=0.8. Furthermore, in the standard version of the evolution code, only the opacity table corresponding to the zero-age metallicity is loaded during an evolution run.
Therefore, we constructed new opacity tables that are valid for H- and He-burning regions and for compositions up to X=1. We took the opportunity to implement the most recent values: OPAL opacities by Iglesias & Rogers (1996) smoothly merged with the low-temperature opacities by Ferguson et al. (2005). These are then combined with updated conductive opacities (Cassisi et al. 2007) by reciprocal addition. The covered range is
![]() and
and
![]() .
At the high end of
.
At the high end of ![]() and
and ![]() ,
where values are missing due to the non-rectangular form of the OPAL tables, we extrapolate linearly.
,
where values are missing due to the non-rectangular form of the OPAL tables, we extrapolate linearly.
For interpolation convenience during the evolution calculations, the tables are made rectangular in (![]() ,
,
![]() ,
Z, XF), where we defined the composition variable
,
Z, XF), where we defined the composition variable
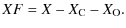
|
X is the hydrogen mass fraction,
We obtained tables for Z = 0, 0.0001, 0.0003, 0.001, 0.002,
0.004, 0.01, 0.02, 0.03, and 0.04. For each metallicity, we built
tables for the compositions: (X,
![]() )
= (1-Z,
0), (0.95, 0), (0.9, 0), (0.8, 0), (0.7, 0), (0.5, 0), (0.35, 0), (0.2,
0), (0.1, 0), (0, 0), (0, 0.1+0), (0, 0.3+0.1), (0, 0.4+0.2), (0,
0.4+0.4), (0, 0.1+0.9-Z). We derived the C/O ratio from a
)
= (1-Z,
0), (0.95, 0), (0.9, 0), (0.8, 0), (0.7, 0), (0.5, 0), (0.35, 0), (0.2,
0), (0.1, 0), (0, 0), (0, 0.1+0), (0, 0.3+0.1), (0, 0.4+0.2), (0,
0.4+0.4), (0, 0.1+0.9-Z). We derived the C/O ratio from a
![]() sdB star during He-burning. Due to the sensitive temperature dependence of the 3
sdB star during He-burning. Due to the sensitive temperature dependence of the 3![]() reactions, the C/O ratio is higher for more massive stars, but luckily,
it is more or less constant within the narrow mass range of sdBs. Thus,
we do not explicitly follow
reactions, the C/O ratio is higher for more massive stars, but luckily,
it is more or less constant within the narrow mass range of sdBs. Thus,
we do not explicitly follow ![]() and
and ![]() separately (as in Eldridge & Tout 2004), but we use the fact that the C/O ratio is a function of
separately (as in Eldridge & Tout 2004), but we use the fact that the C/O ratio is a function of
![]() (as in Pols et al. 1995 and Chen & Tout 2007).
(as in Pols et al. 1995 and Chen & Tout 2007).
We also take into account the effect of metal diffusion on the opacity, and therefore interpolate in metallicity during the evolution. It should be noted that the opacity is still calculated for a fixed metal mixture (Grevesse & Noels 1993), except in the case that Fe is artificially enhanced in the sdB models. This is justified, since the heavy elements diffuse with roughly the same velocities.
The new opacity tables are written in a format suitable for the opacity routine that was originally developed for the CLÉS evolution code by Scuflaire et al. (2008). This routine also calculates accurate opacity derivatives that are necessary for the stability analysis.
3 Solar models
3.1 Calibration of solar models
An important test for a stellar evolution code is provided by the Sun.
In the standard approach of calibrating solar models, the mixing length
parameter ![]() ,
the initial He and metal abundance are adjusted to produce, at the solar age (
,
the initial He and metal abundance are adjusted to produce, at the solar age (
![]() yr, Bahcall et al. 1995), models with observed solar radius (
yr, Bahcall et al. 1995), models with observed solar radius (
![]() cm, Allen 1973), luminosity (
cm, Allen 1973), luminosity (
![]() erg/s, Bahcall et al. 2001) and surface metal fraction
erg/s, Bahcall et al. 2001) and surface metal fraction
![]() (0.0245, Grevesse & Noels 1993).
Because the luminosity of a stellar model is sensitive to the mean
molecular weight, the He-abundance can be adjusted to yield the solar
luminosity. The mixing length parameter determines the efficiency of
energy transport by convection; at a fixed luminosity, a smaller
(0.0245, Grevesse & Noels 1993).
Because the luminosity of a stellar model is sensitive to the mean
molecular weight, the He-abundance can be adjusted to yield the solar
luminosity. The mixing length parameter determines the efficiency of
energy transport by convection; at a fixed luminosity, a smaller ![]() leads to a larger radius and thus a lower effective temperature.
leads to a larger radius and thus a lower effective temperature.
Pols et al. (1995) found an approximate solar model, cooler and fainter within 0.2% and 0.7%, for
![]() ,
,
![]() ,
,
![]() with older opacity tables than used here (Rogers & Iglesias 1992),
and no atomic diffusion. Since the stellar radius is also influenced by
the opacity, stellar models using different opacity tables could
require different values of
with older opacity tables than used here (Rogers & Iglesias 1992),
and no atomic diffusion. Since the stellar radius is also influenced by
the opacity, stellar models using different opacity tables could
require different values of ![]() (Chieffi et al. 1995).
Furthermore, other physical inputs, such as the inclusion of atomic
diffusion, will influence the calibration of solar models. Therefore,
we perform a new solar calibration with the updated input physics
described in Sect. 2.2.
(Chieffi et al. 1995).
Furthermore, other physical inputs, such as the inclusion of atomic
diffusion, will influence the calibration of solar models. Therefore,
we perform a new solar calibration with the updated input physics
described in Sect. 2.2.
We found for
![]() ,
Zi = 0.01928,
Y i = 0.2725 a solar model with a radius and luminosity both within
,
Zi = 0.01928,
Y i = 0.2725 a solar model with a radius and luminosity both within ![]() of the Sun. The surface mass fractions at the solar age are
of the Sun. The surface mass fractions at the solar age are
![]() and
and
![]() ,
which is consistent with Grevesse & Noels (1993). The latest determination of
,
which is consistent with Grevesse & Noels (1993). The latest determination of
![]() by Asplund et al. (2005), although likely to be more accurate, poses a serious problem for helioseismology as pointed out by various authors, e.g. Serenelli et al. (2004), Montalbán et al. (2004) and Christensen-Dalsgaard et al. (2009). Also, the opacity tables use the Grevesse & Noels (1993) metal mixture. We have, therefore, not considered the new solar abundances here.
by Asplund et al. (2005), although likely to be more accurate, poses a serious problem for helioseismology as pointed out by various authors, e.g. Serenelli et al. (2004), Montalbán et al. (2004) and Christensen-Dalsgaard et al. (2009). Also, the opacity tables use the Grevesse & Noels (1993) metal mixture. We have, therefore, not considered the new solar abundances here.
The same ZAMS model evolved without atomic diffusion has at the solar age a radius and luminosity 1.6% smaller than the diffusive model of the Sun. This can be understood in terms of the greater mean molecular weight in the core due to He-settling. Consequently, the nuclear burning rate is higher, giving a larger radius and luminosity for the diffusive solar model.
For the remainder of this paper, we use the mixing length parameter
![]() for all our models. However, one should keep in mind that
for all our models. However, one should keep in mind that ![]() could depend on the specific physical conditions, and could therefore vary with stellar mass and evolutionary phase.
could depend on the specific physical conditions, and could therefore vary with stellar mass and evolutionary phase.
3.2 Diffusion velocities in the solar interior
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12290fg1.eps}
\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12290-09/Timg60.png)
|
Figure 1: The ratio of the approximate diffusion velocities of H to our new exact values, as a function of the solar radius. The solid (MP) and long-dashed (TBL) lines give the ratio of the pressure terms, the short-dashed (MP) and dotted (TBL) lines indicate the temperature term ratios. |
| Open with DEXTER | |
It is illustrative to compare the diffusion velocities obtained with the updated diffusion routine to previous results, using (i) the simplified formulas by Michaud & Proffitt (1993, hereafter MP) for diffusion velocities in a fully ionized H-He mixture; and (ii) the original TBL routine. We calculated the H-diffusion velocity throughout the solar interior using Eq. (17) of MP, where we used the standard solar model as described above. Figure 1 shows the ratio of the MP H-diffusion velocities and our exact values. We evaluate the contributions due to pressure and temperature separately. The ratio of the concentration gradients terms is not shown explicitly, because this almost coincides with the ratio of the pressure terms. Our results are also compared to values obtained with the original TBL routine. It is clear that the largest error in both the MP and the TBL approach is caused by the thermal diffusion term. It has already been noted by TBL that this error is likely caused by their assumption of zij=0.6. MP solved the Burgers equations for a H-He mixture analytically without the heat fluxes, and numerically with the heat fluxes. They then represented the effects of the heat fluxes by an ad hoc correction to the results obtained when neglecting those heat fluxes. It is, therefore, not surprising that their largest error is also in the thermal diffusion term.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12290fg2.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12290-09/Timg61.png)
|
Figure 2: Diffusion velocities throughout the solar radiative interior. Left: the total H diffusion velocity, and right: the total oxygen diffusion velocity, using the three different approaches: TBL (dotted line), MP (dashed line) and our updated TBL approach (solid line). |
| Open with DEXTER | |
In the left panel of Fig. 2,
our total H-diffusion velocity is compared with results by MP and TBL.
Our calculations give a slightly lower H-diffusion velocity. This is
due to the overestimation of the thermal diffusion velocity in the
approximations. A solar model evolved with the same input parameters as
before, i.e.
![]() ,
Zi = 0.01928,
Y i = 0.2725, but using diffusion velocities
from the original TBL routine, results in a radius larger by 0.09% and
is more luminous by 0.15%. Although this effect is small, it becomes
relevant within the desired accuracy of calibrated solar models.
,
Zi = 0.01928,
Y i = 0.2725, but using diffusion velocities
from the original TBL routine, results in a radius larger by 0.09% and
is more luminous by 0.15%. Although this effect is small, it becomes
relevant within the desired accuracy of calibrated solar models.
Equations (18) and (19) of MP give diffusion velocities of trace elements in a H-He background. The deviation between our exact results and the MP and TBL approximations is even worse for heavy element diffusion, as can be seen for oxygen in the right panel of Fig. 2.
4 Progenitors of subdwarf B stars
We distinguish two types of sdB stars: the canonical post-flash sdB star and the newly proposed post-non-degenerate sdB star (Hu et al. 2008; Han et al. 2002; Hu et al. 2007)![]() . The latter type originates from an intermediate mass progenitor (
. The latter type originates from an intermediate mass progenitor (
![]() )
that ignited He quiescently, whereas the progenitor of the canonical sdB star is a low mass star (
)
that ignited He quiescently, whereas the progenitor of the canonical sdB star is a low mass star (
![]() ).
To become an sdB star, a red giant must have lost a lot of mass when
the core was close to He ignition. For a single star this requires an
enhanced stellar wind (D'Cruz et al. 1996). Since the majority of sdBs are observed in binaries (e.g. Maxted et al. 2001; Morales-Rueda et al. 2006),
a more natural mechanism for the mass loss is binary interaction, which
can be either stable Roche lobe overflow or common-envelope ejection (Han et al. 2002). Regardless of the mechanism, we just removed the desired amount of envelope to construct an sdB model.
).
To become an sdB star, a red giant must have lost a lot of mass when
the core was close to He ignition. For a single star this requires an
enhanced stellar wind (D'Cruz et al. 1996). Since the majority of sdBs are observed in binaries (e.g. Maxted et al. 2001; Morales-Rueda et al. 2006),
a more natural mechanism for the mass loss is binary interaction, which
can be either stable Roche lobe overflow or common-envelope ejection (Han et al. 2002). Regardless of the mechanism, we just removed the desired amount of envelope to construct an sdB model.
As representative sdB progenitors, we use a 1 ![]() and a 3
and a 3 ![]() stellar model that we evolved from the ZAMS to the tip of the RGB. At ``zero-age'' the 1
stellar model that we evolved from the ZAMS to the tip of the RGB. At ``zero-age'' the 1 ![]() model is assumed to be chemically homogeneous, while in the 3
model is assumed to be chemically homogeneous, while in the 3 ![]() model 12C has reached equilibrium through the CNO cycle. We used quasi-solar abundances, X=0.70, Y=0.28, Z=0.02.
model 12C has reached equilibrium through the CNO cycle. We used quasi-solar abundances, X=0.70, Y=0.28, Z=0.02.
For comparison we computed for each stellar mass two evolutionary series, one with atomic diffusion as described further in Sect. 2.1, and one without. In the first case, all elements are diffused from the ZAMS to the RGB tip.
4.1 Low mass progenitor
One of the main differences between the 1 ![]() model with and without atomic diffusion is the difference in the
He-core mass at the He-flash, a fact that was already noticed by Michaud et al. (2007). We find that, with atomic diffusion, the red giant has a
model with and without atomic diffusion is the difference in the
He-core mass at the He-flash, a fact that was already noticed by Michaud et al. (2007). We find that, with atomic diffusion, the red giant has a
![]() ,
while without atomic diffusion we get
,
while without atomic diffusion we get
![]() ,
where we defined the He core boundary to be at X=0.10. This
,
where we defined the He core boundary to be at X=0.10. This
![]() difference is caused by the fact that, due to gravitational settling,
the He-abundance at the H-burning shell will be lower. This implies a
smaller mean molecular weight at the shell for the diffusive model.
Thus, the nuclear burning rate will be lower, and hence the maximum
temperature in the core increases more slowly. Consequently, the core
mass can grow to a higher value before the temperature for He-ignition
is reached. We find
difference is caused by the fact that, due to gravitational settling,
the He-abundance at the H-burning shell will be lower. This implies a
smaller mean molecular weight at the shell for the diffusive model.
Thus, the nuclear burning rate will be lower, and hence the maximum
temperature in the core increases more slowly. Consequently, the core
mass can grow to a higher value before the temperature for He-ignition
is reached. We find
![]() ,
a somewhat lower dependence than found by Rood (1972) and Sweigart & Gross (1978),
-0.23 and -0.24, respectively. This could be due to the fact that in
our models the difference in He-abundance grows gradually, while Rood (1972) and Sweigart & Gross (1978)
examined the effect of the initial composition using evolution
calculations without diffusion. Also, different input physics such as
the nuclear reaction rates might play a role.
,
a somewhat lower dependence than found by Rood (1972) and Sweigart & Gross (1978),
-0.23 and -0.24, respectively. This could be due to the fact that in
our models the difference in He-abundance grows gradually, while Rood (1972) and Sweigart & Gross (1978)
examined the effect of the initial composition using evolution
calculations without diffusion. Also, different input physics such as
the nuclear reaction rates might play a role.
In a previous study, Hu et al. (2007) found a He core mass of
![]() at the tip of the RGB for a 1
at the tip of the RGB for a 1 ![]() model. The current lower value is caused by the new conductive opacities by Cassisi et al. (2007).
These authors already mention that their updated conductive opacities
cause a different thermal stratification in the He core than previous
results, leading to a lower He mass at the onset of the flash.
model. The current lower value is caused by the new conductive opacities by Cassisi et al. (2007).
These authors already mention that their updated conductive opacities
cause a different thermal stratification in the He core than previous
results, leading to a lower He mass at the onset of the flash.
We also notice small, but significant, differences in the surface composition, see Fig. 3. Even after the first dredge up some differences remain. At the tip of the RGB, the He surface abundance of the diffusive model is 3% lower than that of the non-diffusive model. The metallicity is lower by 1%.
4.2 Intermediate mass progenitor
For the 3 ![]() model with diffusion, the surface abundances become unrealistic. The
outer layers consist of pure H almost immediately after the ZAMS,
because the envelope is radiative. In reality, this would be prevented
by competing processes such as radiative levitation, turbulence,
rotational mixing, mass loss etc. However, we are not worried by this
as we will remove most of the envelope to construct an sdB star. In any
case, after the first dredge up, the surface abundances become
comparable to the model without diffusion. This is partly because
diffusion has not been efficient in the interior, during the much
shorter evolutionary timescale of the 3
model with diffusion, the surface abundances become unrealistic. The
outer layers consist of pure H almost immediately after the ZAMS,
because the envelope is radiative. In reality, this would be prevented
by competing processes such as radiative levitation, turbulence,
rotational mixing, mass loss etc. However, we are not worried by this
as we will remove most of the envelope to construct an sdB star. In any
case, after the first dredge up, the surface abundances become
comparable to the model without diffusion. This is partly because
diffusion has not been efficient in the interior, during the much
shorter evolutionary timescale of the 3 ![]() model . The 1
model . The 1 ![]() model evolved from the ZAMS to the RGB tip in
model evolved from the ZAMS to the RGB tip in
![]() yr, while it took the 3
yr, while it took the 3 ![]() model only
model only
![]() yr. Furthermore, the convective envelope of the 3
yr. Furthermore, the convective envelope of the 3 ![]() model dredges up more nuclear processed material than in the case of the 1
model dredges up more nuclear processed material than in the case of the 1 ![]() model, washing away the effects of diffusion at the surface.
model, washing away the effects of diffusion at the surface.
We find, with diffusion,
![]() ,
and without
,
and without
![]() .
The difference is 0.0036
.
The difference is 0.0036 ![]() ,
which is larger than for the 1
,
which is larger than for the 1 ![]() model. At first instance this might be surprising, but one should realize that the reason that the diffusive model has a larger
model. At first instance this might be surprising, but one should realize that the reason that the diffusive model has a larger
![]() is different than for the 1
is different than for the 1 ![]() model. In this case, the convective core on the MS becomes larger in
the presence of diffusion. This is mainly caused by chemical
composition changes leading to an increase in the opacity as shown by Richard et al. (2001) and Michaud et al. (2004).
An extended convective core can burn more H, which leads to a larger He
core at the end of the MS, and ultimately, to a larger He core at the
RGB tip.
model. In this case, the convective core on the MS becomes larger in
the presence of diffusion. This is mainly caused by chemical
composition changes leading to an increase in the opacity as shown by Richard et al. (2001) and Michaud et al. (2004).
An extended convective core can burn more H, which leads to a larger He
core at the end of the MS, and ultimately, to a larger He core at the
RGB tip.
![\begin{figure}
\par\includegraphics[width=9cm]{12290fg3.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12290-09/Timg76.png)
|
Figure 3: Surface abundances from
the ZAMS to the tip of the RGB as a function of the stellar age. The
dashed lines are for the model with atomic diffusion, and the solid
lines are for the model without. The left panels are for the model with
|
| Open with DEXTER | |
5 Subdwarf B models
During the evolution up to the RGB tip, all elements were diffused if
diffusion was taken into account. However, on the EHB we must take
special care because in the absence of competing forces gravitational
settling will cause all heavy elements to sink. The outer layers will
consist of pure H, and we know this is not true for sdB stars. Their
atmospheres are usually He deficient, a typical value is
![]() ,
although it can vary from -4 to -1 (Heber & Edelmann 2004; Saffer et al. 1994).
The metal abundances show a wide spread from solar to subsolar by a
factor 100, and different metals show different patterns, see e.g. Fontaine et al. (2004) and O'Toole & Heber (2006).
Current diffusion theory, with radiative levitation and weak stellar
winds, has difficulties explaining the observed abundance anomalies. We
make no such attempt here, but we evaluate how our results are affected
by certain assumptions about the surface abundances. We examine five
cases on the EHB in order to disentangle the impact of different
diffusion processes:
,
although it can vary from -4 to -1 (Heber & Edelmann 2004; Saffer et al. 1994).
The metal abundances show a wide spread from solar to subsolar by a
factor 100, and different metals show different patterns, see e.g. Fontaine et al. (2004) and O'Toole & Heber (2006).
Current diffusion theory, with radiative levitation and weak stellar
winds, has difficulties explaining the observed abundance anomalies. We
make no such attempt here, but we evaluate how our results are affected
by certain assumptions about the surface abundances. We examine five
cases on the EHB in order to disentangle the impact of different
diffusion processes:
- 1a)
- No diffusion, Fe is not enhanced.
- 1b)
- No diffusion, Fe is enhanced.
- 2a)
- Only H and He are diffused, so the surface metallicity stays roughly solar (
 ). Fe is not enhanced.
). Fe is not enhanced.
- 2b)
- Only H and He are diffused, Fe is enhanced.
- 2c)
- All elements are diffused, Fe is not enhanced.
5.1 Post-flash sdB stars
![\begin{figure}
\par\includegraphics[width=18cm]{12290fg4.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12290-09/Timg79.png)
|
Figure 4: Evolutionary tracks for left: the post-flash sdB star, and right: the post-non-degenerate sdB star. The lines correspond to the cases 1a) solid line, 2a), short-dashed line, 2b) long-dashed line and 2c) dotted line as described in the text. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm]{12290fg5.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12290-09/Timg80.png)
|
Figure 5: The effect of diffusion on the the H-profiles at different EHB ages for left: the post-flash sdB star, and right: the post-non-degenerate sdB star. |
| Open with DEXTER | |
The post-flash sdB models are constructed from the 1 ![]() series. If the luminosity due to He-burning exceeds
series. If the luminosity due to He-burning exceeds
![]() ,
it is assumed that the He-flash occurs. The post-flash model is taken
to be a ZAHB star with the same mass, core mass and chemical
composition as the pre-flash model. In reality, the core abundances are
changed slightly due to nuclear burning during the flash. Detailed
calculations of the flash by Piersanti et al. (2004) and Serenelli & Weiss (2005),
suggest that C increases up to 5%. We are not concerned about
this, since the p-modes are shallow envelope modes and do not probe the
core. However, for the g-modes that propagate to deeper interior
regions, the effects of nuclear burning and convective mixing during
the flash (as described in e.g. Dearborn et al. 2006; Mocák et al. 2008) are important. We explored this in Hu et al. (2009).
,
it is assumed that the He-flash occurs. The post-flash model is taken
to be a ZAHB star with the same mass, core mass and chemical
composition as the pre-flash model. In reality, the core abundances are
changed slightly due to nuclear burning during the flash. Detailed
calculations of the flash by Piersanti et al. (2004) and Serenelli & Weiss (2005),
suggest that C increases up to 5%. We are not concerned about
this, since the p-modes are shallow envelope modes and do not probe the
core. However, for the g-modes that propagate to deeper interior
regions, the effects of nuclear burning and convective mixing during
the flash (as described in e.g. Dearborn et al. 2006; Mocák et al. 2008) are important. We explored this in Hu et al. (2009).
For the series without diffusion, the H-envelope is removed just after
He-ignition. The compositions are kept fixed during mass loss, i.e. it
is assumed that the mass loss happens on a timescale shorter than the
nuclear and diffusion timescales. The total amount of H left is
![]() .
In this way, we obtained sdB models with
.
In this way, we obtained sdB models with
![]() .
To obtain sdB models with the same core mass for the series with
diffusion, we had to remove the envelope before He-ignition. Still, the
core mass is large enough so that He is ignited after mass-loss, see Hu et al. (2007).
.
To obtain sdB models with the same core mass for the series with
diffusion, we had to remove the envelope before He-ignition. Still, the
core mass is large enough so that He is ignited after mass-loss, see Hu et al. (2007).
In the left panel of Fig. 4, we show the sdB evolutionary tracks in the
![]() diagram for the cases 1a) solid line, 2a) short-dashed line, 2b) long-dashed line and 2c) dotted line.
We observe the following:
diagram for the cases 1a) solid line, 2a) short-dashed line, 2b) long-dashed line and 2c) dotted line.
We observe the following:
- Compared to 1a) no diffusion, no Fe enhancement, track 2a) with H-He diffusion and no Fe enhancement, is shifted to lower surface gravities and effective temperatures. Due to the outward diffusion of H, the density in the envelope decreases. Consequently the envelope becomes less gravitationally bound, and the sdB star gets larger and cooler.
- Comparing track 2a) to 2b) with H-He diffusion and with Fe enhancement shows that Fe enhancement has only a small effect on the sdB evolution as we already saw in Hu et al. (2008). Due to the increased opacity caused by Fe enhancement there is a slight shift to lower gravities and temperatures.
- Interestingly, track 2c) with all elements diffusing, and no Fe enhancement, is shifted to higher gravities and temperatures compared to 1a). This is because the opacity decreases as the heavy elements sink. Consequently the star becomes more compact and hotter, and apparently this effect is greater than what happens due to H-He diffusion in 2a).
After each 107 years of evolution on the EHB, the pulsational properties were calculated with the non-adiabatic stellar oscillation code MAD (Dupret 2001). In the top panels of Fig. 6, we show the frequencies of pulsation modes
![]() as
a function of the effective temperature. We plotted the results for the
tracks with Fe enhancement in order to evaluate the mode excitation,
namely 1b), no diffusion, with Fe enhancement, and 2b), H-He diffusion, with Fe enhancement. We notice distinct changes in both the frequencies and the frequency range of excited modes.
as
a function of the effective temperature. We plotted the results for the
tracks with Fe enhancement in order to evaluate the mode excitation,
namely 1b), no diffusion, with Fe enhancement, and 2b), H-He diffusion, with Fe enhancement. We notice distinct changes in both the frequencies and the frequency range of excited modes.
To understand the latter, one must realize that the driving is caused by an opacity bump at
![]() .
When H diffuses outwards, the sdB star is cooler and has a lower
temperature gradient due to the lower density in the envelope by
.
When H diffuses outwards, the sdB star is cooler and has a lower
temperature gradient due to the lower density in the envelope by
It should be noted that an increase in the H-fraction tends to increase the opacity, which also affects the radiative energy transport Eq. (6). However, the work of Jeffery & Saio (2006a) indicates that the effect of reducing the mean molecular weight outweighs the effect of increasing the opacity, and our results here regarding the mode excitation support their findings. Thus the opacity bump will be located deeper in the star in the presence of H-He diffusion. For a mode to be driven, the amplitudes of the eigenfunctions must be significant in the driving region, which occurs when the last node is at a certain temperature (
![\begin{figure}
\par\includegraphics[width=9cm]{12290fg6new.eps}
\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12290-09/Timg91.png)
|
Figure 6:
The frequencies of the stable ( |
| Open with DEXTER | |
5.2 Post-non-degenerate sdB stars
For this type of sdB stars, we used the
![]() model as progenitor. The envelope is removed just after He ignited quiescently in the core until the total mass is 0.465
model as progenitor. The envelope is removed just after He ignited quiescently in the core until the total mass is 0.465 ![]() .
.
In the right panel of Fig. 4, we show the sdB evolutionary tracks in the
![]() diagram for the same cases as before. Here, we deduce that;
diagram for the same cases as before. Here, we deduce that;
- Compared to 1a), no diffusion, no Fe enhancement, track 2a), with H-He diffusion and no Fe enhancement,
is drastically shifted to lower gravities and effective temperatures.
In the presence of diffusion the initial low H-abundance (
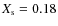 )
in the sdB envelope cannot be maintained. The post-non-degenerate sdB
star has a lot of H ``hidden'' in deeper layers. When this diffuses
outwards, the resulting shift in the
)
in the sdB envelope cannot be maintained. The post-non-degenerate sdB
star has a lot of H ``hidden'' in deeper layers. When this diffuses
outwards, the resulting shift in the
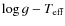 diagram is much more pronounced than for the post-flash sdB star.
diagram is much more pronounced than for the post-flash sdB star.
- Again we find that Fe enhancement shifts track 2b), with H-He diffusion and with Fe enhancement, to slightly lower gravities and effective temperatures compared to 2a).
- Track 2c), with all elements diffusing, and no Fe enhancement, shows an interesting feature. It is shifted to higher gravities and effective temperatures compared to track 2a), but still has lower gravities and temperatures compared to 1a). This is in contrast to what happens in this case for the post-flash sdB star. It is apparent that the decrease in opacity has a smaller impact than the effect of H-He diffusion described in 2a).
In the bottom panels of Fig. 6, we plot the frequencies of pulsation modes
![]() against the effective temperature for the cases 1b) and 2b). The
effects of diffusion on the pulsations are distinct. This is not
surprising considering the great impact diffusion has on the structure
of the post-non-degenerate sdB star. A previous study (Hu et al. 2008)
found that the frequency range of excited modes is one of the main
discriminators between the post-flash and the post-non-degenerate sdB
star. If diffusion is effective, this conclusion must be revised. We
still see differences in the frequency spectrum between models from
different evolutionary channels, but a more detailed study including
more models is necessary to quantify the differences. We plan to
perform such an analysis in the near future.
against the effective temperature for the cases 1b) and 2b). The
effects of diffusion on the pulsations are distinct. This is not
surprising considering the great impact diffusion has on the structure
of the post-non-degenerate sdB star. A previous study (Hu et al. 2008)
found that the frequency range of excited modes is one of the main
discriminators between the post-flash and the post-non-degenerate sdB
star. If diffusion is effective, this conclusion must be revised. We
still see differences in the frequency spectrum between models from
different evolutionary channels, but a more detailed study including
more models is necessary to quantify the differences. We plan to
perform such an analysis in the near future.
We conclude that atomic diffusion causes a larger change of H surface abundance in the post-non-degenerate sdB star than in the post-flash one. So the impact of H-He diffusion on the evolutionary tracks and driving is larger. In contrast to the post-flash case, this cannot be compensated by a possible decrease in the opacity by the heavy elements settling.
6 Conclusions
We have updated the diffusion routine by TBL to make use of diffusion coefficients derived from a screened Coulomb potential (Paquette et al. 1986)
rather than a pure Coulomb potential. The improved accuracy is mainly
in the thermal diffusion term, and this results in slightly lower
diffusion velocities compared to TBL. Although the effect is small, it
becomes important within the accuracy desired for calibrated solar
models. We found an excellent fit to the Sun by evolving a 1 ![]() model with initial abundances Z=0.01928, Y=0.2725 and mixing length parameter
model with initial abundances Z=0.01928, Y=0.2725 and mixing length parameter
![]() with atomic diffusion to the age of
with atomic diffusion to the age of
![]() yr.
yr.
We evolved a 1 and 3 ![]() stellar model from the ZAMS to the RGB tip, with and without atomic
diffusion. By including diffusion, we find an increase in the He core
mass at the RGB tip of 0.0015
stellar model from the ZAMS to the RGB tip, with and without atomic
diffusion. By including diffusion, we find an increase in the He core
mass at the RGB tip of 0.0015 ![]() and 0.0036
and 0.0036 ![]() ,
respectively. Surface mass fractions are slightly changed for the 1
,
respectively. Surface mass fractions are slightly changed for the 1 ![]() model, but not significantly for the 3
model, but not significantly for the 3 ![]() model. The reason is in part the shorter evolutionary timescale of the
higher mass star. More importantly though, is the more efficient mixing
of nuclear processed material during the first dredge up. This is
because for the higher mass star, the inward advance of the convective
envelope reaches regions where the shrinking convective core passed
through during the main sequence.
model. The reason is in part the shorter evolutionary timescale of the
higher mass star. More importantly though, is the more efficient mixing
of nuclear processed material during the first dredge up. This is
because for the higher mass star, the inward advance of the convective
envelope reaches regions where the shrinking convective core passed
through during the main sequence.
From the RGB models, we constructed post-flash and
post-non-degenerate sdB models. Radiative levitation was not included,
but in one set of our calculations we enhanced Fe artificially around
![]() as an approximation to the expected diffusive equilibrium profile (Charpinet et al. 1996).
This allows us to study the excitation of the pulsation modes, while
the effect of such an artificial Fe profile on the sdB evolution is
minimal. Although the question remains if such models are suitable for
a precise seismic analysis, they are very useful for a comparative
study as presented here.
as an approximation to the expected diffusive equilibrium profile (Charpinet et al. 1996).
This allows us to study the excitation of the pulsation modes, while
the effect of such an artificial Fe profile on the sdB evolution is
minimal. Although the question remains if such models are suitable for
a precise seismic analysis, they are very useful for a comparative
study as presented here.
First of all, we see significant shifts in the evolutionary tracks when H-He diffusion is included. If H diffuses outwards, the envelope is less dense and thus less gravitationally bound. This results in larger radii, and therefore lower gravities and effective temperatures. For the post-non-degenerate sdB star the difference is much more pronounced, because the initial (ZAEHB) H-abundance in the envelope was very low, X=0.18, and H extended to deeper layers. In the presence of H-He diffusion in our sdB models, the frequencies of excited modes are lower and the frequency spectrum is more densely spaced. Especially for the post-non-degenerate sdB star the effect is drastic due to the large structural change of the envelope.
We also examined what happens if the metals are allowed to sink due to gravitational settling. The corresponding decrease in opacity will tend to make the star more compact and hotter, thus competing with the effect of He settling. In reality, however, radiative levitation prevents the metals from sinking, so we expect the case of only H-He diffusion to be more realistic. It is clear that consistent modelling of radiative levitation is a missing piece in this study, and we intend to include this in future work. Still, the results presented here, are an improvement to previous sdB models that altogether neglect atomic diffusion. In particular, we find it cannot be ignored in the post-non-degenerate sdB stars as it leads to totally different stellar structures. Furthermore, for H and He, the radiative forces do not play a significant role compared to settling. Therefore, the main conclusion of our work remains valid even when other processes are included: The settling of He leads to a H-rich sdB envelope, which leads to a lower moleculair weight. This results to a lower density at the same pressure and temperature, which changes both the evolution tracks and the stability of the modes in the way presented here.
AcknowledgementsThe authors are indebted to R. Scuflaire and O. Pols for their help on the opacity tables. H.H. thanks S. Kawaler and L. Yungelson for helpful discussions and suggestions. H.H. acknowledges a PhD scholarship through the ``Convenant Katholieke Universiteit Leuven, Belgium - Radboud Universiteit Nijmegen, The Netherlands''. G.N. is supported by NWO VIDI grant 639.042.813. The research leading to these results has received funding from the European Research Council under the European Community's Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no 227224 (PROSPERITY), as well as from the Research Council of K.U. Leuven grant agreement GOA/2008/04. RJS is funded by the Australian Research Council's Discovery Projects scheme under grant DP0879472.
References
- Allen, C. W. 1973, Astrophysical quantities, 3rd edn (London: University of London, Athlone Press) [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. T. G. Barnes, III & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Bahcall, J. N., Pinsonneault, M. H., & Wasserburg, G. J. 1995, Rev. Mod. Phys., 67, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Pinsonneault, M. H., & Basu, S. 2001, ApJ, 555, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Burgers, J. M. 1969, Flow Equations for Composite Gases, Flow Equations for Composite Gases (New York: Academic Press) [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Caughlan, G. R., & Fowler, W. A. 1988, Atomic Data and Nuclear Data Tables, 40, 283 [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 1996, ApJ, 471, L103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 1997, ApJ, 483, L123 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chen, X.-F., & Tout, C. A. 2007, Chin. J. A&A, 7, 245 [Google Scholar]
- Chieffi, A., Straniero, O., & Salaris, M. 1995, ApJ, 445, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., di Mauro, M. P., Houdek, G., et al. 2009, A&A, 494, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D'Cruz, N. L., Dorman, B., Rood, R. T., & O'Connell, R. W. 1996, ApJ, 466, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Dearborn, D. S. P., Lattanzio, J. C., & Eggleton, P. P. 2006, ApJ, 639, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Dupret, M. A. 2001, A&A, 366, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggleton, P. P. 1971, MNRAS, 151, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1972, MNRAS, 156, 361 [NASA ADS] [Google Scholar]
- Eggleton, P. P. 1973, MNRAS, 163, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P., Faulkner, J., & Flannery, B. P. 1973, A&A, 23, 325 [NASA ADS] [Google Scholar]
- Eldridge, J. J., & Tout, C. A. 2004, MNRAS, 348, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G. & Chayer, P. 1997, in The Third Conference on Faint Blue Stars, ed. A. G. D. Philip, J. Liebert, R. Saffer, & D. S. Hayes, 169 [Google Scholar]
- Fontaine, G., Brassard, P., Charpinet, S., et al. 2003, ApJ, 597, 518 [Google Scholar]
- Fontaine, M., Chayer, P., Wesemael, F., Lamontagne, R., & Fontaine, G. 2004, Ap&SS, 291, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Formicola, A., & LUNA Collaboration 2002, in Nuclear Astrophysics, ed. W. Hillebrandt, & E. Müller, 111 [Google Scholar]
- Green, E. M., Fontaine, G., Reed, M. D., et al. 2003, ApJ, 583, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, ed. S. Kubono, & T. Kajino, 15 [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U. 1991, in Evolution of Stars: the Photospheric Abundance Connection, ed. G. Michaud, & A. V. Tutukov, IAU Symp., 145, 363 [Google Scholar]
- Heber, U., & Edelmann, H. 2004, Ap&SS, 291, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F., Austin, S. M., & Lattanzio, J. C. 2006, Phys. Rev. C, 73, 025802 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, H., Nelemans, G., Østensen, R., et al. 2007, A&A, 473, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hu, H., Dupret, M.-A., Aerts, C., et al. 2008, A&A, 490, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hu, H., Nelemans, G., Aerts, C., et al. 2009, A&A, 508, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., Adachi, T., Nakagawa, M., Kohyama, Y., & Munakata, H. 1989, ApJ, 339, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., Mutoh, H., Hikita, A., et al. 1992, ApJ, 395, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffery, C. S., & Saio, H. 2006a, MNRAS, 371, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffery, C. S., & Saio, H. 2006b, MNRAS, 372, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., Koen, C., O'Donoghue, D., et al. 1997, MNRAS, 285, 640 [Google Scholar]
- Maxted, P. F. L., Heber, U., Marsh, T. R., et al. 2001, MNRAS, 326, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., & Proffitt, C. R. 1993, in Inside the Stars, ed. W. W. Weiss, & A. Baglin, ASP Conf. Ser., 40, IAU Colloq., 137, 246 [Google Scholar]
- Michaud, G., & Richer, J. 2008, Mem. Soc. Astron. Ital., 79, 592 [Google Scholar]
- Michaud, G., Vauclair, G., & Vauclair, S. 1983, ApJ, 267, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., Richard, O., Richer, J., et al. 2004, ApJ, 606, 452 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michaud, G., Richer, J., & Richard, O. 2007, ApJ, 670, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Mocák, M., Müller, E., Weiss, A., et al. 2008, A&A, 490, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montalbán, J., Miglio, A., Noels, A., Grevesse, N., & di Mauro, M. P. 2004, in SOHO 14 Helio- and Asteroseismology: Towards a Golden Future, ed. D. Danesy, ESA SP, 559, 574 [Google Scholar]
- Morales-Rueda, L., Maxted, P. F. L., Marsh, T. R., Kilkenny, D., & O'Donoghue, D. 2006, Baltic Astron., 15, 187 [NASA ADS] [Google Scholar]
- O'Toole, S. J., & Heber, U. 2006, A&A, 452, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paquette, C., Pelletier, C., Fontaine, G., et al. 1986, ApJS, 61, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Tornambé, A., & Castellani, V. 2004, MNRAS, 353, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Tout, C. A., Eggleton, P. P., et al. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Tout, C. A., Schroder, K.-P., Eggleton, P. P., & Manners, J. 1997, MNRAS, 289, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Schroder, K.-P., Hurley, J. R., Tout, C. A., & Eggleton, P. P. 1998, MNRAS, 298, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D. 1975, Mem. Soc. Roy. Sci. Liege, 8, 369 [Google Scholar]
- Richard, O., Michaud, G., & Richer, J. 2001, ApJ, 558, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, O., Michaud, G., Richer, J., et al. 2002, ApJ, 568, 979 [Google Scholar]
- Rogers, F. J., & Iglesias, C. A. 1992, ApJS, 79, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Rood, R. T. 1972, ApJ, 177, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Saffer, R. A., Bergeron, P., Koester, D., et al. 1994, ApJ, 432, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Schlattl, H. 2002, A&A, 395, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schröder, K.-P., & Cuntz, M. 2005, ApJ, 630, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, K.-P., Pols, O. R., & Eggleton, P. P. 1997, MNRAS, 285, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Scuflaire, R., Théado, S., Montalbán, J., et al. 2008, Ap&SS, 316, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Serenelli, A., & Weiss, A. 2005, A&A, 442, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serenelli, A. M., Bahcall, J. N., Basu, S., et al. 2004, in SOHO 14 Helio- and Asteroseismology: Towards a Golden Future, ed. D. Danesy, ESA SP, 559, 623 [Google Scholar]
- Stancliffe, R. J. 2006, MNRAS, 370, 1817 [NASA ADS] [CrossRef] [Google Scholar]
- Stancliffe, R. J., & Glebbeek, E. 2008, MNRAS, 389, 1828 [Google Scholar]
- Sweigart, A. V., & Gross, P. G. 1978, ApJS, 36, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Thoul, A., & Montalbán, J. 2007, in EAS Publ. Ser. 26, ed. C. W. Straka, Y. Lebreton, & M. J. P. F. G. Monteiro, 25 [Google Scholar]
- Thoul, A. A., Bahcall, J. N., & Loeb, A. 1994, ApJ, 421, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Turcotte, S., Richer, J., Michaud, G., Iglesias, C. A., & Rogers, F. J. 1998, ApJ, 504, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Unglaub, K., & Bues, I. 2001, A&A, 374, 570 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., & Cassisi, S. 2002, A&A, 392, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Footnotes
- ...
) ![[*]](/icons/foot_motif.png)
- We do not consider sdBs that are merger products.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12290fg1.eps}
\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12290-09/Timg60.png)
|
Figure 1: The ratio of the approximate diffusion velocities of H to our new exact values, as a function of the solar radius. The solid (MP) and long-dashed (TBL) lines give the ratio of the pressure terms, the short-dashed (MP) and dotted (TBL) lines indicate the temperature term ratios. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12290fg2.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12290-09/Timg61.png)
|
Figure 2: Diffusion velocities throughout the solar radiative interior. Left: the total H diffusion velocity, and right: the total oxygen diffusion velocity, using the three different approaches: TBL (dotted line), MP (dashed line) and our updated TBL approach (solid line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12290fg3.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12290-09/Timg76.png)
|
Figure 3: Surface abundances from
the ZAMS to the tip of the RGB as a function of the stellar age. The
dashed lines are for the model with atomic diffusion, and the solid
lines are for the model without. The left panels are for the model with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{12290fg4.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12290-09/Timg79.png)
|
Figure 4: Evolutionary tracks for left: the post-flash sdB star, and right: the post-non-degenerate sdB star. The lines correspond to the cases 1a) solid line, 2a), short-dashed line, 2b) long-dashed line and 2c) dotted line as described in the text. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{12290fg5.eps}
\end{figure}](/articles/aa/full_html/2010/03/aa12290-09/Timg80.png)
|
Figure 5: The effect of diffusion on the the H-profiles at different EHB ages for left: the post-flash sdB star, and right: the post-non-degenerate sdB star. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12290fg6new.eps}
\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/03/aa12290-09/Timg91.png)
|
Figure 6:
The frequencies of the stable ( |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.