| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 6 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/200913597 | |
| Published online | 10 February 2010 | |
LETTER TO THE EDITOR
Protostellar collapse: radiative and magnetic feedbacks on small-scale fragmentation![[*]](/icons/foot_motif.png)
B. Commerçon1,2,3 - P. Hennebelle4 - E. Audit3 - G. Chabrier2 - R. Teyssier3
1 - Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
2 -
École Normale Supérieure de Lyon, CRAL, UMR 5574 CNRS, Université de Lyon,
46 allée d'Italie, 69364 Lyon Cedex 07, France
3 -
Laboratoire AIM, CEA/DSM - CNRS - Université Paris Diderot,
IRFU/SAp, 91191 Gif sur Yvette, France
4 -
Laboratoire de radioastronomie, UMR 8112 CNRS, École Normale Supérieure et Observatoire
de Paris, 24 rue Lhomond, 75231 Paris Cedex 05, France
Received 3 November 2009 / Accepted 12 January 2010
Abstract
Context. Both radiative transfer and magnetic field are
understood to have strong impacts on the collapse and the fragmentation
of prestellar dense cores, but no consistent calculation exists on
these scales.
Aims. We perform the first radiation-magneto-hydrodynamics numerical calculations on a prestellar core scale.
Methods. We present original AMR calculations including that of
a magnetic field (in the ideal MHD limit) and radiative transfer,
within the flux-limited diffusion approximation, of the collapse of a
1 ![]() dense core. We compare the results with calculations performed with a barotropic EOS.
dense core. We compare the results with calculations performed with a barotropic EOS.
Results. We show that radiative transfer has an important impact
on the collapse and the fragmentation, by means of the cooling or
heating of the gas, and its importance depends on the magnetic field. A
stronger field yields a more significant magnetic braking, increasing
the accretion rate and thus the effect of the radiative feedback. Even
for a strongly magnetized core, where the dynamics of the collapse is
dominated by the magnetic field, radiative transfer is crucial to
determine the temperature and optical depth distributions, two
potentially accessible observational diagnostics. A barotropic EOS
cannot account for realistic fragmentation. The diffusivity of the
numerical scheme, however, is found to strongly affect the output of
the collapse, leading eventually to spurious fragmentation.
Conclusions. Both radiative transfer and magnetic field must be
included in numerical calculations of star formation to obtain
realistic collapse configurations and observable signatures.
Nevertheless, the numerical resolution and the robustness of the solver
are of prime importance to obtain reliable results. When using an
accurate solver, the fragmentation is found to always remain inhibited
by the magnetic field, at least in the ideal MHD limit, even when
radiative transfer is included.
Key words: magnetohydrodynamics (MHD) - radiative transfer - stars: formation - stars: low mass - ISM: clouds - ISM: kinematics and dynamics
1 Introduction
Understanding star formation is one of the most challenging problems in
contemporary astrophysics and numerical calculations provide a useful
approach to its investigation. Because of steadily improv computer
performances, numerical
calculations can simulate more and more physical processes of which the
coupling between
matter and radiation is a major issue. Until the formation of
the first Larson core (Larson 1969), the accreting gas can freely radiate
into space and is nearly isothermal (optically
thin regime). Once the gas becomes dense enough (
![]() g cm-3),
the radiation is trapped and the gas begins to heat up (optically
thick regime). The transition between these two regimes controls the
collapse and fragmentation of the cloud. The cooler the gas, the more
important the fragmentation. Another key issue in star formation is the
role of the magnetic field, as dense cores
are observed to exhibit coherent magnetic structures (e.g., Heiles & Crutcher 2005).
g cm-3),
the radiation is trapped and the gas begins to heat up (optically
thick regime). The transition between these two regimes controls the
collapse and fragmentation of the cloud. The cooler the gas, the more
important the fragmentation. Another key issue in star formation is the
role of the magnetic field, as dense cores
are observed to exhibit coherent magnetic structures (e.g., Heiles & Crutcher 2005).
Several authors have investigated the impact of both radiation (Attwood et al. 2009; Bate 2009; Offner et al. 2009; Whitehouse & Bate 2006; Krumholz et al. 2007; Boss et al. 2000) and magnetic field (e.g., Banerjee & Pudritz 2006; Price & Bate 2008; Mellon & Li 2009; Price & Bate 2007; Machida et al. 2008; Hennebelle & Teyssier 2008) on the star-formation process. However, only Price & Bate (2009) have to date performed calculations including both magnetic field and radiative feedback, using a SPH method, although their calculations explore relatively large scales. In this Letter, we present the first full radiation-magneto-hydrodynamics (RMHD) calculations of the protostellar collapse on small scales. We investigate in detail the impact of both magnetic field (in the limit of ideal MHD) and radiative feedback on the fragmentation process and the launching of outflows. The results are compared with those obtained with a barotropic equation of state (EOS), which crudely mimics the transition from the isothermal to adiabatic regime, to assess the importance of a proper treatment of radiative transfer on the collapse.
![\begin{figure}
\includegraphics[width=12cm,clip]{13597fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13597-09/Timg16.png)
|
Figure 1:
Case |
| Open with DEXTER | |
2 Numerical method and initial conditions
We use the RAMSES code (Teyssier 2002) based on a Eulerian formalism (grid based method with adaptive mesh refinement). We solve the transfer equations in the flux-limited diffusion (FLD, Minerbo 1978) in the comoving frame (fluid frame) to evaluate the radiative quantities. The ideal MHD equations are integrated using an unsplit second-order Godunov scheme (Fromang et al. 2006). Coupling terms between matter and radiation, as well as radiation transport, are integrated implicitly to handle the very short heating, cooling, and diffusion timescales. Details of the numerical method and its implementation will be provided in a forthcoming paper.
Calculations were performed using
either the rather diffusive Lax Friedrich (LF) Riemann solver or the more accurate HLLD Riemann solver (Miyoshi & Kusano 2005). Following up on former studies (Commerçon et al. 2008), we impose at least 10 cells per Jeans length as a grid refinement criterion (parameter ![]() ).
The initial resolution of the grid contains 643 cells.
We use the low temperature
opacities of Semenov et al. (2003), parametrized as functions of the gas temperature and density. In contrast, the
non-radiative calculations were performed with a barotropic EOS
).
The initial resolution of the grid contains 643 cells.
We use the low temperature
opacities of Semenov et al. (2003), parametrized as functions of the gas temperature and density. In contrast, the
non-radiative calculations were performed with a barotropic EOS
![]() ,
where
,
where
![]() g cm-3 is the critical density at which the gas
becomes adiabatic,
g cm-3 is the critical density at which the gas
becomes adiabatic, ![]() (set to be 5/3) is the adiabatic index, and
(set to be 5/3) is the adiabatic index, and
![]() is the isothermal sound speed.
is the isothermal sound speed.
We adopt initial
conditions, similar to those chosen in previous studies
(e.g. Commerçon et al. 2008). We consider a
uniform-density sphere of molecular gas,
rotating about the z-axis with a uniform angular velocity. In the present study, the prestellar core mass is fixed at
![]() and the
temperature at 11 K, which corresponds to
and the
temperature at 11 K, which corresponds to
![]() km s-1. To promote fragmentation, we use an
km s-1. To promote fragmentation, we use an ![]() azimuthal
density
perturbation with an amplitude of 10%.
The magnetic field is initially uniform and parallel to the rotation
axis. The strength of the magnetic field is expressed in terms of the
mass-to-flux to critical mass-to-flux ratio
azimuthal
density
perturbation with an amplitude of 10%.
The magnetic field is initially uniform and parallel to the rotation
axis. The strength of the magnetic field is expressed in terms of the
mass-to-flux to critical mass-to-flux ratio
![]() .
The initial energy balance is determined by two
dimensionless parameters, namely the ratio of the
thermal to gravitational energies
.
The initial energy balance is determined by two
dimensionless parameters, namely the ratio of the
thermal to gravitational energies
![]() ,
and rotational over gravitational energies
,
and rotational over gravitational energies
![]() .
The corresponding free-fall time and orbital time are, respectively,
.
The corresponding free-fall time and orbital time are, respectively,
![]() kyr and
kyr and
![]() kyr. The initial density is
kyr. The initial density is
![]() g cm -3.
g cm -3.
3 Results
3.1 Case 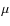 = 20
We first present the results for
= 20
We first present the results for 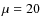 ,
i.e., a weakly magnetized core. We compare FLD calculations performed
with the two Riemann solvers (LF or HLLD) with calculations performed
with the barotropic EOS and the LF solver. The grid refinement
criterion is
,
i.e., a weakly magnetized core. We compare FLD calculations performed
with the two Riemann solvers (LF or HLLD) with calculations performed
with the barotropic EOS and the LF solver. The grid refinement
criterion is
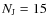 .
Performing similar barotropic calculations, Hennebelle & Teyssier (2008) do not report any fragmentation.
.
Performing similar barotropic calculations, Hennebelle & Teyssier (2008) do not report any fragmentation.
Figure 1 portrays temperature (top) and density (bottom) maps in the equatorial plane for the three aforementioned calculations at the same time ![]() kyr.
The black contours represent the transition between the optically thin
and thick regions (thin contour) and the quasi-adiabatic regions.
The FLD case with the LF solver yields a multiple fragmentation, a
central fragment of mass
kyr.
The black contours represent the transition between the optically thin
and thick regions (thin contour) and the quasi-adiabatic regions.
The FLD case with the LF solver yields a multiple fragmentation, a
central fragment of mass
![]() and several (depending on the time and resolution) orbiting fragments of mass
and several (depending on the time and resolution) orbiting fragments of mass ![]()
![]() having separations ranging from
having separations ranging from ![]() 40 AU to
40 AU to ![]() 100 AU,
whereas no fragmentation occurs in the two other cases. The orbiting
fragments in the FLD-LF simulation are quite warm (
100 AU,
whereas no fragmentation occurs in the two other cases. The orbiting
fragments in the FLD-LF simulation are quite warm (![]() 40 K), while the disc is cold (
40 K), while the disc is cold (![]() 11 K). In all simulations, the central fragment (T > 500 K) corresponds to an adiabatic region, where the gas cannot radiate away its compressional energy.
In the barotropic case, the mass of the central fragment is
11 K). In all simulations, the central fragment (T > 500 K) corresponds to an adiabatic region, where the gas cannot radiate away its compressional energy.
In the barotropic case, the mass of the central fragment is
![]() .
The outer parts of the disc formed are much denser and warmer than for
the two other cases, even though the gas is optically thin and should
cool efficiently, as illustrated in the FLD-LF calculations. The
corresponding values
of the Toomre parameter and Jeans length are greater than in the FLD-LF
case. This heating, however, is spurious and
reflects the approximate treatment of radiative cooling with a
barotropic approximation, where temperature is determined by the
density.
.
The outer parts of the disc formed are much denser and warmer than for
the two other cases, even though the gas is optically thin and should
cool efficiently, as illustrated in the FLD-LF calculations. The
corresponding values
of the Toomre parameter and Jeans length are greater than in the FLD-LF
case. This heating, however, is spurious and
reflects the approximate treatment of radiative cooling with a
barotropic approximation, where temperature is determined by the
density.
The most interesting case is the FLD case with the HLLD Riemann
solver. No fragmentation occurs in that case. The matter falls onto a
central core of mass ![]()
![]() .
With this less diffusive solver, the generation of a toroidal magnetic
field is more efficient. The interplay of magnetic field lines and
velocity gradients leads to the effective expansion of a magnetic
``tower'' in the vertical direction (Hennebelle & Fromang 2008).
The first consequence of this more robust (less diffusive) solver is
that the disc formed is less massive in the equatorial plane than with
the LF solver.
.
With this less diffusive solver, the generation of a toroidal magnetic
field is more efficient. The interplay of magnetic field lines and
velocity gradients leads to the effective expansion of a magnetic
``tower'' in the vertical direction (Hennebelle & Fromang 2008).
The first consequence of this more robust (less diffusive) solver is
that the disc formed is less massive in the equatorial plane than with
the LF solver.
Figure 2 shows
the density, temperature, and both poloidal and toroidal magnetic field
components profiles as a function of height above the
equatorial plane at a cylindrical radius of 10 AU, for the
three aforementioned calculations, at the same time. We note that the
extent of the magnetic tower depends on (increases with) resolution.
The magnetic tower is less dense close to the equatorial plane, since
the gas is spread in the magnetic bubble. In contrast to the barotropic
case, where the temperature falls to 10 K at a distance
>10 AU, the radiative feedback extends vertically up to ![]() 100 AU
with radiative transfer (FLD). Although toroidal magnetic field
generation is more effective with HLLD than with LF, the toroidal
magnetic field in the FLD-LF case is stronger at small radii. This is
because of the denser disc formed, which compresses and twists the
magnetic lines in the region close to the equatorial plane. At a
distance of 100 AU, the toroidal magnetic field component in the
vertical direction is one order of magnitude greater with HLLD than
with LF. This favours the extension of the magnetic tower. The poloidal
magnetic field component is stronger everywhere in the HLLD case, since
matter is less compressed.
100 AU
with radiative transfer (FLD). Although toroidal magnetic field
generation is more effective with HLLD than with LF, the toroidal
magnetic field in the FLD-LF case is stronger at small radii. This is
because of the denser disc formed, which compresses and twists the
magnetic lines in the region close to the equatorial plane. At a
distance of 100 AU, the toroidal magnetic field component in the
vertical direction is one order of magnitude greater with HLLD than
with LF. This favours the extension of the magnetic tower. The poloidal
magnetic field component is stronger everywhere in the HLLD case, since
matter is less compressed.
![\begin{figure}
\par\includegraphics[width=3.6cm,height=2.8cm,clip]{13597fg2.eps}...
...raphics[width=3.6cm,height=2.8cm,clip]{13597fg5.eps}
\vspace{-3mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13597-09/Timg37.png)
|
Figure 2:
Case |
| Open with DEXTER | |
Figure 3 displays the profiles of the magnetic braking force at 10 AU above the equatorial plane and as a function of height above the equatorial plane at a cylindrical radius of 10 AU, for the three same calculations. In the equatorial plane, the magnetic braking obtained with the LF solver or in the barotropic case is barely significant. Magnetic braking favours faster accretion to the central object and thus leads to a larger amount of kinetic energy being radiated away at the first core accretion shock (all the infalling gas kinetic energy is radiated away at the first Larson core accretion shock). The gas is then heated significantly around the central core. In contrast, there is more angular momentum in the (diffusive) FLD-LF case, which promotes fragmentation at the centrifugal barrier. The amount of accretion onto the central fragment is thus lower and the heating caused by accretion is less important. Magnetic braking force as a function of height above the plane is similar for the three calculations. We thus identify two important processes, both quantitatively affected by the numerical treatment: the presence of a magnetic tower, whose extension depends on the numerical resolution, and strong magnetic braking in the equatorial plane, whose strength depends on the diffusivity of the solver.
| Figure 3:
Case |
|
| Open with DEXTER | |
Figure 4 shows the
temperature - density distribution for the FLD calculations with the LF
solver. The isothermal and adiabatic regimes are recovered at low and
high density (
![]() g cm-3 and
g cm-3 and
![]() g cm-3). In-between, we observe a
dispersion in the (T,
g cm-3). In-between, we observe a
dispersion in the (T, ![]() ) plane,
where matter can be hotter at low density and cooler at high density
compared with the barotropic treatment (red solid line). As seen in the
figure, the fragments eventually reach different isentropes. The
central fragment lies on the highest entropy level, while the orbiting
fragments end up on cooler isentropes. The barotropic EOS cannot
reproduce this spread in temperature at a given density. The entropy
and the minimum Jeans mass in that case are determined by the choice of
) plane,
where matter can be hotter at low density and cooler at high density
compared with the barotropic treatment (red solid line). As seen in the
figure, the fragments eventually reach different isentropes. The
central fragment lies on the highest entropy level, while the orbiting
fragments end up on cooler isentropes. The barotropic EOS cannot
reproduce this spread in temperature at a given density. The entropy
and the minimum Jeans mass in that case are determined by the choice of
![]() .
In the FLD-LF case, cooling is more efficient; material in the
equatorial plane cools by radiating in the vertical directions, where
the gas is optically thin. However, this result is mainly affected by
the diffusivity of the Riemann solver. In the FLD-HLLD case, all the
material was heated by the central fragment accretion luminosity and
distributed above the barotropic adiabat. In the FLD-LF case, the
fragmentation is the combined result of the
inefficient magnetic braking
and the efficient cooling caused by the FLD. This illustrates the
importance and complexity
of the interplay between the magnetic field and radiative transfer.
.
In the FLD-LF case, cooling is more efficient; material in the
equatorial plane cools by radiating in the vertical directions, where
the gas is optically thin. However, this result is mainly affected by
the diffusivity of the Riemann solver. In the FLD-HLLD case, all the
material was heated by the central fragment accretion luminosity and
distributed above the barotropic adiabat. In the FLD-LF case, the
fragmentation is the combined result of the
inefficient magnetic braking
and the efficient cooling caused by the FLD. This illustrates the
importance and complexity
of the interplay between the magnetic field and radiative transfer.
| Figure 4:
Case |
|
| Open with DEXTER | |
3.2 Case 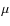 = 5
= 5
We now consider a strongly magnetized core, with
![\begin{figure}
\par\includegraphics[width=8.1cm,height=7cm,clip]{13597fg9.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13597-09/Timg44.png)
|
Figure 5:
Case |
| Open with DEXTER | |
Figure 5 compares temperature and density maps in the yz-plane for the FLD and barotropic calculations, at
![]() kyr.
In both cases, an outflow is launched, with similar propagation and
opening angles. The density patterns are also similar. The temperature
distributions, however, differ drastically. As shown in Hennebelle & Fromang (2008),
a pseudo-warm disc is formed in the equatorial plane in the barotropic
case. We also note the lack of significant heating in the vertical
direction with the barotropic EOS. Since the density within the outflow
is low,
kyr.
In both cases, an outflow is launched, with similar propagation and
opening angles. The density patterns are also similar. The temperature
distributions, however, differ drastically. As shown in Hennebelle & Fromang (2008),
a pseudo-warm disc is formed in the equatorial plane in the barotropic
case. We also note the lack of significant heating in the vertical
direction with the barotropic EOS. Since the density within the outflow
is low,
![]() g cm-3,
this implies a low temperature, which quickly falls to 11 K
10 AU from the center. When including a more proper treatment of
radiation, with the FLD, the radiation escapes preferentially in the
vertical direction (along the z-axis) and heats the gas out to about 100 AU. The highest outflow velocity,
g cm-3,
this implies a low temperature, which quickly falls to 11 K
10 AU from the center. When including a more proper treatment of
radiation, with the FLD, the radiation escapes preferentially in the
vertical direction (along the z-axis) and heats the gas out to about 100 AU. The highest outflow velocity,
![]() km s-1, is obtained in the barotropic case, while
km s-1, is obtained in the barotropic case, while
![]() km s-1
in the FLD calculation. The border line between the outflow and the
infalling gas shows a small spike, where the material is shocked and
heated. The toroidal magnetic field component profiles are in good
agreement with the results of Hennebelle & Fromang (2008) and exhibit a nearly constant plateau in the region of the outflow.
For our present study of a 1
km s-1
in the FLD calculation. The border line between the outflow and the
infalling gas shows a small spike, where the material is shocked and
heated. The toroidal magnetic field component profiles are in good
agreement with the results of Hennebelle & Fromang (2008) and exhibit a nearly constant plateau in the region of the outflow.
For our present study of a 1 ![]() core, radiative cooling in the
core, radiative cooling in the ![]() case is found to be almost inconsequential to the collapse. The cores
are never found to fragment. For more massive cores with stronger
radiative feedback, however, the heating in the outflow is likely to be
more dynamically significant (Krumholz et al. 2007).
case is found to be almost inconsequential to the collapse. The cores
are never found to fragment. For more massive cores with stronger
radiative feedback, however, the heating in the outflow is likely to be
more dynamically significant (Krumholz et al. 2007).
4 Summary and discussion
We have explored the effects of both radiative transfer and magnetic fields (in the limit of ideal MHD) on the fragmentation of a 1In the case ![]() ,
where both the behaviour of the flow and the magnetic field affect the
dynamics of the collapse, weshow that radiative transfer has an
important impact on the final structure. A barotropic approximation can
account for neither the cooling of the dense and rotating gas in the
equatorial plane nor the heating of the less dense gas in the vertical
direction, where radiation is found to escape preferentially. Although
a value
,
where both the behaviour of the flow and the magnetic field affect the
dynamics of the collapse, weshow that radiative transfer has an
important impact on the final structure. A barotropic approximation can
account for neither the cooling of the dense and rotating gas in the
equatorial plane nor the heating of the less dense gas in the vertical
direction, where radiation is found to escape preferentially. Although
a value ![]() is inconsistent with observations, this case clearly illustrates the
impact of a proper treatment of radiative transfer on the collapse and
fragmentation of prestellar cores. For the strongly magnetized
is inconsistent with observations, this case clearly illustrates the
impact of a proper treatment of radiative transfer on the collapse and
fragmentation of prestellar cores. For the strongly magnetized ![]() case, the dynamics of the collapse is dominated by the magnetic field.
In that case, a proper treatment of
radiative cooling is less consequential to the collapse itself but is
crucial for deriving correct optical depth and temperature
distributions, two accessible observational diagnostics. The
temperature distribution with the FLD is indeed found to depend
strongly on the geometry, whereas the barotropic approximation yields a
nearly uniform distribution. We also note that in the
case, the dynamics of the collapse is dominated by the magnetic field.
In that case, a proper treatment of
radiative cooling is less consequential to the collapse itself but is
crucial for deriving correct optical depth and temperature
distributions, two accessible observational diagnostics. The
temperature distribution with the FLD is indeed found to depend
strongly on the geometry, whereas the barotropic approximation yields a
nearly uniform distribution. We also note that in the ![]() case, we always obtain an outflow, even when using the more diffusive
LF Riemann solver. These outflows cannot be obtained using SPH
calculations. We also performed FLD test calculations including the
radiative feedback from a pseudo central newborn star and found that,
for
our 1
case, we always obtain an outflow, even when using the more diffusive
LF Riemann solver. These outflows cannot be obtained using SPH
calculations. We also performed FLD test calculations including the
radiative feedback from a pseudo central newborn star and found that,
for
our 1 ![]() core case, it is inconsequential on the length and time scales of interest.
core case, it is inconsequential on the length and time scales of interest.
The spurious diffusivity caused by either the numerical resolution or the hydrodynamic solver, however, is found to significantly affect the collapse and fragmentation. A less diffusive numerical scheme (HLLD instead of LF) produces strong magnetic braking, which transports angular momentum. Material then falls onto the central core, leading to a higher accretion luminosity. A high numerical resolution is also crucial in the vertical direction to accurately describe the growth of the magnetic tower, which spreads the gas around the central object.
AcknowledgementsWe thank the anonymous referee for comments which have improved the paper significantly. Calculations have been performed at CEA on the DAPHPC cluster. We acknowledge funding from the European Community via the P7/2007-2013 Grant Agreement no. 247060.
References
- Attwood, R. E., Goodwin, S. P., Stamatellos, D., & Whitworth, A. P. 2009, A&A, 495, 201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Banerjee, R., & Pudritz, R. E. 2006, ApJ, 641, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R. 2009, MNRAS, 392, 1363 [NASA ADS] [CrossRef] [Google Scholar]
- Boss, A. P., Fisher, R. T., Klein, R. I., & McKee, C. F. 2000, ApJ, 528, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Commerçon, B., Hennebelle, P., Audit, E., Chabrier, G., & Teyssier, R. 2008, A&A, 482, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S., Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiles, C., & Crutcher, R. 2005, in Cosmic Magnetic Fields, LNP, 664, 137 [Google Scholar]
- Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Teyssier, R. 2008, A&A, 477, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krumholz, M. R., Klein, R. I., & McKee, C. F. 2007, ApJ, 656, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1969, MNRAS, 145, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Tomisaka, K., Matsumoto, T., & Inutsuka, S.-i. 2008, ApJ, 677, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Mellon, R. R., & Li, Z.-Y. 2009, ApJ, 698, 922 [NASA ADS] [CrossRef] [Google Scholar]
- Minerbo, G. N. 1978, J. Quant. Spec. Radiat. Transf., 20, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Miyoshi, T., & Kusano, K. 2005, J. Comp. Phys., 208, 315 [Google Scholar]
- Offner, S. S. R., Klein, R. I., McKee, C. F., & Krumholz, M. R. 2009, ApJ, 703, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., & Bate, M. R. 2007, MNRAS, 377, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., & Bate, M. R. 2008, MNRAS, 385, 1820 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., & Bate, M. R. 2009, MNRAS, 398, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, D., Henning, T., Helling, C., Ilgner, M., & Sedlmayr, E. 2003, A&A, 410, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitehouse, S. C., & Bate, M. R. 2006, MNRAS, 367, 32 [NASA ADS] [CrossRef] [Google Scholar]
Online Material
Appendix A: Note on the influence of both the Riemann solver and the numerical resolution
![\begin{figure}
\par\includegraphics[width=7.4cm,height=8cm,clip]{13597fg10.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13597-09/Timg50.png)
|
Figure A.1:
Case |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12.5cm,height=7cm,clip]{13597fg11.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13597-09/Timg52.png)
|
Figure A.2:
Density and temperature maps in the equatorial plane at time t=38.3 kyr (
|
| Open with DEXTER | |
Figure A.1 portrays the density maps in the equatorial plane for the 4 calculations, at time
![]() .
The calculations performed with the LF solver,
.
The calculations performed with the LF solver,
![]() and
and
![]() clearly diverge from the others, since it fragments. The lack
ofresolution clearly induces inaccurate fragmentation. The three other
calculations are qualitatively similar (no fragmentation) and agree
with Hennebelle & Teyssier (2008)
results (obtained using a Roe-type Riemann solver). This indicates that
the numerical resolution should be enhanced with the LF solver to avoid
spurious effects caused by the diffusivity of the solver. We note that
these differences are more important in the case of FLD calculations,
since depending on the strength of the magnetic braking, radiative
transfer can have two opposite effects. If magnetic braking is
insignificant (with poor resolution and a diffuse Riemann solver), the
material at the centrifugal barrier cools and then fragments. On the
other hand, when the magnetic braking is efficient (with HLLD or a high
resolution), the infall velocity and consequently, the accretion
luminosity, become higher, which prevents fragmentation occurring (as
material loses angular momentum and heats up).
clearly diverge from the others, since it fragments. The lack
ofresolution clearly induces inaccurate fragmentation. The three other
calculations are qualitatively similar (no fragmentation) and agree
with Hennebelle & Teyssier (2008)
results (obtained using a Roe-type Riemann solver). This indicates that
the numerical resolution should be enhanced with the LF solver to avoid
spurious effects caused by the diffusivity of the solver. We note that
these differences are more important in the case of FLD calculations,
since depending on the strength of the magnetic braking, radiative
transfer can have two opposite effects. If magnetic braking is
insignificant (with poor resolution and a diffuse Riemann solver), the
material at the centrifugal barrier cools and then fragments. On the
other hand, when the magnetic braking is efficient (with HLLD or a high
resolution), the infall velocity and consequently, the accretion
luminosity, become higher, which prevents fragmentation occurring (as
material loses angular momentum and heats up).
Appendix B: Case 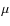 = 1000
= 1000
For this quasi-hydro case, the initial dense core is highly
gravitationally unstable. We performed three types of calculations with
the LF Riemann solver: one with the barotropic EOS and
![]() ,
and two with the FLD and different adiabatic exponents (
,
and two with the FLD and different adiabatic exponents (
![]() and
and
![]() ). The value
). The value
![]() is more appropriate for T> 100 K, when the rotational degrees of freedom of H2 are excited
(e.g., Machida et al. 2008). Using
is more appropriate for T> 100 K, when the rotational degrees of freedom of H2 are excited
(e.g., Machida et al. 2008). Using
![]() yields cooler adiabatic cores than with
yields cooler adiabatic cores than with
![]() at the same density. Higher densities and temperatures in the core are thus reached more rapidly.
at the same density. Higher densities and temperatures in the core are thus reached more rapidly.
Figure A.2 portrays density and temperature maps in the equatorial plane for the three aforementioned calculations at a time t=1.15
![]() .
Temperature maps range from 11.4 K to 20 K. As pointed out in Commerçon et al. (2008),
the horizon of predictability is very short when the initial thermal
support is low. Calculations do not show a convergence to the same
fragmentation pattern, since we do not integrate the same system
equations. The FLD calculations yield different fragmentation modes for
the two values of
.
Temperature maps range from 11.4 K to 20 K. As pointed out in Commerçon et al. (2008),
the horizon of predictability is very short when the initial thermal
support is low. Calculations do not show a convergence to the same
fragmentation pattern, since we do not integrate the same system
equations. The FLD calculations yield different fragmentation modes for
the two values of ![]() 's: for
's: for
![]() ,
we obtain a central object and two satellites (4 at later times), whereas for
,
we obtain a central object and two satellites (4 at later times), whereas for
![]() ,
we obtain a ring fragmentation pattern with orbiting fragments linked
by a bar. The barotropic EOS calculation does not produce a central
object.
From the temperature map of the FLD case with
,
we obtain a ring fragmentation pattern with orbiting fragments linked
by a bar. The barotropic EOS calculation does not produce a central
object.
From the temperature map of the FLD case with
![]() ,
we see that the central region is quite hot. Fragments are compressed more and radiate more energy than for
,
we see that the central region is quite hot. Fragments are compressed more and radiate more energy than for
![]() .
Fragments also form more rapidly than the time required for the
radiative feedback to become significant (at beginning of the second
collapse).
.
Fragments also form more rapidly than the time required for the
radiative feedback to become significant (at beginning of the second
collapse).
Footnotes
- ... fragmentation
![[*]](/icons/foot_motif.png)
- Appendices A and B are only available in electronic form at http://www.aanda.org
All Figures
![\begin{figure}
\includegraphics[width=12cm,clip]{13597fg1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13597-09/Timg16.png)
|
Figure 1:
Case |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=3.6cm,height=2.8cm,clip]{13597fg2.eps}...
...raphics[width=3.6cm,height=2.8cm,clip]{13597fg5.eps}
\vspace{-3mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13597-09/Timg37.png)
|
Figure 2:
Case |
| Open with DEXTER | |
| In the text | |
| |
Figure 3:
Case |
| Open with DEXTER | |
| In the text | |
| |
Figure 4:
Case |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.1cm,height=7cm,clip]{13597fg9.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13597-09/Timg44.png)
|
Figure 5:
Case |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.4cm,height=8cm,clip]{13597fg10.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13597-09/Timg50.png)
|
Figure A.1:
Case |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12.5cm,height=7cm,clip]{13597fg11.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13597-09/Timg52.png)
|
Figure A.2:
Density and temperature maps in the equatorial plane at time t=38.3 kyr (
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


