EDP Sciences
Home All issues Volume 510 (February 2010) A&A, 510 (2010) L3 Online Material
Free Access
Issue
A&A
Volume 510, February 2010
Article Number L3
Number of page(s) 6
Section Letters
DOI https://doi.org/10.1051/0004-6361/200913597
Published online 10 February 2010

Online Material

Appendix A: Note on the influence of both the Riemann solver and the numerical resolution

\begin{figure} \par\includegraphics[width=7.4cm,height=8cm,clip]{13597fg10.eps} \end{figure} Figure A.1:

Case $\mu =20$: density maps in the xy-plane at time $t\sim1.16~t_{\rm ff}$ for 4 barotropic EOS calculations with HLLD, $N_{\rm J}=6$ and $N_{\rm exp}=1$; LF, $N_{\rm J}=20$ and $N_{\rm exp}=4$; LF, $N_{\rm J}=10$ and $N_{\rm exp}=1$; LF, $N_{\rm J}=6$ and $N_{\rm exp}=1$.

Open with DEXTER

\begin{figure} \par\includegraphics[width=12.5cm,height=7cm,clip]{13597fg11.eps} \end{figure} Figure A.2:

Density and temperature maps in the equatorial plane at time t=38.3 kyr ( $1.15~t_{\rm ff}$), for the 3 unmagnetized cases: FLD approximation and $\gamma =7/5$ ( left), the FLD approximation and $\gamma =5/3$ ( middle), and with a barotropic EOS using $\rho _{\rm ad}=2.3\times 10^{-13}$ g cm-3 and $\gamma =5/3$ ( right). Velocity vectors are overplotted on the density maps

Open with DEXTER
We present a short convergence study to investigate the effect of both the Riemann solver and the numerical resolution on the fragmentation process. We show in Sect. 3.1 that the use of the LF Riemann solver leads to inaccurate results. We perform calculations using the barotropic EOS and the HLLD or LF solvers at various numerical resolutions. The latter is determined by 2 parameters: $N_{\rm J}$, the number of points per Jeans length, and $N_{\rm exp}$, which indicates the extent of the mesh around a refined cell (if a cell is flagged for refinement, then the $N_{\rm exp}$ cells around the flagged cell, in each direction, will also be refined). A large $N_{\rm exp}$ provides a smoother transition between the levels of the AMR grid. All calculations presented in Sect. 3.1 have been run with $N_{\rm exp}=4$. We report results of 4 calculations, performed for: HLLD, $N_{\rm J}=6$ and $N_{\rm exp}=1$; LF, $N_{\rm J}=20$ and $N_{\rm exp}=4$; LF, $N_{\rm J}=10$ and $N_{\rm exp}=1$; and LF, $N_{\rm J}=6$ and $N_{\rm exp}=1$.

Figure A.1 portrays the density maps in the equatorial plane for the 4 calculations, at time $t\sim1.16~t_{\rm ff}$. The calculations performed with the LF solver, $N_{\rm J}=6$ and $N_{\rm exp}=1$ clearly diverge from the others, since it fragments. The lack ofresolution clearly induces inaccurate fragmentation. The three other calculations are qualitatively similar (no fragmentation) and agree with Hennebelle & Teyssier (2008) results (obtained using a Roe-type Riemann solver). This indicates that the numerical resolution should be enhanced with the LF solver to avoid spurious effects caused by the diffusivity of the solver. We note that these differences are more important in the case of FLD calculations, since depending on the strength of the magnetic braking, radiative transfer can have two opposite effects. If magnetic braking is insignificant (with poor resolution and a diffuse Riemann solver), the material at the centrifugal barrier cools and then fragments. On the other hand, when the magnetic braking is efficient (with HLLD or a high resolution), the infall velocity and consequently, the accretion luminosity, become higher, which prevents fragmentation occurring (as material loses angular momentum and heats up).

Appendix B: Case 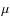$\mu $ = 1000

For this quasi-hydro case, the initial dense core is highly gravitationally unstable. We performed three types of calculations with the LF Riemann solver: one with the barotropic EOS and $\gamma =5/3$, and two with the FLD and different adiabatic exponents ( $\gamma =5/3$ and $\gamma =7/5$). The value $\gamma =7/5$ is more appropriate for T> 100 K, when the rotational degrees of freedom of H2 are excited (e.g., Machida et al. 2008). Using $\gamma =7/5$ yields cooler adiabatic cores than with $\gamma =5/3$ at the same density. Higher densities and temperatures in the core are thus reached more rapidly.

Figure A.2 portrays density and temperature maps in the equatorial plane for the three aforementioned calculations at a time t=1.15 $t_{\rm ff}$. Temperature maps range from 11.4 K to 20 K. As pointed out in Commerçon et al. (2008), the horizon of predictability is very short when the initial thermal support is low. Calculations do not show a convergence to the same fragmentation pattern, since we do not integrate the same system equations. The FLD calculations yield different fragmentation modes for the two values of $\gamma$'s: for $\gamma =7/5$, we obtain a central object and two satellites (4 at later times), whereas for $\gamma =5/3$, we obtain a ring fragmentation pattern with orbiting fragments linked by a bar. The barotropic EOS calculation does not produce a central object. From the temperature map of the FLD case with $\gamma =7/5$, we see that the central region is quite hot. Fragments are compressed more and radiate more energy than for $\gamma =5/3$. Fragments also form more rapidly than the time required for the radiative feedback to become significant (at beginning of the second collapse).

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.