| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 21 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200913120 | |
| Published online | 02 February 2010 | |
The chemical composition of the Orion star forming region
I. Homogeneity of O and Si abundances in
B-type stars![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
S. Simón-Díaz1,2
1 - Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife,
Spain
2 - Departamento de Astrofísica, Universidad de La Laguna,
38205 La Laguna, Tenerife, Spain
Received 14 August 2009 / Accepted 27 October 2009
Abstract
Context. Recent accurate abundance analyses of
B-type main sequence stars in the solar vicinity has shown that
abundances derived from these stellar objects are more homogeneous and
metal-rich than previously thought.
Aims. We investigate whether the inhomogeneity of
abundances previously found in B-type stars in the Ori OB1
association is real (hence a signature of enrichment of the newly
formed stars in an induced star formation scenario) or a consequence of
intrinsic errors induced by the use of photometric indices to establish
the stellar parameters prior to the abundance analysis.
Methods. We obtained a new (improved) spectroscopic
data set comprising 13 B-type stars in the various
Ori OB1 associations, and performed a detailed,
self-consistent spectroscopic abundance analysis by means of the modern
stellar atmosphere code FASTWIND.
Results. We detect systematic errors in the stellar
parameters determined previously which affect the derived abundances.
Once these errors are accounted for, we find a high degree of
homogeneity in the O and Si abundances for stars in the four
Ori OB1 subgroups. The derived abundances are in very good
agreement with recent determinations in other B-type stars in the solar
vicinity. We also compare our results with those obtained for the Sun
during the epoch of the ``solar crisis'', and the Orion nebula.
Key words: stars: early-type - stars: atmospheres - stars: fundamental parameters - stars: abundances
1 Introduction
For many years, our knowledge about the chemical composition of early-B main sequence stars in the solar vicinity has been characterized by two main results: (i) the derived abundances seemed to be highly inhomogeneous (with a dispersion of up to 0.5 dex); and (ii) the mean values indicated lower abundances than the standard (Grevesse & Sauval 1998) set of solar abundances (see reviews by Morel 2009; Herrero & Lennon 2004). These results were not very encouraging, because the inhomogeneity of stellar abundances contradicted with the homogeneity in oxygen abundance found from studying the local diffuse interstellar medium (e.g. Meyer et al. 1998; Cartledge et al. 2006). On the other hand, chemical evolution models of the Galaxy (e.g. Carigi et al. 2005; Chiappini et al. 2003) predict a small enrichment of the ISM in metals during the lifetime of the Sun (i.e. because they are younger than the Sun, nearby OB-type stars are expected to be slightly metal-rich).
Some recent results have began to change this situation. The solar oxygen abundance traditionally considered as a cosmic abundance reference (Grevesse & Sauval 1998) was reviewed by Asplund et al. (2004), who obtained log (O/H) = 8.66 dex, 0.17 dex lower than the standard value. This was the beginning of what has been called the epoch of the``solar crisis'': between 2004 and 2008, several studies by different authors (Ayres 2008; Caffau et al. 2008; Centeno & Socas-Navarro 2008; Socas-Navarro & Norton 2007; Meléndez & Asplund 2008; Ayres et al. 2006; Allende Prieto 2008) presented solar oxygen abundances derived by means of different approaches. The calculated values range from 8.63 dex (Socas-Navarro & Norton 2007) to 8.86 dex (Centeno & Socas-Navarro 2008). The debate about its actual value is still open.
Przybilla et al. (2008)
have recently analyzed a representative sample of six unevolved early
B-type stars in nearby OB associations and the field, and
found a very narrow distribution of abundances, with mean values that
are more metal-rich compared to previous works (e.g.
log (O/H) = 8.76 dex, a value that
is within the range of solar abundances calculated during the ``solar
crisis''). These authors indicate the importance of properly
determining the atmospheric parameters and using robust model atoms to
avoid systematic errors in the abundance determination. (See also Nieva & Przybilla 2009, for
a summary of the main sources of systematic errors affecting the
abundance analyses of B-type stars.) The study by Przybilla
et al. show that the
chemical inhomogeneity previously found for B-type stars in the solar
vicinity
may be spurious and an artificial effect of those systematic errors.
It also reinforces the importance of self-consistent spectroscopic
abundance analyses (i.e., the stellar parameters and the metal
abundances are determined exclusively from spectroscopic diagnostics by
using the same set of stellar atmosphere models). Less accurate
photometric ![]() estimates must be handle
with care (or better avoided whenever possible!) in the abundance
analysis
of B-type stars (see also Nieva
& Przybilla 2008).
estimates must be handle
with care (or better avoided whenever possible!) in the abundance
analysis
of B-type stars (see also Nieva
& Przybilla 2008).
The Orion complex, containing the Orion molecular cloud and
the Orion OB1
(Ori OB1) association, is one of the most massive active
star-forming regions in the 1 kpc centered on the Sun. Blaauw (1964) divided
Ori OB1 into four subgroups of stars - namely Ia, Ib,
Ic, and Id - having different locations in the sky and ages. Brown et al. (1994) derived
mean ages of ![]() ,
,
![]()
![]() ,
,
![]() ,
and <1 Myr for subgroups Ia to Id,
respectively. The youngest subgroup Ori OB1 Id is associated
with the Orion nebula (M 42), the most studied H II
region and the closest ionized nebula to the Sun in which a high
accuracy abundance analysis can be performed.
,
and <1 Myr for subgroups Ia to Id,
respectively. The youngest subgroup Ori OB1 Id is associated
with the Orion nebula (M 42), the most studied H II
region and the closest ionized nebula to the Sun in which a high
accuracy abundance analysis can be performed.
The correlation between the ages of the stellar subgroups,
their location, and the large scale structures in the interstellar
medium around Orion OB1 have been interpreted as features of
sequential star formation and type-II supernovae (Cowie et al.
1979; Brown
et al. 1994; Reynolds & Ogden 1979). Cunha &
Lambert (1994,1992)
obtained C, N, O, Si, and Fe abundances of 18 B-type
main sequence stars from the four subgroups comprising the
Ori OB1 association. They found a range
in oxygen abundances![]() of
of ![]() 0.4 dex,
with the highest values corresponding to the stars in the youngest (Id
and some Ic) subgroups. In this case, the inhomogeneity in
stellar abundances (mainly oxygen and silicon) seemed to be real and
coherent with a scenario of induced star formation in which the new
generation of stars are formed from interstellar material contaminated
by type-II supernovae ejecta.
0.4 dex,
with the highest values corresponding to the stars in the youngest (Id
and some Ic) subgroups. In this case, the inhomogeneity in
stellar abundances (mainly oxygen and silicon) seemed to be real and
coherent with a scenario of induced star formation in which the new
generation of stars are formed from interstellar material contaminated
by type-II supernovae ejecta.
The study by Cunha &
Lambert was based on a photometric estimation of
![]() and the
fitting of the H
and the
fitting of the H![]() line computed from Kurucz (1979)
LTE model atmospheres to the observed one to
derive log g. In a more recent work, Simón-Díaz et al.
(2006) used one of the new generation of NLTE,
line blanketed, model atmosphere codes ( FASTWIND,
Puls
et al. 2005; Santolaya-Rey et al. 1997)
and a self-consistent spectroscopic approach to derive the stellar
parameters and oxygen abundances for the three
B0.5 V stars in Ori OB1d (the youngest and,
supposedly, more metal-rich subgroup). The resulting stellar parameters
were somewhat different and, more important, the derived abundances
were systematically lower than the previous values by Cunha & Lambert (1994) by
line computed from Kurucz (1979)
LTE model atmospheres to the observed one to
derive log g. In a more recent work, Simón-Díaz et al.
(2006) used one of the new generation of NLTE,
line blanketed, model atmosphere codes ( FASTWIND,
Puls
et al. 2005; Santolaya-Rey et al. 1997)
and a self-consistent spectroscopic approach to derive the stellar
parameters and oxygen abundances for the three
B0.5 V stars in Ori OB1d (the youngest and,
supposedly, more metal-rich subgroup). The resulting stellar parameters
were somewhat different and, more important, the derived abundances
were systematically lower than the previous values by Cunha & Lambert (1994) by ![]() 0.2-0.3 dex.
0.2-0.3 dex.
This result motivated us to review the chemical composition of the other B-type stars in Ori OB1 to investigate whether the inhomogeneity of abundances previously found is real or a consequence of intrinsic errors induced by the use of photometric indices to establish the stellar parameters prior to the abundance analysis. To this aim, we obtained a totally new (improved) observational data set and performed a self-consistent abundance analysis of 13 of the stars considered by Cunha & Lambert (1994,1992).
We used FASTWIND to derive the stellar parameters, oxygen, and silicon abundances. The observational data set is described in Sect. 2. The whole spectroscopic analysis is presented in Sect. 3. Then, we compare our stellar parameters and abundance with results from previous works (Sect. 4). The homogeneity of stellar abundances in Ori OB1 and its comparison with other B-type stars in the solar vicinity determinations, the Sun, and the Orion nebula is discussed in Sect. 5. The main conclusions of this work are summarized in Sect. 6.
2 Observational data set
Table 1: List of B-type stars from Ori OB1 considered in this study, ordered by spectral type.
![\begin{figure}
\par\includegraphics[angle=90,scale=0.62]{13120f1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg16.png)
|
Figure 1: Example of FIES@ NOT spectra for three of the observed stars. The complete atlas is available in the electronic version of the paper (Fig. 8). The Si II-IV and O II lines used for the abundance analysis are indicated as solid and dashed vertical lines, respectively. |
| Open with DEXTER | |
The observations used here were carried out with the FIES
cross-dispersed, high-resolution echelle spectrograph attached to the
NOT2.5 m telescope at El Roque de los Muchachos
observatory on La Palma (Islas Canarias, Spain) on
5-8 November 2008. The medium-resolution mode (
R =
46 000, ![]() Å/pix)
was selected, and the entire spectral range 3700-7300 Å was
covered without gaps in a single fixed setting. A sample of
14 stellar candidates was observed, after being selected from
the list of stars in the Ori OB1 association analyzed by Cunha &
Lambert (1994,1992).
These are early-B type, non-evolved, stellar objects
(B0 V-B2 V) with low projected rotational velocities (v sin i
Å/pix)
was selected, and the entire spectral range 3700-7300 Å was
covered without gaps in a single fixed setting. A sample of
14 stellar candidates was observed, after being selected from
the list of stars in the Ori OB1 association analyzed by Cunha &
Lambert (1994,1992).
These are early-B type, non-evolved, stellar objects
(B0 V-B2 V) with low projected rotational velocities (v sin i ![]() 60 km s-1).
The signal-to-noise ratio achieved for all the spectra was always
above 250. The list of observed stars is presented in
Table 1.
Apart from the new set of stars, we re-observed HD 37020 and
HD 37042, two of the three B-type stars
60 km s-1).
The signal-to-noise ratio achieved for all the spectra was always
above 250. The list of observed stars is presented in
Table 1.
Apart from the new set of stars, we re-observed HD 37020 and
HD 37042, two of the three B-type stars![]() analyzed in Simón-Díaz
et al. (2006).
analyzed in Simón-Díaz
et al. (2006).
The spectra were reduced with the FIEStool![]() software in advanced mode.
The FIEStool pipeline provided wavelength calibrated, blaze-corrected,
order-merged spectra of high quality. These spectra were then
normalized with our own developed IDL
programs. An example of the FIES@ NOT
spectra for three of the observed stars is presented in
Fig. 1,
where the Si II-IV and O II
lines used for the abundance analysis are also indicated.
software in advanced mode.
The FIEStool pipeline provided wavelength calibrated, blaze-corrected,
order-merged spectra of high quality. These spectra were then
normalized with our own developed IDL
programs. An example of the FIES@ NOT
spectra for three of the observed stars is presented in
Fig. 1,
where the Si II-IV and O II
lines used for the abundance analysis are also indicated.
3 Spectroscopic analysis
The analyses were performed following a self-consistent spectroscopic approach with the spherically extended, NLTE, line-blanketed stellar atmosphere code FASTWIND (Puls et al. 2005; Santolaya-Rey et al. 1997). Basically, the stellar parameters were derived by comparing the observed H Balmer line profiles and the ratio of Si III-IV and/or Si II-III line equivalent widths with the output from a grid of FASTWIND models. Whenever possible, the He I-II ionizing equilibrium was also considered. Then, the same grid of models was used to derive the stellar abundances by means of the curve-of-growth method.
3.1 Projected rotational velocities
The projected rotational velocities (v sin i)
were obtained by applying
the Fourier method (Gray, 1976; see also Simón-Díaz
& Herrero, 2007,
for its application to OB-type stars) to the Si III ![]() 4552 line.
The 0.03 Å/pix resolution of the FIES spectra implies that the
lowest v sin i
that could be detected is 2-3 km s-1;
however, for those cases with v sin i < 10-15 km s-1,
identifying of the first zero of the Fourier transform was difficult
due to the effect of the noise (an maybe the microturbulence).
4552 line.
The 0.03 Å/pix resolution of the FIES spectra implies that the
lowest v sin i
that could be detected is 2-3 km s-1;
however, for those cases with v sin i < 10-15 km s-1,
identifying of the first zero of the Fourier transform was difficult
due to the effect of the noise (an maybe the microturbulence).
In many cases, an additional extra Gaussian-type broadening (
![]() ) was
needed to properly fit the line profile for the derived value of v sin i.
This extra-broadening account for the microturbulence (and maybe the
macroturbulence), also affecting the shape of the line. The
corresponding derived values are summarized in Table 2.
) was
needed to properly fit the line profile for the derived value of v sin i.
This extra-broadening account for the microturbulence (and maybe the
macroturbulence), also affecting the shape of the line. The
corresponding derived values are summarized in Table 2.
3.2 Measurement of equivalent widths and identification of problematic lines
Table 2: Projected rotational velocities derived for the studied stars.
Table 3: Final results of the HSi analysis: stellar parameters and Si abundances.
The strategy we followed in our analyses is based on the
equivalent widths (EW) of metal lines. Therefore,
proper identification of the lines of interest, along with an accurate
measurement of their EWs (also including the
associated uncertainties), is a very important step. We have developed
IDL routines automatically identifying metal lines in the spectra,
measuring the EWs and their uncertainties, and
detecting the possibility that other lines affect these measurements.
To this aim we compiled a list of C, N, O, Si, Mg, S, Ne, and
Ar lines, extracted from the atomic![]() line list v2.05. For a given line, the program performs a
multi-Gaussian fit of the observed line profile accounting for all the
lines expected to be present in a certain spectral range (
line list v2.05. For a given line, the program performs a
multi-Gaussian fit of the observed line profile accounting for all the
lines expected to be present in a certain spectral range (![]()
![]() [v sin i
[v sin i![]() /c, 0.5
/c, 0.5![]() /R]) around
the wavelength indicated in the line list. The uncertainty in the EW
measurement is obtained by assuming the location of the local continuum
at
/R]) around
the wavelength indicated in the line list. The uncertainty in the EW
measurement is obtained by assuming the location of the local continuum
at ![]() 1/SNR
and, in those cases in which the line is isolated, comparing the value
obtained by means of the Gaussian fitting with the value derived by
integrating the line.
1/SNR
and, in those cases in which the line is isolated, comparing the value
obtained by means of the Gaussian fitting with the value derived by
integrating the line.
The high quality of our spectra allowed us to identify and
measure the EWs of up to 27 Si II-IV
lines and 47 O II lines. Some of
the lines were labeled as problematic because of the presence of one or
more lines from other elements (e.g. the O II ![]() 4673.73 line
may be affected by the C III
4673.73 line
may be affected by the C III ![]() 4673.95 in
same cases; similarly occurs for the O II
4673.95 in
same cases; similarly occurs for the O II ![]() 4641.81
line, coincident with the N III
4641.81
line, coincident with the N III ![]() 4641.85
line). These lines were treated with special care in the abundance
analysis, since they may be giving
wrong values for the abundance.
4641.85
line). These lines were treated with special care in the abundance
analysis, since they may be giving
wrong values for the abundance.
Generally, the Gaussian fit provides reliable results for the EWs; however, in those cases in which the v sin i of the star is above 30-35 km s-1, the use of a Gaussian to fit the profile may result in an under or overestimation of the EW (in a few percent), depending on the line strength. For those cases, the EW resulting from the integration of the observed line profile was preferred.
3.3 A grid of HHeOSi FASTWIND models
For this study, we constructed a grid of FASTWIND
models with ![]() and log g ranging from 17 to 36 kK
(1 kK steps) and 3.7 to 4.3 dex (0.1 dex
steps). As the studied stars are not expected to be evolved, the He
abundance was fixed to 0.09 dex. In addition, since FASTWIND
is a spherically extended code, the radius and other wind parameters
need to be indicated, and are grouped in the Q-parameter.
We fixed this parameter to
and log g ranging from 17 to 36 kK
(1 kK steps) and 3.7 to 4.3 dex (0.1 dex
steps). As the studied stars are not expected to be evolved, the He
abundance was fixed to 0.09 dex. In addition, since FASTWIND
is a spherically extended code, the radius and other wind parameters
need to be indicated, and are grouped in the Q-parameter.
We fixed this parameter to ![]() as a representative value for which the wind effect over the optical
spectrum is practically negligible. (H
as a representative value for which the wind effect over the optical
spectrum is practically negligible. (H![]() and He II
and He II![]() 4686 show no sign of wind
contamination.) The metallicity was assumed to be solar (following the
set of abundances by Grevesse &
Sauval 1998).
4686 show no sign of wind
contamination.) The metallicity was assumed to be solar (following the
set of abundances by Grevesse &
Sauval 1998).
For each pair of stellar parameters, a sub grid of
models varying the microturbulence (
![]() = 1, 3, 5,
7, 9 km s-1), the Si abundance
(
= 1, 3, 5,
7, 9 km s-1), the Si abundance
(
![]() = -5.10,
-4.80, -4.50, -4.20 dex), and the O abundance (
= -5.10,
-4.80, -4.50, -4.20 dex), and the O abundance (
![]() ,
-3.65, -3.30, -2.95 dex) was calculated. The O and Si atomic
models used for the grid came mainly from Becker & Butler (1988,1990).
However, two updates were considered: (a) a extended Si II
model atom (see Trundle et al.
2004), and (b) the most recent log gf values
indicated in the atomic line list v2.05 for the formal solution
calculations.
,
-3.65, -3.30, -2.95 dex) was calculated. The O and Si atomic
models used for the grid came mainly from Becker & Butler (1988,1990).
However, two updates were considered: (a) a extended Si II
model atom (see Trundle et al.
2004), and (b) the most recent log gf values
indicated in the atomic line list v2.05 for the formal solution
calculations.
The final grid consists of
![]() (=560) models
and a total of 2800 formal solutions
(5 microturbulence values per model). It includes line
profiles and EWs
for H , He I-II,
Si II-IV and O II
lines, along with the spectral energy distribution for each set of
stellar parameters.
(=560) models
and a total of 2800 formal solutions
(5 microturbulence values per model). It includes line
profiles and EWs
for H , He I-II,
Si II-IV and O II
lines, along with the spectral energy distribution for each set of
stellar parameters.
3.4 Determining stellar parameters
The use of the Si III-IV and/or
Si II-III ionization equilibrium,
along with the H Balmer lines, for determining the stellar
parameters of early B-type stars is a longstanding method
described elsewhere (see e.g. Kilian et al. 1991; Urbaneja
et al. 2005; Crowther et al. 2006; Markova &
Puls 2008). The ratios EW(Si IV ![]() 4116)/EW(Si III
4116)/EW(Si III ![]() 4552)
and/or EW(Si II
4552)
and/or EW(Si II ![]() 4128)/EW(Si III
4128)/EW(Si III ![]() 4552),
depending on the temperature of the star have been traditionally used
as
4552),
depending on the temperature of the star have been traditionally used
as ![]() indicators. This decision has been probably motivated by the fact that
these are the strongest, unblended lines in the spectral range commonly
observed for the stellar abundance analysis (i.e.
indicators. This decision has been probably motivated by the fact that
these are the strongest, unblended lines in the spectral range commonly
observed for the stellar abundance analysis (i.e. ![]() 4000-5000 Å).
4000-5000 Å).
We derived the stellar parameters, along with the
Si abundance, for all stars in our sample using this
methodology. We initially considered that these Si line ratios
determine the effective temperatures (Cols. 3 and 4
in Table 3).
However, motivated by a couple of problems found when deriving the
stellar parameters in the cooler objects (see discussion below), we
decide to include the EW(Si II ![]() 6347)/EW(Si III
6347)/EW(Si III ![]() 4552) ratio
as a temperature indicator (Col. 5). The measured values are
indicated in brackets in the corresponding
columns. As expected, the Si IV/Si III
ratio decreases when we move to later spectral types, and the
Si II/Si III
behaves in the opposite way. For three of the stars (HD 36959,
HD 35299, and HD 37744), lines from the three ions
are clearly and simultaneously present in the spectra.
4552) ratio
as a temperature indicator (Col. 5). The measured values are
indicated in brackets in the corresponding
columns. As expected, the Si IV/Si III
ratio decreases when we move to later spectral types, and the
Si II/Si III
behaves in the opposite way. For three of the stars (HD 36959,
HD 35299, and HD 37744), lines from the three ions
are clearly and simultaneously present in the spectra.
Four parameters need to be determined at the same time in an
iterative way: ![]() ,
log g,
,
log g,
![]() (Si), and
(Si), and
![]() .
First, we use the Si line ratios indicated above and the wings of the
H Balmer lines (fixing
.
First, we use the Si line ratios indicated above and the wings of the
H Balmer lines (fixing
![]() (Si), and
(Si), and
![]() )
to obtain an initial guess for
)
to obtain an initial guess for
![]() and
log g. Then we apply the curve of
growth method to a proper set of Si II-IV
lines to iteratively obtain final values for the four parameters (a
detailed description of the used lines and the results of the Si
abundance analysis is presented below). Normally, the final values of
and
log g. Then we apply the curve of
growth method to a proper set of Si II-IV
lines to iteratively obtain final values for the four parameters (a
detailed description of the used lines and the results of the Si
abundance analysis is presented below). Normally, the final values of
![]() and
log g are quite close to the initial
values, since the mentioned line ratios are only slightly dependent on
and
log g are quite close to the initial
values, since the mentioned line ratios are only slightly dependent on
![]() and
and
![]() .
.
3.4.1
Hotter objects (
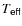
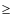 27 000 K)
27 000 K)
In the hotter objects, Si II lines are not
present in the spectra. The EW(Si IV ![]() 4116)/EW(Si III
4116)/EW(Si III ![]() 4552) ratio
is thus used to obtain the initial guess values of
4552) ratio
is thus used to obtain the initial guess values of
![]() for each of
the log g values considered in
the grid. Then, the full set of reliable Si III-IV
lines, along with the H Balmer line profiles, is used for fine
determination of the four parameters indicated above (see an example in
the upper panel of Fig. 2,
and in Fig. 3).
The uncertainties in the EW measurements of the Si
lines have been taken into account for establishing the uncertainties
associated with the derived stellar parameters. Generally, the
for each of
the log g values considered in
the grid. Then, the full set of reliable Si III-IV
lines, along with the H Balmer line profiles, is used for fine
determination of the four parameters indicated above (see an example in
the upper panel of Fig. 2,
and in Fig. 3).
The uncertainties in the EW measurements of the Si
lines have been taken into account for establishing the uncertainties
associated with the derived stellar parameters. Generally, the
![]() and
log g can be determined with an
accuracy better than 500-600 K and 0.1 dex,
respectively. The final results of the analysis are presented in
Table 3.
and
log g can be determined with an
accuracy better than 500-600 K and 0.1 dex,
respectively. The final results of the analysis are presented in
Table 3.
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,clip]{13120f2.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg97.png)
|
Figure 2: Silicon abundance vs. EW diagnostic diagrams for three of the analyzed stars (with representative effective temperatures). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,clip]{13120f3.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg98.png)
|
Figure 3: Example of fitting the H Balmer lines to determine log g. Two FASTWIND models are compared with the observed spectrum (red line) of HD 36960: in black, model with the stellar parameters resulting from the FASTWIND HSi analysis (28 900, 3.9); in blue, model with the stellar parameters derived by Cunha & Lambert (1992), for comparison (28 900, 4.3). |
| Open with DEXTER | |
For main sequence stars with ![]()
![]() 28 000 K
the He I-II ionization equilibrium
can also be used (see e.g. Herrero
et al. 1992; Simón-Díaz et al. 2006).
(Below this temperature,
He II lines are too faint or not
present in the spectrum.) We could determine the stellar parameters in
this way for four of the stars in our sample. An example of this type
of analysis has already been presented in Simón-Díaz et al.
(2006), so we only present here the corresponding results
(see Col. 6 in Table 3). In general,
there is good agreement between the
28 000 K
the He I-II ionization equilibrium
can also be used (see e.g. Herrero
et al. 1992; Simón-Díaz et al. 2006).
(Below this temperature,
He II lines are too faint or not
present in the spectrum.) We could determine the stellar parameters in
this way for four of the stars in our sample. An example of this type
of analysis has already been presented in Simón-Díaz et al.
(2006), so we only present here the corresponding results
(see Col. 6 in Table 3). In general,
there is good agreement between the
![]() determined
through the Si III-IV
and the He I-II ionization balance
with differences in
determined
through the Si III-IV
and the He I-II ionization balance
with differences in ![]() not larger than
not larger than ![]() 500 K.
500 K.
3.4.2 Cooler objects
For the cooler objects, the Si II/Si III
must be used. We initially considered the EW(Si II ![]() 4130)/EW(Si III
4130)/EW(Si III ![]() 4552)
ratio for obtaining a first estimation of the stellar parameters;
however, we found two facts that warned us of a possible problem with
the Si II
4552)
ratio for obtaining a first estimation of the stellar parameters;
however, we found two facts that warned us of a possible problem with
the Si II ![]() 4130
(or the Si II
4130
(or the Si II ![]() 4128) line.
First, it was not possible to properly fit the H Balmer lines
for any of the (
4128) line.
First, it was not possible to properly fit the H Balmer lines
for any of the (
![]() ,
log g)-pairs indicated by the Si II
,
log g)-pairs indicated by the Si II ![]() 4130/Si III
4130/Si III ![]() 4552 line
ratio, because the core of the H synthetic lines were
somewhat narrower than the observed ones (even if high values of
log g are considered). For
these temperatures, the cores of the H Balmer lines begin to be
sensitive to changes in
4552 line
ratio, because the core of the H synthetic lines were
somewhat narrower than the observed ones (even if high values of
log g are considered). For
these temperatures, the cores of the H Balmer lines begin to be
sensitive to changes in ![]() .
For all the cases studied, these lines require somewhat lower effective
temperatures to properly fit their cores.
Second, the
.
For all the cases studied, these lines require somewhat lower effective
temperatures to properly fit their cores.
Second, the ![]() -EW
diagnostic diagrams show two sets of Si II
lines giving different abundances by
-EW
diagnostic diagrams show two sets of Si II
lines giving different abundances by ![]() 0.2 dex (see lower panel in
Fig. 2).
Curiously, each subset of lines corresponds to transitions with very
different energy levels (Si II
0.2 dex (see lower panel in
Fig. 2).
Curiously, each subset of lines corresponds to transitions with very
different energy levels (Si II ![]()
![]() 4128, 4130,
5041, 5056, in one hand, coming from higher energy levels; Si II
4128, 4130,
5041, 5056, in one hand, coming from higher energy levels; Si II ![]()
![]() 6347, 6371,
3856, 3862, on the other, comming from lower energy levels; we suggest
the reader have a Grotrian diagram in hand). This different behavior of
the various lines warned us of possible problems with the Si II
atomic model and of using Si II
6347, 6371,
3856, 3862, on the other, comming from lower energy levels; we suggest
the reader have a Grotrian diagram in hand). This different behavior of
the various lines warned us of possible problems with the Si II
atomic model and of using Si II ![]() 4128 line
alone to establish the stellar temperature.
4128 line
alone to establish the stellar temperature.
Columns 4 and 5 in Table 3 show the different
effective temperatures obtained depending on the Si II
line that is used (Si II ![]() 4128,
Si II
4128,
Si II ![]() 6371).
Temperatures given by the EW(Si II
6371).
Temperatures given by the EW(Si II ![]() 6371)/EW(Si III
6371)/EW(Si III ![]() 4552) ratio
are systematically lower by up to
4552) ratio
are systematically lower by up to ![]() 2000-3000 K. In addition, a proper fit
of the cores of the H Balmer lines can be achieved with these
new values of the temperature.
2000-3000 K. In addition, a proper fit
of the cores of the H Balmer lines can be achieved with these
new values of the temperature.
3.4.3 HD 36595, HD 37744, and HD 35299
These three stars show Si II-III-IV
lines in their spectra, so can contribute with new decisive clues to
the problem mentioned above. In this
case we count with three ![]() indicators. As can be noticed from inspection
of Table 3,
the
indicators. As can be noticed from inspection
of Table 3,
the ![]() indicated by the EW(Si II
indicated by the EW(Si II ![]() 6371)/EW(Si III
6371)/EW(Si III ![]() 4552) ratio
results in better agreement than the other Si II/Si III
ratio
for two of the three cases. For the hotter object (HD 36959),
the Si II
4552) ratio
results in better agreement than the other Si II/Si III
ratio
for two of the three cases. For the hotter object (HD 36959),
the Si II ![]() 6371 is too
faint to be measured. Although the
6371 is too
faint to be measured. Although the
![]() indicated by the EW(Si II
indicated by the EW(Si II ![]() 4130)/EW(Si III
4130)/EW(Si III ![]() 4552) ratio
agrees with the Si IV/Si III
diagnostic in this object, this is not the case for the other objects.
4552) ratio
agrees with the Si IV/Si III
diagnostic in this object, this is not the case for the other objects.
In Fig. 2
(middle panel) we show the
![]() -EW
diagnostic diagram for HD 37744. The stellar parameters
considered in this plot are those indicated by the Si IV/Si III
ratio. The Si II
-EW
diagnostic diagram for HD 37744. The stellar parameters
considered in this plot are those indicated by the Si IV/Si III
ratio. The Si II ![]()
![]() 6371,
3856 lines fit the other Si III-IV
lines perfectly, but not the Si II
6371,
3856 lines fit the other Si III-IV
lines perfectly, but not the Si II ![]()
![]() 4128, 4130
lines.
4128, 4130
lines.
3.4.4 Concluding
We found some indications of a problem in the Si II
model atom
that led to bad modeling of the Si II ![]()
![]() 4128, 4130,
5041, 5056 lines. Fortunately, our observations also include
other Si II lines that seem to
behave properly. A review of the Si II
model atom is needed (and could be tested with the type of detailed
analysis presented here), but in the meantime, several
arguments allow us to trust
4128, 4130,
5041, 5056 lines. Fortunately, our observations also include
other Si II lines that seem to
behave properly. A review of the Si II
model atom is needed (and could be tested with the type of detailed
analysis presented here), but in the meantime, several
arguments allow us to trust![]() the Si II
the Si II ![]()
![]() 6347, 6371,
3856, 3862 set of lines for the stellar parameter determination
and for abundance analysis of the cooler objects in our sample:
(a) the coherence of results between Si IV-III
and Si III-II in terms of
6347, 6371,
3856, 3862 set of lines for the stellar parameter determination
and for abundance analysis of the cooler objects in our sample:
(a) the coherence of results between Si IV-III
and Si III-II in terms of
![]() ;
(b) the good fit of the H Balmer lines for the cooler
stars when the lower
;
(b) the good fit of the H Balmer lines for the cooler
stars when the lower ![]() is considered; (c) the coherence of results in Si and
O abundances that is obtained for all the stars in our sample
when this solution is adopted (see below).
is considered; (c) the coherence of results in Si and
O abundances that is obtained for all the stars in our sample
when this solution is adopted (see below).
3.4.5 Uncertainties
Columns 3 and 5 indicate the uncertainties in
![]() obtained
from considering errors in the EWs
measurement of Si II-IV lines.
These uncertainties, obtained by assuming a fixed gravity are
obtained
from considering errors in the EWs
measurement of Si II-IV lines.
These uncertainties, obtained by assuming a fixed gravity are ![]() 100-600 K.
Gravity can be normally established with an accuracy better
0.1 dex. Uncertainties from both quantities are correlated,
e.g. a positive
variation of log g of 0.1 dex
needs to be compensated by an increase of
100-600 K.
Gravity can be normally established with an accuracy better
0.1 dex. Uncertainties from both quantities are correlated,
e.g. a positive
variation of log g of 0.1 dex
needs to be compensated by an increase of
![]()
![]() 100-300 K
to guarantee again the Si ionization balance. Although in many cases
the formal errors in temperature obtained from the propagation of EWs
errors are smaller than 500 K, our experience warns us to be
conservative (since other parameters can also slightly affect the
derived temperatures, such as the considered microturbulence).
Therefore, we adopt 500 K and 0.1 dex as
characteristic uncertainties in
100-300 K
to guarantee again the Si ionization balance. Although in many cases
the formal errors in temperature obtained from the propagation of EWs
errors are smaller than 500 K, our experience warns us to be
conservative (since other parameters can also slightly affect the
derived temperatures, such as the considered microturbulence).
Therefore, we adopt 500 K and 0.1 dex as
characteristic uncertainties in
![]() and
log g, respectively, from our analyses.
and
log g, respectively, from our analyses.
3.5 Silicon and oxygen stellar abundances
We applied the curve-of-growth method to derive Si and
O abundances. This method considers a grid of models for a
given set of stellar parameters
(
![]() and log g)
in which the microturbulence and
the abundance of the
element to be studied are varied. An abundance is obtained for the
various values of microturbulence for each of the considered lines
(given the measured EW of the lines in the observed
spectrum). Then, the final abundance is given by that microturbulence
that results in all lines giving the same abundance. More details on
this method can be found in e.g. Kilian
(1992) or Simón-Díaz
et al. (2006).
and log g)
in which the microturbulence and
the abundance of the
element to be studied are varied. An abundance is obtained for the
various values of microturbulence for each of the considered lines
(given the measured EW of the lines in the observed
spectrum). Then, the final abundance is given by that microturbulence
that results in all lines giving the same abundance. More details on
this method can be found in e.g. Kilian
(1992) or Simón-Díaz
et al. (2006).
Our preference for this methodology in performing the abundance analysis is that we find the curve-of-growth method very powerful for identifying problematic lines (as shown e.g. in the previous section), which can affect the final abundance determination, and provide precise estimations of the uncertainties associated with the dispersion of line-to-line abundances, microturbulence, and the stellar parameters.
3.5.1 Silicon abundances
As mentioned, silicon abundance is obtained at the same time as
to the stellar parameters. Once a first estimation of the stellar
parameters
was obtained through the EW(Si IV ![]() 4116)/EW(Si III
4116)/EW(Si III ![]() 4552)
and/or EW(Si II
4552)
and/or EW(Si II ![]() 6371)/ EW(Si III
6371)/ EW(Si III ![]() 4552) line
ratios, the curve-of-growth method was applied to a proper set of Si
lines to derive the Si abundance, together with the final
values of the stellar parameters and a microturbulence.
4552) line
ratios, the curve-of-growth method was applied to a proper set of Si
lines to derive the Si abundance, together with the final
values of the stellar parameters and a microturbulence.
Initially, we included all the measured lines in the analysis,
but identified
some problematic lines. By problematic lines we
mean lines giving abundances that are too high or too low compared with
the mean value provide by a set of lines initially considered as
reliable. These problematic lines were removed in the final analysis.
To illustrate the procedure, we consider the case of HD 36960.
The ![]() -EWdiagram
with whole set of measured Si lines (Si III
and Si IV lines, in this case) is
shown in Fig. 4.
As the initial set of reliable lines we consider the Si III
-EWdiagram
with whole set of measured Si lines (Si III
and Si IV lines, in this case) is
shown in Fig. 4.
As the initial set of reliable lines we consider the Si III ![]()
![]() 4552, 4567,
4574 triplet and the Si IV
4552, 4567,
4574 triplet and the Si IV ![]() 4116 line.
The other Si IV lines provide
similar abundances to the first set of reliable lines, except
Si IV
4116 line.
The other Si IV lines provide
similar abundances to the first set of reliable lines, except
Si IV ![]() 6701. The
situation is less encouraging for the other
Si III lines, since all of them lie
below the mean abundance value from
reliable lines. We thus label these lines as problematic. The same
procedure was followed for the selection of reliable Si II
lines (see Sect. 3.4).
6701. The
situation is less encouraging for the other
Si III lines, since all of them lie
below the mean abundance value from
reliable lines. We thus label these lines as problematic. The same
procedure was followed for the selection of reliable Si II
lines (see Sect. 3.4).
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm,clip]{13120f4.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg100.png)
|
Figure 4: Silicon abundance vs. EW diagnostic diagrams for HD 36960. All the observed Si III-IV lines are included in the plot. Uncertainties in the individual line abundances (propagated from the errors in the measured EWs) are indicated as vertical lines. |
| Open with DEXTER | |
A similar behavior is found for the problematic lines in all the
analyzed stars. Since the EW of these lines are
accurately measured and no lines from other elements are expected to be
affecting them![]() ,
we argue that the discrepancy may be related to the definition of the
model atom. For example, the Si III
,
we argue that the discrepancy may be related to the definition of the
model atom. For example, the Si III ![]()
![]() 4813, 4819,
4829 triplet is known to give different results than the Si III
4813, 4819,
4829 triplet is known to give different results than the Si III ![]()
![]() 4552, 4567,
4574 triplet because of the boundary problems of the Si III
model atom (Becker & Butler 1990).
Normally, there is an explanation for the bad behavior of the
problematic lines; therefore, the exclusion of lines from the analysis
is not arbitrary (e.g. lines from the same
multiplets behave in the same way and are normally excluded all
together).
4552, 4567,
4574 triplet because of the boundary problems of the Si III
model atom (Becker & Butler 1990).
Normally, there is an explanation for the bad behavior of the
problematic lines; therefore, the exclusion of lines from the analysis
is not arbitrary (e.g. lines from the same
multiplets behave in the same way and are normally excluded all
together).
It is important to notice that the analysis with the whole set of lines (including the problematic ones) could lead to an incorrect determination of the microturbulence, hence of the final value of Si abundance.
Final results of the Si abundance analysis![]() are indicated in
Table 3
(Cols. 9 and 10). Three sources of errors must be
considered for estimating of the final uncertainty: (1) the
dispersion in the line-by-line abundances; (2) the uncertainty
associated with the microturbulence, (indicated in Table 3, and
Tables 6-18, only available in
the electronic version); and (3) the contribution of
uncertainties in the stellar parameters. These can be added
quadratically to obtain the total uncertainty.
are indicated in
Table 3
(Cols. 9 and 10). Three sources of errors must be
considered for estimating of the final uncertainty: (1) the
dispersion in the line-by-line abundances; (2) the uncertainty
associated with the microturbulence, (indicated in Table 3, and
Tables 6-18, only available in
the electronic version); and (3) the contribution of
uncertainties in the stellar parameters. These can be added
quadratically to obtain the total uncertainty.
Table 4: Final results of the O abundance analysis. Detailed results (line-by-line) of the O abundance analysis are presented in Tables 6 to 18.
For illustrative purposes in the last column of Table 3, we indicate the
effect of a change of ![]() 500 K
in
500 K
in ![]() on the Si abundance if this was derived exclusively by using
Si III lines
on the Si abundance if this was derived exclusively by using
Si III lines![]() .
The minimum effect occurs for
.
The minimum effect occurs for ![]()
![]() 27 000 K
and increases
towards higher and lower temperatures (note the change in the sign of
the uncertainties), reaching values up to 0.12 dex.
This behavior is a consequence of the dependence of the EW
of the Si III lines with temperature. The
maximum EW is achieved around
27 000 K (so the abundance is quite insensitive to
small changes in
27 000 K
and increases
towards higher and lower temperatures (note the change in the sign of
the uncertainties), reaching values up to 0.12 dex.
This behavior is a consequence of the dependence of the EW
of the Si III lines with temperature. The
maximum EW is achieved around
27 000 K (so the abundance is quite insensitive to
small changes in ![]() ), and
decreases towards lower and higher temperatures (also increasing its
sensitivity to
), and
decreases towards lower and higher temperatures (also increasing its
sensitivity to ![]() variations). When lines from two different ions are used, the final Si
abundance can be constrained with better accuracy, since the EW
of lines from different ions behaves in a opposite way for a given
variations). When lines from two different ions are used, the final Si
abundance can be constrained with better accuracy, since the EW
of lines from different ions behaves in a opposite way for a given
![]() .
As a consequence in this case, the uncertainty associated with the
stellar parameters is always negligible compared with the dispersion in
the line-by-line abundances.
.
As a consequence in this case, the uncertainty associated with the
stellar parameters is always negligible compared with the dispersion in
the line-by-line abundances.
3.5.2 Oxygen abundances
Up to 47 O II lines were identified in the observed spectral range. However, not all the lines were finally used for the O abundance determination. The selection of the final set of lines used for the analysis was based on a detailed analysis by multiplets (following similar criteria to the case of Si, but in this case we studied the behavior of lines resulting from different multiplets). We found a similar behavior of lines to the one described in Simón-Díaz et al. (2006).
The derived O abundances are indicated in Table 4, and the results of the line-by-line analyses in Tables 6-18 (in the electronic version). For this element, only lines from one ionization state were available, so we could not test whether the corresponding ionization equilibrium (O III/II or O II/I) is achieved for the considered stellar parameters. We adopt for the oxygen abundance analysis the same stellar parameters as in the Si analysis.
We found (as in many previous works) that the microturbulence
derived from the
O II lines (
![]() (O)) differs from the Si
analysis (
(O)) differs from the Si
analysis (
![]() (Si)), and a somewhat larger
microturbulence is derived. Some authors assume the
(Si)), and a somewhat larger
microturbulence is derived. Some authors assume the
![]() (Si) value
(or a mean value of the microturbulences obtained for
the various elements analyzed) to perform the oxygen abundance
analysis.
In our opinion, this can lead to significant systematic errors in the
analysis.
Since this is an ad-hoc parameter that is still not well understood
(see, however, Cantiello et al.
2009), we adopt the microturbulence derived from
the oxygen analysis itself, for consistency.
(Si) value
(or a mean value of the microturbulences obtained for
the various elements analyzed) to perform the oxygen abundance
analysis.
In our opinion, this can lead to significant systematic errors in the
analysis.
Since this is an ad-hoc parameter that is still not well understood
(see, however, Cantiello et al.
2009), we adopt the microturbulence derived from
the oxygen analysis itself, for consistency.
In fact, determination of the microturbulence value that will
be adopted
in the final steps of the abundance determination is an important task.
Unidentified problems in the O II
line modeling or bad measurements
of the corresponding EWs (due to blends,
noise, or a bad placement
of the continuum) can enormously affect the
![]() value that
produces a zero slope in the
value that
produces a zero slope in the
![]() -EW
diagrams. A detailed analysis by multiplets (see Simón-Díaz
2005) can help identify problematic lines and to better
decide on the final microturbulence to be adopted.
-EW
diagrams. A detailed analysis by multiplets (see Simón-Díaz
2005) can help identify problematic lines and to better
decide on the final microturbulence to be adopted.
Table 4
also indicates the uncertainties associated with errors in
the line-to-line abundance dispersion, the microturbulence, and the
stellar
parameters. In addition, last column shows the derived abundances if
the
effective temperature is varied ![]() 500 K. (Although the exact values are
not shown here, the contribution of the log g
uncertainty to the oxygen abundance can be considered negligible in
comparison with the
500 K. (Although the exact values are
not shown here, the contribution of the log g
uncertainty to the oxygen abundance can be considered negligible in
comparison with the ![]() contribution.) The derived oxygen abundance is very sensitive to
changes in
contribution.) The derived oxygen abundance is very sensitive to
changes in ![]() for the cooler and hotter
objects, and there is a change in the behavior of the oxygen abundance
with
for the cooler and hotter
objects, and there is a change in the behavior of the oxygen abundance
with ![]() around 27 000 K. This behavior is similar to the one
illustrated in Table 3.
around 27 000 K. This behavior is similar to the one
illustrated in Table 3.
4 Comparison with previous works
Two of the stars included in this analysis have already been analyzed
in
Simón-Díaz et al.
(2006). These are HD 37020 and HD 37042. We
observed the two stars again to have spectra with the same
characteristics as the other stars in the sample. The stellar
parameters presented in Table 2 correspond to the
analysis of the new spectra. The new analysis resulted in slightly
higher effective temperatures
(but within the errors) and gravities ![]() 0.1-0.2 dex larger. Several factors
produced this difference in the derived stellar parameters.
First, we based our
0.1-0.2 dex larger. Several factors
produced this difference in the derived stellar parameters.
First, we based our ![]() - log g
determination on the
HSi analysis, instead of using the H and He I-II
lines. The best
- log g
determination on the
HSi analysis, instead of using the H and He I-II
lines. The best ![]() - log g
pair reproducing the Si III-IV
ionization equilibrium and the wings of the H lines
simultaneously is the one indicated
in Table 3.
A lower log g requested an effective
temperature
somewhat lower (which was not fitting the He II
lines).
In addition, the better quality of the new spectra allowed us to better
constrain the gravity of the stars. The wings of the H lines
are not very sensitive to changes of
- log g
pair reproducing the Si III-IV
ionization equilibrium and the wings of the H lines
simultaneously is the one indicated
in Table 3.
A lower log g requested an effective
temperature
somewhat lower (which was not fitting the He II
lines).
In addition, the better quality of the new spectra allowed us to better
constrain the gravity of the stars. The wings of the H lines
are not very sensitive to changes of ![]() 0.1-0.2 dex in log g
in this range of stellar parameters. In Simón-Díaz et al.,
we based
our decision about the best solution on the faint He II
0.1-0.2 dex in log g
in this range of stellar parameters. In Simón-Díaz et al.,
we based
our decision about the best solution on the faint He II ![]() 4541 line;
however, it is better to rely on the HSi criterion, which is more
sensitive in this range of stellar
parameters. In fact, we find that the new
4541 line;
however, it is better to rely on the HSi criterion, which is more
sensitive in this range of stellar
parameters. In fact, we find that the new
![]() - log g
pair
also fits nicely the He I-II lines.
We thus prefer this last solution.
- log g
pair
also fits nicely the He I-II lines.
We thus prefer this last solution.
![\begin{figure}
\par\includegraphics[angle=90,width=17cm,clip]{13120f5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg114.png)
|
Figure 5: Comparison of our derived stellar parameters, Si and O abundances, with those obtained by Cunha & Lambert (1994,1992). Results from both studies for each star are connected by a dashed line. Numbers follow the order of stars presented in Tables 3 and 4. The size of the uncertainties of the various quantities are shown by the crosses. |
| Open with DEXTER | |
We also obtain ![]() 0.05-0.10 dex
higher oxygen abundances. Part of this
difference is caused by the change in stellar parameters; in addition,
we measured sligthly larger EWs for the O II
lines in both stars. Note, however, that the old and new abundances
agree when taking the error bars
into account. The discrepancy for these two objects between Simón-Díaz et al.
(2006) and these new studies serves as an example of the
effect of intrinsic
uncertainties in determination of stellar abundances. Following a
similar methodology the same author can find slightly different results
(but within the errors) when analyzing spectra from two different
observing
campaigns
0.05-0.10 dex
higher oxygen abundances. Part of this
difference is caused by the change in stellar parameters; in addition,
we measured sligthly larger EWs for the O II
lines in both stars. Note, however, that the old and new abundances
agree when taking the error bars
into account. The discrepancy for these two objects between Simón-Díaz et al.
(2006) and these new studies serves as an example of the
effect of intrinsic
uncertainties in determination of stellar abundances. Following a
similar methodology the same author can find slightly different results
(but within the errors) when analyzing spectra from two different
observing
campaigns![]() .
.
Recently, Przybilla
et al. (2008) analyzed a representative sample of
unevolved
early B-type stars in nearby OB associations and the field using a
similar
technique but a different stellar atmosphere code (line blanketed ATLAS9
LTE model atmospheres, Kurucz 1993) and NLTE
line-formation calculations (with updated versions of DETAIL
and SURFACE, Giddings 1981; Butler
& Giddings 1985). They have one star in common with our work,
HD 36591 (HR 1861). We obtain very similar results
for the stellar parameters, as well as the Si and O abundances. They
used several ![]() spectroscopic indicators (apart from Si II-IV),
finding very good overall agreement.
spectroscopic indicators (apart from Si II-IV),
finding very good overall agreement.
Gummersbach et al.
(1998) included a sample of 5 stars from
Ori OB1 in their study of the
abundance gradient of the Galaxy. We have three stars in common. Gummersbach et al. used a
self-consistent spectroscopic approach. We find similar effective
temperatures for the two hotter objects (when Si IV
lines are available), but ![]() 0.2 dex
lower gravities. For these stars (HD 36959 and
HD 36960), the derived Si and O abundances agree
(within the errors) with our values. The difference in gravity could
explain their slightly lower O abundances.
0.2 dex
lower gravities. For these stars (HD 36959 and
HD 36960), the derived Si and O abundances agree
(within the errors) with our values. The difference in gravity could
explain their slightly lower O abundances.
Interestingly, for the cooler object in common
(HD 35039), we obtained lower
![]() and
log g. It is remarkable that they
obtained very low O and Si abundances (8.20 and
7.08 dex, respectively) for this star. Probably, this result
is related to the Si II problem we
described in Sect. 3.4
(see also
lower panel in Fig. 2);
they used line Si II 4130
to establish
and
log g. It is remarkable that they
obtained very low O and Si abundances (8.20 and
7.08 dex, respectively) for this star. Probably, this result
is related to the Si II problem we
described in Sect. 3.4
(see also
lower panel in Fig. 2);
they used line Si II 4130
to establish ![]() ,
so obtained too high a value (23 500 K vs.
19 900 K, the value we obtained). For this range of
stellar parameters, higher
,
so obtained too high a value (23 500 K vs.
19 900 K, the value we obtained). For this range of
stellar parameters, higher ![]() supposes lower O abundances, and a change of
supposes lower O abundances, and a change of ![]() 3000 K in
3000 K in
![]() can
perfectly explain a 0.5 dex variation in the O abundance.
can
perfectly explain a 0.5 dex variation in the O abundance.
Figure 5
presents a comparison our results with those obtained by Cunha &
Lambert (1994,1992)
concerning the stellar parameters, Si and O abundances.
There is a clear discrepancy for the majority of the objects, in terms
not only of effective temperatures, but also of gravities. Cunha &
Lambert (1994,1992)
made use of the calibrations of Strömgen photometry coupled with the
fits to the pressure-broadened line wings of H![]() (from Kurucz 1979, LTE stellar
atmopsheres) to derive
(from Kurucz 1979, LTE stellar
atmopsheres) to derive ![]() and log g. Following Gies
& Lambert (1992), they adjusted the
and log g. Following Gies
& Lambert (1992), they adjusted the
![]() calibrations
by Lester et al.
(1986) and Balona (1984)
upward by 4.2% and 5.2% , respectively. The discrepancy in effective
temperatures obtained through commonly used photometric calibrations
and spectroscopic line diagnostic has already been pointed out by
several authors (e.g. Nieva
& Przybilla 2008; Kilian et al. 1991). Our
result once more brings out these discrepancies.
calibrations
by Lester et al.
(1986) and Balona (1984)
upward by 4.2% and 5.2% , respectively. The discrepancy in effective
temperatures obtained through commonly used photometric calibrations
and spectroscopic line diagnostic has already been pointed out by
several authors (e.g. Nieva
& Przybilla 2008; Kilian et al. 1991). Our
result once more brings out these discrepancies.
Note also the large discrepancy found for the gravity. The Cunha & Lambert values are
systematically higher (![]() 0.3 dex).
As shown by Nieva & Przybilla
(2007), the use of LTE profiles
for the gravity determination lead to overestimated log g
values, in particular for hotter stars. In Fig. 3 we show a comparison
of synthetic hydrogen lines from two FASTWIND
models with the observed profiles for HD 36960 (labeled with
#3 in Fig. 5.
One of the models considers the stellar parameters derived from our
analysis, the other one corresponds to the
0.3 dex).
As shown by Nieva & Przybilla
(2007), the use of LTE profiles
for the gravity determination lead to overestimated log g
values, in particular for hotter stars. In Fig. 3 we show a comparison
of synthetic hydrogen lines from two FASTWIND
models with the observed profiles for HD 36960 (labeled with
#3 in Fig. 5.
One of the models considers the stellar parameters derived from our
analysis, the other one corresponds to the
![]() -log g
pair provided by Cunha & Lambert
(1992). The difference in the wings of the lines is clear.
-log g
pair provided by Cunha & Lambert
(1992). The difference in the wings of the lines is clear.
We also find big discrepancies in the derived Si and
O abundance for most of the stars, with no systematic trend
(i.e. differences are found in both positive and negative directions).
There are several factors to take into account to explain this
disagreement. One of them is the imprecise determination of the stellar
parameters from photometric indices. But maybe the most important one
is the following. Once the stellar parameters were calculated as
described above, Cunha & Lambert
use those values to perform the abundance analysis, computing
line-blanketed LTE model atmospheres with ATLAS6
(Kurucz 1979) for the LTE
case, or using a grid
of EWs based on Gold's models (Gold
1984) for the NLTE abundance
calculations. The risk in this strategy is that the stellar abundance
analysis is decoupled of the
stellar parameter determination, and this could produce inconsistencies
in the
analysis process. Briefly, the calculation of EWs
of those lines used for the abundance determination is based on the
stellar atmosphere structure
defined by a stellar atmosphere model computed for a given set of
stellar parameters; on the other hand, the stellar parameters derived
for a given star will depend on the characteristics of the stellar
atmosphere model we have used![]() .
Therefore, it may be dangerous to do an abundance analysis with a given
stellar atmosphere code using the stellar parameters obtained from a
different code or a photometric calibration. This argument is crucial
in the case of stars with
.
Therefore, it may be dangerous to do an abundance analysis with a given
stellar atmosphere code using the stellar parameters obtained from a
different code or a photometric calibration. This argument is crucial
in the case of stars with ![]()
![]() 30 000 K,
where photometric methods become completely unreliable discriminators
of temperatures and gravities, because of the insensitivity of the
Rayleigh-Jeans tail of the spectral energy distribution on temperature.
30 000 K,
where photometric methods become completely unreliable discriminators
of temperatures and gravities, because of the insensitivity of the
Rayleigh-Jeans tail of the spectral energy distribution on temperature.
A self-consistent spectroscopic approach allows minimizing this problem. In this case, the stellar parameters are determined by fitting certain spectroscopic diagnostics, and then the same models are used for the abundance analysis. This way we are certain that the stellar atmosphere structure used for the computation of the abundance diagnostics is coherent with the derived stellar parameters for the studied star. To a first order, when the whole analysis is performed with stellar atmosphere codes with different characteristics, the derived abundances should be quite similar (although the derived stellar parameters could be somewhat different). This approach can be strengthened if multiple independent spectroscopic indicators are considered (i.e. Si III-IV, He I-II, C II-IV; see e.g. this study or Nieva & Przybilla 2008).
5 Chemical composition of B-type stars in the Ori OB1 association
Figures 6
and 7
again show the derived oxygen and silicon
abundances in our sample of B-type stars in the Ori OB1
association, along
with the results by Cunha &
Lambert (1994). This time, the stars are ordered
following the subgroups suggested by Blaauw
(1964). As discussed in Cunha
& Lambert (1994), they found that the stars in the
youngest group (Id) and some
of the stars in subgroup Ic were enriched in oxygen by
about 40% relative to the stars belonging to the older
subgroups. They interpreted
this result as possible proof of enrichment of the new generation of
stars in the association with the products from supernovae ejecta from
the older subgroups. In addition, they found features of this
enrichment
in silicon (also expected from the triggered star formation scenario).
In contrast, we did not find any systematic difference between the O
and Si abundances in stars from the various associations. In
fact, our results
indicate that the B-type stars in the Ori OB1 association are
chemically
homogeneous (at least in terms of oxygen and silicon), having a
dispersion in
abundances (0.04 and 0.03 dex, respectively) smaller than the
intrinsic uncertainties of the derived abundances (0.10 and
0.08 dex, respectively). The mean abundances are ![]() (O) = 8.73 dex
and
(O) = 8.73 dex
and ![]() (Si) = 7.51 dex.
These values agree with those obtained by Przybilla
et al. (2008) for their sample of six stars in the
solar neighborhood.
(Si) = 7.51 dex.
These values agree with those obtained by Przybilla
et al. (2008) for their sample of six stars in the
solar neighborhood.
![\begin{figure}
\par\includegraphics[angle=90,scale=.53]{13120f6.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg115.png)
|
Figure 6:
Oxygen abundances derived for our sample of early B-type stars in the
Orion association, and comparison with the previous results from Cunha & Lambert (1994).
Vertical lines separates stars from the various subgroups. Solid and
dashed horizontal lines represent the mean value and the dispersion (1 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,scale=.53]{13120f7.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg116.png)
|
Figure 7: As Fig. 2 but for silicon. This time, the reference for the nebular abundance is Rubin et al. (1993) and Garnett et al. (1995) (first and second column, see text). Solar values from Asplund et al. (2005) and Grevesse & Sauval (1998). |
| Open with DEXTER | |
5.1 Comparison with the Sun
We also include in Fig. 6
the resulting solar oxygen abundances appearing in the literature in
the past 4 years (during the so-called solar oxygen crisis![]() epoch, not yet finished).
Various
authors have published values for the solar oxygen abundance based on
improved model atmospheres (either 1D and 3D), line formation codes,
atomic and molecular data, and detailed treatment of blends. In the
plot, we present results by Centeno
& Socas-Navarro (2008), Meléndez
& Asplund (2008), Ayres
(2008), Caffau et al.
(2008), Allende Prieto (2008),
Socas-Navarro & Norton (2007),
Ayres et al. (2006), Asplund et al. (2004), and Grevesse & Sauval (1998).
This last value (marked with an internal black dot) was considered as
the standard solar O abundance until a few years ago. The
derived solar values range from 8.63 dex (Socas-Navarro
& Norton 2007) to 8.86 dex (Centeno & Socas-Navarro 2008).
The O abundances in our sample of stars in Ori OB1
lie in the middle of all these values. In view of the present-day
results, the only thing we can say is that oxygen abundances in the Sun
and B-type stars in the solar vicinity are the same within the
uncertainties.
However, we consider it too premature to draw any firm conclusion or
hypothesis
about the chemical evolution of the local interstellar medium during
the
lifetime of the Sun.
epoch, not yet finished).
Various
authors have published values for the solar oxygen abundance based on
improved model atmospheres (either 1D and 3D), line formation codes,
atomic and molecular data, and detailed treatment of blends. In the
plot, we present results by Centeno
& Socas-Navarro (2008), Meléndez
& Asplund (2008), Ayres
(2008), Caffau et al.
(2008), Allende Prieto (2008),
Socas-Navarro & Norton (2007),
Ayres et al. (2006), Asplund et al. (2004), and Grevesse & Sauval (1998).
This last value (marked with an internal black dot) was considered as
the standard solar O abundance until a few years ago. The
derived solar values range from 8.63 dex (Socas-Navarro
& Norton 2007) to 8.86 dex (Centeno & Socas-Navarro 2008).
The O abundances in our sample of stars in Ori OB1
lie in the middle of all these values. In view of the present-day
results, the only thing we can say is that oxygen abundances in the Sun
and B-type stars in the solar vicinity are the same within the
uncertainties.
However, we consider it too premature to draw any firm conclusion or
hypothesis
about the chemical evolution of the local interstellar medium during
the
lifetime of the Sun.
Figure 7 also shows a comparison of our derived Si abundances with the Solar value. We only present here the old abundance (Grevesse & Sauval 1998) and the new value proposed by Asplund et al. (2005). In contrast to previous results, the mean Si abundance in B-type stars in Ori OB1 is very close to the Solar value (similar to other B-type stars in the solar vicinity Przybilla et al. 2008).
5.2 Comparison with the Orion nebula
The most recent and detailed analysis of the optical spectrum of the
Orion nebula was done by Esteban
et al. (2004). The high-quality UVES@VLT spectrum
they used allowed them to derive the oxygen gas phase abundance of the
nebula by using collisionally excited lines (CELs) and recombination
lines (RLs). The final value they propose is
![]() dex.
This value was calculated assuming the ionic abundances given by
O 2+ RLs and O +
CEL (plus a t2 = 0.022)
dex.
This value was calculated assuming the ionic abundances given by
O 2+ RLs and O +
CEL (plus a t2 = 0.022)![]() . Note, however,
the abundance given by the O 2+ and
O + CELs (and t2=0)
is
. Note, however,
the abundance given by the O 2+ and
O + CELs (and t2=0)
is ![]() dex. These values
have been included in Fig. 6
for comparison with the early B-type stellar abundances presented in
this study. The mean value of the derived stellar oxygen abundances is
0.25 and 0.11 dex higher than the nebular abundances given by
the CELs and RLs, respectively.
dex. These values
have been included in Fig. 6
for comparison with the early B-type stellar abundances presented in
this study. The mean value of the derived stellar oxygen abundances is
0.25 and 0.11 dex higher than the nebular abundances given by
the CELs and RLs, respectively.
Although the mean stellar abundance seems to agree better with the one given by the faint recombination lines, we have to consider that the analysis of the nebular emission line spectrum can only provide abundances for the ionized gas phase of the ISM. This means a lower limit to the actual ISM abundance, since part of the oxygen can be depleted, forming part of the dust grains.
Silicon is one of the elements expected to be more depleted
onto dust grains, along with Mg and Fe (Draine
2003). We can therefore compare our derived Si abundances
with those obtained from the study of the emission line spectrum of the
Orion nebula to try to find some clues about the amount of oxygen
depleted. One should note that the determination of Si nebular
abundances is not straightforward and must be based on results from
photoionization models and certain ionization correction
factors (ICFs). The only determinations of Si abundance in the
Orion nebula we found in the literature are those by Rubin et al. (1993) and Garnett et al. (1995). Both
studies used the same observations of the FUV Si III]
![]() 1883,
1892, and C III]
1883,
1892, and C III]
![]() 1907, 1909 lines to estimate
the Si abundance, and obtained 6.65 and 6.58 dex, respectively. They
computed photoionization models to obtain Si/H (Rubin
et al. 1993) and the ICF needed to transform
Si 2+/C 2+
into Si/C, hence
the C/O and O/H ratios to derive Si/H (Garnett
et al. 1995). In addition, Garnett
et al. (1995)
discuss how the effect of assuming a t2 = 0.04
(Peimbert et al. 1993)
in the
calculation of the C/O and O/H ratios could affect the derived
Si abundance.
They obtained log (Si/H)+12 = 7.14 dex for
this case. These three values of the Si abundance are included in
Fig. 7
for comparison with the stellar abundances. The difference between
stellar and gas phase Si abundances are
1907, 1909 lines to estimate
the Si abundance, and obtained 6.65 and 6.58 dex, respectively. They
computed photoionization models to obtain Si/H (Rubin
et al. 1993) and the ICF needed to transform
Si 2+/C 2+
into Si/C, hence
the C/O and O/H ratios to derive Si/H (Garnett
et al. 1995). In addition, Garnett
et al. (1995)
discuss how the effect of assuming a t2 = 0.04
(Peimbert et al. 1993)
in the
calculation of the C/O and O/H ratios could affect the derived
Si abundance.
They obtained log (Si/H)+12 = 7.14 dex for
this case. These three values of the Si abundance are included in
Fig. 7
for comparison with the stellar abundances. The difference between
stellar and gas phase Si abundances are ![]() 1 dex, or
1 dex, or ![]() 0.3 dex, depending on the nebular
abundances we trust more.
0.3 dex, depending on the nebular
abundances we trust more.
Since a detailed comparison of stellar and nebular abundances in Ori OB1 and the Orion nebula within a dust-depletion scenario requires more extended study, which is beyond the scope of this paper, we decide to present a more detailed discussion in a separate paper (in preparation).
6 Summary and conclusion
In this work, we applied a self-consistent spectroscopic approach to determining of the stellar parameters, the Si and O abundances of a sample of early-B type stars from the various subgroups of the Ori OB1 association. We made use of a high-quality spectroscopic data set, obtained with FIES@ NOT, and the modern NLTE, line-blanketed, spherically extended stellar atmosphere code FASTWIND.
We developed several IDL programs to automatically identify and measure the EW of metal lines in high-resolution spectra. We also constructed a grid of FASTWIND HHeSiO models optimized for the analysis of early B-type, main sequence stars.
The availability of a large number of Si II-III-IV lines in the FIES@ NOT spectra allowed us to obtain the stellar parameters with high accuracy and detect some problems related to some Si lines commonly used for the stellar parameter and Si abundance determination. Once these problems were accounted for, a high degree of homogeneity was found for Si abundances in the analyzed sample of stars.
The oxygen abundance analysis also result in a small dispersion of abundances, in contrast to previous determinations. The mean oxygen and silicon abundances agree with those resulting from a similar analysis of a representative sample of unevolved early B-type stars in the solar vicinity (Przybilla et al. 2008). Both results indicate that abundances derived from these stellar objects are more homogeneous and metal-rich than previously though.
We also compared the O and Si stellar abundance in Ori OB1 with those obtained for the Sun during the epoch of the ``solar crisis''. The O abundances in our sample of stars in Ori OB1 lie in the middle of all these values. In view of the present-day results, the only thing we can say is that oxygen abundances in the Sun and B-type stars in the solar vicinity are the same within the uncertainties. However, we consider it too premature to draw any firm conclusion or hypothesis about the chemical evolution of the local interstellar medium during the lifetime of the Sun. Silicon abundances are also very similar (contrary to what was previously found from the study of B-type stars).
Finally, we compared the stellar abundances with those derived from the study of the emission line spectrum of the Orion nebula. In a forthcoming paper we will present a more detailed discussion accounting for the possible depletion of O, Si, Mg, and Fe into dust.
This work points out one more time the importance of
self-consistent spectroscopic abundance analyses for determining of the
chemical
composition of the photospheres of OB-type stars. Photometric
![]() diagnostics
must be treated with caution in the context of abundance
analyses of these type of objects. It is also dangerous to combine the
stellar parameters determined with any given code and the abundance
analysis performed with a different code. Systematic errors inherent in
those techniques, or possible biases between the various codes, can
lead to incorrect abundances.
diagnostics
must be treated with caution in the context of abundance
analyses of these type of objects. It is also dangerous to combine the
stellar parameters determined with any given code and the abundance
analysis performed with a different code. Systematic errors inherent in
those techniques, or possible biases between the various codes, can
lead to incorrect abundances.
Financial support by the Spanish Ministerio de Ciencia e Innovación under the project AYA2008-06166-C03-01. This work has also been partially funded by the Spanish MICINN under the Consolider-Ingenio 2010 Program grant CSD2006-00070: First Science with the GTC (http://www.iac.es/consolider-ingenio-gtc). I am very grateful to A. Herrero (Spain), G. Stasinska (France), and D. Schaerer (Switzerland) for their support and hospitality during the development of this work. I also acknowledge A. Herrero, M. Urbaneja, D. Lennon, F. Najarro, C. Trundle, and N. Castro for fruitful discussions. J. Puls, N. Przybilla, F. Nieva, and M. Urbaneja for the careful reading of the first version of this paper and all their comments. Finally, I thank J. Puls for allowing me to use the stellar atmosphere code FASTWIND.
References
- Allende Prieto, C. 2008, 14th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, 384, 39 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., Allende Prieto, C., & Kiselman, D. 2004, A&A, 417, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, ASPC, 336, 25 [Google Scholar]
- Ayres, T. R. 2008, ApJ, 686, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R., Plymate, C., & Keller, C. U. 2006, ApJS, 165, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Balona, L. A. 1984, MNRAS, 211, 973 [NASA ADS] [Google Scholar]
- Becker, S. R., & Butler, K. 1988, A&A, 201, 232 [NASA ADS] [Google Scholar]
- Becker, S. R., & Butler, K. 1990, A&A, 235, 326 [NASA ADS] [Google Scholar]
- Blaauw, A. 1964, ARA&A, 2, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Briceño, C., Calvet, N., Hernández, J., et al. 2005, AJ, 129, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, A. G. A., de Geus, E. J., & de Zeeuw, P. T. 1994, A&A, 289, 101 [NASA ADS] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., et al. 2008, A&A, 488, 1031 [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., Langer, N., Brott, I. et al. 2009, A&A, 499, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cartledge, S. I. B., Lauroesch, J. T., Meyer, D. M., et al. 2006, ApJ, 641, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Carigi, L., Peimbert, M., Esteban, C., et al. 2005, ApJ, 623, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Centeno, R., & Socas-Navarro, H. 2008, ApJ, 682, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Romano, D., Matteucci, F. 2003, MNRAS, 339, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Songaila, A., & York, D. G. 1979, ApJ, 230, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Lennon, D. J., & Walborn, N. R. 2006, A&A, 446, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cunha, K., & Lambert, D. L. 1992, ApJ, 399, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., & Lambert, D. L. 1994, ApJ, 426, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Esteban, C., Peimbert, M., García-Rojas, J., et al. 2004, MNRAS, 355, 229 [NASA ADS] [CrossRef] [Google Scholar]
- García-Rojas, J., & Esteban, C. 2007, ApJ, 670, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R., Dufour, R. J., Peimbert, M., et al. 1995, ApJ, 449, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Gies, D. R., & Lambert, D. L. 1992, ApJ, 387, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 1976, The Observation and analysis of Stellar Photospheres, 1st edn (Cambridge University Press) [Google Scholar]
- Gold, M. 1984, Diplomarbeit, Ludwig-Maximilians-Universität München [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Gummersbach, C. A., Kaufer, A., Schaefer, D. R., et al. 1998, A&A, 338, 881 [NASA ADS] [Google Scholar]
- Herrero, A., & Lennon, D. J. 2004, IAUS, 215, 209 [NASA ADS] [Google Scholar]
- Herrero, A., Kudritzki, R. P., Vilchez, J. M., et al. 1992, A&A, 261, 209 [NASA ADS] [Google Scholar]
- Kilian, J. 1992, A&A, 262, 171 [Google Scholar]
- Kilian, J., Becker, S. R., Gehren, T., et al. 1991, A&A, 244, 419 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lester, J. B., Gray, R. O., & Kurucz, R. L. 1986, ApJS, 61, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markova, N., & Puls, J. 2008, A&A, 478, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, D. M., Jura, M., & Cardelli, J. A. 1998, ApJ, 493, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., & Asplund, M. 2008, A&A, 490, 817 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Morel, T. 2009, CoAst, 158, 122 [Google Scholar]
- Nieva, M.-F., & Przybilla, N. 2007, A&A, 467, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nieva, M.-F., & Przybilla, N. 2008, A&A, 481, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nieva M.-F., & Przybilla, N. 2009, in Hot And Cool: Bridging Gaps in Massive Star Evolution, ed. C. Leitherer et al., ASP Conf. Ser. in press [arXiv:0902.2949] [Google Scholar]
- Peimbert, M. 1967, ApJ, 150, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., Storey, P. J., & Torres-Peimbert, S. 1993, ApJ, 414, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Przybilla, N., Nieva, M.-F., & Butler, K. 2008, ApJ, 688, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Urbaneja, M. A., Venero, R., et al. 2005, A&A, 435, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Repolust, T., Puls, J., Herrero, A. 2004, A&A, 415, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynolds, R. J., & Ogden, P. M. 1979, ApJ, 229, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, R. H., Dufour, R. J., & Walter, D. K. 1993, ApJ, 413, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Santolaya-Rey, A. E., Puls, J., & Herrero, A. 1997, A&A, 323, 488 [NASA ADS] [Google Scholar]
- Simón-Díaz, S. 2005, Thesis, Univ. de La Laguna, Spain [Google Scholar]
- Simón-Díaz, S., & Herrero, A. 2007, A&A, 468, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simón-Díaz, S., Herrero, A., Esteban, C., et al. 2006, A&A, 448, 351 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Socas-Navarro, H., & Norton, A. A. 2007, ApJ, 660, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Trundle, C., Lennon, D. J., Puls, J., et al. 2004, A&A, 417, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urbaneja, M. A., Herrero, A., Kudritzki, R.-P., et al. 2005, ApJ, 635, 311 [NASA ADS] [CrossRef] [Google Scholar]
Online Material
Table 5: List of log gf values for the Si II-IV lines considered in this study (from Atomic Line List v2.05). For the O II lines we refer to Simón-Díaz et al. (2006).
Table 6: Results from the abundance analysis of HD 36512 (B0 V).
Table 7: Results from the abundance analysis of HD 37020 (B0.5 V).
Table 8: Results from the abundance analysis of HD 36960 (B0.5 V).
Table 9: Results from the abundance analysis of HD 37042 (B0.7 V).
Table 10: Results from the abundance analysis of HD 36591 (B1 V).
Table 11: Results from the abundance analysis of HD 36959 (B1 V).
Table 12: Results from the abundance analysis of HD 37744 (B1.5 V).
Table 13: Results from the abundance analysis of HD 35299 (B1.5 V).
Table 14: Results from the abundance analysis of HD 36285 (B2 V).
Table 15: Results from the abundance analysis of HD 35039 (B2 V).
Table 16: Results from the abundance analysis of HD 36629 (B2 V).
Table 17: Results from the abundance analysis of HD 36430 (B2 V).
Table 18: Results from the abundance analysis of HD 35912 (B2 V).
![\begin{figure}
\par\includegraphics[angle=180,scale=0.85]{13120f8a.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg123.png)
|
Figure 8: The complete atlas of FIES@ NOT spectra (part 1 of 3). The Si II-IV and O II lines used for the abundance analysis are indicated as solid and dashed vertical lines, respectively. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=180,scale=0.85]{13120f8b.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg124.png)
|
Figure 8: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=180,scale=0.85]{13120f8c.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg125.png)
|
Figure 8: continued. |
| Open with DEXTER | |
Footnotes
- ... stars
![[*]](/icons/foot_motif.png)
- Based on observations made with the Nordic Optical Telescope, operated jointly on the island of La Palma by Denmark, Finland, Iceland, Norway, and Sweden, in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias.
- ...
![[*]](/icons/foot_motif.png)
- Tables 5 to 18, and Fig. 8 are available in electronic form at http://www.aanda.org
- ...
![[*]](/icons/foot_motif.png)
- Briceño et al. (2005)
determined an age for Ori OB1b
 4-6 Myr by studying its low mass, young
stellar population; this value is more consistent with what would be
expected from the presence of the evolved blue supergiant
4-6 Myr by studying its low mass, young
stellar population; this value is more consistent with what would be
expected from the presence of the evolved blue supergiant 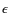 Ori
in this subgroup.
Ori
in this subgroup.
- ... abundances
![[*]](/icons/foot_motif.png)
- Other authors (Gies & Lambert 1992; Gummersbach et al. 1998; Kilian 1992) obtained a similar range in oxygen abundances from the analysis of smaller samples of B-type stars in Orion OB1.
- ... stars
![[*]](/icons/foot_motif.png)
- HD 37023 was also re-observed, but it was not included in the analysis because we found in the new spectrum that the star is is actually a binary system (SB2), hence not optimal for an abundance analysis.
- ... FIEStool
![[*]](/icons/foot_motif.png)
- http://www.not.iac.es/instruments/fies/fiestool/FIEStool.html
- ... atomic
![[*]](/icons/foot_motif.png)
- http://www.pa.uky.edu/ peter/newpage/
- ... trust
![[*]](/icons/foot_motif.png)
- This hypothesis is also supported by a comparison of
 obtained for the cooler objects in our sample from other spectroscopic
diagnostic based on O II/I and
C III/II ratios of lines (F. Nieva,
private communication).
obtained for the cooler objects in our sample from other spectroscopic
diagnostic based on O II/I and
C III/II ratios of lines (F. Nieva,
private communication).
- ... them
![[*]](/icons/foot_motif.png)
- This is not the case for Si IV

 4089, 4631,
and Si II
4089, 4631,
and Si II 
 6347, 3856;
these lines may be blended with O II
6347, 3856;
these lines may be blended with O II  4089,
N II
4089,
N II  4631,
Mg II
4631,
Mg II  6347, and
O II
6347, and
O II 3856, respectively, in some
cases. The high resolution of the FIES@ NOT
spectra normally allows separating both line contributions; however,
results with these lines are always treated with care.
3856, respectively, in some
cases. The high resolution of the FIES@ NOT
spectra normally allows separating both line contributions; however,
results with these lines are always treated with care.
- ... analysis
![[*]](/icons/foot_motif.png)
- Results of the line-by-line analysis are presented in Tables 6-18.
- ... lines
![[*]](/icons/foot_motif.png)
- A similar test assuming a change of 0.1 dex in log g
indicates negligible effects when compared with the
 contribution.
contribution.
- ...
campaigns
![[*]](/icons/foot_motif.png)
- The different results may also be caused by actual changes in the stellar spectra (e.g. due to binarity).
- ...
used
![[*]](/icons/foot_motif.png)
- As an example, we want to mention the consequences that
including the line blanketing and wind blanketing effects in the
stellar atmosphere models of O and early B-type stars had on the
SpT -
 calibrations of these stars (see e.g. Repolust et al. 2004; Martins
et al. 2005).
calibrations of these stars (see e.g. Repolust et al. 2004; Martins
et al. 2005).
- ... crisis
![[*]](/icons/foot_motif.png)
- Ayres et al. (2006)
- ...
![[*]](/icons/foot_motif.png)
- The t2 parameter was introduced by Peimbert (1967) to account for temperature fluctuations in ionized nebulae. The temperature fluctuation scenario has been proposed to explain the CELs vs. RL abundance discrepancy (see García-Rojas & Esteban 2007, and references therein).
All Tables
Table 1: List of B-type stars from Ori OB1 considered in this study, ordered by spectral type.
Table 2: Projected rotational velocities derived for the studied stars.
Table 3: Final results of the HSi analysis: stellar parameters and Si abundances.
Table 4: Final results of the O abundance analysis. Detailed results (line-by-line) of the O abundance analysis are presented in Tables 6 to 18.
Table 5: List of log gf values for the Si II-IV lines considered in this study (from Atomic Line List v2.05). For the O II lines we refer to Simón-Díaz et al. (2006).
Table 6: Results from the abundance analysis of HD 36512 (B0 V).
Table 7: Results from the abundance analysis of HD 37020 (B0.5 V).
Table 8: Results from the abundance analysis of HD 36960 (B0.5 V).
Table 9: Results from the abundance analysis of HD 37042 (B0.7 V).
Table 10: Results from the abundance analysis of HD 36591 (B1 V).
Table 11: Results from the abundance analysis of HD 36959 (B1 V).
Table 12: Results from the abundance analysis of HD 37744 (B1.5 V).
Table 13: Results from the abundance analysis of HD 35299 (B1.5 V).
Table 14: Results from the abundance analysis of HD 36285 (B2 V).
Table 15: Results from the abundance analysis of HD 35039 (B2 V).
Table 16: Results from the abundance analysis of HD 36629 (B2 V).
Table 17: Results from the abundance analysis of HD 36430 (B2 V).
Table 18: Results from the abundance analysis of HD 35912 (B2 V).
All Figures
![\begin{figure}
\par\includegraphics[angle=90,scale=0.62]{13120f1.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg16.png)
|
Figure 1: Example of FIES@ NOT spectra for three of the observed stars. The complete atlas is available in the electronic version of the paper (Fig. 8). The Si II-IV and O II lines used for the abundance analysis are indicated as solid and dashed vertical lines, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,clip]{13120f2.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg97.png)
|
Figure 2: Silicon abundance vs. EW diagnostic diagrams for three of the analyzed stars (with representative effective temperatures). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=9cm,clip]{13120f3.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg98.png)
|
Figure 3: Example of fitting the H Balmer lines to determine log g. Two FASTWIND models are compared with the observed spectrum (red line) of HD 36960: in black, model with the stellar parameters resulting from the FASTWIND HSi analysis (28 900, 3.9); in blue, model with the stellar parameters derived by Cunha & Lambert (1992), for comparison (28 900, 4.3). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=0,width=8.5cm,clip]{13120f4.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg100.png)
|
Figure 4: Silicon abundance vs. EW diagnostic diagrams for HD 36960. All the observed Si III-IV lines are included in the plot. Uncertainties in the individual line abundances (propagated from the errors in the measured EWs) are indicated as vertical lines. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,width=17cm,clip]{13120f5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg114.png)
|
Figure 5: Comparison of our derived stellar parameters, Si and O abundances, with those obtained by Cunha & Lambert (1994,1992). Results from both studies for each star are connected by a dashed line. Numbers follow the order of stars presented in Tables 3 and 4. The size of the uncertainties of the various quantities are shown by the crosses. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,scale=.53]{13120f6.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg115.png)
|
Figure 6:
Oxygen abundances derived for our sample of early B-type stars in the
Orion association, and comparison with the previous results from Cunha & Lambert (1994).
Vertical lines separates stars from the various subgroups. Solid and
dashed horizontal lines represent the mean value and the dispersion (1 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=90,scale=.53]{13120f7.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg116.png)
|
Figure 7: As Fig. 2 but for silicon. This time, the reference for the nebular abundance is Rubin et al. (1993) and Garnett et al. (1995) (first and second column, see text). Solar values from Asplund et al. (2005) and Grevesse & Sauval (1998). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=180,scale=0.85]{13120f8a.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg123.png)
|
Figure 8: The complete atlas of FIES@ NOT spectra (part 1 of 3). The Si II-IV and O II lines used for the abundance analysis are indicated as solid and dashed vertical lines, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=180,scale=0.85]{13120f8b.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg124.png)
|
Figure 8: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=180,scale=0.85]{13120f8c.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13120-09/Timg125.png)
|
Figure 8: continued. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


