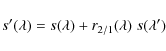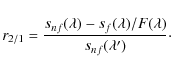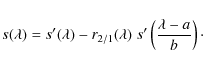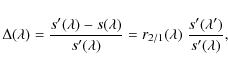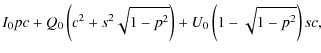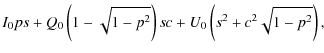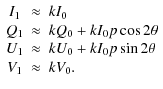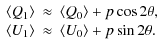EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 510 (February 2010) A&A, 510 (2010) A108 Full HTML
Free Access
Issue
A&A
Volume 510, February 2010
Article Number A108
Number of page(s) 14
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200913083
Published online 18 February 2010
A&A 510, A108 (2010)

VLT spectropolarimetry of the optical transient in NGC 300

Evidence of asymmetry in the circumstellar dust[*]

F. Patat1 - J. R. Maund2 - S. Benetti3 - M. T. Botticella4 - E. Cappellaro3 - A. Harutyunyan3,5 - M. Turatto6

1 - European Organization for Astronomical Research in the Southern Hemisphere (ESO), K. Schwarzschild-str. 2, 85748 Garching b. München, Germany
2 - Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej, 2100 Copenhagen, Denmark
3 - Istituto Nazionale di Astrofisica, Osservatorio Astronomico di Padova, v. Osservatorio n.5, 35122 Padua, Italy
4 - Queen's University - Belfast, BT7 1NN, Northern Ireland, UK
5 - Fundación Galileo Galilei - INAF, Telescopio Nazionale Galileo, 38700 Santa Cruz de la Palma, Tenerife, Spain
6 - Istituto Nazionale di Astrofisica, Osservatorio Astronomico di Catania, v. S. Sofia 78, 95123 Catania, Italy

Received 7 August 2009 / Accepted 2 October 2009

Abstract
Aims. We study possible signs of asymmetry in the bright optical transient in NGC 300, to obtain independent information about the explosion mechanism, the progenitor star and its circumstellar environment.
Methods. Using VLT-FORS1, we obtained low-resolution optical linear spectropolarimetry of NGC 300 OT2008-1 on two epochs, 48 and 55 days after the discovery, covering the spectral range 3600-9330 Å.
Results. The data exhibit a continuum polarization at a very significant level. At least two separate components are identified. The first is characterized by both a strong wavelength dependency and a constant position angle ( $68.6 \pm 0.3$ degrees), which is parallel to the local spiral arm of the host galaxy. The latter is aligned along a completely different position angle ( $151.3 \pm 0.4$). While the former is identified as arising in the interstellar dust associated with NGC 300, the latter is most likely caused by continuum polarization by dust scattering in the circumstellar environment. No line depolarization is detected in correspondence to the most intense emission lines, disfavoring electron scattering as the source of intrinsic polarization. This implies that there is a very small deviation from symmetry in the continuum-forming region. Given the observed level of intrinsic polarization, the transient must be surrounded by a significant amount of dust ($\geq$ $4 \times 10 ^{-5}~M_\odot$), asymmetrically distributed within a few thousand AU. This probably implies that one or more asymmetric outflow episodes took place during the past history of the progenitor.

Key words: supernovae: general - ISM: general - dust, extinction - globular clusters: individual: NGC 300 - techniques: spectroscopic - techniques: polarimetric

1 Introduction

Many surveys have focused their interest on poorly known objects lying in the gap in the absolute magnitude distribution that separates luminous novae ( $M_R \geq -10$) and faint supernovae ( $M_R \leq -14$) (e.g., Rau et al. 2008). Although this gap had been understood to be populated mostly by eruptions of luminous blue variables (LBVs, see Maund et al. 2006), it is now evident that new types of explosions may be responsible for the transient events occurring in this luminosity range, from exotic (LBV-like) outbursts of Wolf-Rayet stars (Pastorello et al. 2007a) to other long duration transients, such as M85 OT2006-1 (Kulkarni et al. 2007; Rau et al. 2008; Ofek et al. 2008; Pastorello et al. 2007b), whose nature remains debated. In this context, a significant impulse to the study of objects in this gap was brought about by the discoveries of two nearby objects, namely SN 2008S in NGC 6946 and the 2008 luminous optical transient in NGC 300 (hereafter NGC 300 OT2008-1).

NGC 300 OT2008-1 was discovered on May 14, 2008 (Monard 2008). A spectrum obtained the day after, revealing H$\alpha $, H$\beta$, Ca II near-IR triplet, forbidden [Ca II] doublet in emission, and Ca II H&K absorptions (Bond et al. 2008), shared striking similarities with that of SN 2008S (Prieto 2008). The photometric and spectroscopic properties of the transient in NGC 300 led to the conclusion that this was not a classical nova, an LBV, or a supernova (Bond et al. 2009). According to Bond et al. (2008, 2009), the spectrum was reminiscent of that of V838 Mon during the early phases of its outburst (Wisniewski et al. 2003). Broad-band optical and near-IR photometric, plus low and intermediate resolution spectroscopic follow-up observations were presented by Bond et al. (2009), while Berger et al. (2009) reported on UV, radio, and X-ray imaging and high resolution spectroscopy. Remarkably, no source was detected at the position of NGC 300 OT2008-1 in the radio and X-ray observations, which indicates that the transient was at least one order of magnitude (in the radio domain) and two orders of magnitudes (in the X-rays region) fainter than any SN discovered to date. In addition, high-resolution spectroscopy suggests the presence of a complex circumstellar environment resulting either from previous asymmetric ejections from the progenitor or from a companion wind (Bond et al. 2009; Berger et al. 2009).

An inspection of pre-explosion, archival HST images revealed that no star was detectable at the outburst position placing stringent upper limits on the progenitor's luminosity, which was interpreted as an additional argument in favor of a non-supernova origin (Berger & Soderberg 2008). However, a progenitor candidate was detected in pre-outburst Spitzer images (Prieto 2008; Berger et al. 2009), and it was identified as a massive star (15-20 $M_\odot$), with a spectral energy distribution very similar to that exhibited by the progenitor of SN 2008S (Prieto et al. 2008; Botticella et al. 2009). By means of an independent method based on the study of the surrounding stellar population, a similar range for the progenitor mass (12-17 $M_\odot$) was found by Gogarten et al. (2009), while Bond et al. (2009) gave a slightly lower mass range (10-15 $M_\odot$). An analysis of the Spitzer/IRS mid-IR spectrum of NGC 300 OT2008-1 obtained three months after the outburst led Prieto et al. (2009) to conclude that, although the presence of a massive star cannot be definitely excluded, a lower mass (6-10 $M_\odot$, carbon-rich AGB/super-AGB, or a post-AGB) precursor would provide a better match to their mid-IR observations.

Albeit with some scatter in the estimate of the progenitor's mass, most studies favor an exotic eruption of a moderate-to-massive star for NGC 300 OT2008-1 (and SN 2008S). However, Botticella et al. (2009) emphasized the overall similarity between the light curves of these transients and those of type II-L SNe. The main argument was the late-time flattening, which is consistent with the slope expected from the radioactive decay of 56Co into 56Fe. If this mechanism plays a role in powering the light curve of these transients, then a SN explosion is the most likely engine (electron-capture SNe, see Botticella et al. 2009; Pumo et al. 2009).

Soon after the discovery, we started an optical/near-IR follow-up using a number of ground-based facilities. The results will be presented and discussed in a forthcoming paper (Pastorello et al. 2009, in prep.). In this paper we focus on the spectropolarimetry of NGC 300 OT2008-1 that we obtained in July 2008 with VLT-FORS1 on two epochs separated by a week, with the aim of detecting possible signs of asymmetries in the ejecta and/or in the circumstellar environment that could provide additional constraints on the progenitor's nature.

The paper is organized as follows. In Sect. 2 we discuss the observations and the data reduction techniques. In Sect. 3 we present the flux spectra, while Sect. 4 deals with the spectropolarimetric data sets. In Sect. 5, we discuss the results, and we summarize our conclusions in Sect. 6. Appendix A contains an analysis of the effects of second order contamination on spectropolarimetry and its application to the data presented in this work, while Appendix B describes the effect of multiple weak polarizers on the resulting polarization signal.

2 Observations and data reduction

We observed the OT in NGC 300 on 2 different epochs, 48 and 55 days after its discovery (Monard 2008), using the FOcal Reducer/low-dispersion Spectrograph (hereafter FORS1), mounted at the Cassegrain focus of the ESO-Kueyen 8.2 m telescope (Appenzeller et al. 1998). In this multi-mode instrument, equipped with a mosaic of two $2048 \times 4096$ pixel (px) E2V CCDs, polarimetry is performed by introducing into the optical path a Wollaston prism (19 $^{\prime\prime}$ throw) and a super-achromatic half-wave plate (HWP). To reduce some known instrumental problems (see Patat & Romaniello 2006), we always used 4 half-wave plate angles ( $\theta_i = 0$, 22.5, 45 and 67.5 degrees). All spectra were obtained with the low-resolution G300V grism coupled with a 1.0 arcsec slit, giving a spectral range 3200-9330 Å, a dispersion of $\sim$3.2 Å px-1, and a resolution of 11.6 Å (FWHM) at 5800 Å. To cover the blue part of the optical spectrum ($\leq$4350 Å), where significant Ca II H&K absorption is clearly evident, we have not used an order sorting filter. Since the object is rather red ( $B-V\sim 1.1$, see Sect. 3), the second order contamination, which for this grism starts at about 6600 Å (O'Brien 2008), is expected to be small and its effects on the spectropolarimetry of NGC 300 OT2008-1 negligible. This is discussed more quantitatively in Appendix A.

Data were bias and flat-field corrected, and wavelength calibrated using standard tasks within IRAF[*]. The rms error in the wavelength calibration is about 0.7 Å. The ordinary (upper) and extraordinary (lower) beams were processed separately. Stokes parameters, linear polarization degree, and position angle were computed by means of specific routines written by us. Finally, polarization bias correction and error estimates were performed following the prescriptions described by Patat & Romaniello (2006), while the HWP zeropoint angle chromatism was corrected using tabulated data (O'Brien 2008). To increase the signal-to-noise ratio, the final Stokes parameters were binned in $\sim$25.8 Å wide bins (8 pixels). This turns into an rms error in the polarization of 0.1% at 6000 Å, where the continuum signal-to-noise ratio per resolution element reaches its maximum (720 and 530 on the first and the second epoch, respectively). The spectra are severely affected by fringing above $\sim$8000 Å, so that the observed noise at the red edge of the wavelength range is significantly greater than the statistical formal errors. The instrument stability (including evolution of the fringing pattern) was checked by comparing $\epsilon_Q$, $\epsilon_U$ pairs (Maund 2008) at the two epochs. Their average differences $\langle \Delta \epsilon\rangle= \langle \epsilon_Q - \epsilon_U\rangle$ were found to be $0.07 \pm 0.02\%$ and $0.13 \pm 0.02\%$ on the first and the second epoch, respectively. These values are within the measurement errors per resolution element (typically $\leq$0.1%), thus confirming the stability of the instrument in the relevant time interval. However, they also imply possible systematic errors of up to about 0.1%, which can be considered as the maximum accuracy one can reach with FORS1 using 4 HWP positions (see also Patat & Romaniello 2006).

Flux calibration was achieved by observing a spectrophotometric standard star and inserting full polarimetric optics (HWP angle set to 0). A log of the observations is given in Table 1.

Table 1:   Log of the VLT-FORS1 observations of NGC 300 OT2008-1.

3 Flux spectra

NGC 300 OT2008-1 was followed up in great detail by Bond et al. (2009) and Berger et al. (2009), to which we refer the reader for a comprehensive account of the spectroscopic properties of this object and its evolution. In the following, we provide a brief description of the flux spectra, while they will be discussed in more detail in the analysis of the whole spectroscopic data set of NGC 300 OT2008-1 (Pastorello et al., in prep.).

The spectra, obtained by coadding for each epoch the ordinary and extraordinary beams for all the four HWP angles, are presented in Fig. 1. Between the two epochs, which are separated by seven days, no evolution is evident and the spectrum consists of a red continuum with a number of superimposed narrow emission lines. As Bond et al. (2008) pointed out, the most prominent spectral lines can be identified with the Balmer series of Hydrogen, Ca II 8498 Å, 8542 Å, 8662 Å, and [Ca II] 7291, 7324 Å. The H lines can be identified to wavelength as sort as H$\delta$ and the Balmer jump at $\sim$3650 Å is clearly detected (Fig. 1). Additionally, our spectra appear to contain He I 3888 Å, 4571 Å, 5015 Å, 5876 Å, 6678 Å, 7065 Å absorption lines, which are clearly seen in the higher resolution spectra presented and discussed by Berger et al. (2009). Finally, Ca II H&K and Na ID are visible in absorption and are contaminated by unresolved features arising in the ISM (see also Berger et al. 2009).

\begin{figure} \par\includegraphics[width=9cm,clip]{13083f01.eps} \end{figure} Figure 1:

Flux spectra of NGC 300 OT2008-1 on 2008 July 1 ( upper) and 2008 July 8 ( lower). For presentation, the spectrum of the second epoch was shifted by -0.4. The main spectral features are identified.

Open with DEXTER

While the absolute flux scales should be compared to broadband photometry when this becomes available, the overall shape of the spectra is expected to be accurate to within 10-15%. The colors deduced from synthetic photometry are B-V = + 1.1, V-R =+0.6, and V-I = + 1.1 for both epochs, with rms uncertainties of about 0.15 mag. These values are fully compatible (within the quoted errors) with the broadband photometry reported by Berger et al. (2009) for June 19 ( $B-V =1.01 \pm 0.03$; see their Table 2). Because of the relatively high value of B-V, the flux contamination by the second order above 6500 Å is expected to be less than a few percent (see Appendix A).

The measured FWHMs of H$\alpha $, H$\beta$, and Ca II 8662 Å are $18.6 \pm 0.3$ Å, $13.8 \pm 0.2$ Å and $23.8 \pm 0.4$ Å, respectively. Once corrected for the instrumental resolution (11.6 Å), these values correspond to expansion velocities of 660, 460, and 720 km s-1. In general, the spectrum of NGC 300 OT2008-1 is very similar to those reported for SN 2008S by Smith et al. (2009). Based on the very low luminosity and expansion velocities, these authors concluded that the object previously designated as SN 2008S is actually a SN impostor (Van Dyk et al. 2000), similar to the giant eruption of a luminous blue variable, and shares the spectral properties of the Galactic hypergiant IRC+10420 (Jones et al. 1993). Here we note that, in general, SN 2008S differs from a classical impostor, in that SN 2008S has a linear and slow evolving luminosity decline, and a spectrum that matches those of LBV eruptions well, excluding its very strong [Ca II] doublet. Based on similar considerations, both Bond et al. (2009) and Berger et al. (2009) concluded that NGC 300 OT2008-1 was the eruption of a dust-enshrouded, massive star. An alternative scenario was proposed by Prieto et al. (2008), Thompson et al. (2009), and Botticella et al. (2009), who argued that SN 2008S and NGC 300 OT2008-1 were generated by the explosion of an electron-capture SN.

4 Spectropolarimetry

The spectropolarimetric data for NGC 300 OT2008-1 are presented in the Q-U plane in Fig. 2. The object exhibits a significant polarization, which reaches a maximum level of about 1.4%. During both epochs, the data cover a range of polarization values which are definitely much higher than expected for a typical Serkowski law (Serkowski et al. 1975, see also next section) with a similar maximum polarization (see Fig. 2 and its caption). No obvious change in polarization is seen across the most prominent emission lines (Sect. 4.2).

\begin{figure} \par\includegraphics[width=100mm,angle=-90]{13083f02.eps} \end{figure} Figure 2:

Observed spectropolarimetry of NGC 300 OT2008-1 at the two epochs on the Stokes Q-U plane. For presentation, the data were binned to 16 pixels (57 Å). The dotted circles are placed at constant polarization levels (0.5, 1.0, 1.5, and 2.0%). The dashed line is a weighted least squares fit to the data in the displayed wavelength range. For comparison, the colored line sequence of dots in the upper left quadrant traces a Serkowski law (Serkowski et al. 1975) for $\lambda_{\max} = 4800$ Å, $P_{\max} = 1.4$%, and K = 0.81 with an arbitrary position angle $\theta = 60$ degrees. The circled dot indicates the position of (Q1,U1) corresponding to the minimum polarization solution (see Sect. 4.1), while the vector indicates the allowed region for (Q1,U1).

Open with DEXTER

4.1 Continuum polarization

The most remarkable aspect of the Q-U plot is the alignment of the data points along a straight line, which is indicative of a polarization component with a clearly defined dominant axis. This does not pass through the origin of the Q-U plane, implying that there must be an additional component with a polarization wavelength dependence which differs from that along the dominant axis (see Appendix B). We also note that the two data sets span similar ranges of values along the dominant direction, but that a rigid shift is present between the two epochs. This is more clearly illustrated in Fig. 3, where we plot the differences $\Delta Q$and $\Delta U$ between the two epochs. The clipped average differences (computed in the wavelength range 3900-9300 Å) are $\langle \Delta Q\rangle = - 0.11 \pm 0.02\%$ (191 spectral bins) and $\langle \Delta U\rangle = + 0.14 \pm 0.02\%$ (193 spectral bins), and the rms deviation from the average is 0.23 and 0.21% for the two Stokes parameters, respectively. Given that the observed grey variation is very small and comparable to the instrument stability between the two epochs ($\sim$0.1%, see Sect. 2), it is unclear whether this is real or caused by an incompletely removed instrumental effect.

\begin{figure} \par\includegraphics[width=80mm,clip]{13083f03.eps} \end{figure} Figure 3:

Differences in Q ( upper panel) and U ( lower panel) Stokes parameters between the two epochs (second minus first). Empty symbols indicate the data points rejected by the k-$\sigma $ clipping.

Open with DEXTER

Table 2:   Dominant axis least squares fit parameters.

To characterize the dominant axis, we fitted the data with a linear relation

\begin{displaymath} U=U_0 \; + Q \; \tan 2\theta. \end{displaymath} (1)

The results of the least squares fitting for the two epochs in the wavelength range 4000-9000 Å are reported in Table 2 (upper part), which includes the rms deviation from the best-fit relation ($\sigma $), the Pearsons linear correlation coefficient (rxy) and $\chi^2$ per degrees of freedom (d.o.f.). To exclude the most deviant data points, we performed a preliminary fit to all data, applied a 1.7-sigma rejection and finally refit the remaining data. The large correlation factors confirm the presence of a dominant axis at a high significance level. This indicates that the main source of polarization is interstellar extinction. Interstellar polarization (ISP), caused by the presence of aligned asymmetric dust grains along the line of sight, is characterized by a wavelength-independent position angle (Serkowski et al. 1975; Whittet et al. 1992). This conclusion is supported by the observed dominant axis being tangential to the spiral arm of NGC 300 close to the outburst position, as shown in Fig. 4. Since dust grains tend to be aligned in the direction of the galactic magnetic field, which in turn follows the spiral pattern (see Scarrot et al. 1987), this strongly indicates that not only the observed polarization is caused by directional extinction, but also that the polarization arises within interstellar material associated with a spiral arm of NGC 300. Similar alignments were detected using spectropolarimetry in two supernovae, namely SN 2001el (Wang et al. 2003) and SN 2006X (Patat et al. 2009). From now on we therefore assume that this component is constant in time.

\begin{figure} \par\includegraphics[width=8cm,clip]{13083f04.eps} \end{figure} Figure 4:

A DSS image of NGC 300. The location of the optical transient is marked by a cross. The arrow indicates the polarization position angle of the dominant axis (the average of the values measured during the two epochs was used: $\theta = 68.6$ degrees).

Open with DEXTER

The estimated position angles at the two epochs differ by $2.0 \pm 0.5$ degrees. Since this variation is only marginally significant, we adopt the average of the two values ( $68.6 \pm 0.5$ degrees) as the representative value. For consistency, we rotated the two data sets by -1.0 and +1.0 degrees, respectively. The results of the least squares fitting after this operation are shown in Table 2 (lower part). The recomputed average differences in Q and U are $\langle \Delta Q\rangle = -0.12\pm 0.02$% and $\langle \Delta U \rangle = + 0.11 \pm 0.02$%. This means that the systematic, wavelength-independent shift observed between the two epochs is not related to this small rotation.

As we said, the position of the points on the Q-U plane requires an additional polarization component. The simplest solution is given by a wavelength-independent polarization, represented by one single point (Q1,U1) on the Q-U plane. In these circumstances, the total, observed Stokes parameters Q and U are given by $Q = Q_1 + Q_2(\lambda)$ and $U = U_1 + U_2(\lambda)$, where Q2 and U2 are the Stokes parameters that characterize the polarization aligned along the dominant axis[*]. Of course, if the ratio of Q2 to U2must remain constant (as required by the wavelength-independent position angle), Q1 and U1 must obey Eq. (1), i.e. (Q1,U1) must be aligned along the observed dominant axis. One additional constraint related to the definitions of Q and U is that all the (Q2,U2) points have to be confined to one single quadrant of the Q-U plane (Wang et al. 2003), which, in our case, is that with Q<0 and U>0. This imposes that Q1 is higher than a certain value $Q_{\min}$, but does not prevent Q1being any higher arbitrary value (see the arrow in Fig. 2). For this reason, although constrained, the solution is not unique. As a consequence, while the position angle of the dominant axis ($\theta_2$) is fixed, the corresponding polarization $P_2(\lambda) = \sqrt{Q_2^2(\lambda)+U_2^2(\lambda)}$ is undefined up to an additive constant, which depends on the particular choice of the wavelength-independent polarization $P_1=\sqrt{Q_1^2+U_1^2}$. Since (Q1,U1) must lie along the dominant axis, the corresponding value of $\theta_1=\arctan U_1/Q_1$is allowed to vary only within a rather limited range (smaller than 10 degrees), regardless how large the value of Q1 is.

4.1.1 Minimum polarization solution

Table 3:   Minimum polarization solutions for the two epochs.

In the following, we consider what we will indicate as minimum polarization solution (MPS), i.e., the solution one obtains for $Q_1=Q_{\min}$, and that leads to the minimum possible values of the polarization degree for both components. Given the wavelength dependency shown by the data (Fig. 2), this means that the MPS corresponds to the case where the polarization is close to zero at the red edge of the observed wavelength range ($\sim$9300 Å). The solution was found as the value of Q1 that produces the minimum constant value of $P_2(\lambda)$ at any given wavelength, while fulfilling the constraints described above. Since we had shown that the two data-sets differ by a wavelength-independent quantity (cf. Fig. 3), we computed Q1 for the second epoch and set the value for the first epoch such that $\Delta Q_1=-0.12\%$ (see above). Within the errors, this ensures that $P_2(\lambda)$ does not change between the two dates. The results of this procedure are presented in Table 3 and illustrated in Fig. 5 for the second epoch. What emerges from this analysis is that the additive, wavelength-independent component is polarized at a highly significant level, which reaches at least 1.2%. Its position angle ( $151.3 \pm 0.4$ degrees, averaged over the two epochs) is very different from that of the dominant component, indicating that they must arise from dissimilar sources (see the discussion in Sect. 5).

\begin{figure} \par\includegraphics[width=8cm,clip]{13083f05.eps} \end{figure} Figure 5:

Minimum polarization solution for 2008 July 8. The dashed line traces the observed dominant axis, while the point (Q1,U1) indicates the wavelength-independent component. The empty circles mark the rejected data points.

Open with DEXTER

When, as in this case, there is a marked dominant direction, it is useful to compute the components parallel ($P_{\rm d}$) and orthogonal ( $P_ {\rm o}$) to this axis, as suggested by Wang et al. (2003). This is achieved by the following roto-translation in the Q-U plane:

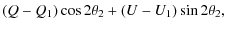
                           $\displaystyle P_{\rm d}$ = $\displaystyle (Q-Q_1) \cos 2\theta_2 + (U-U_1) \sin 2\theta_2,$  
$\displaystyle P_{\rm o}$ = $\displaystyle (U-U_1) \cos 2\theta_2 - (Q-Q_1) \sin 2\theta_2.$  

While $P_{\rm d}$ is undefined up to an additive constant (dependent on the particular choice of Q1), $P_ {\rm o}$is not. Indeed, $P_ {\rm o}$is purely related to the deviations from the dominant axis. The decomposition is shown in Figs. 6 and 7 for the two epochs. Two important results emerge from these plots: i) $P_{\rm d}$ has a smooth wavelength dependence, reaching a maximum ( $2.6 \pm 0.1\%$) at about 4900 Å and decreasing on either sides of the peak much faster than a Galactic Serkowski law (Serkowski et al. 1975); ii) $P_ {\rm o}$ is consistent with a null value. The rms deviations in the wavelength range 4000-9000 Å are 0.13% and 0.16% during the two epochs, respectively. These values are fully compatible with the estimated measurement errors, and thus the two components $\vec{P_1}$ and $\vec{P_2}$ are sufficient to explain all the observed variance in the residuals. During the second epoch, there might be an indication of a mild, smooth wavelength dependency in $P_ {\rm o}$ (see Fig. 7, lower panel), but the statistical significance appears to be marginal. The same is true for a small bump seen at about 7800 Å during the first epoch (Fig. 6, lower panel).

\begin{figure} \par\includegraphics[width=8cm,clip]{13083f06.eps} \end{figure} Figure 6:

Dominant ( upper panel) and orthogonal ( lower panel) polarization on 2008 July 1 after subtracting the wavelength-independent component $\vec{P_1}$. For presentation, the data were binned to 16 pixel (57 Å). The solid curve in the upper panel is a Serkowski law with $P_{\max} =4.8\%$, $\lambda_{\max} = 4250$ Å, and K = 3.0.

Open with DEXTER

\begin{figure} \par\includegraphics[width=8cm,clip]{13083f07.eps} \end{figure} Figure 7:

Same as Fig. 6 for 2008 July 8.

Open with DEXTER

For highly reddened Galactic stars, Serkowski et al. (1975) showed that the linear polarization degree changes with wavelength according to the empirical law

$\displaystyle P(\lambda)=P_{\max} \; \exp\left ( -K\; \ln^2 \; \frac{\lambda_{\max}}{\lambda}\right ),$    

where $\lambda_{\max}$ is the wavelength that corresponds to the maximum polarization $P_{\max}$. Witthet et al. (1992) also demonstrated that $K=0.01 + 1.66\; \lambda_{\max}$, where $\lambda_{\max}$ is expressed in microns. Typical values of K range from 0.7 to 1.4. A comparison between the NGC 300 OT2008-1 data and the behavior expected on the basis of the Serkowski law immediately shows that the observed wavelength dependence is much steeper (Fig. 2), indicative of values of K higher than 5 (see Figs. 6, 7). For comparison, Winsniewski et al. (2003) report $K\simeq 1$ for the Galactic, peculiar variable V838 Monocerotis, for which they could reproduce the observational data with a Serkowski law (see their Fig. 5). Interestingly, $P_{\rm d}$ is reasonably well fitted by a Serkowski law with $P_{\max} = 2.6 \pm 0.1\%$, $\lambda_{\max} = 4880 \pm 40$ Å, and $K = 5.6 \pm 0.1$ (the Witthet et al. relation gives K = 0.82 for the observed $\lambda_{\max}$).

This marked deviation indicates that the dust mixture responsible for the polarization most likely differs from a typical Galactic mixture. Therefore, Serkowski's Galactic relation between color excess and maximum polarization ( $P_{\max}(\%)\geq 9\; E_{B-V}$) probably does not hold for NGC 300 OT2008-1. In this respect, we note that the ISP wavelength dependency observed in several supernovae also clearly deviates from the Galactic Serkowski law (Leonard & Filippenko 2001; Leonard et al. 2002; Maund et al. 2007; Patat et al. 2009). For the hypothesis that the dominant polarization detected in NGC 300 OT2008-1 is produced by dust extinction, as all elements seem to indicate, one can attempt to estimate reddening from the observed level of polarization. Blindly using $P_{\max} = 2.6\%$ in the quoted relation, one obtains an upper limit to the color excess given by $E_{B-V} \leq 0.3$. The observed deviation from a Galactic Serkowski law casts serious doubts on the reliability of this estimate, and what we quote here is just for the sake of completeness. To our knowledge no polarimetric study on NGC 300 exists in the literature. Therefore, it is not possible to tell whether the observed wavelength dependency is typical of the host galaxy or is a peculiarity of the line of sight to NGC 300 OT2008-1. However, we note that the extinction law along the line of sight to young clusters in NGC 300 was reported to be highly variable (Roussel et al. 2005).

Based on photometric considerations, Bond et al. (2009) report EB-V = 0.4, while Berger et al. (2009) derive $E_{B-V} = 0.05 \pm 0.05$ from the equivalent width of the Na I D lines. They conclude that this low value for the reddening is consistent with the lack of obvious evidence of extinction in their optical and UV spectra, and point out that this is in line with evidence of dust destruction in the immediate surroundings of the outbursting star. The extinction arising within the Milky Way is very small ( EB-V = 0.013, Schlegel et al. 1998) and the bulk of reddening has to occur within the host galaxy, and so is most likely the case for interstellar polarization. The compilation of Heiles (1999) contains a few stars close in galactic coordinates to NGC 300[*]. All of them have linear polarizations $\leq$0.1%, in close agreement with the low Galactic extinction along this line of sight.

The best-fit global solution is compared to the observed Stokes parameters and position angle in Fig. 8 for the data acquired on 2008 July 8. The fit is fairly good for this epoch ( $\chi^2 = 1.1$, rms = 0.20%), while for the first epoch the observed data points show higher scatter redwards of $\sim$7000 Å ( $\chi^2 = 2.8$, rms = 0.28%).

\begin{figure} \par\includegraphics[width=8cm,clip]{13083f08.eps} \end{figure} Figure 8:

Best fit solution for 2008 July 8 compared to the observed Stokes parameters ( lower panel), position angle ( upper panel) and polarization level (upper panel). The curves trace the wavelength-independent component $\vec{P_1}$ (dashed), $\vec{P_2}$ (dotted-dashed) and the global solution (solid).

Open with DEXTER

The synthetic B,V,R, and I broad-band polarizations are reported in Table 4. As we have shown for the spectra, the observed variations (all highly significant) can be explained in terms of evolution in the wavelength-independent component. After applying the systematic differences $\langle \Delta Q\rangle$ and $\langle \Delta U\rangle$ to the second epoch and re-computing the synthetic broad-band polarimetry, both the polarization angle and degree are consistent (within the errors) with those derived for the first epoch (Table 4, last row). Interestingly, the variation in Q1 and U1 takes place along a direction (PA =  $154.1 \pm 3.2$) consistent with the average position angle of $\vec{P_1}$( $151.3 \pm 0.4$). If this variation were real, this would imply that the wavelength-independent component evolves just within its polarization level, while the position angle remains practically unchanged. This change in the polarization level is indicative of an intrinsic origin. However, since the observed variation is within the typical instrumental stability limits ($\sim$0.1%, see Sect. 2), no solid conclusion about its nature can be reached.

Table 4:   Synthetic broadband polarimetry of NGC 300 OT2008-1.

4.2 Line polarization

Although the resolution of our spectra is rather low ($\sim$12 Å FWHM), we inspected the data searching for possible line effects corresponding to the most prominent emission lines. In doing this, we first vectorially subtracted the contribution of the component $\vec{P_2}$(which we assumed to be of interstellar origin and to be constant across the line profile) directly estimated fitting the adjacent $Q_2(\lambda)$ and $U_2(\lambda)$ data points and interpolating to the line wavelength[*]. The case of H$\alpha $, the most intense feature (see Fig. 1), is presented in Fig. 9 for the first epoch. Across the line profile there is no evidence of the polarization changes that were previously detected, for instance, in Nova Cygni 1992 (Bjorkman et al. 1994), Nova Scuti 2003 (Kawabata et al. 2006), and V838 Mon (Wisniewski et al. 2003). A similar behavior is observed during the second epoch and for all other prominent emission lines (H$\beta$ and Ca II NIR triplet), in the sense that the observed polarization remains at the wavelength-independent level of $\vec{P_1}$. If the emission line is essentially unpolarized (Harrington & Collins 1968), the ratio of line to continuum polarization is given by the following semi-empirical relation (McLean & Clarke 1979):

$\displaystyle \frac{P(\lambda)}{P_{\rm c}} = \frac{1}{1+F(\lambda)/F_{\rm c}},$    

where $F(\lambda)$ is the line intensity profile and $F_{\rm c}$is the adjacent continuum level. Based on this relation and given that, at the peak of H$\alpha $, $F(\lambda)/F_{\rm c} \simeq 3$(Fig. 9), one would predict the level of polarization to drop to $\sim$0.25 $P_{\rm c}$ at the line center. The relatively high signal-to-noise ratio achieved at the H$\alpha $ line peak ($\sim$700 in the central, 3 pixel bin) allowed us to place an upper limit on the depolarization, which must be smaller than 0.2% during both epochs. This definitely excludes any depolarization at the level predicted by the above relation.

\begin{figure} \par\includegraphics[width=8cm,clip]{13083f09.eps} \end{figure} Figure 9:

Spectropolarimetry of the H$\alpha $ line on 2008 July 1. The data were binned to 3 pixel (9.6 Å). The flux spectrum in the upper panel is unbinned. The thin colored line traces a high-resolution spectrum ( $\Delta \lambda/\lambda \sim 48~000$) obtained with VLT-UVES on 2008 July 2 (Pastorello et al. in preparation).

Open with DEXTER

Finally, we searched for a polarization signal associated with the pronounced Ca II H&K absorption, after vectorially subtracting the adjacent continuum polarization. Although we achieved a marginal detection during the first epoch ( $0.6 \pm 0.2\%$), this signal is not present during the second and, therefore, we do not attach great significance to this finding.

5 Discussion

The data presented in this paper show that the polarization observed in NGC 300 OT2008-1 is generated by at least two, almost perpendicular, components $\vec{P_1}$ and $\vec{P_2}$. Because of the constant polarization angle (rather precisely aligned along the local spiral arm of NGC 300), and the wavelength dependence (reminiscent of a Serkowski law), we have interpreted $\vec{P_2}$ as being caused by ISP. The unusual shape of $P_2(\lambda)$, with its large slope parameter K, might be indicative of a dust mixture that differs in both chemical composition and grain size from that typical of the Milky Way. As of today, there is no consistent model that explains the empirical Serkowski law (Draine 2003a), and it is therefore impossible to derive the dust properties from the observed wavelength dependence.

After reasonably constraining the origin of $\vec{P_2}$, what remains to be clarified is the nature of $\vec{P_1}$.

5.1 Electron scattering

The most natural source of wavelength-independent linear polarization in a stellar envelope is Thomson scattering by free electrons (van den Hulst 1957). This is, for instance, the source of continuum polarization in supernovae (Höflich 1991). More generally, polarization by electron scattering is supposed to originate in stars with ionized and spatially extended atmospheres, such as Be and shell stars, Of and Wolf-Rayet stars, and early-type supergiants (Brown & McLean 1977). A non-null net polarization is indicative of an asymmetry in the continuum emitting region, and can be understood in terms of partial cancellation of the intrinsic polarization generated by the Thomson scattering. In the case of NGC 300 OT2008-1, and based on the assumption of a spheroidal photosphere, the measured level of polarization ( $P_1\geq 1.2\%$) would indicate a substantial asphericity, of axial ratio $\leq$0.8 (Höflich 1991). This geometry would produce a wavelength-independent polarization, characterized by a constant polarization angle (perpendicular to the major axis), similar to what is observed.

Evidences of electron scattering polarization (at a level of about 0.5%) were found in the early phases of Nova Cygni 1992 (Bjorkman et al. 1994) and V838 Mon (Wisniewski et al. 2003). In both cases this was interpreted in terms of asymmetry in the continuum-forming region, identified with a flattened, spheroidal shell ejected during the outburst. Since in the optically thin case the polarization level is proportional to the electron-scattering optical depth (Brown & McLean 1977), the observed decrease in the polarization level is produced by the expansion of the shell. The systematic, gray-decline that we observe between our two epochs (see Sect. 4.1) might be interpreted along the same lines.

An important problem with the electron scattering scenario in NGC 300 OT2008-1 is the absence of line depolarization (Sect. 4.2). This effect is expected when the emission lines arise in an outer ionized region, where Thomson scattering has a lower optical depth (Harrington & Collins 1968; Clarke & McLean 1974). It is observed in a variety of objects, including Be stars (McLean & Clarke 1979), novae (Bjorkman et al. 1994; Kawabata et al. 2006), supernovae (SN 1987A, Cropper et al. 1988), eruptive events such as V838 Mon (Wisniewski et al. 2003), and the post-red supergiant IRC+10420 (Patel et al. 2008). However, we note that there are exceptions, in which continuum polarization is observed but no line effect is detected, both in Be stars (McLean & Clarke 1979; Quirrenbach et al. 1997) and in Nova Sagittarii 1999 (Kawabata et al. 2000).

The narrow absorption profile detected on top of the emission lines (Bond et al. 2009; Berger et al. 2009. For the case of H$\alpha $ see also Fig. 9 here, upper panel) might enhance the polarization within the overall line profile. A similar phenomenon has been proposed to explain the absence of line depolarization in the shell star $\eta$ Cen (McLean & Clarke 1979). Given the modest depth of the narrow absorption, we however propose this is not sufficient to explain the absence of depolarization. Insufficient resolution can also be the responsible for the lack of detection of line effects. However, we tend to exclude this for our data, since the lines are partially resolved.

Another possibility is that the continuum and the emission lines in NGC 300 OT2008-1 arise in similar regions, i.e., that the lines do not form very far above the pseudo-photosphere, so that both the continuum and the lines are subject to roughly the same amount of electron scattering. Although this scenario can only be verified through NLTE calculations, we note that this is quite unlikely. There is indeed strong evidence that in both SN 2008S and in NGC 300 OT2008-1 lines and continuum originate in very different regions. While the photospheric temperature and radius decrease with time, the emission lines evolve very slowly (Berger et al. 2009; Botticella et al. 2009). This and the very high Balmer decrement lead to the conclusion that the emission lines are generated by the interaction between the ejected shell and the pre-existing circumstellar material, while the continuum forms in an inner region (Berger et al. 2009).

Finally, there is a third possibility, i.e., that the polarization source is located outside both the photosphere and the line-forming region. This would probably exclude Thomson scattering by free electrons as the source of the observed polarization and requires an alternative explanation (see next section).

The absence of electron scattering in NGC 300 OT2008-1 can be explained in terms of a spherically symmetric photosphere. Although NGC 300 OT2008-1 and IRC+10420 have similar spectroscopic properties (Smith et al. 2009), the post-red hypergiant has a continuum polarization that is higher than 2%, which is indicative of a significative asymmetry in the continuum-forming region (Patel et al. 2008). Whatever the reason for the lack of line-depolarization in NGC 300 OT2008-1, it definitely indicates a radical difference between the physical conditions in the continuum/line-forming regions of the two objects.

5.2 Dust scattering

To explain the absence of line effects in Nova Sagittarii 1999, Kawabata et al. (2000) proposed that continuum polarization originates in a circumstellar dust cloud. The observed wavelength dependence (a power law with polarization significantly increasing towards the blue) was interpreted as being produced by small dust grains. In the case of SN 2008S, Botticella et al. (2009) found evidence of an extended dust shell, which is understood to be responsible for the large mid-infrared excess observed in the early phases. This was confirmed by radiative transfer calculations applied to mid-IR spectra, showing that a substantial amount of dust must have survived the outburst (Wesson et al. 2009). The existence of a conspicuous dust shell around NGC 300 OT2008-1, pre-dating the outburst, was demonstrated by Prieto et al. (2009) based on a mid-IR Spitzer spectrum obtained three months after the discovery. All of these results infer that dust scattering is a perfectly plausible source of continuum polarization in NGC 300 OT2008-1.

One important problem with the application of the dust-scattering scenario is the pronounced wavelength dependence this is expected to produce. This can be easily understood as follows. If there is dust surrounding the object, part of the light emitted outside the line of sight would be scattered into the observer's direction and add to the radiation traveling directly to her. Since the scattering by dust produces a high degree of linear polarization (see for instance White 1979), depending on the dust geometrical distribution this can turn into a significant non null net polarization. If we consider an infinitesimal dust volume element placed at some distance from the central source and an incoming unpolarized packet of photons at a given wavelength, to a first approximation[*] the fraction of photons scattered into the line of sight (polarized perpendicularly to the plane of scattering) is proportional to $C_{\rm ext}(\lambda) \; \omega(\lambda) \; \Phi(\lambda, \theta)$ (White 1979), where $C_{\rm ext}(\lambda)$ is the dust extinction cross-section, $\omega(\lambda)$ is the dust albedo, and $\Phi(\lambda,\theta)$ is the scattering phase function. This in turn depends on the scattering angle $\theta$ and the degree of forward scattering $g(\lambda)$. Since the albedo is roughly constant in the optical domain and both $C_{\rm ext}$ and $\Phi$ tend to increase significantly in the blue, this implies that the polarization is higher at shorter wavelengths. Using the carbonaceous-silicate grain model by Li & Draine (2001) and Draine (2003b) and adopting the usual parametrization by Henyey & Greenstein (1941) for the scattering phase function, one can estimate this effect more quantitatively. The result is shown in Fig. 10 for two different scattering angles (30 and 70 degrees) and two different Milky Way dust mixtures[*] (RV = 3.1, 5.5). As anticipated, the polarization significantly increases at shorter wavelengths, especially in the case of lower RV, and can be fairly well reproduced by an exponential law $P(\lambda)=P_0 \exp[\beta(\lambda-\lambda_0)/\lambda_0]$. For $\lambda_0 = 4000$ Å, $\beta=-0.7$ for an average scattering angle of $\theta = 50$ degrees (corresponding to the typical value of the forward scattering degree in the optical domain, i.e., $g \simeq 0.6$).

\begin{figure} \par\includegraphics[width=8cm,clip]{13083f10.eps} \end{figure} Figure 10:

Expected polarization wavelength dependence of a Milky Way carbonaceous-silicate dust mixture in a single-scattering approximation for RV = 5.5 ( upper panel) and RV = 3.1 ( lower panel) and two different scattering angles. Dust model is from Li & Draine (2001) and Draine (2003b).

Open with DEXTER

With this result in hand, one can reverse the procedure and, using the observed data, deduce the implied component $\vec{P_2}$. This is shown in Fig. 11, where we have vectorially subtracted from the data the exponential component $\vec{P_1}$ ( $P_0 = 3.7\%$, $\beta=-0.7$ and $\theta_1 = 151$ degrees). As in the wavelength-independent case, we have considered the minimum polarization solution (see Sect. 4.1). As illustrated by Fig. 11, the resulting $\vec{P_2}$ is still well aligned with a dominant axis ( rxy = -0.96): the position angle is $64.7 \pm 0.2$ degrees and the rms deviation is 0.31%, i.e., slightly higher than for the wavelength-independent solution (cf. Table 2). This is fully consistent with an alignment along the local spiral arm of NGC 300, which is indicative of the interstellar nature of this component.

\begin{figure} \par\includegraphics[width=8cm,clip]{13083f11.eps} \end{figure} Figure 11:

Minimum polarization solution with an exponential polarization $\vec{P_1}$ for 2008 July 8. The color-coded segment in the lower right panel is the exponential component $\vec{P_1}$, while the dots trace the corresponding component $\vec{P_2}$. The dashed line traces the best-fit dominant axis.

Open with DEXTER

The position angle $\theta_1$ was fixed by constraining the dominant axis to pass through the origin of the Q-U plane (Wang et al. 2003). As done in the wavelength-independent case (Sect. 4.1), we decomposed $\vec{P_2}$ along the directions parallel and perpendicular to the dominant axis, as shown in Fig. 12 for the second epoch. The rms deviation of the orthogonal component $P_ {\rm o}$ is 0.15%, which is consistent with the typical measurement errors and indicates that there are no statistically significant wavelength dependencies in the residual polarization. As for $P_{\rm d}$, this shows a smooth behavior, and can be reasonably well fitted by a Serkowski law with $P_{\max} =4.8\%$, $\lambda_{\max} = 4250$ Å, and K = 3.0. This value of K is still large compared to what is typical of the Milky Way, but it is significantly smaller than that required by the wavelength-independent component (Sect. 4.1).

\begin{figure} \par\includegraphics[width=8cm,clip]{13083f12.eps} \end{figure} Figure 12:

Dominant ( upper panel) and orthogonal ( lower panel) polarization on 2008 July 8 after subtracting the exponential component $\vec{P_1}$. For presentation, the data were binned to 16 pixel (57 Å). The solid curve on the upper panel is a Serkowski law with $P_{\max} = 2.6\%$, $\lambda_{\max} = 4880$ Å and K = 5.6.

Open with DEXTER

The global solution is compared to the data in Fig. 13 for the second epoch. The fit is reasonably good, even though $\chi^2$(2.5) and the rms deviation (0.3%) are greater than in the wavelength-independent solution (Sect. 4.1). Of course, there is absolutely no reason why the wavelength dependency of dust scattering in the circumstellar environment of NGC 300 OT2008-1 should be similar to that of the Milky Way. However, this illustrates that the wavelength-independent solution, although giving the most accurate reproduction of the data with the minimum number of free parameters, is not unique. One possible argument against a strong wavelength dependence of $\vec{P_1}$ is that this would imply higher polarization values in both components. In the example that we have just discussed, P2 reaches a maximum polarization of about 5% and P1 is $\sim$4% at 4000 Å. These values are quite high, especially considering that the solutions are undefined up to an additive constant and so the derived polarization levels are only lower limits.

\begin{figure} \par\includegraphics[width=8cm,clip]{13083f13.eps} \end{figure} Figure 13:

Best-fit solution for 2008 July 8 compared to the observed Stokes parameters ( lower panel), position angle ( upper panel), and polarization level (upper panel). The curves indicate the exponential component $\vec{P_1}$ (dashed), $\vec{P_2}$(dotted-dashed), and the global solution (solid).

Open with DEXTER

A detailed treatment of the radiation transfer, including light-travel effects, multiple scattering, dust properties, and geometrical distribution (see Patat 2005) would be required for a realistic modeling. However, a lower limit to the amount of dust required to account for the observed level of polarization can be obtained as follows. We assume that the dust is placed at a distance r from the supposedly unpolarized source and is distributed in such a way that all scattered radiation becomes polarized to the maximum possible level $P_{\max}$ (attained for $\theta = \pi$/2 and $P_{\max}\approx 0.5$; see White 1979). Based on this assumption, if $F_s(\lambda)$ is the flux scattered into the line of sight and $F_0(\lambda)$ is the flux isotropically emitted by the source, then the observed degree of polarization is given by

$\displaystyle P(\lambda)\approx \frac{F_s}{F_0+F_s} \approx \frac{P_{\max}}{4\p... ...bda) \; \omega(\lambda) \; C_{\rm ext}(\lambda) \; \frac{M_{\rm H}}{m_{\rm H}},$      

where $M_{\rm H}$ is the implied hydrogen mass (for a given gas-to-dust mass ratio) and $m_{\rm H}$ is the proton mass. Substituting the values for the RV = 3.1 dust mixture (Li & Draine 2001; Draine 2003b) for $\lambda = 5500$ Å ( $\omega = 0.67$, g = 0.54, $C_{\rm ext}/H =5 \times 10 ^{-22}$ cm2) and assuming maximum polarization ( $\theta = \pi$/2), one arrives at the expression:
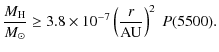
$\displaystyle \frac{M_{\rm H}}{M_\odot}\geq 3.8 \times 10^{-7} \left( \frac{r}{\rm AU} \right)^2\;P(5500).$      

For instance, if the scattering material is placed at r = 1000 AU, one needs $M_{\rm H} \approx 8 \times 10^{-3}~M_\odot$ to reach a 2% polarization. For a gas-to-dust mass ratio of 200 (typical of evolved stars with carbon-rich dust; see Matsuura et al. 2009), this implies a lower limit to the dust mass of $4 \times 10 ^{-5}~M_\odot$. Clearly, if the dust is placed at 100 AU[*], this lower limit would decrease by a factor of 100. As we said, this is only the mass of dust distributed in an asymmetric way, because polarization alone cannot constrain the total amount of dust. For instance, a spherically symmetric dust shell of 10 $^{-2}~M_\odot$ could be present, but this would not produce any measurable polarization. Prieto et al. (2009) came to the conclusion that about 10 $^{-4}~M_\odot$ of circumstellar dust are required to explain the mid-IR excess in NGC 300 OT2008-1. Similar results were found by Wesson et al. (2009) for SN 2008S, while Botticella et al. (2009) derived a dust mass of $\sim$10 $^{-3}~M_\odot$. Our data suggest that a significant fraction of this material (the exact amount depends on the dust distance among other parameters) must be distributed in an asymmetric configuration. Whether this is a torus, a disk, a bipolar outflow (see Bond et al. 2009; Prieto et al. 2009) or a clumpy shell superimposed on an otherwise spherically symmetric distribution, we are unable to decide on the basis of the available data. Spectropolarimetry obtained during earlier epochs might help to differentiate between the various possibilities.

The fiducial date of the outburst is assumed to be April 17, 2008 (Berger et al. 2009), i.e., 75 days before our first epoch. This implies that, at the time of our observations, the expanding radiation front is illuminating dust placed at $\sim$104 AU perpendicular to the line of sight. The light curve peak has a width of about 100 days (Bond et al. 2009), so that the polarized photons that we have detected were scattered in a region that extends between the dust evaporation boundary and about 104 AU. Given that at this large distance the incoming flux is a factor of 100 lower than at 1000 AU, the bulk of the polarization probably comes from material located closer to the source, between the dust evaporation radius and a few thousand AU. In this scenario, the observed decrease in polarization can be understood as being caused by the expansion of the radiation flash, coupled to the confinement of dust close to the object and possible inhomogeneities in its distribution.

If the dust is distributed across a sufficiently large distance from the outbursting object perpendicular to the line of sight, so that the scattering material produces a long integration time, then a case B light echo (Patat et al. 2006) might become observable as the transient fades out. Its evolution with time could help us to better characterize the dust distribution. Unfortunately, the lack of a scattered light echo detection in the HST images obtained more than 4 months after the outburst (Bond et al. 2009) does not allow us to place stringent limits on the circumstellar dust distance. The HST-ACS spatial resolution (50 mas) corresponds to $\sim$105 AU at the distance of NGC 300 (1.88 Mpc; Gieren et al. 2005; Rizzi et al. 2006). Future HST observations might clarify whether there is circumstellar dust at distances greater than $\sim$105 AU from the outburst site. Incidentally, the absence of a resolved light echo indicates that the transient must be placed at a significant distance behind the interstellar dust associated with the local spiral arm of NGC 300.

6 Conclusions

We have presented VLT-spectropolarimetry of NGC 300 OT2008-1 obtained 48 and 55 days after its discovery. The continuum polarization is dominated by a component very well aligned along the local spiral arm of NGC 300, which we have interpreted as originating in interstellar dust. The wavelength dependency of the ISP differs substantially from what is typical of the Milky Way. Once the ISP is subtracted, a substantial signal, reaching about 1.2%, is detected. This polarization component is aligned along a completely different position angle.

The simplest explanation of this continuum polarization is electron scattering coupled with a significantly asymmetric photosphere. Nevertheless, the absence of any line depolarization (very common in sources displaying similar levels of polarization) disfavors this scenario and calls for an alternative origin.

Although we have investigated different possible reasons for the lack of depolarization, the most viable physical mechanism is scattering by a circumstellar, asymmetric dust cloud. If this is the correct picture (also implying that the emitting photosphere does not deviate significantly from spherical symmetry), this means that a significant amount of dust ($\geq$10 $^{-5}~M_\odot$) must be present during the epochs covered by our observations, either because it has re-condensed or because it has survived the radiation flash produced by the outburst.

Besides adding to the growing evidence of substantial amounts of circumstellar dust in a completely independent way, our observations provide direct proof that dust is not only present, but that a significant fraction must have an asymmetric geometry. This implies that one or more asymmetric outflow episodes from the progenitor star must have occurred during its past history.

Acknowledgements
This paper is based on observations made with ESO Telescopes at Paranal Observatory under program ID 281.D-5016. The authors wish to thank ESO's Director General for granting his Discretionary Time to this project. They are also grateful to A. Pastorello and P. Höflich for their kind and competent help, and to H.M. Schmid for the very useful comments provided during the refereeing process.

Appendix A: Effects of second order contamination on spectropolarimetry

The purpose of this Appendix is to evaluate the effect of the second order on spectropolarimetry when no order-sorting filter (hereafter OSF) is used, and to propose a simple technique for its correction.

A.1 Second-order contamination

In general, diffraction-based dispersive elements (such as gratings and grisms) produce replicas of the first-order (FO) spectrum with dispersions that increase proportionally to the order number. While higher orders can usually be neglected, the second-order (SO) spectrum appears as an additive component superimposed on the red part of the first order (FO) spectrum, with a dispersion that is $\sim$2 times that of the first order. In practice, the flux detected at a given wavelength $\lambda$ is the sum of the clean spectrum at $\lambda$and a fraction of the spectrum detected at a bluer wavelength, which we indicate as $\lambda ^\prime $. If $s(\lambda)$ is the spectrum one would record on the detector in the absence of SO contamination, the spectrum which is actually observed $s^\prime(\lambda)$ can be modeled as

\begin{displaymath} s^\prime(\lambda) = s(\lambda) + r_{2/1}(\lambda) \; s(\lambda^\prime) \end{displaymath} (A.1)

where $r_{2/1}(\lambda )$ is a function that we wish to derive. The first step in this procedure is to derive the relationship between $\lambda$ and $\lambda ^\prime $. For this purpose, we used archival FORS1 wavelength-calibration exposures taken with and without the OSF GG435 (O'Brien 2008). After performing the wavelength calibration and identifying 6 isolated blue lines and their red replicas, we derived the relation between their first order wavelength and their apparent wavelength in the second order. The data points are very well fitted by a linear relation

\begin{displaymath} \lambda = a + b\;\lambda^\prime, \end{displaymath} (A.2)

where $a = - 539.5 \pm 0.4$ Å and $b = 2.081 \pm 0.001$. With this result at hand, the ratio r2/1 can be estimated in the following way. We indicate by $S(\lambda)$ the intrinsic spectrum of an astronomical source, by $T(\lambda)$ the transmission function (including atmosphere, instrument optics and detector efficiency), by F$(\lambda)$ the OSF transmission, and by $G_1(\lambda)$ and $G_2(\lambda)$ the grism FO and SO efficiencies, respectively. If $s_{f}(\lambda)$ and $s_{nf}(\lambda)$are the observed spectra obtained with and without OSF, respectively, and based on the assumption that the order-sorting filter completely eliminates the SO (see below), they can be written as
                            $\displaystyle s_{f}(\lambda)$ = $\displaystyle {S}(\lambda) \;{T}(\lambda) \; {F}(\lambda) \; G_1(\lambda)$  
$\displaystyle s_{nf}(\lambda)$ = $\displaystyle {S}(\lambda) \;T(\lambda) \;G_1(\lambda) + {S}(\lambda^\prime) \; {T}(\lambda^\prime) \;G_2(\lambda^\prime).$  

Since r2/1, as defined in Eq. (A.1), is the ratio of the pure SO flux at $\lambda$ to the corresponding FO flux at $\lambda ^\prime $, this can be written as

\begin{displaymath} r_{2/1} = \frac{s_{nf}(\lambda)-s_f(\lambda)/F(\lambda)}{s_{nf}(\lambda^\prime)}\cdot \end{displaymath} (A.3)

The advantages of this formulation are that it is based on measurable or known quantities and is independent of the detector sensitivity function. It can indeed be easily shown that $r_{2/1}(\lambda )$ is the ratio of G2 to G1.

In principle, any bright astronomical target with a continuum spectrum observed with and without the OSF can be used to derive $r_{2/1}(\lambda )$. Nevertheless, because of the lower sensitivity of detectors in the blue and since the effect that we wish to measure is produced by blue photons, the most suitable choice is a hot star. For this reason, and because it is included in the FORS1 calibration plan (O'Brien 2008), we selected the D0p spectrophotometric standard star Feige 110 ( $\alpha_{2000} = 23$:19:58.4, $\delta_{2000} = - 05$:09:55.8), which has a very blue ( B-V = - 0.30) and featureless spectrum (Hamuy et al. 1992, 1994). The FORS1 archival data that we selected were obtained on 2008 October 12 with the grism 300 V, with and without the OSF GG435, which has a cutoff wavelength $\lambda_f \sim 4300$ Å. As for the filter transmission curve, we used the tabulated data provided by the Observatory[*]. One needs to mention that the GG435 OSF does not prevent a small portion of the SO being produced in the red edge of the spectrum. Its blue cut-off corresponds to a SO wavelength of $\sim$8500 Å, so that redward of this value a contribution from photons bluer than 4350 Å is still present. This makes the derivation of $r_{2/1}(\lambda )$ uncertain between 8500 Å and the red edge of the spectral range covered by the detector.

\begin{figure} \par\includegraphics[width=8.4cm,clip]{13083f14.eps} \end{figure} Figure A.1:

Ratio between observed SO and FO as a function of wavelength derived for the 300V grism mounted in FORS1. The upper scale indicates the corresponding FO wavelength  $\lambda ^\prime $. The solid blue curve is a best fit with a fifth order polynomial.

Open with DEXTER

\begin{figure} \par\includegraphics[width=90mm,clip]{13083f15.eps} \end{figure} Figure A.2:

Lower panel: comparison between the observed spectrum of the OT in NGC 300 (dotted line) and the corrected spectrum (solid line). The dashed line traces the $r_{2/1}(\lambda )$ function. Upper panel: the relative SO contamination $\Delta (\lambda )$. The results above 8500 Å are uncertain (see text).

Open with DEXTER

After wavelength calibration, we extracted the two spectra and applied Eq. (A.3) to derive $r_{2/1}(\lambda )$. The result is presented in Fig. A.1. This figure shows that the second-order contamination can be significant for very blue targets: for instance, the SO contamination at 6500 Å is about 35% of the flux detected at 3380 Å. Clearly, the exact amount of contamination depends on the input spectrum, which is in principle unknown. Nevertheless, one must notice that for the SO contamination only the knowledge of the blue part of the spectrum is needed, where the observed and the uncontaminated spectrum are identical ( $s^\prime(\lambda) = s(\lambda)$). The SO begins to contaminate the spectrum at a wavelength $\lambda_{\rm c}$ which corresponds to the detector blue cut-off wavelength $\lambda_b$. For FORS1, it is $\lambda_b\sim 3200$ Å, which, according to Eq. (A.2), corresponds to $\lambda_{\rm c} = 6120$ Å. Below this wavelength, the SO can be considered negligible and so one can set $r_{2/1}(\lambda) = 0$ for $\lambda<\lambda_{\rm c}$.

Therefore, knowing $r_{2/1}(\lambda )$ one can recover the uncontaminated spectrum by simply inverting Eq. (A.1) and using Eq. (A.2), e.g.,

\begin{displaymath} s(\lambda)=s^\prime(\lambda) - r_{2/1}(\lambda) \; s^\prime\left(\frac{\lambda-a}{b}\right)\cdot \end{displaymath} (A.4)

A way of expressing the severity of the SO contamination is to normalize its absolute amount to the flux at any given wavelength, by introducing the quantity  $\Delta (\lambda )$

\begin{displaymath} \Delta(\lambda) = \frac{s^\prime(\lambda)-s(\lambda)}{s^\pri... ...\lambda)\; \frac{s^\prime(\lambda^\prime)}{s^\prime(\lambda)}, \end{displaymath} (A.5)

which is the fraction of the observed flux produced by the SO.

The application of this method to the data discussed in this paper is illustrated in Fig. A.2. To avoid introducing additional noise, we replaced the computed $r_{2/1}(\lambda )$ with a fifth order polynomial fit to the data (solid curve in Fig. A.1). For our object, the contamination reaches a maximum relative value of about $\Delta = 5\%$ at about 8000 Å which, for most purposes is negligible, being smaller than the typical accuracy one can achieve in the flux calibration.

Nevertheless, since polarimetry is in most cases dealing with flux differences of a few percent, the impact of SO contamination needs to be evaluated.

A.2 Effects on spectropolarimetry

In dual-beam instruments such as FORS1, spectropolarimetry is performed by evaluating the so-called normalized flux ratios $F_i (\lambda)$, derived from the ordinary and extraordinary beams produced in the same frame by the Wollaston prism (see Patat & Romaniello 2006, for a general introduction). For the canonical HWP position angles $\theta_i=\frac{\pi}{8} i$ (where i = 0, 1, 2, 3) and for an ideal polarimeter, these ratios are directly related to the Stokes parameters: F0 = Q, F1 = U, F2 = - Q, and F3=-U. Since the observed fluxes in the ordinary ( $f^{\prime, O}_i$) and extraordinary ( $f^{\prime,E}_i$) beams can be modeled with Eq. (A.1), the observed normalized ratios

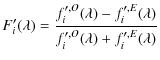
$\displaystyle F^\prime_i(\lambda)=\frac{f^{\prime,O}_i(\lambda)-f^{\prime,E}_i(\lambda)} {f^{\prime,O}_i(\lambda)+f^{\prime,E}_i(\lambda)}$      

after some manipulation can be expressed as
$\displaystyle F^\prime_i(\lambda)=\frac{F_i(\lambda) + g_i(\lambda)\; F_i(\lambda^\prime)} {1+g_i(\lambda)},$     (A.6)

where we have defined
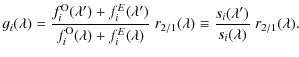
$\displaystyle g_i(\lambda)=\frac{f^{\rm O}_i(\lambda^\prime)+f^E_i(\lambda^\pri... ...1}(\lambda) \equiv \frac{s_i(\lambda^\prime)}{s_i(\lambda)}\; r_{2/1}(\lambda).$      

Equation (A.6) shows that, in general, the effect of SO contamination on the final polarization is not obvious, since it depends on the exact spectral energy distribution and polarization of the source. However, when the SO contamination is moderate ( $\Delta(\lambda)\leq 0.1$), the effect is more readily understood. In those circumstances, it is given by $s(\lambda^\prime)/s(\lambda) \approx s^\prime(\lambda^\prime)/s^\prime(\lambda)$, so that $g(\lambda)\approx \Delta(\lambda)$ (see Eq. (A.5)) and one can write
$\displaystyle F^\prime_i(\lambda)\approx\frac{F_i(\lambda) + \Delta(\lambda)\; ... ...1+\Delta(\lambda)} \approx F_i(\lambda) + \Delta(\lambda)\;F_i(\lambda^\prime).$      

In our case, where $\Delta$ reaches a maximum value of $\sim$0.05 and the polarization in the blue is of the order of 2%, the absolute effect on the derived Stokes parameters is of the order of 0.1%, which is comparable to the maximum accuracy one can reach with instruments such as FORS1 (Patat & Romaniello 2006). For this reason, the SO effect on the data presented in this paper can be neglected. A more rigorous calculation performed by correcting each of the ordinary and extraordinary beams following the procedure outlined in Sect. A.1 leads to the same conclusions.

Appendix B: The effect of multiple weak polarizers

In general, if $\vec{S_0}(I_0,Q_0,U_0,V_0)$ is the Stokes vector that defines the polarization status of an incoming beam, its passage through an optical system can be described by $\vec{S_1} = \vec{M} \cdot \vec{S_0}$, where $\vec{S_1}$ is the emerging Stokes vector and ${\vec M}$is the Mueller matrix that characterizes the system (Chandrasekhar 1950). To a first approximation, a dust cloud can be treated as a partial polarizer. The Mueller matrix for a non-birefringent, non-scattering, partial polarizer with horizontal transmission axis ( $\theta = 0$) is given by the expression

\begin{displaymath} \vec{M(0)}=\frac{1}{2} \left( \begin{array}{cccc} k_1+k_2 & ... ... k_2} & 0 \\ 0 & 0 & 0 & 2\sqrt{k_1 k_2} \end{array} \right) \end{displaymath} (B.1)

where k1 and k2 ( $k_1\geq k_2$; $0 \leq k_1,k_2 \leq 1$) are the principal transmittances (see for instance Keller 2000, Eq. (3.24)). For k1 = 1 and k2 = 0, one obtains a perfect linear, horizontal polarizer, while for k1=k2 = 1, Eq. (B.1) implies an isotropic, non-absorbing medium. The general expression for a generic position angle $\theta$ can be obtained by computing the product $\vec{R(-\theta)} \cdot \vec{M(0)} \cdot \vec{R(\theta)}$ (Chandrasekhar 1950), where $\vec{R(\theta)}$ is the usual rotation matrix
$\displaystyle \vec{R(\theta)}= \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 &... ... 0 & -\sin 2\theta & \cos 2\theta & 0 \\ 0 & 0 & 0 & 1\\ \end{array} \right).$    

After defining $s=\sin 2\theta$, $c=\cos 2\theta$, k=(k1+k2)/2, and p =(k1-k2)/(k1+k2), one can write the matrix product as
$\displaystyle \vec{M(\theta)}= k \left( \begin{array}{cccc} 1 & pc & ps & 0 \\ ... ... & s^2+c^2\sqrt{1-p^2} & 0 \\ 0 & 0 & 0 & \sqrt{1-p^2}\\ \end{array} \right),$    

where $0 \leq k,p \leq1$. For p = 0, one clearly obtains an isotropic medium with transmittance k, while for p = 1 the previous equation provides the general expression of an ideal linear polarizer with position angle $\theta$ (see for instance Keller 2000; Eq. (3.26)).

Using the above matrix, one can compute the resulting Stokes vector to be

                                     sI1/k = I0+Q0pc + U0ps,  
Q1/k = $\displaystyle I_0pc + Q_0\left(c^2+s^2\sqrt{1-p^2}\right) + U_0\left(1-\sqrt{1-p^2}\right)sc,$  
U1/k = $\displaystyle I_0ps+ Q_0\left(1-\sqrt{1-p^2}\right)sc + U_0\left(s^2+c^2\sqrt{1-p^2}\right),$  
V1/k = $\displaystyle V_0 \sqrt{1-p^2}.$  

If the incoming beam is unpolarized, the resulting Stokes vector is $\vec{S_1}(kI_0, kI_0 p \cos 2\theta, kI_0 p \sin 2\theta, 0)$, so that the polarization is p and its position angle is $\theta$. If the beam is polarized (either because the source is intrinsically polarized or because the beam passed already through a polarizing system such as a dust cloud), then the situation becomes more complicated. However, when the incoming polarization and p are far smaller than 1, the previous expressions can be approximated to be
$\displaystyle \begin{array}{ccl} I_1 &\approx& k I_0 \\ Q_1 &\approx& k Q_0 + ... ...+ k I_0p\sin 2\theta\nonumber \\ V_1 &\approx& k V_0. \nonumber\\ \end{array}$      

Therefore, in the case of weak linear polarization, the output normalized Stokes parameters are simply given by
$\displaystyle \begin{array}{ccl} \langle Q_1 \rangle &\approx& \langle Q_0\rang... ... \rangle &\approx& \langle U_0\rangle + p\sin 2\theta. \nonumber\\ \end{array}$      

This implies that the effect of multiple weak polarizers (such as several dust clouds) can be described as a sum of terms, each characterized by a polarization pi and a position angle $\theta_i$. In other words, when the polarization is weak, the components can be considered to be vectorially additive[*].

An interesting consequence follows from this conclusion. If we express the polarization wavelength dependency as $p(\lambda)=p_{\max} f(\lambda)$ and we imagine a beam of unpolarized light passing through a system of interstellar clouds of various $p_{\max}$ and $\theta$(with ${\rm d}\theta/{\rm d}\lambda = 0$), then the resulting normalized Stokes parameters are

                  $\displaystyle \langle Q\rangle$ = $\displaystyle \sum p_{\max,i} \; f_i(\lambda) \;\cos 2\theta_i,$  
$\displaystyle \langle U$ = $\displaystyle \sum p_{\max,i} \; f_i(\lambda) \;\sin 2\theta_i.$  

Therefore, if the dust in the various clouds produces linear polarization with the same wavelength dependency (i.e., dust properties are common to all clouds), then the resulting polarization position angle $\theta=1/2 \arctan (U/Q)$ is wavelength-independent and the entire system is indistinguishable from a single cloud.

On the other hand, if the different clouds produce polarizations that do not obey the same law  $f(\lambda)$, then the resulting polarization position angle $\theta$ will be wavelength-dependent. Once plotted on the Q,U plane, the polarization data will not lie on a straight line passing through the origin and will possibly extend over different quadrants.

An example of a system consisting of two clouds both obeying the empirical Serkowski law (Serkowski et al. 1975), with two different values of the polarization peak wavelength $\lambda_{\max}$ is shown in Fig. B.1.

\begin{figure} \par\includegraphics[width=9cm,clip]{13083f16.eps} \end{figure} Figure B.1:

Example composition of two Serkowski laws: $P_{\max} = 1.8\%$, $\lambda_{\max} = 3500$ Å, $\theta = 70^\circ $ (K=0.59) and $P_{\max} = 1.5$%, $\lambda_{\max} = 9500$ Å, $\theta = 150^\circ $(K=1.59). A Gaussian noise ( $\sigma = 0.1$%) was added to the resulting points. The wavelength step is 100 Å.

Open with DEXTER

References

  1. Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
  2. Berger, E., & Sodergerg, A., 2008, A.Tel., 1544 [Google Scholar]
  3. Berger, E., Soderberg, A. M., Chevalier, R. A., et al. 2009, ApJ, 699, 1850 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bjorkman, K. S., Johansen, K. A., Nordsieck, K. H., Gallager, J. S., & Barger, A. J. 1994, ApJ, 425, 247 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bond, H. E., Walter, F. M., & Velasquez, J., 2008, IAU Circ. n. 8946 [Google Scholar]
  6. Bond, H. E., Bedin, L. R., Bonanos, A. Z., et al. 2009, ApJ, 695, L154 [NASA ADS] [CrossRef] [Google Scholar]
  7. Botticella, M. T., Pastorello, A., Smartt, S. J., et al. 2009, MNRAS, 398, 1041 [NASA ADS] [CrossRef] [Google Scholar]
  8. Brown, J. C., & McLean, I. S. 1977, A&A, 57, 141 [Google Scholar]
  9. Chandrasekhar, S. 1950, Radiative Transfer (Oxford: Oxford University Press) [Google Scholar]
  10. Clarke, D., & McLean, I. S. 1974, MNRAS, 167, 27 [Google Scholar]
  11. Cropper, M., Bailey, J., McCowage, J., Cannon, R. D., & Couch, W. J. 1988, MNRAS, 231, 695 [NASA ADS] [Google Scholar]
  12. Draine, B. T. 2003a, ARA&A, 41, 241 [Google Scholar]
  13. Draine, B. T. 2003b, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
  14. Gieren, W., Pietrzynski, G., Soszynski, I., et al. 2005, ApJ, 628, 695 [NASA ADS] [CrossRef] [Google Scholar]
  15. Gogarten, S. M., Dalcanton, J. J., Murphy, J. W. 2009, ApJ, 703, 300 [NASA ADS] [CrossRef] [Google Scholar]
  16. Hamuy, M., Walker, A. R., & Suntzeff, N. B. 1992, PASP, 104, 533 [NASA ADS] [CrossRef] [Google Scholar]
  17. Hamuy, M., Suntzeff, N. B., Heathcote, S. R., et al. 1994, PASP, 106, 566 [NASA ADS] [CrossRef] [Google Scholar]
  18. Harrington, J. P., & Collins, G. Q. 1968, ApJ, 151, 1051 [NASA ADS] [CrossRef] [Google Scholar]
  19. Heiles, C. 1999, AJ, 119, 923 [Google Scholar]
  20. Henyey, L. C., & Greenstein, J. L. 1941, AJ, 93, 70 [Google Scholar]
  21. Höflich, P. 1991, A&A, 246, 481 [Google Scholar]
  22. Hoffman, J. L., Leonard, D. C., Chornock, R., et al. 2008, ApJ, 688, 1186 [NASA ADS] [CrossRef] [Google Scholar]
  23. Jones, T. J., Humphreys, R. M., Gehrz, R. D., et al. 1993, ApJ, 411, 323 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kawabata, K. S., Hirata, R., Ikeda, Y., et al. 2000, ApJ, 540, 429 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kawabata, K. S., Ohyama, Y., Ebizuka, N., et al., 2006, AJ, 132, 433 [NASA ADS] [CrossRef] [Google Scholar]
  26. Keller, C. U. 2002, in Astrophysical Spectropolarimetry (Cambridge: Cambridge Univ. Press), 303 [Google Scholar]
  27. Kulkarni, S. R., Ofek, E. O., Rau, A., et al. 2007, ApJ, 447, 458 [Google Scholar]
  28. Leonard, D. C., & Filippenko, A. V. 2001, PASP, 113, 920 [Google Scholar]
  29. Leonard, D. C., Filippenko, A. V., Chornock, R., et al. 2002, ApJ, 124, 2506 [Google Scholar]
  30. Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
  31. Matsuura, M., Barlow, M. J., Zijlstra, A. A., et al. 2009, MNRAS, 396, 918 [NASA ADS] [CrossRef] [Google Scholar]
  32. Maund, J. 2008, A&A, 481, 913 [Google Scholar]
  33. Maund, J. R., Smartt, S. J., Kudritzki, R.-P., et al. 2006, MNRAS, 369, 390 [NASA ADS] [CrossRef] [Google Scholar]
  34. Maund, J. R., Wheeler, J. C., Patat, F., et al. 2007, MNRAS, 381, 201 [NASA ADS] [CrossRef] [Google Scholar]
  35. McLean, I. S., & Clarke, D. 1979, MNRAS, 186, 245 [Google Scholar]
  36. Monard, L. A. G. 2008, IAU Circ. n. 8946 [Google Scholar]
  37. O'Brien, K. 2008, FORS1+2 User's Manual, VLT-MAN-ESO-13100-1543, Issue 82.1 [Google Scholar]
  38. Ofek, E. O., Kulkarni, S. R., Rau, A., et al. 2008, ApJ, 674, 447 [NASA ADS] [CrossRef] [Google Scholar]
  39. Pastorello, A., Smartt, S. J., Mattila, S., et al. 2007a, Nature, 447, 829 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  40. Pastorello, A., Della Valle, M., Smartt, S. J., et al. 2007b, Nature, 449, 1 [Google Scholar]
  41. Patat, F. 2005, MNRAS, 357, 1161 [NASA ADS] [CrossRef] [Google Scholar]
  42. Patat, F., & Romaniello, M. 2006, PASP, 118, 146 [NASA ADS] [CrossRef] [Google Scholar]
  43. Patat, F., Benetti, S., Cappellaro, E., et al. 2006, MNRAS, 369, 1949 [NASA ADS] [CrossRef] [Google Scholar]
  44. Patat, F., Baade, D., Höflich, P., et al. 2009, A&A, 508, 229 [Google Scholar]
  45. Patel, M., Oudmaijer, R. D., Vink, J. S., et al. 2008, MNRAS, 385, 967 [NASA ADS] [CrossRef] [Google Scholar]
  46. Prieto, J. L. 2008, A. Tel., n. 1596 [Google Scholar]
  47. Prieto, J. L., Kistler, M. D., Thompson, T., et al. 2008, ApJ, 681, L9 [NASA ADS] [CrossRef] [Google Scholar]
  48. Prieto, J. L., Sellgren, K., Thompson, T. A., et al. 2009, ApJ, 705, 1425 [NASA ADS] [CrossRef] [Google Scholar]
  49. Pumo, M. L., Turatto, M., Botticella, M. T., et al. 2009, ApJ, 705, 138 [Google Scholar]
  50. Quirrenbach, A., Bjorkman, K. S., Bjorkman, J., et al. 1997, ApJ, 479, 477 [NASA ADS] [CrossRef] [Google Scholar]
  51. Rau, A., Ofek, E. O., Kulkarni, S. R., et al. 2008, ApJ, 682, 1205 [NASA ADS] [CrossRef] [Google Scholar]
  52. Rizzi, L., Bresolin, F., Kudritzki, R. P., Gieren, W., & Pietrzynsky, G. 2006, ApJ, 638, 766 [NASA ADS] [CrossRef] [Google Scholar]
  53. Roussel, H., Gil de Paz, A., Seibert, M., et al. 2005, ApJ, 632, 227 [NASA ADS] [CrossRef] [Google Scholar]
  54. Scarrot, S. M., Ward-Thompson, D., & Warren-Smith, R. F. 1987, MNRAS, 224, 299 [NASA ADS] [CrossRef] [Google Scholar]
  55. Serkowski, K., Matheson, D. S., & Ford, V. L. 1975, ApJ, 196, 261 [NASA ADS] [CrossRef] [Google Scholar]
  56. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  57. Smith, N., Ganeshalingam, M., Chornock, R., et al. 2009, ApJ, 697, L49 [NASA ADS] [CrossRef] [Google Scholar]
  58. Thompson, T. A., Prieto, J. L., Stanek, K. Z., et al. 2009, ApJ, 705, 1364 [NASA ADS] [CrossRef] [Google Scholar]
  59. van den Hulst, H. C. 1957, Light Scattering by Small Particles (New York: Wiley & Sons) [Google Scholar]
  60. Van Dyk, S. D., et al. 2000, PASP, 117, 553 [Google Scholar]
  61. Wang, L., et al. 2004, ApJ, 591, 1110 [Google Scholar]
  62. Wesson, R., Barlow, M. J., Ercolano, B., et al. 2009, MNRAS, submitted [arXiv:0907:0246v1] [Google Scholar]
  63. White, R. L. 1979, ApJ, 229, 954 [NASA ADS] [CrossRef] [Google Scholar]
  64. Whittet, D. C. B., Martin, P. G., Hough, J. H., et al. 1992, ApJ, 386, 562 [NASA ADS] [CrossRef] [Google Scholar]
  65. Wisniewski, J. P., Morrison, N. D., Bjorkman, K. S., et al. 2003, ApJ, 588, 486 [NASA ADS] [CrossRef] [Google Scholar]

Footnotes

... dust[*]
Based on observations made with ESO Telescopes at Paranal Observatory under Program ID 281.D-5016.
... IRAF[*]
IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, under contract with the National Science Foundation.
... axis[*]
In the weak polarization approximation the components are vectorially additive. See Appendix B.
... NGC 300[*]
http://vizier.cfa.harvard.edu/viz-bin/VizieR?-source=II/226
... wavelength[*]
Note that this is a pure shift of Q and U that does not modify their shape.
... approximation[*]
If the dust optical depth is high, then multiple scattering becomes important and acts as a depolarizer. See for instance Patat (2005).
... mixtures[*]
Wesson et al. (2009) have shown that the dust around SN 2008S most likely consists of carbon grains. The usage of a carbonaceous-silicate mixture here is just illustrative.
... 100 AU[*]
Prieto et al. (2009) set the outer boundary of dust evaporation for NGC 300 OT2008-1 to be 100 AU, while for SN 2008S Botticella et al. (2009) obtained a significantly larger value (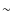$\sim$2000 AU).
... Observatory[*]
http://www.eso.org/sci/facilities/paranal/instruments/fors/inst/Filters/
... additive[*]
The demonstration can be easily extended to the most general form of the Mueller matrix that describes the polarizer.

All Tables

Table 1:   Log of the VLT-FORS1 observations of NGC 300 OT2008-1.

Table 2:   Dominant axis least squares fit parameters.

Table 3:   Minimum polarization solutions for the two epochs.

Table 4:   Synthetic broadband polarimetry of NGC 300 OT2008-1.

All Figures

  \begin{figure} \par\includegraphics[width=9cm,clip]{13083f01.eps} \end{figure} Figure 1:

Flux spectra of NGC 300 OT2008-1 on 2008 July 1 ( upper) and 2008 July 8 ( lower). For presentation, the spectrum of the second epoch was shifted by -0.4. The main spectral features are identified.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=100mm,angle=-90]{13083f02.eps} \end{figure} Figure 2:

Observed spectropolarimetry of NGC 300 OT2008-1 at the two epochs on the Stokes Q-U plane. For presentation, the data were binned to 16 pixels (57 Å). The dotted circles are placed at constant polarization levels (0.5, 1.0, 1.5, and 2.0%). The dashed line is a weighted least squares fit to the data in the displayed wavelength range. For comparison, the colored line sequence of dots in the upper left quadrant traces a Serkowski law (Serkowski et al. 1975) for $\lambda_{\max} = 4800$ Å, $P_{\max} = 1.4$%, and K = 0.81 with an arbitrary position angle $\theta = 60$ degrees. The circled dot indicates the position of (Q1,U1) corresponding to the minimum polarization solution (see Sect. 4.1), while the vector indicates the allowed region for (Q1,U1).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=80mm,clip]{13083f03.eps} \end{figure} Figure 3:

Differences in Q ( upper panel) and U ( lower panel) Stokes parameters between the two epochs (second minus first). Empty symbols indicate the data points rejected by the k-$\sigma $ clipping.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13083f04.eps} \end{figure} Figure 4:

A DSS image of NGC 300. The location of the optical transient is marked by a cross. The arrow indicates the polarization position angle of the dominant axis (the average of the values measured during the two epochs was used: $\theta = 68.6$ degrees).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13083f05.eps} \end{figure} Figure 5:

Minimum polarization solution for 2008 July 8. The dashed line traces the observed dominant axis, while the point (Q1,U1) indicates the wavelength-independent component. The empty circles mark the rejected data points.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13083f06.eps} \end{figure} Figure 6:

Dominant ( upper panel) and orthogonal ( lower panel) polarization on 2008 July 1 after subtracting the wavelength-independent component $\vec{P_1}$. For presentation, the data were binned to 16 pixel (57 Å). The solid curve in the upper panel is a Serkowski law with $P_{\max} =4.8\%$, $\lambda_{\max} = 4250$ Å, and K = 3.0.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13083f07.eps} \end{figure} Figure 7:

Same as Fig. 6 for 2008 July 8.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13083f08.eps} \end{figure} Figure 8:

Best fit solution for 2008 July 8 compared to the observed Stokes parameters ( lower panel), position angle ( upper panel) and polarization level (upper panel). The curves trace the wavelength-independent component $\vec{P_1}$ (dashed), $\vec{P_2}$ (dotted-dashed) and the global solution (solid).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13083f09.eps} \end{figure} Figure 9:

Spectropolarimetry of the H$\alpha $ line on 2008 July 1. The data were binned to 3 pixel (9.6 Å). The flux spectrum in the upper panel is unbinned. The thin colored line traces a high-resolution spectrum ( $\Delta \lambda/\lambda \sim 48~000$) obtained with VLT-UVES on 2008 July 2 (Pastorello et al. in preparation).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13083f10.eps} \end{figure} Figure 10:

Expected polarization wavelength dependence of a Milky Way carbonaceous-silicate dust mixture in a single-scattering approximation for RV = 5.5 ( upper panel) and RV = 3.1 ( lower panel) and two different scattering angles. Dust model is from Li & Draine (2001) and Draine (2003b).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13083f11.eps} \end{figure} Figure 11:

Minimum polarization solution with an exponential polarization $\vec{P_1}$ for 2008 July 8. The color-coded segment in the lower right panel is the exponential component $\vec{P_1}$, while the dots trace the corresponding component $\vec{P_2}$. The dashed line traces the best-fit dominant axis.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13083f12.eps} \end{figure} Figure 12:

Dominant ( upper panel) and orthogonal ( lower panel) polarization on 2008 July 8 after subtracting the exponential component $\vec{P_1}$. For presentation, the data were binned to 16 pixel (57 Å). The solid curve on the upper panel is a Serkowski law with $P_{\max} = 2.6\%$, $\lambda_{\max} = 4880$ Å and K = 5.6.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{13083f13.eps} \end{figure} Figure 13:

Best-fit solution for 2008 July 8 compared to the observed Stokes parameters ( lower panel), position angle ( upper panel), and polarization level (upper panel). The curves indicate the exponential component $\vec{P_1}$ (dashed), $\vec{P_2}$(dotted-dashed), and the global solution (solid).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.4cm,clip]{13083f14.eps} \end{figure} Figure A.1:

Ratio between observed SO and FO as a function of wavelength derived for the 300V grism mounted in FORS1. The upper scale indicates the corresponding FO wavelength  $\lambda ^\prime $. The solid blue curve is a best fit with a fifth order polynomial.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=90mm,clip]{13083f15.eps} \end{figure} Figure A.2:

Lower panel: comparison between the observed spectrum of the OT in NGC 300 (dotted line) and the corrected spectrum (solid line). The dashed line traces the $r_{2/1}(\lambda )$ function. Upper panel: the relative SO contamination $\Delta (\lambda )$. The results above 8500 Å are uncertain (see text).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{13083f16.eps} \end{figure} Figure B.1:

Example composition of two Serkowski laws: $P_{\max} = 1.8\%$, $\lambda_{\max} = 3500$ Å, $\theta = 70^\circ $ (K=0.59) and $P_{\max} = 1.5$%, $\lambda_{\max} = 9500$ Å, $\theta = 150^\circ $(K=1.59). A Gaussian noise ( $\sigma = 0.1$%) was added to the resulting points. The wavelength step is 100 Å.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.