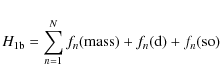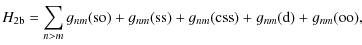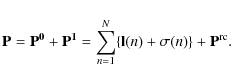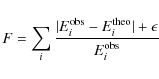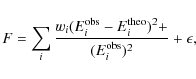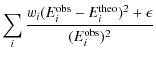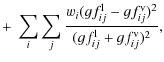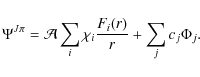| Issue |
A&A
Volume 508, Number 3, December IV 2009
|
|
|---|---|---|
| Page(s) | 1527 - 1537 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/200913179 | |
| Published online | 04 November 2009 | |
A&A 508, 1527-1537 (2009)
Radiative transition rates and collision strengths for Si II![[*]](/icons/foot_motif.png)
M. A. Bautista1 - P. Quinet2,3 - P. Palmeri2 - N. R. Badnell4 - J. Dunn5 - N. Arav5
1 - Department of Physics, Western Michigan University, Kalamazoo, MI
49008-5222, USA
2 - Astrophysique et Spectroscopie, Université de Mons-Hainaut, 7000 Mons, Belgium
3 -
IPNAS, B15 Sart Tilman, Université de Liège, 4000 Liège, Belgium
4 -
Department of Physics, University of Strathclyde, Glasgow G4 0NG, UK
5 -
Department of Physics, Virginia Polytechnic Institute and State University,
Blacksburg, VA 24061, USA
Received 25 August 2009 / Accepted 20 October 2009
Abstract
Aims. This work reports on radiative transition rates and electron impact excitation collision strengths for levels of the 3s23p, 3s3p2, 3s24s, and 3s23d configurations of Si II.
Methods. The radiative data were computed using the
Thomas-Fermi-Dirac-Amaldi central potential, but with the modifications
introduced by Bautista (2008) that account for the effects of
electron-electron interactions. We also introduce new schemes for the
optimization of the variational parameters of the potential. Additional
calculations were carried out with the Relativistic Hartree-Fock and
the multiconfiguration Dirac-Fock methods. Collision strengths in
LS-coupling were calculated in the close coupling approximation with
the R-matrix method. Then, fine structure collision strengths
were obtained by means of the intermediate-coupling frame
transformation (ICFT) method which accounts for spin-orbit coupling
effects.
Results. We present extensive comparisons between the results of
different approximations and with the most recent calculations and
experiments available in the literature. From these comparisons we
derive a recommended set of gf-values and radiative transition
rates with their corresponding estimated uncertainties. We also study
the effects of different approximations in the representation of the
target ion on the electron-impact collision strengths. Our most
accurate set of collision strengths were integrated over a Maxwellian
distribution of electron energies and the resulting effective collision
strengths are given for a wide range of temperatures. Our results
present significant differences from recent calculations with the
B-spline non-orthogonal R-matrix method. We discuss the sources of the differences.
Key words: atomic data - atomic processes - line: formation - quasars: absorption lines - Sun: abundances - ISM: atoms
1 Introduction
Singly ionized silicon (Si II) is prominent in
ultra-violet (UV) and optical spectra of various astrophysical plasmas.
In terms of absorption spectra, in the spectral range longward of
912 Å Si II has 8 absorption line complexes connected to the ground term 3s23p 2P![]() .
In photoionized plasmas with electron temperatures (
.
In photoionized plasmas with electron temperatures (![]() )
of the order of 104 K and electron densities (
)
of the order of 104 K and electron densities (![]() )
) ![]() 104 cm-3 the relative optical depths of troughs from the two ground state levels depend on
104 cm-3 the relative optical depths of troughs from the two ground state levels depend on ![]() .
Hence, this dependence can be used as diagnostic
of
.
Hence, this dependence can be used as diagnostic
of ![]() (e.g. Dunn et al. 2009). On this regard, the lines centered at 1814 Å (3s23p 2P
(e.g. Dunn et al. 2009). On this regard, the lines centered at 1814 Å (3s23p 2P![]() - 3s3p2 2D) are particularly convenient because of their unusually small oscillator strengths, such that these, among all other Si II lines,
are the most likely to be in the linear part of the curve of growth and
their column densities can be accurately measured. Unfortunately,
though, the determination of accurate and reliable oscillator strengths
for these transitions is particularly difficult and has been the
subject of much theoretical and experimental efforts.
- 3s3p2 2D) are particularly convenient because of their unusually small oscillator strengths, such that these, among all other Si II lines,
are the most likely to be in the linear part of the curve of growth and
their column densities can be accurately measured. Unfortunately,
though, the determination of accurate and reliable oscillator strengths
for these transitions is particularly difficult and has been the
subject of much theoretical and experimental efforts.
Si II is also prominent in emission spectra of various kinds of objects.
In the upper chromosphere and lower transition region in the Sun and late-type stars line ratios among the Si II 1814 Å multiplet and the intercombination (3s23p 2P![]() - 3s3p2 4P)
multiplet near 2335 Å are potentially useful density diagnostics.
However, until recently the best electron impact collision strengths of
Dufton & Kingston (1991) led to predicted line ratios that disagreed with observations
(Judge et al. 1991). Similarly, theoretical models of emission spectra of Broad Line Regions
of Active Galactic Nuclei fail to reproduce the observed intensities by factors of a few; a problem that was named by Baldwin et al. (1996) the ``Si II disaster''.
- 3s3p2 4P)
multiplet near 2335 Å are potentially useful density diagnostics.
However, until recently the best electron impact collision strengths of
Dufton & Kingston (1991) led to predicted line ratios that disagreed with observations
(Judge et al. 1991). Similarly, theoretical models of emission spectra of Broad Line Regions
of Active Galactic Nuclei fail to reproduce the observed intensities by factors of a few; a problem that was named by Baldwin et al. (1996) the ``Si II disaster''.
Despite considerable theoretical work on oscillator strengths there is still considerable spread in the results, particularly for those transitions of most astronomical interest, such as those of the 1814 Å complex. This is because the upper 2D term of these transitions is made of a mixture of the 3s3p2 and 3s23d configurations, which produce strong cancellation in the oscillator strengths and makes the f-values very difficult to compute. Also for these transitions, there has been much spread in experimental gf-values. Measurements based on the electron beam phase shift method (Curtis & Smith 1974; Savage & Lawrence 1966) could be inaccurate for very long lifetimes. Absolute emission measurements on an arc (Hofmann 1969) are often uncertain owing to the difficult control and calibration of the instrument. Determinations based in comparisons of equivalent widths of the weak 1810 Å lines to stronger lines in astronomical spectra (Shull et al. 1981; Van Buren 1986) are unreliable due to blends and saturation of the stronger lines (Jenkins 1986). The latest, and probably most accurate determination of gf-values for these lines was done with the time-resolved laser-induced fluorescence technique Bergeson & Lawler (1993).
The oscillator strengths for the intercombination transitions (3s23p 2P![]() - 3s3p2 4P) have also been subject of controversy. These transitions arise due to spin-orbit mixing of the metastable term 3s3p2 4P with the 2S, 2P, and 2D terms. The difficulty then comes from the fact that the gf-values
are sensitive to core-valence and core-core correlations, in addition
to the valence-shell effects. The results of some of the most recent
calculations (Froese Fischer et al. 2006) differ from
experimentally measured transition probabilities (Calamai et al. 1993) by
- 3s3p2 4P) have also been subject of controversy. These transitions arise due to spin-orbit mixing of the metastable term 3s3p2 4P with the 2S, 2P, and 2D terms. The difficulty then comes from the fact that the gf-values
are sensitive to core-valence and core-core correlations, in addition
to the valence-shell effects. The results of some of the most recent
calculations (Froese Fischer et al. 2006) differ from
experimentally measured transition probabilities (Calamai et al. 1993) by ![]() 30%.
30%.
But beyond providing accurate oscillator strengths by tailoring atomic structure representations on each type of transition of interest, it is important to try constructing a single representation that yields reasonably accurate energies and oscillator strengths for all levels and transitions considered simultaneously. This is because various practical applications will require such a general atomic representation for subsequent scattering calculations (e.g. electron impact excitation, photoionization, and recombination). One of the most widely used methods for this purpose is based on the Thomas-Fermi-Dirac-Amaldi (TFDA) central potential to generate optimized one-electron orbitals, which represent the atomic structure through configuration interaction (CI) expansions and can also be used for close-coupling representations of the scattering problem. Recently, Bautista (2008) introduced a correction to the TFDA potential that accounts for the effects of electron-electron interactions on the radial wavefunction and yield a considerably improved representation of the system. It is thus interesting to apply this new approach to get the best possible representation of the important Si II system.
In the present paper, to complement and expand the work with the TFDA potential we also compare with the results of the Hartree-Fock Relativistic (HFR), and the multi-configuration Dirac-Fock (MCDF) methods. This general multiplatform approach was successfully employed in our previous studies of the K-shell spectra of Fe, O, Ne, Mg, Si, S, Ar, Ca, and Ni (e.g. Bautista et al. 2003; García et al. 2005; Palmeri et al. 2003a,2008a,b,2003b). This has the advantage that allows for consistency checks and inter-comparison. It also helps to reveal which physical processes are important for any given transition, since these different platforms employ different approaches to, for example, relativistic effects and orthogonal vs. non-orthogonal orbitals.
The present paper is organized as follows: in the next section we describe the calculations of oscillator strengths and transition rates. In Sect. 3 we present the calculations of collision strengths, including some new techniques specifically designed for the present problem. Our discussion of the results and conclusions are presented in Sect. 4.
2 Radiative calculations
The Breit-Pauli Hamiltonian for an N-electron system is given by
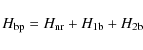
|
(1) |
where
represent the spin-orbit interaction,
usually referred to as the Breit interaction, include, on the one hand, the fine structure terms
The oscillator strengths (f-values) for dipole allowed transitions have equivalent forms in length and velocity gauges as
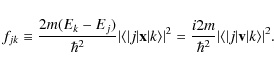
|
(4) |
The radiative rates (A-values) for electric dipole and quadrupole transitions are respectively given in units of s-1 by the expressions
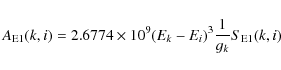
|
(5) |
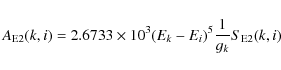
|
(6) |
where S(k,i) is the line strength, gk is the statistical weight of the upper level, and energies are in Rydberg units and lengths in Bohr radii.
Similarly for magnetic dipole and quadrupole transitions, the A-values are
respectively given by
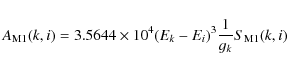
|
(7) |
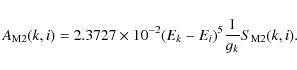
|
(8) |
Due to the strong magnetic interactions in this ion, the magnetic dipole line strength is assumed to take the form
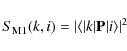
|
(9) |
where
In the present work we employ three different computational packages to study the properties of the strongly correlated configurations 3s23p, 3s3p2, 3s23d, and 3s24s of Si II.
AUTOSTRUCTURE
AUTOSTRUCTURE, an extension by Badnell (1997,1986) of the atomic structure program
SUPERSTRUCTURE (Eissner et al. 1974),
computes fine-structure level energies, radiative and Auger rates in a
Breit-Pauli relativistic framework. Single electron orbitals, Pnl(r), are constructed by diagonalizing the non-relativistic Hamiltonian,
![]() ,
within a statistical Thomas-Fermi-Dirac-Amaldi (TFDA) model potential
,
within a statistical Thomas-Fermi-Dirac-Amaldi (TFDA) model potential
![]() (Eissner & Nussbaumer 1969). The
(Eissner & Nussbaumer 1969). The
![]() scaling parameters are optimized variationally by minimizing a weighted sum of the LS term energies. LS terms are represented by configuration-interaction (CI) wavefunctions of the type:
scaling parameters are optimized variationally by minimizing a weighted sum of the LS term energies. LS terms are represented by configuration-interaction (CI) wavefunctions of the type:
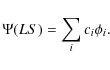
|
(11) |
Bautista (2008) introduced a modification to the TFDA model potential that accounts in part for the effects of electron-electron correlations on the radial wavefunctions by means of additional higher order terms in the potential whose strength is controlled by variational parameters. We will refer to this potential as c-TFDA. This formalism also proposed a new optimization technique of the variational parameters by minimizing the difference between predicted, including spin-orbit coupling and relativistic effects, and experimental term averaged energies. The numerical functional used for this optimization was:
with
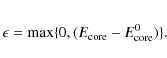
This last term acts as a penalty to the functional whenever the new core energy exceeds that found from the standard TFDA minimization. This numerical functional was modified again for the present work as shown in Sect. 2.2.
HFR
In the Hartree-Fock Relativistic code ( HFR) by Cowan (1981), a set of orbitals are obtained for each electronic configuration by solving the Hartree-Fock equations for the spherically averaged atom. The equations are the result of the application of the variational principle to the configuration average energy. Relativistic corrections are also included in this set of equations, i.e. the Blume-Watson spin-orbit, mass-variation and one-body Darwin terms. The Blume-Watson spin-orbit term comprises the part of the Breit interaction that can be reduced to a one-body operator.
The multi-configuration Hamiltonian matrix is constructed and diagonalized in the ![]() representation
within the framework of the Slater-Condon theory. Each matrix element
is a sum of products of Racah angular coefficients and radial integrals
(Slater and spin-orbit integrals), i.e.
representation
within the framework of the Slater-Condon theory. Each matrix element
is a sum of products of Racah angular coefficients and radial integrals
(Slater and spin-orbit integrals), i.e.
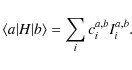
|
(13) |
The radial parameters, Iia,b, can be adjusted to fit the available experimental energy levels in a least-squares approach. The eigenvalues and the eigenstates obtained in this way (ab initio or semi-empirically) are used to compute the wavelength and oscillator strength for each possible transition.
MCDF
The multi-configuration Dirac-Fock (MCDF) method considers the Dirac Hamiltonian for a N-electron atomic system given in au by:
![\begin{displaymath}%
H_{\rm D} \equiv \sum_{i=1}^N \left[c{\bf\alpha}_i \times {...
..._i-1)c^2-{Z\over r_i}\right ]+\sum_{i\ne j}^N {1\over r_{ij}},
\end{displaymath}](/articles/aa/full_html/2009/48/aa13179-09/img41.png)
|
(14) |
where c is the speed of light and
2.1 Energy levels and radiative rates
Our calculations concentrate on the 15 lowest levels, of the Si II system. This is 8 LS terms from configurations 3s23p, 3s3p2, 3s24s, 3s23d, and 3s24p. A Grotrian diagram of the ions is presented in Fig. 1 which shows the levels and the UV optical and intercombination transitions of interest.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13179fig1.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13179-09/Timg44.png)
|
Figure 1: Partial Grotrian diagram of Si II showing the 22 lowest Levels in 8 LS terms and the dipole and intercombination line multiplets observable in the UV spectral region. |
| Open with DEXTER | |
2.1.1 Calculations with HFR
In the physical model adopted in HFR calculations, we suppose that the Si+ ion can be represented by three valence electrons surrounding a Ne-like Si4+ ionic core with ten electrons occupying the 1s22s22p6
closed subshells. The intravalence correlation is then considered by
the explicit introduction, in the model, of the 52 following
configurations: 3s23p + 3s24p + 3s25p + 3s24f + 3s25f + 3s3p3d + 3s3p4d + 3s3p5d + 3s3p4s + 3s3p5s + 3s3d4p + 3s3d5p + 3p24p + 3p25p + 3p24f + 3p25f + 3d24p + 3d25p + 3d24f + 3d25f + 3p3 (odd parity) and 3s3p2 + 3s24s + 3s25s + 3s23d + 3s24d + 3s25d + 3s3p4p + 3s3p5p + 3s3p4f + 3s3p5f + 3s3d2 + 3s4s2 + 3s4p2 + 3s4d2 + 3s4s5s + 3s3d4s + 3s3d5s + 3s3d4d + 3s3d5d + 3p23d + 3p24d + 3p25d + 3p24s + 3p25s + 3p3d4p + 3p4s4p + 3d24s + 3d25s + 3d24d + 3d25d +3d3
(even parity). Core-valence correlation is then considered by including
a core-polarization (CPOL) potential and a correction to the dipole
operator as described in many previous papers (see e.g. Quinet et al. 1999,2002). These corrections are used with a value of the dipole polarizability equal to 0.16 a03, as computed by Johnson et al. (1983) for Si V, and a cut-off radius equal to 0.53 a0 which corresponds to the HFR expectation value of
![]() for the outermost core orbital, i.e. 2p. This method is then
combined with a well-established least-squares optimization of the
radial parameters in order to minimize the discrepancies between the
Hamiltonian eigenvalues and the available experimental energy levels
for the 3s23p, 3s24p, 3s3p2, 3s24s, 3s25s, 3s23d, 3s24d, 3s25d and 3s3p4p configurations.
for the outermost core orbital, i.e. 2p. This method is then
combined with a well-established least-squares optimization of the
radial parameters in order to minimize the discrepancies between the
Hamiltonian eigenvalues and the available experimental energy levels
for the 3s23p, 3s24p, 3s3p2, 3s24s, 3s25s, 3s23d, 3s24d, 3s25d and 3s3p4p configurations.
2.1.2 Calculations with MCDF
Here, we carried out two MCDF calculations. The first one, hereafter
referred to as MCDF1, was focused on our radiative parameters for the
intercombination transitions 3s23p 2P![]() - 3s3p2 4P, and the second one, hereafter referred to as MCDF2, on those of the allowed transitions 3s23p 2P
- 3s3p2 4P, and the second one, hereafter referred to as MCDF2, on those of the allowed transitions 3s23p 2P![]() - 3s3p2 2D.
- 3s3p2 2D.
In MCDF1, CI expansions are built including the valence-valence correlation through single and double excitations from 3s23p J = 1/2, 3/2 + 3s3p2 J = 1/2, 3/2, 5/2 extending the orbital active set up to 5g in 4 steps. The final number of CSFs generated was 2127. For 3 of the steps, we selected an ``extended optimal level'', EOL, optimization option (Dyall et al. 1989; Parpia et al. 1996) on the lowest 5 levels using the same weight for the 5 ASFs. In the first step, no excitation was allowed, the active set was limited up to 3p, and all the core and valence orbitals were variational. The second step consisted in extending the expansion through single and double excitations increasing the active set up to 3d. Here, only the 3d orbital was variational, while freezing all the others to their values of the preceding optimization step. In the third step, the expansions were further extended increasing the active set up to 4f. All n=4 orbitals were optimized while freezing all others in a similar procedure as in the second step. In the final optimization step, only the n=5 were variational freezing all the other orbitals to their preceding step values.
In MCDF2, we used the same procedure as in MCDF1 except that the excitations were from 3s23p J = 1/2, 3/2 + 3s3p2 J = 3/2, 5/2 and the EOL option was selected on the first, second, fifth and sixth levels. Here the final number of CSFs used in the MCDF expansions was 1832.
2.1.3 Calculations with AUTOSTRUCTURE
We performed calculations with various different configurations expansions, starting with models similar to those of previously published work and then evolving to more sophisticated techniques and larger configuration expansions.
Table 1: Configurations included in various expansions used for Si II.
Table 1 presents the configurations included in 7 basic expansions studied. The various configuration expansions (CEs) are named CE1, CE2, ..., CE6 and are tabulated in such a way that each CE includes the configurations of all previous CEs. In other words, CE1 includes the 24 configurations listed at the top of Table 1, CE2 includes all 24 configurations from CE1 plus 2s22p63s24f, CE3 includes the 25 configuration from CE1 and CE2 plus 3 more, and CE6 includes all 48 configurations in the table.
![\begin{figure}
\par\includegraphics[angle=-90,width=17cm,clip]{13179fig2.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13179-09/Timg46.png)
|
Figure 2: Evolution of the gf-values for transitions in Si II from our different calculations AST1, ..., AST9 and comparison with previous determinations. The square points depict our results in the length gauge (blue) and velocity gauge (red). The solid horizontal lines depict experimental determinations by Shull et al. (1981) (magenta), Van Buren (1986) (blue), Schectman et al. (1988) (green), Bergeson & Lawler (1993) (black). The dashed lines depict theoretical results of Froese Fischer et al. (2006), (blue), Tayal (2007) (red), Nahar (1988) (green). |
| Open with DEXTER | |
The rational for these configurations and the progression of various calculations carried is as follows:
- AST1: this calculation uses the expansion CE1 that keeps the 2s and 2p shells closed and promotes the three remaining electrons among orbitals with principal quantum number n = 3-5 and orbital angular momentum l = 0-2. The TFDA potential was used and the orbitals were optimized in the standard AUTOSTRUCTURE procedure minimizing the energies of the lowest 8 LS terms. Fine structure coupling and relativistic corrections are introduced as perturbations after optimizing the orbitals. From this calculation the core energy of the system is -578.40 Ry. Table 1 compares the calculated energies relative to the ground level with experimental values from NIST (2008). The results are rather unsatisfactory with energy differences scattered between -19% and 35%. Even more troublesome are the gf-values that result from this calculation, particularly those for the 1814 Å multiplet, which are considerably overestimated with respect to the experimental determination of Bergeson & Lawler (1993) (see Fig. 2). This is because it is difficult to represent 3s23p and 3s3p2 states simultaneously with orthogonal orbitals, owing to polarization and orbital relaxation effects.
- AST2: for this calculation we use the same expansion CE1 as in AST1 but with the use of the c-TFDA potential of Bautista (2008) optimized against the experimental term energies using the functional of Eq. (12).
This gave a core energy of -578.34 Ry, which is slightly higher
than in AST1. Yet, the calculated energies here agree much better with
experiment than from AST1, with most terms within 5% of experiment
with the exception of the two excited levels 3s23p 2P
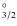 ,
from the ground multiplet, and 3s3p2 4Pj. Together with the changes in calculated energies there are also significant changes in the predicted
gf-values for the 1814 Å and 1531 Å multiplets, as illustrated in Fig. 2.
,
from the ground multiplet, and 3s3p2 4Pj. Together with the changes in calculated energies there are also significant changes in the predicted
gf-values for the 1814 Å and 1531 Å multiplets, as illustrated in Fig. 2.
- AST3: this calculation is just like AST2, but we now add the configurations 3s24f and 3s25f
(i.e. CE2). We find that the f orbitals have an important
effect on increasing the polarizability of configurations that include
d orbitals, such as the 3s3d2, and 3p23d. Thus, by including nf configurations in the expansion we find different optimization for the core. When including these nf orbitals one has to include enough nd configurations
in order to reach convergence in the solution. But, various
configurations such as 3d, 3d2, 4d, and 5d are already
included since CE1. In the course of the calculations we checked
on the contributions of 5d and 5f and they were found to be small.
Thus, we believe that the calculation is nearly converged. In this
calculation the core energy improves to -578.38 Ry and the
agreement between calculated and experimental energies with respect to
the ground level also improves a little. Despite the relatively minor
changes in the calculated energies between this calculation and the
previous one there are large changes in the gf-values for the 1814 Å and 1264 Å multiplets, with a
drop of
 0.8 dex for the former and a rise of
0.8 dex for the former and a rise of 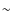 0.9 dex for the latter.
0.9 dex for the latter.
- AST4, AST5, AST6, and AST7:
for these calculations we progressively add new configurations by
opening the 2s and 2p orbitals, with one 2p electron promotions in
AST4 (CE3), two 2p electron promotions in AST5 (CE4), one 1s
electron promotions in AST6 (CE5) and three 2p electron promotions
in AST7 (CE6). By this point the computational time in optimizing
all orbitals of the potential has become exceedingly long, going from a
few minutes in the AST1 calculation to several hours in the
AST7 calculation. For this reason, and with the purpose to see the
effects of increasing CI we did not optimize again the orbitals for
these calculation, but instead chose the same scaling parameters as in
AST3. Despite the large increase in CI in these computations we find no
significant change in either the calculated energies, see Table 2. The calculated core energies also remain constant at -578.38 Ry for AST4, AST5, and AST6 and -578.39 Ry for AST7. The computed f-values
are also unaltered by CI, except for those of the 1814 Å multiplet
which seem to converge asymptotically. Nonetheless, for this and most
of the other transitions the difference between length and velocity
gauges of the f-values is uncomfortably large. It is clear
now that increasing the amount of CI in the calculations beyond that of
the AST7 calculation will not improve the quality of the results.
Instead, we need to turn our attention towards the optimization of the
orbitals.
Table 2: Comparison of level energies (Ry) for Si II.
- AST8: for this calculation we decided to return to the simplest expansion CE1, but
try a different optimization technique. Because the f-values for the 1814 Å multiplet is so sensitive to cancellation in the mixing of the 3s3p2 2D and 3s23d 2D states
it is crucial to reproduce the experimental energies of the levels as
accurately as possible. Thus, we modified the AUTOSTRUCTURE code use an optimization functional of the form
where the sum goes over fine structure energy levels and wi is a user defined weight on different levels. For our calculation we ran this sum for the lowest 15 levels of the Si II system and we weighted the 3s23p 2P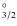 and 3s3p2 2DJ levels
5 times as much as the rest. This kind of optimization provides
much better energies for all levels and nearly exact energies for the 3s23p 2P
and 3s3p2 2DJ levels
5 times as much as the rest. This kind of optimization provides
much better energies for all levels and nearly exact energies for the 3s23p 2P
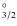 and 3s3p2 2DJ levels
(within 0.2% of experiment). This optimization also provides a
lower core energy than from previous calculations (-578.42 Ry).
Nevertheless, this optimization does not reduce the difference between
length and
velocity forms of the f-values.
and 3s3p2 2DJ levels
(within 0.2% of experiment). This optimization also provides a
lower core energy than from previous calculations (-578.42 Ry).
Nevertheless, this optimization does not reduce the difference between
length and
velocity forms of the f-values.
An alternative optimization functional that is already available in AUTOSTRUCTURE is based on the differences between length and velocity f-values. This, however, does not work because it leaves the level energies to change way off from experiment.
Then, we define a combined functional of the form
where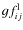 and
and
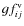 are the length and velocity forms of the gf-value for the transition
are the length and velocity forms of the gf-value for the transition 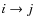 .
An optimization of this kind heavily weighted on the gf-values
for the 1260 Å multiplet yields length and velocity values in very
close agreement with each other. These results also agree very well
with the experimental determination of Bergeson & Lawler (1993). Unfortunately, the obtained gf-values
for transitions involving higher terms seem to deteriorate. This is to
be expected, as the small expansion used here misses important
core-valence and core-core correlations.
.
An optimization of this kind heavily weighted on the gf-values
for the 1260 Å multiplet yields length and velocity values in very
close agreement with each other. These results also agree very well
with the experimental determination of Bergeson & Lawler (1993). Unfortunately, the obtained gf-values
for transitions involving higher terms seem to deteriorate. This is to
be expected, as the small expansion used here misses important
core-valence and core-core correlations.
- AST9: for this last calculation we use the largest expansion CE6 and optimize the orbitals as in AST8. For a model expansion of this size numerical optimization becomes challenging, and the code took 4 days to do so. The resulting energies are slightly better than in the previous calculation, and the core energy is predicted at -572.41 Ry. It is found that the f-values in the length gauge for the 1814 Å multiplet remain in good agreement with the experiment of Bergeson & Lawler (1993) although the velocity f-value departed somewhat. Interestingly, for these transitions the present velocity f-value is lower than the length f-value, contrary to what was seen in previous calculations. The present difference between the two forms of the f-value probably owes to the need of finer optimization of the orbitals, which became computationally prohibitive for the large CI expansion used here. Another interesting set of f-values are those for the 1260 Å multiplet, which in the present calculation result somewhat higher and with greater difference between length and velocity than from previous calculations. The present result seems to favor the experimental determination of Schectman et al. (1988), while the results of previous calculations seemed very stable and in good agreement with Froese Fischer et al. (2006) and Tayal (2007).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13179fig3.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13179-09/Timg54.png)
|
Figure 3: Evolution of the gf-values for intercombination transition in Si II from our different calculations AST1, ..., AST9 and comparison with experimental values of Calamai et al. (1993). The square points depict our results in the length gauge (blue) and velocity gauge (red). The experimental vales are given by the horizontal solid line, with quoted errors given by dashed lines. |
| Open with DEXTER | |
At this point is worth pointing out the detailed study of Dufton et al. (1992) on the LS f-value for the 1814 Å transition. They found that in dealing with the cancelation effects from contributions from the 3s3p2 2D and 3s23d 2D states
one must pay attention to the calculated energy difference between
these states. In this sense we notice that our prefer calculation AST8
and AST9 yield energy separations for the 3s3p2 2D and 3s23d 2D states that differ by
![]() %
from experiment, in contrast with calculations AST3 through AST7 that
reproduce these energy separation significantly better. However,
getting exact energies is neither sufficient nor guarantee of resulting
accurate gf-vaues. Inspection of Table 1 of Dufton et al. (1992) shows that essentially the same gf-value
can obtained when the energy difference with respect to experiment was
less than 2% and nearly 11%. By contrast, calculations that
predicted energies differing from experiment by 5 and 7% got gf-values that were off by roughly a factor of 3. Moreover, we are mostly concerned with the fine structure gf-values and for that we also need accurate energies for the J resolved levels of the 3s23p 2P and 3s3p2 2D terms
and these are best reproduced by the AST8 and AST9 calculations,
as opposed to the AST7 calculation that underestimates the energy
of the 3s23p 2P3/2 level by 15%.
%
from experiment, in contrast with calculations AST3 through AST7 that
reproduce these energy separation significantly better. However,
getting exact energies is neither sufficient nor guarantee of resulting
accurate gf-vaues. Inspection of Table 1 of Dufton et al. (1992) shows that essentially the same gf-value
can obtained when the energy difference with respect to experiment was
less than 2% and nearly 11%. By contrast, calculations that
predicted energies differing from experiment by 5 and 7% got gf-values that were off by roughly a factor of 3. Moreover, we are mostly concerned with the fine structure gf-values and for that we also need accurate energies for the J resolved levels of the 3s23p 2P and 3s3p2 2D terms
and these are best reproduced by the AST8 and AST9 calculations,
as opposed to the AST7 calculation that underestimates the energy
of the 3s23p 2P3/2 level by 15%.
On the other hand, it is also known that in computing gf-values one may not rely only on the agreement between length and velocity values, because such an criterium can be misleading if the model potential is oversimplified. Nonetheless, we believe that the agreement between length and velocity results in our calculations AST8 and, particularly AST9 is very significant. AST9 uses the largest CI expansion that we could handle, which the inner core orbitals to account for polarization. In addition, this calculation uses the c-TFDA potential to account for additional electron-electron correlation. Thus AST9 employs the most complex and complete potential that we can build at this time, then the good agreement between length and velocity seems meaningful.
Now we look at the results for the intercombination transitions 3s23p 2P![]() -3s3p2 4Pj'.
These lines, seen in emission in the 2328-2350 Å spectral range,
are very useful density diagnostics in a variety of astronomical
sources. Though, computation of accurate transition rates, A-values, for these lines is difficult because the transitions are induced by mixing between the 4P and even parity doublet states. Hence, the calculated A-values
for the intercombination transitions depend critically on the quality
of the representation of those even parity doublet states. Figure 3 shows the evolution of the calculated gf-values
in length and velocity forms from our calculations together with the
results of other authors and the experimental determinations of Calamai et al. (1993).
Here we plot our results in the length and velocity gauges, although none of previous
authors present similar comparisons. It is clear, though, that there are considerable discrepancies
between the two gauges, being the length form of the gf-values typically in better agreement
with experiment. Other authors, like Tayal (2007) do not even quote their results in the velocity gauge. Indeed, the velocity form of the gf-value is typically less stable numerically,
since it depends on the first derivative of the radial wavefunction. Thus, we disregard the
velocity gf-values for subsequent analysis. The present gf-values from AUTOSTRUCTURE agree within 0.2 dex with experimental determinations of Calamai et al. (1993),
and the agreement between
MCDF results and experiment is even better, within 0.1 dex.
On the other hand, the HFR results seem as accurate as MCDF for
some transitions, but significantly discrepant for others. The results
of Tayal (2007) and Froese Fischer et al. (2006), using a multiconfiguration Hartree-Fock, are comparable in quality to our HFR results. The results of Dufton & Kingston (1991), based on the multiconfiguration Hartree-Fock method, and Nussbaumer (1977), from the use of the TFDA potential, seem to be of inferior quality.
-3s3p2 4Pj'.
These lines, seen in emission in the 2328-2350 Å spectral range,
are very useful density diagnostics in a variety of astronomical
sources. Though, computation of accurate transition rates, A-values, for these lines is difficult because the transitions are induced by mixing between the 4P and even parity doublet states. Hence, the calculated A-values
for the intercombination transitions depend critically on the quality
of the representation of those even parity doublet states. Figure 3 shows the evolution of the calculated gf-values
in length and velocity forms from our calculations together with the
results of other authors and the experimental determinations of Calamai et al. (1993).
Here we plot our results in the length and velocity gauges, although none of previous
authors present similar comparisons. It is clear, though, that there are considerable discrepancies
between the two gauges, being the length form of the gf-values typically in better agreement
with experiment. Other authors, like Tayal (2007) do not even quote their results in the velocity gauge. Indeed, the velocity form of the gf-value is typically less stable numerically,
since it depends on the first derivative of the radial wavefunction. Thus, we disregard the
velocity gf-values for subsequent analysis. The present gf-values from AUTOSTRUCTURE agree within 0.2 dex with experimental determinations of Calamai et al. (1993),
and the agreement between
MCDF results and experiment is even better, within 0.1 dex.
On the other hand, the HFR results seem as accurate as MCDF for
some transitions, but significantly discrepant for others. The results
of Tayal (2007) and Froese Fischer et al. (2006), using a multiconfiguration Hartree-Fock, are comparable in quality to our HFR results. The results of Dufton & Kingston (1991), based on the multiconfiguration Hartree-Fock method, and Nussbaumer (1977), from the use of the TFDA potential, seem to be of inferior quality.
Table 3:
![]() values for transitions among the 15 lowest levels in Si II.
values for transitions among the 15 lowest levels in Si II.
It seems clear that no one calculation among those performed here and
those reported by other authors can provide ultimate accuracy gf-values
for all transitions simultaneously. Like with the different
calculations, there is significant scatter among the results of various
experimental determinations. Thus, in order to provide the most
reliable set of gf-values possible we take the statistical average among all theoretical results, i.e. our present results from AST8 and
AST9 and those of other authors. In computing the average we discard values that depart by more than 3![]() from the average, where
from the average, where ![]() is the statistical dispersion of the data. Both, length and velocity gf-values, are taken with equal weights in the average. In the case of the
recombination transitions and the 1814 Å multiplet we also include in the averages the experimental data from Calamai et al. (1993) and Bergeson & Lawler (1993)
respectively with twice as much weight as the theoretical values.
It is noted that our calculation AST8 that uses the smaller
configuration expansion is very well optimized on the lowest energy
terms, for instance the 3s23p 2P
is the statistical dispersion of the data. Both, length and velocity gf-values, are taken with equal weights in the average. In the case of the
recombination transitions and the 1814 Å multiplet we also include in the averages the experimental data from Calamai et al. (1993) and Bergeson & Lawler (1993)
respectively with twice as much weight as the theoretical values.
It is noted that our calculation AST8 that uses the smaller
configuration expansion is very well optimized on the lowest energy
terms, for instance the 3s23p 2P![]() and 3s3p2 2D terms, but it deteriorates rapidly for higher excitation terms. Figure 2 depicts our recommended gf-values
for every transition together with the statistical dispersion, which is
probably representative of the true uncertainty. In Table 3
we show our results for transitions among the lowest 15 levels of
the ion from the AST9, AST9, HFR, and MCDF calculations. The AUTOSTRUCTURE
results are given in length and velocity gauges and the
MCDF results are given in the corresponding Coulomb and Babushkin
gauges. In the last column of the table are our recommended values and
estimated uncertainties.
and 3s3p2 2D terms, but it deteriorates rapidly for higher excitation terms. Figure 2 depicts our recommended gf-values
for every transition together with the statistical dispersion, which is
probably representative of the true uncertainty. In Table 3
we show our results for transitions among the lowest 15 levels of
the ion from the AST9, AST9, HFR, and MCDF calculations. The AUTOSTRUCTURE
results are given in length and velocity gauges and the
MCDF results are given in the corresponding Coulomb and Babushkin
gauges. In the last column of the table are our recommended values and
estimated uncertainties.
3 Collision strengths
The collision strengths for electron impact excitation are computed with the ICFT Breit-Pauli R-matrix package ( BPRM) based on the close-coupling approximation of Burke & Seaton (1971) whereby the wavefunctions for states of an N-electron target and a colliding electron with total angular momentum and parity ![]() are expanded in terms of the target eigenfunctions
are expanded in terms of the target eigenfunctions
The functions
One-body Breit-Pauli relativistic corrections have been introduced in the R-matrix suite by Scott & Taylor (1982); Scott & Burke (1980). Inter-channel coupling is equivalent to CI in the atomic structure context.
Because of the large number of configurations and close coupling states in the representation of the target ion the scattering calculation had to be done in LS-coupling. Then, fine structure collision strengths were obtained by means of the intermediate coupling frame transformation (ICFT) method of Griffin et al. (1998).
Since we have produced a large number of target expansion to
study the quality and the wavefunction it is interesting to see the
effects of these various representations on the collision strengths.
This comparison may be used to asses the accuracy of the collision
strengths. Thus, we performed three different scattering calculations
using target orbitals from models AST1, AST8, and AST9. For the first
two calculations we included only the lowest 12 LS terms in the closed
coupling expansion, while for the calculation with the
AST9 target, the most accurate and extensive, we included the
lowest 43 LS terms. All calculations explicitly include
partial waves from states with ![]() and multiplicity 1, 3, 5, and 7. The final collision strengths are produced with an energy resolution of 6
and multiplicity 1, 3, 5, and 7. The final collision strengths are produced with an energy resolution of 6 ![]() 10-5 Ry.
10-5 Ry.
Figure 4 compares the
LS-coupling collision strengths obtained from the target
expansions AST1, AST8, and AST9 for excitation from the ground
term 3s23p 2P![]() to the first four excited terms 3s3p2 4P, 3s3p2 2D, 3s24s 2S, and 3s3p2 2S.
to the first four excited terms 3s3p2 4P, 3s3p2 2D, 3s24s 2S, and 3s3p2 2S.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13179fig4.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13179-09/Timg72.png)
|
Figure 4: Comparison of collision strengths in LS coupling for excitations from the ground term to the first five excite terms in Si II computed with approximations AST1 ( left panels), AST8 ( middle panels), and AST9 ( right panels). |
| Open with DEXTER | |
Table 4:
Comparison of Maxwellian averaged collision strengths in LS-coupling for excitation from the ground term 3s23p 2P![]() .
.
The results, in terms of Maxwellian averaged effective collision
strengths, of AST1, AST8, and AST9 are also compared in Table 4 for excitations from the ground term, 3s23p 2P![]() ,
to the first five excited terms of Si II.
Here, the third column presents the effective collision strengths from
our best model AST9 and columns fourth and five present the
percentage difference from these as obtained from models AST1 and
AST8 respectively. These comparisons are done for temperatures between
5000 K and 20 000 K. Excitation rates for higher
temperatures are
of little practical interest because under these conditions the ionic
fraction in Si II
is
too small. The are two general characteristics of collision strengths
that could lead to variations in their thermal averages: (i) the
background and resonances in the near threshold region, which determine
the low temperature (
,
to the first five excited terms of Si II.
Here, the third column presents the effective collision strengths from
our best model AST9 and columns fourth and five present the
percentage difference from these as obtained from models AST1 and
AST8 respectively. These comparisons are done for temperatures between
5000 K and 20 000 K. Excitation rates for higher
temperatures are
of little practical interest because under these conditions the ionic
fraction in Si II
is
too small. The are two general characteristics of collision strengths
that could lead to variations in their thermal averages: (i) the
background and resonances in the near threshold region, which determine
the low temperature (
![]() )
Maxwellian averaged collision strengths and
depend on the coupling of the target ion with the continuum; and
(ii) the slope of the continuum towards high energies, which in
dipole allowed transitions depend linearly on the oscillator
strength and consequently on the quality of the target representation.
It is interesting to see that the results from AST1 and AST9 agree
rather well in terms of the qualitative shape of the collision
strengths and the quantitative Maxwellian averaged rates, within
)
Maxwellian averaged collision strengths and
depend on the coupling of the target ion with the continuum; and
(ii) the slope of the continuum towards high energies, which in
dipole allowed transitions depend linearly on the oscillator
strength and consequently on the quality of the target representation.
It is interesting to see that the results from AST1 and AST9 agree
rather well in terms of the qualitative shape of the collision
strengths and the quantitative Maxwellian averaged rates, within
![]() ,
except for the 3s23p 2P
,
except for the 3s23p 2P![]() -3s3p2 2S transition. This is in contrast to the large differences in gf-values for essentially all transitions among levels of the N-electron Si II target.
The good agreement in collision strengths is because these are dominated by bound-continuum couplings of the (N+1)-electron system, which seems to be well represented by the large amount CI in the close coupling expansion.
-3s3p2 2S transition. This is in contrast to the large differences in gf-values for essentially all transitions among levels of the N-electron Si II target.
The good agreement in collision strengths is because these are dominated by bound-continuum couplings of the (N+1)-electron system, which seems to be well represented by the large amount CI in the close coupling expansion.
On the other hand, the target expansion AST8 does yield a different lay
out of resonances on the collision strengths. In addition,
AST8 yields steeper rises in the background collision strengths
for excitation to the 3s24s 2S level
and higher levels. This translates into effective collision strengths
from AST8 that are systematically lower than those from AST9 by as much
as
![]() .
.
It is expected that our results from the AST9 expansion
should be the most accurate due to the good quality of the target
representation and the large amount of CI included for the (N+1)-electron
system. Nonetheless, the comparison with results of various target
representation allow us to asses the uncertainties in the collision
strengths to
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13179fig5.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13179-09/Timg76.png)
|
Figure 5:
Collision strengths in JJ-coupling for transitions 3s23p 2P
|
| Open with DEXTER | |
Figure 5 shows the collision strengths for a sample of forbidden, intercombination, and dipole transitions. We chose the same transitions as in Tayal (2008) for direct comparison with that work. Although the collision strengths from both calculations are roughly similar, there are quantitative differences between the two sets in terms of resonance structures and absolute level of the background. It is apparent that the present collision strengths should yield Maxwellian averages somewhat lower than those of Tayal.
Table 5: Comparison of Maxwellian averaged collision strengths in JJ-coupling from present calculation (Present), Tayal (2008; Tayal), and Dufton & Kingston (1991; DK).
In Table 5 we compare the present fine structure Maxwellian averaged collision strengths with those of Tayal (2008) and Dufton & Kingston (1991). For most transitions our results are
![]() lower
than those of Tayal, while the results of Dufton & Kingston lie
inbetween those two. That our results are somewhat lower than those of
Dufton & Kingston can be understood from the much larger
close coupling expansion used in the present work. As more
scattering channels are open in the calculation, the flow of electrons
is redistributed and the collision strength among low lying levels
tends to converge to lower values. The source of the differences found
with respect to Tayal are less clear, and seems to be due to
differences in computational approach used, i.e. between the
orthogonal and non-orthogonal R-matrix methods.
lower
than those of Tayal, while the results of Dufton & Kingston lie
inbetween those two. That our results are somewhat lower than those of
Dufton & Kingston can be understood from the much larger
close coupling expansion used in the present work. As more
scattering channels are open in the calculation, the flow of electrons
is redistributed and the collision strength among low lying levels
tends to converge to lower values. The source of the differences found
with respect to Tayal are less clear, and seems to be due to
differences in computational approach used, i.e. between the
orthogonal and non-orthogonal R-matrix methods.
4 Conclusions
We have carried out extensive calculations of transitions rates and collision strengths for electron impact excitation for the lowest 12 levels of the astrophysically important Si II ion.
In the calculation of radiative data, we paid special attention to the
weak dipole allowed and intercombination transitions, which are of
particular interest for plasma diagnostics. Determination of accurate
data for these transitions is particularly challenging, therefore we
studied the effects of valence-valence, valence-core, and core-core
interactions with three different methods, i.e. MCDF, HFR, and the
central potential method implemented in AUTOSTRUCTURE. With MCDF we could only include valence-valence correlations, as opening of the n=2 core resulted in a large number of states that could not be managed with the computer code GRASP. For this reason,
we were able to obtain accurate transition rates for the 3s23p 2P![]() -3s3p2 4P intercombination transitions only. Both HFR and AUTOSTRUCTURE
allowed us to investigate valence-core and core-core interaction by
building very large configuration expansions. The accuracy of AUTOSTRUCTURE calculations were significantly improved by the use of the c-TFDA potential of Bautista (2008)
and a new technique for optimizing the variational parameters of this
potential. This optimization technique takes into account the
differences between length and velocity gauges of the gf-values, in addition to the accuracy of predicted energy levels. Our most accurate gf-values
were then compared with previous theoretical and experimental
determinations. From these comparisons we derive a recommended set of gf-values and estimate their uncertainties.
-3s3p2 4P intercombination transitions only. Both HFR and AUTOSTRUCTURE
allowed us to investigate valence-core and core-core interaction by
building very large configuration expansions. The accuracy of AUTOSTRUCTURE calculations were significantly improved by the use of the c-TFDA potential of Bautista (2008)
and a new technique for optimizing the variational parameters of this
potential. This optimization technique takes into account the
differences between length and velocity gauges of the gf-values, in addition to the accuracy of predicted energy levels. Our most accurate gf-values
were then compared with previous theoretical and experimental
determinations. From these comparisons we derive a recommended set of gf-values and estimate their uncertainties.
We then proceed to compute electron impact excitation collision strengths with the R-matrix
method. We do so by using various of the targets representations made
from the previous calculations and compare the results. This allows us
to identify the physical effects that affect the
accuracy of the computed collision strengths. We also compare our
results with those of previous calculations. The present results agree
reasonably well with those of Dufton & Kingston (1991), who also used an orthogonal R-matrix
method but with a much smaller close coupling expansion. On the other
hand, the present results for Maxwellian averaged collision strengths
are systematically lower than those of the recent calculation of Tayal (2008) using a non-orthogonal R-matrix method. The reasons for these differences, that typically amount to
![]() ,
are unclear. We argue that
the source of this difference could be in the non-orthogonal R-matrix approach.
,
are unclear. We argue that
the source of this difference could be in the non-orthogonal R-matrix approach.
Tables 6 and 7 containing the present gf-values, A-values,
and effective collision strengths are available in electronic form. The
data and atomic model are also to become available through the TIPTOP![]() database and the XSTAR database Bautista & Kallman (2001).
database and the XSTAR database Bautista & Kallman (2001).
M.A.B. acknowledges financial support from grants from the NASA Astronomy and Physics Research and Analysis Program (award Award NNX09AB99G) and the Space Telescope Science Institute (project GO-11745). Financial support from the Belgian F.R.S.-FNRS is also acknowledged by two of us (P.Q. and P.P.) who are, respectively, Senior Research Associate and Research Associate of this organization.
References
- Badnell, N. R. 1986, J. Phys. B, 19, 3827 [NASA ADS] [CrossRef]
- Badnell, N. R. 1997, J. Phys. B, 30, 1 [NASA ADS] [CrossRef]
- Baldwin, J. A., Ferland, G. J., Korista, K., et al. 1996, ApJ, 461, 664 [NASA ADS] [CrossRef]
- Bautista, M. A. 2008, J. Phys. B: Atom. Mol. Opt. Phys., 41, 065701 [CrossRef]
- Bautista, M. A., & Kallman, T. R. 2001, ApJS, 134, 139 [NASA ADS] [CrossRef]
- Bautista, M. A., Mendoza, C., Kallman, T. R., & Palmeri, P. 2003, A&A, 403, 339 [NASA ADS] [EDP Sciences] [CrossRef]
- Bergeson, S. D., & Lawler, J. E. 1993, ApJ, 414, L137 [NASA ADS] [CrossRef]
- Berrington, K. A., Burke, P. G., Butler, K., et al. 1987, J. Phys. B, 20, 6379 [NASA ADS] [CrossRef]
- Berrington, K. A., Burke, P. G., Chang, J. J., et al. 1974, Comput. Phys. Commun., 8, 149 [NASA ADS] [CrossRef]
- Berrington, K. A., Burke, P. G., Le Dourneuf, M., et al. 1978, Comput. Phys. Commun., 14, 367 [NASA ADS] [CrossRef]
- Berrington, K. A., Burke, P. G., Eissner, W., et al. 1995, Comput. Phys. Commun., 92, 290 [NASA ADS] [CrossRef]
- Burke, P. G., & Seaton, M. J. 1971, Meth. Comp. Phys., 10, 1
- Calamai, A. G., Smith, P. L., & Bergeson, S. D. 1993, ApJ, 415, L59 [NASA ADS] [CrossRef]
- Cowan, R. D. 1981, The Theory of Atomic Structure and Spectra (Berkeley, CA: University of California Press)
- Curtis, L. J., & Smith, W. H. 1974, Phys. Rev. A, 9, 1537 [NASA ADS] [CrossRef]
- Drake, G. W. F. 1971, Phys. Rev. A, 3, 908 [NASA ADS] [CrossRef]
- Dufton, P. L., & Kingston, A. E. 1991, MNRAS, 248, 827 [NASA ADS]
- Dufton, P. L., Keenan, F. P., Hibbert, A., Ojha, P. C., & Stafford, R. P. 1992, ApJ, 387, 414 [NASA ADS] [CrossRef]
- Dunn, J. P., Bautista, M. A., Arav, N., et al. 2009, ApJ, submitted
- Dyall, K. G., Grant, I. P., Johnson, C. T., Parpia, F. A., & Plummer, E. P. 1989, Comput. Phys. Commun., 55, 425 [NASA ADS] [CrossRef]
- Eissner, W., & Nussbaumer, H. 1969, J. Phys. B, 2, 1028 [NASA ADS] [CrossRef]
- Eissner, W., Jones, M., & Nussbaumer, H. 1974, Comput. Phys. Commun., 8, 270 [NASA ADS] [CrossRef]
- Froese Fischer, C., Tachiev, G., & Irimia, A. 2006, At. Data Nucl. Data Tables, 92, 607 [NASA ADS] [CrossRef]
- García, J., Mendoza, C., Bautista, M. A., et al. 2005, ApJS, 158, 68 [NASA ADS] [CrossRef]
- Griffin, D. C., Badnell, N. R., & Pindzola, M. S. 1998, J. Phys. B. At. Mol. Opt. Phys, 31, 3713 [NASA ADS] [CrossRef]
- Hofmann, W. 1969, Z. Nat., 24, 990 [NASA ADS]
- Jenkins, E. B. 1986, ApJ, 304, 739 [NASA ADS] [CrossRef]
- Johnson, W. R., Kolb, D., & Huang, K. N. 1983, At. Data Nucl. Data Tables, 28, 333 [NASA ADS] [CrossRef]
- Jönsson, P., He, X., Froese Fischer, C., & Grant, I. P. 2007, Comput. Phys. Commun., 177, 597 [NASA ADS] [CrossRef]
- Judge, P. G., Carpenter, K. G., & Harper, G. M. 1991, MNRAS, 253, 123 [NASA ADS]
- Luo, D., Pradhan, A. K., & Shull, J. M. 1988, ApJ, 335, 498 [NASA ADS] [CrossRef]
- Nahar, S. N. 1988, At. Data Nucl. Data Tables, 68, 83
- http://physics.nist.gov/PhysRefData/ASD/levels_form.html
- Nussbaumer, H. 1977, A&A, 58, 291 [NASA ADS]
- Palmeri, P., Mendoza, C., Kallman, T. R., & Bautista, M. A. 2003a, A&A, 403, 1175 [NASA ADS] [EDP Sciences] [CrossRef]
- Palmeri, P., Mendoza, C., Kallman, T. R., Bautista, M. A., & Meléndez, M. 2003b, A&A, 410, 359 [NASA ADS] [EDP Sciences] [CrossRef]
- Palmeri, P., Quinet, P., Mendoza, C., et al. 2008a, ApJS, 177, 408 [NASA ADS] [CrossRef]
- Palmeri, P., Quinet, P., Mendoza, C., et al. 2008b, ApJS, 179, 542 [NASA ADS] [CrossRef]
- Parpia, F. A., Froese Fischer, C., & Grant, I. P. 1996, Comput. Phys. Commun., 94, 249 [NASA ADS] [CrossRef]
- Quinet, P., Palmeri, P., Biémont, E., et al. 1999, MNRAS, 307, 934 [NASA ADS] [CrossRef]
- Quinet, P., Palmeri, P., Biémont, E., et al. 2002, J. Alloys Comp., 344, 255 [CrossRef]
- Savage, B. D., & Lawrence, G. M. 1966, ApJ, 146, 940 [NASA ADS] [CrossRef]
- Schectman, R. M., Povolny, H. S., & Curtis, L. J. 1988, ApJ, 504, 921 [NASA ADS] [CrossRef]
- Scott, N. S., & Burke, P. G. 1980, J. Phys. B, 13, 4299 [NASA ADS] [CrossRef]
- Scott, N. S., & Taylor, K. T. 1982, Comput. Phys. Commun., 25, 349 [NASA ADS]
- Shull, J. M., Snow, T. P., & York, D. G. 1981, ApJ, 246, 549 [NASA ADS] [CrossRef]
- Tayal, S. S. 2007, J. Phys. B: Atom. Mol. Opt. Phys., 40, 2551 [NASA ADS] [CrossRef]
- Tayal, S. S. 2008, ApJS, 179, 534 [NASA ADS] [CrossRef]
- Van Buren, D. 1986, ApJ, 311, 400 [NASA ADS] [CrossRef]
Footnotes
- ... II
![[*]](/icons/foot_motif.png)
- Tables 6 and 7 containing the present gf-values, A-values, and effective collision strengths are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?J/A+A/508/1527
- ...
TIPTOP
![[*]](/icons/foot_motif.png)
- http://heasarc.gsfc.nasa.gov/topbase
All Tables
Table 1: Configurations included in various expansions used for Si II.
Table 2: Comparison of level energies (Ry) for Si II.
Table 3:
![]() values for transitions among the 15 lowest levels in Si II.
values for transitions among the 15 lowest levels in Si II.
Table 4:
Comparison of Maxwellian averaged collision strengths in LS-coupling for excitation from the ground term 3s23p 2P![]() .
.
Table 5: Comparison of Maxwellian averaged collision strengths in JJ-coupling from present calculation (Present), Tayal (2008; Tayal), and Dufton & Kingston (1991; DK).
All Figures
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13179fig1.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13179-09/Timg44.png)
|
Figure 1: Partial Grotrian diagram of Si II showing the 22 lowest Levels in 8 LS terms and the dipole and intercombination line multiplets observable in the UV spectral region. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=17cm,clip]{13179fig2.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13179-09/Timg46.png)
|
Figure 2: Evolution of the gf-values for transitions in Si II from our different calculations AST1, ..., AST9 and comparison with previous determinations. The square points depict our results in the length gauge (blue) and velocity gauge (red). The solid horizontal lines depict experimental determinations by Shull et al. (1981) (magenta), Van Buren (1986) (blue), Schectman et al. (1988) (green), Bergeson & Lawler (1993) (black). The dashed lines depict theoretical results of Froese Fischer et al. (2006), (blue), Tayal (2007) (red), Nahar (1988) (green). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13179fig3.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13179-09/Timg54.png)
|
Figure 3: Evolution of the gf-values for intercombination transition in Si II from our different calculations AST1, ..., AST9 and comparison with experimental values of Calamai et al. (1993). The square points depict our results in the length gauge (blue) and velocity gauge (red). The experimental vales are given by the horizontal solid line, with quoted errors given by dashed lines. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13179fig4.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13179-09/Timg72.png)
|
Figure 4: Comparison of collision strengths in LS coupling for excitations from the ground term to the first five excite terms in Si II computed with approximations AST1 ( left panels), AST8 ( middle panels), and AST9 ( right panels). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13179fig5.eps}
\end{figure}](/articles/aa/full_html/2009/48/aa13179-09/Timg76.png)
|
Figure 5:
Collision strengths in JJ-coupling for transitions 3s23p 2P
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.