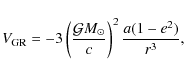| Issue |
A&A
Volume 507, Number 2, November IV 2009
|
|
|---|---|---|
| Page(s) | 1053 - 1065 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200912878 | |
| Published online | 15 September 2009 | |
A&A 507, 1053-1065 (2009)
Constructing the secular architecture of the solar system II: the terrestrial planets
R. Brasser1 - A. Morbidelli1 - R. Gomes2 - K. Tsiganis3 - H. F. Levison4
1 - Dep. Cassiopee, University of Nice - Sophia Antipolis, CNRS, Observatoire de la Côte d'Azur, 06304 Nice, France
2 - Observatório Nacional, Rio de Janeiro, RJ, Brazil
3 - Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
4 - Southwest Research Institute, Boulder, CO, USA
Received 13 July 2009 / Accepted 31 August 2009
Abstract
We investigate the dynamical evolution of the terrestrial planets
during the planetesimal-driven migration of the giant planets.
A basic assumption of this work is that giant planet migration
occurred after the completion of terrestrial planet formation, such as
in the models that link the former to the origin of the late heavy
bombardment. The divergent migration of Jupiter and Saturn causes the g5 eigenfrequency to cross resonances of the form g5=gk with k
ranging from 1 to 4. Consequently these secular resonances
cause large-amplitude responses in the eccentricities of the
terrestrial planets if the amplitude of the g5 mode in Jupiter is similar to the current one. We show that the resonances g5=g4 and g5=g3
do not pose a problem if Jupiter and Saturn have a fast approach and
departure from their mutual 2:1 mean motion resonance. On the
other hand, the resonance crossings g5=g2 and g5=g1 are more of a concern: they tend to yield a terrestrial system incompatible with the current one, with amplitudes of the g1 and g2 modes
that are too large. We offer two solutions to this problem. The first
solution states that a secular resonance crossing can also damp the
amplitude of a Fourier mode if the latter is large originally. We show
that the probability of the g5=g2 resonance damping a primordially excited g2 mode in the Earth and Venus is approximately 8%. Using the same mechanism to also ensure that the g5=g1 resonance keeps the amplitude of the g1 mode
in Mercury within 0.4 reduces the overall probability to
approximately 5%. However, these numbers may change for different
initial excitations and migration speeds of the giant planets.
A second scenario involves a ``jumping Jupiter'' in which
encounters between an ice giant and Jupiter, without ejection of the
former, cause the latter to migrate away from Saturn much faster than
if migration is driven solely by encounters with planetesimals. In this
case, the g5=g2 and g5=g1 resonances
can be jumped over, or occur very briefly. We show that, in this case,
the terrestrial system can have dynamical properties comparable to what
is exhibited today. In the framework of the Nice model, we estimate
that the probability that Jupiter had this kind of evolution is
approximately ![]() .
.
Key words: solar system: formation - planets and satellites: formation
1 Introduction
In this paper we continue our effort to understand the origin of the orbital architecture of the planets of the solar system. In a previous work (Morbidelli et al. 2009), which is henceforth called Paper I, we analysed the secular architecture of the outer solar system and concluded that, in addition to radial migration, encounters between Saturn and one of the ice giants needed to have occurred in order to explain the current properties of the secular dynamics of the outer solar system. Here we investigate the orbital evolution of the terrestrial planets during the changes that occurred in the outer solar system.
A prerequisite for this study is a discussion of whether or not the terrestrial planets existed at the time the giant planets changed their orbital architecture. According to our best models (Chambers & Wetherill 1998; Agnor et al. 1999; Chambers 2001; Raymond et al. 2004, 2005, 2006, 2007; O'Brien et al. 2006; Kenyon & Bromley 2006), the terrestrial planets formed by collisions among a population of intermediate objects called planetary embryos, with masses of the order of 0.01-0.1 Earth masses. This process should have lasted several tens of millions to a hundred million years, in agreement with modern results from the analysis of radioactive chronometers (Touboul et al. 2007; Allègre et al. 2008). In contrast, the giant planets had to have formed in a few million years; otherwise, they could not have trapped the gas from the primordial solar nebula, which typically disappears on this timescale (e.g. Haisch et al. 2001). Once triggered, the migration and the other changes in the orbital structure of the giant planets typically take a few tens of million years (Gomes et al. 2004). Putting all these timescales together, it is legitimate to think that, by the time the terrestrial planets had completed their formation, the giant planets were already on their current orbits. If this is indeed the case, then there is no object for the present study.
However, there is an emerging view that the re-organisation of the orbital structure of the giant planets might have had a delayed start (Gomes et al. 2005; Strom et al. 2005; see also Levison et al. 2001) and therefore it might have postdated the formation of the terrestrial planets. The reason to think so is that the terrestrial planets underwent a late heavy bombardment (LHB) of small bodies. The temporal evolution of this bombardment is still the subject of debate (see for instance Hartman et al. 2000, for a review), but the majority of the evidence points to a cataclysmic nature of the LHB, i.e. to a spike in the cratering rate occurring approximately 3.85 Gyr ago (e.g. Ryder et al. 2000) i.e. approximately 600 Myr after terrestrial planet formation. If this is true, then something ``major'' had to happen in the solar system at that time, and the late change in the orbital structure of the giant planets seems to be a plausible explanation (although, see Chambers, 2007, for an alternative scenario that does not involve a change in the giant planets' orbits).
The study of the evolution of the terrestrial planets during the putative changes of the giant planets' orbits is therefore a key to unveiling the real evolution of the solar system. For instance, if we find that the current orbital architecture of the terrestrial planets is incompatible with giant planet migration, then explanations of the LHB based on a late migration of Jupiter and Saturn (Gomes et al. 2005; Strom et al. 2005) should be rejected. If, on the contrary, we find that some giant planet evolutions, consistent with the constraints of Paper I, are also consistent with the current architecture of the terrestrial planets, then we have made another important step towards building a coherent and consistent scenario of the dynamical history of the solar system. This is precisely the purpose of the present paper.
In the next section, we explain the challenges set by the migration and the orbital excitation of the giant planets on the stability of the terrestrial planets. Then, in Sect. 3 we look in detail at the evolution of the Earth-Venus couple and of Mercury and how their current secular dynamics could be achieved or preserved. Section 4 is devoted to Mars. Section 5 will briefly discuss the evolution of the inclinations. Finally, Sect. 6 is devoted to the discussion of the relative timing of giant planets' migration versus terrestrial planets' formation. The conclusions in light of our results are presented there as well.
2 Giant planet migration and the evolution of the terrestrial planets
2.1 Overview
The evolution of the eccentricities and longitudes of perihelia of the four terrestrial planets can be described, in first approximation, by the Lagrange-Laplace solution of the secular equations of motion (see Chapter 7 in Murray & Dermott 1999):
where the index i refers to the planet in consideration and k ranges from 1 to 8 with
Notice that, because the terrestrial planets exhibit weakly chaotic dynamics (Laskar 1990), the frequencies g1 to g4 and their amplitudes and corresponding phases are not constant with time. The changes are particularly relevant for the frequency g1. Thus, Tables 1 and 2 should be considered as indicative, and only reflect the current dynamics. Their values might have been different in the past, even since the giant planets achieved their current orbital configuration. Consequently, the maximal eccentricities that the planets attain during their secular oscillation could change over time. For instance, the current maximal eccentricity of Venus is 0.072 (as it can be seen by adding together the absolute values of the coefficients of the second line in Table 2). However, over the last 4 Gyr, the eccentricity of Venus had a 10% probability to exceed 0.09; similarly, with the same probability the eccentricity of Mercury could have exceeded 0.4, that of the Earth 0.08 and that of Mars 0.17 (Laskar 2008). Correia & Laskar (2004) argued that some time in the past the eccentricity of Mercury had to be greater than 0.325 to allow it to be captured in its 3:2 spin-orbit resonance. As Mercury should have been in synchronous rotation before the formation of the Caloris basin (Wieczorek et al. 2009), one of the latest big impact events recorded on Mercury, this high-eccentricity phase should have occurred after the LHB.
Table 7: Frequencies and phases for Mercury to Jupiter on their current orbits.
Table 8: Coefficients Mj,k of the Lagrange-Laplace solution for the terrestrial planets.
2.2 Evolution of g5 and its implications
When Jupiter was closer to Saturn, the value of the g5 frequency had to be higher than it is today. Figure 1 shows the value of g5 as a function of the orbital period ratio between Saturn and Jupiter (
![]() ). The values of g5
have been obtained by numerical Fourier analysis of the outputs of a
sequence of 1 Myr integrations of the Jupiter-Saturn pair. The two
planets were migrated from just outside their 3:2 mean motion
resonance to a final, pre-determined period ratio, and
subsequently the end result of that migration run was integrated for
1 Myr to obtain the Fourier spectrum.
). The values of g5
have been obtained by numerical Fourier analysis of the outputs of a
sequence of 1 Myr integrations of the Jupiter-Saturn pair. The two
planets were migrated from just outside their 3:2 mean motion
resonance to a final, pre-determined period ratio, and
subsequently the end result of that migration run was integrated for
1 Myr to obtain the Fourier spectrum.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg1.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg14.png)
|
Figure 25:
The frequency g5 as a function of
|
| Open with DEXTER | |
If the period ratio between Saturn and Jupiter had evolved from
![]() to its current value, at least the secular resonances g5=g2 and g5=g1 had to be crossed at some time, as one can see from the figure. This effect has already been pointed out by Agnor (2005) and Agnor & Lin (2007). For reference, the minimal amplitude of planet migration deduced by Malhotra (1995) from the analysis of the Kuiper belt sets the initial
to its current value, at least the secular resonances g5=g2 and g5=g1 had to be crossed at some time, as one can see from the figure. This effect has already been pointed out by Agnor (2005) and Agnor & Lin (2007). For reference, the minimal amplitude of planet migration deduced by Malhotra (1995) from the analysis of the Kuiper belt sets the initial
![]() equal to
equal to
![]() ;
Minton & Malhotra (2009) in their recent analysis of the evolution of the asteroid belt, also adopted this initial orbital period ratio. Figure 1 shows that the g5 frequency increases when Jupiter and Saturn are closer to their mutual 2:1 resonance (
;
Minton & Malhotra (2009) in their recent analysis of the evolution of the asteroid belt, also adopted this initial orbital period ratio. Figure 1 shows that the g5 frequency increases when Jupiter and Saturn are closer to their mutual 2:1 resonance (
![]() ).
This effect is well known and is caused by the divergence of the
quadratic terms in the masses of the two planets, which are generated
when the equations of motion are averaged over the orbital periods (see
for instance Knezevic et al. 1991).
As a consequence, if Jupiter passed through or was originally close to
the 2:1 resonance with Saturn, as in the Nice model (Tsiganis
et al. 2005; Gomes et al. 2005; Morbidelli et al. 2007) or in the scenario of Thommes et al. (2007), also the secular resonances g5=g4 and g5=g3 had to be crossed.
).
This effect is well known and is caused by the divergence of the
quadratic terms in the masses of the two planets, which are generated
when the equations of motion are averaged over the orbital periods (see
for instance Knezevic et al. 1991).
As a consequence, if Jupiter passed through or was originally close to
the 2:1 resonance with Saturn, as in the Nice model (Tsiganis
et al. 2005; Gomes et al. 2005; Morbidelli et al. 2007) or in the scenario of Thommes et al. (2007), also the secular resonances g5=g4 and g5=g3 had to be crossed.
A secular resonance crossing can significantly modify the amplitudes of the proper modes in the Lagrange-Laplace solution, i.e. the Mi,k's. In fact, the Lagrange-Laplace solution of the secular dynamics is only a good approximation of the secular motion when the planets are far away from secular or mean motion resonances. Thus, if the system passes through a resonance g5=gk, the terrestrial planets follow a Lagrange-Laplace solution before the resonance crossing and another Lagrange-Laplace solution after the resonance crossing, with the two solutions differing mostly in the amplitudes Mi,k of the terms with corresponding frequencies gk. Thus, the crucial question is: are the current amplitudes of the g1 to g4 terms in the terrestrial planets (i.e. the M coefficients in Table 2) compatible with secular resonance crossings having occurred?
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg2.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg18.png)
|
Figure 26:
Evolution of the terrestrial planets during the g5=g2 and g5=g1 resonance crossings. The top panel shows the evolution of
|
| Open with DEXTER | |
As a demonstration of the effect of secular resonances sweeping through
the terrestrial planets system during the migration of Jupiter and
Saturn, we performed a simple experiment: Mercury, Venus, Earth and
Mars were placed on orbits with their current semi-major axes and
inclinations, but with initial eccentricities equal to zero. Jupiter
and Saturn were forced to migrate smoothly from
![]() to their current orbits (Fig. 2, top), so that g5 sweeps through the g4-g1 range (see Fig. 1). Migration is enacted using the technique discussed in Paper I, with a characteristic e-folding timescale
to their current orbits (Fig. 2, top), so that g5 sweeps through the g4-g1 range (see Fig. 1). Migration is enacted using the technique discussed in Paper I, with a characteristic e-folding timescale ![]() Myr, which is somewhat faster than the fastest time found in Tsiganis et al. (2005). The initial eccentricities and longitudes of perihelion of the giant planets were chosen so that the amplitude of the g5 term in Jupiter was close to the current one. We refer the reader to Paper I as to why this is a valid choice.
Myr, which is somewhat faster than the fastest time found in Tsiganis et al. (2005). The initial eccentricities and longitudes of perihelion of the giant planets were chosen so that the amplitude of the g5 term in Jupiter was close to the current one. We refer the reader to Paper I as to why this is a valid choice.
Unlike in Paper I, in all the simulations presented in this work,
we included in the equations of motion the terms resulting from the
additional potential
where
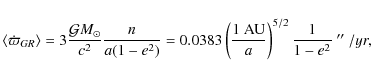
|
(3) |
in accordance with Nobili & Will (1986). This potential term yields a precession rate of the longitude of perihelion of Mercury of 0.43
Returning to Fig. 2 we see that Mercury's eccentricity reaches 0.25 (solid line; middle panel), which is consistent with its current orbit. The current mean value and range in eccentricity of Mercury is displayed by the first, higher bullet with error bars. We should stress that some other simulations, with a similar set up to this one, led to an eccentricity of Mercury exceeding 0.5. Mars' eccentricity (dashed line; middle panel) is excited up to 0.1 very early in the simulation and then oscillates in the 0-0.1 range i.e. slightly smaller in reality (depicted by the second, lower bullet with error bars). Alternatively, Venus acquires a mean eccentricity around 0.1, with a maximal value as large as 0.14 (bottom panel; solid line), while the maximal eccentricity of the Earth exceeds 0.1 (bottom panel; dashed line). Thus, the Earth and Venus become significantly more eccentric than they are, or can be, in the current solar system (Laskar 2008).
The reason for this behaviour is that the amplitudes corresponding to the g1 and g2 frequencies have been strongly excited in Mercury, Venus and Earth by the passage through a resonance with the g5 frequency. Similarly, the g4 mode
in Mars is excited very early on by the same mechanism. A Fourier
analysis done on a 4 Myr continuation of the simulation, with
Jupiter and Saturn on non-migrating orbits, reveals that the amplitude
of the g2 term in Venus is about 0.1, i.e. five times larger than the current value. The amplitude of the g1 term in Mercury is also ![]() ,
which is less than its current value. The evolution of Mercury, though,
is not only influenced very strongly by Jupiter, but also by Venus.
Thus, the amount by which the g1 term is excited is very sensitive to the phase that the g2 term has in Mercury when the g5=g1 resonance occurs. Consequently, it is very easy to excite the amplitude of the g1 mode
in Mercury to a much greater value by slightly changing the set-up of
the simulation so that the time at which the resonance occurs is
somewhat different. In addition, if the terrestrial planets are started
on co-planar orbits, g1 is faster and therefore closer to g2 and consequently the g1 term is excited more easily because of a quasi-resonance between g1 and g2. Conversely, since g5 passes very quickly through the values of g4 and g3, the amplitudes of the corresponding terms in Mars and the Earth are only moderately excited (0.015 for g3 and 0.04 for g4 in Mars). Since the final amplitude of the g2 term is much larger than that of the g3 term, the Earth and Venus are in apsidal libration around
,
which is less than its current value. The evolution of Mercury, though,
is not only influenced very strongly by Jupiter, but also by Venus.
Thus, the amount by which the g1 term is excited is very sensitive to the phase that the g2 term has in Mercury when the g5=g1 resonance occurs. Consequently, it is very easy to excite the amplitude of the g1 mode
in Mercury to a much greater value by slightly changing the set-up of
the simulation so that the time at which the resonance occurs is
somewhat different. In addition, if the terrestrial planets are started
on co-planar orbits, g1 is faster and therefore closer to g2 and consequently the g1 term is excited more easily because of a quasi-resonance between g1 and g2. Conversely, since g5 passes very quickly through the values of g4 and g3, the amplitudes of the corresponding terms in Mars and the Earth are only moderately excited (0.015 for g3 and 0.04 for g4 in Mars). Since the final amplitude of the g2 term is much larger than that of the g3 term, the Earth and Venus are in apsidal libration around ![]() ,
as explained in Paper I.
,
as explained in Paper I.
Thus, this simulation shows that, at least in the case of a fast migration (see Sect. 4), the g5=g4 and g5=g3 resonances are not a severe problem. But the g5=g2 and g5=g1 resonances,
occurring towards the end of the migration, are a more serious concern
for reconstructing the current secular architecture of the terrestrial
planets. For a fast migration speed the excitation of the g2 mode is a linear function of the migration timescale, ![]()
![]() . Consequently, given that with
. Consequently, given that with ![]() Myr the amplitude of the g2 term approximately 0.1, achieving the current excitation would require
Myr the amplitude of the g2 term approximately 0.1, achieving the current excitation would require
![]() Myr. This value of
Myr. This value of ![]() is unrealistic for planetesimal-driven migration of the giant planets.
For example, in the preferred case of Hahn & Malhotra (1999), in which planet migration is driven by a 50
is unrealistic for planetesimal-driven migration of the giant planets.
For example, in the preferred case of Hahn & Malhotra (1999), in which planet migration is driven by a 50
![]() planetesimal disc, it takes more than 30 Myr for the planets to
reach their current orbits. Assuming an exponential fit to the
migration and allowing the migration to be essentially finished after
3 e-folding times, will yield
planetesimal disc, it takes more than 30 Myr for the planets to
reach their current orbits. Assuming an exponential fit to the
migration and allowing the migration to be essentially finished after
3 e-folding times, will yield
![]() Myr. A similar result can be found in Gomes et al. (2004).
The Nice model is the scenario in which the fastest migration is
allowed because the entire planetesimal disc is destabilised at once.
Even in this model, the shortest possible e-folding time measured is
Myr. A similar result can be found in Gomes et al. (2004).
The Nice model is the scenario in which the fastest migration is
allowed because the entire planetesimal disc is destabilised at once.
Even in this model, the shortest possible e-folding time measured is
![]() Myr (Tsiganis et al. 2005; Morbidelli et al. 2005).
Myr (Tsiganis et al. 2005; Morbidelli et al. 2005).
The above analysis implies that the current orbital architecture of the
terrestrial planets is incompatible with a late migration of the giant
planets. However, this may not be the ultimate answer. In fact, it
might be possible that the eccentricities of the terrestrial planets
had been damped after the secular resonance sweeping, due to dynamical
friction exerted by the planetesimals scattered by the giant planets
during their migration. Moreover, as shown in Paper I, the
evolution of the giant planets was not simply a smooth radial
migration, as in the simulation we just presented. Potentially, the
excitation of the g5 mode might have happened late, relative to the g5=g2 and g5=g1 crossings.
Moreover, encounters had to have happened among the gas giants and the
ice giants (see Paper I), so that the radial migration of Jupiter
and Saturn might not have been smooth. Also, unlike the giant planets,
the terrestrial planets might not have formed on circular orbits.
As we reviewed in the Introduction, the terrestrial planets formed
by collisions among massive planetary embryos. As a result of
collisions and encounters among massive bodies, the final orbits might
have been relatively eccentric. The early simulations of this process
(e.g. Chambers 1999) predicted that the orbits of the terrestrial planets were ![]() times more eccentric than the current ones when their accretion ended. More modern simulations (e.g. O'Brien et al. 2006),
accounting for dynamical friction, succeed in producing terrestrial
planets on orbits whose eccentricities and inclinations are comparable to the current values. But nothing guarantees that they had to be the same as now, as well as nothing indicates that they had to be zero. The initial orbital excitation might have been somewhat smaller than now or even greater, probably within a factor of
times more eccentric than the current ones when their accretion ended. More modern simulations (e.g. O'Brien et al. 2006),
accounting for dynamical friction, succeed in producing terrestrial
planets on orbits whose eccentricities and inclinations are comparable to the current values. But nothing guarantees that they had to be the same as now, as well as nothing indicates that they had to be zero. The initial orbital excitation might have been somewhat smaller than now or even greater, probably within a factor of
![]() .
This opens a new degree of freedom to be explored while addressing the effects of secular resonance sweeping.
.
This opens a new degree of freedom to be explored while addressing the effects of secular resonance sweeping.
Below, we will consider all these caveats, while analysing in detail each secular resonance crossing.
3 The g5 = g1 and g5 = g2 resonance crossings
In this section we discuss possibilities to alleviate or circumvent the effects of the secular resonances between the fundamental frequencies of the perihelion of Jupiter (g5) and those of Venus (g2) and Mercury (g1). We discuss these two resonances together, because g2 and g1 have similar values and consequently these resonances both occur during the same phase of Jupiter's evolution. Below, we discuss in sequence four potential mechanisms: (i) the terrestrial planets' eccentricities were damped due to dynamical friction after being excited by the resonance crossing; (ii) the amplitude of the g5 mode in Jupiter, M5,5, was pumped after the secular resonances were crossed; (iii) the amplitudes of the g1 and g2 modes where larger originally, and they were damped down by the secular resonance crossings; (iv) Jupiter and Saturn migrated discontinuously, with jumps in semi-major axes due to encounters with a Uranus-mass planet, so that the g5=g1 and g5=g2 resonances occurred very briefly or did not occur at all.
3.1 Dynamical friction on the terrestrial planets
It might be possible that the eccentricities of the terrestrial planets evolved as in the simulation of Fig. 2,
but were then subsequently decreased due to dynamical friction, exerted
by the large flux of planetesimals scattered by the giant planets from
the outer disc. In all models (Hahn & Malhotra 1999; Gomes et al. 2004; Tsiganis et al. 2005) the mass of the planetesimal disc driving giant planet migration was 30-50
![]() .
About a third of the planetesimals acquired orbits typical of Jupiter family comets (JFCs; perihelion distance q<2.5 AU) some time during their evolution (Levison & Duncan 1997), corresponding to 10-16
.
About a third of the planetesimals acquired orbits typical of Jupiter family comets (JFCs; perihelion distance q<2.5 AU) some time during their evolution (Levison & Duncan 1997), corresponding to 10-16
![]() .
The other planetesimals remained too far from the terrestrial planets to have any influence on them. Given that the g5=g2 and g5=g1 resonances occurred when approximately 2/3 of the full migration of Jupiter and Saturn was completed (see Fig. 1),
the total amount of mass of the planetesimals on JFC orbits that
could exert some dynamical friction on the terrestrial planets after
their excitation was about 3-5
.
The other planetesimals remained too far from the terrestrial planets to have any influence on them. Given that the g5=g2 and g5=g1 resonances occurred when approximately 2/3 of the full migration of Jupiter and Saturn was completed (see Fig. 1),
the total amount of mass of the planetesimals on JFC orbits that
could exert some dynamical friction on the terrestrial planets after
their excitation was about 3-5
![]() .
.
We investigated the magnitude of this dynamical friction in a follow-up simulation of that presented in Fig. 2. A population of 2000 massive objects - with a total mass of
![]() - was added on orbits representative of the steady state orbital distribution of JFCs (Levison & Duncan 1997) and the simulation was continued for 1 Myr. During that time
- was added on orbits representative of the steady state orbital distribution of JFCs (Levison & Duncan 1997) and the simulation was continued for 1 Myr. During that time
![]() of
the JFCs were lost, after being scattered away by the planets. The rest
survived on distant orbits. At the end of the simulation, the amplitude
of the g2 eccentricity term had changed only by
of
the JFCs were lost, after being scattered away by the planets. The rest
survived on distant orbits. At the end of the simulation, the amplitude
of the g2 eccentricity term had changed only by ![]() in Earth and
in Earth and ![]() in Venus. This result is expected to scale linearly with the mass of
the JFCs. Hence, to have a significant dynamical friction that can
reconcile the final orbits of the terrestrial planets with the observed
ones, one would need an enormous and unrealistic mass in the
planetesimal population. Thus we conclude that dynamical friction
cannot be the solution for the excessive excitation of the terrestrial
planets.
in Venus. This result is expected to scale linearly with the mass of
the JFCs. Hence, to have a significant dynamical friction that can
reconcile the final orbits of the terrestrial planets with the observed
ones, one would need an enormous and unrealistic mass in the
planetesimal population. Thus we conclude that dynamical friction
cannot be the solution for the excessive excitation of the terrestrial
planets.
3.2 Late excitation of the g5 mode in Jupiter
The resonances that are responsible for the excitation of the eccentricities of the terrestrial planets are secular resonances. Thus, their effects on the terrestrial planets are proportional to the amplitude of the g5 mode in the secular evolution of the perturber i.e. Jupiter.
We have seen in Paper I that the amplitude of the g5 mode
had to have been excited by close encounters between Saturn
(or Jupiter itself) with a planet with a mass comparable to the
mass of Uranus. In principle, one could think that these encounters
happened relatively late, after the ratio
![]() exceeded 2.25 which, as shown in Fig. 1, corresponds to the last secular resonance crossing (g5=g1).
If this were the case, when the resonance crossing occurred, the
effects would have been less severe than shown in Fig. 2.
exceeded 2.25 which, as shown in Fig. 1, corresponds to the last secular resonance crossing (g5=g1).
If this were the case, when the resonance crossing occurred, the
effects would have been less severe than shown in Fig. 2.
In the framework of the Nice model, we tend to exclude this possibility. In the simulations performed in Tsiganis et al. (2005) and Gomes et al. (2005),
the encounters between gas giants and ice giants start as soon as
Jupiter and Saturn cross their mutual 2:1 mean motion resonance (
![]() )
and end before
)
and end before
![]() .
In the variant of the Nice model proposed in Morbidelli et al. (2007), the encounters start even earlier, when
.
In the variant of the Nice model proposed in Morbidelli et al. (2007), the encounters start even earlier, when
![]() .
We do not know of any other model in which these encounters start after a substantial migration of the giant planets.
.
We do not know of any other model in which these encounters start after a substantial migration of the giant planets.
As a variant of this ``late g5 excitation
scenario'' we can also envision the possibility that the radial
migration of the giant planets and the excitation of their
eccentricities started contemporarily, but the initial separation of
Jupiter and Saturn was such that
![]() from the beginning. For instance, in some of the simulations of Thommes et al. (1999) where Uranus and Neptune are originally in between Jupiter and Saturn, initially
from the beginning. For instance, in some of the simulations of Thommes et al. (1999) where Uranus and Neptune are originally in between Jupiter and Saturn, initially
![]() .
It is likely that the initial separation of Jupiter and Saturn
could have been increased in these simulations to satisfy the condition
.
It is likely that the initial separation of Jupiter and Saturn
could have been increased in these simulations to satisfy the condition
![]() ,
without significant changes of the results. However, the presence of Uranus and Neptune should increase the value of g5 relative to that shown in Fig. 1 for the same value of
,
without significant changes of the results. However, the presence of Uranus and Neptune should increase the value of g5 relative to that shown in Fig. 1 for the same value of
![]() .
Hence the initial value of
.
Hence the initial value of
![]() should have been even larger than 2.25 in order to avoid secular resonances with g1 and g2.
Moreover, we have to re-iterate what we already stressed in
Paper I: hydro-dynamical simulations of the evolution of the giant
planets when they are embedded in the gas disc show that Jupiter and
Saturn should have evolved until they got trapped in their mutual
3:2 resonance (
should have been even larger than 2.25 in order to avoid secular resonances with g1 and g2.
Moreover, we have to re-iterate what we already stressed in
Paper I: hydro-dynamical simulations of the evolution of the giant
planets when they are embedded in the gas disc show that Jupiter and
Saturn should have evolved until they got trapped in their mutual
3:2 resonance (
![]() ;
Pierens & Nelson 2008). Initial conditions with
;
Pierens & Nelson 2008). Initial conditions with
![]() are definitely inconsistent with this result. Hence, the possibility of pumping the g5 mode late i.e. when
are definitely inconsistent with this result. Hence, the possibility of pumping the g5 mode late i.e. when
![]() ,
should probably not be considered as a viable option.
,
should probably not be considered as a viable option.
3.3 Decreasing the amplitudes of the g1 and g2 modes
It is a wide-spread misconception that perihelion secular resonances excite the eccentricities (or, equivalently, the amplitudes of the resonant Fourier modes). This is true only if the initial eccentricities are close to zero: in this case, obviously, the eccentricities can only increase.
The misconception comes from an un-justified use of the
Lagrange-Laplace solution as an adequate integrable approximation,
i.e. as the starting point for studying the full dynamics with
perturbation theory. This linear approach assumes that the frequency of
the eccentricity oscillations is independent of its amplitude, as is
the case with a harmonic oscillator.
This leads to the false prediction that the amplitude of the resonant
mode diverges to infinity at the exact resonance. However, in reality
the dynamics inside or near a secular resonance resemble those of a pendulum (see e.g. Chapter 8 of Morbidelli 2002), which is a non-linear oscillator. Strictly speaking, motion takes place inside a resonance when the corresponding resonant angle, ![]() ,
librates. Let us take as an example the motion of a test particle, with proper secular frequency g, perturbed by the planets. For a resonance between g and gk,
,
librates. Let us take as an example the motion of a test particle, with proper secular frequency g, perturbed by the planets. For a resonance between g and gk,
![]() .
Correlated to the librations of
.
Correlated to the librations of ![]() are large-amplitude periodic
variations of the ``angular momentum'' of the pendulum, which is a
monotonically increasing function of the eccentricity of the particle.
On the other hand, when we are outside but near the g=gk resonance,
are large-amplitude periodic
variations of the ``angular momentum'' of the pendulum, which is a
monotonically increasing function of the eccentricity of the particle.
On the other hand, when we are outside but near the g=gk resonance, ![]() slowly circulates and the eccentricity oscillations are of smaller amplitude. Thus, each resonance has a specified width,
which determines the maximum allowable excursion in eccentricity.
Following this general scheme, a secular resonance between two of the
planetary proper modes (e.g. g2=g5)
can be thought of as a dynamical state, in which two modes exchange
energy in a periodic fashion, according to the evolution of
slowly circulates and the eccentricity oscillations are of smaller amplitude. Thus, each resonance has a specified width,
which determines the maximum allowable excursion in eccentricity.
Following this general scheme, a secular resonance between two of the
planetary proper modes (e.g. g2=g5)
can be thought of as a dynamical state, in which two modes exchange
energy in a periodic fashion, according to the evolution of ![]() .
As
.
As ![]() moves towards one extreme of its libration cycle, one mode gains
``energy'' over the other, and the eccentricity terms related to the
``winning'' mode increase, in expense of terms related to the
``losing'' mode. The situation for the two modes will be reversed,
as
moves towards one extreme of its libration cycle, one mode gains
``energy'' over the other, and the eccentricity terms related to the
``winning'' mode increase, in expense of terms related to the
``losing'' mode. The situation for the two modes will be reversed,
as ![]() will move towards the other extreme of the libration cycle. The total
amount of ``energy'' contained in both modes has to be conserved.
Hence, the eccentricity variations are determined by the initial
conditions, which define a single libration curve.
will move towards the other extreme of the libration cycle. The total
amount of ``energy'' contained in both modes has to be conserved.
Hence, the eccentricity variations are determined by the initial
conditions, which define a single libration curve.
The above scheme is correct in the conservative frame, i.e. as
long as the planets do not migrate. When migration occurs, the system
may be slowly driven from a non-resonant to a resonant regime. This
situation is reminiscent of the one examined in Paper I, where the
slow crossing of a mean motion resonance (MMR) was studied. However,
there is a fundamental difference between the two phenomena, related to
the vastly different libration time-scales. In the case of a MMR
crossing, the migration rate is significantly slower than the libration
frequency of the MMR. Thus, MMR crossing is an adiabatic
process, and adiabatic invariance theory can be used to predict the
final state of the system. When a secular resonance is crossed, things
are not so simple. The crossing time is of the same order as the
libration period. Thus, each moment the planets follow an
``instantaneous'' secular libration curve (i.e. the one that they
would follow if the migration was suddenly stopped), which itself
changes continuously as the planets move radially. Therefore, depending
on the initial phases (i.e., ![]() )
when the resonance is approached, a given eccentricity mode can
decrease or increase, the final amplitude can also do this, depending
on the crossing time. If migration is very slow, the
eccentricities may perform several oscillations, due to repeated
libration cycles. Once the resonance is far away, the Lagrange-Laplace
solution is again valid, but with different amplitudes of the
former-resonant modes.
)
when the resonance is approached, a given eccentricity mode can
decrease or increase, the final amplitude can also do this, depending
on the crossing time. If migration is very slow, the
eccentricities may perform several oscillations, due to repeated
libration cycles. Once the resonance is far away, the Lagrange-Laplace
solution is again valid, but with different amplitudes of the
former-resonant modes.
From the above discussion it is clear that the result of a secular resonance crossing does not always lead to increasing the amplitude of a given secular mode. The final result depends mostly on the initial conditions (eccentricity amplitudes and phases) as well as on the migration speed. In practice, if the initial amplitude of a mode is small compared to possible eccentricity excursion along the libration curve (or, the width of the resonance) the result will be a gain in eccentricity. If, conversely, the initial eccentricity is similar to, or greater than, the resonance width and the migration speed is not too slow, then there can be a large interval of initial phases that would lead to a net loss in eccentricity.
With these considerations in mind, we can envision the possibility that, when they formed, the terrestrial planets had somewhat greater amplitudes of the g1 and g2 modes than now, and that these amplitudes were damped during the g5 secular resonance sweeping. To test this possibility, and estimate the probability that this scenario occurred, we have designed the following experiment.
As initial conditions for the terrestrial planets, we took the outcome of a simulation similar to that presented in Fig. 2, so that the amplitude of the g2 mode in Mercury, Venus and Earth is large (![]() ); the initial eccentricity of Mercury is 0.12. The amplitudes of the g3 and g4 frequencies are, respectively, comparable (g3) and smaller (g4) than the current ones in all planets. Jupiter and Saturn were started with a period ratio
); the initial eccentricity of Mercury is 0.12. The amplitudes of the g3 and g4 frequencies are, respectively, comparable (g3) and smaller (g4) than the current ones in all planets. Jupiter and Saturn were started with a period ratio
![]() and migrated to their current orbits, so that g5 passes through the values of the g2 and g1 frequencies but avoids resonances with g3 and g4. As before, the migration timescale
and migrated to their current orbits, so that g5 passes through the values of the g2 and g1 frequencies but avoids resonances with g3 and g4. As before, the migration timescale ![]() was assumed equal to 1 Myr and the initial eccentricities and
longitudes of perihelia were chosen so that the amplitude of the g5 mode
in Jupiter is correct. With this setup, we did several simulations,
which differ from each other in a rotation of the terrestrial planet
system relative to the Jupiter-Saturn system. This rotation changes the
initial relative phase of the g5 and g2 terms and consequently changes the phase at which the secular resonance
g5=g2 is met. The same principle applies to the g5=g1 resonance.
was assumed equal to 1 Myr and the initial eccentricities and
longitudes of perihelia were chosen so that the amplitude of the g5 mode
in Jupiter is correct. With this setup, we did several simulations,
which differ from each other in a rotation of the terrestrial planet
system relative to the Jupiter-Saturn system. This rotation changes the
initial relative phase of the g5 and g2 terms and consequently changes the phase at which the secular resonance
g5=g2 is met. The same principle applies to the g5=g1 resonance.
Regardless of what happens to Mercury, we found that in about 8% of the simulations the amplitude of the g2 term in Venus was smaller than 0.025 at the end i.e. just 25% of the initial value and comparable to the current one.
To measure the probability that also the final orbit of Mercury is acceptable, we used a successful simulation that damped the g2 mode to construct a new series of simulations as follows. We first measured the value of g5-g2
for the initial configuration. This was done by numerical Fourier
analysis of a 8 Myr simulation with no migration imposed on
Jupiter and Saturn. Defining
![]() ,
we then did a simulation, still without migration of the giant planets, with outputs at multiples of P5,2. All these outputs had, by construction, the same relative phases of the g5 and g2 terms, but different relative phases of the g1 term. We used five consecutive outputs, covering a full
,
we then did a simulation, still without migration of the giant planets, with outputs at multiples of P5,2. All these outputs had, by construction, the same relative phases of the g5 and g2 terms, but different relative phases of the g1 term. We used five consecutive outputs, covering a full ![]() range for the latter, since
range for the latter, since
![]() .
Each of these outputs was used as an initial condition for a new
migration simulation, with the same parameters as before. All of these
simulations led essentially to the same behaviour (i.e. damping)
of the g2 mode, because the secular resonance g5=g2
was encountered at the same phase. But the behaviour of Mercury was
different from one simulation to another. We considered the simulation
successful when the eccentricity of Mercury did not exceed 0.4
during the migration simulation, as well as during a 8 Myr
continuation with no migration of the giant planets; the latter was
performed to determine the Fourier spectra at the end. In total we
found that the evolution of Mercury satisfied these requirements
in 60% of the simulations. Figure 3 shows an example of a successful simulation. In this run, the amplitude of the g2 mode in Venus is damped from 0.1 to 0.025 and the amplitude of the g1 mode in Mercury increases from 0.169 to 0.228.
.
Each of these outputs was used as an initial condition for a new
migration simulation, with the same parameters as before. All of these
simulations led essentially to the same behaviour (i.e. damping)
of the g2 mode, because the secular resonance g5=g2
was encountered at the same phase. But the behaviour of Mercury was
different from one simulation to another. We considered the simulation
successful when the eccentricity of Mercury did not exceed 0.4
during the migration simulation, as well as during a 8 Myr
continuation with no migration of the giant planets; the latter was
performed to determine the Fourier spectra at the end. In total we
found that the evolution of Mercury satisfied these requirements
in 60% of the simulations. Figure 3 shows an example of a successful simulation. In this run, the amplitude of the g2 mode in Venus is damped from 0.1 to 0.025 and the amplitude of the g1 mode in Mercury increases from 0.169 to 0.228.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg3.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg51.png)
|
Figure 27:
Evolution of the terrestrial planets during the g5=g2 and g5=g1 resonance crossings in where the g2 mode is damped down. The top panel shows
|
| Open with DEXTER | |
In summary, we find that there is a probability of 0.08 ![]() 0.6 =
0.6 = ![]() that the migration of the giant planets leads to a damping of the g2 mode
and to an acceptable final orbit of Mercury. This probability should
not be taken very literally. Although it has been measured carefully,
it clearly depends on the properties of the system of terrestrial
planets that we start with and on the migration rate. From the
considerations reported at the beginning of this section we expect that
the probability decreases for reduced initial excitations of the g1 and g2 modes;
also, the probability should decrease if slower migrations are enacted,
unless the initial excitations are increased, approximately in
proportion with
that the migration of the giant planets leads to a damping of the g2 mode
and to an acceptable final orbit of Mercury. This probability should
not be taken very literally. Although it has been measured carefully,
it clearly depends on the properties of the system of terrestrial
planets that we start with and on the migration rate. From the
considerations reported at the beginning of this section we expect that
the probability decreases for reduced initial excitations of the g1 and g2 modes;
also, the probability should decrease if slower migrations are enacted,
unless the initial excitations are increased, approximately in
proportion with ![]() .
We stress that the amplitude of the g2 mode
cannot much exceed 0.1, otherwise the system of the terrestrial
planets becomes violently unstable. Mercury is chaotic and potentially
unstable on a 4 Gyr timescale even in the current system
(Laskar 1990, 1994); if the amplitude of the g2 mode exceeds the current one, it becomes increasingly difficult to find solutions for Mercury that are stable for
.
We stress that the amplitude of the g2 mode
cannot much exceed 0.1, otherwise the system of the terrestrial
planets becomes violently unstable. Mercury is chaotic and potentially
unstable on a 4 Gyr timescale even in the current system
(Laskar 1990, 1994); if the amplitude of the g2 mode exceeds the current one, it becomes increasingly difficult to find solutions for Mercury that are stable for ![]() Myr, which is the putative time at which the migration of the giant planets occurred, as suggested by the LHB.
Myr, which is the putative time at which the migration of the giant planets occurred, as suggested by the LHB.
To conclude, we consider this scenario viable, but with a low probability to have really occurred. An additional puzzling aspect of this mechanism that makes us sceptical, is that it requires the original amplitude of the g2 mode to exceed the amplitude of the g3 mode. As we said above, it is unclear which orbital excitation the terrestrial planets had when they formed. However, given the similarity in the masses of the Earth and Venus, nothing suggests that there should have been a significant imbalance between the amplitudes of these two modes. Actually, it would be very difficult to excite one mode without exciting the other one in a scenario in which the excitation comes from a sequence of collisions and encounters with massive planetary embryos. In fact, as explained in Paper I for the case of Jupiter and Saturn, even if only one planet has a close encounter with a third massive body, both amplitudes abruptly increase to comparable values.
3.4 A jumping Jupiter scenario
In Paper I we have concluded that the current excitation of the g5 and g6 modes in Jupiter and Saturn could be achieved only if at least one of these planets had encounters with a body with a mass comparable to that of Uranus or Neptune. These encounters would have not just excited the eccentricity modes; they would have also provided kicks to the semi-major axes of the planets involved in the encounter. In this section we evaluate the implications of this fact.
If Saturn scatters the ice giant onto an orbit with a greater
semi-major axis, its own semi-major axis has to decrease. Thus, the
![]() ratio
decreases instantaneously. Instead, if Saturn scatters the ice giant
onto an orbit with a smaller semi-major axis, passing it to the control
of Jupiter, and then Jupiter scatters the ice giant onto an orbit with
a larger semi-major axis, the semi-major axis of Saturn has to
increase, that of Jupiter has to decrease, and consequently
ratio
decreases instantaneously. Instead, if Saturn scatters the ice giant
onto an orbit with a smaller semi-major axis, passing it to the control
of Jupiter, and then Jupiter scatters the ice giant onto an orbit with
a larger semi-major axis, the semi-major axis of Saturn has to
increase, that of Jupiter has to decrease, and consequently
![]() has to increase. This opens the possibility that
has to increase. This opens the possibility that
![]() jumps,
or at least evolves very quickly, from less than 2.1 to larger
than 2.25, thus avoiding secular resonances between g5 and g2 or g1 (see Fig. 1).
jumps,
or at least evolves very quickly, from less than 2.1 to larger
than 2.25, thus avoiding secular resonances between g5 and g2 or g1 (see Fig. 1).
We now turn to the Nice model, because this is our favoured model and
the one on which we have data to do more quantitative analysis. In the
Nice model, only in a minority of the successful runs (i.e. the
runs in which both Uranus and Neptune reach stable orbits at locations
close to the current ones) there are encounters between Jupiter and an
ice giant without ejecting it. For instance, this happened in one
simulation out of six in Gomes et al. (2005), and in two simulations out of 14 in Nesvorný et al. (2007).
So, the probability seems to be approximately 15%. In all other
runs, only Saturn encounters an ice giant, which, as we said above,
decreases the
![]() ratio instead of increasing it.
ratio instead of increasing it.
We point the attention of the reader to the fact that Nesvorný et al. (2007)
showed that encounters with Jupiter would explain the capture of the
irregular satellites of this planet and their orbital properties. If
Jupiter never had encounters, only Saturn, Uranus and Neptune should
have captured irregular satellites (unless Jupiter captured them by
another mechanism, but then it would be odd that the system of the
irregular satellites of Jupiter is so similar to those of the other
giant planets; see Jewitt & Sheppard 2006). Moreover, in the Nice
model, the cases where Jupiter has encounters with an ice giant are
those which give final values of
![]() which
best approximate the current solar system, whereas in the other cases
Saturn tends to end its evolution a bit too close to the Sun
(Tsiganis et al. 2005).
These two facts argue that, although improbable, this kind of dynamical
evolution, involving Jupiter encounters with an ice giant, actually
occurred in the real solar system.
which
best approximate the current solar system, whereas in the other cases
Saturn tends to end its evolution a bit too close to the Sun
(Tsiganis et al. 2005).
These two facts argue that, although improbable, this kind of dynamical
evolution, involving Jupiter encounters with an ice giant, actually
occurred in the real solar system.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg4.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg55.png)
|
Figure 28:
Evolution of
|
| Open with DEXTER | |
As an example of what can happen in the Nice model when Jupiter encounters an ice giant, the top panel of Fig. 4 shows the evolution of
![]() ;
the middle panel displays the evolution of the semi-major axis of
Jupiter and in the bottom panel that of Saturn. The time resolution of
the output is 100 yr, though only every 1000 years is shown
here. This new simulation is a ``clone'' of one of the original
simulations of Gomes et al. (2005).
The positions and velocities of the planets were taken at a time when
Jupiter and Saturn had just crossed their 2:1 MMR, but had not yet
experienced encounters with the ice giants - this time is denoted
by t=0 in Fig. 4 and corresponds to t=875.5 Myr in the simulation of Gomes et al. (2005) where the giant planet instability occurred at a time that roughly corresponds to the chronology of the LHB.
;
the middle panel displays the evolution of the semi-major axis of
Jupiter and in the bottom panel that of Saturn. The time resolution of
the output is 100 yr, though only every 1000 years is shown
here. This new simulation is a ``clone'' of one of the original
simulations of Gomes et al. (2005).
The positions and velocities of the planets were taken at a time when
Jupiter and Saturn had just crossed their 2:1 MMR, but had not yet
experienced encounters with the ice giants - this time is denoted
by t=0 in Fig. 4 and corresponds to t=875.5 Myr in the simulation of Gomes et al. (2005) where the giant planet instability occurred at a time that roughly corresponds to the chronology of the LHB.
As one can see in Fig. 4,
![]() evolves very rapidly from
evolves very rapidly from
![]() to
to
![]() around t= 0.25 Myr. Then
around t= 0.25 Myr. Then
![]() decreases again below 2.4, has a rapid incursion into the 2.3-2.4 interval around t= 0.75 Myr and eventually, after t=2.5 Myr, increases smoothly to 2.45. The latter value is a very good approximation of the current value of
decreases again below 2.4, has a rapid incursion into the 2.3-2.4 interval around t= 0.75 Myr and eventually, after t=2.5 Myr, increases smoothly to 2.45. The latter value is a very good approximation of the current value of
![]() .
The striking similarity of the curves in the top and middle panels
demonstrates that the orbital period ratio is essentially dictated by
the dynamical evolution of Saturn. Nevertheless, Saturn can have this
kind of early evolution only if Jupiter has encounters with an ice
giant, which justifies the name of ``jumping Jupiter scenario'' used in
this section. This can be understood by looking at the evolution of the
two planets and of Uranus in details, as we describe below with the
help of the magnification of the dynamics, which is provided
in Fig. 5.
.
The striking similarity of the curves in the top and middle panels
demonstrates that the orbital period ratio is essentially dictated by
the dynamical evolution of Saturn. Nevertheless, Saturn can have this
kind of early evolution only if Jupiter has encounters with an ice
giant, which justifies the name of ``jumping Jupiter scenario'' used in
this section. This can be understood by looking at the evolution of the
two planets and of Uranus in details, as we describe below with the
help of the magnification of the dynamics, which is provided
in Fig. 5.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg5.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg58.png)
|
Figure 29: Magnification of the dynamics of Fig. 4, in the 180 000y-890 000y interval. The top panel now shows the evolution of Uranus' semi-major axis. |
| Open with DEXTER | |
Saturn first has an excursion in semi-major axis from approximately 8.5 AU to 8.8 AU at t=
0.215 Myr. This happens because it has repeated encounters with
Uranus, which lead to a temporary exchange of their orbits, placing
Uranus at a=8.4 AU. Then Saturn kicks Uranus back outwards, which again puts Saturn at ![]() AU.
This series of events shows that, if Jupiter does not participate in
this phase of encounters, the dynamics are characterised by energy
exchange between Saturn and Uranus: if one planet is scattered
outwards, the other is scattered inwards and vice-versa. Given that
Uranus was initially much closer to the Sun than it is now, the net
effect on Uranus had to be an outwards scattering; consequently, in the
absense of encounters with Jupiter, Saturn would have had to move
inwards. So, this evolution could not have led to an increase in
AU.
This series of events shows that, if Jupiter does not participate in
this phase of encounters, the dynamics are characterised by energy
exchange between Saturn and Uranus: if one planet is scattered
outwards, the other is scattered inwards and vice-versa. Given that
Uranus was initially much closer to the Sun than it is now, the net
effect on Uranus had to be an outwards scattering; consequently, in the
absense of encounters with Jupiter, Saturn would have had to move
inwards. So, this evolution could not have led to an increase in
![]() .
.
The situation is drastically different if encounters between Jupiter and Uranus occur. In Fig. 5, this starts to happen at
![]() Myr), when Saturn's semi-major axis evolves rapidly to
Myr), when Saturn's semi-major axis evolves rapidly to ![]() AU and Uranus' semi-major axis to
AU and Uranus' semi-major axis to ![]() AU. Jupiter first exchanges orbits with Uranus: Jupiter moves out to 5.52 AU while
AU. Jupiter first exchanges orbits with Uranus: Jupiter moves out to 5.52 AU while ![]() reaches 3.65 AU and the perihelion distance of Uranus,
reaches 3.65 AU and the perihelion distance of Uranus, ![]() ,
decreases to
,
decreases to ![]() AU.
However, notice that the intrusion of Uranus into the asteroid belt is
not a necessary feature of the jumping Jupiter scenario; some
simulations leading only to
AU.
However, notice that the intrusion of Uranus into the asteroid belt is
not a necessary feature of the jumping Jupiter scenario; some
simulations leading only to
![]() AU. Then Jupiter scatters Uranus outwards to
AU. Then Jupiter scatters Uranus outwards to
![]() AU, itself reaching
AU, itself reaching
![]() AU.
The situation is now very different from the one before: Uranus is back
on a trans-Saturnian orbit and, because this was the result of a
Jupiter-Uranus encounter, Saturn has not moved back to its original
position. Thus, this series of encounters has led to an irreversible
increase of the orbital separation (and period ratio) of Jupiter and
Saturn. The subsequent evolution of the planets, shown in Fig. 5, is dominated by encounters between Saturn and Uranus. These encounters push Uranus' semi-major axis to beyond 200 AU at t= 0.35 Myr and to beyond 100 AU at t= 0.725-0.775 Myr, but in both cases Saturn pulls it back. This erratic motion of
AU.
The situation is now very different from the one before: Uranus is back
on a trans-Saturnian orbit and, because this was the result of a
Jupiter-Uranus encounter, Saturn has not moved back to its original
position. Thus, this series of encounters has led to an irreversible
increase of the orbital separation (and period ratio) of Jupiter and
Saturn. The subsequent evolution of the planets, shown in Fig. 5, is dominated by encounters between Saturn and Uranus. These encounters push Uranus' semi-major axis to beyond 200 AU at t= 0.35 Myr and to beyond 100 AU at t= 0.725-0.775 Myr, but in both cases Saturn pulls it back. This erratic motion of ![]() correlates with the one of
correlates with the one of ![]() .
Eventually Uranus' semi-major axis stabilises at
.
Eventually Uranus' semi-major axis stabilises at ![]() AU.
Thus, Uranus and Neptune switch positions, relative to their initial
configuration. This happened in all our simulations where
Jupiter-Uranus encounters took place.
AU.
Thus, Uranus and Neptune switch positions, relative to their initial
configuration. This happened in all our simulations where
Jupiter-Uranus encounters took place.
We now proceed to simulate the evolution of the terrestrial planets in
the framework of the evolution of Jupiter, Saturn and Uranus discussed
above. However, we cannot simply add the terrestrial planets into the
system and redo the simulation because the dynamics is
chaotic and the outcome for the giant planets would be completely
different. Thus, we need to adopt the strategy introduced by Petit
et al. (2001). More precisely, we have modified the code Swift-WHM (Levison & Duncan 1994),
so that the positions of Jupiter, Saturn and Uranus are computed by
interpolation from the output of the original simulation. Remember that
the orbital elements of the outer planets had been output every
100 yr. The interpolation is done in orbital element space, and
the positions and velocities are computed from the result of the
interpolation. For the orbital elements
![]() ,
and
,
and ![]() ,
which vary slowly, the interpolation is done linearly. For the mean anomaly M, which cycles over several periods in the 100 yr output-interval, we first
compute the mean orbital frequency from the mean semi-major axis (defined as the average between the values of a at the beginning and at the end of the output-interval) and then adjust it so that M matches the value recorded at the end of the output-interval. Then, over the output-interval, we propagate M from one time-step to another, using this adjusted mean orbital frequency.
,
which vary slowly, the interpolation is done linearly. For the mean anomaly M, which cycles over several periods in the 100 yr output-interval, we first
compute the mean orbital frequency from the mean semi-major axis (defined as the average between the values of a at the beginning and at the end of the output-interval) and then adjust it so that M matches the value recorded at the end of the output-interval. Then, over the output-interval, we propagate M from one time-step to another, using this adjusted mean orbital frequency.
To test the performance of this code, we have done two
simulations of the evolution of the 8 planets of the solar system.
In the first one, the planets were started from their current
configuration and were integrated for 1 Myr, using the original
Swift-WHM code. In the second one, an encounters phase was simulated,
by placing Uranus initially in between the orbits of Jupiter and
Saturn, while setting the terrestrial planets on circular and co-planar
orbits, and integrating for 1 Myr. In both simulations the orbital
elements of the planets were recorded every 100 yr. Then, we
re-integrated the terrestrial planets, in both configurations, using
our new code, in which the orbital evolutions of Jupiter, Saturn and
Uranus were being read from the output of the previous integration. We
then compared the outputs of the two simulations, for each initial
planet configuration. Eccentricity differences between the two
simulations of the same configuration are interpreted here as the
``error'' of our new code. In the first configuration (current system),
which represents a quite regular evolution, we found that the
root-mean-square errors in eccentricity are 1.05 ![]() 10-4 for Mercury, 4.3
10-4 for Mercury, 4.3 ![]() 10-5 for Venus, 4.0
10-5 for Venus, 4.0 ![]() 10-5 for the Earth and 8.9
10-5 for the Earth and 8.9 ![]() 10-5
for Mars. In the second simulation (repeated encounters) the evolution
of the terrestrial planets, Mercury in particular, is more violently
chaotic. Consequently, the error remains acceptable (
10-5
for Mars. In the second simulation (repeated encounters) the evolution
of the terrestrial planets, Mercury in particular, is more violently
chaotic. Consequently, the error remains acceptable (![]()
![]() 10-3) for all planets except Mercury, for which the error grows above
10-3) for all planets except Mercury, for which the error grows above ![]()
![]() 10-3 after
10-3 after
![]() Myr.
This is due to a shift in the secular phases of Mercury's orbit in the
two simulations, which changes the outcome of the evolution. Given the
chaotic character of the dynamics, both evolutions are equally likely
and acceptable. Thus, we conclude that our modified integrator is
accurate enough (although the effects of encounters among the giant
planets are ``smeared'' over 100 yr intervals) to be used
effectively for our purposes.
Myr.
This is due to a shift in the secular phases of Mercury's orbit in the
two simulations, which changes the outcome of the evolution. Given the
chaotic character of the dynamics, both evolutions are equally likely
and acceptable. Thus, we conclude that our modified integrator is
accurate enough (although the effects of encounters among the giant
planets are ``smeared'' over 100 yr intervals) to be used
effectively for our purposes.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg6.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg74.png)
|
Figure 30: The evolution of the eccentricities of Mercury ( top), Venus and Earth (respectively solid and dashed lines) in the middle panel, and Mars ( bottom), during the dynamics of Jupiter and Saturn illustrated in Fig. 4. The initial orbits of the terrestrial planets are assumed to be circular and coplanar. The solid circles and vertical bars represent the eccentricity oscillation of Earth and Venus, as in Fig. 2. |
| Open with DEXTER | |
For a comparison with the case illustrated in Fig. 2, we first present a simulation where all terrestrial planets start from coplanar, circular orbits. Figure 6
shows the evolution of the eccentricity of Mercury (top), Venus and
Earth (middle) and Mars (bottom). The eccentricities of the terrestrial
planets increase rapidly but, unlike in the case of smooth migration of
Jupiter and Saturn (Fig. 2), they remain moderate and do not exceed the values characterising their current secular evolutions (see for instance Laskar 1990).
A Fourier analysis of a 4 Myr continuation of the
simulation, with Jupiter and Saturn freely evolving from their final
state, gives amplitudes of the g2 and g3 modes in Venus and the Earth of
![]() ,
in good agreement with the real values. The amplitude of the g4 mode in Mars is smaller than the real one. For Mercury, the analysis is not very significant because the g1 and g5 frequencies are closer to each other than in reality (because
,
in good agreement with the real values. The amplitude of the g4 mode in Mars is smaller than the real one. For Mercury, the analysis is not very significant because the g1 and g5 frequencies are closer to each other than in reality (because
![]() is a bit smaller, which increases g5 faster, and Mercury is more inclined, which decreases g1). Nevertheless, in a 20 Myr simulation, the eccentricity of Mercury does not exceed 0.4.
is a bit smaller, which increases g5 faster, and Mercury is more inclined, which decreases g1). Nevertheless, in a 20 Myr simulation, the eccentricity of Mercury does not exceed 0.4.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg7.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg76.png)
|
Figure 31: The same as Fig. 6, but for terrestrial planets starting from their current orbits. |
| Open with DEXTER | |
Since it is unlikely that the terrestrial planets formed on circular
orbits, but from the beginning should have had some orbital excitation,
remnant of their violent formation process, we have re-enacted the
evolution of the terrestrial planets, but starting from their current
orbits. In this case we assume that their current orbital excitation is
an approximation to their primordial excitation. Again, Jupiter and
Saturn evolve as in Fig. 4. The results are illustrated in Fig. 7.
We find that the eccentricities of the terrestrial planets remain
moderate and comparable to the current values. A Fourier analysis
of the continuation of this simulation shows again that amplitudes of
the g2 and g3 terms in Venus and the Earth are
![]() .
The final amplitude of the g4 term in Mars has preserved the initial value of
.
The final amplitude of the g4 term in Mars has preserved the initial value of
![]() .
The maximal eccentricity of Mercury does not exceed 0.35.
.
The maximal eccentricity of Mercury does not exceed 0.35.
Taken together, these two simulations are a successful demonstration that the rapid evolution of
![]() over the 2.1-2.4 range allows the excitation of the terrestrial planets
to remain comparable to their current values, because the sweeping of
the g5 secular resonance is too fast to have a noticeable effect.
over the 2.1-2.4 range allows the excitation of the terrestrial planets
to remain comparable to their current values, because the sweeping of
the g5 secular resonance is too fast to have a noticeable effect.
We have to stress, though, that not all ``jumping-Jupiter'' evolutions
are favourable for the terrestrial planets. In some cases the rapid
evolution of
![]() ends when the orbital period ratio is
ends when the orbital period ratio is ![]() or less, which is close to the g5=g1 and g5=g2 resonance. In other cases, after having increased to above 2.3,
or less, which is close to the g5=g1 and g5=g2 resonance. In other cases, after having increased to above 2.3,
![]() decreases again and for a long time remains in the range of values for
which these secular resonances occur. In these cases, the destiny of
the terrestrial planets is set: Mercury typically becomes unstable, and
the Earth and Venus become much more eccentric than they are in
reality, due to the excitation of the g2 mode.
decreases again and for a long time remains in the range of values for
which these secular resonances occur. In these cases, the destiny of
the terrestrial planets is set: Mercury typically becomes unstable, and
the Earth and Venus become much more eccentric than they are in
reality, due to the excitation of the g2 mode.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg8.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg79.png)
|
Figure 32: Top panel: the evolution of the period ratio between Saturn and Jupiter in another ``jumping Jupiter'' evolution from the Nice model. Middle and bottom panel: the evolutions of the eccentricities of Mercury and Venus, respectively. |
| Open with DEXTER | |
Nevertheless, the evolution of
![]() does not need to be as fast as in Fig. 4 to lead to ``good'' terrestrial planets. Figure 8 gives another example from a different realisation of the Nice model: the top panel shows the evolution of
does not need to be as fast as in Fig. 4 to lead to ``good'' terrestrial planets. Figure 8 gives another example from a different realisation of the Nice model: the top panel shows the evolution of
![]() ,
the middle and the bottom panel show the evolutions of the
eccentricities of Mercury and Venus, respectively, for a system of
terrestrial planets starting from current orbits. In this case
,
the middle and the bottom panel show the evolutions of the
eccentricities of Mercury and Venus, respectively, for a system of
terrestrial planets starting from current orbits. In this case
![]() evolves rapidly to
evolves rapidly to
![]() ,
but then it returns in the 2.10-2.25 range, where it spends a good
half-a-million years. Subsequently, after evolving again to 2.3,
it returns to 2.25 and starts to increase again, slowly. In
this case the effect of secular resonances is no longer negligible as
in the case illustrated above. But in our terrestrial planet simulation
the eccentricity of Mercury is effectively damped, enacting the
principle formulated in Sect. 3.3. The eccentricity of Venus, via the amplitude of the g2 mode, is excited during the time when
,
but then it returns in the 2.10-2.25 range, where it spends a good
half-a-million years. Subsequently, after evolving again to 2.3,
it returns to 2.25 and starts to increase again, slowly. In
this case the effect of secular resonances is no longer negligible as
in the case illustrated above. But in our terrestrial planet simulation
the eccentricity of Mercury is effectively damped, enacting the
principle formulated in Sect. 3.3. The eccentricity of Venus, via the amplitude of the g2 mode, is excited during the time when
![]() and reaches 0.1. However, it is damped back when
and reaches 0.1. However, it is damped back when
![]() decreases again to 2.5 at
decreases again to 2.5 at ![]() Myr.
At the end, the orbits of the terrestrial planets are again comparable
to their observed orbits, in terms of eccentricity excitation and
amplitude of oscillation.
Myr.
At the end, the orbits of the terrestrial planets are again comparable
to their observed orbits, in terms of eccentricity excitation and
amplitude of oscillation.
At this point, one might wonder what is the fraction of giant planets'
evolutions in the Nice model that are favourable for the terrestrial
planets. This is difficult to evaluate, because we only performed a
limited number of simulations and then cloned the simulations that
seemed to be the most promising. We try, nevertheless, to give a rough
estimate. As we said at the beginning of this section, the jumping
Jupiter evolutions are about 15-20% of the successful Nice model runs.
By successful we mean those runs that, at the end, yielded giant
planets on orbits resembling their observed ones, without considering
terrestrial planets constraints. The successful runs are about 50-70%
of the total runs (Gomes et al. 2005; Tsiganis et al. 2005).
Most of the unsuccessful runs were of the jumping Jupiter category, but
led to the ejection of Uranus. It is possible that, if the planetesimal
disc had been more massive than the one used in the simulation, or
represented by a larger number of smaller particles, so as to better
resolve the process of dynamical friction, Uranus would have been saved
more often, thus leading to a larger fraction of successful jumping
Jupiter cases. Then, by cloning jumping Jupiter simulations after the
time of the first encounter with Uranus, we find that about 1/3 of the
``successful'' jumping Jupiter cases are also successful for the
terrestrial planets, like the cases presented in Figs. 6-8;
![]() evolves very quickly beyond 2.3, and does not exceed 2.5 in
the end. This brings the total probability of having in the Nice model
a giant planet evolution compatible with the current orbits of the
terrestrial planets to about 6%.
evolves very quickly beyond 2.3, and does not exceed 2.5 in
the end. This brings the total probability of having in the Nice model
a giant planet evolution compatible with the current orbits of the
terrestrial planets to about 6%.
4 The g5 = g3 and g5 = g4 resonance crossings
The study described in this section is very similar to that presented at two DPS conferences by Agnor (2005) and Agnor & Lin (2007) and therefore its results are not new. However, Agnor and collaborators never presented their work in a formal publication so, for completeness, we do it here.
As discussed in Sect. 2, when Jupiter and Saturn are close enough to their mutual 2:1 mean motion resonance, the g5 frequency can be of the order of 17-18
![]() /yr (see Fig. 1), and therefore resonances with the proper frequencies of Mars and the Earth (g4 and g3) have to occur. If the migration of Jupiter and Saturn from the 2:1 resonance is sufficiently fast, as shown in Fig. 2, the sweeping of the g5=g4 and g5=g3 does not cause an excessive excitation of the amplitudes of the g4 and g3 mode.
/yr (see Fig. 1), and therefore resonances with the proper frequencies of Mars and the Earth (g4 and g3) have to occur. If the migration of Jupiter and Saturn from the 2:1 resonance is sufficiently fast, as shown in Fig. 2, the sweeping of the g5=g4 and g5=g3 does not cause an excessive excitation of the amplitudes of the g4 and g3 mode.
However, while a fast departure from the 2:1 resonance is likely, in the original version of the Nice model (Gomes et al. 2005) Jupiter and Saturn have to approach the 2:1 resonance very slowly, in order to cross the resonance with sufficient delay to explain the timing of the LHB. During the approach phase the eccentricities of Jupiter and Saturn (and, therefore, also the amplitude of the g5 term) were very small but, nevertheless, the long timescales involved could allow the secular resonances to have a destabilising effect on the terrestrial planets.
To illustrate this point, we repeated the last part of the simulation presented in Gomes et al. (2005),
during which Jupiter and Saturn slowly approach the 2:1 resonance,
and we added the terrestrial planets, Venus to Mars, initially on
circular orbits. The top panel of Fig. 9
shows the evolution of the eccentricities of the terrestrial planets,
while on the bottom panel the evolution of the period ratio between
Saturn and Jupiter over the integrated time-span is depicted. The
initial configuration is very close to the g5=g4 resonance. At this time, Jupiter's eccentricity is oscillating from ![]() to
to
![]() ,
but with a high frequency related to the 2:1 resonance with Saturn. The amplitude of the g5 mode in Jupiter is only 3
,
but with a high frequency related to the 2:1 resonance with Saturn. The amplitude of the g5 mode in Jupiter is only 3 ![]() 10-4. Eventually, the secular resonance (i.e. at
10-4. Eventually, the secular resonance (i.e. at
![]() Gyr) excites the amplitude of the g4 term
in Mars to approximately 0.15, in Earth and Venus to 0.033
and 0.023 respectively, as well as the amplitude of the g5 mode in Jupiter to 2
Gyr) excites the amplitude of the g4 term
in Mars to approximately 0.15, in Earth and Venus to 0.033
and 0.023 respectively, as well as the amplitude of the g5 mode in Jupiter to 2 ![]() 10-3. At the same time, the g4 frequency increases abruptly because of the increase in Mars' eccentricity and becomes approximately 0.2
10-3. At the same time, the g4 frequency increases abruptly because of the increase in Mars' eccentricity and becomes approximately 0.2
![]() /y faster than g5. The long periodic oscillations of the eccentricity of Mars after 0.05 Gyr are precisely related to the g4-g5 beat. As migration proceeds, the g5 frequency increases. Surprisingly, the g4 frequency
increases accordingly, which causes the mean eccentricities of Mars,
Earth and Venus to also increase accordingly. We interpret this
behaviour as if the dynamical evolution is sticking to the outer
separatrix of the g5=g4 resonance, in apparent violation of adiabatic theory. Therefore the g5=g4 resonance
is not crossed again. At the end, the eccentricity of Mars becomes
large enough to drive the terrestrial planets into a global
instability. This is a very serious problem, which seems to invalidate
the original version of the Nice model.
/y faster than g5. The long periodic oscillations of the eccentricity of Mars after 0.05 Gyr are precisely related to the g4-g5 beat. As migration proceeds, the g5 frequency increases. Surprisingly, the g4 frequency
increases accordingly, which causes the mean eccentricities of Mars,
Earth and Venus to also increase accordingly. We interpret this
behaviour as if the dynamical evolution is sticking to the outer
separatrix of the g5=g4 resonance, in apparent violation of adiabatic theory. Therefore the g5=g4 resonance
is not crossed again. At the end, the eccentricity of Mars becomes
large enough to drive the terrestrial planets into a global
instability. This is a very serious problem, which seems to invalidate
the original version of the Nice model.
Fortunately, the new version of the Nice model, presented in Morbidelli et al. (2007) solves this problem. This version was built to remove the arbitrary character of the initial conditions of the giant planets that characterised the original version of the model. In Morbidelli et al. (2007), the initial conditions of the N-body simulations are taken from the output of a hydrodynamical simulation in which the four giant planets, evolving in the gaseous proto-planetary disc, eventually reach a non-migrating, fully resonant, stable configuration. More precisely, Jupiter and Saturn are trapped in their mutual 3:2 resonance (see also Masset & Snellgrove 2001; Morbidelli & Crida 2007; Pierens & Nelson 2008); Uranus is in the 3:2 resonance with Saturn and Neptune is caught in the 4:3 resonance with Uranus. Morbidelli et al. (2007) showed that, from this configuration, the evolution is similar to that of the original version of the Nice model (e.g. Tsiganis et al. 2005; Gomes et al. 2005), but the instability is triggered when Jupiter and Saturn cross their mutual 5:3 resonance (instead of the 2:1 resonance as in the original version of the model). Additional simulations done by our group (Levison et al., in preparation) show that, if the planetesimal disc is assumed as in Gomes et al. (2005), the instability of the giant planets is triggered as soon as a pair of planets leaves their original resonance, and this can happen as late as the LHB chronology seems to suggest.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg9.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg85.png)
|
Figure 33:
The evolution of eccentricities of Venus, Earth and Mars
in a simulation where Jupiter and Saturn approach slowly their 2:1 resonance. The top panel shows the evolution of the eccentricities of Mars (upper curve) and of Earth and Venus
(overlapping almost perfectly in a unique lower curve). The bottom panel shows
|
| Open with DEXTER | |
For our purposes in this paper, the crucial difference between the new and the original version of the Nice model is that Jupiter and Saturn approach their mutual 2:1 resonance fast, because the instability has been triggered before, when Jupiter and Saturn were still close (or more likely locked in) their 3:2 resonance.
To test what this implies for the terrestrial planets, we have run
several simulations, in which Jupiter and Saturn, initially on
quasi-circular orbits, migrate all the way from within the
5:3 resonance to the 2:1 resonance on timescales of a several
million years (corresponding to
![]() Myr).
We stress that we enact a smooth migration of the giant planets
(evolutions of the jumping Jupiter case would be a priori more
favourable) and that the migration time to the 2:1 resonance could
easily be much shorter than we assume (see for instance the bottom
panel of Fig. 8 in Morbidelli et al. 2007). On the other hand, in these simulations the amplitude of the g5 term
in Jupiter is excited through the multiple mean motion resonance
crossings between Jupiter and Saturn, and therefore is about 1/3
of the current value (see Paper I).
Myr).
We stress that we enact a smooth migration of the giant planets
(evolutions of the jumping Jupiter case would be a priori more
favourable) and that the migration time to the 2:1 resonance could
easily be much shorter than we assume (see for instance the bottom
panel of Fig. 8 in Morbidelli et al. 2007). On the other hand, in these simulations the amplitude of the g5 term
in Jupiter is excited through the multiple mean motion resonance
crossings between Jupiter and Saturn, and therefore is about 1/3
of the current value (see Paper I).
We present two simulations here. Both have been obtained with ![]() Myr;
the first one investigates the outcome of initially circular
terrestrial planets while the other uses the current orbits of the
terrestrial planets. The results are presented in Figs. 10 and 11,
respectively. In both figures, the top panel shows the evolution of the
orbital period ratio between Saturn and Jupiter; the middle panel shows
the eccentricities of the terrestrial planets except Mercury, and the
bottom panel the eccentricities of Jupiter and Saturn.
Myr;
the first one investigates the outcome of initially circular
terrestrial planets while the other uses the current orbits of the
terrestrial planets. The results are presented in Figs. 10 and 11,
respectively. In both figures, the top panel shows the evolution of the
orbital period ratio between Saturn and Jupiter; the middle panel shows
the eccentricities of the terrestrial planets except Mercury, and the
bottom panel the eccentricities of Jupiter and Saturn.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg10.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg88.png)
|
Figure 34: The evolution of eccentricities of Venus, Earth and Mars, starting from circular orbits, in a simulation where Jupiter and Saturn migrate from within the 5:3 resonance to the 2:1 resonance. The top panel shows ratio of orbital periods between Saturn and Jupiter. The middle panel shows the evolution of the eccentricities of Mars (short dashed), Earth (long dashed) and Venus (solid). The bottom panel shows the eccentricities of Jupiter (solid) and Saturn (dashed). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg11.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg89.png)
|
Figure 35:
The same as Fig. 10,
but for terrestrial planets starting from their current orbits. Notice
that the evolution for Jupiter and Saturn is not exactly the same as
that of the previous simulation, despite the initial conditions
and |
| Open with DEXTER | |
Notice the little jumps of the
![]() curve and of
curve and of ![]() and
and ![]() when Jupiter and Saturn cross mean motion resonances. Also notice that
in the interim between resonances, the eccentricities of Jupiter and
Saturn decay, as a consequence of a damping term that we introduced on
Saturn to mimic the effect of dynamical friction, and to ensure that
they do not become unstable (see Paper I). In the case where the
terrestrial planets have initially circular orbits (Fig. 10)
we see that they start to be excited after 1.5 Myr, when Jupiter
and Saturn cross their mutual 9:5 resonance and become more
eccentric themselves. The simultaneous increase in the eccentricities
of Venus and Earth is mostly caused by an increase in their g2 terms because of the near-resonance g5=g2 when
when Jupiter and Saturn cross mean motion resonances. Also notice that
in the interim between resonances, the eccentricities of Jupiter and
Saturn decay, as a consequence of a damping term that we introduced on
Saturn to mimic the effect of dynamical friction, and to ensure that
they do not become unstable (see Paper I). In the case where the
terrestrial planets have initially circular orbits (Fig. 10)
we see that they start to be excited after 1.5 Myr, when Jupiter
and Saturn cross their mutual 9:5 resonance and become more
eccentric themselves. The simultaneous increase in the eccentricities
of Venus and Earth is mostly caused by an increase in their g2 terms because of the near-resonance g5=g2 when
![]() (see Fig. 1); the amplitude of their g2 terms becomes approximately 0.02. The effect of the g5=g4 resonance
is visible towards the end of the simulation, when Mars becomes
suddenly more eccentric (dashed line; middle panel) and has its g4 term
increased to about 0.08. However, its eccentricity does not
exceed 0.09, and decreases again in response to the giant planets
crossing the 2:1 resonance. In the next figure, the case where the
terrestrial planets are initially on their current orbits (Fig. 11),
we see almost no changes in the eccentricity evolution of the
terrestrial planets, which remain of the same order as the initial
ones. The most likely reason for this behaviour is that the chaotic
nature of the migration causes the behaviour of Jupiter and Saturn to
be slightly different from one simulation to the next. Indeed, the
value of
(see Fig. 1); the amplitude of their g2 terms becomes approximately 0.02. The effect of the g5=g4 resonance
is visible towards the end of the simulation, when Mars becomes
suddenly more eccentric (dashed line; middle panel) and has its g4 term
increased to about 0.08. However, its eccentricity does not
exceed 0.09, and decreases again in response to the giant planets
crossing the 2:1 resonance. In the next figure, the case where the
terrestrial planets are initially on their current orbits (Fig. 11),
we see almost no changes in the eccentricity evolution of the
terrestrial planets, which remain of the same order as the initial
ones. The most likely reason for this behaviour is that the chaotic
nature of the migration causes the behaviour of Jupiter and Saturn to
be slightly different from one simulation to the next. Indeed, the
value of
![]() has a longer plateau in Figs. 10 than in 11. In addition, in the first simulation the value of M5,5
is slightly larger than in the second, which can be seen from the
slightly larger excursions of Jupiter's eccentricity from its mean. In
addition, the little changes in the eccentricities of the terrestrial
planets in Fig. 10 become nearly invisible if the eccentricities are already quite large.
has a longer plateau in Figs. 10 than in 11. In addition, in the first simulation the value of M5,5
is slightly larger than in the second, which can be seen from the
slightly larger excursions of Jupiter's eccentricity from its mean. In
addition, the little changes in the eccentricities of the terrestrial
planets in Fig. 10 become nearly invisible if the eccentricities are already quite large.
Thus, we conclude that the g5=g4 and g5=g3 secular resonances are not a hazard for the terrestrial planets, at least in the new version of the Nice model.
5 Note on the inclinations of the terrestrial planets
The dynamical excitation of the terrestrial planets at the end of the process of formation is still not known. Simulations (e.g. O'Brien et al. 2006) show that the planets had an orbital excitation comparable to the current one, but this could be an artifact of the poor modelling of dynamical friction. Therefore, any indirect indication of what had to be the real dynamical state of the orbits of the terrestrial planets would be welcome.
In the two previous sections we have seen that original circular orbits cannot be excluded. In fact, if the terrestrial planets had circular orbits after their formation, the current eccentricities and amplitudes of the secular modes could have been acquired during the evolution of the giant planets through secular resonance crossings and reactions to the jumps in eccentricity of Jupiter's orbit. It is interesting to see if the same is true for the inclinations, which are between 2 and 10 degrees for the real terrestrial planets. In fact, if the terrestrial planets had originally quasi-circular orbits (probably as a result of strong dynamical friction with the planetesimals remaining in the inner solar system at the end of the giant collisions phase), presumably they had also inclinations close to zero. If the evolution of the giant planets could not excite the inclinations of the terrestrial planets, then the orbits of these planets had to be excited from the very beginning. In the opposite case, co-planar (and circular) initial orbits cannot be excluded.
Unlike the eccentricity case, there are no first-order secular
resonances affecting the evolution of the inclinations of the
terrestrial planets during the migration of Jupiter and Saturn. In
fact, neglecting Uranus and Neptune, the secular motion of Jupiter and
Saturn in the Lagrange-Laplace theory is characterised by a unique
frequency (s6). Its value is now approximately
![]() /yr
and should have been faster in the past, when the two planets were
closer to each other. The frequencies of the longitudes of the node of
the terrestrial planets are all smaller in absolute value than s6: the frequencies s1 and s2 are about -6 to
/yr
and should have been faster in the past, when the two planets were
closer to each other. The frequencies of the longitudes of the node of
the terrestrial planets are all smaller in absolute value than s6: the frequencies s1 and s2 are about -6 to
![]() /yr; the s3 and s4 frequencies are -18 to
/yr; the s3 and s4 frequencies are -18 to
![]() /yr (Laskar 1990). So, no resonances of the kind s6=sk, with k=1 to 4 were possible.
/yr (Laskar 1990). So, no resonances of the kind s6=sk, with k=1 to 4 were possible.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg12.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg96.png)
|
Figure 36: Evolution of the inclinations of Mercury (solid), Venus (dark dashed) Earth (light dashed) and Mars (dotted), all starting from 0, in the ``jumping Jupiter'' evolution shown in the top panel of Fig. 8. |
| Open with DEXTER | |
Nevertheless, in our simulations with terrestrial planets starting with circular and co-planar orbits in Sect. 3.4 we find (see Fig. 12)
that the inclinations are excited and the current values can be
reproduced, including that of the Mercury (whose mean real inclination
is
![]() ;
Laskar 1988) and Mars (4
;
Laskar 1988) and Mars (4
![]() ).
This is because there are a number of non-linear secular resonances
that can occur, which also involve Uranus or Neptune. The
frequencies s1 and s2 could resonate with s7 or s8, whenever the latter were larger in absolute value than the current values (respectively -2.99 and
).
This is because there are a number of non-linear secular resonances
that can occur, which also involve Uranus or Neptune. The
frequencies s1 and s2 could resonate with s7 or s8, whenever the latter were larger in absolute value than the current values (respectively -2.99 and
![]() /yr now), which is likely when the ice giants had much stronger interactions with Jupiter and Saturn. The frequencies s3 and s4 were close to the 1:2 resonance with s6,
when the latter was larger than now due to the smaller orbital spacing
between the giant planets. As is well known, a resonance
s6 = 2 s4 cannot have dynamical
effects, because the corresponding combination of the angles does not
fulfil the D'Alembert rule (see for instance Morbidelli 2002). However, a resonance like
2 s4=s6+s7 does satisfy the D'Alembert rule and is close to the previous one, due to the current small value of s7.
The variety of dynamical evolutions of Uranus and Neptune that are
possible in the Nice model (even within the subset of jumping-Jupiter
evolutions) precludes us to say deterministically which resonances
really occurred, when and with which effects. But the possibility of
exciting the current inclinations starting from
/yr now), which is likely when the ice giants had much stronger interactions with Jupiter and Saturn. The frequencies s3 and s4 were close to the 1:2 resonance with s6,
when the latter was larger than now due to the smaller orbital spacing
between the giant planets. As is well known, a resonance
s6 = 2 s4 cannot have dynamical
effects, because the corresponding combination of the angles does not
fulfil the D'Alembert rule (see for instance Morbidelli 2002). However, a resonance like
2 s4=s6+s7 does satisfy the D'Alembert rule and is close to the previous one, due to the current small value of s7.
The variety of dynamical evolutions of Uranus and Neptune that are
possible in the Nice model (even within the subset of jumping-Jupiter
evolutions) precludes us to say deterministically which resonances
really occurred, when and with which effects. But the possibility of
exciting the current inclinations starting from ![]() is not remote and therefore, unfortunately, we cannot conclude on what
had to be the initial dynamical state of the orbits of the terrestrial
planets.
is not remote and therefore, unfortunately, we cannot conclude on what
had to be the initial dynamical state of the orbits of the terrestrial
planets.
6 Discussion and conclusions
In this work we have shown that the radial smooth migration of
Jupiter and Saturn tends to excite the eccentricities of the orbits of
Mercury, Venus and the Earth well above the values achievable during
their current evolution. This happens because the g5 frequency decreases during the migration; consequently it enters temporarily in resonance with g2 and g1 when
![]() ,
which excites the amplitudes associated with these two frequencies in
the Fourier spectrum of the terrestrial planets. Conversely, the
amplitude of the g4 frequency
in Mars is not excited too much, provided that Jupiter and Saturn
approached and departed rapidly to/from their mutual 2:1 mean
motion resonance, as in the new version of the Nice model (Morbidelli
et al. 2007).
,
which excites the amplitudes associated with these two frequencies in
the Fourier spectrum of the terrestrial planets. Conversely, the
amplitude of the g4 frequency
in Mars is not excited too much, provided that Jupiter and Saturn
approached and departed rapidly to/from their mutual 2:1 mean
motion resonance, as in the new version of the Nice model (Morbidelli
et al. 2007).
We have found two possible, but low-probability mechanisms that may
make giant planet migration compatible with the current orbital
architecture of the terrestrial planets. One requires that the original
structure of the terrestrial planets was quite strange, with an
amplitude of the g2 mode significantly larger than that of the g3 mode. In this case, the g5=g2 resonance could have
damped the amplitude of the g2 mode (and to some extent also of the g1 mode), for some lucky combination of secular phases. The other requires that
![]() ``jumped'' (or evolved very rapidly across) the 2.1-2.3 interval, as a result of encounters between both
Jupiter and Saturn with either Uranus or Neptune. Some evolutions of
this kind occur in the Nice model, but they are rare (successful
probability approximately
``jumped'' (or evolved very rapidly across) the 2.1-2.3 interval, as a result of encounters between both
Jupiter and Saturn with either Uranus or Neptune. Some evolutions of
this kind occur in the Nice model, but they are rare (successful
probability approximately ![]() ).
).
We are aware that most readers will consider this a first serious drawback of the Nice model. But, before leaving way to critics, we would like to advocate some relevant points.
First, this apparent problem is not confined to the Nice model, but concerns any model which associates the origin of the LHB to a delayed migration of Jupiter and Saturn (e.g. Levison et al. 2001, 2004; Strom et al. 2005; Thommes et al. 2007).
Second, an easy way out of this problem is to deny that the LHB occurred as an impact spike. In this case, giant planet migration might have occurred as soon as the gas disc disappeared, without consequences on the terrestrial planets, which had not formed yet. We warn against this superficial position. It seems to us that there are at least four strong pieces of evidence in favour of the cataclysmic spike of the LHB: (i) basins on the Moon as big as Imbrium and Orientale could not have formed as late as 3.8 Gyr ago if the bombardment rate had been declining monotonically since the time of planet formation at the rate indicated by dynamical models without giant planet migration (Bottke et al. 2007); (ii) old zircons on Earth demonstrate that the climate on Earth 4.3-3.9 Gyr ago was relatively cool (i.e. the impact rate was low; Mojzsis et al. 2001), and that strong heating events, probably associated with impacts, happened approximately 3.8 Gyr ago (Trail et al. 2007); (iii) the most prominent impact basins on Mars occurred after the disappearance of Martian magnetic field (Lillis et al. 2006, 2007); (iv) impact basins on Iapetus occurred after the formation of its equatorial ridge, which is estimated to have formed between t= 200-800 Myr (Castillo-Rogez et al. 2007). Anybody seriously arguing against the cataclysmic nature of the LHB should find an explanation for each of these issues.
Third, one may argue that the origin of the LHB was not determined by a delayed migration of the giant planets, but that it was caused instead by dynamical events that concerned only the inner solar system. The model by Chambers (2007) does precisely this and, in our opinion, it is the most serious alternative to the Nice model, for the origin of the LHB. In Chambers' scenario, the system of terrestrial planets originally contained five planets. The fifth rogue planet, of sub-martian mass, was in between the current orbit of Mars and the inner edge of the asteroid belt. The orbit of this planet became unstable at a late epoch: after crossing the asteroid belt for some time and dislodging most of the asteroids originally resident in that region (which caused the LHB) the rogue planet was eventually removed by a collision with another planet, a collision with the Sun, or ejection from the solar system. Although appealing, this model has never been given much consideration and has never been tested in detail, for instance against the current structure of the asteroid belt and the magnitude of the LHB. We stress that Chambers' model cannot by any means explain the bombardment of Iapetus. Thus, to accept this model one has to find an alternative explanation of the late bombardent of this satellite of Saturn that does not involve or imply a migration of the giant planets or, alternatively, to prove that its ridge formed much earlier than estimated by Castillo-Rogez et al. (2007), so that the heavy bombardment of Iapetus could have occurred early.
As a final note, we remark that it is very dangerous to exclude or adopt a model based on probabilistic arguments on events that concern the habitability of the Earth, such as its orbital excitation. The fact that we are here to study these problems introduces an obvious observational bias: of all possible solar systems, we can be only in one that allows our existence, however improbable was the chain of events that led to its formation. The solar system is full of low-probability properties related to habitability: the presence of the Moon (necessary to stabilise the obliquity of the Earth; Laskar et al. 1993), the quasi-circular orbits of the giant planets (as opposed to the extra-solar planets), the absence of giant planets in the temperate zone, to quote only a few. Therefore, we think that the low probability to preserve a moderately excited orbit of the Earth cannot be used to disqualify the Nice model.
AcknowledgementsWe thank the reviewer C. Beaugé for useful comments. This work is part of the Helmholtz Alliance's ``Planetary evolution and Life'', which R.B. and A.M. thank for financial support. Exchanges between Nice and Thessaloniki have been funded by a PICS programme of France's CNRS, and R.B. thanks the host K.T. for his hospitality during a recent visit. R.G. thanks Brazil's CNPq and FAPERJ for support. H.F.L. is thankful for support from NASA's OSS and OPR programmes. Most of the simulations for this work were performed on the CRIMSON Beowulf cluster at OCA.
References
- Agnor, C. 2005, DPS, 37, 29.01
- Agnor, C., & Lin, D. 2007, BAAS, 38, 537 [NASA ADS]
- Agnor, C., Canup, R., & Levison, H. 1999, Icarus, 142, 219 [CrossRef] [NASA ADS]
- Allègre, C., Manhès, G., & Göpel, C. 2008, E&PSL, 267, 386 [CrossRef] [NASA ADS]
- Bottke, W., Levison, H., Nesvorný, D., & Dones, L. 2007, Icarus, 190, 203 [CrossRef] [NASA ADS]
- Castillo-Rogez, J. C., Matson, D. L., Sotin, C., et al. 2007, Icarus, 190, 179 [CrossRef] [NASA ADS]
- Chambers, J. 1999, MNRAS, 304, 793 [CrossRef] [NASA ADS]
- Chambers, J. 2001, Icarus, 152, 205 [CrossRef] [NASA ADS]
- Chambers, J. 2007, Icarus, 189, 386 [CrossRef] [NASA ADS]
- Chambers, J., & Wetherill, G. 1998, Icarus, 136, 34 [CrossRef]
- Correia, A., & Laskar, J. 2004, Nature, 429, 848 [CrossRef] [NASA ADS]
- Gomes, R., Morbidelli, A., & Levison, H. 2004, Icarus, 170, 492 [CrossRef] [NASA ADS]
- Gomes, R., Levison, H., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [CrossRef]
- Hahn, J., & Malhotra, R. 1999, AJ, 117, 3041 [CrossRef] [NASA ADS]
- Haisch, K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, 153 [CrossRef] [NASA ADS]
- Hartmann, W. K., Ryder, G., Dones, L., & Grinspoon, D. 2000, in Origin of the Earth and Moon, ed. R. Canup, & R. Knighter (Tucson, Arizona: Univ. Arizona Press)
- Jewitt, D., & Sheppard, S. 2005, Sp. Sci. Rev., 116, 441 [CrossRef] [NASA ADS]
- Kenyon, S., & Bromley, B. 2006, AJ, 131, 1837 [CrossRef] [NASA ADS]
- Knezevic, Z., Milani, A., Farinella, P., Froeschle, Ch., & Froeschle, Cl. 1991, Icarus, 93, 316 [CrossRef] [NASA ADS]
- Laskar, J. 1988, A&A, 198, 341 [NASA ADS]
- Laskar, J. 1990, Icarus, 88, 266 [CrossRef] [NASA ADS]
- Laskar, J. 1994, A&A, 287, L9 [NASA ADS]
- Laskar, J. 2008, Icarus, 196, 1 [CrossRef] [NASA ADS]
- Laskar, J., Joutel, F., & Robutel, P. 1993, Nature, 361, 615 [CrossRef] [NASA ADS]
- Levison, H., & Duncan, M. 1994, Icarus, 108, 18 [CrossRef] [NASA ADS]
- Levison, H. F., & Duncan, M. J. 1997, Icarus, 127, 13 [CrossRef] [NASA ADS]
- Levison, H. F., Dones, L., Chapman, C. R., et al. 2001, Icarus, 151, 286 [CrossRef] [NASA ADS]
- Levison, H., Morbidelli, A., & Dones, L. 2004, AJ, 128, 2553 [CrossRef] [NASA ADS]
- Lillis, R. J., Frey, H. V., Manga, M., et al. 2006, AGU Fall Meeting Abstracts A5
- Lillis, R. J., Frey, H. V., Manga, M., et al. 2007, LPI Contributions, 1353, 3090 [NASA ADS]
- Malhotra, R. 1995, AJ, 110, 420 [CrossRef] [NASA ADS]
- Masset, F., & Snellgrove, M. 2001, MNRAS, 320, 55 [CrossRef] [NASA ADS]
- Minton, D., & Malhotra, R. 2009, Nature, 457, 1109 [CrossRef] [NASA ADS]
- Mojzsis, S. J., Harrison, T. M., & Pidgeon, R. T. 2001, Nature, 409, 178 [CrossRef] [NASA ADS]
- Morbidelli, A. 2002, Modern Celestial Mechanics - Aspects of Solar System Dynamics (UK: Taylor & Francis)
- Morbidelli, A., & Crida, A. 2007, Icarus, 191, 158 [CrossRef] [NASA ADS]
- Morbidelli, A., Tsiganis, K., Crida, A., Levison, H., & Gomes, R. 2007, AJ, 134, 1790 [CrossRef] [NASA ADS]
- Murray, C., & Dermott, S. 1999, Solar System Dynamics (Cambridge, UK: Cambridge University Press)
- Nesvorný, D., Vokrouhlický, D., & Morbidelli, A. 2007, AJ, 133, 1962 [CrossRef] [NASA ADS]
- Nobili, A., & Will, C. 1986, Nature, 320, 39 [CrossRef] [NASA ADS]
- O'Brien, P., Morbidelli, A., & Levison, H. 2006, Icarus, 184, 39 [CrossRef] [NASA ADS]
- Petit, J.-M., Morbidelli, A., & Chambers, J. 2001, Icarus, 153, 338 [CrossRef] [NASA ADS]
- Pierens, A., & Nelson, R. 2008, A&A, 482, 333 [EDP Sciences] [CrossRef] [NASA ADS]
- Raymond, S. N., Quinn, T., & Lunine, J. I. 2004, Icarus, 168, 1 [CrossRef] [NASA ADS]
- Raymond, S. N., Quinn, T., & Lunine, J. I. 2005, ApJ, 632, 670 [CrossRef] [NASA ADS]
- Raymond, S. N., Quinn, T., & Lunine, J. I. 2006, Icarus, 183, 265 [CrossRef] [NASA ADS]
- Raymond, S. N., Quinn, T., & Lunine, J. I. 2007, Astrobiology, 7, 66 [CrossRef] [NASA ADS]
- Ryder, G., Koeberl, C., & Mojzsis, S. 2000, in Origin of the Earth and Moon, ed. R. Canup, & R. Knighter (Tucson, Arizona: Univ. Arizona Press)
- Saha, P., & Tremaine, S. 1994, AJ, 108, 1962 [CrossRef] [NASA ADS]
- Strom, R. G., Malhotra, R., Ito, T., Yoshida, F., & Kring, D. A. 2005, Science, 309, 1847 [CrossRef] [NASA ADS]
- Tsiganis, K., Gomes, R., Morbidelli, A., & Levison, H. 2005, Nature, 435, 459 [CrossRef] [NASA ADS]
- Thommes, E., Duncan, M., & Levison, H. 1999, Nature, 402, 635 [CrossRef] [NASA ADS]
- Thommes, E., Nilsson, L., & Murray, N. 2007, ApJ, 656, 25 [CrossRef] [NASA ADS]
- Touboul, M., Kleine, T., Bourdon, B., Palme, H., & Wieler, R. 2007, Nature, 450, 1206 [CrossRef] [NASA ADS]
- Trail, D., Mojzsis, S., & Harrison, T. 2007, GeCoA, 71, 4044 [NASA ADS]
- Wieczorek, M. A., Le Feuvre, M., Rambaux, N., Laskar, J., & Correia, A. C. M. 2009, LPISCA, 40, 1276 [NASA ADS]
Footnotes
- ...
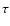
![[*]](/icons/foot_motif.png)
- We have verified this in our simulations.
All Tables
Table 3: Frequencies and phases for Mercury to Jupiter on their current orbits.
Table 4: Coefficients Mj,k of the Lagrange-Laplace solution for the terrestrial planets.
All Figures
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg1.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg14.png)
|
Figure 13:
The frequency g5 as a function of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg2.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg18.png)
|
Figure 14:
Evolution of the terrestrial planets during the g5=g2 and g5=g1 resonance crossings. The top panel shows the evolution of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg3.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg51.png)
|
Figure 15:
Evolution of the terrestrial planets during the g5=g2 and g5=g1 resonance crossings in where the g2 mode is damped down. The top panel shows
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg4.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg55.png)
|
Figure 16:
Evolution of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg5.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg58.png)
|
Figure 17: Magnification of the dynamics of Fig. 4, in the 180 000y-890 000y interval. The top panel now shows the evolution of Uranus' semi-major axis. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg6.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg74.png)
|
Figure 18: The evolution of the eccentricities of Mercury ( top), Venus and Earth (respectively solid and dashed lines) in the middle panel, and Mars ( bottom), during the dynamics of Jupiter and Saturn illustrated in Fig. 4. The initial orbits of the terrestrial planets are assumed to be circular and coplanar. The solid circles and vertical bars represent the eccentricity oscillation of Earth and Venus, as in Fig. 2. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg7.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg76.png)
|
Figure 19: The same as Fig. 6, but for terrestrial planets starting from their current orbits. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg8.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg79.png)
|
Figure 20: Top panel: the evolution of the period ratio between Saturn and Jupiter in another ``jumping Jupiter'' evolution from the Nice model. Middle and bottom panel: the evolutions of the eccentricities of Mercury and Venus, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg9.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg85.png)
|
Figure 21:
The evolution of eccentricities of Venus, Earth and Mars
in a simulation where Jupiter and Saturn approach slowly their 2:1 resonance. The top panel shows the evolution of the eccentricities of Mars (upper curve) and of Earth and Venus
(overlapping almost perfectly in a unique lower curve). The bottom panel shows
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg10.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg88.png)
|
Figure 22: The evolution of eccentricities of Venus, Earth and Mars, starting from circular orbits, in a simulation where Jupiter and Saturn migrate from within the 5:3 resonance to the 2:1 resonance. The top panel shows ratio of orbital periods between Saturn and Jupiter. The middle panel shows the evolution of the eccentricities of Mars (short dashed), Earth (long dashed) and Venus (solid). The bottom panel shows the eccentricities of Jupiter (solid) and Saturn (dashed). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg11.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg89.png)
|
Figure 23:
The same as Fig. 10,
but for terrestrial planets starting from their current orbits. Notice
that the evolution for Jupiter and Saturn is not exactly the same as
that of the previous simulation, despite the initial conditions
and |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{12878fg12.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12878-09/Timg96.png)
|
Figure 24: Evolution of the inclinations of Mercury (solid), Venus (dark dashed) Earth (light dashed) and Mars (dotted), all starting from 0, in the ``jumping Jupiter'' evolution shown in the top panel of Fig. 8. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.