| Issue |
A&A
Volume 507, Number 2, November IV 2009
|
|
|---|---|---|
| Page(s) | 1053 - 1065 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200912878 | |
| Published online | 15 September 2009 | |
Constructing the secular architecture of the solar system II: the terrestrial planets
1
Dep. Cassiopee, University of Nice – Sophia Antipolis, CNRS, Observatoire de la Côte d'Azur, 06304 Nice, France e-mail: brasser_astro@yahoo.com
2
Observatório Nacional, Rio de Janeiro, RJ, Brazil
3
Department of Physics, Aristotle University of Thessaloniki, Thessaloniki, Greece
4
Southwest Research Institute, Boulder, CO, USA
Received:
13
July
2009
Accepted:
31
August
2009
We investigate the dynamical evolution of the terrestrial planets during the planetesimal-driven migration of the giant planets. A basic assumption of this work is that giant planet migration occurred after the completion of terrestrial planet formation, such as in the models that link the former to the origin of the late heavy bombardment. The divergent migration of Jupiter and Saturn causes the g5 eigenfrequency to cross resonances of the form 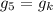 with k ranging from 1 to 4. Consequently these secular resonances cause large-amplitude responses in the eccentricities of the terrestrial planets if the amplitude of the g5 mode in Jupiter is similar to the current one. We show that the resonances
with k ranging from 1 to 4. Consequently these secular resonances cause large-amplitude responses in the eccentricities of the terrestrial planets if the amplitude of the g5 mode in Jupiter is similar to the current one. We show that the resonances 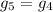 and
and 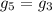 do not pose a problem if Jupiter and Saturn have a fast approach and departure from their mutual 2:1 mean motion resonance. On the other hand, the resonance crossings
do not pose a problem if Jupiter and Saturn have a fast approach and departure from their mutual 2:1 mean motion resonance. On the other hand, the resonance crossings 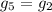 and
and 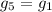 are more of a concern: they tend to yield a terrestrial system incompatible with the current one, with amplitudes of the g1 and g2 modes that are too large. We offer two solutions to this problem. The first solution states that a secular resonance crossing can also damp the amplitude of a Fourier mode if the latter is large originally. We show that the probability of the
are more of a concern: they tend to yield a terrestrial system incompatible with the current one, with amplitudes of the g1 and g2 modes that are too large. We offer two solutions to this problem. The first solution states that a secular resonance crossing can also damp the amplitude of a Fourier mode if the latter is large originally. We show that the probability of the 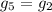 resonance damping a primordially excited g2 mode in the Earth and Venus is approximately 8%. Using the same mechanism to also ensure that the
resonance damping a primordially excited g2 mode in the Earth and Venus is approximately 8%. Using the same mechanism to also ensure that the 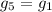 resonance keeps the amplitude of the g1 mode in Mercury within 0.4 reduces the overall probability to approximately 5%. However, these numbers may change for different initial excitations and migration speeds of the giant planets. A second scenario involves a “jumping Jupiter” in which encounters between an ice giant and Jupiter, without ejection of the former, cause the latter to migrate away from Saturn much faster than if migration is driven solely by encounters with planetesimals. In this case, the
resonance keeps the amplitude of the g1 mode in Mercury within 0.4 reduces the overall probability to approximately 5%. However, these numbers may change for different initial excitations and migration speeds of the giant planets. A second scenario involves a “jumping Jupiter” in which encounters between an ice giant and Jupiter, without ejection of the former, cause the latter to migrate away from Saturn much faster than if migration is driven solely by encounters with planetesimals. In this case, the 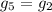 and
and 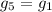 resonances can be jumped over, or occur very briefly. We show that, in this case, the terrestrial system can have dynamical properties comparable to what is exhibited today. In the framework of the Nice model, we estimate that the probability that Jupiter had this kind of evolution is approximately
resonances can be jumped over, or occur very briefly. We show that, in this case, the terrestrial system can have dynamical properties comparable to what is exhibited today. In the framework of the Nice model, we estimate that the probability that Jupiter had this kind of evolution is approximately 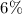 .
.
Key words: solar system: formation / planets and satellites: formation
© ESO, 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


