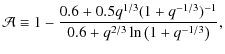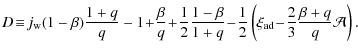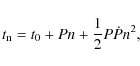| Issue |
A&A
Volume 507, Number 2, November IV 2009
|
|
|---|---|---|
| Page(s) | 617 - 620 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/200912803 | |
| Published online | 15 September 2009 | |
A&A 507, 617-620 (2009)
Constraints on the size of extra dimensions from the orbital evolution of the black-hole X-ray binary XTE J1118+480
T. Johannsen
Physics Department, The University of Arizona, 1118 E. 4th Street, Tucson, AZ 85721, USA
Received 1 July 2009 / Accepted 9 September 2009
Abstract
Context. To constrain Randall-Sundrum type
braneworld gravity models and the expected rapid evaporation of
astrophysical black holes due to the emission of gravitational modes in
the extra dimension.
Aims. It is argued that the black-hole X-ray binary
XTE J1118+480 is suitable for a constraint on the asymptotic
curvature radius of the extra dimension in such braneworld models.
An upper limit on the rate of change of the orbital period of
XTE J1118+480 is obtained.
Methods. The expected black-hole evaporation in the
extra dimension leads to a potentially observable rate of change of the
orbital period in XTE J1118+480. The time-change of the
orbital period is calculated from previous orbital period measurements
from the literature. The lack of observed orbital period evolution is
used to constrain the asymptotic curvature radius of the extra
dimension.
Results. The asymptotic AdS radius of curvature is
constrained to a value comparable to other limits from astrophysical
sources. A unique property of XTE J1118+480 is that the
expected rate of change of the orbital period due to magnetic braking
alone is so large that only one additional measurement of the orbital
period would lead to the first detection of orbital evolution in a
black-hole binary and impose the tightest constraint to date on the
size of one extra dimension of the order of
![]() .
.
Key words: gravitation - black hole physics - X-rays: binaries - stars: individual: J1118+480 - X-rays: stars
1 Introduction
The so-called hierarchy problem is one of the key open questions in the search for a grand theory beyond general relativity and the standard model. The fundamental scale of Einsteinian gravity, the Planck scale, differs from the electroweak scale by 16 orders of magnitude, thus making general relativity and the standard model hard to reconcile in a grand unification scheme. Braneworld gravity, as a candidate for a unified theory, requires the existence of more than three spatial dimensions (see Maartens 2004, for a review), but the size of a potential extra dimension has already been constrained to the sub-mm range by precision tests of Newton's inverse square law (see, e.g., Adelberger et al. 2003, for a review).
One possible solution (Arkani-Hamed et al. 1998) is to demand that extra dimensions be compactified at a scale smaller than those probed by experiment. All standard-model particles are bound to the known four-dimensional world (``the brane''). Only gravity can access the extra dimensions, which accounts for its apparent weakness, because it is spread out through higher-dimensional space (``the bulk''). This approach reconciles the gravitational and the electroweak scales if the extra dimensions are large enough, but it is beyond the scope of astrophysical tests.
A second scenario (Randall & Sundrum 1999) embeds the brane in a five-dimensional anti-de Sitter space, which allows for the extra dimension to be infinite. The bulk is filled with a negative cosmological constant such that the extra dimension only effects the brane on a length scale which is small enough and which is set by the asymptotic curvature radius L of the bulk. This model has striking consequences for astrophysical black holes.
Perturbative solution of the classical bulk equations (Tanaka 2003) indicated that no stable black holes can exist on the brane. A treatment of higher-dimensional black holes via the AdS/CFT correspondence showed that black holes are indeed unstable and lose energy in the extra dimension through the emission of CFT modes (Emparan et al. 2003; see, however, Fitzpatrick et al. 2006). The lifetimes of astrophysical black holes are dramatically reduced and can be as short as a Megayear if the asymptotic curvature L of the extra dimension turns out to be in the sub-mm range.
For a binary system consisting of a black hole and a companion
star, this effect should be observable and lead to a measurable change
of the orbital period (Johannsen et al. 2009). Several
black-hole binaries were identified as candidates, and the system
SXT A0620-00 yielded a constraint on the asymptotic curvature
radius of ![]() at 3
at 3![]() (Johannsen et al. 2009). Similar limits have been obtained
from the age of the black hole XTE J1118+480 (
(Johannsen et al. 2009). Similar limits have been obtained
from the age of the black hole XTE J1118+480 (
![]() ;
Psaltis 2007) and from tabletop experiments of Newton's inverse square
law (Adelberger et al. 2007;
Geraci et al. 2008). The
current 3
;
Psaltis 2007) and from tabletop experiments of Newton's inverse square
law (Adelberger et al. 2007;
Geraci et al. 2008). The
current 3![]() -upper
limit on the AdS radius L is of the order
of
-upper
limit on the AdS radius L is of the order
of
![]() (Kapner et al. 20072007).
(Kapner et al. 20072007).
In this paper, I extend the analysis of Johannsen
et al. (2009) to the black-hole binary XTE J1118+480
and compute an additional constraint on the asymptotic curvature
radius L. In Sect. 2,
I briefly review the results of Johannsen et al.
(2009) for the evolution of the orbital period of a black-hole binary
system with non-conservative mass transfer and black-hole evaporation.
In Sect. 3, I apply this result to the black-hole
binary J1118+480 and I obtain a constraint on the
asymptotic curvature radius of
![]() in Sect. 4.
in Sect. 4.
2 Black-hole binaries in braneworld gravity
For a binary system with a black hole of mass m1
and a companion star of mass m2
on a circular orbit, the orbital angular momentum,
![]() ,
is subject to change because of magnetic braking (e.g., Webbink
et al. 1983) and the evolution of the secondary star (e.g.,
Verbunt 1993). Here,
,
is subject to change because of magnetic braking (e.g., Webbink
et al. 1983) and the evolution of the secondary star (e.g.,
Verbunt 1993). Here, ![]() ,
,
![]() ,
and a is the semi-major axis.
A third effect is the emission of CFT modes in the
extra dimension (Johannsen et al. 2009), where the black-hole
mass loss is given by (Emparan et al. 2003)
,
and a is the semi-major axis.
A third effect is the emission of CFT modes in the
extra dimension (Johannsen et al. 2009), where the black-hole
mass loss is given by (Emparan et al. 2003)
Here, L is the asymptotic AdS radius of curvature.
This leads to a change of the orbital period of (Johannsen
et al. 2009)
where

Here, P is the orbital period,
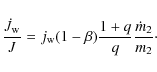
|
(4) |
In this expression,
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12803f1.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12803-09/Timg42.png)
|
Figure 1:
The rate of change of the orbital period P
of the binary systems J1118+480 and A0620-00 versus the
asymptotic curvature radius L in the extra
dimension. The parameters are
|
| Open with DEXTER | |
Observations of the system A0620-00 have been used previously in
conjunction with the above theoretical prediction to constrain the
asymptotic curvature radius to a value of
![]() (Johannsen et al. 2009). In the following, I apply
the formalism above to the system XTE J1118+480.
(Johannsen et al. 2009). In the following, I apply
the formalism above to the system XTE J1118+480.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{12803f2a.eps}\hspace*{1cm}
\...
...eps}\hspace*{1cm}
\includegraphics[width=5.25cm,clip]{12803f2c.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12803-09/Timg45.png)
|
Figure 2:
The rate of change of the orbital period P
(in years) of the binary system J1118+480 versus the specific
angular momentum removed by the stellar wind |
| Open with DEXTER | |
3 The orbital evolution of XTE J1118+480
In order to obtain a constraint on the asymptotic curvature radius L of the extra dimension, it is essential to select a black-hole binary with an unevolved companion star. In that case, the evolution term in Eq. (2) can be neglected, and the binary can be used to constrain the AdS radius as long as the magnetic braking term is negligible compared to the evaporation term. In the following I argue that this approach can be applied to the black-hole binary J1118+480, and I use previous measurements of its orbital period to place a bound on the rate of change of its orbital period.
Table 1: The observed orbital periods and times of measurement for J1118+480.
The system J1118+480 has been monitored for more than a decade
(Remillard & McClintock 2006). The companion star of the black
hole resembles a late-type main-sequence star of spectral
type K7 V-M0 V (Wagner et al.
2001). In addition, the mean density is only ![]() 50% higher than for a usual main-sequence
M0 star (McClintock et al. 2001), and the mass is
only
50% higher than for a usual main-sequence
M0 star (McClintock et al. 2001), and the mass is
only ![]() 50% lower
than that of such a star (see Charles & Coe 2006).
50% lower
than that of such a star (see Charles & Coe 2006).
It is important to note that this is not simply a normal star. It has emerged out of an exeptional evolutionary history (see de Kool et al. 1986, for an example), and it does not evolve on a nuclear timescale. For my analysis, however, it is sufficient that the secondary only behaves like a main-sequence star. Then the evolution term in Eq. (2) is negligible.
Considering only the evaporation term and the magnetic braking
term in Eq. (2),
I plot in Fig. 1
the rate of change of the orbital period versus the asymptotic
curvature radius L in the extra dimension
for the binary systems J1118+480 and A0620-00. The parameters
used in this plot are ![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() .
For values of the asymptotic curvature radius greater than
.
For values of the asymptotic curvature radius greater than
![]() the evaporation term dominates the evolution of the orbital period in
the case of J1118+480. Below that value, the magnetic braking is
predominant. For the binary A0620-00 the transition occurs at
the evaporation term dominates the evolution of the orbital period in
the case of J1118+480. Below that value, the magnetic braking is
predominant. For the binary A0620-00 the transition occurs at
![]() (Johannsen et al. 2009). Consequently, these sources are
similar in constraining the asymptotic curvature radius of the extra
dimension.
(Johannsen et al. 2009). Consequently, these sources are
similar in constraining the asymptotic curvature radius of the extra
dimension.
A measurement of a positive rate of change of the orbital period automatically constrains the asymptotic curvature radius to an interval, as can be seen by simply evaluating the magnetic braking term. For a binary system with a high mass ratio, i.e. m1/m2>5.5, the effect of magnetic braking can only decrease the orbital period (Johannsen et al. 2009). Thus such a measurement actually determines the AdS radius L and would prove the existence of an extra dimension.
In Fig. 2,
I plot the rate of change of the orbital period of J1118+480 as a
function of the parameters ![]() ,
,
![]() ,
and
,
and ![]() .
On varying one of them, the others are held constant at the respective
values
.
On varying one of them, the others are held constant at the respective
values ![]() ,
,
![]() ,
and
,
and ![]() .
For all plots I choose
.
For all plots I choose
![]() and
and ![]() ,
which is the value of the current experimental limit (Kapner
et al. 2007). I am interested in the smallest rate of
orbital period evolution, so in the following I set
the parameters to the respective values
,
which is the value of the current experimental limit (Kapner
et al. 2007). I am interested in the smallest rate of
orbital period evolution, so in the following I set
the parameters to the respective values
![]() (no angular momentum loss due to stellar wind),
(no angular momentum loss due to stellar wind), ![]() (no accretion onto the black hole), and
(no accretion onto the black hole), and ![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12803f3.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12803-09/Timg52.png)
|
Figure 3: The times T0 of the inferior conjunction and residuals versus the orbital cycle number n for the black-hole binary J1118+480. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12803f4.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2009/44/aa12803-09/Timg54.png)
|
Figure 4:
The minimum rate of change of the orbital period P
of the binary J1118+480 versus the asymptotic curvature
radius L in the extra dimension. The
intersection point of the observed 3 |
| Open with DEXTER | |
The orbital period P of J1118+480 has been measured several times over the past decade. Based on those measurements, I calculate the rate of change of the orbital period. Table 1 shows the orbital period measurements for J1118+480. The values are for the most part consistent with each other, indicating an at most small change of the period over the last years.
Assuming a constant rate of change of the orbital period, the
time of the nth orbital cycle is given by
(e.g., Kelley et al. 1983)
where P is the orbital period at time
4 Results
Using the values of the orbital period derivative calculated in
Sect. 3, I compute a limit on the asymptotic
curvature radius of the extra dimension. For the mass of the black hole
I use the best fit value of
![]() (cf. Charles & Coe 2006).
(cf. Charles & Coe 2006).
The 3![]() -upper
limit on the observed rate of change of the orbital period and the
smallest theoretical expectation thereof determine an upper bound on
the AdS curvature radius L. In
Fig. 4,
I plot the rate of change of the orbital period of J1118+480
for the set of parameters that minimizes it
(cf. Sect. 3). The intersection point of this curve
with the 3
-upper
limit on the observed rate of change of the orbital period and the
smallest theoretical expectation thereof determine an upper bound on
the AdS curvature radius L. In
Fig. 4,
I plot the rate of change of the orbital period of J1118+480
for the set of parameters that minimizes it
(cf. Sect. 3). The intersection point of this curve
with the 3![]() -upper
limit on the orbital period evolution yields a constraint on the
AdS curvature radius of
-upper
limit on the orbital period evolution yields a constraint on the
AdS curvature radius of
![]() .
.
This value is comparable to the constraint obtained from
A0620-00 (Johannsen et al. 2009). A refinement of
that upper bound would be easy to obtain and simply requires an
additional measurement of the orbital period. The fact that the period
change due to magnetic braking is so large for J1118+480 in the case
where the black-hole evaporation is negligible (
![]() ;
cf. Fig. 1)
has two important consequences. First, even one additional measurement
of the orbital period in 2009 (n=17 000)
with an error in the ephemeris T0
of the order of
;
cf. Fig. 1)
has two important consequences. First, even one additional measurement
of the orbital period in 2009 (n=17 000)
with an error in the ephemeris T0
of the order of ![]() would prove the period derivative to be negative at
would prove the period derivative to be negative at ![]() ,
hence measuring the first orbital period evolution of a black-hole
X-ray binary. Second, such a measurement would show that black-hole
evaporation is negligible against magnetic braking in this binary,
which would in turn impose a constraint of the order of
,
hence measuring the first orbital period evolution of a black-hole
X-ray binary. Second, such a measurement would show that black-hole
evaporation is negligible against magnetic braking in this binary,
which would in turn impose a constraint of the order of
![]() on the size of one extra dimension, the tightest constraint
to date.
on the size of one extra dimension, the tightest constraint
to date.
The constraint on the asymptotic curvature radius also depends
on the mass of the primary, but since the black-hole mass has been
measured quite precisely (m1=6.8 ![]()
![]() ;
from Charles & Coe 2006), its effect is small.
;
from Charles & Coe 2006), its effect is small.
5 Conclusions
- 1.
- The black-hole binary XTE J1118+480 is well-suited for a constraint on the asymptotic curvature radius of the extra dimension in Randall-Sundrum type braneworld gravity models.
- 2.
- An upper limit on the rate of change of the orbital period
of XTE J1118+480 is calculated based on previous measurements
of the orbital period from the literature. The lack of observed orbital
evolution of this binary imposes a constraint on the asymptotic
curvature radius of
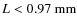 .
.
- 3.
- This constraint can be significantly improved by only one
additional measurement of the orbital period of XTE J1118+480.
This would be the first detection of orbital evolution in a black-hole
binary. The expected predominance of magnetic braking would provide the
best constraint to date on the asymptotic curvature radius of the extra
dimension of the order of
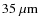 .
.
I would like to thank Dimitrios Psaltis for carefully reading the manuscript. This work was supported by the NSF CAREER award NSF 0746549.
References
- Adelberger, E. G., Heckel, B. R., Hoedl, S., et al. 2007, PRL, 98, 131104 [CrossRef] [NASA ADS]
- Arkani-Hamed, N., Dimopoulos, S., & Dvali, G. 1998, Phys. Lett. B, 429, 263 [CrossRef] [NASA ADS]
- Charles, P. A., & Coe, M. J. 2003, in Compact Stellar X-ray Sources ed. W. H. G. Lewin, & M. van der Klis (Cambridge University Press) [arXiv:0308020]
- de Kool, M., van den Heuvel, E. P. J., & Pylyser, E. 1987, A&A, 183
- Emparan, R., García-Bellido, J., & Kaloper, N. 2003, JHEP, 0301, 079 [CrossRef] [NASA ADS]
- Fitzpatrick, A. L., Randall, L., & Wiseman, T. 2006, JHEP, 0611, 033 [CrossRef] [NASA ADS]
- Gelino, D. M., & Harrison, T. E. 2003, ApJ, 599, 1254 [CrossRef] [NASA ADS]
- Geraci, A. A., Smullin, S. J., Weld, D. M., Chiaverini, J., & Kapitulnik, A. 2008, Phys. Rev. D, in press [arXiv:0802.2350.v1]
- Gonzalez Hernandez, J. I., Rebolo, R., Israelian, G., et al. 2008, ApJ, 679, 732 [CrossRef] [NASA ADS]
- Johannsen, T., Psaltis, D., & McClintock, J. E. 2009, ApJ, 691, 997 [CrossRef] [NASA ADS]
- Kalogera, V., & Webbink, R. F. 1996, ApJ, 458, 301 [CrossRef] [NASA ADS]
- Kapner, D. J., Cook, T. S., Adelberger, E. G., et al. 2007, Phys. Rev. Lett., 98, 021101 [CrossRef] [NASA ADS]
- Kelley, R. L., Rappaport, S., Clark, G. W., & Petro, L. D. 1982, ApJ, 268, 790 [CrossRef] [NASA ADS]
- Maartens, R. 2004, LRR, 7, 7 [NASA ADS]
- McClintock, J. E., & Remillard, R. A. 1986, ApJ, 308, 110 [CrossRef] [NASA ADS]
- McClintock, J. E., Garcia, M. R., Caldwell, N., et al. 2001, ApJ, 551, 147 [CrossRef] [NASA ADS]
- Psaltis, D. 2007, Phys. Rev. Lett., 98, 181101 [CrossRef] [NASA ADS]
- Randall, L., & Sundrum, R. 1999, Phys. Rev. Lett., 83, 4690 [CrossRef] [NASA ADS]
- Rappaport, S., Verbunt, F., & Joss, P. C. 1983, ApJ, 275, 713 [CrossRef] [NASA ADS]
- Tanaka, T. 2003, Prog. Theor. Phys. Suppl., 148, 307 [CrossRef] [NASA ADS]
- Torres, M. A. P., Callanan, P. J., Garcia, M. R., et al. 2004, ApJ, 612, 1026 [CrossRef] [NASA ADS]
- Verbunt, F. 1993, ARA&A, 31, 93 [CrossRef] [NASA ADS]
- Wagner, R. M., Foltz, C. B., Shahbaz, T., et al. 2001, ApJ, 556, 42 [CrossRef] [NASA ADS]
- Webbink, R. F., Rappaport, S., & Savonije, G. J. 1983, ApJ, 270, 678 [CrossRef] [NASA ADS]
- Will, C. M., & Zaglauer, H. W. 1989, ApJ, 346, 366 [CrossRef] [NASA ADS]
- Yungelson, L., & Lasota, J.-P. 2008, New Astron. Rev., 51, 860 [CrossRef] [NASA ADS]
- Zurita, C., Casares, J., Shahbaz, T., et al. 2002, MNRAS, 333, 791 [CrossRef] [NASA ADS]
All Tables
Table 1: The observed orbital periods and times of measurement for J1118+480.
All Figures
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12803f1.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12803-09/Timg42.png)
|
Figure 1:
The rate of change of the orbital period P
of the binary systems J1118+480 and A0620-00 versus the
asymptotic curvature radius L in the extra
dimension. The parameters are
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{12803f2a.eps}\hspace*{1cm}
\...
...eps}\hspace*{1cm}
\includegraphics[width=5.25cm,clip]{12803f2c.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12803-09/Timg45.png)
|
Figure 2:
The rate of change of the orbital period P
(in years) of the binary system J1118+480 versus the specific
angular momentum removed by the stellar wind |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12803f3.eps}
\end{figure}](/articles/aa/full_html/2009/44/aa12803-09/Timg52.png)
|
Figure 3: The times T0 of the inferior conjunction and residuals versus the orbital cycle number n for the black-hole binary J1118+480. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12803f4.eps}
\vspace*{2mm}
\end{figure}](/articles/aa/full_html/2009/44/aa12803-09/Timg54.png)
|
Figure 4:
The minimum rate of change of the orbital period P
of the binary J1118+480 versus the asymptotic curvature
radius L in the extra dimension. The
intersection point of the observed 3 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



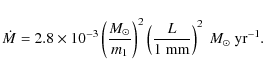
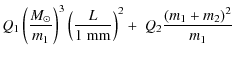
![$\displaystyle \times ~ \left[\frac{0.49q^{-2/3}}{0.6q^{-2/3}+\ln(1+q^{-1/3})}\r...
...gamma}
\left[\frac{\sqrt{G(m_{1}+m_{2})}}{2\pi}P\right]^{\frac{2}{3}(\gamma-5)}$](/articles/aa/full_html/2009/44/aa12803-09/img25.png)
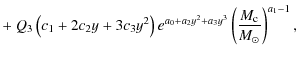
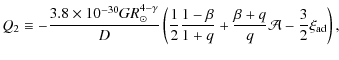
![$\displaystyle Q_{3}\!\equiv\!1.37 \times 10^{-11} \times 4^{a_{1}}
\left[\frac{...
...\beta+q}{q}\mathcal{A}\!-\!\frac{3}{2}\xi_{{\rm ad}}\right)-\frac{3}{2}\right],$](/articles/aa/full_html/2009/44/aa12803-09/img31.png)