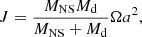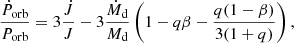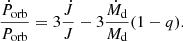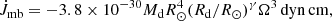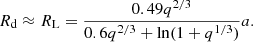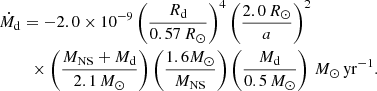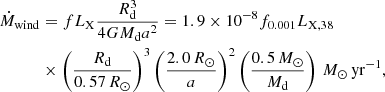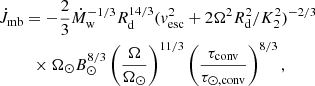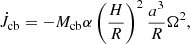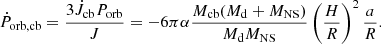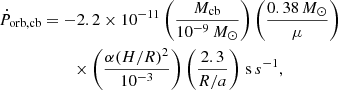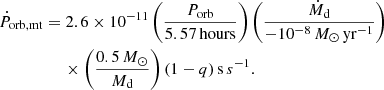| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202346397 | |
| Published online | 09 November 2023 | |
Anomalous orbital expansion of the low-mass X-ray binary 2A 1822-371: the existence of a circumbinary disk?
1
School of Science, Qingdao University of Technology, Qingdao 266525, PR China
e-mail: chenwc@pku.edu.cn
2
School of Physics and Electrical Information, Shangqiu Normal University, Shangqiu 476000, PR China
Received:
13
March
2023
Accepted:
19
September
2023
Source 2A 1822-371 is an eclipsing low-mass X-ray binary (LMXB) consisting of a neutron star (NS) and a ∼0.5 M⊙ donor star in an orbit of 5.57 h. Based on the timing of the eclipse arrival times, this source was found to experience a rapid orbital expansion with an orbital period derivative as Ṗorb = (1.51 ± 0.05) × 10−10 s s−1, implying that the mass-transfer rate is probably higher than at least three times the Eddington accretion rate. The standard magnetic braking (MB) model cannot produce a mass-transfer rate this high. The modified MB model can produce a high mass-transfer rate, resulting in a high Ṗorb. We propose an alternative model to account for the anomalously high mass-transfer rate and Ṗorb of 2A 1822-371. During the mass transfer, a tiny fraction of the transferred material is thought to form a circumbinary (CB) disk around the LMXB, which can efficiently extract orbital angular momentum from the system by the interaction between the CB disk and the binary. We used the MESA code to model the formation and evolution of 2A 1822-371 for different CB-disk masses. When the CB-disk mass is 2.3 × 10−8 M⊙, the simulation can reproduce the observed donor-star mass, orbital period, and orbital period derivative. This CB disk can accelerate the evolution of the binary and produce a high mass-transfer rate of 1.9 × 10−7 M⊙ yr−1, driving the binary to evolve toward a wide-orbit system. Therefore, we propose that CB disks may cause the rapid orbital changes observed in some LMXBs.
Key words: binaries: eclipsing / stars: neutron / stars: mass-loss
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
According to the masses of the companion stars, strong Galactic X-ray sources are mainly classified into two groups: high-mass X-ray binaries, and low-mass X-ray binaries (LMXBs) (Tauris et al. 2006). In LMXBs, a neutron star (NS) or black hole accretes materials from its donor star with a mass lower than 1 − 2 M⊙ by Roche-lobe overflow (RLOF) and emits strong X-rays. Due to the long accretion phase in LMXBs, the accreting NSs are spun up to a millisecond period and evolve into millisecond pulsars (Alpar et al. 1982; Radhakrishnan & Srinivasan 1982). Therefore, the study of LMXBs is significant for understanding the formation and evolution of millisecond pulsars. Furthermore, LMXBs provide much information about mass exchange and angular momentum loss, which makes them ideal probes for testing stellar and binary evolution theory.
Source 2A 1822-371 (sometimes named X 1822-371) is a persistent eclipsing LMXB with a short orbital period of 5.57 h (Mason et al. 1980; White et al. 1981), in which an NS with a relatively low spin frequency of ν ∼ 1.69 Hz (Jonker & van der Klis 2001) is spinning up at a rate of 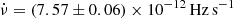 via a mass accretion (Jain et al. 2010; Iaria et al. 2015; Bak Nielsen et al. 2017). According to the partial eclipses, 2A 1822-371 was hypothesized to be an accretion disk corona source (White & Holt 1982), and the inclination angle was inferred to be 81° −85° (Heinz & Nowak 2001; Ji et al. 2011).
via a mass accretion (Jain et al. 2010; Iaria et al. 2015; Bak Nielsen et al. 2017). According to the partial eclipses, 2A 1822-371 was hypothesized to be an accretion disk corona source (White & Holt 1982), and the inclination angle was inferred to be 81° −85° (Heinz & Nowak 2001; Ji et al. 2011).
The mass function of 2A 1822-371 was measured to be f(M) = (2.03 ± 0.03)×10−2 M⊙ (Jonker & van der Klis 2001), resulting in a minimum companion-star mass of Md = 0.33 ± 0.05 M⊙ (Jonker et al. 2003). By studying the K correction for the emission lines formed in the X-ray illuminated atmosphere of the donor star, the masses of the NS and the donor star were constrained to be 1.61 M⊙ ≤ MNS ≤ 2.32 M⊙ and 0.44 M⊙ ≤ Md ≤ 0.56 M⊙, respectively (Muñoz-Darias et al. 2005).
Based on the distance of 2.5 kpc, the unabsorbed X-ray luminosity of 2A 1822-371 was calculated to be LX ≃ 1.0 × 1036 erg s−1, yielding a mean ratio of the X-ray to optical luminosity of LX/Lopt ∼ 20 (Mason & Cordova 1982). This ratio is much lower than the typical luminosity ratio (LX/Lopt ∼ 1000) of LMXBs, implying that the intrinsic luminosity of 2A 1822-371 may exceed the Eddington limit (Bayless et al. 2010; Burderi et al. 2010). Magnetic braking (MB) is the main mechanism driving the mass transfer of LMXBs with long orbital periods. However, it is challenging to produce a super-Eddington mass transfer in this LMXB with a low-mass donor star with the standard MB model given by Rappaport et al. (1983).
The orbital evolution of source 2A 1822-371 also remains mysterious. Based on the analysis of eclipses detected by the HEAO-1, Einstein, Exosat, and Ginga, its orbital period was thought to increase at a rate of Ṗorb = (2.19 ± 0.58) × 10−10 s s−1 (Hellier et al. 1990). Based on an improved ephemeris for the optical eclipses, Bayless et al. (2010) confirmed that its orbital period is rapidly changing at a rate of Ṗorb = 2.12 × 10−10 s s−1. Subsequently, the orbital period derivative of 2A 1822-371 was independently measured to be Ṗorb = (1.50 ± 0.07) × 10−10 s s−1 (Burderi et al. 2010), Ṗorb = (1.59 ± 0.09) × 10−10 s s−1 (Iaria et al. 2011), Ṗorb = (1.464 ± 0.041) × 10−10 s s−1 (Chou et al. 2016), and Ṗorb = (1.475 ± 0.054) × 10−10 s s−1 (Mazzola et al. 2019). Recently, the orbital period derivative was refined to be Ṗorb = (1.51 ± 0.05) × 10−10 s s−1 based on the updated orbital ephemeris joining two new eclipse times related to NuSTAR and Swift observations (Anitra et al. 2021). This orbital-period derivative is three orders of magnitude higher than that derived from conservative mass transfer driven by MB and gravitational radiation, implying that the mass-transfer rate is probably higher than at least three times the Eddington accretion rate of an NS (Burderi et al. 2010; Bayless et al. 2010). As mentioned above, the standard MB model cannot produce such a high mass-transfer rate for a low-mass donor star. Therefore, the formation and evolution of the source 2A 1822-371 challenges the conventional binary evolution theory and may require a new MB description or new physical mechanisms.
2. Analysis of the orbital evolution
The total orbital angular momentum of an LMXB consisting of an NS and a low-mass donor star can be written as
where MNS and Md are the NS mass and the donor-star mass, respectively; Ω = 2π/Porb is the orbital angular velocity of the binary, and a is the orbital separation. When we insert Kepler’s third law (G(MNS + Md)/a3 = Ω2) into Eq. (1) and differentiate it, the orbital period derivative satisfies
where ẋ = dx/dt, q = Md/MNS is the mass ratio of the binary, and β = −ṀNS/Ṁd is the accretion efficiency of the NS.
2.1. Conservative mass transfer
In the case of conservative mass transfer, β = 1, Eq. (2) changes into
The first term on the right-hand side of Eq. (3) would produce a negative Ṗorb because 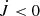 , while the mass transfer from the less massive donor star to the more massive NS would cause a positive Ṗorb since Ṁd < 0 and q < 1 (see also the second term on the right-hand side). The rate of angular momentum loss predicted by the standard MB model is
, while the mass transfer from the less massive donor star to the more massive NS would cause a positive Ṗorb since Ṁd < 0 and q < 1 (see also the second term on the right-hand side). The rate of angular momentum loss predicted by the standard MB model is
where Rd is the donor-star radius, and γ is a dimensionless magnetic braking index from 0 to 4 (Rappaport et al. 1983). We adopted the simplest approximation as γ = 4 (Verbunt & Zwaan 1981). Because the donor star filled its Roche lobe, its radius can be estimated as (Eggleton 1983)
For a binary with an orbital period exceeding 3 h, the rate of angular momentum loss through gravitational radiation is weaker than that by MB. Hence the contribution of gravitational radiation can be ignored. Taking Porb = 5.57 h, Ṗorb = 1.51 × 10−10 s s−1, MNS = 1.6 M⊙, and Md = 0.5 M⊙, we have Rd = 0.57 R⊙, a = 2.0 R⊙, 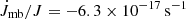 , and Ṗorb/P = 7.5 × 10−15 s−1. Because
, and Ṗorb/P = 7.5 × 10−15 s−1. Because 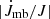 is two orders of magnitude smaller than Ṗorb/P, the contribution of angular momentum loss to Ṗorb of 2A 1822-371 is trivial. Therefore, according to equation (3), the mass-transfer rate can be derived as |Ṁd| = (5.76 ± 0.19) × 10−8 M⊙ yr−1.
is two orders of magnitude smaller than Ṗorb/P, the contribution of angular momentum loss to Ṗorb of 2A 1822-371 is trivial. Therefore, according to equation (3), the mass-transfer rate can be derived as |Ṁd| = (5.76 ± 0.19) × 10−8 M⊙ yr−1.
2.2. Nonconservative mass transfer
The calculated mass-transfer rate of 2A 1822-371 is higher than the Eddington accretion rate (ṀEdd = 1.5 × 10−8 M⊙ yr−1), hence the mass transfer of 2A 1822-371 is probably nonconservative, that is, the accretion efficiency β ≠ 1. To study the influence of the accretion efficiency, we plot the relation between the mass-transfer rate and the accretion efficiency β in Fig. 1 according to Eq. (2) (the contribution of angular momentum loss for Ṗorb is still ignored1). It is clear that a low accretion efficiency tends to require a low mass-transfer rate to produce the observed orbital period derivative. For MNS = 1.6 M⊙ and Md = 0.5 M⊙, β = 1 predicts a mass-transfer rate of ≈ 5.8 × 10−8 M⊙ yr−1, which is consistent with the mass-transfer rate predicted by the conservative mass-transfer case. The mass-transfer rate apparently depends weakly on the accretion efficiency. Even if the NS does not accrete any material (β = 0), it still requires a mass-transfer rate of ∼ (4 − 5) × 10−8 M⊙ yr−1 to produce the observed Ṗorb of 2A 1822-371. Furthermore, the NS mass and the donor star mass can also alter the derived mass-transfer rate. However, the effect of the latter is more significant than that of the former. Therefore, this rapid orbital expansion implies a rapid mass transfer between the donor star and the accreting NS of 2A 1822-371.
 |
Fig. 1. Mass-transfer rate vs. accretion efficiency of the NS of 2A 1822-371. We take Porb = 5.57 h, Ṗorb = 1.51 × 10−10 s s−1. The solid, dashed, and dotted curves represent the cases when (MNS, Md) = (1.6, 0.5),(1.8, 0.5), and (1.6, 0.6) M⊙, respectively. |
2.3. Some possible models
When q = 0.5/1.6 ≈ 0.31, the standard MB model predicts an approximate mass-transfer rate as (Pavlovskii & Ivanova 2016)
For some typical parameters of 2A 1822-371, the estimated mass-transfer rate is 2.0 × 10−9 M⊙ yr−1, which is about one order of magnitude lower than that derived from the observed orbital period derivative. Similarly, the inferred mass-transfer rates of some LMXBs with short orbital periods are found to be at least an order of magnitude higher than theoretically expected values (Podsiadlowski et al. 2002). To solve this discrepancy problem between observation and theory, Van & Ivanova (2019) modified the MB prescription and proposed a convection- and rotation-boosted (CARB) MB model (see also Sect. 2.4).
Chou et al. (2016) argued that the unusual Ṗorb may be caused by the X-ray radiation-driven mass loss proposed by Tavani & London (1993). Assuming that a fraction (f, i.e., the efficiency of irradiation-driving wind) of the X-ray luminosity that the donor star receives conquers the gravitational bind energy of the material on the surface of the donor star and drives a strong wind (with a velocity equal to the escape speed of the donor surface), the loss rate of the irradiation-driving winds is (Chen & Podsiadlowski 2016)
where f0.001 = f/0.001, LX,38 = LX/1038 erg s−1. Tavani & London (1993) obtained the efficiencies of irradiation-driving wind in the range from 0.001 to 0.1. Therefore, it is possible to produce a relatively high wind-loss rate from the donor star because the intrinsic X-ray luminosity of 2A 1822-371 may exceed 1038 erg s−1. The irradiation-driving winds may also play a key role in producing a positive orbital period derivative of the first discovered accreting millisecond pulsar SAX J1808.4-3658 (Chen 2017).
Considering angular momentum loss due to MB by coupling between the strong magnetic field and an irradiation-driving wind (Justham et al. 2006), Xing & Li (2019) used the MESA code to model the evolution of an LMXB consisting of a 1.4 M⊙ NS and a 1.1 M⊙ donor star on an initial orbit of 0.4 days. Taking a wind-driving efficiency of f = 5 × 10−3 and a magnetic field of 900 G, their simulated total mass-loss rate of the donor star is ∼ 10−7 M⊙ yr−1 when the donor star mass is ∼0.5 M⊙. This irradiation-driving wind model can account for the donor mass, orbital period, orbital-period derivative, and high X-ray luminosity of 2A 1822-371.
2.4. CARB MB model
The CARB MB model considered the influence of the donor star rotation on the stellar wind velocity (Matt et al. 2012; Réville et al. 2015) and the influences of the donor star convective-turnover timescale and the donor star rotation on its surface magnetic field (Parker 1971; Noyes et al. 1984; Ivanova 2006; Van et al. 2019). When these mechanisms are included, the rate of angular momentum loss can be written as (Van & Ivanova 2019)
where Ṁw, and vesc are the wind mass-loss rate and the surface escape velocity of the donor star, respectively; K2 = 0.07 is a constant originating from a grid of simulations (Réville et al. 2015); τconv is the turnover time of convective eddies; B⊙ = 1 G is the surface magnetic field strength of the Sun, and the surface-rotation rate and the convective-turnover time of the Sun are Ω⊙ ≈ 3.0 × 10−6 s−1, and τ⊙,conv = 2.8 × 106 s (see also Van et al. 2019), respectively (for some information regarding the inlists and subroutines used to simulate the mass-transfer process of LMXBs in the CARB MB model, see also Mangat et al. 2022).
The CARB MB model can reproduce the observed mass-transfer rates and orbital periods at the detected mass ratio for all observed persistent NS LMXBs in the Galaxy (Van & Ivanova 2019). Using the CARB MB model, Van & Ivanova (2021) investigated the potential progenitors of the observed persistent NS LMXBs and found that these progenitors occupy a small part of the plausible parameter space in the diagram of the initial donor-star mass versus initial orbital period. Deng et al. (2021) also found that the CARB MB model can successfully reproduce the observed characteristics of all persistent NS LMXBs and binary pulsars. Because the CARB MB model can result in a high mass-transfer rate (∼ 10−7 M⊙ yr−1) for persistent NS LMXBs (Van & Ivanova 2019, 2021) that is higher than the required mass-transfer rate (see also Sect. 2.2), the observed parameters of 2A 1822-371 can be reproduced.
We attempt to explore an alternative mechanism that can result in a rapid mass transfer and produce the rapid orbital expansion observed in source 2A 1822-371. Based on a circumbinary (CB) disk model, we present a detailed stellar evolution model for the formation of 2A 1822-371 in Sect. 3. In Sect. 4 we discuss the possible influence of the input parameters and the observed confirmation. Finally, we give a summary in Sect. 5.
3. CB disk model
3.1. CB disk model
During the mass transfer of an LMXB, a tiny fraction of the transferred material may be ejected by the strong radiation pressure of the accreting NS. Because the ejecta possess high orbital angular momentum, they may form a CB disk that surrounds the system and may not completely leave it (van den Heuvel & de Loore 1973; van den Heuvel 1994). The resonant torque produced by the interaction between the CB disk and the binary can extract orbital angular momentum from the orbital motion. Based on an assumption of a standard thin disk, the rate of angular momentum loss via a CB disk can be expressed as (Chen & Podsiadlowski 2019)
where Mcb, α, H, and R are the mass, viscosity parameter, thickness, and half angular momentum radius of the CB disk, respectively.
For simplicity, a CB disk with a constant mass is assumed to surround the LMXB if a mass transfer occurs. Assuming that the ratio between the half angular momentum radius and the orbital separation is a constant (R/a = 2.3) in three black hole LMXBs, Chen & Podsiadlowski (2019) found that the derived CB-disk masses around XTE J1118 and A0620-00 are consistent with the inferred values (Mcb ∼ 10−9 M⊙, Muno & Mauerhan 2006) when α = 0.1, H/R = 0.1. As for the black hole LMXBs, we also took α = 0.1, H/R = 0.1, and R/a = 2.3 for 2A 1822-371. The CB-disk parameters, including α, H/R, and R/a, might be different for NS LMXBs and black hole LMXBs. However, both Mcb and α(H/R)2R/a are degenerate in Eq. (9). Therefore, some uncertainties resulting from α, H/R, and R/a can be compensated for by slightly altering the CB-disk mass.
3.2. Stellar evolution code
We employed the MESA binary module of the code called modules for experiments in stellar astrophysics code (MESA; version r-12115; Paxton et al. 2011, 2013, 2015; Paxton et al. 2018, 2019) to calculate the formation and evolution of source 2A 1822-371. The progenitor of the source was assumed to be a binary system consisting of an NS and a low-mass main-sequence (MS) star on a circular orbit. The code only models the nuclear synthesis and evolution of the MS companion star, and the NS is considered a point mass. The initial chemical composition of the MS companion star was taken to be solar, that is, X = 0.70, Y = 0.28, and Z = 0.02.
During the mass transfer, the mass-growth rate of the NS is limited by the Eddington accretion rate (ṀEdd = 1.5 × 10−8 M⊙ yr−1), that is, the mass-growth rate of the NS Ṁns = (Ṁedd,Ṁtr), where Ṁtr is the mass-transfer rate. During the accretion, the excess material in unit time (Ṁtr − Ṁns) is thought to be reemitted as an isotropic fast wind that carries the specific orbital angular momentum of the NS away (Tauris & van den Heuvel 2023).
Using the MESA code, we modeled the evolution of an LMXB consisting of an NS with a mass of 1.6 M⊙ and an MS donor star with a mass of 1.0 M⊙ for two independent models: the CARB MB, and the CB disk models. In the CARB MB model, angular momentum loss via gravitational radiation and MB (see also Sect. 2.4) is included. For the CB-disk model, a tiny fraction of the transferred material was assumed to form a CB disk with a constant mass when mass transfer occurs. The torque originating from the resonant interaction between the CB disk and the binary can therefore extract orbital angular momentum from the orbital motion at a rate of 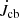 (see also Eq. (10)2. Furthermore, the gravitation radiation and the standard MB mechanism proposed by Rappaport et al. (1983) with γ = 4 were also considered. The MB mechanism (the CARB MB or the standard MB) would work when the donor star possesses both a convective envelope and a radiative core.
(see also Eq. (10)2. Furthermore, the gravitation radiation and the standard MB mechanism proposed by Rappaport et al. (1983) with γ = 4 were also considered. The MB mechanism (the CARB MB or the standard MB) would work when the donor star possesses both a convective envelope and a radiative core.
In the calculation, we altered the initial orbital period and/or the CB-disk mass to obtain a model that can match the observed properties of 2A 1822-371, as listed in Table 1. In the CARB MB description, an NS binary with a donor star of 1.75 M⊙ and an initial orbital period of 0.5 days can evolve into 2A 1822-371 (Van & Ivanova 2021). Therefore, the initial orbital period ranges from 0.31 (the donor star has already filled its Roche lobe at the beginning of the evolution if the initial orbital period is shorter than 0.31 days) to 2.0 days in our models. Similar to the inferred CB-disk mass of three black hole LMXBs (Chen & Podsiadlowski 2019), the CB-disk mass was assumed to be in the range of ∼10−9 − 10−7 M⊙.
Some observed data o source 2A 1822-371.
3.3. Simulation results
Our simulations find that the evolution of a binary consisting of a 1.6 M⊙ NS and a 1.0 M⊙ donor star on an initial orbit of 0.35 days can match the observed properties of 2A 1822-371. The evolution of the orbital period and donor star mass with stellar age is shown in the top and bottom panels of Fig. 2, respectively. Before the donor star fills its Roche lobe, MB causes the orbit to shrink, and the orbital period decreases to ∼0.3 days. The evolutionary tracks with four different CB-disk masses are the same at this stage. When the stellar age is t = 1.28 × 107 yr, the donor star fills its Roche lobe and initiates mass transfer. Because of a tiny outflow from the mass transfer, a CB disk forms that surrounds the binary. Different CB-disk masses result in different rates of angular momentum loss driving the binary to evolve along different evolutionary tracks. A high-mass CB disk results in rapid angular momentum loss and causes the system to evolve into a minimum orbital period on a short timescale. Our simulations indicate that a CB disk with Mcb = 2.3 × 10−8 M⊙ can successfully account for the observed orbital period and donor star mass of 2A 1822-371 when t = 1.59 × 107 yr. The models with Mcb = 1.0 × 10−7 and 1.0 × 10−9 M⊙ also appear to reproduce the observed orbital period in the orbital-expansion stage, but the corresponding donor star masses for Mcb = 1.0 × 10−9 are much lower than observed (see also Fig. 3). It is worth emphasizing that the orbital period with Mcb = 0 (i.e., the mass transfer is only driven by the standard MB mechanism) continuously decreases without experiencing an orbital expansion stage for the observed donor star mass of 2A 1822-371. At the stellar age of t = 1.1 × 107 yr, the CARB MB model can also successfully produce the observed orbital period and donor-star mass of 2A 1822-371. At the current orbital period, the NS masses calculated with the CB-disk and CARB MB models are 1.65 M⊙ and 1.71 M⊙, respectively.
 |
Fig. 2. Evolution of an LMXB consisting of a 1.6 M⊙ NS and a 1.0 M⊙ MS donor star with an initial orbit of 0.35 days in the orbital period vs. stellar age diagram (top panel), and the donor-star mass vs. stellar age diagram (bottom panel). The horizontal short dashed line in the top panel indicates the orbital period of 2A 1822-371, and the horizontal short dashed lines in the bottom panel represent the inferred upper and lower limits of the donor star mass. |
Figure 3 plots the evolution of LMXBs in the diagram of the orbital period versus the donor star mass. Three evolutionary tracks when Mcb = 2.3 × 10−8 M⊙, Mcb = 1.0 × 10−7 M⊙, and the CARB MB agree with the observed data of 2A 1822-371, while the orbit of the binary continuously shrinks for Mcb = 1.0 × 10−9 M⊙, and Mcb = 0, without experiencing an orbital expansion stage in the observed range of the donor star mass.
 |
Fig. 3. Same as in Fig. 2, but for the diagram of the orbital period vs. donor star mass. The solid circle represents the observed data for source 2A 1822-371. |
Figure 4 illustrates the evolution of the orbital period derivative of LMXBs with three different CB-disk masses and the CARB MB model in the Ṗorb − Porb diagram. To compare this with the observation, we only plot the evolution of Ṗorb in the orbital expansion stage (the evolutionary track with Mcb = 0 is not included because the orbital period derivative is negative at the current orbital period). Four orbital periods steadily climb after the minimum orbital periods, resulting in positive orbital period derivatives. Two orbital-period derivatives predicted by the CB-disk model with Mcb = 2.3 × 10−8 M⊙ and the CARB MB model are approximately consistent with the observed value at the current orbital period, while the simulated Ṗorb are greater and smaller than the observation for Mcb = 1.0 × 10−7 M⊙ and 1.0 × 10−9 M⊙, respectively. On the other hand, these orbital period derivatives also show an increasing tendency. The factors leading to an increasing Ṗorb are very complicated, while the main two factors are the increasing orbital period and the decreasing donor star mass. When the contribution of angular momentum loss is ignored, Eq. (2) yields Ṗorb ∝ Ṗorb/Md. Therefore, the increasing orbital period and the decreasing donor star mass might cause the increasing Ṗorb.
 |
Fig. 4. Same as in Fig. 2, but for the diagram of the orbital period derivative vs. orbital period. The solid circle represents the observed data for source 2A 1822-371. |
The evolution of the mass-transfer rates of LMXBs is presented in Fig. 5. When the mass transfer starts, the five evolutionary tracks are different because the angular momentum loss rates are different. The three models with Mcb = 2.3 × 10−8 M⊙, Mcb = 1.0 × 10−7 M⊙, and the CARB MB clearly experience a super-Eddington mass transfer in the current range of the donor star mass. A high CB-disk mass of 1.0 × 10−7 M⊙ produces a high mass-transfer rate of ∼ 10−7 − 10−6 M⊙ yr−1. Therefore, CB disks can accelerate the mass exchange and shorten the evolutionary timescale of LMXBs. The mass-transfer rates produced by the CB-disk model with Mcb = 2.3 × 10−8 M⊙ and the CARB MB model are 1.9 × 10−7 M⊙ yr−1, and 1.6 × 10−7 M⊙ yr−1 at the current donor star mass, respectively. These two mass-transfer rates are approximately one order of magnitude higher than the analytical estimation ((4.3 − 5.8) × 10−8 M⊙ yr−1) in Sect. 2. This difference arises because the torque exerted by the CB disk or the CARB MB causes a significant negative orbital-period derivative. In other words, an efficient angular momentum loss is worthy of a rapier in influencing the orbital evolution of LMXBs as follows: First, it produces a negative Ṗorb,aml due to rapid angular momentum loss, and second, it also results in a positive Ṗorb,mt because the mass transfer from the less massive donor star to the more massive NS is rapid (see also Eq. (2)). To compensate for the influence of the negative Ṗorb,aml, it requires a higher mass-transfer rate to produce the observed Ṗorb. The simulated mass-transfer rates when Mcb = 0, and 1.0 × 10−9 M⊙ are always lower than the Eddington-accretion rate, resulting in a negative orbital period derivative in the observed range of the donor star mass. The main reason is that Ṗorb,mt is smaller than |Ṗorb,aml|, thus the total period derivative (Ṗorb = Ṗorb,aml+ Ṗorb,mt) is still negative. As Md ∼ 0.3 M⊙, the mass-transfer rates produced by the CARB and the standard MB models decrease sharply, which arises from the cut-off of MB when the donor stars become fully convective.
 |
Fig. 5. Same as in Fig. 2, but for the evolution of the mass-transfer rates as a function of the donor star masses. The horizontal short dashed line denotes the Eddington-accretion rate. |
4. Discussion
Our standard model proposes that the progenitor of 2A 1822-371 consists of a 1.6 M⊙ NS and a 1.0 M⊙ MS companion star on an orbit of 0.35 days, which is surrounded by a CB disk with Mcb = 2.3 × 10−8 M⊙ during the mass transfer. In this section, we investigate the influence of the initial parameters, including the initial donor star mass (Md, i) and the initial orbital period (Porb, i). Figure 6 depicts the evolution of NS-MS star binaries with different initial companion star masses and initial orbital periods in the Porb-Md diagram. All five models can evolve to the current orbital period in the orbital expansion stage. The initial orbital periods can be disregarded in the evolution of the binaries toward source 2A 1822-371 in the orbital expansion stage. The models with (Md,i,Porb,i) = (1.0 M⊙,0.6 days), and (1.0 M⊙,1.0 day) can also reproduce the observed orbital period and donor star mass. Another system with a relatively high donor star mass of 1.1 M⊙ and the same orbital period of 0.35 days is the potential progenitor of 2A 1822-371. Three models with (Md,i,Porb,i) = (1.0 M⊙,0.35 days), (1.0 M⊙,6.0 days), and (1.0 M⊙,1.0 day) have a similar evolutionary tendency and slope, resulting in a similar Ṗorb (see also Fig. 8).
 |
Fig. 6. Evolutionary tracks of LMXBs with different initial donor star masses and initial orbital periods in the diagram of the orbital period vs. donor star mass. The solid curves represent our standard model with Md, i = 1.0 M⊙ and Ṗorb,i = 0.35 days. A CB disk with a mass of Mcb = 2.3 × 10−8 M⊙ is included in all models. The solid circle represents the observed data for source 2A 1822-371. |
To account for the current NS mass of 2A 1822-371, both the CB-disk model and the CARB MB model found that the NS was born massive (∼1.6 M⊙). This is very similar to PSR J1614-2230 and PSR J1640+2224, which were proposed to be born with masses of ∼1.95 M⊙ (Tauris et al. 2011) and > 2.0 M⊙ (Deng et al. 2020), respectively. Because the mass-transfer rate in the early stage was relatively low (see also Fig. 5), the accretion efficiency of the CARB MB model is slightly higher than that of the CB-disk model.
The similar evolutionary tendencies of the five curves in Fig. 6 probably originate from similar mass-transfer rates. Figure 7 summarizes the evolution of the mass-transfer rates as a function of the donor star masses. The model with (Md,i,Porb,i) = (0.8 M⊙,0.35 days) appears to possess the highest mass-transfer rate at the current stage of 2A 1822-371. In the observed range of the donor star mass, five models have similar mass-transfer rates (1.7 − 2.1 × 10−7 M⊙ yr−1), which are higher than theoretical estimation in Sect. 2. A high mass-transfer rate naturally results in rapid orbital expansion, which can compensate for the orbital shrinking caused by angular momentum loss. Therefore, the orbital evolution of the five models has an expansion tendency.
 |
Fig. 7. Same as in Fig. 6, but for the evolution of mass-transfer rates as a function of the donor star masses. The horizontal short dashed line denotes the Eddington-accretion rate. |
Figure 8 shows the evolution of LMXBs with different initial donor star masses and initial orbital periods in the Ṗorb − Porb diagram. A low donor star mass appears to produce a high orbital-period derivative at the current orbital period of 2A 1822-371. Three models with a 1.0 M⊙ donor star and initial orbital periods of 0.35, 0.6, and 1.0 day can approximately reproduce the observed orbital-period derivative of 2A 1822-371. In other words, the peculiar observed properties of this source are probably associated with three initial parameters: the initial donor star mass, the initial orbital period, and the CB-disk mass.
 |
Fig. 8. Evolution of orbital period derivatives of LMXBs plotted in Fig. 6 in the Ṗorb − Porb diagram. For simplicity, we only plot the evolutionary tracks in the orbit-expansion stage. The solid circle represents the observed data for source 2A 1822-371. |
To produce the observed orbital period derivative of 2A 1822-371, our CB-disk model predicts a relatively high mass-transfer rate of 1.9 × 10−7 M⊙ yr−1. This mass-transfer rate is higher than the mass-accretion rate (1.6 − 5.0 × 10−8 M⊙ yr−1) derived from the intrinsic luminosity of 2A 1822-371 (Van et al. 2019). This implies a strong outflow during the mass transfer, which would absorb a large fraction of the X-ray radiation, resulting in a low observed luminosity. On the other hand, because the orbital inclination angle of this source is in the range of 81° −85° (Heinz & Nowak 2001; Ji et al. 2011), an edge-on accretion disk may cause the low X-ray luminosity in observations.
Some uncertainties exist in our simulation. The orbital period derivative produced by the mass transfer in our standard model is ![$ \dot{P}_{\mathrm{orb,mt}}=-3P_{\mathrm{orb}}\frac{\dot{M}_{\mathrm{d}}}{M_{\mathrm{d}}}[1-q\beta-\frac{q(1-\beta)}{3(1+q)}]\approx6.5\times10^{-10}\,\rm s\,s^{-1} $](/articles/aa/full_html/2023/11/aa46397-23/aa46397-23-eq15.gif) when we take Md = 0.5 M⊙, MNS = 1.6 M⊙, β = 0.1, and Ṁd = 1.9 × 10−7 M⊙ yr−1. Because the observed donor star mass is Md = 0.5 ± 0.06 M⊙, it has an uncertainty of 12%. The observed mass-transfer rate is Ṁd = (3.3 ± 1.7) × 10−8 M⊙ yr−1, which has an approximate uncertainty of 50%. We can approximately estimate the minimum uncertainty of Ṗorb,mt as
when we take Md = 0.5 M⊙, MNS = 1.6 M⊙, β = 0.1, and Ṁd = 1.9 × 10−7 M⊙ yr−1. Because the observed donor star mass is Md = 0.5 ± 0.06 M⊙, it has an uncertainty of 12%. The observed mass-transfer rate is Ṁd = (3.3 ± 1.7) × 10−8 M⊙ yr−1, which has an approximate uncertainty of 50%. We can approximately estimate the minimum uncertainty of Ṗorb,mt as  3, thus Ṗorb,mt ≈ (6.5 ± 3.3) 10× 10−10 s s−1. The orbital period derivative produced by the CB disk is (Chen & Podsiadlowski 2019)
3, thus Ṗorb,mt ≈ (6.5 ± 3.3) 10× 10−10 s s−1. The orbital period derivative produced by the CB disk is (Chen & Podsiadlowski 2019)
Taking Mcb = 2.3 × 10−8 M⊙, we have Ṗorb,cb = −4.95 × 10−10 s s−1. Some uncertainties also exist in the CB-disk mass and the disk parameters α(H/R)2a/R. In the black hole LMXB XTE J1118+480, a rapid orbital decay with an orbital period derivative as Ṗorb = −(6.01 ± 1.81) 10× 10−11 s s−1 was detected (González Hernández et al. 2014), and its surrounding CB-disk mass was constrained to be 10−9 M⊙. Taking H/R = 0.1, a/R = 1/2.3, Md = 0.18 M⊙, and the black hole mass MBH = 8 M⊙, this yields α = 0.13 ± 0.04 according to equation (10). Therefore, the α = 0.1 that we adopt has an uncertainty of at least ∼30%. Those uncertainties of other parameters are difficult to estimate. For simplicity, the minimum uncertainty of Ṗorb,cb is ∼30%, that is, Ṗorb,cb = (−4.95 ± 1.49) × 10−10 s s−1. Because Ṗorb = Ṗorb,mt + Ṗorb,cb, the minimum error of Ṗorb is 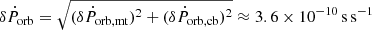 . As a consequence, the orbital period derivative is Ṗorb = (1.55 ± 3.6) × 10−10 s s−1, in which the expected error exceeds our simulated value by a factor of 2 at least.
. As a consequence, the orbital period derivative is Ṗorb = (1.55 ± 3.6) × 10−10 s s−1, in which the expected error exceeds our simulated value by a factor of 2 at least.
Compared with Xing & Li (2019), an NS-MS star binary with a CB disk can evolve into 2A 1822-371 in a wide initial orbital period range (0.35 − 1.0 days). Because the rate of angular momentum loss due to MB by coupling between the strong magnetic field and an irradiation-driving wind is lower than that by a CB disk, it requires a relatively short initial orbital period to reproduce the observed orbital period and orbital period derivative. As a consequence, the excited wind-driving mass-transfer model found that the progenitor of 2A 1822-371 is a narrow-orbit system with a short orbital period of 0.4 days when the surface magnetic field of the donor star is 900 G (Xing & Li 2019). Another difference between these two models is the evolutionary tendency of the mass-transfer rates. In the observed range of the donor star mass, the CB disk model predicts a decreasing mass-transfer rate (see also Figs. 5 and 7); but the rate obtained by the excited wind-driving mass-transfer model is increasing (Xing & Li 2019). Because the mass transfers of both models are super-Eddington, it is hard to test the validity of these two models according to the observed X-ray luminosities.
If a CB disk exists around source 2A 1822-371, the infrared radiation might confirm its existence, as for GG Tau (Roddier et al. 1996). In particular, recent works performed by the Wide-Field Infrared Survey Explorer confirmed that the three black hole LMXBs XTE J1118+480, A0620-00, GRS 1915+105, and NS LMXB 3A 1728-247 are surrounded by CB disks (Wang & Wang 2014). However, the orbital period (1160.8 days) of NS LMXB 3A 1728-247 is much longer than that of 2A 1822-371. Therefore, there still is no observable evidence for the existence of such a CB disk around NS LMXBs similar to 2A 1822-371. Furthermore, because the orbital inclination angle of 2A 1822-371 is in the range of 81° −85° (Heinz & Nowak 2001; Ji et al. 2011), it is challenging to detect an edge-on CB disk. We expect that the powerful new infrared capabilities of the James Webb Space Telescope will confirm or disprove whether a CB disk encloses the source 2A 1822-371.
In theory, a CB disk around LMXBs can not only cause a rapid orbital expansion, but can also lead to fast orbital shrinkage. According to Eq. (11), the angular momentum loss caused by a CB disk results in a negative orbital period derivative as
where μ = MdMNS/(Md + MNS) is the reduced mass of LMXBs. For β = 1, the mass transfer produces a positive orbital period derivative as
The orbital evolution fates of LMXBs would depend on the competition between Ṗorb,cb and Ṗorb,mt. For an LMXB such as 2A 1822-371, Md = 0.5 M⊙, μ = 0.38 M⊙, Porb = 5.57 h, we have Ṗorb,cb = −2.2 × 10−11 s s−1 if the system is surrounded by a CB disk with a mass similar to XTE J1118+480. Similarly, Ṗorb,mt = (0.26 ± 2.6) × 10−11 s s−1 if the system possesses a mass ratio (q = 0.31) similar to 2A 1822-371 and a mass-transfer rate in the range from 10−9 M⊙ yr−1 to 10−8 M⊙ yr−1. As a result, the total orbital period derivative (Ṗorb = Ṗorb,cb + Ṗorb,mt) is in the range from −1.94 × 10−11 s s−1 to 0.4 × 10−11 s s−1. Therefore, the LMXB would evolve toward a wide-orbit binary like 2A 1822-371 for a high mass-transfer rate. Otherwise, the result is a narrow-orbit system like the black hole LMXBs XTE J1118+480 and A0620-00 (Xu & Li 2018; Chen & Podsiadlowski 2019).
5. Summary
According to the observed orbital period derivative of 2A 1822-371, our analysis finds that the mass-transfer rate must be in the range of (4.3 − 5.8) × 10−8 M⊙ yr−1, which is insensitive to the accretion efficiency of the NS. In addition to gravitational radiation and MB, it requires an additional mechanism to efficiently extract angular momentum from the system, resulting in a rapid mass transfer.
We attempted to investigate whether a surrounding CB disk can explain the anomalous orbital-period derivative of 2A 1822-371. For typical CB-disk parameters of α = 0.1, H/R = 0.1, and R/a = 2.3, detailed stellar evolution models show that a CB disk with a mass of Mcb = 2.3 × 10−8 M⊙ can reproduce the observed orbital period, donor star mass, and orbital period derivative of 2A 1822-371. However, the expected error of the orbital period derivative exceeds our simulated value by a factor of 2 at least. According to our simulations, the progenitor of source 2A 1822-371 is probably a binary system including a 1.6 M⊙ NS and a 1.0 M⊙ MS companion star on an initial orbit of 0.35 − 1.0 days. Although the angular momentum loss by the CB disk causes rapid orbital shrinkage, the high mass-transfer rate of 1.9 × 10−7 M⊙ yr−1 from the less massive donor star to the more massive NS causes a more significant orbital expansion. It is noteworthy that there is no direct observational evidence that 2A 1822-371 has such a high mass-transfer rate.
Our calculations also find that CB disks can accelerate the mass exchange of LMXBs and alter their evolutionary fates, which strongly depend on the CB-disk masses and mass-transfer rate. For a system similar to 2A 1822-371, a CB disk with a mass of Mcb = 10−9 M⊙ would cause its orbit to widen for a high mass-transfer rate of 10−8 M⊙ yr−1. However, the orbit of the system would continuously shrink for the same CB disk and a low mass-transfer rate of 10−9 M⊙ yr−1. We stress that observable evidence of a CB disk like this is still absent in NS LMXBs similar to 2A 1822-371.
It is worth emphasizing that the CARB MB model can not only interpret the observed characteristics of all persistent NS LMXBs (Van & Ivanova 2019, 2021) and binary pulsars (Deng et al. 2021), but can also reproduce the anomalous orbital period derivative of 2A 1822-371. Therefore, it might be the best MB model to replace the standard MB model in the binary evolution model in the future.
In principle, a mass-loss rate exceeding Ṁedd would carry away the specific angular momentum of the NS, which contributes ![$ (\dot{J}/J)_{\mathrm{ml}}=(1-\beta)\dot{M}_{\mathrm{d}}q/[(1+q)M_{\mathrm{ns}}] $](/articles/aa/full_html/2023/11/aa46397-23/aa46397-23-eq21.gif) . Therefore, the ratio of the first and second term on the right-hand side of Eq. (2) is (1 − β)q2/[1 − qβ − q(1 − β)/(3 + 3q)]/(1 + q). For 2A 1822-371, this ratio is about 0.075 when we take q = 0.3 and β = 0; hence
. Therefore, the ratio of the first and second term on the right-hand side of Eq. (2) is (1 − β)q2/[1 − qβ − q(1 − β)/(3 + 3q)]/(1 + q). For 2A 1822-371, this ratio is about 0.075 when we take q = 0.3 and β = 0; hence 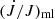 can be ignored.
can be ignored.
Here, the uncertainty of 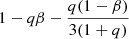 was not considered. We also ignored the uncertainty of angular momentum loss by MB because
was not considered. We also ignored the uncertainty of angular momentum loss by MB because 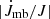 is two orders of magnitude smaller than Ṗorb/P (see also Sect. 2.1).
is two orders of magnitude smaller than Ṗorb/P (see also Sect. 2.1).
Acknowledgments
We are extremely grateful to the anonymous referee for very constructive and detailed comments that improved this manuscript. This work was partly supported by the National Natural Science Foundation of China (under grant numbers 12273014, 12373044, 11733009), Natural Science Foundation (under grant number ZR2021MA013) of Shandong Province.
References
- Alpar, M. A., Cheng, A. F., Ruderman, M. A., & Shaham, J. 1982, Nature, 300, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Anitra, A., Di Salvo, T., Iaria, R., et al. 2021, A&A, 654, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bak Nielsen, A.-S., Patruno, A., & D’Angelo, C. 2017, MNRAS, 468, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Bayless, A. J., Robinson, E. L., Hynes, R. I., Ashcraft, T. A., & Cornell, M. E. 2010, ApJ, 709, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Burderi, L., Di Salvo, T., Riggio, A., et al. 2010, A&A, 515, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, W.-C. 2017, MNRAS, 464, 4673 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, W.-C., & Podsiadlowski, P. 2016, ApJ, 830, 131 [CrossRef] [Google Scholar]
- Chen, W.-C., & Podsiadlowski, P. 2019, ApJ, 876, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Chou, Y., Hsieh, H.-E., Hu, C.-P., Yang, T.-C., & Su, Y.-H. 2016, ApJ, 831, 29 [CrossRef] [Google Scholar]
- Deng, Z.-L., Gao, Z.-F., Li, X.-D., & Shao, Y. 2020, ApJ, 892, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Deng, Z.-L., Li, X.-D., Gao, Z.-F., & Shao, Y. 2021, ApJ, 909, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
- González Hernández, J. I., Rebolo, R., & Casares, J. 2014, MNRAS, 438, L21 [CrossRef] [Google Scholar]
- Heinz, S., & Nowak, M. A. 2001, MNRAS, 320, 249 [CrossRef] [Google Scholar]
- Hellier, C., Mason, K. O., Smale, A. P., & Kilkenny, D. 1990, MNRAS, 244, 39 [NASA ADS] [Google Scholar]
- Iaria, R., Di Salvo, T., Burderi, L., et al. 2011, A&A, 534, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iaria, R., Di Salvo, T., Matranga, M., et al. 2015, A&A, 577, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivanova, N. 2006, ApJ, 653, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Jain, C., Paul, B., & Dutta, A. 2010, MNRAS, 409, 755 [CrossRef] [Google Scholar]
- Ji, L., Schulz, N. S., Nowak, M. A., & Canizares, C. R. 2011, ApJ, 729, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Jonker, P. G., & van der Klis, M. 2001, ApJ, 553, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Jonker, P. G., van der Klis, M., & Groot, P. J. 2003, MNRAS, 339, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Justham, S., Rappaport, S., & Podsiadlowski, P. 2006, MNRAS, 366, 1415 [CrossRef] [Google Scholar]
- Mangat, C. S., Ivanova, N., & Van, K. 2022, Astron. Comput., 42, 100681 [Google Scholar]
- Mason, K. O., & Cordova, F. A. 1982, ApJ, 262, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, K. O., Middleditch, J., Nelson, J. E., et al. 1980, ApJ, 242, L109 [CrossRef] [Google Scholar]
- Matt, S. P., Pinzón, G., Greene, T. P., & Pudritz, R. E. 2012, ApJ, 745, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzola, S. M., Iaria, R., Di Salvo, T., et al. 2019, A&A, 625, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muno, M. P., & Mauerhan, J. 2006, ApJ, 648, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Darias, T., Casares, J., & Martínez-Pais, I. G. 2005, ApJ, 635, 502 [CrossRef] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [Google Scholar]
- Parker, E. N. 1971, ApJ, 164, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlovskii, K., & Ivanova, N. 2016, MNRAS, 456, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Podsiadlowski, P., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Radhakrishnan, V., & Srinivasan, G. 1982, Curr. Sci., 51, 1096 [NASA ADS] [Google Scholar]
- Rappaport, S., Verbunt, F., & Joss, P. C. 1983, ApJ, 275, 713 [Google Scholar]
- Réville, V., Brun, A. S., Matt, S. P., Strugarek, A., & Pinto, R. F. 2015, ApJ, 798, 116 [Google Scholar]
- Roddier, C., Roddier, F., Northcott, M. J., Graves, J. E., & Jim, K. 1996, ApJ, 463, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., & van den Heuvel, E. P. J. 2006, in Compact stellar X-ray sources, eds. W. Lewin, & M. van der Klis (Cambridge: Cambridge Univ. Press), 623 [CrossRef] [Google Scholar]
- Tauris, T. M., & van den Heuvel, E. P. J. 2023, Physics of Binary Star Evolution (Princeton: University Press), 825 [Google Scholar]
- Tauris, T. M., Langer, N., & Kramer, M. 2011, MNRAS, 416, 2130 [NASA ADS] [CrossRef] [Google Scholar]
- Tavani, M., & London, R. 1993, ApJ, 410, 281 [Google Scholar]
- Van, K. X., & Ivanova, N. 2019, ApJ, 886, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Van, K. X., & Ivanova, N. 2021, ApJ, 922, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Van, K. X., Ivanova, N., & Heinke, C. O. 2019, MNRAS, 483, 5595 [NASA ADS] [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J. 1994, in Interacting Binaries, eds. S. N. Shore, et al. (Saas-Fee 22; Berlin: Springer), 263 [NASA ADS] [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J., & de Loore, C. 1973, A&A, 25, 387 [NASA ADS] [Google Scholar]
- Verbunt, F., & Zwaan, C. 1981, A&A, 100, L7 [NASA ADS] [Google Scholar]
- Wang, X., & Wang, Z. 2014, ApJ, 788, 184 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. E., & Holt, S. S. 1982, ApJ, 257, 318 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. E., Becker, R. H., Boldt, E. A., et al. 1981, ApJ, 247, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Xing, Z.-P., & Li, X.-D. 2019, ApJ, 887, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, X.-T., & Li, X.-D. 2018, ApJ, 859, 46 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Mass-transfer rate vs. accretion efficiency of the NS of 2A 1822-371. We take Porb = 5.57 h, Ṗorb = 1.51 × 10−10 s s−1. The solid, dashed, and dotted curves represent the cases when (MNS, Md) = (1.6, 0.5),(1.8, 0.5), and (1.6, 0.6) M⊙, respectively. |
| In the text | |
 |
Fig. 2. Evolution of an LMXB consisting of a 1.6 M⊙ NS and a 1.0 M⊙ MS donor star with an initial orbit of 0.35 days in the orbital period vs. stellar age diagram (top panel), and the donor-star mass vs. stellar age diagram (bottom panel). The horizontal short dashed line in the top panel indicates the orbital period of 2A 1822-371, and the horizontal short dashed lines in the bottom panel represent the inferred upper and lower limits of the donor star mass. |
| In the text | |
 |
Fig. 3. Same as in Fig. 2, but for the diagram of the orbital period vs. donor star mass. The solid circle represents the observed data for source 2A 1822-371. |
| In the text | |
 |
Fig. 4. Same as in Fig. 2, but for the diagram of the orbital period derivative vs. orbital period. The solid circle represents the observed data for source 2A 1822-371. |
| In the text | |
 |
Fig. 5. Same as in Fig. 2, but for the evolution of the mass-transfer rates as a function of the donor star masses. The horizontal short dashed line denotes the Eddington-accretion rate. |
| In the text | |
 |
Fig. 6. Evolutionary tracks of LMXBs with different initial donor star masses and initial orbital periods in the diagram of the orbital period vs. donor star mass. The solid curves represent our standard model with Md, i = 1.0 M⊙ and Ṗorb,i = 0.35 days. A CB disk with a mass of Mcb = 2.3 × 10−8 M⊙ is included in all models. The solid circle represents the observed data for source 2A 1822-371. |
| In the text | |
 |
Fig. 7. Same as in Fig. 6, but for the evolution of mass-transfer rates as a function of the donor star masses. The horizontal short dashed line denotes the Eddington-accretion rate. |
| In the text | |
 |
Fig. 8. Evolution of orbital period derivatives of LMXBs plotted in Fig. 6 in the Ṗorb − Porb diagram. For simplicity, we only plot the evolutionary tracks in the orbit-expansion stage. The solid circle represents the observed data for source 2A 1822-371. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.