JKCS 041: a colour-detected galaxy cluster at ~ 1.9 with deep potential well as confirmed by X-ray data

S. Andreon; B. Maughan; G. Trinchieri; J. Kurk

doi:10.1051/0004-6361/200912299

Home

All issues

Volume 507 / No 1 (November III 2009)

A&A, 507 1 (2009) 147-157

Full HTML

Press Release

Free Access

Issue		A&A Volume 507, Number 1, November III 2009


Page(s)		147 - 157
Section		Cosmology (including clusters of galaxies)
DOI		https://doi.org/10.1051/0004-6361/200912299
Published online		01 October 2009

A&A 507, 147-157 (2009)

JKCS 041: a colour-detected galaxy cluster at 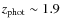${z}_{\rm phot}\sim 1.9$ with deep potential well as confirmed by X-ray data

S. Andreon¹ - B. Maughan² - G. Trinchieri¹ - J. Kurk³

1 - INAF - Osservatorio Astronomico di Brera, via Brera 28, 20121 Milano, Italy
2 - Department of Physics, University of Bristol, Tyndall Ave, Bristol BS8 1TL, UK
3 - Max-Planck-Institut fur Astronomie, Konigstuhl 17, 69117 Heidelberg, Germany

Received 8 April 2009 / Accepted 24 September 2009

Abstract
We report the discovery of JKCS 041, a massive near-infrared selected cluster of galaxies at ${z}_{\rm phot}\sim 1.9$ . The cluster was originally discovered using a modified red-sequence method and also detected in follow-up Chandra data as an extended X-ray source. Optical and near-infrared imaging data alone allow us to show that the detection of JKCS 041 is secure, even in the absence of the X-ray data. We investigate the possibility that JKCS 041 is not a galaxy cluster at $z\sim1.9$ , and find other explanations unlikely. The X-ray detection and statistical arguments rule out the hypothesis that JKCS 041 is actually a blend of groups along the line of sight, and we find that the X-ray emitting gas is too hot and dense to be a filament projected along the line of sight. The absence of a central radio source and the extent and morphology of the X-ray emission argue against the possibility that the X-ray emission comes from inverse Compton scattering of CMB photons by a radio plasma. The cluster has an X-ray core radius of 36.6 ^+8.3_-7.6 arcsec (about 300 kpc), an X-ray temperature of 7.4^+5.3_-3.3 keV, a bolometric X-ray luminosity within R₅₀₀ of $(7.6\pm0.5)$ $\times$ 10⁴⁴ erg s^-1, and an estimated mass of M₅₀₀=2.9^+3.8_-2.4 $\times$ $10^{14}~M_\odot$ , the last derived under the usual (and strong) assumptions. The cluster is composed of 16.4 $\pm$ 6.3 galaxies within 1.5 arcmin (750 kpc) brighter than $K\sim 20.7$ mag. The high redshift of JKCS 041 is determined from the detection colour, from the detection of the cluster in a galaxy sample formed by $z_{\rm phot}>1.6$ galaxies and from a photometric redshift based on 11-band spectral energy distribution fitting. By means of the latter we find the cluster redshift to be 1.84< z<2.12 at 68% confidence. Therefore, JKCS 041 is a cluster of galaxies at ${z}_{\rm phot}\sim 1.9$ with a deep potential well, making it the most distant cluster with extended X-ray emission known.

Key words: galaxies: evolution - galaxies: clusters: general - galaxies: clusters: individual: JKCS 041 - cosmology: dark matter - X-rays: galaxies: clusters - methods: statistical

1 Introduction

Clusters of galaxies are known to harbour red galaxies out to the highest redshifts explored thus far, z=1.45 (Stanford et al. 2006). They owe their colour mostly to their old stellar populations: their luminosity function is passively evolving (de Propris et al. 1999; Andreon 2006a; Andreon et al. 2008) and their colour-magnitude relation evolves in slope, intercept and scatter as expected for a passive evolving population (e.g. Stanford et al. 1999; Kodama et al. 1998). The presence of red galaxies characterises clusters irrespectively of the way they are selected: X-ray selected clusters show a red sequence (see, e.g. Andreon et al. 2004a, 2005, for XMM-LSS cluster samples at 0.3<z<1.2; Ebeling et al. 2007 for MACS; whose red sequence is reported in Stott et al. 2007; and Andreon 2008; see also Stanford et al. 2005; Lidman et al. 2008; Mullis et al. 2005, for some other individual clusters). The first Sunyaev-Zeldovich selected clusters (Staniszewski et al. 2009) have been confirmed thanks to their red sequence, and their photometric redshifts were derived from its colour. The same is often true for shear-selected clusters (e.g. Wittman et al. 2006), starting with the first such example (Wittman et al. 2001).

It is now established that bright red galaxies exist at the appropriate frequency in high redshift clusters and the discussion has now shifted to the faint end of the red population. Current studies aim at establishing whether their abundance evolves with lookback time, with proponents divide into opposite camps (e.g. Andreon 2008; Lidman et al. 2008; Crawford et al. 2009; Tanaka et al. 2008; vs. Gilbank & Balogh 2008; Stott et al. 2007). However, these galaxies are too faint for the purpose of discovering clusters, and thus such discussion is not relevant here.

On the contrary, bright red galaxies are a minority in the field population. Consequently, selections based on galaxy colour enhance the contrast of the large red galaxy population in clusters relative to bluer field galaxies.

The Balmer break is a conspicuous characteristic feature of galaxy spectra. Red colours are observed when a galaxy has a prominent Balmer break and is at the appropriate redshift for the filter pair used. In some circumstances a galaxy may look red, when another spectral break (e.g. Lyman break) falls between the filter pair, but these galaxies are numerically few in actual samples and are not clustered as strongly as the galaxies in clusters. Therefore, their clustering cannot be mistaken as a cluster detection. Indeed, if they were found to be so strongly clustered it would be an interesting discovery in itself. The colour index thus acts as a (digital) filter and removes galaxies with a spectral energy distribution inconsistent with the expected one. One can then select against objects at either a different redshift or having unwanted colours, making the colour selection a very effective way of detecting clusters. Red-sequence-like algorithms, pioneered by Gladders & Yee (2000) for detecting clusters rely precisely on identifying a spatially localised overdensity of galaxies with a pronounced Balmer break.

Several implementations of red-sequence-like algorithms have been used to detect clusters (e.g. Gladders & Yee 2000; Goto et al. 2002; Koester et al. 2007), each one characterised by different assumptions on the cluster model (i.e. on the expected properties of the ``true'' cluster). For example, some models require clusters to follow the Navarro et al. (1997) radial profile with a predicted radius scale. Alternatively the scale (or form of the profile) can be left free (or only weakly bounded). To enlarge the redshift baseline in such cluster surveys, one is simply required to change filters in order to ``follow'' the Balmer break to higher and higher redshifts. One version of these algorithms has been applied in a series of papers by Andreon et al.' to cover the largest redshift range sampled in one study. In Andreon (2003) the technique was applied to the nearby (z<0.3) universe using SDSS g and r filters. With the R and z' filters the medium-distant universe ( $0.3 \la z < 1.1$ ) was probed (Andreon et al. 2004a,b, 2005, 2008, note that the same bands are used by the red sequence survey, Gladders & Yee 2005). To sample the $z\approx 1.2$ universe, infrared bands must be used for the ``red'' filter, because the Balmer break moves into the z' band at $z \sim 1.2$ . This is shown by Andreon et al. (2005), who were able to detect XLSSC 046 (called ``cluster h'' in that paper) at z=1.22 using z' and J, but we missed it in R and z'. XLSSC 046 was later spectroscopically confirmed in Bremer et al. (2006).

Cluster detection by red sequence-like method is observationally cheap: it is possible to image large ( ${\ga}1$ deg² per exposure) sky regions at sufficient depth to detect clusters up to z=1, with short ( ${\la}2$ ks) exposure times on 4 m ground-based telescopes. All-sky X-ray surveys such as the RASS also provide efficient cluster detections, although they do require more expensive space-based observations. For distant clusters, currently operational X-ray observatories are less efficient than red-sequence methods due to the longer exposure times required (e.g. >10 ks) and smaller fields of view (1/9 deg² at most). As a result, red-sequence-like studies are able to follow the cluster mass function down to lower mass limits than is possible with X-ray observations (e.g. Andreon et al. 2005). On the other hand, X-ray detected clusters are less affected by confusion issues, i.e. by the possibility that the detected structure is a line-of-sight blend of smaller structures. Cluster detection by gravitational shear, meanwhile, requires deeper optical data than red-sequence-like algorithms. This is because shear studies require the measuement of subtler quantities (small distortions in shape) of fainter galaxies. Furthermore, detection by shear is affected by confusion (we will return to this issue in Sect. 3.6), and thus may be of limited use for detecting samples of clusters. However, shear measurements offer a more direct probe of cluster mass, provided the shear detection has a sufficient signal to noise to perform the measurement in survey data (although this is currently not common, see e.g. Schirmer et al. 2007).

In this paper, we present the detection of the very distant, $z_{\rm phot}=1.9$ cluster JKCS 041 obtained by adopting redder (J and K) filters to follow the Balmer break to even higher redshifts. Since the Balmer break enters the J filter at $z\sim1.9$ , J-K>2.3 mag (in the Vega system) is a very effective criterion (Saracco et al. 2001; Franx et al. 2003) for selecting $z\ga 2$ galaxies. The spectroscopic study by Reddy et al. (2005), by Papovich et al. (2006) and by Kriek et al. (2008), all confirme that the J-K>2.3 mag criterion selects mainly galaxies at $z\ga 2$ .

The paper is organised as follow: Sect. 2 presents the original cluster discovery. In Sect. 3 we reinforce the cluster detection using different methods and we determined the cluster photometric redshift. In that section, we also show that JKCS 041 is not a blend of two (or more) groups along the line of sight. JKCS 041 is also X-ray detected in follow-up Chandra observations. Section 4 describes these data, confirming the cluster detection, and presents our measurements of basic cluster properties (core radius, luminosity, temperature). We also show here that other possible interpretations of the X-ray emission (unlikely a priori) do not match our data. After a short discussion (Sect. 5), Sect. 6 summarises the results.

We adopt $\Omega_\Lambda=0.7$ , $\Omega_{\rm m}=0.3$ and H₀=70 km s^-1 Mpc^-1. The scale, at z=1.9, is 8.4 kpc arcsec^-1. Magnitudes are quoted in the photometric system in which they were published (Vega for near-infrared photometry, AB for optical photometry), unless stated otherwise.

$\begin{figure} \par\includegraphics[width=5.5cm,clip]{12299f1a.ps}\hspace*{3mm} ... ...1b.ps}\hspace*{3mm} \includegraphics[width=5.5cm,clip]{12299f1c.ps} \end{figure}$

Figure 1:

Number density image of a region of 146 Mpc² (0.16 deg²) area centred on JKCS 041. In the left panel, only 2.1<J-K<2.5 mag galaxies are considered, and all the ancillary photometry ignored. This shows the original cluster detection. In the central panel, we have discarded foreground galaxies, as identified by their spectral energy distribution (SED), using spectroscopy, optical and near-infrared photometry. In the right panel, we only keep galaxies with SEDs similar to the Grasil 1.5 Gyr old ellipticals at z=1.9 and we also use Spitzer photometry. JKCS 041, at the centre of each panel, is clearly detected in all images, independently of the filtering applied. The images have been smoothed with a Gaussian with $\sigma =54$ arcsec for displaying purpose. A 5 arcmin ruler is also marked. The large amount of white/light-gray space in each panel qualitatively shows that the detection is unlikely to result from chance background fluctuations. North is up, East is to the left.

Open with DEXTER

2 Near-infrared UKIDSS data and cluster discovery

JKCS 041 was initially detected in 2006 using J and K UKIRT Infrared Deep Sky Survey (UKIDSS, Lawrence et al. 2007) Early Data Release (Dye et al. 2006) as a clustering of sources of similar colour using our own version (Andreon 2003; Andreon et al. 2004a,b) of the red-sequence method (Gladders & Yee 2000). UKIDSS data used here are complete (5 sigma, point sources, 2 arcsec aperture) to K=20.7 mag and J=22.2 mag (Warren et al. 2008).

Basically, all non-Bayesian cluster detection algorithms (including ours) compute a p-value (called significance in CIAO, the Chandra software package, and detection likelihood in XMMSAS). This is sometimes described as the probability of rejecting the null hypothesis ``no cluster is there'', for a set of parameters. In our case, these parameters are sky location, red-sequence colour, cluster size, red-sequence colour width and limiting magnitude. The N-dimensional volume of the parameter space is explored iterating on all (or many) values of the parameters. For the following analysis, we used a regular grid of parameter values.

JKCS 041 is detected with a p-value of 10^-11 at J-K=2.3 mag and RA, dec = (36.695, -4.68) on a scale of 1 arcmin and with a red-sequence width of 0.2 mag. This would correspond to ${\sim}6.5\sigma$ detection in the classical hypothesis testing sense (assuming a Gaussian distribution). The left panel of Fig. 1 shows the spatial distribution of the number density of galaxies with 2.1<J-K<2.5 centred on JKCS 041. The large amount of white/light-gray space qualitatively shows that the detection is unlikely to be produced by chance background fluctuations.

Since the discovery of JKCS 041, the UKIDSS $4{\rm th}$ data release catalogue (Warren et al. 2008) has been released. We make use of that data here, together with images that we mosaiced from Early Data Release stacks (Dye et al. 2006).

The detection just described makes a very limited use of the available data. In the next sections we show how much we can infer from optical, near-infrared and IRAC data to characterise JKCS 041 in absence of the X-ray data. These methods are of interest for clusters for which X-ray data are not available, or, even worse, their expected X-ray flux is too low to be detected in a reasonable exposure time. The analysis of JKCS 041 X-ray observations is presented in Sect. 4.

3 What can we learn about JKCS 041 without X-ray data?

Multiwavelength coverage is available for JKCS 041 from a) the Canada-France-Hawaii Telescope Legacy Survey (CFHTLS, hereafter) Deep Survey 1 field; b) the Swire (Lonsdale et al. 2003) fields; and c) the VVDS $2^{\rm h}$ spectroscopic field.

CFHTLS gives images (available at the Canadian Astronomy Data Centre) and Ilbert et al. (2006) give catalogues in five bands: u^*,g',r',i',z'. Spitzer gives images and catalogues in four bands ([3.6], [4.5], [5.8] and [8]). We used Spitzer images, as presented in Andreon (2006a), and the Spitzer catalogue, as distributed by Surace et al. (2005), the latter taken (in place of Andreon 2006a catalogue) to make our work easier to reproduce. Le Fèvre et al. (2005) give VVDS spectroscopic redshifts in the general area of JKCS 041 for about 10⁴ galaxies. However, cluster members are not included in the spectroscopic catalogue, because they are fainter than the VVDS limiting magnitude ( $I_{\rm AB}=24$ ). We make use of only those VVDS redshifts that are considered reliable ( ${\rm flag}\ge2$ ).

In order to enhance the cluster detection, we used the above data in two ways: a) to remove foreground objects from the sample, i.e. galaxies that are at much lower (photometric) redshift or; b), to retain galaxies whose observed spectral energy distribution (SED, hereafter) fits that of old (red) galaxies at z=1.9.

3.1 Removing foreground objects

By combining near-infrared photometry, optical photometry and VVDS spectroscopic data we can remove foreground galaxies. We flagged as foreground every galaxy whose SED includes a detection in at least five filters and matches the SED of at least two galaxies with VVDS redshift z<1.6. We require a match to two VVDS galaxies (instead of just one) to make our flagging more robust against VVDS galaxies with (potential) bad photometry in our catalogues (for example, because of a deblending problem). We define two SEDs as matching if they differ by less than 0.05 mag in each colour index (u^*-g', g'-r', r'-i', i'-z', z'-J, J-K). The advantage of this approach, compared to photometric redshift estimates, is that all systematics (due to seeing effects, photometric calibration, templates mismatches, etc.) cancel out in the comparison. The trial sample is from the very same image (and catalogue) as the measured sample, and shares its idiosyncrasies. Furthermore, the above approach does not suffer from redshift degeneracies, which affect photometric redshifts ( $z_{\rm phot}$ ), which attempt an inversion by deriving $z_{\rm phot}$ from SEDs.

The central panel of Fig. 1 shows the spatial distribution of the galaxies whose SEDs do not resemble VVDS z<1.6 galaxies. The noise in the map is reduced after the removal of these foreground galaxies, while JKCS 041 is still prominent. Since galaxy positions are not used to decide whether a galaxy is in the foreground, the spatial structure we see in the image is not a spurious feature of the foreground removal.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12299f2.ps} \end{figure}$

Figure 2:

The J-K colour distribution of galaxies within 1.5 arcmin (750 kpc) of the cluster centre is shown by the solid histogram. The same distribution measured in the control field (a 1.5<r<15 arcmin annulus) and normalised to the cluster area is shown by the dashed histogram with error bars. Foregound galaxies were removed in both cases. A clear excess is seen at $J-K\sim 1.9{-}2.2$ mag. Error bars mark approximate errors, whereas 68% highest posterior credible bounds are marked by the shading. The models represented by the solid curves are described in the text.

Open with DEXTER

Figure 2 shows the colour distributions of galaxies not resembling VVDS galaxies at z<1.6, and brighter than K=20.7, for two different regions: within a 1.5 arcmin radius (750 kpc) from the cluster centre, and in a control annulus from 1.5 to 15 arcmin in radius. The latter distribution was normalised to the area of the cluster region. The control histogram gives the expected number of galaxies unrelated to the cluster (those in the foreground but not identified as resembling z<1.6 VVDS galaxies, plus those in the background). More precisely, this second histogram is the maximum likelihood estimate of the true value of the background. To determine the significance of the cluster detection, we used the Bayesian methods introduced in Andreon et al. (2006b) and used in Andreon et al. (2008) to model the same problem. This removes the approximation of the maximum likelihood estimate (i.e. we allow the background to be as uncertain as the data allow, instead of assuming a perfect knowledge of it). The colour distribution of the background data was fit with a Pearson type IV distribution (that allows a larger flexibility than a Gaussian, allowing non-zero skewness and excess kurtosis) and the colour distribution of galaxies in the cluster region were fit with the background model plus a Gaussian. The intensities of these processes are Poisson, with the obvious constraint that the background rate (i.e. intensity divided by the solid angle) in the cluster region and the control region are the same. As priors, we took uniform distributions for all parameters in their plausible ranges and zero outside them (avoiding, for example, normal distributions with negative variances, a colour scatter lower than the colour errors, negative numbers, etc.). A Marchov-Chains Monte Carlo (Metropolis et al. 1953) with a Metropolis et al. (1953) sampler was used to perform the stochastic computation.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12299f3.ps} \end{figure}$

Figure 3:

The black jagged curve shows the posterior probability of the number of JKCS 041 members. Also plotted is a Gaussian with the same mean and standard deviation (red curve). Note that the Gaussian is a poor approximation to the probability distribution at low $n_{\rm gal}$ values, demonstrating that a Gaussian approximation cannot be used to establish the detection significance in terms of a number of sigma's. The posterior value at $n_{\rm gal}=0$ , normalised by the prior value at that value (about 0.02), gives the relative probability of the two hypotheses: ``no cluster'' vs. ``cluster''. As it is obvious even by inspection of the figure, this ratio is near to zero.

Open with DEXTER

The (blue) curves and yellow shaded regions in Fig. 2 show the best-fitting models and the highest posterior 68% confidence intervals, respectively. There is a clear excess above the background, at $J-K\sim 2.1$ mag. This is quantified in Fig. 3, which shows the probability distribution of the number of cluster galaxies; there are about $n_{\rm gal}=16.4$ $\pm$ 6.3 cluster galaxies. We note that the probability distribution is not normal (the red curve is a Gaussian with matching mean and standard deviation), especially at low $n_{\rm gal}$ values. The peak of the colour distribution, $J-K\sim 2.1$ mag, is slighly bluer than the detection colour, J-K= 2.3 mag, because of the presence of blue members, and because we attribute, for this plot only, J=22.2 mag to galaxies undetected in the J band.

A second peak in the colour distribution is visible at $J-K\sim1.4$ mag. Our model does not account for this feature (supposing it to be real, and not to be another cluster/group on the line of sight), because we have not allowed two peaks in the colour distribution of cluster galaxies. If we added a second Gaussian component in the cluster model, the total number of cluster galaxies is 19.3 $\pm$ 6.3, i.e. there are three additional galaxies, not accounted for in our simpler cluster model. With this exception (a half sigma difference), all of the inferences based on the simpler model are unchanged.

3.2 Detection probability

In Sect. 2 we computed the cluster ``detection significance'' and we found 10^-11. This number is technically known as p-value, and it is the quantity most often quoted in astronomical papers to measure the strength of a detection. By definition, a p-value is the probability of observing, under the null hypothesis, a value at least as extreme as the one that was actually observed. Readers willing to evaluate the strength of our cluster detection compared to other cluster detections should use our p-value. The detection of JKCS 041 cluster is as ``sure'' as other published 10^-11 detections.

Readers desiring to use Bayesian evidence are asked to follow us along a longer path. We have some data (those mentioned above) and we want to know the relative probability (often called evidence hereafter) of two models: one that claims ``a cluster is there'', and another that claims ``no cluster is there''. To evaluate this, we simply need to compute these two probabilities and calculate their ratio. The two models (hypotheses) are nested: ``no cluster is there'' is a (mathematical) special case of ``at least one cluster is there'', when all clusters have precisely zero members each. We assume a priori equal probabilities for the two hypotheses, to express our indifference between the two hypotheses in the absence of any data. When hypotheses are nested, as in our case, the ratio above simplifies to the Savage-Dickey density ratio (see Trotta 2007, for an astronomical introduction). The latter ratio is computationally easier to calculate, because it is the value of the posterior at the null hypothesis (i.e. at $n_{\rm gal}=0$ in Fig. 3) divided by the prior probability of that value. For a uniform prior on $n_{\rm gal}$ between 0 and 50, we find a ratio of 1.9 $\times$ 10^-2. Therefore the probability that a cluster is there is about 50 times larger than the probability that none is there. This constitutes strong evidence on the Jeffreys (1961) scale (see Liddle 2004, for an astronomical introduction to the scale). Our evidence ratio implies that only one in 50 clusters detected at the claimed significance of JKCS 041 is a statistical fluctuation. The precise value of the evidence ratio depends only slightly on the assumed prior, provided a reasonable one is adopted. Let's assume, for example an exponential declining prior, $p(n_{\rm gal})\propto {\rm e}^{-n_{\rm gal}/\tau}$ , to approximate the fact that nature usually produces a lot of small objects (e.g. groups) per each large object (e.g. a rich cluster). With this prior, we found odds of 1 in 50 for all $\tau\ga 5$ (N.B. smaller values of $\tau$ were not considered as they give very low probabilities for $n_{\rm gal}>30$ , which is clearly inconsistent with observations of clusters, e.g. Abell 1958; Abell et al. 1989).

This evidence ratio cannot be compared to p-values. They are fundamentally different quantities, and their numerical values differ by orders of magnitude (nine, in the case of JKCS 041). Evidence ratios are not commonly used in the astronomical literature to quantify the quality of a cluster detection, but we can compute them ourselves using published data for the REFLEX cluster survey (Bohringer et al. 2004). For this, we will use the property mentioned previously that the evidence ratio is the ratio of ``not-confirmed'' to ``confirmed'' clusters. Clusters in REFLEX were selected to be X-ray sources, to positionally match a galaxy overdensity, and to have a spectroscopic redshift. The XMM follow-up of a REFLEX sub-sample of clusters (REXCESS, Bohringer et al. 2007) choose 34 clusters in REFLEX not amongst the worst, and the chosen objects are said to be representative of REFLEX clusters by the authors. They found one AGN among 34 objects previously classified as clusters in REFLEX. The implied quality of a REFLEX cluster detection is therefore 1 in 33, marginally lower than the 1 in 50 computed for the JKCS 041 detection. We emphasise that the good REFLEX performance used X-ray, optical and spectroscopic information on the cluster. Instead, the ``1 in 50'' evidence ratio provided here to measure the strength of the JKCS 041 detection does not make any use of the (available) X-ray data. The JKCS 041 detection is slightly more secure than REFLEX clusters. The introduction of the X-ray evidence only strengthens the cluster detection significance, as JKCS 041 is detected as an extended X-ray source (Sect. 4). This provides a solid confirmation of our probability calculus to asses the significance of its detection.

$\begin{figure} \par\includegraphics[width=6cm,clip]{12299f4.ps} \end{figure}$	Figure 4: Distribution in the generalised colour $\Delta$ for galaxies within 1.5 arcmin from the cluster centre (solid histogram), and of the control field (measured in a 1.5<r<15 arcmin annulus, dashed histogram), normalised to the cluster area. A clear excess is seen at $\Delta <1$ mag.
Open with DEXTER

3.3 SED detection using eleven bands

The second approach to detecting JKCS 041 uses all eleven photometric bands to identify galaxies with a spectral energy distribution similar to a Grasil (Silva et al. 1998) 1.5 Gyr old elliptical galaxy at z=1.9 (i.e. $z_f\sim 3.5$ for the adopted cosmology).

Figures 4 is similar to 2: it shows the colour distribution, but for a generalised colour, $\Delta$ , given by the average distance of the photometry data points from the model SED (a 1.5 Gyr old Grasil elliptical at z=1.9). Had we used just the J and K photometric bands, the x-axis would be J-K (plus an obvious warping, to bring all measurements to a common numerical scale) and Fig. 4 would be identical to Fig. 2, except for the different sample selection. We consider here galaxies with photometric data measured to better than 10% accuracy in at least 4 bands. In the cluster direction there is a clear excess of galaxies having SEDs similar to the 1.5 Gyr old Grasil elliptical (i.e. with small values of $\Delta$ ). For example, we observe 23 galaxies with $\Delta<0.4$ when 9.09 are expected. The probability of observing a larger value by chance alone is 3 $\times$ 10^-5. At first sight, the observed $\Delta$ values are large, of the order of 0.2-0.3 mag for galaxies in the leftmost peak. This is expected, however, primarily because we are sampling the ultraviolet ( 1200-3100 Å) with many data points. This means that small differences between the true history of star formation and the model result in large differences between observed and model SEDs in this wavelength range.

This SED based approach is analogous to the photo-z approach used by Stanford et al. (2005) to detect the z=1.41 ISCS J1438+3414 cluster. Therefore, had we decided to use SED model fitting as our initial detection method, JKCS 041 would still have been detected.

The spatial distribution of these SED-selected galaxies with $\Delta<0.4$ mag is shown in the rightmost panel of Fig. 1. JKCS 041 shows the largest numerical overdensity in the survey area (53 $\times$ 53 arcmin²).

3.4 Cluster redshift

Due to the faintness of JKCS 041 galaxies ( $I\sim 25$ ) and their weak spectral features in the (observer-frame) optical, we failed to measure spectroscopic redshifts even after an exposure of 12 h on FORS2 at VLT (progr. P277.A-5028). We therefore address the determination of the cluster redshift by using galaxy colours.

The original cluster detection colour (Sect. 2), 2.1<J-K<2.5 and the peak of the colour distribution (Sect. 3.1), both imply $z_{\rm phot}\approx 1.9$ either assuming a model spectral energy distribution (e.g. Bruzual & Charlot 2003; or those detailed in the UKIDSS calibration paper, Hewett et al. 2006) or by comparison with J-K colour of red galaxies at $z_{\rm spect}\approx 1.9$ (e.g. Kriek et al. 2008).

We now use our SED approach of Sect. 3.3 to compute the photometric cluster redshift and its uncertainty. For each redshift value we compute the expected Grasil SED for 1.5 Gyr old elliptical galaxy and we compute how many galaxies match ( $\Delta<0.4$ ) this SED in the cluster direction (a circle of 1.5 arcmin), $n_{\rm on+off}$ , and in a reference line of sight, $n_{\rm off}$ , the latter estimated in a corona centred on the cluster and with inner and outer radii of 1.5 and 15 arcmin (and scaled by the solid angle ratio). Assuming that these count processes are Poisson distributed, the posterior probability $p(z\vert n_{\rm on+off},n_{\rm off})$ is computed assuming uniform priors, following simple algrebra (e.g. Prosper 1989; Kraft 1991; Andreon et al. 2006). The posterior distribution is plotted in Fig. 5, for z>1.5 because z<1.6 is already ruled out by having detected the cluster after filtering out $z_{\rm phot}<1.6$ galaxies (Sect. 3.1). The posterior probability distribution has mean equal to z=1.98 and two peaks, one at z=1.93 and one at z=2.08. The 68% shortest confidence interval, shaded in the figure, is [1.84,2.12].

The length of the 68% uncertainty interval on redshift, 0.28, can also be estimated from the error on the mean J-K colour of the red galaxies that compose the excess in Fig. 2, after restricting the sample to J<22.2 mag in order to avoid upper limits. The result is 0.22 mag (the value is derived from the modelling described in Sect. 3.1). Since ${\rm d}(J-K)/{\rm d}z = 1.8$ for old galaxies at $z\approx 2$ (e.g. using models listed in Hewett et al. 2006), this gives $\sigma_z=0.22/1.8=0.12$ (vs. 0.14=0.28/2 for half the 68% shortest confidence interval).

$\begin{figure} \par\includegraphics[width=6cm,clip]{12299f5.ps} \end{figure}$	Figure 5: Photo-z redshift probability distribution, based on 11 bands photometry. The shortest 68% credible interval is marked with a (yellow) shading.
Open with DEXTER

We emphasise that this is the statistical error. However, we expect a systematic error due to our use of a model SED, instead of the true $z\sim2$ old galaxies SED, directly measured on the same data used by us (i.e. UKIDSS+CFHTLS+IRAC). For example, Hewett et al. (2006), describing the photometric calibration of the UKIDSS survey (from which we took J-K), give two predictions of the colour of an elliptical in the UKIRST photometric system at $z\sim2$ which differ by 0.1 mag ( $\Delta z = 0.05$ ). A similar comparison (Kriek et al. 2008), based however on real spectroscopic and J-K measurements, displays $\Delta z \sim0.08$ systematic errors. At much lower redshift EDiSCs clusters have photo-z systematics of $\Delta z \sim0.1$ (White et al. 2005), similar to RCS clusters prior to photometric redshift recalibration (Gilbank et al. 2007).

This source of error has little effect on the width of the posterior redshift distribution: if we model this source of uncertainty with a top-hat filter of width $\Delta z=0.2$ , (i.e. ${\pm}0.1$ ), the 68% confidence interval of JKCS 041 redshift is [1.86,2.18], almost identical to what intially derived ( [1.84,2.12]).

The redshift uncertainty has little effect on our results. It does not change at all the probability that we detected a cluster. Our filtering technique (Sect. 3.1) excludes a redshift similar to that of the ``now'' second most distant cluster of z=1.45 (Stanford et al. 2006). It affects the value of cluster core radius (Sect. 4.1) by less than 1 per cent, because the angular distance is almost constant with redshift at $z\approx 2$ . It introduces an uncertainty on the cluster X-ray luminosity (Sect. 4.2) by about about 15 per cent (if $\delta z \sim 0.1$ ), only three times the uncertainty implied by the uncertainty on $\Omega_{\rm m}$ alone, and by a negligible quantity for the study of $L_{\rm X}-T$ scale relation, because the mentioned 15 per cent error is about five time smaller than the $L_{\rm X}$ scatter at a given T (e.g. Stanek et al. 2006). The redshift uncertainty represents a minor source of error on the cluster temperature (Sect. 4.2.).

When needed for intrinsic quantities, we adopt the lower-redshift peak of the distribution, z=1.9 as the cluster redshift, in place of the posterior average value, z=1.98, which gives conservative estimates of the cluster redshift, X-ray luminosity, and cluster mass.

$\begin{figure} \par\includegraphics[width=6cm,clip]{12299f6.ps} \end{figure}$	Figure 6: Number density radial profile of galaxies selected according to J-K colour ( top panel), dissimilarity from VVDS galaxies SED ( central panel), similarity to old galaxies at z=1.9 ( bottom panel). In all three cases, more galaxies in the cluster line of sight are observed than in adjacent directions.
Open with DEXTER

3.5 A robustness check

We now revisit our cluster detection, using a slighly more stringent magnitude limit and a simplified analysis than applied in previous Sections.

We first consider galaxies with K<20.1 (well within the K-band limit). Those with $J-K\le2.1$ are brighter than the completeness limit in the J band, J=22.2, and removed because they are not of interest. All other K<20.1 galaxies, regardeless of their actual detection in the J band, will have 2.1<J-K<2.5 (we expect minimal contamination from J-K>2.5 sources). Their number density radial profile, shown in the top panel of Fig. 6, indicates an excess in the inner 1 arcmin, where 9 galaxies are found when 2 are expected. This implies a significance (p-value) of 2 $\times$ 10^-4 (about a 3.7 $\sigma$ detection), lower than reported in Sect. 2, but still generally acceptable.

We then consider galaxies with K<20.5 mag. We remove from the sample galaxies with SED matching any pair of z<1.6 VVDS galaxies in at least three bands with good photometric quality (<0.2 mag). Again, the radial distribution of the remaining population (middle panel of Fig. 6) shows an excess in the inner 1': we observe 25 galaxies when 8 are expected. The p-value (significance, detection likelihood) is 10^-6, a $5 \sigma$ detection.

$\begin{figure} \par\includegraphics[width=17cm,clip]{12299f7.ps} \end{figure}$	Figure 7: z' image. Contours of equal number density of galaxies with 2.1<J-K<2.5 mag (irregular yellow contours). North is up and East is to the left.
Open with DEXTER

Last, we consider galaxies with K<20.5 mag, good photometric quality (<0.2 mag) on at least 6 bands, whose SED are similar to a z=1.9 Grasil 2.5 Gyr old galaxy (Sect. 3.3). Figure 6 (bottom panel) shows 13 galaxies in the inner 1' when 2 are expected, giving a p-value (significance, detection likelihood) of 2 $\times$ 10^-7, a $5.3 \sigma$ detection.

Although with reduced statistical significance, due to the reduced sample, we confirm a spatial concentration of objects of similar colour or SED within 1' from the cluster centre. The typical colour of the excess population is $J-K\sim 2.3$ mag, either because this is the selecting colour (first method), because this is the colour of the bulk of the population after foreground removal (second method) or because it is the colour of the template SED used to select the galaxies (third method).

Figure 7 shows a large region around JKCS 041 in the VLT z' band, where the galaxy overdensity is highlighted by the yellow contours. A true-colour image (z'JK) of a slightly smaller region around JKCS 041 is given in Fig. 8.

3.6 A single cluster or a blend of smaller structures?

In the previous section we showed that the detection of JKCS 041 is significant and not just a statistical fluctuation. However, the detection algorithms used do not provide constraints on the size of the detected structure along the line of sight. In particular, they do not distinguish between the observation of a single cluster-size object, or a projection of two (or several) groups. This limitation is common to several other cluster detection methods. The line of sight kernel of cluster detection by gravitational shear is about 1000 Mpc, basically because the detected signal changes little on these scales. Sunyaev-Zeldovich (SZ) cluster searches have an even larger kernel, $\delta z=1$ , basically because the signal depends on the angular size distance, which flatens off at $z\sim0.4$ . In fact, SZ cluster surveys are likely to be confusion-limited at masses below $10^{14}~h^{-1}~M_\odot$ (Holder et al. 2007), below this threshold cluster detections will frequently be blends of clusters along the line of sight. The same is partially true at higher masses, especially considering that the confusion error is highly non-Gaussian with a long tail to the positive side.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12299f8.ps} \end{figure}$	Figure 8: True colour (z'JK) image. Contours of the adaptively smoothed X-ray emission detected by Chandra (white contours). North is up and East is to the left.
Open with DEXTER

Red-sequence-like cluster searches have a redshift kernel that is given by the photometric error of the colour divided by the derivative with redshift of the model colour. This implies $\delta z \sim 0.02$ when photometry S/N is high, the Balmer break is well sampled by the filter pair and filters are taken near to the break (see Andreon 2003; and Andreon et al. 2004, for an observational assessment at z<0.3 and $0.3 \la z \la 1.1$ , respectively). $\delta z \sim 0.02$ error at z=1.9 (which are very optimistic) would still imply a resolution of ${\approx}30$ Mpc along the line of sight. This is too large to discriminate, for example, a single cluster of size of ${\la}3$ Mpc from two structures separated by 10 Mpc. Therefore, red-sequence detected clusters are also prone to confusion, as we quantify below.

The posterior odds (probability ratio) that a detection is a single object or a blend of two objects each carrying about half the total mass is given by the ratio of the probability of observing one object, $p(1\vert\lambda_1)$ over the probability of observing two objects, $p(2\vert\lambda_2)$ , in the given volume, multiplied by the relative a priori probabilities of the two hypotheses. The latter ratio is taken to be 1 to formalise our indifference in absence of any data. $p(i\vert\lambda_i)$ , with i=1,2 are assumed to be Poisson distributed. $\lambda_1$ and $\lambda_2$ are the average volume density of objects (clusters) at the redshift of interest, assumed to be a Jenkins et al. (2001) mass function. The volume is given by $1.84\le z \le 2.12$ (the 68% confidence interval) and $\Delta \alpha = \Delta \delta =60$ arcsec (a larger separation on the sky would mean that the two structures could be distinguished). We also adopt a power spectrum shape parameter $\Gamma=0.6$ and $\sigma_8=0.9$ . To convert the mass of JKCS 041 from M₅₀₀ (derived in Sect. 4.2) to the virial mass, we assume a Navarro et al. (1997) profile of concentration 5. We find $p(1\vert\lambda_1)/p(2\vert\lambda_2)= 4.1$ $\times$ 10³. Our result implies that, on average, one blend occurs every 4100 detections similar to JKCS 041. For three or more objects the odd ratio is even larger. The odds do not change appreciably if we allow blends of similar, but not identical mass (e.g. up to a mass ratio 1:4). Thus, there is ``decisive'' evidence in favour of a single object, when the evidence is measured on the Jeffreys (1961) probability scale. We emphasise once more that quoted probabilities are not p-values, and that probabilities (quoted here) cannot be compared to p-values (often quoted in other studies).

Continuing our survey on cluster detection methods, the size of a structure can obviously also be assessed with spectroscopic data, because even a few galaxies at small $\delta z$ (of the order of 1000 km s^-1) are sufficient to establish with reasonable confidence that most of a given structure is of cluster size. Of course, one should also account for the non negligible possibility that a number of concordant redshifts are found by chance (see e.g. Gal et al. 2008). For example, in the JKCS 041 direction, we found 9 galaxies with redshift $z\sim0.96$ within 2 arcmin from the cluster centre. However, the same number of concordant redshifts is found in almost every other region of the VVDS area ( ${\approx}40$ $\times$ 40 arcmin) that had similar sampling rate (the redshift survey is not spatially uniform). This is just one of the redshift spikes in the general JKCS 041 area (Lefevre et al. 2005), and is not the redshift of every cluster in the area.

$\begin{figure} \par\includegraphics[width=8cm,clip]{12299f9.ps} \end{figure}$

Figure 9:

A background subtracted, exposure corrected [0.3-2] keV Chandra X-ray image of JKCS 041, binned to 4 arcsec pixels. The image is overlaid with contours of the X-ray emission after adaptive smoothing so that all features are significant to at least the 3 $\sigma$ level. The faintest contour was chosen to closely approximate the region enclosing the pixels for which the smoothing kernel contained a signal above the 3 sigma threshold. The square boxes show the positions of 3 radio sources detected in this field, with the box size indicating the spatial resolution of the radio data (see Sect. 4.3).

Open with DEXTER

4 Chandra X-ray observations

JKCS041 was observed by Chandra for 75 ks on 2007 November 23 (ObsID 9368), using the ACIS-S detector. The data were reduced using the standard data reduction procedures as outlined in Maughan et al. (2008). A preliminary examination of the cluster spectrum showed that the 0.3-2.0 keV energy band gave the maximum cluster signal to noise ratio for our image analysis. An image was produced in this energy band, and is shown in Fig. 9. The image was then adaptively smoothed so all features were significant to at least $3\sigma$ , using a version of the Ebeling et al. (2006) algorithm modified to include exposure correction. Contours of this smoothed X-ray image are overlaid in Fig. 9 and on the true-colour image in Fig. 8. The X-ray morphology appears regular, but this should be interpreted with caution due to the relatively large smoothing kernel required by the low signal to noise cluster emission. The $\sigma$ of this Gaussian kernel was ${\la}20$ arcsec within a radius of 30 arcsec of the cluster centre. Within a 1 arcmin radius from the cluster centre there are 223 $\pm$ 31 photons in the 0.3-2 keV band (after subtraction of the background and exclusion of point sources).

4.1 X-ray image analysis

The Chandra image of JKCS041 was fit in Sherpa with a two-dimensional (2D) model chosen to describe the cluster surface brightness distribution. The model used was the Sherpa implimentation of the 2D $\beta$ -profile with an additive constant background component. The model was constrained to be circular and was fit to the data using the Cash (1979) statistic, appropriate for low numbers of counts per bin, including convolution with a model of the Chandra PSF and multiplication by the appropriate exposure map. Point sources were masked out of the data and model during the fitting process. The point source 8 arcsec to the south east of the cluster X-ray centre is relatively bright (and already detected in Chiappetti et al. 2005), contributing ${\sim}100$ photons or ${\sim}30\%$ of the total cluster and point source X-ray flux in the imaging band (the other point sources are much fainter). Fortunately, this emission is easily resolved by Chandra for exclusion from our analysis.

$\begin{figure} \par\includegraphics[angle=-90,width=8.5cm,clip]{12299f10.ps} \end{figure}$	Figure 10: Radial profiles of JKCS 041, and the best fitting 2D model.
Open with DEXTER

An advantage of the 2D fitting used here compared with fitting a model to a one-dimensional (1D) surface brightness profile is that the centre of such a 1D profile is subject to significant uncertainties in low signal to noise data like these. Changes in the central position of the 1D profile have a strong effect on the profile's shape. In a 2D model, those uncertainties can be explicitly included by allowing the centre coordinates of the 2D model to be free parameters. The additional free parameters in our fit were the core radius $r_{\rm c}$ of the model, and the source and background normalisations. The slope $\beta$ of the surface brightness model could not be constrained by the data and was fixed at $\beta=2/3$ . The best fitting model to JKCS 041 had central coordinates of ${\rm RA} = 02{:}26{:}44$ $\pm$ 6 arcsec and ${\rm Dec} = -04{:}41{:}37$ $\pm$ 4 arcsec, with a core radius of 36.6^+8.3_-7.6 arcsec ( 307⁺⁷⁰_-64 kpc). Figure 10 shows a radial profile of the data and the best fitting 2D model. Note that this is simply for visualisation purposes, the model was not fit in this space. This figure demonstrates convincingly that the $r_{\rm c}=37$ arcsec X-ray emission is extended with respect to the 0.5 arcsec Chandra PSF. The cluster core radius, about 300 kpc, is in the range of values observed for local clusters.

4.2 X-ray spectral analysis

Our spectral analysis procedure was chosen to match that of Pacaud et al. (2007) to allow direct comparison with their $L_{\rm X}-T$ relation, presented in Andreon et al. (in preparation). In summary, a cluster spectrum was extracted from an aperture of radius 40 arcsec (336 kpc) (with point sources excluded), chosen to maximise the signal to noise ratio. A background spectrum was extracted from an annular region around the cluster, sufficiently separated to exclude any cluster emission (inner and outer radii: 99'' and 198''; 833 and 1665 kpc). The resulting cluster spectrum contained approximately 210 source photons in the 0.3-7.0 keV band used for spectral fitting, with a signal to noise ratio of 7.4. The source spectrum was fit with an absorbed APEC (Smith et al. 2001) plasma model, with the absorbing column fixed at the Galactic value (2.61 $\times$ 10²⁰ cm^-2), the metal abundance relative to Solar fixed at 0.3 and the redshift of the plasma model fixed at 1.9. The spectrum was grouped to contain a minimum of 5 counts per bin and the model was fit to the background-subtracted data using the XSPEC C-statistic.

The best fitting spectral model had a temperature of 7.6^+5.3_-3.3 keV (plotted in Fig. 11) and gave an unabsorbed bolometric X-ray flux of 1.93 $\times$ 10^-14 erg cm^-2 s^-1 (corrected for area lost to point sources in the spectral aperture). This temperature was used to estimate R₅₀₀=0.52 Mpc (the radius within which the mean density is 500 times the critical density at the cluster redshift), using the scaling relation of Finoguenov et al. (2001) as given in Pacaud et al. (2007; their Eq. (2)). The best fitting 2D surface brightness model was then used to scale the observed flux from the spectral aperture to this radius, including correction for point sources. The bolometric luminosity within R₅₀₀ was thus found to be $(7.4\pm1.7)$ $\times$ 10⁴⁴ erg s^-1, with these errors including the uncertainties on the normalisation of the spectral model, on its temperature and on the core radius of the 2D model used for the aperture correction. This is consistent again with Pacaud et al. (2007) with the exception that we do not include the uncertainties on the surface brightness model slope, which is unconstrained by our data.

$\begin{figure} \par\includegraphics[angle=-90,width=8.5cm,clip]{12299f11.ps} \end{figure}$	Figure 11: The Chandra X-ray spectrum of JKCS 041 and the best fitting model are shown in the top panel, with the residuals from the model shown in the bottom panel. The spectrum is binned for displaying purposes.
Open with DEXTER

Finally, the temperature of JKCS 041 can be used to estimate the cluster's mass. For consistency, we can simply use the definition of R₅₀₀ given above to yield $M_{500}=2.9^{+3.8}_{-2.4} \times 10^{14}~M_\odot$ , under the (strong) assumption that the Finoguenov et al. (2001) relation holds at z=1.9.

4.3 Testing a non-thermal origin for the X-ray emission

Fabian et al. (2001, 2003) interpreted the extended X-ray source coincident with the powerful radio source 3C 294 at z = 1.768 as due to CMB photons scattered at high energy through inverse Compton scattering on non-thermal electrons produced by this radio source. This is the only known case of such a phenomenum. In the case of JKCS 041, the X-ray spectrum alone is unable to rule out a non-thermal emission model, but the latter is an unlikely interpretation for several reasons. Firstly, there is no significant radio source present in the cluster core. Bondi et al. (2003, 2007) present VLA and GMRT radio observations of this field as part of the VVDS-VLA field. The three sources detected close to JKCS 041 are marked in Fig. 9. None of the radio sources appear associated with the extended X-ray emission, although the eastern-most source is associated with a faint X-ray point source with an optical counterpart

Furthermore, the morhopology of the X-ray emission in 3C 294 was found to be hourglass shaped, and contained within a radius of 100 kpc. Within the limits of the Chandra data for JKCS 041, there is no evidence for irregular X-ray morphology, and the X-ray emission is detected to a radius of ${\sim}500$ kpc (see Fig. 10).

$\begin{figure} \par\includegraphics[width=6cm,clip]{12299f12.ps} \end{figure}$	Figure 12: Temperature likelihood of JKCS 041.
Open with DEXTER

4.4 Is JKCS 041 a filament?

We now consider the possibility that JKCS 041 is a filament viewed along the line of sight. In short, the X-ray data rule out this possibility on two fronts: the gas is too dense and too hot.

The density implied by the X-ray emission (as determined from the normalisation of the best fitting spectral model) if the emission were due to a cylindrical filament of uniform density gas of length 10 Mpc along the line of sight and radius 0.326 Mpc (our spectral aperture) is $n_{\rm e}=4.4$ $\pm$ 0.4 $\times$ 10^-4 cm^-3 (giving a mass density of 1.0 $\pm$ 0.1 $\times$ 10^-27 g cm^-3). This is significantly higher than the gas densities found in large scale filaments in e.g. the simulations of Dolag et al. (2006), who found densities typically much lower than 10^-28 g cm^-3.

Second, the measured temperature of the gas implies a deep gravitational potential well, and is inconsistent with the <1 keV temperatures predicted in such filamentary structures (e.g. Pierre et al. 2000; Dolag et al. 2006). To test how strongly the data can rule out <1 keV gas, we need to calculate the ratio of the probability that T<1, as expected for filaments, and the probability that T>1, as usual for clusters. The temperature likelihood (the output of STEPPAR in Xspec), used for the computation, is depicted in Fig. 12. If we adopt an uniform prior in T, to express our indifference on T prior to observing any data, over a range abundantly encompassing all reasonable temperatures (say, from 0.03 to 20 keV), we found odds of 1 in ${\gg}10^4$ . This demonstrates that the filament hypothesis is rejected by the observed X-ray spectrum. Figure 12 shows that this very small probability ratio is insensitive the precise value (e.g. 2 keV vs. 1 keV) of the temperature threshold adopted to define the two hypotheses.

5 Discussion

5.1 The redshift of the X-ray emission

The redshift of the X-ray emitting gas, unless it is directly derived from the X-ray spectrum, is commonly assumed to be the same of the galaxy overdensity spatially coincident with it. This is the tacit assumption made in all but a couple of studies related to cluster gas intrinsic properties, like X-ray luminosity or temperature. We make the same assumption and we further check that no other cluster is in the JKCS 041 line of sight.

JKCS 041 lies in a region rich of photometric data, which have been exploited by several groups independently. Using CFHTLS data, Olsen et al. (2007), Grove et al. (2009) and Mazure et al. (2007) explored the range up to $z \sim 1.1$ using several filters and detection methods. None of their candidate clusters spatially matches JKCS 041, the nearest being 6.5 arcmin away. We also found no matching detection by using R and z' bands and the very same algorithm used with J and K. Therefore, we found no evidence of another cluster on the JKCS 041 line of sight.

5.2 JKCS 041 and cosmological parameters

The detection of JCSK 041 is in line with the expectation of a $\Lambda$ CDM model, with $\sigma_8=0.9$ and power spectral shape parameter $\Gamma=0.6$ and a Jenkins et al. (2001) mass function. In the surveyed area (about 53 $\times$ 53 arcmin²) and within 1.8<z<2.0 about 2.4 clusters with M>10^13.75 h^-1 are expected.

In the past, cosmological parameters have been constrained by the observation of a single high redshift cluster. The argument used is quite simple: cosmological parameters that predict in the studied volume fewer than one cluster more massive than the observed cluster are disregarded in favour of those that make predictions close to the observed number of clusters (i.e. one). Because the first discovered high redshift object is usually extreme (being extreme makes its discovery easier), it is likely to fall in the tail of the distribution. Trying to invert the argument, and constraining cosmological parameter values after having observed a likely extreme object is quite dangerous. This assumes a perfect knowledge of the tail of the distribution from which the object is drawn, which is seldom true on general grounds, and it is certainly not true in this specific case. The halo mass function differs somewhat at the high mass end between different theoretical determinations, e.g. Jenkins et al. (2001), Press & Schechter (1974), Sheth & Tormen (1999) and numerical simulations (see Jenkins et al. 2001).

For this reason, we do not attempt to constrain cosmological parameters from the JKCS 041 discovery, and we simply note that its detection is in line with (model dependent) predictions.

6 Summary

We report the discovery of a massive near-infrared selected cluster of galaxy at ${z}_{\rm phot}\sim 1.9$ . The evidence relies both on eleven band optical, near-infrared and Spitzer photometry, and on the detection of extended X-ray emission in Chandra data. The estimate of the redshift is based on the observed galaxy colours and fitting with SED of old galaxies.

The cluster is centred at ${\rm RA} = 02{:}26{:}44$ and ${\rm Dec} = -04{:}41{:}37$ , and has a bolometric X-ray luminosity within R₅₀₀ of $(7.4\pm1.7)$ $\times$ 10⁴⁴ erg s^-1. Spatial and spectral analysis indicate an X-ray core radius of 36.6^+8.3_-7.6 arcsec (about 300 kpc), an X-ray temperature of 7.6^+5.3_-3.3 keV, and a mass of M₅₀₀=2.9^+3.8_-2.4 $\times$ $10^{14}~M_\odot$ , the latter derived under the usual (and strong) assumptions.

The cluster is originally discovered using a modified red-sequence method based on near-infrared photometry, and is subsequently detected both by removing galaxies with SEDs similar to any two of the 10⁴ VVDS galaxies with z<1.6 in the region, and by using a SED fitting technique to isolate z=1.9 Grasil ellipticals. By means of the latter we find the cluster redshift to be 1.84<z<2.12 at 68% confidence. The X-ray detection from follow-up Chandra observations, together with statistical arguments, discard the hypothesis of a blend of groups or a filament along the line of sight. The absence of a strong radio source makes scattering of CMB photons at X-ray energies also an unlikely explanation for the X-ray emission.

Therefore, we conclude that JKCS 041 is a cluster of galaxies at ${z}_{\rm phot}\sim 1.9$ with a deep potential well, making it the highest redshift cluster currently known, with extended X-ray emission.

X-ray scaling relations of JKCS 041, and other clusters at lower redshift, will be discussed in Andreon et al. (in preparation). Sunyaev-Zeldovich observations of JKCS 041 are in progress at the SZ array.

Acknowledgements

We would like to thank the referee, Harald Ebeling, for a detailed report which allowed us to improve our paper. S.A. thanks Marcella Longhetti and Emanuela Pompei for useful discussions. Most of the Bayesian analysis in this paper benefitted from discussions (mostly by e-mail) with Giulio D'Agostini, Steve Gull, Merrilee Hurn and Roberto Trotta. This paper is based on observations obtained by UKIDSS (see standard acknowledgement at the URL http://www.ukidss.org/archive/archive.html) Chandra (ObsID 9368) and ESO (277.A-5028). B.J.M. was partially supported during this work by NASA through Chandra guest observer grant GO8-9117X. J.K. acknowledges financial support from Deutsche Forschungsgemeinschaft (DFG) grant SFB 439.

References

Abell, G. O. 1958, ApJS, 3, 211 [CrossRef] [NASA ADS]
Abell, G. O., Corwin, H. G., Jr., & Olowin, R. P. 1989, ApJS, 70, 1 [CrossRef] [NASA ADS]
Andreon, S. 2003, A&A, 409, 37 [EDP Sciences] [CrossRef] [NASA ADS]
Andreon, S. 2006a, A&A, 448, 447 [EDP Sciences] [CrossRef] [NASA ADS]
Andreon, S. 2006b, MNRAS, 369, 969 [CrossRef] [NASA ADS]
Andreon, S. 2008, MNRAS, 386, 1045 [CrossRef] [NASA ADS]
Andreon, S. 2009, in Bayesian Methods in Cosmology, ed. M. P. Hobson, et al. (Cambridge, UK: Cambridge University Press), ISBN-13: 9780521887946
Andreon, S., Willis, J., Quintana, H., et al. 2004a, MNRAS, 353, 353 [CrossRef] [NASA ADS]
Andreon, S., Willis, J., Quintana, H., et al. 2004b, in Exploring the Universe. Contents and Structure of the Universe, XXXIX Rencontres de Moriond [arXiv:astro-ph/0405574]
Andreon, S., Valtchanov, I., Jones, L. R., et al. 2005, MNRAS, 359, 1250 [CrossRef] [NASA ADS]
Andreon, S., Quintana, H., Tajer, M., Galaz, G., & Surdej, J. 2006, MNRAS, 365, 915 [CrossRef] [NASA ADS]
Andreon, S., Puddu, E., de Propris, R., & Cuillandre, J.-C. 2008, MNRAS, 385, 979 [CrossRef] [NASA ADS]
Bondi, M., Ciliegi, P., Zamorani, G., et al. 2003, A&A, 403, 857 [EDP Sciences] [CrossRef] [NASA ADS]
Bondi, M., Ciliegi, P., Venturi, T., et al. 2007, A&A, 463, 519 [EDP Sciences] [CrossRef] [NASA ADS]
Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [EDP Sciences] [CrossRef] [NASA ADS]
Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [EDP Sciences] [CrossRef] [NASA ADS]
Bremer, M. N., Valtchanov, I., Willis, J., et al. 2006, MNRAS, 371, 1427 [CrossRef] [NASA ADS]
Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [CrossRef] [NASA ADS]
Cash, W. 1979, ApJ, 228, 939 [CrossRef] [NASA ADS]
Chiappetti, L., Tajer, M., Trinchieri, G., et al. 2005, A&A, 439, 413 [EDP Sciences] [CrossRef] [NASA ADS]
Crawford, S. M., Bershady, M. A, & Hoessel, J. G. 2009, ApJ, 690, 1158 [CrossRef] [NASA ADS]
de Propris, R., Stanford, S. A., Eisenhardt, P. R., Dickinson, M., & Elston, R. 1999, AJ, 118, 719 [CrossRef] [NASA ADS]
Dolag, K., Meneghetti, M., Moscardini, L., Rasia, E., & Bonaldi, A. 2006, MNRAS, 370, 656 [NASA ADS]
Dye, S., Warren, S. J., Hambly, N. C., et al. 2006, MNRAS, 372, 1227 [CrossRef] [NASA ADS]
Ebeling, H., White, D. A., & Rangarajan, F. V. N. 2006, MNRAS, 368, 65 [NASA ADS]
Ebeling, H., Barrett, E., Donovan, D., et al. 2007, ApJ, 661, L33 [CrossRef] [NASA ADS]
Fabian, A. C., Crawford, C. S., Ettori, S., & Sanders, J. S. 2001, MNRAS, 322, L11 [CrossRef] [NASA ADS]
Fabian, A. C., Sanders, J. S., Crawford, C. S., & Ettori, S. 2003, MNRAS, 341, 729 [CrossRef] [NASA ADS]
Feroz, F., & Hobson, M. P. 2008, MNRAS, 384, 449 [CrossRef] [NASA ADS]
Finoguenov, A., Reiprich, T. H., & Bohringer, H. 2001, A&A, 368, 749 [EDP Sciences] [CrossRef] [NASA ADS]
Franx, M., Labbé, I., Rudnick, G., et al. 2003, ApJ, 587, L79 [CrossRef] [NASA ADS]
Gal, R. R., Lemaux, B. C., Lubin, L. M., Kocevski, D., & Squires, G. K. 2008, ApJ, 684, 933 [CrossRef] [NASA ADS]
Gilbank, D. G., & Balogh, M. L. 2008, MNRAS, 385, L116 [NASA ADS]
Gilbank, D. G., Yee, H. K. C., Ellingson, E., et al. 2007, AJ, 134, 282 [CrossRef] [NASA ADS]
Gladders, M. D., & Yee, H. K. C. 2000, AJ, 120, 2148 [CrossRef] [NASA ADS]
Gladders, M. D., & Yee, H. K. C. 2005, ApJS, 157, 1 [CrossRef] [NASA ADS]
Goto, T., Sekiguchi, M., Nichol, R. C., et al. 2002, AJ, 123, 1807 [CrossRef] [NASA ADS]
Jeffreys, H. 1961, Theory of probability, 3rd edn. (Oxford: Oxford Univ. Press)
Jenkins, A., Frenk, C. S., White, S. D. M., et al. 2001, MNRAS, 321, 372 [CrossRef] [NASA ADS]
Hewett, P. C., Warren, S. J., Leggett, S. K., & Hodgkin, S. T. 2006, MNRAS, 367, 454 [CrossRef] [NASA ADS]
Kodama, T., Arimoto, N., Barger, A. J., & Arag'on-Salamanca, A. 1998, A&A, 334, 99 [NASA ADS]
Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 239 [CrossRef] [NASA ADS]
Kraft, R. P., Burrows, D. N., & Nousek, J. A. 1991, ApJ, 374, 344 [CrossRef] [NASA ADS]
Kriek, M., van Dokkum, P. G., Franx, M., et al. 2008, ApJ, 677, 219 [CrossRef] [NASA ADS]
Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [EDP Sciences] [CrossRef] [NASA ADS]
Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [CrossRef] [NASA ADS]
Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [EDP Sciences] [CrossRef] [NASA ADS]
Liddle, A. R. 2004, MNRAS, 351, L49 [CrossRef] [NASA ADS]
Lidman, C., Rosati, P., Tanaka, M., et al. 2008, A&A, 489, 981 [EDP Sciences] [CrossRef] [NASA ADS]
Lonsdale, C. J., Smith, H. E., Rowan-Robinson, M., et al. 2003, PASP, 115, 897 [CrossRef] [NASA ADS]
Maughan, B. J., Jones, C., Forman, W., & Van Speybroeck, L. 2008, ApJS, 174, 117 [CrossRef] [NASA ADS]
Metropolis, N., Rosenbluth, A., Rosenbluth, M., Teller A., & Teller, E. 1953, J. Chem. Phys, 21, 1087 [CrossRef] [NASA ADS]
Mullis, C. R., Rosati, P., Lamer, G., et al. 2005, ApJ, 623, L85 [CrossRef] [NASA ADS]
Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [CrossRef] [NASA ADS]
Pacaud, F., Pierre, M., Adami, C., et al. 2007, MNRAS, 382, 1289 [NASA ADS]
Papovich, C., Moustakas, L. A., Dickinson, M., et al. 2006, ApJ, 640, 92 [CrossRef] [NASA ADS]
Pierre, M., Bryan, G., & Gastaud, R. 2000, A&A, 356, 403 [NASA ADS]
Pierre, M., Valtchanov, I., Altieri, B., et al. 2004, J. Cosmol. Astro-Part. Phys., 9, 11 [CrossRef] [NASA ADS]
Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [CrossRef] [NASA ADS]
Prosper, H. 1998, Phys. Rev. D, 37, 1153 [CrossRef] [NASA ADS]
Reddy, N. A., Erb, D. K., Steidel, C. C., et al. 2005, ApJ, 633, 748 [CrossRef] [NASA ADS]
Regnault, N., Conley, A., Guy, J., et al. 2009, A&A, 506, 999 [EDP Sciences] [CrossRef]
Saracco, P., Giallongo, E., Cristiani, S., et al. 2001, A&A, 375, 1 [EDP Sciences] [CrossRef] [NASA ADS]
Schirmer, M., Erben, T., Hetterscheidt, M., & Schneider, P. 2007, A&A, 462, 875 [EDP Sciences] [CrossRef] [NASA ADS]
Silva, L., Granato, G. L., Bressan, A., & Danese, L. 1998, ApJ, 509, 103 [CrossRef] [NASA ADS]
Surace, J., et al. 2005, see: http://swire.ipac.caltech.edu/swire/astronomers/data_access.html
Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [CrossRef] [NASA ADS]
Stanek, R., Evrard, A. E., Böhringer, H., Schuecker, P., & Nord, B. 2006, ApJ, 648, 956 [CrossRef] [NASA ADS]
Stanford, S. A., Eisenhardt, P. R., & Dickinson, M. 1998, ApJ, 492, 461 [CrossRef] [NASA ADS]
Stanford, S. A., Eisenhardt, P. R., Brodwin, M., et al. 2005, ApJ, 634, L129 [CrossRef] [NASA ADS]
Stanford, S. A., Romer, A. K., Sabirli, K., et al. 2006, ApJ, 646, L13 [CrossRef] [NASA ADS]
Staniszewski, Z., Ade, P. A. R., Aird, K. A., et al. 2009, ApJ, 701, 32 [CrossRef] [NASA ADS]
Sheth, R. K., & Tormen, G. 1999, MNRAS, 308, 119 [CrossRef] [NASA ADS]
Stott, J. P., Smail, I., Edge, A. C., et al. 2007, ApJ, 661, 95 [CrossRef] [NASA ADS]
Tanaka, M., Finoguenov, A., Kodama, T., et al. 2008, A&A, 489, 571 [EDP Sciences] [CrossRef] [NASA ADS]
Trotta, R. 2007, MNRAS, 378, 72 [CrossRef] [NASA ADS]
White, S. D. M., Clowe, D. I., Simard, L., et al. 2005, A&A, 444, 365 [EDP Sciences] [CrossRef] [NASA ADS]
Wilks, S. 1938, Ann. Math. Stat., 9, 60 [CrossRef]
Wittman, D., Tyson, J. A., Margoniner, V. E., Cohen, J. G., & Dell'Antonio, I. P. 2001, ApJ, 557, L89 [CrossRef] [NASA ADS]
Wittman, D., Dell'Antonio, I. P., Hughes, J. P., et al. 2006, ApJ, 643, 128 [CrossRef] [NASA ADS]

Footnotes

... JKCS 041: Cluster names are acronyms indicating the filter pair used for the detection ( gr, Rz, JK) followed by the string CS, for colour selected, followed by the order number in the catalogue. These names are IAU-compliant as the acronyms are registered.
... each: The likelihood ratio theorem, or statistical tests build on it, such as the F-test, cannot be used in our case because the tested model is on the boundary of the parameter space, see e.g. Protassov et al. (2001) or Andreon (2009) for an astronomical introduction.

All Figures

$\begin{figure} \par\includegraphics[width=5.5cm,clip]{12299f1a.ps}\hspace{3mm} ... ...1b.ps}\hspace{3mm} \includegraphics[width=5.5cm,clip]{12299f1c.ps} \end{figure}$	Figure 1: Number density image of a region of 146 Mpc² (0.16 deg²) area centred on JKCS 041. In the left panel, only 2.1<J-K<2.5 mag galaxies are considered, and all the ancillary photometry ignored. This shows the original cluster detection. In the central panel, we have discarded foreground galaxies, as identified by their spectral energy distribution (SED), using spectroscopy, optical and near-infrared photometry. In the right panel, we only keep galaxies with SEDs similar to the Grasil 1.5 Gyr old ellipticals at z=1.9 and we also use Spitzer photometry. JKCS 041, at the centre of each panel, is clearly detected in all images, independently of the filtering applied. The images have been smoothed with a Gaussian with $\sigma =54$ arcsec for displaying purpose. A 5 arcmin ruler is also marked. The large amount of white/light-gray space in each panel qualitatively shows that the detection is unlikely to result from chance background fluctuations. North is up, East is to the left.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12299f2.ps} \end{figure}$	Figure 2: The J-K colour distribution of galaxies within 1.5 arcmin (750 kpc) of the cluster centre is shown by the solid histogram. The same distribution measured in the control field (a 1.5<r<15 arcmin annulus) and normalised to the cluster area is shown by the dashed histogram with error bars. Foregound galaxies were removed in both cases. A clear excess is seen at $J-K\sim 1.9{-}2.2$ mag. Error bars mark approximate errors, whereas 68% highest posterior credible bounds are marked by the shading. The models represented by the solid curves are described in the text.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12299f3.ps} \end{figure}$	Figure 3: The black jagged curve shows the posterior probability of the number of JKCS 041 members. Also plotted is a Gaussian with the same mean and standard deviation (red curve). Note that the Gaussian is a poor approximation to the probability distribution at low $n_{\rm gal}$ values, demonstrating that a Gaussian approximation cannot be used to establish the detection significance in terms of a number of sigma's. The posterior value at $n_{\rm gal}=0$ , normalised by the prior value at that value (about 0.02), gives the relative probability of the two hypotheses: ``no cluster'' vs. ``cluster''. As it is obvious even by inspection of the figure, this ratio is near to zero.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6cm,clip]{12299f4.ps} \end{figure}$	Figure 4: Distribution in the generalised colour $\Delta$ for galaxies within 1.5 arcmin from the cluster centre (solid histogram), and of the control field (measured in a 1.5<r<15 arcmin annulus, dashed histogram), normalised to the cluster area. A clear excess is seen at $\Delta <1$ mag.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6cm,clip]{12299f5.ps} \end{figure}$	Figure 5: Photo-z redshift probability distribution, based on 11 bands photometry. The shortest 68% credible interval is marked with a (yellow) shading.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6cm,clip]{12299f6.ps} \end{figure}$	Figure 6: Number density radial profile of galaxies selected according to J-K colour ( top panel), dissimilarity from VVDS galaxies SED ( central panel), similarity to old galaxies at z=1.9 ( bottom panel). In all three cases, more galaxies in the cluster line of sight are observed than in adjacent directions.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=17cm,clip]{12299f7.ps} \end{figure}$	Figure 7: z' image. Contours of equal number density of galaxies with 2.1<J-K<2.5 mag (irregular yellow contours). North is up and East is to the left.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{12299f8.ps} \end{figure}$	Figure 8: True colour (z'JK) image. Contours of the adaptively smoothed X-ray emission detected by Chandra (white contours). North is up and East is to the left.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{12299f9.ps} \end{figure}$	Figure 9: A background subtracted, exposure corrected [0.3-2] keV Chandra X-ray image of JKCS 041, binned to 4 arcsec pixels. The image is overlaid with contours of the X-ray emission after adaptive smoothing so that all features are significant to at least the 3 $\sigma$ level. The faintest contour was chosen to closely approximate the region enclosing the pixels for which the smoothing kernel contained a signal above the 3 sigma threshold. The square boxes show the positions of 3 radio sources detected in this field, with the box size indicating the spatial resolution of the radio data (see Sect. 4.3).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8.5cm,clip]{12299f10.ps} \end{figure}$	Figure 10: Radial profiles of JKCS 041, and the best fitting 2D model.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[angle=-90,width=8.5cm,clip]{12299f11.ps} \end{figure}$	Figure 11: The Chandra X-ray spectrum of JKCS 041 and the best fitting model are shown in the top panel, with the residuals from the model shown in the bottom panel. The spectrum is binned for displaying purposes.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=6cm,clip]{12299f12.ps} \end{figure}$	Figure 12: Temperature likelihood of JKCS 041.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

JKCS 041: a colour-detected galaxy cluster at with deep potential well as confirmed by X-ray data

1 Introduction

2 Near-infrared UKIDSS data and cluster discovery

3 What can we learn about JKCS 041 without X-ray data?

3.1 Removing foreground objects

3.2 Detection probability

3.3 SED detection using eleven bands

3.4 Cluster redshift

3.5 A robustness check

3.6 A single cluster or a blend of smaller structures?

4 Chandra X-ray observations

4.1 X-ray image analysis

4.2 X-ray spectral analysis

4.3 Testing a non-thermal origin for the X-ray emission

4.4 Is JKCS 041 a filament?

5 Discussion

5.1 The redshift of the X-ray emission

5.2 JKCS 041 and cosmological parameters

6 Summary

References

Footnotes

All Figures

JKCS 041: a colour-detected galaxy cluster at ${z}_{\rm phot}\sim 1.9$ with deep potential well as confirmed by X-ray data