| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 327 - 345 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200912062 | |
| Published online | 08 September 2009 | |
A&A 507, 327-345 (2009)
C2D Spitzer-IRS spectra of disks around T Tauri stars
IV. Crystalline silicates![[*]](/icons/foot_motif.png)
J. Olofsson1 - J.-C. Augereau1 - E. F. van Dishoeck2,3 - B. Merín4 - F. Lahuis5,2 - J. Kessler-Silacci6 - C. P. Dullemond7 - I. Oliveira2,8 - G. A. Blake8 - A. C. A. Boogert 9 - J. M. Brown3 - N. J. Evans II6 - V. Geers10 - C. Knez11 - J.-L. Monin1 - K. Pontoppidan8
1 - Laboratoire d'Astrophysique de Grenoble, Université Joseph Fourier, CNRS, UMR 5571, Grenoble, France
2 -
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
3 -
Max Planck Institut für Extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
4 -
Herschel Science Centre, SRE-SDH, ESA PO Box 78, 28691 Villanueva de la Cañada, Madrid, Spain
5 -
SRON Netherlands Institute for Space Research, PO Box 800, 9700 AV Groningen, The Netherlands
6 -
The University of Texas at Austin, Department of Astronomy, 1 University Station C1400, Austin, Texas 787120259, USA
7 -
Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
8 -
Division of Geological and Planetary Sciences 150-21, California Institute of Technology, Pasadena, CA 91125, USA
9 -
Infrared Processing and Analysis Center, MS 100-22, California Institute of Technology, Pasadena, CA 91125, USA
10 -
Department of Astronomy and Astrophysics, University of Toronto, 50 St. George Street, Toronto, ON, M5S 3H4, Canada
11 -
Department of Astronomy, University of Maryland, College Park, MD 20742, USA
Received 13 March 2009 / Accepted 26 August 2009
Abstract
Aims. Dust grains in the planet-forming regions around young
stars are expected to be heavily processed due to coagulation,
fragmentation, and crystallization. This paper focuses on the
crystalline silicate dust grains in protoplanetary disks for a
statistically significant number of TTauri stars (96).
Methods. As part of the cores to disks (c2d) legacy program, we
obtained more than a hundred Spitzer/IRS spectra of TTauri stars, over
a spectral range of 5-35 ![]() m
where many silicate amorphous and crystalline solid-state features are
present. At these wavelengths, observations probe the upper layers of
accretion disks up to distances of a dozen AU from the central object.
m
where many silicate amorphous and crystalline solid-state features are
present. At these wavelengths, observations probe the upper layers of
accretion disks up to distances of a dozen AU from the central object.
Results. More than 3/4 of our objects show at least one
crystalline silicate emission feature that can be essentially
attributed to Mg-rich silicates. The Fe-rich crystalline silicates are
largely absent in the c2d IRS spectra. The strength and detection
frequency of the crystalline features seen at
![]() m correlate with each other, while they are largely uncorrelated with the observational properties of the amorphous silicate
m correlate with each other, while they are largely uncorrelated with the observational properties of the amorphous silicate ![]() m feature. This supports the idea that the IRS spectra essentially probe two independent disk regions: a warm zone (
m feature. This supports the idea that the IRS spectra essentially probe two independent disk regions: a warm zone (![]() 1 AU) emitting at
1 AU) emitting at
![]() m and a much colder region emitting at
m and a much colder region emitting at
![]() m (
m (![]() 10 AU). We identify a crystallinity paradox, as the long-wavelength (
10 AU). We identify a crystallinity paradox, as the long-wavelength (
![]() m) crystalline silicate features are detected 3.5 times more frequently (
m) crystalline silicate features are detected 3.5 times more frequently (![]() 55% vs.
55% vs. ![]() 15%) than the crystalline features arising from much warmer disk regions (
15%) than the crystalline features arising from much warmer disk regions (
![]() m). This suggests that the disk has an inhomogeneous dust composition within
m). This suggests that the disk has an inhomogeneous dust composition within ![]() 10 AU. The analysis of the shape and strength of both the amorphous
10 AU. The analysis of the shape and strength of both the amorphous ![]() m feature and the crystalline feature around 23
m feature and the crystalline feature around 23 ![]() m provides evidence for the prevalence of
m provides evidence for the prevalence of ![]() m-sized (amorphous and crystalline) grains in upper layers of disks.
m-sized (amorphous and crystalline) grains in upper layers of disks.
Conclusions. The abundant crystalline silicates found far from
their presumed formation regions suggest efficient outward radial
transport mechanisms in the disks around TTauri stars. The presence
of ![]() m-sized
grains in disk atmospheres, despite the short timescales for settling
to the midplane, suggests efficient (turbulent) vertical diffusion,
probably accompanied by grain-grain fragmentation to balance the
expected efficient growth. In this scenario, the depletion of
submicron-sized grains in the upper layers of the disks points toward
removal mechanisms such as stellar winds or radiation pressure.
m-sized
grains in disk atmospheres, despite the short timescales for settling
to the midplane, suggests efficient (turbulent) vertical diffusion,
probably accompanied by grain-grain fragmentation to balance the
expected efficient growth. In this scenario, the depletion of
submicron-sized grains in the upper layers of the disks points toward
removal mechanisms such as stellar winds or radiation pressure.
Key words: stars: pre-main sequence - planetary systems: protoplanetary disks - circumstellar matter - infrared: stars - methods: statistical - techniques: spectroscopic
1 Introduction
The silicate dust grains that are originally incorporated into stellar nebulae and eventually constitute planet-forming disks are thought to have interstellar medium (ISM) size and composition, namely submicron in diameter and extremely amorphous (>99%) in structure (e.g. Gail 1998). Solar System comets, on the other hand, show high crystallinity fractions. The silicate grains in Oort comet Hale-Bopp are, for instance, composed of 40 to 60% of Mg-rich crystalline grains (Crovisier et al. 1997; Wooden et al. 1999,2007), while Jupiter family comets have slightly lower crystalline fractions of about 25-35% (e.g. comet 9P/Tempel 1, Harker et al. 2007). Although the actual crystalline fraction may depend somewhat on the methodology used to calculate the dust's optical properties (e.g. Min et al. 2008), the clear detection of crystalline silicates features in comet spectra indicates that their mass fraction is high compared to the ISM. The amorphous silicate grains that were incorporated into the Solar nebula must have been processed in the very early stages of planet formation before being incorporated into comets. Because of the high temperatures required to thermally anneal amorphous silicates and modify their lattice structure, it is generally accepted that the crystallization of amorphous silicates occurred close to the young Sun. The crystalline silicates were then transported outwards by processes such as turbulence or winds, leading to possible radial variations that may explain some of the mineralogic differences observed between small Solar System bodies today. Other processes could also explain the presence of crystals in the outer regions, such as shock waves triggered by gravitational instabilities in the solar nebula as described in Desch & Connolly (2002) and Harker & Desch (2002). Locally, such shocks could heat up enough surrounding materials to anneal and crystallize amorphous grains. In all these scenarios, silicate crystalline grains can be considered as tracers of the history of the protoplanetary, circumsolar disk.
The detection of silicates in the disks around young stars was notoriously difficult until the Infrared Space Observatory (ISO) and, later, the Spitzer Space Telescope
were launched. Thanks to ISO, mid- to far-IR spectroscopy of disks
around young intermediate mass stars (Herbig Ae/Be stars,
hereafter, HAeBe) could be performed. Acke & van den Ancker (2004) showed that 52% of HAeBe stars exhibit emission in the ![]() m
(amorphous) silicate feature that arises from the upper layers of the
disks, while 23% of these stars show features at
m
(amorphous) silicate feature that arises from the upper layers of the
disks, while 23% of these stars show features at ![]() m, which is associated with forsterite, a Mg-rich crystalline silicate. Using the mid-IR capabilities of MIDI on
the VLT Interferometer, van Boekel et al. (2004) spatially resolved the 10
m, which is associated with forsterite, a Mg-rich crystalline silicate. Using the mid-IR capabilities of MIDI on
the VLT Interferometer, van Boekel et al. (2004) spatially resolved the 10 ![]() m
emission zone for three HAeBe stars. They found a gradient of
crystallinity, with a larger fraction of enstatite and forsterite
crystalline grains located close to the star (1-2 AU) and lower
fractions farther away in the disk (2-20 AU). This was among the
first observations where the disk dust content was proven to be
radially inhomogeneous.
m
emission zone for three HAeBe stars. They found a gradient of
crystallinity, with a larger fraction of enstatite and forsterite
crystalline grains located close to the star (1-2 AU) and lower
fractions farther away in the disk (2-20 AU). This was among the
first observations where the disk dust content was proven to be
radially inhomogeneous.
Although TTauri stars were too faint for observations with the ISO/SWS and LWS, Natta et al. (2000) employed the lower spectral resolution ISOPHOT instrument to detect the broad amorphous silicate emission feature at around ![]() m
for 9 stars in the Chameleon I cloud; but low resolution, low
signal-to-noise ratios and limited spectral range did not allow firm
detection of any crystalline
features in the disks around young solar mass stars. Pioneering
ground-based observations of TTauri stars (hereafter TTs) nevertheless
showed evidence for forsterite emission features in the terrestrial
spectral window around
m
for 9 stars in the Chameleon I cloud; but low resolution, low
signal-to-noise ratios and limited spectral range did not allow firm
detection of any crystalline
features in the disks around young solar mass stars. Pioneering
ground-based observations of TTauri stars (hereafter TTs) nevertheless
showed evidence for forsterite emission features in the terrestrial
spectral window around ![]() m. Honda et al. (2003), for example, clearly identified the presence of crystalline silicate emission features (forsterite at 10.1, 10.5 and
m. Honda et al. (2003), for example, clearly identified the presence of crystalline silicate emission features (forsterite at 10.1, 10.5 and ![]() m, and possibly enstatite at
m, and possibly enstatite at ![]() m) in the N-band spectrum (
m) in the N-band spectrum (![]() )
of Hen 3-600A, and argued that the crystalline grains
represent about 50% (30% enstatite, 20% forsterite) of
the total mass of grains emitting at
)
of Hen 3-600A, and argued that the crystalline grains
represent about 50% (30% enstatite, 20% forsterite) of
the total mass of grains emitting at ![]() m.
Because of the difficulty disentangling grain growth, emission from
PAHs (Polycyclic Aromatic Hydrocarbon) or emission from forsterite as
the main cause of the
m.
Because of the difficulty disentangling grain growth, emission from
PAHs (Polycyclic Aromatic Hydrocarbon) or emission from forsterite as
the main cause of the ![]() m ``feature'' in some disks (see e.g. Sitko et al. 2000; and the discussion in Przygodda et al. 2003),
an unambiguous assessment of the presence of crystalline silicates in
large samples of TTauri disks has awaited the launch of Spitzer.
m ``feature'' in some disks (see e.g. Sitko et al. 2000; and the discussion in Przygodda et al. 2003),
an unambiguous assessment of the presence of crystalline silicates in
large samples of TTauri disks has awaited the launch of Spitzer.
The high sensitivity and large spectral range (
![]() m)
of the IRS spectroscopic instrument onboard Spitzer permits routine
mid-infrared spectroscopy of TTauri disks in nearby molecular clouds.
Surveys of young solar analogs in different star-forming regions such
as those by Furlan et al. (2006) and Watson et al. (2009) for the Taurus cloud, and of amorphous silicate features in other clouds by Kessler-Silacci et al. (2006), were performed. Detailed mineralogic fits
analysing the amorphous and crystalline silicate fractions in TTauri disks were performed by Bouwman et al. (2008, 7 TTs) and Sargent et al. (2009, 65 TTs), as well as for disks around much lower mass objects like the borderline brown dwarf (hereafter, BD) SST-Lup3-1 (Merín et al. 2007), and the BD 2MASS J04442713+2512164 in the Taurus cloud (Bouy et al. 2008), both of which show abundant crystalline silicate grains despite their low (sub-)stellar temperatures. According to Bouwman et al. (2008),
the crystalline content of the inner regions of TTauri disks appear to
be mostly dominated by enstatite silicates while the crystalline
content of the outer region instead seems dominated by forsterite
grains. Such data point toward an inhomogeneous dust content within the
disks which could result from a radial dependence of crystallisation
processes, or a difference in the initial conditions under which these
crystals formed. The evolution of crystalline silicates has also been
studied by Watson et al. (2009, 84 TTs),
who find that within the same environmental conditions, the silicate
crystalline mass fraction varies greatly, from none to
nearly 100%. They find that 90% of the
objects in their sample present crystalline features in the 10
m)
of the IRS spectroscopic instrument onboard Spitzer permits routine
mid-infrared spectroscopy of TTauri disks in nearby molecular clouds.
Surveys of young solar analogs in different star-forming regions such
as those by Furlan et al. (2006) and Watson et al. (2009) for the Taurus cloud, and of amorphous silicate features in other clouds by Kessler-Silacci et al. (2006), were performed. Detailed mineralogic fits
analysing the amorphous and crystalline silicate fractions in TTauri disks were performed by Bouwman et al. (2008, 7 TTs) and Sargent et al. (2009, 65 TTs), as well as for disks around much lower mass objects like the borderline brown dwarf (hereafter, BD) SST-Lup3-1 (Merín et al. 2007), and the BD 2MASS J04442713+2512164 in the Taurus cloud (Bouy et al. 2008), both of which show abundant crystalline silicate grains despite their low (sub-)stellar temperatures. According to Bouwman et al. (2008),
the crystalline content of the inner regions of TTauri disks appear to
be mostly dominated by enstatite silicates while the crystalline
content of the outer region instead seems dominated by forsterite
grains. Such data point toward an inhomogeneous dust content within the
disks which could result from a radial dependence of crystallisation
processes, or a difference in the initial conditions under which these
crystals formed. The evolution of crystalline silicates has also been
studied by Watson et al. (2009, 84 TTs),
who find that within the same environmental conditions, the silicate
crystalline mass fraction varies greatly, from none to
nearly 100%. They find that 90% of the
objects in their sample present crystalline features in the 10 ![]() m region (either the 9.2
m region (either the 9.2 ![]() m enstatite feature or the 11.3
m enstatite feature or the 11.3 ![]() m
forsterite feature). Regarding other crystalline features at longer
wavelengths, they found that 50% of the objects surveyed had
detectable crystalline features at
m
forsterite feature). Regarding other crystalline features at longer
wavelengths, they found that 50% of the objects surveyed had
detectable crystalline features at ![]() 33
33 ![]() m.
Also, no strong correlations between crystalline indices and stellar
parameters have been found, suggesting that some mechanisms
(e.g. X-ray emission, giant planets formation or migration)
operate to erase the correlations that are expected from the standard
models of
crystallisation processes.
m.
Also, no strong correlations between crystalline indices and stellar
parameters have been found, suggesting that some mechanisms
(e.g. X-ray emission, giant planets formation or migration)
operate to erase the correlations that are expected from the standard
models of
crystallisation processes.
Here we present a comprehensive study of crystalline silicates
in more than a hundred disks around young stars based on 5-35 ![]() m IRS spectroscopic observations obtained as part of the c2d Spitzer legacy program from molecular clouds to planets (Evans et al. 2003).
This work is the continuation of a series of c2d/IRS papers,
studying grains, PAHs and gas in inner disk regions around young
stellar objects (class II). Paper I by Kessler-Silacci et al. (2006)
focuses on
amorphous silicate features as a proxy for grain growth in a subsample
of the c2d IRS class II objects. They find that the grain
size is a function of spectral type. Paper II by Geers et al. (2006)
shows evidence for low fractions of PAHs around TTs, indicating low gas
phase PAHs abundance in disks as compared to the ISM. Paper III by
Lahuis et al. (2007) reports the first detections of [Ne II] and [Fe I] gas-phase lines in TTauri disks.
m IRS spectroscopic observations obtained as part of the c2d Spitzer legacy program from molecular clouds to planets (Evans et al. 2003).
This work is the continuation of a series of c2d/IRS papers,
studying grains, PAHs and gas in inner disk regions around young
stellar objects (class II). Paper I by Kessler-Silacci et al. (2006)
focuses on
amorphous silicate features as a proxy for grain growth in a subsample
of the c2d IRS class II objects. They find that the grain
size is a function of spectral type. Paper II by Geers et al. (2006)
shows evidence for low fractions of PAHs around TTs, indicating low gas
phase PAHs abundance in disks as compared to the ISM. Paper III by
Lahuis et al. (2007) reports the first detections of [Ne II] and [Fe I] gas-phase lines in TTauri disks.
In this paper, we present in Sect. 2 IRS observations of the entire c2d/IRS sample of class II objects, and we provide in Sect. 3 an overview of the detection statistics of solid-state emission features, especially those from crystalline silicates. In Sect. 4 we study the properties of crystalline silicate grains, including their size, and search for correlations between amorphous and crystalline silicates and between the SED shape and grain size. We further investigate the difference in crystallinity between the inner and outer regions of disks. In Sect. 5 we discuss the implications of our results for the dynamics of disks at planet-forming radii, and we summarize our results in Sect. 6. In a companion paper (Olofsson et al. 2009b, in prep.), we analyse in more detail the dust mineralogy based on compositional fitting of the complete spectra.
2 Spitzer/IRS observations
We present in this study the infrared spectra of disks around
108 young stellar objects obtained as part of the c2d Spitzer
legacy program. The spectra were obtained using the IRS instrument
onboard
the Spitzer Space Telescope. It was used to expand the early
spectroscopic studies of HAeBe stars with ISO, and of a few TTs
observed from the ground in the ![]()
![]() 10
10 ![]() m
atmospheric
window. Thanks to the high sensitivity of Spitzer, a large sample of
disks around low-mass and solar-mass stars could be efficiently
observed.
m
atmospheric
window. Thanks to the high sensitivity of Spitzer, a large sample of
disks around low-mass and solar-mass stars could be efficiently
observed.
The IRS spectrograph is composed of four different modules that enable a wavelength coverage from 5 to 37 ![]() m.
Two modules, short-low and long-low (SL and LL hereafter), provide a
spectral resolution between 60-127 over ranges of 5.2-14.5
m.
Two modules, short-low and long-low (SL and LL hereafter), provide a
spectral resolution between 60-127 over ranges of 5.2-14.5 ![]() m and 14.0-38.0
m and 14.0-38.0 ![]() m
for SL and LL, respectively. The remaining two modules, Short-High and
Long-High (SH and LH hereafter), have a spectral resolution of
about 600. They cover more limited spectral ranges of
9.9-19.6
m
for SL and LL, respectively. The remaining two modules, Short-High and
Long-High (SH and LH hereafter), have a spectral resolution of
about 600. They cover more limited spectral ranges of
9.9-19.6 ![]() m and 18.7-37.2
m and 18.7-37.2 ![]() m for SH and LH, respectively.
m for SH and LH, respectively.
2.1 Stellar sample
In this paper, we focus on class II objects - young stars no
longer embedded in their protostellar envelope and surrounded by a
circumstellar disk, where the dust may already be significantly
processed. Our selection contains objects classified as class II
according to the literature, but also 10 objects with no known
spectral type. In this sample, 30 objects are sources newly
discovered with the instrument IRAC onboard Spitzer as part of the
mapping phase of the c2d project. All such objects are named with
the prefix SSTc2d, and are classified as class II objects
according to Evans et al. (2009)
except for one source with no known classification
(SSTc2d J182909.8+03446). The object
SSTc2d J162221.0-230403 is characterized as
class I, but shows amorphous 10 ![]() m
emission without additional absorption features. Two other
SSTc2d objects have no classification. However, for the
10 objects with no classification in the literature, they were
retained in the full list as they clearly show amorphous silicate
features in emission.
m
emission without additional absorption features. Two other
SSTc2d objects have no classification. However, for the
10 objects with no classification in the literature, they were
retained in the full list as they clearly show amorphous silicate
features in emission.
The final sample contains 108 stars including 60 TTs, 9 HAeBe and 1 BD. The 38 remaining objects have no spectral classification in the literature, or are new SSTc2d stars discovered with Spitzer. This sample is distributed toward several clouds: Perseus (16 objects), Taurus (9), Chamaeleon (23), Ophiuchus (25), Lupus (16), Serpens (15), and includes 4 isolated stars: 3 HAeBes (BF Ori, HD 132947 and HD 135344) and one TT star (IRAS 08267-3336). All six clouds are young star-forming regions (1-5 Myr), located at distances within 140 and 260 pc from the Sun, with star densities (number of young stellar objects per square parsec) lying between 3 and 13. Some clouds are therefore quite extended, like Taurus or Lupus. The main cloud properties are given in Evans et al. (2009). The complete list of IRS targets analysed in this paper, their classifications and spectral types, as well as details about the observations, are given in Table 4.
Out of the 108 objects, four display spectra unusual for class II objects. These objects are DL Cha, HD 132947, SSTc2d J182849.4+00604 and SSTc2d J182859.5+03003. The first three sources all display spectra reminiscent of those observed toward Oxygen-rich Asymptotic Giant Branch stars (see Sloan et al. 2003, for example spectra) while the fourth object displays a spectrum similar to a C-rich AGB star. Both SSTc2d objects located in the Serpens cloud are objects newly discovered using Spitzer/IRAC surveys. DL Cha is a known variable star in Chamaeleon and HD 132947 is an isolated Herbig star, classified in the literature as a pre-main sequence star (see e.g. Valenti et al. 2003). We do not question here the classification of these four stars, but as they display unusual spectra (see Fig. 24), we decided to remove them from the rest of the study.
2.2 Data reduction
The spectra presented in this paper were extracted from S13 pre-reduced (BCD) data using the c2d legacy team pipeline (Lahuis et al. 2006) which uses two different extraction methods: full aperture extraction and optimal point spread function (PSF) extraction. The full aperture extraction method is applied to both low and high spectral resolution modules. For the low resolution modules, the c2d pipeline implements an extraction with a fixed-width aperture over the whole order. The source position in the slit is determined and the aperture is then centered on the source. The width is such that 99% of the flux of a point-source falls within the window. For the high resolution modules, the full slit width is used for the extraction. One disadvantage of this method is that the reduced spectra present a number of spikes (mainly due to bad pixels response, or ``hot'' pixels on the array, see below) that cannot be easily removed by automated pipelines.
For the PSF extraction, the observed signal is assumed to be
that of a point source or slightly resolved source plus an uniform zero
level. This zero level, in most cases, represents the local extended
emission close to the source, and the typical PSF profile is
calculated from high signal-to-noise ratio calibrator data. As this
zero-level may also contain residuals from, for example, raw pipeline
dark current, we remove this contribution. PSF fitting is less
sensitive to bad data samples and unidentified bad pixels than the
aperture extraction method. The Spitzer Science Center
provides masks with known bad pixels, but they are not all identified.
Our pipeline detects such remaining pixels. The LH array is
particularly affected by this issue, but other modules require
attention. With the PSF extraction method, bad pixels are simply
eliminated, whereas their values are interpolated for the full aperture
extraction method. The PSF extraction method, in addition,
provides an estimate of the data zero level or sky contribution to the
observed spectrum. An important disadvantage of the PSF fitting
method, however, is that for some modules (mainly for the
![]() orders), the PSF is subpixel in size and the extraction method can become unstable. Thus, for some sources, the
orders), the PSF is subpixel in size and the extraction method can become unstable. Thus, for some sources, the
![]() order of the SL module and the
order of the SL module and the
![]() order of the LL module are unavailable, leading to incomplete spectra.
order of the LL module are unavailable, leading to incomplete spectra.
In this paper, we adopt the PSF extraction method in order to obtain
spectra with as few spikes as possible. Where the PSF extraction
method is not available or turns out to be unstable, we use the full
aperture extraction method to build spectra. We then opt for a median
filtering scheme to remove the remaining spikes: for the SL and
SH modules we use a median smoothing over three channels while we
use a median smoothing over five channels for the LL and
LH modules. Some problems were encountered with the data reduction
for two objects in our sample: EC69 and ISO-Cha237. For the latter
source there are two possible explanations: either the LL1 module
spectrum poorly matches
the LL2 module spectrum, or the LL2 module pipeline reduction
failed and its slope is off. The second explanation seems the most
likely, given the shape of the red side of the 10 ![]() m
feature. For EC69, flux values for some orders were null. We decided to
keep these two objects in our sample, first because ISO-Cha237 shows
a 10
m
feature. For EC69, flux values for some orders were null. We decided to
keep these two objects in our sample, first because ISO-Cha237 shows
a 10 ![]() m
feature that can be analysed. For EC69, the spectrum appears
featureless, and as it is classified as a TTauri star, we choose not to
bias our results by removed ``problematic'' spectra.
m
feature that can be analysed. For EC69, the spectrum appears
featureless, and as it is classified as a TTauri star, we choose not to
bias our results by removed ``problematic'' spectra.
![\begin{figure}
\par\includegraphics[angle=90,width=17cm,clip]{12062f1.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg26.png)
|
Figure 1: Example Spitzer/IRS
spectra of 3 T Tauri stars (top spectrum: SL+SH+LH modules,
bottom spectrum: SL+LL). The grey envelopes correspond to 3- |
| Open with DEXTER | |
2.3 Module merging and offset correction
The c2d pipeline corrects for telescope pointing errors that may lead
to important flux offsets between the different modules. Some small
offsets can nevertheless remain between modules even after pointing
correction, and an additionnal post-processing offset correction is
thus applied. This correction depends on the modules available for
every spectrum. Table 1
gives a summary of all the possible configurations, and list the
modules used in all the cases we encountered to obtain the final
spectra. The exact modules used for each individual star are given in
Table 4. A tick-mark (![]() )
means that data provided by this module are used to build the final
spectrum. Priority was given to SL and LL, first because the spectral
resolution is sufficient for detecting crystalline features, and
second, because the high resolution modules provide noisier spectra
than those from the low resolution modules. For each star, a final
spectrum is then obtained by merging all the chosen modules and
correcting manually for small remaining offsets. The spectra themselves
are presented in Figs. 1, 2 and 15-23.
)
means that data provided by this module are used to build the final
spectrum. Priority was given to SL and LL, first because the spectral
resolution is sufficient for detecting crystalline features, and
second, because the high resolution modules provide noisier spectra
than those from the low resolution modules. For each star, a final
spectrum is then obtained by merging all the chosen modules and
correcting manually for small remaining offsets. The spectra themselves
are presented in Figs. 1, 2 and 15-23.
Table 1: Overview of the modules used to obtain the final spectra.
2.4 Estimating the uncertainties
The uncertainties propagated through the c2d pipeline are
dominated by the flux calibration error estimates. As our study is
oriented toward the detection of features in emission from silicates,
we are only concerned with relative uncertainties which are evaluated
by dividing the original spectrum by a smoothed version of itself
obtained using a Savitzky-Golay filter (Savitzky & Golay 1964). This provides an estimate of the signal-to-noise ratio (SNR)
on the spectrum, and is used to assess the presence of features as
follows: the Savitzky-Golay filtering process calculates a local 3
![]() -order
polynomial for every point of the spectrum, based on the four left and
right neighbors. The main advantage of this filter is that it maintains
the shape and contrast of the features, while ``pointy'' features tend
to be rounded out with classical average smoothing, thereby increasing
the uncertainties at the top of every feature and downgrading the
actual quality of the data. The Savitzky-Golay filter has only been
used to calculate the uncertainties displayed as grey envelopes in
Figs. 1, 2 and 15-23, not affecting the spectra themselves presented in these figures and used for the scientific analysis.
-order
polynomial for every point of the spectrum, based on the four left and
right neighbors. The main advantage of this filter is that it maintains
the shape and contrast of the features, while ``pointy'' features tend
to be rounded out with classical average smoothing, thereby increasing
the uncertainties at the top of every feature and downgrading the
actual quality of the data. The Savitzky-Golay filter has only been
used to calculate the uncertainties displayed as grey envelopes in
Figs. 1, 2 and 15-23, not affecting the spectra themselves presented in these figures and used for the scientific analysis.
3 Overview of observed solid-state features
3.1 Observed crystalline silicates
The 104 spectra analysed in this paper are displayed in Figs. 15 to 23, for wavelengths between 5 and 35 ![]() m and in units of Jy (
m and in units of Jy (![]() ). They are sorted by
cloud and increasing Right Ascension. The spectra of the four isolated stars in our sample are displayed in Fig. 23.
). They are sorted by
cloud and increasing Right Ascension. The spectra of the four isolated stars in our sample are displayed in Fig. 23.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12062f2.ps}\hspace*{1.5cm}
\includegraphics[width=7.95cm,clip]{12062f3.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg34.png)
|
Figure 2:
Left panel: examples of the 9.2 (enstatite), 11.3 (forsterite) and 12.5 |
| Open with DEXTER | |
Broad emission features at 10 and 20 ![]() m
from amorphous silicates can be identified in many spectra, as well as
narrower emission features. The latter are identified more easily
beyond 20
m
from amorphous silicates can be identified in many spectra, as well as
narrower emission features. The latter are identified more easily
beyond 20 ![]() m, and are due to crystalline silicates. Figure 1 illustrates the diversity of the spectra seen in our sample. ISO-ChaII 54 (bottom spectrum) shows many
crystalline features, with a weak 10
m, and are due to crystalline silicates. Figure 1 illustrates the diversity of the spectra seen in our sample. ISO-ChaII 54 (bottom spectrum) shows many
crystalline features, with a weak 10 ![]() m
band. In contrast, AS 205 (top spectrum) is almost
``pristine'', with strong amorphous bands and no evidence of
crystalline features
m
band. In contrast, AS 205 (top spectrum) is almost
``pristine'', with strong amorphous bands and no evidence of
crystalline features![]() .
The third spectrum, for SSTc2d J033036.0+303024, has
both amorphous and crystalline features. The crystalline features in
disks can, in most cases, be attributed to Mg-rich silicate minerals
(with a possible contribution from Ca-rich silicates); in agreement
with some model predictions (e.g. Gail 2004, and reference therein), and as observed in solar system comets (e.g. Wooden et al. 2007).
.
The third spectrum, for SSTc2d J033036.0+303024, has
both amorphous and crystalline features. The crystalline features in
disks can, in most cases, be attributed to Mg-rich silicate minerals
(with a possible contribution from Ca-rich silicates); in agreement
with some model predictions (e.g. Gail 2004, and reference therein), and as observed in solar system comets (e.g. Wooden et al. 2007).
Table 2: Summary of the different crystalline silicate features examined in this study.
3.1.1 Mg-rich crystalline silicates: forsterite and enstatite
Table 2 presents the
different crystalline silicate features we searched for in every
spectrum - in addition to the amorphous silicate feature
at 10 ![]() m. In Table 2, ``Peak
m. In Table 2, ``Peak ![]() '' is taken from the literature, ``Measured
'' is taken from the literature, ``Measured ![]() '' and ``
'' and ``
![]() '' values
are the peak positions and equivalent widths measured by our
observations. ``C23'' and ``C28'' refer to silicate features blended in
complexes. Uncertainties are standard
deviations. Here we consider features arising from Mg-rich silicates,
specifically enstatite (inosilicate belonging to the pyroxene group,
with chemical formula MgSiO3) and forsterite, the nesosilicate Mg-rich end-member of the olivine group (Mg2SiO4). Blowups of representative spectral features are shown in Fig. 2.
Using IRS spectra, we cannot disentangle differences between
crystalline structures, for instance, clino-enstatite or
ortho-enstatite. Still, according to Koike et al. (2000), enstatite features are most likely attributed to ortho-enstatite.
'' values
are the peak positions and equivalent widths measured by our
observations. ``C23'' and ``C28'' refer to silicate features blended in
complexes. Uncertainties are standard
deviations. Here we consider features arising from Mg-rich silicates,
specifically enstatite (inosilicate belonging to the pyroxene group,
with chemical formula MgSiO3) and forsterite, the nesosilicate Mg-rich end-member of the olivine group (Mg2SiO4). Blowups of representative spectral features are shown in Fig. 2.
Using IRS spectra, we cannot disentangle differences between
crystalline structures, for instance, clino-enstatite or
ortho-enstatite. Still, according to Koike et al. (2000), enstatite features are most likely attributed to ortho-enstatite.
The example spectrum for ISO-ChaII 54, displayed in Fig. 1 as well as the blowups in the right panel of Fig. 2, shows that the 23.0, 24.5 ![]() m enstatite and the 23.8
m enstatite and the 23.8 ![]() m forsterite features can be blended into one single complex. Similarly, the 27.6
m forsterite features can be blended into one single complex. Similarly, the 27.6 ![]() m forsterite feature can also be blended with the 28.2
m forsterite feature can also be blended with the 28.2 ![]() m enstatite feature. In the following, we
will treat these features as two complexes, at reference positions of 23 and 28
m enstatite feature. In the following, we
will treat these features as two complexes, at reference positions of 23 and 28 ![]() m,
independent of the actual crystals responsible for the observed
emission. We shall note these two complexes, C23 and C28, which
are by far the most frequently detected crystalline features in disks
(Sect. 3.2.1). Figure 2
displays eight example spectra of the C23 and C28 complexes.
Clearly, the shape and peak positions may vary from one object to
another. We
will show in Sect. 4.1
that some of these differences may relate to the mean size of the
emitting grains, although the composition (more or less enstatite
compared to forsterite), grain shape, and strength of the continuum
might also contribute to the diversity of the C23 and C28 features
observed.
m,
independent of the actual crystals responsible for the observed
emission. We shall note these two complexes, C23 and C28, which
are by far the most frequently detected crystalline features in disks
(Sect. 3.2.1). Figure 2
displays eight example spectra of the C23 and C28 complexes.
Clearly, the shape and peak positions may vary from one object to
another. We
will show in Sect. 4.1
that some of these differences may relate to the mean size of the
emitting grains, although the composition (more or less enstatite
compared to forsterite), grain shape, and strength of the continuum
might also contribute to the diversity of the C23 and C28 features
observed.
Beside the features listed in Table 2, other enstatite bands at 10.6, 11.7 and 19.6 ![]() m, as well as forsterite features at 10.1 and 19.7
m, as well as forsterite features at 10.1 and 19.7 ![]() m were also searched for with little success in a subsample of 47 high SNR spectra.
The detection rate of these crystalline features is very low and not
significant. For the two enstatite and forsterite features at
m were also searched for with little success in a subsample of 47 high SNR spectra.
The detection rate of these crystalline features is very low and not
significant. For the two enstatite and forsterite features at ![]() 19.6 and 19.7
19.6 and 19.7 ![]() m,
the main difficulty lies in the added noise where SH and
LH modules merge, which prevents any firm detection of these two
features.
m,
the main difficulty lies in the added noise where SH and
LH modules merge, which prevents any firm detection of these two
features.
3.1.2 Fe-rich components: troilite and fayalite
The formation of Mg-rich crystalline silicates by direct
condensation from a gas of solar composition (as opposed to formation
by thermal annealing) is expected to additionally yield iron-bearing
condensates, in particular FeS (or troilite, see Wooden et al. 2007).
This condensate is of great interest and, while a detailed study of the
ISO spectra of two HAeBe stars (including HD 163296,
Fig. 18) carried out by Keller et al. (2002) indicates FeS in these systems, it remains difficult to detect, in general, because the main feature (between 17-26 ![]() m), centered at 23.5
m), centered at 23.5 ![]() m, is broad, and falls in a region where the IRS spectra are often noisy (due to module merging around 20
m, is broad, and falls in a region where the IRS spectra are often noisy (due to module merging around 20 ![]() m). Further, the disk spectra are often dominated by the presence of the 18
m). Further, the disk spectra are often dominated by the presence of the 18 ![]() m
amorphous silicate feature as well as by frequent C23 emission
features. Therefore, studying the presence or absence of FeS emission
in the c2d sample is beyond the scope of this paper.
m
amorphous silicate feature as well as by frequent C23 emission
features. Therefore, studying the presence or absence of FeS emission
in the c2d sample is beyond the scope of this paper.
Another Fe-rich component that can potentially be detected in
IRS spectra is fayalite, a crystal belonging to the olivine
class (Fe2SiO4). Theoretical opacities from Fabian et al. (2001) show
strong emission features around 30 ![]() m. For small grains, three narrow features are expected at
m. For small grains, three narrow features are expected at ![]() 27, 29.3 and 31.6
27, 29.3 and 31.6 ![]() m. We find there are 4 objects where fayalite may tentatively be present, all four in the Chameleon cloud (Fig. 17):
TW Cha, VZ Cha, WX Cha, and Sz62. Interestingly, the
Sz62 spectrum also shows other features that can be attributed to
fayalite, at roughly 11
m. We find there are 4 objects where fayalite may tentatively be present, all four in the Chameleon cloud (Fig. 17):
TW Cha, VZ Cha, WX Cha, and Sz62. Interestingly, the
Sz62 spectrum also shows other features that can be attributed to
fayalite, at roughly 11 ![]() m and 19
m and 19 ![]() m. All these objects notably display a feature centered at around 30.5
m. All these objects notably display a feature centered at around 30.5 ![]() m, which is at shorter wavelength compared to the feature from pure fayalite which lies at 31.6
m, which is at shorter wavelength compared to the feature from pure fayalite which lies at 31.6 ![]() m (e.g. Fabian et al. 2001; or Koike et al. 2003). This may reflect a small departure from pure Fe-rich crystalline olivine (e.g.
m (e.g. Fabian et al. 2001; or Koike et al. 2003). This may reflect a small departure from pure Fe-rich crystalline olivine (e.g. ![]() 10-15% Mg fraction) as illustrated by the three top spectra in Fig. 1 from Koike et al. (2003)
where it is seen that the feature shifts to smaller wavelengths with
increasing Mg-content. We note that there are other spectra that show
some similar behaviours in the 30
10-15% Mg fraction) as illustrated by the three top spectra in Fig. 1 from Koike et al. (2003)
where it is seen that the feature shifts to smaller wavelengths with
increasing Mg-content. We note that there are other spectra that show
some similar behaviours in the 30 ![]() m
region, but they are of lower signal-to-noise ratio and contain
possible data reduction artifacts (see e.g. RX J0432.8+1735
spectrum, Fig. 16). These
factors make it difficult to conclude whether fayalite is present or
not. Because of the small number of positive detections and because of
the ambiguity between possible noise and real features, we will not
investigate the presence of this component further. We do note,
however, that the compositional fits to seven Spitzer/IRS spectra of
TTs by Bouwman et al. (2008) show no evidence of Fe-rich materials.
m
region, but they are of lower signal-to-noise ratio and contain
possible data reduction artifacts (see e.g. RX J0432.8+1735
spectrum, Fig. 16). These
factors make it difficult to conclude whether fayalite is present or
not. Because of the small number of positive detections and because of
the ambiguity between possible noise and real features, we will not
investigate the presence of this component further. We do note,
however, that the compositional fits to seven Spitzer/IRS spectra of
TTs by Bouwman et al. (2008) show no evidence of Fe-rich materials.
However, the previous conclusion means that we do not observe pure
fayalite in our spectra. Considering the following formula for
crystalline olivine (MgxFe1-x)2SiO4 (with
![]() ), features in the 20-30
), features in the 20-30 ![]() m spectral range become weaker (especially around 23
m spectral range become weaker (especially around 23 ![]() m)
for Mg fractions below 0.6. This means that we are actually
probing crystalline olivine with at least more than 60% of Mg
compared to Fe. Still, as crystalline pyroxene is also
contributing to C23 and C28 complexes, further interpretations
remain difficult.
m)
for Mg fractions below 0.6. This means that we are actually
probing crystalline olivine with at least more than 60% of Mg
compared to Fe. Still, as crystalline pyroxene is also
contributing to C23 and C28 complexes, further interpretations
remain difficult.
3.1.3 Other silicates: diopside and silica
Diopside, a calcium magnesium silicate, and a member of the pyroxene group (CaMg(SiO3)2), can be searched for at ![]()
![]() m.
Because of the presence of the C23 complex, however, the diopside
feature can sometimes be blended with the complex. Even worse, the
shoulder of the complex can be mis-interpreted as a 25
m.
Because of the presence of the C23 complex, however, the diopside
feature can sometimes be blended with the complex. Even worse, the
shoulder of the complex can be mis-interpreted as a 25 ![]() m
feature. We therefore obtain only a lower limit on the frequency at
which this feature is present. The low detection rate of an additional
(but weaker)
m
feature. We therefore obtain only a lower limit on the frequency at
which this feature is present. The low detection rate of an additional
(but weaker) ![]() m diopside feature does not strengthen the confidence level of the detection of diopside in TTauri star disks.
m diopside feature does not strengthen the confidence level of the detection of diopside in TTauri star disks.
Finally, silica (SiO2) has also been identified in our spectra, with a feature arising at 12.5 ![]() m. Attribution of this single feature to amorphous or crystalline silica is not straightforward. Sargent et al. (2009) showed that amorphous silica tends to produce a feature around 12.3-12.4
m. Attribution of this single feature to amorphous or crystalline silica is not straightforward. Sargent et al. (2009) showed that amorphous silica tends to produce a feature around 12.3-12.4 ![]() m, while various crystalline silica polymorphs produce a feature centered at or slightly longward of 12.5
m, while various crystalline silica polymorphs produce a feature centered at or slightly longward of 12.5 ![]() m. Due to the presence of the broad amorphous 10
m. Due to the presence of the broad amorphous 10 ![]() m
feature, disentangling the different contributions is beyond the scope
of our statistical study of the most prominent crystalline silicates.
Example silica features are shown in Fig. 1 and the left panel of Fig. 2.
m
feature, disentangling the different contributions is beyond the scope
of our statistical study of the most prominent crystalline silicates.
Example silica features are shown in Fig. 1 and the left panel of Fig. 2.
3.2 Silicate feature statistics for TTauri stars
3.2.1 The fraction of disks showing silicate(s) feature(s)
We developed a routine that measures the characteristics of both crystalline and amorphous (10 ![]() m)
features. For each feature, it assumes a local continuum which is built
using a two point Lagrange polynomial joining the feet of the feature,
computed as follows:
m)
features. For each feature, it assumes a local continuum which is built
using a two point Lagrange polynomial joining the feet of the feature,
computed as follows:
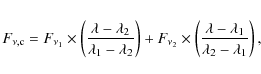
where
Thus, the overwhelming majority (![]() 97%) of the disks do show at least one feature that can be attributed to silicates. Since
97%) of the disks do show at least one feature that can be attributed to silicates. Since ![]() m-sized or larger grains are essentially featureless in the
IRS spectral range (see, for example, the theoretical opacities in Fig. 9),
our results indicate qualitatively that inner disk atmospheres are
populated by grains a few micrometers or less in size, independent of
the age of our stars, and of cloud membership. Some differences between
clouds are nevertheless addressed in Sect. 3.2.2, and a discussion concerning the size of the amorphous and crystalline silicate grains can be found in Sect. 4.1.
m-sized or larger grains are essentially featureless in the
IRS spectral range (see, for example, the theoretical opacities in Fig. 9),
our results indicate qualitatively that inner disk atmospheres are
populated by grains a few micrometers or less in size, independent of
the age of our stars, and of cloud membership. Some differences between
clouds are nevertheless addressed in Sect. 3.2.2, and a discussion concerning the size of the amorphous and crystalline silicate grains can be found in Sect. 4.1.
In the following, we remove the 8 HAeBe stars (plus HD 132947 that we already removed) in our survey from the statistical analysis so that the sample is composed mainly of objects classified as TTs. The statistics in the paper are therefore made on the remaining 96 objects.
3.2.2 The prevalence of crystalline features
Feature-by-feature statistics are displayed in Fig. 3, which shows detection fractions of crystalline features ranging between ![]() 10% and
10% and ![]() 60%. A visual inspection of the 28-29
60%. A visual inspection of the 28-29 ![]() m and 33-35
m and 33-35 ![]() m features for a subset (40 TTs and 7 HAeBes) of the target sample analysed in this paper led Kessler-Silacci et al. (2006) to conclude that
m features for a subset (40 TTs and 7 HAeBes) of the target sample analysed in this paper led Kessler-Silacci et al. (2006) to conclude that ![]() 50%
of the spectra show crystalline silicate features. Considering here the
full 96 star sample and only secure detections with SNR > 20 for the C28 and 33.6
50%
of the spectra show crystalline silicate features. Considering here the
full 96 star sample and only secure detections with SNR > 20 for the C28 and 33.6 ![]() m complexes, we obtain a fraction of
m complexes, we obtain a fraction of ![]() 65%
(63 out of 96) for objects displaying at least one of the two
features. Including all the other crystalline features (still with SNR > 20), this fraction rises to
65%
(63 out of 96) for objects displaying at least one of the two
features. Including all the other crystalline features (still with SNR > 20), this fraction rises to ![]() 78% (75 out of 96 stars). We have checked that these results are not corrupted with
possible PAH emission features, and that the 11.3
78% (75 out of 96 stars). We have checked that these results are not corrupted with
possible PAH emission features, and that the 11.3 ![]() m can be associated with forsterite. Indeed, Geers et al. (2006) identified only three objects in our sample that have potential PAHs emission at 11.3
m can be associated with forsterite. Indeed, Geers et al. (2006) identified only three objects in our sample that have potential PAHs emission at 11.3 ![]() m: LkH
m: LkH![]() 330, T Cha and SR 21. All the other objects cited in Geers et al. (2006) are HAeBe stars and, therefore, not considered in our sample. With additional data, Geers (2007) could confirm the presence of PAHs
for LkH
330, T Cha and SR 21. All the other objects cited in Geers et al. (2006) are HAeBe stars and, therefore, not considered in our sample. With additional data, Geers (2007) could confirm the presence of PAHs
for LkH![]() 330,
T Cha and SR 21, and so these three
objects have then been removed from our statistics for the analysis of
the 11.3
330,
T Cha and SR 21, and so these three
objects have then been removed from our statistics for the analysis of
the 11.3 ![]() m forsterite feature. One other object, EC 82 is identified by Geers (2007) to have a 6.2
m forsterite feature. One other object, EC 82 is identified by Geers (2007) to have a 6.2 ![]() m PAH feature but with no 11.3
m PAH feature but with no 11.3 ![]() m
counterpart, thereby avoiding any possible contamination in this
particular case. Note that we have been as conservative as possible in
identifying features, especially for the crystalline features around
10
m
counterpart, thereby avoiding any possible contamination in this
particular case. Note that we have been as conservative as possible in
identifying features, especially for the crystalline features around
10 ![]() m. Some spectra display a shoulder at around 11.3
m. Some spectra display a shoulder at around 11.3 ![]() m that could possibly be interpreted as a forsterite feature (see e.g. Sz 52 spectrum, Fig. 2, label f).
We choose not to attribute such a shoulder to forsterite. Therefore, we
conclude from our analysis that about 3/4 of the protoplanetary
disks in our sample of young solar-analogs show at least one
crystalline feature in their 5-35
m that could possibly be interpreted as a forsterite feature (see e.g. Sz 52 spectrum, Fig. 2, label f).
We choose not to attribute such a shoulder to forsterite. Therefore, we
conclude from our analysis that about 3/4 of the protoplanetary
disks in our sample of young solar-analogs show at least one
crystalline feature in their 5-35 ![]() m
spectrum, meaning that dust crystallization is not a marginal process
but is instead widespread at this stage of disk evolution.
m
spectrum, meaning that dust crystallization is not a marginal process
but is instead widespread at this stage of disk evolution.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12062f4.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg47.png)
|
Figure 3:
Detection statistics for crystalline silicate features (yellow and red bars) for the 10.0 |
| Open with DEXTER | |
It is interesting to compare these results to those of Watson et al. (2009)
who analysed 84 TTs in the Taurus-Auriga association, also using
Spitzer/IRS. Developing indices measuring the departure from an
ISM-like pristine 10 ![]() m feature, they found that 90% of the Taurus-Auriga disks show either the 9.2
m feature, they found that 90% of the Taurus-Auriga disks show either the 9.2 ![]() m enstatite feature or the 11.3
m enstatite feature or the 11.3 ![]() m forsterite feature, while we obtain about 20% for both features (Fig. 3). In Watson et al. (2009), any departure from the 10
m forsterite feature, while we obtain about 20% for both features (Fig. 3). In Watson et al. (2009), any departure from the 10 ![]() m
pristine reference spectrum is considered as being evidence for
crystalline features, while we argue that this frequent departure that
we also observe has more to do with a grain size effect (see
Sects. 4.1 and 5.3
for further discussions). There is therefore a difference in the
interpretation of the measurements that leads to inconsistent
conclusions. Watson et al. (2009) used the D'Alessio et al. (2006) model to investigate the impact of dust sedimentation on the observed dispersion in equivalent width for the 10
m
pristine reference spectrum is considered as being evidence for
crystalline features, while we argue that this frequent departure that
we also observe has more to do with a grain size effect (see
Sects. 4.1 and 5.3
for further discussions). There is therefore a difference in the
interpretation of the measurements that leads to inconsistent
conclusions. Watson et al. (2009) used the D'Alessio et al. (2006) model to investigate the impact of dust sedimentation on the observed dispersion in equivalent width for the 10 ![]() m
amorphous feature. They could reproduce a broad range of observed
equivalent widths by depleting the dust fraction (that consists of
grains
m
amorphous feature. They could reproduce a broad range of observed
equivalent widths by depleting the dust fraction (that consists of
grains
![]() m in their model) in the upper layers of the disks, thereby mimicking dust settling. In a more recent paper, Dullemond & Dominik (2008) find that sedimentation has a very limited effect on the shape of the 10
m in their model) in the upper layers of the disks, thereby mimicking dust settling. In a more recent paper, Dullemond & Dominik (2008) find that sedimentation has a very limited effect on the shape of the 10 ![]() m
feature as long as a continuous grain size distribution is considered
(as opposed to fixed grain sizes). For longer wavelength
crystalline features, comparison with the work of Watson et al. (2009) is possible for
the 33.6
m
feature as long as a continuous grain size distribution is considered
(as opposed to fixed grain sizes). For longer wavelength
crystalline features, comparison with the work of Watson et al. (2009) is possible for
the 33.6 ![]() m forsterite feature, but not for the features around 23 and 28
m forsterite feature, but not for the features around 23 and 28 ![]() m as they did not study these two complexes. They find that 50% of the Taurus-Auriga objects show the 33.6
m as they did not study these two complexes. They find that 50% of the Taurus-Auriga objects show the 33.6 ![]() m
crystalline feature, compared to 28% for our sample, but this
detection statistic is consistent with the statistics for the
C23 (55%) and C28 (54%) crystalline complexes.
m
crystalline feature, compared to 28% for our sample, but this
detection statistic is consistent with the statistics for the
C23 (55%) and C28 (54%) crystalline complexes.
Figure 4 shows
feature-by-feature statistics sorted by clouds. The largest occurrence
of the C23 complex is found in the Ophiuchus cloud with about 80%
of the objects showing this feature. Disks in Serpens have a prevalence
of crystalline features significantly smaller than in the Perseus,
Chamaeleon, Ophiuchus and Lupus clouds which show comparable fractions
of amorphous and crystalline features. The Taurus cloud shows a
noticeably low frequency of the 10 ![]() m
amorphous feature compared to the other clouds and does not appear to
be balanced by a remarkably high fraction of crystalline grains when
compared to the other regions. Our sample contains only eight objects
in the Taurus cloud, however, which introduces a strong bias. Watson et al. (2009) found that the amorphous 10
m
amorphous feature compared to the other clouds and does not appear to
be balanced by a remarkably high fraction of crystalline grains when
compared to the other regions. Our sample contains only eight objects
in the Taurus cloud, however, which introduces a strong bias. Watson et al. (2009) found that the amorphous 10 ![]() m
feature is present for a large majority of the objects in their survey
of 84 TTs. Therefore, discussing the differences is not
statistically significant for our Taurus sample. One can notice that,
except for Taurus, the five remaining clouds show very similar
behavior. This points toward a rather homogeneous distribution of
amorphous and crystalline silicate dust grains in disks throughout
clouds. Detection statistics in the Serpens cloud are overall smaller,
but the trends are the same as that in the other clouds. Our current
result on the Serpens cloud will be revisited in a forthcoming paper by
Oliveira et al. (in prep.) who analyse a much larger sample
of more than a hundred Serpens objects observed with Spitzer/IRS.
m
feature is present for a large majority of the objects in their survey
of 84 TTs. Therefore, discussing the differences is not
statistically significant for our Taurus sample. One can notice that,
except for Taurus, the five remaining clouds show very similar
behavior. This points toward a rather homogeneous distribution of
amorphous and crystalline silicate dust grains in disks throughout
clouds. Detection statistics in the Serpens cloud are overall smaller,
but the trends are the same as that in the other clouds. Our current
result on the Serpens cloud will be revisited in a forthcoming paper by
Oliveira et al. (in prep.) who analyse a much larger sample
of more than a hundred Serpens objects observed with Spitzer/IRS.
In the following, we will treat all the objects as a single sample. The first reason for this is that cloud-to-cloud differences suffer from low statistics and merging the entire sample will increase the significance of our inferences (96 objects in total). The second reason is that the trends of the different clouds seem to be similar (except for our Taurus cloud smaple which has a low number of stars). Merging the sample will strengthen our conclusions thanks to the large number of class II objects.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12062f5.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg49.png)
|
Figure 4: Same as Fig. 3 but now sorted by clouds. Uncertainties are again Poisson noise, derived from the number of objects per cloud: 15 for Perseus, 8 for Taurus, 20 for Chamaeleon, 16 for Lupus, 24 for Ophiuchus and 12 for Serpens. |
| Open with DEXTER | |
4 Properties of crystalline silicates in the disks around young stars
One may expect that the relatively large spectral range of the IRS instrument (5-35 ![]() m)
implies that the detected short- and long-wavelength emission features
could arise from physically distinct regions in the disk. Kessler-Silacci et al. (2006) and Pinte et al. (2008), among others, have shown that for a typical TTs, the
m)
implies that the detected short- and long-wavelength emission features
could arise from physically distinct regions in the disk. Kessler-Silacci et al. (2006) and Pinte et al. (2008), among others, have shown that for a typical TTs, the ![]() m emission comes from a region about 10 times smaller than the
m emission comes from a region about 10 times smaller than the ![]() m
emitting zone. We examine in this section the correlations between the
detected features. In particular, we inspect the relation between the
properties of the
m
emitting zone. We examine in this section the correlations between the
detected features. In particular, we inspect the relation between the
properties of the ![]() m
silicate
amorphous feature (its energy, the size of its carriers, its
apparition frequency) and those of the crystalline silicate features
at
m
silicate
amorphous feature (its energy, the size of its carriers, its
apparition frequency) and those of the crystalline silicate features
at
![]() m.
m.
4.1 Growth of warm amorphous silicates
The amorphous 10 ![]() m feature is present at a rate of about 70% in our sample. Bouwman et al. (2001), van Boekel et al. (2003) and Kessler-Silacci et al. (2006)
have shown that detailed studies of this feature reveal much
information on dust characteristics. Especially noteworthy is that the
observed shape versus strength relation for the 10
m feature is present at a rate of about 70% in our sample. Bouwman et al. (2001), van Boekel et al. (2003) and Kessler-Silacci et al. (2006)
have shown that detailed studies of this feature reveal much
information on dust characteristics. Especially noteworthy is that the
observed shape versus strength relation for the 10 ![]() m feature can be reproduced by varying the characteristic grain size over the range of
m feature can be reproduced by varying the characteristic grain size over the range of
![]() m. Here we analyse the 10
m. Here we analyse the 10 ![]() m feature by adopting the same continuum normalization and the same computational method for the shape (flux ratio
S11.3/S9.8) and strength (
m feature by adopting the same continuum normalization and the same computational method for the shape (flux ratio
S11.3/S9.8) and strength (
![]() )
of the 10
)
of the 10 ![]() m feature as in Kessler-Silacci et al. (2006). The different values S11.3, S9.8 and
m feature as in Kessler-Silacci et al. (2006). The different values S11.3, S9.8 and
![]() are obtained by normalizing the observed flux
are obtained by normalizing the observed flux ![]() as follows:
as follows:
![]() ,
where
,
where
![]() is the estimated linear
continuum between the red and blue feet of the feature and
is the estimated linear
continuum between the red and blue feet of the feature and
![]() its mean value between the two feet (all fluxes expressed in Jy). We choose a wavelength range of
its mean value between the two feet (all fluxes expressed in Jy). We choose a wavelength range of ![]()
![]() m around 9.8
m around 9.8 ![]() m and 11.3
m and 11.3 ![]() m to calculate S11.3 and S9.8.
m to calculate S11.3 and S9.8.
Figure 5 (left panel) shows the known correlation between the flux ratio
S11.3/S9.8 (![]() m feature shape) and
m feature shape) and
![]() (
(![]() m feature strength). To quantify this correlation we use a Kendall
m feature strength). To quantify this correlation we use a Kendall ![]() test. The Kendall
test. The Kendall ![]() rank correlation coefficient measures the degree of correspondance
between two datasets. If the agreement between the two sets of values
is perfect then
rank correlation coefficient measures the degree of correspondance
between two datasets. If the agreement between the two sets of values
is perfect then ![]() ,
if the disagreement is perfect then
,
if the disagreement is perfect then ![]() .
The Kendall
.
The Kendall ![]() procedure also returns a probability P, computed using the complementary error function of
procedure also returns a probability P, computed using the complementary error function of ![]() (see Press et al. 1992, for further informations on the Kendall
(see Press et al. 1992, for further informations on the Kendall ![]() and P calculations). The P probability is the two-sided significance; the smaller the P value, the more significant the correlation.
and P calculations). The P probability is the two-sided significance; the smaller the P value, the more significant the correlation.
For the shape versus strength of the amorphous 10 ![]() m feature, we find an anti-correlation (
m feature, we find an anti-correlation (
![]() )
with a significance probability P = 3.58
)
with a significance probability P = 3.58 ![]() 10-7. This correlation can be interpreted as larger grains producing a flatter 10
10-7. This correlation can be interpreted as larger grains producing a flatter 10 ![]() m amorphous feature, while smaller grains produce narrower features (e.g. van Boekel et al. 2003). A thorough analysis by Kessler-Silacci et al. (2006) and Kessler-Silacci et al. (2007) of the shape-strength trend showed that more massive stars (HAeBe) tend to have sharper
m amorphous feature, while smaller grains produce narrower features (e.g. van Boekel et al. 2003). A thorough analysis by Kessler-Silacci et al. (2006) and Kessler-Silacci et al. (2007) of the shape-strength trend showed that more massive stars (HAeBe) tend to have sharper ![]() m
features than do TTs and BDs, which cluster in a region more consistent
with micron-diameter grains as the typical emitting grain size. The
comparison of our observations to synthetic
m
features than do TTs and BDs, which cluster in a region more consistent
with micron-diameter grains as the typical emitting grain size. The
comparison of our observations to synthetic ![]() m amorphous features calculated for different grain sizes (see Sect. 4.6
for details on the computation method of grain opacities) confirms this
trend as the bulk of our sample clusters in a region consistent with
grains that have grown to sizes larger than about
m amorphous features calculated for different grain sizes (see Sect. 4.6
for details on the computation method of grain opacities) confirms this
trend as the bulk of our sample clusters in a region consistent with
grains that have grown to sizes larger than about ![]() m (left panel of Fig. 5).
m (left panel of Fig. 5).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12062f6.ps}\hspace*{1cm}
\includegraphics[width=8.5cm,clip]{12062f7.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg62.png)
|
Figure 5:
Left panel: correlations between shape (
S11.3/S9.8) and strength (
|
| Open with DEXTER | |
4.2 Growth of cold crystalline silicates
Although a similar analysis of the ![]() m
amorphous emission features is rendered more difficult because of the
broadness of the feature, the narrower longer-wavelength crystalline
silicate features, especially the C23 complex, show a grain
size-dependent behaviour that can be tested with our disk sample (see
the theoretical opacities in Fig. 9). Similar trends could not be exploited for the C28 complex as its shape is not very sensitive to grain size (over the
0.1-3
m
amorphous emission features is rendered more difficult because of the
broadness of the feature, the narrower longer-wavelength crystalline
silicate features, especially the C23 complex, show a grain
size-dependent behaviour that can be tested with our disk sample (see
the theoretical opacities in Fig. 9). Similar trends could not be exploited for the C28 complex as its shape is not very sensitive to grain size (over the
0.1-3 ![]() m range). For the C23 complex, we build a feature shape index, the
S24/S23 flux ratio, computed using the same approach as for the amorphous 10
m range). For the C23 complex, we build a feature shape index, the
S24/S23 flux ratio, computed using the same approach as for the amorphous 10 ![]() m feature. The S23 normalized flux is obtained by averaging the normalized (local) continuum-subtracted flux between 23.5 and
m feature. The S23 normalized flux is obtained by averaging the normalized (local) continuum-subtracted flux between 23.5 and ![]() m, and between 24.1 and
m, and between 24.1 and ![]() m for S24. Figure 5 (right panel) shows the
S24/S23 ratio as a function of the strength of the C23 complex (C23
m for S24. Figure 5 (right panel) shows the
S24/S23 ratio as a function of the strength of the C23 complex (C23
![]() ). The Kendall test gives
). The Kendall test gives
![]() with a significance probability below 10-38, indicative of a clear anticorrelation between these two quantities.
with a significance probability below 10-38, indicative of a clear anticorrelation between these two quantities.
To better evaluate the relationship between grain size and the C23 shape, we calculate theoretical
S24/S23 ratios for synthetic crystalline silicates opacity curves obtained using the Distribution of Hollow Spheres (DHS) method (Min et al. 2005). We consider grains between 0.1 and ![]() m in radius, and two different compositions: 100% forsterite (Mg2SiO4, using optical constants from Servoin & Piriou 1973) and a mixture composed of 50% forsterite plus 50% enstatite (MgSiO3, optical constants taken from Jaeger et al. 1998). Grains larger than
m in radius, and two different compositions: 100% forsterite (Mg2SiO4, using optical constants from Servoin & Piriou 1973) and a mixture composed of 50% forsterite plus 50% enstatite (MgSiO3, optical constants taken from Jaeger et al. 1998). Grains larger than
![]() m,
for either enstatite or forsterite, do not give striking results, as
the
feature disappears into the continuum. Also, a pure enstatite
composition turns out to be incompatible with the observed shape for
the C23 complex as it shows two unblended features at 23.8
and 24.5
m,
for either enstatite or forsterite, do not give striking results, as
the
feature disappears into the continuum. Also, a pure enstatite
composition turns out to be incompatible with the observed shape for
the C23 complex as it shows two unblended features at 23.8
and 24.5 ![]() m.
This indicates that we are not observing pure enstatite grains in our
sample, a result which seems to first order consistent with Bouwman et al. (2008) who found that the very inner (
m.
This indicates that we are not observing pure enstatite grains in our
sample, a result which seems to first order consistent with Bouwman et al. (2008) who found that the very inner (![]() 1 AU)
warm dust population is dominated by enstatite while the dust
population at large radii is dominated by forsterite. The overall
shape-strength trend for the C23 crystalline complex is better
reproduced for a forsterite/enstatite mixture, with characteristic
grain sizes larger than 1.0
1 AU)
warm dust population is dominated by enstatite while the dust
population at large radii is dominated by forsterite. The overall
shape-strength trend for the C23 crystalline complex is better
reproduced for a forsterite/enstatite mixture, with characteristic
grain sizes larger than 1.0 ![]() m
in order to match the bulk of the measured values. This suggests that
not only have the warm amorphous silicate grains grown in our sample of
TTs (left panel of Fig. 5), but also that the colder crystalline silicate grains have coagulated into
m
in order to match the bulk of the measured values. This suggests that
not only have the warm amorphous silicate grains grown in our sample of
TTs (left panel of Fig. 5), but also that the colder crystalline silicate grains have coagulated into ![]() m-sized particles and remain suspended in the upper layers of the disk atmospheres.
m-sized particles and remain suspended in the upper layers of the disk atmospheres.
The offset in the right panel of Fig. 5
between the data points distribution and the curves obtained using
theoretical opacities may come from various effects. First, we consider
pure
crystalline dust grains, which may be a too restrictive assumption to
reproduce the observations. It allows us to see the impact of
grain size, however, and to show that it matches reasonably well with
the observed trend. Recently, Min et al. (2008)
studied the impact of inclusions of small crystals into larger
amorphous grains, but this is too much of a refinement for our
purposes. Second, we only consider pure Mg-rich crystals (no iron).
According to Chihara et al. (2002), the
24.5 ![]() m feature of crystalline pyroxenes shifts towards slightly larger wavelengths with increasing Fe-content. Also, according to Koike et al. (2003), the peak position of the 23.8
m feature of crystalline pyroxenes shifts towards slightly larger wavelengths with increasing Fe-content. Also, according to Koike et al. (2003), the peak position of the 23.8 ![]() m crystalline olivine feature does not shift unless the Fe-content is larger than 20%. As the S24 index is computed integrating between 24.1 and 24.4
m crystalline olivine feature does not shift unless the Fe-content is larger than 20%. As the S24 index is computed integrating between 24.1 and 24.4 ![]() m, raising the Fe-content will produce a smaller S24 and therefore a smaller
S24/S23, while the strength of the
complex will decrease slightly as the 24.5
m, raising the Fe-content will produce a smaller S24 and therefore a smaller
S24/S23, while the strength of the
complex will decrease slightly as the 24.5 ![]() m
feature shifts to larger wavelengths. To conclude, even if there
is a small shift when comparing the observations to theoretical points,
the trend is well reproduced by varying the grain size.
m
feature shifts to larger wavelengths. To conclude, even if there
is a small shift when comparing the observations to theoretical points,
the trend is well reproduced by varying the grain size.
Interestingly, we find no correlation between the grain size proxy for the amorphous 10 ![]() m feature and the grain size proxy for the C23 complex. Considering the sets of values
m feature and the grain size proxy for the C23 complex. Considering the sets of values
![]() as a function of
as a function of
![]() ,
we obtain a Kendall's
,
we obtain a Kendall's ![]() of 0.07, with a significance probability P
of 0.44. This means that even if grain growth took place in both
components, the growth of the amorphous and crystalline grains,
respectively, does not seem to be correlated.
of 0.07, with a significance probability P
of 0.44. This means that even if grain growth took place in both
components, the growth of the amorphous and crystalline grains,
respectively, does not seem to be correlated.
4.3 Relationship between the 10  m and C23 features with
disk properties
m and C23 features with
disk properties
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12062f8.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg70.png)
|
Figure 6:
Left panel: correlations between the slope of spectra (
F30/F13) as a function of the strength (
|
| Open with DEXTER | |
Young flared disks are expected to show rising spectra in the
mid-IR, as opposed to more evolved, settled systems having
self-shadowed disks with much flatter mid-IR spectra (e.g. Dominik et al. 2003). Here we measure the slope of the spectra by the ratio of the F30 and F13 indexes, where F13 is the mean flux value (in Jy) in the range 13 ![]() m
m ![]()
![]() m, and between 29
m, and between 29 ![]() m and 31
m and 31 ![]() m for F30. The left panel of Fig. 6 shows the correlation between the strength of the amorphous 10
m for F30. The left panel of Fig. 6 shows the correlation between the strength of the amorphous 10 ![]() m feature and the slope of the spectra (
F30/F13 ratio). Taking out the two outliers (blue open circles), which are known cold disks (LkH
m feature and the slope of the spectra (
F30/F13 ratio). Taking out the two outliers (blue open circles), which are known cold disks (LkH![]() 330 and CoKu Tau/4, Brown et al. 2007), we find a correlation coefficient
330 and CoKu Tau/4, Brown et al. 2007), we find a correlation coefficient
![]() with a significance probability P smaller than 5.2
with a significance probability P smaller than 5.2 ![]() 10-4 suggestive of a correlation. A similar trend is found by Bouwman et al. (2008) within their FEPS sample of seven stars, and by Watson et al. (2009) with the Taurus-Auriga sample of 84 TTs. This can be interpreted as smaller grains (large
10-4 suggestive of a correlation. A similar trend is found by Bouwman et al. (2008) within their FEPS sample of seven stars, and by Watson et al. (2009) with the Taurus-Auriga sample of 84 TTs. This can be interpreted as smaller grains (large
![]() values) being probed in flared disks (high values of
F30/F13), while flattened disk (low
F30/F13 values) atmospheres are characterized by larger grains.
values) being probed in flared disks (high values of
F30/F13), while flattened disk (low
F30/F13 values) atmospheres are characterized by larger grains.
If dust sedimentation is the main process responsible for disk
flattening, one would expect the upper layers of the disks to be
depleted in large grains, hence the mid-infrared spectroscopic
signature to be that of very small grains (peaked 10 ![]() m features). The observed trend (Fig. 6) very clearly refutes such a possible trend in the relation between the SED shape and that of the 10
m features). The observed trend (Fig. 6) very clearly refutes such a possible trend in the relation between the SED shape and that of the 10 ![]() m feature. The effect of dust sedimentation on the shape of the 10
m feature. The effect of dust sedimentation on the shape of the 10 ![]() m amorphous silicate feature was recently discussed by Dullemond & Dominik (2008) based on models. They showed that the sedimentation of the larger grains toward the disk midplane is
generally not enough to transform a flat 10
m amorphous silicate feature was recently discussed by Dullemond & Dominik (2008) based on models. They showed that the sedimentation of the larger grains toward the disk midplane is
generally not enough to transform a flat 10 ![]() m
feature into a peaked feature. Our observations tend to support these
results as sedimentation, if assumed to be revealed by disk flattening,
is
generally associated with flat 10
m
feature into a peaked feature. Our observations tend to support these
results as sedimentation, if assumed to be revealed by disk flattening,
is
generally associated with flat 10 ![]() m
features. This trend is in fact valid for the majority of the TTs in
our sample as the objects cluster in the region with flat SEDs and flat
silicate features in Fig. 6.
m
features. This trend is in fact valid for the majority of the TTs in
our sample as the objects cluster in the region with flat SEDs and flat
silicate features in Fig. 6.
For the C23 crystalline complex (right panel of Fig. 6), we find a rather weak anticorrelation, with
![]() and a significance probability P < 0.01. The small crystalline grains with
and a significance probability P < 0.01. The small crystalline grains with
![]() larger than about 1.2 are only found in flat or slowly rising disks (
F30/F13 smaller than about 2),
while the larger grains can be found in all kinds of disks.
Interestingly, the very flared disks which have large crystalline
grains emitting at 23
larger than about 1.2 are only found in flat or slowly rising disks (
F30/F13 smaller than about 2),
while the larger grains can be found in all kinds of disks.
Interestingly, the very flared disks which have large crystalline
grains emitting at 23 ![]() m also show small amorphous grains in their warm component (that is, the region probed at 10
m also show small amorphous grains in their warm component (that is, the region probed at 10 ![]() m).
Seven out of the eight objects (RY Lup,
RX J1615.3-3255, Haro 1-1,
SSTc2d J162148.5-234027,
SSTc2d J162245.4-243124,
SSTc2d J162715.1-245139, Haro 1-16) with
F30/F13 > 3 on the right panel of Fig. 6 indeed have their counterpart in the left panel with
m).
Seven out of the eight objects (RY Lup,
RX J1615.3-3255, Haro 1-1,
SSTc2d J162148.5-234027,
SSTc2d J162245.4-243124,
SSTc2d J162715.1-245139, Haro 1-16) with
F30/F13 > 3 on the right panel of Fig. 6 indeed have their counterpart in the left panel with
![]() larger than about 2 (the last object being DoAr 25).
larger than about 2 (the last object being DoAr 25).
![\begin{figure}
\par\includegraphics[height=5.9cm,width=8.5cm,clip]{12062f9.ps}\h...
...*{1cm}
\includegraphics[height=5.9cm,width=8.5cm,clip]{12062f10.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg75.png)
|
Figure 7:
Left panel: from left to right: correlations between the unitless line fluxes of the 10 |
| Open with DEXTER | |
4.4 Relationship between the 10  m feature and crystallinity
m feature and crystallinity
We find in Sect. 4.2 that the growth of warm amorphous silicates (probed by the ![]() m
feature) is statistically disconnected from the growth of cold
crystalline silicates (probed by the C23 complex). We further
investigate the relationship between the amorphous and crystalline
silicates features by searching for a correlation between the energy
contained in the
amorphous
m
feature) is statistically disconnected from the growth of cold
crystalline silicates (probed by the C23 complex). We further
investigate the relationship between the amorphous and crystalline
silicates features by searching for a correlation between the energy
contained in the
amorphous ![]() m feature and the energy contained in the C23, C28 and the
m feature and the energy contained in the C23, C28 and the ![]() m features. To get rid of possible distance or brightness effects we normalized the line fluxes as follows:
m features. To get rid of possible distance or brightness effects we normalized the line fluxes as follows:
![]() ,
where
,
where
![]() is the mean value of the local feature continuum and
is the mean value of the local feature continuum and ![]() is the measured central wavelength of the considered feature.
is the measured central wavelength of the considered feature.
The unitless line fluxes are displayed in the left panel of Fig. 7, which shows that when both the C23 and the 10 ![]() m feature are present with SNR > 20, their emission energies are not correlated (
m feature are present with SNR > 20, their emission energies are not correlated (
![]() ,
significance probability P = 0.55), although the plot would suggest that objects with low 10
,
significance probability P = 0.55), although the plot would suggest that objects with low 10 ![]() m line flux usually also have a low C23 line flux. The middle panel of Fig. 7 shows a similar result when both the C28 and the 10
m line flux usually also have a low C23 line flux. The middle panel of Fig. 7 shows a similar result when both the C28 and the 10 ![]() m feature are present with SNR > 20:
m feature are present with SNR > 20:
![]() (no correlation between these features) with a significance probability P = 0.83, reflecting the dispersion. Finally, the right panel of Fig. 7 shows a similar trend for the 33.6
(no correlation between these features) with a significance probability P = 0.83, reflecting the dispersion. Finally, the right panel of Fig. 7 shows a similar trend for the 33.6 ![]() m and the amorphous 10
m and the amorphous 10 ![]() m feature:
m feature:
![]() and a significance probability P = 0.15. Therefore, the flux radiated by the 10
and a significance probability P = 0.15. Therefore, the flux radiated by the 10 ![]() m
amorphous feature is largely unrelated to the energy contained in the
crystalline silicates features that appear at wavelengths longer
than 20
m
amorphous feature is largely unrelated to the energy contained in the
crystalline silicates features that appear at wavelengths longer
than 20 ![]() m.
m.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12062f11.ps}\vspace*{5mm}
\includegraphics[width=8.8cm,clip]{12062f12.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg82.png)
|
Figure 8:
Top panel: normalized line fluxes for the 33.6 |
| Open with DEXTER | |
Similarly, the shape of the amorphous 10 ![]() m feature (that is, the
S11.3/S9.8 ratio, which is a proxy for grain size, Sect. 4.1) seems uncorrelated with the emergence of the 23
m feature (that is, the
S11.3/S9.8 ratio, which is a proxy for grain size, Sect. 4.1) seems uncorrelated with the emergence of the 23 ![]() m complex, the 28
m complex, the 28 ![]() m complex, or the 33.6
m complex, or the 33.6 ![]() m forsterite feature. The right panel of Fig. 7, for example, shows the number of positive detections of the C23, C28 and
33.6
m forsterite feature. The right panel of Fig. 7, for example, shows the number of positive detections of the C23, C28 and
33.6 ![]() m features per
S11.3/S9.8 bin, where the
errors bars correspond to Poisson noise (square root of the number of
detections). The fraction of disks with C23 and C28 features is
found
to be independent of the mean grain size probed by the 10
m features per
S11.3/S9.8 bin, where the
errors bars correspond to Poisson noise (square root of the number of
detections). The fraction of disks with C23 and C28 features is
found
to be independent of the mean grain size probed by the 10 ![]() m amorphous feature, further suggesting that the 10
m amorphous feature, further suggesting that the 10 ![]() m feature and the C23, C28 features essentially probe disconnected populations. For the 33.6
m feature and the C23, C28 features essentially probe disconnected populations. For the 33.6 ![]() m
feature, the fraction of objects per bin seems less independent because
of the smaller numbers of detections (23 objects with both the 10
and 33.6
m
feature, the fraction of objects per bin seems less independent because
of the smaller numbers of detections (23 objects with both the 10
and 33.6 ![]() m features).
m features).
Overall, these results suggest that the crystalline features appearing at wavelengths longer than 20 ![]() m and the 10
m and the 10 ![]() m amorphous feature arise from unrelated populations. On the other hand, Fig. 8 shows the correlation between the normalized line fluxes of the C23 and C28 complexes where both are present with SNR > 20, and also their correlation with the 33.6
m amorphous feature arise from unrelated populations. On the other hand, Fig. 8 shows the correlation between the normalized line fluxes of the C23 and C28 complexes where both are present with SNR > 20, and also their correlation with the 33.6 ![]() m feature. The Kendall
m feature. The Kendall ![]() tests and associated significance probabilities confirm the expected
result that the crystalline features at wavelengths longer than 20
tests and associated significance probabilities confirm the expected
result that the crystalline features at wavelengths longer than 20 ![]() m have emission fluxes that correlate to each other.
m have emission fluxes that correlate to each other.
4.5 Feature correlation coefficients
The one-to-one correlation probabilities between the detection frequencies of all the features examined in this study with SNR > 20 are displayed in Table 3.
The diagonal shows the total number of positive detections for any
given feature (these numbers being close to percentages of detections
as we have 96 objects). The lower part of the table displays the
Kendall ![]() values as well as the number of spectra with common detections of the
considered features between parenthesis. The Kendall significance P probabilities are displayed in the upper part.
values as well as the number of spectra with common detections of the
considered features between parenthesis. The Kendall significance P probabilities are displayed in the upper part.
At this point, it is interesting to understand the meaning of the inferred Kendall ![]() values in this table. Some correlations appear possible according to the Kendall
values in this table. Some correlations appear possible according to the Kendall ![]() values but only because both features are absent from spectra. Consider as an example the 11.3
values but only because both features are absent from spectra. Consider as an example the 11.3 ![]() m forsterite feature and the C23 complex, for which we obtain
m forsterite feature and the C23 complex, for which we obtain
![]() and P = 0.001, for 12 detections of the 11.3
and P = 0.001, for 12 detections of the 11.3 ![]() m
feature and 56 detections of the C23 complex, indicating a
weak correlation. Out of the 96 stars, 11 spectra show both
features, one spectrum shows the 11.3
m
feature and 56 detections of the C23 complex, indicating a
weak correlation. Out of the 96 stars, 11 spectra show both
features, one spectrum shows the 11.3 ![]() m feature only, and 45 objects show the C23 complex only. The other 39 (
96-45-1-11) objects show neither the 11.3
m feature only, and 45 objects show the C23 complex only. The other 39 (
96-45-1-11) objects show neither the 11.3 ![]() m
feature nor the C23 complex, and these objects account for
concordant pairs. This explains why we find a weak correlation
(non-zero
m
feature nor the C23 complex, and these objects account for
concordant pairs. This explains why we find a weak correlation
(non-zero ![]() value),
as the number of concordant pairs (50) is of the order of the
number of discordant pairs (46) for this example. In this case, we
could eliminate objects that do not show either of these two features
from the statistics, and we would obtain an anti-correlation with
value),
as the number of concordant pairs (50) is of the order of the
number of discordant pairs (46) for this example. In this case, we
could eliminate objects that do not show either of these two features
from the statistics, and we would obtain an anti-correlation with
![]() and P
= 0.004. Therefore, in order to have comparable numbers for all the
features, irrespective of the number of detections, we decide to
consider the entire sample for the calculation of the correlation
coefficients, even when spectra do not show any of the considered
features.
and P
= 0.004. Therefore, in order to have comparable numbers for all the
features, irrespective of the number of detections, we decide to
consider the entire sample for the calculation of the correlation
coefficients, even when spectra do not show any of the considered
features.
The detection frequencies of the 10 ![]() m amorphous feature and the C23 complex are found to be essentially uncorrelated (
m amorphous feature and the C23 complex are found to be essentially uncorrelated (
![]() with P = 0.47). Similar results are obtained when considering the 10
with P = 0.47). Similar results are obtained when considering the 10 ![]() m feature and the C28 complex (
m feature and the C28 complex (
![]() with P = 0.86), and also the 10
with P = 0.86), and also the 10 ![]() m and 33.6
m and 33.6 ![]() m features (
m features (
![]() with P = 0.44). For the C23, C28 complexes and the 33.6
with P = 0.44). For the C23, C28 complexes and the 33.6 ![]() m feature, we have, respectively, 43, 40 and 22 common detections with the amorphous 10
m feature, we have, respectively, 43, 40 and 22 common detections with the amorphous 10 ![]() m feature (which is observed in 69 spectra). The C23 and C28 complexes, as well as the 33.6
m feature (which is observed in 69 spectra). The C23 and C28 complexes, as well as the 33.6 ![]() m forsterite feature, do therefore appear in spectra independently from the presence of the 10
m forsterite feature, do therefore appear in spectra independently from the presence of the 10 ![]() m feature. On the other hand, the C23 complex appears to be coincident with the C28 complex in our spectra (
m feature. On the other hand, the C23 complex appears to be coincident with the C28 complex in our spectra (
![]() with
P < 10-38), which concurs with our results based on line fluxes (Sect. 4.4). The 33.6
with
P < 10-38), which concurs with our results based on line fluxes (Sect. 4.4). The 33.6 ![]() m feature also appears to be coincident, to a slightly lesser extent with the C23 complex (
m feature also appears to be coincident, to a slightly lesser extent with the C23 complex (
![]() with
P < 10-38), and the C28 features (
with
P < 10-38), and the C28 features (
![]() with P = 3
with P = 3 ![]() 10-3). The number of common detections also confirm these trends.
10-3). The number of common detections also confirm these trends.
Table 3: Correlation coefficients between the features detected with SNR > 20.
Table 3 further shows that the forsterite 11.3 ![]() m feature is anti-correlated with the amorphous 10
m feature is anti-correlated with the amorphous 10 ![]() m feature (
m feature (
![]() ,
only 3 objects show both the 10
,
only 3 objects show both the 10 ![]() m and the 11.3
m and the 11.3 ![]() m features). The anti-correlation between the forsterite 11.3
m features). The anti-correlation between the forsterite 11.3 ![]() m feature and the amorphous 10
m feature and the amorphous 10 ![]() m feature could be explained by a contrast effect. Indeed, the 11.3
m feature could be explained by a contrast effect. Indeed, the 11.3 ![]() m feature could potentially be present but hidden by the stronger amorphous feature (see discussion in Sect. 4.6 for a more detailed analysis of this effect).
m feature could potentially be present but hidden by the stronger amorphous feature (see discussion in Sect. 4.6 for a more detailed analysis of this effect).
Interestingly, the crystalline features in the 10 ![]() m range (9.2 and 11.3
m range (9.2 and 11.3 ![]() m) seem to be correlated with both the C23 and C28 complexes: if crystalline features are present in the 10
m) seem to be correlated with both the C23 and C28 complexes: if crystalline features are present in the 10 ![]() m
spectral range then the presence of the two complexes is highly
probable. Still the reverse is not true, if one of the two
complexes (C23 or C28) is present, it is not guaranteed that
we will find the 9.2 or 11.3
m
spectral range then the presence of the two complexes is highly
probable. Still the reverse is not true, if one of the two
complexes (C23 or C28) is present, it is not guaranteed that
we will find the 9.2 or 11.3 ![]() m
features. This reflects that the correlation is dominated by objects
where none of the considered features is present. Furthermore, as we
find no strong correlation for the line fluxes between these features,
this would mean that there is a general increase of crystallinity for
several objects, compared to the rest of the sample. Also, the two
features at 9.2 and 11.3
m
features. This reflects that the correlation is dominated by objects
where none of the considered features is present. Furthermore, as we
find no strong correlation for the line fluxes between these features,
this would mean that there is a general increase of crystallinity for
several objects, compared to the rest of the sample. Also, the two
features at 9.2 and 11.3 ![]() m do not seem to be correlated with the 33.6
m do not seem to be correlated with the 33.6 ![]() m forsterite feature. The declining quality of the data (lower SNR) at the long wavelength end of the IRS spectra may explain this trend in part, as some (lower contrast) 33.6
m forsterite feature. The declining quality of the data (lower SNR) at the long wavelength end of the IRS spectra may explain this trend in part, as some (lower contrast) 33.6 ![]() m features may not have been detected. Another possible explanation could be that the 33.6
m features may not have been detected. Another possible explanation could be that the 33.6 ![]() m forsterite feature probes an even colder disk region than the population probed by C23 and C28 complexes.
m forsterite feature probes an even colder disk region than the population probed by C23 and C28 complexes.
To summarize, our results show that the C23, C28 and 33.6 ![]() m crystalline features probably arise from the same population of grains. Also, the detections of the 9.2 and 11.3
m crystalline features probably arise from the same population of grains. Also, the detections of the 9.2 and 11.3 ![]() m
crystalline features are correlated with the detections of C23 and C28
(but the presence of one of the longer wavelengths complexes does not
guarantee the detection of 9.2 or 11.3
m
crystalline features are correlated with the detections of C23 and C28
(but the presence of one of the longer wavelengths complexes does not
guarantee the detection of 9.2 or 11.3 ![]() m
features), which can be interpreted as a general increase of
crystallinity in the inner and outer regions of disks. However, this
crystalline population seems to be disjoint from the population of
amorphous silicate grains that produce the 10
m
features), which can be interpreted as a general increase of
crystallinity in the inner and outer regions of disks. However, this
crystalline population seems to be disjoint from the population of
amorphous silicate grains that produce the 10 ![]() m feature.
m feature.
4.6 Degree of crystallinity of the warm versus cold disk regions
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{12062f13.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg95.png)
|
Figure 9:
Example mass opacities (in arbitrary units) used to model the IRS observations. From bottom to top: amorphous olivine, amorphous pyroxene, crystalline forsterite and crystalline enstatite. The left panel shows opacities for a grain size
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12062f14.ps}\hspace*{0.3cm}
\includegraphics[width=8.6cm,clip]{12062f15.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg96.png)
|
Figure 10:
Synthetic spectra, in arbitrary units, for mass fractions of
crystalline silicates from 0% to 50% (steps are: 0, 5, 10, 15, 20, 25,
30, 40, 50%, see Sect. 4.6 for more details). The impact of the grain size on the detectability of the 11.3 |
| Open with DEXTER | |
Both Figs. 3 and 4
show larger occurrences of the C23 and C28 emission features than
of shorter wavelength crystalline silicate features, especially the
9.2 (enstatite) and 11.3 ![]() m
(forsterite) features. As silicates are expected to thermally
anneal close to the star, this result may reflect a counterintuitive
positive gradient of the crystalline silicate fraction toward colder
temperatures. However, the presence of the broad, and generally strong,
amorphous
m
(forsterite) features. As silicates are expected to thermally
anneal close to the star, this result may reflect a counterintuitive
positive gradient of the crystalline silicate fraction toward colder
temperatures. However, the presence of the broad, and generally strong,
amorphous ![]() m
feature may lower the contrast of (or even hide) the shortest
wavelength crystalline features preventing direct conclusions. We
examine in this section this apparent crystallinity paradox by comparing our Spitzer/IRS observations to synthetic spectra.
m
feature may lower the contrast of (or even hide) the shortest
wavelength crystalline features preventing direct conclusions. We
examine in this section this apparent crystallinity paradox by comparing our Spitzer/IRS observations to synthetic spectra.
To better gauge the actual differences between the degrees of crystallinity of the warm (
![]() m) versus cold (
m) versus cold (
![]() m)
disk regions, we generate synthetic spectra
representative of the observations, from which we then extract line
fluxes as was performed for the IRS spectra in Sect. 3.2.1. We consider amorphous species that include silicates of olivine stoichiometry (glassy MgFeSiO4, optical constants from Dorschner et al. 1995), and silicates of pyroxene stoichiometry (glassy MgFeSi2O6, optical constants from Dorschner et al. 1995). For the crystalline species, we use enstatite (MgSiO3) optical constants from Jaeger et al. (1998) and forsterite (Mg2SiO4) optical constants from
Servoin & Piriou (1973). Theoretical mass opacities
m)
disk regions, we generate synthetic spectra
representative of the observations, from which we then extract line
fluxes as was performed for the IRS spectra in Sect. 3.2.1. We consider amorphous species that include silicates of olivine stoichiometry (glassy MgFeSiO4, optical constants from Dorschner et al. 1995), and silicates of pyroxene stoichiometry (glassy MgFeSi2O6, optical constants from Dorschner et al. 1995). For the crystalline species, we use enstatite (MgSiO3) optical constants from Jaeger et al. (1998) and forsterite (Mg2SiO4) optical constants from
Servoin & Piriou (1973). Theoretical mass opacities
![]() are computed using Mie theory (valid for hard spheres) for the
amorphous species and DHS theory (Distribution of Hollow Spheres,
Min et al. 2005) for the crystalline
silicates. Twelve example opacity curves for the four compositions and
three typical (in terms of spectroscopic signature) grain sizes (
are computed using Mie theory (valid for hard spheres) for the
amorphous species and DHS theory (Distribution of Hollow Spheres,
Min et al. 2005) for the crystalline
silicates. Twelve example opacity curves for the four compositions and
three typical (in terms of spectroscopic signature) grain sizes (![]() m,
m, ![]() m and
m and ![]() m) are displayed in Fig. 9.
m) are displayed in Fig. 9.
The synthetic spectra of Fig. 10 have been generated by adding to a representative continuum (![]() ),
the mass opacities of amorphous and crystalline silicates, multiplied
by relative masses and by a blackbody at reference temperatures
(350 K for the warm region, and 100 K for cold region). The
amorphous content is a 50:50 mixture of olivine and pyroxene and the
crystalline content is a 50:50 mixture of enstatite plus
forsterite. The adopted
),
the mass opacities of amorphous and crystalline silicates, multiplied
by relative masses and by a blackbody at reference temperatures
(350 K for the warm region, and 100 K for cold region). The
amorphous content is a 50:50 mixture of olivine and pyroxene and the
crystalline content is a 50:50 mixture of enstatite plus
forsterite. The adopted ![]() m representative continuum is given by the median values (mean slopes and mean offsets:
m representative continuum is given by the median values (mean slopes and mean offsets:
![]()
![]()
![]() )
of all the local continua linearly (
)
of all the local continua linearly (
![]()
![]()
![]() )
estimated in Sect. 3.2.1 for the observed amorphous 10
)
estimated in Sect. 3.2.1 for the observed amorphous 10 ![]() m features:
m features:
![]()
![]()
![]() ,
with
,
with ![]() in Jy and
in Jy and ![]() in
in ![]() m. Similarly, a representative C23/C28 continuum has been derived for cold synthetic spectra:
m. Similarly, a representative C23/C28 continuum has been derived for cold synthetic spectra:
![]()
![]()
![]() (
(![]() in Jy and
in Jy and ![]() in
in ![]() m).
m).
To obtain as representative synthetic spectra as possible, we compute
the median observed continuum over feature ratio (i.e., the continuum
flux divided by the height of the feature) for the 10 ![]() m feature and the C23 complex. For the amorphous 10
m feature and the C23 complex. For the amorphous 10 ![]() m feature, we obtain a
ratio of 2 and we therefore normalize the opacities, before adding them to the continuum (
m feature, we obtain a
ratio of 2 and we therefore normalize the opacities, before adding them to the continuum (![]() ),
so that the synthetic spectra show similar ratios. For the C23, we
measure a median continuum over feature ratio of 20
),
so that the synthetic spectra show similar ratios. For the C23, we
measure a median continuum over feature ratio of 20 ![]() 10, and we normalize the opacities in order to get a ratio
between 10 and 30 in the synthetic spectra. This exercise
could not be reproduced for the large 6.0
10, and we normalize the opacities in order to get a ratio
between 10 and 30 in the synthetic spectra. This exercise
could not be reproduced for the large 6.0 ![]() m
grains because the shapes of their C23/C28 features are not
representative of the observed features (especially for the forsterite
grains, see right panel of Fig. 9),
suggesting such large grains are not the main carriers of these
features. As a final step, the synthetic spectra are degraded by
adding random noise, with a maximum amplitude of 1.8
m
grains because the shapes of their C23/C28 features are not
representative of the observed features (especially for the forsterite
grains, see right panel of Fig. 9),
suggesting such large grains are not the main carriers of these
features. As a final step, the synthetic spectra are degraded by
adding random noise, with a maximum amplitude of 1.8 ![]() 10-3 Jy for the warm spectra and 7.2
10-3 Jy for the warm spectra and 7.2 ![]() 10-3
for the cold spectra, representative of the quadratic sum of the
measured uncertainties on the Spitzer data over in the 10
10-3
for the cold spectra, representative of the quadratic sum of the
measured uncertainties on the Spitzer data over in the 10 ![]() m region and in the C23/C28 spectral range. The synthetic observations displayed in Fig. 10 are then processed as in Sect. 3.2.1 to derive the band fluxes of the crystalline
features.
m region and in the C23/C28 spectral range. The synthetic observations displayed in Fig. 10 are then processed as in Sect. 3.2.1 to derive the band fluxes of the crystalline
features.
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{12062f16.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg110.png)
|
Figure 11:
Signal-to-noise ratio of the 9.2 |
| Open with DEXTER | |
The theoretical SNRs for the 9.2, ![]() m,
C23 and C28 crystalline silicate features, assuming crystalline
mass fractions between 0% and 50% and characteristic grain
sizes, are displayed in Fig. 11. It is seen that the SNR reached in the simulations compare well with the measured SNR values, especially for micron-sized grains (Table 5).
The diagonal-striped areas correspond to crystalline mass fractions
where the continuum over C23/C28 feature ratios could hardly match
the median observed values, or which totally fail to reproduce them.
This means that we are not able to discuss the detectability of
features for crystalline mass fractions smaller than 5
and 15% for grains sizes of 0.1 and 1.5
m,
C23 and C28 crystalline silicate features, assuming crystalline
mass fractions between 0% and 50% and characteristic grain
sizes, are displayed in Fig. 11. It is seen that the SNR reached in the simulations compare well with the measured SNR values, especially for micron-sized grains (Table 5).
The diagonal-striped areas correspond to crystalline mass fractions
where the continuum over C23/C28 feature ratios could hardly match
the median observed values, or which totally fail to reproduce them.
This means that we are not able to discuss the detectability of
features for crystalline mass fractions smaller than 5
and 15% for grains sizes of 0.1 and 1.5 ![]() m, respectively. In the particular case of the 6.0
m, respectively. In the particular case of the 6.0 ![]() m grains, as explained above, we cannot compute SNR for C23 and C28 complexes as opacities do not match typical observations.
m grains, as explained above, we cannot compute SNR for C23 and C28 complexes as opacities do not match typical observations.
We see in Fig. 11 that the SNR of the crystalline features drops with increasing grain size (especially the ![]() m,
m, ![]() m features) and with decreasing crystalline mass fraction, as expected. A crystalline fraction of
m features) and with decreasing crystalline mass fraction, as expected. A crystalline fraction of ![]() % or larger seems to
be enough that all four of the studied crystalline features are observable if the grains are sub-micron in size. For the
% or larger seems to
be enough that all four of the studied crystalline features are observable if the grains are sub-micron in size. For the ![]() m-sized grains, crystalline mass fractions of about 15% are
required, (1) to obtain spectra consistent with observations; and (2) to detect all the features studied with SNR > 20. For higher crystalline mass fractions, they all present very similar
behaviors. For
m-sized grains, crystalline mass fractions of about 15% are
required, (1) to obtain spectra consistent with observations; and (2) to detect all the features studied with SNR > 20. For higher crystalline mass fractions, they all present very similar
behaviors. For ![]() m-sized
grains, it becomes more difficult to trace the detectability of the C23
and C28 features as opacities become much less consistent with
typical observations. For 9.2
m-sized
grains, it becomes more difficult to trace the detectability of the C23
and C28 features as opacities become much less consistent with
typical observations. For 9.2 ![]() m and 11.3
m and 11.3 ![]() m, crystalline fractions larger than 20% and 15%, respectively, are required in order to detect these features with SNR > 20.
m, crystalline fractions larger than 20% and 15%, respectively, are required in order to detect these features with SNR > 20.
Since the observed features in our sample are mainly produced by ![]() m-sized grains (Sect. 4.1), which in particular produce a shoulder at the location of the
m-sized grains (Sect. 4.1), which in particular produce a shoulder at the location of the ![]() m crystalline feature, we conclude that the physical processes that preferentially place
m crystalline feature, we conclude that the physical processes that preferentially place ![]() m-sized
grains in the disk atmospheres do not contribute much to the measured
differences between the number of detections of the
m-sized
grains in the disk atmospheres do not contribute much to the measured
differences between the number of detections of the ![]() m feature compared to the number of detections of the C23 complex (Figs. 3 and 4).
m feature compared to the number of detections of the C23 complex (Figs. 3 and 4).
To summarize, we find an apparent crystallinity paradox, namely a noticeable difference in detection statistics for the ![]() m
and C23 features, with more than 3 times more detections for
C23 compared to the number of detections of the 11.3
m
and C23 features, with more than 3 times more detections for
C23 compared to the number of detections of the 11.3 ![]() m
forsterite feature. This seems counterintuitive as shorter wavelengths
are expected to probe warmer disk regions where grains can crystallize
more efficiently. We investigated the possibility that crystalline
features could be hidden by amorphous features. The effect seems
insufficient to explain the observations, but we cannot predict firmly
the real impact of this effect until the Spitzer observations are
confronted by a more detailed compositional analysis. This is deferred
to a future paper (Olofsson et al. 2009b, in prep.).
m
forsterite feature. This seems counterintuitive as shorter wavelengths
are expected to probe warmer disk regions where grains can crystallize
more efficiently. We investigated the possibility that crystalline
features could be hidden by amorphous features. The effect seems
insufficient to explain the observations, but we cannot predict firmly
the real impact of this effect until the Spitzer observations are
confronted by a more detailed compositional analysis. This is deferred
to a future paper (Olofsson et al. 2009b, in prep.).
5 Discussion
5.1 On the lack of Fe-rich silicates
Because of the large number of objects analysed in this paper, our
results raise challenging questions on the dynamics and (chemical)
evolution of planet-forming disks regions that are in principle not
statistically biased. For instance, the lack of Fe-rich silicates in
our 96 star sample![]() reinforces the result by Bouwman et al. (2008) obtained with their 7-star sample. Silicates crystals studied in this
analysis may contain iron, as seen in Sect. 3.1.2 but magnesium is the most abundant element. Several scenarios can explain this apparent lack of iron. First, Davoisne et al. (2006)
found that a reduction reaction during the thermal annealing of
ferro-magnesian amorphous silicates at temperatures below 1000 K
can produce pure forsterite crystals plus spheroidal metallic
particles. The iron is therefore locked inside a metallic nanophase
that cannot be observed. Secondly, according to Nuth & Johnson (2006),
simple thermal annealing in the warm inner regions of the disk cannot
produce Fe-rich silicate crystals. As the annealing timescale for
iron silicates is
larger than for magnesium silicates (Hallenbeck et al. 2000),
the lifetime of such Fe-rich silicates against the evaporation
timescale is expected to be too short for these grains to crystallize
and then be transported outward in the disk. Still, thermal annealing
induced by shocks may be able to produce both Fe-rich and Mg-rich
crystals at the same time.
reinforces the result by Bouwman et al. (2008) obtained with their 7-star sample. Silicates crystals studied in this
analysis may contain iron, as seen in Sect. 3.1.2 but magnesium is the most abundant element. Several scenarios can explain this apparent lack of iron. First, Davoisne et al. (2006)
found that a reduction reaction during the thermal annealing of
ferro-magnesian amorphous silicates at temperatures below 1000 K
can produce pure forsterite crystals plus spheroidal metallic
particles. The iron is therefore locked inside a metallic nanophase
that cannot be observed. Secondly, according to Nuth & Johnson (2006),
simple thermal annealing in the warm inner regions of the disk cannot
produce Fe-rich silicate crystals. As the annealing timescale for
iron silicates is
larger than for magnesium silicates (Hallenbeck et al. 2000),
the lifetime of such Fe-rich silicates against the evaporation
timescale is expected to be too short for these grains to crystallize
and then be transported outward in the disk. Still, thermal annealing
induced by shocks may be able to produce both Fe-rich and Mg-rich
crystals at the same time.
5.2 On the need for turbulent diffusion and grain-grain fragmentation
The new grain size proxy introduced here for cold crystalline
silicates (via the C23 complex) indicates that the upper layers of
the disks are preferentially populated by ![]() m-sized grains. This result also holds for the warm disk region using the classical size proxy for the carriers of the 10
m-sized grains. This result also holds for the warm disk region using the classical size proxy for the carriers of the 10 ![]() m amorphous feature (Fig. 5).
Adopting a purely sequential evolutionary
approach for the solid constituents in disks, where interstellar-like
grains coagulate to form micron-sized dust aggregates, then pebbles and
planetesimals, a straighforward conclusion from these results would be
that grain agglomeration occurred in the first few AU and that we are
witnessing an intermediate, regular step of the growth of solid
particles along their way to form planets. Nevertheless, this picture
is most certainly an oversimplified view of the processes at work in
planet-forming regions around young stars as it does not fit with basic
dynamical considerations. Indeed, the short settling time-scale of
m amorphous feature (Fig. 5).
Adopting a purely sequential evolutionary
approach for the solid constituents in disks, where interstellar-like
grains coagulate to form micron-sized dust aggregates, then pebbles and
planetesimals, a straighforward conclusion from these results would be
that grain agglomeration occurred in the first few AU and that we are
witnessing an intermediate, regular step of the growth of solid
particles along their way to form planets. Nevertheless, this picture
is most certainly an oversimplified view of the processes at work in
planet-forming regions around young stars as it does not fit with basic
dynamical considerations. Indeed, the short settling time-scale of ![]() m-sized grains in a laminar disk, and their expected fast growth which will accelerate sedimentation (Laibe et al. 2008; Dullemond & Dominik 2005),
both argue in favor of some processes that sustain the disk atmosphere
with grains that have mid-infared spectroscopic signatures (grains
smaller than about 10
m-sized grains in a laminar disk, and their expected fast growth which will accelerate sedimentation (Laibe et al. 2008; Dullemond & Dominik 2005),
both argue in favor of some processes that sustain the disk atmosphere
with grains that have mid-infared spectroscopic signatures (grains
smaller than about 10 ![]() m)
over a few Myr. Therefore, our results support the
replenishment of the disk upper regions by the vertical transport of
dust particles (e.g. turbulent diffusion, Fromang & Nelson 2009), likely combined with grain-grain fragmentation to balance the expected
efficient growth of solid particulates (that accelerates sedimentation, Laibe et al. 2008; Dullemond & Dominik 2005).
In this picture, the grains observed at mid-IR wavelengths would then
result from the destruction of much larger solid particles (an
assumption consistent with the presence of millimeter-sized grains in
most TTauri disks, e.g. review by Natta et al. 2007), rather than from the direct growth from interstellar-like grains.
m)
over a few Myr. Therefore, our results support the
replenishment of the disk upper regions by the vertical transport of
dust particles (e.g. turbulent diffusion, Fromang & Nelson 2009), likely combined with grain-grain fragmentation to balance the expected
efficient growth of solid particulates (that accelerates sedimentation, Laibe et al. 2008; Dullemond & Dominik 2005).
In this picture, the grains observed at mid-IR wavelengths would then
result from the destruction of much larger solid particles (an
assumption consistent with the presence of millimeter-sized grains in
most TTauri disks, e.g. review by Natta et al. 2007), rather than from the direct growth from interstellar-like grains.
5.3 On the depletion of submicron-sized grains
A consequence of the above conclusion is that one would have to explain
the general apparent depletion of submicron-sized grains in the disk
zones probed by mid-IR spectroscopy. The fact that we see a flat, boxy
10 ![]() m
feature profile for most TTs indicates that there cannot be many
submicron-sized grains, because their emission would overwhelm the few
large grains. Grain-grain collisions are nevertheless expected to
produce fragments with a range of sizes that are likely to extend to
the submicron domain (i.e. the size of the monomers that form
m
feature profile for most TTs indicates that there cannot be many
submicron-sized grains, because their emission would overwhelm the few
large grains. Grain-grain collisions are nevertheless expected to
produce fragments with a range of sizes that are likely to extend to
the submicron domain (i.e. the size of the monomers that form ![]() m-sized
aggregates). This effect might be enhanced by the large velocity
fluctuations (a fraction of the local sound speed) found at high
altitudes above the disk midplane in disk simulations with
MHD turbulence (Fromang & Nelson 2009).
Qualitatively, submicron-sized grains, lifted in the disk atmospheres
by turbulent diffusion or produced locally, are therefore expected to
be abundant, which contradicts the IRS observations.
m-sized
aggregates). This effect might be enhanced by the large velocity
fluctuations (a fraction of the local sound speed) found at high
altitudes above the disk midplane in disk simulations with
MHD turbulence (Fromang & Nelson 2009).
Qualitatively, submicron-sized grains, lifted in the disk atmospheres
by turbulent diffusion or produced locally, are therefore expected to
be abundant, which contradicts the IRS observations.
5.3.1 Impact of the size distribution
The above conclusion is based on our single, characteristic grain size approach (Sects. 4.1 and 4.2)
and one may question whether this assumption affects our interpretation
of the observations. To answer that question, we calculate mean
cross-sections as follows:
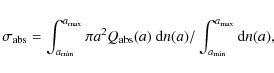
where a is the grain radius,
5.3.2 Impact of the crystallinity
Several studies (e.g. Bouwman et al. 2001; Honda et al. 2006; or van Boekel et al. 2005) mention the possible impact of the crystallinity on the shape versus strength correlation for the 10 ![]() m feature. According to these studies, the presence of crystalline grains can mimic the flattening of the feature. Min et al. (2008) recently investigated in detail this effect by considering inhomogeneous aggregates. Their Fig. 2 shows that
m feature. According to these studies, the presence of crystalline grains can mimic the flattening of the feature. Min et al. (2008) recently investigated in detail this effect by considering inhomogeneous aggregates. Their Fig. 2 shows that
![]() remains approximately constant for crystalline fractions up to 20% (the maximum fraction considered in their study) while
S11.3/S9.8 rises, suggesting a shift along the y-axis of Fig. 12 due to crystallinity rather than along the observed trend.
remains approximately constant for crystalline fractions up to 20% (the maximum fraction considered in their study) while
S11.3/S9.8 rises, suggesting a shift along the y-axis of Fig. 12 due to crystallinity rather than along the observed trend.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12062f17.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg118.png)
|
Figure 12:
Correlation between shape and strength for the amorphous 10 |
| Open with DEXTER | |
In order to further investigate the impact of crystallinity on this
correlation, we use the synthetic spectra described in Sect. 4.6.
The only difference is that we do not normalize opacities anymore to
obtain a constant ratio between feature strength and continuum.
Normalizing opacities would lead to a constant
![]() ,
which is not what we want to characterize here. We therefore normalize
the opacities, for each grain size, so that only the strongest feature
reaches a ratio of 2 between the continuum and the feature
strength. Other features are normalized with the same factor and
obviously present a higher ratio between continuum and feature
strength. This normalization is done in order to reproduce spectra
similar to observations, and still conserve the diversity of feature
strengths. Subsequently, values for S9.8, S11.3 and
,
which is not what we want to characterize here. We therefore normalize
the opacities, for each grain size, so that only the strongest feature
reaches a ratio of 2 between the continuum and the feature
strength. Other features are normalized with the same factor and
obviously present a higher ratio between continuum and feature
strength. This normalization is done in order to reproduce spectra
similar to observations, and still conserve the diversity of feature
strengths. Subsequently, values for S9.8, S11.3 and
![]() are derived in the same way as in Sect. 4.1. Figure 13 shows the impact of crystallinity on the shape versus strength for the 10
are derived in the same way as in Sect. 4.1. Figure 13 shows the impact of crystallinity on the shape versus strength for the 10 ![]() m feature. We consider three grain sizes (0.1, 1.5 and 6.0
m feature. We consider three grain sizes (0.1, 1.5 and 6.0 ![]() m) and the same composition as in Sect. 4.6:
50:50 mixture of olivine and pyroxene for the amorphous content
and 50:50 of enstatite and forsterite for the crystalline
population. The crystallinity fraction varies from 0% to 50% (0,
5, 10, 15, 20, 25, 30, 40 and 50%), and increasing crystallinity
goes from bottom left to top right on the plot. We note that for
6.0
m) and the same composition as in Sect. 4.6:
50:50 mixture of olivine and pyroxene for the amorphous content
and 50:50 of enstatite and forsterite for the crystalline
population. The crystallinity fraction varies from 0% to 50% (0,
5, 10, 15, 20, 25, 30, 40 and 50%), and increasing crystallinity
goes from bottom left to top right on the plot. We note that for
6.0 ![]() m-sized grains the effect is negligible, while it is more dramatic for 0.1
m-sized grains the effect is negligible, while it is more dramatic for 0.1 ![]() m-sized
grains. The spread induced by an increase of crystallinity is almost
orthogonal to the direction of the correlation. This result was also
found by Kessler-Silacci et al. (2006) (Fig. 10e).
The direction of this deviation can be understood when considering
opacities for amorphous and crystalline grains. For the same mass of
dust, crystalline grain emission will be stronger compared to amorphous
grains. Therefore adding some crystalline grains to a purely amorphous
dust content will give a 10
m-sized
grains. The spread induced by an increase of crystallinity is almost
orthogonal to the direction of the correlation. This result was also
found by Kessler-Silacci et al. (2006) (Fig. 10e).
The direction of this deviation can be understood when considering
opacities for amorphous and crystalline grains. For the same mass of
dust, crystalline grain emission will be stronger compared to amorphous
grains. Therefore adding some crystalline grains to a purely amorphous
dust content will give a 10 ![]() m feature stronger and broader (because of crystalline features at, e.g., 11.3
m feature stronger and broader (because of crystalline features at, e.g., 11.3 ![]() m in the case of forsterite). This will thus produce a higher value of
S11.3/S9.8 and at the same time a stronger
m in the case of forsterite). This will thus produce a higher value of
S11.3/S9.8 and at the same time a stronger
![]() .
.
Crystallinity therefore does impact the correlation and may be responsible for a dispersion in the direction orthogonal to the correlation, but according to the opacities, it cannot solely explain the observed trend.
5.3.3 Hypothesis for the depletion of submicron-sized grains
Several solutions could be envisaged to explain the apparent depletion of submicron-sized grains at high altitudes above the disk midplane. The fragmentation time-scale of grains in disk atmospheres may be longer than the grain growth timescale, thereby quickly eliminating the smallest and most freshly produced submicronic grains. The high velocity fluctuations observed in MHD simulations at high altitudes, do not, in principle, work in favor of this scenario. An alternative possibility may be that the submicron-sized grains are evacuated from the upper layers of the disks by stellar winds or radiation pressure. The impact of radiation pressure on grains in young disks has been explored by Takeuchi & Lin (2003) and presents several advantages. First, it acts on short timescales as long as the grain size reaches a threshold, usually referred to as the blowout size limit, below which the radiation pressure force overcomes the gravitational and gas drag forces. Second, the blowout size limit falls in the right regime of grain sizes (close to a micrometer for silicates) for solar-type stars in the presence of some gas.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12062f18.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg119.png)
|
Figure 13:
Correlation between shape and strength for the amorphous 10 |
| Open with DEXTER | |
It is interesting to apply the latter scenario to the case of more luminous stars. According to Kessler-Silacci et al. (2007), HAeBe stars tend to show a widest variety of 10 ![]() m
silicate features, including the peaked features attributed to
submicron-sized grains. Because of their higher temperature and
luminosity, HAeBe stars are expected to have upper layers that are
even more ionized than those of T Tauri stars, thereby enhancing
the turbulence if it is supported by disk magnetic fields, as well as
velocity fluctuations. This would therefore encourage the systematic
production of submicron dust fragments in disk atmospheres. On the
other hand,
silicate grains of a few micrometers and smaller, are in principle more
prone to be eliminated by radiation pressure. Nevertheless, the latter
reasoning assumes an optically thin medium at the wavelengths where
grains absorb most, namely in the UV and visible. The optically thin
region at mid-IR wavelengths is likely to be essentially opaque in the
UV/visible, and this opacity will affect more strongly the most
luminous stars, thereby possibly reducing the blowout size limit.
m
silicate features, including the peaked features attributed to
submicron-sized grains. Because of their higher temperature and
luminosity, HAeBe stars are expected to have upper layers that are
even more ionized than those of T Tauri stars, thereby enhancing
the turbulence if it is supported by disk magnetic fields, as well as
velocity fluctuations. This would therefore encourage the systematic
production of submicron dust fragments in disk atmospheres. On the
other hand,
silicate grains of a few micrometers and smaller, are in principle more
prone to be eliminated by radiation pressure. Nevertheless, the latter
reasoning assumes an optically thin medium at the wavelengths where
grains absorb most, namely in the UV and visible. The optically thin
region at mid-IR wavelengths is likely to be essentially opaque in the
UV/visible, and this opacity will affect more strongly the most
luminous stars, thereby possibly reducing the blowout size limit.
Clearly, the depletion of submicron-sized grains in the disk atmospheres of most T Tauri stars should be further investigated by models to examine the likelihood of the scenarios discussed above (competition between coagulation and fragmentation, stellar winds, radiation pressure, ...).
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12062f19.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg120.png)
|
Figure 14: Schematic view of the TTauri disk regions probed by the Spitzer IRS spectroscopic observations. This illustrates some of the dynamical processes that are discussed in Sect. 5 and summarized in Sect. 6. |
| Open with DEXTER | |
5.4 On radial mixing
The coldest disk component probed by our IRS observations shows a rather high crystallinity fraction. According to Fig. 3, the 23 and 28 ![]() m
complexes are detected in more than 50% of the spectra. In a
scenario where silicate crystals form by thermal annealing, the
production of crystalline silicates can only occur on reasonably short
time-scales near the star
(T > 900 K), namely in regions much hotter than those emitting at
m
complexes are detected in more than 50% of the spectra. In a
scenario where silicate crystals form by thermal annealing, the
production of crystalline silicates can only occur on reasonably short
time-scales near the star
(T > 900 K), namely in regions much hotter than those emitting at
![]() m.
The observed cold crystals would thus have been radially transported
there from the inner disk zone, which according to two-dimensional
models can occur around the midplane of accretion disks (Ciesla 2009, and references therein). Keller & Gail (2004), for example, find that
m.
The observed cold crystals would thus have been radially transported
there from the inner disk zone, which according to two-dimensional
models can occur around the midplane of accretion disks (Ciesla 2009, and references therein). Keller & Gail (2004), for example, find that ![]() to 30% of the total mass that is transported inward at high disk
altitudes is transported outward near the disk midplane. For a solar
mass star with an accretion rate of
to 30% of the total mass that is transported inward at high disk
altitudes is transported outward near the disk midplane. For a solar
mass star with an accretion rate of
![]() /yr, Ciesla (2009) estimates the crystalline fraction at 10 AU to be
about
/yr, Ciesla (2009) estimates the crystalline fraction at 10 AU to be
about ![]() % by the end of his simulations. As the accretion rate becomes smaller, the crystalline fraction drops accordingly:
% by the end of his simulations. As the accretion rate becomes smaller, the crystalline fraction drops accordingly: ![]() % and
% and ![]() % for
% for
![]() /yr and
/yr and
![]() /yr, respectively. However, Watson et al. (2009) find
only a weak correlation between the accretion rate and the crystalline features arising at around 10
/yr, respectively. However, Watson et al. (2009) find
only a weak correlation between the accretion rate and the crystalline features arising at around 10 ![]() m, and no correlation with the 33
m, and no correlation with the 33 ![]() m
feature, leading the authors to suggest that some
mechanisms may be erasing such trends. Alternatively, other
crystallisation processes at colder temperatures (e.g. via nebular
shock, Desch & Connolly 2002) could also contribute to the presence of crystals at significant distances from the central object (e.g. Kimura et al. 2008).
m
feature, leading the authors to suggest that some
mechanisms may be erasing such trends. Alternatively, other
crystallisation processes at colder temperatures (e.g. via nebular
shock, Desch & Connolly 2002) could also contribute to the presence of crystals at significant distances from the central object (e.g. Kimura et al. 2008).
It is noteworthy that the warmer disk zone seems significantly less crystalline than the colder regions, although detailed compositional analysis of the IRS spectra is required before firmly concluding this must be so (Olofsson et al. 2009b, in prep.) Interestingly, compositional fits to some individual IRS spectra by Bouy et al. (2008) and Sargent et al. (2009) do show the need for larger amounts of silicate crystals in the outer regions compared to inner regions (e.g. 2MASS J04442713+2512164 and F04147+2822). If radial mixing leads to the large crystalline fraction in the cold disk component, it leaves the disks with an inhomogeneous chemical composition in the solid phase. Some re-amorphisation processing of the crystalline grains, by X-ray emission or cosmics rays for example, could also contribute to the apparent lack of crystals in the inner regions of disks.
This result of a cold region being more crystalline compared to
the inner warm regions seems, at first glance, to be in contradiction
with the results by van Boekel et al. (2004)
who observed three HAeBe stars with the mid-IR instrument MIDI for
the VLTI interferometer. Using different baselines, they found that the
inner regions (1-2 AU) of the disks are more crystalline compared
to the outer regions (2-20 AU). Beside the fact that their sample
is limited to 3 intermediate mass objects while we analyse a
statistically significant TTs sample, direct comparison of their
observations with ours is not straightforward. They do have spatial
information, but only for the
10 ![]() m
spectral region, while we cover a larger spectral range. We, on the
other hand, are observing the entire disk with Spitzer/IRS, with no
direct spatial information. An ideal and
challenging way to confront such kinds of interferometric data with IRS
would be to repeat similar observations for TTs and even better, at
wavelengths larger than 20
m
spectral region, while we cover a larger spectral range. We, on the
other hand, are observing the entire disk with Spitzer/IRS, with no
direct spatial information. An ideal and
challenging way to confront such kinds of interferometric data with IRS
would be to repeat similar observations for TTs and even better, at
wavelengths larger than 20 ![]() m.
This will ultimately require space-born interferometers because of the
poor atmosphere transmission in the mid-IR. With such observations,
however, we would then be able to constrain the crystalline fraction in
the inner and outer regions of the disk more directly.
m.
This will ultimately require space-born interferometers because of the
poor atmosphere transmission in the mid-IR. With such observations,
however, we would then be able to constrain the crystalline fraction in
the inner and outer regions of the disk more directly.
5.5 On the similarities with Solar System objects
Studies of Solar Sytem asteroids and comets show strong similarities
with our results. First of all, laboratory studies of asteroidal and
cometary solids have show that they contain very little ISM-like
materials. The 81P/Wild 2 samples from the Stardust mission McKeegan et al. (2006),
for example, show that this comet contains high-temperature silicates
and oxide minerals. These authors conclude that such materials could
not have been formed via annealing of presolar amorphous silicates in
the Kuiper belt, and also that they could not have been formed from a
single isotopic reservoir. Overall, this suggests that comet
81P/Wild 2 sampled different regions of the inner solar
protoplanetary disk during its formation. One proposed transportation
mechanism is the combination of winds associated with bipolar outflows.
This hypothesis is also supported by laboratory measurements from Toppani et al. (2006) on condensation under high temperature, low-pressure conditions. Mg-rich silicates crystals can rapidly (![]() h at 4
h at 4 ![]() 10-3 bar)
be produced from the gas phase through condensation, confirming the
fact that crystalline grains can be produced even in bipolar outflows
from evolved stars. In still further work on the 81P/Wild 2
Stardust mission, Zolensky et al. (2006),
found large abundances of crystalline materials. Olivine is present in
most of the studied particles, with grain sizes ranging between
submicron-sized to over 10
10-3 bar)
be produced from the gas phase through condensation, confirming the
fact that crystalline grains can be produced even in bipolar outflows
from evolved stars. In still further work on the 81P/Wild 2
Stardust mission, Zolensky et al. (2006),
found large abundances of crystalline materials. Olivine is present in
most of the studied particles, with grain sizes ranging between
submicron-sized to over 10 ![]() m, and it is concluded that some materials in the comet have seen temperatures possibly higher than 2000 K. Similar to McKeegan et al. (2006),
large-scale radial transportation mechanisms inside the disk are
required to match the derived mineralogy of the olivine samples.
Similar results were found studying other solar system bodies, for
exemple, comet Hale-Bopp. Spectroscopic studies of this object (Wooden et al. 1999; Wooden et al. 2000) revealed the presence of crystalline olivine, crystalline ortho-pyroxene and
crystalline clino-pyroxene, in significant quantities.
m, and it is concluded that some materials in the comet have seen temperatures possibly higher than 2000 K. Similar to McKeegan et al. (2006),
large-scale radial transportation mechanisms inside the disk are
required to match the derived mineralogy of the olivine samples.
Similar results were found studying other solar system bodies, for
exemple, comet Hale-Bopp. Spectroscopic studies of this object (Wooden et al. 1999; Wooden et al. 2000) revealed the presence of crystalline olivine, crystalline ortho-pyroxene and
crystalline clino-pyroxene, in significant quantities.
All these results echo the crystallinity paradox we find in our Spitzer observations, in the sense that the disk dust content is far from being homogeneous, and even far from the simple picture with crystalline grains close to the central object and amorphous content in the outer regions.
6 Summary and conclusion
We have conducted in this paper a comprehensive statistical study of
crystalline silicates in proto-planetary (class II) disks which
was made possible thanks to the high sensitivity of the spectroscopic
instrument IRS (5-35 ![]() m)
onboard the Spitzer Space Telescope. This unprecedented work is among
the first statistical studies of crystalline silicates emission
features over a large sample of young solar-analog stars
(96 objects). We find the following
results:
m)
onboard the Spitzer Space Telescope. This unprecedented work is among
the first statistical studies of crystalline silicates emission
features over a large sample of young solar-analog stars
(96 objects). We find the following
results:
- 1.
- Crystallinity is not a marginal phenomenon in class II
disks around young solar analogs, as more than 3/4 of the
objects show at least one crystalline feature in the IRS spectra.
Crystalline features emitting at wavelengths larger than 20
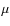 m
are in addition widely present: both the C23 and C28 complexes,
produced by enstatite plus forsterite features, are present at a
frequency larger than 50%.
m
are in addition widely present: both the C23 and C28 complexes,
produced by enstatite plus forsterite features, are present at a
frequency larger than 50%.
- 2.
- The crystalline silicates revealed by the IRS spectra are essentially Mg-rich silicates (forsterite, enstatite), with a small contribution of CaMg-rich silicates (diopside). We find no evidence of Fe-rich silicates (marginal evidence for fayalite) nor troilite (FeS) in our spectra.
- 3.
- We find that the amorphous 10
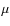 m feature is not correlated with the C23, C28 and 33.6
m feature is not correlated with the C23, C28 and 33.6 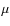 m
crystalline features, neither on the basis of the frequencies at which
they are detected nor on the fluxes they emit. Crystalline features
emitted at wavelengths larger than 20
m
crystalline features, neither on the basis of the frequencies at which
they are detected nor on the fluxes they emit. Crystalline features
emitted at wavelengths larger than 20 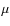 m are, on the other hand, correlated to each other (C23, C28 and 33.6
m are, on the other hand, correlated to each other (C23, C28 and 33.6 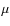 m), based either on detection frequencies and band fluxes.
m), based either on detection frequencies and band fluxes.
- 4.
- From previous results, we conclude that within the spectral
range of the Spitzer/IRS instrument, we are probing essentially
two independent dust populations (see the illustration in Fig. 14): a warm component, which is likely located close to the central object (
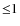 AU), emitting features in the 10
AU), emitting features in the 10 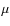 m region, and a second component, located at larger radii (
m region, and a second component, located at larger radii (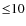 AU)
or deeper inside the disk; the latter cold component being responsible
for the emission of both C23 and C28 complexes plus the 33.6
AU)
or deeper inside the disk; the latter cold component being responsible
for the emission of both C23 and C28 complexes plus the 33.6 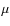 m forsterite feature.
m forsterite feature.
- 5.
- For a large majority of objects, the upper layers of the disks
are populated essentially by micron-sized grains, suggesting that
submicron grains are largely depleted in disks atmospheres. For the
amorphous 10
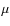 m
feature, we find the known correlation between the shape and the
strength of the feature used as a grain size proxy and showing that the
grains are
m
feature, we find the known correlation between the shape and the
strength of the feature used as a grain size proxy and showing that the
grains are 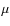 m-sized
or larger. We adapted this relationship to the C23 complex and
find similar results for the crystalline grains producing this complex.
We also noted that the grain size proxies for the 10
m-sized
or larger. We adapted this relationship to the C23 complex and
find similar results for the crystalline grains producing this complex.
We also noted that the grain size proxies for the 10 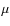 m and C23 features are uncorrelated.
m and C23 features are uncorrelated.
- 6.
- We find a correlation between the shape of the SED (
F30/F13) and the grain size proxy for the 10
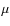 m
feature. We see rather small, warm amorphous silicates for flared disks
and grains becoming larger as disks are flattening. This trend is
almost reversed for the cold, C23 crystalline grains as small
crystals are only found for flattened SEDs.
m
feature. We see rather small, warm amorphous silicates for flared disks
and grains becoming larger as disks are flattening. This trend is
almost reversed for the cold, C23 crystalline grains as small
crystals are only found for flattened SEDs.
- 7.
- We identify an apparent crystallinity paradox since the cold crystalline features (
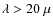 m) are much more frequently detected than the warm ones (
m) are much more frequently detected than the warm ones (
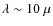 m). We show that crystalline features can be hidden by amorphous features, especially near
m). We show that crystalline features can be hidden by amorphous features, especially near
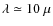 m,
but this contrast effect is insufficient to explain the difference
regarding the apparition frequencies of the C23 complex and the
11.3
m,
but this contrast effect is insufficient to explain the difference
regarding the apparition frequencies of the C23 complex and the
11.3 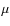 m
forsterite feature, suggesting that the warm grain population is, on
average, intrinsically more amorphous than the cold grain population.
m
forsterite feature, suggesting that the warm grain population is, on
average, intrinsically more amorphous than the cold grain population.
- some mechanisms must supply the upper layers of the disks with micron-sized grains that should otherwise grow and settle rapidly. Vertical turbulent diffusion, accompanied by grain-grain fragmentation, would be natural candidates;
- some mechanisms must act efficiently to remove the submicron-size grains from the regions which are optically thin at IRS wavelengths. Stellar winds and radiation pressure have been suggested as possible processes;
- and, some mechanisms are responsible for rendering the colder disks regions much more crystalline than the warmer zones (crystallinity paradox). If this result has to do with dust radial mixing, it teaches us that the mixing does not result in a disk with a homogenous grain composition, and that it must transport crystals efficiently into the ``comet-forming regions''.
The authors warmly thank Bram Acke for his help on the IDL routine to extract the crystalline features characteristics, Jérome Aléon and Matthieu Gounelle for sharing with us their precious knowledge of small solid Solar System bodies, and Joel Green for the rich discussions we had. We also thank the anonymous referee for the very useful comments that helped improving this study. It is also a pleasure to acknowledge fruitful discussions with the Grenoble FOST team members, as well as the participants to the ANR (Agence Nationale de la Recherche of France) project ANR-07-BLAN-0221. This research is partly supported by the Programme National de Physique Stellaire (PNPS).
References
- Acke, B., & van den Ancker, M. E. 2004, A&A, 426, 151 [EDP Sciences] [CrossRef] [NASA ADS]
- Alcala, J. M., Krautter, J., Schmitt, J. H. M. M., et al. 1995, A&AS, 114, 109 [NASA ADS]
- Andrews, S. M., & Williams, J. P. 2007, ApJ, 659, 705 [CrossRef] [NASA ADS]
- Bouwman, J., Meeus, G., de Koter, A., et al. 2001, A&A, 375, 950 [EDP Sciences] [CrossRef] [NASA ADS]
- Bouwman, J., Henning, T., Hillenbrand, L. A., et al. 2008, ApJ, 683, 479 [CrossRef] [NASA ADS]
- Bouy, H., Huélamo, N., Pinte, C., et al. 2008, A&A, 486, 877 [EDP Sciences] [CrossRef] [NASA ADS]
- Brown, J. M., Blake, G. A., Dullemond, C. P., et al. 2007, ApJ, 664, L107 [CrossRef] [NASA ADS]
- Chen, H., Grenfell, T. G., Myers, P. C., & Hughes, J. D. 1997, ApJ, 478, 295 [CrossRef] [NASA ADS]
- Chihara, H., Koike, C., Tsuchiyama, A., Tachibana, S., & Sakamoto, D. 2002, A&A, 391, 267 [EDP Sciences] [CrossRef] [NASA ADS]
- Ciesla, F. J. 2009, Icarus, 200, 655 [CrossRef] [NASA ADS]
- Crovisier, J., Leech, K., Bockelee-Morvan, D., et al. 1997, Science, 275, 1904 [CrossRef] [NASA ADS]
- D'Alessio, P., Calvet, N., Hartmann, L., Franco-Hernández, R., & Servín, H. 2006, ApJ, 638, 314 [CrossRef] [NASA ADS]
- Davoisne, C., Djouadi, Z., Leroux, H., et al. 2006, A&A, 448, L1 [EDP Sciences] [CrossRef] [NASA ADS]
- Desch, S. J., & Connolly, Jr., H. C. 2002, Meteoritics and Planetary Science, 37, 183 [NASA ADS]
- Dominik, C., Dullemond, C. P., Waters, L. B. F. M., & Walch, S. 2003, A&A, 398, 607 [EDP Sciences] [CrossRef] [NASA ADS]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS]
- Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [EDP Sciences] [CrossRef] [NASA ADS]
- Dullemond, C. P., & Dominik, C. 2008, A&A, 487, 205 [EDP Sciences] [CrossRef] [NASA ADS]
- Evans, II, N. J., Allen, L. E., Blake, G. A., et al. 2003, PASP, 115, 965 [CrossRef] [NASA ADS]
- Evans, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [CrossRef] [NASA ADS]
- Fabian, D., Henning, T., Jäger, C., et al. 2001, A&A, 378, 228 [EDP Sciences] [CrossRef] [NASA ADS]
- Fromang, S., & Nelson, R. P. 2009, A&A, 496, 597 [EDP Sciences] [CrossRef] [NASA ADS]
- Furlan, E., Hartmann, L., Calvet, N., et al. 2006, ApJS, 165, 568 [CrossRef] [NASA ADS]
- Gail, H.-P. 1998, A&A, 332, 1099 [NASA ADS]
- Gail, H.-P. 2004, A&A, 413, 571 [EDP Sciences] [CrossRef] [NASA ADS]
- Geers, V. C. 2007, Ph.D. Thesis, Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
- Geers, V. C., Augereau, J.-C., Pontoppidan, K. M., et al. 2006, A&A, 459, 545 [EDP Sciences] [CrossRef] [NASA ADS]
- Hallenbeck, S. L., Nuth, III, J. A., & Nelson, R. N. 2000, ApJ, 535, 247 [CrossRef] [NASA ADS]
- Harker, D. E., & Desch, S. J. 2002, ApJ, 565, L109 [CrossRef] [NASA ADS]
- Harker, D. E., Woodward, C. E., Wooden, D. H., Fisher, R. S., & Trujillo, C. A. 2007, Icarus, 190, 432 [CrossRef] [NASA ADS]
- Herbig, G. H., & Bell, K. R. 1988, Third catalog of emission-line stars of the Orion population, ed. G. H. Herbig, & K. R. Bell
- Honda, M., Kataza, H., Okamoto, Y. K., et al. 2003, ApJ, 585, L59 [CrossRef] [NASA ADS]
- Honda, M., Kataza, H., Okamoto, Y. K., et al. 2006, ApJ, 646, 1024 [CrossRef] [NASA ADS]
- Hughes, J., & Hartigan, P. 1992, AJ, 104, 680 [CrossRef] [NASA ADS]
- Jaeger, C., Molster, F. J., Dorschner, J., et al. 1998, A&A, 339, 904 [NASA ADS]
- Keller, C., & Gail, H.-P. 2004, A&A, 415, 1177 [EDP Sciences] [CrossRef] [NASA ADS]
- Keller, L. P., Hony, S., Bradley, J. P., et al. 2002, Nature, 417, 148 [CrossRef] [NASA ADS]
- Kessler-Silacci, J., Augereau, J.-C., Dullemond, C. P., et al. 2006, ApJ, 639, 275 [CrossRef] [NASA ADS]
- Kessler-Silacci, J. E., Dullemond, C. P., Augereau, J.-C., et al. 2007, ApJ, 659, 680 [CrossRef]
- Kimura, Y., Miyazaki, Y., Kumamoto, A., Saito, M., & Kaito, C. 2008, ApJ, 680, L89 [CrossRef] [NASA ADS]
- Koike, C., Tsuchiyama, A., Shibai, H., et al. 2000, A&A, 363, 1115 [NASA ADS]
- Koike, C., Chihara, H., Tsuchiyama, A., et al. 2003, A&A, 399, 1101 [EDP Sciences] [CrossRef] [NASA ADS]
- Krautter, J., Wichmann, R., Schmitt, J. H. M. M., et al. 1997, A&AS, 123, 329 [EDP Sciences] [CrossRef] [NASA ADS]
- Lahuis, F., Kessler-Silacci, J. E., Evans, N. J., et al. 2006, c2d Spectroscopy Explanatory Supplement, Tech. rep., Pasadena, Spitzer Science Center
- Lahuis, F., van Dishoeck, E. F., Blake, G. A., et al. 2007, ApJ, 665, 492 [CrossRef] [NASA ADS]
- Laibe, G., Gonzalez, J.-F., Fouchet, L., & Maddison, S. T. 2008, A&A, 487, 265 [EDP Sciences] [CrossRef] [NASA ADS]
- Lawson, W. A., Feigelson, E. D., & Huenemoerder, D. P. 1996, MNRAS, 280, 1071 [NASA ADS]
- McKeegan, K. D., Aléon, J., Bradley, J., et al. 2006, Science, 314, 1724 [CrossRef] [NASA ADS]
- Merín, B., Augereau, J.-C., van Dishoeck, E. F., et al. 2007, ApJ, 661, 361 [CrossRef] [NASA ADS]
- Min, M., Hovenier, J. W., & de Koter, A. 2005, A&A, 432, 909 [EDP Sciences] [CrossRef] [NASA ADS]
- Min, M., Hovenier, J. W., Waters, L. B. F. M., & de Koter, A. 2008, A&A, 489, 135 [EDP Sciences] [CrossRef] [NASA ADS]
- Molster, F. J., Waters, L. B. F. M., & Tielens, A. G. G. M. 2002, A&A, 382, 222 [EDP Sciences] [CrossRef] [NASA ADS]
- Natta, A., Meyer, M. R., & Beckwith, S. V. W. 2000, ApJ, 534, 838 [CrossRef] [NASA ADS]
- Natta, A., Testi, L., Calvet, N., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 767
- Nuth, J. A., & Johnson, N. M. 2006, Icarus, 180, 243 [CrossRef] [NASA ADS]
- Oliveira, I., Merín, B., Pontoppidan, K. M., et al. 2009, ApJ, 691, 672 [CrossRef] [NASA ADS]
- Padgett, D. L., Cieza, L., Stapelfeldt, K. R., et al. 2006, ApJ, 645, 1283 [CrossRef] [NASA ADS]
- Pinte, C., Padgett, D. L., Ménard, F., et al. 2008, A&A, 489, 633 [EDP Sciences] [CrossRef] [NASA ADS]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in C. The art of scientific computing, ed. W. H. Press, S. A. Teukolsky, W. T. Vetterling, & B. P. Flannery
- Przygodda, F., van Boekel, R., Àbrahàm, P., et al. 2003, A&A, 412, L43 [EDP Sciences] [CrossRef] [NASA ADS]
- Salyk, C., Pontoppidan, K. M., Blake, G. A., et al. 2008, ApJ, 676, L49 [CrossRef] [NASA ADS]
- Sargent, B. A., Forrest, W. J., Tayrien, C., et al. 2009, ApJS, 182, 477 [CrossRef] [NASA ADS]
- Savitzky, A., & Golay, M. J. E. 1964, Anal. Chem., 36, 1627 [CrossRef] [NASA ADS]
- Servoin, J., & Piriou, B. 1973, Phys. Stat. Sol. (b), 55, 677 [CrossRef]
- Sitko, M. L., Lynch, D. K., & Russell, R. W. 2000, AJ, 120, 2609 [CrossRef] [NASA ADS]
- Sloan, G. C., Kraemer, K. E., Goebel, J. H., & Price, S. D. 2003, ApJ, 594, 483 [CrossRef] [NASA ADS]
- Takeuchi, T., & Lin, D. N. C. 2003, ApJ, 593, 524 [CrossRef] [NASA ADS]
- Toppani, A., Libourel, G., Robert, F., & Ghanbaja, J. 2006, Geochim. Cosmochim. Acta, 70, 5035 [CrossRef] [NASA ADS]
- Valenti, J. A., Fallon, A. A., & Johns-Krull, C. M. 2003, ApJS, 147, 305 [CrossRef] [NASA ADS]
- van Boekel, R., Waters, L. B. F. M., Dominik, C., et al. 2003, A&A, 400, L21 [EDP Sciences] [CrossRef] [NASA ADS]
- van Boekel, R., Min, M., Leinert, C., et al. 2004, Nature, 432, 479 [CrossRef] [NASA ADS]
- van Boekel, R., Min, M., Waters, L. B. F. M., et al. 2005, A&A, 437, 189 [EDP Sciences] [CrossRef] [NASA ADS]
- Watson, D. M., Leisenring, J. M., Furlan, E., et al. 2009, ApJS, 180, 84 [CrossRef] [NASA ADS]
- Wichmann, R., Krautter, J., Schmitt, J. H. M. M., et al. 1996, A&A, 312, 439 [NASA ADS]
- Wooden, D. H., Harker, D. E., Woodward, C. E., et al. 1999, ApJ, 517, 1034 [CrossRef] [NASA ADS]
- Wooden, D. H., Butner, H. M., Harker, D. E., & Woodward, C. E. 2000, Icarus, 143, 126 [CrossRef] [NASA ADS]
- Wooden, D., Desch, S., Harker, D., Gail, H.-P., & Keller, L. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 815
- Zolensky, M. E., Zega, T. J., Yano, H., et al. 2006, Science, 314, 1735 [CrossRef] [NASA ADS]
Online Material
Table 4: Characteristics of the observations.
Table 5:
Signal-to-noise ratios for detections of crystalline silicate features,
amorphous silicate 10 ![]() m feature and silica.
m feature and silica.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f20.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg135.png)
|
Figure 15:
Spitzer/IRS spectra of young stars in the Perseus cloud, in units of Jy. Gray areas correspond to 3- |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f21.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg136.png)
|
Figure 16: Same as Fig. 15 but for the Taurus star sample. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f22.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg137.png)
|
Figure 17: Same as Fig. 15 but for the Chamaleon star sample. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f23.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg138.png)
|
Figure 18: Spitzer/IRS spectra for the Chamaleon sample: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f24.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg139.png)
|
Figure 19: Same as Fig. 15 but for the Lupus star sample. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f25.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg140.png)
|
Figure 20: Same as Fig. 15 but for the Ophiuchus star sample. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f26.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg141.png)
|
Figure 21: Spitzer/IRS spectra for the Ophiuchus sample: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f27.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg142.png)
|
Figure 22: Same as Fig. 15 but for the Serpens star sample. |
| Open with DEXTER | |
| Figure 23: Same as Fig. 15 but for the 3 isolated stars in our sample. |
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f29.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg144.png)
|
Figure 24: Same as Fig. 15 but for the 4 objects with spectra similar to C-rich and O-rich AGB stars. |
| Open with DEXTER | |
Footnotes
- ... silicates
![[*]](/icons/foot_motif.png)
- Tables 4, 5 and Figs. 15-24 are only available in electronic form at http://www.aanda.org
- ... features
![[*]](/icons/foot_motif.png)
- Extensive, narrow features not discussed in this paper, but
seen between 10 and
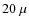 m
in Fig. 1
are attributed to water emission lines (Salyk
et al. 2008).
m
in Fig. 1
are attributed to water emission lines (Salyk
et al. 2008).
- ... sample
![[*]](/icons/foot_motif.png)
- Except 5 marginal detections discussed in Sect. 3.1.2.
All Tables
Table 1: Overview of the modules used to obtain the final spectra.
Table 2: Summary of the different crystalline silicate features examined in this study.
Table 3: Correlation coefficients between the features detected with SNR > 20.
Table 4: Characteristics of the observations.
Table 5:
Signal-to-noise ratios for detections of crystalline silicate features,
amorphous silicate 10 ![]() m feature and silica.
m feature and silica.
All Figures
![\begin{figure}
\par\includegraphics[angle=90,width=17cm,clip]{12062f1.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg26.png)
|
Figure 1: Example Spitzer/IRS
spectra of 3 T Tauri stars (top spectrum: SL+SH+LH modules,
bottom spectrum: SL+LL). The grey envelopes correspond to 3- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12062f2.ps}\hspace*{1.5cm}
\includegraphics[width=7.95cm,clip]{12062f3.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg34.png)
|
Figure 2:
Left panel: examples of the 9.2 (enstatite), 11.3 (forsterite) and 12.5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12062f4.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg47.png)
|
Figure 3:
Detection statistics for crystalline silicate features (yellow and red bars) for the 10.0 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12062f5.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg49.png)
|
Figure 4: Same as Fig. 3 but now sorted by clouds. Uncertainties are again Poisson noise, derived from the number of objects per cloud: 15 for Perseus, 8 for Taurus, 20 for Chamaeleon, 16 for Lupus, 24 for Ophiuchus and 12 for Serpens. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12062f6.ps}\hspace*{1cm}
\includegraphics[width=8.5cm,clip]{12062f7.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg62.png)
|
Figure 5:
Left panel: correlations between shape (
S11.3/S9.8) and strength (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12062f8.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg70.png)
|
Figure 6:
Left panel: correlations between the slope of spectra (
F30/F13) as a function of the strength (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=5.9cm,width=8.5cm,clip]{12062f9.ps}\h...
...*{1cm}
\includegraphics[height=5.9cm,width=8.5cm,clip]{12062f10.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg75.png)
|
Figure 7:
Left panel: from left to right: correlations between the unitless line fluxes of the 10 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12062f11.ps}\vspace*{5mm}
\includegraphics[width=8.8cm,clip]{12062f12.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg82.png)
|
Figure 8:
Top panel: normalized line fluxes for the 33.6 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{12062f13.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg95.png)
|
Figure 9:
Example mass opacities (in arbitrary units) used to model the IRS observations. From bottom to top: amorphous olivine, amorphous pyroxene, crystalline forsterite and crystalline enstatite. The left panel shows opacities for a grain size
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12062f14.ps}\hspace*{0.3cm}
\includegraphics[width=8.6cm,clip]{12062f15.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg96.png)
|
Figure 10:
Synthetic spectra, in arbitrary units, for mass fractions of
crystalline silicates from 0% to 50% (steps are: 0, 5, 10, 15, 20, 25,
30, 40, 50%, see Sect. 4.6 for more details). The impact of the grain size on the detectability of the 11.3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{12062f16.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg110.png)
|
Figure 11:
Signal-to-noise ratio of the 9.2 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12062f17.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg118.png)
|
Figure 12:
Correlation between shape and strength for the amorphous 10 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12062f18.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg119.png)
|
Figure 13:
Correlation between shape and strength for the amorphous 10 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12062f19.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg120.png)
|
Figure 14: Schematic view of the TTauri disk regions probed by the Spitzer IRS spectroscopic observations. This illustrates some of the dynamical processes that are discussed in Sect. 5 and summarized in Sect. 6. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f20.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg135.png)
|
Figure 15:
Spitzer/IRS spectra of young stars in the Perseus cloud, in units of Jy. Gray areas correspond to 3- |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f21.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg136.png)
|
Figure 16: Same as Fig. 15 but for the Taurus star sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f22.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg137.png)
|
Figure 17: Same as Fig. 15 but for the Chamaleon star sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f23.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg138.png)
|
Figure 18: Spitzer/IRS spectra for the Chamaleon sample: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f24.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg139.png)
|
Figure 19: Same as Fig. 15 but for the Lupus star sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f25.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg140.png)
|
Figure 20: Same as Fig. 15 but for the Ophiuchus star sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f26.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg141.png)
|
Figure 21: Spitzer/IRS spectra for the Ophiuchus sample: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f27.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg142.png)
|
Figure 22: Same as Fig. 15 but for the Serpens star sample. |
| Open with DEXTER | |
| In the text | |
| |
Figure 23: Same as Fig. 15 but for the 3 isolated stars in our sample. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{12062f29.ps}
\end{figure}](/articles/aa/full_html/2009/43/aa12062-09/Timg144.png)
|
Figure 24: Same as Fig. 15 but for the 4 objects with spectra similar to C-rich and O-rich AGB stars. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


