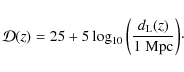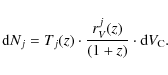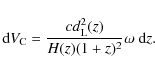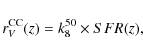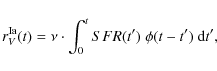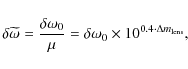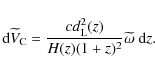| Issue |
A&A
Volume 507, Number 1, November III 2009
|
|
|---|---|---|
| Page(s) | 71 - 83 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200811254 | |
| Published online | 11 August 2009 | |
A&A 507, 71-83 (2009)
Near-IR search for lensed supernovae behind galaxy clusters
II. First detection and future prospects![[*]](/icons/foot_motif.png)
A. Goobar1,2 - K. Paech1,2 - V. Stanishev1,3 - R. Amanullah1,2 - T. Dahlén4 - J. Jönsson5 - J. P. Kneib6 - C. Lidman7 - M. Limousin6,8 - E. Mörtsell1,2 - S. Nobili1 - J. Richard9 - T. Riehm10,2 - M. von Strauss1,2
1 - Department of Physics, Stockholm University, Albanova University
Center, 106 91 Stockholm, Sweden
2 - The Oskar Klein Center, Stockholm University, 106 91 Stockholm,
Sweden
3 - CENTRA - Centro Multidisciplinar de Astrofísica, Instituto Superior
Técnico, Av. Rovisco Pais 1, 1049-001 Lisbon, Portugal
4 - Space Telescope Science Institute, Baltimore, MD 21218, USA
5 - University of Oxford Astrophysics, Denys Wilkinson Building, Keble
Road, Oxford OX1 3RH, UK
6 - Laboratoire d'Astrophysique de Marseille, OAMP, CNRS-Université
Aix-Marseille, 38, rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13,
France
7 - ESO, Vitacura, Alonso de Cordova, 3107, Casilla 19001, Santiago,
Chile
8 - Dark Cosmology Centre, Niels Bohr Institute, University of
Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
9 - Department of Astronomy, California Institute of Technology,
105-24, Pasadena, CA 91125, USA
10 - Department of Astronomy, Stockholm University, Albanova University
Center, 106 91 Stockholm, Sweden
Received 30 October 2008 / Accepted 7 April 2009
Abstract
Aims. Powerful gravitational telescopes in the form
of massive galaxy clusters can be used to enhance the light collecting
power over a limited field of view by about an order of magnitude in
flux. This effect is exploited here to increase the depth of a survey
for lensed supernovae at near-IR wavelengths.
Methods. We present a pilot supernova search
programme conducted with the ISAAC camera at VLT. Lensed galaxies
behind the massive clusters A1689, A1835, and AC114 were observed for a
total of 20 h divided into 2, 3, and 4 epochs respectively,
separated by approximately one month to a limiting magnitude
![]() (Vega).
Image subtractions including another 20 h worth of
archival ISAAC/VLT data were used to search for transients with
lightcurve properties consistent with redshifted supernovae, both in
the new and reference data.
(Vega).
Image subtractions including another 20 h worth of
archival ISAAC/VLT data were used to search for transients with
lightcurve properties consistent with redshifted supernovae, both in
the new and reference data.
Results. The feasibility of finding lensed
supernovae in our survey was investigated using synthetic lightcurves
of supernovae and several models of the volumetric type Ia and
core-collapse supernova rates as a function of redshift. We also
estimate the number of supernova discoveries expected from the inferred
star-formation rate in the observed galaxies. The methods consistently
predict a Poisson mean value for the expected number of supernovae in
the survey of between ![]() and 1.6 for all supernova types, evenly distributed between core
collapse and type Ia supernovae. One transient object was found behind
A1689,
and 1.6 for all supernova types, evenly distributed between core
collapse and type Ia supernovae. One transient object was found behind
A1689, ![]() from a galaxy with photometric redshift
from a galaxy with photometric redshift
![]() .
The lightcurve and colors of the transient are consistent with being a
reddened type IIP supernova at
.
The lightcurve and colors of the transient are consistent with being a
reddened type IIP supernova at
![]() .
The lensing model predicts 1.4 mag of magnification at the
location of the transient, without which this object would not have
been detected in the near-IR ground-based search described in this
paper (unlensed magnitude
.
The lensing model predicts 1.4 mag of magnification at the
location of the transient, without which this object would not have
been detected in the near-IR ground-based search described in this
paper (unlensed magnitude ![]() ).
).
We perform a feasibility study of the potential for lensed
supernovae discoveries with larger and deeper surveys and conclude that
the use of gravitational telescopes is a very exciting path for new
discoveries. For example, a monthly rolling supernova search of a
single very massive cluster with the HAWK-I camera at VLT would yield
![]() lensed
supernova lightcurves per year, where type Ia supernovae would
constitute about half of the expected sample.
lensed
supernova lightcurves per year, where type Ia supernovae would
constitute about half of the expected sample.
Key words: cosmology: observations - stars: supernovae: general - galaxies: clusters: general - gravitational lensing
1 Introduction
Acting as powerful gravitational telescopes, massive galaxy clusters
offer unique opportunities to observe extremely distant galaxies (Kneib
et al. 2004),
as well as distant supernovae (SNe), too faint to be otherwise detected
(Gunnarsson
& Goobar 2003; Kolatt
& Bartelmann 1998;
Kovner
& Paczynski 1988; Sullivan
et al. 2000;
Gal-Yam
et al. 2002). Lensing magnifications of up to a
factor ![]() 40
have been inferred for many multiple images of galaxies (Seitz
et al. 1998)
and typical magnification factors of 5 to
10 are common within the central few arcminutes of the most massive
clusters of galaxies. Exploiting this remarkable boost in flux is an
interesting avenue for probing the rate of exploding stars at
redshifts beyond the detection capabilities of currently available
telescopes. Successful programs detecting intermediate to high redshift
SN at optical wavelengths include SDSS-II (Frieman
et al. 2008),
SNLS (Astier
et al. 2006), and ESSENCE (Miknaitis
et al. 2007),
which all target
40
have been inferred for many multiple images of galaxies (Seitz
et al. 1998)
and typical magnification factors of 5 to
10 are common within the central few arcminutes of the most massive
clusters of galaxies. Exploiting this remarkable boost in flux is an
interesting avenue for probing the rate of exploding stars at
redshifts beyond the detection capabilities of currently available
telescopes. Successful programs detecting intermediate to high redshift
SN at optical wavelengths include SDSS-II (Frieman
et al. 2008),
SNLS (Astier
et al. 2006), and ESSENCE (Miknaitis
et al. 2007),
which all target
![]() supernovae,
mainly type Ia. For higher redshifts, Riess
et al. (2007)
demonstrated the power of space measurements by reporting the discovery
and analysis of 23 type Ia SNe with
supernovae,
mainly type Ia. For higher redshifts, Riess
et al. (2007)
demonstrated the power of space measurements by reporting the discovery
and analysis of 23 type Ia SNe with ![]() ,
although not without significant effort. The project made use of about
750 HST orbits to detect SNe, obtain multi-color lightcurves
and grism spectroscopy with ACS and NICMOS. Dawson et al. (in
prep.) improved the yield of high-z type Ia SN
detections with ACS/HST by targeting SN in massive z>1
clusters. A common feature of both HST
projects was that the search was done in the F850LP filter, i.e., z-band.
Poznanski
et al.
(2007) used the extremely large FoV of the Suprime-Cam at
Subaru 8.2 m to measure SNIa rates up z=1.6.
They reported the discovery of 13 SNIa beyond z=1
with repeated imaging of the Subaru Deep Field at optical wavelengths,
including z-band.
,
although not without significant effort. The project made use of about
750 HST orbits to detect SNe, obtain multi-color lightcurves
and grism spectroscopy with ACS and NICMOS. Dawson et al. (in
prep.) improved the yield of high-z type Ia SN
detections with ACS/HST by targeting SN in massive z>1
clusters. A common feature of both HST
projects was that the search was done in the F850LP filter, i.e., z-band.
Poznanski
et al.
(2007) used the extremely large FoV of the Suprime-Cam at
Subaru 8.2 m to measure SNIa rates up z=1.6.
They reported the discovery of 13 SNIa beyond z=1
with repeated imaging of the Subaru Deep Field at optical wavelengths,
including z-band.
We explore a complementary technique for SN detection and photometric follow-up that involves a near-IR, ``rolling'', SN survey behind intermediate-redshift massive clusters. By exploiting the significant lensing magnification, the redshift discovery limit is enhanced. There are, however, two main limitations to this approach. First, the large lensing magnification is limited to small solid angles around the cluster core, of typically a few arc-minutes. Second, conservation of flux implies that the survey area behind the cluster in the source plane is shrunk due to lensing.
The choice of near-IR filter ensures that the survey has a
potential for SNIa discoveries to unprecedented high redshifts, ![]() ,
and still samples the rest-frame optical part of the spectrum,
potentially allowing a significant increase in the lever arm of the
type Ia SN Hubble diagram. Furthermore, because of the strong lensing
effect, multiple images of high-z SNe with time
separations of between weeks and a few years could be observed. These
rare events could provide strong constraints on the Hubble constant,
using the time-delay technique (Refsdal
1964) and possibly be used as tests of dark matter and dark
energy in an unexplored redshift range (Mörtsell
& Sunesson 2006;
Goobar
et al. 2002). A feasibility study of the potential
for improving the mass models of clusters of galaxies using lensed SNe
will be presented in Riehm et al. in preparation (Paper III).
,
and still samples the rest-frame optical part of the spectrum,
potentially allowing a significant increase in the lever arm of the
type Ia SN Hubble diagram. Furthermore, because of the strong lensing
effect, multiple images of high-z SNe with time
separations of between weeks and a few years could be observed. These
rare events could provide strong constraints on the Hubble constant,
using the time-delay technique (Refsdal
1964) and possibly be used as tests of dark matter and dark
energy in an unexplored redshift range (Mörtsell
& Sunesson 2006;
Goobar
et al. 2002). A feasibility study of the potential
for improving the mass models of clusters of galaxies using lensed SNe
will be presented in Riehm et al. in preparation (Paper III).
In this paper, we describe a pilot program using the ISAAC near-IR imaging camera at ESO's Very Large Telescope (VLT), to detect gravitationally lensed SNe behind very massive clusters of galaxies. The potential for a scaled-up version of this project with the new HAWK-I near-IR instrument at VLT is also studied. A description of the observing strategy, the data-set and data reduction, as well as a full presentation of the photometry of the transient object discussed in Sect. 6.2, are presented in an accompanying paper (Stanishev et al. 2009, Paper I).
Throughout this paper, we adopt the concordance model
cosmology, ![]() ,
,
![]() ,
h=0.7, w=-1. Magnitudes are
given in the Vega system.
,
h=0.7, w=-1. Magnitudes are
given in the Vega system.
2 Supernova subtypes
SN explosions are broadly divided into two classes, core-collapse
supernovae (SN CC), marking the end of very massive stars
![]() ,
and the so-called type Ia supernovae (SNIa), believed to be either the
result of merging white dwarfs or accreting white dwarfs in close
binaries, where thermonuclear explosions are triggered when the system
is close to the Chandrasekhar mass,
,
and the so-called type Ia supernovae (SNIa), believed to be either the
result of merging white dwarfs or accreting white dwarfs in close
binaries, where thermonuclear explosions are triggered when the system
is close to the Chandrasekhar mass,
![]() .
.
Several subtypes of explosions belong to the core-collapse class, including type II SN as well as type Ib/c and hypernovae (HN), which are also interesting because of their association with GRBs. Type II SNe are furthermore subdivided into IIP, IIL, and IIn based on lightcurve and spectroscopic properties. For reviews of SN classification and their general properties, see Filippenko (1997) and Leibundgut (2008).
Table 1: Supernova properties.
In Table 1,
we summarize some of the main properties of the SNe being considered in
this analysis, which are: the peak V-band
brightness, MV;
the one-standard-deviation range around the peak intrinsic luminosity,
![]() (a
Gaussian distribution has been assumed for all types, except for
type IIL supernovae, for which a bi-Gaussian distribution is used, with
the two peak values being labeled IIL and IIL
(a
Gaussian distribution has been assumed for all types, except for
type IIL supernovae, for which a bi-Gaussian distribution is used, with
the two peak values being labeled IIL and IIL
![]() ); and the fraction of the
core-collapse SN subtypes,
); and the fraction of the
core-collapse SN subtypes, ![]() ,
inferred from measurements of the local universe. We adopted the values
of
,
inferred from measurements of the local universe. We adopted the values
of ![]() ,
lightcurve and spectral properties compiled by Peter Nugent
,
lightcurve and spectral properties compiled by Peter Nugent![]() , which in turn are based
on work by Richardson
et al. (2002). We note, however, that the
uncertainty in the relative fractions within the core-collapse types is
quite large. For instance, Smartt
et al. (2009) found a much higher fraction of type
Ib/c (29%) than Richardson
et al. (2002), while their estimate of the number of
type IIL is about a factor 10 lower than what has been assumed here.
Clearly, significantly larger data-sets are needed to determine the CC
rates accurately, both at low and high redshifts.
, which in turn are based
on work by Richardson
et al. (2002). We note, however, that the
uncertainty in the relative fractions within the core-collapse types is
quite large. For instance, Smartt
et al. (2009) found a much higher fraction of type
Ib/c (29%) than Richardson
et al. (2002), while their estimate of the number of
type IIL is about a factor 10 lower than what has been assumed here.
Clearly, significantly larger data-sets are needed to determine the CC
rates accurately, both at low and high redshifts.
Since the peak brightness, lighcurve shape and spectral energy
density vary significantly between SN types, we treat each subtype
separately when computing the expected rates. Synthetic
lightcurves of SNe at a luminosity distance
![]() are
calculated for the observer NIR filters using cross-filter
K-corrections (Kim
et al. 1996)
are
calculated for the observer NIR filters using cross-filter
K-corrections (Kim
et al. 1996)
where Y represents an arbitrary observer filter and the distance modulus is defined as
The luminosity distance,
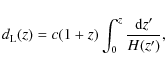
|
(3) |
where c denotes the speed of light in vacuum and the Hubble parameter evolves with redshift as
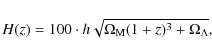
|
(4) |
in units of km s-1 Mpc-1.
We also included in Eq. (1)
the
perturbation
![]() in
the observed magnitude from lensing magnification,
in
the observed magnitude from lensing magnification,
![]() ,
and/or extinction by dust along the line of sight,
,
and/or extinction by dust along the line of sight,
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11254f1.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg42.png)
|
Figure 1:
Synthetic lightcurves in SZ-band of type Ia, type
Ib/c, and type IIP supernovae at z=1.5 and
z=2 at their mean peak brightness. Also shown
is the increased sensitivity for lensing magnification by 1, 2, 3 and
4 mag. The unlensed limit, |
| Open with DEXTER | |
Figure 1
shows examples of synthetic lightcurves for a representative set of SN
types at redshifts z=1.5 and z=2.0
through the ISAAC SZ-filter (
![]() m;
m;
![]() m), a broader and redder
version of the more common Y filter. Due to the
large lensing magnifications from the foreground cluster
(Sect. 4.1),
significantly higher redshifts can be probed, not only for the
intrinsically fainter core-collapse supernovae, but also for type Ia
supernovae beyond
m), a broader and redder
version of the more common Y filter. Due to the
large lensing magnifications from the foreground cluster
(Sect. 4.1),
significantly higher redshifts can be probed, not only for the
intrinsically fainter core-collapse supernovae, but also for type Ia
supernovae beyond ![]() .
.
3 Supernova rates
We now consider two different routes for computing the expected number of SNe in a survey. In Sect. 3.1, the volumetric approach is followed, i.e., the predictions are derived from the volume probed in the field of view of the survey and assumptions about the SN rate per co-moving volume for the various types of SNe as a function of redshift. In Sect. 3.2, we also consider the rates derived from the rest-frame UV luminosities of the resolved galaxies behind the clusters based on the assumption that they trace the star-formation rate in each individual galaxy.
3.1 Volumetric rate estimate
The expected number of SNe of a certain subclass,
![]() ,
in a redshift interval,
,
in a redshift interval, ![]() ,
depends on the monitoring time for that specific SN type, Tj,
the solid angle of the survey,
,
depends on the monitoring time for that specific SN type, Tj,
the solid angle of the survey, ![]() ,
and the volumetric SN rate, rjV
(with units Mpc-3 yr-1),
given by
,
and the volumetric SN rate, rjV
(with units Mpc-3 yr-1),
given by
Furthermore, it is a function of cosmological parameters, since it includes the comoving volume element
Next, we explore the current estimates of the volumetric rates of core-collapse and type Ia supernovae.
3.1.1 Core-collapse SNe
Large scale SN programs such as SDSS, SNLS, ESSENCE, or
GOODS/PANS and even the planned survey at the LSST are rather
inefficient at detecting core-collapse SNe at z>1.
As an example, the two highest-redshift identified CC SNe in the
five-year SNLS survey are at z=0.617 (a probable
Ib/c) and z=0.605 (Ib/c confirmed)![]() . We note, however, that
SNLS specifically targeted type Ia supernovae, and thus was not
optimized for finding CC SNe.
. We note, however, that
SNLS specifically targeted type Ia supernovae, and thus was not
optimized for finding CC SNe.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11254f2.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg51.png)
|
Figure 2:
Predictions for the CC SN rate,
|
| Open with DEXTER | |
The magnification provided by foreground clusters could enable the
exploration of this population for the first time. Since the
progenitors of CC SNe are massive short-lived stars, the CC SN rate,
![]() ,
reflects the ongoing star-formation rate (SFR, units
,
reflects the ongoing star-formation rate (SFR, units
![]() yr-1 Mpc-3).
Thus, we can use the SNR to obtain independent bounds on the cosmic SFR
since
yr-1 Mpc-3).
Thus, we can use the SNR to obtain independent bounds on the cosmic SFR
since
where
The observational results for the CC rates at high-z
(Dahlen
et al. 2004)
show an increase in the range ![]() -0.7, which
is consistent with independent estimates of the SFR. Extending
these measurements to
-0.7, which
is consistent with independent estimates of the SFR. Extending
these measurements to ![]() is clearly important for checking the underlying SFR models.
Observations at near-IR, i.e. in the rest-frame optical, should also
provide a direct probe of the
star formation that could be missed by UV surveys due to extinction by
dust along the line of sight. Since the VLT/ISAAC survey had very
limited sensitivity beyond z > 2, the
smoothly
extrapolated
model of M07 is used mainly for our estimate of the feasibility of
discovering lensed SNe in future surveys in Sect. 7.
is clearly important for checking the underlying SFR models.
Observations at near-IR, i.e. in the rest-frame optical, should also
provide a direct probe of the
star formation that could be missed by UV surveys due to extinction by
dust along the line of sight. Since the VLT/ISAAC survey had very
limited sensitivity beyond z > 2, the
smoothly
extrapolated
model of M07 is used mainly for our estimate of the feasibility of
discovering lensed SNe in future surveys in Sect. 7.
3.1.2 Type Ia SNe
While SNIa have been used extensively for deriving
cosmological parameters, it is unsatisfactory that the progenitor
scenario preceding the SN explosion is still mostly unknown. Existing
models
predict that different scenarios, such as the single degenerate and the
double degenerate models, should have different delay-time
distributions ![]() ,
describing the time between the formation of the progenitor star and
the explosion of the SN. The results of Mannucci
et al. (2005)
and Sullivan
et al. (2006) suggest that the specific SNR (SNR per
unit mass) is significantly higher in young star forming galaxies than
in older galaxies. Pritchet
et al. (2008) used the results from Sullivan
et al. (2006)
to show that the delay-time distribution,
,
describing the time between the formation of the progenitor star and
the explosion of the SN. The results of Mannucci
et al. (2005)
and Sullivan
et al. (2006) suggest that the specific SNR (SNR per
unit mass) is significantly higher in young star forming galaxies than
in older galaxies. Pritchet
et al. (2008) used the results from Sullivan
et al. (2006)
to show that the delay-time distribution, ![]() ,
is consistent with a power-law function and that the specific SNR is at
least a factor of 10 higher in active star-forming galaxies compared to
passive galaxies.
,
is consistent with a power-law function and that the specific SNR is at
least a factor of 10 higher in active star-forming galaxies compared to
passive galaxies.
Using a different method, Strolger
et al. (2004) compare the SFR(t)
and the SNR, ![]() ,
derived in the GOODS fields to derive the delay-time distribution with
the relation
,
derived in the GOODS fields to derive the delay-time distribution with
the relation
where
We note that the main driver of the relatively long delay-time found in the method used by Strolger et al. (2004) is the low number of type Ia SNe found at high redshift z>1.4. Using the extended GOODS survey, Dahlen et al. (2008) also found fewer type Ia SNe at z>1.4 than what is expected if the delay-time is short and SNR follows the SFR. Results for the type Ia rate at z>1.4 were also presented in Poznanski et al. (2007) and Kuznetsova et al. (2008). While both these sets of results show a rate that is consistent with being constant at z>1.4, the large statistical errors can not exclude a rate that declines sharply as suggested by the results in Dahlen et al. (2008).
It is therefore particularly important to search for SNe at
these redshifts, where the predicted rate is most sensitive to the
delay time. If ![]() is large (>3-4 Gyr), there should be a
steep decline in the SNIa rate at z>1.5,
while if
is large (>3-4 Gyr), there should be a
steep decline in the SNIa rate at z>1.5,
while if ![]() is short, the SNR should follow the SFR and remain fairly constant to
is short, the SNR should follow the SFR and remain fairly constant to
![]() .
.
Furthermore, there are also theoretical predictions that the SNIa rate could be significantly suppressed (or even inhibited) at high redshifts (z>2 in spirals and z>2.5 in ellipticals) due to metallicity effects, e.g., Kobayashi et al. (1998). Kobayashi & Nomoto (2008) revised their analysis and found an expected increase of the SNIa rate in elliptical hosts above z=2.5. These results also show that deriving the type Ia rate at high redshift is of great interest.
![\begin{figure}
\par\includegraphics[width=8.85cm,clip]{11254f3.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg67.png)
|
Figure 3:
Extrapolations of available SNIa rate predictions,
|
| Open with DEXTER | |
To calculate the number of detectable type Ia SNe, we use a sample of SNIa rate model predictions and best-fit solutions to the available data, extrapolated to very high redshifts. These models are shown in Fig. 3. As for CC SNe, we used the smoothly extrapolated M07 model as a benchmark for the feasibility studies in Sect. 7.
3.2 SN rates derived from the SFR of observed galaxies
Since the rate of SNe is expected to follow the star-formation rate, we also consider the numbers that can be derived for the SFR in the galaxies detected along the field of view. In Sect. 5, we describe how galaxy catalogs were generated for the resolved objects along the line of sight to massive clusters.
We used the rest-frame UV luminosity as a tracer of the SFR in the observed galaxies, redshifted to the optical bands. Since the UV luminosity is dominated by the most short-lived stars, it is closely related to star formation.
We use L2800, the
flux at rest-frame
![]() ,
to estimate the SFR. We first used the photometric (or spectroscopic)
redshift (see Sect. 5)
to derive which two observed filters straddle the rest-frame L2800
and interpolate between those using the
best-fit spectral template to derive the apparent magnitude
corresponding to the rest-frame L2800
flux. The absolute L2800
magnitude is thereafter derived after correcting for distance modulus
and K-corrections. Next, the lensing magnification is taken into
account, as described in Sect. 4.1.
,
to estimate the SFR. We first used the photometric (or spectroscopic)
redshift (see Sect. 5)
to derive which two observed filters straddle the rest-frame L2800
and interpolate between those using the
best-fit spectral template to derive the apparent magnitude
corresponding to the rest-frame L2800
flux. The absolute L2800
magnitude is thereafter derived after correcting for distance modulus
and K-corrections. Next, the lensing magnification is taken into
account, as described in Sect. 4.1.
Finally, we use the relation between L2800
and SFR from (Dahlen
et al. 2007)
to relate the flux to star formation,
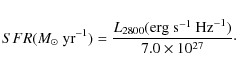
|
(9) |
The expected number of core collapse SNe are calculated using Eq. (7), whereas the SNIa rate is estimated using Eq. (8) for a Gaussian distribution of
4 Clusters as gravitational telescopes
We have investigated the use of some of the most massive clusters of
galaxies as gravitational telescopes; A1689, A1835, and AC114. A1689 (z=0.183)
has the largest Einstein radius of all massive lensing clusters,
![]() .
Broadhurst
et al.
(2005) and Limousin
et al. (2007) performed a strong lensing analysis
using HST data and identified 115 images of 34 multiply lensed
background galaxies in the redshift range 1<z<5.5
based on spectroscopic and photometric redshift estimates. A cluster
mass model of AC114
.
Broadhurst
et al.
(2005) and Limousin
et al. (2007) performed a strong lensing analysis
using HST data and identified 115 images of 34 multiply lensed
background galaxies in the redshift range 1<z<5.5
based on spectroscopic and photometric redshift estimates. A cluster
mass model of AC114
![]() and
several strongly lensed sources, including a 5-image configuration
at z=3.347 were presented in Campusano
et al. (2001).
The mass model for A1835 (z=0.253) yields an
Einstein radius of
and
several strongly lensed sources, including a 5-image configuration
at z=3.347 were presented in Campusano
et al. (2001).
The mass model for A1835 (z=0.253) yields an
Einstein radius of
![]() at
high-z (Richard
et al. 2006).
at
high-z (Richard
et al. 2006).
4.1 Lensing magnification: tunnel vision
To calculate the lensing magnification of the SN lightcurves, the
public LENSTOOL![]() software package was used. The code is specifically developed for
modeling the mass distribution of galaxies and clusters in the strong
and
weak lensing regime (Kneib
et al. 1996). It uses a Monte Carlo Markov Chain
technique (Jullo
et al. 2007) to constrain the parameters of the
cluster model using observational data of the background galaxies as
input. The output can then be used to compute, e.g., the magnification
and time delay function at any given position behind the cluster. For
A1689 the mass
model by Limousin
et al. (2007) was used. The clusters A1835 and AC114
were modeled as in Richard
et al. (2006). Figure 4 shows
the
average lensing magnification as a
function of source redshift in the FOV of the ISAAC camera, which is
software package was used. The code is specifically developed for
modeling the mass distribution of galaxies and clusters in the strong
and
weak lensing regime (Kneib
et al. 1996). It uses a Monte Carlo Markov Chain
technique (Jullo
et al. 2007) to constrain the parameters of the
cluster model using observational data of the background galaxies as
input. The output can then be used to compute, e.g., the magnification
and time delay function at any given position behind the cluster. For
A1689 the mass
model by Limousin
et al. (2007) was used. The clusters A1835 and AC114
were modeled as in Richard
et al. (2006). Figure 4 shows
the
average lensing magnification as a
function of source redshift in the FOV of the ISAAC camera, which is
![]() arcmin2
for the three cluster fields considered.
We note that A1689 seems to be the most promising gravitational lens
for reaching the highest redshifts. For the 2007 observations of A1689,
centered on the cluster itself, the magnification is on average
arcmin2
for the three cluster fields considered.
We note that A1689 seems to be the most promising gravitational lens
for reaching the highest redshifts. For the 2007 observations of A1689,
centered on the cluster itself, the magnification is on average
![]() 2.5 mag
for
2.5 mag
for
![]() in
the ISAAC field of view. The 2003/2004 archival observations that we
used were offset from the cluster core, and therefore the average
magnification for these observations is lower,
in
the ISAAC field of view. The 2003/2004 archival observations that we
used were offset from the cluster core, and therefore the average
magnification for these observations is lower, ![]() 1.5 mag for
1.5 mag for
![]() .
For A1835, the average magnification is
.
For A1835, the average magnification is ![]() 1 mag for
1 mag for
![]() .
The width of the A1689 2003/2004 and A1835 curves indicate the slightly
different pointings and effective FOV of these observations. AC114 has
an average lensing magnification of
.
The width of the A1689 2003/2004 and A1835 curves indicate the slightly
different pointings and effective FOV of these observations. AC114 has
an average lensing magnification of ![]() 0.8 mag for
0.8 mag for
![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11254f4.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg77.png)
|
Figure 4: Average lensing magnification versus redshift for the three observed clusters computed with LENSTOOL (see text) for the ISAAC/VLT field of view. Two curves are shown for A1689, since the pointings in 2003/2004 (dashed red) and 2007 were different. The width of the curve for the A1689 pointings (solid red) in 2003/2004 and the A1835 pointings (orange) indicate that these pointings do not cover the same area, but are slightly shifted between observations and the effective area observed is different (details can be found in Paper I). |
| Open with DEXTER | |
4.2 Monitoring time for SN surveys with gravitational telescopes
Because of flux conservation, large lensing magnifications result in
small observed solid angle ![]() .
.
Therefore, unlike other SN searches, the effective solid angle
![]() in
Eq. (6)
is not constant with redshift when cluster fields are targeted. The
light beam at any given redshift behind the cluster is magnified by a
factor
in
Eq. (6)
is not constant with redshift when cluster fields are targeted. The
light beam at any given redshift behind the cluster is magnified by a
factor
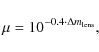
|
(10) |
at the expense of a smaller solid angle
where
The corresponding reduction in the source area as a function of redshift for the strongest (A1689) and weakest (AC114) lens in our survey are shown in Fig. 5. Although A1689 is the the most promising gravitational lens, the figures illustrate that the rapid shrinkage in the solid angle with increasing redshift is also very strong
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11254f5a.eps}\vspace*{2.5mm}
\includegraphics[width=9cm,clip]{11254f5b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg87.png)
|
Figure 5: Source plane area shrinkage behind our strongest gravitational telescope A1689 ( top figure) for various redshifts; z=0.25 (orange), 0.5 (yellow), 2.0 (magenta) and the weakest in the current survey AC114 (bottom figure) for various redshifts (z= 0.5 (yellow), 2.0 (magenta), 3.0 (cyan). The utmost line (red) shows the effective FOV of the observations. |
| Open with DEXTER | |
Thus, as shown in Gunnarsson & Goobar (2003), a gravitational lens does not always enhance the number of SN discoveries. However, it does increase the limiting redshift of a magnitude-limited survey. We exploit this effect to search for SNe at redshifts beyond those explored by ``traditional'' SN searches.
Weaker lenses, such as AC114 and A1835, may not go as deep in redshift, but one may still find a comparable number of SNe as behind A1689 (or even more), although these SNe would be found at somewhat lower average redshifts.
For the unlensed case, the monitoring time above threshold for
a SN of type j, Tj,
is
a function of the SN lightcurve, the detection efficiency, ![]() ,
the extinction by dust,
,
the extinction by dust,
![]() ,
and the intrinsic brightness Mj
with the probability distribution P(Mj).
With
,
and the intrinsic brightness Mj
with the probability distribution P(Mj).
With ![]() being the lightcurve time period when the supernova is above the
detection threshold,
being the lightcurve time period when the supernova is above the
detection threshold,
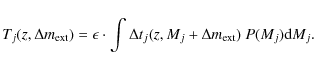
|
(13) |
We assume P(M) to be Gaussian, and to have the mean values and standard deviations listed in Table 1.
Taking into account the lensing effect of the clusters, the monitoring
time becomes
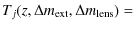 
|
(14) |
keeping in mind that
Thus, the expected number of SNe for a given type j,
using volumetric rates, is then given by
where we assume an overall Milky-Way-like dust extinction (Cardelli et al. 1989) with E(B-V)=0.15 and RV=3.1. In this study, we have assumed a constant optical depth for all supernovae. This choice matches the assumptions used to derive the SFR estimates that we have used.
| Figure 6: Resolved galaxies vs redshift behind A1689, A1835 and AC114. |
|
| Open with DEXTER | |
Table 2: Archival data used to calculate photometric redshifts.
5 Properties of background galaxies
For each one of the three considered clusters, galaxy catalogs were compiled using archival optical and near-IR photometry. The different instruments and filters are listed in Table 2.
The observed magnitudes in at least three bands, optical or near-IR, were used to derive a photometric redshift using the template-fitting technique (e.g., Mobasher et al. 1996; Gwyn 1995). The software used is the code developed by the GOODS team as described in Dahlen et al. (2005, 2009, in prep.)
Figure 6
shows the distribution of galaxies in bins of
![]() for
the three clusters. Furthermore, the restframe UV-flux at
2800 Å of each resolved galaxy was computed and used as a
tracer of the SFR. Similarly, the integrated SFR was calculated in each
redshift bin by summing the resolved galaxies behind each cluster.
Thus, we compute the expected number of SNe with two methods: 1) the
volumetric rate taken from the literature; and 2) the measured
star-formation rate of the resolved galaxies in the FOV.
for
the three clusters. Furthermore, the restframe UV-flux at
2800 Å of each resolved galaxy was computed and used as a
tracer of the SFR. Similarly, the integrated SFR was calculated in each
redshift bin by summing the resolved galaxies behind each cluster.
Thus, we compute the expected number of SNe with two methods: 1) the
volumetric rate taken from the literature; and 2) the measured
star-formation rate of the resolved galaxies in the FOV.
6 The ISAAC pilot survey
During the spring of 2007, three clusters, A1689, AC114 and A1835, were
monitored with the ISAAC instrument at VLT with approximately one-month
intervals, as shown in Table 3. In total,
the
data set consists of 20 h of VLT time on target:
4.5 h, 5.85 h and 10 h for A1689, AC114 and
A1835 respectively. The data is complemented by archival data (also
listed in the table): 8.4 h, 5.7 h and 6.1 h
for A1689, AC114 and A1835. The survey filters in our 2007 program were
chosen to match the deepest reference images. Thus, the SN search was
done using the SZ-filter for A1689 and A1835 and J-band
for AC114. A full description of the data reduction, SN search
efficiency, and limiting magnitude is reported in Paper I. An average
discovery depth at 90 % CL of
![]() mag
(Vega) was derived by Monte Carlo simulations in which artificial stars
were added
to the images.
mag
(Vega) was derived by Monte Carlo simulations in which artificial stars
were added
to the images.
Table 3: Data used for transient search.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{11254f7.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg98.png)
|
Figure 7: Upper: redshift distribution for the number of SNe (for each type) assuming the rates estimates by Mannucci et al. (2007) for A1689 in SZ-band. Lower: gain/loss of using A1689 as a lens compared to an equivalent survey without the lens for different redshifts. The crossing of the curves through the zero line indicates the redshift for which a transition to a net gain in SN discoveries is obtained due to the gravitational telescope. An average Milky-Way like extinction with E(B-V)=0.15 was assumed for both plots. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{11254f8.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg99.png)
|
Figure 8: Upper: redshift distribution of the expected number of SNe (for each type) assuming the rates estimates by Mannucci et al. (2007) for A1835 in SZ-band. Lower: gain/loss of using A1835 as a lens compared to an equivalent survey without the lens for different redshifts. The crossing of the curves through the zero line indicates the redshift for which a transition to a net gain in SN discoveries is obtained due to the gravitational telescope. An average Milky-Way-like extinction with E(B-V)=0.15 was assumed. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{11254f9.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg100.png)
|
Figure 9: Upper: redshift distribution of the expected number of SNe (for each type) assuming the rates estimates by Mannucci et al. (2007) for AC114 in J-band. Lower: gain/loss of using AC114 as a lens compared to an equivalent survey without the lens for different redshifts. The crossing of the curves through the zero line indicates the redshift for which a transition to a net gain in SN discoveries is obtained due to the gravitational telescope. An average Milky-Way-like extinction with E(B-V)=0.15 was assumed. |
| Open with DEXTER | |
6.1 Expected event rate in the survey
One of the most important aspects of the pilot survey is to explore whether the use of gravitational telescopes significantly enhances the survey depth given the observational magnitude limit. In the upper panels of Figs. 7-9, we explore the differential number of SNe expected for each one of the three clusters with lensing magnification. The lower panels of the figures show the gain/loss due to the lensing compared to the same survey without lensing as a function of redshift. In particular, the lower panels indicate the redshift regions where the use of gravitational telescopes enhances the detection probability.
As expected, the boost is most important for the fainter core-collapse supernovae, type Ib/c and IIP in particular, where the detection efficiency is increased for z>0.5. For the brighter SNe, such as type Ia, it is only for z>1 that a net gain is expected. Thus, the foreground massive cluster, besides increasing the flux levels, serves as a high-z filter.
Both AC114 and A1835 (to a somewhat lesser extent) provide comparable total SN rates to A1689, although A1689 is a much stronger lens than the other two clusters. This is because, as already mentioned, the magnification is associated with a shrinkage in the effective volume element.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11254f10.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg101.png)
|
Figure 10: Redshift distribution (including an overall reddening of E(B-V)=0.15 and RV=3.1) for the number of SNe for the various model predictions for the three clusters combined for each SN type separately. |
| Open with DEXTER | |
For simplicity, we restricted this comparison in Figs. 7 to 9 to the volumetric rates estimates in Mannucci et al. (2007). In Fig. 10, the various model predictions for the three clusters combined are shown for each SN type separately.
![\begin{figure}
\par\includegraphics[width=8.25cm,clip]{11254f11a.eps}\vspace*{2.55mm}
\includegraphics[width=8.25cm,clip]{11254f11b.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg102.png)
|
Figure 11: Number of expected SNe for the observations given in Table 3 for (1) the SN rates shown in Figs. 2 and 3, and (2) the SN rates derived from SFR (denoted by SFR) in resolved galaxies described in Sect. 3.2. |
| Open with DEXTER | |
The expected total number of SNe in our survey is shown in
Fig. 11.
The estimated rates assume extinction by Galactic-like dust (Cardelli
et al. 1989)
with an average color excess of
E(B-V)=0.15
and a total-to-selective extinction coefficient RV=3.1,
i.e., AV=0.46 mag.
Since the lensing magnification is typically
![]() ,
the impact from dust extinction accounts for less than a factor two
decrease in the expected number of SN discoveries, compared to the
results where dimming by dust is completely neglected.
,
the impact from dust extinction accounts for less than a factor two
decrease in the expected number of SN discoveries, compared to the
results where dimming by dust is completely neglected.
6.2 A transient candidate
Paper I described the image subtractions used to search for transient objects in our data set. Transients were sought in both the new images, using archival data as a reference, and for transients in the archival images using the period 79 (April-July 2007) data as a reference. The images were geometrically aligned and the point-spread functions and the flux levels of the two images were matched prior to the pixel subtraction.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11254f12.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg104.png)
|
Figure 12:
LENSTOOL lensing magnification map of A1689
based on mass model in Limousin
et al. (2007) superimposed on top of a HAWK-I J-band
image from our P81 program (July 2008). The lensing contours for a
source at z=0.6 for
|
| Open with DEXTER | |
In this process, one transient candidate was found in the A1689 archival images in the SZ-band. One I-band data point of A1689 and two z-band data points were observed with FORS2 and another in J-band with ISAAC at VLT during the time that the transient was bright. We used HAWK-I J-band images from our program in period 81 (July 2008) as a reference to obtain a measurement of the transient flux in that band. Additional reference data from FORS2 and HST/ACS were available for the optical bands. These were used to measure the flux in the region of the transient after it had faded. The transient photometry is summarized in Table 4. The location of the transient and the lensing magnification map is shown in Fig. 12.
Table 4: Transient candidate photometry from Paper I.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11254f13.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg106.png)
|
Figure 13:
Transient candidate photometry (also listed in Table 4)
plotted on
top of redshifted |
| Open with DEXTER | |
All available SN templates and a grid of redshifts (z=[0,3])
and reddening parameters were tested (allowing for an intrinsic
variation in the brightness) and the best fit was found for a type IIP
template based on lightcurves of SN2001cy from Poznanski
et al. (2009),
redshifted to ![]() .
Moreover, the best fit of the transient colors was found by assuming
that the SN is highly reddened, with a low total-to-selective
extinction ratio (AV=1.27,
RV=1.5),
as shown
in Fig. 13.
We note that low values of RV,
although not seen in the Milky Way, were reported for extinction of
quasars (Östman
et al. 2008; Wang
et al. 2004)
and shown to be very common along SN lines of sight (Nobili
& Goobar 2008),
possibly as a result of multiple scattering by circumstellar dust (Goobar 2008).
Another
possibility is that the intrinsic colors of the SN candidate differ
significantly from SN2001cy, in which case a bias could be introduced
in the K-corrections. However, a recent study of 40 low-z
type IIP SN lightcurves (Poznanski
et al. 2009) found a low average value of the total
to selective extinction ratio,
.
Moreover, the best fit of the transient colors was found by assuming
that the SN is highly reddened, with a low total-to-selective
extinction ratio (AV=1.27,
RV=1.5),
as shown
in Fig. 13.
We note that low values of RV,
although not seen in the Milky Way, were reported for extinction of
quasars (Östman
et al. 2008; Wang
et al. 2004)
and shown to be very common along SN lines of sight (Nobili
& Goobar 2008),
possibly as a result of multiple scattering by circumstellar dust (Goobar 2008).
Another
possibility is that the intrinsic colors of the SN candidate differ
significantly from SN2001cy, in which case a bias could be introduced
in the K-corrections. However, a recent study of 40 low-z
type IIP SN lightcurves (Poznanski
et al. 2009) found a low average value of the total
to selective extinction ratio,
![]() ,
in excellent agreement with the best-fit solution for our SN candidate.
,
in excellent agreement with the best-fit solution for our SN candidate.
| Figure 14:
Probability distribution function for the photometric redshift (seven
bands) of the galaxy closest (0.5 arcsec) to the transient, the SN
photo-z assuming a IIP template matching SN2001cy
and the product of the two, yielding
|
|
| Open with DEXTER | |
For the nearest galaxy, at
![]() projected
distance, a photometric redshift
projected
distance, a photometric redshift
![]() is
derived, as shown in Fig. 14. The
closest
galaxy,
is
derived, as shown in Fig. 14. The
closest
galaxy, ![]() away, has a photometric redshift that also peaks at z=0.6.
The distance to the galaxy cores is thus 3.3 and 7.7 kpc,
respectively.
away, has a photometric redshift that also peaks at z=0.6.
The distance to the galaxy cores is thus 3.3 and 7.7 kpc,
respectively.
It should be noted that at z=0.6 because
of the dust extinction the transient (![]() mag, unlensed) would
not have been detected in our survey without the magnification power of
the cluster, 1.4 mag. Taking into account the lensing
magnification and the assumed host galaxy extinction, we find that the
best fit shown in Fig. 13
corresponds to an absolute magnitude
mag, unlensed) would
not have been detected in our survey without the magnification power of
the cluster, 1.4 mag. Taking into account the lensing
magnification and the assumed host galaxy extinction, we find that the
best fit shown in Fig. 13
corresponds to an absolute magnitude
![]() ,
in good agreement with the assumptions in Table 1. It
is striking that the tentative identification of the transient redshift
and type match well the expectations for the survey in terms of SN
subtype and redshift, as shown in Fig. 7.
,
in good agreement with the assumptions in Table 1. It
is striking that the tentative identification of the transient redshift
and type match well the expectations for the survey in terms of SN
subtype and redshift, as shown in Fig. 7.
We now address the alternative possibility that the transient
is at the cluster redshift. A type Ia supernova more than
70 days past lightcurve maximum could potentially match the
observed brightness of the transient. Sharon
et al. (2007) estimated the rate of type Ia
supernovae in intermediate-z clusters to ![]() 0.3 SNu.
For the integrated galaxy luminosity in A1689 of
0.3 SNu.
For the integrated galaxy luminosity in A1689 of
![]() and a
monitoring time of
and a
monitoring time of ![]() 100 days,
about 0.1 type
Ia supernovae were expected in A1689 in our dataset, i.e., a
non-negligible possibility. However, as discussed in paper I, the
decline rate of SNIa lighturves at late times is
0.01-0.02 mag/day, which is inconsistent with the transient
lightcurve.
100 days,
about 0.1 type
Ia supernovae were expected in A1689 in our dataset, i.e., a
non-negligible possibility. However, as discussed in paper I, the
decline rate of SNIa lighturves at late times is
0.01-0.02 mag/day, which is inconsistent with the transient
lightcurve.
To conclude, we find that the match to the photometric redshifts of the potential host galaxy and the supernova lightcurves, along with the fitted peak magnitude being consistent with a type IIP supernova (reddened by dust with RV similar to that found for the nearby sample of type IIP SNe in Poznanski et al. 2009) to represent the most compelling fit to the transient behind A1689.
7 Implications for future near-IR surveys
The pilot survey was completed with the ISAAC instrument at VLT, which
has a FOV of ![]() and a threshold of
and a threshold of ![]() 24 mag (Vega)
for SZ and J-bands and
relatively few observations. We briefly discuss the feasibility of
building up lightcurves of lensed SNe behind clusters of galaxies for
surveys with 8-m class ground-based telescopes and large FOV near-IR
instruments, such as HAWK-I at VLT or MOIRCS at Subaru. We consider a
five-year ``rolling'' search survey, with imaging spaced at intrevals
of 30 days.
24 mag (Vega)
for SZ and J-bands and
relatively few observations. We briefly discuss the feasibility of
building up lightcurves of lensed SNe behind clusters of galaxies for
surveys with 8-m class ground-based telescopes and large FOV near-IR
instruments, such as HAWK-I at VLT or MOIRCS at Subaru. We consider a
five-year ``rolling'' search survey, with imaging spaced at intrevals
of 30 days.
The lensing model of A1689 is used as our baseline for
estimating the number of SNe behind a massive cluster as a function of
redshift. Thus, the results below apply to the most massive clusters,
![]() .
We also consider a survey period of five years since this is optimal
for the discovery of multiple images (Sect. 7.1). In
practice, several clusters would have to be observed to correspond to
``five A1689 years'' since that particular field is behind the Sun part
of the year.
.
We also consider a survey period of five years since this is optimal
for the discovery of multiple images (Sect. 7.1). In
practice, several clusters would have to be observed to correspond to
``five A1689 years'' since that particular field is behind the Sun part
of the year.
During period 81 (P81, July 2008), our team started a survey
targeting lensed SNe behind A1689 using the increased sensitivity and
FOV (![]()
![]() )
of HAWK-I on VLT. The limited availability of the instrument in P81,
only a few, closely spaced observations were completed. Although the
observations were not suited to transient searches, the dataset could
be used to estimate the depth of the point-source search in J-band
that was continued during P82 (early 2009) to
)
of HAWK-I on VLT. The limited availability of the instrument in P81,
only a few, closely spaced observations were completed. Although the
observations were not suited to transient searches, the dataset could
be used to estimate the depth of the point-source search in J-band
that was continued during P82 (early 2009) to ![]() 24.65 mag (Vega)
for 90% detection efficiency, i.e., about 0.65 mag deeper than
the survey done with ISAAC.
24.65 mag (Vega)
for 90% detection efficiency, i.e., about 0.65 mag deeper than
the survey done with ISAAC.
We now examine the feasibility of SN detection with HAWK-I. We
use LENSTOOL to calculate the lensing
magnification map of A1689 for the larger FOV. Although the
magnification decreases with distance from the cluster core, reaching
![]() at
the edges of the FOV, the impact of lensing remains very important
for detecting distant supernovae. In the upper panel of Fig. 15,
the differential number of SNe is shown for the various types of SNe.
The lower part of the figure shows the gain and loss of lensing
compared to the same survey without lensing as a function of redshift.
As expected, fewer SNe are found at low redshifts, while the survey
depth is significantly increased. The integrated number of SNe for the
various models is shown in Fig. 16.
at
the edges of the FOV, the impact of lensing remains very important
for detecting distant supernovae. In the upper panel of Fig. 15,
the differential number of SNe is shown for the various types of SNe.
The lower part of the figure shows the gain and loss of lensing
compared to the same survey without lensing as a function of redshift.
As expected, fewer SNe are found at low redshifts, while the survey
depth is significantly increased. The integrated number of SNe for the
various models is shown in Fig. 16.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{11254f15.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg118.png)
|
Figure 15: Upper: redshift distribution of SN discoveries in a 5-year survey behind a very massive cluster (model of A1689 used). Lower: gain/loss of using a A1689-like cluster as a lens compared to an equivalent survey without the lens for different redshifts. The crossing of the curves through the zero line indicates the redshift for which a transition to a net gain in SN discoveries is obtained due to the gravitational telescope. An average Milky-Way-like extinction with E(B-V)=0.15 was assumed together with SN rates from M07. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11254f16a.eps}\vspace*{3mm}
...
...c.eps}\vspace*{3mm}
\includegraphics[width=8cm,clip]{11254f16d.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg119.png)
|
Figure 16: ( Top) Number of SNe expected in a 5 year monthly survey of one very massive, A1689-like cluster, with HAWK-I. ( Bottom) Number of SNe with z>1.5. |
| Open with DEXTER | |
For HAWK-I (and the A1689 mass model), we expect on the order of 40-70 SNe (depending on the underlying rate estimate for the various SN types) of which about a dozen will be at z > 1.5. In Fig. 17, the potential of the suggested rolling search for generating lensed supernova lightcurves in the redshift range (1<z<2) is shown. The repeated images are used both to discover new supernovae and to build up lightcurves for earlier discoveries. The supernova types and redshift distribution matches the differential rates in Fig. 15.
Surveys for lensed supernovae with space instruments would complement the ground-based approaches since even higher redshifts could be reached due to the deeper point source sensitivity.
7.1 Multiple SN images
When looking through a gravitational lens, multiple images of the same source image can be observed. This is also true for SNe that, due to strong lensing, can potentially be detected to very high redshifts. About one in a hundred SNe behind A1689 in the HAWK-I FOV would have multiple images with time separations of between weeks and a few years. Thus, about 0.5-1.0 SNe with multiple images are expected in a 5 year survey with HAWK-I.
Figure 18
indicates the fraction of the source areas with multiply lensed SNe
that can be observed as a function of survey time for two different
redshifts. For z=1, all SN types show the same
behavior and given a sufficiently large survey time, at least two (or
more) images of the SN could be observed, regardless of its type. At
higher redshifts (z=2), given a sufficiently large
survey time, most of the brighter SNe (Ia and IIn) and about half of
the IIL
![]() and HN will be observable and
have at least two (or more) images. The
other SN types (IIL, Ib/c, and IIP) will be too faint - even with
magnification - to be observed. For all considered redshifts, a
5 year survey (or longer) is optimal for discovering multiple
images of SNe behind clusters.
and HN will be observable and
have at least two (or more) images. The
other SN types (IIL, Ib/c, and IIP) will be too faint - even with
magnification - to be observed. For all considered redshifts, a
5 year survey (or longer) is optimal for discovering multiple
images of SNe behind clusters.
Detecting these rare events could provide important constraints on the Hubble constant with the time-delay technique (Refsdal 1964) as well testing dark matter and energy properties in an unexplored redshift range (Mörtsell & Sunesson 2006; Goobar et al. 2002). Models of lens systems are in general uncertain due to the possibility to rescale the density distribution of the lens and add a circularly symmetric density mass-sheet, while preserving the observed image configuration (Liesenborgs et al. 2008; Gorenstein et al. 1988). This mass-sheet degeneracy can be broken if the absolute magnification of the lens is known. Since SNIa have a very tight dispersion in brightness, these lens systems would constitute an ideal sample for minimizing three major systematic uncertainties in the estimates of H0 using the time-delay technique: accurate time estimates from supernova lightcurves, elimination of the mass-sheet degeneracy, and accurate lens models because of the large number of lensed background galaxies, as discussed in Paper III.
8 Conclusions
Powerful gravitational telescopes in the form of massive galaxy
clusters provide unique opportunities to discover transient objects
such as SNe at redshifts beyond what can be reached with current
telescopes. The lensing magnification ![]() corresponds to a gain factor in exposure length,
corresponds to a gain factor in exposure length, ![]() ,
while at the same time the solid angle at the source planes shrinks by
a factor
,
while at the same time the solid angle at the source planes shrinks by
a factor ![]() for source redshifts higher than the cluster redshift. The net
gain/loss of searching for supernovae behind massive clusters is
therefore a non-trivial combination of FOV, limiting depth, and
supernova luminosity functions. In general, the lens works as a
magnifying glass and high-z filter, i.e., by
reducing the number of detections of bright/close supernovae and
enhancing the detections of distant/faint objects. Thus, to be
successful, a SN survey behind galaxy clusters needs to be optimized.
Clearly, for extremely sensitive (e.g. JWST or ELT) or very large FOV
instruments, the positive impact of the lensing cluster may be
negligible, at least for the brightest types of supernovae. The net
benefit of exploiting the suggested approach will ultimately depend on
the rate and intrinsic brightness of the various types of SNe at
redshifts beyond what is currently known. For type Ia supernovae, an
important parameter determining the rates beyond z=1.5
is the delay time,
for source redshifts higher than the cluster redshift. The net
gain/loss of searching for supernovae behind massive clusters is
therefore a non-trivial combination of FOV, limiting depth, and
supernova luminosity functions. In general, the lens works as a
magnifying glass and high-z filter, i.e., by
reducing the number of detections of bright/close supernovae and
enhancing the detections of distant/faint objects. Thus, to be
successful, a SN survey behind galaxy clusters needs to be optimized.
Clearly, for extremely sensitive (e.g. JWST or ELT) or very large FOV
instruments, the positive impact of the lensing cluster may be
negligible, at least for the brightest types of supernovae. The net
benefit of exploiting the suggested approach will ultimately depend on
the rate and intrinsic brightness of the various types of SNe at
redshifts beyond what is currently known. For type Ia supernovae, an
important parameter determining the rates beyond z=1.5
is the delay time, ![]() .
By increasing the redshift sensitivity beyond that achieved by
``standard'' surveys, we may significantly improve our understanding of
SNIa progenitors. Similarly, little is known about the dimming of
supernovae by dust at very high redshifts. The combination of a longer
wavelength-survey and higher sensitivity to fainter high-z
SNe could thus lead to detections of a different population of objects.
.
By increasing the redshift sensitivity beyond that achieved by
``standard'' surveys, we may significantly improve our understanding of
SNIa progenitors. Similarly, little is known about the dimming of
supernovae by dust at very high redshifts. The combination of a longer
wavelength-survey and higher sensitivity to fainter high-z
SNe could thus lead to detections of a different population of objects.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{11254f17.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg122.png)
|
Figure 17: Simulated lightcurve sampling for supernovae in the redshift range 1<z<2 in a 5-year monthly survey of A1689 and AC114 with HAWK-I. The top panel shows the expected lightcurves sampling SNIa. Core-collapse SNe are shown in the bottom panel. The vertical axis shows the unlensed magnitudes. The symbol colors indicate the SN redshift: blue (z=[1.0,1.2]), cyan (z=[1.2,1.4]), green (z=[1.4,1.6]), orange (z=[1.6,1.8]), and red (z=[1.8,2.0]). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11254f18.eps}
\end{figure}](/articles/aa/full_html/2009/43/aa11254-08/Timg123.png)
|
Figure 18: Fraction of SNe with multiple images that are observable as a function of survey duration. |
| Open with DEXTER | |
A combined 40-h dataset involving archival ISAAC data and new
observations obtained in 2007 for three very massive clusters (A1689,
A1835, and AC114) was used to determine the feasibility of
discovering lensed core-collapse and type Ia SNe. Considering the
monitoring time available, the area surveyed, the lensing
magnification, and the survey magnitud limit, rate estimates of the
various SN subtypes considered were calculated. Synthetic lightcurves
of SNe and several models of the volumetric type Ia and core-collapse
SN rates as a function of redshift were used, all consistently
predicting a Poisson mean value for the expected number of SNe in the
survey of between ![]() and 1.6 for all SNe. One transient object was found behind A1689 on a
galaxy with photometric redshift
and 1.6 for all SNe. One transient object was found behind A1689 on a
galaxy with photometric redshift
![]() ,
the most probable redshift for SN detection in the ISAAC/VLT survey.
The lightcurve is consistent with being a reddened type IIP
supernova at
,
the most probable redshift for SN detection in the ISAAC/VLT survey.
The lightcurve is consistent with being a reddened type IIP
supernova at ![]() .
At the position and redshift of the transient, the lensing model
predicts 1.4 mag of magnification.
.
At the position and redshift of the transient, the lensing model
predicts 1.4 mag of magnification.
Because of the recent deployment of large and sensitive near-IR cameras, such as HAWK-I at VLT, the search for the highest redshift SNe can now be moved to longer wavelengths, thus avoiding the difficulties involved with restframe UV observations, and extending the potential for supernova discoveries, especially type Ia supernovae, beyond z>2. A feasibility study of the potential to build up lightcurves of lensed SNe with larger and deeper surveys shows that this is a very exciting path for new discoveries. The equivalent of a five-year monthly survey of a single very massive cluster with the HAWK-I camera at VLT would yield 40-70 lensed SNe, most of them with good lightcurve sampling. Thus, a dedicated multi-year NIR rolling search targeting several massive clusters would lead to a high rate of very high-z SN discoveries, thus making this approach complementary to deep optical space-based SN surveys (Riess et al. 2007) as well large field-of-view optical SN searches, e.g., (Poznanski et al. 2007).
Although very rare, multiple images of strongly lensed SNe are within reach of such a survey and could offer potentially exciting tests of cosmological parameters as well as improvements to the cluster mass modeling.
AcknowledgementsWe would like to thank Peter Nugent for providing lightcurve and spectral templates used in this analysis. Filippo Mannucci is also thanked for making his SN rate predictions available to us. We are also grateful to Dovi Poznanski for providing us with lightcurves and spectra of SN2001cy and to Avishay Gal-Yam for comments on an earlier draft. K.P. gratefully acknowledges support from the Wenner-Gren Foundation. A.G., V.S. and S.N. acknowledge support from the Gustafsson foundation. V.S. acknowledges financial support from the Fundação para a Ciência e a Tecnologia. A.G. and E.M. acknowledge financial support from the Swedish Research Council. J.P.K. thanks CNRS for support as well as the French-Israeli council for Research, Science and Technology Cooperation.
References
- Astier, P., Guy, J., Regnault, N., et al. 2006, A&A, 447, 31 [EDP Sciences] [CrossRef] [NASA ADS]
- Broadhurst, T., Benítez, N., Coe, D., et al. 2005, ApJ, 621, 53 [CrossRef] [NASA ADS]
- Campusano, L. E., Pelló, R., Kneib, J.-P., et al. 2001, A&A, 378, 394 [EDP Sciences] [CrossRef] [NASA ADS]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [CrossRef] [NASA ADS]
- Chary, R., & Elbaz, D. 2001, ApJ, 556, 562 [CrossRef] [NASA ADS]
- Dahlen, T., Strolger, L.-G., Riess, A. G., et al. 2004, ApJ, 613, 189 [CrossRef] [NASA ADS]
- Dahlen, T., Mobasher, B., Somerville, R. S., et al. 2005, ApJ, 631, 126 [CrossRef] [NASA ADS]
- Dahlen, T., Mobasher, B., Dickinson, M., et al. 2007, ApJ, 654, 172 [CrossRef] [NASA ADS]
- Dahlen, T., Strolger, L.-G., & Riess, A. G. 2008, ApJ, 681, 462 [CrossRef] [NASA ADS]
- Filippenko, A. V. 1997, ARA&A, 35, 309 [CrossRef] [NASA ADS]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [CrossRef] [NASA ADS]
- Frieman, J. A., Bassett, B., Becker, A., et al. 2008, AJ, 135, 338 [CrossRef] [NASA ADS]
- Gal-Yam, A., Maoz, D., & Sharon, K. 2002, MNRAS, 332, 37 [CrossRef] [NASA ADS]
- Giavalisco, M., Dickinson, M., Ferguson, H. C., et al. 2004, ApJ, 600, L103 [CrossRef] [NASA ADS]
- Gnedin, N. Y., Kravtsov, A. V., & Chen, H.-W. 2008, ApJ, 672, 765 [CrossRef] [NASA ADS]
- Goobar, A. 2008, ApJ, 686, L103 [CrossRef] [NASA ADS]
- Goobar, A., Mörtsell, E., Amanullah, R., & Nugent, P. 2002, A&A, 393, 25 [EDP Sciences] [CrossRef] [NASA ADS]
- Gorenstein, M. V., Shapiro, I. I., & Falco, E. E. 1988, ApJ, 327, 693 [CrossRef] [NASA ADS]
- Gunnarsson, C., & Goobar, A. 2003, A&A, 405, 859 [EDP Sciences] [CrossRef] [NASA ADS]
- Gwyn, S. D. J. 1995, Master's thesis, MS Thesis, University of Victoria (1995)
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [CrossRef] [NASA ADS]
- Jullo, E., Kneib, J.-P., Limousin, M., et al. 2007, New Journal of Physics, 9, 447 [CrossRef] [NASA ADS]
- Kim, A., Goobar, A., & Perlmutter, S. 1996, PASP, 108, 190 [CrossRef] [NASA ADS]
- Kneib, J.-P., Ellis, R. S., Smail, I., Couch, W. J., & Sharples, R. M. 1996, ApJ, 471, 643 [CrossRef] [NASA ADS]
- Kneib, J.-P., Ellis, R. S., Santos, M. R., & Richard, J. 2004, ApJ, 607, 697 [CrossRef] [NASA ADS]
- Kobayashi, C., & Nomoto, K. 2008, [arXiv:0801.0215]
- Kobayashi, C., Tsujimoto, T., Nomoto, K., Hachisu, I., & Kato, M. 1998, ApJ, 503, L155 [CrossRef] [NASA ADS]
- Kolatt, T. S., & Bartelmann, M. 1998, MNRAS, 296, 763 [CrossRef] [NASA ADS]
- Kovner, I., & Paczynski, B. 1988, ApJ, 335, L9 [CrossRef] [NASA ADS]
- Kuznetsova, N., et al. 2008, ApJ, 673, 981 [CrossRef] [NASA ADS]
- Leibundgut, B. 2008, General Relativity and Gravitation, 40, 221 [CrossRef] [NASA ADS]
- Lien, A., & Fields, B. D. 2009, J. Cosmol. Astro-Part. Phys., 1, 47 [CrossRef] [NASA ADS]
- Liesenborgs, J., de Rijcke, S., Dejonghe, H., & Bekaert, P. 2008, MNRAS, 386, 307 [CrossRef] [NASA ADS]
- Limousin, M., Richard, J., Jullo, E., et al. 2007, ApJ, 668, 643 [CrossRef] [NASA ADS]
- Mannucci, F., Della Valle, M., Panagia, N., et al. 2005, A&A, 433, 807 [EDP Sciences] [CrossRef] [NASA ADS]
- Mannucci, F., Della Valle, M., & Panagia, N. 2007, MNRAS, 377, 1229 [CrossRef] [NASA ADS]
- Miknaitis, G., Pignata, G., Rest, A., et al. 2007, ApJ, 666, 674 [CrossRef] [NASA ADS]
- Mobasher, B., Rowan-Robinson, M., Georgakakis, A., & Eaton, N. 1996, MNRAS, 282, L7 [NASA ADS]
- Mörtsell, E., & Sunesson, C. 2006, J. Cosmol. Astro-Part. Phys., 1, 12 [CrossRef] [NASA ADS]
- Neill, J. D., Sullivan, M., Balam, D., et al. 2006, AJ, 132, 1126 [CrossRef] [NASA ADS]
- Nobili, S., & Goobar, A. 2008, A&A, 487, 19 [EDP Sciences] [CrossRef] [NASA ADS]
- Östman, L., Goobar, A., & Mörtsell, E. 2008, A&A, 485, 403 [EDP Sciences] [CrossRef] [NASA ADS]
- Poznanski, D., Maoz, D., Yasuda, N., et al. 2007, MNRAS, 382, 1169 [NASA ADS]
- Poznanski, D., Butler, N., Filippenko, A. V., et al. 2009, ApJ, 694, 1067 [CrossRef] [NASA ADS]
- Pritchet, C. J., Howell, D. A., & Sullivan, M. 2008, ApJ, 683, L25 [CrossRef] [NASA ADS]
- Refsdal, S. 1964, MNRAS, 128, 307 [NASA ADS]
- Richard, J., Pelló, R., Schaerer, D., Le Borgne, J.-F., & Kneib, J.-P. 2006, A&A, 456, 861 [EDP Sciences] [CrossRef] [NASA ADS]
- Richardson, D., Branch, D., Casebeer, D., et al. 2002, AJ, 123, 745 [CrossRef] [NASA ADS]
- Riess, A. G., Strolger, L.-G., Casertano, S., et al. 2007, ApJ, 659, 98 [CrossRef]
- Salpeter, E. E. 1955, ApJ, 121, 161 [CrossRef] [NASA ADS]
- Scannapieco, E., & Bildsten, L. 2005, ApJ, 629, L85 [CrossRef] [NASA ADS]
- Seitz, S., Saglia, R. P., Bender, R., et al. 1998, MNRAS, 298, 945 [CrossRef] [NASA ADS]
- Sharon, K., Gal-Yam, A., Maoz, D., Filippenko, A. V., & Guhathakurta, P. 2007, ApJ, 660, 1165 [CrossRef] [NASA ADS]
- Smartt, S. J., Eldridge, J. J., Crockett, R. M., & Maund, J. R. 2009, MNRAS, 395, 1409 [CrossRef] [NASA ADS]
- Stanishev, V., Goobar, A., Paech, K., et al. 2009, A&A, 507, 61 [EDP Sciences] [CrossRef] (Paper I)
- Strolger, L.-G., Riess, A. G., Dahlen, T., et al. 2004, ApJ, 613, 200 [CrossRef] [NASA ADS]
- Sullivan, M., Ellis, R., Nugent, P., Smail, I., & Madau, P. 2000, MNRAS, 319, 549 [CrossRef]
- Sullivan, M., Le Borgne, D., Pritchet, C. J., et al. 2006, ApJ, 648, 868 [CrossRef] [NASA ADS]
- Wang, J., Hall, P. B., Ge, J., Li, A., & Schneider, D. P. 2004, ApJ, 609, 589 [CrossRef] [NASA ADS]
Footnotes
- ... prospects
![[*]](/icons/foot_motif.png)
- Based on observations made with ESO telescopes at the La Silla Paranal Observatory under programme ID 079.A-0192 and ID 081.A-0734.
- ... Nugent
![[*]](/icons/foot_motif.png)
- http://supernova.lbl.gov/ nugent
- ... confirmed)
![[*]](/icons/foot_motif.png)
- Kathy Perrett, private communication.
- ... LENSTOOL
![[*]](/icons/foot_motif.png)
- www.oamp.fr/cosmology/lenstool
- ... viewing
![[*]](/icons/foot_motif.png)
- Throughout
this paper,
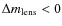 for
for 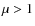 .
.
- ... strong
![[*]](/icons/foot_motif.png)
- Gravity gives, gravity takes!
All Tables
Table 1: Supernova properties.
Table 2: Archival data used to calculate photometric redshifts.
Table 3: Data used for transient search.
Table 4: Transient candidate photometry from Paper I.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.