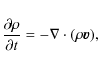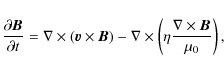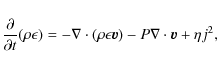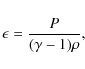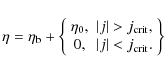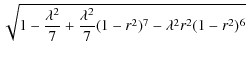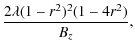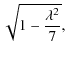| Issue |
A&A
Volume 506, Number 2, November I 2009
|
|
|---|---|---|
| Page(s) | 913 - 925 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200912285 | |
| Published online | 27 August 2009 | |
A&A 506, 913-925 (2009)
Coronal heating by magnetic reconnection in loops with zero net current
A. W. Hood1 - P. K. Browning2 - R. A. M. Van der Linden3
1 -
School of Mathematics and Statistics, St Andrews University, St Andrews, KY16 9SS,
UK
2 -
Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, University of Manchester, Manchester M13 9PL, UK
3 -
SIDC, Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium
Received 6 April 2009 / Accepted 17 August 2009
Abstract
Context. The paper is concerned with heating of the solar
corona by nanoflares: a superposition of small transient events in
which stored magnetic energy is dissipated by magnetic reconnection. It
is proposed that heating occurs in the nonlinear phase of an ideal kink
instability, where magnetic reconnection leads to relaxation to a state
of minimum magnetic energy.
Aims. The aim is to investigate the nonlinear aspects of
magnetic relaxation on a current loop with zero net axial current. The
dynamical processes leading to the establishment of a relaxed state are
explored. The efficiency of loop heating is investigated.
Methods. A 3D magnetohydrodynamic numerical code is used to
simulate the evolution of coronal loops which are initially in ideally
unstable equilibrium. The initial states have zero net current. The
results are interpreted by comparison both with linear stability
analysis and with helicity-conserving relaxation theory.
Results. The disturbance due to the unstable mode is strongly
radially confined when the loop carries zero net current. Strong
current sheets are still formed in the nonlinear phase with dissipation
of magnetic energy by fast reconnection. The nonlinear development
consists first of reconnection in a large scale current sheet, which
forms near the quasi-resonant surface of the equilibrium field.
Subsequently, the current sheet extends and then fragments, leading to
multiple reconnections and effective relaxation to a constant ![]() field.
field.
Conclusions. Magnetic reconnection is triggered in the nonlinear
phase of kink instability in loops with zero net current. Initially,
reconnection occurs in a single current sheet, which then fragments
into multiple reconnection sites, allowing almost full relaxation to
the minimum energy state. The loop is heated to high temperatures
throughout its volume.
Key words: Sun: corona - Sun: magnetic fields - magnetohydrodynamics (MHD) - plasmas
1 Introduction
Nanoflares are often suggested as the mechanism that heats the solar corona (Parker 1988). The idea is that there are many small and rapid releases of magnetic energy, such that a hot corona can be maintained by their combined effect. A very good candidate for the actual energy dissipation mechanism is magnetic reconnection. Indeed, there is now a very compelling body of evidence that reconnection is the primary energy release process in large-scale flares, and it thus seems likely that the same process operating on smaller-scales could be responsible for maintaining the X-ray corona.
Coronal heating must involve both energy storage and energy release. In the case in which energy is stored over timescales longer than an Alfvén travel time, which is expected to be the dominant situation in solar active regions, the field is assumed to evolve quasi-statically through a sequence of equilibria if the coronal footpoints are suitably line-tied by the dense photospheric plasma. Hood et al. (1989) has noted that slow chromospheric motions may violate this condition and Grappin et al. (2008) have shown that the evolution due to slow photospheric motions may lead to a different coronal response to that expected due to line-tying.
To extract energy from the coronal magnetic field, it must be in a
stressed state: that is, at least non-potential (although it is not
necessarily the case that all energy above a potential state can be
effectively dissipated). Relaxation theory predicts that a
non-potential, force-free magnetic field, satisfying
![]() (where
(where
![]() ),
can relax through reconnection events to a lower energy state, while
preserving the magnetic helicity. The field relaxes towards the minimum
energy state, which is a linear or constant-
),
can relax through reconnection events to a lower energy state, while
preserving the magnetic helicity. The field relaxes towards the minimum
energy state, which is a linear or constant-![]() field (Taylor 1974, 1986). Note that free energy is thus associated with non-uniformities in
field (Taylor 1974, 1986). Note that free energy is thus associated with non-uniformities in ![]() .
For this mechanism to work, the magnetic field must initially be
stressed sufficiently beyond the relaxed state so that energy is stored
in the field, before an instability (or other trigger) releases this
stored energy and results in the necessary heating. In fact, the
heating rate depends on how far the free energy can build up
before relaxation takes place (Heyvaerts & Priest 1984).
.
For this mechanism to work, the magnetic field must initially be
stressed sufficiently beyond the relaxed state so that energy is stored
in the field, before an instability (or other trigger) releases this
stored energy and results in the necessary heating. In fact, the
heating rate depends on how far the free energy can build up
before relaxation takes place (Heyvaerts & Priest 1984).
It has been proposed (Browning & Van der Linden 2003) that the trigger for such a relaxation event could be the onset of an ideal kink instability: this was essentially confirmed by Browning et al. (2008), showing that the kink instability could form a helical current sheet that allows reconnection to occur. While there are only one or two phases of highly dynamic activity, the magnetic field does indeed relax towards the predicted state. It has also been demonstrated (Browning et al. 2008) that helicity is very well conserved compared with energy, and thus the primary condition for Taylor relaxation applies: however, for full relaxation to a minimum energy state to be achieved, it is also necessary that there is sufficient means of energy dissipation, which depends on the distribution of reconnection sites. In laboratory plasmas, relaxation theory seems to apply best to plasmas which have relatively high levels of fluctuations associated with instabilities, such as Reverse Field Pinches (Ji et al. 1995) and Spheromaks (Jarboe 2005).
The model magnetic field considered (Browning & Van der Linden 2003; Browning et al.2008)
consisted of a cylindrical loop with two different ![]() values:
values: ![]() inside a radius
inside a radius ![]() ,
,
![]() between
between ![]() and R, and (in some cases) a potential field (zero
and R, and (in some cases) a potential field (zero ![]() )
between R and the outer numerical boundary. Advantages of such a model field are that the degree of non-uniformity in the
)
between R and the outer numerical boundary. Advantages of such a model field are that the degree of non-uniformity in the ![]() profile, associated with free energy above the minimum energy state, is
clearly quantified; also, a wide range of current profiles can be
explored using a two parameter family, for which relevant quantities
such as energy and helicity can be analytically calculated. The
analytical approach, assuming a helicity-conserving relaxation for the
nonlinear phase (Browning & Van der Linden 2003), and using a conducting wall at the loop boundary R,
showed that heating events of a wide range of magnitudes would result,
depending on where the stability boundary is crossed. This naturally
leads to the idea that the corona is heated by a series of transient
events of varying sizes - as in the nanoflare hypothesis.
profile, associated with free energy above the minimum energy state, is
clearly quantified; also, a wide range of current profiles can be
explored using a two parameter family, for which relevant quantities
such as energy and helicity can be analytically calculated. The
analytical approach, assuming a helicity-conserving relaxation for the
nonlinear phase (Browning & Van der Linden 2003), and using a conducting wall at the loop boundary R,
showed that heating events of a wide range of magnitudes would result,
depending on where the stability boundary is crossed. This naturally
leads to the idea that the corona is heated by a series of transient
events of varying sizes - as in the nanoflare hypothesis.
Initial 3D numerical simulations (Browning et al. 2008)
essentially confirmed
the hypothesis that the field undergoes helicity-conserving relaxation
during the nonlinear phase of the kink instability, and that the final
relaxed state is close to
the predicted constant-![]() field. However, the cases selected previously all had a non-zero total
axial current and so there was always an azimuthal component of the
magnetic field in the outermost part of the loop. The kink instability
in these cases was very extensive, with the disturbances reaching all
the way to the numerical boundary. Thus, the entire plasma column is
mixed and the constant-
field. However, the cases selected previously all had a non-zero total
axial current and so there was always an azimuthal component of the
magnetic field in the outermost part of the loop. The kink instability
in these cases was very extensive, with the disturbances reaching all
the way to the numerical boundary. Thus, the entire plasma column is
mixed and the constant-![]() state is nearly reached. What happens if the instability is more
confined? Can the field still relax towards the state predicted by
relaxation theory?
state is nearly reached. What happens if the instability is more
confined? Can the field still relax towards the state predicted by
relaxation theory?
The question of how the magnetic field becomes stressed, to
initially store the required magnetic energy, will influence the form
that the non-linear
![]() takes; Browning et al. (2008)
did not consider this. If the magnetic field is initially potential,
then it is untwisted and, in the cylindrical case, is simply a uniform
axial field. Assuming that photospheric motions twist the field and
introduce an azimuthal field component, if the twisting motions are
confined to a localised region, then the resulting non-potential field
will have a zero total axial current. The cylindrical loop will
be confined only by a surrounding axial field that will not have any
azimuthal component. Thus, zero-net-current fields are far more
realistic representations of the solar coronal field. However, it is
expected that the instability in such cases should be much more
confined (Lionello et al. 1998), and it is important to discover whether a relaxed state can still be
achieved. This cannot be determined from previous work (e.g. Baty & Heyvaerts 1996; Velli et al. 1997; Lionello et al. 1998; Baty 2000a)
since the final state was not analysed and indeed the simulations were
not run for long enough for a quasi-steady-state to be achieved.
takes; Browning et al. (2008)
did not consider this. If the magnetic field is initially potential,
then it is untwisted and, in the cylindrical case, is simply a uniform
axial field. Assuming that photospheric motions twist the field and
introduce an azimuthal field component, if the twisting motions are
confined to a localised region, then the resulting non-potential field
will have a zero total axial current. The cylindrical loop will
be confined only by a surrounding axial field that will not have any
azimuthal component. Thus, zero-net-current fields are far more
realistic representations of the solar coronal field. However, it is
expected that the instability in such cases should be much more
confined (Lionello et al. 1998), and it is important to discover whether a relaxed state can still be
achieved. This cannot be determined from previous work (e.g. Baty & Heyvaerts 1996; Velli et al. 1997; Lionello et al. 1998; Baty 2000a)
since the final state was not analysed and indeed the simulations were
not run for long enough for a quasi-steady-state to be achieved.
This paper considers the nonlinear dynamics of fields which are
initially in unstable equilibrium with zero-net-current (localised
footpoint
twist profiles). We look at three zero-net-current models: the first
case is close to the marginal stability boundary, the second is much
further into the unstable region, as identified by Browning et al.
(2008), while the third case has a smooth
![]() profile. In terms of the framework proposed by Browning & Van der Linden (2003),
the first case might be expected to be most representative of nanoflare
heating, since the field should become unstable as soon as the
stability threshold is crossed. However, if the driving is not so slow,
the field might, in practice, evolve well into the linearly unstable
region before an instability develops. Case 2 thus provides a useful
comparison, to see how the extent to which the field is is linearly
unstable affects the nonlinear development. Finally, Case 3 allows us
to determine whether there are any significant differences between
(more realistic) smooth current profiles and the piecewise-constant-
profile. In terms of the framework proposed by Browning & Van der Linden (2003),
the first case might be expected to be most representative of nanoflare
heating, since the field should become unstable as soon as the
stability threshold is crossed. However, if the driving is not so slow,
the field might, in practice, evolve well into the linearly unstable
region before an instability develops. Case 2 thus provides a useful
comparison, to see how the extent to which the field is is linearly
unstable affects the nonlinear development. Finally, Case 3 allows us
to determine whether there are any significant differences between
(more realistic) smooth current profiles and the piecewise-constant-![]() profiles studied previously.
profiles studied previously.
The main aim of this paper is to explore in detail the dynamics of the process by which a relaxed state of minimum magnetic energy may be attained in a coronal loop, during the nonlinear phase of kink instability, and to determine the extent to which this mechanism works in a loop without net current (i.e. with a localised footpoint twisting profile). This builds on previous results (Browning et al. 2008) but makes some significant new developments: firstly, the study of profiles with zero net current; secondly, consideration of smooth equilibrium current profiles, allowing the applicability of the previously studied profiles (with discontinuous current profiles) to be tested; thirdly, a much more detailed investigation of the dynamics of the reconnection and a determination of how a relaxed state is actually attained; fourthly, an investigation of the loop heating arising from reconnection, including temperature profiles. Haynes & Arber (2007) have investigated the observational consequences of the kink instability for a zero net current loop by constructing synthetic EUV images of intensity but they did not consider this from the viewpoint of relaxation theory.
The paper is structured in the following manner. Section 2 describes the equations used, the numerical method used to solve them and the initial equilibria. Section 3 presents the overall results from the simulations: including a comparison with linear stability results, a discussion of current sheet formation and fieldline evolution, energy dissipation and heating, and a comparison with relaxation theory. Finally, the results are discussed and our conclusions are given in the last section.
2 Numerical procedure and model problem
2.1 Numerical procedure
To run the nonlinear simulations, we use a 3D MHD
code, Lare3d, which solves the MHD equations given by,
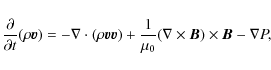 |
(2) |
with specific energy density,
where
The application of this code to relaxation theory has been discussed in Browning et al. (2008).
The equations are made dimensionless by setting
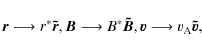
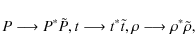
where a tilde denotes a dimensionless variable.
| (6) |
Since the resistivity that we use is not uniform, we keep a normalised
where
Quantities such as magnetic and kinetic energy are calculated by direct integration of the fields, while we calculate the change in the relative helicity (Finn & Antonsen 1985) in the same manner as described in Browning et al. (2008).
For each of the cases investigated, we have taken a computational
domain with sizes
Lx = Ly = 2 or 3 to ensure that the effect of the rigid wall boundary conditions are minimised. In the axial direction we have Lz=20
where line-tying conditions are imposed. Each equilibrium is
represented as a loop of normalised radius 1 and, therefore, each loop
has an aspect-ratio of 20, as in Browning & Van der Linden (2003) and Browning et al. (2008). We have run each simulation with a low resolution
![]() grid (as used in our previous work), a medium resolution
grid (as used in our previous work), a medium resolution
![]() grid and a high resolution
grid and a high resolution
![]() grid. Similar trends are obtained for each resolution, although, as
expected, the highest resolution reveals more fine structures, and the
detailed time evolution is somewhat dependent on the resolution.
The results presented here are actually all for the high resolution
cases, with
Lx=Ly=3 for Case 1 (described below) and
Lx=Ly=2 for Cases 2 and 3. We have also shown that changing Lx from 2 to 3 makes little difference, due to the radially confined nature of the instability.
grid. Similar trends are obtained for each resolution, although, as
expected, the highest resolution reveals more fine structures, and the
detailed time evolution is somewhat dependent on the resolution.
The results presented here are actually all for the high resolution
cases, with
Lx=Ly=3 for Case 1 (described below) and
Lx=Ly=2 for Cases 2 and 3. We have also shown that changing Lx from 2 to 3 makes little difference, due to the radially confined nature of the instability.
2.2 Initial equilibria
As in Browning et al. (2008),
the initial field is assumed to be a force-free equilibrium unstable to
an ideal MHD kink instability. Consistent with the assumption of a
force-free field in order to model ab initio heating, the initial
density is taken as constant while the temperature is zero.
The first two equilibria are modified from the model described in
Browning & Van der Linden (2003) and consist of two constant-![]() regions surrounded by a uniform, axial potential field. The magnetic
field is everywhere continuous; hence the current is always finite,
though discontinuous.
regions surrounded by a uniform, axial potential field. The magnetic
field is everywhere continuous; hence the current is always finite,
though discontinuous.
![]() is obtained from
is obtained from
and, in our dimensionless equations, may be expressed as
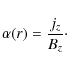
Another useful equilibrium quantity is the twist,
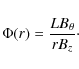
Quasi-mode rational (or quasi-resonant) surfaces exist when
Thus, the initial field consists of two constant-![]() regions, with
regions, with
![]() within the inner core, defined to have radius
within the inner core, defined to have radius ![]() ,
and
,
and
![]() in
the outer layer; outside the loop radius (which is 1 in dimensionless
units), is a potential field region, which extends to a conducting wall
at
in
the outer layer; outside the loop radius (which is 1 in dimensionless
units), is a potential field region, which extends to a conducting wall
at
![]() ,
or a square conducting wall in the case of the numerical simulations. These fields are of the form
,
or a square conducting wall in the case of the numerical simulations. These fields are of the form
where, to ensure continuity of the field components,
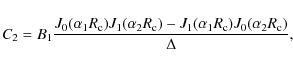 |
(11) |
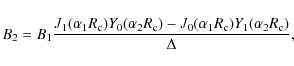 |
(12) |
| (13) |
and,
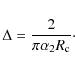 |
(14) |
Here, J0,1 are Bessel functions of the first kind, with orders 0 and 1, respectively, and Y0,1 are Bessel functions of the second kind; B1, B2, C2 and C3 are constant coefficients. Note that the outer vacuum layer has no azimuthal field in the case discussed here, since the loop carries no net axial current (see below). Due to the oscillatory nature of Bessel functions, these equations allow for a wide range of profiles, both with and without reversals of axial and azimuthal field components; however, the particular cases studied here have unidirectional (positive) axial field (see Fig. 1, top), while the azimuthal field is also unidirectional but falls to zero at the loop edge. Figure 1 (bottom) shows the initial profiles for By(x,0,0) which corresponds to the azimuthal field,
We take
![]() ,
B1 = 1 and normally take
,
B1 = 1 and normally take
![]() or 3.0. The values of
or 3.0. The values of ![]() and
and ![]() are not independent here. For example, we can select
are not independent here. For example, we can select ![]() and then
and then ![]() must be chosen so that
must be chosen so that
![]() for r > 1.0. If
for r > 1.0. If
![]() in the outer region, then the total axial current in the loop is zero.
Such a configuration is expected if the magnetic field is stressed by
photospheric footpoint motions that only extend over a finite radius (
in the outer region, then the total axial current in the loop is zero.
Such a configuration is expected if the magnetic field is stressed by
photospheric footpoint motions that only extend over a finite radius (
![]() ). Hence, we must have
). Hence, we must have
where we remember that B2 and C2 depend on
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12285f1a.eps}\vspace*{2mm}
\includegraphics[width=8cm,clip]{12285f1b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg70.png) |
Figure 1: Top: the initial profiles of Bz(x,0,0) are shown as dashed curves and the final numerical simulation profiles are shown as solid curves. Bottom: the initial profiles of By(x,0,0) are shown as dashed curves and the final numerical simulation profiles are shown as solid curves. Case 1 has the initial profiles as black dashed curves, Case 2 as red dot-dashed curves and Case 3 as blue triple-dot dashed curves. |
| Open with DEXTER | |
A third possible zero net current equilibrium has a smooth ![]() profile rather than the piecewise constant profile used above. For Case 3, we take, for r < 1,
profile rather than the piecewise constant profile used above. For Case 3, we take, for r < 1,
and
for r > 1. The value of the constant parameter
Note that the numerical code uses Cartesian coordinates, but that
the analytical equilibria described here are represented in cylindrical
coordinates. The field components thus have to be mapped onto the
Cartesian grid to provide the initial states for the simulations.
The linear stability calculations, and the analytic calculations of
relaxed states, are performed using a cylindrical boundary at
![]() .
Since the position of the outer boundary does not influence either the
linear growth rates or the non linear evolution, there is no issue with
using a Cartesian boundary in the simulations, at
.
Since the position of the outer boundary does not influence either the
linear growth rates or the non linear evolution, there is no issue with
using a Cartesian boundary in the simulations, at
![]() .
.
3 Numerical simulation results
All three cases have been run with a zero background resistivity
![]() ,
and a non-zero background uniform resistivity,
,
and a non-zero background uniform resistivity,
![]() ,
in addition to the non-uniform resistivity,
,
in addition to the non-uniform resistivity, ![]() described by (7).
There are a few differences between the results and the forms of
resistivity but no qualitative differences between the three cases.
Hence, results are presented here for Cases 1 and 2 with
described by (7).
There are a few differences between the results and the forms of
resistivity but no qualitative differences between the three cases.
Hence, results are presented here for Cases 1 and 2 with
![]() and for Case 3 with
and for Case 3 with
![]() .
High resolution runs are presented but we have also run all cases with
reduced resolution. We are confident that the results are qualitatively
similar at lower resolution, except that the current layers are more
spread out and there are differences in the detailed time profiles
(e.g. the time at which the kinetic energy peaks).
.
High resolution runs are presented but we have also run all cases with
reduced resolution. We are confident that the results are qualitatively
similar at lower resolution, except that the current layers are more
spread out and there are differences in the detailed time profiles
(e.g. the time at which the kinetic energy peaks).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12285f2.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg83.png) |
Figure 2:
The |
| Open with DEXTER | |
The 3 test cases are summarised as follows. The initial profiles for Bz are shown in Fig. 1, along with the final profiles from the simulation.
There are
![]() gridpoints in the x, y, z directions. The critical current at which the anomalous resistivity switches on is
gridpoints in the x, y, z directions. The critical current at which the anomalous resistivity switches on is
![]() and the non-uniform resistivity is
and the non-uniform resistivity is
![]() .
.
Case 1: The values of ![]() are
are
![]() for r < 0.5,
for r < 0.5,
![]() for
0.5 < r < 1.0 and
for
0.5 < r < 1.0 and
![]() for r > 1. There is no background resistivity in this experiment. The outer wall dimensions are Lx=Ly=3.
for r > 1. There is no background resistivity in this experiment. The outer wall dimensions are Lx=Ly=3.
Case 2: This case uses
![]() and
and
![]() and is beyond the marginal stability curve, well into the unstable regime. In this case Lx=Ly=2.
and is beyond the marginal stability curve, well into the unstable regime. In this case Lx=Ly=2.
Case 3: This uses a smooth current profile and is described by Eqs. (16) and (17). A background resistivity of
![]() is used. In this case Lx=Ly=2. as well.
is used. In this case Lx=Ly=2. as well.
3.1 Initial phase and comparison with linear stability
Before discussing the results of the nonlinear simulations, we present the results from the linear analysis (see Van der Linden et al. 1999). The linear modes are calculated using the CILTS code, with a cylindrical boundary, and the radial and axial profiles of vx are shown, for Case 1, in Fig. 3.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12285f3a.ps}\vspace*{2mm}
\includegraphics[width=7cm,clip]{12285f3b.ps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg90.png) |
Figure 3: The linear eigenmode of the most unstable mode is in a) vx(x,0,0) and b) vx(0,0,z). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12285f4.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg91.png) |
Figure 4: Plot of -vx as a function of z along x=y=0 at time t=180. -vx is chosen in order to compare with Fig. 3. |
| Open with DEXTER | |
The axial variation of vx is sinusoidal in z (with about 4 periods) with the amplitude modified to satisfy the line tying. Hence, the dominant axial wavenumber is
![]() .
The radial structure is almost parabolic out to r=0.5. Once the second region of
.
The radial structure is almost parabolic out to r=0.5. Once the second region of ![]() is reached the amplitude drops dramatically and is almost zero by r=1.
This may be expected since the disturbance will match the pitch of the
fieldlines in the core and so any perturbation in the outer layer
will cause strong fieldline bending as the pitch varies strongly there.
The region outside the loop, where the field is potential in r
> 1, is barely disturbed. This is also not surprising since there is
no free energy in this region and any disturbance here will only result
in an increase in the potential energy of this region, taking energy
from the instability. Therefore, the instability tries to restrict
itself to the internal region where the currents are non-zero and we
have an internal kink instability. Thus, the position of the outer wall
is not critical in these simulations - in contrast with some of the
cases considered previously (Browning et al. 2008),
where the disturbances reached the wall. This is also confirmed by the
linear results, which show that the growth rate is insensitive to the
wall position once it is beyond about r=1.5.
is reached the amplitude drops dramatically and is almost zero by r=1.
This may be expected since the disturbance will match the pitch of the
fieldlines in the core and so any perturbation in the outer layer
will cause strong fieldline bending as the pitch varies strongly there.
The region outside the loop, where the field is potential in r
> 1, is barely disturbed. This is also not surprising since there is
no free energy in this region and any disturbance here will only result
in an increase in the potential energy of this region, taking energy
from the instability. Therefore, the instability tries to restrict
itself to the internal region where the currents are non-zero and we
have an internal kink instability. Thus, the position of the outer wall
is not critical in these simulations - in contrast with some of the
cases considered previously (Browning et al. 2008),
where the disturbances reached the wall. This is also confirmed by the
linear results, which show that the growth rate is insensitive to the
wall position once it is beyond about r=1.5.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12285f5.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg93.png) |
Figure 5: Plots of a) magnetic energy, b) kinetic energy, c) internal energy, d) maximum current as functions of time for Case 1. |
| Open with DEXTER | |
The dimensionless linear growth rate for Case 1 is
![]() .
This is quite small and means that a general disturbance, as used in the non linear code, will need time (up to t=100)
before the unstable mode finally comes through. The slow growth has
another impact on the way the instability develops non-linearly, which
depends on the actual form of the resistivity chosen. For example, we
consider two forms for the resistivity. Firstly, we assume that there
is a current threshold (taken as 5 to lie above the maximum of the
current in the initial equilibrium) and have an anomalous resistivity
.
This is quite small and means that a general disturbance, as used in the non linear code, will need time (up to t=100)
before the unstable mode finally comes through. The slow growth has
another impact on the way the instability develops non-linearly, which
depends on the actual form of the resistivity chosen. For example, we
consider two forms for the resistivity. Firstly, we assume that there
is a current threshold (taken as 5 to lie above the maximum of the
current in the initial equilibrium) and have an anomalous resistivity
![]() for
for
![]() .
Secondly, we either choose a small background uniform resistivity of
.
Secondly, we either choose a small background uniform resistivity of
![]() or have no background value. If
or have no background value. If
![]() ,
then the slow growth rate means that the equilibrium field can diffuse
slightly before the instability starts. Since the plasma is so close to
marginal stability, this can significantly affect the growth rate of
the linear stage or even remove it entirely.
,
then the slow growth rate means that the equilibrium field can diffuse
slightly before the instability starts. Since the plasma is so close to
marginal stability, this can significantly affect the growth rate of
the linear stage or even remove it entirely.
In Fig. 4 the form of
a perpendicular component of the velocity along the axis is shown from
the non-linear simulation. This has the form of a mode with
![]() ,
namely
,
namely ![]() ,
and agrees well with the form predicted from the linear code (see Fig. 3).
The numerical mode is not clean since it has arisen from a fairly
general initial disturbance and so there are many other (stable) modes
also present. Similarly, the numerical disturbance is highly confined
radially in the early stages, in agreement with the linear results: the
velocity is very close to zero outside r =1.
,
and agrees well with the form predicted from the linear code (see Fig. 3).
The numerical mode is not clean since it has arisen from a fairly
general initial disturbance and so there are many other (stable) modes
also present. Similarly, the numerical disturbance is highly confined
radially in the early stages, in agreement with the linear results: the
velocity is very close to zero outside r =1.
The time evolution of the most important characteristics of the
integrated fields for the numerical simulations is shown for Case 1 in
Fig. 5. The dependence of kinetic energy only is shown for Cases 2 and 3 (Fig. 6),
since this illustrates the key dynamic features. The initial growth
rates for the high resolution case can be estimated from the logarithm
of the kinetic energy, as described in Browning et al. (2008). Initially (for Case 1) the kinetic energy slowly decays until time t=100. (It should be recalled that t = 1 corresponds to the radial Alfvén transit time.) At this point, the unstable mode emerges from the background. Around t=100,
the kinetic energy starts to rise exponentially as the linear
instability is first detected.The growth rate found from the non-linear
code for this case is
![]() and is about half the value from the linear code. This phase lasts until about t = 125, when the kinetic energy growth levels off. A second exponential growth phase starts just before t = 160 and lasts until about t = 190; this has measured growth rate of
and is about half the value from the linear code. This phase lasts until about t = 125, when the kinetic energy growth levels off. A second exponential growth phase starts just before t = 160 and lasts until about t = 190; this has measured growth rate of
![]() ,
much faster than the maximum linear growth rate, and is presumably
driven nonlinearly. It is interesting that a clear period of
exponential growth can be found within the nonlinear phase of the
instability, as also seen previously Browning et al. (2008).
,
much faster than the maximum linear growth rate, and is presumably
driven nonlinearly. It is interesting that a clear period of
exponential growth can be found within the nonlinear phase of the
instability, as also seen previously Browning et al. (2008).
For Case 2, the growth rate is much larger, being around
![]() for the most unstable mode. Here the growth rates predicted from the simulation agree favourably with the linear results.
for the most unstable mode. Here the growth rates predicted from the simulation agree favourably with the linear results.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12285f6a.eps}\par\includegraphics[width=7cm,clip]{12285f6b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg102.png) |
Figure 6: The kinetic energy versus time for a) Case 2 and b) Case3. Note the different scales on the axes. The final values of the kinetic energy are similar for Cases 2 and 3. |
| Open with DEXTER | |
3.2 Current sheet development and reconnection
Consider first the overall evolution of the kinetic energy and other global quantities, as shown in Figs. 5 and 6. The magnetic energy remains at the initial value until round t=180 (for Case 1) when it starts to decrease and the energy from the field is converted into kinetic energy and internal energy. Very similar behaviour is observed for the other cases: always, the magnetic energy starts to drop as the kinetic energy rises, eventually reaching a new, lower, steady-state value. For Case 2, since the initial perturbation has been chosen to be closer to the form of the most unstable mode, the instability develops quicker. In addition, the maximum value of the total kinetic energy is significantly larger for Case 2 than for Cases 1 and 3 (see Figs. 5 and 6), because it is further into the unstable regime. As noted above, the kinetic energy for Case 1 peaks twice, at around t = 200 and t = 230. From then on, the kinetic energy decays, as the plasma heads towards its final relaxed state. Similar multiple peaks in kinetic energy are observed for Cases 2 and 3 (Fig. 6), although the timing and relative sizes of the peaks varies between cases (and is also senstive to the numerical resolution). Although not clear from the curves shown, there are oscillations superimposed on the general trends of the kinetic energy, particularly before the second period of exponential growth. The period is around 2.4 and is related to the propagation of fast modes across the box.
Figure 5c shows that the increase in internal energy starts at the same time as the magnetic energy starts to decrease. The internal energy increases by about 1.5 by the end of the simulation while the magnetic energy has decreased by almost 2. Figure 5d shows the time variation of the maximum current. Note that the maximum current remains below the critical value of 5 until around t=120. So reconnection only starts around this time, as does Ohmic heating.
Consider now the development of the current profile, focusing first on Case 1. The current starts to rise just after t = 100. Analysing the current profile at
the midplane (z = 0), a small spike in current is just discernible at t = 105, at a radius of
![]() .
Since, as discussed above, the unstable linear mode has dominant wavenumber
.
Since, as discussed above, the unstable linear mode has dominant wavenumber
![]() ,
the corresponding quasi-resonant surface occurs where
,
the corresponding quasi-resonant surface occurs where
![]() ,
which is at
,
which is at
![]() (Fig. 2). This is very close to the initial location of the current sheet, as expected (Baty 2000a; Lionello et al. 1998),
since the kink instability with zero-net-current should be the
line-tied analogue of an internal resonant kink mode. It is of interest
to note that the ``resonant surface'' has a clear signature in our
simulations of a finite-length loop (with aspect-ratio L/R = 20), whereas recent work (Huang et al. 2006)
on the linear analysis suggests that resonant surfaces only retain
their significance in much higher aspect-ratio systems. This current
spike is in fact part of an emerging helical current ribbon, whose
pitch matches the helical pitch of the quasi-resonant fieldlines. As
the current builds in magnitude, which happens quite rapidly, the
ribbon also moves radially outwards, as it is carried out by the radial
flow associated with the initial kink disturbance.
For example, after a further 55 Alfven times (at t = 160), the current spike (now larger) appears at about r = 0.694. The initial current sheet formation and subsequent increase in strength and outward movement are shown in Fig. 7.
(Fig. 2). This is very close to the initial location of the current sheet, as expected (Baty 2000a; Lionello et al. 1998),
since the kink instability with zero-net-current should be the
line-tied analogue of an internal resonant kink mode. It is of interest
to note that the ``resonant surface'' has a clear signature in our
simulations of a finite-length loop (with aspect-ratio L/R = 20), whereas recent work (Huang et al. 2006)
on the linear analysis suggests that resonant surfaces only retain
their significance in much higher aspect-ratio systems. This current
spike is in fact part of an emerging helical current ribbon, whose
pitch matches the helical pitch of the quasi-resonant fieldlines. As
the current builds in magnitude, which happens quite rapidly, the
ribbon also moves radially outwards, as it is carried out by the radial
flow associated with the initial kink disturbance.
For example, after a further 55 Alfven times (at t = 160), the current spike (now larger) appears at about r = 0.694. The initial current sheet formation and subsequent increase in strength and outward movement are shown in Fig. 7.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{12285f7.ps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg106.png) |
Figure 7: The magnitude of the current as a function of x, at y=0 and z=0 is shown for t=105 (solid) and t=160 (triple dot dashed). The vertical dotted line indicates where the current sheet due to the kink instability first forms at x=-0.6. |
| Open with DEXTER | |
Thus, the kink instability creates the initial current sheet and the first small-scale structure. The development of the current sheet and the associated flow patterns are shown in Figs. 8 and 9 for Case 3. The initial formation of the current sheet, already clearly visible by about t = 55 (Fig. 8a), happens earlier in this case, but the current and flow patterns are very similar indeed to Case 1 at about t = 110. The flow pattern associated with the kink instability has the form of two vortices. The corresponding fieldlines, together with a current isosurface indicating the three-dimensional current sheet structure, are shown in Fig. 10. At this early stage in the nonlinear development, the loop has developed a clear helical deformation, and a helical current ribbon is present (as described above), especially near the loop apex. Note that this time corresponds to the first (rather small) peak in kinetic energy (Fig. 6b), whereas the matching situation for Case 1 (i.e. initial current ribbon formation) occurs in the main peak of kinetic energy (Fig. 5b).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12285f8a.eps}\includegraphics[width=8cm,clip]{12285f8b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg107.png) |
Figure 8: Case 3: contour plot of the current density, j, at z = 0 at time t=55 and 85. The arrows show the velocity components, vx and vy, scaled by a factor of 5. The length of the arrows are proportional to the magnitude of the horizontal velocity. a) Left is at t=55. b) Right is at t=85. The colour scale for the current density is from 0 (light purple) to 15 (red). |
| Open with DEXTER | |
The fields and currents evolve quite rapidly from this point. By about t = 85 (Figs. 8b and 10b),
the current
sheet has become much stronger but has also stretched and started to
split into two. It is also apparent from the fieldline plot that the
current ribbon has a much greater axial length at this stage, and clear
reconnection of the inner (![]() )
fieldlines with the outer (
)
fieldlines with the outer (![]() )
fieldlines can be seen. This is the beginning of the relaxation process, as each reconnection ``mixes'' the
)
fieldlines can be seen. This is the beginning of the relaxation process, as each reconnection ``mixes'' the ![]() values (or more correctly the parallel current profiles), moving
towards a more uniform profile. It may be seen that the flow pattern -
a remnant of the double vortex pattern of the kink - is such as to pull
the ends of the current sheet around (to the negative x side, in the figure) and then inwards towards the original loop axis.
values (or more correctly the parallel current profiles), moving
towards a more uniform profile. It may be seen that the flow pattern -
a remnant of the double vortex pattern of the kink - is such as to pull
the ends of the current sheet around (to the negative x side, in the figure) and then inwards towards the original loop axis.
As the current sheet is stretched and distorted in this way, it fragments further. By about t
= 150, the sheet has split into several parts, and a distribution of
current sheets of various strengths is starting to fill the loop
cross-section (Fig. 9).
A similar structure is observed through most of the loop length, as can
be discerned from the current isosurface in Fig. 10c.
Note that this figure also shows that the fieldlines have undergone
considerable reconnection by this time, as the fieldline connectivity
is quite different from the initial state. This snapshot is close to
the main peak
in kinetic energy from Fig. 6c.
Thus the strongest flows are associated with the fragmented current
sheet. In Case 1, the fragmented current sheet structure is also
associated with the second peak in kinetic energy (at around t
= 230), although in this case the height of the second peak is lower
than the first. Considering the flow patterns in Fig. 9,
it may be seen that each current sheet has strong reconnection
outflows; these outflows are driving inflows into neighbouring current
sheets, and are thus reinforcing the reconnection. In this stage, ![]() values are mixing across the cross-section, and so the field approaches the constant-
values are mixing across the cross-section, and so the field approaches the constant-![]() state (albeit, at this point, with superimposed spikes of
state (albeit, at this point, with superimposed spikes of ![]() on a profile which is becoming, on average, more uniform).
on a profile which is becoming, on average, more uniform).
Subsequent to this, the current sheets gradually fade away, and the fieldlines assume a state which, away from the footpoints, is close to straight axial field (Fig. 10d). This field is still not fully in equilibrium (note the final kinetic energy still is non-zero as seen in Fig. 6), but is clearly approaching its relaxed state. Since physical viscosity is switched off in these runs, the rate at which the field is relaxing does depend on the values of the resistivity and the shock viscosities, which have been chosen to exceed any numerical diffusion. How close the field is to the relaxed state may be estimated by considering the maximum angle between the current and magnetic field vectors.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12285f9.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg108.png) |
Figure 9: Case 3: contour plot of the current density, j, at z = 0 at time t=150. The arrows show the velocity components, vx and vy. The colour scale for the current density is from 0 (blue) to 15 (red). |
| Open with DEXTER | |
3.3 Heating and temperature profiles
Nothing very much happens to the density and temperature until the first current sheet forms - after about t=105 for Case 1.
A picture of what is happening can be seen by looking at cuts through y=0 and z=0. The temperature as a function of x is shown, for Case 1, in Fig. 11. Initially (t=180), there is only heating at the current sheet with a peak dimensionless temperature of 0.015. The location of the spike corresponds closely to the initial current spike (discussed above). During this time the dimensionless density is of order unity. When the kinetic energy reaches a maximum value around t=200, the maximum temperature reaches a value around 0.06 but now there are more spikes appearing. Eventually, at t=250, the peak temperature is slightly lower, at around 0.02, but it is reasonably uniform across a radius of 1.5.
It is also very instructive to look at contour plots of temperature, taking a cross-section across the loop midplane (z = 0), as shown in Figs. 12 and 13, for Case 3. These snapshots correspond to the same times as the velocity, current and fieldline plots shown in Figs. 8 and 10. There is some initial heating associated with the current sheet formation (though not exactly co-located), see Fig. 12a. Then, when a strong current sheet has formed, around t = 85, there is very localised heating inside the current sheet and within the reconnection outflows (Fig. 12b). Finally, once a fragmented current sheet has been established, a much more distributed temperature profile arises, with hot plasma (albeit still with filamentary structure) across the full cross-section (Fig. 13).
![\begin{figure}
\par\includegraphics[width=14.3cm,clip]{1228510a.eps}\par\includegraphics[width=14.3cm,clip]{1228510b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg109.png) |
Figure 10: Case 3: the yellow fieldlines are drawn from z=-10, centred on x=0, y=0 while the blue fieldlines are drawn from z=10 again centred on x=0, y=0. The red isosurface is the magnitude of the current with a value of 4. a) Top left is at t=55. b) Top right is at t=85. c) Bottom left is at t=150 and d) Bottom right is the final time at t=295. |
| Open with DEXTER | |
Assuming a typical dimensional magnetic field strength of B0 = 50 G, and mass density of
![]() kg, the dimensional value of the temperature is typically around
kg, the dimensional value of the temperature is typically around
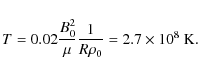
This value is high but it should only be considered as an upper estimate to the actual value. Since the energy equation does not allow thermal energy to leave the system through radiation losses, the resulting temperature is necessarily too high. Haynes & Arber (2007) obtained lower values for their field profile and parameter choices. In addition to radiative losses, thermal conduction will also lower this value and so the predicted temperatures can only give estimates of the maximum values likely in the relaxation process. The inclusion of thermal conduction and radiation is likely to be important during the slow evolution towards the final relaxed state but less so during the phase of rapid energy release.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12285f11.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg112.png) |
Figure 11: Case 1: the temperature, T(x,0,0), as a function of x at y=0 and z = 0 at times t= a) 180, b) 200, c) 250 and d) 280. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1228512a.eps}\includegraphics[width=9cm,clip]{1228512b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg113.png) |
Figure 12: Case 3: contourplot of the temperature at time t=55 ( left and 85 (right) in the mid-plane at z=0. The colour scale for the temperature is from 0 (blue) to 15 (red). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12285f13.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg114.png) |
Figure 13: Case 3: contourplot of the temperature at time t=150 in the mid-plane at z=0. The colour scale for the temperature is from 0 (blue) to 15 (red). |
| Open with DEXTER | |
What about the temperature variation along the loop? Figure 14 shows how the hotter plasma (T=0.02) is near the summit of the loop (corresponding to where the initial ohmic heating occurs). The lower temperature material (T=0.01) is more spread out. There is very little evidence of a temperature rise near the footpoints. However, the inclusion of thermal conduction would mean that the heat was conducted down towards the footpoints.
3.4 Predicted energy release and relaxed states
The relative magnetic helicity is calculated analytically for the
initial states using the method of Finn & Antonsen (1985) (see also
Browning et al. 2008). Then the relaxed states can be calculated by obtaining the constant ![]() force-free field that has the same helicity, while the energy release
is then the difference in energies between the initial and relaxed
states.
As we have seen, the kink instability and subsequent evolution is
strongly radially confined and does not really spread towards the outer
boundary. We predict the magnetic energy released,
force-free field that has the same helicity, while the energy release
is then the difference in energies between the initial and relaxed
states.
As we have seen, the kink instability and subsequent evolution is
strongly radially confined and does not really spread towards the outer
boundary. We predict the magnetic energy released, ![]() ,
the final
,
the final ![]() value and the value of Bz on the axis r=0, as presented in Table 1
based on an outer radius of 3 or 2; in fact, we have shown there is
very little difference between the energies released for the outer
radius of 2 and 3, but it is significantly smaller for a boundary at 1.
Similarly, the predicted
value and the value of Bz on the axis r=0, as presented in Table 1
based on an outer radius of 3 or 2; in fact, we have shown there is
very little difference between the energies released for the outer
radius of 2 and 3, but it is significantly smaller for a boundary at 1.
Similarly, the predicted ![]() values are very close to zero for the larger values of the outer
radius; this is to be expected because
the outer potential layer in this case has exactly zero helicity and
the loop itself has rather small helicity due to the change in sign of
values are very close to zero for the larger values of the outer
radius; this is to be expected because
the outer potential layer in this case has exactly zero helicity and
the loop itself has rather small helicity due to the change in sign of ![]() .
However, the predicted value of the axial magnetic field at the axis is
essentially the same in all three cases. So in simple terms, relaxation
will remove all the azimuthal field and this is essentially the
available energy. The axial flux is conserved and, since the final
state is almost potential,
the axial field will spread out to give an almost uniform value
everywhere. This can indeed be seen in Fig. 10d.
The only reason why a uniform profile cannot be attained is that
line-tying forces the axial field to retain its original prescribed Bz(r)
profile on the top and bottom boundaries. However, the field will
expand away from the loop footpoints, in the manner described by Lothian & Hood (1989) and Browning & Hood (1989),
with most of the axial
variation confined to localised layers near the footpoints. Thus the
final state should be close to a cylinder with almost uniform axial
field and very weak azimuthal field over most of its length.
Note that Case 2 releases more energy than Case 1: this may be
expected, since this field has a larger variation in
.
However, the predicted value of the axial magnetic field at the axis is
essentially the same in all three cases. So in simple terms, relaxation
will remove all the azimuthal field and this is essentially the
available energy. The axial flux is conserved and, since the final
state is almost potential,
the axial field will spread out to give an almost uniform value
everywhere. This can indeed be seen in Fig. 10d.
The only reason why a uniform profile cannot be attained is that
line-tying forces the axial field to retain its original prescribed Bz(r)
profile on the top and bottom boundaries. However, the field will
expand away from the loop footpoints, in the manner described by Lothian & Hood (1989) and Browning & Hood (1989),
with most of the axial
variation confined to localised layers near the footpoints. Thus the
final state should be close to a cylinder with almost uniform axial
field and very weak azimuthal field over most of its length.
Note that Case 2 releases more energy than Case 1: this may be
expected, since this field has a larger variation in ![]() and hence has more free energy.
and hence has more free energy.
The effective heating may thus be estimated as follows. Assuming all
the azimuthal field is eliminated, which is almost the case since the
final
relaxed state ![]() is close to zero, then the energy dissipated is
is close to zero, then the energy dissipated is
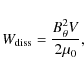
where
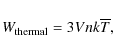
where
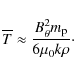 |
(17) |
From the initial profiles, we find
![\begin{figure}
\par\includegraphics[width=4cm,clip]{1228514a.eps}\includegraphic...
...e.eps}\includegraphics[width=4cm,clip]{1228514f.eps}\hspace*{4cm}}\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg122.png) |
Figure 14:
Case 3: isosurface of the temperature, T=0.01 (red), and T=0.02 (green) at times
t=85, 150, 295. The sizes of the boxes are
|
| Open with DEXTER | |
Table 1:
Predicted and numerical values of ![]() ,
,
![]() and
Bz(0,0,0) for the 3 cases.
and
Bz(0,0,0) for the 3 cases.
4 Discussion and conclusions
We have presented 3D MHD simulations of the nonlinear development of the kink instability in a cylindrical model of a coronal loop, for 3 different initial equilibria, each of which is linearly unstable to the ideal kink mode and carries no net current (that is, each has a footpoint twist profile which is localised to the loop). The overall conclusion is that fast reconnection takes place in the nonlinear phase of the kink instability, which effectively dissipates magnetic energy and allows the loop to relax to a minimum energy state that is close to the one predicted by relaxation theory. Although the instability is much more confined in a loop with zero-net-current, the relaxation is still as effective as in previous studies of loops which carried a net current Browning et al. (2008). We have also considerably elucidated the dynamic processes by which the loop relaxes.
Two of the profiles used have a piecewise-constant profile of ![]() ,
based on a model proposed by Browning & Van der Linden (2003), whereas the third has a continuous
,
based on a model proposed by Browning & Van der Linden (2003), whereas the third has a continuous ![]() profile. There are no significant differences between the results,
beyond what would be expected for differing profiles: in other words,
there is no discernible effect of the current discontinuities in the
first two profiles. This confirms that the piecewise-constant
profile. There are no significant differences between the results,
beyond what would be expected for differing profiles: in other words,
there is no discernible effect of the current discontinuities in the
first two profiles. This confirms that the piecewise-constant ![]() profiles are
viable models, both for studying linear stability and for nonlinear
dynamics, and supports the use of the profiles for future studies,
where appropriate.
profiles are
viable models, both for studying linear stability and for nonlinear
dynamics, and supports the use of the profiles for future studies,
where appropriate.
The picture in the early stages is largely in line with previous simulations of nonlinear kink instability (Baty & Heyvaerts 1996; Velli et al. 1997; Lionello et al. 1998; Arber et al. 1999; Baty 2000a,b; Gerrard & Hood 2003; Haynes & Arber 2007), although we have developed a clearer picture of some of the features of this phase, particularly through comparison with results from a linear stability analysis (with line-tying). After a quiescent period, whose duration depends on how far the initial equilibrium lies within the unstable region, a kink mode develops with initial exponential (linear) growth, leading to a helical deformation of the loop and an internal double-vortex flow pattern. As the amplitude increases, a helical current ribbon starts to form, initially very close to the quasi-surface of the most unstable linear mode. The current sheet builds in magnitude and also lengthens (in azimuthal and axial extent).
The subsequent development has not been previously described.
As the current sheet stretches, it initially splits into two. It is
further distorted and
wrapped into the loop interior, eventually splitting and forming a
complex fragmented current sheet structure distributed throughout the
loop cross section.
Reconnection proceeds strongly in this fragmented structure, as the
outflows from one current sheet drive reconnection in another. It is in
this phase that the
most of the fieldlines undergo reconnection, and most of the relaxation
takes place as each reconnection `` mixes'' the values of ![]() ,
leading to the establishment of an almost relaxed state. It is likely
that the higher numerical resolution and longer run-times of our
simulations, compared with previous studies, have allowed us to
identify this important dynamic phase.
,
leading to the establishment of an almost relaxed state. It is likely
that the higher numerical resolution and longer run-times of our
simulations, compared with previous studies, have allowed us to
identify this important dynamic phase.
During the reconnection process, the kinetic energy rises, and
eventually falls (as the reconnection ceases), while the magnetic
energy falls to a new, lower value.
Towards the end of the simulations, the field is in a near equilibrium
state. This is well matched by a constant-![]() field, despite some residual ``spikiness'' in the current profile.
Because the initial profile contains currents of reversed sign, and
because some of the surrounding potential field layer is involved in
the relaxation, the final
field, despite some residual ``spikiness'' in the current profile.
Because the initial profile contains currents of reversed sign, and
because some of the surrounding potential field layer is involved in
the relaxation, the final ![]() value is quite close to zero, and the final field is close to a uniform
axial field (except in boundary layers near the footpoints). This
appears somewhat to contradict previous work (Amari & Luciani 2000; Baty 2000b)
which suggested that the final state of a nonlinear kink was a double
flux tube, with two seperate flux tubes wrapped around each other.
Indeed, this has been used (Amari & Luciani 2000),
as an argument against Taylor relaxation theory. However, it appears
that we do see a similar state, but only at an intermediate stage
(after the first reconnections in the single helical ribbon): this
structure, which clearly must possess localised currents, evolves
further as the current sheet fragments and reconnection proceeds across
the loop volume. We re-iterate that it
is the generation of the fragmented current sheet, with small
length-scales and a complex spatial structure, which is essential in
allowing helicity-conserving relaxation to a minimum energy state -
rather than just the initial helical current ribbon.
value is quite close to zero, and the final field is close to a uniform
axial field (except in boundary layers near the footpoints). This
appears somewhat to contradict previous work (Amari & Luciani 2000; Baty 2000b)
which suggested that the final state of a nonlinear kink was a double
flux tube, with two seperate flux tubes wrapped around each other.
Indeed, this has been used (Amari & Luciani 2000),
as an argument against Taylor relaxation theory. However, it appears
that we do see a similar state, but only at an intermediate stage
(after the first reconnections in the single helical ribbon): this
structure, which clearly must possess localised currents, evolves
further as the current sheet fragments and reconnection proceeds across
the loop volume. We re-iterate that it
is the generation of the fragmented current sheet, with small
length-scales and a complex spatial structure, which is essential in
allowing helicity-conserving relaxation to a minimum energy state -
rather than just the initial helical current ribbon.
A further consequence of the fragmented current sheet is that the loop can be efficiently heated across its cross-section, in contrast with the localised heating produced by the initial single current ribbon. High peak temperatures of over 108 K can be attained, although this would clearly be moderated by the presence of conduction and radiation, which are absent in our model.
The results, in line with Browning et al. (2008), essentially support the framework proposed by Browning & Van der Linden (2003), and, thus, validate the use of modelling based on relaxation theory. The broader coronal heating picture arising is as follows. A loop is stressed by footpoint motions, and evolves quasi-statically until it crosses the stability threshold for the ideal kink. At that point, a dynamic heating episode ensues - as described in our simulations - until a relaxed state is attained. The process then repeats, leading to an intermittent sequence of heating events of various magnitudes. Future simulations will investigate whether this process depends on the time required for the plasma to reach the relaxed state (which is long) or just on the time to release the majority of the magnetic energy (which is short).
The role of fluctuations, often referred to as a turbulent
dynamo, in establishing a relaxed state has been widely discussed in
the context of laboratory plasmas, particularly Reverse Field Pinches,
Spheromaks and Spherical Tokamaks (Taylor 1986; Ji et al. 1995; Jarboe 2005). Indeed, a direct association between the flattening of the ![]() profile and fluctuations with mode number n =1 has been experimentally demonstrated in spheromaks (Willett et al. 1999).
Furthermore,
relaxation associated with helicity-injected current drive in
spheromals and spherical tokamaks has been shown to be associated with
the onset of an ideal kink instability in the open flux region (Brennan et al. 1999). In fact, a oscillation of the
profile and fluctuations with mode number n =1 has been experimentally demonstrated in spheromaks (Willett et al. 1999).
Furthermore,
relaxation associated with helicity-injected current drive in
spheromals and spherical tokamaks has been shown to be associated with
the onset of an ideal kink instability in the open flux region (Brennan et al. 1999). In fact, a oscillation of the ![]() profile across the kink instability boundary has been observed in a spheromak (Willett et al. 1999; Brennan et al. 1999), which is very reminiscent of the repeated relaxation events predicted
by Browning & Van der Linden (2003)
- although in a spheromak, a fully relaxed state is never attained
due to the continual external driving and resistive dissipation. 3D
numerical simulations of spheromak formation also demonstrate the role
of ideal kink instabilities in the onset of relaxation (Sovinec et al. 2001). Our results here are consistent with this scenario.
profile across the kink instability boundary has been observed in a spheromak (Willett et al. 1999; Brennan et al. 1999), which is very reminiscent of the repeated relaxation events predicted
by Browning & Van der Linden (2003)
- although in a spheromak, a fully relaxed state is never attained
due to the continual external driving and resistive dissipation. 3D
numerical simulations of spheromak formation also demonstrate the role
of ideal kink instabilities in the onset of relaxation (Sovinec et al. 2001). Our results here are consistent with this scenario.
The idea that coronal heating arises from the generation of small-scale current sheets due to tangling of coronal field lines (Parker 1972, 1988) has long been discussed. Recently, the development of such current sheets, and a cascade of energy to small-scales, has been demonstrated numerically in reduced MHD simulations (Rappazzo et al. 2007, 2008). However, this relies on rather more complex patterns of footpoint motions, and has continual driving. Our results show that fragmented current sheets, with distributed (but localised) heating can be generated even with very simple smooth footpoint motions. We have found a cascade from the injection length-scale, which is as large as possible in our case, to small-scales of dissipation. Since we deal with an individual heating event, the current sheets appear, and are then removed as the field relaxes to a new, (almost) smooth equilibrium. Such an event is, of course, a single building-block in a scenario by which the corona is heated by a series oftransient events: the field should be repeatedly stressed and relaxed, with a statistical steady-state emerging (Rappazzo et al. 2008). In future, a natural extension of our work will be to investigate the effects of driving footpoint motions, which move the field profile across the stability threshold (Gerrard et al. 2002, 2008).
This work will be developed in a number of other ways in future. An important step will be to include conduction and radiation in the energy balance, and thus find more realistically how the temperature evolves. This will be reported in a future paper.
AcknowledgementsThe computational work was carried out on the joint STFC and SFC (SRIF) funded linux clusters at St Andrews University. A.W.H. and P.K.B. are grateful to UK PPARC/STFC for financial support. We thank the unknown referee for the helpful comments.
References
- Amari, T., & Luciani, J. F. 2000, Phys., Rev. Lett., 84, 1196
- Arber, T. D., Longbottom, A. W., & Van der Linden, R. A. M. 1999, ApJ, 517, 990 [NASA ADS] [CrossRef]
- Arber, T. D., Longbottom, A. W., Gerrard, C. L., & Milne, A. M. 2001, J. Comp. Phys., 171, 151 [NASA ADS] [CrossRef]
- Baty, H. 2000a, A&A, 353, 1074 [NASA ADS]
- Baty, H. 2000b, A&A, 360, 345 [NASA ADS]
- Baty, H., & Heyvaerts, J. 1996, A&A, 308, 935 [NASA ADS]
- Brennan, D. P., Browning, P. K., Van der Linden, R. A. M., & Woodruff, S. 1999, Phys. Plas., 6, 4248 [NASA ADS] [CrossRef]
- Brennan, D. P., Browning, P. K., Gates, J., & Van der Linden, R. A. M. 2009, Plas. Phys. Cont. Fus., 51, 045004 [CrossRef]
- Browning, P. K., & Hood, A. W. 1989, Sol. Phys., 124, 271 [NASA ADS] [CrossRef]
- Browning, P. K., & Van der Linden, R. A. M. 2003, A&A, 400, 355 [NASA ADS] [CrossRef] [EDP Sciences]
- Browning, P. K., Hood, A. W., Gerrard, C., Kevis, R., & Van der Linden, R. A. M. 2008, A&A, 485, 837 [NASA ADS] [CrossRef] [EDP Sciences]
- Evans, C. R., & Hawley, J. F. 1988, ApJ, 332, 659 [NASA ADS] [CrossRef]
- Finn, J. M., & Antonsen, T. A. 1985, Commun. Plas. Phys. Cont. Fus., 9, 111
- Gerrard, C. L., & Hood, A. W. 2003, Sol. Phys. 214, 151
- Gerrard, C. L., Arber, T. D., & Hood, A. W. 2002, A&A, 387, 687 [NASA ADS] [CrossRef] [EDP Sciences]
- Grappin, R., Aulanier, G., & Pinto, R. 2008, A&A, 490, 353 [NASA ADS] [CrossRef] [EDP Sciences]
- Haynes, M., & Arber, T. D. 2007, A&A, 467, 327 [NASA ADS] [CrossRef] [EDP Sciences]
- Heyvaerts, J., & Priest, E. R. 1984, A&A, 137, 63 [NASA ADS]
- Hood, A. W., Van der Linden, R. A. M., & Goossens, M. 1989, Sol. Phys., 120, 261 [NASA ADS] [CrossRef]
- Huang, Y.-M., Zweibel, E. G., & Sovinec, C. R. 2006, Phys. Plas., 12, 092102 [NASA ADS] [CrossRef]
- Jarboe, T. 2005, Phys. Plas., 12, 058103 [NASA ADS] [CrossRef]
- Ji, H., Prager, S. C., & Serff, J. S. 1995, Phys. Rev. Lett., 74, 2945 [NASA ADS] [CrossRef]
- Lionello, R., Velli, M., Einaudi, G., & Mikic, Z. 1998, ApJ, 494, 840 [NASA ADS] [CrossRef]
- Lothian, R., & Hood, A. W. 1989, Sol. Phys., 122, 227 [NASA ADS] [CrossRef]
- Parker, E. N. 1972, ApJ, 174, 499 [NASA ADS] [CrossRef]
- Parker, E. N. 1988, ApJ, 330, 474 [NASA ADS] [CrossRef]
- Rappazzo, A. F., Velli, M., Einaudi, G., & Dahlburg, R.B. 2007, ApJ, 657, L47 [NASA ADS] [CrossRef]
- Rappazzo, A. F., Velli, M., Einaudi, G., & Dahlburg, R.B. 2008, ApJ, 677, 1348 [NASA ADS] [CrossRef]
- Sovinec, C. R., Finn, J. M., & del-Castello-Negrete, D. 2001, Phys. Plas., 8, 475 [NASA ADS] [CrossRef]
- Taylor, J. B. 1974, Phys. Rev. Lett., 33, 1139 [NASA ADS] [CrossRef]
- Taylor, J. B. 1986, Rev. Mod. Phys., 58, 741 [NASA ADS] [CrossRef]
- Van der Linden, R. A. M., & Hood, A. W. 1999, A&A, 346, 303 [NASA ADS]
- Van Leer, B. 1997 J. Comp. Phys., 135, 229
- Velli, M., Lionello, R., & Einaudi, G. 1997, Sol. Phys., 172, 257 [NASA ADS] [CrossRef]
- Willett, D. M., Browning, P. K., Woodruff, S., & Gibson, K. J. 1999, Plas. Phys. Cont. Fus., 41, 595 [CrossRef]
- Wilkins, M. L. 1980, J. Comp. Phys., 36, 281 [NASA ADS] [CrossRef]
All Tables
Table 1:
Predicted and numerical values of ![]() ,
,
![]() and
Bz(0,0,0) for the 3 cases.
and
Bz(0,0,0) for the 3 cases.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12285f1a.eps}\vspace*{2mm}
\includegraphics[width=8cm,clip]{12285f1b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg70.png) |
Figure 1: Top: the initial profiles of Bz(x,0,0) are shown as dashed curves and the final numerical simulation profiles are shown as solid curves. Bottom: the initial profiles of By(x,0,0) are shown as dashed curves and the final numerical simulation profiles are shown as solid curves. Case 1 has the initial profiles as black dashed curves, Case 2 as red dot-dashed curves and Case 3 as blue triple-dot dashed curves. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12285f2.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg83.png) |
Figure 2:
The |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12285f3a.ps}\vspace*{2mm}
\includegraphics[width=7cm,clip]{12285f3b.ps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg90.png) |
Figure 3: The linear eigenmode of the most unstable mode is in a) vx(x,0,0) and b) vx(0,0,z). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12285f4.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg91.png) |
Figure 4: Plot of -vx as a function of z along x=y=0 at time t=180. -vx is chosen in order to compare with Fig. 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12285f5.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg93.png) |
Figure 5: Plots of a) magnetic energy, b) kinetic energy, c) internal energy, d) maximum current as functions of time for Case 1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{12285f6a.eps}\par\includegraphics[width=7cm,clip]{12285f6b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg102.png) |
Figure 6: The kinetic energy versus time for a) Case 2 and b) Case3. Note the different scales on the axes. The final values of the kinetic energy are similar for Cases 2 and 3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{12285f7.ps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg106.png) |
Figure 7: The magnitude of the current as a function of x, at y=0 and z=0 is shown for t=105 (solid) and t=160 (triple dot dashed). The vertical dotted line indicates where the current sheet due to the kink instability first forms at x=-0.6. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12285f8a.eps}\includegraphics[width=8cm,clip]{12285f8b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg107.png) |
Figure 8: Case 3: contour plot of the current density, j, at z = 0 at time t=55 and 85. The arrows show the velocity components, vx and vy, scaled by a factor of 5. The length of the arrows are proportional to the magnitude of the horizontal velocity. a) Left is at t=55. b) Right is at t=85. The colour scale for the current density is from 0 (light purple) to 15 (red). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12285f9.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg108.png) |
Figure 9: Case 3: contour plot of the current density, j, at z = 0 at time t=150. The arrows show the velocity components, vx and vy. The colour scale for the current density is from 0 (blue) to 15 (red). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=14.3cm,clip]{1228510a.eps}\par\includegraphics[width=14.3cm,clip]{1228510b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg109.png) |
Figure 10: Case 3: the yellow fieldlines are drawn from z=-10, centred on x=0, y=0 while the blue fieldlines are drawn from z=10 again centred on x=0, y=0. The red isosurface is the magnitude of the current with a value of 4. a) Top left is at t=55. b) Top right is at t=85. c) Bottom left is at t=150 and d) Bottom right is the final time at t=295. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12285f11.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg112.png) |
Figure 11: Case 1: the temperature, T(x,0,0), as a function of x at y=0 and z = 0 at times t= a) 180, b) 200, c) 250 and d) 280. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1228512a.eps}\includegraphics[width=9cm,clip]{1228512b.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg113.png) |
Figure 12: Case 3: contourplot of the temperature at time t=55 ( left and 85 (right) in the mid-plane at z=0. The colour scale for the temperature is from 0 (blue) to 15 (red). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12285f13.eps}
\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg114.png) |
Figure 13: Case 3: contourplot of the temperature at time t=150 in the mid-plane at z=0. The colour scale for the temperature is from 0 (blue) to 15 (red). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=4cm,clip]{1228514a.eps}\includegraphic...
...e.eps}\includegraphics[width=4cm,clip]{1228514f.eps}\hspace*{4cm}}\end{figure}](/articles/aa/full_html/2009/41/aa12285-09/Timg122.png) |
Figure 14:
Case 3: isosurface of the temperature, T=0.01 (red), and T=0.02 (green) at times
t=85, 150, 295. The sizes of the boxes are
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.