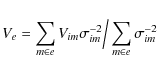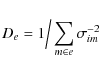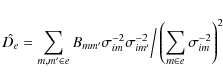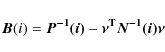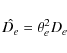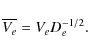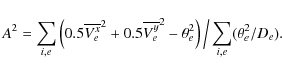| Issue |
A&A
Volume 505, Number 2, October II 2009
|
|
|---|---|---|
| Page(s) | 903 - 918 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200912026 | |
| Published online | 11 August 2009 | |
Precision multi-epoch astrometry with VLT cameras FORS1/2![[*]](/icons/foot_motif.png)
P. F. Lazorenko1
- M. Mayor2 - M. Dominik3,![]() - F. Pepe2 - D. Segransan2
- S. Udry2
- F. Pepe2 - D. Segransan2
- S. Udry2
1 - Main Astronomical Observatory,
National Academy of Sciences of the Ukraine,
Zabolotnogo 27, 03680 Kyiv-127, Ukraine
2 - Observatoire de Geneve, 51 Chemin des Maillettes,
1290 Sauverny, Switzerland
3 - SUPA, University of St Andrews, School of Physics &
Astronomy, North Haugh, St Andrews, KY16 9SS, UK
Received 10 March 2009 / Accepted 1 July 2009
Abstract
Aims. We investigate the astrometric performance of the FORS1 and FORS2 cameras of the VLT at long time scales with emphasis on systematic errors which normally prevent attaining a precision better than 1 mas.
Methods. The study is based on multi-epoch time series of observations of a single sky region imaged with a time spacing of 2-6 years at FORS1 and 1-5 months at FORS2. Images were processed with a technique that reduces atmospheric image motion, geometric distortions, and takes into account relative displacement of reference stars in time.
Results. We performed a detailed analysis of a random error of positions that was shown to be dominated by the uncertainty of the star photocenter determination. The component of the random error corresponding to image motion was found to be caused primarily by optical aberrations and variations of atmospheric PSF size but not by the effect of atmospheric image motion. Comparison of observed and model annual/monthly epoch average positions yielded estimates of systematic errors for which temporal properties and distribution in the CCD plane are given. At frame center, the systematic component is about 25 ![]() as. Systematic errors are shown to be caused mainly by a combined effect of the image asymmetry and seeing variations which therefore should be strongly limited to avoid generating random and systematic errors. For a series of 30 images, we demonstrated presicion of about 50
as. Systematic errors are shown to be caused mainly by a combined effect of the image asymmetry and seeing variations which therefore should be strongly limited to avoid generating random and systematic errors. For a series of 30 images, we demonstrated presicion of about 50 ![]() as stable on daily, monthly, and annual time scales. Small systematic errors and a Gaussian distribution of positional residuals at any time scale indicate that the astrometric accuracy of the VLT is comparable to the precision. Relative proper motion and trigonometric parallaxes of stars in the center of the test field were derived with a precision of 20
as stable on daily, monthly, and annual time scales. Small systematic errors and a Gaussian distribution of positional residuals at any time scale indicate that the astrometric accuracy of the VLT is comparable to the precision. Relative proper motion and trigonometric parallaxes of stars in the center of the test field were derived with a precision of 20 ![]() as yr-1 and 40
as yr-1 and 40 ![]() as for 17-19 mag stars. Therefore, distances at 1 kpc could be determinable at a 4% precision if suitably distant reference objects are in the field.
as for 17-19 mag stars. Therefore, distances at 1 kpc could be determinable at a 4% precision if suitably distant reference objects are in the field.
Conclusions. We prove that the VLT with FORS1/2 cameras are not subject to significant systematic errors at time scales from a few hours to a few years providing that observations are obtained in narrow seeing limits. The astrometric performance of the VLT imaging cameras meets requirements necessary for many astrophysical applications, in particular, exoplanet studies and determination of relative trigonometric distances by ensuring a high accuracy of observations, at least 50 ![]() as attained for image series of 0.5 hour.
as attained for image series of 0.5 hour.
Key words: astrometry - atmospheric effects - instrumentation: high angular resolution - planetary systems
1 Introduction
The availability of astrometric measurements of proper motion and parallactic displacements at 10-100 microarsec precision provide a base for many astrophysical applications, e.g. determination of the distances to stars and their absolute luminosity, detection of planets, microlensing studies of the mass distribution in the Galaxy, dynamics of the Galaxy Center stars, etc.The above studies imply use of very high precision astrometry, requiring both reduction methods that are fairly insensitive to major noise sources as well as telescopes fulfilling the precision requirements and temporal stability. The availability of suitable instruments however hardly matches current demand, and is in large disproportion to envisioned future endeavors. In particular, this hinders programmes studying exoplanet populations by means of astrometry, which would powerfully extend and complement efforts based on other techniques and provide an efficient pathway towards identifying habitable planets.
The best future prospects for high-precision astrometry can be expected
from space telescopes, but the only mission currently planned
is GAIA (Perryman et al. 2001).
Achieving a single-measurement
precision below 10 ![]() as on V < 13 stars, it will offer the
opportunity to discover and study several thousands of planets
(Casertano et al. 2008).
However, GAIA operates as an all-sky
survey and cannot be pointed to a specific target, and its accuracy
degrades rapidly towards fainter stars
(Lindegren et al. 2007).
as on V < 13 stars, it will offer the
opportunity to discover and study several thousands of planets
(Casertano et al. 2008).
However, GAIA operates as an all-sky
survey and cannot be pointed to a specific target, and its accuracy
degrades rapidly towards fainter stars
(Lindegren et al. 2007).
In contrast, pointing to selected targets is possible with ground-based
telescopes, effectively measuring distances in binary star systems by
means of optical interferometry. These achieve accuracies of the order of
those of GAIA at V > 15. VLTI/PRIMA is able to measure distances
between stars separated by 10
![]() with 10
with 10 ![]() as precision
(Delplancke et al. 2000)
with a 30 min integration time; at a similar
20
as precision
(Delplancke et al. 2000)
with a 30 min integration time; at a similar
20 ![]() as h-1
precision, star separations can be measured with the Keck
Interferometer (Boden et al. 1999).
Moreover, at 30
as h-1
precision, star separations can be measured with the Keck
Interferometer (Boden et al. 1999).
Moreover, at 30
![]() separation in pairs
of bright stars, an astrometric precision of 100
separation in pairs
of bright stars, an astrometric precision of 100 ![]() as has been
achieved by Lane et al. (2000)
with the Palomar Testbed Interferometer
(PTI), and Lane & Muterspagh (2004) and
Muterspagh et al. (2006)
reported an accuracy of 20
as has been
achieved by Lane et al. (2000)
with the Palomar Testbed Interferometer
(PTI), and Lane & Muterspagh (2004) and
Muterspagh et al. (2006)
reported an accuracy of 20 ![]() as stable over a few nights.
The availability of and access to ground-based high-precision astrometry
facilities is however extremely limited, so that no exoplanet detection
programme has yet been established.
as stable over a few nights.
The availability of and access to ground-based high-precision astrometry
facilities is however extremely limited, so that no exoplanet detection
programme has yet been established.
Large ground-based monopupil telescopes
that operates in imaging mode also can significantly contribute
to the detection and measurement planetary systems. Unlike
infrared interferometers, these telescopes
measure the position of a target either with reference to a single
star or to a grid of reference stars.
For a long time, however, astrometric measurements with ground-based
imaging telescopes were believed to be
limited by about 1 mas precision due to atmospheric image motion
(Lindegren 1980).
This limitation, however, is not fundamental and rather reflects the performance
of the conventional astrometric technique.
The first high precision observations well below 1 mas were obtained by
Pravdo & Shaklan (1996) at the Hale telescope with a D=5 m aperture.
In the field of 90
![]() ,
they demonstrated precision
of 150
,
they demonstrated precision
of 150 ![]() as h-1.
This precision was further improved by Cameron et al. (2008)
with the use of adaptive optics.
They reached a precision of 100
as h-1.
This precision was further improved by Cameron et al. (2008)
with the use of adaptive optics.
They reached a precision of 100 ![]() as with a 2 min exposure
and showed it to be stable over 2 months.
as with a 2 min exposure
and showed it to be stable over 2 months.
A detailed analysis of the process of differential measurements
affected by image motion allowed Lazorenko & Lazorenko (2004)
to show that the excellent results obtained by
Pravdo & Shaklan (1996)
represent the actual astrometric performance of large telescopes.
It was shown that angular observations
with very large monopupil telescopes are not atmosphere limited
due to effective averaging of phase distortions over the aperture.
For observations in very narrow fields, atmospheric image motion
decreases as D-3/2 (Lazorenko 2002) reaching below
other error components.
Also, the image motion spectrum can be further filtered
in the process of the reduction by using reference field stars
as a specific filter.
Astrometric precision greatly benefits from the use of large
![]() m apertures.
m apertures.
Besides atmospheric image motion, one can list a number of other
systematic and random error sources that could
prevent us to reach a ![]() as level of the precision.
Many sources of error depend on the telescope
and cause long-term astrometric instability of results.
To ascertain the practical feasibility of this new astrometric method, we
have chosen the high performance FORS1/2 cameras
set at the VLT with excellent seeing.
We have undertaken several
tests of various time scales, ranging from a few hours to
several years.
as level of the precision.
Many sources of error depend on the telescope
and cause long-term astrometric instability of results.
To ascertain the practical feasibility of this new astrometric method, we
have chosen the high performance FORS1/2 cameras
set at the VLT with excellent seeing.
We have undertaken several
tests of various time scales, ranging from a few hours to
several years.
The first test (Lazorenko 2006) was based on
a single four-hour series of
FORS2 images in Galactic Bulge obtained by Moutou et al. (2003).
It proved the validity of the basic concept of the new astrometric
method and an astrometric precision of 300 ![]() as
with a 17 s exposure was reached.
as
with a 17 s exposure was reached.
In the second test (Lazorenko et al. 2007),
we investigated the astrometric precision of the FORS1
camera over time scales of a few days. For this study
we used the two-epoch (2000 and 2002) image series
(Motch et al. 2003),
each epoch represented by four consecutive nights. We reached
a positional precision of
![]()
![]() as
and detected no instrumental systematic errors above 30
as
and detected no instrumental systematic errors above 30 ![]() as
at the time scales considered. The precision of a
series of n images was shown to improve as
as
at the time scales considered. The precision of a
series of n images was shown to improve as
![]() at least to n = 30,
which corresponds to a 40-50
at least to n = 30,
which corresponds to a 40-50 ![]() as astrometric precision.
as astrometric precision.
This paper concludes our study of the VLT camera astrometric performance and extends our previous short time scale results to intervals of 1-5 months and 2-6 years. This covers all time scales required for typical microlensing, exoplanet search applications, and Galaxy kinematics studies. In Sect. 2 we outline the strategy of this study, observations, and the computation of the star image photocenters. Astrometric reduction based on the reduction model (Sect. 3) is described in Sect. 4. The random errors of single measurements are analyzed in Sect. 5, where we extract the image motion component, which proved to be of instrumental origin. Systematic errors in epoch monthly/annual average positions, and their spatial and temporal properties are considered in Sect. 6. Astrometric precision in terms of the Allan deviation is discussed in Sect. 7.
2 Observation strategy and computation of photocenters
As a test star field, the best choice is the field
near the neutron star RX J0720.4-3125 whose FORS1/UT1 images
of
![]() angular size obtained
in Dec. 2000 and Dec. 2002 by Motch et al. (2003)
were already used in our previous study (Lazorenko et al. 2007).
Its uniqueness is that it has the best history of observations
available in the ESO/ST ECF Archives
suitable for precision astrometry.
Data are represented by 65 images obtained with the B filter and
obtained with a 2 year epoch difference,
which allows for a reduction with no bias due to
parallax. Also, the field is densely populated,
containing about 200 stars with a high light signal.
We repeatedly observed it in Dec 2006,
at integer differences of years, with FORS1/UT2 (1 px =0.10
angular size obtained
in Dec. 2000 and Dec. 2002 by Motch et al. (2003)
were already used in our previous study (Lazorenko et al. 2007).
Its uniqueness is that it has the best history of observations
available in the ESO/ST ECF Archives
suitable for precision astrometry.
Data are represented by 65 images obtained with the B filter and
obtained with a 2 year epoch difference,
which allows for a reduction with no bias due to
parallax. Also, the field is densely populated,
containing about 200 stars with a high light signal.
We repeatedly observed it in Dec 2006,
at integer differences of years, with FORS1/UT2 (1 px =0.10
![]() scale) and
the same B filter, thus
comparing model predicted and observed positions
at three annual epochs, verifying
the very long-term astrometric stability of the VLT at 2-6 years,
and computing relative proper motions used later on
for the reduction of FORS2 data.
Observations were performed with the LADC optical system
(Avila et al. 1997) that improves image quality by compensating
for the differential chromatic refraction (DCR) of the atmosphere.
scale) and
the same B filter, thus
comparing model predicted and observed positions
at three annual epochs, verifying
the very long-term astrometric stability of the VLT at 2-6 years,
and computing relative proper motions used later on
for the reduction of FORS2 data.
Observations were performed with the LADC optical system
(Avila et al. 1997) that improves image quality by compensating
for the differential chromatic refraction (DCR) of the atmosphere.
The same test star field was imaged five times at FORS2
(1 px =0.126
![]() scale)
with the
scale)
with the
![]() filter with a
T=70 s exposure to keep star fluxes at
approximately the same level as in the FORS1 images.
A one month spacing between time series was chosen to match
the typical sampling for the observation of
astrometric microlensing or of the astrometric shift of stars caused by an
orbiting planet.
The availability of FORS1 images gives us an opportunity to correct
the measured FORS2 positions for highly accurate
relative
proper motions determined at six year time intervals.
This correction is critically important since elimination of proper
motion from FORS2 positions
decreases the number of model parameters, thus greatly improving
the reliability of the subsequent statistical analysis.
After elimination of proper motion obtained as shown,
the positions of 5 series are reduced to a common standard frame
with a model that fits star motion by parallax.
Residuals of star positions (measured minus model)
are then analyzed to detect systematic errors
and any correlations with time or magnitude.
A summary of observation data is given in Table 1.
Note the large variations of seeing which does
not favor high precision astrometry (Sect. 6).
filter with a
T=70 s exposure to keep star fluxes at
approximately the same level as in the FORS1 images.
A one month spacing between time series was chosen to match
the typical sampling for the observation of
astrometric microlensing or of the astrometric shift of stars caused by an
orbiting planet.
The availability of FORS1 images gives us an opportunity to correct
the measured FORS2 positions for highly accurate
relative
proper motions determined at six year time intervals.
This correction is critically important since elimination of proper
motion from FORS2 positions
decreases the number of model parameters, thus greatly improving
the reliability of the subsequent statistical analysis.
After elimination of proper motion obtained as shown,
the positions of 5 series are reduced to a common standard frame
with a model that fits star motion by parallax.
Residuals of star positions (measured minus model)
are then analyzed to detect systematic errors
and any correlations with time or magnitude.
A summary of observation data is given in Table 1.
Note the large variations of seeing which does
not favor high precision astrometry (Sect. 6).
The primary goal of this study is the investigation of random and systematic
positional errors of the FORS cameras. This task
requires a careful reduction of observations, including determination
of proper motion and parallaxes with the combined use of images
obtained with two cameras. We aim to demonstrate that a 300 ![]() as single
measurement precision of narrow-field astrometry translates to about 50
as single
measurement precision of narrow-field astrometry translates to about 50 ![]() as
precision for a series of 30 measurements.
as
precision for a series of 30 measurements.
Table 1: Summary of the test field observations.
Raw images were calibrated (debiased and flat-fielded) using
calibration master files. Star images having even
a single saturated pixel were marked and rejected
for a loss, even small, of positional information.
Positions of star photocenters X,Y were computed
with the profile fitting technique based on the 12-parameter model
specific for the VLT images (Lazorenko 2006).
By careful examination, we developed a three component model
that fits observed profiles to the photon noise limit.
The dominant model component that approximates the core of the
PSF (point spread function) is a relatively compact
Gaussian with width parameters
![]() ,
,
![]() along x,y axes and
a flux
along x,y axes and
a flux ![]() containing 2/3 of the
total star flux I. Two auxiliary
Gaussians, each one multiplied by a
factor x2 or y2, are
co-centered at the dominant component and approximate
wings of the PSF. The model also takes into account the high-frequency oscillating
feature of the PSF, computing it as a systematic discrepancy
between the model and observed star profiles.
Deviations
between the model and observed pixel counts were found
to be at the
containing 2/3 of the
total star flux I. Two auxiliary
Gaussians, each one multiplied by a
factor x2 or y2, are
co-centered at the dominant component and approximate
wings of the PSF. The model also takes into account the high-frequency oscillating
feature of the PSF, computing it as a systematic discrepancy
between the model and observed star profiles.
Deviations
between the model and observed pixel counts were found
to be at the
![]() level.
Determination of star photocenters is a very
important element of the process because, as we show later on,
most of the random and systematic errors occur at this phase.
level.
Determination of star photocenters is a very
important element of the process because, as we show later on,
most of the random and systematic errors occur at this phase.
The precision
![]() of the star photocenter was
estimated by numerical simulation of random images
yielding an expression
similar to that derived by Irwin (1985)
for a single Gaussian profile
of the star photocenter was
estimated by numerical simulation of random images
yielding an expression
similar to that derived by Irwin (1985)
for a single Gaussian profile
This equation is valid in a much wider range of fluxes, seeing, and background signal
Computed model parameters were analyzed to detect and reject
non-standardly shaped images indicating computation errors and
actual image defects caused by blending, cosmic rays, etc.
All images with model parameters and ![]() exceeding some deliberately set
thresholds were discarded. Thresholds were
chosen so that the frequency of rejections
was about 1% for bright images.
At this fixed threshold, the number of rejections
gradually increased with magnitude,
reaching 10-25% for faint images,
which are more sensitive to the background irregularities.
In contrast, filtration based on
exceeding some deliberately set
thresholds were discarded. Thresholds were
chosen so that the frequency of rejections
was about 1% for bright images.
At this fixed threshold, the number of rejections
gradually increased with magnitude,
reaching 10-25% for faint images,
which are more sensitive to the background irregularities.
In contrast, filtration based on ![]() caused excessive rejection
of the brightest images, since the accuracy of the model profile
is insufficient at high light signals and becomes
comparable to the statistical fluctuations of counts.
This gives rise to a
caused excessive rejection
of the brightest images, since the accuracy of the model profile
is insufficient at high light signals and becomes
comparable to the statistical fluctuations of counts.
This gives rise to a ![]() with subsequent false rejection of measurements.
with subsequent false rejection of measurements.
| |
Figure 1:
Ratio
|
| Open with DEXTER | |
Most often, discarded faint star images have excessive size.
This produced a selective effect seen as
a systematic dependence
of image parameters on flux I.
A difference between the mean image size parameter
![]() in the filted star sample and
its mean value
in the filted star sample and
its mean value
![]() in the initial star sample is typical.
The systematic dependence of the
ratio
in the initial star sample is typical.
The systematic dependence of the
ratio
![]() on flux is shown in Fig. 1.
While no difference is seen for bright images, at the faint end
the size
on flux is shown in Fig. 1.
While no difference is seen for bright images, at the faint end
the size
![]() of stars selected for further processing is
systematically 10-30% smaller.
For FORS1 images the effect is stronger due to the larger pixel
scale (lower signal to noise ratio) and many cosmic rays occured over the long
integration time.
The selection described here induces a similar
dependence of the centroiding error on flux (Sect. 5).
of stars selected for further processing is
systematically 10-30% smaller.
For FORS1 images the effect is stronger due to the larger pixel
scale (lower signal to noise ratio) and many cosmic rays occured over the long
integration time.
The selection described here induces a similar
dependence of the centroiding error on flux (Sect. 5).
Further astrometric reduction revealed that some stars show a significant correlation between model minus observed residuals of positions and variations of seeing. This effect, detected primarily for relatively close star pairs, is due to the asymmetry of images caused by the light from the nearby star (see Sect. 6). About 1% of measurements subject to this effect were rejected.
3 Astrometric reduction model
![]() is a sample of
is a sample of
![]() stars
imaged
stars
imaged
![]() fold
in the sky area of angular radius Rcentered on a target star which we denote with a subscript
i=0.
In general,
fold
in the sky area of angular radius Rcentered on a target star which we denote with a subscript
i=0.
In general, ![]() may represent only a portion of the
complete sample of
stars
may represent only a portion of the
complete sample of
stars ![]() seen in the telescope FoV.
Given the measured star centroids Xim, Yim,
we derive, on each CCD image, the differential position of the target,
its
relative parallax, proper motion, and deviations Vim from
the model that may hide the astrometric signal (e.g. planetary
signature).
These quantities are not measured directly and are rather estimates of
model parameters found in a certain reference system set by
the reduction model; therefore, they depend on it.
The image m=0 sets the zero-point
of positions, a grid of reference stars in this image defines
the reference frame. For processing therefore we use relative CCD
positions
xim=Xim-Xi0,
yim=Yim-Yi0.
seen in the telescope FoV.
Given the measured star centroids Xim, Yim,
we derive, on each CCD image, the differential position of the target,
its
relative parallax, proper motion, and deviations Vim from
the model that may hide the astrometric signal (e.g. planetary
signature).
These quantities are not measured directly and are rather estimates of
model parameters found in a certain reference system set by
the reduction model; therefore, they depend on it.
The image m=0 sets the zero-point
of positions, a grid of reference stars in this image defines
the reference frame. For processing therefore we use relative CCD
positions
xim=Xim-Xi0,
yim=Yim-Yi0.
The certain difficulty for astrometric processing is brought by the instability of the reference frame in time due to the atmospheric differential chromatism (e.g. Monet et al. 1992; Pravdo & Shaklan 1996; Lazorenko 2006; Lazorenko et al. 2007), variable geometric distortion, proper motions, etc. In our previous study (Lazorenko et al. 2007), we developed a model that correctly handles this problem and ensures a solution in a uniform system with no distinction between target and reference stars. Here we propose a more general solution that allows an easy readjustment of the system of model parameters and of deviations Vim in a way that is optimal for a particular study. The model deals with atmospheric image motion (Sect. 3.1), geometric distortions (Sect. 3.2), and instability of the reference frame in time (Sect. 3.3). We emphasize that all the data derived from the differential reduction (proper motions, parallaxes, chromatic parameters, etc.) are intrinsically relative (not absolute). This point is discussed in detail in Sect. 3.5.
3.1 Atmospheric image motion
The variance of the atmospheric image motion in positions measured in narrow fields is given by Lindegren's (1980) expressionwhere h is the altitude of the atmospheric turbulent layer generating the image motion and R is a star configuration angular size. For a binary star, R is the star separation. Equation (2) refers to the very narrow angle observations defined by condition
otherwise we have the much worse
We have shown (Lazorenko 2002; Lazorenko & Lazorenko 2004) that
- any arbitrary discrete reference star distribution, of at least three stars, can be symmetrized;
- symmetrization is always implemented by a standard plate reduction with a linear or more complex model;
-
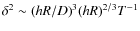 ,
which suggests faster improvement of
,
which suggests faster improvement of  with D in comparison to Lindegren's
prediction for symmetric continuous distributions;
with D in comparison to Lindegren's
prediction for symmetric continuous distributions;
- use of a large
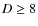 m is required to meet condition (3)
for high stratospheric layers.
m is required to meet condition (3)
for high stratospheric layers.
that inherits the initial modal structure of G(q), and H2s are modal coefficients. Of course, the actual value of
For optical interferometers, the atmospheric noise
decreases as d-2/3 (Shao & Colavita 1992) and
phase fluctuations are mitigated by probing the difference of phase
at ends of the instrument long baseline d. For monopupil telescopes,
a fast decrease of image motion occurs in another way, by
averaging the turbulent phase fluctuations over the aperture.
The efficiency of phase averaging depends on
the symmetry of the star configuration, which requires availability
of the grid of reference stars. We emphasize that, unlike
optical interferometers, monopupil telescopes are not adapted for
precision measurement of the angular offset between a pair of stars
due to the intrinsic
asymmetry of this star configuration, for which ![]() follows
dependence (2).
follows
dependence (2).
From Eq. (4) it follows that
![]() can be reduced by removing (filtering)
the several first most significant modes
can be reduced by removing (filtering)
the several first most significant modes
![]() up to some
optional k/2 spectral mode.
The residual variance
up to some
optional k/2 spectral mode.
The residual variance
![]() obtained in this way
depends on the first high k=2s (k is even integer) active mode
of the image motion spectrum and is therefore of a comparatively small magnitude.
For the VLT, the gain in
obtained in this way
depends on the first high k=2s (k is even integer) active mode
of the image motion spectrum and is therefore of a comparatively small magnitude.
For the VLT, the gain in ![]() is a factor of 100 and
more. The above possibility follows from the next considerations:
the relative position of the target in image m along the x axis
(here and farther on we omit similar expressions for y)
is defined by the quantity
is a factor of 100 and
more. The above possibility follows from the next considerations:
the relative position of the target in image m along the x axis
(here and farther on we omit similar expressions for y)
is defined by the quantity
where prime indicates that index i=0 is omitted. Coefficients a0i meet the normalizing condition
for each
Equations (6). Solution of this redundant system (because usually N>N') is found with a supplementary condition
set on the variance
is valid where I' is the light flux per unit area coming from bright reference stars.
Thus, the quantity V defined by (5) is free from the first
modes of the image motion spectrum untill k/2 providing that
a0i confirm to Eqs. (6), (8).
The variance of V is
Because
which is reached at some optimal size
3.2 Single plate reduction
A standard plate reduction produces effects equivalent to symmetrization
of the reference frame
(Lazorenko & Lazorenko 2004).
Really, the basic equation of the plate model, in vector representation,
is
where
considering that
Residuals of the least square fit is the vector
with the property
The covariance matrix of
defines the variance of reference frame component
The last term is the noise from the reference frame and is a composition of two components, noise from the star i itself with the variance
Equations (15), (14) of the plate model correspond to Eqs. (5), (6) of the image motion filtration and (8) is the least square condition. Therefore both methods are equivalent. However, we imply that the model (12) should include a sequence of all basic functions fw with no omission and at least k=4 (linear plate solution) or above is chosen. The use of higher-order models results in better filtration of image motion, though, as follows from Eq. (9), it increases
3.3 Multi-plate reduction
A single plate model (12) is easily extended to the case of
multiple
![]() images. For this purpose we
specify, for any star i,
a set of
images. For this purpose we
specify, for any star i,
a set of
![]() model parameters
model parameters ![]() which are
zero-points,
relative proper motion
which are
zero-points,
relative proper motion ![]() and
and ![]() ,
relative parallax
,
relative parallax ![]() ,
etc. Thus the position xim of any star i in image m is modelled by
,
etc. Thus the position xim of any star i in image m is modelled by
![]() where
where ![]() are functions of time (of image number) coupled to
are functions of time (of image number) coupled to ![]() and cwm are model
parameters cw in image m. Using matrices similar to
the above quantities, we reach
and cwm are model
parameters cw in image m. Using matrices similar to
the above quantities, we reach
in a concatenated space formed by two types of basic functions, f and
Equation (20) is a set of
![]() equations solvable by the
least square fit with respect to
equations solvable by the
least square fit with respect to
![]() parameters cwm and
parameters cwm and
![]() parameters
parameters ![]() .
Also, for each image m, we introduce
an
.
Also, for each image m, we introduce
an
![]() weight matrix
weight matrix
![]() with elements
with elements
![]() used for the reduction in x, y space and treated like
the matrix
used for the reduction in x, y space and treated like
the matrix ![]() of Sect. 3.2.
Another
of Sect. 3.2.
Another
![]() diagonal matrix
diagonal matrix
![]() related to
a star i takes into account the change in time of the
residuals
related to
a star i takes into account the change in time of the
residuals
![]() .
Diagonal elements
of
.
Diagonal elements
of
![]() are equal to
are equal to
![]() defined by Eqs. (10) or (19) depending on the star type.
When star i measurements are
unavailable at image m, the corresponding elements of matrices
defined by Eqs. (10) or (19) depending on the star type.
When star i measurements are
unavailable at image m, the corresponding elements of matrices
![]() and
and
![]() are put to zero.
are put to zero.
Direct solution of system (20) is, however,
impossible due to the ambiguity between
![]() and
and ![]() .
If some component s of parameters
.
If some component s of parameters ![]() (for example, proper
motion) systematically changes across the CCD, this change can be
fitted by a polynomial and thus is not resolvable from a change in cwm.
And vice versa,
a change in time of some component w of cwm produces an effect
that is similar to a change in
(for example, proper
motion) systematically changes across the CCD, this change can be
fitted by a polynomial and thus is not resolvable from a change in cwm.
And vice versa,
a change in time of some component w of cwm produces an effect
that is similar to a change in ![]() .
Therefore
Eq. (20) is solved under
.
Therefore
Eq. (20) is solved under
![]() conditions
conditions
where
solved iteratively using reference stars only with no contribution from the target due to zero weights P0m and
A simple, non-iterative
solution of Eq. (22) exists, requiring only
that each star measurement is available at each image,
at constant flux and seeing conditions.
In this case
![]() and therefore
and therefore
![]() and
and
![]() providing that
providing that
![]() is set.
is set.
Given solution ![]() and
and
![]() ,
we derive residuals
,
we derive residuals
which are orthogonal to the basic vectors
Putting solution
3.4 Reference frame quality
In very dense reference frames, astrometric precision is limited only by errors of the photocenter determination if image motion is well reduced. For sparsely populated reference frames, the noisewhich depends on the star location in the frame, its brightness, and in extreme cases of
where for simplicity we assumed
| |
Figure 2:
Characteristics of reference frame:
error
|
| Open with DEXTER | |
Figure 2 shows distribution of ![]() as a function
of magnitude for each star processed as a target.
The dependence has a specific decline at the bright end, to
as a function
of magnitude for each star processed as a target.
The dependence has a specific decline at the bright end, to
![]() .
For bright targets
.
For bright targets
![]() even at field center
due to the limited number of reference stars.
It follows that for small
even at field center
due to the limited number of reference stars.
It follows that for small ![]() ,
the resulting variance
,
the resulting variance
![]() significantly exceeds the
centroiding error
significantly exceeds the
centroiding error
![]() since
since
![]() .
In this respect,
.
In this respect, ![]() is a factor that
specifies the quality of the reference frame.
is a factor that
specifies the quality of the reference frame.
3.5 System of output data
Due to the differential reduction, the computed parameters
![]() and positional residuals V are relative.
Weights
and positional residuals V are relative.
Weights
![]() define
the system of parameters
define
the system of parameters ![]() of both target and reference stars.
It follows from Eq. (21) which
allows interpretation of
of both target and reference stars.
It follows from Eq. (21) which
allows interpretation of
![]() as the residual of the least square fit of some
absolute parameters
as the residual of the least square fit of some
absolute parameters
![]() by basic functions f.
Therefore what we measure are not
by basic functions f.
Therefore what we measure are not
![]() but
relative values
but
relative values
where
Noting the similar structure of Eqs. (21) and (24)
(the first equation),
we can apply the above considerations to
the system of residuals V and find that it is
defined by weights Pim.
Residuals V are related to some ``absolute'' residuals
![]() by
the expression of (28) as
by
the expression of (28) as
There is however an essential difference in treating Eqs. (28) and (29). The variance of
System weights Pim and
![]() essentially affect
output residuals V and model parameters
essentially affect
output residuals V and model parameters ![]() ,
which is better
analyzed
from the point of view of signal detection.
,
which is better
analyzed
from the point of view of signal detection.
![]() is a signal in x that generates some response z' in V.
With regard to the target,
the amplitude of z', according to Eq. (15), is
is a signal in x that generates some response z' in V.
With regard to the target,
the amplitude of z', according to Eq. (15), is
![]() since ai0=0. With Eq. (27) defining
the variance of V0, we find that
the signal-to-noise ratio
since ai0=0. With Eq. (27) defining
the variance of V0, we find that
the signal-to-noise ratio
![]() is
is
![]() .
Thus, while the measured
signal z in V0 is independent of properties of the reference field,
the signal-to-noise degrades at low
.
Thus, while the measured
signal z in V0 is independent of properties of the reference field,
the signal-to-noise degrades at low ![]() ,
primarily
for bright targets. Now consider the reference star i. In
this case
,
primarily
for bright targets. Now consider the reference star i. In
this case
![]() according to Eq. (15).
From Eq. (18) and the definition of
according to Eq. (15).
From Eq. (18) and the definition of ![]() we find
we find
![]() hence
hence
![]() and
and
![]() .
We conclude that the signal-to-noise ratio is equal for either type of stars,
but the best 100% response z' in V is detected for targets. For reference
stars, the signal decreases as
.
We conclude that the signal-to-noise ratio is equal for either type of stars,
but the best 100% response z' in V is detected for targets. For reference
stars, the signal decreases as ![]()
![]() ,
especially significant for bright
stars.
,
especially significant for bright
stars.
For some specific studies dealing with a full sample of stars
(kinematics of open cluster members),
uniformity of the system of output model parameters
![]() is much desired.
In this case, the best way is to process
all stars as reference objects (
is much desired.
In this case, the best way is to process
all stars as reference objects (
![]() ,
,
![]() ).
The model solution
).
The model solution
![]() is then related to
is then related to
![]() via Eq. (28). With respect to proper motions, this transformation is
via Eq. (28). With respect to proper motions, this transformation is
![]() where
where
![]() corresponds to the system of weights
corresponds to the system of weights
![]() .
.
Untill now we have discussed reduction with reference to a star grid
within a single isolated circular area
![]() disregarding other stars in the FoV.
In our previous study
(Lazorenko et al. 2007), we considered
reduction with multiple overlapping
reference subframes
disregarding other stars in the FoV.
In our previous study
(Lazorenko et al. 2007), we considered
reduction with multiple overlapping
reference subframes
![]() each centered at each i star seen in the FoV.
In this approach, the star i is processed, at first, as a target (Pi=0)
measured with reference to its own local subframe
each centered at each i star seen in the FoV.
In this approach, the star i is processed, at first, as a target (Pi=0)
measured with reference to its own local subframe
![]() .
At the same time, this star is
a reference object (
.
At the same time, this star is
a reference object (
![]() )
for adjacent subframes.
The solution initially related to local frames
)
for adjacent subframes.
The solution initially related to local frames
![]() is iteratively expanded to a reference grid
is iteratively expanded to a reference grid ![]() (all FoV)
and a single common system
by applying a set of interlinking Eqs. (21).
It can be shown that the final solution in
(all FoV)
and a single common system
by applying a set of interlinking Eqs. (21).
It can be shown that the final solution in ![]() does not
depend on the size of the initial frames
does not
depend on the size of the initial frames
![]() .
Residuals V of this solution in each
image m meet conditions
.
Residuals V of this solution in each
image m meet conditions
![]() .
These conditions correspond to Eq. (24) for reference stars
in
.
These conditions correspond to Eq. (24) for reference stars
in ![]() providing that
providing that
![]() .
Therefore a solution with
overlapping reference subframes is equivalent to that
in a single isolated area
.
Therefore a solution with
overlapping reference subframes is equivalent to that
in a single isolated area
![]() ,
or to a standard solution performed with all stars used as reference only.
Consequently,
no improvement in the signal to noise ratio is expected.
This version of the reduction is useful for
a low number of model parameters (vector
,
or to a standard solution performed with all stars used as reference only.
Consequently,
no improvement in the signal to noise ratio is expected.
This version of the reduction is useful for
a low number of model parameters (vector ![]() is not used
in the model), high uniformity of model parameters and residuals V,
and a fast convergence of iterations. However, assumption
is not used
in the model), high uniformity of model parameters and residuals V,
and a fast convergence of iterations. However, assumption
![]() used here means that Pim is constant in time,
which is not always acceptable.
used here means that Pim is constant in time,
which is not always acceptable.
For this study, we used standard reduction
(Sect. 3.3) computing the target position with weights
P0=0,
![]() to ensure the best response
to systematic errors in V.
to ensure the best response
to systematic errors in V.
Table 2: Minimum and optimal radii of reference fields.
4 Astrometric data reduction
4.1 Reduction of FORS1 images
One of the FORS1 sky images
obtained in Dec. 2000 at a seeing near its mean level was used as a reference.
Photocenters were computed for 180 stars of B=18-24 mag
in the central area.
Reductions were performed with a standard model (Sect. 3.3) that
yields residuals V and model parameters ![]() of a target star i relative to
the local grid of reference stars
of a target star i relative to
the local grid of reference stars
![]() .
Due to the extremely small value of systematic errors, we tried
to improve the statistics by accumulating data over all
stars available.
Therefore, reductions were repeated 180 times, processing each star iin turn, as a target (which till now was denoted by a subscript i=0).
For that reason, the astrometric precision varied depending on
the distance r of the star i from the frame center.
For the brightest stars, this occurred due to
.
Due to the extremely small value of systematic errors, we tried
to improve the statistics by accumulating data over all
stars available.
Therefore, reductions were repeated 180 times, processing each star iin turn, as a target (which till now was denoted by a subscript i=0).
For that reason, the astrometric precision varied depending on
the distance r of the star i from the frame center.
For the brightest stars, this occurred due to
![]() decreasing from
decreasing from
![]() at the frame center to 0.2 at the periphery
(Fig. 2) with a corresponding error increase by 25-50%.
Computations were carried out with all k
from 6 to 16 and all R from some
at the frame center to 0.2 at the periphery
(Fig. 2) with a corresponding error increase by 25-50%.
Computations were carried out with all k
from 6 to 16 and all R from some
![]() (Table 2) that
provides the minimum number of
reference stars needed at a given k, to the maximum
(Table 2) that
provides the minimum number of
reference stars needed at a given k, to the maximum
![]()
![]() .
The first run was performed with zero image motion and afterwards
computations were repeated with the actual estimate of
.
The first run was performed with zero image motion and afterwards
computations were repeated with the actual estimate of ![]() (Sect. 5).
(Sect. 5).
We assumed a 10-parameter model for ![]() with zero-points, proper motions
with zero-points, proper motions
![]() ,
,
![]() ,
atmospheric differential chromatic parameter
,
atmospheric differential chromatic parameter ![]() ,
the LADC compensating displacement
,
the LADC compensating displacement ![]() ,
and with no parallax
for integer year differences between epochs.
Four extra gxx, gxy, gyx, and gyy model terms
for each star were applied to compensate
for a strong, over
,
and with no parallax
for integer year differences between epochs.
Four extra gxx, gxy, gyx, and gyy model terms
for each star were applied to compensate
for a strong, over ![]() 200 px jittering of images.
Jittering induced a large signal in
V, clearly correlated with telescope
displacement
200 px jittering of images.
Jittering induced a large signal in
V, clearly correlated with telescope
displacement ![]() ,
,
![]() along the x, y axes.
This effect increased with R,
reaching several milliarcseconds at
along the x, y axes.
This effect increased with R,
reaching several milliarcseconds at
![]() ,
,
![]() .
The jittering makes the reduction
difficult, and is the reason that we discarded
a linear (k=4) model reduction.
.
The jittering makes the reduction
difficult, and is the reason that we discarded
a linear (k=4) model reduction.
Jittering moves the star field with reference to the camera optics.
This causes a change in the optical distortion (say along x)
at some point x,y from its initial value
![]() to
to
![]() .
A similar expression
is valid for the distortion
.
A similar expression
is valid for the distortion
![]() along the y axis. Naming
the partial derivatives used here as g**, we come to the expression
along the y axis. Naming
the partial derivatives used here as g**, we come to the expression
equally applicable for the correction of positions. Assuming that optical distortions are stable over the observing period, g** terms are included in, and found as components of
| |
Figure 3:
Example of B=20.8 star motion over a CCD traced for
6 years with FORS1 and 5 months with FORS2: measured
positions (open circles with error bars) and
model track (solid curves). Reduction was performed
with parameters k=10 and R=1.5 |
| Open with DEXTER | |
An example of the measured and model star
motion over the CCD surface is shown in Fig. 3
for a red (B=20.8, B-R=2.8) star with
proper motion
![]() mas yr-1,
mas yr-1,
![]() mas yr-1,
and trigonometric parallax
(all relative)
mas yr-1,
and trigonometric parallax
(all relative)
![]() mas which was computed
later based on FORS2 images (Sect. 4.2). This
graph is actually rather simplified because it refers to positions
corrected for polynomial
mas which was computed
later based on FORS2 images (Sect. 4.2). This
graph is actually rather simplified because it refers to positions
corrected for polynomial ![]() and for jitter related terms.
The intricate shape of the track is due mainly to the DCR shift
of images within a single series. In the blue band, this motion exceeds
and for jitter related terms.
The intricate shape of the track is due mainly to the DCR shift
of images within a single series. In the blue band, this motion exceeds
![]() 10 mas while in the red filter the effect is an order lower.
This makes it clear, for instance, why reference star displacements should be
taken into account when processing B images.
10 mas while in the red filter the effect is an order lower.
This makes it clear, for instance, why reference star displacements should be
taken into account when processing B images.
![\begin{figure}
\par {\includegraphics[width=8.5cm,clip]{12026fg4.eps} }\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg217.png) |
Figure 4:
Astrometric precision of
relative proper motions (open circles)
determined from FORS1 images with a six year time span
and trigonometric parallaxes (triangles) derived from FORS2 images with
corrections based on FORS1 proper motions.
Reductions performed with k=10 and R=1.5 |
| Open with DEXTER | |
The dependence on magnitude of the internal precision of proper motions
is shown in Fig. 4. These estimates correspond
to the formal least squares precision and take into account
components
![]() ,
,
![]() ,
and
,
and
![]() of the total random error
of the total random error ![]() .
Due to the large time span between epochs, proper motions were
derived with high precision, reaching 20
.
Due to the large time span between epochs, proper motions were
derived with high precision, reaching 20 ![]() as yr-1 for bright stars.
Systematic errors (Sect. 6) degrade precision little
since their contribution is small in comparison to random errors
(see Sect. 4.2).
as yr-1 for bright stars.
Systematic errors (Sect. 6) degrade precision little
since their contribution is small in comparison to random errors
(see Sect. 4.2).
4.2 Reduction of FORS2 images based on FORS1 proper motions
For processing of FORS2 images we used high-precision proper motions
The reduction was started by finding the FORS2 image
obtained at normal seeing
and best matching the star content of FORS1 images.
This image at epoch T0was used as a reference for the reduction of all FORS2 images.
In most cases, the difference in star content
from the two cameras occured for a small gap
between two CCD chips of FORS2 and
saturation of bright stars in the R filter.
In this way, 152 common stars were selected
for further reduction, which started from applying
corrections
for proper motion occuring in star positions between epochs T0and Tm.
This was performed taking into account
the singularity of astrometric reduction according to which
the i-th target position (and proper motion ![]() )
is related
to a particular subset
)
is related
to a particular subset
![]() of reference
stars
of reference
stars
![]() ,
whose unique model parameters
(denoted by
,
whose unique model parameters
(denoted by ![]() in contrast to
in contrast to ![]() )
are valid within this subset only. Therefore,
to conserve the reference system, a reduction
of FORS2 images for a target i was performed
with reference to the same frame
)
are valid within this subset only. Therefore,
to conserve the reference system, a reduction
of FORS2 images for a target i was performed
with reference to the same frame
![]() as used for FORS1.
Also, we applied
weights
as used for FORS1.
Also, we applied
weights
![]() that are same as those involved in the reduction of
FORS1 images, that is, using average light fluxes in the blue filter.
Thus, each reference (with respect to target i)
star
that are same as those involved in the reduction of
FORS1 images, that is, using average light fluxes in the blue filter.
Thus, each reference (with respect to target i)
star
![]() positions were corrected by
positions were corrected by
This complicated procedure is due to the necessity to conserve the system of model parameters when processing different sets of images. Violation of this principle immediately destroys the accuracy. Thus, direct application of corrections
The reduction model included zero-points, chromatic parameters ![]() ,
,
![]() ,
and trigonometric
parallaxes
,
and trigonometric
parallaxes ![]() .
Formal random precision of FORS2 parallaxes for stars
of different brightness is given by Fig. 4.
For the best stars,
relative parallaxes are
determined with a precision near to 40
.
Formal random precision of FORS2 parallaxes for stars
of different brightness is given by Fig. 4.
For the best stars,
relative parallaxes are
determined with a precision near to 40 ![]() as,
which means that distances at 1 kpc are measurable with
a 4% precision. A few large upward deviations in Fig. 4
for some stars are caused
by a low number of measurements (oversaturation of bright images,
or position in the gap between two chips of the camera)
or by the peripheral position of stars and thus low
as,
which means that distances at 1 kpc are measurable with
a 4% precision. A few large upward deviations in Fig. 4
for some stars are caused
by a low number of measurements (oversaturation of bright images,
or position in the gap between two chips of the camera)
or by the peripheral position of stars and thus low ![]() (large
(large
![]() ).
).
The precision of parallaxes is increased by use of FORS1 proper
motions, allowing us to exclude a component ![]() from model
parameters
from model
parameters ![]() ,
removing in this way a strong correlation between
,
removing in this way a strong correlation between ![]() and
and ![]() .
In other
cases, the expected
precision of parallaxes from the 5-month series of observations is
200
.
In other
cases, the expected
precision of parallaxes from the 5-month series of observations is
200 ![]() as only.
as only.
Systematic errors, of course, affect the accuracy of both proper motion
and parallax determination. In Sect.6 we show that the systematic
error for targets near frame center is about 25 ![]() as, or
a half of the random error of epoch average positions for bright stars,
at months to year time scales.
Translating this estimate to parallaxes, we find that
systematic errors contribute approximately
as, or
a half of the random error of epoch average positions for bright stars,
at months to year time scales.
Translating this estimate to parallaxes, we find that
systematic errors contribute approximately ![]() 20
20 ![]() as to each star parallax
and
as to each star parallax
and ![]() 10
10 ![]() as yr-1 to proper motions irrespective of the star
magnitude.
as yr-1 to proper motions irrespective of the star
magnitude.
4.3 Merged residuals

![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026fg5.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{12026fg6.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg228.png) |
Figure 5:
Image-to-image change of FORS1 residuals Vfor a) a faint 22 mag star (
|
| Open with DEXTER | |
While processing, we computed
residuals V for each star i, each image m,
all reduction modes k from 6 to 16, and several
reference field sizes R, including
![]() .
The best precision
residuals computed at
.
The best precision
residuals computed at
![]() we denote as Vim(k).
In practice, however,
we do not require multiply defined residuals but rather a single
set of residuals
which for a particular star i is the best estimate of the planetary
signal at the moment of image m exposure. For that purpose we merge
Vim(k) into a single system, the possibility of which follows from
the discussion in Sect. 3.5.
we denote as Vim(k).
In practice, however,
we do not require multiply defined residuals but rather a single
set of residuals
which for a particular star i is the best estimate of the planetary
signal at the moment of image m exposure. For that purpose we merge
Vim(k) into a single system, the possibility of which follows from
the discussion in Sect. 3.5.
Let us consider
Fig. 5 that presents an example of the image-to-image
change of Vim(k) computed with different k
for two stars of different brightness.
Residuals corresponding to different k are seen to be highly correlated,
especially for a faint star,
and fluctuate near their average,
![]() being a function of m.
Recall that according to (29),
being a function of m.
Recall that according to (29),
![]() where aij(k) refer to k used.
Therefore
where aij(k) refer to k used.
Therefore
![]() where
where
![]() is an average of aij(k) with respect to k.
Hence
is an average of aij(k) with respect to k.
Hence
![]() .
The variance of this difference, neglecting the second term, is
.
The variance of this difference, neglecting the second term, is
![]() ,
or
,
or
![]() at k given.
Thus, the standard deviation of
at k given.
Thus, the standard deviation of
![]() depends on
depends on
![]() almost linearly. This approximation is confirmed by actual data,
as shown in Fig. 6.
almost linearly. This approximation is confirmed by actual data,
as shown in Fig. 6.
| |
Figure 6:
Standard deviation (scatter with respect to k) of
|
| Open with DEXTER | |
Given 6 sets of
Vim(k) corresponding to k=6...16 for each target i,
we merged them into the
weighted average
![]() using
weights
using
weights
![]() .
Along with V,
merged residuals
.
Along with V,
merged residuals
![]() were
tested for the presence of systematic errors (Sect. 6).
As explained in Sect. 3.5, the merging is not applicable to model
parameters
were
tested for the presence of systematic errors (Sect. 6).
As explained in Sect. 3.5, the merging is not applicable to model
parameters ![]() .
.
For faint stars, the relative amplitude of V fluctuations near
![]() is insignificant (Fig. 5a) since
is insignificant (Fig. 5a) since
![]() .
Therefore
.
Therefore
![]() at any k and the use of
at any k and the use of
![]() instead of V is of low efficiency. For bright stars (Fig. 5b),
the precision of
instead of V is of low efficiency. For bright stars (Fig. 5b),
the precision of
![]() is better
due to the averaging of the reference frame noise.
is better
due to the averaging of the reference frame noise.
5 Random errors
5.1 Calibration of the image centroiding error
 dependence on flux
dependence on flux
In this section, our study was carried out with
images obtained in a narrow seeing range of 0.47-0.78
![]() ,
which
includes almost all FORS1 and about 80% of FORS2 images. The use of
images out of this range leads to
a noticeable increase of random errors.
,
which
includes almost all FORS1 and about 80% of FORS2 images. The use of
images out of this range leads to
a noticeable increase of random errors.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026fg8.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{12026fg9.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg243.png) |
Figure 7:
Initial (dashed lines) and corrected (solid lines) residuals
of the error expansion (32)
computed at minimum reference field size
|
| Open with DEXTER | |
The use of stars of different brightness to
investigate systematic errors requires careful
calibration of
the dependence on flux of the image centroiding error
![]() (1).
For calibration purposes, the best
residuals are V computed at the minimum possible
(1).
For calibration purposes, the best
residuals are V computed at the minimum possible
![]() (Table 2)
since they
contain negligible input of atmospheric image motion
(Table 2)
since they
contain negligible input of atmospheric image motion ![]() .
Using the variance
.
Using the variance
![]() of residuals V computed
for each k at
of residuals V computed
for each k at
![]() ,
we can find the residual discrepancy of the decomposition (25)
into error components
,
we can find the residual discrepancy of the decomposition (25)
into error components
for each target i. The change of this quantity with star magnitude is shown in Fig. 7 by dashed lines for each k. All curves corresponding to different k modes closely follow a common dependence with little scatter. The anomalously large deviation seen for the FORS1 camera at k=6 originates from the large jittering of images which was not completely compensated by the reduction. For high k modes this effect is well removed. While for bright stars, discrepancies
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f10.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{12026f11.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg251.png) |
Figure 8:
Correction
|
| Open with DEXTER | |
A change of
![]() with brightness in Fig. 8
is similar for both cameras. A negative trend
over a 4-5 mag range of brightness
reproduces the dependence of star image size
with brightness in Fig. 8
is similar for both cameras. A negative trend
over a 4-5 mag range of brightness
reproduces the dependence of star image size
![]() on flux (Fig. 1) and therefore probably
is a consequence of selective filtration
based on star profile parameters when star images with excessive size
were discarded (Sect. 2).
The use of more compact images in comparison to
the initial star sample, of course, results in an
improvement of the effective centroiding error
on flux (Fig. 1) and therefore probably
is a consequence of selective filtration
based on star profile parameters when star images with excessive size
were discarded (Sect. 2).
The use of more compact images in comparison to
the initial star sample, of course, results in an
improvement of the effective centroiding error
![]() observed in Fig. 8.
A similar improvement of precision for the brightest images
occurs for the selection based on
observed in Fig. 8.
A similar improvement of precision for the brightest images
occurs for the selection based on ![]() criterion (Sect. 2).
criterion (Sect. 2).
Averaging with respect to k produced final estimates
![]() shown in Fig. 8 by solid lines.
With these corrections, residuals (32) have been recomputed yielding new
discrepancies
shown in Fig. 8 by solid lines.
With these corrections, residuals (32) have been recomputed yielding new
discrepancies
![]() with much smaller
magnitudes (Fig. 7, solid lines).
Having found the calibration factor
with much smaller
magnitudes (Fig. 7, solid lines).
Having found the calibration factor
![]() ,
we can
correctly estimate
,
we can
correctly estimate
![]() at any
at any
![]() simply by adding the image motion variance
simply by adding the image motion variance ![]() :
:
The term
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f12.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg256.png) |
Figure 9:
Astrometric precision of a single photocenter measurement:
observed (open circles) and model estimate
|
| Open with DEXTER | |
The validity of above calibration
is illustrated in Fig. 9 where we compare
the astrometric precision of a single photocenter measurement
restored from observations with its model prediction
![]() in the case of
reductions with R=1.5
in the case of
reductions with R=1.5![]() and k=10.
The measured astrometric precision, for each star, was computed
based on the observed variance
and k=10.
The measured astrometric precision, for each star, was computed
based on the observed variance
![]() of V (mean in x and y),
of V (mean in x and y),
![]() derived in Sect. 5.2, and representation (33).
These results, as for model values
derived in Sect. 5.2, and representation (33).
These results, as for model values
![]() for each target,
were averaged over all data available.
Figure 9 shows a good match of the observed
and model precision over wide range of magnitudes.
This graph matches well our previous results for FORS1 based
on a reduction technique with overlapping reference frames
(Lazorenko et al. 2007).
for each target,
were averaged over all data available.
Figure 9 shows a good match of the observed
and model precision over wide range of magnitudes.
This graph matches well our previous results for FORS1 based
on a reduction technique with overlapping reference frames
(Lazorenko et al. 2007).
We emphasize that both
![]() and
and
![]() are estimates of the
actual precision of the photocenter determination. The difference is
that the first one refers to
the star sample affected by selection while
are estimates of the
actual precision of the photocenter determination. The difference is
that the first one refers to
the star sample affected by selection while
![]() is
related to
the imaginary sample of FORS images with no defects.
In spite of the small value of
is
related to
the imaginary sample of FORS images with no defects.
In spite of the small value of ![]() ,
the subsequent study of
image motion and systematic errors greatly favours its use since it allows us
to incorporate large amount of data from faint stars.
,
the subsequent study of
image motion and systematic errors greatly favours its use since it allows us
to incorporate large amount of data from faint stars.
5.2 Image motion
Taking advantage of the availability of a well calibrated image centroiding error,
we used Eq. (33) to extract the image motion
component ![]() at various R.
This equation was solved numerically for each star
taking into consideration the fact that the reference frame noise
at various R.
This equation was solved numerically for each star
taking into consideration the fact that the reference frame noise
![]() is a function of
is a function of
![]() and
and ![]() .
The results averaged over all stars available and computed for each kand R are shown in Fig. 10.
Comparing estimates
obtained for both cameras, one may note the similarity of results
in spite of the
difference in pixel scale, number and spacing of epochs,
different reduction model parameters, different method of reduction and,
especially, an 8-fold difference in
exposure T (600 and 70 s for FORS1 and FORS2 respectively).
The last aspect raises a doubt about the validity
of relating the measured image motion to atmospheric turbulence.
.
The results averaged over all stars available and computed for each kand R are shown in Fig. 10.
Comparing estimates
obtained for both cameras, one may note the similarity of results
in spite of the
difference in pixel scale, number and spacing of epochs,
different reduction model parameters, different method of reduction and,
especially, an 8-fold difference in
exposure T (600 and 70 s for FORS1 and FORS2 respectively).
The last aspect raises a doubt about the validity
of relating the measured image motion to atmospheric turbulence.
At each fixed k, ![]() estimates were fitted by a power law
estimates were fitted by a power law
assuming that R is given in minutes of arc. Fitting parameters B and b are given in Table 3 for the first few k modes only since the results for k>12 are too uncertain. Excessive estimates of B (in comparison to FORS2) found at k=6 and k=8 could be due to the residual effect of large image jittering of FORS1 images. For comparison, the table contains
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f13.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{12026f14.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg260.png) |
Figure 10:
Image motion |
| Open with DEXTER | |
In a pilot study of FORS2 astrometric performance, Lazorenko (2006) estimated Eq. (34) parameters B' and b'using a single night observation series with T=17 s exposure. Coefficients B' reproduced in Table 3 are approximately twice as large as in this study, possibly due to the different technique of reductions, which now takes into account DCR displacement of reference stars.
Table 3:
Coefficients of Eq. (34):
derived in this study B[![]() as], b;
predicted
as], b;
predicted ![]() ,
,
![]() by atmospheric model (Lazorenko & Lazorenko 2004);
and B', b' obtained from
a single series of FORS2 images (Lazorenko 2006).
by atmospheric model (Lazorenko & Lazorenko 2004);
and B', b' obtained from
a single series of FORS2 images (Lazorenko 2006).
In all cases, the measured powers b of Eq. (34) are
significantly below their predicted values ![]() .
We conclude that the observed image motion at
.
We conclude that the observed image motion at ![]() s is not due to
atmospheric turbulence since it does not decrease as T-1/2and therefore is of instrumental origin.
Very likely, it does not depend on exposure, at least
for
s is not due to
atmospheric turbulence since it does not decrease as T-1/2and therefore is of instrumental origin.
Very likely, it does not depend on exposure, at least
for ![]() s. Due to domination over
the intrinsic atmospheric image motion, the last component
not can be extracted from the present data.
In Sect. 6 we suggest that the image motion detected probably
is caused by star image asymmetry in combination with variations of the PSF.
s. Due to domination over
the intrinsic atmospheric image motion, the last component
not can be extracted from the present data.
In Sect. 6 we suggest that the image motion detected probably
is caused by star image asymmetry in combination with variations of the PSF.
6 Systematic errors at monthly/annual epochs
In our former study (Lazorenko et al. 2007),
systematic errors
in positional observations with the FORS1 camera were shown
to be about 30 ![]() as.
The detection of such weak signals presents a certain
difficulty and limits our search to characterization
of the error component
invariable within each monthly/annual epoch of observations.
Systematic signs in observations may appear for effects
not described by the reduction model. The most troublsome are
long-term instabilities
which differently affect images at distant epochs,
e.g. changes in VLT optical aberrations, star colours, actual PSF shape,
variable background gradient due to light from nearby stars, etc.
as.
The detection of such weak signals presents a certain
difficulty and limits our search to characterization
of the error component
invariable within each monthly/annual epoch of observations.
Systematic signs in observations may appear for effects
not described by the reduction model. The most troublsome are
long-term instabilities
which differently affect images at distant epochs,
e.g. changes in VLT optical aberrations, star colours, actual PSF shape,
variable background gradient due to light from nearby stars, etc.
6.1 Epoch average residuals
| |
Figure 11:
Monthly normal points (average residuals) Ve for stars
observed with FORS2. Symbol size refers to
the expected precision of normal points De1/2,
which changes from better than 100 |
| Open with DEXTER | |
The quantities best suited to this study are the epoch
average weighted residuals
computed for each star at each monthly/annual observation epoch e. A set of these epoch points Ve was investigated to detect and characterize systematic errors. The epoch normal points Ve are formally characterized by variances
equal to the cumulative weight of individual residuals of images
where Bmm' are diagonal elements of a covariance matrix
of residuals Vim for i-th star and
where
It is difficult to
suppose that systematic components follow exactly
the parallax and proper motion displacement of stars.
Therefore, after a fit in time, systematic errors add an extra scatter to
epoch residuals Ve, which is detected as an
excess in the expected value of the variance ![]() .
This excess
we find below based on the well-calibrated (Sect.5) model of
the stochastic-dependent component of the variance.
.
This excess
we find below based on the well-calibrated (Sect.5) model of
the stochastic-dependent component of the variance.
A good idea of analyzed epoch average residuals Ve is given
by graphs of Fig. 11. This plot shows the
typical distribution of
monthly normal points Ve(x), Ve(y)
in the x,y plane for each month, for stars
observed at FORS2, and the reduction with k=10 and
![]() .
This distribution of Ve is typical also
for processing with other k at
.
This distribution of Ve is typical also
for processing with other k at
![]() due to
the high degree of correlation between these sets of residuals (Sect. 4.3).
Normal points are shown by open circles
of three size grades which refer to the
precision De1/2 of normal points
better than 100
due to
the high degree of correlation between these sets of residuals (Sect. 4.3).
Normal points are shown by open circles
of three size grades which refer to the
precision De1/2 of normal points
better than 100 ![]() as (largest circles, usually brightest central stars),
170
as (largest circles, usually brightest central stars),
170 ![]() as (middle size),
and 260
as (middle size),
and 260 ![]() as (small circles, faint or peripheral
stars). Ellipses (dashed curves) with semiaxes
as (small circles, faint or peripheral
stars). Ellipses (dashed curves) with semiaxes
![]() mark
3
mark
3![]() scatter limits expected for least square residuals.
The different scatter of Ve
for different epochs is caused primarily
by seeing (Table 1), which is best for
the second (most compact location of dots)
and worst for the third and last
epoch. For the same reason,
only a few points with
De1/2<100
scatter limits expected for least square residuals.
The different scatter of Ve
for different epochs is caused primarily
by seeing (Table 1), which is best for
the second (most compact location of dots)
and worst for the third and last
epoch. For the same reason,
only a few points with
De1/2<100 ![]() as precision (large signs)
are seen for the middle and the last epoch since only the
best stars are measured well at bad seeing.
Most
normal points of each precision grade are inside of the
corresponding 3
as precision (large signs)
are seen for the middle and the last epoch since only the
best stars are measured well at bad seeing.
Most
normal points of each precision grade are inside of the
corresponding 3![]() limits with no wide dispersions.
limits with no wide dispersions.
Next, we considered the frequency distribution
of Ve. These data however are not uniform in precision
for different light fluxes from stars.
In order to exclude a dependence of the precision on brightness,
we introduced the dimensionless normalized quantities
The standard deviation of
In the case of FORS1,
from Eqs.(36)-(38) we find
that typical values of
![]() are
0.17, 0.48, and 0.27 for epochs e=1,2,3 respectively,
with small variations depending on observing conditions of
the particular target.
Therefore
are
0.17, 0.48, and 0.27 for epochs e=1,2,3 respectively,
with small variations depending on observing conditions of
the particular target.
Therefore
![]() is a
is a ![]() -width parameter for a theoretical Gaussian distribution.
The observed distribution of
-width parameter for a theoretical Gaussian distribution.
The observed distribution of
![]() for FORS1 is slightly wider,
with a 0.61
for FORS1 is slightly wider,
with a 0.61 ![]() -parameter and a few large residuals (Fig. 12a).
-parameter and a few large residuals (Fig. 12a).
In the case of FORS2,
![]() varies for different epochs between 0.22 and 0.76,
with an average
varies for different epochs between 0.22 and 0.76,
with an average
![]() .
The observed distribution is much wider, with a 1.17
.
The observed distribution is much wider, with a 1.17
![]() -width parameter and
a significant widening of wings (Fig. 12b). The observed
distribution of monthly normalized residuals clearly indicates
the presence of large systematic errors which is discussed later on.
-width parameter and
a significant widening of wings (Fig. 12b). The observed
distribution of monthly normalized residuals clearly indicates
the presence of large systematic errors which is discussed later on.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f16.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg281.png) |
Figure 12:
Histograms of
|
| Open with DEXTER | |
The histograms in Fig. 12 are sensitive to
systematic errors providing their magnitude is
comparable to the precision of epoch normal positions, about
50-200 ![]() as. These histograms however are to be considered
primarily as illustrative.
Numerical characterization of systematic error is found
under the assumption that its value Ae for a given star iis constant within
each monthly/annual observation series e. In this case
all measured residuals Vim in images
as. These histograms however are to be considered
primarily as illustrative.
Numerical characterization of systematic error is found
under the assumption that its value Ae for a given star iis constant within
each monthly/annual observation series e. In this case
all measured residuals Vim in images ![]() are systematically
biased by a constant Ae. Therefore
are systematically
biased by a constant Ae. Therefore
![]() and
the expectation of the variance of measured normalized residuals is
and
the expectation of the variance of measured normalized residuals is
![]() .
The second item describing the input of systematic errors
in
.
The second item describing the input of systematic errors
in
![]() dominates for bright stars.
This component was computed for each star and
averaged to derive statistically reliable
dominates for bright stars.
This component was computed for each star and
averaged to derive statistically reliable
![]() .
Averaging was performed over not too faint stars, all epochs, and
all parameters k at
.
Averaging was performed over not too faint stars, all epochs, and
all parameters k at
![]() ,
assuming that the mathematical expectation of
Ae2 does not depend on epoch, star light flux, and axis.
This yielded the representative estimate
,
assuming that the mathematical expectation of
Ae2 does not depend on epoch, star light flux, and axis.
This yielded the representative estimate
For a complete set of FORS2 observations (any seeing conditions), and images in the central r<1
The frequency distribution of epoch average residuals
![]() based on merged residuals
based on merged residuals
![]() (Fig. 12d)
does not differ from that built for Ve (Fig. 12c).
(Fig. 12d)
does not differ from that built for Ve (Fig. 12c).
The estimates of A for stars in CCD
central circular areas of r=40
![]() ,
1
,
1![]() ,
and 1.5
,
and 1.5![]() are given in Table 4.
are given in Table 4.
Table 4:
Systematic component A [![]() as]
in residuals Ve
and in
as]
in residuals Ve
and in
![]() within central CCD zones of r radii.
within central CCD zones of r radii.
According to Table 4, the characteristics of the systematic error Afor both cameras
are similar and show a slight increase
in the direction from the center to the periphery of a frame.
Thus, while at the periphery A is near to 100 ![]() as,
at r<40
as,
at r<40
![]() it does not exceed 50-60
it does not exceed 50-60 ![]() as.
Due to statistical limitations
we not can estimate A at the center
(where the target is usually placed),
but considering the tendency observed we predict it could be about 25
as.
Due to statistical limitations
we not can estimate A at the center
(where the target is usually placed),
but considering the tendency observed we predict it could be about 25 ![]() as
at r<10
as
at r<10
![]() ,
as expected from the following discussion.
The systematic components in
,
as expected from the following discussion.
The systematic components in
![]() and Ve are approximately equal.
and Ve are approximately equal.
An important piece of information on the global distribution of
systematic errors over
the CCD plane was derived applying a low-pass Gaussian spatial filter to
the epoch residuals Ve.
The resulting low-frequency component A(x,y) in Ve for each camera,
some epochs, and reduction versions
is shown in contour plots Figs. 13, 14 with isolines
drawn with 25 ![]() as increments. All graphs refer to the
residuals on the x-axis.
A(x,y) function change is rather complicated and has
several extremums. This behavior, of course, not can be
approximated by polynomials with basic functions
as increments. All graphs refer to the
residuals on the x-axis.
A(x,y) function change is rather complicated and has
several extremums. This behavior, of course, not can be
approximated by polynomials with basic functions ![]() since this dependence is excluded in the course of the
reduction procedure. It is characteristic that
large systematic errors reaching in most cases
100-200
since this dependence is excluded in the course of the
reduction procedure. It is characteristic that
large systematic errors reaching in most cases
100-200 ![]() as tend to concentrate at the periphery.
At the field center, where the target is
usually placed, A(x,y) functions varies rather smoothly
and often fall to <
as tend to concentrate at the periphery.
At the field center, where the target is
usually placed, A(x,y) functions varies rather smoothly
and often fall to <![]() 25
25 ![]() as. No graph was found to have
extremum at the center of the frame.
as. No graph was found to have
extremum at the center of the frame.
| |
Figure 13:
Global pattern of FORS1 systematic error distribution
over the CCD surface: a) in normal points Ve and b) in merged residuals
|
| Open with DEXTER | |
In the case of FORS1, systematic error plots are given
for middle 2002 epoch at which the maximum fluctuations of A(x,y)
are detected. Figure 13a, plotted for Ve computed with
k=10 at
![]() and Fig. 13b for
merged
and Fig. 13b for
merged
![]() residuals have few similar structures
above
residuals have few similar structures
above ![]() 50
50 ![]() as. At the center, errors are
negligibly small. Although we discuss here only
a particular case of the reduction with k=10 or
of merged
as. At the center, errors are
negligibly small. Although we discuss here only
a particular case of the reduction with k=10 or
of merged
![]() ,
our comments (both for FORS1 and FORS2)
are valid also for computations with other
k due to the high correlation of results obtained
at
,
our comments (both for FORS1 and FORS2)
are valid also for computations with other
k due to the high correlation of results obtained
at
![]() (Sect. 4.3).
(Sect. 4.3).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f18.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg301.png) |
Figure 14:
Distribution
over the CCD surface of a systematic component in FORS2 epoch residuals
in Jan. 2007:
a) in Ve computed with k=10 and
|
| Open with DEXTER | |
Figure 14b shows the systematic pattern
after elimination of images with abnormally good and bad seeing
and illustrates the decrease of systematic errors compared to the
use of a complete set of images (Fig. 14a). Few extrema
have vanished and most contrast details are smoothed. These
graphs correspond to the middle of the January 2007 epoch with the
largest variance of monthly residuals (Fig. 11),
which was chosen to show
the worst case of A(x,y). In November 2006 (first epoch)
these errors are much better (Fig. 14e).
The error structure for the merged
![]() residuals
(Fig. 14d) in general is like that for Ve (Fig. 14b)
at the same epoch. Figure 14f refers to Ve computed at
k=6 and
residuals
(Fig. 14d) in general is like that for Ve (Fig. 14b)
at the same epoch. Figure 14f refers to Ve computed at
k=6 and
![]()
![]() .
The distribution shown here is similar
to that for the reduction with k=10 (Fig. 14b) and for
.
The distribution shown here is similar
to that for the reduction with k=10 (Fig. 14b) and for
![]() with
with ![]() 50
50 ![]() as systematic errors at the center,
but much larger peaks at frame boundaries.
as systematic errors at the center,
but much larger peaks at frame boundaries.
The dependence of A(x,y) on x,y could be
a reason for excluding systematic errors
in a secondary iteration;
however we had an
insufficient number of reference stars.
Alternatively, Ae can be treated as additional
components of each star model parameter ![]() to be computed
with other parameters.
This however is not useful for planet search or microlensing
applications due to the complete zeroing of useful astrometric signals.
to be computed
with other parameters.
This however is not useful for planet search or microlensing
applications due to the complete zeroing of useful astrometric signals.
Considering that a change of Ae between two adjacent
epochs at the frame center
is approximately 50 ![]() as (100-200
as (100-200 ![]() as within the entire FoV)
for both cameras,
we can estimate the stability of the FORS astrometric system over short
time scales. Assuming that
a given change occurs at about a month spacing, the daily rate of
systematic change is 1-2
as within the entire FoV)
for both cameras,
we can estimate the stability of the FORS astrometric system over short
time scales. Assuming that
a given change occurs at about a month spacing, the daily rate of
systematic change is 1-2 ![]() as (3-6
as (3-6 ![]() as for the whole FoV).
Our previous study of FORS1 errors
(Lazorenko et al. 2007) have shown that
a difference in the systematic component
over a time scale of four days is either undetectably small or
30
as for the whole FoV).
Our previous study of FORS1 errors
(Lazorenko et al. 2007) have shown that
a difference in the systematic component
over a time scale of four days is either undetectably small or
30 ![]() as atmost. This is about 8
as atmost. This is about 8 ![]() as a day
change in systematic errors
in the whole FoV, which is in accord with the current estimate.
as a day
change in systematic errors
in the whole FoV, which is in accord with the current estimate.
Recall that the amplitude of systematic errors
of 50 ![]() as we referred to corresponds to poor
observing conditions; the estimate of
25
as we referred to corresponds to poor
observing conditions; the estimate of
25 ![]() as is more relevant for normal conditions and
targets at frame center.
as is more relevant for normal conditions and
targets at frame center.
6.2 Instrumental background of systematic errors
Based on the discussion in the previous subsection, we conclude that the characteristics of the systematic component Ae in magnitude and in spatial behavior are identical for FORS1 and FORS2. This is the second identity of these cameras derived based on observations at rather different time scales, CCD type, and photometric bands (the first is a dependence of image motion variance on R), and is evidently due to identical optical design of the cameras.
Systematic errors are probably generated during
image centroiding due to the highly complicated
star profiles, actually indefinite at
the high accuracies at which we work. Consider that
a typical error of 100 ![]() as is only
as is only
![]() fraction
of the FWHM. Although FORS images are appropriate, the definition of the
``image photocenter'' for star profiles distorted by
variable optical aberrations becomes uncertain. Therefore
we use a centroiding procedure (Lazorenko 2006)
specialized for finding the
weighted photocenter of the image which is more
stable to image deformations than the ``profile center''.
fraction
of the FWHM. Although FORS images are appropriate, the definition of the
``image photocenter'' for star profiles distorted by
variable optical aberrations becomes uncertain. Therefore
we use a centroiding procedure (Lazorenko 2006)
specialized for finding the
weighted photocenter of the image which is more
stable to image deformations than the ``profile center''.
At zero or constant geometric distortion, the position of the measured image centroid is subject only to random errors caused primarily by Poisson noise in the number of photons and by atmospheric image motion. Systematic and extra random components in position appear in the following cases of instability:
- small deformation of a star profile (change of asymmetry) in time
due to a slow change of optical aberrations. This results in image
photocenter shift proportional to the gradient of aberrations at the point.
These shifts, correlated in x,y space, are
detected (after a certain filtration introduced
by astrometric reduction) as systematic residuals A(x,y);
their change in time produces A
component. The effect is lowest at frame
center were images are most symmetric due to optimal optical performance;
- a random change of image-to-image atmospheric PSF and seeing (shape and size). This affects image profiles both in size and shape and therefore shifts photocenters by an amount proportional to seeing fluctuation and to the measure of image asymmetry at the point, representing modulation of the optical aberration field by a random signal. The observed effect is random in time and correlated in space, and thus mimics atmospheric image motion. In Sect. 5 we classified it as ``instrumental'' image motion with an amplitude exceeding that of atmospheric image motion and not dependent on exposure time.
Systematic deviations of the average seeing at a single epoch
from its average for a full set of data may produce systematic bias
of positions.
To see whether this exists in our data, we performed
reduction with an expanded set of parameters
![]() adding two extra terms describing the linear dependence of a star's x,y position on seeing. With a full set (all seeing) of images, a new value
of the systematic error A in an r<1
adding two extra terms describing the linear dependence of a star's x,y position on seeing. With a full set (all seeing) of images, a new value
of the systematic error A in an r<1![]() area
decreased from its former 160
area
decreased from its former 160 ![]() as to 90
as to 90 ![]() as, and a much
smoother shape of A(x,y) (Fig. 13c)
was obtained in comparison to the initial pattern (Fig. 13a).
The improvement, however, is seen primarily at the periphery
where geometric distortions are largest.
Thus variations of seeing actually lead to systematic errors in
epoch positions. We however consider the use of the expanded reduction model
insufficiently validated, since it reduces the useful astrometric signal and,
for centrally placed targets, does not leads to a
significant improvement in the accuracy.
as, and a much
smoother shape of A(x,y) (Fig. 13c)
was obtained in comparison to the initial pattern (Fig. 13a).
The improvement, however, is seen primarily at the periphery
where geometric distortions are largest.
Thus variations of seeing actually lead to systematic errors in
epoch positions. We however consider the use of the expanded reduction model
insufficiently validated, since it reduces the useful astrometric signal and,
for centrally placed targets, does not leads to a
significant improvement in the accuracy.
Thus, variations in seeing are a source of systematic errors; for precise astrometry these variations should be limited.
7 Allan precision
Another characterization of
the VLT long-term astrometric stability
is based on the computation of the Allan deviation of residuals Vm.
This quantity is normally used as a powerful indicator of
systematic errors in observations and corresponds
to the astrometric precision of a time series of n images.
Figure 15 presents
plots of this variable as a function of time lag (expressed as
the number of images n) between
subsamples of residuals Vm.
The data in Fig. 15 are the average of each star Allan deviation
taken
over all, except the most peripheral, stars. Before averaging, we
normalized the individual Allan deviations to their values at zero time lag so as
to compensate for the highly varying amplitude
of this variable for stars of different brightness.
The right vertical axis of Fig. 15
is the scale for the normalized Allan deviation
computed as described and is valid for stars of any magnitude.
The left axis is the scale used to find the Allan deviation
for bright stars (B=18 mag at FORS1 and R=16.5 mag at FORS2)
with
![]()
![]() as,
as,
![]()
![]() as and
assuming its location at the frame center, which ensures small
as and
assuming its location at the frame center, which ensures small
![]()
![]() as.
as.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f19.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg305.png) |
Figure 15:
Normalized Allan deviation (right axis)
in positional residuals
and astrometric precision for bright targets
(left axis) expected from a series of n images with standard seeing only.
Estimates are based on: residuals V obtained with
k=6...16 (dashed lines which for FORS2
actually run into a single line); merged residuals
|
| Open with DEXTER | |
For computations, we used Vm residuals obtained with each
reduction parameter k=6...16 and
![]() .
Results for different k are very similar
due to the high degree of correlation between these data sets (dashed curves
in Fig. 15);
for FORS2 they actually run into a single line corresponding to
the Allan deviation of residuals
.
Results for different k are very similar
due to the high degree of correlation between these data sets (dashed curves
in Fig. 15);
for FORS2 they actually run into a single line corresponding to
the Allan deviation of residuals
![]() .
Besides,
due to the normalizing procedure, computations based on a subset of either all or
bright stars only produced similar estimates.
The Allan deviation was found to follow
.
Besides,
due to the normalizing procedure, computations based on a subset of either all or
bright stars only produced similar estimates.
The Allan deviation was found to follow
![]() (FORS1) and
(FORS1) and
![]() (FORS2)
power laws which are near to that
expected for the average of a random variable. A simple comparison
with an n-1/2 law is of course incorrect since least square fit residuals
are correlated and have a non-diagonal covariance matrix
(FORS2)
power laws which are near to that
expected for the average of a random variable. A simple comparison
with an n-1/2 law is of course incorrect since least square fit residuals
are correlated and have a non-diagonal covariance matrix ![]() .
To compare our results with those expected with zero
systematic errors,
we performed a numerical simulation of observations introducing
uncorrelated random noise in model measurements. The obtained dependence
(solid curves in Fig. 15) follow a power law with a
slope
.
To compare our results with those expected with zero
systematic errors,
we performed a numerical simulation of observations introducing
uncorrelated random noise in model measurements. The obtained dependence
(solid curves in Fig. 15) follow a power law with a
slope
![]() for both cameras,
which is near to that obtained from observations.
for both cameras,
which is near to that obtained from observations.
The difference in the observed and expected plots is clearly seen for the FORS2 camera starting from n>15. This divergence is related to systematic errors discussed in Sect. 6. Due to the small magnitude of the errors, they cause only a 5-10% increase in the astrometric error in comparison to that expected in the absence of systematic errors.
Above, in the case of FORS2, we used images with a standard FWHM to avoid any degradation of precision caused by images with abnormal seeing. The Allan deviations with all available measurements used (black dots in Fig. 15) are seen to have an excess of about 30% for n>15.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f20.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg309.png) |
Figure 16:
Astrometric precision (Allan deviation)
for a series of 30 images as a function of magnitude derived from
five-month FORS2 observations
(open circles); the same expected in the case
of a very dense reference frame (
|
| Open with DEXTER | |
Given a series of 30 images (0.5-1 h of telescope time),
the precision of FORS1/2 astrometry
(Fig. 15) is about 50 ![]() as.
At this
fixed number of images, Fig. 16 (open circles)
shows the dependence of the precision on star brightness
computed for each star as the individual Allan deviation. Data refer
to FORS2 for which sufficiently long observation series
are available and for images obtained at normal seeing.
Because precision very much depends on
the reference frame noise (especially for bright targets),
the plot shows only those stars for which
as.
At this
fixed number of images, Fig. 16 (open circles)
shows the dependence of the precision on star brightness
computed for each star as the individual Allan deviation. Data refer
to FORS2 for which sufficiently long observation series
are available and for images obtained at normal seeing.
Because precision very much depends on
the reference frame noise (especially for bright targets),
the plot shows only those stars for which
![]()
![]() as. For that reason, many
of the brightest 16.5-17.0 mag stars were omitted due to their peripheral
location in the frame.
The observed dependence of precision on magnitude shows it to be
better than 100
as. For that reason, many
of the brightest 16.5-17.0 mag stars were omitted due to their peripheral
location in the frame.
The observed dependence of precision on magnitude shows it to be
better than 100 ![]() as for R<19 mag targets and about 50
as for R<19 mag targets and about 50 ![]() as
for
as
for
![]() mag.
mag.
The above estimate includes the error caused by reference frame and optical aberrations
which depend on a particular density of star distribution in the sky,
stability of the optical system, and
variations of seeing conditions at the period of observations.
Precision improves with improved conditions.
A case of interest is the precision expected
at high reference star density (
![]() )
and image motion
)
and image motion
![]()
![]() as, typical for a
reference frame size of 0.7-1.5
as, typical for a
reference frame size of 0.7-1.5![]() .
These estimates,
shown by a solid line in
Fig. 16, prove the feasibility of 50
.
These estimates,
shown by a solid line in
Fig. 16, prove the feasibility of 50 ![]() as astrometric precision
for brightest targets.
as astrometric precision
for brightest targets.
8 Conclusion
Astrometric quantities (residuals of positions, model parameters) derived from the processing of images are intrinsically relative. They are computed in a certain system and relative to the frame of reference objects specific to the particular target. These peculiarities of differential reduction should be taken into account for the interpretation of the output data and in more complicated cases of handling inhomogeneous series of images, for instance obtained in different spectral bands or even with different cameras, which is a case expected for long-term programmes. We demonstrated that a careful processing of B and R images in a common system does not degrade precision.
The precision of astrometric imaging at VLT
depends on several noise sources. Uncertainty of the
image photocenter determination
![]() ,
of course, is the dominant component of
the total error. Our data show that Eq. (1) provides
a correct estimate of this error, at least with an accuracy of
,
of course, is the dominant component of
the total error. Our data show that Eq. (1) provides
a correct estimate of this error, at least with an accuracy of ![]() 5%,
for a wide range of light fluxes and seeing conditions.
5%,
for a wide range of light fluxes and seeing conditions.
![]() depends not on the star magnitude but
on the light flux collected in the star image.
For that reason, the lowest
depends not on the star magnitude but
on the light flux collected in the star image.
For that reason, the lowest
![]() (equally, best astrometric
precision) is expected for images at saturation level, which depends on the
exposure, filter, pixel scale, and seeing. Therefore, having, for example,
dependence
(equally, best astrometric
precision) is expected for images at saturation level, which depends on the
exposure, filter, pixel scale, and seeing. Therefore, having, for example,
dependence
![]() of
of
![]() on magnitude R, it is easy
to apply it to other observations. For instance, in B band
on magnitude R, it is easy
to apply it to other observations. For instance, in B band
![]() where
where ![]() is
the difference of magnitudes of images with equal light flux in B and R bands. This scaling is illustrated in Fig. 9
where
is
the difference of magnitudes of images with equal light flux in B and R bands. This scaling is illustrated in Fig. 9
where
![]() and
and
![]() are seen to be
the same dependences shifted by
are seen to be
the same dependences shifted by
![]() mag.
mag.
Mitigation of atmospheric image motion at ![]() s exposure does not
present a problem due to its small amplitude in comparison to other random
noise components. Quite unexpectedly, however, we found that the measured
image motion variance is the same at the very different T=70 and
s exposure does not
present a problem due to its small amplitude in comparison to other random
noise components. Quite unexpectedly, however, we found that the measured
image motion variance is the same at the very different T=70 and
![]() s
exposure. We consider this as a new type of random error
caused by the combined effect of the telescope-related
asymmetry of star profiles and of random
changes in the atmospheric PSF. We have found that images with abnormally
bad and good seeing are affected by large random and systematic errors
and thus their use should be avoided in precision astrometry.
s
exposure. We consider this as a new type of random error
caused by the combined effect of the telescope-related
asymmetry of star profiles and of random
changes in the atmospheric PSF. We have found that images with abnormally
bad and good seeing are affected by large random and systematic errors
and thus their use should be avoided in precision astrometry.
Estimates of astrometric errors obtained in this study refer rather to precision caused by stochastic error components but not to accuracy. The final astrometric accuracy can degrade compared to precision due to systematic errors incorporated into the reference frame and then propagated by the reduction model. Presently, our astrometric results cannot be cross-compared against independent datasets and analyses of common objects, which could provide direct estimates of the long-term accuracy. In Sect. 6,7, however, we demonstrated that the measured star displacements in space and time are fitted to nearly white noise residuals with a variance predicted by the model, therefore, an extra systematic component (if present) should closely trace both the parallactic and proper motion of each star. A too low probability of this scenario (considering large accumulated Dof) implies that the accuracy of the VLT relative parallax and proper motion determination is comparable to the precision.
We have demonstrated that, with reference to systematic errors,
astrometry at FORS1/2 is accurate to 25 ![]() as at five month
and 6 year time intervals. Due to that fact,
relative
proper motions and trigonometric parallaxes of stars in the test
field were derived
with a precision of 20
as at five month
and 6 year time intervals. Due to that fact,
relative
proper motions and trigonometric parallaxes of stars in the test
field were derived
with a precision of 20 ![]() as yr-1 and 40
as yr-1 and 40 ![]() as respectively
for 17-19 mag stars. Thus distances to stars at 1 kpc
can be measured with a precision of 4%,
providing a correction from relative to absolute parallax is added.
This level of accuracy and, especially, good long-term
stability, has numerous astrometric applications
including measurement of astrometric microlensing,
planet detection and characterization by measuring reflex
motion of the parent star, and kinematics of Galactic stellar populations.
In the context of exoplanet searches, the use of the VLT
to search for planets near brown dwarfs is very efficient.
With a 2 year observation programm,
Saturn mass planets with orbit periods longer than 1 year
and Netpune mass planets with 2 year periods
are detectable for brown dwarfs located at 10-20 pc. These
observations will make a real breakthrough in our understanding of planet
and brown dwarf formation by
probing a separation and mass range that is poorly suited to
other techniques.
as respectively
for 17-19 mag stars. Thus distances to stars at 1 kpc
can be measured with a precision of 4%,
providing a correction from relative to absolute parallax is added.
This level of accuracy and, especially, good long-term
stability, has numerous astrometric applications
including measurement of astrometric microlensing,
planet detection and characterization by measuring reflex
motion of the parent star, and kinematics of Galactic stellar populations.
In the context of exoplanet searches, the use of the VLT
to search for planets near brown dwarfs is very efficient.
With a 2 year observation programm,
Saturn mass planets with orbit periods longer than 1 year
and Netpune mass planets with 2 year periods
are detectable for brown dwarfs located at 10-20 pc. These
observations will make a real breakthrough in our understanding of planet
and brown dwarf formation by
probing a separation and mass range that is poorly suited to
other techniques.
Currently our method has several crucial limitations. It is applicable to moderately populated sky areas with low rates of blending but that are rich enough to provide a sufficient number of reference stars. Also, targets brighter than 15-16 mag not can be measured due to saturation if the exposure time is not too short. Therefore it is not applicable to highly crowded sky areas like those used for microlensing works and to bright, nearby solar-type stars which are objects of interest for planet searches. Most of these limitations originate from the star profile fitting and can be removed with use of a better technique for determination of star photocenters. Precision astrometry is also problematic for telescopes with segmented primary mirrors that produce intrinsic complex and time-variable PSF.
We emphasize that the results of this study do not refer to
a specific telescope, they validate precision astrometry for a whole class
of large ground-based imaging telescopes. Astrometry benefits
highly from the use of large apertures, mitigating in this way both
the principal image centroiding component
of the total error and atmospheric image motion. For future 30 m telescopes,
the astrometric precision is expected to be 10 ![]() as or better for image
series of 0.5 h duration.
At this precision, we are challenged with a wide spectrum of problems,
e.g. the ability to measure bright objects due to saturation
and the predominance of systematic errors caused by optical aberrations.
as or better for image
series of 0.5 h duration.
At this precision, we are challenged with a wide spectrum of problems,
e.g. the ability to measure bright objects due to saturation
and the predominance of systematic errors caused by optical aberrations.
References
- Avila, G., Rupprecht, G., & Beckers, J. M. 1997, Proc. SPIE, 2871, 1135 [NASA ADS] (In the text)
- Boden, A. F., Colavita, M. M., Lane, B. F., et al. 1999, ASP Conf. Ser., 194, 84 [NASA ADS] (In the text)
- Cameron, P. B., Britton, M. C., & Kulkarni, S. R. 2008, AJ, 137, 83 [NASA ADS] [CrossRef] (In the text)
- Casertano, S., Lattanzi, M. G., Sozzetti, A., et al. 2008, A&A, 482, 699 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Delplancke, F., Leveque, S., Kervella, P., et al. 2000, Proc. SPIE 4006, 365 (In the text)
- Irwin, M. J. 1985, MNRAS, 214, 575 [NASA ADS] (In the text)
- Lane, B. F., & Muterspagh, M. W. 2004, ApJ, 601, 1129 [NASA ADS] [CrossRef] (In the text)
- Lane, B. F., Colavita, M. M., Boden, A. F., et al. 2000, Proc. SPIE, 4006, 452 [NASA ADS] (In the text)
- Lazorenko, P. F. 2002, A&A, 382, 1125 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lazorenko, P. F. 2006, A&A, 449, 1271 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lazorenko, P. F., & Lazorenko, G. A. 2004, A&A, 427, 1127 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lazorenko, P. F., Mayor, M., Dominik, M., Pepe, F., et al. 2007, A&A, 471, 1057 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lindegren, L. 1980, A&A, 89, 41 [NASA ADS] (In the text)
- Lindegren, L., Babusiaux, C., Bailer-Jones, C., et al. 2007, in A Giant Step: from Milli- to Micro-arcsecond Astrometry, ed. W. J. Jin, I. Platais, & M. A. C. Perryman, Proc. IAU Symp., 248, 217 (In the text)
- Monet, D. G., Dahn, C. C., Vrba, F. J., et al. 1992, AJ, 103, 638 [NASA ADS] [CrossRef] (In the text)
- Motch, C., Zavlin, V. E., & Haberl, F. 2003, A&A, 408, 323 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Moutou, C., Pont, F., Bouchy, F., & Mayor, M. 2004, A&A, 424, L31 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Muterspagh, M. W., Lane, B. F., Konacki, M., et al. 2006, Proc. SPIE, 6268, 16 (In the text)
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pravdo, S., & Shaklan, S. 1996, AJ, 465, 264 [NASA ADS] [CrossRef] (In the text)
- Shao, M., & Colavita, M. M. 1992, A&A, 262, 353 [NASA ADS] (In the text)
Footnotes
- ... FORS1/2
![[*]](/icons/foot_motif.png)
- Based on observations made with ESO telescopes at the La Silla Paranal Observatory under programme ID 078.C-0074 and observations made with the European Southern Observatory telescopes obtained from the ESO/ST-ECF Science Archive Facility.
- ...
![[*]](/icons/foot_motif.png)
- Royal Society University Research Fellow.
All Tables
Table 1: Summary of the test field observations.
Table 2: Minimum and optimal radii of reference fields.
Table 3:
Coefficients of Eq. (34):
derived in this study B[![]() as], b;
predicted
as], b;
predicted ![]() ,
,
![]() by atmospheric model (Lazorenko & Lazorenko 2004);
and B', b' obtained from
a single series of FORS2 images (Lazorenko 2006).
by atmospheric model (Lazorenko & Lazorenko 2004);
and B', b' obtained from
a single series of FORS2 images (Lazorenko 2006).
Table 4:
Systematic component A [![]() as]
in residuals Ve
and in
as]
in residuals Ve
and in
![]() within central CCD zones of r radii.
within central CCD zones of r radii.
All Figures
| |
Figure 1:
Ratio
|
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
Characteristics of reference frame:
error
|
| Open with DEXTER | |
| In the text | |
| |
Figure 3:
Example of B=20.8 star motion over a CCD traced for
6 years with FORS1 and 5 months with FORS2: measured
positions (open circles with error bars) and
model track (solid curves). Reduction was performed
with parameters k=10 and R=1.5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\includegraphics[width=8.5cm,clip]{12026fg4.eps} }\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg217.png) |
Figure 4:
Astrometric precision of
relative proper motions (open circles)
determined from FORS1 images with a six year time span
and trigonometric parallaxes (triangles) derived from FORS2 images with
corrections based on FORS1 proper motions.
Reductions performed with k=10 and R=1.5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026fg5.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{12026fg6.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg228.png) |
Figure 5:
Image-to-image change of FORS1 residuals Vfor a) a faint 22 mag star (
|
| Open with DEXTER | |
| In the text | |
| |
Figure 6:
Standard deviation (scatter with respect to k) of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026fg8.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{12026fg9.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg243.png) |
Figure 7:
Initial (dashed lines) and corrected (solid lines) residuals
of the error expansion (32)
computed at minimum reference field size
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f10.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{12026f11.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg251.png) |
Figure 8:
Correction
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f12.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg256.png) |
Figure 9:
Astrometric precision of a single photocenter measurement:
observed (open circles) and model estimate
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f13.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{12026f14.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg260.png) |
Figure 10:
Image motion |
| Open with DEXTER | |
| In the text | |
| |
Figure 11:
Monthly normal points (average residuals) Ve for stars
observed with FORS2. Symbol size refers to
the expected precision of normal points De1/2,
which changes from better than 100 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f16.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg281.png) |
Figure 12:
Histograms of
|
| Open with DEXTER | |
| In the text | |
| |
Figure 13:
Global pattern of FORS1 systematic error distribution
over the CCD surface: a) in normal points Ve and b) in merged residuals
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f18.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg301.png) |
Figure 14:
Distribution
over the CCD surface of a systematic component in FORS2 epoch residuals
in Jan. 2007:
a) in Ve computed with k=10 and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f19.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg305.png) |
Figure 15:
Normalized Allan deviation (right axis)
in positional residuals
and astrometric precision for bright targets
(left axis) expected from a series of n images with standard seeing only.
Estimates are based on: residuals V obtained with
k=6...16 (dashed lines which for FORS2
actually run into a single line); merged residuals
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12026f20.eps}
\end{figure}](/articles/aa/full_html/2009/38/aa12026-09/Timg309.png) |
Figure 16:
Astrometric precision (Allan deviation)
for a series of 30 images as a function of magnitude derived from
five-month FORS2 observations
(open circles); the same expected in the case
of a very dense reference frame (
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



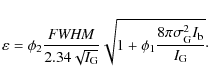
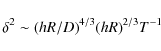
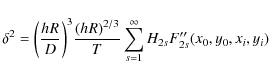
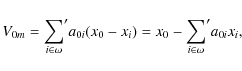
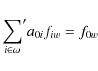
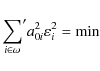
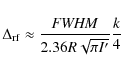
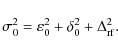

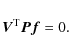
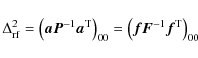
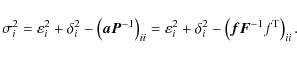
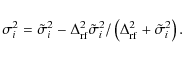
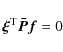
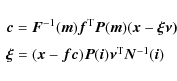
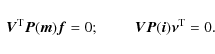
![\begin{displaymath}\begin{array}{l}
\sigma^2_{0m} = \varepsilon_{0}^2 + \delta_...
...\nu } \right]_{mm}
\quad {\rm ref. \; star} \; i.
\end{array}\end{displaymath}](/articles/aa/full_html/2009/38/aa12026-09/img160.png)
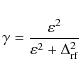
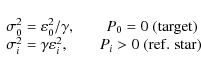
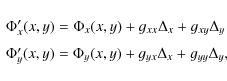
![\begin{displaymath}
\Delta_{\rm {res}}^2=\sigma_{i}^2- \varepsilon_{i}^2-\Delta_...
...vec {\nu}^{\rm T} \vec{N}^{-1}(\vec{i}) \vec{\nu} \right]_{mm}
\end{displaymath}](/articles/aa/full_html/2009/38/aa12026-09/img246.png)
![\begin{displaymath}
\sigma_{ {V}}^2=
(1+\varphi)\varepsilon_{i}^2+ (1+\varphi)...
...ec{\nu}^{\rm T} \vec{N}^{-1}(\vec{i}) \vec{\nu }\right]_{mm} .
\end{displaymath}](/articles/aa/full_html/2009/38/aa12026-09/img254.png)