| Issue |
A&A
Volume 504, Number 3, September IV 2009
|
|
|---|---|---|
| Page(s) | 719 - 726 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200912099 | |
| Published online | 24 July 2009 | |
Metal enrichment of the intra-cluster medium by thermally and cosmic-ray driven galactic winds
An analytical prescription for galactic outflows
W. Kapferer1 - T. Kronberger1 - D. Breitschwerdt2 - S. Schindler1 - E. van Kampen1 - S. Kimeswenger1 - W. Domainko3 - M. Mair1 - M. Ruffert4
1 - Institute for Astro- and Particle Physics, University
of Innsbruck, Technikerstr. 25, 6020 Innsbruck, Austria
2 -
Zentrum für Astronomie und Astrophysik, Technische
Universität Berlin, Hardenbergstrasse 36, 10623 Berlin, Germany
3 -
Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany
4 -
School of Mathematics and Maxwell Institute, University of Edinburgh, Edinburgh EH9 3JZ, Scotland, UK
Received 18 March 2009 / Accepted 14 July 2009
Abstract
Aims. We investigate the efficiency and time-dependence of thermally and cosmic ray driven galactic winds for the metal enrichment of the intra-cluster medium (ICM) using a new analytical approximation for the mass outflow. The spatial distribution of the metals are studied using radial metallicity profiles and 2D metallicity maps of the model clusters as they would be observed by X-ray telescopes like XMM-Newton.
Methods. Analytical approximations for the mass loss by galactic winds driven by thermal and cosmic ray pressure are derived from the Bernoulli equation and implemented in combined N-body/hydrodynamic cosmological simulations with a semi-analytical galaxy formation model. Observable quantities like the mean metallicity, metallicity profiles, and 2D metal maps of the model clusters are derived from the simulations.
Results. We find that galactic winds alone cannot account for the observed metallicity of the ICM. At redshift z=0 the model clusters have metallicities originating from galactic winds which are almost a factor of 10 lower than the observed values. For massive, relaxed clusters we find, as in previous studies, a central drop in the metallicity due to a suppression of the galactic winds by the pressure of the ambient ICM. Combining ram-pressure stripping and galactic winds we find radial metallicity profiles of the model clusters which agree qualitatively with observed profiles. Only in the inner parts of massive clusters the observed profiles are steeper than in the simulations. Also the combination of galactic winds and ram-pressure stripping yields too low values for the ICM metallicities. The slope of the redshift evolution of the mean metallicity in the simulations agrees reasonably well with recent observations.
Key words: galaxies: clusters: general - intergalactic medium - ISM: jets and outflows - methods: numerical
1 Introduction
A well observable consequence of the interaction processes between
galaxies and the hot, thin intra-cluster medium (ICM) is the high
metal abundance (![]() 0.3 in solar units) in the intra-cluster
gas. These heavy elements cannot be primordial but must have been
mostly processed in stars within galaxies, and transported to the
ICM by some interaction processes. Galactic winds were one of the
first origins proposed for metal enriched gas found by X-ray
observations (De Young 1978). Recently, it has been shown (Everett
et al. 2008) that the best model to explain the soft X-ray emission
of the Milky Way halo from ROSAT observations is a cosmic ray driven
galactic wind. Further mechanisms that can act as enrichment process
are ram-pressure stripping (Gunn & Gott 1972), tidal interactions
(Gnedin 1998; Kapferer et al. 2005), active galactic nuclei
(AGNs) (e.g. Moll et al. 2007), and intra-cluster supernovae
(Domainko et al. 2004).
0.3 in solar units) in the intra-cluster
gas. These heavy elements cannot be primordial but must have been
mostly processed in stars within galaxies, and transported to the
ICM by some interaction processes. Galactic winds were one of the
first origins proposed for metal enriched gas found by X-ray
observations (De Young 1978). Recently, it has been shown (Everett
et al. 2008) that the best model to explain the soft X-ray emission
of the Milky Way halo from ROSAT observations is a cosmic ray driven
galactic wind. Further mechanisms that can act as enrichment process
are ram-pressure stripping (Gunn & Gott 1972), tidal interactions
(Gnedin 1998; Kapferer et al. 2005), active galactic nuclei
(AGNs) (e.g. Moll et al. 2007), and intra-cluster supernovae
(Domainko et al. 2004).
With the first generation of X-ray satellites it was just possible
to measure radial metallicity profiles (see e.g. De Grandi et al.
2004; Boehringer et al. 2005; Baldi et al. 2007; Sato et al. 2009).
Using the current satellites XMM and CHANDRA also the 2D spatial
distribution of the metals became measurable, i.e. metallicity maps
(e.g. Schmidt et al. 2002; Furusho et al. 2003; Sanders et al. 2004;
Fukazawa et al. 2004; Hayakawa et al. 2004). These maps show clearly
a non-uniform and non-spherical distribution of the metals, which
agrees with the results of simulations (e.g. Schindler et al. 2005).
Recent observations also shed some light on the redshift evolution
of the metallicity. Balestra et al. (2007) showed that there is a
mild evolution of the Fe content in the ICM with redshift. From
observations of 56 clusters they conclude that the average Fe
content of the ICM in local clusters is a factor of ![]() 2
larger than at
2
larger than at
![]() ,
even though with a large scatter.
Maughan et al. (2007) confirmed this result with a sample of 115
clusters of galaxies in a redshift interval
0.1 < z < 1.3
observed with Chandra.
,
even though with a large scatter.
Maughan et al. (2007) confirmed this result with a sample of 115
clusters of galaxies in a redshift interval
0.1 < z < 1.3
observed with Chandra.
Numerical simulations are widely used to investigate the efficiency and time dependence of the various processes. Several groups have simulated one or more of the possible enrichment mechanisms of an isolated galaxy, e.g. ram-pressure stripping (Abadi et al. 1999; Quilis et al. 2000; Toniazzo & Schindler 2001; Schulz & Struck 2001; Vollmer et al. 2001) or galactic winds (e.g. Tenorio-Tagle & Munoz-Tunon 1998; Strickland & Stevens 2000).
On galaxy cluster scales metal enrichment processes are implemented
into cosmological simulations to explain the overall enrichment of
the ICM. De Lucia et al. (2004) and Nagashima et al. (2005) use
combined semi-analytic techniques and N-body simulations to
calculate the overall ICM metallicity. They find that mainly massive
galaxies contribute to the enrichment and that there is a mild metal
evolution since z=1 and a stronger evolution for z > 1. Tornatore et al. (2004, 2007) and Valdarnini (2003) use smoothed particle
hydrodynamics (SPH) with detailed yields from type Ia and II
supernovae. Cora (2006) also uses combined N-body/SPH simulations
together with a semi-analytic model. Aguirre et al. (2001)
investigated the efficiency of galactic winds at
![]() .
They
did, however, not calculate the distribution of the metals that
arise from the winds. They conclude that there are degeneracies in
the results and that other enrichment processes might lead to the
same result.
.
They
did, however, not calculate the distribution of the metals that
arise from the winds. They conclude that there are degeneracies in
the results and that other enrichment processes might lead to the
same result.
In Kapferer et al. (2007a) we have simulated, for the first time, two enrichment processes (galactic winds and ram-pressure stripping) acting simultaneously. Compared to our previous work (Schindler et al. 2005; Kapferer et al. 2006; Domainko et al. 2006; Moll et al. 2007) this investigation was extended to high redshifts. With this approach a reasonable agreement with observed metallicity profiles was achieved. The wind model adopted in Kapferer et al. (2007a) was, however, a phenomenological one, in which the mass loss scales linearly with the star formation rate of the galaxy. This model does not allow for a deeper insight into the physical processes involved in the outflow and neglects environmental effects such as the possible suppression of galactic winds by high ICM pressure (Schindler et al. 2005). We extend here the work presented in Kapferer et al. (2007a) by introducing a new analytical model for the mass loss due to galactic winds. A major advantage of this implementation of outflows by galactic winds presented in this work compared to the outflow model in Schindler et al. (2005) is the analytical nature of the calculation. Whereas in Schindler et al. (2005) the mass outflow was calculated with an external numerical scheme (Breitschwerdt et al. 1991) individually for each galaxy at each timestep, the scheme presented in this work can be easily implemented on top of semi-analytical models due to its analytical nature.
The paper is organized as follows: in Sect. 2 we present the new analytical model used for this work. In Sect. 3 we present the numerical setup and the implementation of the analytical model. The results are presented and compared to observations in Sect. 4. We end with a summary of the main conclusions in Sect. 5.
2 Analytical wind model
An analytical model for galactic winds driven by thermal, cosmic
ray, and magnetohydrodynamic (MHD) wave pressure has been presented
by Breitschwerdt et al. (1991). To account for the plane-parallel
geometry of the outflow near the disc and the spherical geometry at
large distances from the disc, Breitschwerdt et al. (1991) use a
flux tube geometry, where the area cross section A(z) varies as
![\begin{displaymath}A(z)=A_0 \left[1+\left(\frac{z}{Z_0}\right)^2\right]\cdot
\end{displaymath}](/articles/aa/full_html/2009/36/aa12099-09/img4.png) |
(1) |
Here z denotes the height above the plane of the galaxy, A0 the area at a reference level typically 1kpc above the plane of the galaxy, and Z0 is the height above the galactic plane, at which flux tube divergence becomes significant, taken to be equal to the galactic radius here. In this geometry the conservation of mass and energy of the outflow can be written as
and
where
Using Eq. (3), the Bernoulli equation, we derive an
analytical approximation for the mass loss due to thermally driven
winds. With the continuity equation Eq. (2) and the
assumptions
![]() and
and
![]() ,
Eq. (3)
simplifies to
,
Eq. (3)
simplifies to
where the subscripts 0 refer to the quantities at the reference level, taken to be at z=1 kpc. While the subscript
Here we have also used
where we inserted the relation
for the sound speed c and the definition of the escape velocity
| (8) |
The total mass loss of a galaxy due to galactic winds can be found by integrating Eq. (2) over the galactic disc or the area over which mass loss occurs, i.e.
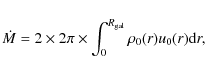 |
(9) |
where
In the same way Breitschwerdt et al. (1991) derived an analytical
approximation for the mass loss due to cosmic ray driven winds, i.e.
the case where
![]() and
and
![]() ,
which reads
,
which reads
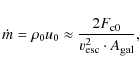 |
(10) |
where
This model is ideally suited for high resolution N-body/hydrodynamic simulations, in which the galaxies and the inter-stellar medium (ISM) are spatially resolved. Most quantities in Eq. (6) would be known directly from the simulations and the initial outflow velocity u0 could be directly measured in such simulations. Our setup, however, does not allow such a procedure, as we do not have the internal velocity field of the ISM near the reference level. Therefore, in the following, we have to rely on several assumptions about the thermodynamic properties of the ejected gas, i.e. its temperature and density. These uncertainties have to be kept in mind when interpreting the presented results.
3 Simulations
We implement the prescription of galactic wind mass loss given by
Eq. (2) into the setup described in Kapferer et al.
(2007a) which was improved with respect to the setup used in
Schindler et al. (2005), Kapferer et al. (2006) and Domainko et al.
(2006) by the use of comoving coordinates in the hydrodynamic code.
In this setup we use different code modules to calculate the main
components of a galaxy cluster in the framework of a standard
![]() CDM cosmology, i.e. using
CDM cosmology, i.e. using
![]() ,
,
![]() ,
h=0.7,
,
h=0.7,
![]() ,
and
,
and
![]() .
In the following subsections we will detail these
code modules and their interplay.
.
In the following subsections we will detail these
code modules and their interplay.
3.1 Dark Matter and galaxy formation models
The non-baryonic dark matter (DM) component is calculated using GADGET2 (Springel 2005) with constrained random field initial conditions (Hoffman & Ribak 1991; implemented by van de Weygaert & Bertschinger 1996). From the resulting DM distribution we calculate at each time step the underlying gravitational potential for the hydrodynamic code by solving the Poisson equation. Additionally we can calculate the dynamically fully described orbits and the merger tree of galaxy haloes from the DM distribution.
The properties of the galaxies are calculated by an improved version (van Kampen et al. 2005) of the galaxy formation code of van Kampen et al. (1999) which is a semi-analytic model in the sense that the merging history of galaxy haloes is taken directly from the cosmological N-body simulation. Halo mergers are identified in the N-body simulations as events in which a new halo is formed that is both virialised and contains at least two progenitors. Gas that cools within virialised haloes is assumed to settle in a disc with an exponential profile. To set the disk-scale length we use the model of Mo et al. (1998), with the distinction that we measure the angular momentum of the dark halo from the N-body simulation data instead of assuming an analytical model for it. Gas-rich galaxies undergo a burst of star formation during a halo merger event. Galaxy-galaxy mergers are treated in a different way: all galaxies within a dark matter halo or subhalo suffer from dynamical friction, and will merge with the central galaxy eventually, triggering a starburst as well. This starburst uses up most of the cold gas left in the satellite, however not all is turned into stars due to supernovae feedback, which heats the surrounding gas. Stars which are formed during halo merger events and galaxy-galaxy mergers contribute to the stellar mass of the bulge. In between merger events star formation is quiescent in discs with a threshold according to the Kennicutt criterion (Kennicutt 1998). Stellar evolution is modelled using the stellar population synthesis models of Bruzual & Charlot (2003). A fraction of the metals formed in stars is ejected by supernovae and stellar winds into the surrounding inter-stellar medium (ISM). The metals that end up in the hot gas component also affect the metallicity dependent cooling rates (Sutherland & Dopita 1993). Yields are taken from the metallicity evolution model of Matteucci & Francois (1989), in a manner as described in van Kampen et al. (1999), which includes SN types I and II. The evolution of the metallicity is followed for the stellar populations as well as for the cold and hot gas reservoirs, and exchanges are tracked as well. Material returned to the cold ISM by stellar winds and supernovae has been chemically enriched by the nuclear processes inside the stars.
3.2 Hydrodynamics
For the treatment of the ICM we use comoving Eulerian hydrodynamic
parts with shock capturing scheme (PPM, Collela & Woodward 1984),
with a fixed mesh refinement (Ruffert 1992) on four levels and
radiative cooling (Sutherland & Dopita 1993). For the initial
conditions of the hydrodynamic simulation we distribute the gas as
the dark matter in a Gaussian random field at z=40. The largest of
the four nested grids covers a comoving volume of (20 Mpc)3. Each
finer grid covers
![]() of the volume of the next larger
grid. Using a resolution of 1283 grid cells on each grid we
obtain a finest spacing of
of the volume of the next larger
grid. Using a resolution of 1283 grid cells on each grid we
obtain a finest spacing of ![]() 19.5 kpc comoving for each cell on
the innermost grid. The N-body and hydrodynamic code are calculated
starting at z=40, while the semi-analytic galaxy formation model
covers the redshift interval from z=20 to z=0.
19.5 kpc comoving for each cell on
the innermost grid. The N-body and hydrodynamic code are calculated
starting at z=40, while the semi-analytic galaxy formation model
covers the redshift interval from z=20 to z=0.
3.3 The model galaxy clusters
With this numerical setup we model a sample of merging systems, from which we draw a non-cooling flow cluster which is a lower mass cluster with several strong sub-cluster mergers. We will name this model cluster hereafter ``model cluster A''. The second model cluster we use for this analysis is a more massive merging system with about twice the mass of model cluster A and several minor merger events. This model cluster will be referred to as ``model cluster B''. These model clusters were also used in Kapferer et al. (2007a), with respect to the initial conditions of the dark matter and the baryonic matter. Main improvements were done regarding the semi-analytical galaxy formation model. One improvement is the change of the IMF, where we now use the IMF proposed by Chabrier (2003). This produces better fits to the luminosity function without large changes to the star formation history. Other improvements include adopting a 40% shorter galaxy merger rate timescale, and a different ratio for the distinction between minor and major mergers, which is now 0.3. In the previous model the metallicity of the cold gas in the disc galaxies was higher, therefore the stripping leads to higher metallicities in the ICM. To constrain the model parameters for the semi-analytical model which is applied, we made sure to reproduce the Tully-Fisher relation and the global star formation history. The luminosity functions in the B-band (star forming galaxies) and the K-band (passively evolving galaxies) are in good agreement around L* in both bands, but overpredict abundances at the bright end. This problem is usually fixed by implementing an AGN feedback recipe, which the model used for this work does not include. For completeness we summarise here the main properties of the two model clusters as described in Kapferer et al. (2007a).
- Model Cluster A: the cluster starts to form at
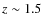 and has two major merger events at z=0.8 and z=0.5. The total mass
at z=0 is
and has two major merger events at z=0.8 and z=0.5. The total mass
at z=0 is
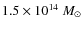 in a sphere with 1 Mpc
radius.
in a sphere with 1 Mpc
radius.
- Model Cluster B: the formation redshift for this
cluster is
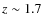 .
Four minor merger events appear at z = 1.4,
z = 1.1, z = 0.5 and z=0.3. The cluster has a final mass of
.
Four minor merger events appear at z = 1.4,
z = 1.1, z = 0.5 and z=0.3. The cluster has a final mass of
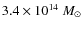 within a sphere of 1 Mpc radius.
within a sphere of 1 Mpc radius.
3.4 Implementation of the analytical wind model into the numerical setup
The semi-analytic galaxy formation model limits the applicability of
Eq. (6), because it does not give spatially resolved
information about the star formation. Instead it gives a global
value for the disc. Density and temperature distributions are also
unknown. Therefore, to make use of Eq. (6) in our
numerical setup, we have to rely on several assumptions. To
calculate the gravitational potential and its escape velocity, we
assume for the dark matter halo a Hernquist (1990) potential:
where a is a scale length and
For the potential of the disc we use a Toomre (1963) model (first derived by Kuzmin 1956), which is given by
where r and z denote the cylindrical coordinates and b is a non-zero scale length. The potential at a certain radius can then be directly calculated from Eqs. (11) and (13), using the total mass of the disc and of the dark matter halo. The scale length a in Eq. (11) follows from the disc scale length of an exponential disc
The terminal velocity of the outflow
![]() is also unknown,
so we assume
is also unknown,
so we assume
![]() .
Breitschwerdt et al. (1991) have
shown that the terminal velocity of the wind
.
Breitschwerdt et al. (1991) have
shown that the terminal velocity of the wind
![]() and the
escape velocity of the system
and the
escape velocity of the system
![]() differ typically by not more
than a factor of two. We have tested the consequences of this
uncertainty by using
differ typically by not more
than a factor of two. We have tested the consequences of this
uncertainty by using
![]() and
and
![]() ,
respectively. We found that quantitatively
the resulting absolute metallicity values change up to a factor of
three. The resulting metal distribution (radial profiles and 2D
metal maps) and the redshift evolution of the metallicity, however,
are only marginally affected. Given all the uncertainties in the
simulation setup, e.g. within the semi-analytical galaxy formation
model, this uncertainty appears acceptable.
,
respectively. We found that quantitatively
the resulting absolute metallicity values change up to a factor of
three. The resulting metal distribution (radial profiles and 2D
metal maps) and the redshift evolution of the metallicity, however,
are only marginally affected. Given all the uncertainties in the
simulation setup, e.g. within the semi-analytical galaxy formation
model, this uncertainty appears acceptable.
To derive the sound speed we would require a pressure and density
distribution through the gaseous disc, which is not available from
the semi-analytic model. Therefore, we follow the argumentation line
of Breitschwerdt et al. (1991), who estimated that for a Milky-Way
type galaxy with a supernova rate of once every 30 years the time
averaged halo filling factor is of order unity. Therefore the
pressure support for a flux tube should be, on average, maintained.
We couple the supernova rate to the star formation rate (SFR) via
the assumption of a Salpeter initial mass function (IMF) with a
slope of -1.35 in the range of 0.1 ![]() and 40
and 40 ![]() .
A
model galaxy is hence having a galactic wind driven purely by
thermal pressure if the SFR exceeds a certain threshold, for which
we adopt here a value of 4
.
A
model galaxy is hence having a galactic wind driven purely by
thermal pressure if the SFR exceeds a certain threshold, for which
we adopt here a value of 4 ![]() /yr. Below this SFR the galaxy
can still have a cosmic ray driven wind, for which we calculate the
mass loss using Eq. (10). As in Breitschwerdt et al. (1991) we then
assume that the flux tubes are homogeneously distributed over the
galactic disc. This obvious oversimplification is necessary, as we
have no information on the location of the supernovae from the
semi-analytical model. We set the temperature and the density at the
reference level to
/yr. Below this SFR the galaxy
can still have a cosmic ray driven wind, for which we calculate the
mass loss using Eq. (10). As in Breitschwerdt et al. (1991) we then
assume that the flux tubes are homogeneously distributed over the
galactic disc. This obvious oversimplification is necessary, as we
have no information on the location of the supernovae from the
semi-analytical model. We set the temperature and the density at the
reference level to
![]() K and
K and
![]() g/cm3, respectively. These are typical values for gas fed into a
galactic wind (e.g. Breitschwerdt et al. 1991). For an outflow to
occur we furthermore demand that the pressure of the outflow exceeds
the pressure of the surrounding ICM.
g/cm3, respectively. These are typical values for gas fed into a
galactic wind (e.g. Breitschwerdt et al. 1991). For an outflow to
occur we furthermore demand that the pressure of the outflow exceeds
the pressure of the surrounding ICM.
4 Results
In the following we investigate the efficiency and the time dependency of galactic winds as enrichment process. In order to compare our results to observed quantities we will present mean metallicities, metallicity profiles, and 2D metal maps of our model clusters. In addition we compare the efficiency of the proposed wind model with ram-pressure stripping as source of metals in the ICM. Metals originating from galaxies, either from galactic winds or ram-pressure stripping, are advected and mixed with the hydrodynamic solution of the ICM for each timestep in the simulation.
4.1 Metallicity profiles
The most basic measure to quantify the metal distribution in the ICM
is its mean metallicity, obtained from emission weighted metallicity
maps. We assume that the X-ray measurements extend to a radius of 1
Mpc and that only galactic winds are acting. Within this volume, the
mean metallicity in solar units (Grevesse & Sauval 1998) is 0.02
and 0.04 at z=0 for model cluster A and B, respectively. For both
model clusters this value is significantly lower than observed
metallicities in real clusters. More information on the metal
distribution is given by radial metallicity profiles, especially by
their slope. The normalisation of the profile depends strongly on
the uncertain ISM metallicity, present in semi-analytic simulations.
In Fig. 1 we present the metallicity profile of model
cluster A and B at redshift z = 0. Note that for these profiles only
metals originating from galactic winds are taken into account. The
metal profiles are obtained from X-ray weighted metal maps (see
Kapferer et al. 2007b). For model cluster A the metallicity is
almost constant up to a radius of ![]() 300 kpc. Beyond
300 kpc. Beyond ![]() 500
kpc the profile decreases constantly. Model cluster B is more
massive than model cluster A and, as a result of a prominent infall
region, the metallicity at a radius of 1 Mpc is with
500
kpc the profile decreases constantly. Model cluster B is more
massive than model cluster A and, as a result of a prominent infall
region, the metallicity at a radius of 1 Mpc is with ![]() 0.03
solar units higher than in cluster A. A striking feature of the
profile is the decreasing metallicity towards the centre of the
cluster. This behaviour is different from model cluster A. Galactic
winds are suppressed by the high central pressure of the ambient
medium, a phenomenon which was already discussed by Schindler et al.
(2005) for quiet (i.e. mainly cosmic-ray driven) galactic winds.
0.03
solar units higher than in cluster A. A striking feature of the
profile is the decreasing metallicity towards the centre of the
cluster. This behaviour is different from model cluster A. Galactic
winds are suppressed by the high central pressure of the ambient
medium, a phenomenon which was already discussed by Schindler et al.
(2005) for quiet (i.e. mainly cosmic-ray driven) galactic winds.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12099_fig1.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12099-09/Timg62.png) |
Figure 1: Radial metallicity profile of model cluster A and B at redshift z=0. For the shown metallicity profiles only metals originating from galactic winds are taken into account. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12099_fig2.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12099-09/Timg63.png) |
Figure 2: Metallicity profiles for observed nearby (z<0.2) clusters (symbols) from Pratt et al. (2007) compared to emission weighted simulated profiles from model cluster A at redshift z=0 with galactic winds (red, solid line) and with combined wind and ram-pressure stripping (red, dashed line) as enrichment processes. |
| Open with DEXTER | |
Finally, we compare the simulated metallicity profiles to observed profiles from Pratt et al. (2007) in Fig. 2. Using only galactic winds as enrichment process (red, solid line), the radial metallicity profile of model cluster A lies at all radii significantly below the observed profiles. The slope agrees reasonably well with the observed values. This result indicates, that additional processes are acting in clusters, presumably ram-pressure stripping and/or AGNs. We calculate the combined effect of galactic winds and ram-pressure stripping and present the result in Fig. 2 (red, dashed line). Ram-pressure stripping was modelled using a Gunn & Gott (1972) criterion, as described in Kapferer et al. (2007a). The profile agrees then reasonably well at most radii. In the very centre (the inner 50 kpc), where our resolution is not sufficient, a central AGN might still be responsible for the observed steepening there. In the very outer parts of the cluster the simulated metallicity profile lies below the observed values.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12099_fig3.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12099-09/Timg64.png) |
Figure 3: Mean metallicity profile from a sample of observed clusters (symbols) from de Grandi et al. (2004) compared to emission weighted simulated profiles from model cluster B with galactic winds (red, solid line) and with combined wind and ram-pressure stripping (red, dashed line) as enrichment processes. |
| Open with DEXTER | |
We carried out the same analysis for model cluster B. However, as
this model cluster is mostly relaxed at redshift z=0, it is not
reasonable to compare it to the set of merging clusters from Pratt
et al. (2007). Therefore we use the mean of cool-core clusters
presented in De Grandi et al. (2004) for comparison. The result is
shown in Fig. 3. Again, with wind as the only
enrichment process, neither the slope nor the absolute values agree
with the observations, especially in the inner parts of the cluster.
Combining winds and ram-pressure stripping leads to reasonable
agreement in the slope of the profiles for radii ![]() kpc. At
smaller radii, however, the mean observed profile is steeper than
our simulated cluster profile. This might be a selection effect, as
we show only a snapshot of one specific model cluster. It may also
indicate, however, that we miss an enrichment process acting in the
centre of massive, relaxed clusters (e.g. enrichment by a central
AGN).
kpc. At
smaller radii, however, the mean observed profile is steeper than
our simulated cluster profile. This might be a selection effect, as
we show only a snapshot of one specific model cluster. It may also
indicate, however, that we miss an enrichment process acting in the
centre of massive, relaxed clusters (e.g. enrichment by a central
AGN).
In the case of the massive galaxy cluster the difference between the phenomenological model for galactic outflow in Kapferer et al. (2007a) and the present work is more striking. In the phenomenological wind model the contribution to the enrichment of the ICM is up to a factor of ten more efficient compared to the wind model presented in this work. The analytical wind model introduced in this work gives much less metallicities compared to the outflow model which scales the outflow linearly with the galaxies' star formation rate. The strong mismatch between the reproduction of the observed metallicity profiles in the case of the massive system B leads to the conclusion that additional sources for metal enrichment in massive galaxy clusters play an important role. In addition the amount of metals originating from ram-pressure stripping is much lower compared to Kapferer et al. (2007a). The explanation lies in the improved semi-analytical model, see Sect. 3.3. The investigation of the metal enrichment through AGNs will be part of an upcoming work.
We note once more, that the absolute values of the profile depend strongly on the adopted parameters of the semi-analytic galaxy formation model and the parameters of the wind model. The slope of the simulated profile, on the contrary, is robust against reasonable changes of the parameters.
Similar studies have been performed by other groups. Tornatore et al. (2007), for example, used an N-body/SPH code. They found generally good agreement of the metallicity profiles with observations. The same is true for Cora (2006), whereas they apply a semianalytical model in their work. Their adopted wind model might, however, overestimate the mass loss caused by galactic winds (see Sect. 4.3).
In Fig. 4 we present the redshift evolution of the mean metallicity of the two model clusters and compare them with the observed evolution of a sample of clusters from Balestra et al. (2007). Both enrichment processes (ram-pressure stripping and galactic winds) are taken into account. For both clusters the evolution agrees with the observational trend but the absolute values are lower than expected from observations. This is especially true at lower redshift (z < 0.5), where the enrichment processes do not seem to be efficient enough. In the observational sample of Balestra et al. (2007) the extraction radius varied roughly from 200-1000 kpc, depending on the signal-to-noise ratio. We assumed a constant extraction radius of 600 kpc, which we also use for comparison of the metallicity profiles with observations. A variation of this radius does not change the general trend significantly. Note that 1 Mpc corresponds roughly to the virial radius of the two galaxy clusters at z = 0.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12099_fig4.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12099-09/Timg66.png) |
Figure 4: Redshift evolution of the mean metallicity of model cluster A (red, dashed line) and model cluster B (red, solid line) compared to the observed evolution of a sample of clusters from Balestra et al. (2007). Both enrichment processes (ram-pressure stripping and galactic winds) are taken into account). |
| Open with DEXTER | |
4.2 X-ray weighted maps
With modern X-ray space telescopes it is feasible to study also the
2D metal distribution. It was found that the metals are not
homogeneously distributed within the ICM (e.g. Sanders et al. 2004;
Durret et al. 2005; O'Sullivan et al. 2005; Sauvageot et al. 2005;
Werner et al. Werner; Sanders & Fabian 2006; Hayakawa et al. 2006;
Finoguenov et al. 2006; Bagchi et al. 2006). In Fig. 5
we present such an X-ray weighted metal map for model cluster A at
redshift z=0. The X-ray surface brightness map is overlayed as
contours and shows the overall ICM distribution. A filament along
which galaxies fall into the cluster is visible at the bottom left.
As the ICM density in the filament is relatively low
(![]()
![]() g/cm3 compared to
g/cm3 compared to
![]()
![]() g/cm3 in the centre), it can be more
easily enriched there (i.e. a higher metal mass fraction is
achieved). In the centre of the cluster the metallicity is slightly
lower.
g/cm3 in the centre), it can be more
easily enriched there (i.e. a higher metal mass fraction is
achieved). In the centre of the cluster the metallicity is slightly
lower.
In Fig. 6 we present the X-ray weighted metal map for model cluster B at redshift z = 0. The X-ray surface brightness map is again overlayed as contours and shows the overall ICM distribution. The suppression of the galactic winds in the centre of the cluster, as discussed in Sect. 4.1, is clearly visible. In the left and upper-right parts of the cluster the outflows of galaxies, falling into the cluster along a filament, cause a complex metallicity pattern with several maxima.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12099_fig5.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12099-09/Timg69.png) |
Figure 5: X-ray weighted metal map for model cluster A at redshift z=0. Overlayed contours indicate the X-ray surface brightness. |
| Open with DEXTER | |
![\begin{figure}
\center
\includegraphics[width=8.8cm,clip]{12099_fig6.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12099-09/Timg70.png) |
Figure 6: X-ray weighted metal map for model cluster B at redshift z=0. Overlayed contours indicate the X-ray surface brightness. |
| Open with DEXTER | |
5 Summary and conclusions
We have investigated the efficiency and time-dependence of thermally and cosmic ray driven galactic winds for the metal enrichment of the intra-cluster medium (ICM) by a combination of a new analytical model and cosmological hydrodynamic simulations. The analytical approximations for the mass loss by galactic winds driven by thermal and cosmic ray pressure were derived from the Bernoulli equation. We extend in this work the previous wind model presented in Kapferer et al. (2007a) by introducing a new analytical model for the mass loss due to galactic winds. This new model does allow a deeper insight into the physical processes involved in the outflow and addresses environmental effects such as the possible suppression of galactic winds by high ICM pressure (Schindler et al. 2005). It is still simple enough to be readily implemented in metal enrichment and semi-analytic galaxy formation models. We simulated the enrichment processes for a galaxy cluster with major merger events (cluster A) and a less merging system (cluster B). Investigating observable quantities, we found that:
- Galactic winds alone cannot account for the observed mean metallicity of the ICM.
At redshift z=0 the model clusters have mean metallicities, which
are almost a factor of 10 lower than observed values. Within a
radius of 1 Mpc model cluster A has a mean metallicity of 0.02 and
model cluster B a metallicity of 0.04 in solar units.
- A central drop in the metallicity of the relatively relaxed model
cluster B is due to a suppression of steady state galactic winds by
the pressure of the ambient ICM. In the merging model cluster A, no
decrease of the metallicity towards the centre is observable.
- 2D metallicity maps reveal important additional information on the metal
distribution, e.g. infalling groups from filaments and
inhomogeneities.
- Combining ram-pressure stripping and galactic winds we
find radial metallicity profiles of the model clusters which agree
in their slopes with observations. In the inner parts of massive
clusters the observed profile is steeper than in the simulations.
- The slope of the redshift evolution of the mean metallicity in the
simulations agrees reasonably well with recent observations of
Balestra et al. (2007).
5.1 What additional processes do enrich the ICM
Ram-pressure stripping and galactic winds, as modelled in this work, are not able to account for the observed metallicities in the ICM. Therefore additional processes need to be taken into account. An important source of enriched matter in the central part of galaxy clusters would be an AGN in a massive central cluster galaxy. The injection of buoyant bubbles in the ICM transports enriched matter from the central cluster galaxy to the surrounding ICM (Roediger et al. 2007). Simionescu et al. (2009) find that 15% of the total amount of Fe in the inner region of the galaxy cluster Hydra A belongs to gas, which is uplifted by buoyant bubbles from the central AGN. This effect would be stronger in relaxed, more massive systems, as the stratification of the ICM is not strongly disturbed by mergers and therefore the bubbles can survive longer.
Ram-pressure stripping, as it is able to trigger star formation in the gaseous wake of stripped galaxies, can enrich the ICM in situ (Kronberger et al. 2008; Kapferer et al. 2008; Kapferer et al. 2009). In the case of strong ram pressures stripping nearly all new stars are formed in the wake of the stripped galaxies. Their influence on the overall metal enrichment is yet unknown, but first simulations of ram-pressure stripping including recipes for star formation point towards the picture that off disc star formation due to ram-pressure stripping is very efficient as an enrichment process of the ICM. Also Intra-cluster stellar populations can enrich the ICM very efficiently as shown in Sivanandam et al. (2009).
Galaxy-galaxy interaction is able to enrich the surroundings by redistributing the ISM kinematically in large volumes around the interacting galaxies (Kapferer et al. 2005). In the model of galactic winds, described in this work, the effect of mergers on the star formation are taken into account, which lead to stronger outflows in the galactic winds. Nevertheless the redistribution of the ISM is not modelled within the presented simulations. The heating of the kinematically redistributed ISM, so that it can contribute to the observed X-ray flux, is not well understood. Hence conclusions on the contribution to the overall enrichment of the ICM due to galaxy interactions have to be investigated in detail.
In a recent paper Fabjan et al. (2008) studied the redshift evolution of the metal content of the ICM with N-body/SPH simulations combined with a detailed model of chemical evolution. They found good agreement with observations for a Salpeter initial mass function. They have shown that gasdynamical processes which redistribute metals, like the sinking of low entropy enriched gas to the central cluster regions, is an additional process that helps explain the increase of the observed emission-weighted metallicity of the ICM at low z. These results also confirm those found by Cora et al. (2008) which were obtained by using a combination of N-body/SPH simulations with an analytic model of galaxy formation.
Concluding, the effects of AGN, ram-pressure stripping induced off-disc star formation and direct enrichment by galaxy-galaxy interactions will be investigated in upcoming works, with the aim to obtain a more complete picture of the relative strength of the enrichment processes in galaxy clusters and the influence on the evolution of the galaxies.
Acknowledgements
We thank the anonymous referee you helped to improve the quality of the paper significantly. The authors further acknowledge the UniInfrastrukturprogramm des BMWF Forschungsprojekt Konsortium Hochleistungsrechnen, the ESO Mobilitätsstipendien des BMWF (Austria), the Austrian Science Foundation (FWF) through grants P18523-N16, P18416-N16, P18493-N08, and P19300-N16, and the Tiroler Wissenschaftsfonds (Gefördert aus Mitteln des vom Land Tirol eingerichteten Wissenschaftsfonds). We also thank Rien van de Weygaert and Ed Bertschinger for allowing us the use of their constrained random field code and Volker Springel for GADGET-2.
References
- Abadi, M. G., Moore, B., & Bower, R. G. 1999, MNRAS, 308, 947 [NASA ADS] [CrossRef] (In the text)
- Aguirre, A., Hernquist, L., Schaye, J., et al. 2001, ApJ, 560, 599 [NASA ADS] [CrossRef] (In the text)
- Bagchi, J., Durret, F., Neto, G. B. L., & Paul, S. 2006, Science, 314, 791 [NASA ADS] [CrossRef] (In the text)
- Baldi, A., Ettori, S., Mazzotta, P., Tozzi, P., & Borgani, S. 2007, ApJ, 666, 835 [NASA ADS] [CrossRef] (In the text)
- Balestra, I., Tozzi, P., Ettori, S., et al. 2007, A&A, 462, 429 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Böhringer, H., Matsushita, K., Finoguenov, A., Xue, Y., & Churazov, E. 2005, Adv. Space Res., 36, 677 [NASA ADS] [CrossRef]
- Breitschwerdt, D., McKenzie, J. F., & Voelk, H. J. 1991, A&A, 245, 79 [NASA ADS] (In the text)
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] (In the text)
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] (In the text)
- Collela, P., & Woodward, P. R. 1984, J. Comp. Phys., 54, 174 [NASA ADS] [CrossRef] (In the text)
- Cora, S. A. 2006, MNRAS, 368, 1540 [NASA ADS] [CrossRef] (In the text)
- Cora, S. A., Tornatore, L., Tozzi, P., & Dolag, K. 2008, MNRAS, 386, 96 [NASA ADS] [CrossRef] (In the text)
- De Grandi, S., Ettori, S., Longhetti, M., & Molendi, S. 2004, A&A, 419, 7 [NASA ADS] [CrossRef] [EDP Sciences]
- De Lucia, G., Kauffmann, G., & White, S. D. M. 2004, MNRAS, 349, 1101 [NASA ADS] [CrossRef]
- De Young, D. S., 1978, ApJ, 223, 47 [NASA ADS] [CrossRef]
- Domainko W., Gitti M., Schindler, S., & Kapferer, W. 2004, A&A 425, L21 (In the text)
- Domainko, W., Mair, M., Kapferer, W., et al. 2006, A&A, 452, 795 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Durret, F., Lima Neto, G. B., & Forman, W. 2005, A&A, 432, 809 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Everett, J. E., Zweibel, E. G., Benjamin, R. A., et al. 2008, ApJ, 674, 258 [NASA ADS] [CrossRef] (In the text)
- Fabjan, D., Tornatore, L., Borgani, S., Saro, A., & Dolag, K. 2008, MNRAS, 386, 1265 [NASA ADS] [CrossRef] (In the text)
- Finoguenov, A., Henriksen, M. J., Miniati, F., Briel, U. G., & Jones, C. 2006, ApJ, 643, 790 [NASA ADS] [CrossRef] (In the text)
- Fukazawa Y., Kawano N., & Kawashima K. 2004, ApJ, 606, L109 [NASA ADS] [CrossRef] (In the text)
- Furusho T., Yamasaki N. Y., & Ohashi T. 2003, ApJ, 596, 181 [NASA ADS] [CrossRef] (In the text)
- Sato, K., Matsushita, K., & Gastaldello, F. 2009, PASJ, 61, 365 (In the text)
- Gnedin, N. Y. 1998, MNRAS, 294, 407 [NASA ADS] [CrossRef] (In the text)
- Gunn J. E., & Gott J. R. III 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] (In the text)
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] (In the text)
- Hayakawa A., Furusho T., Yamasaki N. Y., Ishida M., & Ohashi T. 2004, PASJ, 56, 743 [NASA ADS] (In the text)
- Hayakawa, A., Hoshino, A., Ishida, M., et al. 2006, PASJ, 58, 695 [NASA ADS] (In the text)
- Hernquist, L. 1990, ApJ, 356, 359 [NASA ADS] [CrossRef] (In the text)
- Hoffman Y., & Ribak, E. 1991, ApJ, 380, L5 [NASA ADS] [CrossRef] (In the text)
- Kapferer, W., Knapp, A., Schindler, S., Kimeswenger, S., & van Kampen, E. 2005, A&A, 438, 87 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kapferer, W., Ferrari, C., Domainko, W., et al. 2006, A&A, 447, 827 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kapferer, W., Kronberger, T., Weratschnig, J., et al. 2007a, A&A, 466, 813 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kapferer, W., Kronberger, T., Weratschnig, J., & Schindler, S. 2007b, A&A, 472, 757 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kapferer, W., Kronberger, T., Ferrari, C., Riser, T., & Schindler, S. 2008, MNRAS, 389, 1405 [NASA ADS] [CrossRef] (In the text)
- Kapferer, W., Sluka, C., Schindler, S., Ferrari, C., & Ziegler, B. 2009, A&A, 499, 87 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] (In the text)
- Kronberger, T., Kapferer, W., Ferrari, C., Unterguggenberger, S., & Schindler, S. 2008, A&A, 481, 337 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Kuzmin, G. G. 1956, Astron. Zh., 33, 27 (In the text)
- Martin, C. L. 1999, ApJ, 513, 156 [NASA ADS] [CrossRef]
- Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [NASA ADS] (In the text)
- Maughan, B. J., Jones, C., Forman, W., & Van Speybroeck, L. 2008, ApJS, 174, 117 [NASA ADS] [CrossRef]
- Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 319 [NASA ADS] [CrossRef] (In the text)
- Moll, R., Schindler, S., Domainko, W., et al. 2007, A&A, 463, 513 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Nagashima, M., Lacey, C. G., Baugh, C. M., Frenk, C. S., & Cole, S. 2005, MNRAS, 358, 1247 [NASA ADS] [CrossRef] (In the text)
- O'Sullivan, E., Vrtilek, J. M., Kempner, J. C., David, L. P., & Houck, J. C. 2005, MNRAS, 357, 1134 [NASA ADS] [CrossRef]
- Quilis, V., Moore, B., & Bower, R. 2000, Science, 288, 1617 [NASA ADS] [CrossRef] (In the text)
- Roediger, E., Brüggen, M., Rebusco, P., Böhringer, H., & Churazov, E. 2007, MNRAS, 375, 15 [NASA ADS] [CrossRef] (In the text)
- Ruffert, M. 1992, A&A 265, 82 (In the text)
- Sanders, J. S., & Fabian, A. C. 2006, MNRAS, 371, 1483 [NASA ADS] [CrossRef] (In the text)
- Sanders J. S., Fabian A. C., Allen S., & Schmidt R. W. 2004, MNRAS, 349, 952 [NASA ADS] [CrossRef] (In the text)
- Sauvageot, J. L., Belsole, E., & Pratt, G. W. 2005, A&A, 444, 673 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schindler, S., Kapferes, W., Domainko, W. et al. 2005, A&A, 435, L25 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schmidt R. W., Fabian A. C., & Sanders J. 2002, MNRAS, 337, 71 [NASA ADS] [CrossRef] (In the text)
- Schulz, S., & Struck, C. 2001, MNRAS, 328, 185 [NASA ADS] [CrossRef] (In the text)
- Simionescu, A., Werner, N., Böhringer, H., et al. 2009, A&A, 493, 409 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Sivanandam, S., Zabludoff, A. I., Zaritsky, D., Gonzalez, A. H., & Kelson, D. D. 2009, ApJ, 691, 1787 [NASA ADS] [CrossRef]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] (In the text)
- Springel, V., & Hernquist, L. 2003, MNRAS, 333, 649 [NASA ADS] [CrossRef]
- Strickland, D. K., & Stevens, I. R. 2000, MNRAS, 314, 511 [NASA ADS] [CrossRef] (In the text)
- Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] (In the text)
- Tenorio-Tagle, G., & Munoz-Tunon, C. 1998, MNRAS, 293, 299 [NASA ADS] [CrossRef] (In the text)
- Toniazzo T., & Schindler S. 2001, MNRAS, 325, 509 [NASA ADS] [CrossRef] (In the text)
- Tornatore L., Borgani S., Matteucci F., Recchi S., & Tozzi P. 2004, MNRAS, 349, L19 [NASA ADS] [CrossRef] (In the text)
- Tornatore, L., Borgani, S., Dolag, K., & Matteucci, F. 2007, MNRAS, 382, 1050 [NASA ADS] (In the text)
- Toomre, A. 1963, ApJ, 138, 385 [NASA ADS] [CrossRef] (In the text)
- Valdarnini, R. 2003, MNRAS, 339, 1117 [NASA ADS] [CrossRef] (In the text)
- van de Weygaert R., & Bertschinger E. 1996, MNRAS, 281, 84 [NASA ADS]
- van Kampen, E., Jimenez, R., & Peacock, J. A. 1999, MNRAS, 310, 43 [NASA ADS] [CrossRef]
- van Kampen, E., Percival, W. J., Crawford, M., et al. 2005, MNRAS, 359, 469 [NASA ADS] [CrossRef]
- Vollmer, B., Cayatte, V., Balkowski, C., & Duschl, W. J. 2001, ApJ, 561, 708 [NASA ADS] [CrossRef] (In the text)
- Werner, N., de Plaa, J., Kaastra, J. S., et al. 2006, A&A, 449, 475 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12099_fig1.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12099-09/Timg62.png) |
Figure 1: Radial metallicity profile of model cluster A and B at redshift z=0. For the shown metallicity profiles only metals originating from galactic winds are taken into account. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12099_fig2.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12099-09/Timg63.png) |
Figure 2: Metallicity profiles for observed nearby (z<0.2) clusters (symbols) from Pratt et al. (2007) compared to emission weighted simulated profiles from model cluster A at redshift z=0 with galactic winds (red, solid line) and with combined wind and ram-pressure stripping (red, dashed line) as enrichment processes. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12099_fig3.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12099-09/Timg64.png) |
Figure 3: Mean metallicity profile from a sample of observed clusters (symbols) from de Grandi et al. (2004) compared to emission weighted simulated profiles from model cluster B with galactic winds (red, solid line) and with combined wind and ram-pressure stripping (red, dashed line) as enrichment processes. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12099_fig4.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12099-09/Timg66.png) |
Figure 4: Redshift evolution of the mean metallicity of model cluster A (red, dashed line) and model cluster B (red, solid line) compared to the observed evolution of a sample of clusters from Balestra et al. (2007). Both enrichment processes (ram-pressure stripping and galactic winds) are taken into account). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12099_fig5.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12099-09/Timg69.png) |
Figure 5: X-ray weighted metal map for model cluster A at redshift z=0. Overlayed contours indicate the X-ray surface brightness. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\center
\includegraphics[width=8.8cm,clip]{12099_fig6.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa12099-09/Timg70.png) |
Figure 6: X-ray weighted metal map for model cluster B at redshift z=0. Overlayed contours indicate the X-ray surface brightness. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\displaystyle \rho u A
\left[\frac{1}{2}u^2+\frac{\gamma_{\rm g}}{\gamma_{\rm g}-1}\frac{p_{\rm g}}{\rho}+\Phi\right]$](/articles/aa/full_html/2009/36/aa12099-09/img6.png)
![\begin{displaymath}
\left[\frac{1}{2}u_0^2+\frac{\gamma_{\rm g}}{\gamma_{\rm g}-...
...m g}-1}\frac{p_{g\infty}}{\rho_{\infty}}+\Phi_{\infty}\right],
\end{displaymath}](/articles/aa/full_html/2009/36/aa12099-09/img20.png)
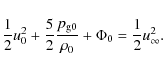
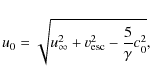
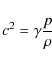
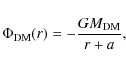
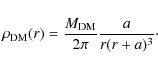
![\begin{displaymath}
\Phi_{\rm disc}(r,z)=-\frac{GM_{\rm disc}}{[r^2+(b+\vert z\vert)^2]^{1/2}},
\end{displaymath}](/articles/aa/full_html/2009/36/aa12099-09/img51.png)