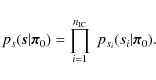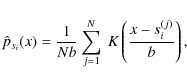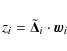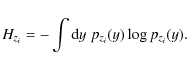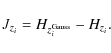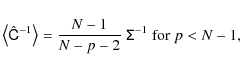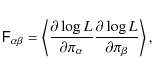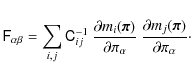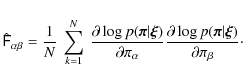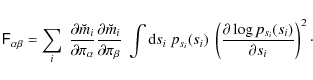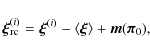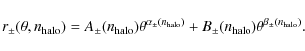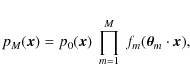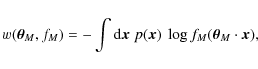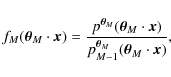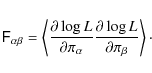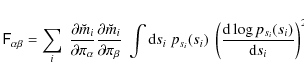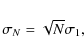| Issue |
A&A
Volume 504, Number 3, September IV 2009
|
|
|---|---|---|
| Page(s) | 689 - 703 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200911697 | |
| Published online | 09 July 2009 | |
The non-Gaussianity of the cosmic shear likelihood or how odd is the Chandra Deep Field South?
J. Hartlap1 - T. Schrabback2,1 - P. Simon3 - P. Schneider1
1 -
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
2 - Leiden Observatory, Universiteit Leiden, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands
3 - The Scottish Universities Physics Alliance (SUPA), Institute for Astronomy, School of Physics, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
Received 20 January 2009 / Accepted 19 June 2009
Abstract
Aims. We study the validity of the approximation of a Gaussian cosmic shear likelihood. We estimate the true likelihood for a fiducial cosmological model from a large set of ray-tracing simulations and investigate the impact of non-Gaussianity on cosmological parameter estimation. We investigate how odd the recently reported very low value of ![]() really is as derived from the Chandra Deep Field South (CDFS) using cosmic shear by taking the non-Gaussianity of the likelihood into account, as well as the possibility of biases coming from the way the CDFS was selected.
really is as derived from the Chandra Deep Field South (CDFS) using cosmic shear by taking the non-Gaussianity of the likelihood into account, as well as the possibility of biases coming from the way the CDFS was selected.
Methods. A brute force approach to estimating the likelihood from simulations must fail because of the high dimensionality of the problem. We therefore use independent component analysis to transform the cosmic shear correlation functions to a new basis, in which the likelihood approximately factorises into a product of one-dimensional distributions.
Results. We find that the cosmic shear likelihood is significantly non-Gaussian. This leads to both a shift of the maximum of the posterior distribution and a significantly smaller credible region compared to the Gaussian case. We re-analyse the CDFS cosmic shear data using the non-Gaussian likelihood in combination with conservative galaxy selection criteria that minimise calibration uncertainties. Assuming that the CDFS is a random pointing, we find
![]() for fixed
for fixed
![]() .
In a WMAP5-like cosmology, a value equal to or lower than this would be expected in
.
In a WMAP5-like cosmology, a value equal to or lower than this would be expected in ![]() 5% of the times. Taking biases into account arising from the way the CDFS was selected, which we model as being dependent on the number of haloes in the CDFS, we obtain
5% of the times. Taking biases into account arising from the way the CDFS was selected, which we model as being dependent on the number of haloes in the CDFS, we obtain
![]() .
Combining the CDFS data with the parameter constraints from WMAP5 yields
.
Combining the CDFS data with the parameter constraints from WMAP5 yields
![]() and
and
![]() for a flat universe.
for a flat universe.
Key words: gravitational lensing - cosmology: cosmological parameters - methods: statistical - methods: numerical
1 Introduction
Weak gravitational lensing by the large-scale structure in the Universe, or cosmic shear, is becoming a more and more important tool to constrain cosmological parameters. It is largely complementary to other cosmological probes like the cosmic microwave background or the clustering of galaxies, and particularly sensitive to the matter density
![]() and the normalisation of the matter power spectrum
and the normalisation of the matter power spectrum ![]() .
Important constraints have already been obtained by Benjamin et al. (2007), who compiled a set of five weak lensing surveys, and from the CFHT Legacy Survey (Hoekstra et al. 2006; Fu et al. 2008; Semboloni et al. 2006). In subsequent years, a new generation of surveys like KIDS or Pan-STARRS (Kaiser & Pan-STARRS Collaboration 2005) will allow cosmic shear to be measured with statistical uncertainties that are much smaller than the systematic errors both on the observational and the theoretical sides. Strong efforts are now being made to find sources of systematics in the process of shape measurement and shear estimation (e.g. Massey et al. 2007a). In addition, new methods of shape measurement are being explored, such as the shapelet formalism (Kuijken 2006; Refregier & Bacon 2003) or the methods proposed in Bernstein & Jarvis (2002) and Miller et al. (2007).
.
Important constraints have already been obtained by Benjamin et al. (2007), who compiled a set of five weak lensing surveys, and from the CFHT Legacy Survey (Hoekstra et al. 2006; Fu et al. 2008; Semboloni et al. 2006). In subsequent years, a new generation of surveys like KIDS or Pan-STARRS (Kaiser & Pan-STARRS Collaboration 2005) will allow cosmic shear to be measured with statistical uncertainties that are much smaller than the systematic errors both on the observational and the theoretical sides. Strong efforts are now being made to find sources of systematics in the process of shape measurement and shear estimation (e.g. Massey et al. 2007a). In addition, new methods of shape measurement are being explored, such as the shapelet formalism (Kuijken 2006; Refregier & Bacon 2003) or the methods proposed in Bernstein & Jarvis (2002) and Miller et al. (2007).
It is equally important to have accurate theoretical model predictions that can be fit to the expected high-quality measurements. Currently, these models are all based on fitting formulae for the three-dimensional matter power spectrum derived from N-body simulations as given by Peacock & Dodds (1996) and more recently by Smith et al. (2003). However, these are only accurate at best to the percent level on the scales relevant to this and similar works when compared to ray-tracing simulations based on state-of-the-art N-body simulations (Hilbert et al. 2009), such as the Millennium Run (Springel et al. 2005). Therefore, there is a strong need for a large ray-tracing effort to obtain accurate semi-numerical predictions for a range of cosmological parameters.
While a tremendous effort is currently being directed to the solution of these problems, the actual process of parameter estimation has so far received relatively little attention. Obviously, the statistical data analysis has to achieve the same accuracy as the data acquisition if the aforementioned efforts are not to be wasted.
The standard procedure for converting measurements of second-order cosmic shear statistics into constraints on cosmological parameters is to write down a likelihood function and to determine the location of its maximum for obtaining estimates of the cosmological parameters of interest. To make this feasible, several approximations are commonly made. Despite the shear field being non-Gaussian due to nonlinear structure growth, lacking an analytical description the likelihood is most often approximated by a multivariate Gaussian distribution. The covariance matrix for the Gaussian likelihood then remains to be determined, which is an intricate issue by itself.
In most previous studies, the dependence of the covariance matrix on cosmological parameters has been ignored when writing down the likelihood function. Instead, it was kept fixed to some fiducial cosmological model. The dependence of the covariance matrix on the cosmological parameters has been investigated in Eifler et al. (2009) for the case of Gaussian shear fields. The authors find that this has a significant effect on the constraints on cosmological parameters (reducing the size of the credible regions) and will be particularly important for future large-area surveys.
There are several approaches to determine the covariance for the fiducial set of parameters: Hoekstra et al. (2006) use the covariance matrix derived for a Gaussian shear field. Although this is rather easy to compute (Joachimi et al. 2008), the errors are strongly underestimated particularly on small scales. Another option is to estimate the covariance from the data itself (e.g. Massey et al. 2007b). This will become sensible and feasible mostly for the upcoming large surveys, which can be safely split into smaller subfields without severely underestimating cosmic variance. A third possibility, which currently seems to be the most accurate, is to measure the covariance matrix from a large sample of ray-tracing simulations. Semboloni et al. (2007) have provided a fitting formula which allows one to transform covariances computed for Gaussian shear fields into covariances including non-Gaussianity. Another promising way, which would also easily allow one to take into account the dependence on cosmological parameters, is the semi-analytical computation using the halo model (Takada & Jain 2009; Scoccimarro et al. 1999; Cooray & Hu 2001).
However, all these works are based on the assumption that the likelihood is well approximated by a Gaussian. In this paper, we study the impact of this assumption on the shape of the posterior probability distribution of the matter density parameter
![]() and the power spectrum normalisation
and the power spectrum normalisation ![]() .
Furthermore, we compute Fisher matrix constraints for the four-dimensional parameter space spanned by
.
Furthermore, we compute Fisher matrix constraints for the four-dimensional parameter space spanned by
![]() ,
,
![]() ,
h100
and
,
h100
and
![]() .
We propose a method to numerically compute the likelihood function from a large set of ray-tracing simulations based on the technique of independent component analysis (ICA, e.g. Jutten & Hérault 1991; Comon et al. 1991). ICA is a technique for the separation of independent source signals underlying a set of observed random variables, a statistical method related to factor analysis and principal component analysis (PCA). An approach similar to ours, called projection pursuit density estimation, which we use to verify our results, was proposed by Friedman et al. (1984).
.
We propose a method to numerically compute the likelihood function from a large set of ray-tracing simulations based on the technique of independent component analysis (ICA, e.g. Jutten & Hérault 1991; Comon et al. 1991). ICA is a technique for the separation of independent source signals underlying a set of observed random variables, a statistical method related to factor analysis and principal component analysis (PCA). An approach similar to ours, called projection pursuit density estimation, which we use to verify our results, was proposed by Friedman et al. (1984).
In their cosmic shear analysis of the combined HST GEMS and GOODS data of the
CDFS, Schrabback et al. (2007) (S07, from hereon) have found a very low value of
![]() .
In the second part of this paper, we present a re-analysis of the cosmic shear data of S07. Using our estimate of the non-Gaussian likelihood, we investigate whether cosmic variance alone is responsible for producing the low
.
In the second part of this paper, we present a re-analysis of the cosmic shear data of S07. Using our estimate of the non-Gaussian likelihood, we investigate whether cosmic variance alone is responsible for producing the low ![]() -estimate or whether the criteria applied by Giacconi et al. (2001) to select a field suitable for deep X-ray observations have a share in this.
-estimate or whether the criteria applied by Giacconi et al. (2001) to select a field suitable for deep X-ray observations have a share in this.
The outline of our paper is as follows: in Sect. 2, we describe our sample of ray-tracing simulations which we use for the likelihood estimation. In Sect. 3, we briefly review the lensing quantities relevant for this paper and Bayesian parameter estimation. We introduce our method of estimating the ``true'' likelihood and illustrate the impact of non-Gaussianity on parameter estimation using the example of a CDFS-like survey. In Sect. 4, we present the improved cosmic shear analysis of the CDFS and investigate possible reasons for the low power spectrum normalisation found in S07.
2 Ray-tracing simulations
We have performed a set of 10 N-body simulations using the publically available code GADGET-2 (Springel 2005), all of which are realisations of the same WMAP-5-like cosmology (
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
h100=0.73).
The simulation boxes are
,
h100=0.73).
The simulation boxes are
![]() on a side, populated by
on a side, populated by
![]() dark matter particles with masses of
dark matter particles with masses of
![]() .
We have started the simulations at z=50 and obtained snapshots from z=0 to z=4.5 in intervals of
.
We have started the simulations at z=50 and obtained snapshots from z=0 to z=4.5 in intervals of ![]() corresponding to the box size, so that a suitable snapshot is available for each lens plane.
corresponding to the box size, so that a suitable snapshot is available for each lens plane.
In the following, we only give a brief description of our ray-tracing algorithm and refer the reader to, for example, Jain et al. (2000) or Hilbert et al. (2009) for a more detailed introduction.
The ray-tracing is performed by dividing the dark matter distribution into redshift slices and projecting each slice onto a lens plane. Starting at the observer, light rays are shot through this array of lens planes. We assume that deflections only take place at the planes themselves, and that the rays propagate on straight lines in the space between two planes. In our case, each redshift slice corresponds to one output box of the N-body simulation and was projected as a whole onto a lens plane, preserving the periodic boundary conditions of the simulation box. To avoid repetition of structure along the line of sight, the planes were randomly shifted and rotated. The light rays are shot from the observer through the set of lens planes, forming a regular grid on the first plane. We then use FFT methods to compute the lensing potential on each lens plane, from which we obtain the deflection angle and its partial derivatives on a grid. The ray position and the Jacobian of the lens mapping for each ray are obtained by recursion: given the ray position on the current lens plane, its propagation direction (known from the position on the previous plane), and the deflection angle on the current plane interpolated onto the ray, we immediately obtain the ray position on the next plane. Differentiation of this recursion formula with respect to the image plane coordinates yields a similar relation for the Jacobian of the lens mapping, which takes into account the previously computed tidal deflection field (for a detailed description of the formalism used, see Hilbert et al. 2009). The recursion is performed until we reach the redshift cut-off at z=4.5.
We obtain the final Jacobian for a given source redshift distribution by performing a weighted average over the Jacobians for the light paths to each lens plane.
Since our aim is to create mock catalogues comparable to those of the CDFS field, we use the redshift distribution found for our revised galaxy catalogues (Smail et al. 1995, see Sect. 4.1):
![\begin{displaymath}p(z_{\rm s}) = A~\left(\frac{z_{\rm s}}{z_0}\right)^\alpha \exp\left[-\left(\frac{z_{\rm s}}{z_0}\right)^\beta\right],
\end{displaymath}](/articles/aa/full_html/2009/36/aa11697-09/img49.png)
where z0=1.55,
3 The non-Gaussianity of the cosmic shear likelihood
3.1 Cosmic shear
Perhaps the most common way to extract the lensing information from the measured shapes of distant galaxies is to estimate the two-point correlation functions of the distortion field. One defines two shear correlation functions (for more details, see e.g. Schneider 2006)
where
Here, i and j label galaxies at angular positions
3.2 Parameter estimation
Let us assume that we have measured the shear correlation functions
Adopting a Bayesian point of view, our aim is to compute the posterior likelihood, i.e. the probability distribution of a parameter vector ![]() given the information provided by the data
given the information provided by the data ![]() :
:
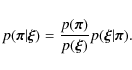 |
(3) |
Here,
where
3.3 Estimating the likelihood
The choice of the functional form of the likelihood as given by Eq. (4) is only approximate. Since the underlying shear field in the correlation function measurement becomes non-Gaussian in particular on small scales due to nonlinear structure formation, there is no good reason to expect the distribution of the shear correlation function to be Gaussian. Our aim therefore is to use a very large sample of ray-tracing simulations to estimate the likelihood and explore the effects of the deviations from a Gaussian shape on cosmological parameter constraints.
In this work, we have to sustain the approximation that the functional form of the likelihood does not depend on cosmology in order to keep computation time manageable.
Our ray-tracing simulations were all done for identical cosmological parameters, which is our fiducial parameter vector ![]() .
Thus, as in Eq. (5) the likelihood depends on cosmology only through the difference
.
Thus, as in Eq. (5) the likelihood depends on cosmology only through the difference
![]() .
.
Since
![]() is the probability of obtaining the data
is the probability of obtaining the data ![]() given the parameters
given the parameters
![]() ,
we in principle have to estimate the p-dimensional distribution
of
,
we in principle have to estimate the p-dimensional distribution
of ![]() from our sample of N ray-tracing simulations. However, due to the high dimensionality of the problem, a brute force approach to estimate the full joint distribution is hopeless.
The problem would simplify considerably if we could find a transformation
from our sample of N ray-tracing simulations. However, due to the high dimensionality of the problem, a brute force approach to estimate the full joint distribution is hopeless.
The problem would simplify considerably if we could find a transformation
such that
Here,
where
Our likelihood estimation procedure is as follows: the first step is to remove first-order correlations from the data vector by performing a PCA (e.g. Press et al. 1992). This yields a basis in which the components of ![]() are uncorrelated. If we knew that the distribution
of
are uncorrelated. If we knew that the distribution
of ![]() were Gaussian, this would be sufficient, because in this case uncorrelatedness is equivalent to statistical independence. However, for a general distribution, uncorrelatedness is only a necessary condition for independence. Since we suspect that the likelihood is non-Gaussian, a second change of basis, determined by the ICA technique (described in detail in the next section), is carried out which then results in the desired independence.
We then use a kernel density method (see e.g. Hastie et al. 2001; Venables & Ripley 2002, and references therein) to estimate and tabulate the one-dimensional distributions
were Gaussian, this would be sufficient, because in this case uncorrelatedness is equivalent to statistical independence. However, for a general distribution, uncorrelatedness is only a necessary condition for independence. Since we suspect that the likelihood is non-Gaussian, a second change of basis, determined by the ICA technique (described in detail in the next section), is carried out which then results in the desired independence.
We then use a kernel density method (see e.g. Hastie et al. 2001; Venables & Ripley 2002, and references therein) to estimate and tabulate the one-dimensional distributions
![]() in this new basis. The density estimate is constructed by smoothing the empirical distribution function of the observations of si,
in this new basis. The density estimate is constructed by smoothing the empirical distribution function of the observations of si,
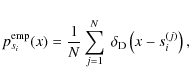 |
(9) |
where si(j) is the jth of N observations of si and
where si(j) is the jth of N observations of si and b is the bandwidth. For the kernel K we use a Gaussian distribution. It has been shown that the shape of the Kernel K is of secondary importance for the quality of the density estimate; much more important is the choice of the bandwidth b. If b is too small,
Constraints on cosmological parameters can now be derived as follows: we transform our set of model vectors and the measured correlation function to the new ICA basis:
| (11) |
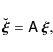 |
(12) |
so that
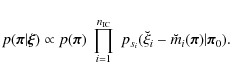 |
(13) |
3.4 Independent component analysis
We now briefly outline the ICA method (Hyvärinen & Oja 2000; Hyvärinen et al. 2001), which we use to find the new basis inwhere
An intuitive, though slightly hand-waving way to understand how ICA works is to note that a set of linear combinations Yi of independent, non-Gaussian random variables Xj will usually have distributions that are more Gaussian than the original distributions of the Xj (central limit theorem). Reversing this argument, this suggests that the Xj could be recovered from a sample of the Yi by looking for linear combinations of the Yi that have the least Gaussian distributions. These linear combinations will also be close to statistically independent. A more rigorous justification of the method can be found in Hyvärinen et al. (2001).
The ICA algorithm consists of two parts, the first of which is a preprocessing step: after subtracting the mean
![]() from
from
![]() ,
the data is whitened, i.e. a linear transformation
,
the data is whitened, i.e. a linear transformation
![]() is introduced such that
is introduced such that
![]() ,
where
,
where ![]() is the unit matrix. This can be achieved by the eigen-decomposition of the covariance matrix
is the unit matrix. This can be achieved by the eigen-decomposition of the covariance matrix
![]() of
of
![]() ,
where
,
where
![]() ,
by choosing
,
by choosing
![]() .
Note that
.
Note that ![]() is orthonormal and that
is orthonormal and that ![]() for all i. As will be discussed below, each source signal si can only be determined up to a multiplicative constant using ICA. We choose these factors such that
for all i. As will be discussed below, each source signal si can only be determined up to a multiplicative constant using ICA. We choose these factors such that
![]() .
The effect of the whitening is that the new mixing matrix
.
The effect of the whitening is that the new mixing matrix
![]() between
between
![]() and
and ![]() is orthogonal. This can be seen as follows:
is orthogonal. This can be seen as follows:
![]() .
Since we have chosen
.
Since we have chosen
![]() ,
the claim follows.
,
the claim follows.
After the preprocessing, the components of
![]() are uncorrelated. This would be equivalent to statistical independence if their distributions were Gaussian. However, as this is not the case here, a further step is needed. It consists of finding a new set of orthogonal vectors
are uncorrelated. This would be equivalent to statistical independence if their distributions were Gaussian. However, as this is not the case here, a further step is needed. It consists of finding a new set of orthogonal vectors ![]() (the row vectors of
(the row vectors of
![]() )
such that the distributions
pzi(zi) of
)
such that the distributions
pzi(zi) of
maximise a suitable measure of non-Gaussianity. A common method to achieve this is to minimise the entropy (or approximations thereof) of the zi, which is defined by
Since it can be shown that the Gaussian distribution has the largest entropy of all distributions of equal variance, this can be rewritten as maximising the so-called negentropy of the zi, defined by
Here,
ICA suffers from several ambiguities, none of which, however, is crucial for this work. First of all, the amplitudes of the source signals cannot be determined, since any
prefactor ![]() to the signal si can be cancelled by multiplication of the corresponding column of the mixing matrix by
to the signal si can be cancelled by multiplication of the corresponding column of the mixing matrix by ![]() .
Secondly, the order of the independent components is not determined, since any permutation of the si can be accommodated by corresponding changes to
.
Secondly, the order of the independent components is not determined, since any permutation of the si can be accommodated by corresponding changes to ![]() .
Thirdly, ICA does not yield a unique answer if at least some of
the si are Gaussian - the subset of Gaussian signals is only determined up to an orthogonal transformation.
This is not an issue in our context, since the Gaussian signals will be uncorrelated thanks to the preprocessing steps, and uncorrelatedness implies statistical independence for Gaussian random variables.
.
Thirdly, ICA does not yield a unique answer if at least some of
the si are Gaussian - the subset of Gaussian signals is only determined up to an orthogonal transformation.
This is not an issue in our context, since the Gaussian signals will be uncorrelated thanks to the preprocessing steps, and uncorrelatedness implies statistical independence for Gaussian random variables.
Several interpretations of ICA and algorithms exist and are described in detail in Hyvärinen et al. (2001).
In this work, we use an implementation of the fastICA algorithm (Hyvärinen & Oja 1997) for the R language (R Development Core Team 2007)![]() .
.
3.5 Tests
In this section, we present the results of a number of tests we have performed to insure that our results are not affected by convergence issues or statistical biases of any kind.
The fastICA algorithm requires a set of randomly chosen directions ![]() as initial conditions. It then iteratively computes corrections to these vectors in order to increase the negentropy of the projections of the data vectors onto these directions (Eq. (15)), followed by an orthonormalisation step. It is not clear a priori whether the algorithm will settle in the same negentropy maxima for different sets of initial vectors. This concern is backed by the fact that at least some of the
as initial conditions. It then iteratively computes corrections to these vectors in order to increase the negentropy of the projections of the data vectors onto these directions (Eq. (15)), followed by an orthonormalisation step. It is not clear a priori whether the algorithm will settle in the same negentropy maxima for different sets of initial vectors. This concern is backed by the fact that at least some of the
![]() might be very close to Gaussian, which might hamper convergence even further.
We have therefore tested whether we obtain the same set of basis vectors from a large number of different initial conditions. We find that this is indeed the case for those
might be very close to Gaussian, which might hamper convergence even further.
We have therefore tested whether we obtain the same set of basis vectors from a large number of different initial conditions. We find that this is indeed the case for those ![]() for which the distribution of
for which the distribution of
![]() departs significantly from a Gaussian. As expected, the directions leading to a rather Gaussian pzi are different for different starting values, reflecting the inability of ICA to distinguish between Gaussian source signals.
However, the posterior distributions derived using our algorithm do not differ notably when using different initial conditions. This is even true if the fastICA algorithm does not formally converge (i.e. when the differences of some of the basis vectors between two iterations is not small): after a few hundred iterations, the non-Gaussian directions are determined and do not change anymore. The reason for not reaching convergence is that the algorithm still tries to find negentropy maxima in the subspace of Gaussian directions.
departs significantly from a Gaussian. As expected, the directions leading to a rather Gaussian pzi are different for different starting values, reflecting the inability of ICA to distinguish between Gaussian source signals.
However, the posterior distributions derived using our algorithm do not differ notably when using different initial conditions. This is even true if the fastICA algorithm does not formally converge (i.e. when the differences of some of the basis vectors between two iterations is not small): after a few hundred iterations, the non-Gaussian directions are determined and do not change anymore. The reason for not reaching convergence is that the algorithm still tries to find negentropy maxima in the subspace of Gaussian directions.
As has been noted in Hartlap et al. (2007), statistical biases can become significant already for the Gaussian approximation of the likelihood (Eq. (4)): care has to be taken if the covariance matrix of the correlation function (given on p bins) is estimated from a finite set of N simulations or observations. Inverting the estimated covariance yields a biased estimate of the inverse:
where
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[angle=270]{11697f01.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg136.png) |
Figure 1:
Area of the |
| Open with DEXTER | |
Our method to estimate the likelihood crucially depends on the assumption that a linear transformation makes the components of the shear correlation vectors statistically independent. A necessary condition for mutual statistical independence of all si is pairwise independence. The components i and j are called pairwise statistical independent if p(si,sj)=psi(si) psj(sj). We therefore compare the joint pairwise distributions p(si,sj) to the product distributions psi(si) psj(sj), where we estimate p(si,sj) using a two-dimensional extension (using a bi-variate Gaussian kernel) of the kernel density method given by Eq. (10). We give two examples in Fig. 2, where we compare the joint and product distributions of the two most-non-Gaussian components and two nearly Gaussian components. As expected, a simple PCA is not enough to achieve pairwise statistical independence in the non-Gaussian case. Only after performing the ICA, pairwise independence is achieved.
A more rigorous test for mutual statistical independence for the multivariate, continuous case was proposed by Chiu et al. (2003).
It is based on the observation that if x is a continuous random variable and P(x) is its cumulative distribution function (CDF), then z=P(x) is uniformly distributed in [0,1]. If we are given a set of statistically independent random variables si, this means that the joint distribution of
zi=Pi(si), where again Pi is the CDF of si, is uniform in the multidimensional unit cube. On the other hand,
if the assumption of statistical independence of the si is violated, the joint density
![]() of the zi is given by
of the zi is given by
| |
= | ||
| = | 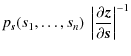 |
||
| = | (19) |
Here, pi(si) is the distribution function of si only and
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[angle=270]{11697f02.eps}}...
....5cm}
\resizebox{8cm}{!}{\includegraphics[angle=270]{11697f03.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg145.png) |
Figure 2: Comparison of the joint distributions p(si,sj) (black dashed contours) and the product psi(si) psj(sj) (solid red contours) for the two most non-Gaussian components (i=1, j=2) and two rather Gaussian ones (i=9, j=10), after performing ICA ( left panels) and PCA ( right panels). The components have been ranked and labelled according to their non-Gaussianity; the ith PCA component is in general not the same as ith ICA-component. In the right panel of each plot, the distributions with respect to the PCA basis vectors are shown and in the left panel, the distributions in the ICA basis are displayed. Statistical independence is indicated by p(si,sj)=psi(si) psj(sj). |
| Open with DEXTER | |
Applying the test to the si that we have obtained from our ICA procedure, we have to reject statistical independence at ![]() confidence. This means that the ICA does not remove all dependencies between the components of the shear correlation function. This result, however, does not give an indication of how these residual dependencies affect our likelihood estimate and the conclusions regarding constraints on cosmological parameters.
We therefore compare the constraints derived from the ICA likelihood with the constraints from the likelihood estimated using an alternative method, called projection pursuit density estimation (PPDE; Friedman et al. 1984), which we describe in detail in Appendix A. This method is free from any assumptions regarding statistical independence and therefore provides an an ideal cross-check for the ICA method.
For the comparison, we have computed the shear correlation functions with p=10, and we also use
confidence. This means that the ICA does not remove all dependencies between the components of the shear correlation function. This result, however, does not give an indication of how these residual dependencies affect our likelihood estimate and the conclusions regarding constraints on cosmological parameters.
We therefore compare the constraints derived from the ICA likelihood with the constraints from the likelihood estimated using an alternative method, called projection pursuit density estimation (PPDE; Friedman et al. 1984), which we describe in detail in Appendix A. This method is free from any assumptions regarding statistical independence and therefore provides an an ideal cross-check for the ICA method.
For the comparison, we have computed the shear correlation functions with p=10, and we also use
![]() independent components. The resulting contours in the
independent components. The resulting contours in the
![]() -plane are shown in Fig. 3. Both posterior likelihoods are very similar, although the credible regions of the PPDE posterior have a slightly smaller area than the contours of the ICA posterior (which actually supports the findings presented in the next section). Given the good agreement of the two methods, we will henceforth only make use of the ICA procedure, which is considerably faster and numerically less contrived than PPDE.
-plane are shown in Fig. 3. Both posterior likelihoods are very similar, although the credible regions of the PPDE posterior have a slightly smaller area than the contours of the ICA posterior (which actually supports the findings presented in the next section). Given the good agreement of the two methods, we will henceforth only make use of the ICA procedure, which is considerably faster and numerically less contrived than PPDE.
3.6 Results on the posterior
![\begin{figure}
\par\resizebox{8.6cm}{!}{\includegraphics[angle=270]{11697f04.ps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg148.png) |
Figure 3:
Comparison of the posterior likelihoods for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm]{11697f05.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg149.png) |
Figure 4:
Comparison of the posterior likelihoods for
|
| Open with DEXTER | |
The most interesting question is how much the posterior distribution computed from the non-Gaussian ICA likelihood will differ from the Gaussian approximation. We have investigated this for the case of the CDFS and the parameter set
![]() .
Here and henceforth, we use 15 angular bins for
.
Here and henceforth, we use 15 angular bins for ![]() and
and ![]() in the range from
in the range from
![]() to
to
![]() ,
i.e. p=30. For the data vector, we do not use the correlation functions from our simulations, but take the theoretical prediction for our fiducial parameter set instead. This allows us to study the shape of the posterior likelihood independent of noise in the data and biases due to the fact that the theoretical model does not quite match the mean correlation function from the simulations. In Fig. 4, we show the contours of the posterior computed in this way from the likelihood estimated using our ICA method (left panel) and from the Gaussian likelihood. We have assumed
,
i.e. p=30. For the data vector, we do not use the correlation functions from our simulations, but take the theoretical prediction for our fiducial parameter set instead. This allows us to study the shape of the posterior likelihood independent of noise in the data and biases due to the fact that the theoretical model does not quite match the mean correlation function from the simulations. In Fig. 4, we show the contours of the posterior computed in this way from the likelihood estimated using our ICA method (left panel) and from the Gaussian likelihood. We have assumed
![]() for the dispersion of the intrinsic galaxy ellipticities.
The shape of the ICA posterior is different from that of the Gaussian approximation in three respects: it is steeper (leading to smaller credible regions), the maximum is shifted towards higher
for the dispersion of the intrinsic galaxy ellipticities.
The shape of the ICA posterior is different from that of the Gaussian approximation in three respects: it is steeper (leading to smaller credible regions), the maximum is shifted towards higher ![]() and lower
and lower
![]() ,
and the contours are slightly tilted. The first two differences can be traced back to the shape of the distributions of the individual ICA components: most of the distribution functions psi are generally slightly steeper than a Gaussian and most of the non-Gaussian components are in addition strongly skewed, thus shifting the peak of the posterior. Generally, these differences are more pronounced in the direction of the
,
and the contours are slightly tilted. The first two differences can be traced back to the shape of the distributions of the individual ICA components: most of the distribution functions psi are generally slightly steeper than a Gaussian and most of the non-Gaussian components are in addition strongly skewed, thus shifting the peak of the posterior. Generally, these differences are more pronounced in the direction of the
![]() -
-![]() -degeneracy and towards lower values of both parameters, where the posterior is shallower.
-degeneracy and towards lower values of both parameters, where the posterior is shallower.
Of more practical relevance is how the parameter constraints change when the ICA likelihood is used for the analysis of large weak lensing surveys. Here, we consider surveys consisting
of ![]() CDFS-like fields.
Bayesian theory states that if
CDFS-like fields.
Bayesian theory states that if ![]() is large enough, the posterior probability distribution of the parameters becomes Gaussian, centred on the true parameter values, with covariance matrix
is large enough, the posterior probability distribution of the parameters becomes Gaussian, centred on the true parameter values, with covariance matrix
![]() (e.g. Gelman et al. 2004). Here,
(e.g. Gelman et al. 2004). Here, ![]() is the Fisher matrix (Kendall et al. 1987), which is defined by
is the Fisher matrix (Kendall et al. 1987), which is defined by
where
Equation (20) provides us with a way to estimate the Fisher matrix for the non-Gaussian likelihood. For each ray-tracing realisation of the CDFS, we compute the logarithm of the posterior distribution
In Appendix B, we show that the expression for the Fisher matrix of the ICA likelihood can be evaluated further to be
This equation allows a simpler, alternative computation of
![\begin{figure}
\par\includegraphics[width=12cm]{11697f06.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg166.png) |
Figure 5:
Fisher matrix constraints for a hypothetical 1500-
|
| Open with DEXTER | |
We have used Eqs. (21) and (23) to compute the Fisher matrices for a 1500-
![]() survey (
survey (
![]() ). We fit for four cosmological parameters (
). We fit for four cosmological parameters (
![]() ), keeping all other parameters fixed to their true values.
To visualise the posterior, we compute two-dimensional marginalised posterior distributions for each parameter pair as well as the one-dimensional marginals for each parameter.
The results are shown in Fig. 5. A general feature of the ICA likelihood, which has already been apparent in the 2D-analysis (Fig. 4), is that the credible intervals are significantly smaller than the ones derived from the Gaussian likelihood. For the two-dimensional marginal distributions, the area of the
), keeping all other parameters fixed to their true values.
To visualise the posterior, we compute two-dimensional marginalised posterior distributions for each parameter pair as well as the one-dimensional marginals for each parameter.
The results are shown in Fig. 5. A general feature of the ICA likelihood, which has already been apparent in the 2D-analysis (Fig. 4), is that the credible intervals are significantly smaller than the ones derived from the Gaussian likelihood. For the two-dimensional marginal distributions, the area of the ![]() credible regions derived from the ICA likelihood are smaller by
credible regions derived from the ICA likelihood are smaller by ![]()
![]() .
The one-dimensional constraints are tighter by
.
The one-dimensional constraints are tighter by ![]()
![]() .
In addition we find that the ICA Fisher ellipses in some cases are slightly tilted with respect to those computed using the Gaussian likelihood. This is particularly apparent for parameter combinations involving the Hubble parameter. Note that the shift of the maximum observed in the two-dimensional case for a single CDFS-like field is absent here because it was assumed for the Fisher analysis that the posterior is centred on the true parameter values.
.
In addition we find that the ICA Fisher ellipses in some cases are slightly tilted with respect to those computed using the Gaussian likelihood. This is particularly apparent for parameter combinations involving the Hubble parameter. Note that the shift of the maximum observed in the two-dimensional case for a single CDFS-like field is absent here because it was assumed for the Fisher analysis that the posterior is centred on the true parameter values.
4 How odd is the Chandra Deep Field South?
4.1 The CDFS cosmic shear data
The second part of this work is based on the cosmological weak lensing analysis of the
combined HST GEMS and GOODS data of the CDFS (Rix et al. 2004; Giavalisco et al. 2004), which was presented in S07. The mosaic comprises 78 ACS/WFC tiles imaged in F606W, covering a total area of ![]()
![]() .
We refer the reader to the original publication for details on the
data and weak lensing analysis, which applies the KSB+ formalism (Luppino & Kaiser 1997; Kaiser et al. 1995; Hoekstra et al. 1998).
.
We refer the reader to the original publication for details on the
data and weak lensing analysis, which applies the KSB+ formalism (Luppino & Kaiser 1997; Kaiser et al. 1995; Hoekstra et al. 1998).
In S07, the cosmic shear analysis was performed using two different signal-to-noise and magnitude cuts. The first one selects galaxies with S/N>4 and has no magnitude cut, and the second one applies a more conservative selection with S/N>5 and
m606<27.0, where S/N is the shear measurement signal-to-noise ratio as defined in Erben et al. (2001).
The drizzling process in the data reduction introduces correlated noise in adjacent pixels. While these correlations are ignored in the computation of S/N, an approximate correction factor (see S07) is taken into account for
![]() ,
making the above cuts
,
making the above cuts
![]() and
and
![]() respectively.
The two selection criteria yielded moderately different
respectively.
The two selection criteria yielded moderately different ![]() -estimates of
0.52+0.11-0.15 and
0.59+0.11-0.14 for
-estimates of
0.52+0.11-0.15 and
0.59+0.11-0.14 for
![]() (median of the posterior), not assuming a flat Universe. The errors include the statistical and redshift uncertainties. This translates to
(median of the posterior), not assuming a flat Universe. The errors include the statistical and redshift uncertainties. This translates to
![]() and
0.65+0.12-0.15 for our fiducial cosmology with
and
0.65+0.12-0.15 for our fiducial cosmology with
![]() .
The difference of the two estimates was considered as a measure for the robustness and hence systematic accuracy of our shear measurement pipeline.
While the analysis of the ``Shear TEsting Programme 2
.
The difference of the two estimates was considered as a measure for the robustness and hence systematic accuracy of our shear measurement pipeline.
While the analysis of the ``Shear TEsting Programme 2
![]() (STEP2) image simulations (Massey et al. 2007a) indicated no significant average shear calibration bias for our method, a detected dependence on galaxy magnitude and size could effectively bias a cosmic shear analysis through the redshift dependence of the shear signal (see also Semboloni et al. 2009).
In order to better understand the difference between the two estimates found in S07, and to
exclude any remaining calibration uncertainty in the current analysis, we further investigate the shear recovery accuracy as a function of the signal-to-noise ratio using the STEP2 simulations in Appendix C.
Here we conclude that our KSB+ implementation under-estimates gravitational shear for very noisy galaxies with
(STEP2) image simulations (Massey et al. 2007a) indicated no significant average shear calibration bias for our method, a detected dependence on galaxy magnitude and size could effectively bias a cosmic shear analysis through the redshift dependence of the shear signal (see also Semboloni et al. 2009).
In order to better understand the difference between the two estimates found in S07, and to
exclude any remaining calibration uncertainty in the current analysis, we further investigate the shear recovery accuracy as a function of the signal-to-noise ratio using the STEP2 simulations in Appendix C.
Here we conclude that our KSB+ implementation under-estimates gravitational shear for very noisy galaxies with
![]() ,
which likely explains the lower signal found in S07 when all galaxies with S/N>4 (
,
which likely explains the lower signal found in S07 when all galaxies with S/N>4 (
![]() )
were considered.
For the more conservative selection criteria we find no significant mean shear calibration bias and a variation as a function of magnitude and size of
)
were considered.
For the more conservative selection criteria we find no significant mean shear calibration bias and a variation as a function of magnitude and size of ![]()
![]()
![]() .
Therefore we base our current analysis on the more robust galaxy sample with S/N>5 (
.
Therefore we base our current analysis on the more robust galaxy sample with S/N>5 (
![]() )
and
m606<27.0, which yields a galaxy number density of
)
and
m606<27.0, which yields a galaxy number density of
![]() .
Based on the simulations, any remaining calibration uncertainty should be negligible compared to the statistical uncertainty.
.
Based on the simulations, any remaining calibration uncertainty should be negligible compared to the statistical uncertainty.
Note that Heymans et al. (2005) found a higher estimate of
![]() from GEMS, where they extrapolated the redshift distribution from the relatively shallow COMBO-17 photometric redshifts (Wolf et al. 2004). Using deeper data from the GOODS-MUSIC sample (Grazian et al. 2006), S07 were able to show that the COMBO-17 extrapolation significantly underestimates the mean redshift for GEMS, leading to the difference in the results for
from GEMS, where they extrapolated the redshift distribution from the relatively shallow COMBO-17 photometric redshifts (Wolf et al. 2004). Using deeper data from the GOODS-MUSIC sample (Grazian et al. 2006), S07 were able to show that the COMBO-17 extrapolation significantly underestimates the mean redshift for GEMS, leading to the difference in the results for ![]() .
.
In Fig. 6, we show the posterior distribution for ![]() based on this sample of galaxies. For the fit, all other cosmological parameters were held fixed at the fiducial values chosen for our ray-tracing simulations. This avoids complications in the discussion of cosmic variance and field selection biases due to the effect of parameter degeneracies. We choose a flat prior for
based on this sample of galaxies. For the fit, all other cosmological parameters were held fixed at the fiducial values chosen for our ray-tracing simulations. This avoids complications in the discussion of cosmic variance and field selection biases due to the effect of parameter degeneracies. We choose a flat prior for ![]() ,
with a lower boundary of
,
with a lower boundary of
![]() to cut off the tail of the posterior distribution towards small values of the power spectrum normalisation, which is caused by the fact that the difference (and therefore the likelihood) between the data and the model vectors changes only very little when
to cut off the tail of the posterior distribution towards small values of the power spectrum normalisation, which is caused by the fact that the difference (and therefore the likelihood) between the data and the model vectors changes only very little when ![]() (and therefore the shear correlation function) is very small. We have performed the fit for the ICA likelihood as well as for the Gaussian approximation to the likelihood. For the latter, the covariance matrix was in one case estimated from the full sample of our ray-tracing simulations, and in the other case computed analytically assuming that the shear field is a Gaussian random field (Joachimi et al. 2008).
The striking similarity of the posterior densities derived from the ICA likelihood and using the Gaussian covariance matrix for this particular data vector is merely a coincidence and is in general not seen for our set of simulated correlation functions.
(and therefore the shear correlation function) is very small. We have performed the fit for the ICA likelihood as well as for the Gaussian approximation to the likelihood. For the latter, the covariance matrix was in one case estimated from the full sample of our ray-tracing simulations, and in the other case computed analytically assuming that the shear field is a Gaussian random field (Joachimi et al. 2008).
The striking similarity of the posterior densities derived from the ICA likelihood and using the Gaussian covariance matrix for this particular data vector is merely a coincidence and is in general not seen for our set of simulated correlation functions.
For estimates of ![]() ,
we use the maximum of the posterior (henceforth we write ICA-MAP for the maximum of the non-Gaussian likelihood, and Gauss-MAP if the Gaussian approximation is used), although we also quote the median (ICA median) for comparison with S07. In the first case, our credible intervals are highest posterior density intervals, whereas for the median we choose to report the interval for which the probability of
,
we use the maximum of the posterior (henceforth we write ICA-MAP for the maximum of the non-Gaussian likelihood, and Gauss-MAP if the Gaussian approximation is used), although we also quote the median (ICA median) for comparison with S07. In the first case, our credible intervals are highest posterior density intervals, whereas for the median we choose to report the interval for which the probability of ![]() of being below the lower interval boundary is as high as being above the upper boundary. The results are summarised in Table 1.
of being below the lower interval boundary is as high as being above the upper boundary. The results are summarised in Table 1.
Table 1:
Estimates of ![]() from the CDFS.
from the CDFS.
4.2 Cosmic variance
The original estimates for
To begin, we determine the probability of finding a low ![]() in a CDFS-like field if the pointing is completely random. We estimate the sampling distribution of the
in a CDFS-like field if the pointing is completely random. We estimate the sampling distribution of the ![]() -MAP estimators for Gaussian and ICA likelihoods from the full sample of our ray-tracing simulations.
We compute the posterior likelihood for
-MAP estimators for Gaussian and ICA likelihoods from the full sample of our ray-tracing simulations.
We compute the posterior likelihood for ![]() using a uniform prior in the range
using a uniform prior in the range
![]() and determine the MAP estimator
and determine the MAP estimator
![]() .
As in the previous sections, we do this using both the Gaussian and the ICA likelihoods. To separate possible biases of the estimators from biases that might arise because the model prediction based on Smith et al. (2003) does not quite fit our simulations, we correct the simulated correlation functions for this: if
.
As in the previous sections, we do this using both the Gaussian and the ICA likelihoods. To separate possible biases of the estimators from biases that might arise because the model prediction based on Smith et al. (2003) does not quite fit our simulations, we correct the simulated correlation functions for this: if
![]() is the correlation function measured in the ith realisation, then
is the correlation function measured in the ith realisation, then
is the ``re-centred'' shear correlation, where
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[]{11697f07.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg197.png) |
Figure 6:
Posterior distributions for |
| Open with DEXTER | |
The resulting sampling distributions of
![]() are shown in Figs. 7 (original
are shown in Figs. 7 (original ![]() )
and 8 (re-centred
)
and 8 (re-centred ![]() ). All the distributions are well fit by a Gaussian. With the original correlation functions, we obtain estimates
). All the distributions are well fit by a Gaussian. With the original correlation functions, we obtain estimates
![]() which are too high on average. This reflects the fact that the power spectrum fitting formula by Smith et al. (2003) underpredicts the small scale power in the simulations (see also Hilbert et al. 2009). If we correct for this, we see that the maximum of the ICA likelihood is a nearly unbiased estimator of
which are too high on average. This reflects the fact that the power spectrum fitting formula by Smith et al. (2003) underpredicts the small scale power in the simulations (see also Hilbert et al. 2009). If we correct for this, we see that the maximum of the ICA likelihood is a nearly unbiased estimator of ![]() in the one-dimensional case considered here, and in addition has a lower variance than the maximum of the Gaussian likelihood.
in the one-dimensional case considered here, and in addition has a lower variance than the maximum of the Gaussian likelihood.
We estimate the probability of obtaining a power spectrum normalisation as low as the one measured in the CDFS or lower,
![]() ,
by the ratio of the number of realisations which fulfil this condition to the total number of simulations. These estimates agree very well with those computed from the best fitting Gaussian distribution. The results for the MAP and median estimators are summarised in
Table 2. As expected from the above considerations, we find higher probabilities for the re-centred correlation functions. In this case, the ICA-MAP estimator yields
,
by the ratio of the number of realisations which fulfil this condition to the total number of simulations. These estimates agree very well with those computed from the best fitting Gaussian distribution. The results for the MAP and median estimators are summarised in
Table 2. As expected from the above considerations, we find higher probabilities for the re-centred correlation functions. In this case, the ICA-MAP estimator yields ![]() for the probability of obtaining an equally low or lower
for the probability of obtaining an equally low or lower ![]() than the CDFS. This reduces to
than the CDFS. This reduces to
![]() when the uncorrected correlation functions are used, because the misfit of our theoretical correlation functions to the simulations biases the
when the uncorrected correlation functions are used, because the misfit of our theoretical correlation functions to the simulations biases the ![]() -estimates high. If we assume that our simulations are a reasonable representation of the real Universe, we can expect the same bias when we perform fits to real data. Therefore,
-estimates high. If we assume that our simulations are a reasonable representation of the real Universe, we can expect the same bias when we perform fits to real data. Therefore,
![]() as derived from the uncorrected correlation functions is most likely closest to reality. The probabilities computed from the Gauss-MAP estimates are generally smaller than the ICA-MAP values because of the lower value of
as derived from the uncorrected correlation functions is most likely closest to reality. The probabilities computed from the Gauss-MAP estimates are generally smaller than the ICA-MAP values because of the lower value of
![]() found using these estimators, even though the sampling
distributions of the Gauss estimators are broader.
found using these estimators, even though the sampling
distributions of the Gauss estimators are broader.
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[]{11697f08.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg204.png) |
Figure 7:
Sampling distributions of the MAP estimators of |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[]{11697f09.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg205.png) |
Figure 8: Same as Fig. 7, but using re-centred correlation functions. |
| Open with DEXTER | |
4.3 Influence of the CDFS selection criteria
We now investigate if and by how much the way in which the CDFS was selected can bias our estimates of the power spectrum normalisation low. Several local criteria had to be fulfilled by the future CDFS, such as a low galactic H I density, the absence of bright stars and observability from certain observatory sites. Since these conditions do not reach beyond our galaxy, we do not expect them to affect the lensing signal by the cosmological large-scale structure.
Furthermore, the field was chosen such that no extended X-ray sources from the ROSAT All-Sky Survey (RASS), in particular galaxy clusters, are in the field of view. This is potentially important, since it is known from halo-model calculations that the cosmic shear power spectrum on intermediate and small scales is dominated by group- and cluster-sized haloes. Therefore, the exclusion of X-ray clusters might bias the selection of a suitable line of sight towards under-dense fields. On the other hand, the RASS is quite shallow and thus only contains very luminous or nearby clusters, which have a limited impact on the lensing signal due to their low number or low lensing efficiency. We quantify the importance of this criterion using the halo catalogues of our N-body-simulations. To each halo, we assign an X-ray luminosity in the energy range from 0.1 to
![]() using the mass-luminosity relation given in Reiprich & Böhringer (2002) and convert this into X-ray flux using the halo redshift. We then compute the average of the
using the mass-luminosity relation given in Reiprich & Böhringer (2002) and convert this into X-ray flux using the halo redshift. We then compute the average of the ![]() estimates from all fields which do not contain a cluster brighter than a certain flux limit. It is difficult to define an exact overall flux limit to describe the CDFS selection, because the RASS is rather heterogeneous. However, it is apparent from Fig. 9 that even a very conservative limit of
estimates from all fields which do not contain a cluster brighter than a certain flux limit. It is difficult to define an exact overall flux limit to describe the CDFS selection, because the RASS is rather heterogeneous. However, it is apparent from Fig. 9 that even a very conservative limit of
![]() will change the average
will change the average ![]() estimate by at most
estimate by at most ![]() .
This bias is therefore most likely not large enough to explain our CDFS result alone.
.
This bias is therefore most likely not large enough to explain our CDFS result alone.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=0]{11697f10.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg209.png) |
Figure 9:
The average values of the ICA-MAP (solid black line) and Gauss-MAP (solid red line) estimators computed from CDFS realisations that do not contain clusters with an X-ray flux larger than
|
| Open with DEXTER | |
Table 2:
![]() for the CDFS.
for the CDFS.
Finally, the CDFS candidate should not contain any ``relevant NED source''. This is very hard to translate into a quantitative criterion, in particular because our simulations contain only dark matter. We model the effect of imposing this requirement by demanding that there be less than
![]() group- or cluster-sized haloes (
group- or cluster-sized haloes (
![]() )
in the redshift range from z=0 and z=0.5 in a CDFS candidate. The impact of this criterion on the estimated value of
)
in the redshift range from z=0 and z=0.5 in a CDFS candidate. The impact of this criterion on the estimated value of
![]() using the ICA- and Gauss-MAP estimators is shown in
Fig. 10. As expected, the median
using the ICA- and Gauss-MAP estimators is shown in
Fig. 10. As expected, the median
![]() is a monotonically increasing function of
is a monotonically increasing function of
![]() .
For fields with less than
.
For fields with less than
![]() massive haloes, the probability of obtaining a power spectrum normalisation as low as in the CDFS rises above
massive haloes, the probability of obtaining a power spectrum normalisation as low as in the CDFS rises above
![]() .
Given that the average number of massive haloes in the specified redshift range is 18.5, it does not seem to be too unreasonable that fields with less than
.
Given that the average number of massive haloes in the specified redshift range is 18.5, it does not seem to be too unreasonable that fields with less than
![]() such haloes could be obtained by selecting ``empty'' regions in the NED.
This is also in qualitative agreement with Phleps et al. (2007), who find that the CDFS is underdense by a factor of
such haloes could be obtained by selecting ``empty'' regions in the NED.
This is also in qualitative agreement with Phleps et al. (2007), who find that the CDFS is underdense by a factor of ![]() 2 in the redshift range from
2 in the redshift range from
![]() to
to
![]() .
.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=0]{11697f11.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg226.png) |
Figure 10:
Dependence of the ICA-MAP-estimator for |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=270]{11697f12.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg227.png) |
Figure 11:
Ratios r+ ( upper panel) and r- ( lower panel) of the shear correlation functions in a particular
|
| Open with DEXTER | |
We estimate the impact of this selection criterion on the estimates of cosmological parameters by treating the number of haloes in the CDFS as a nuisance parameter in the process of parameter estimation. Similar to what we did to obtain Fig. 10, we bin the realisations of the CDFS according to the number of group-sized haloes in the realisations. For each bin, we obtain the mean shear correlation function and its ratio to the mean shear correlation function of all realisations,
![]() .
The functions r+ and r- are shown in Fig. 11. The realisations with fewer (more) haloes than the average generally display a smaller (larger) shear correlation function. We fit the ratios in each bin with a double power law of the form
.
The functions r+ and r- are shown in Fig. 11. The realisations with fewer (more) haloes than the average generally display a smaller (larger) shear correlation function. We fit the ratios in each bin with a double power law of the form
For values of
Having corrected for the field selection, we can now recompute the probabilities given in Table 2 for drawing the CDFS at random. We find for the ICA-MAP estimate
![]() for the original shear correlation functions and
for the original shear correlation functions and
![]() for the re-centred ones. For the Gaussian likelihood, we find
for the re-centred ones. For the Gaussian likelihood, we find
![]() (original) and
(original) and
![]() (re-centred), respectively.
(re-centred), respectively.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=270]{11697f13.eps}}
\resizebox{8.8cm}{!}{\includegraphics[angle=0]{11697f14.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg239.png) |
Figure 12:
Upper panel: posterior density for
|
| Open with DEXTER | |
With this (approximate) treatment of the systematic effects caused by the field selection, we can now put the CDFS in context with the results from the WMAP five-year data. For this, we fit the shear correlation function for
![]() and
and ![]() ,
marginalising
over h100 (with a Gaussian prior centred on
h100=0.7 and
,
marginalising
over h100 (with a Gaussian prior centred on
h100=0.7 and
![]() ,
as suggested by the Hubble Key Project; Freedman et al. 2001) and
,
as suggested by the Hubble Key Project; Freedman et al. 2001) and
![]() with a uniform prior. We use the WMAP Markov chain for a flat
with a uniform prior. We use the WMAP Markov chain for a flat ![]() CDM model (lcdm+sz+lens; Komatsu et al. 2009; Dunkley et al. 2009), where again we marginalise over all parameters except
CDM model (lcdm+sz+lens; Komatsu et al. 2009; Dunkley et al. 2009), where again we marginalise over all parameters except
![]() and
and ![]() .
The resulting posterior distributions for the CDFS only (blue dashed contours), WMAP only (red contours) and the combination of both measurements (thick black contours) are shown in Fig. 13. Clearly, the joint posterior is dominated by the WMAP data; however, the constraints from the CDFS allow us to exclude parameter combinations where both
.
The resulting posterior distributions for the CDFS only (blue dashed contours), WMAP only (red contours) and the combination of both measurements (thick black contours) are shown in Fig. 13. Clearly, the joint posterior is dominated by the WMAP data; however, the constraints from the CDFS allow us to exclude parameter combinations where both
![]() and
and ![]() are large. We find the MAP estimates
are large. We find the MAP estimates
![]() and
and
![]() when marginalising over the other parameter.
when marginalising over the other parameter.
Finally, note that the two criteria discussed in this section are not strictly independent. However, it is highly improbable that a single field will contain more than one massive halo above the X-ray flux limit. Therefore, selecting fields without an X-ray-bright cluster prior to performing the steps that lead to Fig. 10 would change the halo numbers that go into the analysis by at most one and would not significantly influence the foregoing discussion.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=0]{11697f15.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg243.png) |
Figure 13:
Posterior density for
|
| Open with DEXTER | |
5 Summary and discussion
In this paper, we have investigated the validity of the approximation of a Gaussian likelihood for the cosmic shear correlation function, which is routinely made in weak lensing studies. We have described a method to estimate the likelihood from a large set of ray-tracing simulations. The algorithm tries to find a new set of (non-orthogonal) basis vectors with respect to which the components of the shear correlation functions become approximately statistically independent. This then allows us to estimate the high-dimensional likelihood as a product of one-dimensional probability distributions. A drawback of this method is that quite a large sample of realistically simulated correlation functions is required to get good results for the tails of the likelihood. However, this should become less problematic in the near future when increasingly large ray-tracing simulations will become available.
We have investigated how the constraints on matter and vacuum energy density, Hubble parameter and power spectrum normalisation depend on the shape of the likelihood for a survey composed of
![]() fields and a redshift distribution similar to the CDFS. We find that if the non-Gaussianity of the likelihood is taken into account, the posterior likelihood becomes more sharply peaked and skewed. When fitting only for
fields and a redshift distribution similar to the CDFS. We find that if the non-Gaussianity of the likelihood is taken into account, the posterior likelihood becomes more sharply peaked and skewed. When fitting only for
![]() and
and ![]() ,
the maximum of the posterior is shifted towards lower
,
the maximum of the posterior is shifted towards lower
![]() and higher
and higher ![]() ,
and the area of the
,
and the area of the ![]() highest posterior density credible region decreases by about
highest posterior density credible region decreases by about ![]() compared to the case of a Gaussian likelihood. For the four-dimensional parameter space, we have conducted a Fisher matrix analysis to obtain lower limits on the errors achievable with a
compared to the case of a Gaussian likelihood. For the four-dimensional parameter space, we have conducted a Fisher matrix analysis to obtain lower limits on the errors achievable with a
![]() survey. As in the two-dimensional case, we find the most important effect to be that the error bars decrease by
survey. As in the two-dimensional case, we find the most important effect to be that the error bars decrease by ![]() compared to the Gaussian likelihood. Less severe is the slight tilt of the Fisher ellipses when marginalising over two of the four parameters, particularly when h100 is involved.
compared to the Gaussian likelihood. Less severe is the slight tilt of the Fisher ellipses when marginalising over two of the four parameters, particularly when h100 is involved.
In the second part of this work, we have presented a re-analysis of the CDFS-HST data.
Using the non-Gaussian likelihood, we find
![]() for
for
![]() (keeping all other parameters fixed to their fiducial values), compared to
(keeping all other parameters fixed to their fiducial values), compared to
![]() obtained from the Gaussian likelihood with a covariance matrix estimated from the ray-tracing simulations. We have then tried to quantify how (un-)likely it is to randomly select a field with the characteristics of the Chandra Deep Field South with a power spectrum normalisation this low. We have used 9600 ray-tracing realisations of the CDFS to estimate the sampling distribution of the ICA-MAP estimator for
obtained from the Gaussian likelihood with a covariance matrix estimated from the ray-tracing simulations. We have then tried to quantify how (un-)likely it is to randomly select a field with the characteristics of the Chandra Deep Field South with a power spectrum normalisation this low. We have used 9600 ray-tracing realisations of the CDFS to estimate the sampling distribution of the ICA-MAP estimator for ![]() .
For our fiducial, WMAP5-like cosmology, we find that
.
For our fiducial, WMAP5-like cosmology, we find that
![]() ,
assuming that the location of the CDFS on the sky was chosen randomly. The fact that the CDFS was selected not to contain an extended X-ray source in the ROSAT All-Sky Survey can lead to a bias of the estimated
,
assuming that the location of the CDFS on the sky was chosen randomly. The fact that the CDFS was selected not to contain an extended X-ray source in the ROSAT All-Sky Survey can lead to a bias of the estimated ![]() by at most
by at most ![]() .
This is because the clusters excluded by this criterion are rare and mostly at low redshifts, and therefore not very lensing-efficient. The second relevant selection criterion is that the CDFS should not contain any relevant NED source. We model this by selecting only those fields which contain a specific number
.
This is because the clusters excluded by this criterion are rare and mostly at low redshifts, and therefore not very lensing-efficient. The second relevant selection criterion is that the CDFS should not contain any relevant NED source. We model this by selecting only those fields which contain a specific number
![]() of group- and cluster-sized haloes. We find that for those realisations for which the number of such haloes is below the average, the estimates of
of group- and cluster-sized haloes. We find that for those realisations for which the number of such haloes is below the average, the estimates of ![]() can be biased low by about 5-
can be biased low by about 5-![]() .
We include this effect in our likelihood analysis by extending our model shear correlation function by a correction factor depending on
.
We include this effect in our likelihood analysis by extending our model shear correlation function by a correction factor depending on
![]() and treating
and treating
![]() as a nuisance parameter. This increases the estimate of
as a nuisance parameter. This increases the estimate of ![]() by
by ![]() to
to
![]() for the ICA likelihood and by
for the ICA likelihood and by ![]() to
to
![]() for the Gaussian likelihood. This procedure also yields tentative evidence that the number of massive haloes in the CDFS is only
for the Gaussian likelihood. This procedure also yields tentative evidence that the number of massive haloes in the CDFS is only
![]() of the average, in qualitative agreement with the findings of Phleps et al. (2007).
of the average, in qualitative agreement with the findings of Phleps et al. (2007).
Finally, we combine the CDFS cosmic shear results with the constraints on cosmological parameters from the WMAP experiment. We fit for
![]() and
and ![]() ,
where we marginalise over the Hubble constant and take into account the field selection bias by marginalising also over
,
where we marginalise over the Hubble constant and take into account the field selection bias by marginalising also over
![]() .
While the posterior is clearly dominated by the WMAP data, the CDFS still allows us to exclude parts of the parameter space with high values of both
.
While the posterior is clearly dominated by the WMAP data, the CDFS still allows us to exclude parts of the parameter space with high values of both
![]() and
and ![]() .
Assuming a flat Universe, the MAP estimates for these two parameters are
.
Assuming a flat Universe, the MAP estimates for these two parameters are
![]() and
and
![]() .
.
Acknowledgements
We would like to thank Tim Eifler for useful discussions and the computation of the Gaussian covariance matrix, and Sherry Suyu for careful reading of the manuscript. We thank Richard Massey and William High for providing the STEP2 image simulations. JH acknowledges support by the Deutsche Forschungsgemeinschaft within the Priority Programme 1177 under the project SCHN 342/6 and by the Bonn-Cologne Graduate School of Physics and Astronomy. T.S. acknowledges financial support from the Netherlands Organization for Scientific Research (NWO) and the German Federal Ministry of Education and Research (BMBF) through the TR33 ``The Dark Universe''. We acknowledge the use of the Legacy Archive for Microwave Background Data Analysis (LAMBDA). Support for LAMBDA is provided by the NASA Office of Space Science.
Appendix A: Projection pursuit density estimation
In order to have an independent check of the ICA-based likelihood estimation algorithm, we employ the method of projection pursuit density estimation (PPDE; Friedman et al. 1984). Like our ICA method, PPDE aims to estimate the joint probability density ![]() of a random
vector
of a random
vector ![]() ,
given a set of observations of
,
given a set of observations of ![]() .
As starting point, an initial model
.
As starting point, an initial model
![]() for the multidimensional probability distribution
for the multidimensional probability distribution ![]() has to be provided, for which a reasonable choice is e.g. a multivariate Gaussian with a covariance matrix estimated from the data. The method then identifies the direction
has to be provided, for which a reasonable choice is e.g. a multivariate Gaussian with a covariance matrix estimated from the data. The method then identifies the direction
![]() along which the marginalised model distribution differs most from the marginalised density of the data points and corrects for the discrepancy along the direction
along which the marginalised model distribution differs most from the marginalised density of the data points and corrects for the discrepancy along the direction
![]() by multiplying p0 with a correction factor. This yields a refined density estimate
by multiplying p0 with a correction factor. This yields a refined density estimate
![]() ,
which can be further improved by iteratively applying the outlined procedure.
,
which can be further improved by iteratively applying the outlined procedure.
More formally, the PPDE density estimate is of the form
where pM is the estimate after M iterations of the procedure and p0 is the initial model. The univariate functions
![\begin{displaymath}D_{\rm KL}[p,p_M] = \int{\rm d}\vec x\;p(\vec x)~\log \frac{p(\vec x)}{p_M(\vec x)},
\end{displaymath}](/articles/aa/full_html/2009/36/aa11697-09/img262.png) |
(A.2) |
as a goodness-of-fit measure. The Kullback-Leibler divergence provides a ``distance measure'' between two probability distribution functions, since it is non-negative and zero only if
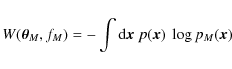 |
(A.3) |
of the K-L divergence is relevant for the minimisation, all other terms do not depend on
which is the expectation value of
 |
(A.5) |
For fixed
where
- choosing a direction
 ;
;
- computing the marginal densities
 and
and
 ;
;
- computing
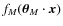 according to Eq. (A.6);
according to Eq. (A.6);
- computing
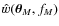 ;
;
- choosing a new
 that decreases
that decreases 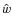 ;
;
- continuing from step 2 until a convergence criterion is fulfilled.
Note that the PPDE technique, although using very similar methodology as our ICA-based procedure, is different in the important point that it does not rely on the assumption that a linear transformation of the data leads to statistical independence of the components of the transformed data vectors. It therefore comprises a good test of the validity of this approximation.
Appendix B: Fisher matrix of the ICA likelihood
In this appendix, we give the derivation of Eq. (23). In
the general case, the Fisher matrix is given by (e.g. Kendall et al. 1987)
In our case, the likelihood depends on cosmological parameters only through the difference between data and model vector, i.e.
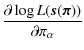 |
= | 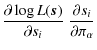 |
(B.2) |
| = | 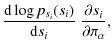 |
(B.3) |
where in the last step we have made use of the fact that the likelihood factorises in the ICA basis. The expression for the Fisher matrix then can be written as
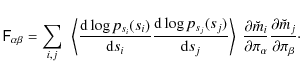 |
(B.4) |
Next, we compute the expectation value on the right hand side and obtain
| |
= | 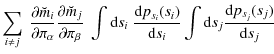 |
(B.5) |
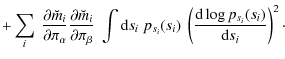 |
(B.6) |
The integrals in the first term of the right hand side vanish since the psi drop to zero for very large and small values of si. This leaves us with
The derivatives in Eq. (B.7) can be strongly affected by noise in the estimated psi(si), in particular in the tails of the distributions. For their numerical computation, we therefore choose the following four-point finite difference operator (Abramowitz & Stegun 1964):
| (B.8) |
which we find to be more stable against this problem than its more commonly used two-point counterpart. Because of this potential difficulty, we cross-check our results with the alternative method provided by Eq. (22). This method is significantly slower, but numerically simpler. This is because the derivatives of the log-likelihood in Eq. (22) are on average computed close to the maximum-likelihood point, where the likelihood estimate is well sampled. Reassuringly, we find excellent agreement between the two methods. Finally, we have investigated the influence of the choice of the Kernel function K in Eq. (10), which might affect the computation of the numerical derivatives. Our results prove to be stable against variation of K, provided that we chose a differentiable Kernel function.
Appendix C: Further conclusions for our KSB+ pipeline from the STEP simulations
In this appendix we assume that the reader is familiar with basic KSB notation. For a short introduction and a summary of differences between various implementations see Heymans et al. (2006).
Within the Shear TEsting
Programme![]() (STEP) simulated images containing sheared galaxies are analysed in blind
tests, in order to test the shear measurement accuracy of weak lensing
pipelines.
In these analyses the shear recovery accuracy has been quantified in terms
of a multiplicative calibration bias m and additive PSF residuals c.
From the analysis of the first set of simulations (STEP1, Heymans et al. 2006),
which mimic simplified ground-based observations, we
find that our KSB+ implementation significantly under-estimates
gravitational shear on average if no calibration correction is applied.
After the elimination of selection and weighting-related effects this shear
calibration bias amounts to a relative under-estimation of
(STEP) simulated images containing sheared galaxies are analysed in blind
tests, in order to test the shear measurement accuracy of weak lensing
pipelines.
In these analyses the shear recovery accuracy has been quantified in terms
of a multiplicative calibration bias m and additive PSF residuals c.
From the analysis of the first set of simulations (STEP1, Heymans et al. 2006),
which mimic simplified ground-based observations, we
find that our KSB+ implementation significantly under-estimates
gravitational shear on average if no calibration correction is applied.
After the elimination of selection and weighting-related effects this shear
calibration bias amounts to a relative under-estimation of ![]() .
According to our testing the largest contribution to this bias originates
from the inversion of the
.
According to our testing the largest contribution to this bias originates
from the inversion of the ![]() -tensor, which describes the response of
galaxy
ellipticity to gravitational shear. While a full-tensor inversion reduces
this bias, it strongly increases the measurement noise (see also
Erben et al. 2001) and dependence on galaxy selection criteria.
We therefore decided to stick to the commonly applied approximation of
-tensor, which describes the response of
galaxy
ellipticity to gravitational shear. While a full-tensor inversion reduces
this bias, it strongly increases the measurement noise (see also
Erben et al. 2001) and dependence on galaxy selection criteria.
We therefore decided to stick to the commonly applied approximation of
![]() ,
which we measure from individual galaxies, and correct the shear estimate using a
multiplicative calibration factor of
,
which we measure from individual galaxies, and correct the shear estimate using a
multiplicative calibration factor of
![]() in the S07 analysis.
This average calibration correction was found to be stable to the
in the S07 analysis.
This average calibration correction was found to be stable to the ![]()
![]() -level between
different STEP1 simulation subsets. However, note that the bias depends on the
details of the KSB implementation, which might explain some of the scatter
between the results for different KSB codes in STEP1.
In particular, we identified a strong dependence on the choice of the
Gaussian filter scale
-level between
different STEP1 simulation subsets. However, note that the bias depends on the
details of the KSB implementation, which might explain some of the scatter
between the results for different KSB codes in STEP1.
In particular, we identified a strong dependence on the choice of the
Gaussian filter scale ![]() ,
which is used in the computation of
the KSB brightness moments. For example changing from our default
,
which is used in the computation of
the KSB brightness moments. For example changing from our default
![]() ,
where
,
where ![]() is the flux
radius as measured by SExtractor
(Bertin & Arnouts 1996),
to
is the flux
radius as measured by SExtractor
(Bertin & Arnouts 1996),
to
![]() ,
worsens the bias to
,
worsens the bias to ![]() .
.
The average calibration correction likewise proved to be robust for the second set of image simulations (STEP2, Massey et al. 2007a), which also mimics ground-based data but takes into account more complex PSFs and galaxy morphologies by applying the shapelets formalism (Massey et al. 2004). Yet, the STEP2 analysis revealed a significant magnitude dependence of the shear recovery accuracy for our implementation, with a strong deterioration at faint magnitudes. In this analysis we applied the same signal-to-noise cut S/N>4.0 as in STEP1 (KSB S/N as defined in Erben et al. 2001), where we however ignored the strong noise correlations present in the STEP2 data, which was added to mimic the influence of drizzle.
![\begin{figure}
\par\includegraphics[width=5.4cm]{11697f16.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg296.png) |
Figure C.1:
Estimate of the effective influence of the noise correlations in
the STEP2 simulations: plotted is the ratio of the pixel value dispersion
|
| Open with DEXTER | |
In the case of uncorrelated noise the dispersion of the sum over the pixel
values of N pixels
scales as
where
In order to estimate the effective influence
of the noise correlations in STEP2, we use a pure noise image which was
provided together with the simulated images.
We compute the rms of the pixel sum
![]() in independent quadratic
sub-regions of the image with side length
in independent quadratic
sub-regions of the image with side length
![]() and determine the ratio
and determine the ratio
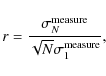 |
(C.2) |
which in the absence of correlated noise would be equal to 1 for all N. In the presence of noise correlations it will for large N converge to the factor by which
![\begin{figure}
\par\includegraphics[width=5cm]{11697f17.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg304.png) |
Figure C.2:
Calibration bias m as a function of the uncorrected
KSB signal-to-noise
S/N for the TS analysis of the STEP2
simulations.
Thin solid (dashed) lines show |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm]{11697f18.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg305.png) |
Figure C.3:
Calibration bias m and PSF residuals c as a function of input
galaxy magnitude and size for our refined analysis of the STEP2
data.
Thin solid (dashed) lines show |
| Open with DEXTER | |
We plot the dependence of our STEP2 shear estimate on the (uncorrected)
S/Nin Fig. C.2.
For
![]() ,
corresponding to
,
corresponding to
![]() ,
a significant
deterioration of the shear signal occurs, with a mean calibration bias
,
a significant
deterioration of the shear signal occurs, with a mean calibration bias
![]() and a large scatter between the different PSF models.
We conclude that this approximately marks the limit down to which our KSB+ implementation
can reliably measure shear.
If we apply a modified cut
S/N>7.0 to the STEP2
galaxies, the resulting magnitude and size dependence of the shear calibration bias
is
and a large scatter between the different PSF models.
We conclude that this approximately marks the limit down to which our KSB+ implementation
can reliably measure shear.
If we apply a modified cut
S/N>7.0 to the STEP2
galaxies, the resulting magnitude and size dependence of the shear calibration bias
is ![]()
![]() 5% (top panels in Fig. C.3).
The remaining galaxies are best corrected with a slightly
reduced calibration factor
5% (top panels in Fig. C.3).
The remaining galaxies are best corrected with a slightly
reduced calibration factor
![]() ,
which we apply for
the plots shown in this appendix and the updated shear analysis presented in
this paper.
The
difference between the
calibration corrections derived from STEP1 and STEP2 agrees with the estimated
,
which we apply for
the plots shown in this appendix and the updated shear analysis presented in
this paper.
The
difference between the
calibration corrections derived from STEP1 and STEP2 agrees with the estimated ![]()
![]() accuracy.
Note that the error increases for the highly elliptical PSFs D and E
(
accuracy.
Note that the error increases for the highly elliptical PSFs D and E
(
![]() )
in STEP2, for which in addition significant PSF
anisotropy residuals occur (bottom panels in
Fig. C.3). This should however not affect our
analysis given that typical ACS PSF ellipticities rarely exceed
)
in STEP2, for which in addition significant PSF
anisotropy residuals occur (bottom panels in
Fig. C.3). This should however not affect our
analysis given that typical ACS PSF ellipticities rarely exceed
![]() ,
see e.g. S07.
,
see e.g. S07.
References
- Abramowitz, M., & Stegun, I. A. 1964, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, ninth edn. (New York: Dover) (In the text)
- Benjamin, J., Heymans, C., Semboloni, E., et al. 2007, MNRAS, 381, 702 [NASA ADS] [CrossRef] (In the text)
- Bernstein, G. M., & Jarvis, M. 2002, AJ, 123, 583 [NASA ADS] [CrossRef] (In the text)
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Chiu, K.-C., Liu, Z.-Y., & Xu, L. 2003, in Proc. 4th International Symposium on Independent Component Analysis and Blind Signal Separation (ICA2003), Nara, Japan, 751 (In the text)
- Comon, P., Jutten, C., & Hérault, J. 1991, Signal Processing, 24, 11 [CrossRef]
- Cooray, A., & Hu, W. 2001, ApJ, 554, 56 [NASA ADS] [CrossRef]
- Davison, A. C. 2003, Statistical Models, Cambridge Series in Statistical and Probabilistic Mathematics (Cambridge University Press)
- Dunkley, J., Komatsu, E., Nolta, M. R., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef] (In the text)
- Eifler, T., Schneider, P., & Hartlap, J. 2009, A&A, 502, 721 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Erben, T., van Waerbeke, L., Bertin, E., Mellier, Y., & Schneider, P. 2001, A&A, 366, 717 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] (In the text)
- Friedman, J., Stuetzle, W., & Schroeder, A. 1984, J. Am. Stat. Assoc., 79, 599 [CrossRef] (In the text)
- Fu, L., Semboloni, E., Hoekstra, H., et al. 2008, A&A, 479, 9 [NASA ADS] [CrossRef] [EDP Sciences]
- Gelman, A., Carlin, J. B., Stern, H., & Rubin, D. B. 2004, Bayesian Data Analysis (Chapman & Hall/CRC) (In the text)
- Giacconi, R., Rosati, P., Tozzi, P., et al. 2001, ApJ, 551, 624 [NASA ADS] [CrossRef] (In the text)
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef]
- Grazian, A., Fontana, A., de Santis, C., et al. 2006, A&A, 449, 951 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hartlap, J., Simon, P., & Schneider, P. 2007, A&A, 464, 399 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hastie, T., Tibshirani, R., & Friedman, J. 2001, The Elements of Statistical Learning (Springer)
- Heymans, C., Brown, M. L., Barden, M., et al. 2005, MNRAS, 361, 160 [NASA ADS] [CrossRef] (In the text)
- Heymans, C., Van Waerbeke, L., Bacon, D., et al. 2006, MNRAS, 368, 1323 [NASA ADS] [CrossRef] (In the text)
- Hilbert, S., Hartlap, J., White, S. D. M., & Schneider, P. 2009, A&A, 499, 31 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Hoekstra, H., Franx, M., Kuijken, K., & Squires, G. 1998, ApJ, 504, 636 [NASA ADS] [CrossRef]
- Hoekstra, H., Mellier, Y., van Waerbeke, L., et al. 2006, ApJ, 647, 116 [NASA ADS] [CrossRef]
- Hyvärinen, A. & Oja, E. 1997, Neural Computation, 9(7), 1438 (In the text)
- Hyvärinen, A. & Oja, E. 2000, Neural Networks, 13(4-5), 411
- Hyvärinen, A., Karhunen, J., & Oja, E. 2001, Independent Component Analysis (Wiley Interscience)
- Jain, B., Seljak, U., & White, S. 2000, AJ, 530, 547 [NASA ADS] [CrossRef] (In the text)
- Joachimi, B., Schneider, P., & Eifler, T. 2008, A&A, 477, 43 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jutten, C., & Hérault, J. 1991, Signal Processing, 24, 1 [CrossRef]
- Kaiser, N., & Pan-STARRS Collaboration 2005, in BAAS, 37, 465 (In the text)
- Kaiser, N., Squires, G., & Broadhurst, T. 1995, ApJ, 449, 460 [NASA ADS] [CrossRef]
- Kendall, M. G., Stuart, A., & Ord, J. K. (eds.) 1987, Kendall's advanced theory of statistics (New York, NY, USA: Oxford University Press, Inc.) (In the text)
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef]
- Kuijken, K. 2006, A&A, 456, 827 [NASA ADS] [CrossRef] [EDP Sciences]
- Kullback, S., & Leibler, R. A. 1951, Annals of Mathematical Statistics, 22, 79 [CrossRef] (In the text)
- Liang, J.-J., Fang, K.-T., Hickernell, F. J., & Li, R. 2001, Math. Comput., 70, 337 [NASA ADS] (In the text)
- Luppino, G. A., & Kaiser, N. 1997, ApJ, 475, 20 [NASA ADS] [CrossRef]
- Massey, R., Refregier, A., Conselice, C. J., David, J., & Bacon, J. 2004, MNRAS, 348, 214 [NASA ADS] [CrossRef] (In the text)
- Massey, R., Heymans, C., Bergé, J., et al. 2007a, MNRAS, 376, 13 [NASA ADS] [CrossRef] (In the text)
- Massey, R., Rhodes, J., Leauthaud, A., et al. 2007b, ApJS, 172, 239 [NASA ADS] [CrossRef] (In the text)
- Miller, L., Kitching, T. D., Heymans, C., Heavens, A. F., & van Waerbeke, L. 2007, MNRAS, 382, 315 [NASA ADS] [CrossRef] (In the text)
- Peacock, J. A., & Dodds, S. J. 1996, MNRAS, 280, 19 [NASA ADS] (In the text)
- Phleps, S., Wolf, C., Peacock, J. A., Meisenheimer, K., & van Kampen, E. 2007, in Cosmic Frontiers, ed. N. Metcalfe, & T. Shanks, ASP Conf. Ser., 379, 327 (In the text)
- Press, W., et al. 1992, Numerical Recipes in C (Cambridge University Press) (In the text)
- R Development Core Team. 2007, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria (In the text)
- Refregier, A., & Bacon, D. 2003, MNRAS, 338, 48 [NASA ADS] [CrossRef]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] (In the text)
- Rix, H.-W., Barden, M., Beckwith, S. V. W., et al. 2004, ApJS, 152, 163 [NASA ADS] [CrossRef]
- Schneider, P. 2006, in Saas-Fee Advanced Course 33: Gravitational Lensing: Strong, Weak and Micro, ed. G. Meylan, P. Jetzer, P. North, P. Schneider, C. S. Kochanek, & J. Wambsganss, 269 (In the text)
- Schneider, P., van Waerbeke, L., Kilbinger, M., & Mellier, Y. 2002, A&A, 396, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schrabback, T., Erben, T., Simon, P., et al. 2007, A&A, 468, 823 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Scoccimarro, R., Zaldarriaga, M., & Hui, L. 1999, ApJ, 527, 1 [NASA ADS] [CrossRef]
- Scott, D. W. 1992, Multivariate Density Estimation: Theory, Practice, and Visualization (New York: John Wiley & Sons)
- Semboloni, E., Mellier, Y., van Waerbeke, L., et al. 2006, A&A, 452, 51 [NASA ADS] [CrossRef] [EDP Sciences]
- Semboloni, E., van Waerbeke, L., Heymans, C., et al. 2007, MNRAS, 375, 6 [NASA ADS] (In the text)
- Semboloni, E., Tereno, I., van Waerbeke, L., & Heymans, C. 2009, MNRAS, 397, 608 [NASA ADS] [CrossRef] (In the text)
- Silverman, B. W. 1986, Density Estimation (London: Chapman and Hall)
- Smail, I., Hogg, D. W., Yan, L., & Cohen, J. G. 1995, ApJ, 449, 105 [NASA ADS] [CrossRef] (In the text)
- Smith, R. E., Peacock, J. A., Jenkins, A., et al. 2003, MNRAS, 341, 1311 [NASA ADS] [CrossRef] (In the text)
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] (In the text)
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] (In the text)
- Takada, M., & Jain, B. 2009, MNRAS, 395, 2065 [NASA ADS] [CrossRef]
- Venables, W., & Ripley, B. 2002, Modern Applied Statistics with S (Springer)
- Wolf, C., Meisenheimer, K., Kleinheinrich, M., et al. 2004, A&A, 421, 913 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Footnotes
- ...(R Development Core Team 2007)
![[*]](/icons/foot_motif.png)
- http://www.r-project.org/
- ...
Programme
![[*]](/icons/foot_motif.png)
- http://www.physics.ubc.ca/~heymans/step.html
All Tables
Table 1:
Estimates of ![]() from the CDFS.
from the CDFS.
Table 2:
![]() for the CDFS.
for the CDFS.
All Figures
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[angle=270]{11697f01.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg136.png) |
Figure 1:
Area of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[angle=270]{11697f02.eps}}...
....5cm}
\resizebox{8cm}{!}{\includegraphics[angle=270]{11697f03.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg145.png) |
Figure 2: Comparison of the joint distributions p(si,sj) (black dashed contours) and the product psi(si) psj(sj) (solid red contours) for the two most non-Gaussian components (i=1, j=2) and two rather Gaussian ones (i=9, j=10), after performing ICA ( left panels) and PCA ( right panels). The components have been ranked and labelled according to their non-Gaussianity; the ith PCA component is in general not the same as ith ICA-component. In the right panel of each plot, the distributions with respect to the PCA basis vectors are shown and in the left panel, the distributions in the ICA basis are displayed. Statistical independence is indicated by p(si,sj)=psi(si) psj(sj). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8.6cm}{!}{\includegraphics[angle=270]{11697f04.ps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg148.png) |
Figure 3:
Comparison of the posterior likelihoods for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm]{11697f05.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg149.png) |
Figure 4:
Comparison of the posterior likelihoods for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm]{11697f06.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg166.png) |
Figure 5:
Fisher matrix constraints for a hypothetical 1500-
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[]{11697f07.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg197.png) |
Figure 6:
Posterior distributions for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[]{11697f08.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg204.png) |
Figure 7:
Sampling distributions of the MAP estimators of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{9cm}{!}{\includegraphics[]{11697f09.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg205.png) |
Figure 8: Same as Fig. 7, but using re-centred correlation functions. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=0]{11697f10.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg209.png) |
Figure 9:
The average values of the ICA-MAP (solid black line) and Gauss-MAP (solid red line) estimators computed from CDFS realisations that do not contain clusters with an X-ray flux larger than
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=0]{11697f11.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg226.png) |
Figure 10:
Dependence of the ICA-MAP-estimator for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=270]{11697f12.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg227.png) |
Figure 11:
Ratios r+ ( upper panel) and r- ( lower panel) of the shear correlation functions in a particular
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=270]{11697f13.eps}}
\resizebox{8.8cm}{!}{\includegraphics[angle=0]{11697f14.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg239.png) |
Figure 12:
Upper panel: posterior density for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=0]{11697f15.eps}}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg243.png) |
Figure 13:
Posterior density for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5.4cm]{11697f16.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg296.png) |
Figure C.1:
Estimate of the effective influence of the noise correlations in
the STEP2 simulations: plotted is the ratio of the pixel value dispersion
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=5cm]{11697f17.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg304.png) |
Figure C.2:
Calibration bias m as a function of the uncorrected
KSB signal-to-noise
S/N for the TS analysis of the STEP2
simulations.
Thin solid (dashed) lines show |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm]{11697f18.eps}
\end{figure}](/articles/aa/full_html/2009/36/aa11697-09/Timg305.png) |
Figure C.3:
Calibration bias m and PSF residuals c as a function of input
galaxy magnitude and size for our refined analysis of the STEP2
data.
Thin solid (dashed) lines show |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



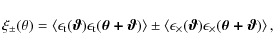
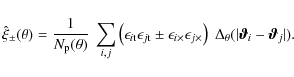
![$\displaystyle p(\vec{\xi} \vert \vec{\pi}) = \frac{1}{(2\pi)^{p/2}\det \tens C(...
... \tens{C}^{-1}(\vec{\pi})~ \left[\vec{\xi}-\vec{m}(\vec{\pi})\right] \right\} ,$](/articles/aa/full_html/2009/36/aa11697-09/img75.png)
![\begin{displaymath}
p(\vec{\xi} \vert \vec{\pi}) = L_{\vec{\pi}_0}\left[\vec{\Delta}(\vec{\pi})\right].
\end{displaymath}](/articles/aa/full_html/2009/36/aa11697-09/img79.png)