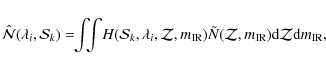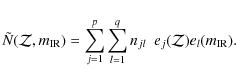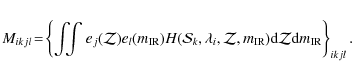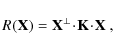EDP Sciences
Home All issues Volume 504 / No 3 (September IV 2009) A&A, 504 3 (2009) 727-740 Full HTML
Highlight
Free Access
Issue
A&A
Volume 504, Number 3, September IV 2009
Page(s) 727 - 740
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200809945
Published online 09 July 2009

Cosmic star-formation history from a non-parametric inversion of infrared galaxy counts[*]

D. Le Borgne1,2,3 - D. Elbaz1 - P. Ocvirk1,4 - C. Pichon2,3

1 - CEA/Saclay, DSM/IRFU/SAp, 91191 Gif-sur-Yvette, France
2 - UPMC Univ. Paris 06, UMR7095, Institut d'Astrophysique de Paris, 75014 Paris, France
3 - CNRS, UMR7095, Institut d'Astrophysique de Paris, 75014 Paris, France
4 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany

Received 10 April 2008 / Accepted 17 April 2009

Abstract
Aims. This paper aims at providing new conservative constraints on the cosmic star-formation (SF) history from the empirical modeling of recent observations in the mid and far infrared.
Methods. We present a new empirical method based on a non-parametric inversion technique. It primarily uses multi-wavelength galaxy counts in the infrared and sub-mm (15, 24, 70, 160, 850 $\mu $m), and it does not require any redshift information. This inversion can be considered as a ``blind'' search for all possible evolutions and shapes of the infrared luminosity function of galaxies, from which the evolution of the star-formation rate density (SFRD) and its uncertainties are derived. The cosmic infrared background (CIRB) measurements are used a posteriori to tighten the range of solutions. The inversion relies only on two hypotheses: (1) the luminosity function remains smooth both in redshift and luminosity; (2) a set of infrared spectral energy distributions (SEDs) of galaxies must be assumed, with a dependency on the total luminosity alone.
Results. The range of SF histories recovered at low redshift is well-constrained and consistent with direct measurements from various redshift surveys. Redshift distributions are recovered without any input into the redshifts of the sources making the counts. A peak of the SFRD at $z\simeq 2$ is preferred, although higher redshifts are not excluded. We also demonstrate that galaxy counts at 160 $\mu $m present an excess around 20 mJy that is not consistent with counts at other wavelengths under the hypotheses cited above. Finally, we find good consistency between the observed evolution of the stellar mass density and the prediction from our model of SF history.
Conclusions. Multi-wavelength counts and CIRB (both projected observations) alone, interpreted with a luminosity-dependent library of SEDs, contain enough information to recover the cosmic evolution of the infrared luminosity function of galaxies, and therefore the evolution of the SFRD, with quantifiable errors. Moreover, the inability of the inversion to model perfectly and simultaneously the multi-wavelength infrared counts implies either (i) the existence of a sub-population of colder galaxies; (ii) a larger dispersion of dust temperatures among local galaxies than expected; (iii) a redshift evolution of the infrared SED of galaxies.

Key words: galaxies: high-redshift - galaxies: evolution - Galaxy: formation - infrared: galaxies - submillimeter - galaxies: luminosity function, mass function

1 Introduction

Some key questions remain concerning the formation of galaxies, such as when and how galaxies formed their stars over the past 13 Gyr. Thanks to recent ultra-deep surveys at various wavelengths, some phenomena are now quite accurately measured and described, at least at relatively low redshift. For instance, it is well-established that massive galaxies have experienced most of their SF activity at early epochs, whereas the SF activity in small galaxies keeps a more constant level, on average. This so-called ``downsizing'' has been subject to many studies over the past few years (Madau et al. 1996; Steidel et al. 1999; Le Floc'h et al. 2005; Lilly et al. 1996; Juneau et al. 2005) and various signs of this downsizing are now seen. But precise measurements of the rate of stellar formation occurring at high redshift are still needed to efficiently challenge the latest models of galaxy formation. In other words, additional constraints on the modeling of the evolution of the cosmic SF history should be inspired by observations.

Recently, very deep surveys were designed to probe SF in the distant universe. For instance, mid-infrared light (at 15 and 24 $\mu $m) collected by the ISO and Spitzer telescopes has been used extensively to measure the star-formation rate (SFR) of both nearby and distant galaxies. The evolution of the infrared (IR) luminosity functions (hereafter LF), parameterized in shape (e.g. with Schechter functions), has been measured up to z=2 with, again, a parameterization for the evolution that can be both in luminosity ( $(1+z)^{\alpha_{\rm L}}$) or in density ( $(1+z)^{\alpha_{\rm D}}$). From these studies (Caputi et al. 2007; Babbedge et al. 2006; Le Floc'h et al. 2005), several values of $\alpha_{\rm L}$ and $\alpha_{\rm D}$ have been measured in various redshift ranges and used to derive the evolution of the SFRD. Such works give a very solid basis to our understanding of galaxy evolution, but they are generally limited to relatively low redshifts for two reasons. First, they are very expensive in observation time if spectroscopic redshifts are used to derive the luminosities of the sources. Photometric redshifts can also be used to complement spectroscopic redshifts, but their uncertainties are well-quantified only at low redshift, where spectroscopic redshifts are available to calibrate them. The second reason is that k-corrections of 24 $\mu $m light becomes large and hazardous at z>2 where the restframe wavelength falls in the PAH features. The derivations of total infrared luminosities and SFRs are therefore uncertain. In the following, we call this approach ``direct method'' and it consists in deriving luminosity functions and SFRD from mid-IR light collected in redshift surveys.

However, these studies present some severe limitations. First, a full multi-wavelength approach has not yet been used to measure these quantities. Indeed, the studies cited above only use observations in one mid-IR band to extrapolate to a total IR luminosity and derive an SFR from uncertain calibrations (e.g. Kennicutt 1998). Moreover, various depths and areas must be explored simultaneously. On the one hand, only very deep surveys are able to probe the lowest levels of SF in distant galaxies, which is necessary to account for the total volume-average SF activity potentially dominated by numerous galaxies with low SFRs. But these very deep surveys necessarily probe only a small area in the sky. On the other hand, large (and therefore shallow) surveys are also needed to probe the populations of sources presenting a low density on the sky. It is the case for very low-redshift sources and it might also be the case for the distant populations of ULIRGS[*] for instance.

A natural way of exploiting this multi-wavelength and multi-scale information all-together is to adopt a global modeling approach. Ideally, the models (defined as the combination of a library of IR SEDs and of an evolving LF) must be able to simultaneously account for all the counts observed at all IR wavelengths, from faint to bright sources. In addition, they must also account for the constraints brought by measurements of the CIRB, and from LFs measured with the ``direct method''. For instance, Chary & Elbaz (2001, hereafter CE01) and Lagache et al. (2003, hereafter LDP03) or Franceschini et al. (2001) have found models that are able to reproduce most of these constraints. However, some adjustments of the LFs or even of the SEDs by these authors were needed to reproduce the most up-to-date observations. This modeling approach is powerful but it is also subject to caveats. Indeed, some important choices must be made for how to parameterize the shape (e.g. a double power law, a Schechter function, or the local 15 $\mu $m LF from Xu 2000, converted into $L_{\rm IR}$) and the evolution of the LFs (e.g. with factors $(1+z)^{\alpha_{\rm L}}$ and $(1+z)^{\alpha_{\rm D}}$). These parameterizations rely mainly on physical intuition and sometimes require adding more degrees of freedom. This is the case for the two populations of sources introduced by LDP03, with their LFs evolving separately from each other. Moreover, these models cannot claim to be the only possible representation of the true cosmic LFs or of the true SEDs. They are generally good enough to reproduce current observations, but they are never provided with a range of uncertainties.

In this paper, we add new constraints to the decomposition of the ``Lilly-Madau'' SFRD diagram using a powerful non-parametric inversion technique that blindy and simultaneously exploits the information from the published multi-wavelength IR galaxy counts in deep and small, as well as large and shallow, surveys. From these counts alone, and without any input information on redshifts, we derive the range of all possible evolutions and shapes of the IR LF.

In Sect. 2, we present the inversion method in the general case (see also Appendix A). We present in Sect. 3 the data and our choice for an SED library used in this study. Sect. 4 contains our results: the counts inversion and the corresponding IR LFs, together with the inferred cosmic SF history. In Sect. 5, we validate our inversion by comparing our empirical modeling of counts, LFs, SFRD, and stellar-mass density evolution to bibliographic data (see also Appendix B for the robustness of the inversion). Finally, we discuss the results and give our conclusions in Sect. 6. Some predictions for forthcoming Herschel observations are also given in Appendix C. We use a cosmology defined by H0= 70 km s-1 Mpc-1, $\Lambda= 0.7$, $\Omega_{\rm m}=0.3$. The IMF is assumed to be Salpeter (1955) unless otherwise stated (i.e. in Sect. 5.4).

2 Method: non-parametric inversion of deep multi-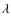$\lambda $ IR galaxy counts

In this section, we present a new approach to infer the evolution of IR LFs of galaxies from multi-wavelength and multi-scale observations of galaxy counts. It consists in a phenomenological modeling approach, similar to the works of CE01, LDP03, and others[*]. However, the modeling is made here in a global and flexible way: assuming that a given library of SEDs is able to account for the spectra of galaxies at any redshift (an assumption tested from the limits of the method's success), we search blindly for all shapes and evolutions of the total IR LF that are able to reproduce the multi-wavelength IR counts and the CIRB. This method is non-parametric; i.e., it does not depend on a parameterization of the LF (in shape or evolution). It must be noted, however, that the underlying model of SEDs (on which the inversion depends) can, itself, involve one or several parameters that must be fixed for the inversion.

Our method exploits data from infrared surveys designed to probe high-redshift populations by using their observed galaxy number counts. However, the redshifts of the sources are not required, which makes this method quite versatile[*].

An important advantage of this technique, one that makes it different from all previous models for IR galaxy number counts, is that it provides an automatic, hence objective, way of sampling the range of possible histories of the IR luminosity function. While previous studies have always presented their favorite model for fitting the IR galaxy counts, the present work spans the range of all possible evolutions that are consistent with the observations. This results in two major improvements. First, the modeled cosmic SFR history or luminosity functions per redshift bin are presented with their error bars. Second, it will allow us to discuss the limitation of local IR SEDs at reproducing the properties of distant galaxies. Indeed, if after spanning all possibilities, we still find that the fit is not complete, this will demonstrate that the IR SEDs must be revised, either because they provide an incomplete description of local galaxies or because they evolve with redshift.

In this section, as well as in Appendix A, we present the technical and mathematical aspects of our counts modeling.

2.1 Linear matrix modeling of the counts

The deep galaxy counts can be seen as the projection on a flux scale of the SEDs of galaxies of various luminosities, masses, types, etc., distributed in redshift. Therefore, to reproduce counts, one needs at least a description of the number of galaxies at various redshifts per unit volume, the SEDs of these galaxies[*], and a cosmology.

In the following, to describe the numbers of galaxies in space and time, we use total infrared luminosity functions (LF$_{\rm IR}$). Doing so, we simultaneously assume that the SED of a galaxy seen in the IR can be efficiently described by the sheer knowledge of its redshift and $L_{\rm IR}$. Although such a description can be regarded as simple-minded, the current knowledge of galaxy SEDs in the IR is not much better than an empirical description parameterized only by $L_{\rm IR}$. Therefore, the model description that we have chosen is suited to the current limitations of our understanding.

For a galaxy (which IR SED is known) lying at redshift z0 with a luminosity $L^{\rm IR}_0$, we can easily compute a k-correction and a distance modulus to obtain the flux density S0 that one would measure in a given IR filter centered at the wavelength $\lambda_0$. This conversion only depends on the cosmology and on the SED of the galaxy.

A luminosity function being only the description of the number of sources per comoving Mpc3 as a function of redshift and infrared luminosity $L_{\rm IR}$, we can then compute a matrix that converts this evolving LF$_{\rm IR}$ into numbers of galaxies seen at various fluxes and through different IR filters. This matrix is simply the response function of the conversion from $(z, L_{\rm IR})$ to $(S,\lambda)$presented above. Again, this matrix depends only on the cosmology and on the library of SEDs. Since it includes k-correction, distance effects (dimming as a function of the square of the luminosity distance), and redshift effects (flux density stretching and dimming), we call it the ``k+d'' matrix in the following[*].

After discretization, and using a matrix notation, the inverse problem can be formalized as


\begin{displaymath}\mathbf{Y}(\lambda,S) = \mathbf{M}(\lambda,S,z,L_{\rm IR}) \cdot \mathbf{X}(z,L_{\rm IR}), \end{displaymath} (1)

where Y is the matrix containing the number counts at fluxes S in bands $\lambda $, M is the above-mentioned ``k+d'' transformation matrix, and X is the LF$_{\rm IR}$ that is a function of only z and $L_{\rm IR}$ (see Appendix A for details).

Therefore, our problem involves inverting this linear equation to find the evolving LFs (i.e. redshift dependent number counts per unit volume), X, from the known values of Y (the wavelength dependent observed number counts per unit area). Because the matrix, M, is not square, and because the number counts are noisy and must be positive, the solution is not quite as simple as using the pseudo inverse: $\mathbf{X} = \mathbf{M}^{(-1)} \cdot \mathbf{Y}$, and requires computing a regularized solution as discussed bellow and explained in Appendix A. The reader may also refer to, e.g. Pichon et al. (2002) or Ocvirk et al. (2006b). The uncertainties on the observed counts Y are taken into account through an additional error matrix W that makes it possible to compute a $\chi^2$ between the model X and the data Y and to derive uncertainties on the recovered LF.

In this formalism, we choose to describe the luminosity function in a logarithmic scale, taking $\log_{10}$ $L_{\rm IR}$ instead of $L_{\rm IR}$ everywhere. This is justified by the better conditioning of the inversion in this case because the LF$_{\rm IR}$ generally spans several orders of magnitudes in luminosity. For the same reason, the counts are treated numerically through their Euclidian differential form ${\rm d}{N}/{\rm d}{S} \times S^{2.5}$ (units of mJy1.5 deg-2) which varies slowly with flux. The evolution is measured as a function of $\log_{10}(1+z)$. Indeed, in the following, we impose a smooth evolution in redshift of the luminosity function and we need to define the temporal parameter on which this smoothing applies. We find that the simplest redshift description that corresponds roughly to a regular time sampling is actually $\log_{10}(1+z)$. A parameterization with z or with $\log_{10} z$ would leave too much room for strong variations in LF$_{\rm IR}$ at early and late times, respectively. More quantitatively, we discretize the problem in bins regular in $\delta \log_{10}$ $L_{\rm IR}$ = 0.1 and in $\delta \log_{10} (1+z)=0.015$, which corresponds to the sampling that is good enough to produce counts with regular flux sampling of $\delta \log_{10}$ S=0.1.

2.2 Regularizing the inverse problem

In practice, provided the number of bins in LF$_{\rm IR}$ is large enough, this problem is ``ill-posed'': there is possibly a large number of LFs that are able to satisfy Eq. (1) perfectly, hence overfitting the noisy counts. However, many of these solutions are unlikely and not physical so that we need to ``regularize'' the problem to obtain valid solutions. The first natural constraint is the positivity of the LF$_{\rm IR}$ (there are no such things as negative numbers of galaxies). This imposes an iterative, CPU-costly approach to the problem, and a choice for an initial guess (see below). Moreover, we want to avoid solutions that are not meaningful given our noisy finite set of counts, such as LFs that are chaotically varying as a function of $L_{\rm IR}$ or redshift. Therefore, we penalize the inversion with an extra term, added to the formal $\chi^2$, which enforces the smoothness of the LF$_{\rm IR}$ both in $L_{\rm IR}$ and in z (see Appendix A and Ocvirk et al. 2006b, for the details of the formalism). With these constraints, the solutions, X (which depend on the choice of the initial guess required for the nonlinear optimization), are reasonable and can serve as a solid basis for future works. We can also optionally impose external constraints as supplementary priors, namely the low-redshift luminosity functions obtained from direct methods.

To obtain the range of all realistic solutions for the nonlinear optimization problem, we explore a wide range of random initial guesses, in a Monte-Carlo approach with at least 100 realizations. The range of LFs spanned by the initial guesses is much wider than the range of the final LF$_{\rm IR}$ (X) obtained after convergence, which lends credibility to our study's completeness[*].

Finally, some of the solutions do not match the constraints brought by CIRB measurements. We filter out these invalid solutions, a posteriori, leaving only the most realistic luminosity functions.

3 Data and SEDs used in this work

3.1 Input multi-wavelength counts

 \begin{figure} \par\includegraphics[width=17cm,clip]{09945f1.ps} \end{figure} Figure 1:

Observed 15/16 $\mu $m, 24 $\mu $m, 70 $\mu $m, 160 $\mu $m, and 850 $\mu $m counts of galaxies from various surveys. The shaded area representing 1$\sigma $ uncertainty area are determined semi-automatically from the data points (smoothed envelopes of the data points after excluding the strongest outliers, particularly at 15 $\mu $m), and are used as an input for the inversions. Instruments/fields: ISO LW3/various fields (Elbaz et al. 1999), ISO LW3/ELAIS-S (Gruppioni et al. 2002), SPITZER IRS/GOODS (Teplitz et al. 2006), SPITZER MIPS24/GOODS (Chary et al. 2004), SPITZER MIPS24/various fields (Papovich et al. 2004), SPITZER MIPS24/GOODS (Le Floc'h et al. 2005), SPITZER MIPS70/FLS (Frayer et al. 2006a), SPITZER MIPS70/GOODS-N (Frayer et al. 2006b), ISO ISOPHOT170/FIRBACK (Dole et al. 2001), SPITZER MIPS160/MARANO+CDFS (Dole et al. 2004), JCMT SCUBA/SXDF+LH (Coppin et al. 2006).

Open with DEXTER

The multi-wavelength counts that we invert in this work are presented in Fig. 1. They summarize bibliographic observed galaxy counts at 15, 24, 70, 160, and 850 $\mu $m. This compilation is not exhaustive but we retained significant surveys for each IR band, mixing wide and shallow ones to avoid cosmic variance effects as much as possible, and deep ones for faint source detections. The data shown in Fig. 1 are actual observations, except for the 70 and 160 $\mu $m points from Dole (private communication; and also Dole et al. 2006), which are obtained from stacking 24 $\mu $m sources in several flux bins and using an MIR-FIR observed correlation. Although these points are not strict measurements, the MIR-FIR relationship is tight enough (down to less than 0.1 mJy) to be confident in the stacking results. We group the 15 and 16 $\mu $m counts, as well as the 160/170 $\mu $m counts, thus neglecting the small differences to the counts (a few percent) that are caused by the slightly different k-corrections. Our inversion is applied to this compilation.

3.2 Library of SEDs

The IR SEDs that we use in this study are taken from the empirical library of CE01, which defines a bijection between $L_{\rm IR}$ and the IR SED from 3 to 1000  $\mu $m. Although this library is based on correlations observed in local galaxies, we suppose in the following that the SEDs of galaxies with a given $L_{\rm IR}$ do not change with redshift. It does not necessarily mean that SEDs of individual galaxies do not evolve, but that they must evolve along the local SED- $L_{\rm IR}$ correlation. It is worth noting that when a description of the evolving IR SEDs of galaxies becomes available (e.g. with Herschel), the technique that we use can be applied to these evolving SED libraries.

Moreover, we ``clip'' this library for the highest IR luminosities, using the $L_{\rm IR}$ = 1012.2 $L_\odot$ SED shape for galaxies more luminous than this value. This makes the SEDs colder than in CE01 for ULIRGs and makes it compatible with most of the known data, from low-redshift, low-luminosity to high-redshift luminous galaxies (see CE01; Papovich et al. 2007). Figure 2 presents the relation between 24 $\mu $m and total IR luminosities that is predicted by the ``clipped'' CE01 library, together with observations from (Papovich et al. 2007) in the range z=1.5-2.5. This clipping can be justified by the SEDs of high luminosity galaxies (ULIRGs) like those seen at high redshift being poorly known in the local universe: their dust temperature can only be measured by Herschel. Therefore, the CE01 SEDs are extrapolated within this luminosity range. We chose to clip the IR dust temperatures of the CE01 library to those of the luminosity range really observed in the local universe, rather than extrapolating them.

 \begin{figure} \par\includegraphics[width=8.9cm,clip]{09945f2.ps} \end{figure} Figure 2:

24 $\mu $m vs. total IR luminosities (or the SFR equivalent of these luminosities assuming a Salpeter IMF). The shaded gray area represents the observations of Papovich et al. (2007) Fig. 11, considering that most of this intense SF is probed by the IR light, neglecting the UV contribution. The solid lines correspond to the ``clipped'' CE01 library for a set of virtual galaxies at redshifts z=1.5, 1.8, 2.2 and 2.5 (from left to right) with fluxes fainter than 1 mJy, for which the Papovich et al. (2007) observations are valid. A pure CE01 library would have followed the one-to-one slope.
Open with DEXTER

4 Results

In this section, we present the counts, luminosity functions, and SF history that are modeled from the counts inversion, as well as the effect of using or not using low-z luminosity functions as priors. We compare these results and their redshift decompositions to measurements obtained from direct methods and bibliographic data only in Sect. 5.

4.1 Counts inversion

 \begin{figure} \par\includegraphics[width=17cm,clip]{09945f3.ps} \end{figure} Figure 3:

Mid- and Far-IR counts obtained from the non-parametric inversion of the observed counts. The data counts that are the basis of the inversion are represented by the shaded blue zones (fitted values $\pm $1$\sigma $, corresponding to the zones of Fig. 1). The best fit to the counts is shown by the solid red lines, together with the range of allowed solutions (red dashed areas). The vertical gray zones delimit the flux ranges where some counts are observed. All the counts modeled here satisfy the CIRB constraints. The oblique dashed line corresponds to a statistical limit of a one square degree survey (less than 2 sources per decade in flux).
Open with DEXTER

This inversion model has been designed to reproduce infrared galaxy counts and as a result to derive a range of possible total IR LF as a function of redshift, that can be converted afterwards into a range of cosmic SF histories. The success of the model can be visually tested by comparing the range of predicted galaxy counts with the observed number counts and their dispersion (see Fig. 3).

At first glance, one can see that the observed counts are well-fitted over the whole IR range, from 15 to 850 $\mu $m. In particular, the bumps at 15 and 24 $\mu $m are reproduced simultaneously. The 850 $\mu $m differential counts are well-fitted too: negative k-corrections make it possible to see a high-redshift population of galaxies, namely ULIRGS and HLIRGS ( $L_{\rm IR}$ $>10^{12}~L_\odot$) at z>2, which are hardly seen at other wavelengths except in faint 24 and 70 $\mu $m counts.

Interestingly, one can see from Fig. 3 that, while the only strong constraint that is imposed on the model is to keep a smooth dependence of the LF with redshift and luminosity, the model is unable to perfectly fit the observed number counts and their dispersion at all flux densities and wavelengths even though the whole range of possible LF and associated redshift evolution has been spanned blindly. Some solutions tend not to fit the 15 $\mu $m counts perfectly, the 70 $\mu $m counts are slightly overproduced, and more strikingly, the 160 $\mu $m counts are underproduced around 20 mJy.

A major strength of this model is to provide an objective and statistically significant way to test a given library of template SED. Indeed, the discrepancy between the model and observed counts cannot arise from the LF itself since it was allowed to vary both with luminosity and redshift with a high degree of freedom (see also Ocvirk et al. 2006a, for a discussion on the corresponding biases in a slightly different context). It must therefore arise from the library of template SEDs that is used as an input for fitting the number counts (through the ``k+d'' matrix M). The CE01 library of template SEDs that is used here reflects the median trend of local galaxies and was found to be statistically consistent with the radio-infrared correlation up to $z\sim 1.3$ (Appleton et al. 2004; Elbaz et al. 1999), with the mid-infrared observations of galaxies up to $z\sim 1$ with moderate variations (Marcillac et al. 2006) and with massive galaxies selected with the BzK technique (Daddi et al. 2007b). The origin of the discrepancy can therefore come from three possible origins. The first two possibilities compatible with no evolution of the infrared SED of galaxies are (i) a bias towards cold galaxies due to the shallow depth at 160 $\mu $m within the dispersion already existing at $z\sim0$; (ii) the existence of a subpopulation of cold galaxies, already present locally but not yet identified due to limited constraints on both sides of the peak emission in the far infrared. A third possibility would be that the infrared SEDs of galaxies evolve as a function of redshift (see e.g. Chapman et al. 2002).

It is not possible to disentangle between the three possibilities based on the present dataset. However, a forthcoming paper will study this issue in detail using a stacking analysis at 160 $\mu $m (Magnelli et al., in preparation). It must be noted though that the method described here is versatile enough to allow its user to test any library of template SED against existing constraints from galaxy counts and the infrared background. It will therefore be a straightforward matter to check whether any change or evolution in the SEDs can reproduce the number counts at all wavelengths and flux densities. We refrained from making these adjustments to the counts at this stage since any of the previously mentioned alternatives is equally possible.

4.2 Solutions: range of evolving luminosity functions

 \begin{figure} \par\includegraphics[width=17cm,clip]{09945f4.ps} \end{figure} Figure 4:

All possible solutions for the evolving LFs that best reproduce all the IR counts of Fig. 3 and the CIRB constraints. As in Fig. 3, the thick red line and the dashed red areas represent the best-fitting solution and the range of allowed solutions, respectively. By construction, no conclusion on the LF can be made in the vertical gray-shaded areas where a divergence is expected because these objects are not seen in the counts because of the flux limits of current IR surveys. At the top of each panel, the ranges of $L_{\rm IR}$ probed by IR counts are shown as horizontal lines, from 15 to 850 $\mu $m (bottom to top). Diamonds, triangles, and filled circles correspond to 0.1, 0.3, and 3 mJy fluxes, respectively. Bottom right panel: range of CIRB corresponding to the inverted LFs. Data points (in gray) are taken from ilation by Dole et al. (2006).
Open with DEXTER

Looking now at the main output of the model, i.e. the evolution of the total IR luminosity function with redshift, we note that large parts of the LF are constrained very well by the inversion (see Fig. 4). In particular, the number density of galaxies with $10.5 < \log_{10} L_{\rm IR} < 11.5$ at z<0.5 is tightly constrained, as are the numbers of galaxies with higher luminosities at higher redshift.

We will present in Sect. 5.2 a comparison of these solutions to the LF$_{\rm IR}$s obtained from direct measurements at low redshift.

But before doing so, we note that a fraction of the solutions present a knee in the LF, particularly at 0.3<z<1 around $10^{10}{-}10^{11} L_\odot$, which is partly responsible for the bump seen in the number counts at 24 and 15 $\mu $m at the corresponding flux densities. However, not all solutions of the inversion technique present such a strong knee, which might be seen as an artifact.

4.3 Evolution of the star-formation activity

 \begin{figure} \par\includegraphics[width=12.8cm,clip]{09945f5.ps} \end{figure} Figure 5:

Star-formation rate density since z=5 derived from the counts inversions. The SFRD is obtained from the range of all possible luminosity functions derived from the counts and respecting the CIRB constraints. The solid lines correspond to the best fit to the counts and the transparent shaded areas show the range of uncertainties. From top to bottom at z=0.8: black = all galaxies, green = LIRGS, blue = normal star-forming galaxies, orange = ULIRGS, red = HLIRGS.
Open with DEXTER

The SFRD can now be estimated from the LFs that were obtained from the counts inversion. The total infrared LFs are integrated over the whole range of luminosities down to 107 $L_\odot$. The resulting total infrared luminosity density is then converted into a SFRD using formula (2) (Kennicutt 1998):

\begin{displaymath}{\it SFR ~[M}_{\odot}~ {\rm yr}^{-1}]=1.72 \times 10^{-10} ~ L_{\rm IR} ~[L_{\odot}]. \end{displaymath} (2)

Therefore, the regions shown in Fig. 5 effectively represent the range of all possible SF histories that are compatible with the multi-$\lambda $ counts and the CIRB. The SFRD history obtained from the LF$_{\rm IR}$ that produces the best fit to the counts is also shown for each luminosity class of galaxies.

This inversion shows that, indeed, an IR downsizing is at work: ``normal'' galaxies dominate the SFRD at low redshift (although the contribution of ULIRGS and HLIRGS are poorly constrained in the low-z range because they would correspond to bright and very rare sources, not easily seen in the counts of current deep surveys). At z>0.8, LIRGS dominate the SFRD, whereas the contribution of ULIRGS peaks at $z \gtrsim 2$. These results will be compared in detail to measurements from direct methods and bibliographic data in Sect. 5.3.

As mentioned before, it is also possible to use an additional prior for the inversion: direct measurements of the 8 or 15 $\mu $m LF below z=2. Although subject to many caveats (e.g. the strong dependency on the PAH modeling of the SEDs), they can be used as a prior to guide the inversion, and at least constrain the solutions at low redshift[*].

We checked the effect of using this prior from direct measurements at low redshift. We observe that some uncertainties in the LIRGS and ULIRGS contributions are slightly tightened, but we also note that the trends are basically unchanged. We interpret this surprising result as follows: the leverage that we have access to by inverting galaxy counts on a very wide wavelength-basis (from 15 to 850 $\mu $m) is large enough to provide a realistic description of the redshift distribution of the sources on a statistical basis. This is likely to only be possible because the library of SEDs that we use seems close to the real SEDs of galaxies, on average (again, in the statistical sense) at any redshift lower than $z\simeq3$, thus avoiding a complete blurring of the de-projection of multi-wavelength galaxy counts onto the luminosity function space. Therefore, various populations of galaxies at different redshifts are seen at various wavelengths, which considerably reduces degeneracies and enables us to recover the history of IR galaxies as a whole.

Since the philosophy of this paper is to remain as conservative as possible, we choose not to use the low-redshift LF measured from direct methods as a prior in the following. Indeed, doing so would only slightly change our results, and it would introduce a source of potential additional errors propagating from the errors intrinsic to direct methods (k-corrections in the mid-infrared or redshifts).

5 Validation: comparison with direct measurements at low redshift

After presenting the global outputs of the model in the previous section, we detail here the redshift decomposition of the inversion results and we compare them to measurements obtained from direct (redshift-based) methods. This comparison is particularly challenging since no redshift information was used as an input in the inversion.

5.1 Redshift decomposition of the mid-IR counts

 \begin{figure} \par\includegraphics[width=16cm,clip]{09945f6.ps} \end{figure} Figure 6:

Top and bottom left: counts at 16, 24, and 70 $\mu $m modeled (solid lines) from the inversion, on the one hand, and observed (dotted lines) in GOODS fields, on the other. The counts are decomposed in redshift bins (black = all redshifts, blue =z<0.5, green  =0.5<z<1.5, orange = 1.5<z<2.5, red = z>2.5). Bottom right: CIRB decomposed in redshift (same color-coding). The oblique dashed line corresponds to the limit in statistics due to the smallness of a field like GOODS North+South or 0.07 square degrees: less than 2 galaxies per flux bin of width $\delta \log F=0.1$ dex are expected below this limit.
Open with DEXTER

To validate our inversion results, we need to compare the redshift decomposition of the IR counts to observations from a direct method. To do so, we compared our results to data from the GOODS survey (P.I. Dickinson for GOODS-Spitzer, P.I. M.Giavalisco for GOODS-HST) originally presented in Giavalisco et al. (2004). This survey consists of two fields which have been subject to several studies at various wavelengths in the past few years. We investigated the redshift decomposition of the counts at 16, 24, and 70 $\mu $m using the optical counterparts of these sources in GOODS and making use of the spectroscopic and photometric redshifts. The sample that we used covers a total area of 0.07 square degree on the sky. Although this area is quite small and cosmic variance might affect our study, we found that the luminosity functions measured from the direct method are similar in both GOODS fields, making them compatible within 2$\sigma $. The spectroscopic completeness is high (60% at $S_{24~\mu {\rm m}}=30$ $\mu $Jy for z<1.5 sources), and we complemented them with photometric redshifts computed with the code Z-Peg (Le Borgne & Rocca-Volmerange 2002) with a precision $\Delta z/(1+z) \simeq 0.04$ to 0.1 depending on the redshift of the sources. We then used the $V_{\rm max}$ formalism to correct from incompleteness at the lower flux limit. The galaxies showing signs of AGNs (identified from X-rays or optical emission lines), were excluded from the sample of 24 $\mu $m sources. Doing so enabled us to use SEDs of galaxies to compute k-corrections and only slightly affects our results, mainly at the very high-luminosity end of the luminosity function at moderate (z=1) or high (z>2) redshifts.

Figure 6 presents the resulting comparison of the redshift decomposition of the counts obtained from direct and inverse methods. At 24 $\mu $m, our best solution for the recovered LF$_{\rm IR}$ indeed produces a redshift decomposition of the counts that is compatible with the observed ones. The match of 15 $\mu $m counts as a function of redshift is poorer because CE01 templates represent the fluxes at this wavelength less well for 0.5<z<1 galaxies (e.g. Marcillac et al. 2006). As for the 70 $\mu $m counts, the observed decomposition is not complete at faint fluxes, making the comparison hazardous.

5.2 Comparison to direct measurements of the infrared luminosity functions

We now compare the range of luminosity functions LF$_{\rm IR}$ obtained from our inversion to some measurements of the LF$_{\rm IR}$ obtained from the direct method. As noted before, several studies (Caputi et al. 2007; Babbedge et al. 2006; Le Floc'h et al. 2005) have measured the 15 or 8 $\mu $m luminosity functions, which can be converted to LF$_{\rm IR}$ if a library of SEDs is assumed. We show in Fig. 7 the results from (Le Floc'h et al. 2005) for reference. We also provide on the same figure our own direct measurements of the evolving LF$_{\rm IR}$ that we derived from 24 $\mu $m galaxies seen in the GOODS fields (North+South). We chose to do these direct measurements again for two reasons. First, for consistency with our inversion, we used the same library of templates for the k-corrections (used for MIR to total LIR conversion)[*]. Second, our data at 24 $\mu $m reaches a depth of 24 $\mu $Jy instead of 80 $\mu $Jy in previous works, extending the LF to the faint end. The completeness at this depth is 85% (Chary 2007). Not surprisingly, our direct measurements of the LF$_{\rm IR}$ from 24 $\mu $m fluxes are compatible with previous studies that used the same method. In particular, we find the same values as Le Floc'h et al. (2005) who explored the z<1 domain. However, we reach higher redshift galaxies thanks to the depth of our sample. However, k-corrections are very uncertain for these high-z sources (24 $\mu $m corresponds to less than 8 $\mu $m at z>2, a range where the library of SEDs is not validated). Therefore, we use these high-redshift measurements with caution, as mentioned earlier.

 \begin{figure} \par\includegraphics[width=15.5cm,clip]{09945f7.ps} \end{figure} Figure 7:

Total IR luminosity functions derived independently from the counts inversion and from direct measurements. ``Clipped'' CE01 templates are used for the 24 $\mu $m fluxes to $L_{\rm IR}$ conversion (filled black dots). The measurements from Le Floc'h et al. (2005) are also shown for reference. The model (counts inversion) curves (dashed lines) are given at the mean redshift of each bin. The shaded areas represent the range of uncertainties on our modeled LF at the mean redshift of each bin.
Open with DEXTER

It is striking in Fig. 7 that the LF obtained from the direct method is consistent with the best-fitting LF derived from the counts inversion in the common range that they probe. This is remarkable because no information on the redshift of the sources was used in the inversion. This means that all the constraints that one can get from these direct measurements are not really needed for the inversion: although we do not use the redshift of the sources, we recover the observed redshift distributions that are here expressed equivalently in terms of evolving luminosity functions. The interpretation is the same as for the redshift decomposition of the counts, which are different views of the same phenomenon.

The meaningfulness of the agreement between the observed and the recovered LFs is strengthened by the fact that that both $L_{\rm IR}$ luminosity functions are measured or estimated using the same library of SEDs, thus using the same k-correction in a consistent way. Using another library of SEDs for both methods would produce the same kind of agreement, although the precise shape of the LFs would be slightly different from what we obtain here with the ``clipped'' CE01 library.

5.3 Cosmic star-formation history vs literature

In this section, we compare the SFRD history that we derived from the multi-$\lambda $ counts inversion to ``direct'' measurements at low redshift.

5.3.1 Total SFRD

The comparison of the total SFRD derived with this inversion technique matches the compilation of direct measurements from Hopkins & Beacom (2006, Fig. 8). Moreover, we also show in Fig. 8 the SFRD that we derived from 24 $\mu $m data in the GOODS fields. We must stress here that these measurements, obtained with the ``direct'' method, are independent of the SFRD inferred by the counts inversion[*]. We only present them here for comparison to the inversion results in this subsection. The total infrared luminosities measured for individual 24 $\mu $m sources in the GOODS fields were summed up in redshift bins and converted to SFRDs. Like several authors before us (e.g. Pérez-González et al. 2005; Flores et al. 1999; Le Floc'h et al. 2005), we could have extrapolated the measured luminosity functions in the faint end to obtain the total SFRD. But this is somewhat dangerous and depends strongly on the parameterization of the LF fits, so we chose not to extrapolate the luminosity functions at faint fluxes to estimate the SFRD. Instead, we used only the sources brighter than our flux limit at 24 $\mu $m (24 $\mu $Jy) to estimate lower-limits for the SFRD at every redshift. Therefore, all the points in this figure should be considered as lower limits.

Our inversion technique, on the other hand, makes it possible to partially avoid such caveats. First, unlike direct methods, more than one band is used to estimate the total IR LF. Second, the extrapolation of the LF in the faint-end is achieved automatically via the only constraint of having a smooth variation in $L_{\rm IR}$ and z. Therefore, the area of uncertainties we propose here are very likely more robust than previous estimates because they use more data and are less dependent on parameterization for both the shape of the LF and its evolution.

The SFRD obtained from the counts inversion and our measurements with the ``direct'' method in GOODS are in rather good agreement, which tends to give credit to the inversion. One might note, however, that the data points are systematically lower than the inversion results, which illustrates the choice of not extrapolating the measured LFs at faint luminosities to estimate the SFRD.

 \begin{figure} \par\includegraphics[width=12cm,clip]{09945f8.ps} \end{figure} Figure 8:

Total SFRD regions compared to ilation of direct measurements from Hopkins & Beacom (2006) (empty circles and error bars only for z>1.5 for clarity purposes). The outer light-gray regions corresponds to all possible LFs fitting the counts. The inner darker region includes 68% of these models. The dashed line corresponds to the LF producing the best-fit to the multi-$\lambda $ IR counts. The solid triangles with error bars show the integrated SFRD that we measured in the GOODS fields in several redshift bins (see also Fig. 9 for a luminosity decomposition of these measurements).
Open with DEXTER

5.3.2 Luminosity decomposition of the SFRD

Figure 9 presents a detailed comparison of the history of the SFRD inferred from our inversion and decomposed in luminosity classes to what can be independently obtained from the ``direct'' method with 24 $\mu $m sources in GOODS.

Let us first consider the reliability of the direct measurements used for comparison. Because we chose not to extrapolate the LFs at low luminosity, several points in this figure must be considered as lower limits. It is not the case, however, for the z<1.2 points for LIRGS and the 1<z<2.5 points for ULIRGS. Overall, we are limited at very low redshift by small statistics and at high redshift by flux limits. Moreover, the contribution of HLIRGS should be taken with caution. Indeed, by inspecting these luminous high-redshift sources, we came to the conclusion that a large fraction of the photometric redshifts computed for these IR-bright sources have poor precision, leading to catastrophic failures for almost half of the HLIRG sources at z>1.5. This poor performance of the photometric redshifts is not too surprising for this class of galaxies at such high redshifts since the templates used in the fitting procedure have a relatively low level of dust, compatible with most galaxies seen in the current optical and NIR surveys. These direct measurements present a nice picture of the ``IR downsizing'', where the cosmic SFRD was dominated by brighter and brighter galaxies in the IR as we go back in time. Our results confirms the IR view of the cosmic SF history that was explored in previous works up to z=2 e.g. Caputi et al. (2007). At z=2, we confirm that ULIRGS seem to dominate the budget of the SF activity.

 \begin{figure} \par\includegraphics[width=11.5cm,clip]{09945f9.ps} \end{figure} Figure 9:

History of the SFRD decomposed in four infrared luminosity classes. The inversion results (full set of models and 68% inner region) are shown with gray-shaded areas. The total SFRD history (68% inner region) is also shown for reference in each panel as dotted lines. Our direct (and independent) measurements from the GOODS survey are shown as triangles. Empty triangles are used for bins affected by completeness. The z=3 point for HLIRGS is subject to caveats (see text for details) so is probably overestimated.
Open with DEXTER

A number of interesting remarks arise from the comparison of the ``inverted'' SFRD to the ``direct'' measurements. First, it is comforting to see that both methods give consistent views of the IR downsizing. In both cases, low luminosity galaxies dominate the SFRD at z<0.5, and ULIRGS are dominant at z>2. However, a more detailed comparison of both results provides interesting clues to what is really seen in current deep surveys. One can easily notice that most data points (``direct'' measurements) are at the lower limit of the area allowed by the inversion. This means that the 24 $\mu $Jy limited sample of 24 $\mu $m galaxies probe almost all the cosmic SFRD. However, the same remark also opens up the possibility that up to 50% of the SFRD is not yet resolved in sources down to our flux limit, especially for low-luminosity galaxies at z>0.5.

Another interesting point is that the inversion does not allow the population of HLIRGS to contribute much to the CIRB at any redshift. This somewhat contradicts the direct measurements for the same objects, which tend to indicate an increasing contribution of these extreme sources at z>2. But again, we must stress that many uncertainties lie in the observations of these distant sources (photometric redshifts, validity of the SEDs, contribution of AGNs, etc.). Therefore, we must conclude that this population cannot be too numerous to reproduce the deep IR counts, including the 850 $\mu $m ones, if the ``clipped'' CE01 SEDs are used at any redshift. We checked that allowing more HLIRGS at these redshifts, at a level comparable to the observed number, overproduces the 850 $\mu $m counts. This means that either these objects do not exist (and indeed, as we mentioned before, about half of these HLIRGS have a wrong photometric redshift, hence a wrong luminosity), or the SEDs for these objects are very different from the templates in the SED library that we use. Of course, both reasons may be at work simultaneously. Interestingly, if the original CE01 library is used (both for the inversion and for direct measurements), the situation is similar: the SFRD of HLIRGS inferred by the inversion of the multi-wavelength counts is still smaller (by a factor of 4) than the value inferred from direct measurements of 24 $\mu $m sources. The main difference, in this case, is that the SFRD of HLIRGS are roughly a factor of 5 to 10 larger than what is derived with the clipped CE01 library.

Finally, we notice that the measured SFRD for ULIRGS at z<1.5 (see Fig. 9) is smaller than the range allowed by the inversion. This could be explained by cosmic variance due to the small area covered by our GOODS sample.

5.4 Evolution of the stellar mass density

In this section, we address the question of the consistency of the SFR history that we derive from the inversion model with the independent observational constraints existing on its integral, namely the evolution of the comoving density of stars per unit comoving volume. After assuming an initial mass function (IMF) and computing the mass of stellar remnants after the death of massive stars, it is straightforward to compute the total amount of stars that must be locked into galaxies as a function of redshift, on the basis of the SFR history. In our computation of stellar masses, we account for the recycling of stellar material into the ISM, for the mass of stellar remnants (which account for about 15% of the total stellar mass at z=0) and for the evolution of the metallicity, using the spectral synthesis code PÉGASE.2 (Fioc & Rocca-Volmerange 1997,1999).

This is not the first time that such a computation has been performed, but we believe that this is an important test that has been the source of discussions in the recent past, in particular with the claim that both histories - SF and stellar masses - were not consistent with the integral of the SF history producing more stars than actually observed at any redshift. Our paper now proves this claim to be incorrect.

Before discussing our own computation, we wish to emphasize an important point regarding the effect of the choice of a particular IMF in this process. Although various IMFs have been proposed in the past, including top-heavy IMFs for starbursting galaxies (see e.g. Rieke et al. 1993; Elbaz et al. 1995,1992; Davé 2008; Lacey et al. 2008), no definitive evidence has been provided yet for a non-universality of the IMF. The main difference that is now commonly accepted with respect to the pioneering work of Salpeter (1955) is the finding that the slope of the IMF changes around 1 $M_{\odot}$, in the direction of having a lower contribution of low mass stars to the total mass of stars formed, or equivalently a larger contribution of stars more massive than 1 $M_{\odot}$ (see the review by Chabrier 2003). Nonetheless, such a change in the IMF almost equivalently affects both the conversion factor used to determine the SFR from LF$_{\rm IR}$ and the mass-to-light ratio used to derive the stellar mass. In the present study, the SFR is derived from the total IR luminosity assuming the coefficient computed for a Salpeter IMF by Kennicutt (1998, see Eq. (2)). For a different IMF, such as the Baldry & Glazebrook (2003, hereafter BG03) one which shows a flattening below 1 $M_{\odot}$ as discussed above, the SFR would be 0.45 lower and the M/L ratio would also be reduced by a similar factor (0.6, computed using the PEGASE.2 code).

The evolution of the cosmic stellar mass density with redshift that we computed by integrating the SFR history resulting from the inversion model is found to be in good agreement with the latest direct measurements of galaxy masses of e.g. Pérez-González et al. (2008). Their published stellar mass densities were multiplied by a factor 0.61 since they were estimated with a Salpeter (1955) IMF, which corresponds to the difference in mass-to-light ratios in the Kband. It is clear that, at all redshifts probed, the range of SF histories that result from the inversion technique are consistent with the measured stellar mass density. This consistency indirectly reinforces the likelihood that the inversion technique spans a reasonable range of possible histories.

Finally, we note that after submission of the present paper, an erratum was published by Hopkins & Beacom (2006) in which they recognize that their computation was erroneous and that, contrary to their initial claim, the two histories do not exhibit any inconsistency, apart from possibly at the largest redshifts. Hence their study is now consistent with our finding, which is not surprising since our SFR history globally agrees with their compilation (see Fig. 8).

6 Discussion and conclusions

This paper presents measurements of the evolving infrared luminosity function and of the corresponding cosmic SFRD using a non-parametric inversion of the galaxy counts in the mid and far infrared.

For the first time, we have exhaustively derived the range of possible evolutions for these quantities with a non-parametric inversion technique. The input data that were used simultaneously to derive these set of allowed models cover a wide range of wavelengths: deep infrared counts observed at various wavelengths (from 15 to 850 $\mu $m), the cosmic infrared background measurements, and optionally the low-redshift measurements of the IR luminosity function that are derived from the 24 $\mu $m fluxes. We derived from this inversion the allowed range of SF histories, together with the range of stellar mass density evolutions that are consistent considering all this multi-$\lambda $ data. This approach is to be contrasted with previous modeling works that were based on predictions from a single preferred model: a range of models is given here.

The inversion technique does not use any redshift information as input, although such an option can be (and has been) considered through a prior constructed on the low-redshift LF. Despite this arguably questionable lack of information about the redshift of the sources, the inversion technique recovers the known redshift distributions surprisingly well up to z=2. The reason for this success probably lies in the very broad basis of wavelengths used in the inversion: 15 $\mu $m, 160 $\mu $m, and 850 $\mu $m (and intermediate wavelengths) do not probe the same populations of galaxies at the same redshifts because of very different k-corrections. The uncertainties inherent in the library of SEDs that we used seem to be masked, at first order, by the extent of the data set that we considered.

We find new constraints for the SFRD and its decomposition. Our method shows that the IR downsizing must be at work, even though only the IR counts are considered. Quantitatively, we are in good agreement with direct measurements of the SFRD at low and high redshifts. Again the clear advantage of our approach is its exhaustivity: the range of possible SF histories inferred from the inversion does not suffer from incompleteness, in contrast to surveys based on spectroscopic and photometric redshifts. This range matches recent measurements of the evolution of the stellar mass density very well, when a non-evolving IMF is used and stellar remnants are taken into account, in contrast to previous works.

Then by comparing the results on the SFRD from the ``direct'' (redshift-based) and ``indirect'' (counts inversion) methods, we showed that the population of HLIRGS tentatively seen at z>2 is excluded, at least with SEDs similar to local ULIRGS. Either the photometric redshifts of these peculiar sources are systematically wrong, or their SED is very different from the local equivalents. Both reasons contribute probably to the observed discrepancy.

Moreover, a strong contribution from obscured AGNs to the mid-IR counts, especially at 24 $\mu $m as shown by Daddi et al. (2007a) cannot be excluded. For this reason, the objects that seem to be HLIRGS at z=2-3may also be actually obscured AGNs. Solid identifications of AGNs from far-IR diagnostics will be needed for further modeling work.

The set of galaxy SEDs that we used in the inversion (CE01) was calibrated at z=0 for $\lambda < 100$ $\mu $m. Moreover, the SFR predictions made with these templates are compatible with radio estimates up to z=1 (Appleton et al. 2004; Elbaz et al. 2002). Although the multi-$\lambda $ IR counts are reproduced reasonably well with the inverted luminosity functions, the 160 $\mu $m counts cannot be satisfactorily reproduced by any SF history satisfying the rest of the counts. At this wavelength, the counts are systematically under-produced by models. As noted by LDP03, a population of objects colder than those included in the CE01 library is needed to produce these counts. We can therefore decide either on an evolution of the SEDs that were different - presumably colder for the same $L_{\rm IR}$ - at high redshift, or on a poor calibration of the CE01 SEDs in this range (which is actually expected). This strongly confirms the tentative evidence from previous works on modeling (LDP03) or observational Papovich et al. (2007) grounds. The recent works of Pope et al. (2008) on submillimeter galaxies go in the same direction: these high-redshift IR galaxies are colder than previously thought. But only Herschel will enable the characterization of the dust temperature of these objects at these wavelengths. In fact, Herschel studies of local galaxies will be very helpful for high-redshift studies of galaxy evolution.

 \begin{figure} \par\includegraphics[width=8.9cm,clip]{09945f10.ps} \end{figure} Figure 10:

Range of allowed evolutions of the stellar mass density computed with the range of cosmic SF histories of Fig. 5. The dashed lines corresponds to the best-fit to the IR counts. The data points with error bars are measurements from Pérez-González et al. (2008) (empty circles) and Elsner et al. (2008) (filled dots). The realistic Baldry & Glazebrook (2003) IMF is used both for the data points and to derive the stellar mass density from the SFR density.
Open with DEXTER

Moreover, the inversion does not completely take the special case of AGNs into account. Implicitly, we assumed that their SEDs are close enough to the templates of star-forming galaxies represented in the CE01 library. Obviously, the AGNs have different SEDs, with a flatter SED in the mid and far-IR. However, our results are not very sensitive to this issue. First, the contribution of AGNs (as identified from X-rays or optical spectra) to the mid-IR counts is small, especially for faint fluxes. Therefore, a small correction to the bibliographic counts should be made, but remains difficult at all wavelengths. Moreover, as noted above, the global trends derived for the LF or the cosmic SFRD compare well with independent measurements at low redshift, which seems to indicate that the inversion is relatively insensitive to the precise shape of the SEDs. Of course, there are limits to this statement, but we believe that the small fraction of AGNs found in the counts, combined with this statement, should only weakly affect our findings.

After checking that the predicted redshift distributions of the sources making the counts at 16, 24, and 70 $\mu $m are compatible with the real redshift distributions, we then made predictions for the future surveys to come with Herschel, SPICA, SCUBA2, and Artemis (see Appendix C where we explain the bivariate distributions in z and $L_{\rm IR}$ of the sources as a function of flux, and we give the fraction of the CIRB that will be resolved by future confusion limited surveys).

Finally, we stress that, although the LF$_{\rm IR}$ and the SF history derived from the inversion actually depend (slightly) on the library of SEDs chosen for the work, the use of a new, updated, SED library would be straightforward: unlike previous modeling approaches, it would not imply a whole new work to refine parameters in order to obtain a good modeling of the counts.

Acknowledgements
We wish to thank A. Hopkins for making available his compilation of cosmic SFRs. We also thank Hervé Dole for providing unpublished results from stacking at 70 and 160 $\mu $m. We are grateful to E. Daddi, R. Chary, H. Dole, G. Lagache, B. Magnelli, K. Glazebrook, and I. Baldry for fruitful discussions. D. Le Borgne and D. Elbaz wish to thank the Centre National d'Etudes Spatiales for his support. D. Elbaz thanks the Spitzer Science Center at Caltech University for support. We would also like to thank D. Munro for freely distributing his Yorick programming language (available at http://yorick.sourceforge.net/), which was used during the course of this work. We also thank E. Thiebaut for his optimization package optimpack (Thiébaut 2005).

References

Online Material

Appendix A: The inverse problem

A.1 The model

As argued in the main text, (Sect. 2.1) the formal equation relating the number of counts of galaxies $\mathcal{N}(\lambda_i,S_k)$ with the flux Sk (within ${\rm d}{S}$) at wavelength $\lambda_i$ (within ${\rm d}{\lambda}$) to the number of counts of galaxies, $N(z,L_{\rm IR})$, at redshift z (within ${\rm d}{z}$) and IR luminosity $L_{\rm IR}$ (within ${\rm d}{L_{\rm IR}} $) is given by

\begin{displaymath}\mathcal{N}(\lambda_i,S_k) = \!\!\int\!\!\!\int\!\delta_{\rm ... ...R}{})\right]\!N(z,L_{\rm IR}){\rm d}{z}~ {\rm d}{L_{\rm IR}} , \end{displaymath} (A.1)

where $\delta_{\rm D}$ is the standard Dirac function, F the flux observed in a photometric band centered on wavelength $\lambda_i$ of a galaxy at redshift z with a $L_{\rm IR}$ luminosity:

\begin{displaymath}F(\lambda_i,z,L_{\rm IR}{})= A / D_{\rm L}^2(z) K(\lambda_i,z,L_{\rm IR}{}). \end{displaymath} (A.2)

Here, $D_{\rm L}(z)$ is the luminosity distance for an object at redshift zwith the standard cosmology used in this paper, A is the solid angle corresponding to one square degree, and K corresponds to the k-corrections:

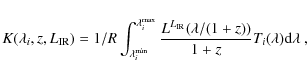\begin{displaymath}K(\lambda_i,z,L_{\rm IR}{})= 1/R \int_{\lambda_i^{\rm min}}^... ...rm IR}{}} (\lambda/(1+z))}{1+z} T_i(\lambda) {\rm d}\lambda~, \end{displaymath} (A.3)

where $T_i(\lambda)$ is the transmission curve for the filter centered on $\lambda_i$, $R=\int_{\lambda_i^{\rm min}}^{\lambda_i^{\rm max}} T_i(\lambda) {\rm d}\lambda$, and $L^{L_{\rm IR}{}}(\lambda)$ is the underlying library of SEDs (CE01) for which the SED of a galaxy depends only on its total luminosity $L_{\rm IR}$.

As mentioned in the main text, from the point of view of the conditioning of the inverse problem, it is preferable to reformulate Eq. (A.1) in terms of $\mathcal{Z}\equiv \log_{10}(1+z)$, $\mathcal{S}\equiv \log_{10}(S)$ and $m_{\rm IR}\equiv\log_{10} L_{\rm IR}{}$:

\begin{displaymath}{\hat \mathcal{N}}(\lambda_i,\mathcal{S}_k) = \!\!\int\!\!\!\... ...thcal{Z},m_{\rm IR}){\rm d}{ \mathcal{Z}} {\rm d}{m_{\rm IR}}, \end{displaymath} (A.4)

where the kernel of Eq. (A.4) reads

\begin{displaymath}H(\mathcal{S},\lambda,\mathcal{Z},m_{\rm IR})\equiv 10^{2.5 \... ... D}\!\left[S-F(\lambda,10^\mathcal{Z},10^{m_{\rm IR}})\right] \end{displaymath}

with

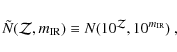\begin{displaymath}{\tilde N}(\mathcal{Z},m_{\rm IR})\equiv N(10^\mathcal{Z},10^{m_{\rm IR}})~, \end{displaymath} (A.5)

\begin{displaymath}{\hat \mathcal{N}}(\lambda_i,\mathcal{S}_k)\equiv{\mathcal{N}}(\lambda_i,10^{\mathcal{S}_k}) 10^{2.5 \mathcal{S}_k}. \end{displaymath} (A.6)

Here we have introduced the Euclidian-normalized number count, ${\hat \mathcal{N}}$, by multiplying the number count by the expected S2.5 power law.

A.2 Discretization

Let us project ${\tilde N}(\mathcal{Z},m_{\rm IR})$ onto a complete basis of $p \times q$ functions

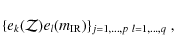
\begin{displaymath}\{e_k(\mathcal{Z}) e_l(m_{\rm IR})\}_{ j=1,\ldots,p \ l=1,\ldots,q}~,\end{displaymath}

of finite (asymptotically zero) support, which are chosen here to be piecewise constant step functions:

\begin{displaymath}{\tilde N}(\mathcal{Z},m_{\rm IR}) = \sum_{j=1}^{p} \sum_{l=1}^{q} n_{jl} ~ ~ e_{j}(\mathcal{Z}) e_{l}(m_{\rm IR}). \end{displaymath} (A.7)

The parameters to fit are the weights njl. Calling  ${\mathbf{X}}=\{ n_{jl}\}_{j=1,..p,l=1,..q}$(the $p \times q$ parameters) and  ${\mathbf{Y}}=\{ {\hat \mathcal{N}}(\lambda_i,\mathcal{S}_k)\}_{i=1,..r,k=1,..s}$ (the $r \times s$ measurements), Eq. (A.4) then becomes formally

\begin{displaymath}{\mathbf{Y}}= {\mathbf{M}}\cdot {\mathbf{X}}, \end{displaymath} (A.8)

where M is a $(r,s)\times (p,q)$ matrix with entries given by

 \begin{eqnarray*}M_{i k j l}\! = \! \left\{ {\int \!\!\! {\int} ~ e_{j}(\mathcal... ...R}) {\rm d}{\mathcal{Z}}{\rm d}{m_{\rm IR}}} \right\}_{i k j l}. \end{eqnarray*}


A.3 Penalties

Assuming that the noise in ${\hat \mathcal{N}}$ can be approximated to be Normal, we can estimate the error between the measured counts and the non-parametric model by

\begin{displaymath}{\mathit{L}}_{\mathit{}}({\mathbf{X}}) \equiv \chi^2({\mathbf... ...\!\cdot\!({{\mathbf{Y}}} - {\mathbf{M}}\!\cdot\!{\mathbf{X}}), \end{displaymath} (A.9)

where the weight matrix W is the inverse of the covariance matrix of the data (which is diagonal for uncorrelated noise with diagonal elements equal to one over the data variance). Since we are interested here in a non-parametric inversion, the decomposition in Eq. (A.7) typically involves many more parameters than constraints, such that each parameter controls the shape of the function, ${\tilde N}$, only locally. As mentioned in the main text, some trade-off must therefore be found between the level of smoothness imposed on the solution in order to deal with the artefacts induced by the ill-conditioning, on the one hand, and the level of fluctuations consistent with the amount of information in the counts, on the other hand. Between two solutions yielding equivalent likelihood, the smoothest is chosen on the basis of the quadratic penalty:

\begin{displaymath}{\mathit{R}}_{\mathit{}}({\mathbf{X}}) = {{{{\mathbf{X}}}}^{\bot}} \!\cdot\!{\mathbf{K}} \!\cdot\!{\mathbf{X}}~, \end{displaymath} (A.10)

where K is a positive definite matrix, which is chosen so that R in Eq. (A.10) should be non zero when X is strongly varying as a function of its indices. In practice, we use a square Laplacian penalization D2 norm as defined by Eq. (30) of Ocvirk et al. (2006b). Indeed, a Tikhonov penalization does not explicitly enforce smoothness of the solution, and a square gradient penalization favors flat solutions that are unphysical in our problem.

As mentioned in the main text, for a range of redshifts, a direct measurement, X0, which can be used as a prior for ${\tilde N}$, is available. We may therefore add as a supplementary constraint that

\begin{displaymath}{\mathit{P}}_{\mathit{}}({\mathbf{X}}) = {({{\mathbf{X}}} -... ...ot\!{\mathbf{W}}_2 \!\cdot\!({{\mathbf{X}}} - {\mathbf{X}}_0) \end{displaymath} (A.11)

should remain small, where the weight matrix, W2, is the inverse of the covariance matrix of the prior, X0, and should be non zero over the appropriate redshift range. In short, the penalized non-parametric solution of Eq. (A.8) accounting for both penalties is found by minimizing the so-called objective function

\begin{displaymath}Q({\mathbf{X}})=L({\mathbf{X}})+\lambda~R({\mathbf{X}})+\mu~P({\mathbf{X}}), \end{displaymath} (A.12)

where L(X), R(X), and P(X) are the likelihood and regularization terms given by Eqs. (A.9)- (A.11), respectively. The Lagrange multipliers $\lambda, \mu\geq0$ allow us to tune the level of smoothness of the solution (in practice, we set $\lambda=0.02$ for the reasons given below) and the requirement that X should remain close to its prior for the range of redshifts for which data is available. The introduction of the Lagrange multipliers is formally justified by our wanting to minimize the objective function Q(X), subject to the constraint that L(X) and P(X) should fall in the range $N_{\mathit{\rm data}}\pm\sqrt{2~N_{\mathit{\rm data}}}$ and $N_{\mathit{\rm param}}\pm\sqrt{2~N_{\mathit{\rm param}}}$, respectively.

The minimum of the objective function, Q(X), given by Eq. (A.12) reads formally as

 \begin{eqnarray*}\hat {\mathbf{X}} = ({{{{\mathbf{M}}}}^{\bot}} \!\cdot\!{\mathb... ...{\mathbf{Y}}\!+\mu {\mathbf{W}}_2\!\cdot\!{\mathbf{X}}_0\right). \end{eqnarray*}


This equation clearly shows that the solution tends towards X0when $\mu \rightarrow \infty$, while the smoothing Lagrange multiplier, $\lambda $, damps counterparts of the components of Y corresponding to the higher singular vectors of M (Ocvirk et al. 2006b). When dealing with noisy datasets, the non-parametric inversion technique may produce negative coefficients for the reconstructed luminosity function. To avoid such effects, positivity is imposed on those coefficients njl in Eq. (A.7), see for instance Ocvirk et al. (2006b) or Pichon et al. (2002). In practice, the minimum of the objective function is found iteratively, using optimpack (Thiébaut 2005). The relative weight on the likelihood and the two penalties is chosen so that the three quantities have a comparable contribution to the total likelihood after convergence. This corresponds to a reasonably smooth variation in the LF both in redshift and $L_{\rm IR}$, and imposes a solution that is always within 1$\sigma $ of the observed low-redshift LF, X0, when $\mu $ is not set to zero in Eq. (A.12).

Appendix B: Test of robustness

To quantify the confidence level of the inversion technique, we test its robustness. Starting from an arbitrary LF, we produce IR counts in the bands and flux ranges corresponding to the observations from this LF. Then, we add some random Gaussian noise to the simulated counts, using the real uncertainty on the observations as the $\sigma $of the error distribution for each flux bin. Finally, we apply the inversion technique described in Sect. 2.1 to these noisy counts and obtain an output LF.

The comparison of the input and output LFs is shown in Fig. B.1. The error on the absolute difference in $\log_{10} LF_{\rm in} - \log_{10} LF_{\rm out}$ is represented in gray levels and contours. The difference is generally less than 0.4 dex (factor 2.5) in the range where the LF can be constrained from the observed counts (range of the z-L plane encompassed by the dashed lines). A noticeable exception is the very low-redshift range (z<0.1), which corresponds to bright sources. For such large fluxes, the considerable noise in the observed counts produces large errors on the recovered LF. At high redshift, recall that the ultra-luminous population of galaxies appears as rare and very bright objects, in a flux range where the number counts are poorly known.

 \begin{figure} \par\includegraphics[width=9cm,clip]{09945f11.ps} \end{figure} Figure B.1:

Estimated robustness of the LF inversion used in this paper. The relative difference between the input LF and the recovered LF (when a realistic noise is added to the corresponding input counts) is larger for darker parts of the diagram. This difference is relatively small (<0.4 dex) in the region of the z-L space effectively constrained by observations: the dotted and dashed lines correspond to the extreme fluxes considered at 24 $\mu $m and 850 $\mu $m, respectively, for this study. See main text for details.
Open with DEXTER

Appendix C: Model predictions for Herschel

In Sect. 4, we have inverted the known IR counts to obtain constraints on the evolving total IR LF. We have seen that the LF obtained through this inversion is realistic and matches most of the recent observations (counts, CIRB, Mid-IR LF at low redshift). Then, in Sect. 5.2, we have shown how we can measure directly a part of this LF with a good confidence and that the LF resulting from the inversion is in good agreement with this solid measurement, validating the LF obtained by this empirical modeling approach. In this section, we use the median LF obtained from the inversions to predict some counts which should be observed with future observations in the FIR with Herschel or SCUBA2.

At the time of publication, several new facilities are in preparation to observe the Universe in the far-IR to sub-mm regimes. The differential counts (normalized to Euclidean) at wavelengths ranging from 16 to 850 $\mu $m, which we derived from the inversion technique, are presented in Fig. C.3. The separation of the contribution of local, intermediate, and distant galaxies in different colors illustrates the expected trend that larger wavelengths are sensitive to higher redshifts, hence the relative complementarity of all IR wavelengths. There will be a bias towards more luminous and distant objects with increasing wavelength, illustrated here for the Herschel passbands (see Fig. C.4), but this may be used to pre-select the most distant candidates expected to be detected only at the largest wavelengths. In the following, we discuss the predictions of the inversion technique for those instruments, as well as their respective confusion limits, which is the main limitation of far-IR extragalactic surveys.

The ESA satellite Herschel is scheduled to be launched within the next year, while the next-generation IR astronomical satellite of the Japanese space agency, SPICA, is scheduled for 2010, with a contribution by ESA under discussion, including a mid-IR imager named SAFARI. Both telescopes share the same diameter of 3.5 m, but the lower telescope temperature of SPICA, combined with projected competitive sensitivities, will make it possible to reach confusion around 70 $\mu $m (where Herschel is limited by integration time). The 5$\sigma $-1hour limits of the instruments SAFARI onboard SPICA (50 $\mu $Jy, 33-210 $\mu $m, dashed line), PACS (3mJy, 55-210 $\mu $m, light blue line) and SPIRE (2 mJy, 200-670 $\mu $m, blue line) onboard Herschel are compared in Fig. C.1 to the confusion limits that we derive from the best-fit model of the inversion, at all wavelengths between 30 and 850 $\mu $m, assuming the the confusion limit definition given below.

 \begin{figure} \par\includegraphics[width=9cm,clip]{09945f12.ps} \end{figure} Figure C.1:

Confusion limit for a 3.5 m telescope. The 5$\sigma $-1 h limits of SPICA-SAFARI (50 $\mu $Jy, 33-210 $\mu $m, dashed line), Herschel PACS (3 mJy, 55-210 $\mu $m, light blue line) and SPIRE (2 mJy, 200-670 $\mu $m, blue line) are shown together with their wavelength ranges. The blue part of the curve is determined by the source density criterion (i.e. the requirement to have less than 30% of the sources closer than 0.8 $\times $ FWHM), the red part is defined by the photometric criterion, i.e. sources must be brighter than 5 times the rms due to very faint sources below the detection limit.
Open with DEXTER

The definition of the confusion limit is not trivial, in particular because it depends on the level of clustering of galaxies; the optimum way to define it would be to perform simulations to compute the photometric error as a function of flux density, and then decide that the confusion limit is e.g. the depth above which 68% of the detected sources are measured with a photometric accuracy better than 20%. In the following, we only consider a simpler approach that involves computing the two sources of confusion that were discussed in Dole et al. (2003):

  • the photometric confusion noise: the noise produced by sources fainter than the detection threshold. The photometric criterion corresponds to the requirement that sources are detected with an S/N(photometric) > 5;
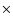  • the fraction of blended sources: a requirement for the quality of the catalog of sources will be that less than N % of the sources are closer than 0.8 $\times $ FWHM, i.e. close enough to not be separated.
We tested various levels for N and found that N=30% was equivalent to the above requirement that 68% of the detected sources are measured with a photometric accuracy better than 20% using realistic simulations in the far IR for Herschel. We therefore use the value N=30%. The confusion limit is then defined as the flux density above which both criteria are respected. As a result, it is found that the main limitation is the fraction of blended sources at $\lambda=50{-}105$ $\mu $m (blue part of the curve in Fig. C.1) and the photometric confusion noise below and above this range, i.e. at $\lambda= 33{-}50$ and $\lambda=105{-}210$ $\mu $m (red parts of curve in Fig. C.1). As a result of their smaller beam, shorter IR wavelength are more efficient at detecting faint star-forming galaxies than longer ones (see Fig. C.2). This is at the expense of observing farther away from the peak of the far IR emission, which implies larger uncertainties on the derivation of the total IR luminosity due to the uncertain dust temperature.

 \begin{figure} \par\includegraphics[width=8.7cm,clip]{09945f13.ps} \end{figure} Figure C.2:

Detection limits for confusion limited surveys from 70 to 850 $\mu $m. The curves show the minimum IR luminosity (8-1000 $\mu $m), or equivalently SFR (= $L_{\rm IR}\times 1.72 \times 10^{-10}$), that can be detected for a star-forming galaxy assuming that it has an SED similar to the Chary & Elbaz (2001) ones. The 70, 100, 160, 250, 350 and 500 $\mu $m limits correspond to a 3.5 m telescope diameter, such as Herschel or SPICA, while the 400 $\mu $m is for a 12 m class telescope such as APEX (e.g. ARTEMIS, we show the average between the two bands at 350 or 450 $\mu $m to avoid confusion with Herschel) and the 850 $\mu $m is for a 15 m telescope as the JCMT (SCUBA).
Open with DEXTER

Table C.1:   Fraction of the CIRB resolved by confusion-limited Herschel surveys.

We note that the confusion limit for a 3.5 m-class telescope, such as Herschel, is ten times more than the depth it can reach in one hour (5$\sigma $). With a source density of 12.8 sources per square degree at the 500 $\mu $m confusion limit (25 mJy), or equivalently one source in a field of 17 arcmin on a side, this shows that the best strategy at this wavelength is to go for very large and moderately shallow surveys, in order to identify the rare and very luminous distant galaxies.

 \begin{figure} \par\includegraphics[width=16.5cm,clip]{09945f14.ps} \end{figure} Figure C.3:

Counts predicted from the inversion in the far-infrared and sub-mm (solid line). The counts are decomposed in redshift bins (blue = z<0.5; green = 0.5<z<1.5; orange = 1.5<z<2.5; red = z>2.5). The oblique dashed line corresponds to the limit in statistics due to the smallness of a field like GOODS North+South or 0.07 square degrees: less than 2 galaxies per flux bin of width $\delta \log F=0.1$ dex are expected below this limit.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=16.6cm,clip]{09945f15.ps} \end{figure} Figure C.4:

Differential counts predicted from the non-parametric inversion for future Herschel observations: PACS 100 $\mu $m (solid black), SPIRE 250 $\mu $m (dotted blue), SPIRE 350 $\mu $m (dashed green), SPIRE 500 $\mu $m (dot-dashed red) decomposed simultaneously in redshift and $L_{\rm IR}$.
Open with DEXTER

For comparison, we also illustrated the ground-based capacity of ARTEMIS built by CEA-Saclay which will operate at the ESO 12 m-telescope facility APEX (Atacama Pathfinder EXperiment) at 200, 350 and 450 $\mu $m and SCUBA-2 that will operate at the 15 m telescope JCMT at 450 and 850 $\mu $m. To avoid confusion between all instruments, we only show the average wavelength 400 $\mu $m for a 12 m-class telescope and 850 $\mu $m for a 15 m-class telescope (Fig. C.1). Although the confusion limit in the 850 $\mu $m passband is ten times below that of Herschel at the longest wavelengths, this band is not competitive with the $\sim$400 $\mu $m one, which should be priorities for ARTEMIS and SCUBA-2 for the study of distant galaxies, or with the 70 and 100 $\mu $m ones for a 3.5 m space experiment such as SPICA and Herschel, for redshifts below $z\sim5$. We also note that only in these two passbands will the cosmic IR background be resolved with these future experiments (see Table C.1), which suggests that a larger telescope size should be considered for a future experiment to observe the far IR Universe above 100 $\mu $m and below the wavelength domain of ALMA. We did not mention here ALMA since it will not be affected by these confusion issue: due to its very good spatial resolution, it will be limited to either small ultradeep survey, hence missing rare objects or follow-ups of fields observed with single dish instruments, e.g. ARTEMIS. Finally, the JWST that will operate in the mid IR will be a very powerful instrument for probing the faintest star-forming galaxies in the distant Universe, but predictions are difficult to produce at the present stage since it has already been found that extrapolations from the mid to far IR become less robust already at $z\sim 2$ (e.g. Papovich et al. 2007; Pope et al. 2008; Daddi et al. 2007b).


Footnotes

... counts[*]
Appendices are only available in electronic from at http://www.aanda.org
... ULIRGS[*]
We adopt the following notation in this paper:
``Normal'' galaxies have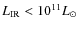 $L_{\rm IR}{}<10^{11} L_\odot$;
``LIRGS'':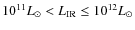 $10^{11} L_\odot < L_{\rm IR}{} \leq 10^{12} L_\odot$;
``ULIRGS'':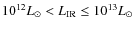 $10^{12} L_\odot < L_{\rm IR}{} \leq 10^{13} L_\odot$;
``HLIRGS'':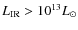 $L_{\rm IR}{}>10^{13} L_\odot$.
... others[*]
This approach is at variance with the classical ``direct'' methods used for this purpose, in which luminosities of individual sources are derived from their measured redshifts and fluxes in a single mid-IR band.
... versatile[*]
It is worth noting that we can take (optionally and when available) the redshift information into account by using as priors the luminosity functions measured at low redshifts from direct methods. We will show in Sect. 4 that this knowledge of the luminosity-redshift distribution at low redshift (z<2) brings actually little new to our results.
... galaxies[*]
In this subsection presenting the formalism in the general case, an evolution of the SEDs is considered as possible.
... following[*]
If the SEDs vary not only with 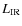$L_{\rm IR}$ but also with z, we could call it the ``e+k+d'' matrix.
... completeness[*]
We could also have used a more classical approach to characterize the uncertainties in the recovered LFs by computing the posterior variance covariance of the parameters away from the itterative nonlinear solution, and compared it to the corresponding initial prior (hence constructing the so called information matrix). These uncertainties naturally arise from the uncertainties on the observed counts through the error matrix W. Instead, we favor here Monte-Carlo simulations because they yield similar - if not more robust (since we span ranges of possible nonlinear solutions) - constraints on the recovered LF.
... redshift[*]
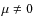Technically, this supplementary prior involves again penalizing the formal $\chi^2$ by adding an extra term that measures the distance between the observed LF and the solution (this corresponds to $\mu\neq 0$ in Appendix A). The LFs that are too different from the known low-redshift LF are therefore strongly penalized, so excluded de facto.
... conversion)[*]
Note that Le Floc'h et al. (2005) errors bars are rather large because they partly reflect the uncertainties in the SEDs of galaxies. We checked that using another library of SEDs (e.g. the LDP03 library) produces differences in our LFs comparable to the error bars of Le Floc'h et al. (2005).
... inversion[*]
The datasets are independent, indeed. But strictly speaking, it is actually not the case for the SFRD measurements because the libraries of SEDs used for k-corrections are the same in both methods.

All Tables

Table C.1:   Fraction of the CIRB resolved by confusion-limited Herschel surveys.

All Figures

  \begin{figure} \par\includegraphics[width=17cm,clip]{09945f1.ps} \end{figure} Figure 1:

Observed 15/16 $\mu $m, 24 $\mu $m, 70 $\mu $m, 160 $\mu $m, and 850 $\mu $m counts of galaxies from various surveys. The shaded area representing 1$\sigma $ uncertainty area are determined semi-automatically from the data points (smoothed envelopes of the data points after excluding the strongest outliers, particularly at 15 $\mu $m), and are used as an input for the inversions. Instruments/fields: ISO LW3/various fields (Elbaz et al. 1999), ISO LW3/ELAIS-S (Gruppioni et al. 2002), SPITZER IRS/GOODS (Teplitz et al. 2006), SPITZER MIPS24/GOODS (Chary et al. 2004), SPITZER MIPS24/various fields (Papovich et al. 2004), SPITZER MIPS24/GOODS (Le Floc'h et al. 2005), SPITZER MIPS70/FLS (Frayer et al. 2006a), SPITZER MIPS70/GOODS-N (Frayer et al. 2006b), ISO ISOPHOT170/FIRBACK (Dole et al. 2001), SPITZER MIPS160/MARANO+CDFS (Dole et al. 2004), JCMT SCUBA/SXDF+LH (Coppin et al. 2006).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.9cm,clip]{09945f2.ps} \end{figure} Figure 2:

24 $\mu $m vs. total IR luminosities (or the SFR equivalent of these luminosities assuming a Salpeter IMF). The shaded gray area represents the observations of Papovich et al. (2007) Fig. 11, considering that most of this intense SF is probed by the IR light, neglecting the UV contribution. The solid lines correspond to the ``clipped'' CE01 library for a set of virtual galaxies at redshifts z=1.5, 1.8, 2.2 and 2.5 (from left to right) with fluxes fainter than 1 mJy, for which the Papovich et al. (2007) observations are valid. A pure CE01 library would have followed the one-to-one slope.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{09945f3.ps} \end{figure} Figure 3:

Mid- and Far-IR counts obtained from the non-parametric inversion of the observed counts. The data counts that are the basis of the inversion are represented by the shaded blue zones (fitted values $\pm $1$\sigma $, corresponding to the zones of Fig. 1). The best fit to the counts is shown by the solid red lines, together with the range of allowed solutions (red dashed areas). The vertical gray zones delimit the flux ranges where some counts are observed. All the counts modeled here satisfy the CIRB constraints. The oblique dashed line corresponds to a statistical limit of a one square degree survey (less than 2 sources per decade in flux).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=17cm,clip]{09945f4.ps} \end{figure} Figure 4:

All possible solutions for the evolving LFs that best reproduce all the IR counts of Fig. 3 and the CIRB constraints. As in Fig. 3, the thick red line and the dashed red areas represent the best-fitting solution and the range of allowed solutions, respectively. By construction, no conclusion on the LF can be made in the vertical gray-shaded areas where a divergence is expected because these objects are not seen in the counts because of the flux limits of current IR surveys. At the top of each panel, the ranges of $L_{\rm IR}$ probed by IR counts are shown as horizontal lines, from 15 to 850 $\mu $m (bottom to top). Diamonds, triangles, and filled circles correspond to 0.1, 0.3, and 3 mJy fluxes, respectively. Bottom right panel: range of CIRB corresponding to the inverted LFs. Data points (in gray) are taken from ilation by Dole et al. (2006).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12.8cm,clip]{09945f5.ps} \end{figure} Figure 5:

Star-formation rate density since z=5 derived from the counts inversions. The SFRD is obtained from the range of all possible luminosity functions derived from the counts and respecting the CIRB constraints. The solid lines correspond to the best fit to the counts and the transparent shaded areas show the range of uncertainties. From top to bottom at z=0.8: black = all galaxies, green = LIRGS, blue = normal star-forming galaxies, orange = ULIRGS, red = HLIRGS.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16cm,clip]{09945f6.ps} \end{figure} Figure 6:

Top and bottom left: counts at 16, 24, and 70 $\mu $m modeled (solid lines) from the inversion, on the one hand, and observed (dotted lines) in GOODS fields, on the other. The counts are decomposed in redshift bins (black = all redshifts, blue =z<0.5, green  =0.5<z<1.5, orange = 1.5<z<2.5, red = z>2.5). Bottom right: CIRB decomposed in redshift (same color-coding). The oblique dashed line corresponds to the limit in statistics due to the smallness of a field like GOODS North+South or 0.07 square degrees: less than 2 galaxies per flux bin of width $\delta \log F=0.1$ dex are expected below this limit.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=15.5cm,clip]{09945f7.ps} \end{figure} Figure 7:

Total IR luminosity functions derived independently from the counts inversion and from direct measurements. ``Clipped'' CE01 templates are used for the 24 $\mu $m fluxes to $L_{\rm IR}$ conversion (filled black dots). The measurements from Le Floc'h et al. (2005) are also shown for reference. The model (counts inversion) curves (dashed lines) are given at the mean redshift of each bin. The shaded areas represent the range of uncertainties on our modeled LF at the mean redshift of each bin.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{09945f8.ps} \end{figure} Figure 8:

Total SFRD regions compared to ilation of direct measurements from Hopkins & Beacom (2006) (empty circles and error bars only for z>1.5 for clarity purposes). The outer light-gray regions corresponds to all possible LFs fitting the counts. The inner darker region includes 68% of these models. The dashed line corresponds to the LF producing the best-fit to the multi-$\lambda $ IR counts. The solid triangles with error bars show the integrated SFRD that we measured in the GOODS fields in several redshift bins (see also Fig. 9 for a luminosity decomposition of these measurements).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=11.5cm,clip]{09945f9.ps} \end{figure} Figure 9:

History of the SFRD decomposed in four infrared luminosity classes. The inversion results (full set of models and 68% inner region) are shown with gray-shaded areas. The total SFRD history (68% inner region) is also shown for reference in each panel as dotted lines. Our direct (and independent) measurements from the GOODS survey are shown as triangles. Empty triangles are used for bins affected by completeness. The z=3 point for HLIRGS is subject to caveats (see text for details) so is probably overestimated.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.9cm,clip]{09945f10.ps} \end{figure} Figure 10:

Range of allowed evolutions of the stellar mass density computed with the range of cosmic SF histories of Fig. 5. The dashed lines corresponds to the best-fit to the IR counts. The data points with error bars are measurements from Pérez-González et al. (2008) (empty circles) and Elsner et al. (2008) (filled dots). The realistic Baldry & Glazebrook (2003) IMF is used both for the data points and to derive the stellar mass density from the SFR density.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{09945f11.ps} \end{figure} Figure B.1:

Estimated robustness of the LF inversion used in this paper. The relative difference between the input LF and the recovered LF (when a realistic noise is added to the corresponding input counts) is larger for darker parts of the diagram. This difference is relatively small (<0.4 dex) in the region of the z-L space effectively constrained by observations: the dotted and dashed lines correspond to the extreme fluxes considered at 24 $\mu $m and 850 $\mu $m, respectively, for this study. See main text for details.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{09945f12.ps} \end{figure} Figure C.1:

Confusion limit for a 3.5 m telescope. The 5$\sigma $-1 h limits of SPICA-SAFARI (50 $\mu $Jy, 33-210 $\mu $m, dashed line), Herschel PACS (3 mJy, 55-210 $\mu $m, light blue line) and SPIRE (2 mJy, 200-670 $\mu $m, blue line) are shown together with their wavelength ranges. The blue part of the curve is determined by the source density criterion (i.e. the requirement to have less than 30% of the sources closer than 0.8 $\times $ FWHM), the red part is defined by the photometric criterion, i.e. sources must be brighter than 5 times the rms due to very faint sources below the detection limit.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.7cm,clip]{09945f13.ps} \end{figure} Figure C.2:

Detection limits for confusion limited surveys from 70 to 850 $\mu $m. The curves show the minimum IR luminosity (8-1000 $\mu $m), or equivalently SFR (= $L_{\rm IR}\times 1.72 \times 10^{-10}$), that can be detected for a star-forming galaxy assuming that it has an SED similar to the Chary & Elbaz (2001) ones. The 70, 100, 160, 250, 350 and 500 $\mu $m limits correspond to a 3.5 m telescope diameter, such as Herschel or SPICA, while the 400 $\mu $m is for a 12 m class telescope such as APEX (e.g. ARTEMIS, we show the average between the two bands at 350 or 450 $\mu $m to avoid confusion with Herschel) and the 850 $\mu $m is for a 15 m telescope as the JCMT (SCUBA).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16.5cm,clip]{09945f14.ps} \end{figure} Figure C.3:

Counts predicted from the inversion in the far-infrared and sub-mm (solid line). The counts are decomposed in redshift bins (blue = z<0.5; green = 0.5<z<1.5; orange = 1.5<z<2.5; red = z>2.5). The oblique dashed line corresponds to the limit in statistics due to the smallness of a field like GOODS North+South or 0.07 square degrees: less than 2 galaxies per flux bin of width $\delta \log F=0.1$ dex are expected below this limit.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=16.6cm,clip]{09945f15.ps} \end{figure} Figure C.4:

Differential counts predicted from the non-parametric inversion for future Herschel observations: PACS 100 $\mu $m (solid black), SPIRE 250 $\mu $m (dotted blue), SPIRE 350 $\mu $m (dashed green), SPIRE 500 $\mu $m (dot-dashed red) decomposed simultaneously in redshift and $L_{\rm IR}$.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.