The simulated H I sky at low redshift

A. Popping; R. Davé; R. Braun; B. D. Oppenheimer

doi:10.1051/0004-6361/200911811

Free Access

Issue		A&A Volume 504, Number 1, September II 2009


Page(s)		15 - 32
Section		Cosmology (including clusters of galaxies)
DOI		https://doi.org/10.1051/0004-6361/200911811
Published online		09 July 2009

The simulated H I sky at low redshift

A. Popping^1,2 - R. Davé³ - R. Braun² - B. D. Oppenheimer³

1 - Kapteyn Astronomical Institute, PO Box 800, 9700 AV Groningen, The Netherlands
2 - Australia Telescope National Facility, CSIRO, PO Box 76, Epping, NSW 1710, Australia
3 - Astronomy Department, University of Arizona, Tucson, AZ 85721, USA

Received 8 February 2009 / Accepted 15 June 2009

Abstract
Context. Observations of intergalactic neutral hydrogen can provide a wealth of information about structure and galaxy formation, potentially tracing accretion and feedback processes on Mpc scales. Below a column density of $N_{\rm {HI}} \sim 10^{19}$ cm^-2, the ``edge'' or typical observational limit for H I emission from galaxies, simulations predict a cosmic web of extended emission and filamentary structures. Current observations of this regime are limited by telescope sensitivity, which will soon advance substantially.
Aims. We study the distribution of neutral hydrogen and its 21-cm emission properties in a cosmological hydrodynamic simulation, to gain more insight into the distribution of H I below $N_{\rm {HI}} \sim 10^{19}$ cm^-2. Such Lyman limit systems are expected to trace out the cosmic web and are relatively unexplored.
Methods. Beginning with a 32 h^-1 Mpc simulation, we extract the neutral hydrogen component by determining the neutral fraction, including a post-processed correction for self-shielding based on the thermal pressure. We take molecular hydrogen into account, assuming an average density ratio $\Omega_{{\rm H}_{\rm 2}}/\Omega_{\rm HI} = 0.3$ at z = 0. The statistical properties of the H I emission are compared with observations, to assess the reliability of the simulation. We then make predictions for upcoming surveys.
Results. The simulated H I distribution robustly describes the full column density range between $N_{\rm {HI}} \sim 10^{14}$ and $N_{\rm {HI}} \sim 10^{21}$ cm^-2 and agrees very well with available measurements from observations. Furthermore there is good correspondence in the statistics when looking at the two-point correlation function and the H I mass function. The reconstructed maps are used to simulate observations of existing and future telescopes by adding noise and accounting for the sensitivity of the telescopes.
Conclusions. The general agreement in statistical properties of H I suggests that neutral hydrogen, as modelled in this hydrodynamic simulation, is a fair representation of neutral hydrogen in the Universe. Our method can be applied to other simulations, to compare different models of accretion and feedback. Future H I observations will be able to probe the regions where galaxies connect to the cosmic web.

Key words: intergalactic medium - cosmology: miscellaneous - galaxies: structure

1 Introduction

Current cosmological models ascribe only about 4% of the density in the Universe to baryons (Spergel et al. 2007). The majority of these baryons reside outside of galaxies, with stars and cold galactic gas possibly accounting for about about one third (Fukugita et al. 1998). Intergalactic baryons have historically been traced in absorption, such as the Ly $\alpha$ forest arising from diffuse photo-ionised gas that may account for up to 30% of baryons. The remaining baryons are predicted to exist in a warm-hot intergalactic medium (WHIM) (e.g. Cen & Ostriker 1999; Davé et al. 1999,2001), which is shock-heated during the collapse of density perturbations that give rise to the cosmic web. Nonetheless, absorption probes yield only one-dimensional redshift-space information, or in rare cases several probes through common structures. Mapping intergalactic baryons in emission can in principle provide morphological and kinematic information on accreting (and perhaps out-flowing) gas within the cosmic web.

Unfortunately, emission from intergalactic baryons is difficult to observe, because current telescope sensitivities result in a detection limit of column densities $N_{\rm {HI}} \ga 10^{19}$ cm^-2, which are the realm of damped Ly $\alpha$ (DLA) systems and sub-DLAs. Below column densities of $\sim$ $N_{\rm {HI}} \sim 10^{19.5}$ cm^-2, the neutral fraction of hydrogen decreases rapidly because of the transition from optically-thick to optically-thin gas ionised by the metagalactic ultraviolet flux. At lower densities, the gas is no longer affected by self-shielding and the atoms are mostly ionised. This sharp decline in neutral fraction from almost unity to less than a percent happens within a few kpc (Dove & Shull 1994). Below $N_{\rm {HI}} \sim 10^{17.5}$ cm^-2, the gas is optically thin and the decline in neutral fraction with total column is much more gradual. A consequence of this rapid decline in neutral fraction is a plateau in the H I column density distribution function between $N_{\rm {HI}} \sim 10^{17.5}$ and $N_{\rm {HI}} \sim 10^{19.5}$ cm^-2, where the relative surface area at these columns shows only modest growth. This behaviour is confirmed in QSO absorption studies tabulated by Corbelli & Bandiera (2002) and in H I emission by Braun & Thilker (2004). Below $N_{\rm {HI}} \sim 10^{17.5}$ cm^-2 the relative surface area increases rapidly, reaching about a factor of 30 larger at $N_{\rm {HI}} \sim 10^{17}$ compared with $N_{\rm {HI}} \sim 10^{19}$ cm^-2.

This plateau in the distribution function is a critical issue for observers of neutral hydrogen in emission. Although telescope sensitivities have increased substantially over the past decades, the detected surface area of galaxies observed in the 21-cm line has only increased modestly (eg. Dove & Shull 1994). Clearly there is a flattening in the distribution function near $N_{\rm {HI}} \sim 10^{19.5}$ cm^-2 which has limited the ability of even deep observations to detect hydrogen emission from a larger area. By establishing that a steeper distribution function is again expected below about $N_{\rm {HI}} \sim 10^{17.5}$ , it provides a clear technical target for what the next generation of radio telescopes needs to achieve to effectively probe diffuse gas.

Exploration of the $N_{\rm {HI}} < 10^{17.5}$ cm^-2 regime is essential for gaining a deeper understanding of the repository of baryons that drive galaxy formation and evolution. This gas, residing in filamentary structures, is the reservoir that fuels future star formation, and could provide a direct signature of smooth cold-mode accretion predicted to dominate gas acquisition in star-forming galaxies today (Dekel et al. 2009; Keres et al. 2005,2009). Furthermore, the trace neutral fraction in this phase may provide a long-lived fossil record of tidal interactions and feedback processes such as galactic winds and AGN-driven cavities.

Several new large facilities to study 21cm emission are under development today. In view of the observational difficulties in probing the low H I column regime, it is particularly important to have reliable numerical simulations to aid in planning new observational campaigns, and eventually to help interpret such observations within a structure formation context. While simulations of galaxy formation are challenging, historically they have had much success predicting the more diffuse baryons residing in the cosmic web (e.g. Davé et al. 1999). If such simulations display statistical agreement with key existing H I emission data, then they can be used to make plausible predictions for the types of structures that may be detected, along with suggesting optimum observing strategies.

In this paper, we employ a state-of-the art cosmological hydrodynamic simulation to study H I emission from filamentary large-scale structure and the galaxies within them. The simulation used here include a well-constrained prescription for galactic outflows that has been shown to reproduce the observed metal and H I absorption line properties from $z\sim 6\rightarrow 0$ (Oppenheimer & Davé 2008,2006,2009). We develop a method to produce H I maps from these simulations, and compare statistical properties of the reconstructed H I data with the statistics of real H I observations, to assess the reliability of the simulation. For this purpose we will primarily use the H I Parkes All Sky Survey (HIPASS) (Barnes et al. 2001) since this is the largest available H I survey. This work is intended to provide an initial step towards a more thorough exploration of model constraints that will be enabled by comparisons with present and future H I data.

Note that current spatial resolution of simulations having cosmologically-representative volumes cannot reproduce a galaxy as would be seen with H I observations having sub-kpc resolution. Therefore we do not consider the internal kinematics or detailed shapes of the objects associated with simulated galaxies. We can only assess the statistical properties of the diffuse H I phase and predict how the gas is distributed on multi-kpc scales. We particularly focus on lower column density material that may be probed with future H I surveys, which primarily reside in cosmic filaments within which galaxies are embedded.

Our paper is organised as follows. In section two we briefly describe the particular simulation that has been analysed. In section three we describe our method to extract the neutral hydrogen from the simulations. The neutral fraction is determined from both a general ionisation balance as well as a local self-shielding correction. We also model the transition from atomic to molecular hydrogen We present our results, showing the statistical properties of the recovered H I in section four, where they are compared with similar statistics obtained from observations. The distribution of neutral hydrogen is compared with the distribution of dark matter and stars in this section as well. In the fifth section we discuss the results and outline the implications. Finally, section six reiterates our main conclusions.

2 Simulation code

A modified version of the N-body+hydrodynamic code Gadget-2 is employed, which uses a tree-particle-mesh algorithm to compute gravitational forces on a set of particles, and an entropy-conserving formulation of smoothed particle hydrodynamics (SPH: Springel & Hernquist 2002) to simulate pressure forces and shocks in the baryonic gaseous particles. This Lagrangian code is fully adaptive in space and time, allowing simulations with a large dynamic range necessary to study both high-density regions harbouring galaxies and the lower-density IGM. It includes a prescription for star formation following Springel & Hernquist (2003b) and galactic outflows as described below. The code has been described in detail in Oppenheimer & Davé (2006, 2008); we will only summarise the properties here.

The novel feature of our simulation is that it includes a well-constrained model for galactic outflows. The implementation follows Springel & Hernquist (2003a), but employs scaling of outflow speed and mass loading factor with galaxy mass as expected for momentum-driven winds (Murray et al. 2005). Our simulations using these scalings have been shown to successfully reproduce a wide range of IGM and galaxy data, including IGM enrichment as traced by $z\sim2$ -6 C IV absorbers (Oppenheimer & Davé 2006), the galaxy mass-metallicity relation (Finlator & Davé 2008), the early galaxy luminosity function and its evolution (Davé et al. 2006), O VI absorption at low-z (Oppenheimer & Davé 2009), and enrichment and entropy levels in galaxy groups (Davé et al. 2008). Such outflows are expected to impact the distribution of gas in the large-scale structure around galaxies out to typically $\sim$ 100 kpc (Oppenheimer & Davé 2008,2009), so are important for studying the regions expected to yield detectable H I emission.

The simulation used here is run with cosmological parameters consistent with the 3-year WMAP results (Spergel et al. 2007). The parameters are $\Omega_0 = 0.25$ , $\Omega_{\Lambda} = 0.75$ , $\Omega_{\rm b} = 0.044$ , H₀ = 71 km s^-1 Mpc^-1, $\sigma_8 = 0.83$ , and n = 0.95. The periodic cubic volume has a box length of 32 h^-1 Mpc (comoving), and the gravitational softening length is set to 2.5 h^-1kpc (comoving). Dark matter and gas are represented using 256³particles each, yielding a mass per dark matter and gas particle of $1.57\times 10^8~M_\odot$ and $3.35\times 10^7~M_\odot$ , respectively. The simulation was started in the linear regime at z=129, with initial conditions established using a random realisation of the power spectrum computed following Eisenstein & Hu (1999), and evolved to z=0.

3 Method for making H I maps

We now describe the algorithm used to extract the neutral hydrogen component from this simulation. The method developed is general, and can be applied to any simulation that has a similar set of output parameters. In our analysis, we set the total hydrogen number density to $n_{\rm {H}} = 0.74\rho_g/m_{\rm {H}}$ where $m_{\rm {H}}$ is the mass of the hydrogen atom. The factor 0.74 assumes a helium abundance of Y = 0.26 by mass, and that all the helium is in the form of He I and He II with a similar neutral fraction as hydrogen. Apart from this factor the presence of helium is not taken into account in our calculations. We will describe how we determine the neutral fraction of the gas particles, including applying a correction for self shielding in high density regions and taking into account molecular hydrogen formation where relevant. This allows reconstruction of the neutral hydrogen distribution, by mapping the particles onto a three dimensional grid.

3.1 Neutral fraction of hydrogen

We begin by calculating the neutral fraction from the density and temperature of gas in the simulations, together with the H I photo-ionisation rate provided by the cosmic UV background. Dove & Shull (1994) found that the radial structure of the column density of H I is more sensitive to the extra-galactic radiation field than to the distribution of mass in the host galaxy. When calculating the neutral fraction, we assume that all photo-ionisation is due to radiation external to the disk and that internal stellar sources are not significant. In this case the nebular model as described in Osterbrock (1989) is a very good approximation, since the typical number density in the outer parts of galaxies, approximately 10^-2cm^-3, is so low that collisional ionisation is negligible. When going further out, the densities become even lower. Inside galaxies the volume densities are so high, that the neutral fraction is of order unity owing to self-shielding.

In the IGM, hydrogen becomes ionised when the extreme ultraviolet (UV) radiation ionises and heats the surrounding gas. On the other hand, the recombination of electrons leads to neutralisation. The degree of ionisation is determined by the balance between photo-ionisation and radiative recombination. Only photons more energetic than $h\nu > 13.6$ eV can ionise hydrogen. The ionisation equilibrium equation is given by e.g. Osterbrock (1989) as:

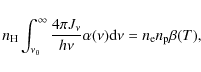$\begin{displaymath}n_{\rm {H}} \int^{\infty}_{\nu_0} \frac{4\pi J_{\nu}}{h\nu}\alpha(\nu) {\rm d}\nu = n_{\rm e} n_{\rm p} \beta(T), \end{displaymath}$

(1)

where $J_{\nu}$ is the mean intensity of ionising photons, $\alpha(\nu)$ is the ionisation cross section and $\beta(T)$ is the recombination rate coefficient to all levels of atomic hydrogen at temperature T. $\nu_0$ is the ionisation threshold frequency. Only radiation with frequency $\nu > \nu_0$ is effective in photo-ionisation of hydrogen from the ground level. Summarising, the integral represents the number of photo-ionisations per unit time and the right hand side of the equation gives the number of recombinations per unit time. The neutral hydrogen, $n_{\rm {H}}$ , electron, $n_{\rm e}$ , and proton, $n_{\rm p}$ , densities are related through the charge conservation and hydrogen abundance equations,

$\begin{displaymath}n_{\rm e} = n_{\rm p} = (1-\xi)n \end{displaymath}$

(2)

where $\xi$ is the neutral fraction, so

$\begin{displaymath}n_{\rm {H}} = \xi n \end{displaymath}$

(3)

with n the total density.

We can write the ionisation balance for neutral hydrogen as

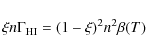$\begin{displaymath}\xi n \Gamma_{\rm {HI}} = (1-\xi)^2n^2 \beta(T) \end{displaymath}$

(4)

where $\Gamma_{\rm {HI}}$ is the ionisation rate for neutral hydrogen.
With this equation it is easy to determine the neutral fraction, which is given by

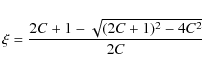$\begin{displaymath}\xi = \frac{2C + 1 - \sqrt{(2C+1)^2-4C^2}}{2C} \end{displaymath}$

(5)

using

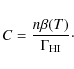$\begin{displaymath}C = \frac{n \beta(T)}{\Gamma_{\rm {HI}}}\cdot \end{displaymath}$

(6)

Obviously the neutral fractions that we calculate are closely related to the values we use for the photo-ionisation and recombination rate. The photo-ionisation rate at low redshift is not well constrained observationally; by combining Ly $\alpha$ forest data and simulations, Davé & Tripp (2001) obtain a photo-ionisation rate of $\Gamma_{\rm {HI}} \sim 10^{-13.3 \pm 0.7}$ s^-1 for redshift $z \sim 0.17$ . We will use the photo-ionisation rate given by the CUBA model of Haardt & Madau (2001), which is $\Gamma_{\rm {HI}} \sim 10^{-13}$ s^-1 for $z \sim 0$ .

The recombination rate coefficients are dependent on temperature. We make use of an analytic function described by Verner & Ferland (1996), that fits the coefficients in the temperature range form 3 K to 10¹⁰ K:

$\begin{displaymath}\beta(T) = a \Big[ \sqrt{T/T_0}\big(1+\sqrt{T/T_0}\big)^{1-b}\big(1+\sqrt{T/T_1}\big)^{1+b} \Big] ^{-1} \end{displaymath}$

(7)

where a, b, T₀ and T₁ are the fitting parameters. For the H I ion the fitting parameters are: $a=7.982 \times 10^{-11}$ cm³ s^-1, b=0.7480, T₀=3.148 K and $T_1 = 7.036 \times 10^{5}$ K.

The neutral fraction is plotted for different temperatures as function of density of H atoms in Fig. 1. For temperatures below 10⁴ K, the neutral fraction is still significant (a few percent) at reasonably low densities of 0.01 cm^-3 but at higher temperatures most of the gas is ionised, and the neutral fraction drops very quickly.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{11811f01.eps} \end{figure}$	Figure 1: Neutral fraction as a function of density for different temperatures between 10⁴ and 10⁹ K.
Open with DEXTER

3.2 Molecular hydrogen

When gas has cooled sufficiently, it coexists in the molecular (H₂) and atomic (H I) phases. The H₂ regions are found in dense molecular clouds where star formation occurs. Unfortunately there is large uncertainty in the average amount of H₂ in galaxies, as estimates have to rely on indirect tracers and conversion factors, for which the dependancies are not well-understood. As a result, there is substantial variance in estimates of the average density ratio at z=0, $\eta_{\rm universe} = \Omega_{{\rm H}_{\rm 2}} / \Omega_{\rm HI}$ (e.g. 0.42 and 0.26 stated respectively by Keres et al. 2003 and Obreschkow & Rawlings 2009). It is beyond the scope of this paper to revisit these determinations, therefore we will adopt a value of $\Omega_{{\rm H}_{\rm 2}}/\Omega_{\rm HI} = 0.3$ that falls within the error bars of current estimates. Given the observed local value of the atomic mass density, of $\rho_{\rm HI}=6.1\times 10^7~h~M_{\odot}$ Mpc^-3 (Zwaan et al. 2003), this implies a molecular mass density of $\rho_{{\rm H}_{\rm 2}}=1.8\times 10^7~h~M_{\odot}$ Mpc^-3.

To define the regions of molecular hydrogen, we use a threshold based on the thermal pressure (P/k = nT). Wong & Blitz (2002), Blitz & Rosolowsky (2004) and more recently Blitz & Rosolowsky (2006) have made the case that the amount of molecular hydrogen that is formed in galaxies is determined by only one parameter, the interstellar gas pressure. In hydrostatic pressure equilibrium, the hydrostatic pressure is balanced by the sum of all contributions to the gas pressure: magnetic pressure, cosmic ray pressure and kinetic pressure terms (of which the thermal pressure is relatively small) (e.g. Walterbos & Braun 1996, and references therein). However, thermal pressure is directly coupled to energy dissipation via radiation, and therefore thermal pressure can track the total pressure due to various equipartition mechanisms. An evaluation of the various contributions to the total hydrostatic pressure is given by Boulares & Cox (1990).

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{11811f02.eps} \end{figure}$

Figure 2:

Temperatures are plotted against densities for every 200 th. particle in the simulation. The dashed (blue) and dash-dotted (red) lines correspond to constant thermal pressures of P/k = 155 and 810 cm^-3 K, that were found empirically to reproduce the observed mass densities of atomic and molecular gas at z = 0. The solid (green) line shows where the recombination time is equal to the sound-crossing time at a physical scale of one kpc. Particles above/left of the green line are unlikely to be neutral or molecular.

Open with DEXTER

Two lines of constant thermal pressure are shown in Fig. 2 where temperatures are plotted against density for individual particles in the simulation. When following these lines, they cross two regions, one with high densities and low temperatures and one with moderate densities, but very high temperatures. These two regions are distinguished by the solid green line in Fig. 2, where the radiative recombination time is equivalent to the sound-crossing time on a kilo-parsec scale. The radiative recombination time is given in Tielens (2005) by:

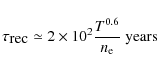$\begin{displaymath}\tau_{\textrm{rec}} \simeq 2 \times 10^2 \frac{T^{0.6}}{n_{\rm e}} \textrm{ years} \end{displaymath}$

(8)

where $n_{\rm e}$ is the electron density which is comparable to the total density for low neutral fractions. The sound crossing time is given by $\tau_{\textrm{s}} = R/C_{\textrm{s}}$ , where R is the relevant scale (assumed here to be one kpc) and $C_{\textrm{s}} \simeq 1.4 \times 10^4 T^{1/2}$ cm s^-1 is the sound velocity. All particles right of the green line have a recombination time that is shorter than the sound crossing time. Particles with a recombination time that is larger than the sound crossing time are unlikely to be neutral or molecular.

For each particle the thermal pressure can be calculated and particles with a pressure exceeding the threshold value and satisfying $\tau_{\rm {rec}}<\tau_{\textrm{s}}$ are considered molecular. By exploring different pressure values as shown in Fig. 3, the threshold can be tuned to yield the required molecular mass density, $\rho_{{\rm H}_{\rm 2}}=1.8\times 10^7~h~M_{\odot}$ Mpc^-3. The threshold thermal pressure value we empirically determine is P/k = 810 cm^-3 K. We must stress, that this value is very likely not a real physical value, as the resolution in our simulation is not sufficient to resolve the scales of molecular clouds. Molecular clouds have smaller scales with higher densities, which will likely have significantly enhanced pressures.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{11811f03.eps} \end{figure}$

Figure 3:

The average molecular density at z = 0 is plotted against the threshold thermal pressure, where molecular hydrogen is assumed to form from atomic, while also satisfying the condition that $\tau _{\textrm {rec}}<\tau _{\textrm {s}}$ . The dashed line indicates a pressure of P/k = 810 cm^-3 K, where $\rho_{{\rm H}_{\rm 2}}=1.8\times 10^7~h~M_{\odot}$ Mpc^-3 which is shown by the dotted line.

Open with DEXTER

3.3 Correction for self-shielding

Although the ionisation state and kinetic temperature are determined self-consistently within the simulation, it has been necessary to assume that each gas particle is subjected to the same all-pervasive radiation field. At both extremely low and high particle densities this approximation is sufficient, since local conditions will dominate. However, at intermediate densities, the ``self-shielding'' of particles by their neighbours may play a critical role in permitting local recombination, when the same particle would be substantially ionised in isolation. Present cosmological simulations are not capable of solving the full radiative transfer equations, although it is now becoming possible to post-process radiative transfer on individual galaxies (e.g. Pontzen et al. 2008). Because we want to study emission from the IGM as well as galaxies, we must instead adopt a simple correction based on density and temperature to approximate self-shielding. We adopt a similar approach to the one that was used to model the atomic to molecular transition above, using the thermal pressure as a proxy for the hydrostatic pressure. Only gas at a sufficiently high thermal pressure and for which the recombination time is shorter than the sound crossing time on kpc scales is assumed to recombine. Particles that satisfy the pressure and time-scale condition are considered to be fully self-shielded, and their neutral fraction is set to unity.

We will assume that the highest pressure regions which satisfy $\tau _{\textrm {rec}}<\tau _{\textrm {s}}$ have already provided $\rho_{{\rm H}_{\rm 2}}=1.8\times 10^7~h~M_{\odot}$ Mpc^-3 as discussed above. We subsequently calculate the atomic density as function of the thermal pressure threshold, as shown in Fig. 4. It is empirically found, that a threshold value of P/k = 155 cm^-3 K results in an H I density of $\rho=6.1\times 10^7~h~M_{\odot}$ Mpc^-3, that is similar to the derived value in Zwaan et al. (2003). We will adopt this threshold value for our further analysis.

The typical densities and temperatures where self-shielding becomes important are not accurately defined. When looking at Fig. 2, the typical temperatures and densities which satisfy our empirical thermal pressure criterion for local recombination are temperatures of $\sim$ 10⁴ K and densities of $\sim$ 0.01 cm^-3. These values agree well with various estimates from literature (e.g. Weinberg et al. 1997; Wolfire et al. 2003; Pelupessy 2005).

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{11811f04.eps} \end{figure}$

Figure 4:

The average H I mass density at z = 0 is plotted against the threshold thermal pressure, where atomic hydrogen is assumed to recombine from ionised, while also satisfying the condition that $\tau _{\textrm {rec}}<\tau _{\textrm {s}}$ (and accounting for a molecular density of $\rho_{{\rm H}_{\rm 2}}=1.8~\times~ 10^7~h~M_{\odot}$ Mpc^-3). At a pressure of P/k = 155 cm^-3 K (dashed line), $\rho_{\rm HI}=6.1~\times~10^7~h~M_{\odot}$ Mpc^-3 (dotted line), which is consistent with the H I density from Zwaan et al. (2003).

Open with DEXTER

3.4 Gridding method

To reconstruct the density fields, we have employed a grid-based method, in which the value of the density field is calculated at a set of locations defined on a regular grid. The mass of each particle is spread over this grid in accordance with a particular weighting function W, to yield

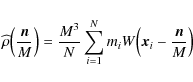$\begin{displaymath}\widehat{\rho}\Big(\frac{\vec{n}}{M}\Big) = \frac{M^3}{N} \sum_{i=1}^N m_i W \Big(\vec{x}_i - \frac{\vec{n}}{M} \Big) \end{displaymath}$

(9)

where $\vec{n} = (n_x,n_y,n_z)$ denotes the grid-cell, M is the number of cells of the grid in each dimension, N is the number of particles and m_i is the mass of particle i.

We adopt the weighting function directly from what is used for SPH in Gadget-2, namely a spline kernel defined by Monaghan & Lattanzio (1985):

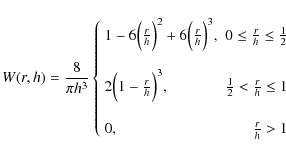$\begin{displaymath}W(r,h) = \frac{8}{\pi h^3} \left\{ \begin{array}{lr} 1-6\Big(... ...\\ & \\ 0\textrm{,} & \frac{r}{h} >1\\ \end{array} \right. \end{displaymath}$

(10)

where r is the distance from the position of a particle and h is the smoothing length for each particle (which in Gadget-2 is the radius that encloses 32 gas particle masses). Furthermore we set a limit to the size of the smoothing length: the smoothing length of a particle has to be at least 1.5 times the resolution of the grid-cells, which means that a particle is distributed over at least three grid-cells in each dimension. This adversely affects the highest density regions in the reconstructed field (when insufficient gridding resolution is employed), but gives a more realistic representation of resolved objects and transitions without shot noise or step functions. We note that our procedure explicitly conserves total mass.

4 Results

Reconstructed density fields are gridded in three dimensions, for the total hydrogen component (ionised plus neutral) the neutral component and the molecular component. This makes it possible to compare the distribution of the total and neutral hydrogen budget and permits determination of neutral fractions for the volume and column densities. Initially the full 32 h^-1 Mpc cubes is gridded with a cell size of 80 kpc. This allows visualisation of the distribution on large scales and determination of the average density of neutral hydrogen in the simulation volume $\bar{\rho}_{\rm {HI}}$ . The degree of clustering can be determined by looking at the two-point correlation function. However, this low resolution grid is not suitable to resolve the high density regions and small structures, as we will describe later. High density regions of the simulation volume were selected and gridded with a cell-size of 2 kpc. The H I column density distribution function and the H I mass function can be determined from these regions. The properties of the simulated H I gas will be described and the statistics will be compared with the statistical properties of observational data, mostly from the H I Parkes All Sky Survey (HIPASS) (Barnes et al. 2001).

Apart from gas or SPH particles, the simulations contain star and dark matter particles as well. We will adopt a relatively simple gridding scheme to reconstruct the distribution of stars and dark matter. This can be very useful to verify whether the stars, but especially the gas (or reconstructed H I) trace the distribution of Dark Matter.

$\begin{figure} \par\mbox{\includegraphics[width=7.2cm,clip]{11811f05.eps} \includegraphics[width=7.2cm,clip]{11811f06.eps} } \end{figure}$

Figure 5:

Left panel: H I distribution function after gridding to 80 kpc (dashed (red) line). The solid (blue) line corresponds to data gridded to a 2 kpc cell size. Filled dots correspond to the QSO absorption line data (Corbelli & Bandiera 2002). Right panel: combined H I distribution functions of the simulation, gridded to a resolution of 2 kpc (solid (blue) line) and 80 kpc (dashed (purple) line). Overlaid are distribution function from observational data of M 31 (Braun & Thilker 2004), WHISP (Swaters et al. 2002; Zwaan et al. 2005) and QSO absorption lines (Corbelli & Bandiera 2002) respectively. The reconstructed H I distribution function corresponds very well to all observed distribution functions.

Open with DEXTER

4.1 Mean H I density

The average H I density is an important property, as this single number gives the amount of neutral hydrogen that is reconstructed without any further analysis. The H I density is very well determined from the 1000 brightest HIPASS galaxies in Zwaan et al. (2003) They deduce an H I density due to galaxies in the local universe of $\bar{\rho}_{\rm {HI}} = (6.9 \pm 1.1)\times 10^7~h~M_\odot$ Mpc^-3or $\bar{\rho}_{\rm {HI}} = (6.1 \pm 1.0)\times 10^7~h~M_\odot$ Mpc^-3 when taking into account biases like selection bias, Eddington effect, H I self absorption and cosmic variance. From Rosenberg & Schneider (2002) a value of $\bar{\rho}_{\rm {HI}} = 7.1 \times 10^7~h~M_\odot$ Mpc^-3 can be derived for the average H I density in the universe. We will adopt the value of $\bar{\rho}_{\rm {HI}} = (6.1 \pm 1.0)\times 10^7~h~M_\odot$ Mpc^-3. The pressure thresholds for molecular and atomic hydrogen are tuned to reproduce this density as is described earlier in this paper.

4.2 H I distribution function

As mentioned above, the low and intermediate column densities $(N_{\rm {HI}} < 10^{19}$ cm^-2) do not have a very significant contribution to the total mass budget of H I.

For comparison with our simulation, the H I distribution function derived from QSO absorption line data will be used as tabulated in Corbelli & Bandiera (2002). For the QSO data the column density distribution function $f(N_{\rm {HI}})$ is defined such that $f(N_{\rm {HI}}){\rm d}N_{\rm {HI}}{\rm d}X$ is the number of absorbers with column density between $N_{\rm {HI}}$ and $N_{\rm {HI}} + {\rm d}N_{\rm {HI}}$ over an absorption distance interval ${\rm d}X$ . We derive $f(N_{\rm {HI}})$ from the statistics of our reconstructed H I emission. The column density distribution function in a reconstructed cube can be calculated from,

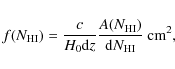$\begin{displaymath}f(N_{\rm {HI}}) = \frac{c}{H_0 {\rm d}z} \frac{A(N_{\rm {HI}})}{{\rm d}N_{\rm {HI}}} \textrm{ cm}^2, \end{displaymath}$

(11)

where ${\rm d}X = {\rm d}z H_0/c$ and $A(N_{\rm {HI}})$ is the surface area subtended by H I in the column density interval ${\rm d}N_{\rm {HI}}$ centred on $N_{\rm {HI}}$ .

As the simulations contain H I column densities over the full range between $N_{\rm {HI}} = 10^{14}$ and 10²¹ cm^-2, we can plot the H I column density distribution function $f(N_{\rm {HI}})$ over this entire range with excellent statistics, in contrast to what has been achieved observationally. In the left panel of Fig. 5 we overlay the H I distribution functions we derive from the simulations with the data values obtained from QSO absorption lines as tabulated by Corbelli & Bandiera (2002) (black dots). The horizontal lines on the QSO data points correspond to the bin-size over which each data point has been derived. Vertical error bars are not shown, as these have the same size as the dot. Around $N_{\rm {HI}} = 10^{19}$ cm^-2 there is only one data bin covering two orders of magnitude in column density, illustrating the difficulty of sampling this region with observations. This corresponds to the transition between optically thick and thin gas, where only a small increase in surface covering is associated with a large decrease in the column density.

The dashed (red) line corresponds to data gridded to a 80 kpc cell size. At low column densities the simulated distribution function agrees very well with the QSO absorption line data. The transition from optically thick to optically thin gas happens within just a few kpc of radius in a galaxy disk (Dove & Shull 1994). Clearly a reconstructed cube with a 80 kpc cell size does not have enough resolution to resolve such transitions. Some form of plateau can be recognised in the coarsely gridded data above $N_{\rm HI}=10^{16}$ cm^-2, however it is not a smooth transition. Furthermore because of the large cell size, no high column density regions can be reconstructed at all. The cores of galaxies have high column densities, but these are severely diluted within the 80 kpc voxels.

To circumvent these limitations, structures with an H I mass exceeding $5\times10^8$ $M_\odot$ in an 80 kpc voxel have been identified for individual high resolution gridding. This mass limit is chosen to match the mass-resolution of the simulation. The mass of a typical gas particle is $\sim$ $2.5 \times 10^7~M_\odot$ , when taking into account the abundance of hydrogen with respect to helium, we need at least 20 gas particles to form a $5\times10^8~M_\odot$ structure. As the neutral fraction is much less than one for most of the particles, the number of particles in one object is much larger. We find 719 structures above the mass limit and grid a 300 kpc box around each object with a cell size of 2 kpc.

We emphasise that gridding to a higher resolution does not mean that the physics is computed at a higher resolution. We are still limited by the simplified physics and finite mass resolution of the particles. A method of accounting for structure or clumping below the resolution of the simulation is described in e.g. Mellema et al. (2006). To derive the clumping factor, they have used another simulation, with the same number of particles, but a much smaller computational volume, and thus higher resolution. In our analysis, we accept that we cannot resolve the smallest structures, since we are primarily interested in the diffuse outer portions of galactic disks. We have chosen a 2 kpc voxel size, as this number represents the nominal spatial resolution of the simulation. The simulation has a gravitational softening length of 2.5 kpc h^-1, but note that the smoothing lengths can go as low as 10% of the gravitational softening length.

Distribution functions are plotted for simulated H I using the two different voxel sizes of 80 and 2 kpc in the left panel of Fig. 5. When using a 80 kpc voxel size, the reconstructed maps are unable to resolve structures with high densities, causing erratic behaviour at column densities above $N_{\rm {HI}} \sim 10^{17}$ cm^-2. When using the smaller voxel size of 2 kpc, there is an excellent fit to the observed data between about $N_{\rm {HI}} = 10^{15} \textrm{ and } 10^{20.5}$ cm^-2. The lower column densities are not reproduced within the sub-cubes (although they are in the coarsely-gridded full simulation cube), while the finite mass and spatial resolution of the simulation do not allow a meaningful distribution function to be determined above about $N_{\rm {HI}} = 10^{21}$ cm^-2.

Below $N_{\rm {HI}} = 10^{20}$ cm^-2 a transition can be seen with the distribution function becoming flatter. The effect of self-shielding is decreasing, which limits the amount of neutral hydrogen at these column densities. Around $N_{\rm {HI}} = 10^{17}$ cm^-2 the optical depth to photons at the hydrogen ionisation edge is equal to 1 (Zheng & Miralda-Escudé 2002). Self-shielding no longer has any effect below this column density and a second transition can be seen. Now the neutral fraction is only determined by the balance between photo-ionisation and radiative recombination. The distribution function is increasing again as a power law toward the very low column densities of the Lyman-alpha forest. The slope in this regime agrees very well with the QSO data. Note that the 2 kpc gridded data are slightly offset to lower occurrences compared to the 80 kpc gridded data. This is because we only considered the vicinity of the largest mass concentrations in the simulation for high resolution sampling. For the same reason the function is not representative below $N_{\rm {HI}} \sim 3 \times 10^{14}$ cm^-2, while for the full, 80 kpc gridded cube it can be traced to $N_{\rm {HI}} \sim 5 \times 10^{13}$ cm^-2. Of course, lower column density systems can be produced in these simulations when artificial spectra are constructed (e.g. Oppenheimer & Davé 2009; Davé & Tripp 2001), but our focus here is on the high column density systems that are well-described by our gridding approach.

The distribution functions after gridding to 2 kpc (solid line), and the low column density end of the 80 kpc gridding (dotted line) are plotted again in the right panel of Fig. 5, but now with several observed distributions overlaid. The high column density regime is covered by the WHISP data (Noordermeer et al. 2005; Swaters et al. 2002) in H I emission; a Schechter function fit to this data by Zwaan et al. (2005) is shown by the dashed line. The dash-dotted line shows H I emission data from the extended M 31 environment after combining data from a range of different telescopes (Braun & Thilker 2004). Since this curve is based on only a single, highly inclined system, it may not be as representative as the curves based on larger statistical samples. Our simulated data agrees very well with the various observed data sets. The distribution function indicates that there is less H I surface area with a column density of $N_{\rm {HI}} \sim 10^{19}$ cm^-2 than at higher column densities of a few times 10²⁰ cm^-2. This is indeed the case, which can be seen if the relative occurrence of different column densities is plotted. In Fig. 6 the fractional area is plotted (dashed line) as function of column density on logarithmic scale, which is given by:

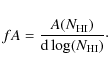$\begin{displaymath}fA = \frac{A(N_{\rm HI})}{{\rm d}\log(N_{\rm HI})}\cdot \end{displaymath}$

(12)

The surface area first increases from the highest column densities (which are poorly resolved in any case above 10²¹ cm^-2) down to a column density of a few times 10²⁰ cm^-2, but then remains relatively constant (per logarithmic bin). Only below column densities of a few times 10¹⁸ cm^-2 does the surface area per bin start to increase again, indicating that the probability of detecting emission with a column density near $N_{\rm {HI}} \sim 10^{17}$ cm^-2 is significantly larger compared to detecting emission with a column density of $N_{\rm {HI}} \sim 10^{19}$ cm^-2. Also of interest are plots of the cumulative H I mass and surface area.

$\begin{figure} \par\includegraphics[width=9cm,clip]{11811f07.eps} \end{figure}$

Figure 6:

Fractional area of reconstructed H I (dashed line, right-hand axis) and cumulated surface area (solid line, left-hand axis) plotted against column density on a logarithmic scale with a bin size of ${\rm d}\log(N_{\rm HI})=0.2$ . The probability of detecting emission with a column density near $N_{\rm {HI}} \sim 10^{17}$ cm^-2 is significantly larger than around $N_{\rm {HI}} \sim 10^{19.5}$ cm^-2. The cumulated surface area is normalised to that at a column density of $N_{\rm HI}=10^{16}$ cm^-2. At column densities of $N_{\rm {HI}} \sim 10^{17}$ cm^-2, the area subtended by H I emission is much larger than at a limit of $N_{\rm {HI}} \sim 10^{19.5}$ cm^-2, which is the sensitivity limit of most current observations of nearby galaxies.

Open with DEXTER

The solid line in Fig. 6 shows the total surface area subtended by H I exceeding the indicated column density. The plot is normalised to unity at a column density of $N_{\rm HI}=10^{16}$ cm^-2. At high column densities the cumulative fractional area increases only moderately. Below a column density of $N_{\rm {HI}} \sim 10^{18}$ cm^-2 there is a clear bend and the function starts to increase more rapidly. At column densities of $N_{\rm {HI}} \sim 10^{17}$ cm^-2, the area subtended by H I emission is much larger than at a limit of $N_{\rm {HI}} \sim 10^{19.5}$ cm^-2, which corresponds to the sensitivity limit of most current observations of nearby galaxies.

4.3 H I column density

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{11811f08.eps}\hspace*{4mm}... ...m}\includegraphics[width=7.2cm,clip]{11811f10.eps}\hspace*{3.6cm}}\end{figure}$

Figure 7:

Top left panel: column density of total H gas integrated over a depth of 32 h^-1 Mpc on a logarithmic scale, gridded to a resolution of 80 kpc. Top right panel: molecular hydrogen component. Only very dense regions in the total hydrogen component contain molecular hydrogen. Bottom panel: neutral atomic hydrogen component of the same region. In the neutral hydrogen distribution the highest densities are comparable to the densities in the total hydrogen distribution, but there is a very sharp transition to low neutral column densities as the gas becomes optically thin. Note the very different scales, the total hydrogen spanning only 2 orders of magnitude and the neutral hydrogen, eight.

Open with DEXTER

$\begin{figure} \par\mbox{\includegraphics[width=6cm]{figures/11811f11.eps}\hspac... ...}\hspace*{4mm} \includegraphics[width=5cm]{figures/11811f22.ps} } \end{figure}$

Figure 8:

Four examples of high density regions in the reconstructed data, gridded to a cell size of 2 kpc. The left panels show the total hydrogen, while the middle panels show only the neutral component. Some objects have many satellites, as in the top panels, while others are much more isolated. All examples have extended H I at column densities around $\log(N_{\rm HI}) = 16$ -17 cm^-2. In the right panel, the individual H I column density distribution function is shown for each of the examples. Black dots correspond to the QSO absorption line data (Corbelli & Bandiera 2002).

Open with DEXTER

In Fig. 7 column density maps are shown of the total and the neutral hydrogen distribution. The maps are integrated over the full 32 h^-1 Mpc depth of the cube, with the colour-bar showing logarithmic column density in units of cm^-2. The total hydrogen map reaches maximum values of $N_{\rm {H}} \sim 10^{21}$ cm^-2, while the connecting filaments have column densities of approximately an order of magnitude less. In the intergalactic medium, the column densities are still quite high, $N_{\rm {H}} \sim 10^{19}$ cm^-2, yielding a very large mass fraction when the large surface area of the intergalactic medium is taken into account.

In the column density map of neutral hydrogen it can be seen that it is primarily the peaks which remain. At the locations of the peaks of the total hydrogen map, we can see peaks in the H I map with comparable column densities, that correspond to the massive galaxies and groups. The filaments connecting the galaxies can still be recognised, but with neutral column densities of the order of $N_{\rm {HI}} \sim 10^{16}$ cm^-2. Here the gas is still relatively dense, but not dominated by self-shielding, resulting in a lower neutral fraction. In the intergalactic regime, the neutral fraction drops dramatically. The gas is highly ionised with neutral columns of only $N_{\rm {HI}} \sim 10^{14}$ cm^-2, yielding only a very small neutral mass contribution.

Figure 8 shows similar maps chosen from several high-resolution regions, gridded to 2 kpc instead of 80 kpc. The left panels show a column density map of all the gas, while in the middle panels the H I column densities are plotted. The right panels show the H I column density distribution function of the individual examples. The most complete distribution function is obtained by summing the distribution functions of all the individual objects, but even the individual distribution functions already display the general trend of a flattening plateau around $N_{\rm {HI}} \sim 10^{19}$ cm^-2. Some objects have just a bright core with extended emission, like the second example from the top. There are many objects with small diffuse companions with maximum peak column densities of $N_{\rm {HI}} \sim 10^{18}$ cm^-2. These companions are typically 20-40 kpc in size and are connected with filaments that have column densities of $N_{\rm {HI}} \sim 10^{17}$ cm^-2 or even less. Comparing the plots containing all the hydrogen and just the neutral hydrogen it can be seen that the edge between low and high densities is much sharper for the neutral hydrogen. The surface covered by column densities of $N_{\rm {HI}} \sim 10^{17}$ cm^-2 is much larger than the surface covered by column densities of $N_{\rm {HI}} \sim 10^{19}$ cm^-2.

4.3.1 Neutral fraction

The neutral fraction is plotted in a particularly instructive way in Fig. 9. Neutral fraction of the hydrogen gas is plotted against H I column density, where the colour-bar represents the relative likelihood on a logarithmic scale of detecting a given combination of neutral column and neutral fraction. The most commonly occurring conditions are a neutral column density around $N_{\rm {HI}} \sim 10^{14}$ cm^-2 with a neutral fraction of $\sim$ 10^-5, representing Ly $\alpha$ forest gas. The cut-off at low column densities is artificial, owing to our gridding scheme.

At high densities, $N_{\rm {HI}} > 10^{20}$ cm^-2, the gas is almost fully neutral and just below $N_{\rm {HI}} \sim 10^{19}$ cm^-2, the neutral fraction starts to drop very steeply below the 10 percent level. This is exactly the column density that is considered to be the ``edge'' of H I galaxies, that defines the border between optically thick and thin gas. This transition from high to low neutral density happens on very small scales of just a few kpc (Dove & Shull 1994). The surface area with column densities in the range from $N_{\rm {HI}} \sim 10^{17}$ to 10¹⁹ cm^-2 is relatively small. At lower column densities, the probability of detecting H I in any given direction increases. The well-defined correlation of neutral fraction with neutral column for $N_{\rm {HI}} > 10^{16}$ cm^-2 defines a straightforward correction for total gas mass accompanying an observed neutral column density.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{11811f23.eps} \end{figure}$	Figure 9: Neutral fraction plotted against H I column density. The colour-bar represents the probability of detecting a certain combination of H I column density and neutral fraction on logarithmic scale. At the highest densities $N_{\rm {HI}} > 10^{20}$ cm^-2, the neutral fraction is almost unity. Column densities around $N_{\rm {HI}} \sim 10^{19}$ cm^-2have the smallest detectionprobability.
Open with DEXTER

In Fig. 10 the cumulative mass is plotted as function of total hydrogen column density (left panel) and the column density of the H I gas (right panel). Note that the vertical scale is different in the two panels. The plot is divided in different regions, the galaxies or Damped Lyman- $\alpha$ Absorbers (DLA) are coloured light grey. In neutral hydrogen, these are the column densities above log $(N_{\rm {HI}})$ = 20.3. Lower column densities belong to the Super Lyman Limit systems (SLLS), or sub-DLAs. In the plot showing the neutral hydrogen an inflection point can be seen at a column density of log $(N_{\rm {HI}})$ = 19. This is where the effect of self shielding starts to decrease rapidly and the Lyman Limit regime begins. At the lower end, below column densities of log $(N_{\rm {HI}})$ = 16 is the Lyman alpha forest, which is coloured dark grey. As can be seen there is a huge difference in mass contribution for the different phases, when comparing the neutral gas against the total gas budget. In H I, about 99 percent of the mass is in DLAs, Lyman Limit Systems account for about 1 percent of the mass and the Lyman alpha forest contributes much less than a percent. When looking at the total gas mass budget all three components (DLAs, LLSs and the Ly- $\alpha$ forest) have approximately the same mass fraction.

$\begin{figure} \par\mbox{ \includegraphics[width=8cm,clip]{11811f24.eps}\hspace*{4mm} \includegraphics[width=8cm,clip]{11811f25.eps} } \end{figure}$

Figure 10:

Left panel: cumulative mass of total hydrogen as function of column density, the different phases are shown with different colours. The Ly $\alpha$ forest, the Lyman Limit System and galaxies have approximately the same mass component when considering all the gas. Right panel: cumulative mass of neutral atomic hydrogen as function of column density. Although the surface covered by the LLSs is large, it contains only 1% off all the neutral gas mass, while about 99% resides in the galaxies.

Open with DEXTER

4.4 Two-point correlation function

The two-point correlation function measures the degree of clustering of galaxies in the spatial direction $(\xi (r))$ , which relates directly to the power spectrum through a Fourier transform (e.g. Davis & Huchra 1982; Groth & Peebles 1977). The spatial two-point correlation function is defined as the excess probability, compared with that expected for a random distribution, of finding a pair of galaxies at a separation r_1,2. For H I, the clustering is weaker compared to optical galaxies (Meyer et al. 2007). On scales between $\sim$ 0.5 kpc and 12 Mpc, the correlation function for optical galaxies has been determined in SDSS (Zehavi et al. 2005) and 2dFGS (Norberg et al. 2002). For the H I-rich galaxies in the HIPASS catalogue, a scale length is obtained of $r_0 = 3.45 \pm 0.25~h^{-1}$ Mpc and a slope of $\gamma = 1.47 \pm 0.08$ .

In the past, several estimators have been given for the two-point correlation function, we will use the Landy & Szalay estimator as described in Landy & Szalay (1993) as this estimator is used in Meyer et al. (2007) to determine the correlation for H I galaxies. This estimator is given by:

$\begin{displaymath}\xi_{\rm {LS}} = \frac{1}{RR}[DD - 2DR + RR ] \end{displaymath}$

(13)

where DD are the galaxy-galaxy pairs, RR the random-random pairs and DR the galaxy-random pairs. This estimator has to be normalised with the number of correlations in the simulated and random distributions:

$\begin{displaymath}\xi_{\rm {LS}} = \frac{1}{RR}\Big[\frac{DD}{(n_{\rm d}n_{\rm d}-1))/2} - \frac{2DR}{n_{\rm r} n_{\rm d}} + RR \Big] \end{displaymath}$

(14)

where $n_{\rm d}$ is the number of detections or simulated objects and $n_{\rm r}$ is the number of galaxies in the random sample.

In Fig. 11 the two-point correlation function is plotted; the black dots represent the values obtained from the simulation, while the dashed red line corresponds to the correlation function that is fit to galaxies in the HIPASS catalogue by Meyer et al. (2007). The solid line is our best fit, with a scale length of $r_0 = 3.3 \pm 0.2~h^{-1}$ Mpc and a slope of $\gamma = 1.7 \pm 0.2$ , only data points where the radius is smaller than 6 Mpc have been used for the fit.

There is very good correspondence between the simulated and observed H I-correlation functions on scales between $\sim$ 0.5 Mpc and $\sim$ 5 Mpc. Accuracy at smaller scales is limited by the finite resolution of the simulation. On the other hand, the representation of large scales is limited by the physical size of the box. In a 32 h^-1 Mpc box, the largest well-sampled structures are about 5 Mpc in size. This difference is not surprising, because Meyer et al. (2007) are able to sample structures up to 10 Mpc, given their significantly larger survey volume. Meyer et al. (2007) also looked at a limited sample of galaxies, applying the parameter cuts $M_{\rm HI} > 10^{9.05} M_{\odot}$ and D < 30 Mpc. This limited sample is very similar to our sample of simulated objects and the power law parameters in this case are $r_0 = 3.2 \pm 1.4~h^{-1}$ Mpc and $\gamma = 1.5 \pm 1.1$ . Although the errors are larger, the results are very similar to the full sample and in excellent agreement with our simulations.

4.5 H I mass function

The H I Mass Function $\theta(M_{\rm {HI}})$ is defined as the space density of objects in units of h³Mpc^-3. For fitting purposes a Schechter function (Schechter 1976) can be used of the form:

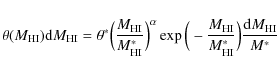$\begin{displaymath}\theta(M_{\rm {HI}}){\rm d}M_{\rm {HI}} = \theta^*\Big(\frac{... ...m {HI}}}{M_{\rm {HI}}^{*}}\Big)\frac{{\rm d}M_{\rm {HI}}}{M^*} \end{displaymath}$

(15)

characterised by the parameters $\alpha$ , $M^{*}_{\rm {HI}}$ and $\theta^*$ , which define the slope of the power law, the H I mass corresponding to the ``knee'' and the normalisation respectively. In a logarithmic form the H I Mass function can be written as:

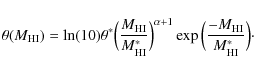$\begin{displaymath}\theta(M_{\rm {HI}}) = \ln(10)\theta^*\Big(\frac{M_{\rm {HI}}... ...lpha+1}\exp\Big(\frac{-M_{\rm {HI}}}{M^*_{\rm {HI}}}\Big)\cdot \end{displaymath}$

(16)

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{11811f26.eps} \end{figure}$	Figure 11: Two-point correlation function of H I-rich objects in our simulation, contrasted with a power-law fit to the observed relation of Meyer et al. (2007).
Open with DEXTER

The reconstructed structures in our high resolution grids can be used to determine a simulated H I Mass Function for structures above $\sim$ $5\times10^8$ $M_\odot$ . The result is plotted in the left panel of Fig. 12, where the H I Mass Function is shown with a bin size of 0.1 dex. Overlaid is the best fit to the data, the fitting parameters that have been used are $\theta^* = 0.059~\pm~0.047$ , $\log(M^*_{\rm {HI}}) = 9.2 ~\pm~ 0.3$ and $\alpha = -1.16 \pm 0.45$ . Note that in this case the value of $\alpha$ is not very well-constrained, as this parameter defines the slope of the lower end of the H I Mass Function, but our simulation is unable to sample the mass function below a mass of $M_{\rm HI} \approx 5\times10^8 M_{\odot}$ . The result is compared with the H I mass function from Zwaan et al. (2003) (dash-dotted line). The reconstructed mass function corresponds reasonably well with the mass functions obtained from galaxies in HIPASS around M^*. At masses around 10¹⁰ $M_\odot$ , the error bars are very large due to small number statistics. A much larger simulation volume is required to sample this regime properly. There is a hint of an excess in the simulation near our resolution limit, this may simply reflect cosmic variance and will be addressed in future studies. Zwaan et al. (2003) compared four different quadrants of the southern sky and found that at $M_{\rm HI} \sim 10^9 M_{\odot}$ the estimated space density varies by a factor of about three, which is comparable to the factor $\sim$ 2 difference we see between the simulation and observations.

4.5.1 H₂ mass function

The H₂ Mass Function can be determined in a similar way as the H I Mass Function. The result is shown in the right panel of Fig. 12 where the simulated data points are fitted with a Schechter function. Our best fit parameters are $\theta^*$ = $0.036~\pm~0.036$ , $\log(M^*_{\rm {{\rm H}_{\rm 2}}}) = 8.7 \pm 0.3$ and $\alpha = -1.01 ~\pm~0.57$ . At the high end of the mass function the results are affected by low number statistics. The simulated fit is compared with the fits as determined by Obreschkow & Rawlings (2009) (dashed line) and Keres et al. (2003) (dash-dotted line). There is very good agreement over the full mass range.

In Fig. 13 the derived H₂ masses are plotted as function of H I mass. The dashed vertical line represents the completeness limit of H I masses. The data can be fitted using a power law (solid line) which looks like $M_{{\rm H}_{\rm 2}} = (M_{\rm HI}/m_0)^\beta$ with a scaling parameter of $m_0=158\pm43$ and a slope of $\beta = 1.2\pm 0.1$ .

$\begin{figure} \par\mbox{\includegraphics[width=8.2cm,clip]{11811f27.eps} \includegraphics[width=8.2cm,clip]{11811f28.eps} } \end{figure}$

Figure 12:

Left panel: H I Mass Function of the simulated data (black dots) with the best-fit Schechter function (solid black line), compared with the HIMF from Zwaan et al. (2003) (dash-dotted red line). Our best fit line is dashed below $10^9~M_{\odot}$ , because there are no data points there and the function is only an extrapolation. Right panel: H₂ Mass Function of the simulated data (black dots) and the best fit, compared with the H₂MF from Keres et al. (2003) (dash-dotted (blue) line) and Obreschkow & Rawlings (2009) (dashed (red) line). Both simulated Mass Functions show agreement with observations over about a decade in mass.

Open with DEXTER

4.6 Stars, dark matter and molecular hydrogen

In addition to the SPH-particles, the simulations also contain dark matter and stars. The distribution of these components can be reconstructed and compared with the distribution of neutral hydrogen. For reconstructing the dark matter and stars a very simple adaptive gridding scheme has been used. This gridding scheme was adopted, because the dark matter and star particles do not have a variable smoothing kernel like the gas particles. They do have a smoothing kernel defined by the softening length of 2.5 kpc h^-1, however this is a fixed value. The gridding method as described in Sect. 3.3 using a spline kernel can not be used for this reason. Exactly the same regions have been gridded as those previously determined H I objects. First the objects have been gridded with a cell size of 10 kpc using a nearest grid-point algorithm. The resulting moment maps have been used to determine which high density regions contain many particles. In a second step the particles have been gridded to five independent cubes using a 2 kpc cell size. Based on the density of simulation particles in the 10 kpc resolution cube, an individual particle is assigned to one of five different cubes for gridding. The density threshold is determined by the number of particles in the 10 kpc resolution cube integrated along the line of sight. The threshold numbers are 2, 6, 18, 54 and everything above 54 particles respectively. The five cubes are integrated along the line of sight and smoothed using a Gaussian kernel with a standard deviation of 7, 5, 3.5, 2.5 and 1.5 pixels of 2 kpc respectively. Finally the five smoothed maps are added together. These smoothing kernels where chosen to insure that each individual cube covering a different density regime has a smooth density distribution, but preserves as much resolution as practical.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{11811f29.eps} \end{figure}$	Figure 13: Derived H₂ masses are plotted against H I masses for individual simulated objects. The distribution can be fit using a simple power law (solid (red) line), although the scatter is very large. The dashed vertical line represents the sample cut-off for H I masses in the simulated data.
Open with DEXTER

In Fig. 14 four examples are shown of the dark matter and stellar distributions overlaid on the of H I column density maps. The right panels in this image show the contours of molecular hydrogen. The stars are concentrated in the bright and dense parts of the H I objects corresponding to the bulges and disks of galaxies. The third example shows an edge-on extended gas disk (its thickness is likely an artefact of our numerical resolution). The neutral hydrogen is much more extended than the stars, and the smaller, more diffuse H I clouds do not have a stellar counterpart in general. Many objects have H I satellites or companions, as in the first two examples. These companions or smaller components do not always have a stellar or molecular counterpart, although the H I column densities can reach high values up to $N_{\rm HI} \sim 10^{20}$ cm^-2 as seen in Galactic high velocity clouds.

Interestingly, these H I clouds only occasionally trace dark matter substructures, hence in many cases they are not obvious large-scale accretion events (since the most massive accreting clumps should be accompanied by dark matter). The origin of these diffuse clouds, perhaps analogous to high velocity clouds, may be from a ``halo fountain" of gas cycling in and out of galaxies owing to galactic outflows, as speculated in Oppenheimer & Davé (2008), or represent more diffuse accretion from the extended environment. Studying the kinematics and metallicities of these clouds may reveal signatures of their origin. In the future we plan to investigate such signatures in the simulations to assess how observations of diffuse H I clouds around galaxies can inform our understanding of the processes of galaxy assembly.

$\begin{figure} \par\mbox{\includegraphics[width=6cm]{figures/11811f30.eps} \incl... ...11f40.eps} \includegraphics[width=6cm]{figures/11811f41.eps} } \par \end{figure}$

Figure 14:

Column density maps of four reconstructed objects as seen in neutral hydrogen with contours of Dark Matter ( left panels), Stars ( middle panels) and molecular hydrogen ( right panels). For both the Dark Matter and the stars contour levels are at N = 3, 5, 10, 20, 30, 50 and $100 \times 10^6~M_{\odot}$ kpc^-2. For the molecular hydrogen contours are drawn at $N_{{\rm H}_{\rm 2}}= 10^{18}$ , 10¹⁹, 10²⁰ and 10²¹ cm^-2. Stars are concentrated in the very dense parts of the H I objects, dark matter is more extended, however the extended H I does not always trace the dark matter. The H I satellites or companions are within the same Dark Matter Halo, but do not always contain stars.

Open with DEXTER

5 Discussion

To make observational predictions based on numerical simulations, the first essential step is to establish that the simulation can adequately reproduce all observational constraints. We have carried out a critical comparison of our simulated H I data with observations using a wide range of statistical measures. Essential in creating simulated data is the minimisation of the number of free parameters over and above the many that are already inherent in the simulation; (Oppenheimer & Davé 2008,2006). In our analysis, the only additional assumptions we make are that the transitions from ionised to atomic and from atomic to molecular hydrogen can be described by a simple threshold effect at two different values of the thermal pressure, while demanding that the recombination time be less than the sound-crossing time. The threshold values are determined by fixing the average H I density and the density ratio $\Omega_{{\rm H}_{\rm 2}}/\Omega_{\rm HI}$ at z = 0 to those determined observationally. In choosing this simple prescription we are strongly limited by current numerical capabilities. Although we did not solve the complete radiative transfer problem, we do get quite complex behaviour emerging. The range of threshold values we explored are consistent with expected values in literature.

The statistics of the reconstructed and observed H I distributions agree quite well, making it plausible that the associated H I structures in the simulation may be similar to those occurring in nature. The simulation cannot reproduce structures that resemble actual galaxies in detail. Besides the finite mass resolution of the SPH-particles of $\sim$ $10^7~M_\odot$ , there are the inevitable limitations on the included physical processes and their practical implementation. Nonetheless, we may begin to explore the fate of partially neutral gas in at least the diffuse outskirts of major galaxies.

Despite the limitations, the simulations can reproduce many observed statistical aspects of H I in galaxies, which is very encouraging for further exploration of this approach. The adopted self-shielding threshold provides good results for this one simulation. Future work will test the variations that are encountered with different feedback mechanisms. The method can also be applied to look at the evolution of neutral hydrogen with redshift. Furthermore, mock observations can be created to make predictions for what future telescopes should detect. This is particularly relevant for assessing performance requirements for the various facilities now under development with a strong H I focus, such as the Square Kilometre Array (SKA) and many of the SKA pathfinders.

5.1 Resolution effects

Table 1: Sensitivity limits for four different telescopes for an assumed line-width of 25 km s^-1 after a total integration time of 500 h to image an area of 30 square degrees.

$\begin{figure} \par\mbox{\includegraphics[angle=270,width=6cm]{figures/11811f42.... ...} \includegraphics[angle=270,width=6cm]{figures/11811f44.eps} } \par\end{figure}$	Figure 15: Left panel: simulated object at a distance of 6 Mpc, with a 6 kpc intrinsic beam size. Middle panel: simulated object smoothed to a 8.7 kpc beam size, corresponding to the ASKAP beam at 6 Mpc. Right panel: noise is added corresponding to the ASKAP sensitivity limit after a 500 h observation of 30 square degrees.
Open with DEXTER

Simulations are limited by their volume and the mass resolution of the particles (over and above the limitations that result from incomplete physics). Although we are able to reconstruct structures of several Mpc in scale, the simulated volume is relatively small. To be able to reconstruct the largest structures encountered in the universe, and effectively overcome cosmic variance, a simulated volume is needed that is about about 300 (rather than 32) Mpc on a side. In the current volume, the most massive structures are suffering from low number statistics. A drawback of using a larger volume is that the mass resolution of individual particles decreases rapidly, making it impossible to resolve structures on even multi-kilo-parsec scales. The approach we have employed to approximate the effects of self-shielding is extremely simple. The actual processes acting on sub-kilo-parsec scales are undoubtedly much more complex. Clumping will occur on the scales of molecular clouds, which will dramatically increase the local densities. The threshold thermal-pressure we determine to approximate the atomic to molecular hydrogen transition only has possible relevance on the kilo-parsec scales of our modelled gas particles. At the smaller physical scales where the transition actually occurs, the physical pressures will likely be substantially different.

We note that realistic simulations of cosmological volumes are extremely challenging, and that even the current state-of-the-art is not particularly successful at reproducing objects that resemble observed galaxies in great detail. The simulation we employ represents a very good compromise between simulations focused on larger and smaller scales. We are mainly interested in the diffuse intergalactic structures on multi-kilo-parsec scales, that would be observable when doing 21-cm H I observations with sufficient sensitivity. We have enough resolution to map and resolve these structures and to reconstruct the extended environments of galaxies and galaxy groups. Our simulation is not suitable for making predictions about the inner cores of galaxies or resolving the star formation process in molecular clouds.

Future work will test our analysis method on both larger and smaller scales. Simulations in a larger volume can provide a more sensitive test of the reconstructed H I Mass function and the two-point correlation function. Simulations in a smaller volume will probably require a more advanced method of modelling the atomic to molecular hydrogen transition. However, substantial insights into the more diffuse phenomena, such as accretion and feedback processes around individual galaxies, are very likely within reach.

5.2 Future observations

This simulation can not only be used for getting a better understanding of the H I distribution, especially at low column densities, but is also very suitable for making predictions for future observations. Currently many radio telescopes are being built as pathfinders toward the SKA. A few examples are the Australia SKA Pathfinder (ASKAP), the Allen Telescope Array (ATA), Karoo Array Telescope (MeerKAT) and the Low frequency array (LOFAR), and many more. Although the SKA will be the final goal, each of these telescopes is a good detector on its own and is planned to be operational in the relatively near future. Of course each telescope will have different characteristics, but in general it will be possible to do surveys deeper, faster and over a broader bandwidth.

We will discuss the simulated maps of two current single dish telescopes, Parkes and Arecibo, and compare these with the capabilities of two future telescopes, the ASKAP and the SKA. Parkes and Arecibo are both single dish telescopes with a multi-beam receiver that have recently been used to do large area surveys, the H I Parkes All Sky Survey (HIPASS, Barnes et al. 2001) and the Arecibo Legacy Fast ALFA Survey (ALFALFA Giovanelli et al. 2005).

To make a fair comparison, all four telescope will get 500 h of observing time to map 30 square degrees of the sky. These numbers are chosen as 500 h is a reasonable time scale to make a deep image and a 30 square degree field is needed to map the extended environment of a galaxy. Furthermore, 30 square degrees is the planned instantaneous field-of-view of ASKAP.

We focus on two cases that illustrate the capabilities of present and upcoming telescopes. In the first example, observations will be simulated at a distance where the beam of the telescopes has a physical size of 25 kpc. This approximate beam size is needed to resolve diffuse filaments and extended companions from the simulation. In the second example observations will be simulated at a fixed distance of 6 Mpc, which is the limiting distance for the Parkes telescope according to the above argument.

Right ascension and declination coordinates are added according to the distance, centred on an RA of 12 h and a Dec of 0 degrees. For each telescope the sensitivity is determined that can be achieved using the given conditions. The technical properties are listed in Table 1. For the Parkes telescope we use the sensitivity that is achieved when re-reducing HIPASS data (Popping 2009, in prep.), which corresponds to $\sim$ 10 mJy/Beam over 26 km s^-1 for a typical HIPASS field after integrating over $\sim$ 560 s per square degree. For the Arecibo telescope we used the sensitivity of the Arecibo Galaxy Environment Survey (AGES) (Auld et al. 2006) assuming 0.95 mJy/beam over 10 km s^-1 after integrating for 10 h per square degree. The expected sensitivities for ASKAP are described in the initial Array Configuration paper which can be found on http://www.atnf.csiro.au/projects/askap/newdocs/configs-3.pdf. ASKAP is expected to achieve a sensitivity of 7.3 mJy/beam over 21 km s^-1 after one hour of integration time. For the SKA we assume a $A_{\rm eff}/T_{\rm sys} = 2000$ m² K^-1 at 2.5 arcmin resolution, which is 20 times higher than ASKAP. Furthermore we assume a field of view similar to ASKAP, 30 square degrees instantaneous.

All the flux densities can be converted into brightness temperature using the equation:

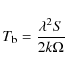$\begin{displaymath}T_{\rm b} = \frac{\lambda^2S}{2k\Omega} \end{displaymath}$

(17)

where $\lambda$ is the observed wavelength, S is the flux density, k the Boltzmann constant and $\Omega$ is the beam solid angle of the telescope. When using the 21-cm line of H I, this equation can be written as:

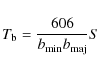$\begin{displaymath}T_{\rm b} = \frac{606}{b_{\rm min}b_{\rm maj}}S \end{displaymath}$

(18)

where $b_{\rm min}$ and $b_{\rm maj}$ are respectively the beam minor and major axis in arcsec and S is the flux in units of mJy/Beam. The integrated 21cm line intensity can directly be converted into an H I column density using:

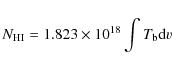$\begin{displaymath}N_{\rm HI} = 1.823 \times 10^{18} \int T_{\rm b} {\rm d}v \end{displaymath}$

(19)

with $[N_{\rm HI}]$ = cm^-2, $[T_{\rm b}]$ = K and $[{\rm d}v]$ = km s^-1.

The second column in Table 1 gives the beam size of each telescope, the third column gives the distance at which the beam has a physical size of 25 kpc, and the fourth column gives the physical beam size at a distance of 6 Mpc. The sensitivities in column five are converted to a column density limit when sampling a line of approximately 25 km s^-1 width in the last column. We assume that in any analysis only the channels will be selected containing diffuse emission and that the line width of diffuse regions will be of the order of 25 km s^-1. Galaxies can have a much larger line-width, however detecting these is not an observational challenge. The reconstructed maps have an intrinsic resolution of 2 kpc with a minimum smoothing kernel size of three pixels. This yields an initial beam size of 6 kpc, which will be smoothed to the appropriate beam size of each telescope, corresponding to the simulated distance. Using the calculated sensitivity limits random Gaussian noise is generated and added to the maps. The steps are shown in Fig. 15, the left panel shows the original reconstructed column density map that is smoothed to the beam of ASKAP in the middle panel. At this stage most of the diffuse and extended emission can still be recognised. Noise is added in the right panel, most of the diffuse emission disappears in the noise.

$\begin{figure} \par\mbox{\includegraphics[angle=270,width=7.4cm,clip]{11811f45.e... ...4mm} \includegraphics[angle=270,width=7.4cm,clip]{11811f48.eps} }\end{figure}$

Figure 16:

Simulated observations of the same object at a distance at which the beam size corresponds to 25 kpc for Parkes ( top left), Arecibo ( top right), ASKAP ( bottom left) and the SKA ( bottom right). All contours begin at a 3 $\sigma$ level, after a 500 h observation of a 30 square degree field with each telescope. Every subsequent contour level is a factor 3 higher than the previous one. Note that the angular scale is different in each panel.

Open with DEXTER

$\begin{figure} \par\mbox{\includegraphics[angle=270,width=7.4cm,clip]{11811f45.e... ...{4mm} \includegraphics[angle=270,width=7.4cm,clip]{11811f51.eps} }\end{figure}$

Figure 17:

Simulated observations of the same object at a fixed distance of 6 Mpc for Parkes ( top left), Arecibo ( top right), ASKAP ( bottom left) and the SKA ( bottom right). Contour levels start at a 3 $\sigma$ level after 500 h observation of a 30 square degree field. For Parkes every subsequent contour is a factor 3 higher than the previous one. For ASKAP and Arecibo, the contours interval is a factor 7. For the SKA the contours start a $4 \times 10^{16}$ cm^-2 and increase by a factor 6. Parkes is not really competitive in detecting substructures at this distance. The other telescopes all have sufficient resolution, however only the SKA is sensitive enough to detect the faint diffuse sub-structures.

Open with DEXTER

In Fig. 16 the same field is shown as in Fig. 15, placed at a distance where the beam has a size of 25 kpc. This means that the object looks similar for all four telescopes as it fills the same number of beams, although there is a big difference in angular scale.

For each panel contour levels are drawn starting at 3 $\sigma$ and increasing as noted in the figure caption, so the actual values are different in each panel, but can be determined using the sensitivity limits given in Table 1. All panels look very similar, as most of the structure and substructure of the original map is smoothed into two large blobs and essentially all the diffuse structures are lost in the noise. Only with the SKA can some extended contours still be recognised at the top of the left object. However, it is very difficult to distinguish extended emission from companions, unless the companions are clearly separated by at least a beam width from the primary object.

An example of this can be seen in Fig. 17 where the same object is shown simulated with four telescopes but now at a similar distance of 6 Mpc. A smaller beam size now yields higher resolution and more detected structure. The differences between the four panels are now obvious. Observed with Parkes in the top left panel the object has essentially no resolved structure. Clearly the beam size is too large and only suitable for very nearby galaxies, closer than 6 Mpc. Arecibo, with a much smaller beam, can resolve the inner core of the object and can just detect the brightest companion. Again the contour levels have values starting at 3 $\sigma$ , so the outer contour in the top right panel corresponds to $9~\times~10^{17}$ cm^-2. ASKAP has a very similar sensitivity limit as Arecibo with a comparable beam size. However it is notable that it reaches Arecibo sensitivities with a much smaller collecting area. Furthermore, these deep integrations have not really been explored, so the given sensitivities are theoretical limits. It is very likely that correcting for systematic effects, like the shape of the spectral bandpass, will be more achievable with an interferometer like ASKAP rather than a large single dish telescope. In the SKA image essentially all companions can be clearly distinguished down to a contour level of $\sim$ $4 \times 10^{16}$ cm^-2. Note that this value is lower than the 3 $\sigma$ value in Table 1, this is because the beam size of the SKA is smaller than the beam size of the simulation at a distance of 6 Mpc. To adjust for this we adopt the beam size of the reconstructed data and smooth the noise to this larger beam size. In this case the noise value will decrease, resulting in a higher sensitivity of $1.3 \times 10^{16}$ cm^-2.

6 Conclusion

We have used a hydrodynamic simulation to predict the neutral hydrogen distribution in the universe. The simulation employs a random cube of 32 h^-1 Mpc on a side at redshift zero, with an SPH mass resolution of $\sim$ $10^7~M_\odot$ . The physics in the simulation includes sub-grid treatments of star formation and feedback mechanisms.

We have developed a method to extract the neutral hydrogen component from the total gas budget. At low volume densities the balance is calculated between photo-ionisation and radiative recombination. For high densities a correction has to be applied for self-shielding, as the gas becomes optically thick for ionising photons. In the densest regions, the atomic hydrogen is turned into molecular hydrogen that will subsequently form stars. The molecular hydrogen and the self-shielding transition are both modelled by a critical thermal pressure. Above the first threshold limit (P/k = 155 cm^-3 K), the gas is assumed to recombine and the neutral fraction is set to unity. At even higher pressures (P/k = 810 cm^-3 K), the atomic hydrogen is assumed to become molecular hydrogen, so the atomic fraction becomes zero. These processes only apply to simulated particles for which the recombination time is shorter than the sound-crossing time on kpc scales. The two threshold pressures are tuned to reproduce the observed average H I density of $\bar{\rho}_{\rm HI} = 6.1 \times 10^7~h~M_{\odot}$ Mpc^-3 and an assumed molecular density of $\bar{\rho}_{{\rm H}_{\rm 2}} = 1.8 \times 10^7~h$ $M_\odot$ Mpc^-3, corresponding to a molecular to atomic density ratio of $\eta_{z=0}=0.3$ .

A wide range of statistical comparisons have been made between the reconstructed H I distribution and existing observational constraints including: the two-point correlation function, the H I mass function and the H I column density distribution. There is agreement between all these statistical measures of the observations and the simulations, which is a very encouraging result. Based on this agreement, the simulated H I distribution may be a plausible description of the H I universe, at least on the intermediate spatial scales that are both well-resolved and well-sampled.

We also compare the distribution of neutral and molecular hydrogen with the distribution of dark matter and stars in the simulation. Massive H I structures generally have associated stars, but the more diffuse clouds do not contain large stellar components or in many cases even concentrations of dark matter. The method to extract neutral hydrogen from an SPH output cube can be applied to other simulations, to allow comparison of different models of galaxy formation. Furthermore, the results can be used to create mock observations and make predictions for future observations. This preliminary study shows that as H I observations of diffuse gas outside of galactic disks continue to improve, simulations will play a vital role in guiding and interpreting such data to help us better understand the role that H I plays in galaxy formation.

Acknowledgements

We would like to thank Thijs van der Hulst for useful discussions and comments on the original manuscript. We appreciate the constructive comments of the anonymous referee.

References

Auld, R., Minchin, R. F., Davies, J. I., et al. 2006, MNRAS, 371, 1617 [NASA ADS] [CrossRef] (In the text)
Barnes, D. G., Staveley-Smith, L., de Blok, W. J. G., et al. 2001, MNRAS, 322, 486 [NASA ADS] [CrossRef] (In the text)
Blitz, L., & Rosolowsky, E. 2004, ApJ, 612, L29 [NASA ADS] [CrossRef] (In the text)
Blitz, L., & Rosolowsky, E. 2006, ApJ, 650, 933 [NASA ADS] [CrossRef] (In the text)
Boulares, A., & Cox, D. P. 1990, ApJ, 365, 544 [NASA ADS] [CrossRef] (In the text)
Braun, R., & Thilker, D. A. 2004, A&A, 417, 421 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Cen, R., & Ostriker, J. P. 1999, ApJ, 514, 1 [NASA ADS] [CrossRef]
Corbelli, E., & Bandiera, R. 2002, ApJ, 567, 712 [NASA ADS] [CrossRef] (In the text)
Davé, R., & Tripp, T. M. 2001, ApJ, 553, 528 [NASA ADS] [CrossRef] (In the text)
Davé, R., Hernquist, L., Katz, N., & Weinberg, D. H. 1999, ApJ, 511, 521 [NASA ADS] [CrossRef]
Davé, R., Cen, R., Ostriker, J. P., et al. 2001, ApJ, 552, 473 [NASA ADS] [CrossRef]
Davé, R., Finlator, K., & Oppenheimer, B. D. 2006, MNRAS, 370, 273 [NASA ADS] (In the text)
Davé, R., Oppenheimer, B. D., & Sivanandam, S. 2008, MNRAS, 391, 110 [NASA ADS] [CrossRef] (In the text)
Davis, M., & Huchra, J. 1982, ApJ, 254, 437 [NASA ADS] [CrossRef]
Dekel, A., Birnboim, Y., Engel, G., et al. 2009, Nature, 457, 451 [NASA ADS] [CrossRef]
Dove, J. B., & Shull, J. M. 1994, ApJ, 423, 196 [NASA ADS] [CrossRef] (In the text)
Eisenstein, D. J., & Hu, W. 1999, ApJ, 511, 5 [NASA ADS] [CrossRef] (In the text)
Finlator, K., & Davé, R. 2008, MNRAS, 385, 2181 [NASA ADS] [CrossRef] (In the text)
Fukugita, M., Hogan, C. J., & Peebles, P. J. E. 1998, ApJ, 503, 518 [NASA ADS] [CrossRef] (In the text)
Giovanelli, R., Haynes, M. P., Kent, B. R., et al. 2005, AJ, 130, 2598 [NASA ADS] [CrossRef] (In the text)
Groth, E. J., & Peebles, P. J. E. 1977, ApJ, 217, 385 [NASA ADS] [CrossRef]
Haardt, F., & Madau, P. 2001, in Clusters of Galaxies and the High Redshift Universe Observed in X-rays (In the text)
Keres, D., Yun, M. S., & Young, J. S. 2003, ApJ, 582, 659 [NASA ADS] [CrossRef] (In the text)
Keres, D., Katz, N., Weinberg, D. H., & Davé, R. 2005, MNRAS, 363, 2 [NASA ADS] [CrossRef]
Keres, D., Katz, N., Fardal, M., Dave, R., & Weinberg, D. H. 2009, MNRAS, 395, 160 [NASA ADS] [CrossRef]
Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] (In the text)
Mellema, G., Iliev, I. T., Pen, U.-L., & Shapiro, P. R. 2006, MNRAS, 372, 679 [NASA ADS] [CrossRef] (In the text)
Meyer, M. J., Zwaan, M. A., Webster, R. L., Brown, M. J. I., & Staveley-Smith, L. 2007, ApJ, 654, 702 [NASA ADS] [CrossRef] (In the text)
Monaghan, J. J., & Lattanzio, J. C. 1985, A&A, 149, 135 [NASA ADS] (In the text)
Murray, N., Quataert, E., & Thompson, T. A. 2005, ApJ, 618, 569 [NASA ADS] [CrossRef] (In the text)
Noordermeer, E., van der Hulst, J. M., Sancisi, R., Swaters, R. A., & van Albada, T. S. 2005, A&A, 442, 137 [NASA ADS] [CrossRef] [EDP Sciences]
Norberg, P., Baugh, C. M., Hawkins, E., et al. 2002, MNRAS, 332, 827 [NASA ADS] [CrossRef] (In the text)
Obreschkow, D., & Rawlings, S. 2009, MNRAS, 394, 1857 [NASA ADS] [CrossRef] (In the text)
Oppenheimer, B. D., & Davé, R. 2006, MNRAS, 373, 1265 [NASA ADS] [CrossRef]
Oppenheimer, B. D., & Davé, R. 2008, MNRAS, 387, 577 [NASA ADS] [CrossRef]
Oppenheimer, B. D., & Davé, R. 2009, MNRAS, 395, 1875 [NASA ADS] [CrossRef]
Osterbrock, D. E. 1989, Astrophysics of gaseous nebulae and active galactic nuclei, Research supported by the University of California, John Simon Guggenheim Memorial Foundation, University of Minnesota, et al. (Mill Valley, CA: University Science Books), 422 (In the text)
Pelupessy, F. I. 2005, Ph.D. thesis, Leiden University (In the text)
Pontzen, A., Governato, F., Pettini, M., et al. 2008, MNRAS, 390, 1349 [NASA ADS] (In the text)
Rosenberg, J. L., & Schneider, S. E. 2002, ApJ, 567, 247 [NASA ADS] [CrossRef] (In the text)
Schechter, P. 1976, ApJ, 203, 297 [NASA ADS] [CrossRef] (In the text)
Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] (In the text)
Springel, V., & Hernquist, L. 2002, MNRAS, 333, 649 [NASA ADS] [CrossRef] (In the text)
Springel, V., & Hernquist, L. 2003a, MNRAS, 339, 289 [NASA ADS] [CrossRef] (In the text)
Springel, V., & Hernquist, L. 2003b, MNRAS, 339, 312 [NASA ADS] [CrossRef] (In the text)
Swaters, R. A., van Albada, T. S., van der Hulst, J. M., & Sancisi, R. 2002, A&A, 390, 829 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (In the text)
Verner, D. A., & Ferland, G. J. 1996, ApJS, 103, 467 [NASA ADS] [CrossRef] (In the text)
Walterbos, R. A. M., & Braun, R. 1996, in The Minnesota Lectures on Extragalactic Neutral Hydrogen, 106, 1 (In the text)
Weinberg, D. H., Miralda-Escude, J., Hernquist, L., & Katz, N. 1997, ApJ, 490, 564 [NASA ADS] [CrossRef] (In the text)
Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [NASA ADS] [CrossRef] (In the text)
Wong, T., & Blitz, L. 2002, ApJ, 569, 157 [NASA ADS] [CrossRef] (In the text)
Zehavi, I., Eisenstein, D. J., Nichol, R. C., et al. 2005, ApJ, 621, 22 [NASA ADS] [CrossRef] (In the text)
Zheng, Z., & Miralda-Escudé, J. 2002, ApJ, 568, L71 [NASA ADS] [CrossRef] (In the text)
Zwaan, M. A., Staveley-Smith, L., Koribalski, B. S., et al. 2003, AJ, 125, 2842 [NASA ADS] [CrossRef] (In the text)
Zwaan, M. A., van der Hulst, J. M., Briggs, F. H., Verheijen, M. A. W., & Ryan-Weber, E. V. 2005, MNRAS, 364, 1467 [NASA ADS] [CrossRef] (In the text)

All Tables

Table 1: Sensitivity limits for four different telescopes for an assumed line-width of 25 km s^-1 after a total integration time of 500 h to image an area of 30 square degrees.

All Figures

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{11811f01.eps} \end{figure}$	Figure 1: Neutral fraction as a function of density for different temperatures between 10⁴ and 10⁹ K.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{11811f02.eps} \end{figure}$	Figure 2: Temperatures are plotted against densities for every 200 th. particle in the simulation. The dashed (blue) and dash-dotted (red) lines correspond to constant thermal pressures of P/k = 155 and 810 cm^-3 K, that were found empirically to reproduce the observed mass densities of atomic and molecular gas at z = 0. The solid (green) line shows where the recombination time is equal to the sound-crossing time at a physical scale of one kpc. Particles above/left of the green line are unlikely to be neutral or molecular.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{11811f03.eps} \end{figure}$	Figure 3: The average molecular density at z = 0 is plotted against the threshold thermal pressure, where molecular hydrogen is assumed to form from atomic, while also satisfying the condition that $\tau _{\textrm {rec}}<\tau _{\textrm {s}}$ . The dashed line indicates a pressure of P/k = 810 cm^-3 K, where $\rho_{{\rm H}_{\rm 2}}=1.8\times 10^7~h~M_{\odot}$ Mpc^-3 which is shown by the dotted line.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{11811f04.eps} \end{figure}$	Figure 4: The average H I mass density at z = 0 is plotted against the threshold thermal pressure, where atomic hydrogen is assumed to recombine from ionised, while also satisfying the condition that $\tau _{\textrm {rec}}<\tau _{\textrm {s}}$ (and accounting for a molecular density of $\rho_{{\rm H}_{\rm 2}}=1.8~\times~ 10^7~h~M_{\odot}$ Mpc^-3). At a pressure of P/k = 155 cm^-3 K (dashed line), $\rho_{\rm HI}=6.1~\times~10^7~h~M_{\odot}$ Mpc^-3 (dotted line), which is consistent with the H I density from Zwaan et al. (2003).
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=7.2cm,clip]{11811f05.eps} \includegraphics[width=7.2cm,clip]{11811f06.eps} } \end{figure}$	Figure 5: Left panel: H I distribution function after gridding to 80 kpc (dashed (red) line). The solid (blue) line corresponds to data gridded to a 2 kpc cell size. Filled dots correspond to the QSO absorption line data (Corbelli & Bandiera 2002). Right panel: combined H I distribution functions of the simulation, gridded to a resolution of 2 kpc (solid (blue) line) and 80 kpc (dashed (purple) line). Overlaid are distribution function from observational data of M 31 (Braun & Thilker 2004), WHISP (Swaters et al. 2002; Zwaan et al. 2005) and QSO absorption lines (Corbelli & Bandiera 2002) respectively. The reconstructed H I distribution function corresponds very well to all observed distribution functions.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm,clip]{11811f07.eps} \end{figure}$	Figure 6: Fractional area of reconstructed H I (dashed line, right-hand axis) and cumulated surface area (solid line, left-hand axis) plotted against column density on a logarithmic scale with a bin size of ${\rm d}\log(N_{\rm HI})=0.2$ . The probability of detecting emission with a column density near $N_{\rm {HI}} \sim 10^{17}$ cm^-2 is significantly larger than around $N_{\rm {HI}} \sim 10^{19.5}$ cm^-2. The cumulated surface area is normalised to that at a column density of $N_{\rm HI}=10^{16}$ cm^-2. At column densities of $N_{\rm {HI}} \sim 10^{17}$ cm^-2, the area subtended by H I emission is much larger than at a limit of $N_{\rm {HI}} \sim 10^{19.5}$ cm^-2, which is the sensitivity limit of most current observations of nearby galaxies.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{11811f08.eps}\hspace{4mm}... ...m}\includegraphics[width=7.2cm,clip]{11811f10.eps}\hspace{3.6cm}}\end{figure}$	Figure 7: Top left panel: column density of total H gas integrated over a depth of 32 h^-1 Mpc on a logarithmic scale, gridded to a resolution of 80 kpc. Top right panel: molecular hydrogen component. Only very dense regions in the total hydrogen component contain molecular hydrogen. Bottom panel: neutral atomic hydrogen component of the same region. In the neutral hydrogen distribution the highest densities are comparable to the densities in the total hydrogen distribution, but there is a very sharp transition to low neutral column densities as the gas becomes optically thin. Note the very different scales, the total hydrogen spanning only 2 orders of magnitude and the neutral hydrogen, eight.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=6cm]{figures/11811f11.eps}\hspac... ...}\hspace*{4mm} \includegraphics[width=5cm]{figures/11811f22.ps} } \end{figure}$	Figure 8: Four examples of high density regions in the reconstructed data, gridded to a cell size of 2 kpc. The left panels show the total hydrogen, while the middle panels show only the neutral component. Some objects have many satellites, as in the top panels, while others are much more isolated. All examples have extended H I at column densities around $\log(N_{\rm HI}) = 16$ -17 cm^-2. In the right panel, the individual H I column density distribution function is shown for each of the examples. Black dots correspond to the QSO absorption line data (Corbelli & Bandiera 2002).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{11811f23.eps} \end{figure}$	Figure 9: Neutral fraction plotted against H I column density. The colour-bar represents the probability of detecting a certain combination of H I column density and neutral fraction on logarithmic scale. At the highest densities $N_{\rm {HI}} > 10^{20}$ cm^-2, the neutral fraction is almost unity. Column densities around $N_{\rm {HI}} \sim 10^{19}$ cm^-2have the smallest detectionprobability.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{ \includegraphics[width=8cm,clip]{11811f24.eps}\hspace*{4mm} \includegraphics[width=8cm,clip]{11811f25.eps} } \end{figure}$	Figure 10: Left panel: cumulative mass of total hydrogen as function of column density, the different phases are shown with different colours. The Ly $\alpha$ forest, the Lyman Limit System and galaxies have approximately the same mass component when considering all the gas. Right panel: cumulative mass of neutral atomic hydrogen as function of column density. Although the surface covered by the LLSs is large, it contains only 1% off all the neutral gas mass, while about 99% resides in the galaxies.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{11811f26.eps} \end{figure}$	Figure 11: Two-point correlation function of H I-rich objects in our simulation, contrasted with a power-law fit to the observed relation of Meyer et al. (2007).
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=8.2cm,clip]{11811f27.eps} \includegraphics[width=8.2cm,clip]{11811f28.eps} } \end{figure}$	Figure 12: Left panel: H I Mass Function of the simulated data (black dots) with the best-fit Schechter function (solid black line), compared with the HIMF from Zwaan et al. (2003) (dash-dotted red line). Our best fit line is dashed below $10^9~M_{\odot}$ , because there are no data points there and the function is only an extrapolation. Right panel: H₂ Mass Function of the simulated data (black dots) and the best fit, compared with the H₂MF from Keres et al. (2003) (dash-dotted (blue) line) and Obreschkow & Rawlings (2009) (dashed (red) line). Both simulated Mass Functions show agreement with observations over about a decade in mass.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{11811f29.eps} \end{figure}$	Figure 13: Derived H₂ masses are plotted against H I masses for individual simulated objects. The distribution can be fit using a simple power law (solid (red) line), although the scatter is very large. The dashed vertical line represents the sample cut-off for H I masses in the simulated data.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=6cm]{figures/11811f30.eps} \incl... ...11f40.eps} \includegraphics[width=6cm]{figures/11811f41.eps} } \par \end{figure}$	Figure 14: Column density maps of four reconstructed objects as seen in neutral hydrogen with contours of Dark Matter ( left panels), Stars ( middle panels) and molecular hydrogen ( right panels). For both the Dark Matter and the stars contour levels are at N = 3, 5, 10, 20, 30, 50 and $100 \times 10^6~M_{\odot}$ kpc^-2. For the molecular hydrogen contours are drawn at $N_{{\rm H}_{\rm 2}}= 10^{18}$ , 10¹⁹, 10²⁰ and 10²¹ cm^-2. Stars are concentrated in the very dense parts of the H I objects, dark matter is more extended, however the extended H I does not always trace the dark matter. The H I satellites or companions are within the same Dark Matter Halo, but do not always contain stars.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[angle=270,width=6cm]{figures/11811f42.... ...} \includegraphics[angle=270,width=6cm]{figures/11811f44.eps} } \par\end{figure}$	Figure 15: Left panel: simulated object at a distance of 6 Mpc, with a 6 kpc intrinsic beam size. Middle panel: simulated object smoothed to a 8.7 kpc beam size, corresponding to the ASKAP beam at 6 Mpc. Right panel: noise is added corresponding to the ASKAP sensitivity limit after a 500 h observation of 30 square degrees.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[angle=270,width=7.4cm,clip]{11811f45.e... ...4mm} \includegraphics[angle=270,width=7.4cm,clip]{11811f48.eps} }\end{figure}$	Figure 16: Simulated observations of the same object at a distance at which the beam size corresponds to 25 kpc for Parkes ( top left), Arecibo ( top right), ASKAP ( bottom left) and the SKA ( bottom right). All contours begin at a 3 $\sigma$ level, after a 500 h observation of a 30 square degree field with each telescope. Every subsequent contour level is a factor 3 higher than the previous one. Note that the angular scale is different in each panel.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[angle=270,width=7.4cm,clip]{11811f45.e... ...{4mm} \includegraphics[angle=270,width=7.4cm,clip]{11811f51.eps} }\end{figure}$	Figure 17: Simulated observations of the same object at a fixed distance of 6 Mpc for Parkes ( top left), Arecibo ( top right), ASKAP ( bottom left) and the SKA ( bottom right). Contour levels start at a 3 $\sigma$ level after 500 h observation of a 30 square degree field. For Parkes every subsequent contour is a factor 3 higher than the previous one. For ASKAP and Arecibo, the contours interval is a factor 7. For the SKA the contours start a $4 \times 10^{16}$ cm^-2 and increase by a factor 6. Parkes is not really competitive in detecting substructures at this distance. The other telescopes all have sufficient resolution, however only the SKA is sensitive enough to detect the faint diffuse sub-structures.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

The simulated H I sky at low redshift

1 Introduction

2 Simulation code

3 Method for making H I maps

3.1 Neutral fraction of hydrogen

3.2 Molecular hydrogen

3.3 Correction for self-shielding

3.4 Gridding method

4 Results

4.1 Mean H I density

4.2 H I distribution function

4.3 H I column density

4.3.1 Neutral fraction

4.4 Two-point correlation function

4.5 H I mass function

4.5.1 H2 mass function

4.6 Stars, dark matter and molecular hydrogen

5 Discussion

5.1 Resolution effects

5.2 Future observations

6 Conclusion

References

All Tables

All Figures

4.5.1 H₂ mass function