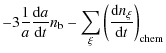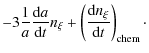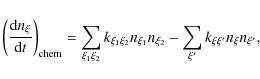| Issue |
A&A
Volume 503, Number 1, August III 2009
|
|
|---|---|---|
| Page(s) | 47 - 59 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200811297 | |
| Published online | 02 July 2009 | |
Chemistry of heavy elements in the Dark Ages
P. Vonlanthen1 - T. Rauscher2 - C. Winteler2 - D. Puy1 - M. Signore3 - V. Dubrovich4
1 - Université Montpellier II - GRAAL, CNRS - UMR 5024, Place Eugène Bataillon, 34095 Montpellier, France
2 -
Department of Physics, University of Basel, 4056 Basel, Switzerland
3 - LERMA, Observatoire de Paris, 75014 Paris, France
4 -
SPb Branch of Special Astrophysical Observatory, RAS, St Petersburg, Russia
Received 5 November 2008 / Accepted 17 June 2009
Abstract
Context. Primordial molecules were formed during the Dark Ages, i.e. the time between recombination and reionization in the early Universe. They were the constituents of the first proto-stellar clouds. Standard Big Bang nucleosynthesis predicts the abundances of hydrogen, helium, lithium, beryllium, and their isotopes in the early Universe. Heavier nuclei such as carbon, nitrogen, or oxygen are only formed in trace amounts. In nonstandard Big Bang nucleosynthesis models, it is possible to synthesize greater quantities of these heavier elements. The latter are interesting because they can form molecules with a high electric dipole moment which can increase the cooling in collapsing protostellar structures.
Aims. The purpose of this article is to analyze the formation of primordial molecules based on heavy elements during the Dark Ages, with elemental abundances taken from different nucleosynthesis models.
Methods. We present calculations of the full nonlinear equation set governing the primordial chemistry. We considered the evolution of 45 chemical species and used an implicit multistep method of variable order of precision with an adaptive stepsize control.
Results. The cosmological recombination of heavy elements is presented for the first time. We find that the most abundant Dark Age molecules based on heavy elements are CH and OH. When considering initial conditions given by the standard Big Bang nucleosynthesis model, we obtain relative abundances
![]() and
and
![]() at z = 10, where
at z = 10, where
![]() is the total number density. But nonstandard nucleosynthesis can lead to higher heavy element abundances, while still satisfying the observed primordial light abundances. In that case, we show that the abundances of molecular species based on C, N, O, and F can be enhanced by two orders of magnitude, leading to a CH relative abundance higher than that of HD+ or H2D+.
is the total number density. But nonstandard nucleosynthesis can lead to higher heavy element abundances, while still satisfying the observed primordial light abundances. In that case, we show that the abundances of molecular species based on C, N, O, and F can be enhanced by two orders of magnitude, leading to a CH relative abundance higher than that of HD+ or H2D+.
Key words: astrochemistry - early Universe - cosmology: theory
1 Introduction
The formation of light elements is a central problem in modern cosmology. Big Bang nucleosynthesis (BBN) provides an important testing ground for the physics of the primordial Universe. The proceedings of nucleosynthesis are relatively well understood. Nucleosynthesis is connected to two important cosmological events. The first one is the freeze-out, at
![]() MeV, of the weak interactions that interconvert neutrons and protons, thus setting the initial proton-to-neutron ratio for nucleosynthesis. The second event is the annihilation of thermal e--e+ pairs in the temperature range 1 MeV-20 keV, delaying the onset of nucleosynthesis by releasing additional heat but eliminating the possibility of positron captures.
MeV, of the weak interactions that interconvert neutrons and protons, thus setting the initial proton-to-neutron ratio for nucleosynthesis. The second event is the annihilation of thermal e--e+ pairs in the temperature range 1 MeV-20 keV, delaying the onset of nucleosynthesis by releasing additional heat but eliminating the possibility of positron captures.
Thereafter, thermal fusion reactions in the plasma first produce deuterium nuclei:
| (1) |
and then helium ( 3He, 4He), lithium ( 7Li), and beryllium ( 7Be). Cosmological expansion plays a crucial role during the whole process and determines the timescale for the nucleosynthesis during the cooling of the Universe. Observations agree well with the predicted abundances of the standard BBN model; see for example Burles et al. (2001), but also Steigman (2007) for the latest observations (and in particular his Fig. 13).
Due to the proton-rich freeze-out from high temperature, standard BBN predicts the highest abundance for the nucleus with the greatest binding energy, which is 4He. Beyond 4He, charged particle reactions are inefficient because of the rising Coulomb barrier and the low density. Therefore, only tiny amounts of heavier nuclei are produced in standard BBN, if any. However, many extensions to the standard BBN have been suggested, among which we find nonstandard Big Bang nucleosynthesis (hereafter NSBBN) scenarios considering density fluctuations in the early Universe. Some of these models show increased abundances of heavy elements (see e.g. Khlopov & Kouvaris 2008; Jedamzik et al. 1994; Rauscher et al. 1994; Dolgov & Silk 1993, and references therein). The original motivation for these studies was to obtain an average baryon density equal to the critical density for a flat universe and to simultaneously satisfy the constraints given by primordial abundance observations. While this was shown to be unfeasible (and unnecessary), density fluctuations are present in the cosmic microwave background. The density fluctuations affecting BBN are of different magnitude, but many different mechanisms have been suggested, acting during the inflationary phase, during baryogenesis, or later. Thus, NSBBN with density fluctuations remains an interesting model for obtaining primordial heavy elements.
During the recombination period, the nuclei became progressively neutralized, which led to molecular formation. However, at early epochs, where a total absence of dust grains appears justified, the chemistry is different from the typical interstellar medium astrochemistry.
Several groups proposed an assembled, comprehensive set of reactions for the early Universe (Glover & Savin 2009; Lepp & Shull 1984; Signore & Puy 1999; Stancil et al. 1998b; Lepp et al. 2002; Galli & Palla 1998; Puy et al. 1993; Puy & Signore 2007; Glover & Abel 2008; Pfenniger & Puy 2003). The chemical network is coupled with the matter and radiation temperatures and with the matter density. Primordial chemistry of heavy nuclei has been poorly studied, although Lipovka et al. (2007) analyzed the possibility of detecting rotational lines of primordial CH, and Puy et al. (2007) analyzed the possibility of forming molecular fluorine HF in the early Universe.
In this paper we will discuss the chemistry of eight elements (hydrogen, deuterium, helium, lithium, carbon, nitrogen, oxygen and fluorine) in the early Universe, for two different contexts: the standard Big Bang nucleosynthesis model and nonstandard nucleosynthesis based on baryon density fluctuations. Heavier elements are particularly interesting because they can form molecules with a high electric dipole moment. Even if their abundances are proven to be quite low, they could still furnish an interesting cooling agent in the gravitational collapse of protostructures, as molecular abundances are prone to drastic variations in such environments. In Sect. 2, we summarize the standard and nonstandard BBN models we used and the predicted abundances. We describe and calculate, in Sect. 3, the mechanisms of recombination and primordial chemistry which act for the eight elements H, D, He, Li, C, N, O and F. In Sect. 4 we discuss our results.
2 Big Bang nucleosynthesis
2.1 Standard model of primordial nucleosynthesis
Standard BBN assumes a homogeneous baryon density throughout the expanding and cooling Universe. The abundance ratio of protons and neutrons is set by the freeze-out of the weak interaction and subsequent decay of the neutrons until the onset of nucleosynthesis. At initially high temperature a nuclear statistical equilibrium is established, favoring the
formation of the strongly bound 4He as soon as the photodisintegrations cease. All neutrons are consumed but a large fraction of protons remains because of the higher initial proton abundance. Due to the high entropy, i.e. low density, the triple-![]() reaction is inefficient and the formation of elements beyond He is suppressed. For this reason, there are few accounts of standard BBN heavy element abundances in literature.
reaction is inefficient and the formation of elements beyond He is suppressed. For this reason, there are few accounts of standard BBN heavy element abundances in literature.
Here, we will consider BBN results by Winteler (2007), obtained with a code based on a modified version of the Basel network code. Modifications include a consistent evolution of temperature and density in the early universe, including weak freeze-out, based on methods by Kawano (1992), and an improved reaction network with updated reaction rates, for details see Winteler (2007). The abundances were calculated for
![]() ,
in accordance with the latest result of the Wilkinson Microwave Anisotropy Probe (WMAP) experiment (
,
in accordance with the latest result of the Wilkinson Microwave Anisotropy Probe (WMAP) experiment (
![]() ,
giving
,
giving
![]() ,
see Dunkley et al. 2009). The weak freeze-out process was carefully followed until the nucleosynthesis phase, thus setting the initial neutron and proton abundances consistently. The first column of Table 1 gives the relative abundances for this SBBN case.
Here and throughout this paper, we consider relative abundances for species
,
see Dunkley et al. 2009). The weak freeze-out process was carefully followed until the nucleosynthesis phase, thus setting the initial neutron and proton abundances consistently. The first column of Table 1 gives the relative abundances for this SBBN case.
Here and throughout this paper, we consider relative abundances for species ![]() such as:
such as:
| (2) |
where
In Table 1 we also quote the amounts of the elements C to F produced in this standard BBN, as they are included in the SBBC calculations.
Table 1:
Relative abundances
![]() of the elements
at the end of Big Bang nucleosynthesis for the SBBN and for two nonstandard BBN scenarios.
of the elements
at the end of Big Bang nucleosynthesis for the SBBN and for two nonstandard BBN scenarios.
2.2 Nonstandard Big Bang nucleosynthesis
While heavy elements are not produced at high levels in SBBN, BBN models assuming density fluctuations allow for different baryon densities
To study the impact of elevated levels of heavy nuclei, we used the same code by Winteler (2007) as for the SBBN but followed nucleosynthesis in zones promising for synthesizing heavy elements. Table 1 shows the results for two models, representative for two extreme cases. The abundances shown in the table are already the final abundances, mixed from the two zones in each model:
![\begin{displaymath}\left[\xi\right]=\frac{f_{\rm v}\eta^{(1)}\left[\xi\right]^{(...
...)\eta^{(2)}\left[\xi\right]^{(2)}}{\eta_{10}^{\rm WMAP}} \cdot
\end{displaymath}](/articles/aa/full_html/2009/31/aa11297-08/img58.png) |
(3) |
The first case (
The second case investigated here (
![]() ,
R=1000) comprises the other end of the allowed spectrum, tiny pockets of extremely high density embedded in a background with almost standard density. This is similar to the scenario originally introduced by Jedamzik et al. (1994) and later also discussed by Matsuura et al. (2005,2007,2004). In the high density pocket the path to heavy elements is opened by an efficient triple-
,
R=1000) comprises the other end of the allowed spectrum, tiny pockets of extremely high density embedded in a background with almost standard density. This is similar to the scenario originally introduced by Jedamzik et al. (1994) and later also discussed by Matsuura et al. (2005,2007,2004). In the high density pocket the path to heavy elements is opened by an efficient triple-![]() reaction. At the same time, increased destruction of 7Li keeps its abundance low. This simultaneously allows the model to achieve light element abundances compatible with those of the SBBN and to increase the heavy element production considerably. However, due to the small volume fraction of the high density zone (which is necessary to obtain the proper global baryon density) the final heavy element abundances after complete mixing remain low, although two orders of magnitude higher than for the standard case.
reaction. At the same time, increased destruction of 7Li keeps its abundance low. This simultaneously allows the model to achieve light element abundances compatible with those of the SBBN and to increase the heavy element production considerably. However, due to the small volume fraction of the high density zone (which is necessary to obtain the proper global baryon density) the final heavy element abundances after complete mixing remain low, although two orders of magnitude higher than for the standard case.
In the following, we will use the abundance values from both NSBBN scenarios as initial conditions for our calculations of the nonstandard Big Bang chemistry (hereafter NSBBC1 and NSBBC2 respectively).
3 Primordial chemistry
3.1 Equations of evolution
The primordial gas is a mixture of hydrogen, deuterium, helium, lithium, ...![]() so there are many possibilities of reactions. Change in the number density of a given chemical species due to chemical reactions depends on the densities of the species involved in these reactions and on the reaction rates, which themselves depend on the matter and radiation temperatures. But of course cosmic expansion also plays a crucial role. Thus, it is necessary to take into account the following set of differential equations (see for example Puy et al. 1993) in the context of the expanding Universe, characterized by the scale factor a:
so there are many possibilities of reactions. Change in the number density of a given chemical species due to chemical reactions depends on the densities of the species involved in these reactions and on the reaction rates, which themselves depend on the matter and radiation temperatures. But of course cosmic expansion also plays a crucial role. Thus, it is necessary to take into account the following set of differential equations (see for example Puy et al. 1993) in the context of the expanding Universe, characterized by the scale factor a:
In these equations,
where
This system of ordinary differential equations governing the chemical abundances is stiff. We use an implicit multistep method of variable order of precision with an adaptive stepsize control. This method has excellent stability properties and is widely used for solving chemical kinetic problems (Hindmarsh & Petzold 1995). We solve the set of Eqs. (4) to (7) from the initial redshift
![]() ,
when the Universe was still totally ionized, to the final redshift
,
when the Universe was still totally ionized, to the final redshift
![]() (about the epoch of reionization).
(about the epoch of reionization).
Moreover, we consider the standard ![]() CDM model, with Hubble parameter H0 = 71 km s-1 Mpc-1, total matter density
CDM model, with Hubble parameter H0 = 71 km s-1 Mpc-1, total matter density
![]() (including dark matter density
(including dark matter density
![]() = 0.226 and baryon density
= 0.226 and baryon density
![]() = 0.044) and dark energy density
= 0.044) and dark energy density
![]() (Komatsu et al. 2009).
(Komatsu et al. 2009).
3.2 Cosmological recombination
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297fg1.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg88.png) |
Figure 1: Successive cosmological recombination for hydrogen, deuterium, helium and lithium in the standard model of primordial chemistry. |
| Open with DEXTER | |
Primordial chemistry begins with the appearance of the first neutral species. Once a neutral species is formed, charge transfers with ions become efficient and lead to the formation of other neutral species and then molecular ions. Figure 1 shows the evolution of the chemical abundances during the successive periods of recombination for the light elements H, D, He and Li in the standard model. Helium nuclei are the first to recombine because of their high electronic binding energy![]() . The recombination and photoionization rates for H and D are taken from Abel et al. (1997). We use the rates of Galli & Palla (1998) for He and for the reactions Li+ + e-
. The recombination and photoionization rates for H and D are taken from Abel et al. (1997). We use the rates of Galli & Palla (1998) for He and for the reactions Li+ + e-
![]() Li +
Li + ![]() .
Higher lithium recombinations and photoionisations are treated with the recombination rates of Verner et al. (1996) and the photoionisation cross sections of Verner & Ferland (1996). The recombination pattern for the two nonstandard cases NSBBC1 and NSBBC2 are very similar, since the initial abundances of H, D, He and Li are almost identical to the SBBC model.
We define the recombination redshift
.
Higher lithium recombinations and photoionisations are treated with the recombination rates of Verner et al. (1996) and the photoionisation cross sections of Verner & Ferland (1996). The recombination pattern for the two nonstandard cases NSBBC1 and NSBBC2 are very similar, since the initial abundances of H, D, He and Li are almost identical to the SBBC model.
We define the recombination redshift
![]() as the redshift when the abundance of a given species equals the one of its corresponding ion. Table 2 summarizes the different recombination redshifts for the standard calculation. Due to its low ionization energy and to the fact that charge transfer reactions between lithium and hydrogen remain active, lithium does not recombine totally, and both neutral and ionized Li tend to match their abundances (see Fig. 1).
as the redshift when the abundance of a given species equals the one of its corresponding ion. Table 2 summarizes the different recombination redshifts for the standard calculation. Due to its low ionization energy and to the fact that charge transfer reactions between lithium and hydrogen remain active, lithium does not recombine totally, and both neutral and ionized Li tend to match their abundances (see Fig. 1).
Table 2: Recombination redshifts for hydrogen, deuterium and helium.
Moreover, we also investigated, for the first time, the primordial recombinations of the carbon, nitrogen and oxygen ions. The photoionization rates are calculated from the cross sections evaluated by Verner et al. (1996). The recombination rates are taken from Verner & Ferland (1996) for the CVI, CV, CIV, NVII, NVI, NV, OVIII, OVII and OVI recombinations. They come from the work of Péquignot et al. (1991) for the CIII, CII, NIV, NIII, NII and for all other oxygen recombinations. Finally, the recombination rates come from Omukai (2000) for the CI recombination and from the UMIST database![]() (Woodall et al. 2007) for the NI recombination. We plot in Figs. 2-4 the successive recombinations of carbon, nitrogen and oxygen ions in the SBBC model. Recombinations in the NSBBC scenarios are very close to the standard recombinations, the only difference being a shift in relative abundances corresponding to the difference in the initial conditions.
(Woodall et al. 2007) for the NI recombination. We plot in Figs. 2-4 the successive recombinations of carbon, nitrogen and oxygen ions in the SBBC model. Recombinations in the NSBBC scenarios are very close to the standard recombinations, the only difference being a shift in relative abundances corresponding to the difference in the initial conditions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11297fg2.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg95.png) |
Figure 2: Successive recombinations of the carbon ions in the standard model. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11297fg3.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg96.png) |
Figure 3: Successive recombinations of the nitrogen ions in the standard model. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11297fg4.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg97.png) |
Figure 4: Successive recombinations of the oxygen ions in the standard model. |
| Open with DEXTER | |
Since the ionization potential of carbon (
![]() eV) is smaller than that of hydrogen (
eV) is smaller than that of hydrogen (
![]() eV), C+ recombination occurs later than H+ recombination. Figure 2 shows that carbon is singly ionized at the beginning of the primordial chemistry. We conclude that it is not necessary to compute all the successive recombinations when calculating the evolution of the carbon species. Thus, we will consider that all the carbon ions are present as C+ at
eV), C+ recombination occurs later than H+ recombination. Figure 2 shows that carbon is singly ionized at the beginning of the primordial chemistry. We conclude that it is not necessary to compute all the successive recombinations when calculating the evolution of the carbon species. Thus, we will consider that all the carbon ions are present as C+ at
![]() .
For similar arguments drawn from Figs. 3 and 4, we will start our calculations of the primordial chemistry of nitrogen and oxygen with the singly ionized nitrogen and oxygen ions at
.
For similar arguments drawn from Figs. 3 and 4, we will start our calculations of the primordial chemistry of nitrogen and oxygen with the singly ionized nitrogen and oxygen ions at
![]() .
.
3.3 Molecular formation
After hydrogen recombination, the decrease of the electron density leads to the inefficiency of thermal coupling between matter and radiation. The chemical processes occuring during this post-recombination period are essentially collisional (ionizations, radiative recombinations, attachments, etc.) and radiative, due to the active presence of the CMB photons. The chemical network leads gradually to the formation of the first molecules in the Universe (Glover & Savin 2009; Lepp & Shull 1984; Signore & Puy 1999; Stancil et al. 1998b; Lepp et al. 2002; Galli & Palla 1998; Puy et al. 1993; Puy & Signore 2007; Glover & Abel 2008; Pfenniger & Puy 2003).
In this section, we will consider the primordial chemistry of hydrogen, deuterium, helium, lithium, carbon, nitrogen, oxygen and fluorine in the SBBN and NSBBN contexts. We list in the Appendix the sets of reactions that we consider.
3.3.1 Hydrogen
The cosmological production of H2 molecules proceeds mainly through two mechanisms which are catalyzed by H- and H2+ (Peebles & Dicke 1968; Saslaw & Zipoy 1967). It is generally considered that the H2+ mechanism produces molecular hydrogen at
![]() ,
while the H- mechanism is responsible for the H2 peak at
,
while the H- mechanism is responsible for the H2 peak at
![]() .
.
The reaction rates we consider for hydrogen are taken from Galli & Palla (1998), except for the recombination and photoionization rates H1 and H2 (Abel et al. 1997), and for the reaction H4 (
![]() ). For that reaction, we consider the important correction described in Hirata & Padmanabhan (2006) that takes into account the effects of the non-thermal radiation emitted during hydrogen recombination.
). For that reaction, we consider the important correction described in Hirata & Padmanabhan (2006) that takes into account the effects of the non-thermal radiation emitted during hydrogen recombination.
Figure 5 shows the evolution of the hydrogen chemistry in the standard model. The amount of H2 molecules created during the Dark Ages is important and converge to the following values at z = 10: [H2]
![]() =
=
![]() = 2.7
= 2.7
![]() .
The effect of the correction of Hirata & Padmanabhan (2006) is shown on Fig. 5. The enhancement of the rate H4 is responsible for the efficient destruction of H- via photodetachment. As a consequence, the contribution of the H- channel to the final amount of molecular hydrogen is strongly reduced at
.
The effect of the correction of Hirata & Padmanabhan (2006) is shown on Fig. 5. The enhancement of the rate H4 is responsible for the efficient destruction of H- via photodetachment. As a consequence, the contribution of the H- channel to the final amount of molecular hydrogen is strongly reduced at
![]() and the value of the standard final abundance is lower than the values usually seen in the literature (about a factor 4). Table 3 gives the abundances at redshifts z=1000, z=100 and z=10. The initial relative abundance of hydrogen is very close in our three chemistry models SBBC, NSBBC1 and NSBBC2 (see Table 1), as is the case for deuterium, helium and to some extent lithium. For that reason we only show the results of the standard chemistry calculation for these four light elements.
and the value of the standard final abundance is lower than the values usually seen in the literature (about a factor 4). Table 3 gives the abundances at redshifts z=1000, z=100 and z=10. The initial relative abundance of hydrogen is very close in our three chemistry models SBBC, NSBBC1 and NSBBC2 (see Table 1), as is the case for deuterium, helium and to some extent lithium. For that reason we only show the results of the standard chemistry calculation for these four light elements.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297fg5.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg108.png) |
Figure 5: Standard primordial chemistry of hydrogen species. The dotted lines for H2, H- and H3+ show the abundances we would obtain without the correction of Hirata & Padmanabhan (2006) relative to the radiation emitted during the hydrogen recombination. |
| Open with DEXTER | |
Table 3:
Relative abundances
![]() of hydrogen species at redshifts z=1000, z=100 and z=10 in the SBBC model.
of hydrogen species at redshifts z=1000, z=100 and z=10 in the SBBC model.
3.3.2 Deuterium
We take the reaction rates for deuterium chemistry from Galli & Palla (1998), except for the recombination and photoionization rates D1 and D2 (Abel et al. 1997), which are the same as H1 and H2 (see Appendix A). Figure 6 and Table 4 show the evolution of the deuterium chemistry. The fact that the abundance of molecular hydrogen is reduced compared to the usual value of the literature has a direct implication on the HD quantity. Indeed, reactions D6 and D8 are the most important formation channels of HD. These reactions are collisions between neutral or charged D with H2. As a consequence, the standard final amount of HD molecules is also smaller (by a factor of 2) than the canonical value and we get [HD]
![]() .
.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297fg6.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg131.png) |
Figure 6: Standard primordial chemistry of deuterium species. As in Fig. 5, the dotted lines for HD and H2D+ show the abundances without the correction of Hirata & Padmanabhan (2006) relative to the radiation emitted during the hydrogen recombination. |
| Open with DEXTER | |
Table 4:
Relative abundances
![]() of deuterium species at redshifts z=1000, z=100 and z=10 in the SBBC model.
of deuterium species at redshifts z=1000, z=100 and z=10 in the SBBC model.
3.3.3 Helium
The reaction rates we consider for helium are taken from Galli & Palla (1998). The results of the standard helium chemistry are shown in Fig. 7. In the first nonstandard BBN model we consider (Sect. 2.2), the formation of helium nuclei during the primordial nucleosynthesis is extremely efficient in the neutron-rich, low-density regions. But primordial chemistry begins after the zones with different densities are mixed by baryon diffusion and the nonstandard initial relative abundance of helium is identical to the standard one (see Table 1). The main feature of helium chemistry is the production of molecule HeH+ ([HeH+]
![]() =
=
![]() at z = 10). Table 5 gives the abundances at redshifts z=1000, z=100 and z=10.
at z = 10). Table 5 gives the abundances at redshifts z=1000, z=100 and z=10.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297fg7.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg151.png) |
Figure 7: Standard primordial chemistry of helium species. |
| Open with DEXTER | |
Table 5:
Relative abundances
![]() of helium species at redshifts z=1000, z=100 and z=10 in the SBBC model
of helium species at redshifts z=1000, z=100 and z=10 in the SBBC model
3.3.4 Lithium
We take the reaction rates for lithium chemistry from Galli & Palla (1998). Figure 8 and Table 6 show the evolution of the lithium species. As said before, lithium never recombines completely, and this is the reason why LiH is less abundant than LiH+ at low redshift: [LiH]
![]() and [LiH+]
and [LiH+]
![]() at z = 10.
at z = 10.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297fg8.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg162.png) |
Figure 8: Standard primordial chemistry of lithium species. |
| Open with DEXTER | |
Table 6:
Relative abundances
![]() of lithium species at redshifts z=1000, z=100 and z=10 in the SBBC model.
of lithium species at redshifts z=1000, z=100 and z=10 in the SBBC model.
Table 7:
Relative abundances
![]() of carbon species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
of carbon species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
3.3.5 Carbon
The presence of neutral or ionized carbon at high redshift is important to determinate the cosmic background temperature at ![]() in order to compare the result with models. Songaila et al. (1994,1995) used this technique to prove the existence of carbon in some high redshift diffuse gas. In the second paper, the detection of absorption due to the first level of neutral carbon fine structure, in a z = 1.776 cloud toward quasar Q1331+170, allows them to deduce that the background temperature is
in order to compare the result with models. Songaila et al. (1994,1995) used this technique to prove the existence of carbon in some high redshift diffuse gas. In the second paper, the detection of absorption due to the first level of neutral carbon fine structure, in a z = 1.776 cloud toward quasar Q1331+170, allows them to deduce that the background temperature is
![]() K at z = 1.776. This result agrees with the theoretical value (7.58 K). The same method was used by Molaro et al. (2002), who studied the fine structure levels of
K at z = 1.776. This result agrees with the theoretical value (7.58 K). The same method was used by Molaro et al. (2002), who studied the fine structure levels of ![]() in a Ly-
in a Ly-![]() system at z = 3.025 toward Q0347-3819. Their result (
system at z = 3.025 toward Q0347-3819. Their result (
![]() K) agrees with the standard temperature limits.
K) agrees with the standard temperature limits.
A gas phase chemical model of the chemistry of CH and CH+ was presented by Dalgarno (1976), then Prasad & Huntress (1980) presented a gas phase chemical model of the chemistry in interstellar clouds, including the C, N and O species. We consider here the evolution of the following carbon species: C, C+, C-, CH, CH+, CH2 and CH2+. The reaction rates are taken from the UMIST database (Woodall et al. 2007), except for five reactions: reaction C7 (Lipovka et al. 2007), the two charge transfers C8 and C9 between C, H and their respective ions (Stancil et al. 1998a), the recombination C48 (Omukai 2000) and the photoionisation C49, whose cross section is taken from Verner et al. (1996, see Table A.5 of the Appendix#. The main reaction leading to the synthesis of CH is clearly the radiative association C15 (C + H
![]() CH +
CH + ![]() ), but we also include the neutral reaction C12 and the two associative detachments C17 and C27. Among the numerous reactions destroying CH, the destructive collisional reactions with atomic hydrogen (reactions C10 and C11), and the charge exchange with H+ (reaction C16) are the most important. The molecular ion CH+ is created by the radiative association C+ + H
), but we also include the neutral reaction C12 and the two associative detachments C17 and C27. Among the numerous reactions destroying CH, the destructive collisional reactions with atomic hydrogen (reactions C10 and C11), and the charge exchange with H+ (reaction C16) are the most important. The molecular ion CH+ is created by the radiative association C+ + H
![]() CH+ +
CH+ + ![]() (reaction C23), the collisional reactions C14 and C18, and the charge exchanges C16 (with H+) and C19 (with H2+), the main ones being C16 and C23. Destruction of CH+ occurs mainly by collisions with H (reaction C25) and dissociative recombination (reaction C26).
(reaction C23), the collisional reactions C14 and C18, and the charge exchanges C16 (with H+) and C19 (with H2+), the main ones being C16 and C23. Destruction of CH+ occurs mainly by collisions with H (reaction C25) and dissociative recombination (reaction C26).
In the reaction sets for carbon, nitrogen and oxygen chemistries (see Appendix A), we do not include photoionizations or photodissociations of primordial molecules (e.g. CH+ + ![]()
![]() C+ + H, NH2 +
C+ + H, NH2 + ![]()
![]() NH2+ + e-). These processes are especially important in the interstellar medium, where strong UV photons constitute the background radiation, whereas the primordial molecules are embedded in a background radiation that is made of much softer microwave photons. In order to be sure not to neglect important photoprocesses, we made test calculations including photoionizations of the neutral molecules and photodissociations of all the molecules based on C, N and O. We computed the rates of these reactions using the CMB intensity and the constant cross section
NH2+ + e-). These processes are especially important in the interstellar medium, where strong UV photons constitute the background radiation, whereas the primordial molecules are embedded in a background radiation that is made of much softer microwave photons. In order to be sure not to neglect important photoprocesses, we made test calculations including photoionizations of the neutral molecules and photodissociations of all the molecules based on C, N and O. We computed the rates of these reactions using the CMB intensity and the constant cross section
![]() cm2. Indeed, this cross section gives a good order of magnitude estimate for the photoionization rates (van Dishoeck 1988) and constitutes an upper limit for photodissociation processes. The results of the chemistry calculations were not changed when considering these photoprocesses.
cm2. Indeed, this cross section gives a good order of magnitude estimate for the photoionization rates (van Dishoeck 1988) and constitutes an upper limit for photodissociation processes. The results of the chemistry calculations were not changed when considering these photoprocesses.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297ca.eps}\\
\vspace{3mm}
\includegraphics[width=9cm,clip]{11297cb.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg250.png) |
Figure 9:
Primordial chemistry of carbon species for the SBBC ( upper panel) and NSBBC2 models ( lower panel). The main difference between the two frames is a global increase of every relative abundance by a factor |
| Open with DEXTER | |
Table 7 gives the abundances of the carbon species at redshifts z=1000, z=100 and z=10 for the three models SBBC, NSBBC1 and NSBBC2. Figure 9 shows the evolution of these abundances as a function of redshift in the standard case and in the NSBBC2 case. We observe that the main difference between the standard and NSBBC2 runs is a global increase of every relative abundance by a factor ![]() 30 in the NSBBC2 run. Except for this shift, the evolution of every carbon species is quite similar in the two scenarios. This is not surprising, since the carbon chemistry is mainly determined by reactions with much more abundant hydrogen species like H, H+, H-, H2 or H2+, and these species have the same abundances in all our models. The results of the NSBBC1 run are quite close to the standard one. We also note that the final amount of CH is about 20 times smaller than the LiH abundance in the standard model. This ratio is about 7.5 for HD+ and H2D+. But we note that in the NSBBC2 case, molecule CH is as abundant as LiH and more abundant than HD+ and H2D+ (about 4.5 times).
30 in the NSBBC2 run. Except for this shift, the evolution of every carbon species is quite similar in the two scenarios. This is not surprising, since the carbon chemistry is mainly determined by reactions with much more abundant hydrogen species like H, H+, H-, H2 or H2+, and these species have the same abundances in all our models. The results of the NSBBC1 run are quite close to the standard one. We also note that the final amount of CH is about 20 times smaller than the LiH abundance in the standard model. This ratio is about 7.5 for HD+ and H2D+. But we note that in the NSBBC2 case, molecule CH is as abundant as LiH and more abundant than HD+ and H2D+ (about 4.5 times).
We note that the formation of carbon molecules is comparatively as efficient as the formation of H2 or HD. Indeed, the ratio of the most abundant carbon molecule CH to C is
![]() at z = 10 in our three models. For comparison, we have the following ratios fot the most abundant molecule based on each one of the light elements:
at z = 10 in our three models. For comparison, we have the following ratios fot the most abundant molecule based on each one of the light elements:
![]() ,
,
![]() ,
,
![]() and
and
![]() at z = 10.
at z = 10.
Lipovka et al. (2007) investigated the formation of carbon molecules but with a higher initial ratio [C]/[H] = 10-10. They found a final CH abundance of 10-14, which means a similar efficiency toward molecular formation, even if their chemical model is different.
3.3.6 Nitrogen
We take the reaction rates for nitrogen chemistry from the UMIST database, except for the photoionisation N41 (Verner et al. 1996, see Table A.6 of the Appendix) and study the evolution of N, N+, NH, NH+, NH2 and NH2+. The main reactions responsible for the creation of NH are collisions of nitrogen atoms with H2 and H- (reactions N5 and N14 respectively). We consider many processes that can lead to the destruction of NH, the most important of them being collisions with H (reaction N4) and the charge exchange H+ + NH
![]() NH+ + H (reaction N10). The latter reaction is at the same time one of the main processes responsible for the synthesis of the molecular ion NH+, together with the two collisional reactions N6 (between N and H2+) and N7 (between N+ and molecular hydrogen). Among the different processes destroying NH+, the dissociative recombination N13 appears to be the most efficient.
NH+ + H (reaction N10). The latter reaction is at the same time one of the main processes responsible for the synthesis of the molecular ion NH+, together with the two collisional reactions N6 (between N and H2+) and N7 (between N+ and molecular hydrogen). Among the different processes destroying NH+, the dissociative recombination N13 appears to be the most efficient.
Figure 10 shows the evolution of the nitrogen chemistry as a function of redshift in the standard and NSBBC2 cases. The molecular ion NH+ dominates the nitrogen chemistry from
![]() down to
down to ![]() ,
and is then surpassed by NH, which has a peak around z=40. The final relative abundances at z = 10 are [NH]
,
and is then surpassed by NH, which has a peak around z=40. The final relative abundances at z = 10 are [NH]
![]() and [NH]
and [NH]
![]() .
As for carbon, the main difference between the SBBC and NSBBC2 scenarios is a global increase of every relative abundance (by a factor about 150) in the NSBBC2. Apart from this shift, the evolution of all the nitrogen species is quite similar in the two models. The results of the NSBBC1 run are almost identical to the standard one, since nitrogen nuclei are produced in the same amount in the two corresponding nucleosynthesis scenarios (Table 1). Table 8 gives the abundances at redshifts z=1000, z=100 and z=10 for the three models.
.
As for carbon, the main difference between the SBBC and NSBBC2 scenarios is a global increase of every relative abundance (by a factor about 150) in the NSBBC2. Apart from this shift, the evolution of all the nitrogen species is quite similar in the two models. The results of the NSBBC1 run are almost identical to the standard one, since nitrogen nuclei are produced in the same amount in the two corresponding nucleosynthesis scenarios (Table 1). Table 8 gives the abundances at redshifts z=1000, z=100 and z=10 for the three models.
The formation of molecules based on N is less effective than the formation of carbon molecules. When considering the most abundant species, NH, one has indeed:
![]() for the three scenarios.
for the three scenarios.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297na.eps}\\
\vspace{4mm}
\includegraphics[width=9cm,clip]{11297nb.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg261.png) |
Figure 10: Primordial chemistry of nitrogen species for the SBBC ( upper panel) and NSBBC2 models ( lower panel). The formation of molecules based on nitrogen is less effective than the formation of carbon molecules. The main difference between the two models shown here is a global increase of every relative abundance by more than two orders of magnitude in the nonstandard model. Except for this shift, the evolution of the nitrogen species is similar in the two scenarios. The results of the NSBBC1 model are identical to the standard ones. |
| Open with DEXTER | |
Table 8:
Relative abundances
![]() of nitrogen species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
of nitrogen species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297oa.eps}\\
\vspace{3mm}
\includegraphics[width=9cm,clip]{11297ob.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg312.png) |
Figure 11: Primordial chemistry of oxygen species for the SBBC ( upper panel) and NSBBC2 models ( lower panel). OH is clearly the most abundant oxygen molecule. Primordial water molecules show a peak around z = 30 but are then greatly depleted at lower redshifts. The main difference between the two models is a global increase of every relative abundance by more than two orders of magnitude in the nonstandard NSBBC2 model. Except for this shift, the evolution of the oxygen species is similar in the two scenarios. The results of the NSBBC1 model are very close to the standard ones. |
| Open with DEXTER | |
3.3.7 Oxygen
We consider the following species for oxygen chemistry: O, O+, O-, OH, OH+, H2O and H2O+. Table A.7 shows the reactions we include in our chemical model. The rates for reactions O61 and O62 come from Le Bourlot et al. (1993). The rate for recombination O58 is taken from Péquignot et al. (1991) and the cross section for photoionisation O59 from Verner et al. (1996). All other reaction rates come from the UMIST database. The results of oxygen chemistry are shown in Fig. 11 and Table 9 shows the relative abundances of the oxygen species at redshift z=1000, z=100 and z=10 for the three models. OH and OH+ are the main molecular species based on oxygen at the end of the Dark Ages. In order to synthesize OH, we consider, among many other reactions, the radiative association O9, collisions between H and O- (reaction O10) and between H- and O (reaction O13), and the collisional reaction O15. Note that the first two processes are clearly the most effective. Numerous reactions destroy OH molecules, but collisions with H (reactions O11, O12 and O47) and H+ (reaction O14) dominate. The molecular ion OH+ is produced via the charge exchange O14 (H+ + OH
![]() OH+ + H), the other reactions being less important. OH+ is mainly destroyed by dissociative recombination (reaction O22). The collisions with hydrogen atoms (OH+ + H
OH+ + H), the other reactions being less important. OH+ is mainly destroyed by dissociative recombination (reaction O22). The collisions with hydrogen atoms (OH+ + H
![]() O+ + H2) are efficient at very high redshift only (z > 300). The very strong depletion of O- is caused by the photoprocess O- +
O+ + H2) are efficient at very high redshift only (z > 300). The very strong depletion of O- is caused by the photoprocess O- + ![]()
![]() O + e- (reaction O5). But the UMIST rate for that process assumes an interstellar UV background which obviously is inappropriate for our study. We thus expect a final O- abundance much higher than plotted in Fig. 11.
O + e- (reaction O5). But the UMIST rate for that process assumes an interstellar UV background which obviously is inappropriate for our study. We thus expect a final O- abundance much higher than plotted in Fig. 11.
Table 9:
Relative abundances
![]() of oxygen species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
of oxygen species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
The tendency toward molecular formation is quite strong: we observe
![]() at z = 10 in our three standard and nonstandard calculations, and even if the initial oxygen abundances at z = 104 are very weak, OH is only one order of magnitude less abundant than HD+ and H2D+ in the NSBBC2 run. We note the formation of primordial water molecules around z = 30. They are mainly synthesized by reaction O47 (H + OH
at z = 10 in our three standard and nonstandard calculations, and even if the initial oxygen abundances at z = 104 are very weak, OH is only one order of magnitude less abundant than HD+ and H2D+ in the NSBBC2 run. We note the formation of primordial water molecules around z = 30. They are mainly synthesized by reaction O47 (H + OH
![]() H2O +
H2O + ![]() )
but at lower redshifts their abundance severly drops due to the destructive effect of reaction O60 (H+ + H2O
)
but at lower redshifts their abundance severly drops due to the destructive effect of reaction O60 (H+ + H2O
![]() H2O+ + H). Again, as for carbon and nitrogen, the SBBC and NSBBC2 runs differ mainly by a global shift in relative abundance (by more than two orders of magnitude).
H2O+ + H). Again, as for carbon and nitrogen, the SBBC and NSBBC2 runs differ mainly by a global shift in relative abundance (by more than two orders of magnitude).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297fa.eps}\\
\vspace{3mm}
\includegraphics[width=9cm,clip]{11297fb.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg370.png) |
Figure 12: Primordial chemistry of fluorine species for the SBBC ( upper panel) and NSBBC2 models ( lower panel). HF is more efficiently created by a factor 500 in the NSBBC2. The results of the NSBBC1 model are almost identical to the standard ones. |
| Open with DEXTER | |
3.3.8 Fluorine
Even if the abundance of primary fluorine is much below the abundances of primordial C, N and O at the end of the Big Bang nucleosynthesis, the molecule HF could be efficiently formed in the early Universe for two reasons: the ionization potential of F is greater than that of hydrogen, and the binding energy of the hydrogen atom in HF is greater than the binding energy of H2. The chemistry of fluorine in the post-recombination epoch has been studied in Puy et al. (2007). We use here the same set of reactions (see Table A.8 of the Appendix).
Figure 12 and Table 10 show the evolution of the fluorine chemistry as a function of redshift in the standard and NSBBC2 cases. We clearly see that the fluorine chemistry is comparatively more efficient than the CNO chemistries:
![]() in the three models. The enhancement factor for HF in the NSBBC2 model compared to the standard value is 500.
in the three models. The enhancement factor for HF in the NSBBC2 model compared to the standard value is 500.
4 Summary and conclusion
Molecules play an important role in the process of gravitational collapse through the mechanism of thermal instability (see Abel et al. 2000; Silk 1977; Field 1965; Uehara et al. 1996; Fall & Rees 1985; Puy & Signore 1996). They provide an important cooling mechanism for primordial metal-free gas in different primordial contexts such as small halos virializing at high redshift (e.g. Bromm & Larson 2004; Ciardi & Ferrara 2005; Barkana & Loeb 2001) or early structure formation (Glover & Jappsen 2007; Maio et al. 2007).
The H2 molecule has long been recognized as the most important cooling agent, despite the absence of dipole moment, due to its high relative abundance in comparison with other molecules. For this reason H2 molecules are a key component of many dynamical situations and particularly in the context of a gravitational collapse. However, several studies (Yoshida et al. 2006; Abel et al. 2000; Tegmark et al. 1997; Ripamonti et al. 2002; Omukai & Nishi 1998) consider H2 as the only molecular coolant of the primordial gas, although HD can play an important role at low temperature. Indeed, Puy & Signore (1997) showed that, if the primordial gas cools below 200 K, HD molecules are the main cooling agent, despite their low number abundance. These results were confirmed in different astrophysical mediums (Ripamonti 2007; Uehara & Inutsuka 2000; Flower 2000; Nakamura & Umemura 2000; Nagakura & Omukai 2005; Flower & Pineau des Forêts 2001; Lipovka et al. 2005; Shchekinov & Vasiliev 2006). Recently, Prieto et al. (2008) analyzed the effects of H2, HD and LiH molecules in the cooling of primordial gas. Their simulations clearly showed that the gas, at low densities, reaches temperatures about 100 K and that the main coolant is H2. But at higher densities (n > 102 cm-3) HD dominates and the gas cools well below 100 K. The effects of LiH are negligible in all cases.
Table 10:
Relative abundances
![]() of fluorine species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
of fluorine species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
We analyzed in this paper the primordial chemistry of eight elements (hydrogen, deuterium, helium, lithium, carbon, nitrogen, oxygen and fluorine), with the aim of determining the amount of primordial molecules based on elements heavier than lithium. Heavier molecules with high electric dipole moments could be important, if created in sufficient quantities, during the formation of the first structures in the Universe. We considered initial elemental abundances taken from two different nucleosynthesis contexts: the standard Big Bang nucleosynthesis model and nonstandard nucleosynthesis based on baryon density fluctuations. In both contexts, the baryon-to-photon ratio ![]() (the averaged value for the nonstandard model) was in accordance with the latest result of the WMAP experiment (
(the averaged value for the nonstandard model) was in accordance with the latest result of the WMAP experiment (
![]() ), and the resulting abundances agreed with the observed primordial abundances of deuterium and helium.
), and the resulting abundances agreed with the observed primordial abundances of deuterium and helium.
The most abundant primordial molecules based on elements heavier than lithium are CH and OH. Chemistry calculation assuming standard BBN initial abundances yields
![]() and
and
![]() at z = 10. NH molecules are less abundant:
at z = 10. NH molecules are less abundant:
![]() .
.
We also made two nonstandard chemistry calculations, considering two specific cases of inhomogenous BBN. In the first one, primordial nucleosynthesis abundances for C, N, O and F are only very slightly higher than in the standard case. For that reason, the chemistry of elements heavier than lithium in that context is very similar to the standard chemistry. But in the second nonstandard BBN case, the final heavy element abundances are enhanced by globally two orders of magnitude. In that case, the relative abundances of molecular species based on carbon, nitrogen, oxygen or fluorine are modified by essentially the same factor, and molecules CH are as abundant as LiH and more abundant than HD+ and H2D+:
![]() at z = 10. The details of the chemistry (e.g. the most important species, the most effective reactions, ...) are weakly affected.
at z = 10. The details of the chemistry (e.g. the most important species, the most effective reactions, ...) are weakly affected.
Glover & Abel (2008) investigated the effects of the chemical rate coefficient uncertainties in the primordial chemistry of light elements. They showed that the large uncertainties in the associative detachment and mutual neutralization rates have an impact on the thermal evolution of the gas. As regards the heavy molecules discussed in the present work, the main reactions creating or destroying them are affected by uncertainties that can come to a factor 2. Moreover, some of the rates included in our model are given for a more restricted temperature range than the one of our calculations (from z = 104 to z = 10 the Universe cools from
![]() K down to a few Kelvins). We nonetheless assumed that these rates were valid everywhere in that range. Concerning oxygen chemistry, the UMIST rate for reaction O5 (O
K down to a few Kelvins). We nonetheless assumed that these rates were valid everywhere in that range. Concerning oxygen chemistry, the UMIST rate for reaction O5 (O
![]()
![]() O + e-) is largely not appropriate to the chemistry of the Dark Ages. As one of the two main reactions creating OH is H + O-
O + e-) is largely not appropriate to the chemistry of the Dark Ages. As one of the two main reactions creating OH is H + O-
![]() OH + e-, the use of a better rate for O5 could increase the OH relative abundance obtained in this work.
OH + e-, the use of a better rate for O5 could increase the OH relative abundance obtained in this work.
Knowledge of primordial molecular abundances of heavy molecules could be important in different contexts, cosmologically as well as for the formation of the first structures and stars. A cosmological influence of primordial molecules was suggested by Dubrovich (1977). The measure of CMB anisotropies gives accurate indications on the fluctuation spectrum which led to present great structures. In this way, it is possible that primordial molecular clouds affect the anisotropy spectrum at small scales via resonant scattering of CMB photons on primordial molecules (Schleicher et al. 2008; Maoli et al. 1996,1994; for a review see Basu 2007; or Signore & Puy 2009). The first spectral line surveys searching for primordial signals have been done with the Odin satellite (Persson et al. 2009). Their work may be considered as a pilot study for the forthcoming observations with the Herschel Space Observatory launched on May 14, 2009. One of the most promising molecule has been proven to be HeH+. Molecules such as CH, NH or OH have electric dipole moments of the same order as HeH+. We have shown in this work that their abundances are lower by several orders of magnitude than HeH+ abundance. But the fact that CH could be more abundant than molecules such as HD+ and H2D+ could open new interesting perspectives and detailed calculations have still to be done. In addition to molecules, heavy atoms and ions can also be used as a tool of probing the early Universe. Basu et al. (2004) considered the opacity generated by the scattering of CMB photons on heavy atoms like carbon, oxygen, silicon or iron (and on their respective ions). They found that the Planck HFI detectors will be able to get strong constraints (
10-3-10-4 solar abundance) on the most important atoms and ions (CNO) in the interval
![]() .
Harwit & Spaans (2003) also examined the possibility of detecting the imprint left by the presence of carbon or oxygen on the CMB during the Dark Ages.
.
Harwit & Spaans (2003) also examined the possibility of detecting the imprint left by the presence of carbon or oxygen on the CMB during the Dark Ages.
Numerical simulations of star formation are a very important and popular problem in modern cosmology. If solved successfully, it can add a lot of information to our knowledge of the evolution of all kinds of cosmic structures and the Universe as a whole. Star formation is determined by complex chemical, dynamical and thermodynamical processes (see McGreer & Bryan 2008), each of which plays an important role during some or all parts of the whole process, and the impact of cooling by heavier molecules on the formation of the first (Population III) stars is a new open question. Moreover, it is interesting to note that these first stars were themselves an important source of metallicity (Cooke et al. 2009), and cooling by heavier molecules could be even more important for later star formation.
Acknowledgements
We acknowledge the PNCG (Programme National Cosmologie et Galaxies) and the PNPS (Programme National de Physique Stellaire) for their financial assistance, and Daniel Pfenniger, Anton Lipovka and Dahbia Talbi for fruitful discussions. This work was in part supported by the Swiss National Science Foundation (grant 200020-122287).
Appendix A: Reaction rates for the post-recombination chemistry
We list in Tables A.1 to A.8 the chemical reactions considered in our calculations.
Table A.1: List of reactions for the hydrogen chemistry.
Table A.2: List of reactions for the deuterium chemistry.
Table A.3: List of reactions for the helium chemistry.
Table A.4: List of reactions for the lithium chemistry.
Table A.5: List of reactions for the carbon chemistry.
Table A.6: List of reactions for the nitrogen chemistry.
Table A.7: List of reactions for the oxygen chemistry.
Table A.8: List of reactions for the fluorine chemistry.
References
- Abel, T., Anninos, P., Zhang, Y., & Norman, M. L. 1997, New Astron., 2, 181 [NASA ADS] [CrossRef] (In the text)
- Abel, T., Bryan, G. L., & Norman, M. L. 2000, ApJ, 540, 39 [NASA ADS] [CrossRef]
- Affleck, I., & Dine, M. 1985, Nucl. Phys. B, 249, 361 [NASA ADS] [CrossRef]
- Applegate, J. H., & Hogan, C. J. 1985, Phys. Rev. D, 31, 3037 [NASA ADS] [CrossRef]
- Barkana, R., & Loeb, A. 2001, Phys. Rep., 349, 125 [NASA ADS] [CrossRef]
- Basu, K. 2007, New Astron. Rev., 51, 431 [NASA ADS] [CrossRef] (In the text)
- Basu, K., Hernández-Monteagudo, C., & Sunyaev, R. A. 2004, A&A, 416, 447 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bromm, V., & Larson, R. B. 2004, ARA&A, 42, 79 [NASA ADS] [CrossRef]
- Burles, S., Nollett, K. M., & Turner, M. S. 2001, ApJ, 552, L1 [NASA ADS] [CrossRef] (In the text)
- Ciardi, B., & Ferrara, A. 2005, Space Sci. Rev., 116, 625 [NASA ADS] [CrossRef]
- Cooke, J., Cooray, A., Chary, R.-R., et al. 2009,[ArXiv e-prints 0902.4602] (In the text)
- Cyburt, R. H., Fields, B. D., & Olive, K. A. 2003, Phys. Lett. B, 567, 227 [NASA ADS] [CrossRef]
- Dalgarno, A. 1976, in Atomic processes and applications, ed. P. G. Burke (Amsterdam, Netherlands: North-Holland Publ. Co.), 109 (In the text)
- Dolgov, A., & Silk, J. 1993, Phys. Rev. D, 47, 4244 [NASA ADS] [CrossRef]
- Dubrovich, V. K. 1977, Sov. Astron. Lett., 3, 128 [NASA ADS] (In the text)
- Dunkley, J., Komatsu, E., Nolta, M. R., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef] (In the text)
- Fall, S. M., & Rees, M. J. 1985, ApJ, 298, 18 [NASA ADS] [CrossRef]
- Fendt, W. A., Chluba, J., Rubiño-Martín, J. A., & Wandelt, B. D. 2009, ApJS, 181, 627 [NASA ADS] [CrossRef]
- Field, G. B. 1965, ApJ, 142, 531 [NASA ADS] [CrossRef]
- Flower, D. R. 2000, MNRAS, 318, 875 [NASA ADS] [CrossRef]
- Flower, D. R., & Pineau des Forêts, G. 2001, MNRAS, 323, 672 [NASA ADS] [CrossRef]
- Galli, D., & Palla, F. 1998, A&A, 335, 403 [NASA ADS]
- Glover, S. C. O., & Abel, T. 2008, MNRAS, 388, 1627 [NASA ADS] [CrossRef]
- Glover, S. C. O., & Jappsen, A.-K. 2007, ApJ, 666, 1 [NASA ADS] [CrossRef]
- Glover, S. C. O., & Savin, D. W. 2009, MNRAS, 393, 911 [NASA ADS] [CrossRef]
- Harwit, M., & Spaans, M. 2003, ApJ, 589, 53 [NASA ADS] [CrossRef] (In the text)
- Hindmarsh, A. C., & Petzold, L. R. 1995, Comput. Phys., 9, 34 [NASA ADS] [CrossRef] (In the text)
- Hirata, C. M., & Padmanabhan, N. 2006, MNRAS, 372, 1175 [NASA ADS] [CrossRef] (In the text)
- Jedamzik, K., Fuller, G. M., Mathews, G. J., & Kajino, T. 1994, ApJ, 422, 423 [NASA ADS] [CrossRef]
- Kawano, L. 1992, Fermilab-Pub-92/004-A (In the text)
- Khlopov, M. Y., & Kouvaris, C. 2008, Phys. Rev. D, 77, 065002 [NASA ADS] [CrossRef]
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] (In the text)
- Kompaneets, A. S. 1957, Sov. Phys. JETP, 4, 730
- Le Bourlot, J., Pineau Des Forets, G., Roueff, E., & Flower, D. R. 1993, A&A, 267, 233 [NASA ADS] (In the text)
- Lepp, S., & Shull, J. M. 1984, ApJ, 280, 465 [NASA ADS] [CrossRef]
- Lepp, S., Stancil, P. C., & Dalgarno, A. 2002, J. Phys. B Atom. Mol. Phys., 35, 57 [NASA ADS] [CrossRef]
- Lipovka, A., Núñez-López, R., & Avila-Reese, V. 2005, MNRAS, 361, 850 [NASA ADS] [CrossRef]
- Lipovka, A., Saucedo, J., & Lipovka, N. M. 2007, ArXiv e-prints 0703547 (In the text)
- Maio, U., Dolag, K., Ciardi, B., & Tornatore, L. 2007, MNRAS, 379, 963 [NASA ADS] [CrossRef]
- Malaney, R. A., & Fowler, W. A. 1988, ApJ, 333, 14 [NASA ADS] [CrossRef]
- Maoli, R., Melchiorri, F., & Tosti, D. 1994, ApJ, 425, 372 [NASA ADS] [CrossRef]
- Maoli, R., Ferrucci, V., Melchiorri, F., Signore, M., & Tosti, D. 1996, ApJ, 457, 1 [NASA ADS] [CrossRef]
- Matsuura, S., Dolgov, A. D., & Nagataki, S. 2004, Progr. Theor. Phys., 112, 971 [NASA ADS] [CrossRef]
- Matsuura, S., Fujimoto, S.-I., Nishimura, S., Hashimoto, M.-A., & Sato, K. 2005, Phys. Rev. D, 72, 123505 [NASA ADS] [CrossRef]
- Matsuura, S., Fujimoto, S.-I., Hashimoto, M.-A., & Sato, K. 2007, Phys. Rev. D, 75, 068302 [NASA ADS] [CrossRef]
- McGreer, I. D., & Bryan, G. L. 2008, ApJ, 685, 8 [NASA ADS] [CrossRef] (In the text)
- Molaro, P., Levshakov, S. A., Dessauges-Zavadsky, M., & D'Odorico, S. 2002, A&A, 381, 64 [NASA ADS] [CrossRef] (In the text)
- Nagakura, T., & Omukai, K. 2005, MNRAS, 364, 1378 [NASA ADS] [CrossRef]
- Nakamura, F., & Umemura, M. 2000, in The First Stars, ed. A. Weiss, T. G. Abel, & V. Hill, 263
- Omukai, K. 2000, ApJ, 534, 809 [NASA ADS] [CrossRef] (In the text)
- Omukai, K., & Nishi, R. 1998, ApJ, 508, 141 [NASA ADS] [CrossRef]
- Peebles, P. J. E. 1968, ApJ, 153, 1 [NASA ADS] [CrossRef]
- Peebles, P. J. E., & Dicke, R. H. 1968, ApJ, 154, 891 [NASA ADS] [CrossRef]
- Péquignot, D., Petitjean, P., & Boisson, C. 1991, A&A, 251, 680 [NASA ADS] (In the text)
- Persson, C. M., Maoli, R., Encrenaz, P., et al. 2009, A&A, submitted (In the text)
- Pfenniger, D., & Puy, D. 2003, A&A, 398, 447 [NASA ADS] [CrossRef] [EDP Sciences]
- Prasad, S. S., & Huntress, Jr., W. T. 1980, ApJS, 43, 1 [NASA ADS] [CrossRef] (In the text)
- Prieto, J. P., Infante, L., & Jimenez, R. 2008, ArXiv e-prints (In the text)
- Puy, D., Alecian, G., Le Bourlot, J., Leorat, J., & Pineau Des Forets, G. 1993, A&A, 267, 337 [NASA ADS]
- Puy, D., Dubrovich, V., Lipovka, A., Talbi, D., & Vonlanthen, P. 2007, A&A, 476, 685 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Puy, D., & Signore, M. 1996, A&A, 305, 371 [NASA ADS]
- Puy, D., & Signore, M. 1997, New Astron., 2, 299 [NASA ADS] [CrossRef]
- Puy, D., & Signore, M. 2007, New Astron. Rev., 51, 411 [NASA ADS] [CrossRef]
- Rauscher, T., Applegate, J. H., Cowan, J. J., Thielemann, F.-K., & Wiescher, M. 1994, ApJ, 429, 499 [NASA ADS] [CrossRef]
- Ripamonti, E. 2007, MNRAS, 376, 709 [NASA ADS] [CrossRef]
- Ripamonti, E., Haardt, F., Ferrara, A., & Colpi, M. 2002, MNRAS, 334, 401 [NASA ADS] [CrossRef]
- Saslaw, W. C., & Zipoy, D. 1967, Nature, 216, 976 [NASA ADS] [CrossRef]
- Schleicher, D. R. G., Galli, D., Palla, F., et al. 2008, A&A, 490, 521 [NASA ADS] [CrossRef] [EDP Sciences]
- Shchekinov, Y. A., & Vasiliev, E. O. 2006, MNRAS, 368, 454 [NASA ADS]
- Signore, M., & Puy, D. 1999, New Astron. Rev., 43, 185 [NASA ADS] [CrossRef]
- Signore, M., & Puy, D. 2009, EPJ C, 59, 117 [NASA ADS] (In the text)
- Silk, J. 1977, ApJ, 211, 638 [NASA ADS] [CrossRef]
- Songaila, A., Cowie, L. L., Vogt, S., et al. 1994, Nature, 371, 43 [NASA ADS] [CrossRef]
- Songaila, A., Hu, E. M., & Cowie, L. L. 1995, Nature, 375, 124 [NASA ADS] [CrossRef]
- Stancil, P. C., Havener, C. C., Krstic, P. S., et al. 1998a, ApJ, 502, 1006 [NASA ADS] [CrossRef] (In the text)
- Stancil, P. C., Lepp, S., & Dalgarno, A. 1998b, ApJ, 509, 1 [NASA ADS] [CrossRef]
- Steigman, G. 2007, Ann. Rev. Nuclear and Particle Science, 57, 463 [NASA ADS] [CrossRef] (In the text)
- Tegmark, M., Silk, J., Rees, M. J., et al. 1997, ApJ, 474, 1 [NASA ADS] [CrossRef]
- Uehara, H., & Inutsuka, S.-I. 2000, ApJ, 531, L91 [NASA ADS] [CrossRef]
- Uehara, H., Susa, H., Nishi, R., Yamada, M., & Nakamura, T. 1996, ApJ, 473, L95 [NASA ADS] [CrossRef]
- van Dishoeck, E. F. 1988, in Rate coefficients in astrochemistry (Dordrecht and Norwell, MA: Kluwer Academic Publishers), 49 (In the text)
- Verner, D. A., & Ferland, G. J. 1996, ApJS, 103, 467 [NASA ADS] [CrossRef] (In the text)
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] (In the text)
- Winteler, C. 2007, Master Thesis, University of Basel, Switzerland (In the text)
- Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 466, 1197 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Yoshida, N., Omukai, K., Hernquist, L., & Abel, T. 2006, ApJ, 652, 6 [NASA ADS] [CrossRef]
Footnotes
- ... abundances
![[*]](/icons/foot_motif.png)
- Alternative abundances for 4He and 7Li are written in parentheses.
- ... energy
![[*]](/icons/foot_motif.png)
- New results on the complex helium and hydrogen recombinations are given in Fendt et al. (2009, see also references therein).
- ... database
![[*]](/icons/foot_motif.png)
- http://www.udfa.net
All Tables
Table 1:
Relative abundances
![]() of the elements
at the end of Big Bang nucleosynthesis for the SBBN and for two nonstandard BBN scenarios.
of the elements
at the end of Big Bang nucleosynthesis for the SBBN and for two nonstandard BBN scenarios.
Table 2: Recombination redshifts for hydrogen, deuterium and helium.
Table 3:
Relative abundances
![]() of hydrogen species at redshifts z=1000, z=100 and z=10 in the SBBC model.
of hydrogen species at redshifts z=1000, z=100 and z=10 in the SBBC model.
Table 4:
Relative abundances
![]() of deuterium species at redshifts z=1000, z=100 and z=10 in the SBBC model.
of deuterium species at redshifts z=1000, z=100 and z=10 in the SBBC model.
Table 5:
Relative abundances
![]() of helium species at redshifts z=1000, z=100 and z=10 in the SBBC model
of helium species at redshifts z=1000, z=100 and z=10 in the SBBC model
Table 6:
Relative abundances
![]() of lithium species at redshifts z=1000, z=100 and z=10 in the SBBC model.
of lithium species at redshifts z=1000, z=100 and z=10 in the SBBC model.
Table 7:
Relative abundances
![]() of carbon species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
of carbon species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
Table 8:
Relative abundances
![]() of nitrogen species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
of nitrogen species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
Table 9:
Relative abundances
![]() of oxygen species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
of oxygen species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
Table 10:
Relative abundances
![]() of fluorine species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
of fluorine species at redshifts z=1000, z=100 and z=10 in the SBBC (left), NSBBC1 (middle) and NSBBC2 (right) models.
Table A.1: List of reactions for the hydrogen chemistry.
Table A.2: List of reactions for the deuterium chemistry.
Table A.3: List of reactions for the helium chemistry.
Table A.4: List of reactions for the lithium chemistry.
Table A.5: List of reactions for the carbon chemistry.
Table A.6: List of reactions for the nitrogen chemistry.
Table A.7: List of reactions for the oxygen chemistry.
Table A.8: List of reactions for the fluorine chemistry.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297fg1.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg88.png) |
Figure 1: Successive cosmological recombination for hydrogen, deuterium, helium and lithium in the standard model of primordial chemistry. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11297fg2.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg95.png) |
Figure 2: Successive recombinations of the carbon ions in the standard model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11297fg3.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg96.png) |
Figure 3: Successive recombinations of the nitrogen ions in the standard model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11297fg4.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg97.png) |
Figure 4: Successive recombinations of the oxygen ions in the standard model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297fg5.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg108.png) |
Figure 5: Standard primordial chemistry of hydrogen species. The dotted lines for H2, H- and H3+ show the abundances we would obtain without the correction of Hirata & Padmanabhan (2006) relative to the radiation emitted during the hydrogen recombination. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297fg6.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg131.png) |
Figure 6: Standard primordial chemistry of deuterium species. As in Fig. 5, the dotted lines for HD and H2D+ show the abundances without the correction of Hirata & Padmanabhan (2006) relative to the radiation emitted during the hydrogen recombination. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297fg7.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg151.png) |
Figure 7: Standard primordial chemistry of helium species. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297fg8.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg162.png) |
Figure 8: Standard primordial chemistry of lithium species. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297ca.eps}\\
\vspace{3mm}
\includegraphics[width=9cm,clip]{11297cb.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg250.png) |
Figure 9:
Primordial chemistry of carbon species for the SBBC ( upper panel) and NSBBC2 models ( lower panel). The main difference between the two frames is a global increase of every relative abundance by a factor |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297na.eps}\\
\vspace{4mm}
\includegraphics[width=9cm,clip]{11297nb.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg261.png) |
Figure 10: Primordial chemistry of nitrogen species for the SBBC ( upper panel) and NSBBC2 models ( lower panel). The formation of molecules based on nitrogen is less effective than the formation of carbon molecules. The main difference between the two models shown here is a global increase of every relative abundance by more than two orders of magnitude in the nonstandard model. Except for this shift, the evolution of the nitrogen species is similar in the two scenarios. The results of the NSBBC1 model are identical to the standard ones. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297oa.eps}\\
\vspace{3mm}
\includegraphics[width=9cm,clip]{11297ob.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg312.png) |
Figure 11: Primordial chemistry of oxygen species for the SBBC ( upper panel) and NSBBC2 models ( lower panel). OH is clearly the most abundant oxygen molecule. Primordial water molecules show a peak around z = 30 but are then greatly depleted at lower redshifts. The main difference between the two models is a global increase of every relative abundance by more than two orders of magnitude in the nonstandard NSBBC2 model. Except for this shift, the evolution of the oxygen species is similar in the two scenarios. The results of the NSBBC1 model are very close to the standard ones. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{11297fa.eps}\\
\vspace{3mm}
\includegraphics[width=9cm,clip]{11297fb.eps}
\end{figure}](/articles/aa/full_html/2009/31/aa11297-08/Timg370.png) |
Figure 12: Primordial chemistry of fluorine species for the SBBC ( upper panel) and NSBBC2 models ( lower panel). HF is more efficiently created by a factor 500 in the NSBBC2. The results of the NSBBC1 model are almost identical to the standard ones. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.