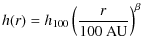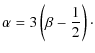| Issue |
A&A
Volume 502, Number 1, July IV 2009
|
|
|---|---|---|
| Page(s) | 367 - 383 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200810782 | |
| Published online | 13 May 2009 | |
Tracing the potential planet-forming regions around
seven pre-main-sequence stars![[*]](/icons/foot_motif.png) ,
,![[*]](/icons/foot_motif.png)
A. A. Schegerer1,2 - S. Wolf3,2 - C. A. Hummel4 - S. P. Quanz2 - A. Richichi4
1 - Helmholtz Zentrum München, German Research Center for
Environmental Health, Ingolstädter Landstraße 1, 85758 Neuherberg,
Germany
2 - Max Planck Institute for Astronomy (MPIA),
Königstuhl 17, 69117 Heidelberg, Germany
3 -
University of Kiel, Institute of Theoretical Physics and Astrophysics, Leibnizstraße 15, 24098 Kiel, Germany
4 - European Organisation for Astronomical Research in the Southern Hemisphere (ESO), Karl-Schwarzschild-Straße 2, 85748 Garching, Germany
Received 11 August 2008 / Accepted 7 April 2009
Abstract
Aims. We investigate the nature of the innermost regions with radii of several AUs of seven circumstellar disks around pre-main-sequence stars, T Tauri stars in particular. Our object sample contains disks apparently at various stages of their evolution. Both single stars and spatially resolved binaries are considered. In particular, we search for inner disk gaps as proposed for several young stellar objects (YSOs). When analyzing the underlying dust population in the atmosphere of circumstellar disks, the shape of the
![]() feature should additionally be investigated.
feature should additionally be investigated.
Methods. We performed interferometric observations in N band (
![]() )
with the Mid-Infrared Interferometric Instrument (MIDI) at the Very Large Telescope Interferometer (VLTI) using baseline lengths of between
)
with the Mid-Infrared Interferometric Instrument (MIDI) at the Very Large Telescope Interferometer (VLTI) using baseline lengths of between
![]() and
and
![]() .
The data analysis is based on radiative-transfer simulations using the Monte Carlo code MC3D by modeling simultaneously the spectral energy distribution (SED), N band spectra, and interferometric visibilities. Correlated and uncorrelated N band spectra are compared to investigate the radial distribution of the dust composition of the disk atmosphere.
.
The data analysis is based on radiative-transfer simulations using the Monte Carlo code MC3D by modeling simultaneously the spectral energy distribution (SED), N band spectra, and interferometric visibilities. Correlated and uncorrelated N band spectra are compared to investigate the radial distribution of the dust composition of the disk atmosphere.
Results. Spatially resolved mid-infrared (MIR) emission was detected in all objects. For four objects (DR Tau, RU Lup, S CrA N, and S CrA S), the observed N band visibilities and corresponding SEDs could be simultaneously simulated using a parameterized active disk-model. For the more evolved objects of our sample, HD 72106 and HBC 639, a purely passive disk-model provides the closest fit. The visibilities inferred for the source RU Lup allow the presence of an inner disk gap. For the YSO GW Ori, one of two visibility measurements could not be simulated by our modeling approach. All uncorrelated spectra reveal the
![]() silicate emission feature. In contrast to this, some correlated spectra of the observations of the more evolved objects do not show this feature, indicating a lack of small silicates in the inner versus the outer regions of these disks. We conclude from this observational result that more evolved dust grains can be found in the more central disk regions.
silicate emission feature. In contrast to this, some correlated spectra of the observations of the more evolved objects do not show this feature, indicating a lack of small silicates in the inner versus the outer regions of these disks. We conclude from this observational result that more evolved dust grains can be found in the more central disk regions.
Key words: infrared: stars - accretion, accretion disks - planetary systems: protoplanetary disks - astrochemistry - instrumentation: interferometer - radiative transfer
1 Introduction
In this study we present the results of highly spatially resolved observations of seven pre-main-sequence stars acquired with the instrument MIDI at the VLTI. Our study is focused on YSOs, T Tauri stars in particular, because this class of object is considered to represent the progenitors of solar-type stars. Studying the evolution of the disks around these stars with MIDI will provide us with an insight into the innermost and most dynamical regions where the earliest stages of the formation of a planetary system can be found.
In terms of spatial resolution, sensitivity, and spectral coverage, MIDI is the only instrument suitable to the simultaneous investigation of the temperature and density distributions in the innermost disk regions, accretion effects, and dust properties, i.e., in determining the evolutionary status of circumstellar disks. Even the presence of a (stellar) companion and its location can be investigated using MIDI. The analysis of (interferometric) observations of more than one YSO at different evolutionary stages provide the opportunity of verifying and constraining disk evolution and planet-formation models (e.g., Leinert et al. 2004).
Table 1: Object properties derived in previous measurements or in this study.
MIDI, operating in the atmospheric N band, is sensitive to warm
(
![]()
![]() )
matter, dust in particular,
located in the inner few AUs of young circumstellar disks.
It is generally assumed that the formation of planetary systems starts in these inner disk regions (Klahr 2004; Wünsch et al. 2005; Nagasawa et al. 2006). As a consequence of the planet-formation process, the disk structure and the composition of the dust population is assumed to evolve (Lissauer 1993; Gail 2003; Wolf 2007). The dust composition and density distribution of old T Tauri objects with an age of >
)
matter, dust in particular,
located in the inner few AUs of young circumstellar disks.
It is generally assumed that the formation of planetary systems starts in these inner disk regions (Klahr 2004; Wünsch et al. 2005; Nagasawa et al. 2006). As a consequence of the planet-formation process, the disk structure and the composition of the dust population is assumed to evolve (Lissauer 1993; Gail 2003; Wolf 2007). The dust composition and density distribution of old T Tauri objects with an age of >
![]() are assumed to have been
strongly modified. In these systems, the accretion onto the star is strongly reduced or has even stopped (Hartmann et al. 1993). Furthermore, the former circumstellar envelope of Class I objects as well as the
innermost disk regions (Calvet et al. 2002) may have disappeared in these objects. In contrast, in YSOs with an age of
are assumed to have been
strongly modified. In these systems, the accretion onto the star is strongly reduced or has even stopped (Hartmann et al. 1993). Furthermore, the former circumstellar envelope of Class I objects as well as the
innermost disk regions (Calvet et al. 2002) may have disappeared in these objects. In contrast, in YSOs with an age of ![]()
![]() ,
the accretion process usually plays a dominant role.
,
the accretion process usually plays a dominant role.
Binarity is a common phenomenon in YSOs. Extensive studies in the near-infrared (NIR) wavelength range, where a spatial resolution of between 0.005
![]() and 10
and 10
![]() was
reached, showed that between 23% and 55% of YSOs are binaries or even multiple systems (Simon et al. 1995; Köhler & Leinert 1998; Dûchene et al. 1999; Ratzka et al. 2005). In a theoretical study, Artymowicz & Lubow (1994) highlighted modifications to the structure of circumstellar and circumbinary disks resulting from a close companion. Furthermore, the nature of the infrared companions of T Tauri stars remains a matter of debate in terms of the structure and orientation of their circumstellar disks as well as their evolutionary stage (Koresko et al. 1997; McCabe et al. 2006).
was
reached, showed that between 23% and 55% of YSOs are binaries or even multiple systems (Simon et al. 1995; Köhler & Leinert 1998; Dûchene et al. 1999; Ratzka et al. 2005). In a theoretical study, Artymowicz & Lubow (1994) highlighted modifications to the structure of circumstellar and circumbinary disks resulting from a close companion. Furthermore, the nature of the infrared companions of T Tauri stars remains a matter of debate in terms of the structure and orientation of their circumstellar disks as well as their evolutionary stage (Koresko et al. 1997; McCabe et al. 2006).
Simultaneous modeling of the spectral energy distribution (SED) - averaged over the entire disk - and of interferometric measurements - sensitive to the inner, warm regions - is the main goal of this study. Modeling the SED alone does not allow us to constrain unambiguously the disk density and temperature structure (e.g., Thamm et al. 1994). Spatially resolved observations, such as interferometric observations with MIDI are needed to reduce the ambiguity caused by considering solely the SED. The modeling approach should be as simple as possible to reduce the mathematical underdetermination of the model. A key issue of this study is to determine whether all objects in our heterogeneous sample can be modeled with one single approach or if modifications and extensions of the model must also be considered. Finally, it has not yet been shown whether any quantities of the objects, such as the stellar luminosity, stellar temperature, and mass accretion rate derived in previous, spatially unresolved observations can also be confirmed with interferometric, small-scale (range of AU) observations.
Table 2: Overview of our observations with MIDI.
Any deviations in the outcome of a homogeneous disk model from the (spectral and spatial) measurements point to (small-scale) perturbations of the disk structure. A non-representative selection of potential perturbations are an inner-disk gap (Calvet et al. 2002; Mathieu et al. 1991), vortices (Klahr 2004), a puffed-up inner-rim wall (Dullemond et al. 2001), and a close stellar companion (Mathieu et al. 1997; Artymowicz & Lubow 1994). Non-homologous evolution of the disk produces these perturbations (Wood et al. 2002; McCabe et al. 2006).
MIDI provides both correlated, i.e., coherent spectra sensitive to the inner part, and uncorrelated spectra sensitive to regions that can be non-interferometrically resolved. For the T Tauri objects TW Hya (Ratzka et al. 2007) and RY Tau (Schegerer et al. 2008), an
increase in the relative crystalline mass contribution to the
![]() silicate feature could be determined for an increasing spatial resolution obtained with MIDI. This result was even found for
the active object FU Ori (Quanz et al. 2005). This
finding was explained by the
hypothesis that silicate dust evolves more rapidly in inner disk regions, i.e., at small radii r, than in outer regions of the disk (e.g., van Boekel et al. 2004) assuming similar initial dust compositions. It is not
known, so far, if this increase occurs
only for intermediate-mass YSOs such as RY Tau or if such a
correlation exists even for fainter (
silicate feature could be determined for an increasing spatial resolution obtained with MIDI. This result was even found for
the active object FU Ori (Quanz et al. 2005). This
finding was explained by the
hypothesis that silicate dust evolves more rapidly in inner disk regions, i.e., at small radii r, than in outer regions of the disk (e.g., van Boekel et al. 2004) assuming similar initial dust compositions. It is not
known, so far, if this increase occurs
only for intermediate-mass YSOs such as RY Tau or if such a
correlation exists even for fainter (![]()
![]() ),
younger (
),
younger (![]() 1 Myr old), and less active T Tauri
objects. Radial mixing could reverse the increase in evolved dust
towards the more inner regions (Gail 2003). In this study, we compare silicate features that effectively arise at different disk
radii within an object. By focusing on one single object, the results of this investigation do not depend on disk properties such as the
evolutionary stage, initial composition, and disk inclination but only on the origin of the feature.
1 Myr old), and less active T Tauri
objects. Radial mixing could reverse the increase in evolved dust
towards the more inner regions (Gail 2003). In this study, we compare silicate features that effectively arise at different disk
radii within an object. By focusing on one single object, the results of this investigation do not depend on disk properties such as the
evolutionary stage, initial composition, and disk inclination but only on the origin of the feature.
This paper is structured in the following way. In
Sect. 2, we present the object sample and briefly describe our observations and data reduction. In
Sect. 3, our modeling approach is outlined. The derived individual disk parameters are presented in Sect. 4. An analysis of the
![]() silicate feature is given in Sect. 5, followed by a summary in
Sect. 6. The Appendix lists some further properties of the objects in our sample.
silicate feature is given in Sect. 5, followed by a summary in
Sect. 6. The Appendix lists some further properties of the objects in our sample.
2 Interferometric observations and data reduction
Most of our objects are well-known T Tauri stars. They belong to various star-forming regions such as the Taurus-Auriga (e.g., DR Tau) and ![]() Ophiuchi (e.g., HBC 639) region. Selected object parameters are compiled in Table 1 (see Appendix A for more details). Different models of an object are provided in roman digits. In this Table 1, the coordinates (RA
and Dec. in J2000.0), distance (d), visual extinction (
Ophiuchi (e.g., HBC 639) region. Selected object parameters are compiled in Table 1 (see Appendix A for more details). Different models of an object are provided in roman digits. In this Table 1, the coordinates (RA
and Dec. in J2000.0), distance (d), visual extinction (![]() ), spectral type (SpTyp), stellar mass (
), spectral type (SpTyp), stellar mass (![]() ), effective stellar temperature (
), effective stellar temperature (![]() ), stellar luminosity (
), stellar luminosity (![]() ), and age are listed. Footnotes are references and point
to the previous measurements. The footnotes ``det.'' and ``ass.''
represent parameter values that were determined and assumed in this study, respectively. Apart from one, all objects are between 0.1 and 3 million years old. The exception is HD 72106 B with an age of 10 million years. Highly spatially resolved measurements in the NIR and mid-infrared (MIR) wavelength range have shown that the objects DR Tau and RU Lup do not have any stellar companion (e.g., Ghez et al. 1997). In contrast, HD 72106 and S CrA at least are well-known binary systems. Considering the stellar mass, GW Ori with
), and age are listed. Footnotes are references and point
to the previous measurements. The footnotes ``det.'' and ``ass.''
represent parameter values that were determined and assumed in this study, respectively. Apart from one, all objects are between 0.1 and 3 million years old. The exception is HD 72106 B with an age of 10 million years. Highly spatially resolved measurements in the NIR and mid-infrared (MIR) wavelength range have shown that the objects DR Tau and RU Lup do not have any stellar companion (e.g., Ghez et al. 1997). In contrast, HD 72106 and S CrA at least are well-known binary systems. Considering the stellar mass, GW Ori with
![]() would be the only Herbig Ae/Be object (
would be the only Herbig Ae/Be object (
![]() )
in our sample, while in terms of spectral type only HD 72106 B would be a Herbig Ae/Be object (Vieira et al. 2003).
)
in our sample, while in terms of spectral type only HD 72106 B would be a Herbig Ae/Be object (Vieira et al. 2003).
The date and the observing time (UT) with MIDI, as well as telescope pairs (TP), and both the projected (effective) length (B) and angle of the baseline (PA, measured from North to East) during the
observations are presented for targets and corresponding calibrator stars in Table 2. The given airmass (AM) is an average value for the observation. We also add the diameter of the
calibrator star and the corresponding references. The diameters were derived from fitting the SED of the objects. In the last column of this Table 2, we also provide comments
concerning the observation and data
reduction. A detailed description of an observing sequence with MIDI is given in Leinert et al. (2004).
The calibration was completed using data for all calibrator stars that were observed during one night with the
same observational mode as the scientific target and
show clear visibility signals. The error bars in the visibility curves, which are presented below, represent the standard deviation when using the ensemble of calibrator measurements. Since the sample contains various objects with known close-by infrared companions, we checked whether these companions affect the visibility measurements. This examination was necessary because of the relatively wide field-of-view of MIDI, of about 1![]() .
The companions do not affect the measurements.
We used the MIA package (MIDI Interactive Analysis Software) for data reduction (Leinert et al. 2004;
Ratzka 2005). The results were confirmed by using the independent EWS software. Both reduction software
packages are publicly available
.
The companions do not affect the measurements.
We used the MIA package (MIDI Interactive Analysis Software) for data reduction (Leinert et al. 2004;
Ratzka 2005). The results were confirmed by using the independent EWS software. Both reduction software
packages are publicly available![]() .
Several target/calibrator pairs were observed at different airmasses (Table 2). Therefore, a correction to the
airmass was performed by multiplying the uncorrelated spectra
with the inverse of the cosine of the zenith angle. The visibility spectra do not need to be corrected because the correlated flux is normalized by the uncorrelated flux.
.
Several target/calibrator pairs were observed at different airmasses (Table 2). Therefore, a correction to the
airmass was performed by multiplying the uncorrelated spectra
with the inverse of the cosine of the zenith angle. The visibility spectra do not need to be corrected because the correlated flux is normalized by the uncorrelated flux.
3 Modeling approach
In the data analysis, we used the radiative-transfer code MC3D, which is based on a Monte Carlo method (Wolf et al. 1999) and was more recently developed to its present form (Schegerer et al. 2008). A predefined, parameterized model of a passive disk is the basic ingredient of our modeling approach. We use the disk model of Shakura & Sunyaev (1973), where the density distribution is given as:
The quantities r and z are the radius measured from the disk center and the vertical distance from the disk midplane, respectively. The quantity
with
The latter relation results from the coupling of surface density and temperature of the disk (Shakura & Sunyaev 1973). We note that the approach established by Shakura & Sunyaev is correct only for geometrically thin disks, i.e., where
For all objects besides HD 72106 B and HBC 639, accretion effects were also considered. The potential energy of a particle on its way towards the star is partly released in the disk midplane assuming the canonical modeling approach of a geometrically thin, active disk as formerly established by Lynden-Bell & Pringle (1974), and
Pringle (1981). Considering the ``magnetically mediated'' modeling approach (e.g., Uchida & Shibata 1984; Bertout et al. 1988; Calvet & Gullbring 1998), the accretion disk is truncated by the stellar magnetic field at a radius
![]() .
Thereupon, more than half of the potential energy of the accreting particles is released in a boundary region above the stellar surface. This boundary region is heated to a temperature of
.
Thereupon, more than half of the potential energy of the accreting particles is released in a boundary region above the stellar surface. This boundary region is heated to a temperature of
![]() by the accreting material. The effects of the this
approach were described and applied by Schegerer et al. (2008) in modeling the circumstellar disk around RY Tau. Calvet & Gullbring (1998) theoretically derived reasonable ranges for the latter both accretion values, i.e.,
by the accreting material. The effects of the this
approach were described and applied by Schegerer et al. (2008) in modeling the circumstellar disk around RY Tau. Calvet & Gullbring (1998) theoretically derived reasonable ranges for the latter both accretion values, i.e.,
![]() and
and
![]() .
We note that the effects of any variations in the boundary temperature
.
We note that the effects of any variations in the boundary temperature
![]() and the magnetic truncation radius
and the magnetic truncation radius
![]() on the SED and MIR visibilities can be neglected in the above-mentioned ranges
(D'Alessio et al. 1998). In our modeling approach, we always used standard values for the boundary temperature and truncation radius, i.e.,
on the SED and MIR visibilities can be neglected in the above-mentioned ranges
(D'Alessio et al. 1998). In our modeling approach, we always used standard values for the boundary temperature and truncation radius, i.e.,
![]() and
and
![]() .
These values were applied by
Akeson et al. (2005) and Schegerer et al. (2008) for other T Tauri stars. The accretion rate
.
These values were applied by
Akeson et al. (2005) and Schegerer et al. (2008) for other T Tauri stars. The accretion rate ![]() ,
which determines the total accretion luminosity
,
which determines the total accretion luminosity
![]() ,
is not an independent model parameter. But its value is constrained by the results of previous
measurements. Correspondingly, the stellar mass
,
is not an independent model parameter. But its value is constrained by the results of previous
measurements. Correspondingly, the stellar mass
![]() ,
the effective stellar temperature
,
the effective stellar temperature
![]() ,
and the stellar luminosity
,
and the stellar luminosity
![]() ,
which were derived in previous studies were starting parameters in the modeling. In some cases, it was necessary to deviate from these results to be able to simulate the measurements considered in this study. These deviations are discussed below.
,
which were derived in previous studies were starting parameters in the modeling. In some cases, it was necessary to deviate from these results to be able to simulate the measurements considered in this study. These deviations are discussed below.
In our modeling approach, we assumed a dust mixture of ``astronomical silicate'' and graphite with relative abundances of 62.5% and 37.5%, respectively (Draine & Malhotra 1993). We used a two-layer disk model, i.e., the disk interior, where the optical
depth in N band fulfills the condition
![]() ,
contains dust grains with a maximum particle size
of
,
contains dust grains with a maximum particle size
of
![]() .
A maximum particle size of
.
A maximum particle size of
![]() was found for several T Tauri stars with millimeter observations using the Very Large Array (Rodmann et al. 2006). Here, the optical depth
was found for several T Tauri stars with millimeter observations using the Very Large Array (Rodmann et al. 2006). Here, the optical depth ![]() is
measured for constant radii, from the disk
atmosphere vertically to the disk midplane. The
surface regions consist of interstellar, non-evolved dust with
is
measured for constant radii, from the disk
atmosphere vertically to the disk midplane. The
surface regions consist of interstellar, non-evolved dust with
![]() as found in the interstellar medium (Mathis et al. 1977). In both the disk interior and the disk surface layer a minimum grain size of
as found in the interstellar medium (Mathis et al. 1977). In both the disk interior and the disk surface layer a minimum grain size of
![]() and a
grain size distribution of a-3.5 for
and a
grain size distribution of a-3.5 for
![]() was adopted (MRN grain-size distribution; Mathis et al. 1977).
was adopted (MRN grain-size distribution; Mathis et al. 1977).
Table 3: Parameters of the models that simulate the measured SED and MIR visibilities best.
After the temperature distribution was determined assuming a
density given by Eq. (1), the SED, the projected
image of the star, and its circumstellar environment, assuming an
inclination angle ![]() ,
were calculated. In the modeled images from which the visibilities result, we generally used a spatial resolution of <
,
were calculated. In the modeled images from which the visibilities result, we generally used a spatial resolution of <
![]() in the MIR range, which is a factor
in the MIR range, which is a factor ![]() 10 higher than the spatial resolution reached in our MIDI observations. For the images from which we derived the NIR visibilities, we used a resolution of <
10 higher than the spatial resolution reached in our MIDI observations. For the images from which we derived the NIR visibilities, we used a resolution of <
![]() ,
i.e., a factor of 10 higher than the resolution reached by any existing NIR interferometer.
,
i.e., a factor of 10 higher than the resolution reached by any existing NIR interferometer.
Independent model parameters of our approach are the outer radius
![]() ,
the scale-height
,
the scale-height
![]() ,
the exponent
,
the exponent ![]() ,
and the inclination angle
,
and the inclination angle ![]() of the circumstellar disk
of the circumstellar disk![]() . Assuming a
certain dust mixture in the models, the disk mass is fixed predominantly by the flux in the millimeter wavelength range. Considering a stellar temperature
. Assuming a
certain dust mixture in the models, the disk mass is fixed predominantly by the flux in the millimeter wavelength range. Considering a stellar temperature ![]() ,
the quadratic distance law, a mean dust sublimation temperature of
,
the quadratic distance law, a mean dust sublimation temperature of
![]() ,
and the specific absorption coefficients
,
and the specific absorption coefficients ![]() of the adopted dust
set, the temperature of single dust grains at each radius can be
determined. However, our approach is only valid for optically thin
media. For optically thick media, the grain temperature at the inner-disk edge is even higher because back radiation from outer dust grains produces an additional heating of the grains at the inner edge. The resulting sublimation radius
of the adopted dust
set, the temperature of single dust grains at each radius can be
determined. However, our approach is only valid for optically thin
media. For optically thick media, the grain temperature at the inner-disk edge is even higher because back radiation from outer dust grains produces an additional heating of the grains at the inner edge. The resulting sublimation radius
![]() is the initial value of
is the initial value of
![]() in our modeling approach.
in our modeling approach.
 |
Figure 1:
SED and MIR visibilities for a projected baseline of
|
| Open with DEXTER | |
Initially, the simulation grid of independent parameters is scanned coarsely during modeling. Simultaneously, we consider parameter values that were derived in preceding studies. By means of manual modifications of the model parameters, we search for the model that reproduces most successfully the measured SED and
MIR visibilities, simultaneously. The SED and the MIR visibilities that we try to model are complex functions of many different disk and dust parameters. However, the effects of any modification of the parameters on modeled SED and visibilities can be estimated. A manual modification is necessary because a disk model with a specific SED and images at different wavelengths![]() takes about an hour to compute. In our search for the best-fit model the uniqueness of our final models cannot therefore be proven. However, we verified whether the modeling results can be improved by varying the model parameters using the following step widths:
takes about an hour to compute. In our search for the best-fit model the uniqueness of our final models cannot therefore be proven. However, we verified whether the modeling results can be improved by varying the model parameters using the following step widths:
| |
= | ||
| = | |||
| = |
Considering the error bars of the measurements, the modeling results could not be improved using finer step widths. The step widths can be considered as the precision to which the local minimum in the
4 Results
All scientific targets could be well resolved, i.e., the visibilities are lower than unity. Table 3 presents the parameters resulting from our effort to model the circumstellar disks of seven YSOs.Values that are marked with (det.) in the list are determined in this study. In the following, we present and discuss our modeling results for each object in our sample, in detail. Previous observations, including photometric measurements, are mentioned in Appendix A.
 |
Figure 2:
SED and MIR visibilities for the projected baselines of
|
| Open with DEXTER | |
4.1 DR Tau
Considering the low gradient of the SED at wavelengths
![]() (Fig. 1), it is evident that the (measured) SED of
DR Tau is represented by a black body with the stellar temperature of
(Fig. 1), it is evident that the (measured) SED of
DR Tau is represented by a black body with the stellar temperature of
![]() and an additional radiation source.
The accretion process is the other strong influence on the radiation emitted
in this wavelength range. In addition to
the stellar luminosity and the accretion rate, the parameters of the model (I) of our approach confirm the values derived in the
previous study of Akeson et al. (2005) using long-baseline NIR
interferometry from the Palomar Testbed Interferometer (PTI). However, they found a stellar luminosity of
and an additional radiation source.
The accretion process is the other strong influence on the radiation emitted
in this wavelength range. In addition to
the stellar luminosity and the accretion rate, the parameters of the model (I) of our approach confirm the values derived in the
previous study of Akeson et al. (2005) using long-baseline NIR
interferometry from the Palomar Testbed Interferometer (PTI). However, they found a stellar luminosity of
![]() ,
which is a factor
of
,
which is a factor
of ![]() 2 lower than the value found in our model. Simultaneously, the accretion rate of their model, i.e.,
2 lower than the value found in our model. Simultaneously, the accretion rate of their model, i.e.,
![]() ,
is four times higher than the value determined in our first model. However, SED and MIR
visibilities can also be reproduced by a model (II) by considering the stellar
luminosity and the accretion rate found by Akeson et al. (2005) while keeping all other model parameters constant. Both models similarly fit MIR visibilities and SED to
within the error bars. We conclude that the intrinsic stellar luminosity and the accretion luminosity cannot be disentangled considering SED and MIR visibilities, only. The derived accretion luminosity
,
is four times higher than the value determined in our first model. However, SED and MIR
visibilities can also be reproduced by a model (II) by considering the stellar
luminosity and the accretion rate found by Akeson et al. (2005) while keeping all other model parameters constant. Both models similarly fit MIR visibilities and SED to
within the error bars. We conclude that the intrinsic stellar luminosity and the accretion luminosity cannot be disentangled considering SED and MIR visibilities, only. The derived accretion luminosity
![]() depends on the applied accretion rate
depends on the applied accretion rate ![]() :
the model (I) has an accretion luminosity of
:
the model (I) has an accretion luminosity of
![]() for
for
![]() while an
accretion luminosity of
while an
accretion luminosity of
![]() for
for
![]() is emitted by the model (II). The sum of the intrinsic stellar luminosity
is emitted by the model (II). The sum of the intrinsic stellar luminosity
![]() and the accretion luminosity
and the accretion luminosity
![]() in both models equals
in both models equals ![]()
![]() .
Finally, we mention
that Mohanty et al. (2005) derived an accretion rate of
.
Finally, we mention
that Mohanty et al. (2005) derived an accretion rate of
![]() analysing Ca II lines. Robitaille et al. (2007) determined a lower and upper
limit to
analysing Ca II lines. Robitaille et al. (2007) determined a lower and upper
limit to ![]() ,
i.e.,
,
i.e.,
![]() assuming
the SED, only. If the NIR visibility data obtained by Akeson et al. (2005) is simultaneously taken into account, we find that the disks of models (I) and (II) appear too spatially resolved, resulting in too low NIR visibilities. Only an additional reduction in the inner disk radius to
assuming
the SED, only. If the NIR visibility data obtained by Akeson et al. (2005) is simultaneously taken into account, we find that the disks of models (I) and (II) appear too spatially resolved, resulting in too low NIR visibilities. Only an additional reduction in the inner disk radius to
![]() improves our fit to the NIR visibility data in the model (II). A similar
improvement cannot be reached in model (I) by reducing its inner disk
radius. Our model of DR Tau with
improves our fit to the NIR visibility data in the model (II). A similar
improvement cannot be reached in model (I) by reducing its inner disk
radius. Our model of DR Tau with
![]() ,
,
![]() ,
and
,
and
![]() is called
model (III). The lower right panel in Fig. 1 shows
measurements and model output for the
NIR visibility of model (III). We note that the fit to the MIR visibility data
at wavelengths of
is called
model (III). The lower right panel in Fig. 1 shows
measurements and model output for the
NIR visibility of model (III). We note that the fit to the MIR visibility data
at wavelengths of
![]() becomes poorer in model (III) and deviates from the measured data by <7% as the gradient of the modeled MIR visibility curve decreases. We summarize that model (III) is the only model that reproduces all available data sets apart from slight deviations in the MIR visibilities at
becomes poorer in model (III) and deviates from the measured data by <7% as the gradient of the modeled MIR visibility curve decreases. We summarize that model (III) is the only model that reproduces all available data sets apart from slight deviations in the MIR visibilities at ![]()
![]() .
.
As we mentioned in Sect. 3, the sublimation
radius is approximated considering a stellar temperature of
![]() and the absorption
coefficients of the dust composition that we used in our two-layer disk model. This
approach is only an approximation because we assume an optically thin disk in
determining of the sublimation radius
and the absorption
coefficients of the dust composition that we used in our two-layer disk model. This
approach is only an approximation because we assume an optically thin disk in
determining of the sublimation radius
![]() .
The true
sublimation radius
.
The true
sublimation radius
![]() should be larger because the back radiation of
adjacent grains is neglected. We obtain a sublimation radius of
should be larger because the back radiation of
adjacent grains is neglected. We obtain a sublimation radius of
![]() even for the dust for which
even for the dust for which
![]() because of a low number of large
grains with
because of a low number of large
grains with
![]() .
Since the inner radius
.
Since the inner radius
![]() of the modeled disk is slightly smaller than the sublimation
radius, this value of
of the modeled disk is slightly smaller than the sublimation
radius, this value of
![]() could imply that
larger grains exist
in the disk, in the innermost disk in particular, than the MRN grain-size
distribution predicts (Mathis et al. 1977). This result is also found
in Sect. 5 and predicted by Isella &
Natta (2005). However, the hint for larger grains is only weak since the
large error bars of the NIR data still allow a slightly larger inner-disk
radius
could imply that
larger grains exist
in the disk, in the innermost disk in particular, than the MRN grain-size
distribution predicts (Mathis et al. 1977). This result is also found
in Sect. 5 and predicted by Isella &
Natta (2005). However, the hint for larger grains is only weak since the
large error bars of the NIR data still allow a slightly larger inner-disk
radius
![]() than we have assumed in model (III).
than we have assumed in model (III).
As the disk crosses the line of sight of the observer with increasing
inclination angle, the NIR flux at ![]()
![]() of the model of DR Tau decreases by 38% in steps of
of the model of DR Tau decreases by 38% in steps of
![]() for small inclinations.
Therefore, the inclination angle can be determined with high accuracy. If the measured visual extinction
for small inclinations.
Therefore, the inclination angle can be determined with high accuracy. If the measured visual extinction
![]() (Muzerolle et al. 2003) can be ascribed exclusively to the circumstellar disk around DR Tau that crosses the line of sight of the observer, an inclination of
(Muzerolle et al. 2003) can be ascribed exclusively to the circumstellar disk around DR Tau that crosses the line of sight of the observer, an inclination of
![]() can be derived. If the extinction is also caused by interstellar media outside
the system, which is not considered in the model, the derived inclination
angle is correspondingly smaller.
can be derived. If the extinction is also caused by interstellar media outside
the system, which is not considered in the model, the derived inclination
angle is correspondingly smaller.
Our observation of DR Tau with MIDI achieved a theoretical spatial
resolution of ![]()
![]() (
(![]()
![]() ). To this
limit, the visibility data do not provide any evidence of a companion with a brightness ratio close to unity, which would have produced a characteristic sinusoidal signature in the visibility (e.g., Schegerer et al. 2008). We note that the detection of a close binary is difficult when the binary is oriented nearly orthogonal to the
baseline vector of our interferometric observations.
). To this
limit, the visibility data do not provide any evidence of a companion with a brightness ratio close to unity, which would have produced a characteristic sinusoidal signature in the visibility (e.g., Schegerer et al. 2008). We note that the detection of a close binary is difficult when the binary is oriented nearly orthogonal to the
baseline vector of our interferometric observations.
Our finding confirms the results of former speckle-interferometric
measurements in the NIR range (Ghez et al. 1997), where a theoretical
spatial resolution of
![]() could be achieved. Two
previously unpublished lunar occultation data sets of high quality (
could be achieved. Two
previously unpublished lunar occultation data sets of high quality (
![]() -40) are available for DR Tau from the
-40) are available for DR Tau from the
![]() telescope in Calar Alto, the first one recorded in November 1997 with an
InSb fast photometer and the second one in September 1999 with the IR array
OmegaCass in fast readout for a
telescope in Calar Alto, the first one recorded in November 1997 with an
InSb fast photometer and the second one in September 1999 with the IR array
OmegaCass in fast readout for a
![]() pixel window. A detailed
analysis allows us to conclude that the source appeared point-like with an
upper limit of
pixel window. A detailed
analysis allows us to conclude that the source appeared point-like with an
upper limit of
![]() ,
i.e.,
,
i.e.,
![]() and
and
![]() ,
i.e.,
,
i.e.,
![]() in
both data sets. Upper limits can also be set to the flux because of a
possible circumstellar emission, and they are
in
both data sets. Upper limits can also be set to the flux because of a
possible circumstellar emission, and they are
![]() 5% over
5% over
![]() and
and
![]() 2.5% over
2.5% over
![]() ,
for
both observations.
,
for
both observations.
4.2 GW Ori
As former millimeter measurements have shown (Mathieu et al. 1995) and can be confirmed by this study, the circumstellar disk around GW Ori is very massive,
i.e.,
![]() .
Furthermore, compared to other objects in this study, the disk of
GW Ori has the largest outer radius
.
Furthermore, compared to other objects in this study, the disk of
GW Ori has the largest outer radius
![]() .
Besides the luminosity, all other stellar parameters
and the accretion rate found in this study are consistent with the result of Calvet et al. (2004), who analyzed the UV spectrum of this source. The accretion luminosity is
.
Besides the luminosity, all other stellar parameters
and the accretion rate found in this study are consistent with the result of Calvet et al. (2004), who analyzed the UV spectrum of this source. The accretion luminosity is
![]() in our model. If an intrinsic stellar luminosity of
in our model. If an intrinsic stellar luminosity of
![]() is
used, as was determined by Calvet et al. (2004), the resulting flux in K band would exceed the
photometric measurement by 20%. In Fig. 2,
the SED and MIR visibilities of a model
with a stellar luminosity of
is
used, as was determined by Calvet et al. (2004), the resulting flux in K band would exceed the
photometric measurement by 20%. In Fig. 2,
the SED and MIR visibilities of a model
with a stellar luminosity of
![]() is also shown (model (II): gray
curves/visibility bars). Although both the SED and the visibilities for
is also shown (model (II): gray
curves/visibility bars). Although both the SED and the visibilities for
![]() can be reproduced, no model could be found that reproduces simultaneously the visibilities of a baseline of
can be reproduced, no model could be found that reproduces simultaneously the visibilities of a baseline of
![]() .
For spectroscopic measurements, Mathieu et al. (1997) found that GW Ori has a stellar companion at a
projected separation
.
For spectroscopic measurements, Mathieu et al. (1997) found that GW Ori has a stellar companion at a
projected separation
![]() between
between
![]() and
and
![]() and of stellar mass between
and of stellar mass between
![]() and
and
![]() .
According to Mathieu et al. (1997), this companion creates a dust-free ring in the circumstellar disk between
.
According to Mathieu et al. (1997), this companion creates a dust-free ring in the circumstellar disk between
![]() and
and
![]() .
By means of a theoretical investigation, Artymowicz & Lubow (1994) determined an inner radius of
.
By means of a theoretical investigation, Artymowicz & Lubow (1994) determined an inner radius of ![]()
![]() for the circumbinary disk of the system. They claimed that each component has its own circumstellar disk of outer radii of
for the circumbinary disk of the system. They claimed that each component has its own circumstellar disk of outer radii of
![]() and
and
![]() .
.
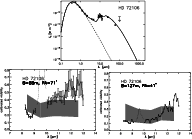 |
Figure 3:
SED and MIR visibilities for the projected baselines of
|
| Open with DEXTER | |
In our approach, the inner disk radius equals the sublimation
radius (
![]() ). We do not consider a dust-free inner gap as proposed by Mathieu et al. (1997) and Artymowicz & Lubow (1994). However, in another model a dust-free,
ring-shaped gap is cut in our disk model. We assumed the same disk parameters
). We do not consider a dust-free inner gap as proposed by Mathieu et al. (1997) and Artymowicz & Lubow (1994). However, in another model a dust-free,
ring-shaped gap is cut in our disk model. We assumed the same disk parameters ![]() and
and
![]() for the circumbinary and circumstellar disk. The disk gap extends from the radius
for the circumbinary and circumstellar disk. The disk gap extends from the radius
![]() to
to
![]() .
In the latter model, we obtained the following results (not shown in the figure): the NIR flux obtained from this model
decreases by 70% and cannot fit the NIR range of the SED
anymore. Although the modeled visibilities
.
In the latter model, we obtained the following results (not shown in the figure): the NIR flux obtained from this model
decreases by 70% and cannot fit the NIR range of the SED
anymore. Although the modeled visibilities
![]() for
the long baseline
for
the long baseline
![]() correspond to a positive gradient, the visibilities for the short baseline
correspond to a positive gradient, the visibilities for the short baseline
![]() decrease by 20% across the complete N band. Any modifications of the radii that limit the disk gap could not even improve our model considering the
measurements.
decrease by 20% across the complete N band. Any modifications of the radii that limit the disk gap could not even improve our model considering the
measurements.
![\begin{figure}
\par {\hspace*{3.75cm}\includegraphics[width=7.5cm,clip]{003fig11...
...,clip]{003fig14.ps}\includegraphics[width=7.5cm,clip]{003fig15.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10782-08/Timg265.png) |
Figure 4:
SED and MIR visibilities for the projected baselines of
|
| Open with DEXTER | |
We assume that the disk gap is probably neither dust-free nor ring-shaped. In a theoretical study, it was shown that material streams between the circumbinary and the circumstellar disks guarantee the accretion onto each component (Günther & Kley 2002). Even the stellar companion that is not implemented in our approach could affect the MIR visibilities and SED. A strong concentration of MIR intensity in the innermost disk regions that could not be spatially resolved with MIDI and an abrupt truncation of the MIR intensity distribution potentially caused by a disk gap result in the increase of the MIR visibility on long baselines.
To reveal the innermost disk region of GW Ori, more complicated modeling approaches as well as additional interferometric observations are essential. Measurements with the NIR interferometer AMBER at the VLTI, for instance, could provide information about the small-scale structures of the innermost regions that potentially deviate from axial symmetry.
4.3 HD 72106 B
HD 72106 B is the least well-studied object in our sample. In our modeling
approach, we use a luminosity of
![]() .
This value results directly from a fit by a Planck function of temperature
.
This value results directly from a fit by a Planck function of temperature
![]() (Schütz et al. 2005) to the photometric measurements in U-, V- and R-band. Two properties make HD 72106 B a special object in our sample:
(Schütz et al. 2005) to the photometric measurements in U-, V- and R-band. Two properties make HD 72106 B a special object in our sample:
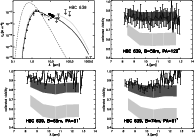 |
Figure 5:
SED and MIR visibility for the projected baselines of
|
| Open with DEXTER | |
First, with an age of
![]() ,
HD 72106 B is a relatively old T Tauri
object with weak infrared excess. The equivalent width of the H
,
HD 72106 B is a relatively old T Tauri
object with weak infrared excess. The equivalent width of the H![]() line that is smaller than 10 Å (Vieira et al. 2003) is a sign of weak accretion. Our model of HD 72106 B consists of a passive disk without considering any accretion
effects. For several T Tauri objects of similar age (e.g., TW Hya; s. Calvet et al. 2002) an inner, dust-free gap in the range of
line that is smaller than 10 Å (Vieira et al. 2003) is a sign of weak accretion. Our model of HD 72106 B consists of a passive disk without considering any accretion
effects. For several T Tauri objects of similar age (e.g., TW Hya; s. Calvet et al. 2002) an inner, dust-free gap in the range of
![]() 1 AU, i.e., larger than the sublimation radius could be detected. However, because the SED and MIR
visibilities of HD 72106 B can be simulated by assuming that the inner edge of
the (dust) disk equals the sublimation radius, a shift in the
inner-disk edge to larger radii is not obvious.
1 AU, i.e., larger than the sublimation radius could be detected. However, because the SED and MIR
visibilities of HD 72106 B can be simulated by assuming that the inner edge of
the (dust) disk equals the sublimation radius, a shift in the
inner-disk edge to larger radii is not obvious.
Second, HD 72106 B is the infrared companion of HD 72106 A with a projected distance of 280 AU. HD 72106 A has already developed into a main-sequence star (Wade et al. 2005). The main component is probably responsible for the truncation of the outer disk around the B component considering an outer radius of 40 AU. The small outer radius of the disk finally produces a strong decrease in the FIR flux (s. Fig. 3).
4.4 RU Lup
As Lamzin et al. (1996) has shown, RU Lup was at least
temporarily a strongly accreting object. By
analyzing its SED, they derived an accretion rate of
![]() .
In this context, Reipurth et al. (1996) found that the H
.
In this context, Reipurth et al. (1996) found that the H![]() emission has broad wings of up to
emission has broad wings of up to
![]() in width. Furthermore, the H
in width. Furthermore, the H![]() emission of RU Lup shows one of the broadest equivalent widths among T Tauri stars (Giovannelli et al. 1995). However, by considering SED and MIR visibilities, we can exclude such a high accretion rate
emission of RU Lup shows one of the broadest equivalent widths among T Tauri stars (Giovannelli et al. 1995). However, by considering SED and MIR visibilities, we can exclude such a high accretion rate ![]() .
We determine a maximum value of
.
We determine a maximum value of
![]() with an accretion
luminosity of only
with an accretion
luminosity of only
![]() .
Herczeg et al. (2005) found that
.
Herczeg et al. (2005) found that
![]() which supports our result. A higher accretion rate produces a decrease in the MIR visibility because the irradiation of the disk increases. Simultaneously, the NIR and MIR flux would exceed the photometric measurements. Figure 4 represents our best-fit model with
which supports our result. A higher accretion rate produces a decrease in the MIR visibility because the irradiation of the disk increases. Simultaneously, the NIR and MIR flux would exceed the photometric measurements. Figure 4 represents our best-fit model with
![]() (black curve/visibility bars). The stellar luminosity of
(black curve/visibility bars). The stellar luminosity of
![]() corresponds to a value
derived by Gras-Velázquez & Ray (2005). It represents the average of previous measurements (Herczeg et al. 2005:
corresponds to a value
derived by Gras-Velázquez & Ray (2005). It represents the average of previous measurements (Herczeg et al. 2005:
![]() ;
Nürnberger et al. 1997:
;
Nürnberger et al. 1997:
![]() ). A model that simulates the flux in the N band, i.e., the silicate feature, could
not be found. The relative deviation in the MIR range is 37%. The visibilities obtained on the baselines
). A model that simulates the flux in the N band, i.e., the silicate feature, could
not be found. The relative deviation in the MIR range is 37%. The visibilities obtained on the baselines
![]() and
and
![]() and for similar position angles significantly differ, which could be due to a measurement error.
and for similar position angles significantly differ, which could be due to a measurement error.
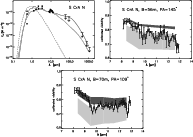 |
Figure 6:
SED and MIR visibilities for the projected baselines of
|
| Open with DEXTER | |
Based on spectro-astrometric observations, Takami et al. (2001) suggested that an inner gap in the circumstellar disk of RU Lup exists between ![]() 2 AU and
2 AU and ![]() 4 AU (20-30 mas) as justified by the following arguments. Because of the positional displacement of the extended wings, the emission of forbidden lines such as [OI] and [SII] in the spectra of RU Lup is assumed to arise in a collimated large-scale outflow. The apparent lack of redshifted line components results from an obscuration of the dorsal outflow by the circumstellar disk (Eislöffel et al. 2000). Takami et al. (2001) found that the H
4 AU (20-30 mas) as justified by the following arguments. Because of the positional displacement of the extended wings, the emission of forbidden lines such as [OI] and [SII] in the spectra of RU Lup is assumed to arise in a collimated large-scale outflow. The apparent lack of redshifted line components results from an obscuration of the dorsal outflow by the circumstellar disk (Eislöffel et al. 2000). Takami et al. (2001) found that the H![]() line in the spectrum of RU Lup, which is evident predominatly in the innermost regions, shows both blueshifted and redshifted wings. This finding is explained by an inner disk gap that allows regions behind the disk to be observed. The gap could be evoked by an unseen (planetary) companion. Since the wings of the H
line in the spectrum of RU Lup, which is evident predominatly in the innermost regions, shows both blueshifted and redshifted wings. This finding is explained by an inner disk gap that allows regions behind the disk to be observed. The gap could be evoked by an unseen (planetary) companion. Since the wings of the H![]() line shows the same positional displacement as the forbidden lines, Takami et al. (2001) suggested that the H
line shows the same positional displacement as the forbidden lines, Takami et al. (2001) suggested that the H![]() line originates predominantly in the outflow.
line originates predominantly in the outflow.
 |
Figure 7:
SED and MIR visibilities for a projected baseline of
|
| Open with DEXTER | |
Similar to our modeling approach of GW Ori, we defined a dust-free gap in the disk model that is presented in Fig. 4
(Tables 1,3). The gap size was varied using values of
![]() of up to
of up to
![]() for the inner gap radius, and
for the inner gap radius, and
![]() and
and
![]() for the outer gap radius. An outflow
was not considered in our model. The resulting
changes can be summarized as follows: as shown in
Fig. 4, a gap lowers the NIR flux by
for the outer gap radius. An outflow
was not considered in our model. The resulting
changes can be summarized as follows: as shown in
Fig. 4, a gap lowers the NIR flux by ![]() 7%. We note that
the NIR flux is highly variable during a year (Giovannelli et al. 1995). Previous photometric measurements (Giovannelli et al. 1995) would be consistent with lower NIR fluxes. A disk gap as used here would even lower the MIR
flux and slightly improve our fit to the N band. The MIR visibility simultaneously decreases at wavelengths <10.5
7%. We note that
the NIR flux is highly variable during a year (Giovannelli et al. 1995). Previous photometric measurements (Giovannelli et al. 1995) would be consistent with lower NIR fluxes. A disk gap as used here would even lower the MIR
flux and slightly improve our fit to the N band. The MIR visibility simultaneously decreases at wavelengths <10.5 ![]() m as the relative MIR
flux contribution of outer disk regions in relation increases. For longer wavelengths
>10.5
m as the relative MIR
flux contribution of outer disk regions in relation increases. For longer wavelengths
>10.5 ![]() m, the disk becomes more compact as the visibilities slightly increase. Our visibility measurements are inconsistent with a disk gap and an inner radius
of
m, the disk becomes more compact as the visibilities slightly increase. Our visibility measurements are inconsistent with a disk gap and an inner radius
of
![]() ,
only, but a gap of between 2 AU and 4 AU fits the visibility data as well as the model without gap.
,
only, but a gap of between 2 AU and 4 AU fits the visibility data as well as the model without gap.
Although there are observational hints for a disk gap, we are unable to
conclude whether the model with a disk gap of inner radius
![]() 2 AU or a model
disk without gap provide a closer fit to the data. Further interferometric observations
and simultaneous photometric measurements in the NIR wavelength range would
allow a final confirmation or rejection of the presence of a gap in the
disk of RU Lup.
2 AU or a model
disk without gap provide a closer fit to the data. Further interferometric observations
and simultaneous photometric measurements in the NIR wavelength range would
allow a final confirmation or rejection of the presence of a gap in the
disk of RU Lup.
4.5 HBC 639
Apart from HD 72106 B, the source HBC 639 is the only object where accretion has not been considered. Although HBC 639 has an age of between 1 and 3 million
years (Gras-Velázquez & Ray 2005), we can neglect the derived accretion rate (Prato et al. 2003), for which we estimate an upper limit of
![]() .
Since the
equivalence width of the H
.
Since the
equivalence width of the H![]() line is smaller than 10 Å, HBC 639 is not a classical T Tauri star but belongs to the class of weak-line T Tauri stars.
line is smaller than 10 Å, HBC 639 is not a classical T Tauri star but belongs to the class of weak-line T Tauri stars.
![\begin{figure}
\par\mbox{\hspace*{2.5cm}\includegraphics[scale=0.29]{003fig25.ps...
...ig38.ps} \includegraphics[scale=0.29]{003fig39.ps}\hspace*{2.5cm}}\end{figure}](/articles/aa/full_html/2009/28/aa10782-08/Timg292.png) |
Figure 8:
Uncorrelated and correlated N band spectra obtained from the objects that were observed with MIDI for this study (black lines). Correlated spectra are designated by the additional information about the baseline length B (Table 2). Because of the remaining ozone band in several spectra the wavelength interval from |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\hspace*{2.5cm}\includegraphics[scale=0.29]{003fig40.ps...
...45.ps} \includegraphics[scale=0.29]{003fig46.ps}\hspace*{2.5cm}}
\end{figure}](/articles/aa/full_html/2009/28/aa10782-08/Timg293.png) |
Figure 8: continued. |
| Open with DEXTER | |
The parameter combination listed in Table 3 could reproduce the MIR visibilities. However, this model produces a strong decline in the FIR flux and is therefore unable to reproduce the photometric upper limits in the FIR range. HBC 639 has an infrared companion at a projected distance of 320 AU (s. Appendix A). The strong decline in the FIR flux could be explained by the presence of an infrared companion that truncates the outer-disk region of the main component. In the latter case, the measured flux in the FIR (s. Fig. 5) can mainly be ascribed to this infrared companion. The companion is again a binary, as well, and deeply embedded in a circumbinary envelope.
A larger value for the disk parameter ![]() results in a more flared disk. Outer disk regions can be more
effectively heated and the intensity distribution in the MIR range therefore decreases less strongly. A consequence is a decrease in the MIR visibilities. Figure 5 also shows the results of a model with
results in a more flared disk. Outer disk regions can be more
effectively heated and the intensity distribution in the MIR range therefore decreases less strongly. A consequence is a decrease in the MIR visibilities. Figure 5 also shows the results of a model with ![]() for which none of the other parameters were modified. We note that the visibilities decrease by at least 10% for all baselines and the FIR flux increases by almost a factor of 2.
for which none of the other parameters were modified. We note that the visibilities decrease by at least 10% for all baselines and the FIR flux increases by almost a factor of 2.
4.6 S CrA N
Only the photometric measurements in the NIR and MIR range can exclusively
be ascribed to the Northern
component of this binary. All other photometric measurements could not spatially resolve
the individual components of the binary system. The visual extinction ![]() and the effective stellar temperature
and the effective stellar temperature
![]() used in the model are within the 1
used in the model are within the 1![]() -deviations (
-deviations (
![]() and 400 K) of the previously derived results of Prato et al. (2003). The NIR flux that results from our model deviates by
and 400 K) of the previously derived results of Prato et al. (2003). The NIR flux that results from our model deviates by ![]() from the measurements (s. Fig. 6). The accretion luminosity is equal to
from the measurements (s. Fig. 6). The accretion luminosity is equal to
![]() .
.
A second model for S CrA N (grey curve/bars in Fig. 6) with
![]() and
and
![]() does not reproduce the visibility measurements as well as the first model (deviations from the measurements are 6%) but the SED for
does not reproduce the visibility measurements as well as the first model (deviations from the measurements are 6%) but the SED for
![]() can be simulated more accurately. In contrast to HBC 639, the FIR flux must then originate in the Southern component. Furthermore, to
reproduce the visual wavelength range, the second model still allows an inclination angle of up to
can be simulated more accurately. In contrast to HBC 639, the FIR flux must then originate in the Southern component. Furthermore, to
reproduce the visual wavelength range, the second model still allows an inclination angle of up to
![]() ,
while only lower inclinations
angles of
,
while only lower inclinations
angles of
![]() can be used in the first model.
can be used in the first model.
4.7 S CrA S
The Southern component of S CrA is the fainter component in the NIR and MIR
wavelength range. An investigation of the Br![]() line showed that this component is as active as the Northern component (Prato & Simon 1997). A value for the
accretion rate had not yet been derived. The accretion luminosity in
our model is
line showed that this component is as active as the Northern component (Prato & Simon 1997). A value for the
accretion rate had not yet been derived. The accretion luminosity in
our model is
![]() .
The corresponding accretion rate of
.
The corresponding accretion rate of
![]() is already an upper limit because higher values would produce an increase in the disk irradiation and
a decrease in the visibilities. If accretion is not considered in our model, the MIR visibilities increase by only
is already an upper limit because higher values would produce an increase in the disk irradiation and
a decrease in the visibilities. If accretion is not considered in our model, the MIR visibilities increase by only ![]() .
Figure 7
represents our best-fit model.
.
Figure 7
represents our best-fit model.
5 Radial gradient of the dust composition in circumstellar disks around T Tauri stars
![\begin{figure}
\par\includegraphics[width=10.5cm,clip]{aa10782-fig9.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10782-08/Timg309.png) |
Figure 9:
Uncorrelated and correlated MIDI spectra after subtraction of a black body that represents the underlying continuum and is fitted to the extended wings of the emission features (black lines). The gray curves represent TIMMI 2 data (Przygodda et al. 2003) after subtraction of a black body and the spectral contribution of small amorphous dust grains found in the preceeding study of Schegerer et al. (2006). For clarity, we only show the results obtained for the single-dish spectra and the correlated spectra that were obtained for the longest effective baseline length. The vertical lines designate features of enstatite (at
|
| Open with DEXTER | |
For each single interferometric observation with MIDI and for each single telescope, one uncorrelated N band spectrum can be obtained. For each interferometric observation, we also obtained a
correlated spectrum reflecting the flux emitted by regions that are not spatially resolved by the interferometer. An increasing effective baseline length B of the
interferometer results in a higher resolution. The uncorrelated, i.e., single-dish spectra as well as the correlated spectra contain spectral contributions of the N band from the entire disk, while the contributions from the hotter
and brighter, i.e., inner regions increase with increasing
effective baseline length B assuming a homogeneous, axial-symmetric disk. It was shown by Schegerer et al. (2008) that the local silicate
dust composition in the circumstellar disk around RY Tau depends on the radial distance from the star, i.e., the relative contribution of crystalline and large dust grains increases towards the star![]() . Small and large dust grains are assumed to have a radius of
. Small and large dust grains are assumed to have a radius of
![]() and
and
![]() ,
respectively. In the following, we
investigate whether a corresponding correlation between radial location and dust composition can also be found in the T Tauri stars of our sample.
,
respectively. In the following, we
investigate whether a corresponding correlation between radial location and dust composition can also be found in the T Tauri stars of our sample.
The (averaged) uncorrelated spectra and the correlated
spectra are shown in Fig. 8.
All uncorrelated and correlated spectra exhibit the silicate emission feature apart from the correlated spectra of HD 72106 and HBC 639 that were obtained with the longest interferometric baseline. The uncorrelated spectra obtained during different nights differ in absolute flux scale by 4% for S CrA N and up to 35% for GW Ori, while the shape of the spectra does not change. We assume that the variation in
the absolute flux scale of a spectrum is caused by an erroneous photometric calibration
during data reduction. Przygodda (2004) indeed confirmed that the scale factor of the photometric calibration can vary by more than 15% during a single night. If available, spectra acquired by the Thermal Infrared Multi Mode Instrument 2 (TIMMI 2) at
ESO's observatory La Silla (Przygodda et al. 2003; Schegerer et al. 2006) are also plotted in Fig. 8. The spectra obtained with TIMMI 2 can be used in the following comparison. With respect to the TIMMI 2 data, the shapes of the uncorrelated MIDI spectra are largely preserved for GW Ori (deviation: 6%), RU Lup (9%), S CrA N (18%), and S CrA S (25%) and differ only in absolute scale. However, the shapes of the spectra of
DR Tau, and of HBC 639 in particular, differ significantly in a way
that could be due to an intrinsically temporal variation. We
note that the TIMMI 2 spectra were obtained ![]() 3 years before our
MIDI observations. However, the difference could also be caused by a doubling
of the spatial resolution power using a
3 years before our
MIDI observations. However, the difference could also be caused by a doubling
of the spatial resolution power using a
![]() -single-dish of
MIDI in contrast to the
-single-dish of
MIDI in contrast to the
![]() -telescope of TIMMI 2. Therefore,
observations with a single-dish of the VLTI allows us to observe exclusively
more central regions of the source, where more evolved grains are assumed to
exist. We should mention that a spatial resolution of
-telescope of TIMMI 2. Therefore,
observations with a single-dish of the VLTI allows us to observe exclusively
more central regions of the source, where more evolved grains are assumed to
exist. We should mention that a spatial resolution of ![]()
![]() at a distance of
at a distance of ![]()
![]() can theoretically be achieved with a
single-dish observation with the VLT.
With respect to the TIMMI 2 spectrum, the flattening of the MIDI spectrum of
HBC 639 could originate from an increase in the mass contribution of
large silicate grains in the more central regions considering their
specific absorption efficiency
can theoretically be achieved with a
single-dish observation with the VLT.
With respect to the TIMMI 2 spectrum, the flattening of the MIDI spectrum of
HBC 639 could originate from an increase in the mass contribution of
large silicate grains in the more central regions considering their
specific absorption efficiency ![]() (Dorschner et al. 1995).
Our latter assumption is also confirmed by the correlated spectra of
the objects HD 72106 B and HBC 639 obtained with the longest
interferometric baseline. These spectra are flat
and do not show any silicate emission band. We refer to a
study of Min et al. (2006), where it was found that the silicate band disappears if the averaged dust grain size exceeds
(Dorschner et al. 1995).
Our latter assumption is also confirmed by the correlated spectra of
the objects HD 72106 B and HBC 639 obtained with the longest
interferometric baseline. These spectra are flat
and do not show any silicate emission band. We refer to a
study of Min et al. (2006), where it was found that the silicate band disappears if the averaged dust grain size exceeds ![]()
![]() .
.
The origin of the evolved dust contributing to the
TIMMI 2 spectra can be derived by considering the following comparison with the MIDI spectra. A black body ![]() that represents the putative underlying continuum (Schegerer et al. 2006) and is fitted to the extended wings of the emission features
that represents the putative underlying continuum (Schegerer et al. 2006) and is fitted to the extended wings of the emission features ![]() of TIMMI 2 as well as correlated and uncorrelated MIDI spectra, is subtracted from N band. We derive normalized features using:
of TIMMI 2 as well as correlated and uncorrelated MIDI spectra, is subtracted from N band. We derive normalized features using:
This normalization procedure preserves the shape of the emission feature (Przygodda et al. 2003). According to Schegerer et al. (2006), the contributions of amorphous and crystalline dust to the TIMMI 2 spectra are determined using a
- 1.
- The normalized TIMMI 2 spectra reproduce well the normalized uncorrelated and normalized correlated MIDI spectra. The evolved grains that contribute to the TIMMI 2 spectra originate therefore in more central regions. Since the normalized TIMMI 2 spectra similarly correspond to the normalized uncorrelated and normalized correlated MIDI spectra, a further evolution of dust in regions that MIDI is able to study, cannot be determined. DR Tau and S CrA N belong to this class.
- 2.
- The normalized TIMMI 2 and MIDI spectra of HBC 639 differ at
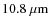 ,
where
the crystalline compound enstatite generally shows a specific emission
feature. If the remaining feature at
,
where
the crystalline compound enstatite generally shows a specific emission
feature. If the remaining feature at 
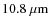 in the
normalized TIMMI 2 spectrum can be ascribed to enstatite, our comparison suggests
that enstatite has its origin in more outer disk regions. These outer
regions can already be resolved with a single-dish of MIDI and do not
appear in the MIDI spectra. S CrA S could also be ascribed to this class
by considering its correlated, normalized spectra. This result is based on
the assumption that the spectral resolution power of MIDI is high enough to resolve the
in the
normalized TIMMI 2 spectrum can be ascribed to enstatite, our comparison suggests
that enstatite has its origin in more outer disk regions. These outer
regions can already be resolved with a single-dish of MIDI and do not
appear in the MIDI spectra. S CrA S could also be ascribed to this class
by considering its correlated, normalized spectra. This result is based on
the assumption that the spectral resolution power of MIDI is high enough to resolve the
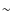
 feature of enstatite in the inner regions.
feature of enstatite in the inner regions.
- 3.
- An increasing flattening of the emission feature and an
increasing amplitude of the forsterite feature at
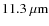 with increasing
baseline length B suggest grain evolution towards more central regions
(e.g., GW Ori). The comparison with the corresponding normalized TIMMI 2 spectra shows, however, that the contribution of small amorphous dust grains, emitting a
triangular emission feature with the maximum at
with increasing
baseline length B suggest grain evolution towards more central regions
(e.g., GW Ori). The comparison with the corresponding normalized TIMMI 2 spectra shows, however, that the contribution of small amorphous dust grains, emitting a
triangular emission feature with the maximum at
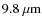 ,
is
still large even in the correlated spectrum that were obtained with the longest
baselines. GW Ori, RU Lup, and S Cr A S belong to this class.
,
is
still large even in the correlated spectrum that were obtained with the longest
baselines. GW Ori, RU Lup, and S Cr A S belong to this class.
Considering a measurement error in the visibility of
![]() as well as the low signal-to-noise ratio of
as well as the low signal-to-noise ratio of ![]() 4 and the low spectral resolution reached, we avoid fitting the uncorrelated and correlated MIDI spectra using a linear combination of different-sized, amorphous and crystalline silicate grains. The latter procedure was presented by Schegerer et al. (2006) and Schegerer et al. (2008).
However, we conclude that the local silicate dust composition in the circumstellar disks around the T Tauri objects of our sample
depends on the radial disk location. Features
of crystalline and large silicate grains indeed originate predominantly in more central disk regions of several AUs in size. However, the features of enstatite
could originate in more outer regions, and the spectral contribution of small, non-evolved dust grains from the inner disk region could remain high.
4 and the low spectral resolution reached, we avoid fitting the uncorrelated and correlated MIDI spectra using a linear combination of different-sized, amorphous and crystalline silicate grains. The latter procedure was presented by Schegerer et al. (2006) and Schegerer et al. (2008).
However, we conclude that the local silicate dust composition in the circumstellar disks around the T Tauri objects of our sample
depends on the radial disk location. Features
of crystalline and large silicate grains indeed originate predominantly in more central disk regions of several AUs in size. However, the features of enstatite
could originate in more outer regions, and the spectral contribution of small, non-evolved dust grains from the inner disk region could remain high.
6 Summary
We have presented MIR visibilities of seven pre-main-sequence stars observed with MIDI at the VLTI. We modeled the SEDs and the spectrally resolved MIR visibilities of these YSOs, and in particular T Tauri objects. The density distributions of the circumstellar disks were derived using the parametrized approach of Shakura & Sunyaev (1973, Eq. (1)). The results of this study are:
- 1.
- All objects could be spatially resolved with MIDI.
- 2.
- We showed that the results of highly spatially resolved observations
in the MIR range probing small-scale structures in the range of several
AUs, and the SED from the visual to the millimeter wavelength
range can simultaneously be reproduced by a single model except for
one source (see vi.). We note that the SED does not generally
provide any spatial information. The number of models that simulate
the SED, solely, can be strongly reduced by the measurements with
MIDI. Furthermore, the results of previous investigations based
on large-scale observations in the range of several
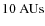 ,
were confirmed by our modeling results in most cases. Any differences
between the results of previous measurements and our modeling approach
(e.g., the accretion rate of RU Lup) could be caused by a time-dependent
variability.
,
were confirmed by our modeling results in most cases. Any differences
between the results of previous measurements and our modeling approach
(e.g., the accretion rate of RU Lup) could be caused by a time-dependent
variability.
- 3.
- For five of seven objects, the modeling approach of a purely passive disk is insufficient to reproduce the SED and the MIR visibilities of the sources. The implementation of accretion effects also significantly improves the simulation of the measurements.
- 4.
- For two objects in this study, i.e., HD 72106 B and HBC 639, the approach of a passive disk without accretion is sufficient. HD 72106 B is 10 million years old and its low accretion rate and high mass contributions from crystalline and large dust grains, have already been mentioned in previous investigations (Vieira et al. 2003; Schütz et al. 2005). In contrast, HBC 639 is still a relatively young object (Gras-Velázquez & Ray et al. 2005) but belongs to the class of weak-line T Tauri stars.
- 5.
- For some targets (e.g., DR Tau, and S CrA N), the MIR data do not constrain all model parameters. However, further modeling constraints can be obtained from additional measurements, e.g., NIR visibilities as shown for our modeling approach for DR Tau, where PTI data were additionally taken into account.
- 6.
- The modeling result for the source GW Ori illustrates the need for an individual extension to our approach. According to Mathieu et al. (1997), GW Ori has a stellar companion at a (projected) distance of
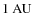 .
Therefore, in a second model we
considered a combination of a
circumstellar and circumbinary disk. The circumstellar and circumbinary disk are determined by the same disk parameters
.
Therefore, in a second model we
considered a combination of a
circumstellar and circumbinary disk. The circumstellar and circumbinary disk are determined by the same disk parameters 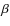 and
and
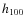 and are seperated by a dust-free gap. However, a model that reproduces all the measurements could not be found. We recommend
acquiring
additional high spatial resolution observations including phase
measurements to clarify the complex inner-disk structure
of this object.
and are seperated by a dust-free gap. However, a model that reproduces all the measurements could not be found. We recommend
acquiring
additional high spatial resolution observations including phase
measurements to clarify the complex inner-disk structure
of this object.
- 7.
- Our measurements of RU Lup can be simulated equally with an active disk model with or without a dust-free gap. A disk model with a gap was formerly proposed by Takami et al. (2001) based on spectro-astrometric observations.
- 8.
- Each single component of the binary system S CrA could be seperately observed with MIDI. Considering inner disk regions on
small scales that could be resolved with MIDI, basic differences between this binary system and other objects in our sample
without a companion could not be
found. Only the SEDs of the sources HD 72106 B, HBC 639, and S CrA N
that decline strongly at
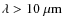 support the idea that a stellar companion truncates the
outer disk regions of these sources.
support the idea that a stellar companion truncates the
outer disk regions of these sources.
- 9.
- The relative mass contribution of evolved dust in the systems of fainter T Tauri objects is higher in the inner disk regions close to the central star than in the outer regions. However, enstatite could already be enriched and stimulated in outer disk regions and the spectral contribution from non-evolved dust grains could still be high in the inner regions.
Acknowledgements
A.A. Schegerer and S. Wolf were supported by the German Research Foundation (DFG) through the Emmy-Noether grant WO 857/2 (``The evolution of circumstellar dust disks to planetary systems''). We gratefully acknowledge O. Chesneau, Ch. Leinert, S. A. Lamzin, G. Meeus, F. Przygodda, Th. Ratzka, and O. Schütz who have generously given their time to provide valuable assistance during the proposal and observation preparation phase as well as during data analysis and discussions. We thank R. Akeson who send us the reprocessed PTI data. We also thank the anonymous referee for her/his suggestions for improvement.
References
- Akeson, R. L., Walker, C. H., Wood, K., et al. 2005, ApJ, 622, 440 [NASA ADS] [CrossRef] (In the text)
- Andrews, S. M., & Williams, J. P. 2005, ApJ, 631, 1134 [NASA ADS] [CrossRef]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] (In the text)
- Beckwith, S. V. W., Sargent, A. I., Chini, R. S., & Güsten, R. 1990, AJ, 99, 924 [NASA ADS] [CrossRef]
- Bernacca, P. L., Lattanzi, M. G., Porto, I., Neuhäuser, R., & Bucciarell, B. 1995, A&A, 299, 933 [NASA ADS] (In the text)
- Bertout, C., Basri, G., & Bouvier, J. 1988, ApJ, 330, 350 [NASA ADS] [CrossRef] (In the text)
- Bouvier, J., & Appenzeller, I. 1992, A&ASS, 92, 481 [NASA ADS]
- Burrows, C. J., Stapelfeldt, K. R., Watson, A. L., et al. 1996, ApJ, 473, 437 [NASA ADS] [CrossRef] (In the text)
- Calvet, N., & Gullbring, E. 1998, ApJ, 509, 802 [NASA ADS] [CrossRef] (In the text)
- Calvet, N., D'Alessio, P., Hartmann, L., et al. 2002, ApJ, 568, 1008 [NASA ADS] [CrossRef] (In the text)
- Calvet, N., Muzerolle, J., Briceño, C., et al. 2004, AJ, 128, 1294 [NASA ADS] [CrossRef] (In the text)
- Chelli, A., Zinnecker, H., Carrasco, L., Cruz-Gonzalez, I., & Perrier, C. 1988, A&A, 207, 46 [NASA ADS] (In the text)
- Chini, R., Kämpgen, K., Reipurth, B., et al. 2003, A&A, 409, 235 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cohen, M. 1973, MNRAS, 161, 97 [NASA ADS]
- Cohen, M. 1975, MNRAS, 173, 279 [NASA ADS]
- Cohen, M., Walker, R. G., Carter, B., et al. 1999, AJ, 117, 1864 [NASA ADS] [CrossRef]
- Cotera, A. S., Whitney, B. A., Young, E., et al. 2001, ApJ, 556, 958 [NASA ADS] [CrossRef] (In the text)
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, in 2MASS All Sky Catalog of point sources
- D'Alessio, P., Cantó, J., Calvet, N., & Lizano, S. 1998, ApJ, 500, 411 [NASA ADS] [CrossRef] (In the text)
- Deep Near Infrared Survey of the Southern Sky (DENIS), DENIS Databasis, 3rd release 2005
- Dolan, Ch. J., & Mathieu, R. D. 2001, AJ, 121, 2124 [NASA ADS] [CrossRef] (In the text)
- Dorschner, J., Begemann, B., Henning, Th., Jäger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS] (In the text)
- Draine, B. T., & Malhotra, S. 1993, ApJ, 414, 632 [NASA ADS] [CrossRef] (In the text)
- Duchêne, G. 1999, A&A, 341, 547 [NASA ADS] (In the text)
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 967 [NASA ADS] [CrossRef] (In the text)
- Edwards, S., Ray, T. P., & Mundt, R. 1993 in PPIII, ed. E. H. Levy, & J. I. Lunine, 567 (In the text)
- Eiroa, C., Oudmaijer, R. D., Davies, J. K., et al. 2002, A&A, 384, 1038 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Eislöffel, J., Mundt, R., Ray, T. P., & Rodríguez, L. F. 2000, in Protostars and Planets IV, ed. V. Mannings, A. Boss, & S. S. Russell (In the text)
- Fabricius, C., & Makarov, V. V. 2000, A&A, 365, 141 [NASA ADS] (In the text)
- Folsom, C. P. 2007, Ph.D. Thesis, Queen's University, Kingston, Canada (In the text)
- Gail, H.-P. 2003 in Astromineralogy, LNP, Hrsg.: Th. Henning, 609, 55 (In the text)
- Gahm, G. F., Gullbring, E., Fischertröm, C., Lindroos, K. P., & Lodén, K. 1993, A&AS, 100, 371 [NASA ADS]
- Gezari, D. Y., Pitts, P. S., & Schmitt, M. 1999, 5
- Ghez, A. M., McCarthy, D. W., Patience, J. L., & Beck, T. L. 1997, ApJ, 481, 295 [CrossRef] (In the text)
- Giovannelli, F., Vittone, A. A., Rossi, C., et al. 1995, A&AS, 114, 269 (In the text)
- Grankin, K. N., Melnikov, S. Yu., Bouvier, J., Herbst, W., & Shevchenko, V. S. 2007, A&A, 461, 183 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gras-Velázquez, A., & Ray, T. P. 2005, A&A, 443, 541 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Greaves, J. S. 2004, MNRAS, 351, 99 [NASA ADS] [CrossRef]
- Günther, R., & Kley, W. 2002, A&A, 387, 550 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Gullbring, E., Calvet, N., Muzerolle, J., & Hartmann, L. 2000, ApJ, 544, 927 [NASA ADS] [CrossRef] (In the text)
- Hartkopf, W. I., Mason, B. D., McAlister, H. A., et al. 1996, AJ, 111, 936 [NASA ADS] [CrossRef] (In the text)
- Hartmann, L., Kenyon, S. J., & Calvet, N. 1993, ApJ, 407, 219 [NASA ADS] [CrossRef] (In the text)
- Hartmann, L., Megeath, S. T., Allen, L., et al. 2005, ApJ, 629, 881 [NASA ADS] [CrossRef]
- Herczeg, G. J., Walter, F. M., Linsky, J. L., et al. 2005, AJ, 129, 2777 [NASA ADS] [CrossRef] (In the text)
- IRAS Explanatory Supplement to the Catalogs and Atlasses 1985, ed. C. Beichmann, G. Neugebauer, H. J. Habing, P. E. Clegg, & T. J. Chester, NASA RP-1190, 1
- Isella, A., & Natta, A. 2005, A&A, 438, 899 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- ISO Data Archive of the Infrared Space Observatory, European Space Agency (ESA)
- Jensen, E. L. N., Mathieu, R. D., & Fuller, G. A. 1996, ApJ, 458, 312 [NASA ADS] [CrossRef]
- Jensen, E. L. N., Mathieu, R. D., Donar, A. X., & Dullighan, A. 2004, ApJ, 600, 789 [NASA ADS] [CrossRef] (In the text)
- Johns-Krull, C. M., Valenti, J. A., & Linsky, J. L. 2000, ApJ, 539, 815 [NASA ADS] [CrossRef]
- Joy, A. H., & Biesbrock, G. 1944, PASP, 56, 123 [NASA ADS] [CrossRef] (In the text)
- Joy, A. H. 1945, ApJ, 102, 168 [NASA ADS] [CrossRef] (In the text)
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef]
- Klahr, H. 2004, ApJ, 606, 1070 [NASA ADS] [CrossRef] (In the text)
- Koehler, R., & Leinert, Ch. 1998, A&A, 331, 977 [NASA ADS] (In the text)
- Koresko, C. D., Herbst, T. M., & Leinert, Ch. 1997, ApJ, 480, 741 [NASA ADS] [CrossRef] (In the text)
- Koresko, C. D. 2002, AJ, 124, 1082 [NASA ADS] [CrossRef] (In the text)
- Kwan, J., & Tademaru, E. 1988, ApJ, 332, 41 [NASA ADS] [CrossRef] (In the text)
- Kwan, J., Edwards, S., & Fischer, W. 2007, ApJ, 657, 897 [NASA ADS] [CrossRef] (In the text)
- Lamzin, S. A., Bisnovatyi-Kogan, G. S., Errico, L., et al. 1996, A&A, 306, 877 [NASA ADS] (In the text)
- Leinert, Ch., van Boekel, R., Waters, L. B. F. M., et al. 2004, A&A, 423, 537 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lissauer, J. J. 1993, ARA&A, 31, 129 [NASA ADS] [CrossRef] (In the text)
- Lommen, D., Wright, C. M., Maddison, S. T., et al. 2007, A&A, 462, 211 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] (In the text)
- Mathieu, R. D., Adams, F. C., & Latham, D. W. 1991, AJ, 101, 6 [CrossRef] (In the text)
- Mathieu, R. D., Adams, F. C., Fuller, G. A., et al. 1995, AJ, 109, 2655 [NASA ADS] [CrossRef] (In the text)
- Mathieu, R. D., Stassen, K., Basri, G., et al. 1997, AJ, 113, 1841 [NASA ADS] [CrossRef] (In the text)
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] (In the text)
- McCabe, C., Ghez, A. M., Prato, L., et al. 2006, ApJ, 636, 932 [NASA ADS] [CrossRef] (In the text)
- Min, M., Dominik, C., Hovenier, J. W., de Koter, A., & Waters, L. B. F. M. 2006, A&A, 445, 1005 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mohanty, S., Jayawardhana, R., & Basri, G. 2005, ApJ, 626, 498 [NASA ADS] [CrossRef] (In the text)
- Muzerolle, J., Calvet, N., Hartmann, L., & D'Alessio, P. 2003, ApJ, 597, 149 [NASA ADS] [CrossRef] (In the text)
- Nagasawa, M., Thommes, E. W., Kenyon, S. J., Bromley, B. C., & Lin, D. N. C. 2006, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (In the text)
- Natta, A., Testi, L., & Randich, S. 2006, A&A, 447, 609 [CrossRef] [EDP Sciences] (In the text)
- Nürnberger, D., Chini, R., & Zinnecker, H. 1997, A&A, 324, 1036 [NASA ADS] (In the text)
- Perryman, M. A. C. 1997, in The Hipparcos and Tycho catalogues, ESA SP Series, 1200
- Prato, L., & Simon, M. 1997, ApJ, 474, 455 [NASA ADS] [CrossRef] (In the text)
- Prato, L., Greene, T. P., & Simon, M. 2003, ApJ, 584, 853 [NASA ADS] [CrossRef] (In the text)
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] (In the text)
- Przygodda, F., van Boekel, R., Ábráham, P., et al. 2003, A&A, 412, 43 [NASA ADS] [CrossRef] (In the text)
- Przygodda, F. 2004, Ph.D. Thesis, Ruprecht-Karls-Universität, Heidelberg (In the text)
- Quanz, S. P., Henning, Th., Bouwman, J., et al. 2007, ApJ, 668, 359 [NASA ADS] [CrossRef] (In the text)
- Ratzka, Th. 2005, Ph.D. Thesis, Ruprecht-Karls-Universität, Heidelberg, Germany (In the text)
- Ratzka, T., Köhler, R., & Leinert, Ch. 2005, A&A, 437, 611 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ratzka, Th., Leinert, Ch., Henning, Th., et al. 2007, A&A, 471, 173 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Reipurth, B., & Zinnecker, H. 1993, A&A, 278, 81 [NASA ADS] (In the text)
- Reipurth, B., Pedrosa, A., & Lago, M. T. V. T. 1996, A&AS, 120, 229 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Rodmann, J., Henning, Th., Chandler, C. J., Mundy, L. G., & Wilner, D. J. 2006, A&A, 446, 211 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Robitaille, Th. P., Whitney, B. A., Indebetouw, R., & Wood, K. 2007, ApJSS, 169, 328 [NASA ADS] [CrossRef] (In the text)
- Rydgren, A. E., Strom, S. E., & Strom, K. M. 1976, ApJS, 30, 30 [NASA ADS] [CrossRef]
- Rydgren, A. E., & Vrba, R. J. 1983, AJ, 88, 1017 [NASA ADS] [CrossRef]
- Schegerer, A., Wolf, S., Voshchinnikov, N. V., Przygodda, F., & Kessler-Silacci, J. E. 2006, A&A, 456, 535 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schegerer, A. A., Wolf, S., Ratzka, Th., & Leinert, Ch. 2008, A&A, 478, 779 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schütz, O., Meeus, G., & Sterzik, M. F. 2005, A&A, 431, 165 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Simon, M., Ghez, A. M., Leinert, Ch., et al. 1995, ApJ, 443, 625 [NASA ADS] [CrossRef] (In the text)
- Shakura, N. I., & Sunyaev, R. A. 1973, AAP, 24, 337 [NASA ADS] (In the text)
- Siess, L., Forestini, M., & Bertout, C. 1999, A&A, 342, 480 [NASA ADS] (In the text)
- Smith, K. W., Lewis, G. F., Bonnell, I. A., Bunclark, P. S., & Emerson, J. P. 1999, MNRAS, 304, 367 [NASA ADS] [CrossRef] (In the text)
- Sonnhalter, C. 1993, Master Thesis, Julius-Maximilian-Universität, Würzburg, Germany (In the text)
- Stempels, H. C., Gahm, G. F., & Petrov, P. P. 2007, A&A, 461, 253 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Takami, M., Bailey, J., Gledhill, T. M., Chrysostomou, A., & Hough, J. H. 2001, MNRAS, 323, 177 [NASA ADS] [CrossRef] (In the text)
- Takami, M., Bailey, J., & Chrysostomou, A. 2003, A&A, 397, 675 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Thamm, E., Steinacker, J., & Henning, Th. 1994, A&A, 287, 493 [NASA ADS] (In the text)
- Torres, C. A. O., Quast, G., de la Reza, R., Gregorio-Hetem, J., & Lépine, J. R. D. 1995, AJ, 109, 2146 [NASA ADS] [CrossRef] (In the text)
- Uchida, Y., & Shibata, K. 1984, PASJ, 36, 105 [NASA ADS] (In the text)
- Ultchin, Y., Regev, O., & Bertout, C. 1997, ApJ, 486, 397 [NASA ADS] [CrossRef] (In the text)
- van Boekel, R., Min, M., Leinert, Ch., et al. 2004, Nature, 432, 479 [NASA ADS] [CrossRef] (In the text)
- Vieira, S. L. A., Corradi, W. J. B., Alencar, S. H. P., et al. 2003, AJ, 126, 2971 [NASA ADS] [CrossRef] (In the text)
- Vink, J. S., Drew, J. E., Harries, T. J., Oudmaijer, R. D., & Unruh, Y. 2005, MNRAS, 359, 1049 [NASA ADS] [CrossRef] (In the text)
- Wade, G. A., Drouin, D., Bagnulo, S., et al. 2005, A&A, 442, 31 [NASA ADS] [CrossRef] (In the text)
- Wade, G. A., Bagnulo, S., Drouin, D., Landstreet, J. D., & Monin, D. 2007, MNRAS, 376, 1145 [NASA ADS] [CrossRef] (In the text)
- Wolf, S., Henning, Th., & Stecklum, B. 1999, A&A, 349, 839 [NASA ADS] (In the text)
- Wolf, S., Padgett, D. L., & Stapelfeldt, K. R. 2003, ApJ, 588, 373 [NASA ADS] [CrossRef] (In the text)
- Wolf, S. 2007, Habil. Thesis, Karl-Ruprecht-Universität Heidelberg (In the text)
- Wood, K., Kenyon, S. J., Whitney, B., & Turnbull, M. 1998, ApJ, 497, 404 [NASA ADS] [CrossRef] (In the text)
- Wood, K., Lada, C. J., Bjorkman, J. E., et al. 2002, ApJ, 567, 1183 [NASA ADS] [CrossRef] (In the text)
- Wünsch, R., Klahr, H., & Rózyczka, M. 2005, MNRAS, 362, 361 [NASA ADS] [CrossRef] (In the text)
Online Material
Appendix A: Previous measurements:
DR Tau:
The 2.5 million-year-old object DR Tau belongs to the Taurus-Auriga star-forming region at a distance of ![]() 140 pc (Siess et al. 1999). Numerous publications illustrate that DR Tau is one of the most well-studied T Tauri objects. Strong veiling has been found in the visual and NIR wavelength range: the flux in V band, for instance, exceeds the intrinsic stellar flux by a factor of five (Edwards et al. 1993). Apart from the excessive flux in the visual, the profiles of several emission
lines, such as the Pf
140 pc (Siess et al. 1999). Numerous publications illustrate that DR Tau is one of the most well-studied T Tauri objects. Strong veiling has been found in the visual and NIR wavelength range: the flux in V band, for instance, exceeds the intrinsic stellar flux by a factor of five (Edwards et al. 1993). Apart from the excessive flux in the visual, the profiles of several emission
lines, such as the Pf![]() -line, points to material accreting onto the central star while the profiles of further emission lines such as the He I line (Kwan et al. 2007) and the H
-line, points to material accreting onto the central star while the profiles of further emission lines such as the He I line (Kwan et al. 2007) and the H![]() lines (Vink et al. 2005) are evidence of outflowing stellar/disk winds. Based on a modeling study, Edwards et al. (1993)
determined an accretion rate of
lines (Vink et al. 2005) are evidence of outflowing stellar/disk winds. Based on a modeling study, Edwards et al. (1993)
determined an accretion rate of
![]() ,
while a mass of
,
while a mass of
![]() is lost by stellar/disk winds. A strongly collimated
outflow was also found by Kwan & Tademaru (1988). DR Tau is photometrically and spectrally variable on short terms, i.e., in the range of weeks (
is lost by stellar/disk winds. A strongly collimated
outflow was also found by Kwan & Tademaru (1988). DR Tau is photometrically and spectrally variable on short terms, i.e., in the range of weeks (
![]() mag; Grankin et al. 2007; Eiroa et al. 2002; Smith et al. 1999). This variability is also ascribed to the formation and movement of stellar spots on this star (Ultchin et al. 1997).
mag; Grankin et al. 2007; Eiroa et al. 2002; Smith et al. 1999). This variability is also ascribed to the formation and movement of stellar spots on this star (Ultchin et al. 1997).
GW Ori: GW Ori, also known as HD 244138, belongs to the star-forming region B 30 in a ring-shaped molecular cloud close to
HD 72106 B: The object HD 72106 is a visual binary (angular distance
RU Lup: RU Lup is a classical T Tauri star in the star-forming region Lupus. Visual and millimeter measurements showed that the object does not have a (remaining) circumstellar envelope (Giovannelli et al. 1995; Lommen et al. 2007). A secondary could not be found with speckle interferometry down to a minimal distance of
HBC 639: HBC 639, also known as DoAr 24 E, belongs to the star-forming region
S CrA: The source S CrA belongs to the Southern Region of the Corona Australis Complex (e.g., Chini et al. 2003). The source was already defined as a T Tauri object by Joy et al. (1945) who pointed to an infrared companion at a projected distance of
Table A.1: Photometric flux measurements of DR Tau.
Table A.2:
Photometric flux measurements of GW Ori. The value that is marked with the symbol ``
![]() '' is an upper flux limit.
'' is an upper flux limit.
Table A.3:
Photometric flux measurements of HD 72106 B. The value that is marked with the symbol ``
![]() '' is an upper limit.
'' is an upper limit.
Table A.4: Photometric flux measurements of RU Lup.
Table A.5: Photometric flux measurement of HBC 639. The flux can be ascribed to the main component up to wavelengths in L band.
Table A.6:
Photometric flux measurement of S CrA N and S CrA S. For the photometric observations of wavelengths
![]() and
and
![]() ,
both components could not be spatially resolved.
,
both components could not be spatially resolved.
Footnotes
- ... stars
![[*]](/icons/foot_motif.png)
- Based on observations made with Telescopes of the European Organisation for Astronomical Research in the Southern Hemisphere (ESO) at the Paranal Observatory, Chile, under the programs 074.C-0342(A), 075.C-0064(A,B), 075.C-0413(A,B), and 076.C-0356(A).
- ...
![[*]](/icons/foot_motif.png)
- Appendix A is only available in electronic form at http://www.aanda.org
- ... available
![[*]](/icons/foot_motif.png)
- Software packages are available at http://www.mpia-hd.mpg.de/MIDISOFT/ and http://www.strw.leidenuniv.nl/~koehler/MIA+EWS-Manual/
- ... scale-height
![[*]](/icons/foot_motif.png)
- The scale-height is defined as the vertical distance from the midplane, where the density has decreased by a factor
 (Euler's constant).
(Euler's constant).
- ... disk
![[*]](/icons/foot_motif.png)
- An inclination angle of 0
 corresponds to a face-on disk.
corresponds to a face-on disk.
- ... wavelengths
![[*]](/icons/foot_motif.png)
- Used for the calculation of the modeled visibility.
- ... star
![[*]](/icons/foot_motif.png)
- In this study, crystalline and large grains are called evolved dust grains.
- ... spectra
![[*]](/icons/foot_motif.png)
- For simplicity, the modified TIMMI 2 spectra after normalization and after subtraction of the contribution of small amorphous grains are called normalized TIMMI 2 spectra.
All Tables
Table 1: Object properties derived in previous measurements or in this study.
Table 2: Overview of our observations with MIDI.
Table 3: Parameters of the models that simulate the measured SED and MIR visibilities best.
Table A.1: Photometric flux measurements of DR Tau.
Table A.2:
Photometric flux measurements of GW Ori. The value that is marked with the symbol ``
![]() '' is an upper flux limit.
'' is an upper flux limit.
Table A.3:
Photometric flux measurements of HD 72106 B. The value that is marked with the symbol ``
![]() '' is an upper limit.
'' is an upper limit.
Table A.4: Photometric flux measurements of RU Lup.
Table A.5: Photometric flux measurement of HBC 639. The flux can be ascribed to the main component up to wavelengths in L band.
Table A.6:
Photometric flux measurement of S CrA N and S CrA S. For the photometric observations of wavelengths
![]() and
and
![]() ,
both components could not be spatially resolved.
,
both components could not be spatially resolved.
All Figures
 |
Figure 1:
SED and MIR visibilities for a projected baseline of
|
| Open with DEXTER | |
| In the text | |
 |
Figure 2:
SED and MIR visibilities for the projected baselines of
|
| Open with DEXTER | |
| In the text | |
 |
Figure 3:
SED and MIR visibilities for the projected baselines of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par {\hspace*{3.75cm}\includegraphics[width=7.5cm,clip]{003fig11...
...,clip]{003fig14.ps}\includegraphics[width=7.5cm,clip]{003fig15.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10782-08/Timg265.png) |
Figure 4:
SED and MIR visibilities for the projected baselines of
|
| Open with DEXTER | |
| In the text | |
 |
Figure 5:
SED and MIR visibility for the projected baselines of
|
| Open with DEXTER | |
| In the text | |
 |
Figure 6:
SED and MIR visibilities for the projected baselines of
|
| Open with DEXTER | |
| In the text | |
 |
Figure 7:
SED and MIR visibilities for a projected baseline of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\hspace*{2.5cm}\includegraphics[scale=0.29]{003fig25.ps...
...ig38.ps} \includegraphics[scale=0.29]{003fig39.ps}\hspace*{2.5cm}}\end{figure}](/articles/aa/full_html/2009/28/aa10782-08/Timg292.png) |
Figure 8:
Uncorrelated and correlated N band spectra obtained from the objects that were observed with MIDI for this study (black lines). Correlated spectra are designated by the additional information about the baseline length B (Table 2). Because of the remaining ozone band in several spectra the wavelength interval from |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\hspace*{2.5cm}\includegraphics[scale=0.29]{003fig40.ps...
...45.ps} \includegraphics[scale=0.29]{003fig46.ps}\hspace*{2.5cm}}
\end{figure}](/articles/aa/full_html/2009/28/aa10782-08/Timg293.png) |
Figure 8: continued. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=10.5cm,clip]{aa10782-fig9.eps}
\end{figure}](/articles/aa/full_html/2009/28/aa10782-08/Timg309.png) |
Figure 9:
Uncorrelated and correlated MIDI spectra after subtraction of a black body that represents the underlying continuum and is fitted to the extended wings of the emission features (black lines). The gray curves represent TIMMI 2 data (Przygodda et al. 2003) after subtraction of a black body and the spectral contribution of small amorphous dust grains found in the preceeding study of Schegerer et al. (2006). For clarity, we only show the results obtained for the single-dish spectra and the correlated spectra that were obtained for the longest effective baseline length. The vertical lines designate features of enstatite (at
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\displaystyle \rho(r,z)=\rho_{0} \left( \frac{R_{\star}}{r} \right)^{\alpha}
\exp \left[ - \frac{1}{2} \left( \frac{z}{h(r)} \right)^{2} \right]\cdot$](/articles/aa/full_html/2009/28/aa10782-08/img146.png)