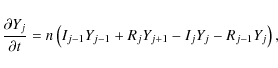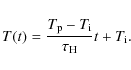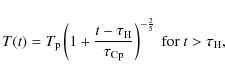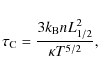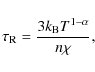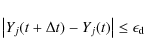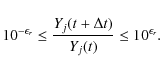| Issue |
A&A
Volume 502, Number 1, July IV 2009
|
|
|---|---|---|
| Page(s) | 409 - 418 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/200810735 | |
| Published online | 27 May 2009 | |
A numerical tool for the calculation of non-equilibrium ionisation states in the solar corona and other astrophysical plasma environments
S. J. Bradshaw
1 - NASA Goddard Space Flight Center, Solar Physics Lab., Code 671, 8800 Greenbelt Road, Greenbelt, MD 20771, USA
2 - Department of Computational and Data Sciences, George Mason University, 4400 University Drive, MSN 6A2, Fairfax, VA 22030, USA
Received 1 August 2008 / Accepted 19 May 2009
Abstract
Context. The effects of non-equilibrium processes on the ionisation state of strongly emitting elements in the solar corona can be extremely difficult to assess and yet they are critically important. For example, there is much interest in dynamic heating events localised in the solar corona because they are believed to be responsible for its high temperature and yet recent work has shown that the hottest (
![]() K) emission predicted to be associated with these events can be observationally elusive due to the difficulty of creating the highly ionised states from which the expected emission arises. This leads to the possibility of observing instruments missing such heating events entirely.
K) emission predicted to be associated with these events can be observationally elusive due to the difficulty of creating the highly ionised states from which the expected emission arises. This leads to the possibility of observing instruments missing such heating events entirely.
Aims. The equations describing the evolution of the ionisaton state are a very stiff system of coupled, partial differential equations whose solution can be numerically challenging and time-consuming. Without access to specialised codes and significant computational resources it is extremely difficult to avoid the assumption of an equilibrium ionisation state even when it clearly cannot be justified. The aim of the current work is to develop a computational tool to allow straightforward calculation of the time-dependent ionisation state for a wide variety of physical circumstances.
Methods. A numerical model comprising the system of time-dependent ionisation equations for a particular element and tabulated values of plasma temperature as a function of time is developed. The tabulated values can be the solutions of an analytical model, the output from a numerical code or a set of observational measurements. An efficient numerical method to solve the ionisation equations is implemented.
Results. A suite of tests is designed and run to demonstrate that the code provides reliable and accurate solutions for a number of scenarios including equilibration of the ion population and rapid heating followed by thermal conductive cooling. It is found that the solver can evolve the ionisation state to recover exactly the equilibrium state found by an independent, steady-state solver for all temperatures, resolve the extremely small ionisation/recombination timescales associated with rapid temperature changes at high densities, and provide stable and accurate solutions for both dominant and minor ion population fractions. Rapid heating and cooling of low to moderate density plasma is characterised by significant non-equilibrium ionisation conditions. The effective ionisation temperatures are significantly lower than the electron temperature and the values found are in close agreement with the previous work of others. At the very highest densities included in the present study an assumption of equilibrium ionisation is found to be robust.
Conclusions. The computational tool presented here provides a straightforward and reliable way to calculate ionisation states for a wide variety of physical circumstances. The numerical code gives results that are accurate and consistent with previous studies, has relatively undemanding computational requirements and is freely available from the author.
Key words: Sun: corona - Sun: UV radiation - atomic processes - methods: numerical
1 Introduction
Recent interest in the detectability of dynamic heating events localised in the solar corona (Bradshaw & Cargill 2006;
Reale & Orlando 2008), believed to be responsible for its high temperature, has brought the importance of non-equilibrium ionisation (NEI) states to the forefront of research concerning the nature of coronal heating. One example of such heating is the reconnection of adjacent magnetic field lines that have become twisted and braided in the corona due to the random motions of their photospheric footpoints. Often called nanoflares (Parker 1988; Cargill 1993, 1994 1997; Klimchuk 2006), with reference to the fraction of energy released in comparison to a large scale flare, models have shown that they may heat the corona to temperatures
![]() K (Cargill & Klimchuk 2004; Patsourakos & Klimchuk 2005, 2006; Bradshaw & Cargill 2006; Klimchuk 2006).
K (Cargill & Klimchuk 2004; Patsourakos & Klimchuk 2005, 2006; Bradshaw & Cargill 2006; Klimchuk 2006).
The major obstacle to the overall acceptance of the idea of a dynamically heated corona is the lack of direct observational evidence. A key piece of evidence that is currently missing and would support the idea of dynamic heating is extremely hot (
![]() K) coronal emission. In recent work Schmelz et al. (2009) report the detection of an extremely weak component of hot emission in a quiet Sun differential emission measure (DEM) curve constructed from Hinode-XRT (Golub et al. 2007) data. However their result, though certainly suggestive, is inconclusive at present because it lies at the very extreme of what DEM techniques can reliably reconstruct. However, a further study based on Hinode-XRT data by Reale et al. (2009), who used filter ratios to construct maps of temperature and emission measure in the quiet Sun, provides independent and corroborating evidence for the presence of a hot, but weak, component of the coronal emission. The lack of strong hot emission may be due to the difficulty of creating the ionisation states from which the expected hot emission would arise. Since the corona is optically thin the processes of ionisation and recombination are dominated by electron collisions, which in low density plasma can occur on timescales significantly longer than those associated with heating and cooling. Under these circumstances the ionisation state of the plasma becomes decoupled from the electron temperature and remains out of equilibrium until the density increases and the ionisation and recombination timescales become comparable with the timescale for temperature changes. For example, if plasma is heated and cooled on timescales much shorter than the ionisation and recombination timescales then changes in the ionisation state lag the change in temperature. At the peak temperature reached during heating the ions that would be present under equilibrium conditions will not have been created and, since thermal conduction then rapidly cools the plasma, there can be no associated hot component of the coronal emission.
K) coronal emission. In recent work Schmelz et al. (2009) report the detection of an extremely weak component of hot emission in a quiet Sun differential emission measure (DEM) curve constructed from Hinode-XRT (Golub et al. 2007) data. However their result, though certainly suggestive, is inconclusive at present because it lies at the very extreme of what DEM techniques can reliably reconstruct. However, a further study based on Hinode-XRT data by Reale et al. (2009), who used filter ratios to construct maps of temperature and emission measure in the quiet Sun, provides independent and corroborating evidence for the presence of a hot, but weak, component of the coronal emission. The lack of strong hot emission may be due to the difficulty of creating the ionisation states from which the expected hot emission would arise. Since the corona is optically thin the processes of ionisation and recombination are dominated by electron collisions, which in low density plasma can occur on timescales significantly longer than those associated with heating and cooling. Under these circumstances the ionisation state of the plasma becomes decoupled from the electron temperature and remains out of equilibrium until the density increases and the ionisation and recombination timescales become comparable with the timescale for temperature changes. For example, if plasma is heated and cooled on timescales much shorter than the ionisation and recombination timescales then changes in the ionisation state lag the change in temperature. At the peak temperature reached during heating the ions that would be present under equilibrium conditions will not have been created and, since thermal conduction then rapidly cools the plasma, there can be no associated hot component of the coronal emission.
Hansteen (1993), Bradshaw & Mason (2003), Bradshaw et al. (2004), Bradshaw & Cargill (2006) and Reale & Orlando (2008) have used numerical hydrodynamic models to examine the implications of NEI for the observable signatures and the detectability of hot emission associated with nanoflare heating localised in the solar corona. They found that NEI does indeed make nanoflares extremely difficult (and in some cases impossible) to detect directly, which certainly explains the lack of observational evidence, and one must instead rely upon secondary signatures predicted by the models in order to infer their presence.
These studies are of particular relevance to current and upcoming solar observing missions that have been specifically designed to detect hot signatures of dynamic coronal heating by making the instruments sensitive to wavelength ranges that contain emission lines from ions that are formed at high temperatures in equilibrium. For example: the long wavelength band of Hinode-EIS (Culhane et al. 2007) is sensitive to emission from ions of iron up to Fe XVI (peak abundance at
T=106.4 K in equilibrium); Hinode-XRT (Golub et al. 2007) has multiple filters sensitive to emission from Fe ions formed in the range
![]() K in equilibrium; and SDO-AIA (Weber et al. 2004) has multiple filters sensitive to emission from Fe ions formed in the range
K in equilibrium; and SDO-AIA (Weber et al. 2004) has multiple filters sensitive to emission from Fe ions formed in the range
![]() K in equilibrium. The success of these instruments at detecting the hottest components of the coronal emission associated with dynamic heating depends critically on the importance of NEI. If the ionisation state of the plasma is not in (or near) equilibrium then the choice of wavelength ranges for these instruments may not reveal any information at all about the heating process.
K in equilibrium. The success of these instruments at detecting the hottest components of the coronal emission associated with dynamic heating depends critically on the importance of NEI. If the ionisation state of the plasma is not in (or near) equilibrium then the choice of wavelength ranges for these instruments may not reveal any information at all about the heating process.
Analysing and understanding the contribution of NEI to any set of observational data from which one hopes to identify signatures of the coronal heating mechanism in operation is undoubtedly important. If the heating mechanism dynamically releases energy directly into the corona then NEI becomes absolutely critical. However, NEI can be extremely difficult to deal with because the equations that describe the evolution of the ionisaton state are a very stiff system of coupled, partial differential equations whose solution can be numerically challenging and time-consuming. Without access to specialised codes and significant computational resources it is extremely difficult to avoid the assumption of an equilibrium ionisation state, even when it clearly cannot be justified, and for this reason NEI is often left out of numerical models and observational data analyses, or at best it is considered via order-of-magnitude estimates of timescales.
The aim of the current work is to develop a computational tool to allow calculation of the time-dependent ionisation state for a wide variety of physical circumstances. Though the solar corona is the focus of the work presented here, the computational tool is intended for application to any optically thin, astrophysical plasma environment (stellar coronae or the nebular phase of expanding nova shells, for example). The numerical model and solver upon which the code is based is described in Sect. 2, the results of a series of tests designed to demonstrate that the model provides accurate and reliable solutions are discussed in Sect. 3, and a summary of the work and conclusions are presented in Sect. 4.
2 Numerical model
The approach adopted here is to consider a zero dimensional (0D) model (e.g. Cargill 1994). The relative abundances (population fractions) of the ions of a particular element are given by
where n is the electron number density, which will be assumed constant for the remainder of the current work and so the focus will be on timescales for temperature changes that are significantly shorter than the inertial timescales for the onset of bulk flows over which density changes may occur. The velocity terms have also been omitted from Eq. (1) for this reason. Y denotes the element (H, He, C, Fe, etc.) and j the ionisation stage. Yj=1 denotes neutral Y (or Y I in spectroscopic notation) and Yj=2 denotes the first ionisation stage of Y (Y II), etc. Values of Y1=0.25 and Y2=0.75, for example, would mean that 25% of element Y is present in the form of neutral Y and 75% is present in the form of singly-ionised Y. I and R are the temperature dependent ionisation and recombination rates, respectively. The collisional ionisation and excitation-autoionisation rates of Dere (2007) and the radiative and dielectronic recombination rates of Mazzotta et al. (1998) are tabulated in intervals of 0.01 dex in the range
Equation (1) must be solved using a set of tabulated values that describe the evolution of the temperature during a particular process such as heating or cooling. [T(t)] could be the solution to an analytical model, the output from a numerical code or a set of observational measurements. In the numerical tests to follow in Sect. 3 the heating process is represented by linearly raising the temperature of the plasma from an initial value ![]() to a peak value
to a peak value ![]() over a timescale
over a timescale
![]() .
Thus:
.
Thus:
The cooling process is represented by the analytical solution to the equation for cooling by thermal conduction in the non-evaporative limit, given by Antiochos & Sturrock (1976):
where
where L1/2 the loop half-length,
Equation (1) represents an extremely stiff set of coupled differential equations and their solution can be a computationally demanding problem. It is worth noting that many numerical methods for the solution of stiff sets of equations rely upon the use of implicit integration schemes. The additional computational expense of implicit schemes is considered outweighed by the permittance of large timesteps and guaranteed numerical stability. One point often overlooked is that implicit schemes only guarantee convergence to equilibrium and the solution at
![]() may not represent the true state of the system if the timesteps are too large. The condition for accuracy for an implicit scheme is equivalent to the condition for stability for an explicit scheme, or: there's no such thing as a free numerical lunch. If one is interested in the detailed evolution of the system before any equilibrium state is reached, which in the present work is most certainly the case, then the principle timescale must be resolved. This condition can be efficiently satisfied by using an adaptive method (MacNeice et al. 1984) for choosing the integration timestep (see Appendix A) and linearly interpolating between the tabulated values [T(t)] to find the exact temperature at each timestep. The NEI module from the HYDRAD code (Bradshaw & Cargill 2006, and references therein), which has been documented and used extensively in the published literature, is used to solve these equations and the solutions are output at time intervals corresponding to [T(t)].
may not represent the true state of the system if the timesteps are too large. The condition for accuracy for an implicit scheme is equivalent to the condition for stability for an explicit scheme, or: there's no such thing as a free numerical lunch. If one is interested in the detailed evolution of the system before any equilibrium state is reached, which in the present work is most certainly the case, then the principle timescale must be resolved. This condition can be efficiently satisfied by using an adaptive method (MacNeice et al. 1984) for choosing the integration timestep (see Appendix A) and linearly interpolating between the tabulated values [T(t)] to find the exact temperature at each timestep. The NEI module from the HYDRAD code (Bradshaw & Cargill 2006, and references therein), which has been documented and used extensively in the published literature, is used to solve these equations and the solutions are output at time intervals corresponding to [T(t)].
3 Numerical tests
3.1 Ionisation equilibration
A suite of numerical tests has been devised in order to demonstrate that the numerical code provides accurate and reliable solutions. The first test checks that it can accurately reproduce and maintain appropriate equilibria. Equilibrium solutions to Eq. (1) are well established and can easily be found from sets of ionisation and recombination rates, giving the ionisation state for a fixed temperature which can then be tabulated and compared with the equilibria found by time-stepping Eq. (1). The effective ionisation temperature
![]() is used as a measure of the strength of departures from equilibrium of the ionisation state. Here
is used as a measure of the strength of departures from equilibrium of the ionisation state. Here
![]() is calculated by choosing the equilibrium ionisation state from a set of values tabulated as a function of temperature (in steps of 0.01 dex in the range
is calculated by choosing the equilibrium ionisation state from a set of values tabulated as a function of temperature (in steps of 0.01 dex in the range
![]() )
that most closely matches the current NEI state. Reale & Orlando (2008) adopt a similar approach but choose to compare only the three most populated stages of the NEI state in order to determine the most closely matching equilibrium state. In the current work all ionisation stages will be compared in order to identify the most closely matching equilibrium state. This provides a far more rigorous set of conditions to be satisfied because an accurate match requires the solver to properly handle both the dominant and the minor ion population fractions. Iron (Fe) will be used as the example element in the current work since it has many ionisation stages (27 in all) and dominates the spectrum of coronal emission.
)
that most closely matches the current NEI state. Reale & Orlando (2008) adopt a similar approach but choose to compare only the three most populated stages of the NEI state in order to determine the most closely matching equilibrium state. In the current work all ionisation stages will be compared in order to identify the most closely matching equilibrium state. This provides a far more rigorous set of conditions to be satisfied because an accurate match requires the solver to properly handle both the dominant and the minor ion population fractions. Iron (Fe) will be used as the example element in the current work since it has many ionisation stages (27 in all) and dominates the spectrum of coronal emission.
To test the ability of the solver to find and maintain equilibrium solutions Eq. (2) was used to generate a set of values [T(t)] such that
![]() K and
K and
![]() K, to represent heating, which were solved with Eq. (1) for
n=[108, 1010, 1012] cm-3. Figure 1 shows that this requirement is satisfied because
K, to represent heating, which were solved with Eq. (1) for
n=[108, 1010, 1012] cm-3. Figure 1 shows that this requirement is satisfied because
![]() in all cases. At n=1012 cm-3
in all cases. At n=1012 cm-3
![]() for all T, which shows that an assumption of ionisation equilibrium is valid at high densities, and at n=1010 cm-3 the ionisation state equilibrates during the first 100 s. Note that the T and
for all T, which shows that an assumption of ionisation equilibrium is valid at high densities, and at n=1010 cm-3 the ionisation state equilibrates during the first 100 s. Note that the T and
![]() data points are plotted in intervals of 100 s. At n=108 cm-3 the equilibration timescale tends to increase with temperature due to the difficulty of freeing the strongly bound inner-shell electrons. A direct comparison of the population fractions as
data points are plotted in intervals of 100 s. At n=108 cm-3 the equilibration timescale tends to increase with temperature due to the difficulty of freeing the strongly bound inner-shell electrons. A direct comparison of the population fractions as
![]() shows that the solver recovers their equilibrium values exactly and this can readily be confirmed by users of the numerical code. Through a comparison of T and
shows that the solver recovers their equilibrium values exactly and this can readily be confirmed by users of the numerical code. Through a comparison of T and
![]() ,
at t=10 s and n=1010 cm-3, with the equilibration timescale for the corresponding n=108 cm-3 curve the results in Fig. 1 also indicate a trend for the equilibration timescale to scale with inverse proportion to the density, as expected from Eq. (1).
,
at t=10 s and n=1010 cm-3, with the equilibration timescale for the corresponding n=108 cm-3 curve the results in Fig. 1 also indicate a trend for the equilibration timescale to scale with inverse proportion to the density, as expected from Eq. (1).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f01.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg32.png) |
Figure 1:
The temperature equilibration rate for the ionisation state of Fe for heating to a range of temperatures at several densities. The diamonds show the actual electron temperature T and the lines show the effective ionisation temperature
|
| Open with DEXTER | |
Since the numerical code is also expected to be used for cooling studies (post flare, for example), Eq. (2) was used to generate a set of [T(t)] such that
![]() K and
K and
![]() K which were solved with Eq. (1) for the same density range as before. The results are shown in Fig. 2 and confirm the ability of the solver to find and maintain equilibrium solutions at all temperatures. Again, a direct comparison of the population fractions as
K which were solved with Eq. (1) for the same density range as before. The results are shown in Fig. 2 and confirm the ability of the solver to find and maintain equilibrium solutions at all temperatures. Again, a direct comparison of the population fractions as
![]() shows that the solver recovers the exact equilibrium solutions.
shows that the solver recovers the exact equilibrium solutions.
The final equilibration test in this section assesses the ability of the solver to follow the temperature when it varies rapidly, over several orders of magnitude, by maintaining the ionisation state in equilibrium at high densities. This is a particularly stringent test; it requires extremely small timescales to be resolved because the ionisation state needs to rapidly evolve to keep up with the temperature changes. Furthermore, stable and accurate solutions for the dominant and minor population fractions are essential because the minor population fractions can quickly become dominant and vice versa. Without accurate solutions errors would quickly accumulate. [T(t)] was calculated with the temperature varying sinusoidally between 104 K and 108 K for periods
![]() s. Figure 3 shows
s. Figure 3 shows
![]() compared with T for n=1010 cm-3 and, clearly, the ionisation state is far from equilibrium for all
compared with T for n=1010 cm-3 and, clearly, the ionisation state is far from equilibrium for all
![]() s. This is expected because the first test (Fig. 1) showed that the timescale for equilibration is of O(100) s for a temperature change of 104 K to 108 K at n=1010 cm-3. However, at n=1012 cm-3 these results showed that the ionisation state should be in equilibrium and this expectation is indeed satisfied in Fig. 4 where
s. This is expected because the first test (Fig. 1) showed that the timescale for equilibration is of O(100) s for a temperature change of 104 K to 108 K at n=1010 cm-3. However, at n=1012 cm-3 these results showed that the ionisation state should be in equilibrium and this expectation is indeed satisfied in Fig. 4 where
![]() for
for
![]() s.
s.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f02.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg37.png) |
Figure 2: The temperature equilibration rate for the ionisation state of Fe for cooling to a range of temperatures at several densities. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f03.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg38.png) |
Figure 3:
The variation of the effective ionisation temperature
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f04.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg39.png) |
Figure 4: As Fig. 3 for n=1012 cm-3. |
| Open with DEXTER | |
The tests carried out in this section confirm the ability of the numerical code to find and maintain appropriate equilibria, to resolve the extremely small ionisation/recombination timescales associated with rapid temperature changes at high densities, and to provide stable and accurate solutions for both dominant and minor ion population fractions.
3.2 Rapid heating and efficient cooling
A traditional test of the accuracy of numerical solutions is to compare them with appropriate analytical solutions. However, since no analytical solutions to Eq. (1) exist a convenient test is instead to check for consistency between alternative codes. This is useful because it can serve to verify the results or highlight any discrepancies that may need to be investigated, which is of particular importance if the codes are in common use but have not previously been benchmarked/calibrated. The work of Reale & Orlando (2008) is chosen to serve as the basis for comparison. Their study was performed using a 1D code and solutions to the NEI equations in such circumstances, coupled as they are to the hydrodynamic equations, require long run times of hours or days depending upon the parameters of the run (number of elements included in the NEI treatment, grid resolution). Conversely, the numerical code presented here can complete a run in a few seconds. If consistent solutions can be obtained for several orders of magnitude less computational time then the code can be a valuable addition to the selection of modeling tools that are available to the community.
The remainder of this section will be devoted to describing a new study, following Reale & Orlando (2008) and the earlier work of Bradshaw & Cargill (2006), that was carried out with the code described here. The purpose of this study is (a) to provide corroboration of the results of the independent, earlier work and (b) to demonstrate that consistent results can be obtained with the current, far less computationally demanding code.
As discussed in Sect. 1 concerns regarding the detectability of coronal nanoflares have promoted recent interest in NEI studies because the lack of significant hot emission, that would otherwise be expected to provide corroborating evidence for coronal heating by nanoflares, can be explained by the difficulties of creating the associated highly charged ionisation states. Rapid, non-evaporative, nanoflare-like heating of coronal plasma to high temperatures is represented by setting
![]() K,
K,
![]() K and
K and
![]() s in Eq. (2) and generating [T(t)]. Equation (1) is then solved for
n=[108, 109, 1010, 1012] cm-3. This parameter space has been chosen so that a range of possible heating scenarios (fast to relatively slow) and coronal conditions (tenuous to very dense) can be investigated since there are open questions regarding the heating rate and the initial (pre-heating) coronal density (e.g. Bradshaw & Cargill 2006; Hudson et al. 2008). Results for the ionisation state of Fe are presented in Figs. 5 to 8 for each region of the parameter space. A limited number of ions (Fe IX, Fe XII, Fe XV, Fe XIX and Fe XXIV) were selected for the sake of readability of the figures.
s in Eq. (2) and generating [T(t)]. Equation (1) is then solved for
n=[108, 109, 1010, 1012] cm-3. This parameter space has been chosen so that a range of possible heating scenarios (fast to relatively slow) and coronal conditions (tenuous to very dense) can be investigated since there are open questions regarding the heating rate and the initial (pre-heating) coronal density (e.g. Bradshaw & Cargill 2006; Hudson et al. 2008). Results for the ionisation state of Fe are presented in Figs. 5 to 8 for each region of the parameter space. A limited number of ions (Fe IX, Fe XII, Fe XV, Fe XIX and Fe XXIV) were selected for the sake of readability of the figures.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f05.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg41.png) |
Figure 5:
The ionisation state of Fe during a heating phase of
|
| Open with DEXTER | |
Figure 5 shows the ionisation state of Fe in plasma of density 108 cm-3 as it is raised from a temperature of 104 K (though the x-axis scale begins at 105 K) to 107 K in 5 s. The solid lines in the figure are the solutions to Eq. (1) for each ion and the dotted lines show the corresponding equilibrium solutions (the solutions for
![]() )
for comparison. The order-of-magnitude displacement in temperature between each solid and corresponding dotted line makes it immediately clear that the ionisation state of Fe is far from equilibrium at all times during the heating phase. The population of Fe IX peaks at
T=105.8 K in equilibrium (dotted line), yet at this temperature in Fig. 5 (upper-left panel) its population fraction is negligible (
<10-10) and doesn't approach a peak until T=107 K. The same behaviour is true of Fe XII and Fe XV. The population fractions of Fe XIX and Fe XXIV are negligible throughout the heating phase and so do not appear on the plot.
)
for comparison. The order-of-magnitude displacement in temperature between each solid and corresponding dotted line makes it immediately clear that the ionisation state of Fe is far from equilibrium at all times during the heating phase. The population of Fe IX peaks at
T=105.8 K in equilibrium (dotted line), yet at this temperature in Fig. 5 (upper-left panel) its population fraction is negligible (
<10-10) and doesn't approach a peak until T=107 K. The same behaviour is true of Fe XII and Fe XV. The population fractions of Fe XIX and Fe XXIV are negligible throughout the heating phase and so do not appear on the plot.
The upper-right panel of Fig. 5 shows the ionisation state of Fe in plasma of density 109 cm-3 subject to the same rate of heating. The peaks in the population fractions of Fe IX, Fe XII and Fe XV have shifted to lower temperatures, though the displacements remain almost an order-of-magnitude, and a somewhat more significant amount of Fe XIX begins to emerge near T=107 K. This trend continues at 1010 cm-3, although there is still a marked displacement between the peak Fe IX to XIX population fractions and their equilibrium temperatures. The population fraction of Fe XXIV remains negligible to 1010 cm-3. At 1012 cm-3 the ionisation state of Fe is close to equilibrium during the heating phase. The temperatures of peak relative abundance for each of the ions are in good agreement with their equilibrium values. There is a marked deviation between the Fe IX population fractions below
T=105.5 K. The time taken to reach this temperature (given the parameter values for ![]() ,
,
![]() and
and
![]() )
is 0.3 s, which is short enough for the rate of ionisation to Fe IX to lag the rate of temperature change.
)
is 0.3 s, which is short enough for the rate of ionisation to Fe IX to lag the rate of temperature change.
As the heating timescale increases (Figs. 6 to 8) the ionisation state of Fe tends more closely to equilibrium, as would be expected. However, the departures from equilibrium at densities up to 1010 cm-3 are still significant at 60 s. The steep gradients of the ion population fraction curves, away from the peak value, mean that even a slight shift of the peak in temperature can result in large differences from the values for the population fractions in equilibrium.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f06.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg43.png) |
Figure 6:
As Fig. 5 for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f07.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg44.png) |
Figure 7:
As Fig. 5 for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f08.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg45.png) |
Figure 8:
As Fig. 5 for
|
| Open with DEXTER | |
The results for heating presented here are certainly consistent with the findings of Reale & Orlando (2008). For example, in their Fig. 1 after 5 s of heating the corona reaches a temperature of 107 K at s=109 cm, where
![]() cm-3, and their Fig. 4 shows that
cm-3, and their Fig. 4 shows that
![]() for Fe is between 1 and 2 MK. In the present work Fig. 5 shows that for
for Fe is between 1 and 2 MK. In the present work Fig. 5 shows that for
![]() s and densities near 108 cm-3 the most abundant ions at the end of the heating phase are in the range Fe IX to Fe XV, which have peak equilibrium populations in the region of the 1 to 2 MK temperature range. Calculations of
s and densities near 108 cm-3 the most abundant ions at the end of the heating phase are in the range Fe IX to Fe XV, which have peak equilibrium populations in the region of the 1 to 2 MK temperature range. Calculations of
![]() for the parameter space of heating explored in the current study confirm this good agreement. Figure 9 shows that
for the parameter space of heating explored in the current study confirm this good agreement. Figure 9 shows that
![]() for
for
![]() cm-3 (obtained by interpolating between
cm-3 (obtained by interpolating between
![]() for
for
![]() cm-3) is expected to be in the region of 1 MK. Note that the temperature at t=0 s, s=109 cm in Reale & Orlando (2008) is 105.7 K, whereas in the current work the initial temperature is 104 K. Therefore, one would expect
cm-3) is expected to be in the region of 1 MK. Note that the temperature at t=0 s, s=109 cm in Reale & Orlando (2008) is 105.7 K, whereas in the current work the initial temperature is 104 K. Therefore, one would expect
![]() found by Reale & Orlando (2008) to be systematically higher than in the current work.
found by Reale & Orlando (2008) to be systematically higher than in the current work.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f09.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg49.png) |
Figure 9:
The evolution of the electron temperature T (solid) from 104 K to 107 K during heating phases of
|
| Open with DEXTER | |
The evidence from these independent studies supports the conclusion that for rapid heating of plasma at densities
![]() cm-3 the effective ionisation temperature can be significantly lower than the electron temperature and even at relatively high densities (around 1010 cm-3) there may still be important differences between these values. Furthermore, Reale & Orlando (2008) show that for elements of lower atomic number than Fe, but of similar abundance (e.g. C, N, O, Ne, Mg, Si) in the solar corona, the differences between the effective ionisation temperature and the electron temperature can be even greater. At very high densities (around 1012 cm-3) the effective ionisation temperature and the electron temperature are expected to be identical.
cm-3 the effective ionisation temperature can be significantly lower than the electron temperature and even at relatively high densities (around 1010 cm-3) there may still be important differences between these values. Furthermore, Reale & Orlando (2008) show that for elements of lower atomic number than Fe, but of similar abundance (e.g. C, N, O, Ne, Mg, Si) in the solar corona, the differences between the effective ionisation temperature and the electron temperature can be even greater. At very high densities (around 1012 cm-3) the effective ionisation temperature and the electron temperature are expected to be identical.
Following heating, coronal plasma is assumed to at first cool rapidly by thermal conduction and at later times to cool more slowly by optically thin radiation (Cargill 1993). Equation (4) shows that thermal conduction operates far more efficiently in short, tenuous, hot loops than it does in long, dense, cool loops. If the energy release for heating is on sufficiently short timescales that the loop enters its cooling phase before any significant evaporation of chromospheric material then thermal conduction is expected to be an extremely effective cooling mechanism for the coronal plasma, even in relatively long loops.
In the current work the plasma is allowed to cool by thermal conduction until the associated timescale exceeds the timescale for radiative cooling, at which point it is assumed that radiation takes over as the dominant cooling mechanism and the model run is ended. Equation (3) is used to generate suitable sets of tabulated values [T(t)]. The radiative cooling timescale is given by
where
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f10.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg56.png) |
Figure 10:
The ionisation state of Fe during thermal conductive cooling following a heating phase of
|
| Open with DEXTER | |
Table 1 shows thermal conductive cooling timescales evaluated from Eq. (4) for a range of densities and loop half-lengths at the peak temperature ![]() reached for the nanoflare-like heating profiles. The limits of the density range of interest have been shifted to lower values because at higher densities (
reached for the nanoflare-like heating profiles. The limits of the density range of interest have been shifted to lower values because at higher densities (
![]() cm-3)
cm-3)
![]() for
for
![]() K and the range of loop half-lengths considered. It is pure thermal conductive cooling that is of interest in the present study.
K and the range of loop half-lengths considered. It is pure thermal conductive cooling that is of interest in the present study.
Figures 10 to 13 show the ionisation state of Fe during thermal conductive cooling for the density range in Table 1 and for heating timescales and loop half-lengths at the extremes of the parameter space, hence:
![]() s; and
s; and
![]() cm. The properties of the ionisation state for intermediate regions of the parameter space can easily be inferred from the figures. The condition
cm. The properties of the ionisation state for intermediate regions of the parameter space can easily be inferred from the figures. The condition
![]() is generally satisfied for higher densities at higher temperatures, as reflected by the truncated extent of the solid curves in Figs. 10 to 13.
is generally satisfied for higher densities at higher temperatures, as reflected by the truncated extent of the solid curves in Figs. 10 to 13.
Table 1:
The thermal conductive cooling timescale at
![]() K for a range of loop half-lengths and plasma densities.
K for a range of loop half-lengths and plasma densities.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f11.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg66.png) |
Figure 11:
As Fig. 10 for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f12.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg67.png) |
Figure 12:
As Fig. 10 for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f13.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg68.png) |
Figure 13:
As Fig. 10 for
|
| Open with DEXTER | |
Figures 10 and 11 show that the ionisation state of Fe remains far from equilibrium during thermal conductive cooling in the shortest and most tenuous loops. The ion populations considered to be characteristic of the high temperature at the onset of cooling could not be created during the heating phase and the cooling timescale is initially too short (
![]() s) to allow the ionisation state to equilibrate. As cooling progresses its timescale increases, approaching the ionisation / recombination timescale and eventually drives the ionisation state towards equilibrium. This effect becomes clear at higher densities (
n=[108, 109] cm-3) in Figs. 10 and 11 where the ionisation state remains out of equilibrium in the range
s) to allow the ionisation state to equilibrate. As cooling progresses its timescale increases, approaching the ionisation / recombination timescale and eventually drives the ionisation state towards equilibrium. This effect becomes clear at higher densities (
n=[108, 109] cm-3) in Figs. 10 and 11 where the ionisation state remains out of equilibrium in the range
![]() K and the ion populations of lower charge state gradually equilibrate when T < 106 K. For n=1010 cm-3 the ionisation state remains close to equilibrium throughout most of the cooling phase with exceptions being the most highly charged (
K and the ion populations of lower charge state gradually equilibrate when T < 106 K. For n=1010 cm-3 the ionisation state remains close to equilibrium throughout most of the cooling phase with exceptions being the most highly charged (![]() Fe XXIV) ion populations during the initial stage of cooling when
T > 106.5 K. The effect of increasing the heating timescale simply ensures a more highly charged ion population at the onset of cooling and consequently a more highly charged population during the cooling phase until the ionisation state begins to equilibrate due to high density and / or increasing cooling timescale.
Fe XXIV) ion populations during the initial stage of cooling when
T > 106.5 K. The effect of increasing the heating timescale simply ensures a more highly charged ion population at the onset of cooling and consequently a more highly charged population during the cooling phase until the ionisation state begins to equilibrate due to high density and / or increasing cooling timescale.
Figures 12 and 13 show the effect of increasing the loop half-length by a factor of 8. The cooling timescale is substantially increased, yet for lower densities (
![]() cm-3) the ionisation state still shows significant departures from equilibrium during the initial stage of cooling. The ion populations of lower charge state gradually equilibrate at later times when T < 106 K. For n = 109 cm-3) the ionisation state undergoes a period of rapid equilibration during the initial stage of cooling, due to the relatively long cooling timescale, and remains close to equilibrium thereafter with exceptions again being the most highly charged (
cm-3) the ionisation state still shows significant departures from equilibrium during the initial stage of cooling. The ion populations of lower charge state gradually equilibrate at later times when T < 106 K. For n = 109 cm-3) the ionisation state undergoes a period of rapid equilibration during the initial stage of cooling, due to the relatively long cooling timescale, and remains close to equilibrium thereafter with exceptions again being the most highly charged (![]() Fe XXIV) ion populations. For n=1010 cm-3 the ionisation state remains in equilibrium throughout the cooling phase.
Fe XXIV) ion populations. For n=1010 cm-3 the ionisation state remains in equilibrium throughout the cooling phase.
As before the overall behaviour of the ionisation state can be understood by comparing the effective ionisation temperature with the electron temperature. Figures 14 to 17 show the effective ionisation temperature
![]() of Fe corresponding to each of the ionisation states shown in Figs. 10 to 13 for the first 5 min of the cooling phase (which begins at t=0 s in the figures).
of Fe corresponding to each of the ionisation states shown in Figs. 10 to 13 for the first 5 min of the cooling phase (which begins at t=0 s in the figures).
![]() is clearly shown to increase with density, heating timescale and loop half-length since increasing each of these parameters leads to an overall more highly charged ionisation state either at the onset of cooling or during this phase. During the initial stage of cooling
is clearly shown to increase with density, heating timescale and loop half-length since increasing each of these parameters leads to an overall more highly charged ionisation state either at the onset of cooling or during this phase. During the initial stage of cooling
![]() regardless of density, heating timescale and loop half-length. The end of this initial stage is characterised by a transition to
regardless of density, heating timescale and loop half-length. The end of this initial stage is characterised by a transition to
![]() .
The temperature at which this transition takes place marks the highest ionisation state created during the entire heating and cooling phase and, consequently, the maximum temperature of the observable emission.
.
The temperature at which this transition takes place marks the highest ionisation state created during the entire heating and cooling phase and, consequently, the maximum temperature of the observable emission.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f14.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg75.png) |
Figure 14:
The evolution of the electron temperature T (solid) and the corresponding effective ionisation temperature
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f15.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg76.png) |
Figure 15:
As Fig. 14 for
|
| Open with DEXTER | |
The period of cooling that elapses before the transition takes place becomes shorter with increasing density and heating timescale (as expected from increasing
![]() )
but longer with increasing loop half-length. The nature of the dependence on the half-length is due to the longer cooling timescale and the additional time required to reach the more highly charged ionisation states characteristic of coronal plasma that maintains a high temperature. Consequently, for short loops one may expect to observe
)
but longer with increasing loop half-length. The nature of the dependence on the half-length is due to the longer cooling timescale and the additional time required to reach the more highly charged ionisation states characteristic of coronal plasma that maintains a high temperature. Consequently, for short loops one may expect to observe
![]() for most of the cooling phase unless the density is particularly low and the heating timescale particularly short, in which case the condition
for most of the cooling phase unless the density is particularly low and the heating timescale particularly short, in which case the condition
![]() may persist for a significant length of time.
may persist for a significant length of time.
![]() can become substantially greater than T for longer heating timescales in short loops. However, for long loops one may expect to observe
can become substantially greater than T for longer heating timescales in short loops. However, for long loops one may expect to observe
![]() for most of the cooling phase at low densities and for a significant period of time at intermediate densities regardless of the heating rate. The differences between
for most of the cooling phase at low densities and for a significant period of time at intermediate densities regardless of the heating rate. The differences between
![]() and T become negligible with increasing density, as expected, regardless of heating timescale and loop half-length.
and T become negligible with increasing density, as expected, regardless of heating timescale and loop half-length.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f16.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg78.png) |
Figure 16:
As Fig. 14 for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f17.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg79.png) |
Figure 17:
As Fig. 14 for
|
| Open with DEXTER | |
4 Summary and conclusions
A computational tool has been developed to allow straightforward calculation of the time-dependent ionisation state for a wide variety of physical circumstances. The numerical model comprises the system of time-dependent ionisation equations for a particular element and tabulated values of plasma temperature as a function of time. The tabulated values [T(t)] can be the solutions of an analytical model, the output from a numerical code or a set of observational measurements. An efficient numerical method to solve the ionisation equations has been implemented and subjected to a suite of tests which demonstrated that it can find and maintain appropriate equilibria, resolve the extremely small ionisation/recombination timescales associated with rapid temperature changes at high densities, and provide stable and accurate solutions for both dominant and minor ion population fractions.
In the case of rapid heating at densities
![]() cm-3 the effective ionisation temperature
cm-3 the effective ionisation temperature
![]() can be significantly lower than the electron temperature and even at relatively high densities (around 1010 cm-3) important differences between these values may still arise. As a result the highest temperatures reached during the period of heating can be missed because there simply isn't time to create the ionisation states responsible for the expected emission. Values of
can be significantly lower than the electron temperature and even at relatively high densities (around 1010 cm-3) important differences between these values may still arise. As a result the highest temperatures reached during the period of heating can be missed because there simply isn't time to create the ionisation states responsible for the expected emission. Values of
![]() were found that are in good agreement with those of Reale & Orlando (2008), thus establishing the consistency of the codes. Furthermore, it was found that
were found that are in good agreement with those of Reale & Orlando (2008), thus establishing the consistency of the codes. Furthermore, it was found that
![]() during the initial stage of thermal conductive cooling (which is thus far too rapid to allow the ionisation state time to equilibrate) and the temperature of the transition at which
during the initial stage of thermal conductive cooling (which is thus far too rapid to allow the ionisation state time to equilibrate) and the temperature of the transition at which
![]() later reaches/exceeds T marks the equilibrium temperature of the highest ionisation state created during the entire heating and cooling phase. The transition temperature is then the maximum temperature of the observable emission and can be significantly less than the peak temperature reached during heating, except for at the very highest densities.
later reaches/exceeds T marks the equilibrium temperature of the highest ionisation state created during the entire heating and cooling phase. The transition temperature is then the maximum temperature of the observable emission and can be significantly less than the peak temperature reached during heating, except for at the very highest densities.
This certainly explains the lack of an observed hot (
![]() K) component of the emission associated with heating events, cited as evidence against the nanoflare heating scenario, and is a conclusion in agreement with Bradshaw & Cargill (2006) and Reale & Orlando (2008). It is important to note that the results presented here are consistent with this earlier work and yet have been achieved for significantly (several orders of magnitude) less demanding computational requirements than are necessary to run a traditional 1D hydrodynamic code with an NEI solver. The implications of this work are of particular importance to current and upcoming solar observing missions (Hinode, SDO) that have been specifically designed to carry out high cadence studies of highly dynamic coronal processes and to detect signatures of coronal heating by making the instruments (EIS, XRT, AIA) sensitive to wavelength ranges that contain emission lines from ions that are formed at high temperatures in equilibrium.
K) component of the emission associated with heating events, cited as evidence against the nanoflare heating scenario, and is a conclusion in agreement with Bradshaw & Cargill (2006) and Reale & Orlando (2008). It is important to note that the results presented here are consistent with this earlier work and yet have been achieved for significantly (several orders of magnitude) less demanding computational requirements than are necessary to run a traditional 1D hydrodynamic code with an NEI solver. The implications of this work are of particular importance to current and upcoming solar observing missions (Hinode, SDO) that have been specifically designed to carry out high cadence studies of highly dynamic coronal processes and to detect signatures of coronal heating by making the instruments (EIS, XRT, AIA) sensitive to wavelength ranges that contain emission lines from ions that are formed at high temperatures in equilibrium.
There are processes to be investigated that may help to mitigate the difficulties associated with NEI. In a recent study West et al. (2008) considered the effect of a non-local model for thermal conduction on cooling timescales for hot coronal plasma associated with nanoflare heating. They found that cooling timescales can be increased due to a bottling up of energy in the corona, although whether this process can maintain the coronal temperature long enough for the ionisation state to equilibrate and to obtain sufficient photon counts for the detection of any hot emission associated with nanoflare heating has yet to be determined. The effect of evaporative cooling would be twofold in driving the ionisation state towards equilibrium and
![]() towards T. The increasing coronal density would shorten the ionisation/recombination timescale and reduce the efficacy of thermal conduction resulting in longer cooling timescales. An earlier transition to radiative cooling would also be expected, with increasing density and decreasing temperature leading to shorter cooling timescales. However, the radiative cooling timescale and the ionisation/recombination timescale have the same density dependence, so if the ionisation state had reached equilibrium at the onset of the radiative cooling phase then significant deviations would not be expected to arise thereafter, unless the radiative emissivity had a particularly strong temperature dependence.
towards T. The increasing coronal density would shorten the ionisation/recombination timescale and reduce the efficacy of thermal conduction resulting in longer cooling timescales. An earlier transition to radiative cooling would also be expected, with increasing density and decreasing temperature leading to shorter cooling timescales. However, the radiative cooling timescale and the ionisation/recombination timescale have the same density dependence, so if the ionisation state had reached equilibrium at the onset of the radiative cooling phase then significant deviations would not be expected to arise thereafter, unless the radiative emissivity had a particularly strong temperature dependence.
Future work should proceed along both observational and theoretical/numerical lines. Observationally it is of crucial importance to constrain values for the density prior to the onset of heating (Hudson et al. 2008). If the densities are low the problems associated with making measurements due to low photon counts and the subsequent consequences of NEI become particularly challenging. Theoretically and numerically the next step will be to investigate the effects of an evaporative model along the lines of the EBTEL code (Klimchuk et al. 2008), which can provide both [T(t)] and [n(t)]. EBTEL itself also requires several orders of magnitude fewer computations than traditional 1D codes and in tandem with the code presented here will constitute a powerful tool for the study of NEI in the solar corona, stellar coronae and potentially other astrophysical plasma environments.
The numerical code, atomic data, and IDL plotting routines used in this work are freely available from the author in order that the interested reader may make a detailed assessment of the importance of NEI to their own investigations.
Acknowledgements
The author thanks the referee for their helpful comments and is grateful to the STFC for their support through the award of a Post-Doctoral Fellowship.
Appendix A: Determining the integration timestep
The integration timestep ![]() can be made adaptive by the introduction of two control parameters
can be made adaptive by the introduction of two control parameters
![]() and
and
![]() .
.
![]() is then chosen sufficiently small such that:
is then chosen sufficiently small such that:
and
The parameter
![]() controls the accuracy of the ions with the greatest population fraction and
controls the accuracy of the ions with the greatest population fraction and
![]() controls the accuracy of the minor ions. Condition A.1 could, if necessary, be made stricter by substituting
controls the accuracy of the minor ions. Condition A.1 could, if necessary, be made stricter by substituting
![]() ,
since
,
since ![]() .
In the current work
.
In the current work
![]() (since the dominant ions generally have populations fractions of O(1)) and
(since the dominant ions generally have populations fractions of O(1)) and
![]() ,
which are the values suggested by MacNeice et al. (1984) and are found to work well for all of the examples considered here. To ensure stability while maintaining efficiency the largest value of
,
which are the values suggested by MacNeice et al. (1984) and are found to work well for all of the examples considered here. To ensure stability while maintaining efficiency the largest value of ![]() consistent with A.1 and A.2 for all Yj is chosen for the integration timestep.
consistent with A.1 and A.2 for all Yj is chosen for the integration timestep.
An additional parameter
![]() can further improve the efficiency of the scheme by helping to avoid waste of time calculations for ions of negligible population (and associated underflows and overflows):
can further improve the efficiency of the scheme by helping to avoid waste of time calculations for ions of negligible population (and associated underflows and overflows):
If
![]() then it is set equal to zero until another Yj brings it above
then it is set equal to zero until another Yj brings it above
![]() .
This makes the equations significantly less stiff, though with the minor drawback that particle conservation is satisfied only to a few times
.
This makes the equations significantly less stiff, though with the minor drawback that particle conservation is satisfied only to a few times
![]() rather than to machine accuracy. In the current work
rather than to machine accuracy. In the current work
![]() .
This choice ensures that particle conservation does not become an issue since it is close to the lower limit representable by a 32 bit, double precision, floating point value. In addition, the values Yj are renormalised after each timestep to guarantee
.
This choice ensures that particle conservation does not become an issue since it is close to the lower limit representable by a 32 bit, double precision, floating point value. In addition, the values Yj are renormalised after each timestep to guarantee
![]() ,
where Z is the atomic number of element Y.
,
where Z is the atomic number of element Y.
References
- Antiochos, S. K., & Sturrock, P. A. 1976, Sol. Phys., 49, 359 [NASA ADS] [CrossRef] (In the text)
- Bradshaw, S. J., & Cargill, P. J. 2006, A&A, 458, 987 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bradshaw, S. J., & Mason, H. E. 2003, A&A, 407, 1127 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bradshaw, S. J., Del Zanna, G., Mason, H. E., & Cargill, P. J. 2004, in SOHO 15 Coronal Heating, ed. R. W. Walsh, J. Ireland, D. Danesy, & B. Fleck, ESA Special Publication, 575, 539 (In the text)
- Cargill, P. J. 1993, Sol. Phys., 147, 263 [NASA ADS] [CrossRef] (In the text)
- Cargill, P. J. 1994, ApJ, 422, 381 [NASA ADS] [CrossRef] (In the text)
- Cargill, P. J., & Klimchuk, J. A. 1997, ApJ, 478, 799 [NASA ADS] [CrossRef] (In the text)
- Cargill, P. J., & Klimchuk, J. A. 2004, ApJ, 605, 911 [NASA ADS] [CrossRef] (In the text)
- Culhane, J. L., Harra, L. K., James, A. M., et al. 2007, Sol. Phys., 243, 19 [NASA ADS] [CrossRef] (In the text)
- Dere, K. P. 2007, A&A, 466, 771 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Golub, L., Deluca, E., Austin, G., et al. 2007, Sol. Phys., 243, 63 [CrossRef] (In the text)
- Hansteen, V. 1993, ApJ, 402, 741 [NASA ADS] [CrossRef] (In the text)
- Hudson, H. S., Hannah, I. G., DeLuca, E. E., & Weber, M. 2008, in First Results from Hinode, ASP Conf. Ser., 397, 130 (In the text)
- Klimchuk, J. A. 2006, Sol. Phys., 234, 41 [NASA ADS] [CrossRef] (In the text)
- Klimchuk, J. A., Patsourakos, S., & Cargill, P. J. 2008, ApJ, 682, 1351 [NASA ADS] [CrossRef] (In the text)
- MacNeice, P., Burgess, A., McWhirter, R. W. P., & Spicer, D. S. 1984, Sol. Phys., 90, 357 [NASA ADS] [CrossRef] (In the text)
- Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Parker, E. N. 1988, ApJ, 330, 474 [NASA ADS] [CrossRef] (In the text)
- Patsourakos, S., & Klimchuk, J. A. 2005, ApJ, 628, 1023 [NASA ADS] [CrossRef] (In the text)
- Patsourakos, S., & Klimchuk, J. A. 2006, ApJ, 647, 1452 [NASA ADS] [CrossRef] (In the text)
- Reale, F., & Orlando, S. 2008, ApJ, 684, 715 [NASA ADS] [CrossRef] (In the text)
- Reale, F., Testa, P., Klimchuk, J. A., & Parenti, S. 2009, ArXiv e-prints (In the text)
- Schmelz, J. T., Saar, S. H., DeLuca, E. E., et al. 2009, ApJ, 693, L131 [NASA ADS] [CrossRef] (In the text)
- Weber, M. A., Caldwell, D., Deluca, E. E., Golub, L., & Sette, A. L. 2004, in BAAS, 36, 795 (In the text)
- West, M. J., Bradshaw, S. J., & Cargill, P. J. 2008, Sol. Phys., 252, 89 [NASA ADS] [CrossRef] (In the text)
All Tables
Table 1:
The thermal conductive cooling timescale at
![]() K for a range of loop half-lengths and plasma densities.
K for a range of loop half-lengths and plasma densities.
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f01.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg32.png) |
Figure 1:
The temperature equilibration rate for the ionisation state of Fe for heating to a range of temperatures at several densities. The diamonds show the actual electron temperature T and the lines show the effective ionisation temperature
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f02.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg37.png) |
Figure 2: The temperature equilibration rate for the ionisation state of Fe for cooling to a range of temperatures at several densities. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f03.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg38.png) |
Figure 3:
The variation of the effective ionisation temperature
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f04.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg39.png) |
Figure 4: As Fig. 3 for n=1012 cm-3. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f05.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg41.png) |
Figure 5:
The ionisation state of Fe during a heating phase of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f06.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg43.png) |
Figure 6:
As Fig. 5 for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f07.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg44.png) |
Figure 7:
As Fig. 5 for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f08.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg45.png) |
Figure 8:
As Fig. 5 for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f09.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg49.png) |
Figure 9:
The evolution of the electron temperature T (solid) from 104 K to 107 K during heating phases of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f10.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg56.png) |
Figure 10:
The ionisation state of Fe during thermal conductive cooling following a heating phase of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f11.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg66.png) |
Figure 11:
As Fig. 10 for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f12.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg67.png) |
Figure 12:
As Fig. 10 for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f13.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg68.png) |
Figure 13:
As Fig. 10 for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f14.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg75.png) |
Figure 14:
The evolution of the electron temperature T (solid) and the corresponding effective ionisation temperature
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f15.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg76.png) |
Figure 15:
As Fig. 14 for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f16.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg78.png) |
Figure 16:
As Fig. 14 for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{10735f17.ps}
\end{figure}](/articles/aa/full_html/2009/28/aa10735-08/Timg79.png) |
Figure 17:
As Fig. 14 for
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.