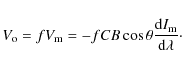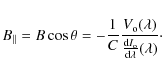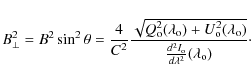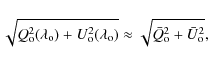EDP Sciences
Home All issues Volume 501 / No 3 (July III 2009) A&A, 501 3 (2009) 1113-1121 Full HTML
Free Access
Issue
A&A
Volume 501, Number 3, July III 2009
Page(s) 1113 - 1121
Section The Sun
DOI https://doi.org/10.1051/0004-6361/200911800
Published online 27 May 2009

Magnetic field strength of active region filaments

C. Kuckein1 - R. Centeno2 - V. Martínez Pillet1 - R. Casini2 - R. Manso Sainz1 - T. Shimizu3

1 - Instituto de Astrofísica de Canarias, vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
2 - High Altitude Observatory (NCAR), Boulder, CO 80301, USA
3 - Institute of Space and Astronautical Science, JAXA, Sagamihara, Kanagawa 229-8510, Japan

Received 5 February 2009 / Accepted 28 April 2009

Abstract
Aims. We study the vector magnetic field of a filament observed over a compact active region neutral line.
Methods. Spectropolarimetric data acquired with TIP-II (VTT, Tenerife, Spain) of the 10 830 Å spectral region provide full Stokes vectors that were analyzed using three different methods: magnetograph analysis, Milne-Eddington inversions, and PCA-based atomic polarization inversions.
Results. The inferred magnetic field strengths in the filament are around 600-700 G by all these three methods. Longitudinal fields are found in the range of 100-200 G whereas the transverse components become dominant, with fields as high as 500-600 G. We find strong transverse fields near the neutral line also at photospheric levels.
Conclusions. Our analysis indicates that strong (higher than 500 G, but below kG) transverse magnetic fields are present in active region filaments. This corresponds to the highest field strengths reliably measured in these structures. The profiles of the helium 10 830 Å  lines observed in this active region filament are dominated by the Zeeman effect.

Key words: Sun: filaments - Sun: photosphere - Sun: chromosphere - Sun: magnetic fields - techniques: polarimetric

1 Introduction

The magnetic field strength of active region (AR) filaments has long remained poorly known or understood. The situation for quiescent filaments is notably more satisfactory since the early measurements back in the 70s (see, e.g., the review by López Ariste & Aulanier 2007). Field strengths measured in quiescent structures, mostly using the Hanle effect on the linear polarization of He I D3 at 5876 Å (e.g., Sahal-Brechot et al. 1977), were found to be in the range of 3-15 G (Leroy et al. 1983; see also the review by Anzer & Heinzel 2007). However, more recent measurements, which also took circular polarization into account, consistently show a tendency towards stronger field strengths. For example, the He I 10 830 Å investigation of Trujillo Bueno et al. (2002) and the He I D3 of Casini et al. (2003) found, respectively, field strengths of 20-40 G and 10-20 G (with field strengths up to 80 G in the latter set of observations). With similar techniques, using carefully inverted observations of the He I 10 830 Å lines, Merenda et al. (2006) find field strengths of about 30 G. Other recent works that also obtained relatively strong filament magnetic fields as compared with older measurements are Paletou et al. (2001) and Wiehr & Bianda (2003). Of particular interest are the high field strength areas revealed by Zeeman-dominated Stokes V profiles in conjunction with scattering dominated Q and U linear polarization signals obtained by Casini et al. (2003), showing how important it is to use all four Stokes parameters for a proper determination of the field strength in prominences.

Well-established properties of AR filaments are their systematically stronger field strengths as compared to their quiescent counterparts, and they lie lower in the atmosphere (see, e.g., Aulanier & Démoulin 2003). Zeeman observations, using coronagraphs, provided field strengths for AR prominences in the range of 50-200 G (Tandberg-Hanssen & Malville 1974, and references therein). However, the intrinsic difficulties of observing such low-lying structures near the limb and the use of H$\alpha$ magnetography render these results somewhat questionable (see López Ariste et al. 2005, for the problems associated with using a Zeeman-based formulation of the measurements made in H$\alpha$). Perhaps the most relevant modern estimate of the field strength in AR prominences has been provided by Wiehr & Stellmacher (1991), who measured the longitudinal magnetic field using the Stokes I and V profiles of the Ca II IR triplet, finding a value of 150 G, compatible with previous measurements. It is important for the discussion presented in our paper to note that, in that observational study, linear polarization signals (Q and U) were not included. The only measurements of strong magnetic fields using an He I 10 830 Å full Stokes vector that we are aware of belong to a multicomponent flaring active region and reached values of ${\approx}380$ G (see Sasso et al. 2007).

Because measurements are scarce, we are still far from having a complete picture of the field strengths that permeate solar filaments. Some progress has come from using photospheric distributions of (mostly longitudinal) fields that are extrapolated into the corona (usually using models of constant-$\alpha$ force-free field). The study by Aulanier & Démoulin (2003) is of particular relevance to the present work. According to these authors, the field strength of filaments found from the extrapolations is about 3 G for the quiescent case, 40 G for active filaments (called ``plage case'' in their work) and 15 G for intermediate cases. The typical height in the atmosphere of a filament base ranges from 20 to 10 Mm, or even lower, as one moves from quiescent to AR structures. These authors also find positive field gradients with height that result in values of 0.1-1 G Mm-1, i.e., stronger fields are higher up in the atmosphere. If these gradients are used to extrapolate down into the photosphere, the fields there would be very similar to those found some Mm up in the corona. For example a 10 Mm-height active filament with 100 G in the corona would have no less than 90 G close to the photosphere. The argument could also be turned around to start from the fields measured near the photosphere, close to AR neutral lines (NLs), and infer what the fields could be high in the corona. In the case of kG-strong plage fields, with high density areal filling factors (that can reach up to 50%; Martínez Pillet et al. 1997), one could expect fields of several hundred Gauss within the filaments. Indeed, Aulanier & Démoulin (1998, 2003) provide arguments supporting a relationship between the photospheric fields at the base of the filament and the filament fields up in the corona. They conclude that the stronger the photospheric fields at the base of the filament, the stronger the field in the filament itself. Similarly, the separation of the two opposite polarity regions scales inversely with the field strength of the filament, the latter being greater whenever the two polarities are closer together. Dense (highly packed) fields in the photosphere correspond indeed to the photospheric configuration found below AR filaments as observed recently by Lites (2005) and Okamoto et al. (2008). In both cases, they find opposite polarity ``abutted'' plage fields at the NL, with sheared horizontal fields in the hecto-Gauss range and relatively high filling factors. These abutted field configurations seem to also correspond with low-lying filaments structures. Lites (2005) comments that the height of the filaments on top of the abutted plage fields is no more than 2.5 Mm. Thus, high density (i.e., large filling factor) horizontal plage fields near AR NLs, together with the inferences from theoretical modeling (Aulanier & Démoulin 1998, 2003), would indicate that fields of several hundred Gauss can be expected in low-lying AR filaments.

Given the observation that energetic coronal mass ejections (CMEs) are often associated with AR filament eruptions (see, e.g., Manchester et al. 2008; and Low 2001, for a review), it is highly desirable to develop diagnostic tools for direct measurements of the AR filament magnetic field and its evolution, from its emergence (see Okamoto et al. 2008) to the erupting phase. In this work, we present a clear diagnostic tool of how this can be achieved using full Stokes polarimetry of the He I 10 830 Å lines.

 \begin{figure} \par {\hspace*{5mm}\includegraphics[width=6.9cm,clip]{11800f11.ps... ....ps}\hspace*{4.9mm} \includegraphics[width=7.4cm,clip]{11800f16.ps} \end{figure} Figure 1:

Top left: slit reconstructed continuum intensity map centered at the NL where the pores and penumbral-like formations can be identified. The location of the slit for the time series map is displayed. Top right: Si I Stokes V map normalized to the continuum intensity. Bottom: Stokes profiles observed at the slit position indicated in the top images and averaged over the time series (comprising 100 scans). The gray scale bar only applies to the polarization signals. The Zeeman-like signature of Stokes Q and Uare evident in this picture (He I lines are centered at 0 and 1.2 Å approximately. The zero in the wavelength scale corresponds to 10 829.09 Å). The arrows indicate the position of the presented Stokes profiles in Figs. 3 and 4.
Open with DEXTER

2 Observations

The observations described in this paper were carried out at the German Vacuum Tower Telescope (VTT, Tenerife, Spain) on the 3rd and the 5th of July, 2005, using the Tenerife Infrared Polarimeter (TIP-II, Collados et al. 2007). TIP-II allows to measure the full Stokes vector (almost) simultaneously for all the pixels along the spectrograph slit. The slit (0 $.\!\!^{\prime\prime}$5 wide and 35 $^{\prime\prime}$ long) was placed over the target, a filament lying over the NL of active region NOAA 10781 situated close to disk center (at coordinates N13-W4 around $\mu=0.97$ on July 3rd and at N13-W29 or $\mu=0.92$ on July 5th) with the help of context H$\alpha$ and continuum images. The H$\alpha$ frames showed the filament lying always on top of bright plage regions visible immediately to either side of the absorption feature. It is likely that the results presented in this paper particularly apply to such an ``active'' filament configuration. SOHO/MDI (Scherrer et al. 1995) magnetograms and continuum frames have been used to follow the evolution of the active region as it crossed the visible surface. The active region was identified to be in its slow decay mode, encompassing a round symmetric leader sunspot and a follower, spotless, plage region. At the location of the NL, sporadic pore-like formations and penumbral-like configurations (with no evident radially symmetric link to an umbral or pore structure as normal penumbra or partial penumbrae do) were seen, especially on the 5th of July data-sets. Pores near the NL with both polarities are identified and the penumbral-like region seems to correspond to field lines connecting them. The NL was oriented in the N-E direction and showed a very compact configuration, with the two polarities always remaining in close contact. The leader sunspot became invisible on the 6th of July after decreasing in size while approaching the west solar limb.

Two observing strategies were used to map the NL region. Several spatial scans that covered the whole AR were carried out in the course of the 3 days, and one time series (with the slit fixed over the filament) was taken on July 5th. This data-set was averaged in time in order to improve the signal-to-noise (S/N) ratio of the spectral profiles. The pixel size along the slit was 0 $.\!\!^{\prime\prime}$17 and the scanning step (in the case of the rasters) was 0 $.\!\!^{\prime\prime}$3 per step. The exposure time per slit position was 8 seconds. The adaptive optics system (KAOS, von der Lühe et al. 2003) was locked on nearby pores during all the runs, substantially improving the image quality of the observations carried out during relatively poor seeing conditions, and providing a final estimated spatial resolution of $\sim$1 $^{\prime\prime}$. Flat-field and dark current corrections were performed for all the data-sets and, in order to compensate for the telescope instrumental polarization, we also carried out the standard polarimetric calibration (Collados 1999; Collados 2003) for this instrument.

The observed spectral range spanned from 10 825 to 10 836 Å, with a spectral sampling of $\sim$11.1 mÅ px-1. However, a 3px binning in the spectral domain was applied to all the data to increase the S/N while still preserving subcritical sampling. The 10 830 Å spectral region is a powerful diagnostic window of the solar atmospheric properties since it contains valuable information coming simultaneously from the photosphere (carried by the Si I line at 10 827 Å) and the chromosphere (encoded in the He I 10 830 Å  triplet). This He multiplet originates between a lower term 23S1 and an upper term 23P2,1,0. Thus, it comprised three spectral lines, namely a ``blue'' component at 10 829.09 Å  ( $J_L=1 \rightarrow J_U=0$) and a ``red'' component at ${\sim} 10~830.3$ Å  that results from the remaining two transitions ( $J_L=1 \rightarrow J_U=1,2$), which appear completely blended at typical solar atmospheric temperatures. This multiplet is formed in the high chromosphere (Avrett et al. 1994) with no contribution from photospheric levels, and serves as a unique diagnostic tool for chromospheric magnetic fields. In filament structures, the height of formation of this multiplet corresponds to the height of the opaque material inside them, which might well correspond to typical coronal heights.

2.1 Predominance of Zeeman-like signatures in AR filament He I 10 830 Å Stokes profiles

The most striking finding encountered during the analysis of the data from this campaign was the ubiquitous presence of Zeeman-like signatures in the Stokes Q and U profiles of the He I lines in the AR filament (see Fig. 1). Recent observations of this triplet carried out with the same instrument (Trujillo Bueno et al. 2002) have shown quiescent filament Stokes profiles dominated by atomic level polarization (and its modification through the Hanle effect). These forward-scattering signatures (see Fig. 4 of Trujillo Bueno et al. 2002) correspond to one-lobe profiles that are positive for the red component of the He triplet and negative for the blue one (in the positive Stokes Qreference system) due, respectively, to selective emission and absorption processes induced by the anisotropic illumination of the He atoms. However, in the present case, the Stokes Q and U signals of the blue and red components of the multiplet, exhibit the usual three-lobe profile that is expected from the Zeeman effect (right panel of Fig. 1). While some influence of atomic polarization in these profiles cannot be ruled out a priory, it is clear that an explanation of their shapes should rely mainly on the Zeeman and Paschen-Back effects. This fact, interesting in itself, will be briefly discussed below (Sect. 3.3).

The continuum frame in the top panel of Fig. 1 was reconstructed from the various slit scan positions (thus reflecting the real spatial resolution of the data) of a map centered at the NL. This data-set was taken on the 5th of July, 2005. The presence of pores and penumbral-like structures is evident in this frame and their location corresponds to the NL. Right after this map, a time series with the slit fixed over the NL was performed in order to produce high S/N Stokes profiles. The bottom four panels of Fig. 1 correspond to the Stokes parameters obtained after averaging over the full time series (100 scans), which resulted in a S/N of about 4000. The inversions performed later in this work were carried out on the spectral profiles extracted from this time-averaged data-set. The location of the NL had to be guessed in real-time during the observations. The chosen slit position for the time series is represented by a vertical black line in the continuum frame of Fig. 1. Posterior analysis has shown that this location was a few arcsec off at one side of the actual NL, and that the slit would have been more correctly placed at x=18 $^{\prime\prime}$ (referred to the abscissa coordinates in the continuum panel) instead of at x=20 $^{\prime\prime}$. Nevertheless, indications of polarity changes along the slit in the Si I line (evident around y=13 $^{\prime\prime}$ in the Stokes V map of the same figure) show that we were not very far away from it.

Inspection of the profiles at other slit locations, and of similar maps taken on the 3rd of July, consistently exhibited Zeeman-dominated linear polarization signals in those regions where the He line showed strong absorption features. However, in regions with weak He absorption (typically near the boundaries of the filament), we often find linear profiles dominated by scattering polarization signatures, similar to those observed by Trujillo Bueno et al. (2002). This indicates that, in general, the profiles obtained in AR filaments can have significant contributions from various competing physical processes: the atomic level polarization due to the anisotropic illumination of the He atoms, the modification of these population imbalances induced by the presence of a magnetic field inclined with respect to the axis of symmetry (Hanle effect), and the Zeeman splitting characteristic of strong magnetic fields. A detailed study with these physical ingredients for all the maps observed at this NL is beyond the scope of this paper. In the present work, we concentrate on the implications of the clear Zeeman-dominated signatures observed almost everywhere in this filament.

One point is worth mentioning after a simple visual inspection of Fig. 1. A comparison of the signs displayed by the linear polarization profiles of the He I and Si I lines shows that the orientation of the vector magnetic field is different in the filament than in the underlying photosphere. In the Stokes Q frame, the He I 3-lobed profiles have the same sign all along the slit whereas the Si I line (and all the other smaller photospheric features at redder wavelengths) exhibits a change in sign around y=23 $^{\prime\prime}$. Conversely, in the Stokes U frame, the photospheric signals have a 3-lobed sign distribution that remains constant almost all along the spatial domain while the He I lines now show a sign reversal near the middle of the slit. An analysis based on the formula for the azimuth angle by Auer et al. (1977) gives an estimate of this difference between the azimuths inferred from the Si I and He I lines. Around y = 5 $^{\prime\prime}$ we obtain values of the azimuth which differ in ${\sim}50^{\circ}$. This readily shows that the 10 830 Å spectral region has a great potential to diagnose the orientation of the magnetic field from the photosphere all the way up to the filament. We postpone this study to a future paper.

3 Vector magnetic field near the AR neutral line

Several analyses with various levels of complexity have been performed on the reduced data. The first approach was a simple magnetograph-like analysis based on the assumption of the weak-field approximation as formulated below. This method was applied to all the points in one of the maps obtained during the campaign. We subsequently performed an analysis of the high S/N spectral profiles obtained from the averaged time series with a Milne-Eddington (ME) code and later with a more sophisticated inversion procedure based on principal component analysis (PCA) of a statistically generated database of spectral profiles that account for the physics of atomic level polarization and the Hanle effect. All these different methods consistently yield transverse field strengths in the filament well above 500 G.

3.1 Magnetograph analysis

Typical Doppler widths for the red He I line are in the range of 200-300 mÅ. The Landé factors are 1.75 and 1.25 for the $J_L=1 \rightarrow J_U=1$ and the $J_L=1 \rightarrow J_U=2$ transitions, respectively. If the transitions are weighted with their line strengths, an average Landé factor of $g_{\rm eff}=$1.42 for the red component of the helium multiplet is obtained. This Landé factor translates the above Doppler widths to field strengths in the range of 2000-3000 G, which is much stronger than the fields we expect for AR filaments. Together with the assumption that the observed signals are due to the Zeeman effect, these large Doppler widths justify the use of the well-known weak field approximation (see, e.g., Landi Degl'Innocenti 1992) as a first approach to infer the magnetic field from the data. In this approximation, the relation between the longitudinal field strength and Stokes V profile is given by:

\begin{displaymath}V_{\rm o}=f V_{\rm m}= - f C B \cos\theta {{{\rm d}I_{\rm m}}\over{{\rm d}\lambda}}\cdot \end{displaymath} (1)

The subscript ``o'' stands for the observed profile, while ``m'' represents the profile generated in the magnetic component that fills a fraction f of the resolution element; B is the field strength, $\theta$the angle between the line-of-sight (LOS) and the magnetic field direction and C the constant $4.67 \times 10^{-13} g_{\rm eff}\lambda_{\rm o}^2$ (which forces the wavelength to be expressed in Å and the field strength in G). The observed Stokes I profile is given by:

\begin{displaymath}I_{\rm o}=f I_{\rm m} +(1-f) I_{\rm nm} \end{displaymath} (2)

with the subscript ``nm'' referring to the non-magnetic component. The last factor in the right-hand-side of Eq. (1) is the derivative of $I_{\rm m}$with respect to the wavelength. However, observations only provide the compound profile $I_{\rm o}$, product of the coexistence of magnetic and non-magnetic components in the same resolution element. The present He I analysis benefits from the fact that the non-magnetic areas of the Sun display a very weak He absorption, so the derivative of the Stokes $I_{\rm nm}$ profile with respect to $\lambda$ can be neglected (we note that, in non-magnetic regions, d $I_{\rm nm}/{\rm d}\lambda$ is found to peak at one order of magnitude smaller values than d $I_{{\rm m}}/{\rm d}\lambda$ as observed in the filament). This nicely eliminates any dependence of the inferred longitudinal field on the unknown filling factor. Following this argument of ignoring the derivative of the $I_{\rm nm}$ profile with respect to wavelength, the longitudinal field is directly inferred as

\begin{displaymath}B_{\parallel} =B \cos\theta= - {{1}\over{C}} {{V_{\rm o}(\la... ...over{{{{\rm d}I_{\rm o}}\over{{\rm d}\lambda}}(\lambda)}}\cdot \end{displaymath} (3)

The $\lambda$ dependence in the last ratio is written explicitly to emphasize that each point within the profile provides an estimate of the longitudinal field. Thus, the way to solve Eq. (3) is through a least-square fit to all the observed points within the profile.

 \begin{figure} \par\includegraphics[width=5.6cm,clip]{11800f21.ps}\hspace*{2.8mm... ...25.ps}\hspace*{2.5mm} \includegraphics[width=6cm,clip]{11800f26.ps} \end{figure} Figure 2:

From left to right and top to bottom: He I Doppler width, Si I LOS magnetic field, He I LOS magnetic field, He I core intensity, Si I transverse magnetic field and He I transverse magnetic field. The corresponding continuum intensity frame can be seen in the top panel of Fig. 1.

Open with DEXTER

For transverse fields, a similar equation applies including the quadratic dependence of the linear polarization signals on the transverse component of the field and the second derivative of the Stokes I profile with respect to $\lambda$. A similar argument gives:

\begin{displaymath}B^2_{\perp} =B^2 \sin^2\theta= {{4}\over{C^2}}{\sqrt{Q^2_{\rm... ...over{{{d^2I_{\rm o}}\over{d\lambda^2}}(\lambda_{\rm o})}}\cdot \end{displaymath} (4)

Like in the equation for the longitudinal field, the filling factor (of a non-magnetic component) is absent. On the other hand, and in contrast to Eq. (3), the right hand side of Eq. (4) must be computed at the central wavelength, $\lambda_{\rm o}$, as this equation can only be formally derived there (Landi Degl'Innocenti 1992). Having only one wavelength point to compute the transverse fields prevents the use of a least square approach, unlike in the case of the longitudinal field equation. This, in turn, complicates the determination of the transverse component because the Stokes Q and U signals are often found to be at, or close to, the noise level. The quadratic average of the linear polarization signals in Eq. (4) hinders any possible noise reduction and generates a veil of noise-induced transverse fields that proves problematic in the use of this equation in many cases. This is particularly true for the He I line, whose second derivative of the (broad) Stokes $I_{\rm o}$ profile is very small. This derivative in the denominator in Equation (4) results in values of the noise-induced transverse fields as high as 300-400 G, only slightly lower than the actual values measured in the filament region. Note that this 300-400 G noise level corresponds to a S/N of 1000 in the map in Fig. 2, whereas in Fig. 1 the S/N is four times higher.

Thus, and in order to obtain high S/N maps of the chromospheric transverse fields, we averaged the unsigned Q and U signals over three wavelengths, the central wavelength and two wavelengths at 278 mÅ on each side of line center, corresponding approximately to the locations of the peak signals in the linear polarization profiles, so

\begin{displaymath}\sqrt{Q^2_{\rm o}(\lambda_{\rm o})+U^2_{\rm o}(\lambda_{\rm o})}\approx\sqrt{{\bar Q}^2_{\rm o}+{\bar U}^2_{\rm o}}, \end{displaymath} (5)

where ${\bar Q_{\rm o}}$ and $\bar{U_{\rm o}}$ are the averaged linear polarization signals over these three wavelength points. We emphasize that this approach reduces the noise level considerably while at the same time preserves the distribution of transverse fields already present when directly applying Eq. (4). The results obtained from this approach have been validated by the ME inversions presented in the next section.

A similar approach was followed with the Si I line to obtain the photospheric magnetic field. The Landé factor for this line is 1.5. The spectral profiles arising from this transition are broad enough to partly justify the application of the weak-field approximation. However, like for any other photospheric line, the vector-magnetograph data obtained with this method have to be interpreted with caution. In particular, the results for this line are affected by filling factor effects as is the case for commonly used photospheric magnetograph data. For the Si I line, the exact formulation of Eq. (4) was used. The intrinsically greater photospheric magnetic field strengths together with the fact that the Si I Stokes I profile has a sizeable second derivative, makes the determination of $B_{\perp}$ less affected by noise when using only the central wavelength point of the linear polarization profiles for its determination.

Lastly, the Stokes I profiles of both He I and Si I were fitted with Gaussian functions from which the line center, line width and strength were inferred. In the case of the He I, this approach proved very useful to identify the location of the filament above the NL.

The results from this approach are presented in Fig. 2 for the map observed on the 5th of July. The He I Doppler width and line core frames show that the line becomes deeper and narrower inside the filament. This could be an indication of the presence of a denser and cooler plasma than in its immediate plage surroundings. These frames also reveal that the filament has a highly twisted topology, with filamentary threads running at almost 45 degrees from the direction defined by the NL. This becomes evident when compared to the Si and He LOS magnetograms. The twist in the filament is more obvious in the bottom half of the frames than in the top part, where a more diffuse linear topology is observed. These twisted signatures could be clearly seen in the observations from the 5th of July, while they were hardly visible in the maps obtained two days earlier. The Si I LOS magnetogram shows that the separation between the two polarities is less than 5 $^{\prime\prime}$ at photospheric levels when the magnetogram is scaled at $\pm$1000 G. A tighter scaling with a smaller threshold would provide a much narrower NL channel. In the He I LOS magnetograms, with a scaling of $\pm$400 G, the channel is practically absent, showing how intense the plage surrounding this AR filament was. A thread-like structure in the longitudinal component running parallel to the direction of the twist (i.e. at 45 degrees from the NL) in the mid range of the frame is observed. Note that the AR is 22 degrees off disk center so horizontal threads in the filament can give rise to sizeable Stokes V signals. The intrinsic LOS magnetic field strength at the NL (we stress that no filling factor effect is included in these estimates) is typically 100 G for each of the two polarities (in agreement with older measurements of AR filaments that did not include transverse field measurements). The neighboring plage displays an intrinsic longitudinal field strength of 200-400 G. If we assume an intrinsic photospheric field strength in the plage of 1400 G (see Martínez Pillet et al. 1997), this would indicate a filling factor of about 20% in this layer.

In both, the photospheric and chromospheric magnetograms, the region where the longitudinal field becomes weaker corresponds to the region with very strong transverse fields. The somewhat wider photospheric NL channel corresponds to a wider photospheric area occupied with strong transverse fields, while the transverse fields in the chromosphere fill a narrower region. These transverse fields seem to follow the structures observed in the He line core frame: a more linear topology in the top part and a twisted formation in the bottom half. What becomes readily surprising is the magnitude of the transverse fields observed in the chromosphere (and to the extent that the weak field approximation is valid, in the photosphere as well). The photosphere shows fields in the range of up to kG in the region between abscissae x=15 $^{\prime\prime}$ to x=20 $^{\prime\prime}$ in the frames of Fig. 2. This area shows penumbral-like structures and pores in the white light image. It is clear that these orphan penumbral-like regions are magnetically linked to the main body of the AR filament and correspond to horizontal field lines at the photospheric surface. The transverse fields derived from the Si I line undoubtedly show the twist configuration similar to that observed in the He I lines. In the chromosphere, the transverse fields are also strong. The present analysis yields transverse fields with strengths in the range of 500-600 G, strongly concentrated in the narrow NL channel. Note that this region, at best, a few arcsec wide, is below the low resolutions of old observations. These high transverse magnetic fields are well above most, if not all, of past field strength measurements in AR filaments.

The various maps for the observations on the 3rd of July support the hypothesis that an AR filament corresponds to a narrow channel characterized with strong (${\sim}500$ G) transverse fields. There is a clear spatial correlation between strong absorption signatures in He I (measured by the line core intensities), and narrow (or ``abutted'') plage regions with strong transverse fields in the chromosphere. A complete description of all these maps is postponed to a future paper. But it is interesting to point out the following main differences with the map of Fig. 2: the absence of evident twisted threads, the absence of penumbral-like regions in white-light maps, weaker and more diffuse transverse fields at the photosphere (not reaching kG levels) and the presence of weaker He I absorption signatures in regions outside the intense NL channel that display atomic polarization signals.

 \begin{figure} \par\includegraphics[width=12.2cm,clip]{11800fg3.ps} \end{figure} Figure 3:

Stokes profiles of the He I 10 830 Å triplet at a height of 8 arcsec in Fig. 1 in the mid portion of the twisted region of the filament. The dots represent the observed profiles obtained after averaging the time series in order to achieve a higher S/N. The solid line corresponds to the best fit achieved with a Milne-Eddington inversion code that takes into account the IPB effect. The magnetic field obtained from this particular fit is $B = 626\pm 10$ G, $\theta = 80.2^{\circ }\pm 0.1^{\circ }$ and $\chi =174.9^{\circ }\pm 0.1^{\circ }$ (the origin of azimuths being the local solar radial direction). The dot-dashed line shows the best fit obtained from an inversion in a slab model of constant properties that accounts for the joint action of scattering polarization and the Hanle Zeeman effects. This fit provided for the magnetic parameters $B = 667\pm 16$ G, $\theta = 81.1^{\circ }\pm 0.3^{\circ }$ and $\chi = 174.8^{\circ }\pm 0.5^{\circ }$.

Open with DEXTER

3.2 Milne-Eddington inversions

The interest of the magnetograph analysis is that it is easily computed over a complete map with a very low computational effort. However, in order to validate the weak-field approximation inferences of the magnetic field strength in the filament, we carried out a Milne-Eddington (ME) inversion of the He I Stokes profiles of the averaged time series. These high S/N data correspond to the location of the vertical line at x=20 $^{\prime\prime}$ in the map of Fig. 1. The inversion code we used (MELANIE; Socas-Navarro 2001) computes the Zeeman-induced Stokes spectra - in the incomplete Paschen-Back (IPB) effect regime - that emerge from a model atmosphere described by the Milne-Eddington approximation. This assumes a semi-infinite constant-property atmosphere whose source function varies linearly with optical depth, $\tau$. This approach does not account for the atomic-level polarization induced by the anisotropic radiation pumping of the He atoms from the underlying photospheric continuum.

For magnetic fields between 400 and 1500 G the Zeeman splitting of the upper J-levels of the He I triplet is comparable to their energy separation. Thus, it is crucial to compute the energy levels in the IPB regime to avoid an under-estimation of the magnetic field strength when carrying out the inversion to interpret observations (Socas-Navarro et al. 2004; Sasso et al. 2006).

The Milne-Eddington model atmosphere uses a set of eleven free parameters that the inversion code modifies in an iterative manner in order to obtain the best fits to the observed Stokes profiles. These free parameters are: the magnetic field strength (B), its inclination ($\theta$) and azimuth ($\chi$) angles in the reference system of the observer (the azimuth is measured with respect to the local solar radial direction), the line strength ($\eta_0$), the Doppler width ( $\Delta\lambda_{\rm D}$), a damping parameter, the LOS velocity, the source function at $\tau=0$ and its gradient, a macroturbulence factor and a stray light fraction f. An initial guess model must be provided to the code. In order to prevent the inversion scheme from getting locked into local minima, we carried out the inversions using several different initializations, in which B, $\theta$ and $\chi$ were taken from the above-described magnetograph analysis and the remaining parameters were obtained from random perturbations of reasonable pre-set values. All parameters were free except for the stray light fraction, which was set to zero (i.e., assuming a filling factor of 1; we refer to the explanation in Sect 3.1). We stress that, even if the data is contaminated with stray-light from the surroundings, using a filling factor of unity allows a direct comparison with the results given in the previous section.

Figures 3 and 4 show the results of the ME inversion of the full Stokes vector for two positions along the filament (only two fits are shown but the complete set of profiles from Fig. 1 were inverted). The excellent performance of the ME inversion tells us that there are barely any scattering polarization signatures in these profiles, and that the formation physics of the multiplet is adequately described in the IPB regime. As expected, the magnetic field strengths inferred from all the inversions are around 600-700 G with very high inclinations ( ${\sim}80^{\circ}$) with respect to the line-of-sight, thus confirming the existence of strong transverse fields in this AR filament. The exact values obtained for Fig. 3 are $B_{\parallel}=109$ G and $B_{\perp}=616$ G while for Fig. 4 we obtain $B_{\parallel}=176$ G and $B_{\perp}=602$ G. In the solar reference frame, the magnetic field vector turns out to be close to horizontal, 59$^\circ$ and 99$^\circ$ of inclination with respect to the local vertical, respectively.

The magnetic field strengths derived from the weak field regime analysis are systematically under-estimated by ${\sim}100{-}150$ G, but the retrieved inclinations and azimuths are in very good agreement with those obtained from the ME-IPB inversions. This means that the weak field approximation yields a reliable magnetic field topology and a low-end value for the field strength.

3.3 PCA-based atomic polarization inversion

The observations described above were also independently inverted using the principal component analysis (PCA) approach described by López Ariste & Casini (2002). In fact, pattern recognition techniques are particularly well suited to attack ill-defined inversion problems characterized by computationally intensive forward problems. This is exactly the case for spectropolarimetric inversions in prominences and filaments, where the Stokes profiles are often formed by the scattering of resonant radiation. The computation of the emergent polarization in such case requires the preliminary solution of the non-LTE problem of atomic-level excitation by anisotropic illumination of the plasma from the underlying photosphere. The presence of a magnetic field further modifies the ensuing atomic polarization through the Hanle effect (see, e.g. Landi Degl'Innocenti & Landolfi 2004, for a review of atomic polarization effects). This problem, which is totally by-passed in the ME approach to spectropolarimetric inversion, completely dominates the numerical computation of line polarization in radiation scattering. For this reason, pattern recognition techniques provide a very attractive strategy to Stokes inversion for radiation scattering, since the numerically intensive forward problem is solved once and for all for a comprehensive set of illumination, thermodynamic, and magnetic conditions in the plasma for the problem at hand. The goal of these techniques is thus to build universal databases of profiles that can be searched for the solution to any given Stokes inversion problem. Principal component analysis additionally provides a way of compressing database information, by reducing it to a few principal component profiles that contain all the fundamental physics of the formation of the emergent Stokes profiles (López Ariste & Casini 2002; Casini et al. 2005).

 \begin{figure} \par\includegraphics[width=13cm,clip]{11800fg4.ps} \end{figure} Figure 4:

Same as Fig. 3 but for a profile near the bottom portion of the twisted region of the filament (at a height of 5 arcsec). The fitted parameters for the ME case are $B = 627\pm 10$ G, $\theta = 73.7^{\circ }\pm 0.3^{\circ }$ and $\chi =5.7^{\circ }\pm 0.1^{\circ }$. The PCA-based algorithm including Hanle effect provided: $B = 664 \pm 15$ G, $\theta = 74.9^{\circ }\pm 0.6^{\circ }$ and $\chi = 5.1^{\circ }\pm 0.8^{\circ }$.

Open with DEXTER

For the inversion of the observations illustrated in this paper, we created a database of 250 000 profiles, spanning all possible orientations of the magnetic field, with strengths between 0 and 2000 G. The illumination conditions were set by the radiation temperature and center-to-limb variation (CLV) profile of the photospheric radiation at 1 $\mu$m (Cox 2000), and by assuming a range of scattering heights between 0 and 0.06 $R_\odot$ (42 Mm). The LOS inclination in the database used for the inversion of the July 5, 2005, observations spanned between 20$^\circ$ and 30$^\circ$. The thermal Doppler width and micro-turbulent velocity, responsible for the overall profile broadening, were accounted for by introducing an equivalent temperature spanning between 104 and $2\times 10^4$ K. Finally, the database Stokes profiles were calculated by integrating the polarized radiation emerging from a homogeneous slab with optical depth at line center varying between 0.2 and 1.4. Very soon it was realized that such conventional scattering scenario could not fit satisfactorily the observations, unless some additional depolarizing mechanism could be accounted for to explain the surprisingly low level of atomic polarization revealed by the Zeeman-like shape of the Stokes Q and Uprofiles. For this reason, in the creation of the inversion database we introduced an ad-hoc weight factor for the anisotropy of the photosphere radiation, ranging between 0 and 1. Extensive inversion tests that were run over the entire filament map consistently gave anisotropy weight factors significantly smaller than unity, with a predominance of values around 0.2, thus confirming the presence of some unidentified depolarizing mechanism in the formation of the observed profiles. The possible physical origin of such depolarization has been extensively discussed by Casini et al. (2009), but see also Trujillo Bueno & Asensio Ramos (2007).

The results of the PCA inversion are overplotted to the ME inversions as dot-dashed lines in Figs. 3 and 4. The PCA inversion provides a magnetic field of B=667 G in the first case and B = 664 G in the second. The inclination angles are almost the same as the ones obtained by the ME inversions, ${\sim}59^{\circ}$ and ${\sim}99^{\circ}$ with respect to the local vertical, respectively. The inferred magnetic field azimuths are also in very good agreement.

4 Conclusions

The He I 10 830 Å lines observed in a filament at the NL of active region NOAA 10 781 exhibit linear polarization profiles dominated by the Zeeman effect. Three different independent analyses (magnetograph approximation, ME inversion and PCA inversion including atomic polarization) of the four Stokes profiles consistently support inferred field strengths in the range 600-700 G at the formation height of the helium triplet. These fields are 3 to 7 times higher than those measured heretofore in AR filaments. The field strengths found at the NL are largely horizontal with 500-600 G transverse fields. The longitudinal component is typically measured to be in the range of 100-200 G, in agreement with past measurements. It must be stressed that these previous observations of AR filaments did not include transverse field estimates. Thus, it is clear that the inclusion of the Stokes Q and U profiles in our analysis is what has allowed the detection of such strong magnetic fields in AR filaments. While the role played by the linear polarization signals was evident already from the magnetograph analysis, a further test was made with the ME inversion to prove this point. Using as input the observed I and V profiles but replacing the Stokes Q and U profiles with noisy data, the ME inversions resulted in fields strengths in the range of 100-200 G. We thus propose that the lack of full Stokes polarimetry was the main reason why past measurements did not find the high field strengths reported in this work. Note also that the spatial extent that displays such strong fields is not more than a few arcsec wide, which would be hardly visible in low resolution measurements. It is also clear that it becomes crucial to search for the signatures of these high field strengths in different spectral windows such as H$\alpha$ and the Ca II triplet.

A similar trend to infer higher field strengths (albeit in a lower range) is presented in modern measurements of quiescent filaments that is also ascribed to the use of full Stokes polarimetry (Casini et al. 2003). In the case of quiescent filaments, observations are dominated by atomic polarization and its modification through the Hanle effect. In the study presented here, however, the linear polarization profiles are dominated by the Zeeman effect as long as the profiles are coming from the regions of strong helium absorption. The reason why atomic polarization signatures are almost absent from these profiles is not yet well understood. On the one hand, the observed high field strengths are approaching the values where the Zeeman effect dominates over atomic level polarization (Trujillo Bueno & Asensio Ramos 2007), but even at this high field strengths, one would have expected a clearer atomic polarization signature. On the other hand, some mechanism to reduce the anisotropy of the radiation field could be present. For example, Trujillo Bueno & Asensio Ramos (2007) suggested that, if the radiation comes from a high opacity region, the isotropy of the radiation field will be such that a much reduced atomic polarization would be induced. A more recent proposal by Casini et al. (2009) suggests that the presence of a randomly oriented field entangled with the main filament field, and of a similar magnitude, could also explain the absence of atomic polarization signatures in these profiles. It is interesting to note that the ad-hoc anisotropy weight factor introduced in the PCA inversions was found to be in the range 0.1-0.5 over the filament region, with a predominant value of 0.2. Although the various atomic processes generating polarization signals cannot be cleanly separated, this persisting value of 0.2 is evidence of their presence in our profiles (note that a weight factor of 1 corresponds to an anisotropic illumination described by the standard CLV of the photospheric radiation field). We also stress that the reason for the absence of atomic level polarization signatures is not simply due to what is commonly referred to as a Van-Vleck configuration of the vector field. For example, whereas the profiles inverted in Fig. 3 give an inclination (with respect to the local vertical) close to the Van-Vleck angle (59$^\circ$; Van-Vleck angle corresponds to $\sim$55$^\circ$), those in Fig. 4 yield an inclination very far from it (99$^\circ$).

What is the origin of these strong transverse fields? This question relates directly to the problem of filament formation and mass loading. Two basic scenarios are commonly used to explain how these structures are formed: photospheric (shearing) motions and flux emergence (see the recent review by Lites 2008). The first one uses photospheric plasma flows that move, tangle and reconnect the field lines of an already emerged active region to form the filament directly in the corona. These processes include in one way or another some form of magnetic cancellation and reconnection that provides a source for mass upload of the filament. In this scenario, the presence of such strong magnetic fields must be related to the existence of a dense plage configuration at the NL and the low gradients inferred by Aulanier & Démoulin (2003) for their model of AR filaments. Our observations pose the question of how filament field strengths in the range of 600-700 G may be generated in this scenario from a surrounding ``abutted'' plage that has a longitudinal field of no more than 400 G at the height of formation of the helium lines. The emergence of a flux rope from below the photosphere scenario has recently received strong support from the observations of Okamoto et al. (2008). If the flux ropes are formed below the surface, the answer to the observed field strengths could be related to the balance between buoyancy forces and gravity acting over the flux system. Although this balance is not yet fully understood, it is clear that the stronger the fields the easier is for the flux system to emerge into the corona and carry a significant amount of trapped photospheric mass (Archontis et al. 2004). Note that the photospheric transverse fields observed at the NL are also very strong (including pore-like structures) and could represent the bottom part of the flux rope system once emerged into the atmosphere.

It remains to be studied whether the observed strong transverse field strengths presented in this paper are common to all AR filaments or only to those surrounded by exceptionally dense plages. An extension of the present study to other ARs with different degrees of activity is mandatory.

Acknowledgements

Based on observations made with the VTT operated on the island of Tenerife by the KIS in the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias. This research has been supported by the Spanish Ministry of Science and Innovation (MICINN) under the project ESP2006-13030-C06-01. The National Center for Atmospheric Research (NCAR) is sponsored by the National Science Foundation. Help received by C. Kuckein during his stay at HAO/NCAR is gratefully acknowledged. R. Manso Sainz has been partially supported by the MICINN through project AYA2007-63881. H. Socas-Navarro helped with the implementation of theMELANIE code and with the interpretation of the obtained results. Comments on the manuscript by B. C. Low and J. Trujillo Bueno are gratefully acknowledged.

References

All Figures

  \begin{figure} \par {\hspace*{5mm}\includegraphics[width=6.9cm,clip]{11800f11.ps... ....ps}\hspace*{4.9mm} \includegraphics[width=7.4cm,clip]{11800f16.ps} \end{figure} Figure 1:

Top left: slit reconstructed continuum intensity map centered at the NL where the pores and penumbral-like formations can be identified. The location of the slit for the time series map is displayed. Top right: Si I Stokes V map normalized to the continuum intensity. Bottom: Stokes profiles observed at the slit position indicated in the top images and averaged over the time series (comprising 100 scans). The gray scale bar only applies to the polarization signals. The Zeeman-like signature of Stokes Q and Uare evident in this picture (He I lines are centered at 0 and 1.2 Å approximately. The zero in the wavelength scale corresponds to 10 829.09 Å). The arrows indicate the position of the presented Stokes profiles in Figs. 3 and 4.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=5.6cm,clip]{11800f21.ps}\hspace*{2.8mm... ...25.ps}\hspace*{2.5mm} \includegraphics[width=6cm,clip]{11800f26.ps} \end{figure} Figure 2:

From left to right and top to bottom: He I Doppler width, Si I LOS magnetic field, He I LOS magnetic field, He I core intensity, Si I transverse magnetic field and He I transverse magnetic field. The corresponding continuum intensity frame can be seen in the top panel of Fig. 1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12.2cm,clip]{11800fg3.ps} \end{figure} Figure 3:

Stokes profiles of the He I 10 830 Å triplet at a height of 8 arcsec in Fig. 1 in the mid portion of the twisted region of the filament. The dots represent the observed profiles obtained after averaging the time series in order to achieve a higher S/N. The solid line corresponds to the best fit achieved with a Milne-Eddington inversion code that takes into account the IPB effect. The magnetic field obtained from this particular fit is $B = 626\pm 10$ G, $\theta = 80.2^{\circ }\pm 0.1^{\circ }$ and $\chi =174.9^{\circ }\pm 0.1^{\circ }$ (the origin of azimuths being the local solar radial direction). The dot-dashed line shows the best fit obtained from an inversion in a slab model of constant properties that accounts for the joint action of scattering polarization and the Hanle Zeeman effects. This fit provided for the magnetic parameters $B = 667\pm 16$ G, $\theta = 81.1^{\circ }\pm 0.3^{\circ }$ and $\chi = 174.8^{\circ }\pm 0.5^{\circ }$.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=13cm,clip]{11800fg4.ps} \end{figure} Figure 4:

Same as Fig. 3 but for a profile near the bottom portion of the twisted region of the filament (at a height of 5 arcsec). The fitted parameters for the ME case are $B = 627\pm 10$ G, $\theta = 73.7^{\circ }\pm 0.3^{\circ }$ and $\chi =5.7^{\circ }\pm 0.1^{\circ }$. The PCA-based algorithm including Hanle effect provided: $B = 664 \pm 15$ G, $\theta = 74.9^{\circ }\pm 0.6^{\circ }$ and $\chi = 5.1^{\circ }\pm 0.8^{\circ }$.

Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.