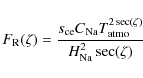| Issue |
A&A
Volume 501, Number 2, July II 2009
|
|
|---|---|---|
| Page(s) | 793 - 799 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/200811411 | |
| Published online | 29 April 2009 | |
Dependence of sodium laser guide star photon return on the geomagnetic field
N. Moussaoui1,2 - R. Holzlöhner1 - W. Hackenberg1 - D. Bonaccini Calia1
1 - European Southern Observatory, Karl-Schwarzschild-Stra![]() e 2, 85748, Garching bei München, Germany
e 2, 85748, Garching bei München, Germany
2 -
Faculty of Physics, University of Sciences and Technology Houari Boumediene, BP32 El-Alia, Bab-Ezzouar, Algiers, Algeria
Received 24 November 2008 / Accepted 10 February 2009
Abstract
Aims. The efficiency of optical pumping that increases the backscatter emission of mesospheric sodium atoms in continuous wave (cw) laser guide stars (LGSs) can be significantly reduced and, in the worst case, eliminated by the action of the geomagnetic field. Our goal is to present an estimation of this effect for several telescope sites.
Methods. Sodium atoms precess around magnetic field lines that cycle the magnetic quantum number, reducing the effectiveness of optical pumping. Our method is based on calculating the sodium magnetic sublevel populations in the presence of the geomagnetic field and on experimental measurements of radiance return from sodium LGS conducted at the Starfire optical range (SOR).
Results. We propose a relatively simple semi-empirical formula for estimating the effect of the geomagnetic field on enhancing the LGSs photon return due to optical pumping with a circularly polarized cw single-frequency laser beam. Starting from the good agreement between our calculations and the experimental measurements for the geomagnetic field effect, and in order to more realistically estimate the sodium LGSs photon return, we introduce the effect of the distance to the mesospheric sodium layer and the atmospheric attenuation. The combined effect of these three factors is calculated for several telescope sites.
Conclusions. In calculating the return flux of LGSs, only the best return conditions are often assumed, relying on strong optical pumping with circularly polarized lasers. However, one can only obtain this optimal return along one specific laser orientation on the sky, where the geomagnetic field lines are parallel to the laser beam. For most of the telescopes, the optimum can be obtained at telescope orientations beyond the observation limit. For the telescopes located close to the geomagnetic pole, the benefit of the optical pumping is much more important than for telescopes located close to the geomagnetic equator.
Key words: instrumentation: adaptive optics - atmospheric effects - atomic processes
1 Introduction
Optical pumping of atomic sodium with circularly polarized light can significantly increase the effective absorption cross section compared to non-polarized excitation of the F = 2 hyperfine ground state Milonni et al. (1998). The increase in the return light for circularly over linearly polarized light has been reported by Ge et al. (1998) to be 30%, Rabien et al. (2000) find 30-50%. Drummond et al. (2007) measured a return flux increase of factor 2.25 in the starfire optical range (SOR) when switching from linear to circular polarization. The exact return flux gain reached with optical pumping in practice depends strongly on the continuous wave (cw) laser spectral format, the direction of the magnetic field with respect to the direction of the laser beam propagation Denman et al. (2006a), and atomic effects.
In this paper, we extend our previous analysis of the effect of the geomagnetic field on the enhancement of the sodium LGS return caused by the optical pumping, Moussaoui et al. (2008). In this work, we study the reduction of the LGS return flux due to the geomagnetic field, including the effects of airmass and atmospheric absorption. The geomagnetic field intensities and orientations are obtained from the British Geological Survey.
In Sect. 2, we present the laser excitation of the sodium atoms and the role of the optical pumping by circularly polarized light. In Sect. 3, we calculate the redistribution of the atomic population of the magnetic sublevels relevant to optical pumping due to the geomagnetic field. Section 4 presents the relatively simple formulation that we propose for estimating the net effect of the geomagnetic field. Section 5 finally shows the results of our calculating the combined effects caused by the geomagnetic field, the distance to the mesospheric sodium layer and, the atmospheric attenuation on the relative enhancement of the sodium LGSs photon return flux due to optical pumping by circularly polarized laser beams for several telescopes.
2 Sodium atom excitation
Atomic sodium has a total of 11 electrons with a single valence electron
outside closed shells. The complete term symbol of the ground state is
![]() ,
and of the first excited
state,
,
and of the first excited
state,
![]() .
The interaction
of the magnetic moment of the electron with the magnetic field associated
with the orbital motion of the electron leads to the energy level splitting
within the first excited state,
.
The interaction
of the magnetic moment of the electron with the magnetic field associated
with the orbital motion of the electron leads to the energy level splitting
within the first excited state,
![]() ,
,
![]() .
The
two states are separated in energy by about 520 GHz. The transitions between
the upper state
.
The
two states are separated in energy by about 520 GHz. The transitions between
the upper state
![]() and the ground state
and the ground state
![]() cause the sodium
cause the sodium ![]() emission or absorption at 589.2 nm, while the
transitions between the lower state
emission or absorption at 589.2 nm, while the
transitions between the lower state
![]() and the ground state
cause the sodium
and the ground state
cause the sodium ![]() emission or absorption at 589.6 nm.
emission or absorption at 589.6 nm.
The total electronic angular momentum of the ground state and first excited
state are J = 1/2 and
J = 1/2, 3/2, respectively. Naturally occurring sodium is
composed virtually 100% of one isotope, which has a nuclear spin of
I = 3/2. The interaction of an electron with the nuclear magnetic moment
leads to the hyperfine structures associated with the ground and excited
states of the sodium atom. The total angular momentum quantum number F is the
sum of nuclear spin I and the electron spin J yielding the total momentum
The resulting total angular momentum quantum numbers are F = 1, 2 for the sodium ground state
The sodium ![]() transitions are chosen for the generation of sodium laser
guide stars because they have a factor of two greater total line strength
than the
transitions are chosen for the generation of sodium laser
guide stars because they have a factor of two greater total line strength
than the ![]() transitions. Furthermore, the
transitions. Furthermore, the ![]() transitions have much
better optical pumping characteristics, which results in more efficient
excitation of the sodium atoms in the mesospheric sodium layer.
transitions have much
better optical pumping characteristics, which results in more efficient
excitation of the sodium atoms in the mesospheric sodium layer.
 |
Figure 1: Schematic diagram of the sodium D transitions (from Hillman et al. 2008). |
| Open with DEXTER | |
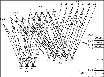 |
Figure 2:
Magnetic substates of the hyperfine levels of the sodium |
| Open with DEXTER | |
Each of the F levels splits up into 2F+1 magnetic quantum levels. For linearly
polarized light, only transitions with
![]() are permitted, whereas for
circularly polarized light,
are permitted, whereas for
circularly polarized light, ![]() must be either +1 or -1. Atoms at a given
m level in the upper state can fall back according to the rule
must be either +1 or -1. Atoms at a given
m level in the upper state can fall back according to the rule
![]() .
In the presence of a
.
In the presence of a ![]() polarized laser beam, for instance,
population migrate of toward the
polarized laser beam, for instance,
population migrate of toward the
![]() states, and this transition has the largest relative
oscillator strength. This well-known optical pumping process can be used to
produce an ensemble of two-state atoms, each of which is in either the
states, and this transition has the largest relative
oscillator strength. This well-known optical pumping process can be used to
produce an ensemble of two-state atoms, each of which is in either the
![]() (
F = 2, m = 2) state or the
(
F = 2, m = 2) state or the
![]() (
F = 3, m = 3) state
(Milonni et al. 1999; Bradley 1992; Quivers 1986).
(
F = 3, m = 3) state
(Milonni et al. 1999; Bradley 1992; Quivers 1986).
If a single-frequency laser, tuned to the exact frequency of the
![]() transition, is used to excite the sodium atoms,
unfortunately, it is still possible to optically pump the atoms from the
F = 2 to the F = 1 ground state. While atoms traveling approximately orthogonal to
the laser beam can only cycle between the F = 2 ground state and the F = 3 upper
state until they change direction by collision, atoms moving in other
directions can excite various atomic transitions to the F = 2 or F = 1 upper state.
Once excited to these levels, they can fall back either to the F = 2 or F = 1 ground
state, and after only a few cycles will end up trapped in the F = 1 ground state
(see Fig. 2).
transition, is used to excite the sodium atoms,
unfortunately, it is still possible to optically pump the atoms from the
F = 2 to the F = 1 ground state. While atoms traveling approximately orthogonal to
the laser beam can only cycle between the F = 2 ground state and the F = 3 upper
state until they change direction by collision, atoms moving in other
directions can excite various atomic transitions to the F = 2 or F = 1 upper state.
Once excited to these levels, they can fall back either to the F = 2 or F = 1 ground
state, and after only a few cycles will end up trapped in the F = 1 ground state
(see Fig. 2).
A magnetic field causes the sodium atoms to precess, leading to a cyclic probability redistribution of finding the atom in a certain m-state. It is important to have a quantitative assessment of the extent to which the geomagnetic field can reduce the degree of optical pumping.
3 Magnetic sublevel populations in the presence of a geomagnetic field
The interaction Hamiltonian for an atom with angular momentum F in a weak magnetic field B is Milonni et al. (1999)
where
![]() is the Bohr magneton, and gF is
the hyperfine Landé factor.
is the Bohr magneton, and gF is
the hyperfine Landé factor.
The weak static field B can only cause transitions between
states with different m and the same F. The probability
![]() that an atom, initially
in state (F,m), assumes the state (F,m') after time t without any intermediate
perturbation depends on the strength of the magnetic field B and the angle
that an atom, initially
in state (F,m), assumes the state (F,m') after time t without any intermediate
perturbation depends on the strength of the magnetic field B and the angle
![]() between the magnetic field vector and the laser beam direction
(Eq. (2))
between the magnetic field vector and the laser beam direction
(Eq. (2))
where
 |
Figure 3: Larmor precession of the mesospheric sodium atoms. |
| Open with DEXTER | |
Figure 4 presents the probability evolution of the magnetic sublevel
32S1/2 (F=2, m=2) population in the presence of a static field
of 0.23 G into the other magnetic sublevels
![]() for the case of
for the case of
![]() .
.
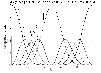 |
Figure 4:
Occupation probabilities of the magnetic sublevels (F = 2,
m' = 2, 1, 0, -1, -2) as a function of the normalized time
|
| Open with DEXTER | |
In Fig. 5, we display the probability evolution for the excited state (
F=3,
m = 3) into the seven m-states
![]() .
.
 |
Figure 5:
Occupation probabilities of the magnetic sublevels
(F = 3, m' = 3, 2, 1, 0, -1, -2, -3) as a function of the
normalized time |
| Open with DEXTER | |
Figures 4 and 5 indicate that the geomagnetic field redistributes the
magnetic sublevel populations in a time scale of ![]()
![]() .
In the
following we focus on the evolution of the populations of the magnetic
sublevels
(F=2, m=2) and
(F=3, m=3). Figure 6 presents the occupation
probabilities of respectively
(F=2, m =2) and (F=3, m=3) as functions of
time for various values of
.
In the
following we focus on the evolution of the populations of the magnetic
sublevels
(F=2, m=2) and
(F=3, m=3). Figure 6 presents the occupation
probabilities of respectively
(F=2, m =2) and (F=3, m=3) as functions of
time for various values of ![]() .
.
To illustrate the redistribution of the atomic population under the effect
of the geomagnetic field, we have calculated the occupation probabilities of
the magnetic sublevels
(F=2, m=2) and
(F=3, m=3) as functions of both
t and ![]() .
We remind the reader that emission and absorption are
ignored in these calculations. The occupation probabilities are presented in
Fig. 7.
.
We remind the reader that emission and absorption are
ignored in these calculations. The occupation probabilities are presented in
Fig. 7.
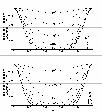 |
Figure 6:
Occupation probability of the magnetic sublevels (F = 2, m = 2) and
(
F = 3, m = 3) as a function of normalized time
|
| Open with DEXTER | |
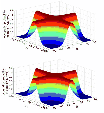 |
Figure 7:
Occupation probabilities of the magnetic sublevels (
F = 2, m = 2) and
(F = 3, m = 3) as functions of both
|
| Open with DEXTER | |
4 Effect of the geomagnetic field on the LGS photon return
As shown in Sect. 2, the optical pumping process produces an ensemble of two-state atoms, each of which is in either the 32S1 / 2 (F = 2, m = 2) state or the 32P3 / 2 (F = 3, m = 3) state. The photon return flux of sodium laser guide stars pumped with single-frequency cw circularly polarized laser beam is proportional to the atomic population of the upper magnetic sublevel. The atomic population of the lower magnetic sublevel 32S1 / 2 (F = 2, m = 2) constitutes the reservoir from which the laser beam populates the upper magnetic sublevel 32P3/2 (F= 3, m = 3). We can see from Fig. 7 that the occupation probabilities of both the lower magnetic sublevel and the upper magnetic sublevel depend on
the angle between the laser beam propagation direction and the geomagnetic field lines. Because of the very short lifetime of the sodium excited state 32P3 / 2 of
![]() ns compared to the time in which the geomagnetic field starts to redistribute the population of the
magnetic sublevels (
ns compared to the time in which the geomagnetic field starts to redistribute the population of the
magnetic sublevels (![]() 1
1 ![]() s), the action of the geomagnetic field is much more important on the sodium ground state 32S1 / 2 than on the excited state, for which the spontaneous emission is faster. Nevertheless the geomagnetic field affects the population of the upper
magnetic sublevel by affecting its reservoir (the population of the lower magnetic sublevel).
s), the action of the geomagnetic field is much more important on the sodium ground state 32S1 / 2 than on the excited state, for which the spontaneous emission is faster. Nevertheless the geomagnetic field affects the population of the upper
magnetic sublevel by affecting its reservoir (the population of the lower magnetic sublevel).
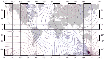 |
Figure 8: Geomagnetic field declinations from the World Magnetic Model (WMM2005). Credit: British Geological Survey (Natural Environment Research Council). |
| Open with DEXTER | |
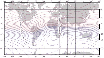 |
Figure 9: Geomagnetic field inclinations from the World Magnetic Model (WMM2005). Credit: British Geological Survey (Natural Environment Research Council). |
| Open with DEXTER | |
It is intuitive that the return flux of a sodium atom that is pumped with
circularly polarized light and still derives most of its fluorescence from
the 32P3 / 2 (F= 3, m= 3) ![]() 32S1 /2 (F = 2, m =2) transition depends on the occupation probability
P(F = 2,m = 2) of the ground state. The effect of the geomagnetic field on the enhancement of the sodium laser guide star photon return due to optical pumping and temporarily neglecting all other factors could be represented by a
geomagnetic field factor
32S1 /2 (F = 2, m =2) transition depends on the occupation probability
P(F = 2,m = 2) of the ground state. The effect of the geomagnetic field on the enhancement of the sodium laser guide star photon return due to optical pumping and temporarily neglecting all other factors could be represented by a
geomagnetic field factor
![]() .
From the above considerations about the
geomagnetic field effect on the atomic populations, and starting from our
previous work Moussaoui et al. (2008) based on the model proposed by
Drummond et al. (2007), we propose the following semi-empirical
formula for
.
From the above considerations about the
geomagnetic field effect on the atomic populations, and starting from our
previous work Moussaoui et al. (2008) based on the model proposed by
Drummond et al. (2007), we propose the following semi-empirical
formula for
![]() ,
Eq. (5). This relatively simple formulation is based on
calculation of the atomic sodium population of the lower magnetic sublevel
and on the observations of the geomagnetic field effect on the sodium LGS
return at SOR, (Denman et al. 2006a, 2004)
,
Eq. (5). This relatively simple formulation is based on
calculation of the atomic sodium population of the lower magnetic sublevel
and on the observations of the geomagnetic field effect on the sodium LGS
return at SOR, (Denman et al. 2006a, 2004)
where a and b are fitting parameters chosen according to the experimental measurements and P(F = 2,m = 2) is the occupation probability of the magnetic sublevel (F=2, m=2). This probability oscillates at the Larmor frequency. If the atom is in the (F=2, m=2) state at a given time, the probability of finding it again in (F=2, m=2) state after time t has elapsed, taking into account only the Larmor precession has been calculated using Eq. (4).
To derive the coefficients of Eq. (5) we calculate the effect of the geomagnetic field on the enhancement of the sodium laser guide star photon return due to optical pumping with circularly polarized laser beam for the SOR telescope (Albuquerque, New Mexico, USA) (Denman et al. 2006a, 2004).
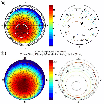 |
Figure 10: a) Polar plot of radiance return from a 30 W, circularly polarized sodium LGS, SOR (Albuquerque, New Mexico, USA) Denman et al. (2006a). The legend indicates the radiance in photon/s/cm2. b) Relative radiance enhancement of the sodium LGS due to optical pumping with circularly polarized laser beam in presence of the geomagnetic field. Calculations using Eq. (5) for the SOR. |
| Open with DEXTER | |
5 Results
5.1 Effect of the geomagnetic field
The intensity, declination, and inclination of the geomagnetic field depend on the geographic location. The magnetic declination is the angle between true north and the compass needle, where positive values indicate that compass points east of true north, while the inclination is the vertical angle of magnetic field lines against the ground, positive numbers indicate that the compass needle points towards the ground, Figs. 8, 9.
Figure 10a shows experimental measurements of the geomagnetic field's impact
on the enhancement of the sodium laser guide star photon return due to
optical pumping with a circularly polarized laser beam for the
SOR Denman et al. (2006a). The polar diagram represents the sky over the
telescope site. The maximum return is observed at the location in the sky
where the earth's magnetic field lines are pointing directly at the SOR,
hence when the laser beam propagation direction in the mesosphere is
parallel with B. The magnetic field has no effect when the
LGS is produced with a linearly polarized beam. According to
Denman et al. (2006b), these experimental results show that the resultant
peak returns are obtained at approximately 198![]() azimuth and 71
azimuth and 71![]() elevation. Starting from this observation, we have used 18
elevation. Starting from this observation, we have used 18![]() as
declination and 71
as
declination and 71![]() as inclination instead of the 10
as inclination instead of the 10![]() and 62
and 62![]() given by the British Geological Survey website to calculate the relative
radiance return for SOR using Eq. (4). Figure 11 shows the results of our
calculations for the coefficients a=1.25, b=1 and at normalized time
given by the British Geological Survey website to calculate the relative
radiance return for SOR using Eq. (4). Figure 11 shows the results of our
calculations for the coefficients a=1.25, b=1 and at normalized time
![]() .
.
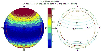 |
Figure 11: Polar plot of the relative radiance enhancement of the sodium LGS due to optical pumping with circularly polarized laser beams in the presence of the geomagnetic field for the VLT telescope, Cerro Paranal (Chile). |
| Open with DEXTER | |
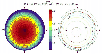 |
Figure 12: Polar plot of the relative radiance enhancement of the sodium LGS due to optical pumping with circularly polarized laser beams in the presence of the geomagnetic field for the Dome C, Antarctica, telescope. |
| Open with DEXTER | |
Figure 10b represents the relative sodium return enhancement of optical pumping with a circularly polarized laser beam in the presence of the geomagnetic field. The red circle indicates the observation limit of the telescope (60![]() zenith angle). The maximum relative enhancement of the sodium LGSs due to optical pumping with a circularly polarized laser beam is assumed to be 2.25 as measured by Denman et al. (2006b), when switching from linear to circular polarization. No effect of the geomagnetic field on the sodium LGSs produced by linearly polarized laser beams.
zenith angle). The maximum relative enhancement of the sodium LGSs due to optical pumping with a circularly polarized laser beam is assumed to be 2.25 as measured by Denman et al. (2006b), when switching from linear to circular polarization. No effect of the geomagnetic field on the sodium LGSs produced by linearly polarized laser beams.
We calculate the effect of the geomagnetic field on the enhancement of the circularly polarized sodium laser guide star return for several telescopes. The results of our calculations are presented in the following figures.
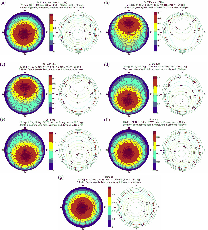 |
Figure 13: Combined effects of geomagnetic field, the airmass, and the atmospheric attenuation on the relative radiance enhancement of the sodium LGS due to optical pumping with circularly polarized laser beams. |
| Open with DEXTER | |
We present in Fig. 12, our calculations for the Dome C telescope in
Antarctica, for which the angle between the geomagnetic field lines and
zenith is less than 10![]() ,
and we expect less disruption of the relative
radiance enhancement of the sodium LGS due to optical pumping with
circularly polarized lasers under the effect of the geomagnetic field
compared to the VLT or the SOR telescopes.
,
and we expect less disruption of the relative
radiance enhancement of the sodium LGS due to optical pumping with
circularly polarized lasers under the effect of the geomagnetic field
compared to the VLT or the SOR telescopes.
5.2 Effect of the geomagnetic field, the airmass and the distance to the Na layer
To model realistic distributions of the sodium LGSs return, we include the
effects of the airmass and the atmospheric attenuation in our calculations.
The specific return flux on the ground per watt of launched laser power is
given by
where
We now combine Eqs. (5) and (7). To simplify our calculations we
consider for all the telescope sites that the coupling efficiency of light
at 589 nm to sodium atoms, and the vertical column density of the sodium
atoms in the mesosphere
![]() are both constant, and we also assume that
the vertical distance from the telescope to the sodium centroid
are both constant, and we also assume that
the vertical distance from the telescope to the sodium centroid
![]() is
the same for all the telescopes. The single-pass transmission of the
atmosphere at 589 nm at zenith
is
the same for all the telescopes. The single-pass transmission of the
atmosphere at 589 nm at zenith
![]() is assumed equal to 0.84, which is
slightly worse than the measured value for a photometric night in Paranal
(0.89) Patat (2004). The combined effects of the geomagnetic field, the
airmass, and the atmospheric attenuation on the enhancement of the sodium
laser guide star photon return caused by the optical pumping with circularly
polarized laser beams can be represented by the expression
is assumed equal to 0.84, which is
slightly worse than the measured value for a photometric night in Paranal
(0.89) Patat (2004). The combined effects of the geomagnetic field, the
airmass, and the atmospheric attenuation on the enhancement of the sodium
laser guide star photon return caused by the optical pumping with circularly
polarized laser beams can be represented by the expression
where
6 Conclusion
To estimate the effect of the geomagnetic field on the enhancement of the
LGSs photon return, we have proposed a semi-empirical formula for the
geomagnetic field factor based on the calculation of the sodium magnetic
sublevel population whose coefficients are calibrated using the experimental
measurements conducted at the Starfire Optical Range. Starting from the good
agreement between our results and the experiments, we extended our
calculations to several other astronomical telescopes. Our calculations show that, for most of the telescopes, the maximum relative enhancement of the
sodium laser guide stars pumped by circularly polarized laser beam can be
obtained at telescope orientations close to the observation limit (60![]() ).
For Paranal, the optimum is obtained for an altitude below the observation
limit of the VLT telescope.
).
For Paranal, the optimum is obtained for an altitude below the observation
limit of the VLT telescope.
To gain a more realistic estimate of the sodium LGSs photon return, we introduced the effect of the distance to mesospheric sodium layer and the effect of the atmospheric attenuation for several telescopes. The results show that, when observing at zenith, the telescope located closer to the geomagnetic pole (Dome C for example) benefits much more from optical pumping than telescopes located close to the geomagnetic equator (Paranal, Cerro Pachon, La Palma, etc.), at least when using a single-frequency cw circularly polarized laser beam.
The intensity of the geomagnetic field varies significantly around the globe. At the VLT, in Paranal, northern Chile, it is quite weak B = 0.23 G, and hence optical pumping may be disrupted less severely than for instance at the SOR in Albuquerque, New Mexico (USA) (B = 0.51 G), or in Hawaii (B=0.35 G). Experimental results will ultimately be needed to assess the effect of the magnetic field strength. Numerical studies are underway to quantify the return flux further Kibblewhite (2008a). In this context, we acknowledge ongoing helpful interaction with Kibblewhite (2008b).
Acknowledgements
The authors are grateful to anonymous referees for their substantive comments that improved the content and presentation of the paper.
References
- Bradley, L. C. 1992, J. Opt. Soc. Am. B, 9, 1931 [NASA ADS] [CrossRef] (In the text)
- British Geological Survey magnetic maps, available athttp://www.geomag.bgs.ac.uk
- Denman, C. A., Moore G., Drummond, J., et al. 2006a, Two-Frequency Sodium Guide star Excitation at the Starfire Optical Range, CfAO workshop (In the text)
- Denman, C. A., Drummond, J., Eickhoff, M. L., et al. 2006b, Proc. SPIE., 6272, L1 (In the text)
- Drummond, J., Denman, C., Hillman, P., et al. 2007, AMOS Conference Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Wailea, Maui, Hawaii, September 12-15, E67, ed. S. Ryan, The Maui Economic Development Board (In the text)
- Drummond, J., Telle, J. M., Denman, C., et al. 2004, in Advancements in Adaptive Optics, ed. D. Bonaccini Calia, B. L. Ellerbroek, & R. Ragazzoni, Proc. SPIE, 5490, 12 (In the text)
- Ge, J., Jacobsen, B. P., Angel, J. R. P., et al. 1998, Proc. SPIE, 3353, 242 [NASA ADS] (In the text)
- Gottfried, K. 1977, Quantum Mechanics (Reading, Mass.: Benjamin), 269 (In the text)
- Hillman, P. D., Drummond, J. D., Denman, C. A., & Fugate, R. Q. 2008, Proc. SPIE, 7015, L1 (In the text)
- Kibblewhite, E. 2008a, SPIE, Marseille, Proc. SPIE, 7015, 1 (In the text)
- Kibblewhite, E. 2008b, Report for ESO (In the text)
- Milonni, P. W., Fugate, R. Q., & Telle, J. M. 1998, J. Opt. Soc. Am. A, 15, 217 [NASA ADS] [CrossRef] (In the text)
- Milonni, P. W., Fearn, H., Telle, J. M., & Fugat,e R. Q. 1999, J. Opt. Soc. Am. A, 16, 2555 [NASA ADS] [CrossRef] (In the text)
- Morris, J. R. 1994, J. Opt. Soc. Am. A, 11, 832 [NASA ADS] [CrossRef] (In the text)
- Moussaoui, N., Holzlöhner, R., Hackenberg, W., & Bonaccini Calia, D. 2008, Proc. SPIE, 7015, 1 (In the text)
- Patat F. 2004, The Messenger, 118, ESO monthly newsletter, 11, http://www.eso.org/sci/publications/messenger/archive/no.118-dec04/messenger-no118.pdf (In the text)
- Quivers W. W. 1986, Phys. Rev. A, 34, 3822 [NASA ADS] [CrossRef] (In the text)
- Rabien S., Ott T., Hackenberg W., et al. 2000, The ALFA Laser and AnalysisTools, ExA 10, 78 (In the text)
- Steck D. A. 2008, Sodium D Line Data, http://steck.us/alkalidata (In the text)
- Ungar P. J., Weiss D. S., Riis E., & Chu S. 1989, J. Opt. Soc. Am. B, 6, 11 [CrossRef] (In the text)
All Figures
 |
Figure 1: Schematic diagram of the sodium D transitions (from Hillman et al. 2008). |
| Open with DEXTER | |
| In the text | |
 |
Figure 2:
Magnetic substates of the hyperfine levels of the sodium |
| Open with DEXTER | |
| In the text | |
 |
Figure 3: Larmor precession of the mesospheric sodium atoms. |
| Open with DEXTER | |
| In the text | |
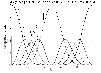 |
Figure 4:
Occupation probabilities of the magnetic sublevels (F = 2,
m' = 2, 1, 0, -1, -2) as a function of the normalized time
|
| Open with DEXTER | |
| In the text | |
 |
Figure 5:
Occupation probabilities of the magnetic sublevels
(F = 3, m' = 3, 2, 1, 0, -1, -2, -3) as a function of the
normalized time |
| Open with DEXTER | |
| In the text | |
 |
Figure 6:
Occupation probability of the magnetic sublevels (F = 2, m = 2) and
(
F = 3, m = 3) as a function of normalized time
|
| Open with DEXTER | |
| In the text | |
 |
Figure 7:
Occupation probabilities of the magnetic sublevels (
F = 2, m = 2) and
(F = 3, m = 3) as functions of both
|
| Open with DEXTER | |
| In the text | |
 |
Figure 8: Geomagnetic field declinations from the World Magnetic Model (WMM2005). Credit: British Geological Survey (Natural Environment Research Council). |
| Open with DEXTER | |
| In the text | |
 |
Figure 9: Geomagnetic field inclinations from the World Magnetic Model (WMM2005). Credit: British Geological Survey (Natural Environment Research Council). |
| Open with DEXTER | |
| In the text | |
 |
Figure 10: a) Polar plot of radiance return from a 30 W, circularly polarized sodium LGS, SOR (Albuquerque, New Mexico, USA) Denman et al. (2006a). The legend indicates the radiance in photon/s/cm2. b) Relative radiance enhancement of the sodium LGS due to optical pumping with circularly polarized laser beam in presence of the geomagnetic field. Calculations using Eq. (5) for the SOR. |
| Open with DEXTER | |
| In the text | |
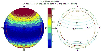 |
Figure 11: Polar plot of the relative radiance enhancement of the sodium LGS due to optical pumping with circularly polarized laser beams in the presence of the geomagnetic field for the VLT telescope, Cerro Paranal (Chile). |
| Open with DEXTER | |
| In the text | |
 |
Figure 12: Polar plot of the relative radiance enhancement of the sodium LGS due to optical pumping with circularly polarized laser beams in the presence of the geomagnetic field for the Dome C, Antarctica, telescope. |
| Open with DEXTER | |
| In the text | |
 |
Figure 13: Combined effects of geomagnetic field, the airmass, and the atmospheric attenuation on the relative radiance enhancement of the sodium LGS due to optical pumping with circularly polarized laser beams. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\displaystyle g_{F}=g_{J}\displaystyle \left[\frac{F(F + 1) + J(J + 1) - I(I + 1)}{2F(F + 1)}\right],$](/articles/aa/full_html/2009/26/aa11411-08/img22.png)
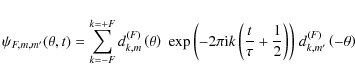
![\begin{displaymath}\begin{array}{l} P_{(F=2,m=m'=2)} (\theta ,\tilde{t})=\\ \dis...
...\left(2\pi \tilde{t}\right)} \end{array}\right]^{2}.\end{array}\end{displaymath}](/articles/aa/full_html/2009/26/aa11411-08/img56.png)