EDP Sciences
Home All issues Volume 499 / No 1 (May III 2009) A&A, 499 1 (2009) L1-L3 Full HTML
Free Access
Issue
A&A
Volume 499, Number 1, May III 2009
Page(s) L1 - L3
Section Letters
DOI https://doi.org/10.1051/0004-6361/200911638
Published online 29 April 2009

LETTER TO THE EDITOR

Can angular momentum loss cause the period change of NN Serpentis?

W.-C. Chen

Department of Physics and Information Engineering, Shangqiu Normal University, Shangqiu 476000, PR China

Received 9 January 2009 / Accepted 15 April 2009

Abstract
NN Ser is a non mass-transferring pre-cataclysmic variable containing a white dwarf with a mass of $\sim$0.5 $M_{\odot}$ and an M dwarf secondary star with a mass of $\sim$0.2 $M_{\odot}$. Based on the data obtained with the high-speed CCD camera ULTRACAM, it was observed that the orbital period of NN Ser is decreasing, which may be caused by a genuine angular momentum loss or by the presence of a third body. However, neither gravitational radiation nor magnetic braking can fully account for the period change of NN Ser. Here, we search for a mechanism which could drain the angular momentum from NN Ser. We propose that a fossil circumbinary disk (CB disk) around the binary may have been established at the end of the common envelope phase, and the tidal torques caused by the gravitational interaction between the disk and the binary can efficiently extract the orbital angular momentum from the system. We find that only if M dwarf has an ultra-high wind loss rate of $\sim$10 $^{-10}~M_{\odot}~\rm yr^{-1}$, and a large fraction ( $\delta\sim 10\%$) of wind loss is fed into the CB disk, can the loss rates of angular momentum via the CB disk explain the period change observed in NN Ser. Such a wind loss rate and $\delta$-value seem to be highly unlikely. Hence it seems that the presence of a third body in a long orbit around the binary might account for the changing period of NN Ser.

Key words: binaries: eclipsing - pulsars: individual: N Serpentis - stars: evolution - white dwarfs - stars: winds, outflows

1 Introduction

From the Palomar-Green survey, NN Ser (PG 1550+131) was determined to have clear emission lines in its spectra. Based on the broad H, He I profiles, and Balmer jumps in the emission lines, NN Ser was classified as a U Gem-like object (see Green et al. 1982). Through the observations of NN Ser, Wilson et al. (1986) found that there exists a rapid decline its the brightness of $\sim$0.6 mag, which was believed to be a characteristic of cataclysmic variable stars.

Based on photometric observations in 1988 July, a strong heating effect ($\sim$0.6 mag) and very deep primary eclipses ($\ga$0.4 mag) have been seen, which show that NN Ser is a detached white dwarf binary with an orbital period of 3.12 h, i.e. it is a pre-cataclysmic variable (Haefner 1989). Through low-resolution IUE observations for NN Ser, Wood & Marsh (1991) derived that the mass of the white dwarf is in the range of $0.47{-}0.60~M_{\odot}$, and the secondary star is an M 4.7-M 6.1 dwarf with a mass of $0.09{-}0.14~M_{\odot}$ and a temperature of 2775-3050 K. Using the phase-resolved blue and far red spectra, Catalan et al. (1994) inferred the radial velocities, and discussed the physical and orbital parameters for both components of NN Ser. Haefner et al. (2004) redetermined all system parameters of NN Ser by using the VLT and the multi-mode FORS instruments.

Using the high speed CCD camera ULTRACAM, Brinkworth et al. (2006) have detected 13 primary eclipses of NN Ser. After fitting of light curve models, they concluded that the orbital period of the binary is decreasing, with a mean change rate $\dot{P}=(9.06\pm 0.06)\times 10^{-12}$ ss-1, and a current change rate $\dot{P}=(2.85\pm 0.15)\times 10^{-11}$ ss-1 during the past 2 years. Generally, period changes in binary systems may be caused by three mechanisms: Applegate's mechanism (Applegate 1992), the presence of a third body around the binary, and an orbital angular momentum loss. After excluding Applegate's mechanism, Brinkworth et al. (2006) concluded that a third body with a mass of $0.0043{-}0.18~M_{\odot}$ and an orbital period of 30-285 yr may be responsible for the period change of NN Ser. Furthermore, the standard magnetic braking model proposed by Rappaport et al. (1983) can also account for NN Ser's period change if the magnetic braking mechanism still applies to at a secondary star with mass lower than $0.3~M_{\odot}$ (Brinkworth et al. 2006).

Grossman et al. (1974) suggested that main-sequence stars with masses $\la$0.3 $M_{\odot}$ have convective cores, therefore the magnetic field lines cannot be locked to the core and magnetic braking should be cut off. From the observed angular momentum loss properties of cataclysmic variables (CVs), Andronov et al. (2003) noted that there is no evidence for a cut-off in magnetic braking when the stellar mass is below $0.3~M_{\odot}$. In addition, if gravitational radiation is the only mechanism draining angular momentum from CVs with a short period, it would result in two serious consequences: (1) the inferred minimum orbital period would be at 1.1 h instead of the observed value of 1.3 h; (2) there should exist a significant fraction of CVs with a minimum period, which is not consistent with the observations (Patterson 1998). Therefore, it is a controversial issue as to whether magnetic braking still works for NN Ser.

It is the purpose of this paper to search for a feasible mechanism extracting the orbital angular momentum from NN Ser, and present an alternative interpretation for its orbital period change. In Sect. 2.1, our analytic results indicate that the magnetic braking cannot explain the observed data of NN Ser. In Sect. 2.2 we investigate if a circumbinary (CB) disk around the binary system can be responsible for the period change of NN Ser. We provide a brief discussion and summary in Sect. 3.

2 The orbital angular momentum loss

2.1 Magnetic braking

Single low-mass main-sequence stars would be expected to undergo magnetic braking due to the coupling between the stellar winds and the magnetic field (Verbunt & Zwaan 1981). The specific angular momentum loss in the stellar winds is very large because the outflow material is bound in the magnetic field lines to co-rotate with the stars out to a long distance (see Kalogera 1999; Mestel & Spruit 1987; Weber & Davis 1967).

Assuming that magnetic braking still works for NN Ser, we estimate the loss rates of orbital angular momentum. The magnetospheric radius of an M dwarf can be derived as (Justham et al. 2006)

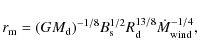\begin{displaymath}r_{\rm m}=(GM_{\rm d})^{-1/8}B_{\rm s}^{1/2}R_{\rm d}^{13/8}\dot{M}_{\rm wind}^{-1/4}, \end{displaymath} (1)

where G is the gravitational constant, $B_{\rm s}$ is the surface magnetic field of the star, $M_{\rm d}$ and $R_{\rm d}$ are the mass and the radius of the star, respectively, $\dot{M}_{\rm wind}$ is the stellar wind loss rates.

In a binary system, the angular momentum loss by magnetic braking would cause the evolved star to spin down. However, the tidal forces between the two components would continuously act to spin the star back up into co-rotation with the orbital rotation (Patterson 1984). The spin-up takes place at the expense of the orbital angular momentum. Hence magnetic braking indirectly carries away the orbital angular momentum of the binary system. Assuming that the stellar wind with the angular velocity of the donor star at magnetosphere depart from the magnetic lines, the loss rates of orbital angular momentum is given by (Justham et al. 2006)

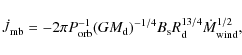\begin{displaymath}\dot{J}_{\rm mb}=-2\pi P_{\rm orb}^{-1}(GM_{\rm d})^{-1/4}B_{\rm s}R_{\rm d}^{13/4}\dot{M}_{\rm wind}^{1/2}, \end{displaymath} (2)

where $P_{\rm orb}$ is the orbital period of the binary.

For NN Ser, the mass and radius of the M dwarf are $\sim$0.15 $M_{\odot}$ and $\sim$0.18 $R_{\odot}$, respectively (Haefner et al. 2004). Detection of Zeeman splitting of Fe lines in very active M dwarfs indicates a magnetic field of 2-4 kG (Johns-Krull & Valenti 1996). Based on data from the James Clerk Maxwell Telescope, Mullan et al. (1992) proposed that the flaring M dwarf stars have a ultra-high wind loss rates of $\sim$ $ 10^{-10}~M_{\odot}$ yr-1. Hence we can obtain the loss rates of orbital angular momentum by magnetic braking

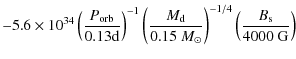                                    $\displaystyle \dot{J}_{\rm mb}$ = $\displaystyle -5.6\times 10^{34} \left(\frac{P_{\rm orb}}{0.13\rm d}\right)^{-1... ...{\rm d}}{0.15~M_{\odot}}\right)^{-1/4}\left(\frac{B_{\rm s}}{4000~\rm G}\right)$  
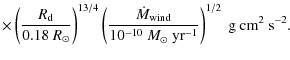    $\displaystyle \times \left(\frac{R_{\rm d}}{0.18~R_{\odot}}\right)^{13/4}\left(... ...}_{\rm wind}}{10^{-10}~M_{\odot}~\rm yr^{-1}}\right)^{1/2}~\rm g~cm^{2}~s^{-2}.$ (3)

Since $10^{-10}~M_{\odot}~\rm yr^{-1}$ is indeed the upper limit of the wind loss rate for an M dwarf (see Sect. 2.2), $5.6\times 10^{34}~\rm g~cm^{2}~s^{-2}$ is the absolute maximum of $\dot{J}$. Equation (3) shows that magnetic braking is not likely to account for the period change of NN Ser, in which the average angular momentum loss rates is in the range of $0.84{-}2.09\times 10^{35}~\rm g~cm^{2}~s^{-2}$ (Brinkworth et al. 2006). The standard magnetic braking model proposed by Rappaport et al. (1983) overestimates angular momentum loss rates for low-mass stars with high rotation rates. However, with the saturated magnetic braking by Sills et al. (2000) and Andronov et al. (2003), the rate of angular momentum loss is too low to explain the period change in NN Ser (Brinkworth et al. 2006). Hence there should be a more efficient angular momentum loss mechanism to explain the current orbital evolution of NN Ser.

2.2 Circumbinary disk

Recently, a new mechanism to extract angular momentum from binary stars - the CB disk - was developed. CB disks were first proposed by van den Heuvel & de Loore (1973) and van den Heuvel (1994), and they argued that part of the transferred material with orbital angular momentum may form a disk around the binary rather than leaving it. The rotating disk around a binary is called the CB disk, whose schematic diagram was presented by Hayasaki & Okazaki (2009) (see their Fig. 1). If the CB disk follows Keplerian rotation, its angular velocity $\Omega \propto r^{-3/2}$ (r is the distance between the CB disk and the mass center of the binary system), then the angular velocity of the CB disk is less than that of the binary. The gravitational interaction between the inner edge $r_{\rm i}$of the CB disk and the binary causes the disk to spin up, and causes the binary to spin down. Hence the tidal torques caused by the gravitational interaction may extract the orbital angular momentum from the binary to the CB disk. Spruit & Taam (2001) and Taam & Spruit (2001) invoked the CB disk to explain the large spread of the mass transfer rate for a given orbital period in CVs. Our recent work also shows that CB disks can efficiently extract orbital angular momentum from binaries, and hence enhance the mass transfer rates (Chen & Li 2006,2007; Chen et al. 2006).

In the standard scenario for the birth of cataclysmic variables, the progenitor systems were assumed to include an intermediate mass star and a low mass companion. After the more massive star fills its Roche lobe, the mass transfer rate is very high because of the large mass ratio between the two components, and the binary systems will evolve into a common envelope phase (for a review Iben & Livio 1993). Ejecting the envelope due to friction dissipation, a compact binary with a low mass white dwarf was formed. NN Ser was proposed to be a post common envelope binary (Schreiber & Gnäsicke 2003). Since the common envelope may not be entirely ejected, a fossil CB disk may have been established (Spruit & Taam 2001).

Assuming that a fraction $\delta$ of the stellar wind loss from the M dwarf feeds into the CB disk, the loss rates of angular momentum via the CB disk can be written as (Taam & Spruit 2001; Spruit & Taam 2001)

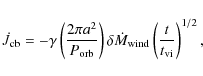\begin{displaymath}\dot{J}_{\rm cb}=-\gamma\left(\frac{2\pi a^2}{P_{\rm orb}}\ri... ...elta\dot{M}_{\rm wind}\left(\frac{t}{t_{\rm vi}}\right)^{1/2}, \end{displaymath} (4)

where $\gamma=\sqrt{r_{\rm i}/a}$ (a is the binary separation), t is the mass input timescale of the disk. Under the assumption of a standard thin disk, the viscous timescale $t_{\rm vi}$ at the inner edge of the CB disk is given by $t_{\rm vi}=2\gamma^{3}P_{\rm orb}/(3\pi\alpha_{\rm SS}\beta^{2})$, where $\beta=H_{\rm i}/r_{\rm i}$, $\alpha_{\rm SS}$ and $H_{\rm i}$ are the viscosity parameter and the scale height of the CB disk, respectively (Chen & Li 2007).

For NN Ser, Haefner et al. (2004) suggested that the cooling time of the white dwarf is $\sim$ $1.3\times 10^{6}$ yr, which is consistent with the age of the white dwarf estimated by Wood & Marsh (1991). Setting $\gamma = 1.3, \alpha_{\rm SS}=0.01$, and $\beta = 0.03$ (Chen & Li 2006), $t_{\rm vi}\approx 18$ yr. Inserting typical values for the parameters into Eq. (4), we have

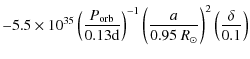                                    $\displaystyle \dot{J}_{\rm cb}$ = $\displaystyle -5.5\times 10^{35} \left(\frac{P_{\rm orb}}{0.13\rm d}\right)^{-1}\left(\frac{a}{0.95~R_{\odot}}\right)^{2}\left(\frac{\delta}{0.1}\right)$  
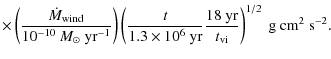    $\displaystyle \times \left(\frac{\dot{M}_{\rm wind}}{10^{-10}~M_{\odot}~\rm yr^... ...es 10^{6}~\rm yr}\frac{18~\rm yr}{t_{\rm vi}}\right)^{1/2}~\rm g~cm^{2}~s^{-2}.$ (5)

According to Eq. (5), the CB disk can explain the loss rates of angular momentum seen in NN Ser for a large  $\delta=0.1$ and an ultra-high wind loss rate ( $10^{-10}~M_{\odot}~\rm yr^{-1}$).

The above order-of-magnitude estimate obviously contains substantial uncertainties in $\delta$ and the wind loss rates. Firstly, the loss rates of angular momentum relies strongly on the stellar wind loss rates, which may be overestimated by Mullan et al. (1992). Based on the observations for several M dwarf flare stars, an upper limit of $\sim$ $ 10^{-12}~M_{\odot}\rm yr^{-1}$was derived (van den Oord & Doyle 1997; Lim & White 1996). Analysis of the data from Chandra and Hubble observations showed that the M 5.5 dwarf Proxima Centauri has a wind loss rate of $\sim$ $ 10^{-14}{-}10^{-15}~M_{\odot}\rm yr^{-1}$ (Wargelin & Drake 2002; Wood et al. 2001). Assuming that the white dwarf accretes wind material through Bondi-Hoyle accretion, Debes (2006) presented a wind loss rates range of $\sim$ $ 10^{-14}{-}10^{-16}~M_{\odot}~\rm yr^{-1}$ for three M dwarfs. We expect that future observations of P Cygni profiles, optical and molecular emission lines, infrared and radio excesses, and absorption lines can provide further constraints for the wind loss rates of NN Ser (Lamers & Cassinelli 1999). Secondly, even if the wind loss rates derived by Mullan et al. (1992) are the same as NN Ser, the CB disk mechanism still requires a large $\delta$, which is about 2-3 orders of magnitude larger than that used by Spruit & Taam (2001). Such wind loss rates and $\delta$-values are overly large, so it seems that the presence of a CB disk is not the main cause of the period change of NN Ser.

3 Discussion and summary

Brinkworth et al. (2006) suggested that the standard magnetic braking model may explain the period change observed in NN Ser if the magnetic braking cut-off is ignored. Here, we estimate the loss rates of angular momentum via magnetic braking with an analytic approach. Our result shows that, even if the M dwarf in NN Ser possesses a strong magnetic field of 4000 G and an ultra-high wind loss rate of $\sim$ $10^{-10}~M_{\odot}~\rm yr^{-1}$, the loss rates of angular momentum via magnetic braking are an order of magnitude less than that of observation. However, for the same wind loss rates, if a large fraction ($\sim$10%) of wind loss was delivered to the CB disk, the loss rates of angular momentum seen in NN Ser could be interpreted by the tidal torques caused by the gravitational interaction between the CB disk and the binary.

However, the stellar wind loss rates of M dwarfs determine if a CB disk can account for the period change of NN Ser. Several authors have subsequently derived wind loss rates of 2-6 mag lower than the one given by Mullan et al. (1992) (Wargelin & Drake 2002; van den Oord & Doyle 1997; Debes 2006; Wood et al. 2001; Lim & White 1996). Based on recent inferred wind loss rates for M dwarfs, the CB disk is not the main mechanism causing the period change of NN Ser. In the absence of evidence for a more efficient mechanism extracting angular momentum from the binary, the presence of a third body in a long orbit around NN Ser may be the best candidate mechanism for its period change (Brinkworth et al. 2006).

Though a CB disk is ruled out in NN Ser, the existence of CB disks might be a key issue in studying the evolution of the CVs. As the result of a continuum contribution of the dust emission, the CB disk may be detected in the L waveband (Spruit & Taam 2001). Recently, Hayasaki & Okazaki (2009) suggested a new channel to probe a CB disk in which the emission profiles may be caused to vary by prograde and nonaxisymmetric waves. Through interferometric observations, the direct imaging of CB disks has been successfully obtained in some young binaries such as GG Tau (Dutrey et al. 1994) and UY Aur (Duvert et al. 1998). When the Spitzer data for CVswith a strong magnetic field were analyzed, the flux density of four and five polars in mid-infrared wavelengths was discovered to be in excess. Howell et al. (2006) and Brinkworth et al. (2007) proposed that the CB dust disks are the most likely origin of these excesses (but the source of optically thin cyclotron radiation cannot be ruled out). Dubus et al. (2007) found that the infrared emission from the magnetic CV AE Aqr is larger than the expected value from the companion, and they thought that the thermal emission from the CB material might be a candidate. Therefore, as the progenitor of CVs, NN Ser may also be surrounded by a CB disk. We expect further detailed multi-waveband observations for this pre-CVs to confirm or negate our idea in the future.

Acknowledgements
We thank the anonymous referee for his/her helpful comments improving this manuscript, and thank Stephen Justham, Li X. D., Liu X. W., and Zuo Z. Y. for their help in improving English of this paper. This work has been supported in part by the National Natural Science Foundation of China (Grant No 10873011), and sponsored by Program for Science & Technology Innovation Talents in Universities of Henan Province, China.

References

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.