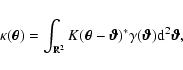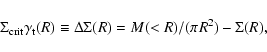EDP Sciences
Home All issues Volume 498 / No 2 (May I 2009) A&A, 498 2 (2009) L33-L36 Full HTML
Free Access
Issue
A&A
Volume 498, Number 2, May I 2009
Page(s) L33 - L36
Section Letters
DOI https://doi.org/10.1051/0004-6361/200911841
Published online 08 April 2009

LETTER TO THE EDITOR

A weak lensing study of the Coma cluster[*]

R. Gavazzi1 - C. Adami2 - F. Durret1 - J.-C. Cuillandre3 - O. Ilbert2 - A. Mazure2 - R. Pelló4 - M. P. Ulmer5

1 - Institut d'Astrophysique de Paris, CNRS UMR 7095 & Univ. Paris 6, 98bis Bd Arago, 75014 Paris, France
2 - LAM, OAMP, Université Aix-Marseille & CNRS, 38 rue Frédéric Joliot-Curie, 13388 Marseille 13 Cedex, France
3 - Canada-France-Hawaii Telescope Corporation, Kamuela, HI 96743, USA
4 - Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse, CNRS, 14 Av. Edouard Belin, 31400 Toulouse, France
5 - Department Physics & Astronomy, Northwestern University, Evanston, IL 60208-2900, USA

Received 12 February 2009 / Accepted 28 March 2009

Abstract
Context. Due to observational constraints, dark matter determinations in nearby clusters based on weak lensing are still extremely rare, in spite of their importance for the determination of cluster properties independent of other methods.
Aims. We present a weak lensing study of the Coma cluster (redshift $\sim$0.024) based on deep images obtained at the CFHT.
Methods. After obtaining photometric redshifts for the galaxies in our field based on deep images in the u* (1 $\times$ 1 deg2), and in the B, V, R and I bands (42' $\times$ 52'), allowing us to eliminate foreground galaxies, we apply weak lensing calculations on shape measurements performed in the u* image.
Results. We derive a map of the mass distribution in Coma, as well as the radial shear profile, and the mass and concentration parameter at various radii. We obtain $M_{\rm 200c}= 5.1^{+4.3}_{-2.1}$ $\times$ $10^{14}~h_{70}^{-1}{M}_{\odot}$ and $c_{\rm 200c}=5.0^{+3.2}_{-2.5}$, in good agreement with previous measurements.
With deep wide field images it is now possible to analyze nearby clusters with weak lensing techniques, thus opening a broad new field of investigation.

Key words: gravitational lensing - galaxies: clusters: individual: Coma

1 Introduction

Although weak lensing studies are of great importance in cosmology, in particular concerning various aspects of the analysis of large scale structures in the universe (e.g.  Schneider 2006; Mellier 1999; Bartelmann & Schneider 2001), dark matter determinations in clusters based on weak lensing have been limited to relatively distant objects, usually with redshifts larger than about 0.15. This is mainly due to the fact that the cluster lensing strength is maximized if the angular diameter distance to the foreground cluster is about half that of the background source galaxies, and to the requirement of large field images, in order to cover the full cluster in a single exposure. Very few low redshift clusters have been analyzed until now in detail through weak lensing: Abell 3667 at redshift 0.055 (Joffre et al. 2000), and clusters observed in the shallow Sloan Digital Sky Survey (Sheldon et al. 2001), including Coma (Kubo et al. 2007). We present here a weak lensing study of the Coma cluster at $z_{\rm Coma}=0.024$ based on deep exposures in several bands obtained with the CFH12k and Megaprime/Megacam large cameras at the Canada France Hawaii Telescope. The J2000 location of the brightest cluster galaxy NGC 4874 is RA = 12:59:35.67, Dec = +27:57:33.7. In the following we assume the ``concordance model'' cosmological background with $H_0 = 70~{\rm km~s}^{-1}~{\rm Mpc}^{-1}$, $\Omega_{\rm m}=0.3$ and $\Omega_\Lambda=0.7$, for which $1\hbox{$^{\prime\prime}$ }$ on the sky corresponds to a transverse scale of $0.79~{\rm kpc}$. All magnitudes are in the AB system.

2 Data analysis

2.1 Cluster membership and background sources

Multiband imaging for this cluster was obtained at CFHT, both in the inner parts made of two CFH12k camera pointings in BVRI bands resulting in about 0.54 deg2 coverage and with Megacam (1 $\times$ $1~{\rm deg}^2$ fov) in the u* band (see Adami et al. 2006,2008,2007, for a detailed description of these data).

We were able to estimate photometric redshifts of all sources down to $R \la 23$ in the area covered by the CFH12k images (Adami et al. 2008). This allowed us to separate the population of faint background sources from nearby objects with $z_{\rm phot}\le0.04$ and to eliminate the bulk of the cluster members that could bias the weak lensing study (e.g.  Medezinski et al. 2007). Adami et al. (2008) used the same technique to discriminate between z<0.2 and z>0.2 galaxies. Here, we push the limit to $z_{\rm phot}=0.04$ to increase the number of background sources although a more conservative cut at 0.2 would not produce noticeable changes given the small number of added objects.

This photometric redshift separation is possible only in the innermost 0.54 deg2. However we found that none of our results below could be significantly biased due to the extreme prevalence of distant sources in the faint end of the magnitude counts (a factor  ${\sim}10{-}20$) despite some incompleteness for $u^* \ga 24.5$. We thus apply a magnitude selection $23.5 \le u^*\le25$ everywhere in the field but we complement the selection by removing the few objects in the inner regions that are known to be at $z_{\rm phot}\le0.04$.

A clear advantage of lensing by nearby deflectors is that the geometric distance factor  $D_{\rm LS}/D_{\rm S}$ (e.g.  Bartelmann & Schneider 2001), which is the ratio of angular distances between deflector and source  $D_{\rm LS}$ and to the source $D_{\rm S}$, is almost constant and close to unity for most of the faint background sources. Given the low redshift of Coma, even a source at $z\sim0.2$ will experience lensing effects with $D_{\rm LS}/D_{\rm S}\simeq 0.87$. In order to check this small redshift dependance, we used the CFHTLS-deep photometric redshifts (Ilbert et al. 2006) measured in four independent 1 deg2 fields to infer the redshift distribution of sources having $23.5 \le u^*\le25$. The mean and median photometric redshifts are 0.87 and 0.92 respectively and the sample contains a negligible amount of low redshift (z<0.04) galaxies. We estimate the mean $\overline{w}=\langle D_{\rm LS}/D_{\rm S}\rangle$ averaged over the whole population of sources to be $\overline{w}\simeq 0.962$. This is the value we will consider below for further weak lensing mass calibrations.

2.2 Shear measurement

In Adami et al. (2009), we presented measurements of the systematic orientation of faint Coma cluster galaxies. The small size of these galaxies required a careful deconvolution of the Point Spread Function (PSF) smearing effect which was done with the same procedure we use here. It is based on the KSB technique (Kaiser et al. 1995) and the pipeline has been applied to ground-based imaging from CFH12k and Megacam cameras (e.g.  Gavazzi & Soucail 2007; Gavazzi et al. 2004). We used the u* channel to measure shapes because it is the one with largest spatial coverage, and also the most homogeneous since the images in the other bands are built from two adjacent pointings. The median u* band seeing FWHM is $1\hbox{$.\!\!^{\prime\prime}$ }02$. Despite this relatively poor value, we were able to successfully correct for PSF smearing.

The quality of PSF anisotropy corrections can be seen in the left panels of Fig. 1 in Adami et al. (2009). The good overall image quality is reflected in the raw and corrected ellipticities of stars. The low scatter in the corrected ellipticities, 0.0028 rms, is also a good assessment of the controled systematics.

Based on mock images designed to simulate Megacam data for the CFHTLS survey and kindly made available to us by Rowe, we were able to assess the reliability of our shear measurements, especially for the isotropic part of the PSF smearing effect. These simulations are similar to STEP2 simulations (Massey et al. 2007) as they capture the complex shape of sources by the use of shapelet models. Following notations of the STEP shear measurement project (Massey et al. 2007; Heymans et al. 2006), residual additive calibration errors are found to be $c\le 0.003$ and multiplicative $m \le 0.05$, which is significantly smaller than the statistical errors present in our data (see below).

 \begin{figure} \par\includegraphics[width=7cm,clip]{check_eieu.eps} \end{figure} Figure 1:

Corrected ellipticities of galaxies measured in Megacam-u* and CFH12k-I bands in the inner parts of the field. A close consistancy is found with $e_I= (1.009 \pm 0.026) e_{u^*}$ with a ${\sim }0.77$ correlation coefficient.
Open with DEXTER

Because redder bands are usually used for weak lensing studies, we checked that PSF-corrected ellipticities of central objects measured in both Megacam-u* and CFH12k-I bands are consistent. This is found to be the case with great accuracy as shown in Fig. 1. We checked that the ellipticity difference  eI -eu* (for both components 1 and 2 taken together or considered individually) does not correlate with either eu*, u* magnitude, I magnitude or rh,u* the u*-band half light radius.

 \begin{figure} \par\includegraphics[width=7.5cm,clip]{kappa+cmemb.eps}\par\includegraphics[width=7.5cm,clip]{light+cmemb+Xneumann.eps} \end{figure} Figure 2:

Top panel: convergence map for the Coma cluster. Green contours represent signal-to-noise ratios of $1,~2,\ldots5$, corresponding to $\kappa=0.01,~0.02,\ldots0.05$. Red crosses represent the bright cluster members lying on the red sequence. Bottom panel: gray-scale view of the luminosity distribution of cluster red sequence members with the overlaid contours in green. The blue dotted contours show the excess X-ray emission over a smooth $\beta $-model X-ray emissivity map (Neumann et al. 2003).
Open with DEXTER

2.3 Convergence map

From the source catalogue, we can infer the shear field  $\gamma(\vec{\theta})$ and deduce the associated convergence field  $\kappa(\vec{\theta})$ which is the projected surface mass density expressed in units of the critical density $\Sigma_{\rm crit}= c^2 (4\pi G)^{-1} D_{\rm S}/(D_{\rm L} D_{\rm LS})$. Here $D_{\rm S}/D_{\rm LS}$ is replaced by the source population average inverse  $1/\overline{w}$ which leads to a critical density $\Sigma_{\rm crit}=1.69$ $\times$  $10^{10}~h_{70}~{M}_{\odot}/{\rm kpc}^2$.

Shear and convergence are related by:

\begin{displaymath}% \kappa(\vec{\theta}) = \int_{\mathbb{R}^2} K(\vec{\theta}-\... ...theta})^* \gamma(\vec{\vartheta}) {\rm d}^2 \vec{\vartheta}, \end{displaymath} (1)

$K(\vec{\theta})=\frac{1}{\pi}\frac{-1}{(\theta_1-{\rm i} \theta_2)^2}$ is a complex convolution kernel (Kaiser & Squires 1993). The shear field is smoothed with a Gaussian $G(\theta)\propto\exp(-\frac{\theta^2}{2\theta_{\rm s}^2})$ with $\theta_{\rm s}=170\hbox{$^{\prime\prime}$ }\simeq80~h_{70}^{-1}~{\rm kpc}$. The convergence field is smoothed by the same filter. The convergence map presents correlated noise properties (van Waerbeke 2000) characterised by $n_{\rm bg}\simeq11~{\rm arcmin}^{-2}$, the number density of background sources. By bootstrapping the orientation of background sources, we estimated this noise level to be $\sigma_{\kappa}=0.0134$ with little variation over the field (except near edges and masked bright stars).

The top panel of Fig. 2 shows the reconstructed convergence map 1 $\times$ $1~{\rm deg}^2$ field of view with contours showing a  ${>}5\sigma$ significance central peak along with various substructures. The high physical resolution of ${\sim}80~h_{70}^{-1}~{\rm kpc}$ that is made possible by the vicinity of Coma somewhat balances the low associated lensing efficiency. The position of the brightest cluster galaxies with $r\le 14$ is shown as red crosses. For comparison we also show in the lower panel of Fig. 2 the luminosity-weighted r-band luminosity distribution coming from bright $r\le 19$ cluster members that lie on the Red Sequence defined by the relation $0.72 \le (g-r)+(r-14)*0.035 \le 0.87$. The convergence contours are overlaid. For this latter study we used the more extended SDSS DR7 photometry, which is better suited for investigation of the bright end of the luminosity function[*]. This panel also shows contours of X-ray emissivity in excess of a smooth $\beta $-model profile (Neumann et al. 2003).

3 Radial mass profile

We now investigate the azimuthally-averaged tangential shear profile  $\gamma_{\rm t}(R)$ which is simply related to the azimuthally-averaged projected surface mass density profile $\Sigma(R)$ by the relation

\begin{displaymath}% \Sigma_{\rm crit}\gamma_{\rm t}(R) \equiv \Delta \Sigma(R) = M(<R)/(\pi R^2) - \Sigma(R), \end{displaymath} (2)

where we have defined the frequently used rescaled shear  $\Delta \Sigma$ and M(<R) is the projected mass enclosed by radius R.

We measure the radial shear profile average in circular annuli centered on the peak of the convergence map ($\alpha$ = 12:59:39.007, $\delta$ = +27:57:55.93) which is only 40 $\hbox{$^{\prime\prime}$ }$ east of NGC 4874, i.e. in the direction of NGC 4889, which are respectively the brightest and second brightest member galaxies. Figure 3 shows the radial shear profile  $\gamma_{\rm t}(R)$ out to the edge of the Megacam field of view ($\sim$1 Mpc). The bottom panel of this figure shows the same profile once galaxies are rotated by 45$^\circ$, which is the curl or B-mode component of the ellipticity field. In the absence of systematic PSF correction residuals, this rotated shear profile should be consistent with zero at all scales. This is what we observe.

 \begin{figure} \par\includegraphics[height=6cm,width=8.5cm,clip]{c-prof.ps} \end{figure} Figure 3:

Top panel: radial shear profile measured in Coma as a function of projected distance. The best-fit NFW profile is overlaid. Bottom panel: B-mode shear profile showing the negligible residuals in the rotated shear component.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=9cm,clip]{c-errors.ps} \end{figure} Figure 4:

$M_{\rm 200c}$ and $c_{\rm 200c}$ parameters constraints of the NFW density profile. The M-c relation predicted by simulation and WMAP5 cosmology (with its $1\sigma $ scatter) are shown in red.
Open with DEXTER

We attempted to fit a radial shear profile as predicted by the NFW mass density profile of the form

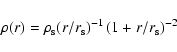\begin{displaymath}% \rho(r) = \rho_{\rm s} (r/r_{\rm s})^{-1} \left( 1 + r/r_{\rm s}\right)^{-2} \end{displaymath} (3)

coming from cosmological simulations (Navarro et al. 1997). The corresponding lensing quantities were derived by Bartelmann (1996). The two relevant quantities that we fit are the mass  $M_{\rm 200c}$ enclosed in the radius  $r_{\rm 200c}$ in which the mean density is 200 times the critical density  $\rho_{\rm crit}$ and the concentration parameter $c_{\rm 200c} = r_{\rm 200c}/r_{\rm s}$. This implies that $\rho_{\rm s}$ = $\rho_{\rm crit} \frac{200}{3} c^3 / \left[ \ln(1+c) - c/(1+c)\right]$. Figure 4 shows the constraints we obtain on these two parameters. Marginal distributions yield the following constraints[*]: $M_{\rm 200c}= 5.1^{+4.3}_{-2.1}$ $\times$  $10^{14}~h_{70}^{-1}{M}_{\odot}$ and $c_{\rm 200c}=5.0^{+3.2}_{-2.5}$, which corresponds to $r_{\rm 200c}=1.8^{+0.6}_{-0.3}~{\rm Mpc}$. Figure 4 also shows the mass-concentration relation and its $1\sigma $ dispersion that were recently reported by Macciò et al. (2008) assuming WMAP5 cosmological parameters (Komatsu et al. 2008). The two-dimensional contours are in good agreement with these predictions. Taking the conditional  $p(c_{\rm 200c}\vert M_{\rm 200c})$ from Macciò et al. (2008) as a prior on $c_{\rm 200c}$, we marginalize again over the poorly constrained concentration parameter and obtain constraints on the mass $M^\prime_{\rm 200c}= 9.7^{+6.1}_{-3.5}$ $\times$ $10^{14}~h_{70}^{-1}{M}_{\odot}$ or again $r_{\rm 200c}=2.2^{+0.3}_{-0.2}~{\rm Mpc}$.

In order to allow a comparison with other mass estimates in the literature, we calculate the virial mass $M_{\rm vir}\equiv M_{\rm 100c}$ and the corresponding concentration $c_{\rm vir}\equiv c_{\rm 100c}$, since a density contrast $\Delta_{\rm vir}\simeq100$ is better suited for the assumed cosmology. All our results regarding both $(M_{\rm 200c},c_{\rm 200c})$ and $(M_{\rm vir},c_{\rm vir})$ as well as corresponding $r_{\rm 200c}$ and $r_{\rm vir}$ values are given in Table 1.

Table 1:   Summary of mass estimates with and without priors on the mass-concentration relation (Macciò et al. 2008).

These results are in good agreement with mass estimates in the literature. Kubo et al. (2007) performed a weak lensing mass estimate of Coma based on the much shallower SDSS data - resulting in $n_{\rm bg}\simeq 1~{\rm arcmin}^{-2}$ - but extending out to ${\sim}14~h_{70}^{-1}~{\rm Mpc}$. They report a mass $M_{\rm 200c}= 2.7^{+3.6}_{-1.9}$ $\times$ $10^{15}~h_{70}^{-1}{M}_{\odot}$ and concentration index $c_{\rm 200c}=3.8^{+13.1}_{-1.8}$ that are statistically consistent with our estimates. In addition, an earlier X-ray study by Hughes (1989) gave $M_{\rm vir}=13$ $\pm$ 2 $\times$ $10^{14}~h_{70}^{-1}{M}_{\odot}$, and is consistent with our estimate. Mass measurements coming from galaxy kinematics are also in good agreement with our mass constraints (e.g.  Geller et al. 1999; The & White 1986; okas & Mamon 2003). Note however that these latter authors report a concentration parameter $c_{\rm vir}\simeq 9$, slightly larger that our best-fit value though statistically consistent.

4 Discussion and conclusion

We have performed a weak lensing analysis of the Coma cluster, based on a deep u* exposure and on images in other bands which allowed to derive photometric redshifts in order to remove as many foreground galaxies as possible from the background population. We thus obtain a map of the mass distribution in Coma, the radial shear profile, as well as the mass and concentration parameter.

The peak of the convergence map is nearly coincident with the X-ray center (Neumann et al. 2003) or the brightest galaxy NGC 4874. The difference is ${\sim}27~h_{70}^{-1}~{\rm kpc}$, below the spatial resolution of the convergence map. We can also notice the correspondence between the ($\alpha$ $\sim$ 194.4, $\delta$ $\sim$ 27.82) 2$\sigma$ detection and the G12/G14 groups of Adami et al. (2005) and between the ($\alpha$ $\sim$ 194.5, $\delta$ $\sim$ 28.03) 2$\sigma$ detection and the northern part of the westX-ray substructure (Neumann et al. 2003). Finally, the convergence map shows a 4$\sigma$ ($\alpha$ $\sim$ 195, $\delta$ $\sim$ 28) extension overlapping the position of NGC 4889, confirming the existence of a mass concentration around this galaxy. Other substructures visible in X-rays and in the optical (e.g. the NGC 4911 group) do not show up in the convergence map, indicating that we are dealing with low mass systems.

The south-west extension of the convergence map is more puzzling. It does not match the light distribution. The groups G8 and G9 from Adami et al. (2005) explain part of this extension, but are not luminous enough to fully account for this mass concentration. Another explanation would be massive low redshift structures (in order to still efficiently induce a weak lensing signal and to be spread largely enough over the sky) but that would not belong to Coma. The SDSS data used by Gott et al. (2005) exhibit such a $z \sim 0.08$ ``Great Wall'', probably not luminous enough though to explain the south west mass concentration. Moreover, the magnitude limit of the SDSS spectroscopy is not very deep, leaving room for other possible large scale structures not appearing in the SDSS sample. This will have to be confirmed by a more detailed knowledge of the immediate background of the Coma cluster (Adami et al., in preparation).

Acknowledgements
R.G. acknowledges Barnaby Rowe for providing mock realistic Megacam images for shear calibration assessments and T. Futamase and N. Okabe for interesting discussion about weak lensing in Coma. We are grateful to the CFHT and Terapix teams, and to the French CNRS/PNG for financial support. M.P.U. also acknowledges support from NASA Illinois space grant NGT5-40073 and from Northwestern University.

References

Footnotes

... cluster[*]
Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l'Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is also partly based on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.
... function[*]
http://cas.sdss.org/astro/en/tools/
... constraints[*]
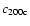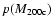
Assuming a flat uniform prior in $\log M_{\rm 200c}$ betwen 13 and 16 and on $c_{\rm 200c}$ between 0.01 and 20 to infer respectively the marginal PDFs p(c) and $p(M_{\rm 200c})$

All Tables

Table 1:   Summary of mass estimates with and without priors on the mass-concentration relation (Macciò et al. 2008).

All Figures

  \begin{figure} \par\includegraphics[width=7cm,clip]{check_eieu.eps} \end{figure} Figure 1:

Corrected ellipticities of galaxies measured in Megacam-u* and CFH12k-I bands in the inner parts of the field. A close consistancy is found with $e_I= (1.009 \pm 0.026) e_{u^*}$ with a ${\sim }0.77$ correlation coefficient.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{kappa+cmemb.eps}\par\includegraphics[width=7.5cm,clip]{light+cmemb+Xneumann.eps} \end{figure} Figure 2:

Top panel: convergence map for the Coma cluster. Green contours represent signal-to-noise ratios of $1,~2,\ldots5$, corresponding to $\kappa=0.01,~0.02,\ldots0.05$. Red crosses represent the bright cluster members lying on the red sequence. Bottom panel: gray-scale view of the luminosity distribution of cluster red sequence members with the overlaid contours in green. The blue dotted contours show the excess X-ray emission over a smooth $\beta $-model X-ray emissivity map (Neumann et al. 2003).
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[height=6cm,width=8.5cm,clip]{c-prof.ps} \end{figure} Figure 3:

Top panel: radial shear profile measured in Coma as a function of projected distance. The best-fit NFW profile is overlaid. Bottom panel: B-mode shear profile showing the negligible residuals in the rotated shear component.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{c-errors.ps} \end{figure} Figure 4:

$M_{\rm 200c}$ and $c_{\rm 200c}$ parameters constraints of the NFW density profile. The M-c relation predicted by simulation and WMAP5 cosmology (with its $1\sigma $ scatter) are shown in red.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.