| Issue |
A&A
Volume 498, Number 2, May I 2009
|
|
|---|---|---|
| Page(s) | 489 - 500 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200810703 | |
| Published online | 18 February 2009 | |
Spectroscopic binaries among Hipparcos M giants![[*]](/icons/foot_motif.gif)
III. The eccentricity - period diagram and mass-transfer signatures
A. Jorissen
- A. Frankowski![]() - B. Famaey
- B. Famaey![]() - S. Van Eck
- S. Van Eck![]()
Institut d'Astronomie et d'Astrophysique, Université Libre de Bruxelles, CP. 226, Boulevard du Triomphe, 1050 Bruxelles, Belgium
Received 29 July 2008 / Accepted 20 December 2008
Abstract
Context. This paper is the third one in a series devoted to studying the properties of binaries involving M giants.
Aims. We use a new set of orbits to construct the first
![]() diagram of an extensive sample of M giant binaries, to obtain their mass-function distribution, and to derive evolutionary constraints for this class of binaries and related systems.
diagram of an extensive sample of M giant binaries, to obtain their mass-function distribution, and to derive evolutionary constraints for this class of binaries and related systems.
Methods. The orbital properties of binaries involving M giants were analysed and compared with those of related families of binaries (K giants, post-AGB stars, barium stars, Tc-poor S stars).
Results. The orbital elements of post-AGB stars and M giants are not very different, which may indicate that, for the considered sample of post-AGB binaries, the post-AGB star left the AGB at quite an early stage (M4 or so). Neither are the orbital elements of post-mass-transfer binaries like barium stars very different from those of M giants, suggesting that the mass transfer did not alter the orbital elements much, contrary to current belief. Finally, we show that binary systems with
![]() (with periods expressed in days) are predominantly post-mass-transfer systems, because (i) the vast majority of barium and S systems match this condition; and (ii) these systems have companion masses peaking around 0.6
(with periods expressed in days) are predominantly post-mass-transfer systems, because (i) the vast majority of barium and S systems match this condition; and (ii) these systems have companion masses peaking around 0.6 ![]() ,
as expected for white dwarfs. The latter property has been shown to hold as well for open-cluster binaries involving K giants, for which a lower bound on the companion mass may easily be set.
,
as expected for white dwarfs. The latter property has been shown to hold as well for open-cluster binaries involving K giants, for which a lower bound on the companion mass may easily be set.
Key words: stars: binaries: spectroscopic - stars: AGB and post-AGB - stars: late-type - stars: binaries: symbiotic
1 Introduction
This paper is the third in our series discussing the
spectroscopic-binary content of a sample of M giants drawn from the
Hipparcos Catalogue (ESA 1997), for which CORAVEL radial velocities
have been obtained in a systematic way (Famaey et al. 2005; Udry et al. 1997).
The availability of an extensive set of orbital
elements for M giants, assembled in Paper I (Famaey et al. 2009),
allows us to address here evolutionary issues through the study
of the eccentricity - period diagram (denoted
![]() in the following).
in the following).
The comparison in Sect. 2 of such
![]() diagrams for K and M giants will reveal the
operation of tidal effects, whereas a comparison of the diagrams of
pre-mass-transfer systems with post-mass-transfer
systems (like post-AGB stars in Sect. 2.2 and barium stars in Sect. 2.3)
will illustrate the impact of the mass-transfer process on the orbital elements.
diagrams for K and M giants will reveal the
operation of tidal effects, whereas a comparison of the diagrams of
pre-mass-transfer systems with post-mass-transfer
systems (like post-AGB stars in Sect. 2.2 and barium stars in Sect. 2.3)
will illustrate the impact of the mass-transfer process on the orbital elements.
Finally, we will show that the impact of mass transfer on orbital elements is
also readily apparent when considering how mass functions distribute across the
![]() diagram
(Sect. 3). This paper presents for the first time compelling evidence
that the lower-right corner
of the
diagram
(Sect. 3). This paper presents for the first time compelling evidence
that the lower-right corner
of the
![]() diagram contains mostly post-mass-transfer objects
with presumably white-dwarf companions. This demonstration is based on
the analysis of the mass functions from K giants in open clusters (Mermilliod et al. 2007).
diagram contains mostly post-mass-transfer objects
with presumably white-dwarf companions. This demonstration is based on
the analysis of the mass functions from K giants in open clusters (Mermilliod et al. 2007).
2 The (e - log P) diagram of M giants: insights into binary evolution
![\begin{figure}
\par\includegraphics[width=9cm]{10703f1.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg15.gif) |
Figure 1:
The
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{10703f2.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg16.gif) |
Figure 2:
Same as Fig. 1 in sequential order, with the
addition of field K giants from the Ninth Catalogue of Spectroscopic
Binary Orbits (Pourbaix et al. 2004), from which the systems with
sdO/sdB or white dwarf companions (like barium stars) have been
removed (since they are plotted in the bottom panel).
For the sake of clarity, all panels start at a period of 30 d,
although field K giants may be found in binary systems with periods
as short as 4 d (see Fig. 6 of Paper II, Frankowski et al. 2009).
The lines and symbols are as in
Fig. 1 except for the the S and Ba star panel
where the
crosses denote S stars with an unexpectedly large mass function
(HD 191 589 and HDE 332 077), open triangles denote mild Barium stars,
and filled triangles strong barium stars and Tc-poor S stars.
Mild and strong barium
stars are separated according to the photometric DDO index
|
| Open with DEXTER | |
The
![]() diagram offers good diagnostics about physical
processes at work in binary systems.
The
diagram offers good diagnostics about physical
processes at work in binary systems.
The
![]() diagram of M giants, constructed from the new and
literature orbital data collected in
Table 8 of Paper I
diagram of M giants, constructed from the new and
literature orbital data collected in
Table 8 of Paper I![]() , is presented in
Fig. 1. Important clues can be obtained
about the evolution of binaries when comparing the location of M
giants in this diagram with that of other classes of binary stars, namely
K giants in open clusters (Mermilliod et al. 2007) or in the
field
, is presented in
Fig. 1. Important clues can be obtained
about the evolution of binaries when comparing the location of M
giants in this diagram with that of other classes of binary stars, namely
K giants in open clusters (Mermilliod et al. 2007) or in the
field![]() (from the Ninth Catalogue of Spectroscopic Binary Orbits; Pourbaix et al. 2004), barium and
(Tc-poor) S stars
(Jorissen et al. 1998), symbiotic stars with
M-giant primaries (Belczynski et al. 2000; Fekel et al. 2007; Mikoajewska 2003) and
post-AGB stars (Van Winckel 2007).
For the sake of clarity, these different stellar classes are presented
again in separate panels in Fig. 2.
In that figure, mild and strong barium stars are separated
according to the DDO index (Lü 1991)
(from the Ninth Catalogue of Spectroscopic Binary Orbits; Pourbaix et al. 2004), barium and
(Tc-poor) S stars
(Jorissen et al. 1998), symbiotic stars with
M-giant primaries (Belczynski et al. 2000; Fekel et al. 2007; Mikoajewska 2003) and
post-AGB stars (Van Winckel 2007).
For the sake of clarity, these different stellar classes are presented
again in separate panels in Fig. 2.
In that figure, mild and strong barium stars are separated
according to the DDO index (Lü 1991)
![]() being respectively
being respectively
![]() -0.11 or >-0.11 (see Jorissen & Boffin 1992, and the Appendix
of Jorissen et al. 1998).
If the DDO indices C(38-41) and C(42-45) needed to construct the
-0.11 or >-0.11 (see Jorissen & Boffin 1992, and the Appendix
of Jorissen et al. 1998).
If the DDO indices C(38-41) and C(42-45) needed to construct the
![]() index are not available, the Warner
Ba index has been used instead (respectively Ba
index are not available, the Warner
Ba index has been used instead (respectively Ba ![]() or Ba
or Ba ![]() for mild and strong barium stars).
for mild and strong barium stars).
The various classes of binary stars presented in Figs. 1 and 2 are very likely linked through what may be called the mass transfer scenario (McClure 1983): the evolution followed by a system consisting initially of two low- or intermediate-mass main-sequence stars will go through the various phases listed above, along the sequence illustrated in Fig. 3. At point 5 in this evolution, part of the mass lost by the asymptotic giant branch (AGB) component will be accreted by the companion, thus increasing the abundances of those elements produced by the AGB nucleosynthesis, most notably C, F and s-process elements. Note that red symbiotics apparently do not exhibit such enhancements and their exact status in this sequence is still debated (see Jorissen 2003a; Frankowski & Jorissen 2007; Jorissen & Van Eck 2005, for recent reviews).
In some systems (most probably the closest), the binary evolution may branch to an Algol configuration at phases 2, 3 or 4 on Fig. 3. This branching is not discussed here (see instead Fig. 10 of Jorissen & Mayor 1992; Eggleton 2006). In yet other systems, phase 5 of Fig. 3 may give rise to a common envelope, and those systems then end their evolution as cataclysmic variables or even coalesce. This situation is thought to occur for systems where a component with a deep convective envelope fills its Roche lobe (Eggleton 2006; Pastetter & Ritter 1989). This is supposed to have occurred in some barium systems, and yet these systems did not end up as cataclysmic variables. Why barium and Tc-poor S stars did escape this dramatic fate has remained unclear so far (but see Frankowski & Jorissen 2007).
![\begin{figure}
\par\includegraphics[width=9cm]{10703f3.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg21.gif) |
Figure 3: One among the various possible evolution channels for a system consisting initially of two low- or intermediate-mass main-sequence stars. The left column corresponds to the normal evolutionary sequence of single stars, while the right column represents the various classes of stars with chemical peculiarities specifically produced by mass transfer across the binary system. Hatched circles denote stars with atmospheres enriched in carbon or heavy elements (see Jorissen 2003a, for a detailed description of the various stellar families involved). Other evolutionary channels would end with a cataclysmic variable or go through an Algol phase, and are not depicted here (see, e.g., Nelson & Eggleton 2001; Eggleton 2006, for details). |
| Open with DEXTER | |
As binary stars evolve along the sequence displayed in Fig. 3, their orbital elements are expected to vary, be it due to tidal effects, to interaction with a circumbinary disc, or to mass loss or mass transfer (through wind accretion or Roche Lobe overflow - RLOF; see Eggleton 2006; Frankowski & Jorissen 2007, for recent discussions). Therefore, the comparison of orbital elements for binary stars located at different stages in the sequence is expected to shed light on the various physical processes that have occurred along their evolution. The availability of the extensive set of orbital elements for M giants obtained in the present study brings an important element to this comparison.
2.1 Smooth evolution KIII - MIII - Ba/S
Figures 1 and 2 reveal a smooth
evolution along the sequence KIII - MIII - Ba/S, in
the sense that the upper boundary of the populated region in the
![]() diagram
moves towards longer periods (this is reflected by the three curved
lines which roughly delineate the regions populated by these three
classes, their exact definition being given below).
This is clearly a consequence of the larger radii
reached by stars evolving along this sequence. In the case of Ba and
Tc-poor S giants,
it is actually their white dwarf (WD) companions which reached very large radii
while evolving on the AGB. For K giants, the situation is
in principle somewhat more complex, since this class mixes stars on the first
giant branch and stars in the core He-burning phase. Low-mass stars belonging to the latter category have gone through the RGB tip, where they reached a very large radius (similar to, or even larger than that of M giants).
Therefore, if those low-mass, core-He burning stars were to dominate among K giants, their distribution in the
diagram
moves towards longer periods (this is reflected by the three curved
lines which roughly delineate the regions populated by these three
classes, their exact definition being given below).
This is clearly a consequence of the larger radii
reached by stars evolving along this sequence. In the case of Ba and
Tc-poor S giants,
it is actually their white dwarf (WD) companions which reached very large radii
while evolving on the AGB. For K giants, the situation is
in principle somewhat more complex, since this class mixes stars on the first
giant branch and stars in the core He-burning phase. Low-mass stars belonging to the latter category have gone through the RGB tip, where they reached a very large radius (similar to, or even larger than that of M giants).
Therefore, if those low-mass, core-He burning stars were to dominate among K giants, their distribution in the
![]() diagram should be characterised by an envelope located at even longer periods than that for M giants. Figure 2 shows that this is not the case, because the sample of open-cluster K giants plotted in Fig. 2 is in fact dominated by intermediate-mass stars, as may be judged from the turnoff masses of the corresponding clusters, most of them being larger than 2
diagram should be characterised by an envelope located at even longer periods than that for M giants. Figure 2 shows that this is not the case, because the sample of open-cluster K giants plotted in Fig. 2 is in fact dominated by intermediate-mass stars, as may be judged from the turnoff masses of the corresponding clusters, most of them being larger than 2 ![]() (Mermilliod et al. 2007). The complication introduced by the mixture of evolutionary states among K giants
is thus not a concern.
(Mermilliod et al. 2007). The complication introduced by the mixture of evolutionary states among K giants
is thus not a concern.
Equating the stellar radius to the
Roche radius results in a threshold period (for given component
masses) below which the primary star
undergoes RLOF. Adopting Paczynski's usual expression
for the Roche radius RR,1 around star 1
where q = M1/M2 and A is the orbital separation, one finds that a star of radius 40
It may seem surprising that the ``periastron envelope''
[A(1-e) = constant, or
P2/3(1-e) = constant] represents a better fit
to the data than the ``circularisation envelope'' [A(1-e2) = constant,
or
P2/3(1-e2) = constant; see Fig. 6 of Paper II],
resulting from the fact that circularisation keeps the angular
momentum per unit reduced mass constant
(Zahn 1977; Hut 1981; Duquennoy et al. 1992). Indeed, as the star gets
closer to its Roche lobe, it should circularise first and then fill
its Roche lobe, and possibly disappear from the sample due to
cataclysmic mass transfer. The samples of K-giant binaries clearly
favour the periastron envelope over the circularisation envelope.
The reason for this may be the following. When a system is close to
filling its Roche lobe at periastron, circularisation proceeds
fast at this moment. But since the circularisation path in
the
![]() diagram is steeper than the periastron line (see Fig. 6 of Paper II),
circularisation drags the system away from Roche lobe filling at periastron
and thus also slows down its own rate.
Circularisation can accelerate only when other effects bring the star
and its Roche lobe closer again. Therefore an ensemble of binaries traces
on their e -
diagram is steeper than the periastron line (see Fig. 6 of Paper II),
circularisation drags the system away from Roche lobe filling at periastron
and thus also slows down its own rate.
Circularisation can accelerate only when other effects bring the star
and its Roche lobe closer again. Therefore an ensemble of binaries traces
on their e - ![]() diagram the current periastron envelope rather
than any circularisation path (see also Paper II, Sect. 2.5).
diagram the current periastron envelope rather
than any circularisation path (see also Paper II, Sect. 2.5).
The role played by periastron RLOF in shaping the
![]() diagram is nicely
illustrated by the M4III star HD 41 511 (=SS Lep). With P = 260.3 d and e
= 0.02 (Welty & Wade 1995), it is the fourth shortest orbital period among the
spectroscopic systems involving an M giant. Verhoelst et al. (2007)
provided convincing evidence that the M giant, having a radius of
diagram is nicely
illustrated by the M4III star HD 41 511 (=SS Lep). With P = 260.3 d and e
= 0.02 (Welty & Wade 1995), it is the fourth shortest orbital period among the
spectroscopic systems involving an M giant. Verhoelst et al. (2007)
provided convincing evidence that the M giant, having a radius of
![]()
![]() derived from interferometric measurements and from the
Hipparcos parallax (Table 1), fills its Roche lobe.
This is consistent with the Roche limit set at 125
derived from interferometric measurements and from the
Hipparcos parallax (Table 1), fills its Roche lobe.
This is consistent with the Roche limit set at 125 ![]() in Figs. 1 and 2.
As a further evidence to
this claim, these authors show that the A-type companion appears to be
a main-sequence star, which has swollen as a result of accretion from the
lobe-filling M giant. Indeed, its radius is ten times that of a
typical A1V star, but its mass, derived from the surface gravity and
radius, is not that of a massive supergiant. Finally, the system is
surrounded by a circumbinary disc (Verhoelst et al. 2007; Jura et al. 2001),
probably fed by the RLOF, which
thus appears to be non conservative.
The A star is rapidly rotating (
in Figs. 1 and 2.
As a further evidence to
this claim, these authors show that the A-type companion appears to be
a main-sequence star, which has swollen as a result of accretion from the
lobe-filling M giant. Indeed, its radius is ten times that of a
typical A1V star, but its mass, derived from the surface gravity and
radius, is not that of a massive supergiant. Finally, the system is
surrounded by a circumbinary disc (Verhoelst et al. 2007; Jura et al. 2001),
probably fed by the RLOF, which
thus appears to be non conservative.
The A star is rapidly rotating (
![]() km s-1; Royer et al. 2002), possibly as a result of spin accretion or, alternatively,
as the primordial rotation speed of the main sequence star. All these features are very suggestive of a scenario outlined by
Frankowski & Jorissen (2007) for an evolving M giant binary.
km s-1; Royer et al. 2002), possibly as a result of spin accretion or, alternatively,
as the primordial rotation speed of the main sequence star. All these features are very suggestive of a scenario outlined by
Frankowski & Jorissen (2007) for an evolving M giant binary.
For M giants with radii somewhat smaller than that of SS Lep, but
still representing a fair fraction of the Roche radius, tidal effects
will take place, and the star will then be seen as an ellipsoidal
variable. The M2.5III star
HD 190 658 (V1472 Aql) is such a case (Samus 1997). It has the second shortest orbital period among M giants (P = 199 d, e = 0.05; Lucke & Mayor 1982).
A rotational velocity of
![]() km s-1 is found from the CORAVEL cross-correlation dip width calibrated by Benz & Mayor (1981).
Assuming that the giant star rotates in synchronism with the orbital
motion, a radius of 59
km s-1 is found from the CORAVEL cross-correlation dip width calibrated by Benz & Mayor (1981).
Assuming that the giant star rotates in synchronism with the orbital
motion, a radius of 59 ![]() /
/![]() is derived, corresponding to
R/A1 = 1.16, where A1 is the semi-major axis of the giant's
orbit around the centre of mass of the system
(Lucke & Mayor 1982). Adopting typical masses of 1.7
is derived, corresponding to
R/A1 = 1.16, where A1 is the semi-major axis of the giant's
orbit around the centre of mass of the system
(Lucke & Mayor 1982). Adopting typical masses of 1.7 ![]() for
the giant and 1.0
for
the giant and 1.0 ![]() for the companion, one obtains
R/A = 0.43and R/RR = 1 !
for the companion, one obtains
R/A = 0.43and R/RR = 1 !
Table 1:
Radii of M giants in binary systems derived from the Stefan-Boltzmann
law (
![]() )
and from high-angular resolution measurements (
)
and from high-angular resolution measurements (
![]() ).
The labels
``UD'' and ``LD'' refer to uniform discs or limb-darkened discs, respectively.
Luminosities are derived from the
Hipparcos parallaxes
).
The labels
``UD'' and ``LD'' refer to uniform discs or limb-darkened discs, respectively.
Luminosities are derived from the
Hipparcos parallaxes ![]() ,
from the 2MASS K magnitudes and bolometric corrections
BCK derived from the (V-K , BCK) analytical relation from
Bessell & Wood (1984), which is in good agreement with
the more recent calibration of Bessell et al. (1998). The Johnson VJmagnitude from the Hipparcos catalogue has been used. Effective
temperatures are derived from the VJ-K indices using the ``bcd'' calibration of Bessell et al. (1998).
,
from the 2MASS K magnitudes and bolometric corrections
BCK derived from the (V-K , BCK) analytical relation from
Bessell & Wood (1984), which is in good agreement with
the more recent calibration of Bessell et al. (1998). The Johnson VJmagnitude from the Hipparcos catalogue has been used. Effective
temperatures are derived from the VJ-K indices using the ``bcd'' calibration of Bessell et al. (1998).
Interestingly, the Ba/S star HD 121 447 (with an
effective temperature equivalent to that of a M0III giant) is another
example: with P = 185.7 d and e = 0, it falls just besides
HD 190 658 in the
![]() diagram and seems to be an ellipsoidal variable
as well (Jorissen et al. 1995), although that interpretation has been
challenged by Adelman (2007), based on the presence of chromatic
variations.
diagram and seems to be an ellipsoidal variable
as well (Jorissen et al. 1995), although that interpretation has been
challenged by Adelman (2007), based on the presence of chromatic
variations.
HD 9053 (=![]() Phe), with P= 193.8 d and e = 0, has the shortest period among M-giant binaries.
Jancart et al. (2005) used the spectroscopic elements and the Hipparcos data to derive a combined orbit yielding a precise inclination
Phe), with P= 193.8 d and e = 0, has the shortest period among M-giant binaries.
Jancart et al. (2005) used the spectroscopic elements and the Hipparcos data to derive a combined orbit yielding a precise inclination
![]() .
The system cannot therefore be eclipsing, so that the eclipsing-like light curve reported by Otero (2007) should in fact be re-interpreted in terms of ellipsoidal variations, a possibility mentioned by Otero (2007). The angular radius measured by Richichi & Percheron (2005) is
.
The system cannot therefore be eclipsing, so that the eclipsing-like light curve reported by Otero (2007) should in fact be re-interpreted in terms of ellipsoidal variations, a possibility mentioned by Otero (2007). The angular radius measured by Richichi & Percheron (2005) is
![]() mas, yielding 50
mas, yielding 50 ![]() when combined with the Hipparcos parallax of
when combined with the Hipparcos parallax of
![]() mas, to be compared with a Roche radius of 78
mas, to be compared with a Roche radius of 78 ![]() (adopting masses of 1.3 and 0.6
(adopting masses of 1.3 and 0.6 ![]() for the giant and its companion, respectively). The giant should therefore be well within its Roche lobe. Nevertheless, HD 9053 is a
``hybrid star'' (Ayres 2005): despite being
located to the right of the ``dividing line'' between hot coronae and massive winds (Reimers et al. 1996; Hünsch & Schroeder 1996), the star exhibits signatures of hot gas, like X-ray flux and C IV line. One may wonder whether these could be signatures of matter being accreted by the companion in this close binary system. Also note that arguments were presented in Sect. 2.5 of Paper II that the usual expressions for the Roche radius (e.g., Eggleton 1983) may actually overstimate it when an extra-force (like radiation pressure) is present in the system (see also Dermine et al. 2009).
for the giant and its companion, respectively). The giant should therefore be well within its Roche lobe. Nevertheless, HD 9053 is a
``hybrid star'' (Ayres 2005): despite being
located to the right of the ``dividing line'' between hot coronae and massive winds (Reimers et al. 1996; Hünsch & Schroeder 1996), the star exhibits signatures of hot gas, like X-ray flux and C IV line. One may wonder whether these could be signatures of matter being accreted by the companion in this close binary system. Also note that arguments were presented in Sect. 2.5 of Paper II that the usual expressions for the Roche radius (e.g., Eggleton 1983) may actually overstimate it when an extra-force (like radiation pressure) is present in the system (see also Dermine et al. 2009).
We will come back to the
relationship between ellipsoidal variables and the periastron envelope
observed in the
![]() diagram when we will show in
Sect. 2.4 that the so-called long secondary periods (also
called sequence D) in the
diagram when we will show in
Sect. 2.4 that the so-called long secondary periods (also
called sequence D) in the
![]() diagram of long-period variables (LPVs) in the Large
Magellanic Cloud (Wood 2000; Wood et al. 1999) may be identified with the
periastron envelope in the
diagram of long-period variables (LPVs) in the Large
Magellanic Cloud (Wood 2000; Wood et al. 1999) may be identified with the
periastron envelope in the
![]() diagram of galactic M giants
(see also Soszynski 2007).
diagram of galactic M giants
(see also Soszynski 2007).
No similar evidence for RLOF or ellipsoidal variations has been found for the other two short-period M giants (HD 89 758 and HD 147 395).
The periastron-distance envelope seen in the
![]() diagram
(Fig. 2) is also apparent in the radius -
orbital-period diagram (Fig. 4).
The radii plotted in Fig. 4 are derived from the
Stefan-Boltzmann law and
are in very good agreement with those derived by combining the
uniform-disc diameters listed in the ``updated Catalogue of High
Angular Resolution Measurements'' (CHARM2; Richichi et al. 2005) and the
Hipparcos parallaxes (Table 1).
Figure 4 shows that, for a given value of the
radius, there is a lower bound on the orbital
period
diagram
(Fig. 2) is also apparent in the radius -
orbital-period diagram (Fig. 4).
The radii plotted in Fig. 4 are derived from the
Stefan-Boltzmann law and
are in very good agreement with those derived by combining the
uniform-disc diameters listed in the ``updated Catalogue of High
Angular Resolution Measurements'' (CHARM2; Richichi et al. 2005) and the
Hipparcos parallaxes (Table 1).
Figure 4 shows that, for a given value of the
radius, there is a lower bound on the orbital
period![]() , simply because stars with large
radii cannot reside in too close systems, or they would undergo RLOF
and would disappear from the sample by transforming into
cataclysmic variables.
The lines in Fig. 4 correspond to the limit imposed by equating
the stellar radius to the Roche
radius (Eq. (1), adopting M1 = 1.3
, simply because stars with large
radii cannot reside in too close systems, or they would undergo RLOF
and would disappear from the sample by transforming into
cataclysmic variables.
The lines in Fig. 4 correspond to the limit imposed by equating
the stellar radius to the Roche
radius (Eq. (1), adopting M1 = 1.3 ![]() and M2 =
0.6
and M2 =
0.6 ![]() ,
or M1 = 1.0
,
or M1 = 1.0 ![]() and M2 =
0.6
and M2 =
0.6 ![]() ),
the stellar radius being computed using
the Stefan-Boltzmann relation as explained before.
),
the stellar radius being computed using
the Stefan-Boltzmann relation as explained before.
![\begin{figure}
\par\includegraphics[width=9cm]{10703f4.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg50.gif) |
Figure 4: The orbital-period - radius diagram for M giants in binary systems. The radii are derived from the Stefan-Boltzmann law applied on the effective temperatures and luminosities presented in Fig. 5. The solid lines display the Roche radii for the corresponding period, for two different choices of the component masses. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm]{10703f5.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg51.gif) |
Figure 5:
Comparison of the location of M giants in binary systems (open circles) and Tc-rich S stars (filled triangles) in the HR diagram. The filled circle
corresponds to the M giant HD 165 374 which possibly hosts a WD companion. Star symbols correspond to Tc-poor S stars and crosses to S
stars with Tc doubtful. The data for S stars are from Van Eck et al. (1998). For M stars, they are derived as explained in the caption of Table 1. The evolutionary tracks are from
Charbonnel et al. (1996) for Z=0.02 stars with masses 1.25 and 1.5 |
| Open with DEXTER | |
Finally, it is noteworthy that the solid line in
Figs. 1 and 2 does not match
well the upper boundary of the region occupied by barium and Tc-poor S stars,
thus suggesting that for these classes of post-mass-transfer binaries,
tidal processes and periastron mass-transfer were, as expected, not the only ones to operate.
Mass transfer and interaction with a circumbinary disc must have
played a role for these (Frankowski & Jorissen 2007). One mild barium star
(HD 77 247: P = 80.5 d; e = 0.09) deviates markedly from the rest of the sample of
barium stars. One may
wonder whether the location of HD 77 247 in the
![]() diagram
along the periastron envelope of K giants is just accidental, or whether it
indicates instead that this system might not be a post-mass-transfer
system after all, as are the other barium stars, but that its barium anomaly may
rather be inherited from the gas out of which it formed, and be unrelated to its binary nature. HD 77 247 would thus join the small number of (mostly dwarf) barium stars with no evidence for being binaries (see the review by Jorissen 2003a, and individual cases discussed by Tomkin et al. 1989; Edvardsson et al. 1993; North et al. 1992, 2000).
diagram
along the periastron envelope of K giants is just accidental, or whether it
indicates instead that this system might not be a post-mass-transfer
system after all, as are the other barium stars, but that its barium anomaly may
rather be inherited from the gas out of which it formed, and be unrelated to its binary nature. HD 77 247 would thus join the small number of (mostly dwarf) barium stars with no evidence for being binaries (see the review by Jorissen 2003a, and individual cases discussed by Tomkin et al. 1989; Edvardsson et al. 1993; North et al. 1992, 2000).
2.2 Relation with post-AGB stars
Binary post-AGB stars (Van Winckel 2007,2003) are the immediate
descendants of the binary M giants (Fig. 3), and indeed
they share almost exactly the same location in the
![]() diagram.
diagram.
The M4III + A system SS Lep already mentioned in Sect. 2.1 is very interesting in this respect, since it shares with post-AGB stars the presence of a circumbinary disc and its position in a group of binaries with the shortest orbital periods among both families. It may thus be considered as a system linking binary M giants and post-AGB systems in the sense that the M-giant component in SS Lep should shortly evolve into a post-AGB star.
On the contrary, one may wonder whether some among the post-AGB stars from panel 4 in Fig. 2 with circular orbits and
![]() d like SS Lep (these are HD 101 584, HD 213 985 and
IRAS 05208-2035, although in the case of HD 101 584, the eccentricity is not well constrained) would not be genuine post-AGB stars, but rather be
accreting main-sequence or white-dwarf stars which have swollen to
giant dimensions in RLOF systems (as expected when the accreting
main-sequence star has a
radiative envelope: Jorissen 2003a; Kippenhahn & Meyer-Hofmeister 1977, or when the WD accretion rate is large enough to
trigger shell H-burning: Paczynski & Rudak 1980; Iben &
Tutukov 1996). The post-AGB stars in those systems would thus be the analogs of the A-type companion of SS Lep.
d like SS Lep (these are HD 101 584, HD 213 985 and
IRAS 05208-2035, although in the case of HD 101 584, the eccentricity is not well constrained) would not be genuine post-AGB stars, but rather be
accreting main-sequence or white-dwarf stars which have swollen to
giant dimensions in RLOF systems (as expected when the accreting
main-sequence star has a
radiative envelope: Jorissen 2003a; Kippenhahn & Meyer-Hofmeister 1977, or when the WD accretion rate is large enough to
trigger shell H-burning: Paczynski & Rudak 1980; Iben &
Tutukov 1996). The post-AGB stars in those systems would thus be the analogs of the A-type companion of SS Lep.
The spectrum of HD 101 584 is very complex, combining emission lines with P-Cygni profiles indicative of ongoing mass loss and absorption lines. The remarkable characteristic of the optical spectrum of
HD 101 584 is the fact that different spectral regions resemble different spectral types. There is therefore no agreement about the effective temperature of the central star, with proposed values ranging from 8500 K (Sivarani et al. 1999) to 12000 K (Bakker et al. 1996), or
![]() K for the post-AGB star and about 11000 K for its companion (Kipper 2005). There is thus no clear evidence from recent works for the companion of the post-AGB star HD 101 584 to be an M giant, despite the early suggestion by Humphreys (1976).
K for the post-AGB star and about 11000 K for its companion (Kipper 2005). There is thus no clear evidence from recent works for the companion of the post-AGB star HD 101 584 to be an M giant, despite the early suggestion by Humphreys (1976).
In the spectral energy distributions presented by de Ruyter et al. (2006) for HD 213 985 and
IRAS 05208-2035, neither is there evidence for the presence of a cool giant
companion, as it was the case for SS Lep
(Verhoelst et al. 2007).
Nevertheless, if the luminosity ratio between the
post-AGB and the giant components is of the order 5 to 10![]() , one may wonder whether the cool giant could at all be
noticed (fitting the complex spectral energy distributions of post-AGB systems is a delicate operation involving many free parameters -like the reddening- with no unique solution; Van Winckel, priv. comm.).
For the SS Lep system, the luminosity ratio is 1.6 in favour of the A component (Verhoelst et al. 2007).
HD 172 481 is another example of a F2Ia
supergiant traditionally considered to be a post-AGB star, but which
is more likely a white dwarf burning hydrogen accreted from its AGB
companion (Whitelock & Marang 2001).
For that system, the presence of
an M giant companion is apparent from the detection of TiO bands, from the
SB2 nature of the CORAVEL cross-correlation dip (Reyniers & Van Winckel 2001),
and from Mira-type
pulsations with a period of 312 d. From the SED, the
luminosity ratio turns out to be similar to SS Lep:
, one may wonder whether the cool giant could at all be
noticed (fitting the complex spectral energy distributions of post-AGB systems is a delicate operation involving many free parameters -like the reddening- with no unique solution; Van Winckel, priv. comm.).
For the SS Lep system, the luminosity ratio is 1.6 in favour of the A component (Verhoelst et al. 2007).
HD 172 481 is another example of a F2Ia
supergiant traditionally considered to be a post-AGB star, but which
is more likely a white dwarf burning hydrogen accreted from its AGB
companion (Whitelock & Marang 2001).
For that system, the presence of
an M giant companion is apparent from the detection of TiO bands, from the
SB2 nature of the CORAVEL cross-correlation dip (Reyniers & Van Winckel 2001),
and from Mira-type
pulsations with a period of 312 d. From the SED, the
luminosity ratio turns out to be similar to SS Lep:
![]() (although that ratio is somewhat dependent upon the adopted
reddening). No radial-velocity
variations hinting at a period of a few hundred days have been
detected for HD 172 481 (Reyniers & Van Winckel 2001).
(although that ratio is somewhat dependent upon the adopted
reddening). No radial-velocity
variations hinting at a period of a few hundred days have been
detected for HD 172 481 (Reyniers & Van Winckel 2001).
The papers mentioned above suggest different types of accreting components in SS Lep and HD 172 481 but, in the absence of stringent constraints on the mass and luminosity of the accreting star, there is in fact no easy way to distinguish between WD and main-sequence accretors.
In summary, we conclude that some systems currently flagged as hosting a post-AGB star could in fact be better described as systems where an M giant dumps matter on its white-dwarf or main-sequence companion which then acquires supergiant dimensions, thus mimicking a post-AGB star. Such systems, currently plotted in panel 3 of Fig. 2 (post-AGB systems), do in fact belong to panel 2 (M giants), were it not for the light of the M giant being lost in the glow of its supergiant-like companion. In this scenario, one might however worry whether the accreting component could indeed become more luminous than the moss-losing giant.
Another possible scenario to account for systems like HD 172 481 could therefore be as follows, now stating instead that the post-AGB star is genuine, but its giant companion is fake. In a system with components of initial masses
(M1,M2) = (3,1) ![]() ,
the star of mass M1 > M2 evolves faster, fills its Roche lobe on the AGB around the first thermal pulse and becomes a white dwarf (WD) with a mass of 0.55
,
the star of mass M1 > M2 evolves faster, fills its Roche lobe on the AGB around the first thermal pulse and becomes a white dwarf (WD) with a mass of 0.55 ![]() (Blöcker 1995). It is not exactly clear what happens to the orbit,
although Frankowski & Jorissen (2007) presented arguments for the orbital period remaining
more or less unchanged (see also the discussion in Sect. 2.3). Then the star of mass M2 (which could by now have reached 2-3
(Blöcker 1995). It is not exactly clear what happens to the orbit,
although Frankowski & Jorissen (2007) presented arguments for the orbital period remaining
more or less unchanged (see also the discussion in Sect. 2.3). Then the star of mass M2 (which could by now have reached 2-3 ![]() as a result of accretion)
evolves in turn along the AGB, but having a lighter companion it can grow bigger and brighter
without filling its Roche lobe, say up to a core mass of 0.6
as a result of accretion)
evolves in turn along the AGB, but having a lighter companion it can grow bigger and brighter
without filling its Roche lobe, say up to a core mass of 0.6 ![]() .
Eventually star M2 fills its Roche lobe
and ejects most of its envelope, transferring part of it back to star M1 (a few
0.01
.
Eventually star M2 fills its Roche lobe
and ejects most of its envelope, transferring part of it back to star M1 (a few
0.01 ![]() is enough for M1 to reignite its H shell and to swell again to giant dimensions; Frankowski 2003).
There are now two cores with comparable envelope masses, both burning hydrogen
in shells, the younger (M2, i.e. the true-post AGB) burning it faster (as it has a more massive core). The younger core is brighter and evolves (contracts) faster.
The difference in evolutionary speed becomes enormous as star M2 gets to its
post-AGB stage
(3000 years off the AGB, the 0.6
is enough for M1 to reignite its H shell and to swell again to giant dimensions; Frankowski 2003).
There are now two cores with comparable envelope masses, both burning hydrogen
in shells, the younger (M2, i.e. the true-post AGB) burning it faster (as it has a more massive core). The younger core is brighter and evolves (contracts) faster.
The difference in evolutionary speed becomes enormous as star M2 gets to its
post-AGB stage
(3000 years off the AGB, the 0.6 ![]() core has already a temperature of
core has already a temperature of
![]() ;
Blöcker 1995) while star M1 still sits on the AGB. Soon we are
left with a giant configuration around M1's core and a hot, brighter
post-AGB M2. In this particular case the brightness difference is
a factor of 3 to 5.
The mass function would be high (0.16
;
Blöcker 1995) while star M1 still sits on the AGB. Soon we are
left with a giant configuration around M1's core and a hot, brighter
post-AGB M2. In this particular case the brightness difference is
a factor of 3 to 5.
The mass function would be high (0.16 ![]() for the sample case above,
assuming
for the sample case above,
assuming
![]() - which makes it very similar to SS Lep, which has
f(M) = 0.26
- which makes it very similar to SS Lep, which has
f(M) = 0.26 ![]() ).
).
In any case, the suggestion that some stars flagged as post-AGB could in fact be components of binary systems caught in the act of mass transfer would have several interesting consequences. It could explain the unexpectedly large number of post-AGB systems (as compared to their short evolution time scale), the similarity between the orbital elements of post-AGB and M binaries (if post-AGB stars were post-mass-transfer systems rather than systems with on-going mass transfer as we suggest, the orbital elements should have been altered, at least to some extent). It would also explain why we could not find any other systems with characteristics similar to SS Lep (namely, early-type star with cool dust in a disc and spectral features typical of (super)giants), since they would all already have been flagged as post-AGB systems! The star 3 Pup (HD 62 623) is sometimes presented as the twin of SS Lep (Jura et al. 2001), but the exact nature of this star is still much debated. At this point, it should be mentioned that the d' symbiotic systems could be related as well to post-AGB systems and SS Lep: they host a warm, fast-rotating giant (F to early K) with a hot compact companion which just left the AGB, as suggested by the presence of cool dust and, often, a planetary nebula. The fast rotation of the giant is very likely the signature of a recent mass-transfer episode (Zamanov et al. 2006; Jorissen et al. 2005).
![\begin{figure}
\par\includegraphics[width=9cm]{10703f6.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg59.gif) |
Figure 6:
Same as Fig. 5 but in terms of V-K and
|
| Open with DEXTER | |
Actually, the shape of the
![]() diagram of post-AGB stars, when
compared to that of binary M and K giants, may be interpreted in two
different ways.
The first interpretation assumes that
the location of post-AGB stars in the
diagram of post-AGB stars, when
compared to that of binary M and K giants, may be interpreted in two
different ways.
The first interpretation assumes that
the location of post-AGB stars in the
![]() diagram is
controlled by the periastron envelope corresponding to 200
diagram is
controlled by the periastron envelope corresponding to 200 ![]() (solid
line in Fig. 2), with some circular systems at
shorter periods plus some among these which had their
eccentricities pumped upwards as a result of the interaction with the
circumbinary disc (Frankowski 2008; Artymowicz et al. 1991; de Ruyter et al. 2006). In this
scenario, the AGB precursors were thus allowed to evolve far up the
AGB, up to at least 200
(solid
line in Fig. 2), with some circular systems at
shorter periods plus some among these which had their
eccentricities pumped upwards as a result of the interaction with the
circumbinary disc (Frankowski 2008; Artymowicz et al. 1991; de Ruyter et al. 2006). In this
scenario, the AGB precursors were thus allowed to evolve far up the
AGB, up to at least 200 ![]() .
The similarity
between the
.
The similarity
between the
![]() diagrams of M giants and post-AGB systems would
thus be purely accidental.
diagrams of M giants and post-AGB systems would
thus be purely accidental.
The second interpretation assumes that this similarity is not
accidental, and states that mass transfer or disc interaction has not dramatically
altered the location of post-AGB binaries in the
![]() diagram
(or as suggested above, some might even be in the course of the
mass-transfer process). This case then differs from the
first interpretation by implying that the AGB precursors
must have left the AGB at a rather early
stage in their evolution,
given their location in the
diagram
(or as suggested above, some might even be in the course of the
mass-transfer process). This case then differs from the
first interpretation by implying that the AGB precursors
must have left the AGB at a rather early
stage in their evolution,
given their location in the
![]() diagram between the tidal
envelopes corresponding to 85 and 200
diagram between the tidal
envelopes corresponding to 85 and 200 ![]() (Fig. 1).
Like the M giants, binary post-AGB stars do not show evidence for s-process
enrichment (despite the confusion introduced by the depletion
pattern; Van Winckel 2007). We believe that the absence of
s-process enrichments in both classes of stars is not a coincidence.
In fact, it may be inferred that neither M giants nor post-AGB binaries reached a point on the AGB where
s-process and dredge-ups were operating
(Fig. 1).
Like the M giants, binary post-AGB stars do not show evidence for s-process
enrichment (despite the confusion introduced by the depletion
pattern; Van Winckel 2007). We believe that the absence of
s-process enrichments in both classes of stars is not a coincidence.
In fact, it may be inferred that neither M giants nor post-AGB binaries reached a point on the AGB where
s-process and dredge-ups were operating![]() .
This argument may actually be checked by locating M giants and post-AGB stars
in the
Hertzsprung-Russell (HR) diagram (Figs. 5 and 6) and comparing their
location with that of Tc-rich S stars (from Van Eck et al. 1998),
which are thermally-pulsing AGB (TP-AGB)
stars enriched in s-process elements.
Luminosities of post-AGB stars are extremely scarce.
When available (e.g., from LMC objects and from a
luminosity-period relationship for RV Tau stars calibrated on
LMC stars; de Ruyter et al. 2006; Alcock et al. 1998) however, they are of the order
of 4000
.
This argument may actually be checked by locating M giants and post-AGB stars
in the
Hertzsprung-Russell (HR) diagram (Figs. 5 and 6) and comparing their
location with that of Tc-rich S stars (from Van Eck et al. 1998),
which are thermally-pulsing AGB (TP-AGB)
stars enriched in s-process elements.
Luminosities of post-AGB stars are extremely scarce.
When available (e.g., from LMC objects and from a
luminosity-period relationship for RV Tau stars calibrated on
LMC stars; de Ruyter et al. 2006; Alcock et al. 1998) however, they are of the order
of 4000 ![]() (
(
![]() ). This luminosity lies in the middle of the range covered by Tc-rich S stars (Fig. 5), so that this argument does not really support a non-TP-AGB origin for post-AGB stars. However, the argument strongly relies on the adopted (uncertain) value for the typical luminosity of post-AGB stars.
). This luminosity lies in the middle of the range covered by Tc-rich S stars (Fig. 5), so that this argument does not really support a non-TP-AGB origin for post-AGB stars. However, the argument strongly relies on the adopted (uncertain) value for the typical luminosity of post-AGB stars.
2.3 Relation with S and barium stars
We now compare M giants in binaries with Tc-rich S stars.
As expected, M giants are always
less evolved than Tc-rich S stars. As already discussed by
Van Eck et al. (1998), Tc-rich S stars are indeed found beyond the onset
of the TP-AGB (i.e., to the right of the early AGB evolutionary tracks
in Fig. 5). There is one exception, though (HIP 38 502 = NQ Pup, a Tc-rich S star with
![]() ),
which illustrates the possible impact of biases when
considering the individual locations of stars with non-negligible
relative errors on their parallaxes (see Van Eck et al. 1998, and references therein).
Nevertheless, overall, the segregation between Tc-rich S stars and
M giants is very clear.
),
which illustrates the possible impact of biases when
considering the individual locations of stars with non-negligible
relative errors on their parallaxes (see Van Eck et al. 1998, and references therein).
Nevertheless, overall, the segregation between Tc-rich S stars and
M giants is very clear.
When M giants evolve further on the AGB, they will indeed turn into Tc-rich
S stars, but at the same time are likely to become long-period variables
(LPVs, Little et al. 1987). As discussed in Papers I and II,
binary systems among LPVs are very difficult to detect for two
reasons. First, given their large
radii, only long-period systems may host them (see
Fig. 4), but these systems necessarily have small
values for the radial-velocity semi-amplitude K (smaller than
about 10 km s-1; see Fig. 5 in Paper II and the
discussion about Fig. 9.4 in Jorissen 2003a). Secondly, since they are
LPVs, shock waves move across their atmospheres, and induce
radial-velocity variations with amplitudes of 10 to 20 km s-1 (Hinkle et al. 1997; Alvarez et al. 2001). Hence they are very
difficult to detect. Spectroscopic binaries involving LPVs are not included in the present
discussion since very few cases are known, and usually their orbital
elements are not known (the supposed post-AGB + Mira system HD 172 481 discussed
in Sect. 2.2 is no exception). The list of AGB stars with composite
spectra compiled by Jorissen (2003a) includes for instance the
Tc-rich S stars W Aql, WY Cas and T Sgr, and the carbon stars SZ Sgr,
TU Tau and BD -26![]() 2983, but orbital periods
are not known for them yet. Symbiotic stars hosting a Mira variable
(the so-called d-type symbiotics; Whitelock 1987; Allen 1982) are perfect examples of binaries
involving a very evolved AGB star. Schmid & Schild (2002) have
succeeded in detecting the orbital motion of these systems using Raman
polarimetry, and concluded that the orbital periods in these systems
are of the order of 150 yr or 55000 d.
Intriguingly,
Goldin & Makarov (2007) find a very short period of 141 d (from
a fit to the Hipparcos Intermediate Astrometric Data) for the M5III
semiregular variable star HIP 34 922 (=HD 56 096 = L2 Pup), possibly
a TP-AGB star since Little et al. (1987) find Tc to be possibly
present. The period - eccentricity pair obtained by
Goldin & Makarov (2007)
2983, but orbital periods
are not known for them yet. Symbiotic stars hosting a Mira variable
(the so-called d-type symbiotics; Whitelock 1987; Allen 1982) are perfect examples of binaries
involving a very evolved AGB star. Schmid & Schild (2002) have
succeeded in detecting the orbital motion of these systems using Raman
polarimetry, and concluded that the orbital periods in these systems
are of the order of 150 yr or 55000 d.
Intriguingly,
Goldin & Makarov (2007) find a very short period of 141 d (from
a fit to the Hipparcos Intermediate Astrometric Data) for the M5III
semiregular variable star HIP 34 922 (=HD 56 096 = L2 Pup), possibly
a TP-AGB star since Little et al. (1987) find Tc to be possibly
present. The period - eccentricity pair obtained by
Goldin & Makarov (2007)
![]() d,
d,
![]() is, however, totally inconsistent with the
values found for the other M giants in Fig. 2,
so that its validity must be questioned, as discussed in the Appendix.
is, however, totally inconsistent with the
values found for the other M giants in Fig. 2,
so that its validity must be questioned, as discussed in the Appendix.
It must be emphasised at this point that Tc-poor S stars![]() (star symbols in Fig. 5) are post-mass-transfer
systems, and as such, may not be directly compared to M giants
and Tc-rich S stars. Nevertheless, the above discussion, stating that
binaries involving Tc-rich S stars and LPVs should have long orbital periods, leads to a
very surprising conclusion: extrinsic, Tc-poor S stars occupy the region of the
(star symbols in Fig. 5) are post-mass-transfer
systems, and as such, may not be directly compared to M giants
and Tc-rich S stars. Nevertheless, the above discussion, stating that
binaries involving Tc-rich S stars and LPVs should have long orbital periods, leads to a
very surprising conclusion: extrinsic, Tc-poor S stars occupy the region of the
![]() diagram where binary Tc-rich S stars are expected
(Fig. 1). This
implies that the mass-transfer episode must have had little
impact on the orbital elements. This is quite surprising at first
sight, since either the orbital period must have shorten dramatically
(for the so-called ``case C'' RLOF) or it must have increased considerably (for wind
accretion), according to standard evolutionary prescriptions
(e.g., Boffin & Jorissen 1988).
This
conclusion is clearly not compatible with the present data, and calls
for alternative mass-transfer prescriptions,
as it was already known for quite some time. Jorissen (2003a),
Frankowski & Jorissen (2007) and Podsiadlowski & Mohamed (2007) have proposed new
avenues to explore. For instance, in the context of the ``transient torus'' scenario
proposed by Frankowski & Jorissen (2007), a near constancy of the orbital
period is not unexpected.
diagram where binary Tc-rich S stars are expected
(Fig. 1). This
implies that the mass-transfer episode must have had little
impact on the orbital elements. This is quite surprising at first
sight, since either the orbital period must have shorten dramatically
(for the so-called ``case C'' RLOF) or it must have increased considerably (for wind
accretion), according to standard evolutionary prescriptions
(e.g., Boffin & Jorissen 1988).
This
conclusion is clearly not compatible with the present data, and calls
for alternative mass-transfer prescriptions,
as it was already known for quite some time. Jorissen (2003a),
Frankowski & Jorissen (2007) and Podsiadlowski & Mohamed (2007) have proposed new
avenues to explore. For instance, in the context of the ``transient torus'' scenario
proposed by Frankowski & Jorissen (2007), a near constancy of the orbital
period is not unexpected.
If it is correct that the mass transfer process does not alter much the orbital period, then the existence of mild barium stars with rather short orbital periods (i.e., the open triangles to the left of the solid line in Fig. 2) may be explained by the fact that their polluting companion did not evolve far up the TP-AGB, hence the AGB envelope was not much enriched in s-process elements. This hypothesis is especially appealing since the other possibility, suggested by Jorissen & Boffin (1992) and Jorissen et al. (1998) - namely, that mild barium stars belong to a more metal-rich population than strong barium stars, because the s-process is more efficient in low-metallicity stars (Goriely & Mowlavi 2000) - has been dismissed by the detailed abundance analysis of mild barium stars by Smiljanic et al. (2007), who conclude that there is no obvious metallicity difference between mild and strong barium stars.
The intriguing absence of s-process enrichment in red symbiotics
(e.g., Jorissen 2003b; Frankowski & Jorissen 2007), despite the
fact that they are likely post-mass-transfer systems like barium
stars, may perhaps be understood by invoking the same argument: as
they fall in the same region as the (non-s-process-enriched) post-AGB stars
in the
![]() diagram (Fig. 2), it is
possible that their companion did not evolve far up enough on the AGB
to activate dredge-ups and s-process.
diagram (Fig. 2), it is
possible that their companion did not evolve far up enough on the AGB
to activate dredge-ups and s-process.
2.4 Radius, period and Wood's sequence D in the period - luminosity diagram
Interestingly enough, our data may be used to shed light on the much debated nature of the so-called ``sequence D'' found by Wood et al. (1999) and Wood (2000) in the period - luminosity diagram of LPVs in the Large Magellanic Cloud (LMC). This sequence (also called ``long secondary periods'') is located to the right of the period - luminosity relationship for Miras pulsating in the fundamental mode (``sequence C''). Sequence D can thus not be associated with higher harmonics, which have shorter periods (``sequences A'' and ``B''). A possible relation between Wood's sequence D and the Roche limit in binary systems (via ellipsoidal variations or dust obscuration events) was originally proposed by Wood et al. (1999) and Wood (2000), and more recently again by Soszynski et al. (2004), Derekas et al. (2006) and Soszynski (2007).
Figure 7 is a variant of Fig. 4 that makes
it easy to compare our data with the period - luminosity diagram of
LPVs in the LMC (Wood 2000; Wood et al. 1999). The ordinate
axis of Fig. 7 corresponds to the K magnitude that our
M giants would have if they were at the distance of the LMC, i.e.,
![]() ,
where the McNamara et al. (2007) LMC distance modulus
has been adopted. It is quite interesting to notice that Wood's
sequence D does match the upper envelope of
the region occupied by the galactic binary M giants. Our finding
of a clear relationship between Wood's D sequence and the Roche limit in
binary systems involving M giants
supports the similar suggestion made by Soszynski et al. (2004) and Soszynski (2007).
,
where the McNamara et al. (2007) LMC distance modulus
has been adopted. It is quite interesting to notice that Wood's
sequence D does match the upper envelope of
the region occupied by the galactic binary M giants. Our finding
of a clear relationship between Wood's D sequence and the Roche limit in
binary systems involving M giants
supports the similar suggestion made by Soszynski et al. (2004) and Soszynski (2007).
2.5 Near absence of circular orbits among M III binaries
A striking difference between K and M giants apparent
on Fig. 1 is the lack, among binaries involving M giants, of the many circular systems
at the short end of the period range that are
observed among the K giants.
The short-period circular systems observed among K giants result from
tidal effects which circularise the orbit when the giant star is close
to filling its Roche lobe (e.g., North & Duquennoy 1992).
The difference between K and M giants is surprising, since
both stellar families involve
stars with deep convective envelopes which should react similarly to
tidal effects.
M giants, however, have shorter lifetimes than K giants, because the former suffer from a much more severe wind mass loss, and this difference offers perhaps
a clue to account for the differences observed at short periods in
their
![]() diagrams. Tidal forces may not have enough time to efficiently operate in the case of M giants.
Indeed, the many circular systems observed
among post-AGB stars seem to be the circular population missing among the M giants. This hints at mass loss and tidal effects operating on
similar time scales: shortly after the system has
been circularised, the envelope is lost and the primary star no longer
looks as an M giant but rather as a post-AGB star.
The very existence of a system like SS Lep does lend support to the above suggestion.
In Fig. 8 investigating a possible correlation
between dust excess and position of the binary M giants in the
diagrams. Tidal forces may not have enough time to efficiently operate in the case of M giants.
Indeed, the many circular systems observed
among post-AGB stars seem to be the circular population missing among the M giants. This hints at mass loss and tidal effects operating on
similar time scales: shortly after the system has
been circularised, the envelope is lost and the primary star no longer
looks as an M giant but rather as a post-AGB star.
The very existence of a system like SS Lep does lend support to the above suggestion.
In Fig. 8 investigating a possible correlation
between dust excess and position of the binary M giants in the
![]() diagram, SS Lep, having a large K - [12] excess, appears as the big circle along the tidal boundary.
diagram, SS Lep, having a large K - [12] excess, appears as the big circle along the tidal boundary.
![\begin{figure}
\par\includegraphics[width=8.8cm]{10703f7.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg67.gif) |
Figure 7:
The orbital-period as a function of (absolute)
K magnitude for
galactic M giants in binary
systems. The ordinate
axis corresponds to the K magnitude that the
M giants would have if they were put at the distance of the LMC (see
text).
The dashed line labelled ``D'' corresponds to Wood's
sequence of long secondary periods.
The solid and dotted lines correspond to the limit on the
orbital period imposed by the Roche radius (for M1 = 1.3 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{10703f8.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg69.gif) |
Figure 8:
The
|
| Open with DEXTER | |
Similarly, it is interesting to note that circular orbits are common among red symbiotics as well, albeit with somewhat longer periods. The implications of this result actually depend on whether the red symbiotics are pre-mass-transfer systems (i.e., with a main-sequence companion) or post-mass-transfer systems (i.e., with a WD companion). This issue has not been solved yet (Frankowski & Jorissen 2007). In the former case, the longer periods are simply a consequence of the fact that the M giants in red symbiotics are on average of later types (i.e., later than M3) than those in our binary sample (Belczynski et al. 2000). Hence, they cannot be hosted by systems as close as those hosting earlier giants (Fig. 7). The absence of s-process enrichments in those red symbiotics - another puzzling issue (Jorissen 2003b; Frankowski & Jorissen 2007) - would then be explained naturally as previously for the post-AGB stars: the M giant has simply not yet reached the TP-AGB phase. In the latter case (the companion is a WD), the orbital periods fall in the short-period tail of the distribution of periods for post-mass-transfer systems like Tc-poor S stars, as expected, but then, the absence of s-process enrichment is puzzling unless these systems had not very evolved AGB progenitors.
![\begin{figure}
\par\includegraphics[width=8.8cm]{10703f9.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg70.gif) |
Figure 9: The cumulative distribution of the mass function for M giants (solid line), K giants from open clusters (dashed line; Mermilliod et al. 2007) and S stars with WD companions (thus excluding the peculiar systems HD 191 589 and HD 332 077; Jorissen et al. 1998, dotted line). |
| Open with DEXTER | |
2.6 The long-period, small-eccentricity gap in the (e - log P) diagram
To conclude this discussion of the
![]() diagram,
it must be pointed out that, for pre-mass-transfer binaries hosting
main sequence stars, there is a void in this diagram
at P > 400 d, e < 0.1. This gap is especially
apparent in the
diagram,
it must be pointed out that, for pre-mass-transfer binaries hosting
main sequence stars, there is a void in this diagram
at P > 400 d, e < 0.1. This gap is especially
apparent in the
![]() diagram of G and K dwarfs of the solar
neighbourhood (Duquennoy & Mayor 1991).
The situation is quite different for post-mass-transfer systems like barium and
Tc-poor S stars.
Figure 1 of North et al. (2000)
clearly shows that barium dwarfs fall almost exclusively within this gap.
Similarly, Barium and Tc-poor S stars fill this gap almost completely
(Fig. 2). Red symbiotics fill the gap till 1000 d
with circular systems, but as discussed in
Sect. 2.5, this may result as well from tidal effects.
diagram of G and K dwarfs of the solar
neighbourhood (Duquennoy & Mayor 1991).
The situation is quite different for post-mass-transfer systems like barium and
Tc-poor S stars.
Figure 1 of North et al. (2000)
clearly shows that barium dwarfs fall almost exclusively within this gap.
Similarly, Barium and Tc-poor S stars fill this gap almost completely
(Fig. 2). Red symbiotics fill the gap till 1000 d
with circular systems, but as discussed in
Sect. 2.5, this may result as well from tidal effects.
There are in fact a few binaries involving K and M giants (most notably HD 165 374, with P = 2741 d, e = 0.05 and a M2III primary) which fall in the long-period tail of this gap, as can be seen on Fig. 2. It is very likely that these systems are in fact post-mass-transfer binaries, a possibility that would be worth testing by looking for Ba-like abundance anomalies in these giants.
An indirect way to confirm the post-mass-transfer nature of the
binaries with long periods and small eccentricities is
to look for the presence of WD
companions. McClure & Woodsworth (1990) have convincingly shown that
the cumulative distribution of the mass functions may be used for that
purpose: since WDs have masses spanning a rather narrow range
(0.5-1.4 ![]() ,
with a peak around 0.6
,
with a peak around 0.6 ![]() ,
at least for single
WDs), the mass functions of binaries involving a giant primary and a WD
secondary may be expected to be much more peaked than in the case of
main-sequence companions, which do not obey a similar constraint on
their masses (except for being less massive than the primary, giant
component). This is illustrated on Fig. 9, which compares
the cumulative mass-function distributions for M giants, K giants in
open clusters (Mermilliod et al. 2007) and S stars with WD companions (Jorissen et al. 1998). The sample of M giants may clearly be split in two subsamples, one with small mass functions matching those of Tc-poor S stars with
WD companions, and the other with larger mass functions typical of main-sequence companions, like the remarkable system SS Lep discussed in this paper (
f(M) = 0.26
,
at least for single
WDs), the mass functions of binaries involving a giant primary and a WD
secondary may be expected to be much more peaked than in the case of
main-sequence companions, which do not obey a similar constraint on
their masses (except for being less massive than the primary, giant
component). This is illustrated on Fig. 9, which compares
the cumulative mass-function distributions for M giants, K giants in
open clusters (Mermilliod et al. 2007) and S stars with WD companions (Jorissen et al. 1998). The sample of M giants may clearly be split in two subsamples, one with small mass functions matching those of Tc-poor S stars with
WD companions, and the other with larger mass functions typical of main-sequence companions, like the remarkable system SS Lep discussed in this paper (
f(M) = 0.26 ![]() ).
).
![\begin{figure}
\par\includegraphics[width=8.8cm]{10703f10.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg71.gif) |
Figure 10: The eccentricity-period diagram for spectroscopic binaries involving K giants in open clusters (filled squares; Mermilliod et al. 2007), and Ba and S stars (open triangles, from Jorissen et al. 1998). The vertical segments have lengths corresponding to mass functions expressed in solar masses. The diagonal dashed line delineates the region where most of the Ba/S stars are found. |
| Open with DEXTER | |
Conversely, with a mass function of 0.078 ![]() ,
HD 165 374 could certainly host a WD companion of (minimum) mass 0.73
,
HD 165 374 could certainly host a WD companion of (minimum) mass 0.73 ![]() (respectively 0.78
(respectively 0.78 ![]() ),
adopting a mass of 1.5
),
adopting a mass of 1.5 ![]() (respectively 1.7
(respectively 1.7 ![]() )
for the M2 giant,
according to its location in the HR diagram of Fig. 5.
)
for the M2 giant,
according to its location in the HR diagram of Fig. 5.
HD 108 907 (4 Dra) is probably a post-mass transfer
system as well, since it hosts a blue, hot
companion, either a cataclysmic variable (Reimers et al. 1988) or more likely a single WD accreting from the wind of its red giant companion, as in normal
symbiotic systems (Wheatley et al. 2003; Skopal 2005b,a).
Its position in the
![]() diagram (
e= 0.33, P= 1703 d) does
not by itself hints at its post-mass-transfer nature, although it
lies just at the border of the region occupied by barium and Tc-poor
S stars, and close to that of the mild barium stars discussed above.
It does not seem, however, to bear chemical anomalies typical
of barium stars. It may therefore be yet another example of a system
containing all the necessary ingredients for being a barium star,
but which is not. Again, one may invoke the possibility that the
AGB progenitor did not evolve far enough on the TP-AGB.
diagram (
e= 0.33, P= 1703 d) does
not by itself hints at its post-mass-transfer nature, although it
lies just at the border of the region occupied by barium and Tc-poor
S stars, and close to that of the mild barium stars discussed above.
It does not seem, however, to bear chemical anomalies typical
of barium stars. It may therefore be yet another example of a system
containing all the necessary ingredients for being a barium star,
but which is not. Again, one may invoke the possibility that the
AGB progenitor did not evolve far enough on the TP-AGB.
Section 3 furthers the considerations of the present subsection by showing that the long-period,
low-eccentricity region of the
![]() diagram mostly contains systems
with small mass functions hinting at WD companions.
diagram mostly contains systems
with small mass functions hinting at WD companions.
3 A clear signature of mass transfer in the (e - log P) diagram of binaries involving K giants in open clusters
Mermilliod et al. (2007) provided an extensive set of orbital elements
for 135 spectroscopic binaries with K giant primaries belonging to open clusters.
The major asset of this sample, over one involving field K giants as
available from the Ninth Catalogue of Spectroscopic Binary Orbits
(Pourbaix 2004), is that the mass of the K giant is known: with
a good accuracy, it may be identified with the cluster main-sequence
turnoff mass (it is therefore essential to keep only cluster members
in our study). A lower bound on the mass of the companion may then be
easily obtained from the mass function f(M) by setting
![]() .
The distribution of the companion masses in different regions of the
.
The distribution of the companion masses in different regions of the
![]() diagram may then be compared. An obvious way to divide the
diagram may then be compared. An obvious way to divide the
![]() diagram is through the line of equation
diagram is through the line of equation
![]() [connecting the
[connecting the
![]() pairs (0, 2.5) and (0.6, 4)] under which
lie most of the barium and Tc-poor S stars (Fig. 10). The result of this procedure is shown in Figs. 11 and 12.
pairs (0, 2.5) and (0.6, 4)] under which
lie most of the barium and Tc-poor S stars (Fig. 10). The result of this procedure is shown in Figs. 11 and 12.
![\begin{figure}
\par\includegraphics[width=8.5cm]{10703f11.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg75.gif) |
Figure 11:
The cumulative distribution of the companion masses for open-cluster K binaries, assuming an inclination of 90 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm]{10703f12.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg76.gif) |
Figure 12:
Same as Fig. 11, but in the form of histograms (thick solid line:
systems in the non-post-mass-transfer zone; thin solid line and shaded histogram: post-mass-transfer
systems).
In the post-mass-transfer region, all companions are less massive than
1.5 |
| Open with DEXTER | |
It is quite clear already from Fig. 10 that the systems
involving K giants and located in the same region of the
![]() diagram as the barium and Tc-poor S stars have a
mass-function distribution which is significantly different from the
distribution of the full sample. This is confirmed by Fig. 11. Moreover, these systems lying in
the post-mass-transfer region have companions masses below 1.5
diagram as the barium and Tc-poor S stars have a
mass-function distribution which is significantly different from the
distribution of the full sample. This is confirmed by Fig. 11. Moreover, these systems lying in
the post-mass-transfer region have companions masses below 1.5 ![]() (with one exception discussed below), and peaking at 0.5
(with one exception discussed below), and peaking at 0.5 ![]() ,
as expected for WD companions
(Figs. 11 and 12). Since most of the clusters making up this supposedly post-mass-transfer sample have turn-off masses well above 1.5
,
as expected for WD companions
(Figs. 11 and 12). Since most of the clusters making up this supposedly post-mass-transfer sample have turn-off masses well above 1.5 ![]() ,
the 1.5
,
the 1.5 ![]() threshold observed for the companion masses cannot be due to a selection effect.
Star 170 (with
threshold observed for the companion masses cannot be due to a selection effect.
Star 170 (with
![]() d,
d,
![]() and
and
![]()
![]() )
in NGC 129 (a young cluster with a
turnoff mass of 5.5
)
in NGC 129 (a young cluster with a
turnoff mass of 5.5 ![]() ;
Mermilliod et al. 1987) is the
only outlier, with a >4.5
;
Mermilliod et al. 1987) is the
only outlier, with a >4.5 ![]() companion in a KII + BV pair.
companion in a KII + BV pair.
With a maximum vertical distance of 0.25 between the cumulative frequency distributions of the two samples displayed in Fig. 11 (containing 29 and 106 stars), the Kolmogorov-Smirnov statistics leads to reject the null hypothesis that the two samples are extracted from the same parent population with a significance level of 10% (Performing the same comparison without star 170 in NGC 129 yields a maximum difference of 0.29 and a significance level of about 4%).
4 Conclusions
The main results of this paper are the following:
- 1.
- The
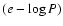 diagram of pre-mass transfer binaries like most of the K binaries in open clusters and the binary M giants is bounded by an upper left envelope corresponding to a constant periastron distance. This distance corresponds to the maximum radius reached at a given spectral type, as shown from the similar boundary observed in the radius - orbital period diagram. Systems lying along that boundary often host a giant (nearly) filling its Roche lobe, and exhibiting either ellipsoidal variations (HD 9053, HD 190 658) or mass-transfer signatures (like an inflated companion; SS Lep). The mass-transfer binary SS Lep (MIII + A), with its circumbinary disc most probably fed by non-conservative RLOF, represents a transition case between binary M giants and genuine post-AGB stars.
diagram of pre-mass transfer binaries like most of the K binaries in open clusters and the binary M giants is bounded by an upper left envelope corresponding to a constant periastron distance. This distance corresponds to the maximum radius reached at a given spectral type, as shown from the similar boundary observed in the radius - orbital period diagram. Systems lying along that boundary often host a giant (nearly) filling its Roche lobe, and exhibiting either ellipsoidal variations (HD 9053, HD 190 658) or mass-transfer signatures (like an inflated companion; SS Lep). The mass-transfer binary SS Lep (MIII + A), with its circumbinary disc most probably fed by non-conservative RLOF, represents a transition case between binary M giants and genuine post-AGB stars.
- 2.
- Systems similar to SS Lep and HD 172 481, hosting an accreting star mimicking a (super)giant star, should be searched for among post-AGB systems lying along the upper envelope of the
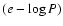 diagram. We suggest that the family of binary post-AGB stars might include systems in an active phase of mass transfer, where the accreting component has swollen to giant dimensions, thus mimicking a genuine post-AGB star.
diagram. We suggest that the family of binary post-AGB stars might include systems in an active phase of mass transfer, where the accreting component has swollen to giant dimensions, thus mimicking a genuine post-AGB star.
- 3.
- The so-called Wood's sequence D in the period - luminosity diagram of LMC LPVs is closely linked to the upper envelope of the
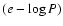 diagram for M giants.
diagram for M giants.
- 4.
- The post-mass transfer systems like barium and Tc-poor S stars have orbital elements very similar to the pre-mass-transfer systems (binary M giants), suggesting that the mass transfer does not alter them much, in line with the new transient-torus scenario for mass transfer proposed by Frankowski & Jorissen (2007).
- 5.
- The lower right region of the
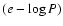 diagram, as defined by the location of the barium and Tc-poor S stars, hosts mainly post-mass-transfer systems, also among K binaries in open clusters. This is very clearly seen from the fact that these systems have low mass functions consistent with WD companions. Whether these giants bear chemical signatures of mass transfer as do barium stars remains to be checked.
diagram, as defined by the location of the barium and Tc-poor S stars, hosts mainly post-mass-transfer systems, also among K binaries in open clusters. This is very clearly seen from the fact that these systems have low mass functions consistent with WD companions. Whether these giants bear chemical signatures of mass transfer as do barium stars remains to be checked.
Acknowledgements
We thank J.-Cl. Mermilliod for sending us his orbital data for K giants in open clusters in advance of publication. This work has been partly funded by an Action de recherche concertée (ARC) from the Direction générale de l'Enseignement non obligatoire et de la Recherche scientifique - Direction de la recherche scientifique - Communauté française de Belgique.
Appendix: Dismissing the binary nature of L2 Pup
The intringuing finding by
Goldin & Makarov (2007) of a very short period of 141 d in
the Hipparcos Intermediate Astrometric Data for the M5III
semiregular variable star HIP 34 922 (=HD 56 096 = L2 Pup) deserves
a specific discussion.
This 141 d period is clearly
related to pulsation, since that periodicity is found in both the
light and radial-velocity curves
(Lebzelter et al. 2005; Cummings et al. 1999). The light curve has a large
amplitude (about 2.5 mag in the visual), which cannot therefore be
attributed to ellipsoidal variations. According to
Lebzelter et al. (2005), the 141 d period moreover falls on sequence C
of the period-luminosity diagram of Wood (2000), which
corresponds to the fundamental pulsation mode of long-period variables
(see Sect. 2.4). Assuming that the 141 d period corresponds
as well to an orbital motion (in the case of a tidal lock between
orbital motion and pulsations) leads, however, to major
inconsistencies. The absolute semi-major axis for the photocentre of
the system, inferred from Goldin & Makarov's angular value a0 =
9.5 mas and from the parallax of
![]() mas, is 0.58 AU,
which may be considered as the absolute semi-major axis of the orbit
of the giant if one assumes that the companion contributes no light to
the system. According to Dumm & Schild (1998), the minimum radius of
an M5 giant is 60
mas, is 0.58 AU,
which may be considered as the absolute semi-major axis of the orbit
of the giant if one assumes that the companion contributes no light to
the system. According to Dumm & Schild (1998), the minimum radius of
an M5 giant is 60 ![]() (but the radius predicted by Dumm &
Schild from the Barnes-Evans relationship for L2 Pup is more like
125
(but the radius predicted by Dumm &
Schild from the Barnes-Evans relationship for L2 Pup is more like
125 ![]() ;
Barnes & Evans 1976). The giant could just fit in the
binary system, filling its Roche lobe at periastron, assuming a
reasonable mass ratio of 1.5 and implying a semi-major axis A =
1.45 AU for the relative orbit. But then, according to Kepler's third
law, the total mass of the system would be 20.4
;
Barnes & Evans 1976). The giant could just fit in the
binary system, filling its Roche lobe at periastron, assuming a
reasonable mass ratio of 1.5 and implying a semi-major axis A =
1.45 AU for the relative orbit. But then, according to Kepler's third
law, the total mass of the system would be 20.4 ![]() ,
or
12.2
,
or
12.2 ![]() for the giant and 8.2
for the giant and 8.2 ![]() for its companion, which is
inconsistent with the M5III classification of the former. We thus
conclude that, although the Hipparcos data are clearly inconsistent
with a single point source (with residuals from the single-star
solution amounting up to 10 mas), Goldin & Makarov's astrometric
orbit is impossible to reconcile with current knowledge about this
system. It could well be that the Hipparcos data have been confused by
the asymmetric surface brightness typical of late-type stars
(Ragland et al. 2006), especially so for a star as extended as
L2Pup having a (predicted) apparent angular radius of 9.6 mas
(Dumm & Schild 1998). A further argument against the binary
nature of L2 Pup is the detection of all three masers SiO, H2O
and OH (Jura et al. 2002), since a binary companion, when orbiting in
the layers where the maser activity should originate, prevents its
operation (Schwarz et al. 1995; Lewis et al. 1987; Herman & Habing 1985).
for its companion, which is
inconsistent with the M5III classification of the former. We thus
conclude that, although the Hipparcos data are clearly inconsistent
with a single point source (with residuals from the single-star
solution amounting up to 10 mas), Goldin & Makarov's astrometric
orbit is impossible to reconcile with current knowledge about this
system. It could well be that the Hipparcos data have been confused by
the asymmetric surface brightness typical of late-type stars
(Ragland et al. 2006), especially so for a star as extended as
L2Pup having a (predicted) apparent angular radius of 9.6 mas
(Dumm & Schild 1998). A further argument against the binary
nature of L2 Pup is the detection of all three masers SiO, H2O
and OH (Jura et al. 2002), since a binary companion, when orbiting in
the layers where the maser activity should originate, prevents its
operation (Schwarz et al. 1995; Lewis et al. 1987; Herman & Habing 1985).
References
- Adelman, S. J. 2007, The Journal of Astronomical Data, 13, 3 [NASA ADS] (In the text)
- Alcock, C., Allsman, R. A., Alves, D. R., et al. 1998, AJ, 115, 1921 [NASA ADS] [CrossRef]
- Allen D. A. 1982, in The Nature of Symbiotic Stars, ed. M. Friedjung, & R. Viotti (Dordrecht: Reidel), IAU Coll., 70, 27
- Alvarez, R., Jorissen, A., Plez, B., et al. 2001, A&A, 379, 305 [NASA ADS] [CrossRef] [EDP Sciences]
- Artymowicz, P., Clarke, C. J., Lubow, S. H., & Pringle, J. E. 1991, ApJ, 370, L35 [NASA ADS] [CrossRef]
- Ayres, T. R. 2005, ApJ, 618, 493 [NASA ADS] [CrossRef] (In the text)
- Bakker, E. J., Lamers, H. J. G. L. M., Waters, L. B. F. M., et al. 1996, A&A, 307, 869 [NASA ADS] (In the text)
- Barnes, T. G., & Evans, D. S. 1976, MNRAS, 174, 489 [NASA ADS] (In the text)
- Belczynski, K., Mikoajewska, J., Munari, U., Ivison, R. J., & Friedjung, M. 2000, A&AS, 146, 407 [NASA ADS] [CrossRef] [EDP Sciences]
- Benz, W., & Mayor, M. 1981, A&A, 93, 235 [NASA ADS] (In the text)
- Bessell, M. S., & Wood, P. R. 1984, PASP, 96, 247 [NASA ADS] [CrossRef] (In the text)
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] (In the text)
- Blöcker, T. 1995, A&A, 297, 727 [NASA ADS] (In the text)
- Boffin, H. M. J., & Jorissen, A. 1988, A&A, 205, 155 [NASA ADS] (In the text)
- Charbonnel, C., Meynet, G., Maeder, A., & Schaerer, D. 1996, A&AS, 115, 339 [NASA ADS] (In the text)
- Cummings, I. N., Hearnshaw, J. B., Kilmartin, P. M., & Gilmore, A. C. 1999, in Precise Stellar Radial Velocities, ed. J. B. Hearnshaw, & C. D. Scarfe, IAU Colloq. 170, ASP Conf. Ser., 185, 204
- de Ruyter, S., van Winckel, H., Maas, T., et al. 2006, A&A, 448, 641 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Derekas, A., Kiss, L. L., Bedding, T. R., et al. 2006, ApJ, 650, L55 [NASA ADS] [CrossRef] (In the text)
- Dermine, T., Jorissen, A., Siess, L., & Frankowski, A. 2009, A&A, submitted (In the text)
- Dumm, T., & Schild, H. 1998, New Astr., 3, 137 [NASA ADS] [CrossRef] (In the text)
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] (In the text)
- Duquennoy, A., Mayor, M., & Mermilliod, J. 1992, in Binaries as Tracers of Stellar Formation, ed. A. Duquennoy, & M. Mayor (Cambridge: Cambridge University Press), 52
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS]
- Eggleton P. 2006, Evolutionary Processes in Binary and Multiple Stars (Cambridge University Press)
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] (In the text)
- ESA 1997, The Hipparcos and Tycho Catalogues, ESA (In the text)
- Famaey, B., Jorissen, A., Luri, X., et al. 2005, A&A, 430, 165 [NASA ADS] [CrossRef] [EDP Sciences]
- Famaey, B., Pourbaix, D., Frankowski, A., et al. 2009, A&A, 498, 627 [NASA ADS] [CrossRef] [EDP Sciences] (Paper I) (In the text)
- Fekel, F. C., Hinkle, K. H., Joyce, R. R., Wood, P. R., & Lebzelter, T. 2007, AJ, 133, 17 [NASA ADS] [CrossRef]
- Frankowski, A. 2003, A&A, 406, 265 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Frankowski, A. 2008, in Asymmetrical Planetary Nebulae IV, ed. R. Corradi, A. Manchado, & N. Soker, electronic publication available at http://www.iac.es/project/apn4/
- Frankowski, A., & Jorissen A. 2007, Balt Astron., 16, 104 [NASA ADS]
- Frankowski, A., Famaey, B., Van Eck, S., et al. 2009, A&A, 498, 479 [NASA ADS] [CrossRef] [EDP Sciences] (Paper II) (In the text)
- Goldin, A., & Makarov, V. V. 2007, ApJS, 173, 137 [NASA ADS] [CrossRef] (In the text)
- Goriely, S., & Mowlavi, N. 2000, A&A, 362, 599 [NASA ADS] (In the text)
- Herman, J., & Habing, H. J. 1985, Phys. Rep., 124, 255 [NASA ADS] [CrossRef]
- Hinkle, K. H., Lebzelter, T., & Scharlach, W. W. G. 1997, AJ, 114, 2686 [NASA ADS] [CrossRef]
- Humphreys, R. M. 1976, ApJ, 206, 122 [NASA ADS] [CrossRef] (In the text)
- Hünsch, M., & Schroeder, K.-P. 1996, A&A, 309, L51 [NASA ADS]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS]
- Iben, I. J., & Tutukov, A. V. 1996, ApJS, 105, 145 [NASA ADS] [CrossRef]
- Jancart, S., Jorissen, A., Babusiaux, C., & Pourbaix, D. 2005, A&A, 442, 365 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Jorissen A. 2003a, in Asymptotic Giant Branch Stars, ed. H. Habing, & H. Olofsson (New York: Springer Verlag), 461
- Jorissen A. 2003b, in Symbiotic stars probing stellar evolution, ed. R. L. M. Corradi, J. Mikoajewska, & T. J. Mahoney, San Francisco, ASP Conf. Ser., 303, 25
- Jorissen, A., & Boffin, H. M. J. 1992, in Binaries as Tracers of Stellar Formation, ed. A. Duquennoy, & M. Mayor (Cambridge: Cambridge University Press), 110 (In the text)
- Jorissen, A., & Mayor, M. 1992, A&A, 260, 115 [NASA ADS] (In the text)
- Jorissen, A., & Van Eck, S. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ASP Conf. Ser., 336, San Francisco, 207
- Jorissen, A., Hennen, O., Mayor, M., Bruch, A., & Sterken, C. 1995, A&A, 301, 707 [NASA ADS] (In the text)
- Jorissen, A., Van Eck, S., Mayor, M., & Udry, S. 1998, A&A, 332, 877 [NASA ADS] (In the text)
- Jorissen, A., Zacs, L., Udry, S., Lindgren, H., & Musaev, F. A. 2005, A&A, 441, 1135 [NASA ADS] [CrossRef] [EDP Sciences]
- Jura, M., Webb, R. A., & Kahane, C. 2001, ApJ, 550, L71 [NASA ADS] [CrossRef]
- Jura, M., Chen, C., & Plavchan, P. 2002, ApJ, 569, 964 [NASA ADS] [CrossRef] (In the text)
- Kippenhahn, R., & Meyer-Hofmeister, E. 1977, A&A, 54, 539 [NASA ADS]
- Kipper T. 2005, Baltic Astronomy, 14, 223 [NASA ADS] (In the text)
- Lebzelter, T., Hinkle, K. H., Wood, P. R., Joyce, R. R., & Fekel, F. C. 2005, A&A, 431, 623 [NASA ADS] [CrossRef] [EDP Sciences]
- Lewis, B. M., Eder, J., & Terzian, Y. 1987, AJ, 94, 1025 [NASA ADS] [CrossRef]
- Little, S. J., Little-Marenin, I. R., & Bauer, W. H. 1987, AJ, 94, 981 [NASA ADS] [CrossRef] (In the text)
- Lü, P. K. 1991, AJ, 101, 2229 [NASA ADS] [CrossRef] (In the text)
- Lucke, P. B., & Mayor, M. 1982, A&A, 105, 318 [NASA ADS] (In the text)
- McClure, R. D. 1983, ApJ, 268, 264 [NASA ADS] [CrossRef] (In the text)
- McClure, R. D., & Woodsworth, A. W. 1990, ApJ, 352, 709 [NASA ADS] [CrossRef] (In the text)
- McNamara, D. H., Clementini, G., & Marconi, M. 2007, AJ, 133, 2752 [NASA ADS] [CrossRef] (In the text)
- Mermilliod, J. C., Mayor, M., & Burki, G. 1987, A&AS, 70, 389 [NASA ADS] (In the text)
- Mermilliod, J.-C., Andersen, J., Latham, D. W., & Mayor, M. 2007, A&A, 473, 829 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Mikoajewska, J. 2003, in Symbiotic stars probing stellar evolution, ed. R. L. M. Corradi, J. Mikoajewska, & T. J. Mahoney, ASP Conf. Ser., 303, San Francisco, 9
- Nelson, C. A., & Eggleton, P. P. 2001, ApJ, 552, 664 [NASA ADS] [CrossRef]
- North, P., & Duquennoy, A. 1992, in Binaries as Tracers of Stellar Formation, ed. A. Duquennoy, & M. Mayor (Cambridge: Cambridge University Press), 202 (In the text)
- North, P., Jorissen, A., & Mayor, M. 2000, in The Carbon Star Phenomenon, ed. R. F. Wing (Dordrecht: Kluwer), IAU Symp., 177, 269 (In the text)
- Otero, S. A. 2007, Open European Journal on Variable Stars, 72, 1 [NASA ADS] (In the text)
- Paczynski, B., & Rudak, B. 1980, A&A, 82, 349 [NASA ADS]
- Pastetter, L., & Ritter, H. 1989, A&A, 214, 186 [NASA ADS]
- Podsiadlowski, P., & Mohamed, S. 2007, Baltic Astronomy, 16, 26 [NASA ADS] (In the text)
- Pourbaix, D. 2004, in Spectroscopically and Spatially Resolving the Components of Close Binary Stars, ed. R. W. Hilditch, H. Hensberge, & K. Pavlovski, ASP Conf. Ser., 318, San Francisco, 132 (In the text)
- Pourbaix, D., Tokovinin, A. A., Batten, A. H., et al. 2004, A&A, 424, 727 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ragland, S., Traub, W. A., Berger, J.-P., et al. 2006, ApJ, 652, 650 [NASA ADS] [CrossRef] (In the text)
- Reimers, D., Griffin, R. F., & Brown, A. 1988, A&A, 193, 180 [NASA ADS] (In the text)
- Reimers, D., Huensch, M., Schmitt, J. H. M. M., & Toussaint, F. 1996, A&A, 310, 813 [NASA ADS]
- Reyniers, M., & Van Winckel, H. 2001, A&A, 365, 465 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Richichi, A., & Percheron, I. 2005, A&A, 434, 1201 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Richichi, A., Percheron, I., & Khristoforova, M. 2005, A&A, 431, 773 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Royer, F., Grenier, S., Baylac, M.-O., Gómez, A. E., & Zorec, J. 2002, A&A, 393, 897 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Samus, N. N. 1997, Informational Bulletin on Variable Stars, 4501, 1 (In the text)
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [NASA ADS] (In the text)
- Schmid, H. M., & Schild, H. 2002, A&A, 395, 117 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schwarz, H. E., Nyman, L.-A., Seaquist, E. R., & Ivison, R. J. 1995, A&A, 303, 833 [NASA ADS]
- Sivarani, T., Parthasarathy, M., García-Lario, P., Manchado, A., & Pottasch, S. R. 1999, A&AS, 137, 505 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Skopal A. 2005a, in The Astrophysics of Cataclysmic Variables and Related Objects, ed. J.-M. Hameury, & J.-P. Lasota, ASP Conf. Ser., 330, San Francisco, 463
- Skopal, A. 2005b, A&A, 440, 995 [NASA ADS] [CrossRef] [EDP Sciences]
- Smiljanic, R., Porto de Mello, G. F., & da Silva, L. 2007, A&A, 468, 679 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Soker, N. 2000, A&A, 357, 557 [NASA ADS] (In the text)
- Soszynski, I. 2007, ApJ, 660, 1486 [NASA ADS] [CrossRef] (In the text)
- Soszynski, I., Udalski, A., Kubiak, M., et al. 2004, Acta Astron., 54, 347 [NASA ADS] [CrossRef] (In the text)
- Tomkin, J., Lambert, D. L., Edvardsson, B., Gustafsson, B., & Nissen, P. E. 1989, A&A, 219, L15 [NASA ADS]
- Torres, G., Neuhäuser, R., & Guenther, E. W. 2002, AJ, 123, 1701 [NASA ADS] [CrossRef]
- Udry, S., Mayor, M., Andersen, J., et al. 1997, in Hipparcos - Venice '97 (ESA SP-402), ESA, Noordwijk, ed. M. Perryman, 693
- Van Eck, S., & Jorissen, A. 1999, A&A, 345, 127 [NASA ADS]
- Van Eck, S., Jorissen, A., Udry, S., Mayor, M., & Pernier, B. 1998, A&A, 329, 971 [NASA ADS] (In the text)
- Van Winckel, H. 2003, ARA&A, 41, 391 [NASA ADS] [CrossRef]
- Van Winckel, H. 2007, Baltic Astronomy, 16, 112 [NASA ADS] (In the text)
- Verhoelst, T., van Aarle, E., & Acke, B. 2007, A&A, 470, L21 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Welty, A. D., & Wade, R. A. 1995, AJ, 109, 326 [NASA ADS] [CrossRef] (In the text)
- Wheatley, P. J., Mukai, K., & de Martino, D. 2003, MNRAS, 346, 855 [NASA ADS] [CrossRef]
- Whitelock, P., & Marang, F. 2001, MNRAS, 323, L13 [NASA ADS] [CrossRef] (In the text)
- Whitelock, P. A. 1987, PASP, 99, 573 [NASA ADS] [CrossRef]
- Wood P. R. 2000, PASA, 17, 18 [NASA ADS]
- Wood, P. R., Alcock, C., Allsman, R. A., et al. 1999, in Asymptotic Giant Branch Stars, IAU Symp., 191, 151
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS]
- Zamanov, R. K., Bode, M. F., Melo, C. H. F., et al. 2006, MNRAS, 365, 1215 [NASA ADS]
Footnotes
- ... M giants
![[*]](/icons/foot_motif.gif)
- Based on observations carried out at the Swiss telescope installed at the Observatoire de Haute Provence (OHP, France), and at the 1.93-m OHP telescope.
- ... Frankowski
![[*]](/icons/foot_motif.gif)
- Postdoctoral Researcher, FNRS, Belgium. Currently at Department of Physics, Technion-Israel Institute of Technology, Haifa 32000, Israel.
- ... Famaey
![[*]](/icons/foot_motif.gif)
- Postdoctoral Researcher, FNRS, Belgium.
- ... Eck
![[*]](/icons/foot_motif.gif)
- Research Associate, FNRS, Belgium.
- ... Paper I
![[*]](/icons/foot_motif.gif)
- Note that the short-period orbit of HD 115521, whose Keplerian nature is in fact questionable (see Sect. 3.3.2 of Paper I), has not been included in the figure.
- ...
field
![[*]](/icons/foot_motif.gif)
- Systems with sdO/sdB or white dwarf companions (like barium stars) have been removed from that sample (in order not to duplicate systems between the bottom and the top panels of Fig. 2).
- ...
field
![[*]](/icons/foot_motif.gif)
- In the sample of KIII binaries in the field, there are several systems with non-zero eccentricities falling to the left of the periastron envelope. Most of these systems are either pre-main sequence (PMS) binaries (mostly from Torres et al. 2002) or Algols (Nelson & Eggleton 2001; Eggleton 2006), i.e., (post-)mass-transfer systems (see also the discussion in relation with Fig. 6 of Paper II). The successive panels in Fig. 2 are meant to illustrate the evolution of the orbital elements as the system evolves from both components on the main sequence to one component being a white dwarf. Therefore, the Algols or PMS systems present in the sample of field KIII stars distort the picture, and should actually be disregarded.
- ...
period
![[*]](/icons/foot_motif.gif)
- Pourbaix et al. (2004) have presented a spectacular figure (their Fig. 4) showing the minimum orbital period as a function of the B-V index for the whole Ninth Catalogue of Spectroscopic Binary Orbits (SB9).
- ... 10
![[*]](/icons/foot_motif.gif)
- de Ruyter et al. (2006) suggest that
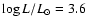 may be typical for post-AGB stars, and Fig. 5
reveals that M giants may be as dim as
may be typical for post-AGB stars, and Fig. 5
reveals that M giants may be as dim as
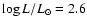 .
.
- ... operating
![[*]](/icons/foot_motif.gif)
- Among
the 4 MIII stars checked for the presence/absence of Tc (HD 2411 =
TV Psc; HD 132 813 = RR UMi; HD 187 076 =
 Sge;
HD 42 995 =
Sge;
HD 42 995 =  Gem; Little et al. 1987), none has been flagged as exhibiting
Tc lines (only in HD 2411 is the presence of Tc qualified as doubtful;
note that this M3III star falls beyond the 200
Gem; Little et al. 1987), none has been flagged as exhibiting
Tc lines (only in HD 2411 is the presence of Tc qualified as doubtful;
note that this M3III star falls beyond the 200 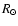 tidal envelope in Figs. 1 and 2,
i.e., in the region occupied by barium stars).
tidal envelope in Figs. 1 and 2,
i.e., in the region occupied by barium stars).
- ... S stars
![[*]](/icons/foot_motif.gif)
- Tc-poor S stars owe their chemical peculiarities to mass transfer in a binary system; they are thus called extrinsic S stars in what follows (Van Eck & Jorissen 1999).
All Tables
Table 1:
Radii of M giants in binary systems derived from the Stefan-Boltzmann
law (
![]() )
and from high-angular resolution measurements (
)
and from high-angular resolution measurements (
![]() ).
The labels
``UD'' and ``LD'' refer to uniform discs or limb-darkened discs, respectively.
Luminosities are derived from the
Hipparcos parallaxes
).
The labels
``UD'' and ``LD'' refer to uniform discs or limb-darkened discs, respectively.
Luminosities are derived from the
Hipparcos parallaxes ![]() ,
from the 2MASS K magnitudes and bolometric corrections
BCK derived from the (V-K , BCK) analytical relation from
Bessell & Wood (1984), which is in good agreement with
the more recent calibration of Bessell et al. (1998). The Johnson VJmagnitude from the Hipparcos catalogue has been used. Effective
temperatures are derived from the VJ-K indices using the ``bcd'' calibration of Bessell et al. (1998).
,
from the 2MASS K magnitudes and bolometric corrections
BCK derived from the (V-K , BCK) analytical relation from
Bessell & Wood (1984), which is in good agreement with
the more recent calibration of Bessell et al. (1998). The Johnson VJmagnitude from the Hipparcos catalogue has been used. Effective
temperatures are derived from the VJ-K indices using the ``bcd'' calibration of Bessell et al. (1998).
All Figures
![\begin{figure}
\par\includegraphics[width=9cm]{10703f1.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg15.gif) |
Figure 1:
The
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{10703f2.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg16.gif) |
Figure 2:
Same as Fig. 1 in sequential order, with the
addition of field K giants from the Ninth Catalogue of Spectroscopic
Binary Orbits (Pourbaix et al. 2004), from which the systems with
sdO/sdB or white dwarf companions (like barium stars) have been
removed (since they are plotted in the bottom panel).
For the sake of clarity, all panels start at a period of 30 d,
although field K giants may be found in binary systems with periods
as short as 4 d (see Fig. 6 of Paper II, Frankowski et al. 2009).
The lines and symbols are as in
Fig. 1 except for the the S and Ba star panel
where the
crosses denote S stars with an unexpectedly large mass function
(HD 191 589 and HDE 332 077), open triangles denote mild Barium stars,
and filled triangles strong barium stars and Tc-poor S stars.
Mild and strong barium
stars are separated according to the photometric DDO index
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10703f3.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg21.gif) |
Figure 3: One among the various possible evolution channels for a system consisting initially of two low- or intermediate-mass main-sequence stars. The left column corresponds to the normal evolutionary sequence of single stars, while the right column represents the various classes of stars with chemical peculiarities specifically produced by mass transfer across the binary system. Hatched circles denote stars with atmospheres enriched in carbon or heavy elements (see Jorissen 2003a, for a detailed description of the various stellar families involved). Other evolutionary channels would end with a cataclysmic variable or go through an Algol phase, and are not depicted here (see, e.g., Nelson & Eggleton 2001; Eggleton 2006, for details). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10703f4.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg50.gif) |
Figure 4: The orbital-period - radius diagram for M giants in binary systems. The radii are derived from the Stefan-Boltzmann law applied on the effective temperatures and luminosities presented in Fig. 5. The solid lines display the Roche radii for the corresponding period, for two different choices of the component masses. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10703f5.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg51.gif) |
Figure 5:
Comparison of the location of M giants in binary systems (open circles) and Tc-rich S stars (filled triangles) in the HR diagram. The filled circle
corresponds to the M giant HD 165 374 which possibly hosts a WD companion. Star symbols correspond to Tc-poor S stars and crosses to S
stars with Tc doubtful. The data for S stars are from Van Eck et al. (1998). For M stars, they are derived as explained in the caption of Table 1. The evolutionary tracks are from
Charbonnel et al. (1996) for Z=0.02 stars with masses 1.25 and 1.5 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{10703f6.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg59.gif) |
Figure 6:
Same as Fig. 5 but in terms of V-K and
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{10703f7.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg67.gif) |
Figure 7:
The orbital-period as a function of (absolute)
K magnitude for
galactic M giants in binary
systems. The ordinate
axis corresponds to the K magnitude that the
M giants would have if they were put at the distance of the LMC (see
text).
The dashed line labelled ``D'' corresponds to Wood's
sequence of long secondary periods.
The solid and dotted lines correspond to the limit on the
orbital period imposed by the Roche radius (for M1 = 1.3 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{10703f8.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg69.gif) |
Figure 8:
The
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{10703f9.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg70.gif) |
Figure 9: The cumulative distribution of the mass function for M giants (solid line), K giants from open clusters (dashed line; Mermilliod et al. 2007) and S stars with WD companions (thus excluding the peculiar systems HD 191 589 and HD 332 077; Jorissen et al. 1998, dotted line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{10703f10.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg71.gif) |
Figure 10: The eccentricity-period diagram for spectroscopic binaries involving K giants in open clusters (filled squares; Mermilliod et al. 2007), and Ba and S stars (open triangles, from Jorissen et al. 1998). The vertical segments have lengths corresponding to mass functions expressed in solar masses. The diagonal dashed line delineates the region where most of the Ba/S stars are found. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{10703f11.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg75.gif) |
Figure 11:
The cumulative distribution of the companion masses for open-cluster K binaries, assuming an inclination of 90 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.6cm]{10703f12.eps}
\end{figure}](/articles/aa/full_html/2009/17/aa10703-08/Timg76.gif) |
Figure 12:
Same as Fig. 11, but in the form of histograms (thick solid line:
systems in the non-post-mass-transfer zone; thin solid line and shaded histogram: post-mass-transfer
systems).
In the post-mass-transfer region, all companions are less massive than
1.5 |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


