| Issue |
A&A
Volume 497, Number 2, April II 2009
|
|
|---|---|---|
| Page(s) | 537 - 543 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200811183 | |
| Published online | 05 March 2009 | |
Time-dependent hydrodynamical simulations of slow solar wind, coronal inflows, and polar plumes
R. Pinto1 - R. Grappin1 - Y.-M. Wang2 - J. Léorat1
1 - Observatoire de Paris, LUTH, CNRS, 92195 Meudon, France
2 - Space Science Division, Naval
Research Laboratory,Washington, DC
20375-5352, USA
Received 17 October 2008 / Accepted 21 February 2009
Abstract
Aims. We explore the effects of varying the areal expansion rate and coronal heating function on the solar wind flow.
Methods. We use a one-dimensional, time-dependent hydrodynamical code. The computational domain extends from near the photosphere, where nonreflecting boundary conditions are applied, to 30  ,
and includes a transition region where heat conduction and radiative losses dominate.
,
and includes a transition region where heat conduction and radiative losses dominate.
Results. We confirm that the observed inverse relationship between asymptotic wind speed and expansion factor is obtained if the coronal heating rate is a function of the local magnetic field strength. We show that inflows can be generated by suddenly increasing the rate of flux-tube expansion and suggest that this process may be involved in the closing-down of flux at coronal hole boundaries. We also simulate the formation and decay of a polar plume, by including an additional, time-dependent heating source near the base of the flux tube.
Key words: interplanetary medium - solar wind - Sun: corona - Sun: magnetic fields
1 Introduction
The origin of the slow solar wind is the subject of much ongoing debate. Because it has different compositional properties and shows greater temporal and spatial variability, its sources are often assumed to lie outside the coronal holes that produce high-speed wind, with closed field regions being a favored choice (see Zurbuchen 2007, and references therein). However, an alternative viewpoint is that both high- and low-speed winds come from coronal holes (defined as open field regions), and that it is the rate of flux-tube expansion (Whang et al. 2005; Arge & Pizzo 2000; Wang & Sheeley 1990; Poduval & Zhao 2004; Levine et al. 1977) and/or the location of the coronal heating (Wang 1994b; Leer & Holzer 1980; Hammer 1982; Sandbaek et al. 1994; Hollweg 1986; Wang 1994a; Withbroe 1988; Cranmer et al. 2007; Wang 1993) that controls the wind speed at 1 AU. Thus, the slow wind tends to be highly variable because it emanates from just inside the boundaries of large coronal holes and from the small, rapidly evolving holes that form near active regions at sunspot maximum. Both of these sources are characterized by rapidly diverging fields.
Adopting the view that open field regions may give rise to a wide variety of solar wind flows, we employ a time-dependent hydrodynamical code that includes the chromospheric-coronal transition region to further explore the dependence of the flow properties on the expansion factor and the form of the coronal heating function. The one-dimensional code (discussed in detail by Grappin et al., in preparation) incorporates nonreflecting boundary conditions and allows us to generate nonsteady transonic wind flows by varying the coronal parameters in time. After describing the equations and procedure in Sect. 2, we review the relationship between wind speed, flux-tube divergence, and coronal heating (Sect. 3), show how coronal inflows can be generated by rapid changes in the heating rate and expansion factor (Sect. 4), and construct a simple model for the growth and decay of a polar plume (Sect. 5). Our conclusions are summarized in Sect. 7.
2 Method
The one-fluid flow is taken to be along the radially oriented axis of
a diverging flux tube, so that the bulk velocity u, (proton or
electron) number density n, mass density
 ,
temperature T, thermal pressure p = 2nkT, and magnetic field Bare functions of heliocentric distance r and time t only. Wave
acceleration is omitted. The mass, momentum, and energy conservation
equations are then given by
,
temperature T, thermal pressure p = 2nkT, and magnetic field Bare functions of heliocentric distance r and time t only. Wave
acceleration is omitted. The mass, momentum, and energy conservation
equations are then given by
In the energy equation, the ratio of specific heats has been set to 5/3, while
 ,
,
 ,
and
,
and  respectively denote
the mechanical heating flux, the
conductive heating flux, and the radiative loss rate.
respectively denote
the mechanical heating flux, the
conductive heating flux, and the radiative loss rate.
The magnetic field is assigned the form
where
 and
and

 .
The field strength
thus falls off as
.
The field strength
thus falls off as  for
for

 and as
r-2 for
and as
r-2 for 
 .
.
The mechanical heating flux  function is assigned
different forms
in the subsequent sections. Firstly, we assign it a standard
phenomenological form (see, e.g., Withbroe 1988)
function is assigned
different forms
in the subsequent sections. Firstly, we assign it a standard
phenomenological form (see, e.g., Withbroe 1988)
where
 represents an arbitrary damping length and
represents an arbitrary damping length and
 is given by Eq. (4),
is given by Eq. (4),
 being the fluxtube's cross sectional area.
Secondly, we assume the heating rate to be proportional to a power
of B such that
being the fluxtube's cross sectional area.
Secondly, we assume the heating rate to be proportional to a power
of B such that
We also consider a combination of these two forms at a later time to study the effects of two separate heating sources and simulate the formation and decay of a polar plume. We assume a Spitzer-Härm conductive heating flux
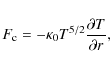 |
(7) |
where
 (in cgs units), but we modify it in two
ways: a) at distances larger than 5 solar radii we limit the flux to 2/3
the Spitzer-Härm value, the width of the transition being 1 solar
radius, so to prevent it from being larger than its collisionless
estimation (see, e.g., Hollweg 1986,1976); b) we use an additional numerical
conductive term of the form
(in cgs units), but we modify it in two
ways: a) at distances larger than 5 solar radii we limit the flux to 2/3
the Spitzer-Härm value, the width of the transition being 1 solar
radius, so to prevent it from being larger than its collisionless
estimation (see, e.g., Hollweg 1986,1976); b) we use an additional numerical
conductive term of the form
 such that
such that
 at the transition region
(hereafter TR), where
at the transition region
(hereafter TR), where  is the
sound speed and
is the
sound speed and  the width of the TR. This term is negligible
compared to the Spitzer-Härm term everywhere except around the
Transition Region, where it
moderates the conductive flux and helps in keeping the mesh
size not too small (see e.g, Linker et al. 2001, for comparable prescriptions).
The radiative loss function is given by
the width of the TR. This term is negligible
compared to the Spitzer-Härm term everywhere except around the
Transition Region, where it
moderates the conductive flux and helps in keeping the mesh
size not too small (see e.g, Linker et al. 2001, for comparable prescriptions).
The radiative loss function is given by
![\begin{displaymath}\Lambda(T) = 10^{-22}10^{[\log_{10}(T/T_{\rm M})]^2}\chi(T)
\end{displaymath}](/articles/aa/full_html/2009/14/aa11183-08/img56.png) |
(8) |
(based on Athay 1986), where
 equals unity for T>0.02 MK
and varies linearly from 0 to 1 for
0.01<T<0.02 MK.
equals unity for T>0.02 MK
and varies linearly from 0 to 1 for
0.01<T<0.02 MK.
 equals 0.2 MK.
equals 0.2 MK.
We employ a nonuniform grid of 640 points between the solar surface
(where
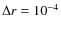
 )
and
31.5
)
and
31.5  (where
(where
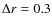
 ). Time integration is
done with a Runge-Kutta scheme of order 3, while an implicit
finite-difference scheme of order 6 is used for the spatial dimension,
except when computing temperature gradients in the conductive term,
when an explicit scheme of order 2 is applied. Numerical filtering is
employed to increase the stability of the schemes (Lele 1992).
). Time integration is
done with a Runge-Kutta scheme of order 3, while an implicit
finite-difference scheme of order 6 is used for the spatial dimension,
except when computing temperature gradients in the conductive term,
when an explicit scheme of order 2 is applied. Numerical filtering is
employed to increase the stability of the schemes (Lele 1992).
Boundary conditions are imposed by integrating the characteristic forms of Eqs. (1)-(3), as in Grappin et al. (1997). At the inner boundary, disturbances may propagate freely out of the system but not into it.
Starting with a cool (6000 K), static atmosphere, the corona and
transition region are constructed as follows. During the first phase,
which lasts for
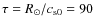 min (
min (
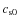 being the isothermal sound speed corresponding to 1 MK), the
medium is heated and only
being the isothermal sound speed corresponding to 1 MK), the
medium is heated and only
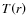 is solved for, with
is solved for, with
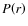 being given by the equation of hydrostatic
equilibrium. This preliminary phase allows considerable CPU time
savings. During the second phase (
being given by the equation of hydrostatic
equilibrium. This preliminary phase allows considerable CPU time
savings. During the second phase (
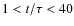 ), the full
equations are integrated, and a supersonic wind is generated by
lowering the pressure at the outer boundary using the ingoing
characteristics; this artificial suction stops as soon as the flow
there becomes supersonic, since thereafter no signal can propagate
into the computational domain from outside. The simulations described
here were performed by starting at the end of the second phase and
varying the coronal parameters. We note that, even at
), the full
equations are integrated, and a supersonic wind is generated by
lowering the pressure at the outer boundary using the ingoing
characteristics; this artificial suction stops as soon as the flow
there becomes supersonic, since thereafter no signal can propagate
into the computational domain from outside. The simulations described
here were performed by starting at the end of the second phase and
varying the coronal parameters. We note that, even at
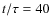 ,
the velocities are still decreasing with time in the transition zone;
however, a steady-state equilibrium has been established near the top
of this region (T = 0.5 MK), which we henceforth refer to as the
``coronal base''.
Other details of the model will be discussed
thoroughly in a forthcoming paper.
,
the velocities are still decreasing with time in the transition zone;
however, a steady-state equilibrium has been established near the top
of this region (T = 0.5 MK), which we henceforth refer to as the
``coronal base''.
Other details of the model will be discussed
thoroughly in a forthcoming paper.
3 Dependence of the wind speed on the coronal parameters
For trial purposes, the coronal heating flux is first assigned the
standard phenomenological form given by Eq. (5). The
effect of varying
the parameters
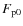 ,
,
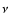 ,
and
,
and  is illustrated by the four
steady-state wind solutions in Fig. 1. When the magnitude
is illustrated by the four
steady-state wind solutions in Fig. 1. When the magnitude
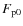 of the heating is raised from 4 to
of the heating is raised from 4 to
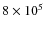 erg cm-2 s-1 but the other parameters are fixed, the
maximum temperature
erg cm-2 s-1 but the other parameters are fixed, the
maximum temperature
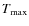 (attained at
(attained at
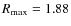
 )
increases by 17%, while the flow speed u1 at the
outer boundary increases by 14%. The main effect, however, is to
double the mass flux at the coronal base: because of the dominance of
the gravitational potential energy near the solar surface,
)
increases by 17%, while the flow speed u1 at the
outer boundary increases by 14%. The main effect, however, is to
double the mass flux at the coronal base: because of the dominance of
the gravitational potential energy near the solar surface,
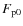 scales roughly as
scales roughly as
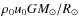 .
.
If now the magnetic falloff index 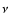 is increased from 2 to 3 while
keeping
is increased from 2 to 3 while
keeping
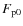 fixed
at
fixed
at
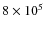 erg cm-2 s-1, the result (dashed
curves in Fig. 1) is that
erg cm-2 s-1, the result (dashed
curves in Fig. 1) is that
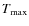 falls by 11%
(mainly due
to the effect of adiabatic expansion), n0u0 remains essentially
unchanged, and u1 decreases by 6%. This result differs from that
obtained when the flux-tube divergence rate is increased but the
coronal temperature is arbitrarily held fixed, in which case the mass
flux at the Sun rises steeply and the asymptotic wind speed undergoes
a much larger decrease (Wang & Sheeley 1991).
falls by 11%
(mainly due
to the effect of adiabatic expansion), n0u0 remains essentially
unchanged, and u1 decreases by 6%. This result differs from that
obtained when the flux-tube divergence rate is increased but the
coronal temperature is arbitrarily held fixed, in which case the mass
flux at the Sun rises steeply and the asymptotic wind speed undergoes
a much larger decrease (Wang & Sheeley 1991).
The dotted curves in Fig. 1 show the solution obtained when
 is decreased from 1 to 0.5
is decreased from 1 to 0.5  ,
keeping
,
keeping 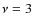 and
and
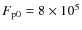 erg cm-2 s-1. The location of
the temperature maximum moves inward as expected (from 1.73 to
1.48
erg cm-2 s-1. The location of
the temperature maximum moves inward as expected (from 1.73 to
1.48  ),
),
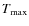 decreases by 4%, while the
temperatures fall significantly in the region
decreases by 4%, while the
temperatures fall significantly in the region
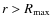 .
At
the same time, n0u0 increases by 32% and u1 drops steeply from
373 to 274 km s-1.
.
At
the same time, n0u0 increases by 32% and u1 drops steeply from
373 to 274 km s-1.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig1.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg71.png) |
Figure 1:
Four steady-state wind solutions obtained by varying the
base flux density
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig2.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg72.png) |
Figure 2:
Three steady-state wind solutions obtained by varying the
magnetic falloff index in the coronal heating function
|
| Open with DEXTER | |
These calculations suggest that the parameter to which the asymptotic
wind speed is most sensitive is the location of the coronal heating.
In particular, depositing the bulk of the energy near the coronal base
results in lower wind speeds and higher mass fluxes, whereas
depositing it near the sonic point produces higher wind speeds and
lower mass fluxes (see Leer & Holzer 1980). Here, the damping length
 has
been treated as an arbitrary parameter. However, if the source of the
heating is magnetic in nature, its spatial distribution might be
expected to depend on
has
been treated as an arbitrary parameter. However, if the source of the
heating is magnetic in nature, its spatial distribution might be
expected to depend on
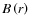 ,
with the damping length being
smaller, the more rapidly the field strength falls off with height
(for example,
,
with the damping length being
smaller, the more rapidly the field strength falls off with height
(for example,
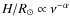 ,
where
,
where
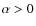 ). Indeed, Cranmer et al. (2007) have developed a self-consistent model for
coronal heating and solar wind acceleration, in which the wind speed
and mass flux are determined by the radial gradient of the Alfvén
speed. In this model, the coronal hole is heated by the damping of
Alfvén waves via a turbulent cascade; the turbulent heating rate
is inversely proportional to the transverse correlation length
). Indeed, Cranmer et al. (2007) have developed a self-consistent model for
coronal heating and solar wind acceleration, in which the wind speed
and mass flux are determined by the radial gradient of the Alfvén
speed. In this model, the coronal hole is heated by the damping of
Alfvén waves via a turbulent cascade; the turbulent heating rate
is inversely proportional to the transverse correlation length
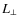 ,
which in turn varies as B-1/2 (cf. Hollweg 1986).
,
which in turn varies as B-1/2 (cf. Hollweg 1986).
To demonstrate that a coronal mechanical heating flux that depends
mainly on the
local magnetic field strength will necessarily lead to an inverse
relationship between wind speed and expansion factor, let us use the
heating flux as given by Eq. (6)
where, for illustrative purposes, we take 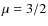 .
Figure 2 shows
the steady-state wind solutions obtained by setting
.
Figure 2 shows
the steady-state wind solutions obtained by setting 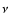 equal to 2,
3, 4 and 5. As the magnetic falloff rate increases, the location of the
temperature maximum moves inward, its peak value decreases, n0u0increases, the outer region
equal to 2,
3, 4 and 5. As the magnetic falloff rate increases, the location of the
temperature maximum moves inward, its peak value decreases, n0u0increases, the outer region
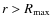 becomes cooler, and the flow velocity at the outer
boundary drops. Similar results are obtained for any
becomes cooler, and the flow velocity at the outer
boundary drops. Similar results are obtained for any 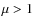 .
.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig3.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg79.png) |
Figure 3:
Time evolution of the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig4}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg80.png) |
Figure 4:
Here, the magnetic falloff index |
| Open with DEXTER | |
4 Generating coronal inflows
During times of high solar activity, white-light coronagraph
observations often show swarms of small-scale features moving sunward
in the region 2
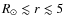
 (Sheeley & Wang 2002). These inflow events are concentrated around the
heliospheric current/plasma sheet. They characteristically start as
small density enhancements that accelerate from rest and leave a
narrow, dark trail in their wake, subsequently decelerating as they
approach the inner edge of the coronagraph field of view. Although
some of these events are clearly CME-associated, the majority do not
occur in the immediate aftermath of CMEs and appear to represent the
closing-down of magnetic flux at coronal hole boundaries.
(Sheeley & Wang 2002). These inflow events are concentrated around the
heliospheric current/plasma sheet. They characteristically start as
small density enhancements that accelerate from rest and leave a
narrow, dark trail in their wake, subsequently decelerating as they
approach the inner edge of the coronagraph field of view. Although
some of these events are clearly CME-associated, the majority do not
occur in the immediate aftermath of CMEs and appear to represent the
closing-down of magnetic flux at coronal hole boundaries.
In the simulation shown in Fig. 3, we have started with
the  wind solution of Fig. 2 and then
instantaneously
reduced
wind solution of Fig. 2 and then
instantaneously
reduced
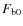 from 8 to
from 8 to
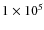 erg cm-2 s-1(see Eq. (6)).
The radial
profiles of T, u, and n are plotted at a succession of times
erg cm-2 s-1(see Eq. (6)).
The radial
profiles of T, u, and n are plotted at a succession of times
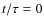 ,
2, 4, 10, 20 and 40 where
,
2, 4, 10, 20 and 40 where
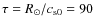 min and t = 0 is here defined as the moment when the heating is
turned down. Although the temperatures almost immediately drop toward their
new equilibrium values, the flow velocities and densities require on
the order of a global sound-crossing time (
min and t = 0 is here defined as the moment when the heating is
turned down. Although the temperatures almost immediately drop toward their
new equilibrium values, the flow velocities and densities require on
the order of a global sound-crossing time (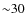
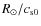 )
to adjust to the greatly reduced heating rate. In the
expanding subsonic regime, the flow separates into inward- and
outward-moving components, and the density falls. Outflow from the Sun
is reestablished after
)
to adjust to the greatly reduced heating rate. In the
expanding subsonic regime, the flow separates into inward- and
outward-moving components, and the density falls. Outflow from the Sun
is reestablished after
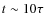 ,
and the system reaches a steady
state with reduced velocities and densities by
,
and the system reaches a steady
state with reduced velocities and densities by
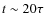 .
While
this simulation produces modest inflows near the Sun, it is unclear
how a large decrease in
.
While
this simulation produces modest inflows near the Sun, it is unclear
how a large decrease in
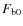 might be effected in reality.
might be effected in reality.
The closing-down of magnetic flux requires that open field lines of
opposite polarity be brought together and reconnected with each other.
Since the local field strength is small in the vicinity of the
polarity reversal, any flux tube that undergoes this merging process
must diverge rapidly with radial distance, and the outward extension
of this flux tube must experience a large reduction in its heating
rate according to Eq. (6). Instead of
decreasing the amplitude of the heating function as in the simulation
of Fig. 3, let us now keep
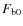 fixed at
fixed at
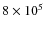 erg cm-2 s-1 but increase the magnetic falloff index
erg cm-2 s-1 but increase the magnetic falloff index
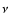 from 2 to 10. As shown in Fig. 4, the velocity
profile again
collapses and inflows are generated below the sonic point, which moves
progressively outward. In this case, because the heating remains
strong near the solar surface, the density increases with time at low
heights, where hydrostatic equilibrium is approached. Above
from 2 to 10. As shown in Fig. 4, the velocity
profile again
collapses and inflows are generated below the sonic point, which moves
progressively outward. In this case, because the heating remains
strong near the solar surface, the density increases with time at low
heights, where hydrostatic equilibrium is approached. Above 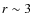
 ,
however, the inward velocities continue to grow to
amplitudes of nearly 100 km s-1 and n(r) falls sharply. The
squeezing-out of plasma from the flux
tubes in this region should facilitate the merging and reconnection
process.
,
however, the inward velocities continue to grow to
amplitudes of nearly 100 km s-1 and n(r) falls sharply. The
squeezing-out of plasma from the flux
tubes in this region should facilitate the merging and reconnection
process.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig5.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg88.png) |
Figure 5:
Effect of an additional heating term near the coronal base,
of the form
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig6.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg89.png) |
Figure 6: Radial profiles of the heating function, conductive heating flux, and enthalpy flux for the plume and interplume solutions. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig7.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg90.png) |
Figure 7:
Formation of a plume. With the initial state being given by
the interplume solution (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig8.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg91.png) |
Figure 8:
Decay of a plume. With the initial state now being given by
the plume solution (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig9}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg92.png) |
Figure 9:
Peak inflow amplitude
|
| Open with DEXTER | |
5 Formation of a polar plume
Coronal plumes are raylike features aligned along open field lines and
characterized by densities  2-5 times higher than the
surrounding interplume regions of the coronal hole. As shown in
Wang (1994a), the enhanced densities in plumes require the presence of
a strong heating source near their bases. Indeed, plumes are found to
overlie EUV bright points, and these small bipoles appear to be
undergoing interchange reconnection with the unipolar flux
concentrations inside coronal holes.
2-5 times higher than the
surrounding interplume regions of the coronal hole. As shown in
Wang (1994a), the enhanced densities in plumes require the presence of
a strong heating source near their bases. Indeed, plumes are found to
overlie EUV bright points, and these small bipoles appear to be
undergoing interchange reconnection with the unipolar flux
concentrations inside coronal holes.
The effect of two separate heating sources, one spread over a distance
on the order of a solar radius, the other concentrated at the base of
the flux tube, is illustrated by the steady-state wind solution in
Fig. 5. Here the total heating function is taken to be
of the form
![\begin{displaymath}F_{\rm plume} = F_{\rm b0}\left(B/B_0\right)^{3/2} +
F_{\rm...
.../B_0\right)\exp\left[-\left(r-R_\odot\right)/H_{\rm p}\right],
\end{displaymath}](/articles/aa/full_html/2009/14/aa11183-08/img94.png) |
(9) |
with
 erg cm-2 s-1 and
erg cm-2 s-1 and  .
The ``interplume'' solution, for which
.
The ``interplume'' solution, for which
 ,
is indicated
by the dotted curves. The plume solution (solid curves) has
,
is indicated
by the dotted curves. The plume solution (solid curves) has
 erg cm-2 s-1 and
erg cm-2 s-1 and

 .
The extra base heating causes T(r) to
increase near the coronal base but to decrease at greater heights; at
the same time, u(r) falls and n(r) rises everywhere. The factor of
.
The extra base heating causes T(r) to
increase near the coronal base but to decrease at greater heights; at
the same time, u(r) falls and n(r) rises everywhere. The factor of
 4 increase in the density is accompanied by a sharp rise in the
conductive heating flux
4 increase in the density is accompanied by a sharp rise in the
conductive heating flux
 conducted
downward into
the transition region and by a large increase in the outward enthalpy
flux
conducted
downward into
the transition region and by a large increase in the outward enthalpy
flux
 (Fig. 6).
(Fig. 6).
Figure 7 shows how the plume forms as the base heating
rate
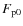 is suddenly raised from 0 to
is suddenly raised from 0 to
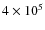 erg cm-2 s-1. The velocities increase during the
first several hours, but subsequently fall below the initial
(interplume) values as the densities continue to rise and the plasma
above the coronal base cools. The reverse process, in which the base
heating is suddenly switched off, is shown in Fig. 8. The
velocities initially decrease, even becoming slightly negative
(
erg cm-2 s-1. The velocities increase during the
first several hours, but subsequently fall below the initial
(interplume) values as the densities continue to rise and the plasma
above the coronal base cools. The reverse process, in which the base
heating is suddenly switched off, is shown in Fig. 8. The
velocities initially decrease, even becoming slightly negative
(
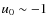 km s-1) near the coronal base; the equilibrium
profile, in which the speeds are everywhere higher than the plume
values, is attained only after
km s-1) near the coronal base; the equilibrium
profile, in which the speeds are everywhere higher than the plume
values, is attained only after  1 day. We note that it takes as
long as
1 day. We note that it takes as
long as  5 h. for the densities to drop by a factor of two, a
result that is consistent with the observed tendency for EUV ``plume
haze'' to linger well after the underlying bright point has faded.
5 h. for the densities to drop by a factor of two, a
result that is consistent with the observed tendency for EUV ``plume
haze'' to linger well after the underlying bright point has faded.
6 Heating timescale and inflow amplitudes
The inflows observed in Figs. 3, 4 and 8,
as well as the ``jet'' shown in
Fig. 7, are transient structures which propagate away
from a well defined region where the volumetric heating rate
changes. These sound wavefronts are the response to the pressure variations
which correspond to the volumetric heating rate changes within that
region. Take for example the case described in Fig. 4,
where the magnetic falloff index 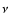 was increased abruptly from 2
to 10, which translates into a decrease in the heating rate in the
region between
was increased abruptly from 2
to 10, which translates into a decrease in the heating rate in the
region between
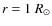 and
and
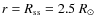 (for
(for
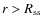 ,
,
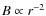 at all times; see Eq. (4) for the
definition of the magnetic field and Eq. (6) for the
heating flux used). We observe the evolution of a negative velocity
perturbation
at all times; see Eq. (4) for the
definition of the magnetic field and Eq. (6) for the
heating flux used). We observe the evolution of a negative velocity
perturbation
 which is superposed on the background
wind flow. The wind slows down as the wavefront passes through. The
resulting total velocity can then be negative, especially in the
lower corona (below
which is superposed on the background
wind flow. The wind slows down as the wavefront passes through. The
resulting total velocity can then be negative, especially in the
lower corona (below
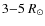 )
where the solar wind speed is
still low. This produces a transient accretion event. Figure 9
shows the maximum inflow amplitude as a function of
the transition time
)
where the solar wind speed is
still low. This produces a transient accretion event. Figure 9
shows the maximum inflow amplitude as a function of
the transition time 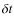 for the variation of the magnetic
falloff index
for the variation of the magnetic
falloff index 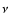 .
The transient inflow amplitude
decreases as
.
The transient inflow amplitude
decreases as 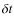 increases, i.e, as the heating variation
becomes less and less abrupt. The inflow peak velocity only
drops down to zero for
increases, i.e, as the heating variation
becomes less and less abrupt. The inflow peak velocity only
drops down to zero for
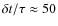 ,
which
is much longer than the sound-crossing time
,
which
is much longer than the sound-crossing time
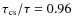 of
the region where the heating rate changes. The position of the inflow
peak velocity (
of
the region where the heating rate changes. The position of the inflow
peak velocity (
 ), its spatial width (
), its spatial width (
 )
and the final stationary state do not depend on
)
and the final stationary state do not depend on  .
.
7 Conclusions
We have used a one-dimensional hydrodynamic code to demonstrate how variations in the coronal heating function can produce a wide variety of solar wind flows. In particular, we find that:
- 1.
- The observed inverse correlation between wind speed and expansion factor can be explained if the heating rate depends mainly on the local magnetic field strength. In that case, most of the heating in a rapidly diverging field will occur well inside the sonic point, resulting in a large mass flux at the coronal base and a low flow speed far from the Sun.
- 2.
- Strong inflows can be generated in the subsonic region by decreasing the local heating rate. Such a decrease might occur during the closing-down of flux, when opposite-polarity field lines merge at a neutral sheet. The evacuation of the flux tubes would further accelerate the merging and reconnection process.
- 3.
- Densities comparable to those observed in polar plumes can be
obtained by depositing a large amount of energy just above the coronal
base. When this extra heating is switched on, the temperature rises
locally but falls at greater heights, the densities progressively
increase all along the flux tube, while the velocities initially
increase but subsequently decrease below their initial values. The
process is reversed when the base heating is switched off. In either
case, a steady-state equilibrium is reached only after
 1 day,
which may explain why coronal plumes appear to evolve more slowly than
their underlying EUV bright points.
1 day,
which may explain why coronal plumes appear to evolve more slowly than
their underlying EUV bright points.
Our future objective is to extend the numerical code to two and three dimensions, while solving the full MHD equations with consistent dissipative terms. It may then be possible to provide a more physical description of the coronal heating process, generalizing the one-dimensional model of Suzuki & Inutsuka (2006), in which Alfvén waves drive compressional waves that dissipate in the corona.
Acknowledgements
This work was supported by CNRS, NASA, and the Office of Naval Research.
References
- Arge, C. N., & Pizzo, V. J. 2000, J. Geophys. Res., 105, 10465 In the text
- Athay, R. G. 1986, ApJ, 308, 975 In the text
- Cranmer, S. R., van Ballegooijen, A. A., & Edgar, R. J. 2007, ApJS, 171, 520 In the text
- Crooker, N. U., Huang, C.-L., Lamassa, S. M., et al. 2004, J. Geophys. Res. (Space Physics), 109, 3107 In the text
- Grappin, R., Cavillier, E., & Velli, M. 1997, A&A, 322, 659 In the text
- Hammer, R. 1982, ApJ, 259, 767 In the text
- Hollweg, J. V. 1976, J. Geophys. Res., 81, 1649 In the text
- Hollweg, J. V. 1986, J. Geophys. Res., 91, 4111 In the text
- Leer, E., & Holzer, T. E. 1980, J. Geophys. Res., 85, 4681 In the text
- Lele, S. K. 1992, J. Comput. Phys., 103, 16 In the text
- Levine, R. H., Altschuler, M. D., & Harvey, J. W. 1977, J. Geophys. Res., 82, 1061 In the text
- Linker, J. A., Lionello, R., Mikic, Z., & Amari, T. 2001, J. Geophys. Res., 106, 25165 In the text
- Poduval, B., & Zhao, X. P. 2004, J. Geophys. Res. (Space Physics), 109, 8102 In the text
- Sandbaek, O., Leer, E., & Hansteen, V. H. 1994, ApJ, 436, 390 In the text
- Sheeley, Jr., N. R., & Wang, Y.-M. 2002, ApJ, 579, 874 In the text
- Suzuki, T. K., & Inutsuka, S.-i. 2006, J. Geophys. Res. (Space Physics), 111, 6101 In the text
- Wang, Y.-M. 1993, ApJ, 410, L123 In the text
- Wang, Y.-M. 1994a, ApJ, 435, L153 In the text
- Wang, Y.-M. 1994b, ApJ, 437, L67 In the text
- Wang, Y.-M., & Sheeley, Jr., N. R. 1990, ApJ, 355, 726 In the text
- Wang, Y.-M., & Sheeley, Jr., N. R. 1991, ApJ, 372, L45 In the text
- Wang, Y.-M., Sheeley, Jr., N. R., Walters, J. H., et al. 1998, ApJ, 498, L165 In the text
- Whang, Y. C., Wang, Y.-M., Sheeley, N. R., & Burlaga, L. F. 2005, J. Geophys. Res. (Space Physics), 110, 3103 In the text
- Withbroe, G. L. 1988, ApJ, 325, 442 In the text
- Zurbuchen, T. H. 2007, ARA&A, 45, 297 In the text
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig1.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg71.png) |
Figure 1:
Four steady-state wind solutions obtained by varying the
base flux density
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig2.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg72.png) |
Figure 2:
Three steady-state wind solutions obtained by varying the
magnetic falloff index in the coronal heating function
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig3.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg79.png) |
Figure 3:
Time evolution of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig4}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg80.png) |
Figure 4:
Here, the magnetic falloff index |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig5.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg88.png) |
Figure 5:
Effect of an additional heating term near the coronal base,
of the form
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig6.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg89.png) |
Figure 6: Radial profiles of the heating function, conductive heating flux, and enthalpy flux for the plume and interplume solutions. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig7.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg90.png) |
Figure 7:
Formation of a plume. With the initial state being given by
the interplume solution (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig8.eps}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg91.png) |
Figure 8:
Decay of a plume. With the initial state now being given by
the plume solution (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{1183fig9}
\end{figure}](/articles/aa/full_html/2009/14/aa11183-08/Timg92.png) |
Figure 9:
Peak inflow amplitude
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



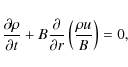
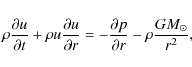
![$\displaystyle 3nk\left(\frac{\partial T}{\partial t} + u\frac{\partial T}{\part...
...ial r}\left[\frac{\left(F_{\rm h}+F_{\rm c}
\right)}{B}\right] - n^2\Lambda(T).$](/articles/aa/full_html/2009/14/aa11183-08/img35.png)
![\begin{displaymath}
B(r) = B_0\left(\frac{R_\odot}{r}\right)^\nu\left[\frac{1 +...
...\nu-2}}{1 +
\left(R_\odot/R_{\rm ss}\right)^{\nu-2}}\right],
\end{displaymath}](/articles/aa/full_html/2009/14/aa11183-08/img39.png)
![\begin{displaymath}
F_{\rm h} = F_{\rm p0}
\left(\frac{B}{B_0}\right)
\exp\left[-\frac{r-R_\odot}{H_{\rm p}}\right]
\end{displaymath}](/articles/aa/full_html/2009/14/aa11183-08/img45.png)
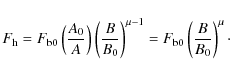
![$F_{\rm
h}(r) = F_{\rm p0}(B/B_0)\exp[-(r-R_\odot)/H]$](/articles/aa/full_html/2009/14/aa11183-08/img70.png) .
Thin solid
lines:
.
Thin solid
lines:
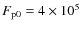 erg cm-2 s-1,
erg cm-2 s-1, 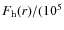 erg cm-2 s-1),
u(r)/(100 km s-1), and T(r)/(1 MK); bottom panel shows
erg cm-2 s-1),
u(r)/(100 km s-1), and T(r)/(1 MK); bottom panel shows
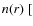 cm-3] and
cm-3] and
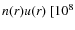 cm-2 s-1].
cm-2 s-1].
 erg cm-2 s-1
(B/B0)3/2.
Thin solid lines:
erg cm-2 s-1
(B/B0)3/2.
Thin solid lines: 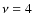 .
Dotted lines:
.
Dotted lines: 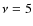 .
.![$F_{\rm p0}(B/B_0)\exp[-(r-R_\odot)/H_{\rm p}]$](/articles/aa/full_html/2009/14/aa11183-08/img87.png) .
Solid curves: steady-state ``plume'' solution with
.
Solid curves: steady-state ``plume'' solution with
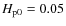
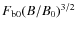 ,
with
,
with
 as a function of the
heating timescale
as a function of the
heating timescale
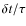 ,
where
,
where 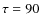 min, for the
variation of the magnetic falloff
index
min, for the
variation of the magnetic falloff
index 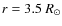 - doesn't
depend on the value of
- doesn't
depend on the value of