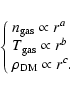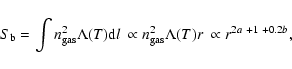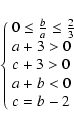| Issue |
A&A
Volume 496, Number 2, March III 2009
|
|
|---|---|---|
| Page(s) | 343 - 349 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361:200811177 | |
| Published online | 14 January 2009 | |
The outer regions of galaxy clusters: Chandra constraints on the X-ray surface brightness
S. Ettori1,2 - I. Balestra3
1 - INAF, Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
2 - INFN, Sezione di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
3 - Max-Planck-Institut für extraterrestrische Physik, Giessenbachstr. 1, 85748 Garching, Germany
Received 17 October 2008 / Accepted 20 November 2008
Abstract
Context. We study the properties of the X-ray surface brightness profiles in a sample of galaxy clusters that were observed with Chandra and have emission detectable with a signal-to-noise ratio higher than 2 per radial bin at a radius beyond
![]() .
.
Aims. Our study aims to measure the slopes in both the X-ray surface brightness and gas density profiles in the outskirts of massive clusters. These constraints are compared with similar results obtained from observations and numerical simulations of the temperature and dark-matter density profiles with the intention of presenting a consistent picture of the outer regions of galaxy clusters.
Methods. We extract the surface brightness profiles
![]() of 52 X-ray luminous galaxy clusters at z>0.3 from X-ray exposures obtained with Chandra. These objects, which are of both high X-ray surface brightness and high redshift, allow us to use Chandra either in ACIS-I or even ACIS-S configuration to survey the cluster outskirts. We estimate R200 using both a
of 52 X-ray luminous galaxy clusters at z>0.3 from X-ray exposures obtained with Chandra. These objects, which are of both high X-ray surface brightness and high redshift, allow us to use Chandra either in ACIS-I or even ACIS-S configuration to survey the cluster outskirts. We estimate R200 using both a ![]() -model that reproduces the surface brightness profiles and scaling relations from the literature. The two methods converge to comparable values. We determine the radius,
-model that reproduces the surface brightness profiles and scaling relations from the literature. The two methods converge to comparable values. We determine the radius,
![]() ,
at which the signal-to-noise ratio is higher than 2, and select the objects in the sample that satisfy the criterion
,
at which the signal-to-noise ratio is higher than 2, and select the objects in the sample that satisfy the criterion
![]() .
For the eleven selected objects, we model by a power-law function the behaviour of
.
For the eleven selected objects, we model by a power-law function the behaviour of
![]() to estimate the slope at several characteristic radii expressed as a fraction of R200.
to estimate the slope at several characteristic radii expressed as a fraction of R200.
Results. We measure a consistent steepening of the
![]() profile moving outward from
0.4R200, where an average slope of -3.6 (
profile moving outward from
0.4R200, where an average slope of -3.6 (
![]() )
is estimated. At R200, we evaluate a slope of -4.3 (
)
is estimated. At R200, we evaluate a slope of -4.3 (
![]() )
that implies a slope in the gas density profile of
)
that implies a slope in the gas density profile of ![]() -2.6 and a predicted mean value of the surface brightness in the 0.5-2 keV band of
-2.6 and a predicted mean value of the surface brightness in the 0.5-2 keV band of
![]() erg s-1 cm-2 deg-2.
erg s-1 cm-2 deg-2.
Conclusions. Combined with estimates of the outer slope of the gas temperature profile and expectations about the dark matter distribution, these measurements lie well within the physically allowed regions, allowing us to describe properly how X-ray luminous clusters behave out to the virial radius.
Key words: galaxies: clusters: general - intergalactic medium - X-rays: galaxies: clusters: - cosmology: observations - dark matter
1 Introduction
Galaxy clusters form by the hierarchical accretion of cosmic matter. The end products of this process are virialized structures that, in the X-ray band, exhibit similar radial profiles of surface brightness (e.g. Vikhlinin et al. 1999; Neumann 2005), plasma temperature (e.g. Allen et al. 2001; Vikhlinin et al. 2005) and dark matter distribution (e.g. Pointecouteau et al. 2005). These measurements have been improved due to the arcsec resolution and large collecting area of the X-ray satellites, such as Chandra and XMM-Newton, but still remain difficult because of the high signal-to-noise ratio required. On the other hand, the X-ray surface brightness is a far easier quantity to observe and define, which is rich in physical information being proportional to the emission measure of the emitting source. Recent work focused on a few local bright objects with ROSAT PSPC observations, which have low instrumental background and large field of view, to recover and characterise the X-ray surface brightness profile over a significant fraction of the virial radius (Vikhlinin et al. 1999; Neumann 2005).
In this work, we study the X-ray emission of a sample of galaxy clusters in the redshift range 0.3-1.3 observed with the arcsec resolution of Chandra (see Balestra et al. 2007), with the purpose of mapping, even at high redshift, a region out to R200and place reasonable constraints on the slope of the gas density in the outskirts of hot (kT > 3 keV) galaxy clusters.
We assume a Hubble constant of 70 h70 km s-1 Mpc-1 in a flat universe
with
![]() equal to 0.3.
All quoted errors are presented as the 1 sigma confidence level, unless otherwise stated.
equal to 0.3.
All quoted errors are presented as the 1 sigma confidence level, unless otherwise stated.
2 Preparation of the dataset
![\begin{figure}
\par\includegraphics[width=5.2cm,clip]{1177f1a.ps}\hspace*{2.3mm}...
...7f1b.ps}\hspace*{1.5mm}
\includegraphics[width=5cm,clip]{1177f1c.ps}\end{figure}](/articles/aa/full_html/2009/11/aa11177-08/Timg35.gif) |
Figure 1:
( Left) Expected R200 for an object with 4 ( dashed line)
and 8 keV ( solid line) and radius corresponding to 4 and 8 ( thickest line)
arcmin for the assumed |
| Open with DEXTER | |
Table 1:
Sample of galaxy clusters, which satisfies the criterion
![]() .
The columns show: the name of the cluster,
the observation IDs, in which ACIS configuration has been observed,
the exposure time, the adopted X-ray center,
the Galactic absorption from Dickey & Lockman (1990) in correspondence
of the X-ray center, the redshift, the gas temperature, the mean
local background, B, in counts observed in the 0.5-5 keV band,
and the average distance
.
The columns show: the name of the cluster,
the observation IDs, in which ACIS configuration has been observed,
the exposure time, the adopted X-ray center,
the Galactic absorption from Dickey & Lockman (1990) in correspondence
of the X-ray center, the redshift, the gas temperature, the mean
local background, B, in counts observed in the 0.5-5 keV band,
and the average distance ![]() of the regions used
to estimate the local background from the X-ray center.
of the regions used
to estimate the local background from the X-ray center.
To study the outskirts of X-ray emitting galaxy clusters, possibly out to the
virial region, we require bright objects located at an appropriate redshift
to allow the Chandra field-of-view to encompass the interesting area.
As shown in Fig. 1 (panel on the left) for a typical massive
object, we should expect to resolve the region within an
overdensity of 200, estimated with respect to the critical density at the
cluster redshift, using instruments with a field-of-view of radius
larger than 8 arcmin above redshift 0.2.
In the same figure, we plot the expected dependence of the radius
(as a function of R200) on both the cluster overdensity (central panel)
and the gas temperature and redshift for a given surface brightness (panel
on the right). These plots indicate that any overdensity is mapped
within a fixed fraction of R200 regardless of the cluster temperature
and/or mass concentration
(e.g.
![]() is reached at about
0.65 R200 for any
T of interest, and with variations of 2 per cent with
a concentration parameter in the range 4-8 for a given
Navarro-Frenk-White mass profile; e.g. Navarro et al. 2004),
and the surface brightness that a galaxy cluster is expected
to emit for a given T and z with respect to the value measured
at z=0 in an object with T=5 keV (e.g. the same
is reached at about
0.65 R200 for any
T of interest, and with variations of 2 per cent with
a concentration parameter in the range 4-8 for a given
Navarro-Frenk-White mass profile; e.g. Navarro et al. 2004),
and the surface brightness that a galaxy cluster is expected
to emit for a given T and z with respect to the value measured
at z=0 in an object with T=5 keV (e.g. the same ![]() value
is expected in a 10 keV system at
value
is expected in a 10 keV system at ![]() ).
).
In the present work, we consider a sample of hot (
![]() keV),
high-redshift (
0.3 < z < 1.3) galaxy clusters described in Balestra et al. (2007).
We refer to that work for details of the data reduction. We recall
that the spectral analysis was performed by extracting
the spectrum from a circular region of radius
keV),
high-redshift (
0.3 < z < 1.3) galaxy clusters described in Balestra et al. (2007).
We refer to that work for details of the data reduction. We recall
that the spectral analysis was performed by extracting
the spectrum from a circular region of radius ![]() 0.15-
0.3 R200
defined in order to maximize the signal-to-noise ratio in each cluster.
These regions contain the core emission, which has not been removed
due to the low count statistics for the high redshift systems under
consideration. On the other hand, results from observations and
numerical simulations (e.g. Santos et al. 2008; Ettori & Brighenti 2008)
indicate a lower incidence of cooling cores in clusters at higher redshift,
suggesting that our overall estimates of
0.15-
0.3 R200
defined in order to maximize the signal-to-noise ratio in each cluster.
These regions contain the core emission, which has not been removed
due to the low count statistics for the high redshift systems under
consideration. On the other hand, results from observations and
numerical simulations (e.g. Santos et al. 2008; Ettori & Brighenti 2008)
indicate a lower incidence of cooling cores in clusters at higher redshift,
suggesting that our overall estimates of
![]() should not be significantly
biased towards low values. Moreover, the measurements of the gas temperature
were used in our analysis only to infer a physical radius, which depends on the square
root of
should not be significantly
biased towards low values. Moreover, the measurements of the gas temperature
were used in our analysis only to infer a physical radius, which depends on the square
root of
![]() .
Therefore, any error affecting our temperature estimates propagates
only half of its value as a relative error on the physical radius of interest.
.
Therefore, any error affecting our temperature estimates propagates
only half of its value as a relative error on the physical radius of interest.
We prepare the exposure-corrected images in the energy band 0.5-5 keV
as described in Tozzi et al. (2003) and Ettori et al. (2004).
The exposure maps for each cluster were computed by combining different
instrumental maps at given energy, using weights defined from a thermal spectrum
with the best-fit parameters obtained from our spectral analysis.
The variations in the exposure map were not expected to be significant
in the adopted energy band
![]() .
We masked any detectable point sources with circular regions of radii
large enough to include all the emission and, in any case, larger than 2
arcsec.
We preferred to remove the point sources manually to avoid any possible
confusion with detections by automatic algorithms (i.e. wavedetect)
in proximity or within the extended emission of the clusters.
.
We masked any detectable point sources with circular regions of radii
large enough to include all the emission and, in any case, larger than 2
arcsec.
We preferred to remove the point sources manually to avoid any possible
confusion with detections by automatic algorithms (i.e. wavedetect)
in proximity or within the extended emission of the clusters.
The center of the cluster was defined to correspond to the centroid of the raw image
estimated in a box of width ![]() 10-20 arcsec around the maximum of the
image itself that had been smoothed with a moving average
in a square box of width equal to 3-5 arcsec.
10-20 arcsec around the maximum of the
image itself that had been smoothed with a moving average
in a square box of width equal to 3-5 arcsec.
The surface brightness profiles were extracted by requiring a fixed number of a minimum 50 counts per bin in the inner 10 radial bins and then collecting the counts within annulii for which the outer radius was increased at each step by a factor of 1.2.
A local background, B, was defined for each exposure by considering a region far from the X-ray center that covered a significant portion of the exposed CCD with negligible cluster emission. The estimated average value of B, its relative error, and the mean distance from the X-ray center of the region analysed to determine the background are quoted in Table 1.
We define the ``signal-to-noise'' ratio, S2N, to be the ratio of the observed surface
brightness value in each radial bin,
![]() ,
after subtraction of the estimated background,
B, to the Poissonian error in the evaluated surface brightness,
,
after subtraction of the estimated background,
B, to the Poissonian error in the evaluated surface brightness,
![]() ,
summed in quadrature with the error in the background,
,
summed in quadrature with the error in the background,
![]() :
:
![]() /
/
![]() .
The outer radius at which the signal-to-noise ratio remained above 2 was defined
to be the limit of the extension of the detectable X-ray emission,
.
The outer radius at which the signal-to-noise ratio remained above 2 was defined
to be the limit of the extension of the detectable X-ray emission,
![]() .
.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{1177f2.ps} \end{figure}](/articles/aa/full_html/2009/11/aa11177-08/Timg73.gif) |
Figure 2:
In the first column, we plot the surface brightness profiles
of the objects under examination with the fitted background
( horizontal dotted line) and the radius R200( vertical dashed line).
The panels in the second column show the signal-to-noise profiles, evaluated
as
|
| Open with DEXTER | |
We note that the local background is about a factor of 2 higher
in the ACIS-S field than in ACIS-I.
We observe no significant correlation of B with the Galactic absorption
(<
![]() cm-2 in the selected objects; a random deviation
from the null value of no-correlation is expected with probability of
0.19), indicating that we were dominated by cosmic and instrumental background.
A negligible (with probability of 0.69) correlation
is also noticed between B and the mean distance
cm-2 in the selected objects; a random deviation
from the null value of no-correlation is expected with probability of
0.19), indicating that we were dominated by cosmic and instrumental background.
A negligible (with probability of 0.69) correlation
is also noticed between B and the mean distance ![]() (see Table 1)
of the region from which the local background is extracted.
A slightly positive trend (significance of
(see Table 1)
of the region from which the local background is extracted.
A slightly positive trend (significance of
![]() )
was instead present between the estimated
uncertainty
)
was instead present between the estimated
uncertainty
![]() and the exposure time of the observation, as expected.
and the exposure time of the observation, as expected.
To scale the radial quantity with respect to a physical radius,
we estimated R200 by using the single temperature measurement
(see Table 1) and the best-fit description of
![]() with a
with a ![]() -model
(the best-fit parameters are shown in Table 2, obtained
after fitting the background-subtracted profile over all positive values
above 40 kpc) following the equation in Ettori (2000):
-model
(the best-fit parameters are shown in Table 2, obtained
after fitting the background-subtracted profile over all positive values
above 40 kpc) following the equation in Ettori (2000):
where
Table 2:
Best-fit results of the X-ray surface brightness profiles
modelled with a ![]() -model.
-model.
![]() is estimated from the scaling laws in Arnaud et al. (2005);
R200 from Eq. (1);
is estimated from the scaling laws in Arnaud et al. (2005);
R200 from Eq. (1);
![]() and
and ![]() are quoted
in unit of R200.
are quoted
in unit of R200.
For comparison, we also estimated R200 by adopting
the scaling relation with
![]() obtained
for massive clusters in Arnaud et al. (2005; similar
results were presented in Vikhlinin et al. 2005):
obtained
for massive clusters in Arnaud et al. (2005; similar
results were presented in Vikhlinin et al. 2005):
![]() kpc.
The value of
kpc.
The value of
![]() was estimated and quoted
in Table 2.
No appreciable differences were present between the different estimates of R200,
such that the mean and standard deviation of the ratio of
the two values were 1.02 and 0.06, respectively.
was estimated and quoted
in Table 2.
No appreciable differences were present between the different estimates of R200,
such that the mean and standard deviation of the ratio of
the two values were 1.02 and 0.06, respectively.
3 The surface brightness at r > R500
We investigated the X-ray surface-brightness profiles
of massive clusters at
![]() (see Fig. 1),
selecting the 11 objects with
(see Fig. 1),
selecting the 11 objects with
![]() .
The properties of these clusters are shown in Tables 1 and 2.
Examples of the analysed dataset are shown in Fig. 2.
.
The properties of these clusters are shown in Tables 1 and 2.
Examples of the analysed dataset are shown in Fig. 2.
We performed a linear least-squares fit between the logarithmic values of the radial bins and the background-subtracted X-ray surface brightness, taking into account the data errors in both coordinates with the routine FITEXY (Press et al. 1992; as implemented in IDL).
The distribution of the error-weighted mean slopes above a fixed fraction
of R200 and within
![]() is shown in Fig. 3 and
quoted in Table 3.
Overall, the error-weighted mean slope is -2.91 (with a standard deviation
in the distribution of 0.46) at
r > 0.2 R200 and
-3.59 (0.75)at
r > 0.4 R200.
For the only 3 objects for which a fit between
0.5 R200 and
is shown in Fig. 3 and
quoted in Table 3.
Overall, the error-weighted mean slope is -2.91 (with a standard deviation
in the distribution of 0.46) at
r > 0.2 R200 and
-3.59 (0.75)at
r > 0.4 R200.
For the only 3 objects for which a fit between
0.5 R200 and
![]() was possible, we measured a further steepening of the profiles, with a
mean slope of -4.43 and a standard deviation of 0.83.
was possible, we measured a further steepening of the profiles, with a
mean slope of -4.43 and a standard deviation of 0.83.
We also fitted linearly the derivative (from numerical differentiation
using three-point Lagrangian interpolation as described in Hildebrand 1987, and
implemented in the IDL function DERIV) of the logarithm
![]() over the radial range
over the radial range
![]() ,
excluding in this way the
influence of the core emission
(see values s0 and s1 in Table 3).
The average (and standard deviation
,
excluding in this way the
influence of the core emission
(see values s0 and s1 in Table 3).
The average (and standard deviation ![]() )
values of the extrapolated slopes are
then
-3.15 (0.46),
-3.86 (0.70), and
-4.31 (0.87)
at
0.4 R200,
0.7 R200 and R200, respectively.
)
values of the extrapolated slopes are
then
-3.15 (0.46),
-3.86 (0.70), and
-4.31 (0.87)
at
0.4 R200,
0.7 R200 and R200, respectively.
These values are comparable to these obtained in previous analyses.
Vikhlinin et al. (1999) found that a ![]() -model with
-model with
![]() -0.85described the surface brightness profiles in the range 0.3-1 R180 of
39 massive local galaxy clusters observed with ROSAT PSPC.
These values translate in a range of the estimate of the power-law slope
(-2.9/-4.1, from
-0.85described the surface brightness profiles in the range 0.3-1 R180 of
39 massive local galaxy clusters observed with ROSAT PSPC.
These values translate in a range of the estimate of the power-law slope
(-2.9/-4.1, from
![]() )
that includes
our estimates.
)
that includes
our estimates.
Neumann (2005) found that the stacked profiles of a few massive nearby systems
located in regions of low (<
![]() cm-3) Galactic absorption
observed by ROSAT PSPC still provided values of
cm-3) Galactic absorption
observed by ROSAT PSPC still provided values of ![]() around 0.8 at
R200, with a power-law slope that increased from -3, when the fit was
done over the radial range
[0.1, 1] R200, to
-5.7+1.5-1.2 over
[0.7, 1.2] R200.
around 0.8 at
R200, with a power-law slope that increased from -3, when the fit was
done over the radial range
[0.1, 1] R200, to
-5.7+1.5-1.2 over
[0.7, 1.2] R200.
These observational results were supported by hydrodynamical simulations
of X-ray emitting galaxy clusters
performed with the Tree+SPH code GADGET-2 from Roncarelli et al. (2006).
In the most massive systems, they measured a steepening of
![]() ,
independently
from the physics adopted in treating the baryonic mass, with a slope of
-4, -4.5, and -5.2 when estimated for the radial range 0.3-
1.2 R200,
0.7-
1.2 R200, and 1.2-
2.7 R200, respectively.
In particular, we note the good agreement between the slope of the simulated
surface brightness profile of the representative massive cluster
in the radial bin 0.7-
1.2 R200 (see values of
,
independently
from the physics adopted in treating the baryonic mass, with a slope of
-4, -4.5, and -5.2 when estimated for the radial range 0.3-
1.2 R200,
0.7-
1.2 R200, and 1.2-
2.7 R200, respectively.
In particular, we note the good agreement between the slope of the simulated
surface brightness profile of the representative massive cluster
in the radial bin 0.7-
1.2 R200 (see values of ![]() in Table 4 of
Roncarelli et al. 2006, ranging between -4.29 and -4.54)
and our mean extrapolated value at R200 of -4.31.
in Table 4 of
Roncarelli et al. 2006, ranging between -4.29 and -4.54)
and our mean extrapolated value at R200 of -4.31.
In Table 3, we quote the estimated surface brightness value
at R200 in CGS units. They were obtained by extrapolating the
measured ![]() at
at ![]() 0.7 R200 out to R200 by using
the best-fit values quoted in the same table. The conversion from the
count rate to the flux was completed by adopting an absorbed thermal component
at the cluster redshift with an assumed metallicity and temperature equal to
(i) the ones measured and (ii) one third of the measured values.
We predict an average surface brightness of about
0.7 R200 out to R200 by using
the best-fit values quoted in the same table. The conversion from the
count rate to the flux was completed by adopting an absorbed thermal component
at the cluster redshift with an assumed metallicity and temperature equal to
(i) the ones measured and (ii) one third of the measured values.
We predict an average surface brightness of about
![]() erg s-1 cm-2 deg-2 in the 0.5-2 keV band, corresponding
to about half of the value associated with the total
cosmic background observed (e.g. Hickox & Markevitch 2006) and consistent
with the estimates measured in the hydrodynamical simulations of massive
galaxy clusters (Roncarelli et al. 2006).
Converting this surface brightness to counts in the 0.5-5 keV band,
we predict that at R200 the X-ray emission from a cluster
is responsible of
erg s-1 cm-2 deg-2 in the 0.5-2 keV band, corresponding
to about half of the value associated with the total
cosmic background observed (e.g. Hickox & Markevitch 2006) and consistent
with the estimates measured in the hydrodynamical simulations of massive
galaxy clusters (Roncarelli et al. 2006).
Converting this surface brightness to counts in the 0.5-5 keV band,
we predict that at R200 the X-ray emission from a cluster
is responsible of ![]() 5 per cent of the total counts
observable with Chandra.
5 per cent of the total counts
observable with Chandra.
Table 3:
Best-fit values of the slope of the surface brightness
profile in the radial range
![]() and
and
![]() .
The best-fit results of the first derivative of
.
The best-fit results of the first derivative of
![]() over the entire radial range are indicated as
over the entire radial range are indicated as
![]() and shown in Fig. 2.
The predicted slopes from the best-fit results at 0.4, 0.7, and
and shown in Fig. 2.
The predicted slopes from the best-fit results at 0.4, 0.7, and
![]() are quoted.
In the last two columns, we present the expected surface brightness
in the 0.5-2 keV band and the fraction fc200 of the clusters counts with
respect to the total count rate measured in the 0.5-5 keV at R200.
are quoted.
In the last two columns, we present the expected surface brightness
in the 0.5-2 keV band and the fraction fc200 of the clusters counts with
respect to the total count rate measured in the 0.5-5 keV at R200.
4 Physical properties of the outer cluster regions
We combine the measured slope of the
surface brightness in the cluster outskirts with the predicted
slopes of the gas temperature and dark matter profiles.
We have demonstrated that the slope depends on the radius at which it
is measured. Thus, we focus hereafter on the properties at R200,
by representing with power-laws the radial dependence of the gas
density,
![]() ,
temperature,
,
temperature,
![]() ,
and
dark matter,
,
and
dark matter,
![]() ,
profiles:
,
profiles:
The surface brightness, ![]() ,
is the integral along the line of sight
of the square of the gas density and can be written,
assuming spherical geometry, as
,
is the integral along the line of sight
of the square of the gas density and can be written,
assuming spherical geometry, as
where we consider the weak dependence (
Hydrostatic polytropic gas can be described by the relation
![]() ,
with a polytropic index
,
with a polytropic index
![]() that relates the ratio of specific heats in a adiabatic gas and
equals 5/3 for a monoatomic ideal gas. If the intracluster
gas is not entirely adiabatic, the polytropic index can be used
as a fitting parameter to describe the relative behaviour of the
gas temperature and density profile.
In particular, if the thermal conduction is an efficient process, the gas
tends to be isothermal and
that relates the ratio of specific heats in a adiabatic gas and
equals 5/3 for a monoatomic ideal gas. If the intracluster
gas is not entirely adiabatic, the polytropic index can be used
as a fitting parameter to describe the relative behaviour of the
gas temperature and density profile.
In particular, if the thermal conduction is an efficient process, the gas
tends to be isothermal and ![]() ,
whereas the entropy per atom will be
constant if the thermal conduction is slow and the gas is well mixed.
Moreover, when
,
whereas the entropy per atom will be
constant if the thermal conduction is slow and the gas is well mixed.
Moreover, when
![]() ,
the gas becomes convectively unstable and mixing
occurs within several sound crossing times, which are in general quite short
compared to the overall age of the cluster.
Therefore, this ``polytropic condition'' requires that
,
the gas becomes convectively unstable and mixing
occurs within several sound crossing times, which are in general quite short
compared to the overall age of the cluster.
Therefore, this ``polytropic condition'' requires that
![]() and translates into the request that
and translates into the request that
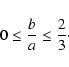 |
(4) |
Further constraints are provided by the integrated masses. The gas mass estimate,
| a + 3 > 0. | (5) |
The total gravitating mass can be expressed both as an integral of the dark matter profile over the cluster volume
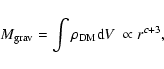 |
(6) |
and with the assumption of hydrostatic equilibrium between dark matter and spherically symmetric intracluster gas
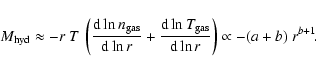 |
(7) |
The request for a gravitational mass increasing radially implies that c + 3 >0 and a + b <0. Moreover, by equating the two definitions of the gravitational mass, we find that the exponents of the radial dependence must to satisfy the condition c+3=b+1, which directly relates the slope of the dark matter profile to that of the gas temperature profile.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1177f3.ps}
\end{figure}](/articles/aa/full_html/2009/11/aa11177-08/Timg162.gif) |
Figure 3:
Error-weighted mean and standard deviation of the distribution
of the values of the slope of the surface brightness in the radial range
|
| Open with DEXTER | |
Overall, these conditions can be summarized by the following
inequalities among the indices of the assumed power-laws:
we show in Fig. 4 the allowed regions in the a-b-c plane.
It is worth noting that the permitted values shown in these plots
also satisfy the requests
that the sound-crossing time,
![]() ,
the cooling time,
,
the cooling time,
![]() ,
and the equipartition time for Coulomb collisions,
,
and the equipartition time for Coulomb collisions,
![]() ,
increase with radius in the cluster outskirts.
,
increase with radius in the cluster outskirts.
Some observational constraints are available and can be located in these
graphs: (1) the mean value of the slope in the surface brightness at
R200 is
![]() ,
equal to
,
equal to
![]() as inferred by Eq. (3), and implies that
as inferred by Eq. (3), and implies that
![]() ;
(2) the dark matter profile behaves as
;
(2) the dark matter profile behaves as
![]() as discussed
and shown in Fig. 3 of Navarro et al. (2004);
(3) a polytropic index
as discussed
and shown in Fig. 3 of Navarro et al. (2004);
(3) a polytropic index
![]() is measured in the outskirts of
temperature profiles (e.g. Markevitch et al. 1998; De Grandi & Molendi 2002,
out to about
is measured in the outskirts of
temperature profiles (e.g. Markevitch et al. 1998; De Grandi & Molendi 2002,
out to about
![]() ;
a value of
;
a value of
![]() is estimated in one of the first spectral determination
of the temperature profile at R200, obtained for the cluster PKS0745-191
with Suzaku in George et al. 2008).
These further constraints are also shown in Fig. 4.
is estimated in one of the first spectral determination
of the temperature profile at R200, obtained for the cluster PKS0745-191
with Suzaku in George et al. 2008).
These further constraints are also shown in Fig. 4.
The expected slope of the dark matter profile, combined with
the observed slope in surface brightness, places constraints
on the predicted behaviour of the temperature profile (Eq. (8))
and its polytropic index,
![]() .
For the values quoted above,
we expect that
.
For the values quoted above,
we expect that
![]() and
and
![]() .
These values agree well with the constraints obtained from observed data-sets
(e.g. Markevitch et al. 1998; Vikhlinin et al. 2005; Leccardi & Molendi 2008,
Reiprich et al. 2008; George et al. 2008); hydrodynamical simulated objects
(e.g. Loken et al. 2002; Roncarelli et al. 2006) and analytical model of the ICM
(e.g. Ostriker et al. 2005).
.
These values agree well with the constraints obtained from observed data-sets
(e.g. Markevitch et al. 1998; Vikhlinin et al. 2005; Leccardi & Molendi 2008,
Reiprich et al. 2008; George et al. 2008); hydrodynamical simulated objects
(e.g. Loken et al. 2002; Roncarelli et al. 2006) and analytical model of the ICM
(e.g. Ostriker et al. 2005).
Finally, the entropy profiles,
![]() ,
both from smooth and hierarchical accretion models
(e.g. Tozzi & Norman 2001; Voit 2005)
are predicted to increase with radius as
,
both from smooth and hierarchical accretion models
(e.g. Tozzi & Norman 2001; Voit 2005)
are predicted to increase with radius as
![]() .
This shape of the entropy profile outside the core, but well within the
virial radius, is also observed in high quality cluster
exposures with the XMM-Newton satellite (Pratt & Arnaud 2003).
By using our power-law expressions, we find that
.
This shape of the entropy profile outside the core, but well within the
virial radius, is also observed in high quality cluster
exposures with the XMM-Newton satellite (Pratt & Arnaud 2003).
By using our power-law expressions, we find that
![]() ,
with a predicted value of the slope
of
,
with a predicted value of the slope
of
![]() and 1.12 for the simulated dark matter distribution
and the observed polytropic index, respectively.
and 1.12 for the simulated dark matter distribution
and the observed polytropic index, respectively.
5 Summary and conclusions
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1177f4.ps}\end{figure}](/articles/aa/full_html/2009/11/aa11177-08/Timg181.gif) |
Figure 4:
Constraints on the outer slopes of the gas density (index a),
temperature (index b) and dark matter (index c = b - 2) profiles.
The shaded area shows the physically allowed regions for
the index values as discussed in the text.
The hatched regions indicate the |
| Open with DEXTER | |
We have selected 11 massive galaxy clusters in the redshift range
0.3< z <0.7observed with Chandra, which is convenient to survey the X-ray emission
out to a significant fraction of the virial radius and, in all the cases,
to radii beyond
![]() .
.
By fitting a single power-law function to the X-ray surface brightness profile
![]() in different radial ranges, we have detected a consistent steepening in
in different radial ranges, we have detected a consistent steepening in
![]() moving outward, with a mean slope of
moving outward, with a mean slope of
![]() when the radial range
when the radial range
![]() is considered, and -3.6 (rms 0.8) when
the lower limit of the radial range is
0.4R200.
The mean slope estimated from the linear fit to the derivative of
is considered, and -3.6 (rms 0.8) when
the lower limit of the radial range is
0.4R200.
The mean slope estimated from the linear fit to the derivative of
![]() is -3.2, -3.9, and -4.3 at
0.4R200,
0.7R200, and R200,
respectively. These values, corrected by the weak dependence of the cooling
function on gas temperature in the considered energy band [0.5,5] keV,
imply a slope in the gas density profile of
is -3.2, -3.9, and -4.3 at
0.4R200,
0.7R200, and R200,
respectively. These values, corrected by the weak dependence of the cooling
function on gas temperature in the considered energy band [0.5,5] keV,
imply a slope in the gas density profile of
![]() (
(
![]() ),
),
![]() (
(
![]() )
and
)
and
![]() (
(
![]() )
at
0.4R200,
0.7R200 and R200, respectively.
)
at
0.4R200,
0.7R200 and R200, respectively.
Combined with previous estimates of the outer slope of the gas temperature
profile (e.g. Vikhlinin et al. 2005, from an observational point of view;
Roncarelli et al. 2006, for hydrodynamically simulated clusters)
and the expectations for the dark matter distribution (e.g. Navarro et al. 2004),
and modelling of the gas density, temperature and dark matter profiles
with single power laws (
![]() ),
we have defined a physically-allowed region in the a-b-c plane, with a
predicted behaviour at R200 described by power-law indices of
),
we have defined a physically-allowed region in the a-b-c plane, with a
predicted behaviour at R200 described by power-law indices of
![]() and
and
![]() .
.
Acknowledgements
We acknowledge the financial contribution from contracts ASI-INAF I/023/05/0 and I/088/06/0. Paolo Tozzi and Silvano Molendi are thanked for reading the manuscript and providing useful comments. We thank the anonymous referee for very useful comments that improved the presentation of the work.
References
- Allen, S. W., Schmidt, R. W., & Fabian, A. C. 2001, MNRAS, 328, L37 [NASA ADS] [CrossRef] (In the text)
- Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2005, A&A, 441, 893 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Balestra, I., Tozzi, P., Ettori, S., et al. 2007, A&A, 462, 429 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- De Grandi, S., & Molendi, S. 2002, ApJ, 567, 163 [NASA ADS] [CrossRef]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] (In the text)
- Ettori, S. 2000, MNRAS, 311, 313 [NASA ADS] [CrossRef] (In the text)
- Ettori, S., & Brighenti, F. 2008, MNRAS, 387, 631 [NASA ADS] [CrossRef] (In the text)
- Ettori, S., Tozzi, P., Borgani, S., & Rosati, P. 2004, A&A, 417, 13 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- George, M. R., Fabian, A. C., Sanders, J. S., Young, A. J., & Russell H. R. 2008, MNRAS, submitted [arXiv:0807.1130] (In the text)
- Hickox, R. C., & Markevitch, M. 2006, ApJ, 645, 95 [NASA ADS] [CrossRef] (In the text)
- Hildebrand, F. B. 1987, Introduction to Numerical Analysis (New York: Dover Publishing), 80
- Leccardi, A., & Molendi, S. 2008, A&A, 486, 359 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Loken, C., Norman, M. L., Nelson, E., et al. 2002, ApJ, 579, 571 [NASA ADS] [CrossRef] (In the text)
- Markevitch, M., Forman, W. R., Sarazin, C. L., & Vikhlinin, A. 1998, ApJ, 503, 77 [NASA ADS] [CrossRef] (In the text)
- Navarro, J. F., Hayashi, E., Power, C., et al. 2004, MNRAS, 349, 1039 [NASA ADS] [CrossRef] (In the text)
- Neumann, D. M. 2005, A&A, 439, 465 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ostriker, J. P., Bode, P., & Babul, A. 2005, ApJ, 634, 964 [NASA ADS] [CrossRef] (In the text)
- Pointecouteau, E., Arnaud, M., & Pratt, G. W. 2005, A&A, 435, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Pratt, G. W., & Arnaud, M. 2003, A&A, 408, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Press, W. H., Teukolsky, S. A., Vetterling, S. A., & Flannery, B. P. 1992, Numerical Recipes in Fortran, second edition, 660 (In the text)
- Reiprich T. H., Hudson D. S., Zhang Y. Y., et al. 2008, A&A, submitted [arXiv:0806.2920] (In the text)
- Roncarelli, M., Ettori, S., Dolag, K., et al. 2006, MNRAS, 373, 1339 [NASA ADS] [CrossRef] (In the text)
- Santos, J. S., Rosati, P., Tozzi, P., et al. 2008, A&A, 483, 35 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Tozzi, P., & Norman, C. 2001, ApJ, 546, 63 [NASA ADS] [CrossRef] (In the text)
- Tozzi, P., Rosati, P., Ettori S., et al. 2003, ApJ, 593, 705 [NASA ADS] [CrossRef] (In the text)
- Vikhlinin, A., Forman, W., & Jones, C. 1999, ApJ, 525, 47 [NASA ADS] [CrossRef] (In the text)
- Vikhlinin, A., Markevitch, M., Murray, S. S., et al. 2005, ApJ, 628, 655 [NASA ADS] [CrossRef] (In the text)
- Voit, G. M. 2005, AdSpR, 36, 701 [NASA ADS] (In the text)
Footnotes
- ... band
![[*]](/icons/foot_motif.gif)
- See, for example, Fig. 2a in http://cxc.harvard.edu/ciao3.4/download/doc/expmap_intro.ps
All Tables
Table 1:
Sample of galaxy clusters, which satisfies the criterion
![]() .
The columns show: the name of the cluster,
the observation IDs, in which ACIS configuration has been observed,
the exposure time, the adopted X-ray center,
the Galactic absorption from Dickey & Lockman (1990) in correspondence
of the X-ray center, the redshift, the gas temperature, the mean
local background, B, in counts observed in the 0.5-5 keV band,
and the average distance
.
The columns show: the name of the cluster,
the observation IDs, in which ACIS configuration has been observed,
the exposure time, the adopted X-ray center,
the Galactic absorption from Dickey & Lockman (1990) in correspondence
of the X-ray center, the redshift, the gas temperature, the mean
local background, B, in counts observed in the 0.5-5 keV band,
and the average distance ![]() of the regions used
to estimate the local background from the X-ray center.
of the regions used
to estimate the local background from the X-ray center.
Table 2:
Best-fit results of the X-ray surface brightness profiles
modelled with a ![]() -model.
-model.
![]() is estimated from the scaling laws in Arnaud et al. (2005);
R200 from Eq. (1);
is estimated from the scaling laws in Arnaud et al. (2005);
R200 from Eq. (1);
![]() and
and ![]() are quoted
in unit of R200.
are quoted
in unit of R200.
Table 3:
Best-fit values of the slope of the surface brightness
profile in the radial range
![]() and
and
![]() .
The best-fit results of the first derivative of
.
The best-fit results of the first derivative of
![]() over the entire radial range are indicated as
over the entire radial range are indicated as
![]() and shown in Fig. 2.
The predicted slopes from the best-fit results at 0.4, 0.7, and
and shown in Fig. 2.
The predicted slopes from the best-fit results at 0.4, 0.7, and
![]() are quoted.
In the last two columns, we present the expected surface brightness
in the 0.5-2 keV band and the fraction fc200 of the clusters counts with
respect to the total count rate measured in the 0.5-5 keV at R200.
are quoted.
In the last two columns, we present the expected surface brightness
in the 0.5-2 keV band and the fraction fc200 of the clusters counts with
respect to the total count rate measured in the 0.5-5 keV at R200.
All Figures
![\begin{figure}
\par\includegraphics[width=5.2cm,clip]{1177f1a.ps}\hspace*{2.3mm}...
...7f1b.ps}\hspace*{1.5mm}
\includegraphics[width=5cm,clip]{1177f1c.ps}\end{figure}](/articles/aa/full_html/2009/11/aa11177-08/Timg35.gif) |
Figure 1:
( Left) Expected R200 for an object with 4 ( dashed line)
and 8 keV ( solid line) and radius corresponding to 4 and 8 ( thickest line)
arcmin for the assumed |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{1177f2.ps} \end{figure}](/articles/aa/full_html/2009/11/aa11177-08/Timg73.gif) |
Figure 2:
In the first column, we plot the surface brightness profiles
of the objects under examination with the fitted background
( horizontal dotted line) and the radius R200( vertical dashed line).
The panels in the second column show the signal-to-noise profiles, evaluated
as
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1177f3.ps}
\end{figure}](/articles/aa/full_html/2009/11/aa11177-08/Timg162.gif) |
Figure 3:
Error-weighted mean and standard deviation of the distribution
of the values of the slope of the surface brightness in the radial range
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1177f4.ps}\end{figure}](/articles/aa/full_html/2009/11/aa11177-08/Timg181.gif) |
Figure 4:
Constraints on the outer slopes of the gas density (index a),
temperature (index b) and dark matter (index c = b - 2) profiles.
The shaded area shows the physically allowed regions for
the index values as discussed in the text.
The hatched regions indicate the |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}R_{200} = r_{\rm c} \times \left[ \left( \frac{195.45 ~ \beta...
...z^2 ~ h_{70}^2 ~ r_{\rm c}^2} \right)^\alpha -1 \right]^{0.5},
\end{displaymath}](/articles/aa/full_html/2009/11/aa11177-08/img76.gif)