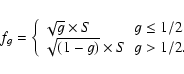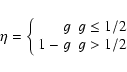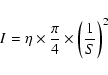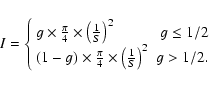Design, analysis, and testing of a microdot apodizer for the Apodized Pupil Lyot Coronagraph

P. Martinez; C. Dorrer; E. Aller Carpentier; M. Kasper; A. Boccaletti; K. Dohlen; N. Yaitskova

doi:10.1051/0004-6361:200810918

Free Access

Issue		A&A Volume 495, Number 1, February III 2009


Page(s)		363 - 370
Section		Astronomical instrumentation
DOI		https://doi.org/10.1051/0004-6361:200810918
Published online		22 December 2008

Design, analysis, and testing of a microdot apodizer for the Apodized Pupil Lyot Coronagraph

P. Martinez^1,2,5 - C. Dorrer³ - E. Aller Carpentier¹ - M. Kasper¹ - A. Boccaletti^2,5 - K. Dohlen⁴ - N. Yaitskova¹

1 - European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
2 - LESIA, Observatoire de Paris Meudon, 5 pl. J. Janssen, 92195 Meudon, France
3 - Laboratory for Laser Energetics-University of Rochester, 250 East River Rd, Rochester, NY, 14623-USA, USA
4 - LAM, Laboratoire d´Astrophysique de Marseille, 38 rue Frédéric Joliot Curie, 13388 Marseille Cedex 13, France
5 - Groupement d´intérêt scientifique PHASE (Partenariat Haute résolution Angulaire Sol Espace)

Receved 5 September 2008 / Accepted 29 October 2008

Abstract
Context. Coronagraphic techniques are required for detecting exoplanets with future Extremely Large Telescopes. One concept, the Apodized Pupil Lyot Coronagraph (APLC), combines an apodizer in the entrance aperture with a Lyot opaque mask in the focal plane. This paper presents the manufacturing and testing of a microdots apodizer optimized for the near IR.
Aims. We attempt to demonstrate the feasibility and performance of binary apodizers for the APLC. This study is also relevant to coronagraph using amplitude pupil apodization.
Methods. A binary apodizer was designed using a halftone-dot process, where the binary array of pixels with either 0% or 100% transmission was calculated to fit the required continuous transmission, i.e. local transmission control was obtained by varying the relative density of the opaque and transparent pixels. An error-diffusion algorithm was used to optimize the distribution of pixels that approximated the required field transmission. The prototype was tested with a coronagraphic setup in the near IR.
Results. The transmission profile of the prototype agrees with the theoretical shape to within 3% and is achromatic. The observed apodized and coronagraphic images are consistent with theory. However, binary apodizers introduce high frequency noise that is a function of the pixel size. Numerical simulations were used to specify pixel size and minimize this effect, and validated by experiment.
Conclusions. This paper demonstrates that binary apodizers are well suited for use in high-contrast imaging coronagraphs. The correct choice of pixel size is important and must be addressed by considering the scientific field of view.

Key words: techniques: high angular resolution - instrumentation: high angular resolution - telescopes - instrumentation: adaptive optics

1 Introduction

Direct detection and characterization of faint objects around bright astrophysical sources is challenging due to the high flux ratios and small angular separations. For instance, self-luminous giant planets are typically 10⁶ times fainter than the parent star in the near-infrared. Even higher contrasts as high as 10¹⁰ are needed to reach the realm of mature giant or telluric planets. To achieve these contrast levels, dedicated instruments for large ground-based telescopes such as SPHERE or GPI (Beuzit et al. 2006; Macintosh et al. 2006), or EPICS (Kasper et al. 2008) for the future European-Extremely Large Telescope (E-ELT) will use powerful Adaptive Optics (extreme AO or XAO) systems coupled with coronagraphs.

While the XAO system corrects for atmospheric turbulence and instrument aberrations, the coronagraph attenuates the starlight diffracted by the telescope in the image plane. Since the invention of the stellar Lyot coronagraph (Lyot 1939), there has been impressive progress in the field leading to a wealth of different coronagraphs that can be divided into different families. In particular, the Apodized Pupil Lyot Coronagraph (APLC) (Soummer et al. 2003a; Aime et al. 2002) appears to be well suited to ELTs and has been studied theoretically (Soummer 2005; Martinez et al. 2007). The APLC features amplitude apodization in the entrance aperture for reducing diffraction, and a small Lyot mask in the focal plane. It is the baseline coronagraph for e.g. SPHERE, GPI, and the Lyot Project (Oppenheimer et al. 2004). Martinez et al. (2008) further demonstrated that the APLC is well suited for use with ELTs considering their particular pupil shapes and segmented mirrors.

A major issue with the APLC, and other coronagraphs using apodization such as is the dual zone coronagraph, Soummer et al. (2003b), is the manufacture of the apodizer itself. Three concepts have been explored in manufacturing apodizers: (1/) a metal layer of spatially variable thickness, (2/) electron-sensitized HEBS glass (high-electron-beam-sensitive glass), and (3/) an array of opaque pixels with spatially variable density. The third concept has several advantages over the first and second ones because it is intrinsically achromatic and avoids wavefront phase errors introduced by a metal layer of variable thickness or the process of writing a HEBS pattern. Simplicity and reproducibility of the technique are also major advantages.

A binary design using a halftone-dot process can in principle be generalized to any apodizer masks (APLC, Dual zone) and even a conventional pupil apodization coronagraph (Aime 2005; Nisenson & Papaliolios 2001; Jacquinot & Roisin-Dossier 1964), or as an alternative manufacturing solution for binary-shaped pupil-coronagraph masks (Enya et al. 2007,2008; Kasdin et al. 2003; Vanderbei et al. 2003,2004).

In this paper, we report on the development (design and laboratory tests) of a binary apodizer for the APLC using a halftone-dot process. We first describe the binary mask principle and the algorithm used to distribute pixels across the pupil (Sect. 2). Optimization of the design (i.e. pixels size issue) is discussed in Sect. 3, while in Sect. 4 we report on laboratory results obtained with a prototype using a near-IR bench that reproduces the Very Large Telescope (VLT) pupil. Finally, we conclude on the suitability of this technique for planet finder instruments in Sect. 5.

2 Principle of microdots apodizer

A binary apodizer is made of an array of opaque pixels (i.e. dots) on a transparent substrate. It is fabricated by lithography of a light-blocking metal layer deposited on a transparent glass substrate. Spatially variable transmission is obtained by varying pixel density. An error-diffusion algorithm was used to calculate the density distribution that reproduces most effectively the required field transmission (Floyd & Steinberg 1976; Ulichney 1987; Dorrer & Zuegel 2007). This algorithm chooses the transmission of a given pixel of the apodizer (either 0 $\%$ or 100 $\%$ ) by comparing the transmission required at this location to a 50 $\%$ threshold, i.e. the transmission is set to zero if the required transmission is smaller than 50 $\%$ , and to one otherwise (see Fig. 1). The induced transmission error is diffused into adjacent pixels that have not yet been processed by biasing the transmission required at the corresponding locations. This locally cancels the error of the binary optics introduced by the process of writing the required transmission (in gray-levels) into binary values. This procedure is used in gray-level reproduction with black-and-white printing techniques (Ulichney 1987), and further details about the algorithm principle are presented in Dorrer & Zuegel (2007).

The shaping of coherent laser beams has also been demonstrated (Dorrer & Zuegel 2007) using this technique. The error-diffusion algorithm has the advantage that the introduced noise is blue, i.e., the noise spectral density is only significant at high spatial frequencies. This allows the accurate generation of gray levels and rapidly varying shaping functions. In the specific case of the design of a coronagraph, the algorithm allows us to reproduce well the PSF of the binary apodizer to the required apodized PSF to a certain radial distance, which could be chosen to be the control radius of the AO system. In theory, higher quality shaping results are obtained with smaller pixels (i.e. sampling problem, Dorrer & Zuegel 2007), since this allows finer control of the local transmission and increases spatial frequency of the binarization noise. This will be discussed further in Sect. 3.

3 Design optimization

Assuming a VLT-like pupil, the apodizer is defined for a 15 $\%$ central obscuration pupil (bagel regime, Soummer 2005). We consider a 4.5 $\lambda/D$ APLC (Martinez et al. 2007). The apodizer shape is illustrated in Fig. 1 (left image). The inner-working angle of this configuration is $\sim$ $2.3 \lambda/D$ .

$\begin{figure} \par\includegraphics[width=4cm]{FIGURES/0918F1.eps}\includegraphi... .../0918F2.eps}\par\includegraphics[width=8.15cm]{FIGURES/0918F3.eps} \end{figure}$	Figure 1: Left: shaper target (continuous apodizer). Right: resulting microdots pattern using algorithm discussed in Sect. 2. The spatial scale of these maps is 600 $\times$ 600 pixels. The scale of transmission is given in $\%$ .
Open with DEXTER

The manufactured apodizer has a diameter of 3mm due to constraints on our optical bench (Sects. 3.3 and 4). For microdots, the performance is related to the ratio of the smallest feature to the pixel size. Hence, for the sake of clarity, we denote by S the scaling factor, the ratio between the apodizer useful diameter (i.e. pupil diameter, denoted $\Phi$ hereafter), and the pixel spacing, i.e. pixel size (dot size), denoted p hereafter:

$\begin{displaymath}S = \frac{\Phi}{p} \cdot \end{displaymath}$

(1)

The individual pixels of a binary apodizer scatter light towards spatial frequencies that depend on the pixel size. The smaller the pixels are, the higher are the spatial frequencies at which the light is scattered, and the more closely the achieved transmission profile matches the desired one.

We also note that the high-frequency noise might have different distributions at different wavelengths. This would be a situation similar to diffraction gratings, where only diffracted orders (i.e. corresponding to large values of the transverse wavevector k) are frequency-dependent. To be able to complete a more detailed analysis, Fresnel propagators and a thorough modeling of the binary shaper (including process errors on the shape and size of each dot such as edge effects resulting from the isotropic wet etching process, Sect. 3.3) would be required.

3.1 Microdots diffraction stray light

The microdots apodizer is modeled as an aperiodic, under-filled, two-dimensional grating, which exhibits blue-noise properties because of the error-diffusion algorithm used (Ulichney 1987; Dorrer & Zuegel 2007). The binary pattern produces an averaged gray level ( $g = \sqrt{T}$ , i.e. averaged amplitude transmission) from an apodizer profile with intensity transmission T. The resulting pattern spectral energy is determined by g (i.e. by the minority pixels present on the device: non-metal pixels when g < 0.5 and by metal pixels conversely). The spectral energy increases as the number of minority pixels increases, peaking at g=0.5 (Ulichney 1987,1988). Most of the energy in the power spectrum of the pattern will be concentrated around the first-order diffraction, which would appear in the field of view at the spatial frequency f_g (in $\lambda/D$ units):

$\begin{displaymath}f_g = \left\{ \begin{array}{ll} \sqrt{g}\times S & g \leq 1/2 \\ \sqrt{(1-g)}\times S & g > 1/2 .\\ \end{array}\right. \end{displaymath}$

(2)

Therefore, for a given g, the pattern power spectrum has a peak in its diffraction at f_g (Ulichney 1987,1988). As the gray level, g, increases from 0 to 0.5, the peak diffraction moves to further angular distance (Fig. 2) with an increase in energy. Above g = 0.5, the situation is similar to that for (1-g), minority pixels has only changed from non-metal dots to metal dots. The PSF of a microdots device can be therefore expressed as a function of a deterministic effect (the first-order diffraction peak) bordered by speckles due to a stochastic effect (i.e. the dot distribution is irregular). Higher-order diffraction peaks are irrelevant since they are out of the science field of view. The intensity of the first-order diffraction peak in the final coronagraphic image is also function of g. The model presented hereafter is based on a study performed by Dohlen (2008), where effects of micro-obscurations, such as dust or cosmetic errors, are analytically described for the SPHERE-instrument image quality.

$\begin{figure} \par\includegraphics[width=9cm]{FIGURES/0918F4.eps} \end{figure}$	Figure 2: First-order peak diffraction f_g position in $S \times \lambda /D$ units as a function of gray level g. Typical domain of application of apodizer masks are reported on the plot.
Open with DEXTER

The coronagraphic halo intensity (I) of the first-order peak diffraction for N dots normalized to the stellar peak intensity is $N_{\rm dots} \times \left(\frac{p}{\Phi}\right)^{4}$ (Dohlen 2008, assuming halos from all the dots add incoherently). The total number of minority dots present in the pattern ( $N_{\rm dots}$ ) can be easily calculated to be the product of the surface ratio of the pupil to a square dot, and the density of minority dots ( $\eta$ , hereafter). The minority dot density can be expressed as:

$\begin{displaymath}\eta = \left\{ \begin{array}{rl} g & g \leq 1/2 \\ 1-g & g > 1/2 \\ \end{array}\right. \end{displaymath}$

(3)

where $N_{\rm dots}$ is given by:

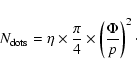$\begin{displaymath}N_{\rm dots} = \eta \times \frac{\pi}{4} \times \left(\frac{\Phi}{p}\right)^{2}\cdot \end{displaymath}$

(4)

The resulting relative halo intensity is then:

$\begin{displaymath}I = \eta \times \frac{\pi}{4} \times \left(\frac{1}{S}\right)^{2} \end{displaymath}$

(5)

therefore, using Eq. (3) one finally obtains:

$\begin{displaymath}I = \left\{ \begin{array}{lr} g \times \frac{\pi}{4} \times ... ...\left(\frac{1}{S}\right)^{2} & g > 1/2. \\ \end{array}\right. \end{displaymath}$

(6)

Considering our APLC apodizer ( $T = 51 \%$ , g = 0.71), the first-order diffraction peak would be therefore localized at $f_g \sim S/2$ in $\lambda/D$ units with an intensity of $I \sim 1/(4\times S^{2})$ . For the Dual Zone coronagraph ( $T \sim 80\%$ , therefore $g \sim 0.9$ ), the first-order, diffraction-peak position moves closer to the central core of the PSF, while its intensity decreases with respect to the APLC case: $f_g \sim S/3$ in $\lambda/D$ with an intensity of $I \sim 1/(13\times S^{2})$ . For Conventional pupil apodization ( $T \sim 25\%$ , hence $g \sim 0.5$ ), the first-order diffraction peak moves further away from the central core of the PSF while its intensity increases: $f_g \sim 1/\sqrt{2} \times S$ in $\lambda/D$ with an intensity of $I \sim 2/(5\times S^{2})$ .

$\begin{figure} \par\includegraphics[width=9cm]{FIGURES/0918F5.eps}\includegraphics[width=9cm]{FIGURES/0918F6.eps} \vspace*{3mm} \end{figure}$	Figure 3: Apodized PSFs ( left) and APLC coronagraphic PSFs ( right) using several dot sizes for the binary apodizer compared to that with continuous apodizer (i.e. theory, in black). Simulation assumes a pupil with 15 $\%$ central obscuration. Profiles presented are azimuthal averages.
Open with DEXTER

Table 1: High frequency noise properties as a function of the pixel size.

3.2 Numerical simulations

Our simulations make use of Fraunhofer propagators between pupil and image planes, which is implemented as fast Fourier transforms (FFTs) generated with an IDL code. In the following, pixels describe the resolution element of the simulation, while dots describe the physical units forming the apodizer. We use 0.3 $\lambda/D$ per pixel, while dots are sampled by a sufficient 4 pixels to allow field of view for imaging the first-order diffraction peak for each S. Validity of the numerical dot sampling has been verified by comparing simulations with different dot sampling (1, 4, and 16 pixels per dot for S = 150).

We first analyze how the dot size affects the apodized PSF (Fig. 3, left) and the coronagraphic PSF (Fig. 3, right) with respect to an ideal, continuous apodizer. The intent of these simulations is to derive relevant information about S and specify this pattern by preserving from noise, low and mid-range frequencies that are critical to coronagraphy. Since the APLC combines a conventional Lyot-type design with pupil apodization to shape the intensity in the Lyot plane, the specification of S must be tackled at the level where the coronagraphic effect appears, i.e. in the coronagraphic images.

All plots confirm agreement with theory (continuous model), until a given angular separation where pixellation noise appears. This angular separation is a function of S as predicted by theoretical models (Eqs. (2) and (6)). From the results summarized in Table 1, we derive the following conclusions:

reduction in the dot size by a factor of 2 increases the radial distance, providing adequate agreement with the specification by a factor of 2 for the coronagraphic image. Equation (2) has been confirmed by simulations;
the analytical model given by Eq. (6) is consistent with simulation predictions. This model is representative of the APLC situation;
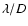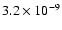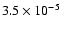at a given frequency in the coronagraphic images, the level of noise decreases in proportion to S⁴ (for instance, at 80 $\lambda/D$ , noise increases from $3.2\times10^{-9}$ to $3.5\times10^{-5}$ , while increases S by a factor of 8)

In practice, for the selection of S (dots size), we modeled in simulation our specific pupil (VLT-like including the secondary support, i.e. contrast accessibility issue), taking into account the field of view of interest (constrained by the AO correction domain: 20 $\lambda/D$ as in SPHERE). As expected we found that, the radial distance corresponding to adequate agreement with the specification (ideal model) moved to larger angular separations, while the intensity level at which the noise appears remains similar to the previous case. In our context, S=600 ( $5~\rm\mu m$ dots) meets our specifications. The S = 1200 configuration produces an extremely small dot size (2.5 $\mu$ m). When the dot size is of the order or lower than the operating wavelength (1.65 $\mu$ m for our application), a Rigorous Coupled-Wave Analysis (RCWA) is mandatory to know how the field reacts to small perturbations in the shaper (Huang & Zhu 2007; Genet & Ebbesen 2007). Gratings with small periods generally have missing diffracted orders in visible and IR light.

3.3 Other specifications

The microdots apodizer was fabricated by Precision Optical Imaging in Rochester, New York. To reduce the effect of misaligning the apodizer with the telescope pupil, the designed profile of the apodizer ( $\Phi=3~\rm mm$ ) was not obscured at the center by the central obscuration (no 0 $\%$ transmission values) and was extrapolated by a Gaussian function in its outer part (from 1.5 mm to 3 mm in radius, i.e. above the apodizer function radius) to reduce the transmission slowly to zero. Having a sharp edge on the apodizer might be detrimental to the characterization process (inspection of the profile), because of strong diffraction effects. The shaper was fabricated using wet-etch contact lithography of a Chrome layer (Optical Density of 4.0) deposited on a BK7 glass substrate ( $\lambda$ /20 peak-to-valley). The back face of the apodizer has an antireflection coating for the H band (1.2 to 1.8 $\mu$ m, $R<1\%$ ). In contrast to other techniques (HEBS glass or deposition of spatially varying metal thickness), no wavefront errors are introduced by the microdots apodizer, while its substrate has the highest quality requirement of all components used in our experiment.

In the case of wet-etch lithography, etching can cause a reduction in the light-blocking metal dot-sizes (smaller than specified in the digital design), which potentially leads to increased transmission. Dot spacing remains the same, while opaque dot size are reduced in size due to an undercut of the masking layer that form cavities with sloping sidewalls. To minimize the impact of this effect on the obtained transmission, the mask design was numerically precompensated by estimating the feature size that would be obtained after fabrication (Dorrer & Zuegel 2007). In practice, we adopted a pixel grid of 6 $\mu\rm m$ (i.e. dot size, S = 500), and several runs were necessary to calibrate the process and reach the specification. Reproducibility was confirmed by a final test after optimal conditions had been set.

The 4.5 $\lambda/D$ hard-edge opaque Lyot mask was fabricated by GEPI, Paris Observatory (360 $\mu$ m $\pm$ 1 $\mu$ m in diameter, OD = 6.0 at 1.65 $\mu$ m using two metallic layers of Chrome (20 nm) and Gold (200 nm)).

$\begin{figure} \par\includegraphics[width=9.cm]{FIGURES/0918F7.eps}\par\includegraphics[width=9.cm]{FIGURES/0918F8.eps} \end{figure}$	Figure 4: Top: picture of the IR coronagraphic test-bench on HOT. The red dot line shows the IR coronagraphic path, while the blue dot line shows the pupil imager system path when placing a mirror on a magnetic mount before the external IR filter. Bottom: schematic setup of the coronagraphic testbench.
Open with DEXTER

4 Experiment

4.1 Optical setup

The experiment configuration is shown is Fig. 4, where the optical IR coronagraphic path is indicated (top) by dot red line. The optical setup was designed to simulate the 8 m VLT pupil. The 3 mm entrance aperture diameter was made in a laser-cut, stainless-steel sheet to an accuracy of 0.002 mm. The central obscuration was scaled to be 0.47 mm $\pm$ 0.002 mm and the spider-vane thickness is 15 $\mu$ m $\pm$ 4 $\mu$ m. The coronagraphic mask was installed at an F/48.4 beam. Re-imaging optics were made with $\lambda$ /10 achromatic IR doublets. The quality of the collimation in the pupil plane and re-imaged pupil plane (where the pupil stop is placed) was checked and adjusted using an HASO 64 Shack-Hartmann sensor. A pupil-imager system (see Fig. 4, where a dotted blue line indicates its optical path) was implemented to align the pupil-stop mask with the entrance-pupil mask (to complete alignment in the x and y direction, orientation of the spider vanes and focalisation).

We installed the entrance-pupil mask and the apodizer in the same collimated beam. Hence, the apodizer is not perfectly inside the pupil plane. The apodizer was placed inside a rotating adjustable-length lens tube that allows a translation of $\sim$ 3.5 mm from the pupil mask.

We used a white-light source combined either with an IR narrow-band filter of $\Delta \lambda /\lambda = 1.4\%$ , central wavelength of 1.64 $\mu$ m, and a peak transmission of 64.4 $\%$ , or IR filters (J, H, K), installed inside the filter wheel of the IR camera, where the H filter was centered on 1.6 $\mu$ m, $\Delta \lambda /\lambda = 20\%$ . The camera used was the ESO Infrared Test Camera (ITC), cooled to 103 K degree with a vacuum pressure of 10^-5 mbar. Internal optics were designed to reach a pixel scale of 5.3 mas. The Strehl ratio was evaluated to be 94 $\%$ .

The APLC pupil stop mimics the VLT pupil mask with a spider-vane thickness that is larger by a factor 4 (60 $\mu$ m $\pm$ 4 $\mu$ m), an outer diameter that is smaller by a factor $0.96\times \Phi$ (2.88 mm $\pm$ 0.002 mm), and a central obscuration that is equal to $0.16\times \Phi$ (0.49 mm $\pm$ 0.002 mm). The pupil stop throughput is about 90 $\%$ .

$\begin{figure} \par\includegraphics[width=8.5cm]{FIGURES/0918F9.eps}\includegraphics[width=8.56cm]{FIGURES/0918F10.eps} \end{figure}$	Figure 5: Left: simulation map of the binary apodizer with $5\times 5~\mu$ m dots. Right: shadowgraph inspection of the manufactured microdots apodizer ( $\times$ 50). For the sake of clarity, only a quarter of the apodizer is shown.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=9cm]{FIGURES/0918F11.eps}\includegraphics[width=9cm]{FIGURES/0918F12.eps} \end{figure}$	Figure 6: Left: apodizer azimuthally average profile (from center to the edges) using different filters (J, H and narrow H band) compared to specification (black curve). Right: corresponding average amplitude error as function of the position using the same filters.
Open with DEXTER

4.2 Quality of the binary apodizer

The size of the square chrome dots has been determined to be $4.5 \times 4.5$ $\mu$ m using a microscopic inspection. The dot spatial distribution across the pupil diameter was also analyzed using a shadowgraph ( $\times$ 50, Fig. 5) and compared with a simulation map ( $5 \times 5$ $\mu$ m dots). Figure 6 shows that the accuracy of the profile matches that expected, and the transmission error is about 3 $\%$ . Achromaticity of the profile is also demonstrated: the profile error increases by only about 2 $\%$ between the narrow H filter and the broadband J filter. A smaller pixel size than that of the digital design ( $6\times 6$ $\mu$ m) was expected (Sect. 3.3) and demonstrates that precompensation of the transmission error due to the feature size was necessary and works well. The global shape of the binary apodizer is illustrated in Fig. 7.

4.3 Coronagraphic results and discussion

4.3.1 Effect on the PSF

The intention behind this first series of tests was to demonstrate the effect of the binary apodizer on the PSF. We only compare the PSF in the absence of the apodizer to that with the apodizer. Qualitatively (Fig. 9), it is demonstrated that the apodizer works well: the wings of the apodized PSF are reduced in intensity, while the core of the apodized PSF becomes larger (exposure time are identical, no neutral density is applied). This behavior agrees well with the theoretical predictions. Although there are some discrepancies between theory and measurements (Fig. 8, bottom, for $\Delta \lambda /\lambda = 20\%$ in H band), the gain between PSF and apodized PSF is consistent with theory. This results has been demonstrated in the H-band with a narrow-band filter ( $\Delta \lambda /\lambda = 1.4\%$ ) and with a broadband filter ( $\Delta \lambda /\lambda = 20\%$ ). Its achromaticity in the H band is therefore confirmed. The fact that we are using a real optical system and the presence of a 3.5 mm defocus between the apodizer and the entrance pupil may explain the discrepancies.

4.3.2 Effect on the coronagraphic PSF

The second series of tests were intended to demonstrate the coronagraphic behavior of the APLC using the microdots apodizer.

Qualitatively, the profile of the coronagraphic image (Fig. 10, H band with $\Delta \lambda/\lambda$ = 1.4 $\%$ ) agrees well with theoretical predictions: a PSF-like pattern homogeneously reduced in intensity with most of the energy inside the first rings. In this observed raw image, a local contrast as large as $6.5\times 10^{-7}$ has been reached between the diffraction spikes. In Fig. 11, we present apodized PSFs and coronagraphic images recorded on the bench using a narrow ( $\Delta \lambda /\lambda = 1.4\%$ ) and broadband filter ( $\Delta \lambda /\lambda = 20\%$ ) in the H band. Most of the time, an order of magnitude discrepancy (mostly in the halo) is found between theory and measured data (Table 2), when we compare intensity levels at 3, 12, and 20 $\lambda/D$ . The contrast is defined to be the ratio of the local intensity (i.e. at a given angular separation) on the coronagraphic image to the maximum intensity of the apodized PSF image. The total rejection rate (ratio of the total intensity of the PSF image to the total intensity of the coronagraphic image, in practice limited to 20 $\lambda/D$ ) differs only by a factor of 2 and 1.8 from theory, for the narrow and broad band filters respectively. This discrepancy is reduced when considering the peak rejection (ratio of the maximum intensity of the PSF to the maximum intensity of the coronagraphic image) to a factor of 1.7 and 1.2, respectively. The impact of chromatism is evident only slightly at small angular separations (of less than 4 $\lambda/D$ ), otherwise achromaticity can be seen in the halo in H band.

$\begin{figure} \par\includegraphics[width=5.43cm]{FIGURES/0918F13.eps} \end{figure}$	Figure 7: Top: infrared recorded image of the apodizer.
Open with DEXTER

The discrepancy may find its origin in different error sources (we discuss here only the main ones): (1/) apodizer profile error ( $\sim$ $3\%$ ), (2/) quality of the bench ( ${\rm Strehl} = 94\%$ ), and (3/) defocus between the apodizer and the pupil plane ( $\sim$ $3.5~\rm mm$ ). Simulations were carried out to analyze independently the impact of the two first ones. For the impact of the defocus, we refer to a sensitivity analysis performed for SPHERE (Boccaletti et al. 2008), where the apodizer mask positioning requirement in defocus is set to be the nominal position $\pm$ $0.1~\rm mm$ . This positioning error affects mainly the halo. As also in simulations, the measured profile of the apodizer (Fig. 6) reduces the discrepancy from 1.7 to 1.2 for the peak rejection and from $\sim$ 10 to $\sim$ 3 in the halo. When the Strehl ratio is set to $94\%$ ( $\lambda/25$ nm rms) while the apodizer is perfect, the discrepancy is reduced to 1.08 for the peak rejection and to $\sim$ 4 in the halo. It is therefore difficult to ascertain the dominant source of error. The discrepancy with theory is certainly a result of a combination of all theses error sources.

$\begin{figure} \par\includegraphics[width=9cm]{FIGURES/0918F14.eps}\includegraphics[width=9cm]{FIGURES/0918F15.eps} \end{figure}$	Figure 8: Left: PSF and apodized PSF recorded on the bench (blue lines) compared to theoretical ones (black lines) with narrow H filter ( $\lambda = 1.64$ $\mu$ m, $\Delta \lambda /\lambda = 1.4\%$ ). Right: same measurements as previous ones but with broadband H filter ( $\Delta \lambda /\lambda = 20\%$ ).
Open with DEXTER

During our laboratory tests, no high frequency noise due to apodizer pixellation was revealed. However, the simulation analysis presented in Sect. 3 predicted pixellation noise of 20 $\lambda/D$ in the coronagraphic image at a contrast level between 10^-7 and 10^-8 (S = 600). In our case, the contrast level was insufficiently high even between diffraction spikes, to reveal the predicted noise. Therefore, draw conclusions only about performance and suitability of our configuration for HOT (the High Order Testbench developed at ESO), and even for SPHERE, but not about the pixellation noise predicted simultaneously by analytical development (Eqs. (2) and (6)) and simulations. We note that a smaller pixel size (< $5~\mu$ m) would certainly help in reducing the 3 $\%$ error in the profile, which could potentially improve performance. Despite the discrepancy discussed above, these first results of APLC using a microdot apodizer (raw contrast profiles) exceed already the SPHERE requirements (Boccaletti et al. 2008).

$\begin{figure} \par\includegraphics[width=4.0cm]{FIGURES/0918F16.eps}\includegraphics[width=4.01cm]{FIGURES/0918F17.eps} \end{figure}$	Figure 9: Images recorded on the bench ( $\lambda = 1.64$ $\mu$ m, $\Delta \lambda /\lambda = 1.4\%$ ), left: VLT-like pupil PSF, right: VLT-like pupil apodized PSF.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=5.05cm]{FIGURES/0918F18.eps}\includegraphics[width=1.39cm]{FIGURES/0918F19.eps} \end{figure}$	Figure 10: Observed raw coronagraphic image (log scale) with its scale of contrast ( $\lambda = 1.64$ $\mu$ m, $\Delta \lambda /\lambda = 1.4$ $\%$ ).
Open with DEXTER

5 Conclusion

We have described the development and laboratory experiments of an Apodized Pupil Lyot Coronagraph using a microdot apodizer in the near-IR. Halftone-dot process has been shown to be a promising alternative solution to continuous metal-layer deposition. Using a diffusion-error algorithm, and both optimized-pixel-size and fabrication techniques, we demonstrate impressive agreement between the specified and measured transmission profiles, as well as the achromatic behavior of this apodizer. Coronagraphic properties are consistent with expected properties, and have already reached the SPHERE requirements. Achromaticity in H band has also been demonstrated.

$\begin{figure} \par\includegraphics[width=9cm]{FIGURES/0918F20.eps} \end{figure}$	Figure 11: Azimuthally averaged coronagraphic profiles at $\lambda = 1.64$ $\mu$ m, $\Delta \lambda /\lambda = 1.4$ % (black lines) and $\Delta \lambda / \lambda = 20$ % (blue lines).
Open with DEXTER

Table 2: Summary of coronagraphic results and comparison with theory.

Additionally, pixellated apodizers do not produce a spatially-varying phase aberration, which could diminish the coronagraphic effect at all radial distances.

We therefore conclude that microdots apodizers represent an excellent choice for the APLC.

Although this study was carried out in the context of Research & Development for future near IR instruments on E-ELT, it is already applicable to other instruments such as SPHERE and other coronagraphs such as the Dual Zone. Finally, we note that a RCWA analysis would be mandatory for a more refined analysis of the dependency of optimal pixel size on wavelength.

Acknowledgements

P.M. would like to thank Sebastien Tordo and Christophe Dupuy from ESO for their helpful support with the ITC and metrology inspection. This activity is supported by the European Community under its Framework Programme 6, ELT Design Study, Contract No. 011863.

References

Aime, C. 2005, A&A, 434, 785 [NASA ADS] [CrossRef] [EDP Sciences]
Aime, C., Soummer, R., & Ferrari, A. 2002, A&A, 389, 334 [NASA ADS] [CrossRef] [EDP Sciences]
Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2006, The Messenger, 125, 29 [NASA ADS]
Boccaletti, A., Abe, L., Baudrand, J., et al. 2008, Proc. SPIE (In the text)
Dohlen, K. 2008, Proc. SPIE (In the text)
Dorrer, C., & Zuegel, J. D. 2007, J. Opt. Soc. Am. B, 24, 1268 [NASA ADS] [CrossRef]
Enya, K., Tanaka, S., Abe, L., & Nakagawa, T. 2007, A&A, 461, 783 [NASA ADS] [CrossRef] [EDP Sciences]
Enya, K., Abe, L., Tanaka, S., et al. 2008, A&A, 480, 899 [NASA ADS] [CrossRef] [EDP Sciences]
Floyd, R. W., & Steinberg, L. 1976, J. Soc. Inf. Disp., 17, 7577
Genet, C., & Ebbesen, T. W. 2007, Nature, 445, 39 [NASA ADS] [CrossRef]
Huang, C.-P., & Zhu, Y.-Y. 2007
Jacquinot, P., & Roisin-Dossier, B. 1964, Prog. Opt., 3, 29
Kasdin, N. J., Vanderbei, R. J., Spergel, D. N., & Littman, M. G. 2003, ApJ, 582, 1147 [NASA ADS] [CrossRef]
Kasper, M., Beuzit, J.-L., Verinaud, C., et al. 2008, Proc. SPIE (In the text)
Lyot, B. 1939, MNRAS, 99, 580 [NASA ADS] (In the text)
Macintosh, B., Graham, J., Palmer, D., et al. 2006, in Advances in Adaptive Optics II, Presented at the Society of Photo-Optical Instrumentation Engineers (SPIE) Conference, ed. B. L. Ellerbroek, & D. Bonaccini Calia, Proc. SPIE, 6272, 62720L
Martinez, P., Boccaletti, A., Kasper, M., Baudoz, P., & Cavarroc, C. 2007, A&A, 474, 671 [NASA ADS] [CrossRef] [EDP Sciences]
Martinez, P., Boccaletti, A., Kasper, M., et al. 2008, A&A, 492, 289 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Nisenson, P., & Papaliolios, C. 2001, ApJ, 548, L201 [NASA ADS] [CrossRef]
Oppenheimer, B. R., Digby, A. P., Newburgh, L., et al. 2004, in Advancements in Adaptive Optics, Presented at the Society of Photo-Optical Instrumentation Engineers (SPIE) Conference, ed. D. Bonaccini Calia, B. L. Ellerbroek, & R. Ragazzoni, Proc. SPIE, 5490, 433 (In the text)
Soummer, R. 2005, ApJ, 618, L161 [NASA ADS] [CrossRef]
Soummer, R., Aime, C., & Falloon, P. E. 2003a, A&A, 397, 1161 [NASA ADS] [CrossRef] [EDP Sciences]
Soummer, R., Dohlen, K., & Aime, C. 2003b, A&A, 403, 369 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Ulichney, R. 1987, The MIT Press
Ulichney, R. 1988, Proc. IEEE, 76, 1, 56
Vanderbei, R. J., Spergel, D. N., & Kasdin, N. J. 2003, ApJ, 590, 593 [NASA ADS] [CrossRef]
Vanderbei, R. J., Kasdin, N. J., & Spergel, D. N. 2004, ApJ, 615, 555 [NASA ADS] [CrossRef]

All Tables

Table 1: High frequency noise properties as a function of the pixel size.

Table 2: Summary of coronagraphic results and comparison with theory.

All Figures

$\begin{figure} \par\includegraphics[width=4cm]{FIGURES/0918F1.eps}\includegraphi... .../0918F2.eps}\par\includegraphics[width=8.15cm]{FIGURES/0918F3.eps} \end{figure}$	Figure 1: Left: shaper target (continuous apodizer). Right: resulting microdots pattern using algorithm discussed in Sect. 2. The spatial scale of these maps is 600 $\times$ 600 pixels. The scale of transmission is given in $\%$ .
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{FIGURES/0918F4.eps} \end{figure}$	Figure 2: First-order peak diffraction f_g position in $S \times \lambda /D$ units as a function of gray level g. Typical domain of application of apodizer masks are reported on the plot.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{FIGURES/0918F5.eps}\includegraphics[width=9cm]{FIGURES/0918F6.eps} \vspace*{3mm} \end{figure}$	Figure 3: Apodized PSFs ( left) and APLC coronagraphic PSFs ( right) using several dot sizes for the binary apodizer compared to that with continuous apodizer (i.e. theory, in black). Simulation assumes a pupil with 15 $\%$ central obscuration. Profiles presented are azimuthal averages.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9.cm]{FIGURES/0918F7.eps}\par\includegraphics[width=9.cm]{FIGURES/0918F8.eps} \end{figure}$	Figure 4: Top: picture of the IR coronagraphic test-bench on HOT. The red dot line shows the IR coronagraphic path, while the blue dot line shows the pupil imager system path when placing a mirror on a magnetic mount before the external IR filter. Bottom: schematic setup of the coronagraphic testbench.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm]{FIGURES/0918F9.eps}\includegraphics[width=8.56cm]{FIGURES/0918F10.eps} \end{figure}$	Figure 5: Left: simulation map of the binary apodizer with $5\times 5~\mu$ m dots. Right: shadowgraph inspection of the manufactured microdots apodizer ( $\times$ 50). For the sake of clarity, only a quarter of the apodizer is shown.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{FIGURES/0918F11.eps}\includegraphics[width=9cm]{FIGURES/0918F12.eps} \end{figure}$	Figure 6: Left: apodizer azimuthally average profile (from center to the edges) using different filters (J, H and narrow H band) compared to specification (black curve). Right: corresponding average amplitude error as function of the position using the same filters.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=5.43cm]{FIGURES/0918F13.eps} \end{figure}$	Figure 7: Top: infrared recorded image of the apodizer.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{FIGURES/0918F14.eps}\includegraphics[width=9cm]{FIGURES/0918F15.eps} \end{figure}$	Figure 8: Left: PSF and apodized PSF recorded on the bench (blue lines) compared to theoretical ones (black lines) with narrow H filter ( $\lambda = 1.64$ $\mu$ m, $\Delta \lambda /\lambda = 1.4\%$ ). Right: same measurements as previous ones but with broadband H filter ( $\Delta \lambda /\lambda = 20\%$ ).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4.0cm]{FIGURES/0918F16.eps}\includegraphics[width=4.01cm]{FIGURES/0918F17.eps} \end{figure}$	Figure 9: Images recorded on the bench ( $\lambda = 1.64$ $\mu$ m, $\Delta \lambda /\lambda = 1.4\%$ ), left: VLT-like pupil PSF, right: VLT-like pupil apodized PSF.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=5.05cm]{FIGURES/0918F18.eps}\includegraphics[width=1.39cm]{FIGURES/0918F19.eps} \end{figure}$	Figure 10: Observed raw coronagraphic image (log scale) with its scale of contrast ( $\lambda = 1.64$ $\mu$ m, $\Delta \lambda /\lambda = 1.4$ $\%$ ).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=9cm]{FIGURES/0918F20.eps} \end{figure}$	Figure 11: Azimuthally averaged coronagraphic profiles at $\lambda = 1.64$ $\mu$ m, $\Delta \lambda /\lambda = 1.4$ % (black lines) and $\Delta \lambda / \lambda = 20$ % (blue lines).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.