| Issue |
A&A
Volume 495, Number 1, February III 2009
|
|
|---|---|---|
| Page(s) | 271 - 286 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361:200810665 | |
| Published online | 22 December 2008 | |
Diagnoses to unravel secular hydrodynamical processes in rotating main sequence stars
T. Decressin1,2 - S. Mathis3,8 - A. Palacios4 - L. Siess5 - S. Talon6 - C. Charbonnel1,7 - J.-P. Zahn8
1 - Geneva Observatory, University of Geneva, chemin des
Maillettes 51, 1290 Sauverny, Switzerland
2 -
Argelander Institute for Astronomy (AIfA), Auf dem
Hügel 71, 53121 Bonn, Germany
3 -
Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot, IRFU/SAp Centre de Saclay, 91191 Gif-sur-Yvette, France
4 -
GRAAL, Université Montpellier II, CNRS, Place
E. Bataillon, 34095 Montpellier Cedex 05, France
5 -
IAA-ULB, Université Libre de Bruxelles, Boulevard du
Triomphe, CP 26, 1050 Bruxelles, Belgium
6 -
Réseau Québécois de Calcul de Haute Performance,
Université de Montréal (DGTIC), CP 6128, succ. Centre-ville,
Montréal H3C 3J7, Canada
7 -
LATT, CNRS UMR 5572, Université de Toulouse, 14 Av. Edouard
Belin, 31400 Toulouse Cedex 04, France
8 -
LUTH, Observatoire de Paris-CNRS-Université Paris-Diderot, Place Jules Janssen, 92195 Meudon, France
Recived 24 July 2008 / Accepted 18 November 2008
Abstract
Context. Recent progress and constraints brought by helio and asteroseismology call for a better description of stellar interiors and an accurate description of rotation-driven mechanisms in stars.
Aims. We present a detailed analysis of the main physical processes responsible for the transport of angular momentum and chemical species in the radiative regions of rotating stars. We focus on cases where meridional circulation and shear-induced turbulence all that are included in the simulations (i.e., no either internal gravity waves nor magnetic fields). We put special emphasis on analysing the angular momentum transport loop and on identifying the contribution of each of the physical process involved.
Methods. We develop a variety of diagnostic tools designed to help disentangle the role of the various transport mechanisms. Our analysis is based on a 2-D representation of the secular hydrodynamics, which is treated using expansions in spherical harmonics. By taking appropriate horizontal averages, the problem reduces to one dimension, making it implementable in a 1D stellar evolution code, while preserving the advective character of angular momentum transport. We present a full reconstruction of the meridional circulation and of the associated fluctuations of temperature and mean molecular weight, along with diagnosis for the transport of angular momentum, heat, and chemicals. In the present paper these tools are used to validate the analysis of two main sequence stellar models of 1.5 and 20
![]() ,
for which the hydrodynamics has previously been extensively studied in the literature.
,
for which the hydrodynamics has previously been extensively studied in the literature.
Results. We obtain a clear visualisation and a precise estimation of the different terms entering the angular momentum and heat transport equations in radiative zones of rotating stars. This enables us to corroborate the main results obtained over the past decade by Zahn, Maeder, and collaborators concerning the secular hydrodynamics of such objects. We focus on the meridional circulation driven by angular momentum losses and structural readjustments. We confirm quantitatively for the first time through detailed computations and separation of the various components that the advection of entropy by this circulation is balanced very well by the barotropic effects and the thermal relaxation during most of the main sequence evolution. This enables us to simplify for the thermal relaxation on this phase. The meridional currents in turn advect heat and generate temperature fluctuations that induce differential rotation through thermal wind, thus closing the transport loop. We plan to make use of our refined diagnosis tools in forthcoming studies of secular (magneto-)hydrodynamics of stars at various evolutionary stages.
Key words: hydrodynamics - turbulence - stars: evolution - stars: rotation
1 The impact of rotation on stellar evolution
Rotation, and more precisely differential rotation, has a major impact on the internal dynamics of stars, in several ways. It induces large-scale circulations both in radiative and convective zones that simultaneously advect angular momentum, nuclides, and magnetic fields (Mestel 1953; Maeder & Zahn 1998; Busse 1982; Sweet 1950; Zahn 1992; Palacios et al. 2003; Garaud 2002b; Palacios et al. 2006; Talon et al. 1997; Mathis & Zahn 2005; Meynet & Maeder 2000; Eddington 1925; Espinosa Lara & Rieutord 2007; Rieutord 2006a; Talon 1997; Mathis & Zahn 2004; Mathis et al. 2007; Vogt 1925). When the star rotates differentially, various instabilities develop (secular and dynamical shear instabilities, baroclinic, and multidiffusive instabilities) that generate hydrodynamical turbulence in radiative zones, in addition to these circulations. Just as in the terrestrial atmosphere and in laboratory experiments, this turbulence acts to reduce its cause, namely the gradients of angular velocity and of chemical composition. This explains why its effect may be described as a diffusion process (Talon 2007; Talon & Zahn 1997; Maeder 2003; Mathis et al. 2004, and references therein).
Rotating stars have an equator that is cooler than the poles, which has a strong effect on radiatively driven stellar winds and hence on the loss of mass and angular momentum (Maeder 1999). If rotation is large enough, the stars can even reach the break-up limit, when centrifugal force balances the gravity, and matter is ejected through an equatorial mechanical winds that create a circumstellar disk (Ekström et al. 2008; Maeder & Meynet 2000a; Meynet et al. 2007).
Rotation also has a strong impact on the stellar magnetism. In radiative zones, rotation interacts with the magnetic field and is able to trigger magnetohydrodynamical instabilities, which could play a role in the transport of angular momentum and nuclides (Maeder & Meynet 2004; Spruit 2002; Braithwaite & Spruit 2005; Brun & Zahn 2006; Menou et al. 2004; Zahn et al. 2007; Braithwaite 2006; Eggenberger et al. 2005; Garaud 2002a; Mathis & Zahn 2005; Spruit 1999; Charbonneau & MacGregor 1993). Furthermore, internal gravity waves and gravito-inertial waves that are excited at the edge of the convection zones may also contribute to the transport of angular momentum. They propagate inside radiative zones and extract or deposit angular momentum in the region where they are damped, thus modifying the angular velocity profile and the vertical distribution of chemicals (Talon & Charbonnel 2003; Charbonnel & Talon 2005; Mathis et al. 2008; Talon et al. 2002; Rogers & Glatzmaier 2005; Talon & Charbonnel 2004; Schatzman 1993; Talon & Charbonnel 2005; Press 1981; Pantillon et al. 2007; Talon & Charbonnel 2008).
All these effects significantly modify the evolution of rotating stars. They affect their surface velocities and chemical abundances, and change their paths across the colour-magnitude diagram (Maeder 2009; Maeder & Meynet 2000b). They also modify the internal structure of stars in a way that we will soon be able to test thanks to asteroseismology over a broader range of evolutionary phases.
In this paper we present a set of diagnosis tools adapted to the analysis of stellar evolution with rotation and use them to compare the efficiency of different transport processes. The present study focuses on ``type I rotational transport'', where magnetic fields and waves are not accounted for and where the angular momentum and the nuclides are both transported exclusively by meridional circulation and shear-induced turbulence. These diagnoses and tools rely on a specific expansion of the equations for the transport of angular momentum, heat, and chemicals that are briefly recalled in Sect. 2. In Sect. 3, we validate our method by applying our tools to two specific stellar models for which the hydrodynamics has already been extensively studied in the literature. Conclusions and perspectives are presented in Sect. 4.
2 Modelling the secular processes
2.1 Scale separation
To simulate the dynamical processes in a star in full details, would require including length scales and time scales spanning many orders of magnitude. This is clearly not feasible, even with the most powerful computers. Either one chooses to describe what occurs on a dynamical time scale, such as a convective turnover time or one focuses on the long time evolution, as we do here, where the typical time is either the Kelvin-Helmholtz time or that characterising the dominant nuclear reactions. The same is true for the length scales, at least in the vertical direction, where we take the resolution that adequately represents the steepest gradients that develop during the evolution.
The situation is somewhat different in the horizontal direction - i.e. in latitude, since we consider only the axisymmetric case here. Stellar radiative zones are stably stratified regions, and the buoyancy, which is the restoring force, acts to inhibit turbulent motions in the vertical direction. This leads to a strongly anisotropic turbulent transport that is more efficient in the horizontal direction (along isobars) than in the vertical one. As a result, the horizontal gradients of all scalar fields (temperature, angular velocity, etc.) are much smaller than their vertical gradients, which allows their expansion in a few spherical harmonics. This scale separation, both in space and in time, is illustrated in Fig. 1.
Considering the axisymmetric case, each scalar field is thus written as the
sum of its horizontal average on an isobar, and its associated fluctuation,
which is expanded in the Legendre polynomials basis
![]() ,
up
to some maximum order
,
up
to some maximum order
![]() .
For simplicity's sake, we present
here the results keeping a single scale
.
For simplicity's sake, we present
here the results keeping a single scale ![]() ,
which is dominant.
Let us note that there are circumstances where we have to include
many more components, for instance when dealing with magnetic fields.
,
which is dominant.
Let us note that there are circumstances where we have to include
many more components, for instance when dealing with magnetic fields.
The unresolved scales intervene in the turbulent transport, for which a prescription is applied that is derived, whenever possible, from laboratory experiments or numerical simulations, and if not through phenomenological considerations.
![\begin{figure}
\par\includegraphics[height=8.5cm,clip]{0665fig1}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg31.gif) |
Figure 1:
Modelling strategy to study dynamical stellar evolution. The
diagram presents time scales of the typical physical processes as a
function of the angular resolution needed to properly describe these
processes. The angular resolution is expressed in terms of the l index
of the spherical harmonics
|
| Open with DEXTER | |
2.2 Linearization and expansion in spherical harmonics
Let us briefly recall how these expansions are performed in practice; for
more details, we refer the reader to Mathis & Zahn (2004) and Maeder (2009).
We begin with the macroscopic velocity field, which is split into 3 components:
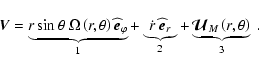 |
(1) |
Term 1 represents the azimuthal velocity field associated with the differential rotation. Term 2 corresponds to the radial Lagrangian velocity due to the structural readjustments of the star during its evolution. Term 3 is the meridional circulation velocity field.
In radiative zones, because of the strong stratification, the turbulent
transport is highly anisotropic, which leads to a ``shellular'' rotation
profile (Zahn 1992). The angular velocity thus varies little on an
isobar, allowing to expand it as
![\begin{displaymath}\Omega(r, \theta) = \overline\Omega(r)+\Omega_2(r)\left[P_2(\cos
\theta)-{1/ 5}\right] ,
\end{displaymath}](/articles/aa/full_html/2009/07/aa10665-08/img35.gif) |
(2) |
where
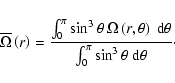 |
(3) |
As usual, the meridional velocity field is projected on spherical functions, of which we show here only that of lowest order:
where P2 is the second-order Legendre polynomial. The anelastic approximation is adopted, filtering out the acoustic waves, which is amply justified for this slow meridional circulation. Therefore, the continuity equation reduces to
Moreover, since
which leads to
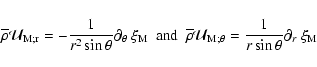 |
(7) |
with
The quantity
Finally, all other variables are expanded as shown here for the temperature
and the mean molecular weight:
and
here,
2.3 The transport equations
Using these notations, the transport equations for angular momentum and chemicals may thus be expanded in the following way.
2.3.1 Transport of angular momentum and thermal-wind
We first consider the azimuthal projection of the momentum equation. By
averaging it over an isobar, we obtain the following advection-diffusion
equation for the mean angular momentum:
Term 1 represents the transport of angular momentum by the meridional circulation; note that the advective character of that transport is preserved. The diffusion term 2 is associated with the action of the shear-induced turbulence, where
This equation shows the relation between the meridional circulation and the transport of angular momentum. In the asymptotic regime, the left hand side term is zero and the transport of angular momentum by meridional circulation is exactly balanced by that through shear turbulence. In the limit of vanishing turbulent viscosity, the rotation profile would adjust so that no meridional currents appear (Busse 1982). In reality, because of the loss of angular momentum by the wind and/or its redistribution by structural changes, the left hand side term is non zero.
By integrating Eq. (11) over a surface of radius r, it can be recast in an equation for the fluxes:
where
is the flux transported by the meridional circulation, and
is what is carried by the vertical shear induced turbulence. The term
From Eq. (12) it is also possible to extract the radial component of the meridional circulation velocity:
Finally, by taking the curl of the momentum equation and again filtering out the fast time scales, we obtain the so-called thermal wind equation:
where
2.3.2 Thermal relaxation
Likewise, by expanding the energy conservation equation over spherical
functions, we establish the following equation for the temperature
perturbation represented here by ![]() (Eq. (101) in Mathis & Zahn 2004;
see Zahn 1992):
(Eq. (101) in Mathis & Zahn 2004;
see Zahn 1992):
where NT, the buoyancy frequency linked with the entropy stratification, is given by
For diagnostic purposes (and also for historical reasons; see the discussion in Zahn 1992, after Eq. (3.32)), we split the diffusion term into two pieces, whose expressions are given in Appendix B:
-
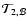 corresponds to the divergence of the
radiative flux associated to the deformation of the isobar induced by the
perturbing force, which here is the centrifugal acceleration. This term
subsists in the case of solid body rotation; for this reason, we called it
the barotropic term following Zahn (1992).
corresponds to the divergence of the
radiative flux associated to the deformation of the isobar induced by the
perturbing force, which here is the centrifugal acceleration. This term
subsists in the case of solid body rotation; for this reason, we called it
the barotropic term following Zahn (1992).
-
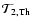 contains the highest derivatives of the
diffusion operator, and according to the thermal wind
Eq. (17), it vanishes in an homogeneous star when the rotation
is uniform. It is referred to as the thermic or baroclinic term
(Zahn 1992).
contains the highest derivatives of the
diffusion operator, and according to the thermal wind
Eq. (17), it vanishes in an homogeneous star when the rotation
is uniform. It is referred to as the thermic or baroclinic term
(Zahn 1992).
Equation (18) can finally be written in the following form
where
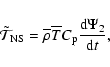 |
(20) |
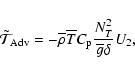 |
(21) |
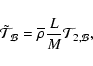 |
(22) |
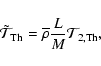 |
(23) |
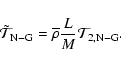 |
(24) |
This will be used in Sect. 3.4. in our diagnosis tools.
![\begin{figure}
\par\mbox{\includegraphics[width=8cm]{0665fig2}\hspace*{4mm}
\includegraphics[width=8cm]{0665fig3} }\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg88.gif) |
Figure 2:
Evolutionary path in the HR diagram of a 20
|
| Open with DEXTER | |
2.3.3 Transport of nuclides
The expansion of the transport equation for the nuclides on an isobar leads
to an equation for the evolution of the mass fraction of each considered
chemical (see also Meynet & Maeder 2000):
where d
where
Equation (25) is complemented by an equation for the time evolution
of the relative fluctuation of the mean molecular weight, expressed here in
terms of ![]() :
:
where
2.3.4 Turbulence modelling
The details of turbulence modelling have already been extensively discussed in previous papers (Palacios et al. 2006; Talon et al. 1997), so that we just recall here the expressions we have chosen.
For the vertical turbulent diffusion coefficients (
![]() ), we
use the expression by Talon & Zahn (1997):
), we
use the expression by Talon & Zahn (1997):
where
For the horizontal turbulent viscosity, we used two different
prescriptions:
after Mathis et al. (2004), and
after Zahn (1992). Here the parameter
We stress that the advective character of the transport of angular momentum by the meridional circulation makes the interpretation of the whole hydrodynamics more complex than when the diffusive approximation is used (e.g., Heger et al. 2000; Pinsonneault et al. 1989; Endal & Sofia 1978). This is one of the reasons we developed the tools that we describe in the following section.
3 Numerical simulation of secular transport
In this section, we apply the formalism described in Sect. 2 to
the evolution of rotating stars with initial masses of 20 and 1.5
![]() and
metallicity close to solar value (Z = 0.017 and 0.02 for the 20 and the
1.5
and
metallicity close to solar value (Z = 0.017 and 0.02 for the 20 and the
1.5
![]() respectively). In the Hertzsprung-Russell diagram shown in
Fig. 2, the black dots indicate the evolutionary points where a
snapshot on the internal structure will be taken and analysed in
detail. These points are associated with central hydrogen mass fractions
respectively). In the Hertzsprung-Russell diagram shown in
Fig. 2, the black dots indicate the evolutionary points where a
snapshot on the internal structure will be taken and analysed in
detail. These points are associated with central hydrogen mass fractions
![]() as indicated on the tracks.
as indicated on the tracks.
A number of results for the hydrodynamics of such rotating models have already been published (Meynet & Maeder 2000; Palacios et al. 2003,2006; Decressin et al. 2007; Mathis et al. 2004; Talon 1997; Talon & Charbonnel 1998), and we rely on this experience to prove the relevance of the diagnosis tools that we have developed. The models presented here were computed with the stellar evolution code STAREVOL V2.90, and the reader is referred to Siess et al. (2000), Palacios et al. (2006), and Siess (2006) for a detailed description of the input physics. We simply recall the main characteristics and parameters used for the modelling.
The reference solar composition we use follows Grevesse et al. (1996).
The standard mixing length theory is used to model the temperature gradient
in the convection zones and the parameter
![]() .
The
atmosphere is treated in the gray approximation and integrated up to an
optical depth
.
The
atmosphere is treated in the gray approximation and integrated up to an
optical depth
![]() .
.
In both simulations, mass loss is included from the zero age main sequence
on. We use the Reimers (1975) prescription for the low-mass star, with a
parameter
![]() (see also Palacios et al. 2006) and the
prescriptions by Vink et al. (2000) for the massive star. Rotation effects on
mass loss are accounted for following Maeder & Meynet (2001). Angular momentum losses
associated with mass loss are also accounted for, but their anisotropy
(Maeder 2002) is not included in the computations.
(see also Palacios et al. 2006) and the
prescriptions by Vink et al. (2000) for the massive star. Rotation effects on
mass loss are accounted for following Maeder & Meynet (2001). Angular momentum losses
associated with mass loss are also accounted for, but their anisotropy
(Maeder 2002) is not included in the computations.
For the transport of angular momentum and nuclides, we use
Eq. (29) as the prescription for Dh for the 20
![]() model.
For the 1.5
model.
For the 1.5
![]() model, we use Eq. (30) as in Palacios et al. (2003)
who shows that it yields to a very good
agreement with the surface velocity and the light nuclides (Li, Be) surface
abundances that are observed in open clusters such as the Hyades. The
expression for the vertical turbulent diffusion coefficient is given by
Eq. (28) in both models. For the transport of nuclides, we do
not account for atomic diffusion.
model, we use Eq. (30) as in Palacios et al. (2003)
who shows that it yields to a very good
agreement with the surface velocity and the light nuclides (Li, Be) surface
abundances that are observed in open clusters such as the Hyades. The
expression for the vertical turbulent diffusion coefficient is given by
Eq. (28) in both models. For the transport of nuclides, we do
not account for atomic diffusion.
In our framework, the evolution of the angular velocity profile and of the
meridional circulation in the radiative zones is governed by a system of
five first-order partial differential equations. These equations are obtained by
splitting Eq. (11) into first-order equations that are complemented
by Eqs. (17) and (27). We use a Newton-Raphson
relaxation method (Heyney et al. 1964) to solve these equations. In
convection zones we assume solid-body rotation (
![]() )
and do
not solve the aforementioned system. The boundary conditions at the
radiative zone limits are the same as those described in Palacios et al. (2003).
)
and do
not solve the aforementioned system. The boundary conditions at the
radiative zone limits are the same as those described in Palacios et al. (2003).
We choose initial velocities on the ZAMS that reflect an average velocity
for main sequence B and F stars (Gaigé 1993; Abt et al. 2002; Fukada 1982).
The adopted initial velocity on the ZAMS are
![]() km s-1 and
km s-1 and
![]() km s-1
for the 20
km s-1
for the 20 ![]() and the 1.5
and the 1.5 ![]() ,
respectively.
,
respectively.
![\begin{figure}
\par\mbox{\includegraphics[width=8cm]{0665fig4}\hspace*{4mm}
\includegraphics[width=8cm]{0665fig5} }\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg113.gif) |
Figure 3:
Angular velocity profile inside the 20
|
| Open with DEXTER | |
The evolution of the surface velocity can be affected by the magnetic
torques exerted at the surface of the star during its early evolution
(Schatzman 1962). This magnetic braking is generally associated with the
presence of a convective envelope; it will thus only be applied to the
low-mass star model, following Kawaler's (1988)
formalism as described in Palacios et al. (2003). In the case of massive stars,
it is only very recently that magnetic fields have been detected in
normal O and B stars, and they appear to be very weak or nonexistent
(Bouret et al. 2008; Schnerr et al. 2008). Moreover, O and B stars with measured
![]() appear to be fast rotators. For these reasons, we have
decided not to account for magnetic braking in the 20
appear to be fast rotators. For these reasons, we have
decided not to account for magnetic braking in the 20
![]() model.
model.
In the following sections, we present new diagnosis tools to better understand and quantify the processes responsible for the building up of differential rotation in stellar interiors.
3.1 Rotational profiles and differential rotation
3.1.1 20 M model
model
The 20
![]() model does not undergo magnetic braking and thus
remains a fast rotator during its main sequence (MS) evolution, with
model does not undergo magnetic braking and thus
remains a fast rotator during its main sequence (MS) evolution, with
![]() km s-1. Similarly to what was obtained by
Meynet & Maeder (2000), differential rotation rapidly develops in the
interior, as firsts meridional flow transports
angular momentum inwards.
After a transient phase that lasts
km s-1. Similarly to what was obtained by
Meynet & Maeder (2000), differential rotation rapidly develops in the
interior, as firsts meridional flow transports
angular momentum inwards.
After a transient phase that lasts ![]() 1 Myr following the arrival on
the ZAMS, the morphology of the rotation profile is not significantly
affected until the star reaches the turn-off, as shown in
Fig. 3 (left panel).
1 Myr following the arrival on
the ZAMS, the morphology of the rotation profile is not significantly
affected until the star reaches the turn-off, as shown in
Fig. 3 (left panel).
Above the radial coordinate 5
![]() (resp. 6
(resp. 6
![]() and 10
and 10
![]() )
for
)
for
![]() (resp.
(resp.
![]() and
and
![]() ), the
angular velocity gradient becomes positive due to very efficient
transport of angular momentum by the meridional circulation in a region
where the density is low (see Sect. 3.2). This inversion of
the angular velocity gradient should be counteracted by the shear
turbulence that tends to smooth out this profile. However, the shear can only
operate if the flow is turbulent, i.e., if the Reynolds condition
), the
angular velocity gradient becomes positive due to very efficient
transport of angular momentum by the meridional circulation in a region
where the density is low (see Sect. 3.2). This inversion of
the angular velocity gradient should be counteracted by the shear
turbulence that tends to smooth out this profile. However, the shear can only
operate if the flow is turbulent, i.e., if the Reynolds condition
![]() is satisfied where Re
is satisfied where Re
![]() is the critical Reynolds
number and
is the critical Reynolds
number and ![]() and
and ![]() the shear and microscopic viscosities,
respectively. Below the convective envelope (where
the shear and microscopic viscosities,
respectively. Below the convective envelope (where
![]() ), this condition is not fulfilled,
and the shear is unable to connect the region with positive angular
velocity gradient with the one where
), this condition is not fulfilled,
and the shear is unable to connect the region with positive angular
velocity gradient with the one where
![]() (see
the dip in the profile of
(see
the dip in the profile of ![]() in Fig. 15). This explains
the persistence of this positive gradient. Computations done without taking
into account the Reynolds criterion show that this positive gradient is
reduced (by a factor 3 to 5) but is still present, although at a lower
level. It should be noted that this inversion has already been obtained by
Talon et al. (1997) in the asymptotic regime for a 9
in Fig. 15). This explains
the persistence of this positive gradient. Computations done without taking
into account the Reynolds criterion show that this positive gradient is
reduced (by a factor 3 to 5) but is still present, although at a lower
level. It should be noted that this inversion has already been obtained by
Talon et al. (1997) in the asymptotic regime for a 9
![]() with an
equatorial angular velocity of 425 km s-1. This feature can be linked to
the Gratton-Öpik term in the meridional circulation (see Sect. 3.4.1).
with an
equatorial angular velocity of 425 km s-1. This feature can be linked to
the Gratton-Öpik term in the meridional circulation (see Sect. 3.4.1).
The decrease in the angular velocity during the MS evolution is due to two
factors: (1) mass and angular momentum losses by the stellar winds and (2)
structural changes that lead to an overall expansion of the star. It should
be noted, however, that up to the point where
![]() ,
the
contrast in
,
the
contrast in ![]() between the centre and the surface is small, not
exceeding 20% .
between the centre and the surface is small, not
exceeding 20% .
3.1.2 1.5 M model
model
In contrast to the 20
![]() star, the 1.5
star, the 1.5
![]() star undergoes magnetic
braking at its arrival on the ZAMS, resulting in a strong extraction
of angular momentum, as shown in Talon & Charbonnel (1998) and
Palacios et al. (2006,2003). During the first 800 Myr, the surface equatorial
velocity drops from 100 km s-1 to 78 km s-1, in agreement with observations
in open clusters like the Hyades (i.e., Gaigé 1993). Beyond this point,
the braking becomes less efficient and the surface rotational velocity
continues to decrease slowly until the star reaches the turn-off with
star undergoes magnetic
braking at its arrival on the ZAMS, resulting in a strong extraction
of angular momentum, as shown in Talon & Charbonnel (1998) and
Palacios et al. (2006,2003). During the first 800 Myr, the surface equatorial
velocity drops from 100 km s-1 to 78 km s-1, in agreement with observations
in open clusters like the Hyades (i.e., Gaigé 1993). Beyond this point,
the braking becomes less efficient and the surface rotational velocity
continues to decrease slowly until the star reaches the turn-off with
![]() km s-1 at age 2.35 Gyr.
km s-1 at age 2.35 Gyr.
The right panel of Fig. 3 presents the evolution of the
angular velocity profile on the MS. When
![]() ,
i.e. when
the star is
,
i.e. when
the star is ![]() 200 Myr old, the core already rotates 1.5 times faster
than the surface. While the angular velocity in the convective core slowly
increases, the extraction of angular momentum at the surface slows down the
surface layers and differential rotation increases during the MS. When the
convective core disappears at central H-exhaustion, the contraction of the
inner shells produces a much steeper
200 Myr old, the core already rotates 1.5 times faster
than the surface. While the angular velocity in the convective core slowly
increases, the extraction of angular momentum at the surface slows down the
surface layers and differential rotation increases during the MS. When the
convective core disappears at central H-exhaustion, the contraction of the
inner shells produces a much steeper ![]() -gradient (right panel,
Fig. 3) with
-gradient (right panel,
Fig. 3) with
![]() .
.
3.2 Meridional circulation
In this section, we isolate the processes that are at the origin of meridional circulation.
3.2.1 20 M model
model
Figure 4 shows the meridional flows in the radiative
interior of the 20
![]() when the central hydrogen mass fraction reaches
when the central hydrogen mass fraction reaches
![]() .
They are represented in terms of the stream function
.
They are represented in terms of the stream function
![]() (see Eq. (8)). The circulation
consists of a single counterclockwise loop, by which matter is transported
inward along the rotational axis, and is conveyed outward in the equatorial
plane. These flows thus extract angular momentum from the deep interior to
the surface. Matter is conserved in the meridional circulation currents and
(see Eq. (8)). The circulation
consists of a single counterclockwise loop, by which matter is transported
inward along the rotational axis, and is conveyed outward in the equatorial
plane. These flows thus extract angular momentum from the deep interior to
the surface. Matter is conserved in the meridional circulation currents and
![]() along the
flux lines (shown in Fig. 4). The abrupt jump in density
occurring near the surface produces an increase in the meridional
circulation velocity as illustrated by Fig. 5. This in
turn forces the inversion of the angular velocity gradient mentioned in
Sect. 3.1 via the Gratton-Öpik term
(
along the
flux lines (shown in Fig. 4). The abrupt jump in density
occurring near the surface produces an increase in the meridional
circulation velocity as illustrated by Fig. 5. This in
turn forces the inversion of the angular velocity gradient mentioned in
Sect. 3.1 via the Gratton-Öpik term
(
![]() ,
see Eq. (B.1) in Appendix B). The velocities are maximum in the low-density regions
(i.e. below the surface) where they reach
,
see Eq. (B.1) in Appendix B). The velocities are maximum in the low-density regions
(i.e. below the surface) where they reach
![]()
![]() 1.6 m s-1.
1.6 m s-1.
![\begin{figure}
\par\includegraphics[width=8.5cm]{0665fig6}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg133.gif) |
Figure 4:
Meridional circulation currents in the 20
|
| Open with DEXTER | |
After a short adjustment phase, which depends on the initial conditions that have been imposed on the ZAMS (uniform rotation), the meridional circulation settles into a counterclockwise regime, as was noticed by Meynet & Maeder (2000). This flow thus carries angular momentum outwards, in order to compensate for the structural changes, i.e. the inflation of the envelope and the contraction of the core.
Figure 5 shows the a posteriori reconstruction of
the meridional circulation based on the integration of the equation for the
evolution of angular momentum (Eq. (16)), at
![]() .
.
![]() represents the angular momentum extraction
and UV what is due to the shear. In the inner part of the
radiative zone, below 7
represents the angular momentum extraction
and UV what is due to the shear. In the inner part of the
radiative zone, below 7
![]() ,
the meridional circulation is powered by the
extraction of angular momentum, as
,
the meridional circulation is powered by the
extraction of angular momentum, as
![]() .
Near the
surface, UV becomes negative and the same order as
.
Near the
surface, UV becomes negative and the same order as
![]() .
This inversion of UV is correlated with the sign
change of the angular velocity gradient since
.
This inversion of UV is correlated with the sign
change of the angular velocity gradient since
![]() .
.
![]() may be considered
as a measure of the departure from a stationary regime, where angular
momentum transport by shear (UV) and meridional circulation
(U2) compensate for each other. This balance is barely achieved in the
uppermost part of the star (above 8
may be considered
as a measure of the departure from a stationary regime, where angular
momentum transport by shear (UV) and meridional circulation
(U2) compensate for each other. This balance is barely achieved in the
uppermost part of the star (above 8
![]() ), but the bulk of the radiative
interior is not in a stationary state, as already pointed out in
Talon et al. (1997) and Meynet & Maeder (2000) on the basis of an asymptotic
analysis. Here, we confirm this result but also track down the importance
of the shear versus angular momentum transport in shaping the meridional
circulation.
), but the bulk of the radiative
interior is not in a stationary state, as already pointed out in
Talon et al. (1997) and Meynet & Maeder (2000) on the basis of an asymptotic
analysis. Here, we confirm this result but also track down the importance
of the shear versus angular momentum transport in shaping the meridional
circulation.
![\begin{figure}
\par\includegraphics[width=8.5cm]{0665fig7}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg136.gif) |
Figure 5:
Decomposition of the meridional circulation based on the equation
of angular momentum evolution in the 20
|
| Open with DEXTER | |
3.2.2 1.5 M model
model
The wind-driven meridional flows are depicted in Fig. 6
for the low-mass star at the three evolutionary stages indicated in
Fig. 2. Compared to the 20
![]() model, the topology of the
meridional circulation is more complex. In panels 1 and 3, the circulation
presents two loops: a small clockwise loop in the central regions and a
large counterclockwise loop connecting the interior to the surface. As in
the massive star model, the counterclockwise loop carries angular momentum
outward and is driven by the strong extraction of angular momentum (here
largely due to the magnetic braking). The clockwise loop corresponds to
matter flowing from the equator to the pole, which results in deposition of
angular momentum in this region. Such loops appear only in the centre and
do not persist over the whole evolution on the main sequence.
model, the topology of the
meridional circulation is more complex. In panels 1 and 3, the circulation
presents two loops: a small clockwise loop in the central regions and a
large counterclockwise loop connecting the interior to the surface. As in
the massive star model, the counterclockwise loop carries angular momentum
outward and is driven by the strong extraction of angular momentum (here
largely due to the magnetic braking). The clockwise loop corresponds to
matter flowing from the equator to the pole, which results in deposition of
angular momentum in this region. Such loops appear only in the centre and
do not persist over the whole evolution on the main sequence.
At the beginning of the MS evolution, the meridional circulation velocity
is maximal in a thin layer below the surface as a result of the applied
magnetic torque. The amplitude of the meridional circulation velocity
||U2|| does not exceed 0.5 m s-1 at its maximum and is
approximately of 10-4 in the bulk of the radiative zone. As the star
spins down, the braking becomes less efficient and the meridional
circulation weakens by 3 orders of magnitude. The large difference in
meridional velocity between the low-mass and the massive star is due to
the
L/M factor (Eq. (18)), which increases with stellar mass, and to
the higher initial angular velocity of the 20
![]() star.
star.
Figure 7 is similar to Fig. 5 but
for the 3 models selected during the MS evolution of the 1.5
![]() star. As
for the 20
star. As
for the 20
![]() model, the meridional circulation is driven by the local
loss of angular momentum (
model, the meridional circulation is driven by the local
loss of angular momentum (![]() term that matches the U2 profile),
the contribution of the vertical shear (UV) being always much smaller,
except in the central regions where it can be about
term that matches the U2 profile),
the contribution of the vertical shear (UV) being always much smaller,
except in the central regions where it can be about ![]() .
This figure
confirms that the inward transport of angular momentum (clockwise
meridional circulation loops) is associated with a positive value
of
.
This figure
confirms that the inward transport of angular momentum (clockwise
meridional circulation loops) is associated with a positive value
of ![]() ,
corresponding to a local gain of angular momentum (see
Eq. (16)). In most of the radiative zone,
,
corresponding to a local gain of angular momentum (see
Eq. (16)). In most of the radiative zone,
![]() ,
and contrary to what was found in the massive star model, the circulation
in the upper part of the radiative zone never approaches the stationary
regime. As shown by Talon et al. (1997), the extraction of angular momentum by
magnetic braking together with the very small meridional velocities prevent
the inversion of the angular velocity gradient in the regions of low
density as was the case in the massive star model. Consequently,
,
and contrary to what was found in the massive star model, the circulation
in the upper part of the radiative zone never approaches the stationary
regime. As shown by Talon et al. (1997), the extraction of angular momentum by
magnetic braking together with the very small meridional velocities prevent
the inversion of the angular velocity gradient in the regions of low
density as was the case in the massive star model. Consequently,
![]() always remains
positive. Besides, during the main sequence the differential rotation
remains too small to ensure an efficient transport of angular momentum by
the shear turbulence.
always remains
positive. Besides, during the main sequence the differential rotation
remains too small to ensure an efficient transport of angular momentum by
the shear turbulence.
![\begin{figure}
\par\includegraphics[width=16cm]{0665fig8}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg139.gif) |
Figure 6:
Meridional circulation flow in the 1.5
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm]{0665fig9}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg140.gif) |
Figure 7:
Decomposition of the vertical component of the meridional
circulation U2 according to Eq. (16) for the 1.5
|
| Open with DEXTER | |
3.3 Angular momentum transport
In Sect. 3.2 we already compared the respective contributions of meridional circulation and turbulence in the transport of angular momentum, in agreement with results from the literature. We now examine the problem from a different perspective, based on the fluxes carried by the two processes (Eq. (12)).
3.3.1 20 M model
model
Figure 8 shows the two components of the angular momentum
flux associated with the meridional circulation and shear.
In this model the
meridional circulation presents only one counterclockwise loop so the
transport occurs in the same direction in the whole radiative zone and
carries angular momentum from the core to the surface (
![]() ). Below
). Below
![]() the turbulent shear works in the same
direction (
the turbulent shear works in the same
direction (
![]() ), but its contribution is
negligible compared to that of the meridional circulation. Above
), but its contribution is
negligible compared to that of the meridional circulation. Above
![]() ,
the angular velocity gradient changes sign and shear takes over
the advection of angular momentum.
,
the angular velocity gradient changes sign and shear takes over
the advection of angular momentum.
Both ![]() and
and
![]() are of opposite sign below the convective
envelope during the MS evolution and grow in amplitude due to the radial
expansion of the outer low-density layers (see Eqs. (13)
and (14)). This configuration tends to impose a stationary
circulation in this region. On the other hand, these fluxes have the
same sign deeper in the interior and act jointly to compensate for
the structural changes of the star by redistributing the total angular
momentum.
are of opposite sign below the convective
envelope during the MS evolution and grow in amplitude due to the radial
expansion of the outer low-density layers (see Eqs. (13)
and (14)). This configuration tends to impose a stationary
circulation in this region. On the other hand, these fluxes have the
same sign deeper in the interior and act jointly to compensate for
the structural changes of the star by redistributing the total angular
momentum.
![\begin{figure}
\par\includegraphics[width=8cm]{0665fi10}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg148.gif) |
Figure 8:
The total flux of angular momentum (solid black line) decomposed
into its meridional circulation
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm]{0665fi11}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg149.gif) |
Figure 9:
Same as Fig. 8 for the 1.5
|
| Open with DEXTER | |
3.3.2 1.5 M model
model
In the low-mass model, the meridional circulation dominates the angular
momentum transport and
![]() at all times on the
main sequence (Fig. 9). The bold parts of the curves
indicate positive, outward fluxes that are associated with the
counterclockwise meridional currents described in Fig. 6.
at all times on the
main sequence (Fig. 9). The bold parts of the curves
indicate positive, outward fluxes that are associated with the
counterclockwise meridional currents described in Fig. 6.
Unlike in the massive star model, shear extracts angular momentum
everywhere because of the monotonous decrease in ![]() with
radius. Nevertheless, its contribution remains negligible. At the turn-off,
the meridional circulation and angular velocities have dropped in the outer
parts of the radiative zone because of the braking of the surface layers
and structural changes. This weakens
with
radius. Nevertheless, its contribution remains negligible. At the turn-off,
the meridional circulation and angular velocities have dropped in the outer
parts of the radiative zone because of the braking of the surface layers
and structural changes. This weakens
![]() ,
while
,
while ![]() remains
almost unaltered. In the central regions, both
remains
almost unaltered. In the central regions, both ![]() and
and
![]() substantially increase leading to a concomitant rise in
substantially increase leading to a concomitant rise in
![]() and
and ![]() .
The increase and sign change in
.
The increase and sign change in
![]() between r = 0.05
between r = 0.05
![]() and r = 0.4
and r = 0.4
![]() is partly due to the
off-centre displacement of the nuclear energy production region when H is
exhausted in the core.
is partly due to the
off-centre displacement of the nuclear energy production region when H is
exhausted in the core.
In summary, our diagnostic tools applied on two well-known cases allow us to give quantitative estimates for the main properties of angular momentum transport already discussed in the literature (see e.g., Meynet & Maeder 2000; Palacios et al. 2003). In low-mass stars, angular momentum transport is ensured by meridional currents that are primarily generated by the action of the applied torques resulting from the action of magnetic braking. In the massive star, owing to the differences in structure (density stratification, radius) and in surface velocities, the gradient of angular velocity becomes positive in the outer layers of the star, and there shear turbulence takes over the transport of angular momentum.
3.4 Thermal relaxation
Let us now analyse how thermal relaxation is achieved, as described by the
heat Eq. (18), which rules the temperature perturbations.
As explained previously, the meridional circulation is mainly driven
by the extraction of angular momentum due to angular momentum losses
at the surface (i.e. by the external torques) and to structural
readjustments (such as the expansion of the star on the MS). This
circulation advects specific entropy, which perturbs the thermal
equilibrium and induces temperature fluctuations described
by ![]() .
These are linked to the differential rotation through the
baroclinic Eq. (17), so that the heat equation is
actually tightly coupled with the equation of angular momentum
transport (11).
We examine how this works in our models.
.
These are linked to the differential rotation through the
baroclinic Eq. (17), so that the heat equation is
actually tightly coupled with the equation of angular momentum
transport (11).
We examine how this works in our models.
3.4.1 20 M model
model
![\begin{figure}
\par\includegraphics[width=15cm]{0665fi12}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg160.gif) |
Figure 10:
Representation of the different components of the heat equation
(Eq. (18)) for the 20
|
| Open with DEXTER | |
Each term of Eq. (19) is represented in Fig. 10
(left panel). The plot is separated into two panels, the upper and lower
ones showing the positive and negative parts of each profile respectively,
on a logarithmic scale. The differential rotation adjusts itself so that
the advection of entropy by the meridional circulation (
![]() )
is almost exactly compensated for by the thermal
readjustment via the barotropic (
)
is almost exactly compensated for by the thermal
readjustment via the barotropic (
![]() )
and
thermic (
)
and
thermic (
![]() )
terms. The other terms, associated
with the non-stationarity (
)
terms. The other terms, associated
with the non-stationarity (
![]() )
and with the
nuclear and gravitational energy generation (
)
and with the
nuclear and gravitational energy generation (
![]() ), are several orders of magnitude smaller and thus can be neglected
during the main sequence evolution. From this simplification, splitting the
divergence of the radiative flux (third term on the right hand side of
Eq. (18)) into barotropic and thermic (baroclinic) components thus
appears to be somewhat artificial.
), are several orders of magnitude smaller and thus can be neglected
during the main sequence evolution. From this simplification, splitting the
divergence of the radiative flux (third term on the right hand side of
Eq. (18)) into barotropic and thermic (baroclinic) components thus
appears to be somewhat artificial.
The temperature perturbations ![]() quickly relax to
the asymptotic regime, which involves only the source (
quickly relax to
the asymptotic regime, which involves only the source (
![]() )
and diffusion
(
)
and diffusion
(
![]() )
terms
(see also Appendix B for description of these terms), and
Eq. (18) gives
)
terms
(see also Appendix B for description of these terms), and
Eq. (18) gives
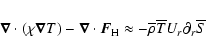 |
(31) |
and
To explicitly disentangle the role played by each component in shaping the entropy transport, we split the barotropic term as
where
and
Here,
Next, the thermic term is decomposed as
where
and
The term
Middle and left panels of Fig. 10 display these components
for the barotropic (
![]() )
and thermic
(
)
and thermic
(
![]() )
terms. We first note that the behaviour of
)
terms. We first note that the behaviour of
![]() closely follows that of
closely follows that of
![]() .
This result is expected, as the terms
.
This result is expected, as the terms
![]() and
and
![]() are driven by the T- and
are driven by the T- and ![]() -fluctuations, which remain small
in main sequence stars (see below). Moreover the term
-fluctuations, which remain small
in main sequence stars (see below). Moreover the term
![]() scales with
scales with
![]() (i.e.,
the ratio of energy production at a given radius with respect to the total
energy enclosed in the sphere of this radius), which remains small as the
(nuclear) energy production is mainly located in the convective core. It
should also be noted that the relative strength of the two baroclinic
corrections scales with
(i.e.,
the ratio of energy production at a given radius with respect to the total
energy enclosed in the sphere of this radius), which remains small as the
(nuclear) energy production is mainly located in the convective core. It
should also be noted that the relative strength of the two baroclinic
corrections scales with
![]() ,
which is always very small (between
10-14 and 10-10 in the whole radiative region and mainly varies
via the
,
which is always very small (between
10-14 and 10-10 in the whole radiative region and mainly varies
via the
![]() dependence). This explains why the term
dependence). This explains why the term
![]() does not appear in
Fig. 10 (middle panel) and can be neglected during the main
sequence evolution.
does not appear in
Fig. 10 (middle panel) and can be neglected during the main
sequence evolution.
The thermic term (
![]() )
requires more attention as
no specific component dominates in the whole radiative layer. Below the
surface and above the convective core the term
)
requires more attention as
no specific component dominates in the whole radiative layer. Below the
surface and above the convective core the term
![]() dominates while
dominates while
![]() is driven by
is driven by
![]() in the centre of the radiative zone. As
discussed in the next section, this result strongly depends on the
in the centre of the radiative zone. As
discussed in the next section, this result strongly depends on the
![]() ratio.
ratio.
Figure 11 presents the two-dimensional reconstruction of
the temperature perturbations in the meridional plane, i.e.
![]() .
These
are directly connected to the behaviour of
.
These
are directly connected to the behaviour of
![]() -gradient: the
temperature is higher at the poles (closer to the rotational axis) than at
the equator where
-gradient: the
temperature is higher at the poles (closer to the rotational axis) than at
the equator where
![]() ,
i.e. where the
angular velocity decreases with increasing radius. Near the surface, the
situation is reversed since
,
i.e. where the
angular velocity decreases with increasing radius. Near the surface, the
situation is reversed since
![]() is positive
there.
is positive
there.
![\begin{figure}
\par\includegraphics[width=8.3cm]{0665fi13}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg185.gif) |
Figure 11:
Two-dimensional reconstruction of the temperature fluctuations
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm]{0665fi14}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg186.gif) |
Figure 12:
Same as Fig. 10 for the 1.5
|
| Open with DEXTER | |
3.4.2 1.5 M model
model
Figure 12 is similar to Fig. 10 for the
1.5
![]() model, but contrary to the 20
model, but contrary to the 20
![]() model,
model,
![]() is now the same order of magnitude as
is now the same order of magnitude as
![]() and
and
![]() .
This is because
magnetic braking forces a larger extraction of angular momentum. Let us
note that the reversal of the meridional circulation shown in
Figs. 6 and 7 is proven by the sign
change of
.
This is because
magnetic braking forces a larger extraction of angular momentum. Let us
note that the reversal of the meridional circulation shown in
Figs. 6 and 7 is proven by the sign
change of
![]() .
Also in contrast to the massive
star, the nuclear and gravitational term,
.
Also in contrast to the massive
star, the nuclear and gravitational term,
![]() ,
becomes comparable to the advective one near the convective core, and
should thus not be neglected. Finally, except near turn-off where it
becomes important in the interior, the non-stationary term,
,
becomes comparable to the advective one near the convective core, and
should thus not be neglected. Finally, except near turn-off where it
becomes important in the interior, the non-stationary term,
![]() ,
is generally several orders of magnitudes
smaller than the other terms during most of the main sequence.
,
is generally several orders of magnitudes
smaller than the other terms during most of the main sequence.
Equation (19) is thus left with four terms balancing each
other. The thermic (baroclinic) and barotropic terms have similar
amplitudes and opposite signs and their sum balances the sum of the
advective term and the nuclear and gravitational heating:
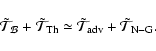 |
(41) |
We finally note that this situation is no longer valid at the turn-off as seen in the third column of Fig. 12. There, the non-stationary terms become dominant in the deep interior and must not be neglected anymore for the following evolutionary phase.
Figure 12 also displays the components of the barotropic and
thermic term in the same way as in Fig. 10. In most of the
radiative interior,
![]() follows the
barotropic component,
follows the
barotropic component,
![]() ,
except below
the surface where the contribution of the second baroclinic correction
,
except below
the surface where the contribution of the second baroclinic correction
![]() becomes relevant. As in the 20
becomes relevant. As in the 20
![]() model,
model,
![]() is negligible during the main
sequence. However, in the last model (
is negligible during the main
sequence. However, in the last model (
![]() ), this term dominates in
the centre due to the release of (a) nuclear energy by the hydrogen-burning
shell and (b) gravitational energy by the contracting core.
), this term dominates in
the centre due to the release of (a) nuclear energy by the hydrogen-burning
shell and (b) gravitational energy by the contracting core.
In contrast to the 20
![]() ,
the heat diffusion,
,
the heat diffusion,
![]() (
(
![]() ), plays no role in the thermic term,
), plays no role in the thermic term,
![]() ,
which is solely driven by the Laplacian
component,
,
which is solely driven by the Laplacian
component,
![]() .
The 1.5
.
The 1.5
![]() model has been
computed with the Zahn (1992) prescription for the horizontal turbulent
diffusion coefficient Dh leading to
model has been
computed with the Zahn (1992) prescription for the horizontal turbulent
diffusion coefficient Dh leading to
![]() ,
whereas this ratio amounts to about 10 for the 20
,
whereas this ratio amounts to about 10 for the 20
![]() ,
where the
Mathis et al. (2004) prescription was used (see Sect. 3.5). At the centre of the
last shown model, the Laplacian component presents a very complex behaviour
as it is sensitive to the first, second, and third radial derivatives of
,
where the
Mathis et al. (2004) prescription was used (see Sect. 3.5). At the centre of the
last shown model, the Laplacian component presents a very complex behaviour
as it is sensitive to the first, second, and third radial derivatives of
![]() .
Figure 3 reveals that the profile of
.
Figure 3 reveals that the profile of
![]() presents some rapid variations in this region which
explain this intricate feature.
presents some rapid variations in this region which
explain this intricate feature.
![\begin{figure}
\par\includegraphics[width=17cm]{0665fi15}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg190.gif) |
Figure 13:
The temperature fluctuation
|
| Open with DEXTER | |
Figure 13 displays the temperature fluctuations that
essentially follow the gradient of
![]() as in the 20
as in the 20 ![]() case. The main difference
is due to the presence of a second circulation loop. The amplitude of
the fluctuations remains globally of the same while the star is on the
MS, and amount to about a few percent.
case. The main difference
is due to the presence of a second circulation loop. The amplitude of
the fluctuations remains globally of the same while the star is on the
MS, and amount to about a few percent.
3.4.3 Possible simplifications
From the previous analysis of the 1.5 and 20
![]() models, during the
quiescent main sequence evolution, the relaxation of
models, during the
quiescent main sequence evolution, the relaxation of ![]() is then ruled
approximately by
is then ruled
approximately by
Note that
In conclusion, the picture of the heat transport presented here differs radically from the classical Eddington-Sweet vision where the thermal imbalance induced by the centrifugal acceleration is considered to be at the origin of the meridional circulation. Actually, the circulation is induced by the angular momentum losses and the structural adjustments. Then, it advects entropy, which leads, after thermal relaxation, to a new temperature state and thus to a new differential rotation profile (cf. Eq. (17)). There then remains a circulation induced by the angular momentum losses and the structural adjustments, and the concomitant evolution of the rotation and thermal states.
3.5 Transport of chemicals
Once a composition gradient builds up, due to gravitational settling (not
accounted for in the present calculations) or
nuclear burning, the meridional circulation creates a latitudinal
perturbation of the molecular weight distribution, as described by
Eq. (27). The sign of these ![]() -fluctuations depends on the
orientation of the circulation, and we thus expect some differences between
the two models.
-fluctuations depends on the
orientation of the circulation, and we thus expect some differences between
the two models.
![\begin{figure}
\par\includegraphics[width=8.5cm]{0665fi16}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg194.gif) |
Figure 14:
Two-dimensional reconstruction of the |
| Open with DEXTER | |
3.5.1 20 M model
model
In that model, the meridional circulation always transports matter with
low-![]() down to the interior near the rotational axis, while high-
down to the interior near the rotational axis, while high-![]() matter is carried outward along the equator. As a result, a horizontal
matter is carried outward along the equator. As a result, a horizontal
![]() -gradient appears near the convective core (see
Fig. 14), which is directed from pole to equator,
i.e. opposite to that of the temperature fluctuations. These
-gradient appears near the convective core (see
Fig. 14), which is directed from pole to equator,
i.e. opposite to that of the temperature fluctuations. These
![]() -fluctuations remain small (less than 1%), which justifies the
perturbative approach.
-fluctuations remain small (less than 1%), which justifies the
perturbative approach.
We already mentioned in Sect. 2.3.4 that the strong turbulent
transport in the horizontal direction interferes with the meridional
circulation, rendering the vertical transport of diffusive nature,
characterised by an effective diffusivity
![]() (Chaboyer & Zahn 1992).
This description makes the comparison between the two processes that contribute to the
transport of chemical elements (vertical shear and combination of advection
and horizontal shear) easier since it suffices to compare their respective
diffusivities.
(Chaboyer & Zahn 1992).
This description makes the comparison between the two processes that contribute to the
transport of chemical elements (vertical shear and combination of advection
and horizontal shear) easier since it suffices to compare their respective
diffusivities.
This is done in Fig. 15, where we see that in most of the
stellar interior the vertical shear turbulence largely dominates the
combination of advection and horizontal shear (
![]() ),
except in the vicinity of the convective core, where the strong
),
except in the vicinity of the convective core, where the strong
![]() -stratification inhibits the shear instability, and in the region
where the gradient of
-stratification inhibits the shear instability, and in the region
where the gradient of
![]() changes sign (and where Dvreduces to the molecular diffusivity).
changes sign (and where Dvreduces to the molecular diffusivity).
This figure can be compared with Fig. 6 of Meynet & Maeder (2000), where the same
profiles are presented for a 20
![]() star at
Z = 0.02, with initial
equatorial velocity
star at
Z = 0.02, with initial
equatorial velocity
![]() km s-1. In their simulation,
Meynet and Maeder use the prescription given by Eq. (30) for the
horizontal turbulent viscosity. While we obtain very similar profiles for
the vertical shear diffusion coefficient, Dv, and for the thermal
diffusivity, KT, the diffusion coefficients associated with horizontal
turbulence, Dh, and meridional circulation,
km s-1. In their simulation,
Meynet and Maeder use the prescription given by Eq. (30) for the
horizontal turbulent viscosity. While we obtain very similar profiles for
the vertical shear diffusion coefficient, Dv, and for the thermal
diffusivity, KT, the diffusion coefficients associated with horizontal
turbulence, Dh, and meridional circulation,
![]() ,
differ by
several orders of magnitude. The Mathis et al. (2004) prescription results in
higher horizontal turbulent viscosity, which also translates into
lower
,
differ by
several orders of magnitude. The Mathis et al. (2004) prescription results in
higher horizontal turbulent viscosity, which also translates into
lower
![]() .
This very same result was first obtained by
Maeder (2003), where using energetic considerations, he derived a new
expression for Dh that is very similar to Eq. (29) (see
also Mathis et al. 2007). It should be noted that the anisotropic turbulence
assumption (
.
This very same result was first obtained by
Maeder (2003), where using energetic considerations, he derived a new
expression for Dh that is very similar to Eq. (29) (see
also Mathis et al. 2007). It should be noted that the anisotropic turbulence
assumption (
![]() )
is always satisfied.
)
is always satisfied.
![\begin{figure}
\par\includegraphics[width=7.5cm]{0665fi17}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg198.gif) |
Figure 15:
Profiles of the thermal diffusivity (KT dotted-dashed green
line) and the one that associated to the meridional circulation (
|
| Open with DEXTER | |
3.5.2 1.5 M model
model
Figure 16 shows that the diffusion coefficients in the
1.5 ![]() star are much smaller than in the massive star as a result of
lower angular velocity and degree of differential rotation. The diffusion
coefficients
star are much smaller than in the massive star as a result of
lower angular velocity and degree of differential rotation. The diffusion
coefficients
![]() and Dv are much closer in this model, partly
due to the adoption of Zahn's (1992)
prescription for Dh (see Eqs. (29) and (30) and Mathis
et al. 2004, for more details). However, the decreasing efficiency of the
meridional transport as the star evolves on the main sequence results in
the shear turbulence dominating the distribution of chemicals
(see Palacios et al. 2003). The inhibiting action of the composition gradient is
visible near the convective core where Dv drops to its microscopic
value, indicating that turbulence is suppressed. It should also be noted
that the anisotropic turbulence assumption (
and Dv are much closer in this model, partly
due to the adoption of Zahn's (1992)
prescription for Dh (see Eqs. (29) and (30) and Mathis
et al. 2004, for more details). However, the decreasing efficiency of the
meridional transport as the star evolves on the main sequence results in
the shear turbulence dominating the distribution of chemicals
(see Palacios et al. 2003). The inhibiting action of the composition gradient is
visible near the convective core where Dv drops to its microscopic
value, indicating that turbulence is suppressed. It should also be noted
that the anisotropic turbulence assumption (
![]() )
is also always
satisfied in this model.
)
is also always
satisfied in this model.
The sign of the ![]() -perturbation depends on the orientation of the
circulation near the convective core. In the lower mass model,
differences arise from the development of a secondary loop, as seen at
-perturbation depends on the orientation of the
circulation near the convective core. In the lower mass model,
differences arise from the development of a secondary loop, as seen at
![]() and
and
![]() .
.
Although the meridional circulation and Dh are both smaller in the
low-mass star, the ratio U2/Dh, which governs the relative strength
of vertical advection by meridional circulation and of horizontal diffusion
(see Eq. (27)), is larger in the 1.5
![]() compared to the
20
compared to the
20
![]() .
This results in larger
.
This results in larger ![]() -imbalance in the lower-mass model.
-imbalance in the lower-mass model.
![\begin{figure}
\par\includegraphics[width=17cm]{0665fi18}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg199.gif) |
Figure 16:
Same as Fig. 15 for the 1.5
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=18cm]{0665fi19}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg200.gif) |
Figure 17:
Two-dimensional reconstruction of the |
| Open with DEXTER | |
4 Conclusion
The paper presents a complete set of diagnostic tools that provide a comprehensive and coherent understanding of the secular hydrodynamical transport processes operating in the radiative zones of rotating stars. The framework is that of ``type I rotational mixing'', where angular momentum and nuclides are transported by the same mechanisms, namely large-scale meridional circulation and shear-induced turbulence.
To validate our new approach, the first analysis presented here
is performed on two well-studied cases of a low-mass
(1.5
![]() )
(see Palacios et al. 2003) and a massive (20
)
(see Palacios et al. 2003) and a massive (20
![]() )
star
(Meynet & Maeder 2000). It allows us to disentangle the main processes at the origin of
meridional circulation and driving angular momentum, heat and chemicals transports
in the stellar interior,
and to confirm results previously established in the literature.
In particular, the angular momentum loss (either by radiation-driven wind
as in the massive
star or by magnetic braking as in the low-mass star) combined with
structural readjustments are the sources responsible for generating
meridional circulation (Fig. 18). The direction of the flow
is such that it transports angular momentum outward to the surface, except
in the deep interior of the 1.5
)
star
(Meynet & Maeder 2000). It allows us to disentangle the main processes at the origin of
meridional circulation and driving angular momentum, heat and chemicals transports
in the stellar interior,
and to confirm results previously established in the literature.
In particular, the angular momentum loss (either by radiation-driven wind
as in the massive
star or by magnetic braking as in the low-mass star) combined with
structural readjustments are the sources responsible for generating
meridional circulation (Fig. 18). The direction of the flow
is such that it transports angular momentum outward to the surface, except
in the deep interior of the 1.5
![]() star where it can reverse, producing
a steeper angular velocity gradient.
star where it can reverse, producing
a steeper angular velocity gradient.
This circulation advects heat, and thus generates latitude-dependent temperature fluctuations. These tend to be damped out by radiative diffusion, until they establish a subtle balance between advection and diffusion, which allows them to induce differential rotation through the baroclinic torque (Eq. (17)). This differential rotation is shear-unstable and generates turbulence that participates in the transport of angular momentum, thus closing the loop (Fig. 18). This picture thus differs drastically from the classical Eddington-Sweet circulation, where the circulation is deemed to originate from the thermal imbalance due to the centrifugal force. If turbulent transport and extraction of angular momentum were absent, the circulation would die altogether, as pointed out by Busse (1982).
Thanks to the diagnostic tools we have developed, the present investigation helped to clarify a number of other points. We confirm that it is mainly the meridional circulation that transports angular momentum in the low-mass star (see also Palacios et al. 2003). It is thus crucial to describe that transport as an advective process, as in the approach developed by Zahn, Maeder, and collaborators. In the massive star, where the redistribution of angular momentum due to the star's expansion plays a much more important role than its extraction by the radiative wind, advection and diffusion make comparable contributions, though in different regions. The advective transport dominates in the inner layers of the star, whereas the diffusive transport is the prime actor in the upper part and, moreover, works there in the opposite direction.
![\begin{figure}
\par\includegraphics[height=8.5cm,clip]{0665fi20}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg201.gif) |
Figure 18: Rotational mixing of type I in the radiative zone of a rotating star, where the transport of angular momentum is achieved by meridional circulation and turbulent diffusion. |
| Open with DEXTER | |
For the first time, through detailed computation and separation of the different components, we confirm that the advection of entropy by meridional circulation is almost exactly balanced by the thermal relaxation (barotropic and thermic terms) during most of the main sequence. This was generally assumed prior to the Maeder & Zahn (1998) work integrating the time-dependency of the temperature fluctuations, but not actually verified through the computation. Grounding our detailed analysis in advanced graphical tools, we were also able to propose a simplified expression for the thermal relaxation on the main sequence.
On the other hand, the transport of
chemicals is shown to be dominated by the shear-induced turbulence while
the star evolves on the main sequence. This is particularly clear for a
massive star such as the 20
![]() star.
star.
In the near future, we plan to apply the same tools to type II rotational mixing, where we shall include the transport of angular momentum by internal gravity waves and magnetic stresses and to advanced phases of stellar evolution.
Acknowledgements
We thank the referee A. Maeder for useful remarks that helped in improving the final version of this paper. This work received financial support from the Programme National de Physique Stellaire of CNRS/INSU (France). T.D. and C.C. acknowledge financial support from Swiss FNS. L.S. is FNRS Research Associate. This research has made use of NASA's Astrophysics Data System Bibliographic Services.
Appendix A: Meridional circulation and angular momentum transport
Let us consider the Eq. (11) for the angular momentum transport:
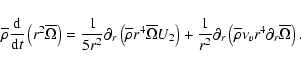 |
(A.1) |
Integrating over a spherical shell, we get
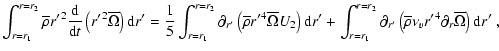 |
(A.2) |
r1 and r2 being respectively its inner and outer radius. Then, introducing the elementary mass element
![$\displaystyle \frac{1}{4\pi}\int_{m=m\left(r_1\right)}^{m=m\left(r_2\right)}\fr...
...t(\overline\rho\nu_{v}r^4\partial_{r}\overline{\Omega}\right)_{r=r_1}\right]~ .$](/articles/aa/full_html/2009/07/aa10665-08/img205.gif) |
(A.3) |
We apply the following identity
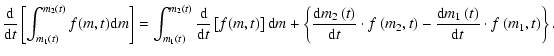 |
(A.4) |
In our Lagrangian description, the mass is conserved,
To obtain the value of the meridional circulation at m(r), we set r1=0 and r2=r :
![\begin{displaymath}U_{2}=\frac{5}{\overline \rho r^4 \overline{\Omega}}\left[\Ga...
...t)-\overline\rho\nu_{v}r^4\partial_{r}\overline{\Omega}\right]
\end{displaymath}](/articles/aa/full_html/2009/07/aa10665-08/img209.gif) |
(A.6) |
where
![\begin{displaymath}\Gamma\left(m\right)=\frac{1}{4\pi}\frac{\rm d}{{\rm d}t}\lef...
..._{0}^{m\left(r\right)}{r'}^2\overline{\Omega}{\rm d}m'\right].
\end{displaymath}](/articles/aa/full_html/2009/07/aa10665-08/img210.gif) |
(A.7) |
Appendix B: Components
 of the heat equation
of the heat equation
These terms intervene in the heat relaxation Eq. (18) and their derivation may be found in Zahn (1992) or Mathis & Zahn (2004). They include:
the barotropic term,
the thermic term,
the term associated with local energy sources,
![$\displaystyle {\mathcal T}_{2,{\rm N-G}}=\frac{\left(\overline{\epsilon}+\overl...
...
+(f_{\epsilon}\epsilon_{\mu}+f_{\epsilon}\varphi - \varphi)\Lambda_{2}\right],$](/articles/aa/full_html/2009/07/aa10665-08/img214.gif) |
where
| (B.3) |
Here,
References
- Abt, H. A., Levato, H., & Grosso, M. 2002, ApJ, 573, 359 [NASA ADS] [CrossRef]
- Bouret, J. -C., Donati, J. -F., Martins, F., et al. 2008, MNRAS, 389, 75 [NASA ADS] [CrossRef]
- Braithwaite, J. 2006, A&A, 449, 451 [NASA ADS] [CrossRef] [EDP Sciences]
- Braithwaite, J., & Spruit, H. 2005, Nature, 431, 819 [NASA ADS] [CrossRef]
- Brun, A.-S., & Zahn, J.-P. 2006, A&A, 457, 665 [NASA ADS] [CrossRef] [EDP Sciences]
- Busse, F. H. 1982, ApJ, 259, 759 [NASA ADS] [CrossRef]
- Chaboyer, B., & Zahn, J.-P. 1992, A&A, 253, 173 [NASA ADS] (In the text)
- Charbonnel, C., & Talon, S. 2005, Science, 309, 2189 [NASA ADS] [CrossRef]
- Charbonneau, P., & MacGregor, K. B. 1993, ApJ, 417, 762 [NASA ADS] [CrossRef]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences]
- Eddington, A. S. 1925, Obs, 48, 73 [NASA ADS]
- Ekström, S., Meynet, G., Maeder, A., & Barblan, F. 2008, A&A, 478, 467 [NASA ADS] [CrossRef] [EDP Sciences]
- Eggenberger, P., Maeder, A., & Meynet, G. 2005, A&A, 440, L9 [NASA ADS] [CrossRef] [EDP Sciences]
- Endal, A. S., & Sofia, S. 1978, ApJ, 220, 279 [NASA ADS] [CrossRef]
- Espinosa Lara, F., & Rieutord, M. 2007, A&A, 470, 1013 [NASA ADS] [CrossRef] [EDP Sciences]
- Fukada, I. 1982, PASP, 94, 271 [NASA ADS] [CrossRef]
- Gaigé, Y. 1993, A&A, 269, 267 [NASA ADS]
- Garaud, P. 2002a, MNRAS, 329, 1 [NASA ADS] [CrossRef]
- Garaud, P. 2002b, MNRAS, 335, 707 [NASA ADS] [CrossRef]
- Grevesse, N., Noels, A., & Sauval, A. J. 1996, Cosmic Abundances, 99, 117 [NASA ADS] (In the text)
- Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef]
- Henyey, L. G., Forbes, J. E., & Gould, N. L. 1964, ApJ, 139, 306 [NASA ADS] [CrossRef] (In the text)
- Kawaler, S. D. 1988, ApJ, 333, 236 [NASA ADS] [CrossRef] (In the text)
- Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Springer-Verlag) (In the text)
- Maeder, A. 1999, A&A, 347, 185 (In the text)
- Maeder, A. 2002, A&A, 392, 575 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Maeder, A. 2003, A&A, 399, 263 [NASA ADS] [CrossRef] [EDP Sciences]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Springer-Verlag)
- Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS]
- Maeder, A., & Meynet, G. 2000a, A&A, 361, 159 [NASA ADS]
- Maeder, A., & Meynet, G. 2000b, ARA&A, 38, 143 [NASA ADS] [CrossRef]
- Maeder, A., & Meynet, G. 2001, A&A, 373, 555 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Maeder, A., & Meynet, G. 2004, A&A, 422, 225 [NASA ADS] [CrossRef] [EDP Sciences]
- Mathis, S., & Zahn, J.-P. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences]
- Mathis, S., & Zahn, J.-P. 2005, A&A, 440, 653 [NASA ADS] [CrossRef] [EDP Sciences]
- Mathis, S., Palacios, A., & Zahn, J.-P. 2004, A&A, 425, 243 [NASA ADS] [CrossRef] [EDP Sciences]
- Mathis, S., Palacios, A., & Zahn, J.-P. 2007, A&A, 462, 1063 [NASA ADS] [CrossRef] [EDP Sciences]
- Mathis, S., Talon, S., Pantillon, F.-P., & Zahn, J.-P. 2008, Sol. Phys., 251, 101 [NASA ADS] [CrossRef]
- Menou, K., Balbus, S. A., & Spruit, H. C. 2004, ApJ, 607, 564 [NASA ADS] [CrossRef]
- Mestel, L. 1953, MNRAS, 113, 716 [NASA ADS]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS]
- Meynet, G., Ekström, S., Maeder, A., & Barblan, F. 2007, ASP, 361, 325 [NASA ADS]
- Palacios, A., Talon, S., Charbonnel, C., & Forestini, M. 2003, A&A, 399, 603 [NASA ADS] [CrossRef] [EDP Sciences]
- Palacios, A., Charbonnel, C., Talon, S., & Siess, L. 2006, A&A, 453, 261 [NASA ADS] [CrossRef] [EDP Sciences]
- Pantillon, F. P., Talon, S., & Charbonnel, C. 2007, A&A, 474, 155 [NASA ADS] [CrossRef] [EDP Sciences]
- Pinsonneault, M. H., Kawaler, S. D., Sofia, S., & Demarque, P. 1989, ApJ, 338, 424 [NASA ADS] [CrossRef]
- Press, W.-H. 1981, ApJ, 245, 286 [NASA ADS] [CrossRef]
- Reimers, D. 1975, Mémoires de la Société Royale des Sciences de Liège, 8, 369 (In the text)
- Rieutord, M. 2006a, Stellar Fluid Dynamics and Numerical Simulations: from the Sun to Neutron Stars, ed. M. Rieutord, & B. Dubrulle, EAS, 21, 275
- Rieutord, M. 2006b, A&A, 451, 1025 [NASA ADS] [CrossRef] [EDP Sciences]
- Rogers, T., & Glatzmaier, G. 2005, MNRAS, 364, 1135 [NASA ADS] [CrossRef]
- Schatzman, E. 1962, Ann. Astrophys., 25, 18 [NASA ADS] (In the text)
- Schatzman, E. 1993, A&A, 279, 431 [NASA ADS]
- Schnerr, R. S., Henrichs, H. F., Neiner, C., et al. 2008, A&A, 483, 857 [NASA ADS] [CrossRef] [EDP Sciences]
- Spruit, H. C. 1999, A&A, 349, 189
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences]
- Siess, L. 2006, A&A, 448, 717 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] (In the text)
- Sweet, P. A. 1950, MNRAS, 110, 548 [NASA ADS]
- Talon, S. 1997, Ph.D. Thesis, Université Paris 7
- Talon, S. 2008, in EAS Publications Series, ed. C. Charbonnel, & J.-P. Zahn, EAS Publ. Ser., 32, 81
- Talon, S., & Zahn, J.-P. 1997, A&A, 317, 749
- Talon, S., & Charbonnel, C. 1998, A&A, 335, 959 [NASA ADS]
- Talon, S., & Charbonnel, C. 2003, A&A, 405, 1025 [NASA ADS] [CrossRef] [EDP Sciences]
- Talon, S., & Charbonnel, C. 2004, A&A, 418, 1051 [NASA ADS] [CrossRef] [EDP Sciences]
- Talon, S., & Charbonnel, C. 2005, A&A, 440, 981 [NASA ADS] [CrossRef] [EDP Sciences]
- Talon, S., & Charbonnel, C. 2008, Proc. IAU Symp., 252 [arXiv:0805.4697]
- Talon, S., Kumar, P., & Zahn, J.-P. 2002, ApJ, 574, L175 [NASA ADS] [CrossRef]
- Talon, S., Zahn, J.-P., Maeder, A., & Meynet, G. 1997, A&A, 322, 209
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [NASA ADS] (In the text)
- Vogt, H. 1925, AN, 223, 229 [NASA ADS]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS]
- Zahn, J.-P., Brun, A. S., & Mathis, S. 2007, A&A, 474, 145 [NASA ADS] [CrossRef] [EDP Sciences]
Footnotes
- ...
gravity
![[*]](/icons/foot_motif.gif)
- In a rotating star, the centrifugal force diminishes the
local gravity, and the effective gravity
 is then
given by horizontally averaging the hydrostatic equilibrium:
is then
given by horizontally averaging the hydrostatic equilibrium:
 ,
where
,
where  is the gravitational potential.
is the gravitational potential.
All Figures
![\begin{figure}
\par\includegraphics[height=8.5cm,clip]{0665fig1}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg31.gif) |
Figure 1:
Modelling strategy to study dynamical stellar evolution. The
diagram presents time scales of the typical physical processes as a
function of the angular resolution needed to properly describe these
processes. The angular resolution is expressed in terms of the l index
of the spherical harmonics
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8cm]{0665fig2}\hspace*{4mm}
\includegraphics[width=8cm]{0665fig3} }\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg88.gif) |
Figure 2:
Evolutionary path in the HR diagram of a 20
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=8cm]{0665fig4}\hspace*{4mm}
\includegraphics[width=8cm]{0665fig5} }\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg113.gif) |
Figure 3:
Angular velocity profile inside the 20
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{0665fig6}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg133.gif) |
Figure 4:
Meridional circulation currents in the 20
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{0665fig7}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg136.gif) |
Figure 5:
Decomposition of the meridional circulation based on the equation
of angular momentum evolution in the 20
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm]{0665fig8}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg139.gif) |
Figure 6:
Meridional circulation flow in the 1.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm]{0665fig9}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg140.gif) |
Figure 7:
Decomposition of the vertical component of the meridional
circulation U2 according to Eq. (16) for the 1.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm]{0665fi10}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg148.gif) |
Figure 8:
The total flux of angular momentum (solid black line) decomposed
into its meridional circulation
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=16cm]{0665fi11}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg149.gif) |
Figure 9:
Same as Fig. 8 for the 1.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm]{0665fi12}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg160.gif) |
Figure 10:
Representation of the different components of the heat equation
(Eq. (18)) for the 20
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm]{0665fi13}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg185.gif) |
Figure 11:
Two-dimensional reconstruction of the temperature fluctuations
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{0665fi14}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg186.gif) |
Figure 12:
Same as Fig. 10 for the 1.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{0665fi15}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg190.gif) |
Figure 13:
The temperature fluctuation
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{0665fi16}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg194.gif) |
Figure 14:
Two-dimensional reconstruction of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm]{0665fi17}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg198.gif) |
Figure 15:
Profiles of the thermal diffusivity (KT dotted-dashed green
line) and the one that associated to the meridional circulation (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{0665fi18}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg199.gif) |
Figure 16:
Same as Fig. 15 for the 1.5
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=18cm]{0665fi19}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg200.gif) |
Figure 17:
Two-dimensional reconstruction of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=8.5cm,clip]{0665fi20}
\end{figure}](/articles/aa/full_html/2009/07/aa10665-08/Timg201.gif) |
Figure 18: Rotational mixing of type I in the radiative zone of a rotating star, where the transport of angular momentum is achieved by meridional circulation and turbulent diffusion. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



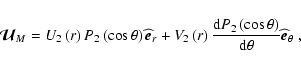
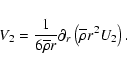
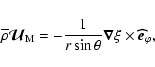
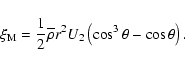
![\begin{displaymath}T\left(r,\theta\right)\!=\!{\overline T}\left(r\right)\!+\!\d...
...\left(r\right){\overline T}\right]P_{2}\left(\cos\theta\right)
\end{displaymath}](/articles/aa/full_html/2009/07/aa10665-08/img48.gif)
![\begin{displaymath}\mu\left(r,\theta\right)\!=\!{\overline \mu}\left(r\right)\!+...
...eft(r\right)\overline{\mu}\right]P_{2}\left(\cos\theta\right);
\end{displaymath}](/articles/aa/full_html/2009/07/aa10665-08/img49.gif)
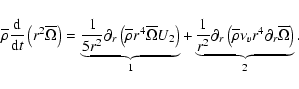
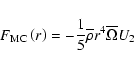
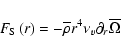
![\begin{displaymath}\Gamma\left(m\right)=\frac{1}{4\pi}\frac{\rm d}{{\rm d}t}\lef...
...}^{m\left(r\right)}{r'}^2\overline{\Omega}~ {\rm d}m'\right] .
\end{displaymath}](/articles/aa/full_html/2009/07/aa10665-08/img65.gif)
![\begin{displaymath}U_{2}=U_\Gamma+U_V=\frac{5}{\overline\rho r^4 \overline{\Omeg...
...-\overline\rho\nu_{v}r^4\partial_{r}\overline{\Omega}\right] .
\end{displaymath}](/articles/aa/full_html/2009/07/aa10665-08/img66.gif)
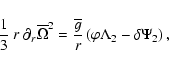
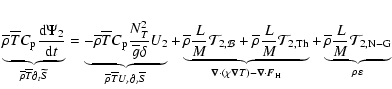
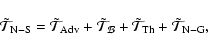
![$\displaystyle \left(\frac{{\rm d} X_i}{{\rm d}t}\right)_{M_r}= \frac{\partial}{...
..._i}{\partial M_r}\right] + \left(\frac{{\rm d}X_i}{{\rm d}t}\right)_{\rm nucl},$](/articles/aa/full_html/2009/07/aa10665-08/img89.gif)
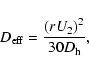
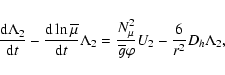
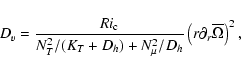
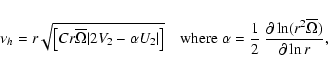
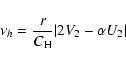
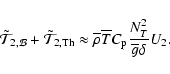
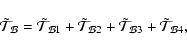
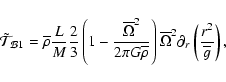
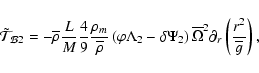
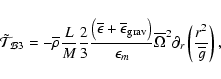
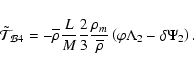
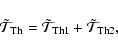
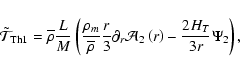
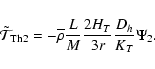
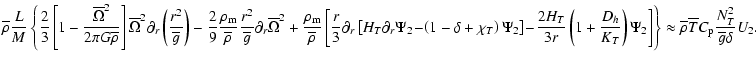
![$\displaystyle \frac{1}{4\pi}\frac{{\rm d}}{{\rm d}t}\left[\int_{m=m\left(r_1\ri...
...t(\overline\rho\nu_{v}r^4\partial_{r}\overline{\Omega}\right)_{r=r_1}\right]~ .$](/articles/aa/full_html/2009/07/aa10665-08/img208.gif)
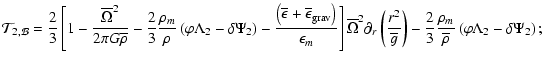
![$\displaystyle {\mathcal T}_{2,{\rm Th}}=\frac{\rho_{m}}{\overline{\rho}}\left[\...
...ght)
-\frac{2 H_{T}}{3 r}\left(1 +
\frac{D_{h}}{K_{T}}\right){\Psi_{2}}\right];$](/articles/aa/full_html/2009/07/aa10665-08/img213.gif)